Link fault tolerability of 3-ary n-cube based on g-good-neighbor r-component edge-connectivity

Abstract

High-performance computing relies heavily on parallel and distributed systems, which promptes us to establish both qualitative and quantitative criteria to assess the fault tolerability and vulnerability of the system’s underlying interconnection networks. Consider the scenario in which large-scale link failures split the interconnection network into several components and each processor has multiple good neighboring processors. In this scenario, the fault tolerability of the system can be measured by g-good-neighbor r-component edge-connectivity, denoted by $\lambda _{g,r}(G)$, which is defined as the minimum number of edges whose removal results in a disconnected network with at least r connected components and each vertex has at least g good neighbors. It combines the strategies of g-good-neighbor edge-connectivity and component edge-connectivity. In this paper, the g-good-neighbor $(r+1)$-component edge-connectivity of 3-ary n-cube is investigated. This work is the first attempt enhancing link fault tolerability for 3-ary n-cube under double constraints in the presence of the large-scale faulty links, which breaks down the inherent idea that poses one limitation on the resulting network. In addition, our results cover the work of Xu et al. (IEEE Trans Reliab, 71(3):1230–1240, 2022) and Li et al. (J Parallel Distrib Comput, 27:104886, 2024). Finally, the compared results reveal that the g-good-neighbor $(r+1)$-component edge-connectivity is almost r times the size of g-good-neighbor edge-connectivity and much larger than $(r+1)$-component edge-connectivity in 3-ary n-cube.

1 Introduction

Massively parallel computing systems employing hundreds to thousands of processors are commercially available today and offer substantially higher raw computing power than the fastest sequential supercomputers. Availability of such systems has fueled interest in investigating the performance of parallel and distributed systems containing a large number of processors. Parallel computing architectures for large-scale parallel and distributed systems have advanced significantly during the last decades. The interconnection network is well recognized to be critical in large-scale parallel and distributed systems, since its design has a direct impact on the system’s performance and cost-effectiveness [3]. Topological structure is generally deemed a key design concern for interconnection networks. A large number of topological structures have been proposed and explored, most notably the hypercube structure and its variants, such as k-ary n-cube, folded hypercube, crossed cube, and so on. The k-ary n-cube, especially the 3-ary n-cube, has attracted a great deal of interest due to its many appealing attributes [11], including its capacity to minimize message latency and ease of implementation. A variety of parallel and distributed systems, including the J-machine [18], the Cray T3D [12], the Cray T3E [2], and the IBM supercomputer BlueGene/L [1], have been constructed with the k-ary n-cube as the underlying topological structure. The IBM supercomputer BlueGene/L’s fundamental architecture is the 3-ary n-cube.

With the increasing of network scale and business traffic, interconnection network is facing a lot of challenges, among which fault tolerability is of the most importance. Actually, the network malfunction, especially for link failure, is common and always inevitable. In a large-scale parallel and distributed system, the link failure on the data plane occurs more occasionally and frequently, and some links are likely to fail every half hour on average [9]. Link failure results in the interruption of traffic transmission and further degrades the network performance. Therefore, considering the seriousness and inevitability of link failure, both academia and industry pay great attention to the link fault tolerability.

There are several metrics that characterize the link fault tolerability of interconnection networks, such as classical edge-connectivity, extra edge-connectivity, component edge-connectivity, g-good-neighbor edge-connectivity, cycle edge-connectivity, embedded edge-connectivity, and so on. Among these metrics, extra edge-connectivity, component edge-connectivity and g-good-neighbor edge-connectivity of many prominent networks have been widely investigated over the years. The h-extra edge-connectivity $\lambda _h(G)$ was proposed by Fàbrega et al. [8], which is defined as the minimum number of edges whose removal results in a disconnected network and each component has at least $h+1$ vertices. Many scholars have studied its h-extra edge-connectivity in diverse networks, such as bijective connection networks $B_n$ [28], folded hypercube $FQ_n$ [29], augmented cube $AQ_n$ [23, 31], 3-ary n-cube $Q_n^3$ [22], folded crossed cube $FCQ_n$ [19]. The g-good-neighbor edge-connectivity $\lambda ^g(G)$ was proposed by Latifi [13], which is defined as the minimum number of edges whose removal results in a disconnected network and each vertex has at least g neighbors. The g-good-neighbor edge-connectivities of many networks, such as bijective connection networks $B_n$ [14], modified bubble-sort networks $MB_n$ [5], augmented cube $AQ_n$ [30], k-ary n-cube [15], have been determined. By the minimality of edge-cuts, the two types of conditional edge-connectivities mentioned above allow only two components to be generated after deleting the smallest conditional edge-cut. Generally speaking, a disconnected network with two components may not be as bad as a disconnected network with many more components. By constraining the number of components of the disconnected network, the r-component edge-connectivity $c\lambda _r(G)$ was proposed by Sampathkumar [20], which is defined as the minimum number of edges whose removal results in a disconnected network with at least r connected components. A lot of related work on specific networks have been studied, including hypercube $Q_n$ [33], locally twisted cube $LTQ_n$ [21], augmented cube $AQ_n$ [31], bijective connection networks $B_n$ [16], 3-ary n-cube $Q_n^3$ [22], hamming graph $K_L^n$ [25], folded Petersen networks $P^n$ [24]. Note that this metric only puts a limit on the number of components but not on the structure of each component, i.e., it may produce sub-networks that have only one vertex, but for which it is not able to perform any of the tasks assigned by the system.

As a result, in order to establish a balance between the number of components and their structure, Yang et al. [26] and Liu et al. [17] proposed two new concepts, namely h-extra r-component edge-connectivity and g-good-neighbor r-component edge-connectivity, by integrating the strategies of r-component edge-connectivity and one of h-extra edge-connectivity and g-good-neighbor edge-connectivity, respectively. Both emphasize the double constraints on the resulting network after removing the smallest edge-cut. The h-extra r-component edge-connectivity, denoted by $c\lambda _r^h(G)$, is defined as the minimum number of edges whose removal results in a disconnected network with at least r connected components and each component has at least $h+1$ vertices. The g-good-neighbor r-component edge-connectivity, denoted by $\lambda _{g,r}(G)$, is defined as the minimum number of edges whose removal results in a disconnected network with at least r connected components and each vertex has at least g neighbors. In particular, $c\lambda _r^0(G)$ and $\lambda _{0,r}(G)$ reduce to r-component edge-connectivity $c\lambda _r(G)$, while $c\lambda _2^h(G)$ and $\lambda _{g,2}(G)$ degrade into h-extra edge-connectivity $\lambda _h(G)$ and g-good-neighbor edge-connectivity $\lambda ^g(G)$, respectively. As applications, Yang et al. [26] explored the h-extra 3-component edge-connectivities of bijective connection networks $B_n$ and folded hypercube $FQ_n$ for specific ranges of h. Moreover, Liu et al. [17] investigated the g-good-neighbor r-component edge-connectivity of hypercube in the same specific ranges with regarded to g and r. For all the related work mentioned above, we present all the results in Table 1 to facilitate the knowledge of the progress of the related work.

In this paper, we focus on the g-good-neighbor $(r+1)$-component edge-connectivity of 3-ary n-cube. More specifically, we obtain $\lambda _{g, r+1}(Q_n^3)=(2-d)(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-[\frac{1}{2}ex_{(2-d)r}(Q_n^3)-(1-d)r]\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }$ for $n\ge 3$, $1\le (2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le (2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil -1}$ or $r=3^{k_0}, 0\le k_0\le \left\lfloor \frac{n}{2}\right\rfloor -1$ and $0\le g\le 2(n-2k_0-1)$, where $d~\equiv g \pmod {2}$, $ex_{(2-d)r}(Q_n^3)$ represents the maximum degree sum of the subgraph induced by $(2-d)r$ vertices of $Q_n^3$ whose exact value is determined by Xu et al. [22].

The rest of this paper is organized as follows. Section 2 reviews some notations and the structure and properties of the 3-ary n-cube. Section 3 constructs a g-good-neighbor $(r+1)$-component edge-cut. Section 4 determines g-good-neighbor $(r+1)$-component edge-connectivity of 3-ary n-cube. Section 5 presents some examples. Section 6 concludes the work.

2 Preliminaries

First of all, we assume that all parameters are nonnegative integers. Let G(V(G), E(G)) be a network or graph, where |V(G)|, |E(G)| denote the order and size of G, respectively. For $W \subseteq V(G) (\text {resp}., E(G))$, G[W] denotes the subgraph of G induced by W, and $G-W$ denotes the subgraph of G induced by $V(G)\setminus W$ (resp., $E(G)\setminus W$). For vertex subsets $T_1, T_2,\ldots , T_r\subset V(G)$, we denote by $E(T_1,T_2,\ldots , T_r)$ the edge set of G with one vertex in $T_i$, and the other in $T_j$, where $T_i\cap T_j =\varnothing , 1\le i<j \le r$. The degree of a vertex v, denoted by $d_G(v)$, is the number of vertices incident to v. We denote by $\delta (G)$ the minimum degree of graph G. A graph G is k-regular if $d_G(v)=k$ for any vertex $v\in V(G)$. The component of G is the maximal connected subgraph of G. The graph $G_1$ is isomorphic to $G_2$ which is indicated by the notation $G_1 \cong G_2$. Let $S_r$ be the set $\{0, 1, 2, \ldots , r-1\}$, $L_l^n$ be the set $\{t_i^n\}_{i=0}^{l-1}$, where $t_i^n$ is the n-ternary string conversed by the decimal number i. Let D(u, v) be the number of different positions in the n-ternary strings u and v. For graph definitions and notations not defined here, we follow [4].

Table 1 The summary of the progress of the related work

The definition of 3-ary n-cube is recalled as follows.

Definition 1

[10] The 3-ary n-cube, denoted by $Q_n^3$, has $3^n$ vertices, where each vertex has form $\{z_nz_{n-1} \ldots z_1 ~|~ z_i\in S_3, 1\le i\le n\}$. For any two vertices u, v, $(u,v)\in E(Q_n^3)$ if and only if $D(u,v)=1$.

The 3-ary n-cube $Q_n^3$ is a 2n-regular 2n-connected graph [6]. $Q_n^3$ can be decomposed into three vertex and edge-disjoint 3-ary $(n-1)$-cubes, denoted by $Q_n^3[0]$, $Q_n^3[1]$, and $Q_n^3[2]$, which are induced by the vertices of $Q_n^3$ with the ith coordinate 0, 1, and 2, respectively. Clearly, $Q_n^3[i]$ and $Q_n^3[j]$ are joined by one perfect matching, so $|E(V(Q_n^3[i]),V(Q_n^3[j]))|=3^{n-1}$ for $i\ne j\in S_3$. For convenience, we denote $Q_n^3$ as $Q_n^3[0]\bigoplus Q_n^3[1]\bigoplus Q_n^3[2]$. We denote by $t_l^{n-m}Z^m$ the vertex set

$$\{x_nx_{n-1}\ldots x_{m+1}z_m\ldots z_2z_1 ~|~ z_i\in S_3, 1\le i \le t\},$$

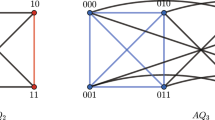
where $x_nx_{n-1}\ldots x_{m+1}$ is $(n-m)$-ternary string conversed by the decimal number l, Z represents variable in $S_3$. By the definition of the $Q_n^3$, the subgraph $Q_n^3[t_l^{n-m}Z^m]\cong Q_m^3$. The 3-ary 3-cube $Q_3^3$ is illustrated in Fig. 1.

Fig. 1

3-ary 3-cube $Q_3^3$

Denote by $\frac{ex_l(Q_n^3)}{2}$ the maximum size (the number of edges) of the subgraph induced by a vertex set with a given size l in $Q_n^3$, where $ex_l(Q_n^3)$ represents the maximum degree sum of the subgraph induced by l vertices of $Q_n^3$, i.e.,

$$ex_l(Q_n^3)=\max \{2|E(Q_n^3[W])| ~|~ W \subseteq V(Q_n^3)~ \text {and}~ |W| = l\}.$$

Fan et al. [7] showed that $\frac{ex_l(Q_n^3)}{2}$ can be achieved by the induced subgraph $Q_n^3[L_l^n]$, i.e., $E(Q_n^3[L_l^n])=\frac{ex_l(Q_n^3)}{2}$. Whereafter, Zhang et al. [32] characterized structural features of subgraph $Q_n^3[L_l^n]$ in accordance with the ternary decomposition of l. Let $l =\sum _{i=0}^{s} a_i3^{k_i}$ be the ternary decomposition of l such that $k_0 = [\log _3 l]$, $a_0 = [l-2\cdot 3^{k_0}]^++1$ and $k_i=[\log _3(l -\sum _{j=0}^{i-1} a_j3^{k_j})]$, $a_i=[l-\sum _{j=0}^{i-1} a_j3^{k_j}- 2\cdot 3^{k_i}]^++1$ for $1\le i\le s$, where

$$\begin{aligned}{}[x]^+= \left\{ \begin{array}{ll} 1, &{}\quad \text {if}~ x\ge 0;\\ 0, &{}\quad \text {if}~ x<0.\\ \end{array} \right. \end{aligned}$$

In [32], $L_l^n$ can be expressed as $V(Q^0\cup Q^1\cup \cdots \cup Q^s)$, where each $Q^i$ is a subgraph induced by vertex set with $a_i3^{k_i}$ vertices, that is, each $Q^i$ is either 3-ary $k_i$-subcube or disjoint union of two 3-ary $k_i$-subcubes connected by a perfect matching. In particular, the single vertex is deemed to 3-ary 0-subcube. In addition, $Q^i$ is taken from a 3-ary n-cube which is obtained from $Q^{i-1}$ by changing the 0 of $(t_i+1)th$ coordinate of $Q^{i-1}$ to 1 or the 0 and 1 of $(t_i+1)th$ coordinate of $Q^{i-1}$ to 2 for $1\le i\le s$. So there exists at least one edge between the vertices in different $Q^i$s. We present some examples in the Table 2 to illustrate this structure.

Table 2 The relationship between ternary decomposition of l and structure of $Q_3^3[L_l^3]$

Motivated by the idea of Fan et al. [7], Xu et al. [22] determined the exact expression of $ex_l(Q_n^3)$ as follows.

Lemma 1

[22] Let $1\le l\le 3^n$ and $l=\sum _{i=0}^s a_i3^{k_i}$ be the ternary decomposition of l. Then, we have $\frac{1}{2}ex_l(Q_n^3)=|E(Q_n^3[L_l^n])|=\sum _{i=0}^s(a_ik_i+a_i-1)3^{k_i}+\sum _{i=1}^s\left( \sum _{j=0}^{i-1}a_j\right) a_i3^{k_i}.$

3 Construction of g-good-neighbor $(r+1)$-component edge-cut

In this section, we will construct a g-good-neighbor $(r+1)$-component edge-cut in the 3-ary n-cube.

Lemma 2

[32] For two positive integers n, l, let $\overline{L_l^n}=V(Q_n^3)\setminus L_l^n$. Both $Q_n^3[L_l^n]$ and $Q_n^3[\overline{L_l^n}]$ are connected.

3.1 $g=0 \pmod {2}$

First of all, we define some notations. Let n, g, r be three integers such that $(r+1)\cdot 3^{\frac{g}{2}}\le 3^n$. For any $i\in S_r$, let $T_i=t_i^{n-\frac{g}{2}}Z^{\frac{g}{2}}$ and $G_i=Q_n^3[T_i]$. Let $T_r=V(Q_n^3)-\bigcup _{i\in S_r}T_i$ and $G_r=Q_n^3[T_r]$. Obviously, $G_i\cong Q_{\frac{g}{2}}^3$ for any $i\in S_r$ and $T_i\cap T_j=\varnothing$ for $i\ne j \in S_r$. We contract each $T_i$ into a vertex $t_i$ for $i\in S_r$ and delete the multiple edges between $T_i$ and $T_j$ when $E(T_i, T_j)\ne \varnothing$ for $i\ne j \in S_r$. Then the graph $G^*$ induced by $\{t_0, t_1, \ldots , t_{r-1}\}$ is isomorphic to $Q_n^3[L_r^n]$. Note that $(t_i,t_j)\in E(G^*)$ if and only if $|E(T_i, T_j)|=3^{\frac{g}{2}}$, hence, $|E(T_0, T_1, \ldots , T_{r-1})|=|E(G^*)|\cdot 3^{\frac{g}{2}}=\frac{1}{2}ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}$.

Lemma 3

If $g=0 \pmod {2}$, then

$$ex_{r\cdot 3^{\frac{g}{2}}}(Q_n^3)=r\cdot ex_{3^{\frac{g}{2}}}(Q_n^3)+ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}.$$

Proof

Let $T_i$ be defined as above for $i\in S_r$. In light of definition of $T_i$, we have $\bigcup _{i\in S_r}T_i=L_{r\cdot 3^{\frac{g}{2}}}^n$. By Lemma 1, $2|E(Q_n^3[\bigcup _{i\in S_r}T_i])|=ex_{r\cdot 3^{\frac{g}{2}}}(Q_n^3)$. Therefore,

$$\begin{aligned} \begin{aligned} ex_{r\cdot 3^{\frac{g}{2}}}(Q_n^3)&=2|E(Q_n^3[\bigcup _{i\in S_r}T_i])|\\&=2\sum _{i=0}^{r-1}|E(Q_n^3[T_i])|+2|E(T_0, T_1, \ldots , T_{r-1})|\\&=r\cdot ex_{3^{\frac{g}{2}}}(Q_n^3)+ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}. \end{aligned} \end{aligned}$$

$\square$

Lemma 4

For any $i\in S_{r+1}$, the subgraph $G_i$ is connected and $\delta (G_i)\ge g$.

Proof

For any $i\in S_r$, $G_i\cong Q_{\frac{g}{2}}^3$, thereby, $G_i$ is connected and $\delta (G_i)\ge g$. In light of definition of $T_i$, we have $\bigcup _{i\in S_r}T_i=L_{r\cdot 3^{\frac{g}{2}}}^n$ and $T_r=\overline{L_{r\cdot 3^{\frac{g}{2}}}^n}$. By Lemma 2, $G_r$ is connected. Let $r=\sum _{j=0}^{s}a_j3^{k_j}$ be the ternary decomposition of r, $k_j+\frac{g}{2}=l_j$. Then,

$$r'=3^n-r\cdot 3^{\frac{g}{2}}=3^n-\sum _{j=0}^{s}a_j3^{l_j}=b_03^{n-1}+b_13^{n-2}+\ldots +b_h3^{n-1-h},$$

where $n-1-h=l_s, b_h=3-a_s$ and

$$\begin{aligned} b_i= \left\{ \begin{array}{ll} 2-a_j, &{}\quad \text {if} ~l_j=n-1-i;\\ 2, &{}\quad \text {otherwise},\\ \end{array} \right. \end{aligned}$$

for $0\le i\le h-1$. According to the above expression of $r'$, $b_i=0$ for some i’s. Therefore, $r'$ can be rephrased as $r'=\sum _{i=0}^{h'}b_i'3^{q_i}$, where $q_0>q_1>\ldots >q_{h'}=l_s$ and $b_{h'}'=3-a_s$. According to the construction of $G_r$, each vertex in $G_r$ falls in some $Q_{q_i}^3$. In view of $q_i\ge l_s=k_s+\frac{g}{2}$ for any $i\in S_{h'+1}$, $\delta (G_r)\ge g$. $\square$

Lemma 5

Let n, g, r be three integers such that $(r+1)\cdot 3^{\frac{g}{2}}\le 3^n$, where $g=0 \pmod {2}$. Then

$$\lambda _{g, r+1}(Q_n^3)\le (2n-g)r\cdot 3^{\frac{g}{2}}-\frac{1}{2}ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}.$$

Proof

We prove this lemma by constructing a g-good-neighbor $(r+1)$-component edge-cut with size $(2n-g)r\cdot 3^{\frac{g}{2}}-\frac{1}{2}ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}$. Suppose that $G_i$ and $T_i$ for any $i\in S_{r+1}$ are defined as above. Then, by Lemma 4, $Q_n^3-E(T_0, T_1, \ldots , T_r)$ is disconnected and has exactly $r+1$ components $G_0, G_1, \ldots , G_r$ and $\delta (G_i)\ge g$ for any $i\in S_{r+1}$. Moreover, $|E(T_0, T_1, \ldots , T_{r-1})|=|E(G^*)|\cdot 3^{\frac{g}{2}}=\frac{1}{2}ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}$. Therefore, we have

$$\begin{aligned} \begin{aligned} |E(T_0, T_1, \ldots , T_r)|&=\sum _{i=0}^{r-1}|E(T_i,\overline{T_i})|-|E(T_0, T_1, \ldots , T_{r-1})|\\&=r(2n-g)3^{\frac{g}{2}}-\frac{1}{2}ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}. \end{aligned} \end{aligned}$$

Thus, the edge set $E(T_0, T_1, \ldots , T_r)$ is a g-good-neighbor $(r+1)$-component edge-cut with size $(2n-g)r\cdot 3^{\frac{g}{2}}-\frac{1}{2}ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}$. By the definition of $\lambda _{g, r+1}(Q_n^3)$, we have $\lambda _{g, r+1}(Q_n^3)\le (2n-g)r\cdot 3^{\frac{g}{2}}-\frac{1}{2}ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}.$ $\square$

Algorithm 1

Find one perfect matching in $Q_{n}^3[L_{2r}^{n}]$

3.2 $g=1 \pmod {2}$

Similarly, we define some notations. Let n, g, r be three integers such that $2(r+1)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le 3^n$. For any $i\in S_{2r}$, let $T_i=t_i^{n-\left\lfloor \frac{g}{2}\right\rfloor }Z^{\left\lfloor \frac{g}{2}\right\rfloor }$. Obviously, $T_i\cap T_j=\varnothing$ for $i\ne j \in S_{2r}$. We contract each $T_i$ into a vertex $t_i$ for $i\in S_{2r}$ and delete the multiple edges between $T_i$ and $T_j$ when $E(T_i, T_j)\ne \varnothing$ for $i\ne j \in S_{2r}$. Then the graph $G^*$ induced by $\{t_0, t_1, \ldots , t_{2r-1}\}$ is isomorphic to $Q_n^3[L_{2r}^n]$. Note that $(t_i,t_j)\in E(G^*)$ if and only if $|E(T_i, T_j)|=3^{\left\lfloor \frac{g}{2}\right\rfloor }$, so a perfect matching in $Q_n^3[L_{2r}^n]$ corresponds to a paired-partitiom of $\{T_0, T_1, \ldots , T_{2r-1}\}$ such that each pairwise paired induced subgraph is isomorphic to $Q_{\left\lfloor \frac{g}{2}\right\rfloor +1}^3[0]\oplus Q_{\left\lfloor \frac{g}{2}\right\rfloor +1}^3[1]$.

Theorem 1

Algorithm 1 outputs one perfect matching M in $Q_n^3[L_{2r}^n]$.

Proof

By Algorithm 1, it is easy to see that M covers all vertices in $L_{2r}^n$. Next, it suffices to show that for each $(x,y)\in M$, $(x,y)\in E(Q_n^3[L_{2r}^n])$. Obviously, $D(t_0^n, t_1^n)=1$ and $D(t_0^n, t_{3^a}^n)=1$. By the definitions of $Q_n^3$ and $t_j^n$, if $r=1$, then $(t_0^n, t_1^n)\in E(Q_n^3[L_{2r}^n])$, while if $r>1$, $(t_0^n, t_{3^a}^n)\in E(Q_n^3[L_{2r}^n])$. According to the lines 7 to 13 in Algorithm 1 and choice of w, if $l=k_s$, then $a_s\ne 2$. Thus, $D(t_w^n, t_{w+3^l}^n)=1$, which implies that $(t_w^n, t_{w+3^l}^n)\in E(Q_n^3[L_{2r}^n])$. $\square$

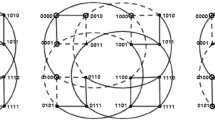
For example, let $n=3$ and $r=8$, then by Algorithm 1, we can find one perfect matchinig in $Q_3^3[L_{16}^3]$, that is $\{(000,100), (001,002), (010,020), (011,012), (021,022), (101,102), (110,120), (111,112)\}$ (see Fig. 2).

Fig. 2

perfect matching in $Q_3^3[L_{16}^3]$

By Theorem 1, there are r pairs of subgraphs $G_0, G_1, \ldots , G_{r-1}$ such that $G_j \cong Q_{\left\lfloor \frac{g}{2}\right\rfloor +1}^3[0]\oplus Q_{\left\lfloor \frac{g}{2}\right\rfloor +1}^3[1]$, for any $j\in S_r$. Let $T_{2r}=V(Q_n^3)-\bigcup _{i\in S_{2r}}T_i$ and $G_{r}=Q_n^3[T_{2r}]$.

Lemma 6

If $g=1 \pmod {2}$, then

$$ex_{2r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)=r\cdot ex_{2\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)+(\frac{1}{2}ex_{2r}(Q_n^3)-r)\cdot 2\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }.$$

Proof

Let $T_i$ and $G_j$ be defined as above for any $i\in S_{2r}$ and $j\in S_r$, respectively. In light of definition of $T_i$, we have $\bigcup _{i\in S_{2r}}T_i=L_{2r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}^n$. By Lemma 1, $2|E(Q_n^3[\bigcup _{i\in S_{2r}}T_i])|=ex_{2r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)$. Therefore,

$$\begin{aligned} \begin{aligned} ex_{2r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)&=2|E(Q_n^3[\bigcup _{i\in S_{2r}}T_i])|\\&=2\sum _{j=0}^{r-1}|E(G_j)|+2|E(V(G_0), V(G_1), \ldots , V(G_{r-1}))|\\&=r\cdot ex_{2\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)+ (\frac{1}{2}ex_{2r}(Q_n^3)-r)\cdot 2\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }. \end{aligned} \end{aligned}$$

$\square$

Lemma 7

For any $i\in S_{r+1}$, the subgraph $G_i$ is connected and $\delta (G_i)\ge g$.

Proof

For any $i\in S_r$, $G_i\cong Q_{\left\lfloor \frac{g}{2}\right\rfloor +1}^3[0]\oplus Q_{\left\lfloor \frac{g}{2}\right\rfloor +1}^3$ [1], thereby, $G_i$ is connected and $\delta (G_i)\ge g$. In light of definition of $T_i$, we have $\bigcup _{i\in S_{2r}}T_i=L_{2r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}^n$ and $T_{2r}=\overline{L_{2r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}^n}$. By Lemma 2, $G_r$ is connected. Let $2r=\sum _{j=0}^{s}a_j3^{k_j}$ be the ternary decomposition of 2r, $k_j+\left\lfloor \frac{g}{2}\right\rfloor =l_j$. Then,

$$r'=3^n-2r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }=3^n-\sum _{j=0}^{s}a_j3^{l_j}=b_03^{n-1}+b_13^{n-2}+\ldots +b_h3^{n-1-h},$$

where $n-1-h=l_s, b_h=3-a_s$ and

$$\begin{aligned} b_i= \left\{ \begin{array}{ll} 2-a_j, &{}\quad \text {if} ~l_j=n-1-i;\\ 2, &{}\quad \text {otherwise},\\ \end{array} \right. \end{aligned}$$

for $0\le i\le h-1$. According to the above expression of $r'$, $b_i=0$ for some i’s. Therefore, $r'$ can be rephrased as $r'=\sum _{i=0}^{h'}b_i'3^{q_i}$, where $q_0>q_1>\ldots >q_{h'}=l_s$ and $b_{h'}'=3-a_s$. According to the construction of $G_r$, each vertex in $G_r$ falls in some $Q_{q_i}^3$. Because of $2(r+1)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le 3^n$, $|G_r|\ge 2\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }$. If $q_{h'}=l_s=\left\lfloor \frac{g}{2}\right\rfloor$, then each vertex in $Q_{q_{h'}}^3$ has at least one neighbor outside $Q_{q_{h'}}^3$, and so $\delta (G_r)\ge g$. If $q_{h'}= l_s>\left\lfloor \frac{g}{2}\right\rfloor$, then $\delta (G_r)\ge g$ in view of $q_i\ge l_s>\left\lfloor \frac{g}{2}\right\rfloor$ for any $i\in S_{h'+1}$. $\square$

Lemma 8

Let n, g, r be three integers such that $2(r+1)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le 3^n$, where $g=1 \pmod {2}$. Then

$$\lambda _{g, r+1}(Q_n^3)\le 2(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-\Big (\frac{1}{2}ex_{2r}(Q_n^3)-r\Big )\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }.$$

Proof

We prove this lemma by constructing a g-good-neighbor $(r+1)$-component edge-cut with size $2(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-(\frac{1}{2}ex_{2r}(Q_n^3)-r)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }$. Suppose that $G_i$ is defined as above for any $i\in S_{r+1}$. Then, by Lemma 7, $Q_n^3-E(V(G_0), V(G_1), \ldots , V(G_r))$ is disconnected and has exactly $r+1$ components $G_0, G_1, \ldots , G_r$ and $\delta (G_i)\ge g$ for any $i\in S_{r+1}$. Moreover, $|E(V(G_0), V(G_1), \ldots , V(G_{r-1}))|=(\frac{1}{2}ex_{2r}(Q_n^3)-r)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }$. Therefore, we have

$$\begin{aligned} \begin{aligned} |E(V(G_0), V(G_1), \ldots , V(G_r))|&=\sum _{i=0}^{r-1}|E(V(G_i),\overline{V(G_i)})|\\&\quad -|E(V(G_0), V(G_1), \ldots , V(G_{r-1}))|\\&=2r(2n-g)3^{\left\lfloor \frac{g}{2}\right\rfloor }-\Big (\frac{1}{2}ex_{2r}(Q_n^3)-r)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }. \end{aligned} \end{aligned}$$

Thus, the edge set $E(V(G_0), V(G_1), \ldots , V(G_r))$ is a g-good-neighbor $(r+1)$-component edge-cut with size $2(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-(\frac{1}{2}ex_{2r}(Q_n^3)-r)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }$. By the definition of $\lambda _{g, r+1}(Q_n^3)$, we have $\lambda _{g, r+1}(Q_n^3)\le 2(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-(\frac{1}{2}ex_{2r}(Q_n^3)-r)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }.$ $\square$

4 g-good-neighbor $(r+1)$-component edge-connectivity

Define

$$\zeta _h(Q_n^3) = \min \{|[W, \overline{W}]| ~|~ W\subset V(G), |W| = h, ~\text {both}~ Q_n^3[W] ~\text {and}~ Q_n^3[\overline{W}] ~\text {are connected}\}.$$

As $Q_n^3$ is 2n-regular, by the definition of $ex_h(Q_n^3)$, we have

$$\zeta _h(Q_n^3)=2nh-ex_h(Q_n^3).$$

Fig. 3

Image of $\zeta _h(Q_7^3)$

In this section, we will endeavor to establish the lower bound of g-good-neighbor $(r+1)$-component edge-connectivity in $Q_n^3$. In this process, we observe that the value of the lower bound is closely related to the function $\zeta _h(Q_n^3)$. More specifically, it relies heavily on the monotonicity of $\zeta _h(Q_n^3)$. Figure 3 depicts the image of the function $\zeta _h(Q_7^3)$, it possesses a fractal structure and symmetry. In order to determine the exact value of $\lambda _{g, r+1}(Q_n^3)$, based on a series of results by Xu et al. [22] and Zhang et al. [32] concerning the properties of the function $\zeta _h(Q_n^3)$, we consider only two special cases that $1\le (2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le (2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil -1}$ and $r=3^{k_0}, 0\le k_0\le \left\lfloor \frac{n}{2}\right\rfloor -1$, $0\le g\le 2(n-2k_0-1)$. In what follows, we review some properties of the function $\zeta _h(Q_n^3)$.

We define

$$\begin{aligned} c= \left\{ \begin{array}{ll} 1, &{}\quad \text {if}~ n =1 ~(\bmod {2});\\ 0, &{}\quad \text {if}~ n =0 ~(\bmod {2}),\\ \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} d= \left\{ \begin{array}{ll} 1, &{}\quad \text {if}~ g =0~(\bmod {2});\\ 0, &{}\quad \text {if}~ g =1~(\bmod {2}).\\ \end{array} \right. \end{aligned}$$

Lemma 9

[22] $\zeta _h(Q_n^3)$ is increasing with respect to h in the interval $[1, (2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil }-2]$.

Lemma 10

[22] If $(2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil }-3\le h\le 3^{\big \lceil \frac{n+2-c}{2}\big \rceil }$ for $n\ge 3$, then $\zeta _h(Q_n^3)\ge \zeta _{(2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil }}(Q_n^3)$. In particular, $\zeta _{(2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil }}(Q_n^3)=\zeta _{(2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil }-3}(Q_n^3)$.

Lemma 11

[22, 32] If $3^k\le h \le 2\cdot 3^{n-1}$ for $0\le k\le n-1$ and $n\ge 3$, then $\zeta _h(Q_n^3)\ge \zeta _{3^k}(Q_n^3)$. If $2\cdot 3^k\le h \le 3^{n-1}$ for $0\le k\le n-2$ and $n\ge 3$, then $\zeta _h(Q_n^3)\ge \zeta _{2\cdot 3^k}(Q_n^3)$.

Lemma 12

[27] For $n\ge 3$ and $0\le g\le 2n$, if H is a connected subgraph in $Q_n^3$ with $\delta (H)\ge g$, then $|V(H)|\ge (2-d)3^{\left\lfloor \frac{g}{2}\right\rfloor }$.

Lemma 13

For $n\ge 3$, if $1\le (2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le (2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil -1}$ or $r=3^{k_0}, 0\le k_0\le \left\lfloor \frac{n}{2}\right\rfloor -1$ and $0\le g\le 2(n-2k_0-1)$, then

$$\lambda _{g, r+1}(Q_n^3)\ge (2-d)(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-[\frac{1}{2}ex_{(2-d)r}(Q_n^3)-(1-d)r]\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }.$$

Proof

Let F be minimum g-good-neighbor $(r+1)$-component edge-cut of $Q_n^3$. By the minimality of F, $Q_n^3-F$ has exactly $r+1$ components, denoted by $H_0, H_1, \ldots , H_r$, satisfying that the minimum degree of each component is at least g. Let $|V(H_i)|=p_i$ for $i\in S_{r+1}$. By Lemma 12, we have $p_i\ge (2-d)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }$. Without loss of generality, suppose that $p_0\ge p_1\ge \ldots \ge p_r$. Note that $\bigg \lceil \frac{3^n}{r+1}\bigg \rceil \le p_0\le 3^n-r\cdot p_r$, we have

$$(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le r\cdot p_r\le \sum _{i=1}^{r}p_i\le 3^n-\bigg \lceil \frac{3^n}{r+1}\bigg \rceil =\left\lfloor \frac{r\cdot 3^n}{r+1}\right\rfloor .$$

Therefore,

$$\begin{aligned} |F|&=\sum _{i=1}^{r}|E(V(H_i), \overline{V(H_i)})|-|E(V(H_1), V(H_2), \ldots , V(H_r))|\\&=2n\sum _{i=1}^{r}p_i-2\sum _{i=1}^{r}|E(H_i)|-\left( \left| E\Big (\bigcup _{i=1}^{r}H_i\Big )\right| -\sum _{i=1}^{r}|E(H_i)|\right) \\&=2n\sum _{i=1}^{r}p_i-\sum _{i=1}^{r}|E(H_i)|-\left| E\Big (\bigcup _{i=1}^{r}H_i\Big )\right| \\&\ge 2n\sum _{i=1}^{r}p_i-\frac{1}{2}\sum _{i=1}^{r}ex_{p_i}(Q_n^3)-\frac{1}{2}ex_{\sum _{i=1}^{r}p_i}(Q_n^3)\\&=\frac{1}{2}\sum _{i=1}^{r}\zeta _{p_i}(Q_n^3)+\frac{1}{2}\zeta _{\sum _{i=1}^{r}p_i}(Q_n^3)\\&\ge \frac{1}{2}\sum _{i=1}^{r}\zeta _{(2-d)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)+\frac{1}{2}\zeta _{\sum _{i=1}^{r}p_i}(Q_n^3)~~(\text {by Lemma } 11)\\&=\frac{1}{2}(2-d)(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }+\frac{1}{2}\zeta _{\sum _{i=1}^{r}p_i}(Q_n^3). \end{aligned}$$

Case 1. $(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le \sum _{i=1}^{r}p_i\le 2\cdot 3^{n-1}$.

In this scenario, by iteratively using Lemmas 9, 10 and 11, we have

$$\zeta _{\sum _{i=1}^{r}p_i}(Q_n^3)\ge \zeta _{(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3) =2n(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-ex_{(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3).$$

Therefore,

$$\begin{aligned} \begin{aligned} |F|&\ge \frac{1}{2}(2-d)(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }+\frac{1}{2}[2n(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-ex_{(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)]\\&=(2-d)(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-[\frac{1}{2}ex_{(2-d)r}(Q_n^3)-(1-d)r]\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }. \end{aligned} \end{aligned}$$

Case 2. $2\cdot 3^{n-1}<\sum _{i=1}^{r}p_i\le \left\lfloor \frac{r\cdot 3^n}{r+1}\right\rfloor$.

Case 2.1. $1\le (2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le (2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil -1}$.

In this scenario, we have

$$(2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil -1}\le \bigg \lceil \frac{3^n}{\frac{1}{(2-d)}(2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil -1-\left\lfloor \frac{g}{2}\right\rfloor }+1}\bigg \rceil \le \bigg \lceil \frac{3^n}{r+1}\bigg \rceil \le 3^n-\sum _{i=1}^{r}p_i\le 3^{n-1}.$$

By the symmetry of edge-cut, we have $\zeta _{\sum _{i=1}^{r}p_i}(Q_n^3)=\zeta _{3^n-\sum _{i=1}^{r}p_i}(Q_n^3)$. By Lemmas 9 and 11,

$$\zeta _{3^n-\sum _{i=1}^{r}p_i}(Q_n^3)\ge \zeta _{(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3) =2n(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-ex_{(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)$$

holds. Therefore, by Lemmas 3 and 6, we have

$$|F|\ge (2-d)(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-[\frac{1}{2}ex_{(2-d)r}(Q_n^3)-(1-d)r]\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }.$$

Case 2.2. $r=3^{k_0}$ and $0\le g\le 2(n-2k_0-1)$, where $0\le k_0\le \left\lfloor \frac{n}{2}\right\rfloor -1$.

In this scenario, we have

$$(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le 2\cdot 3^{n-k_0-1}\le \bigg \lceil \frac{3^n}{3^{k_0}+1}\bigg \rceil \le \bigg \lceil \frac{3^n}{r+1}\bigg \rceil \le 3^n-\sum _{i=1}^{r}p_i\le 3^{n-1}.$$

By the symmetry of edge-cut, we have $\zeta _{\sum _{i=1}^{r}p_i}(Q_n^3)=\zeta _{3^n-\sum _{i=1}^{r}p_i}(Q_n^3)$. By Lemma 11,

$$\zeta _{3^n-\sum _{i=1}^{r}p_i}(Q_n^3)\ge \zeta _{(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3) =2n(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-ex_{(2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }}(Q_n^3)$$

holds. Therefore, by Lemmas 3 and 6, we have

$$|F|\ge (2-d)(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-[\frac{1}{2}ex_{(2-d)r}(Q_n^3)-(1-d)r]\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }.$$

Summing up above, we have

$$\lambda _{g, r+1}(Q_n^3)\ge (2-d)(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-\left[ \frac{1}{2}ex_{(2-d)r}(Q_n^3)-(1-d)r\right] \cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }.$$

$\square$

Combining Lemma 13 with Lemmas 5 and 8, the following result is immediately obtained.

Theorem 2

Let n, g, r be three integers such that $n\ge 3$, $1\le (2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le (2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil -1}$ or $r=3^{k_0}, 0\le k_0\le \left\lfloor \frac{n}{2}\right\rfloor -1$ and $0\le g\le 2(n-2k_0-1)$. Then,

$$\begin{aligned} \lambda _{g, r+1}(Q_n^3)= \left\{ \begin{array}{ll} (2n-g)r\cdot 3^{\frac{g}{2}}-\frac{1}{2}ex_r(Q_n^3)\cdot 3^{\frac{g}{2}}, &{}\text {if} ~g=0~(\bmod {2});\\ 2(2n-g)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }-(\frac{1}{2}ex_{2r}(Q_n^3)-r)\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }, &{}\text {if} ~g=1~(\bmod {2}),\\ \end{array} \right. \end{aligned}$$

Corollary 1

[15, 22] (1) For $n\ge 2$ and $g\le n$, $\lambda ^g(Q_n^3)=(2-d)(2n-g)3^{\left\lfloor \frac{g}{2}\right\rfloor }$.

(2) For $n\ge 6$ and $r\le 3^{\big \lceil \frac{n}{2}\big \rceil }$, $c\lambda _{r+1}(Q_n^3)=2nr-\frac{ex_r(Q_n^3)}{2}$.

Table 3 The value of $\lambda _{g,r+1}(Q_n^3)$, $\lambda ^{g}(Q_{n}^3)$ and $c\lambda _{g+1}(Q_{n}^3)$

5 Application and comparisons

This work concentrates on the g-good-neighbor $(r+1)$-component edge-connectivity under the conditions $1\le (2-d)r\cdot 3^{\left\lfloor \frac{g}{2}\right\rfloor }\le (2-c)\cdot 3^{\big \lceil \frac{n}{2}\big \rceil -1}$ or $r=3^{k_0}, 0\le k_0\le \left\lfloor \frac{n}{2}\right\rfloor -1$ and $0\le g\le 2(n-2k_0-1)$. In what follows, we present an example in each of these two cases. For instance, let $r=2$ and $n=10$. In this case, $r=2$ satisfies the former condition, hence, we have $0\le g\le 8$. Based on the formulas of Theorem 2 and Corollary 1, we derive the corresponding values of $\lambda _{g,3}(Q_{10}^3)$, $\lambda ^{g}(Q_{10}^3)$ and $c\lambda _{g+1}(Q_{10}^3)$ with respect to $0\le g \le 8$ (see Table 3). Another example is $r=3$ and $n=9$. In this case, $r=3$ satisfies the latter condition, hence, we deduce that $0\le g\le 12$. Subsequently, we obtain the corresponding values of $\lambda _{g,4}(Q_{9}^3)$, $\lambda ^{g}(Q_{9}^3)$ and $c\lambda _{g+1}(Q_{9}^3)$ with respect to $0\le g \le 12$ in the same manner (see Table 3). As can be seen from Table 3, the value of $\lambda _{g,3}(Q_{10}^3)$ is almost twice as large as $\lambda ^{g}(Q_{10}^3)$ and much larger than the value of $c\lambda _{g+1}(Q_{10}^3)$ regardless of the value of g. A similar conclusion can be drawn in $Q_9^3$, the value of $\lambda _{g,4}(Q_{9}^3)$ is almost three times the value of $\lambda ^{g}(Q_{9}^3)$ and much larger than the value of $c\lambda _{g+1}(Q_{9}^3)$.

The quantitative relationship among $\lambda _{g,r+1}(Q_n^3)$, $\lambda ^{g}(Q_{n}^3)$ and $c\lambda _{g+1}(Q_{n}^3)$ can be clearly observed from Table 3. Next, we plot Figs. 4 and 5 to better present the growth rates of these three indicators as g increases. Consistent results can be observed that when r and n are fixed, $\lambda _{g,r+1}(Q_n^3)$ grows at a rapid rate as g increases, whereas $c\lambda _{g+1}(Q_{n}^3)$ is relatively flat. This implies that only a few failed links can disrupt this network to generate multiple components, but to allow each processor to communicate with more processors would require large-scale link failures. In addition, Figs. 6 and 7 depict the variation of $\lambda _{g,r+1}(Q_n^3)$ with the growth of g for fixed n and r, respectively.

Fig. 4

Illustration that $r=2$, $n=10$ and $0\le g\le 8$

Fig. 5

Illustration that $r=3$, $n=9$ and $0\le g\le 12$

Fig. 6

Illustration that $2\le r\le 5$, $n=10$ and $0\le g\le 8$

Fig. 7

Illustration that $r=3$, $10\le n\le 13$ and $0\le g\le 8$

6 Concluding Remarks

This work suggests a novel indicator, namely g-good-neighbor r-component edge-connectivity, for measuring network reliability and fault tolerability of 3-ary n-cube, which is proposed by Liu et al. [17]. This concept breaks down the inherent idea to emphasize the double constraints on the resulting network in the presence of the large-scale faulty links, which not only limits the number of component in the resulting network, but also requires that each vertex is adjacent to at least g fault-free links. More importantly, g-good-neighbor $(r+1)$-component edge-connectivity is almost r times the size of g-good-neighbor edge-connectivity and much larger than $(r+1)$-component edge-connectivity in 3-ary n-cube. As a consequence, this metric offers a more refined quantitative indicator of the robustness of a multiprocessor system in the presence of link disruption.