Reliability evaluation of generalized exchanged X-cubes under the $R_g$-conditional restriction

Abstract

In the realm of multiprocessor systems, the evaluation of interconnection network reliability holds utmost significance, both in terms of design and maintenance. The intricate nature of these systems calls for a systematic assessment of reliability metrics, among which, two metrics emerge as vital: connectivity and diagnosability. The $R_g$-conditional connectivity is the minimum number of processors whose deletion will disconnect the multiprocessor system and every processor has at least g fault-free neighbors. The $R_g$-conditional diagnosability is a novel generalized conditional diagnosability, which is the maximum number of faulty processors that can be identified under the condition that every processor has no less than g fault-free neighbors. In this paper, we first investigate the $R_g$-conditional connectivity of generalized exchanged X-cubes $G\!E\!X(s,t)$ and present the lower (upper) bounds of the $R_g$-conditional diagnosability of $G\!E\!X(s,t)$ under the PMC model. Applying our results, the $R_g$-conditional connectivity and the lower (upper) bounds of $R_g$-conditional diagnosability of generalized exchanged hypercubes, generalized exchanged crossed cubes, and locally generalized exchanged twisted cubes under the PMC model are determined. Our comparative analysis highlights the superiority of $R_g$-conditional diagnosability, showcasing its effectiveness in guiding reliability studies across a diverse set of networks.

1 Introduction

Increasingly, the complex functionalities of emerging real-time applications, such as in automotive, industrial automation, and robotics domains, require multiprocessor systems (MPS for short) to be implemented. Compared to the uniprocessor, multiprocessor systems provide a multitude of advantages, such as superior performance and reliability, enhanced reconfigurability, and scalability. With advancements in very large-scale integration (VLSI for short) and software technologies, multiprocessor systems may incorporate tens of thousands of processors. However, as multiprocessor systems scale up, the likelihood of processor failures doubles or even grows geometrically. Once the processor fails, it may significantly compromise the reliability of the system, such as data transmission failure, packet loss, and increased latency. It is important to quantify the effect of the faults so that fault-tolerant designs can be pursued. One fundamental criterion in the design of MPS is reliability [1]. However, the accurate identification and replacement of faulty processors remain a key challenge in maintaining the system’s reliability.

As we all know, connectivity refers to the ability of the interconnection network to establish and maintain communication between processors when failures occur, which is an important metric to assess the fault tolerance of MPS. In general, connectivity is denoted by $\kappa (G)$, which is the minimum number of processors that make the system disconnected. However, the traditional connectivity in actual network applications has been subject to significant limitations. Specifically, it overlooks the practical possibility of all adjacent processors to a processor malfunctioning simultaneously [2]. To overcome this drawback, Esfahanian and Hakimi [3] introduced a novel measure known as the restricted connectivity, which restricts the simultaneous failure of adjacent processors of arbitrary one processor. Subsequently, Latifi et al. [4] proposed a generalized restricted connectivity notion, the g-restricted connectivity (i.e., $R_{g}$-conditional connectivity), which mandates that each processor should have at least g fault-free neighbors in the system. The $R_{g}$-conditional connectivity offers a more refined and comprehensive means of evaluating the resilience and robustness of a multiprocessor system against failures.

In addition, system-level diagnostics is a crucial technique to diagnose a system, as it enables the identification of all faulty processors within the system. Such a fault location method, based on test outcomes, possesses the potential for real-time diagnostics and can be automated. The diagnosability of a system is a pivotal metric in assessing its reliability, which refers to the maximum number of faulty processors that the system can self-identify. A system is said to be t-diagnosable when all faulty processors can be accurately detected, provided that the number of faulty processors does not exceed t [5]. The PMC model, proposed by Preparata et al. [5], is utilized to identify the faulty processors. To execute fault diagnosis in a system, this model assumes that a processor, acting as a tester u, sends a test message to its neighbor, acting as a testee v, where the ordered pair $\langle u,v\rangle$ represents the test. When u is fault-free, the outcome of $\langle u,v\rangle$ can be used to deduce the state of v. Specifically, if the outcome of $\langle u,v\rangle$ is 1 (resp. 0), then v is faulty (resp. fault-free). However, if u is faulty, then the outcome of $\langle u,v\rangle$ becomes unreliable, rendering the state of v unreliable as well. Meanwhile, Maeng and Malek [6] proposed a comparison-based model, the MM model, for diagnosing a system. In this model, a processor w called comparator, sends the same test to its neighbors u, v and then compares their responses. Assume that such a comparison is denoted by $(u,v)_w$. Specifically, $(u,v)_w=0$ (resp. $(u,v)_w=1$) indicates that the test outcomes for u and v are identical (resp. distinct). For a fault-free comparator w, $(u,v)_w=0$ implies that both u and v are fault-free, whereas $(u,v)_w=1$ reveals that there exists at least one faulty processor between u and v. If the comparator w is faulty, then the result of $(u,v)_w$ is unreliable. Based on the MM model, Sengupta et al. [7] introduced the MM* model as a special case of the MM model, in which each processor must test any pair of adjacent processors. In this paper, we focus on the PMC model for diagnosing faulty processors in a system.

The distribution pattern of faulty processors has a significant impact on the diagnosability of a system. However, the classical diagnosability of a system is often limited due to the lack of restrictions on the distribution pattern of faulty processors. To address this limitation, Lai et al. [8] introduced the concept of conditional diagnosability, which imposes a restriction on the system such that all the neighbors of any processor cannot be faulty at the same time. Peng et al. [9] further extended this concept by proposing the g-good-neighbor conditional diagnosability, which aims to identify the maximum number of faulty processors under the condition that every fault-free processor has at least g fault-free neighbors. Over the years, researchers have conducted extensive studies on the conditional diagnosability and g-good-neighbor conditional diagnosability of various interconnection networks, such as star graph, alternating group networks, BC networks, dual cubes, and so on [4, 10,11,12,13,14,15,16,17]. In particular, Guo et al. [18] proposed a novel generalized system-level diagnosis measure called $R_g$-conditional diagnosability, which assumes that every processor has at least g good neighbors. This measure builds upon the concept of g-good-neighbor conditional diagnosability and extends it to cover a broader range of scenarios. Guo et al. also conducted a study of the $R_g$-conditional diagnosability of hypercubes under the PMC model. That is, the $R_g$-conditional diagnosability of n-dimensional hypercubes under the PMC model is $s^{2g}(n-2g)+2^{2g-1}-1$. Later, Wang et al. [19] proposed that the lower bound of $R_g$-conditional diagnosability of n-dimensional hypercubes is $2^{2g-2}(2n-2^{2g}+1)+(n-g)2^{g-1}-1$ under the PMC model when $g\ge 1$ and $2^{2g}\le n-1$. Yuan et al. [20] studied the relationships between the $R_g$-conditional connectivity $\kappa ^g(G)$ and the $R_g$-conditional diagnosability $t_{R_g}(G)$ under the PMC model and MM* model and showed that $t_{R_g}(G)=\kappa ^{2g+1}(G)+g$ under some reasonable conditions, except $t_{R_1}(G)$ under the MM* model. They also investigated the $R_g$-conditional diagnosability of star graphs and bubble-sort graphs under the PMC model and MM* model. In addition, Yuan et al. [21] also investigated the $R_g$-conditional diagnosability of general networks, such as hypercubes and exchanged hypercubes under the PMC model, and presented the lower and upper bounds of $R_g$-conditional diagnosability of networks under some reasonable conditions.

Fig. 1

The generalized exchanged X-cubes structure contains various popular networks

The study of fault tolerance in interconnection networks is of great importance for improving the reliability and stability of computer systems. Recently, Li et al. [22] proposed a new framework, called the generalized exchanged X-cubes $G\!E\!X(s,t)$, which enables the construction of network architectures using various connecting rules. The g-good-neighbor conditional diagnosability of the generalized exchanged X-cubes framework was also determined under the PMC model and MM* model. Generalized exchanged X-cubes possess several excellent properties, including small diameter, fewer edges, low cost, and low latency. These properties indicate that the framework offers a well-balanced consideration of the network’s hardware and communication costs. In addition, the generalized exchanged X-cube $G\!E\!X(s,t)$ is designed around the BC network, comprising three principal interconnection network types: generalized exchanged hypercubes [23], generalized exchanged crossed cubes and locally generalized exchanged twisted cubes (the detailed definitions are provided in Sect. 5). As shown in Fig. 1, the dual-cube-like network is a special case of generalized exchanged hypercubes, which has attracted several researchers to study its properties [24]. Also, the locally exchanged twisted cube [25] is a novel interconnection that scales upward with lower edge costs than the locally twisted cube and provides more interconnection flexibility. Observably, the generalized exchanged X-cube framework integrates numerous established, contemporary, and extensively embraced interconnection networks. This emphasizes the need for a thorough investigation into the reliability of $G\!E\!X(s,t)$, which stands as a universal approach for analyzing reliability across diverse networks.

To further enhance the reliability index of generalized exchanged X-cubes, this paper investigates the $R_g$-conditional connectivity and establishes the lower and upper bounds of $R_g$-conditional diagnosability under the PMC model. Overall, our study demonstrates the usefulness and applicability of the $R_g$-conditional diagnosability measure for evaluating the reliability of various interconnection networks. The major contributions of our work are as follows.

• We investigate the $R_g$-conditional connectivity of BC networks and generalized exchanged X-cubes $G\!E\!X(s,t)$.

• We establish the lower and upper bounds of $R_g$-conditional diagnosability of $G\!E\!X(s,t)$ under the PMC model.

• As applications, we determine the $R_g$-conditional connectivity, and the lower and upper bounds of $R_g$-conditional diagnosability of generalized exchanged hypercubes, generalized exchanged crossed cubes, and locally generalized exchanged twisted cubes under the PMC model.

• We compare the $R_g$-conditional connectivity (resp. diagnosability) with the traditional connectivity (resp. diagnosability) and g-good-neighbor conditional connectivity (resp. diagnosability) in $G\!E\!X(s,t)$. Moreover, for generalized exchanged hypercubes, the most typical case of $G\!E\!X(s,t)$, we conduct comprehensive comparisons involving $R_g$-conditional diagnosability, g-component diagnosability, and g-extra diagnosability in $G\!E\!H(s,t)$, along with evaluating $R_g$-conditional connectivity against a spectrum of novel connectivity.

• The comparative findings highlight the notable reliability of $G\!E\!X(s,t)$ under the $R_g$ restriction, surpassing the performance of a majority of established connectivity and diagnosability.

Organization. The rest of this paper is organized as follows. Basic notations and definitions for generalized exchanged X-cubes, $R_g$-conditional diagnosability, and other terms are provided in Sect. 2. Section 3 demonstrates the $R_g$-conditional connectivity of generalized exchanged X-cubes. Section 4 shows the lower and upper bounds of $R_g$-conditional diagnosability of generalized exchanged X-cubes. Section 5 gives some applications based on the results regarding the $R_g$-conditional connectivity and the $R_g$-conditional diagnosability. Moreover, we draw some comparisons in Sect. 6. Finally, we offer some concluding remarks in the last section.

2 Preliminaries

2.1 Terminologies and notations

Table 1 Notations

In this subsection, we provide Table 1 that describes some of the important notations used in this paper. It is a standard method to regard the multiprocessor system as a simple undirected graph $G=(V(G), E(G))$. For any node $u\in V(G)$, we define the neighborhood $N_{G}(u)$ of u in G to be the set of nodes adjacent to u. Also, we set $N_{G}(R)=\{v\in V(G)\setminus R \vert (u,v)\in E(G)$ and $u\in R\}=\bigcup _{u\in R} N_{G}(u){\setminus } R$ and $N_{G}[R]=N_{G}(R)\cup R$ with $R\subseteq V(G)$. For neighborhoods, we always omit the subscript for the graph when no confusion arises. A graph G is called n-regular if $deg_G(u)=n$ for any node $u\in V(G)$. $G-R$ is denoted as $G[V(G)\backslash R]$, where R is called a node cut if $G-R$ is disconnected. Two binary strings $u=u_1u_0$ and $v=v_1v_0$ are pair related, denoted by $u\sim v$, if and only if $u,v\in \{(00,00),(01,11),(10,10),(11,01)\}$. The case that u and v are not pair related is denoted by $u \not \sim v$. A component is defined as a maximally connected subgraph of a graph. A matching M in G is a set of pairwise nonadjacent edges. M is a perfect matching of G if each node in V(G) is incident with an edge in M. Given two sets $F_1,F_2\subset V(G)$, the symmetric difference of $F_1$ and $F_2$ is denoted by $F_1\bigtriangleup F_2 = (F_1{\setminus } F_2)\cup (F_2{\setminus } F_1)$.

2.2 Generalized exchanged X-cubes

In this subsection, we review the definition and properties of generalized exchanged X-cubes. Since generalized exchanged X-cubes are derived by bijective connection networks (BC networks for short), we first review the definition and properties of the BC networks. Specifically, BC networks are a class of cube-based graphs including several well-known interconnection graphs such as hypercubes [9], M$\ddot{\text {o}}$bius cubes [26], crossed cubes [27], and locally twisted cubes [28]. An n-dimensional BC network, denoted by $X_{n}$, is an n-regular graph with $2^{n}$ nodes and $n\times 2^{n-1}$ edges. The set of all the n-dimensional BC networks is called the family of the n-dimensional BC networks, denoted by $\mathbb {L}_n$. $X_n$ and $\mathbb {L}_n$ can be recursively defined as follows.

Definition 1

(See [29]). The one-dimensional BC network $X_{1}$ contains only two nodes that form an edge. The family of the one-dimensional BC network is defined as $\mathbb {L}_{1}=\{X_{1}\}$. A graph G belongs to the family of n-dimensional BC networks $\mathbb {L}_{n}$ if and only if there exist $V_{0}, V_{1}\subset V(G)$ such that the following two conditions hold:

• (1) $V(G)=V_{0}\cup V_{1}$, $V_{0}\ne \emptyset$, $V_{1}\ne \emptyset$, $V_{0}\cap V_{1}=\emptyset$, and $G[V_{0}], G[V_{1}] \in \mathbb {L}_{n-1}$; and

• (2) $E(V_{0}, V_{1})=\{(u,v)\vert u\in V_0,v\in V_1,(u,v)\in E(G)\}$ is a perfect matching M of G.

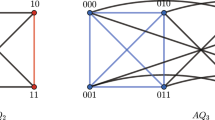
We illustrate two three-dimensional BC networks in Fig. 2. In addition, for any $X_{n}\in \mathbb {L}_{n}$, there exist $V_{0}, V_{1}$ and M satisfying the above two conditions by Definition 1. It is clear that $G[V_{0}]$ and $G[V_{1}]$ are both $(n-1)$-dimensional BC networks, as well as $E(G[V_{0}])$, $E(G[V_{1}])$ and M are a decomposition of $E(X_{n})$. Thus, we use $X_{n-1}^{0}$ (resp. $X_{n-1}^{1}$) to denote the induced subgraph $G[V_{0}]$ (resp. $G[V_{1}]$) and define the decomposition as $X_{n}=G(X_{n-1}^{0},X_{n-1}^{1};M)$.

Fig. 2

Two three-dimensional BC networks

Lemma 1

(See [30]). Suppose that $0\le g\le n$ and $Y\subset V(X_{n})$. If $\delta (X_{n}[Y])\ge g$, then $\vert Y\vert \ge 2^{g}$.

Lemma 2

(See [31]). If S is a subgraph of $X_{n}$ with $\vert V(S)\vert =g+1$ for $0\le g \le n$, then $\vert N_{X_{n}}(V(S))\vert \ge (g+1)n-\frac{g(g-1)}{2}-2\,g$.

Lemma 3

(See [32]). Suppose that $0\le g\le n$, $n\ge 1$ and $Y\subset V(X_{n})$. If $\delta (X_{n}[Y])= g$, then $\vert N_{X_{n}}[Y]\vert \ge (n-g+1)2^{g}$.

Next, we introduce the definition and properties of generalized exchanged X-cubes.

Definition 2

(See [22]). The (s, t)-dimensional generalized exchanged X-cube is defined as a graph $G\!E\!X(s,t) =(V(G\!E\!X(s,t))$, $E(G\!E\!X(s,t)))$ with $s,t\ge 1$. $G\!E\!X(s,t)$ consists of two disjoint subgraphs $\widetilde{L}$ and $\widetilde{R}$, where $\widetilde{L}$ consists of $2^{t}$ subgraphs, denoted by $\widetilde{L}_{i}$ for $i\in [1, 2^{t}]$. Similarly, $\widetilde{R}$ consists of $2^{s}$ subgraphs, denoted by $\widetilde{R}_{j}$ for $j\in [1, 2^{s}]$. Moreover, $G\!E\!X(s,t)$ satisfies the following conditions:

• (1) For any $1\le i\le 2^{t}$ and $1\le j\le 2^{s}$, $\widetilde{L}_{i}\cong X_{s}$ and $\widetilde{R}_{j}\cong X_{t}$. Further, $\vert V(\widetilde{L}_{i})\vert =2^{s}$ and $\vert V(\widetilde{R}_{j})\vert =2^{t}$;

• (2) Each node in $V(\widetilde{L})$ has a unique neighbor in $V(\widetilde{R})$ and vice versa. In addition, for distinct nodes in each $\widetilde{L}_{i}$, their neighbors locate in different $\widetilde{R}_{j}$;

• (3) For any two different subgraphs $\widetilde{L}_{i}$ and $\widetilde{L}_{i'}$ with $i\ne i'$, there exists no edge between them. Similar for $\widetilde{R}_{j}$ and $\widetilde{R}_{j'}$ with $j\ne j'$.

Fig. 3

a The partition of $G\!E\!X(s,t)$, where the rectangle boxes indicate the clusters; b The contraction of $G\!E\!X(s,t)$, where each cluster is represented as a node

According to Definition 2, we can deduce that $\vert V(G\!E\!X(s,t))\vert =2^{s+t+1}$. Let each $\widetilde{L}_{i}$ and $\widetilde{R}_{j}$ be a cluster of $G\!E\!X(s,t)$. Obviously, $G\!E\!X(s,t)$ consists of $2^{t}+2^{s}$ clusters. If we contract each cluster into a node, then $G\!E\!X(s,t)$ can be abstracted as a complete bipartite graph $K_{2^{t},2^{s}}$ (see Fig. 3). The edges that connect different clusters are called cross edges. In the following discussion, we consider $s\le t$. Thus, $\delta (G\!E\!X(s,t))=s+1$ and $\Delta (G\!E\!X(s,t))=t+1$.

Lemma 4

(See [22]). For any integers $3\le s\le t$ and $1 \le g \le s-2$, $t_{g}(G\!E\!X(s,t))=(s-g+2)2^g-1$ under the PMC model.

2.3 The $R_{g}$-conditional diagnosability

Guo et al. [18] proposed a novel conditional diagnosability named $R_g$-conditional diagnosability, which requires every processor to have at least g good neighbors. In what follows, some concepts and results on $R_{g}$-conditional diagnosability of a system are listed.

Suppose that G is an n-regular graph and a set of faulty nodes is called a faulty set. Given a node $u\in V(G)$, $\mathcal {A}_u$ is called a forbidden faulty set of u if and only if $\mathcal {A}_u\subset N(u)$ and $\vert \mathcal {A}_u\vert \ge n-g$ when $0< g \le n$ [33]. Let $R_g =\{Y\subset V(G)\vert \mathcal {A}_u \not \subset Y, \mathcal {A}_u \ \text {is a forbidden faulty set of} \ u, \text {for any} \ u \in V(G)\}$. Thus, if $F \in R_{g}$, then every node, including fault-free and faulty nodes, has at least g good neighbors (i.e., fault-free nodes). A faulty set F is called an $R_g$-conditional faulty set if $F \in R_g$. A node cut R is called an $R_g$-cut of G if $R\in R_g$.

Definition 3

(See [4]). A system G is $R_g$-connected if G has an $R_g$-cut. The $R_g$-conditional connectivity of G, denoted by $\kappa ^{g}(G)$, is the minimum cardinality of all $R_g$-cuts in G.

Definition 4

(See [18]). A system G is $R_g$-conditionally t-diagnosable if an arbitrary pair of distinct $R_g$-conditional faulty sets $(F_1, F_2)$ is distinguishable with $\vert F_1\vert ,\vert F_2\vert \le t$. The $R_g$-conditional diagnosability of G, denoted by $t_{R_g}(G)$, is the maximum t such that G is $R_g$-conditionally t-diagnosable.

Lemma 5

(See [18]). For any two distinct indistinguishable $R_g$-conditional faulty sets $F_1$ and $F_2$ of $G=(V(G),E(G))$, the following conditions are satisfied:

• (1) Each component U of $F_1 \bigtriangleup F_2$ has $\delta (U)\ge 2g$; and

• (2) Each component C of $V(G){\setminus }(F_1\cup F_2)$ has $\delta (C)\ge g$.

In addition, we give a sufficient and necessary condition for two distinct subsets $\hat{F}_1$ and $\hat{F}_2$ to be a distinguishable pair under the PMC model.

Lemma 6

(See [34]). For any two distinct subsets $\hat{F}_1$ and $\hat{F}_2$ in a system $G =(V(G), E(G))$, the sets $\hat{F}_1$ and $\hat{F}_2$ are distinguishable under the PMC model if and only if there exists at least one edge from $V(G)\setminus (\hat{F}_1\cup \hat{F}_2)$ to $\hat{F}_1 \bigtriangleup \hat{F}_2$.

3 The $R_{g}$-conditional connectivity of $G\!E\!X(s,t)$

In this section, we will investigate the $R_g$-conditional connectivity of $G\!E\!X(s,t)$. Before that, we first discuss the $R_g$-conditional connectivity of BC networks $X_n$ and propose Lemma 7 as follows.

Lemma 7

For BC networks $X_n$ with $n\ge 3$ and $0\le g\le \left\lfloor \frac{n}{2}\right\rfloor$, the $R_g$-conditional connectivity of $X_n$ is $\kappa ^{g}(X_{n})=(n-g)2^{g}$.

Proof

At first, we prove that $\kappa ^{g}(X_n)\le (n-g)2^{g}$. Let F be a set of all neighbors of $V(X_g)$, that is $F=\{N_{X_n}(u){\setminus } V(X_g) \ \text {for}\ u\in V(X_g)\}$. Since $X_n$ is an n-regular graph with $2^n$ nodes, we can deduce that $X_n-F$ is disconnected and $\vert F\vert =(n-g)2^{g}$. Then, we now verify that $F\in R_g$. Obviously, every node in $X_g$ has at least g good neighbors. According to the structural properties of $X_n$, F is composed of $n-g$ disjoint subgraphs $X_g$. Hence, each node in F has at most g neighbors u with $u\in V(F)$ and has at least $n-g$ neighbors in $X_n-F$. Further, since $g\le \left\lfloor \frac{n}{2} \right\rfloor$ and $n-g\ge g$, it is clear that every node in F has at least g good neighbors. Also, each node in $X_n-F-X_g$ has at most $n-g$ neighbors in F and $n-g\ge g$, thus any node in $X_n-F-X_g$ has at least g neighbors in $X_n-F$. This proves that such an F belongs to $R_g$.

Next, we prove $\kappa ^{g}(X_n)\ge (n-g)2^{g}$ by induction on g. Assume that S is a minimum $R_g$-cut of $X_n$, Y is the node set of a minimum connected component of $X_n-S$, and the node set $Z=V(X_n-S-Y)$. Let $S_i=S\cap V(X_{n-1}^i)$, $Y_i=Y\cap V(X_{n-1}^i)$ and $Z_i=Y\cap V(X_{n-1}^i)$ for $i\in \{0,1\}$. It is obvious that the result is true for $g=0$. We assume that the result is true for $g-1$ with $g\ge 1$. The following two cases are considered.

Case 1: $Y_0=\emptyset$ or $Y_1=\emptyset$.

Without loss of generality, suppose that $Y_1\!=\!\emptyset$, that is $Y\subseteq V(X_{n-1}^0)$. By Lemma 3 and $X_{n}=G(X_{n-1}^{0},X_{n-1}^{1};M)$, we can deduce that $\vert N_{X_{n}}(Y)\vert =\vert N_{X_{n-1}^0}(Y)\vert +\vert N_{X_{n-1}^1}(Y)\vert =\vert N_{X_{n-1}^0}[Y]\vert \ge ((n-1)-g+1)2^g=(n-g)2^g$. Since S is an $R_g$-cut, it shows that $N_{X_{n}}(Y)\subseteq S$. Thus, $\vert S\vert \ge \vert N_{X_{n}}(Y)\vert \ge (n-g)2^{g}$.

Case 2: $Y_0\ne \emptyset$ and $Y_1\ne \emptyset$.

Subcase 2.1: $Z_0\ne \emptyset$ and $Z_1\ne \emptyset$.

As S is an $R_g$-cut of $X_n$, for each $i\in \{0,1\}$, every node $v\in Y_i\cup Z_i$ has at least g neighbors in $X_n-S$, as well as every node $u\in S_i$ has at least g neighbors in $X_n-S$. If a node v has at most one neighbor in $X_{n-1}^0-S$ (resp. $X_{n-1}^1-S$), then v has at least $g-1$ neighbors in $X_{n-1}^1-S$ (resp. $X_{n-1}^0-S$). Moreover, a node $u\in S$ has at least $g-1$ neighbors in $X_{n-1}^0-S$ (resp. $X_{n-1}^1-S$), which implies that $S_0$ (resp. $S_1$) is an $R_{g-1}$-cut of $X_{n-1}^0$ (resp. $X_{n-1}^1$). By the induction hypothesis, $\vert S_0\vert \ge [(n-1)-(g-1)]2^{g-1}=(n-g)2^{g-1}$ and $\vert S_1\vert \ge 2^{g-1}(n-g)$. Hence, $\vert S\vert =\vert S_0\cup S_1\vert \ge (n-g)2^{g}$.

Subcase 2.2: $Z_0=\emptyset$ or $Z_1=\emptyset$.

Without loss of generality, suppose that $Z_0\ne \emptyset$ and $Z_1=\emptyset$. As discussed in Subcase 2.1, $S_0$ is an $R_{g-1}$-cut of $X_{n-1}^1$ and $\vert S_0\vert \ge (n-g)2^{g-1}$. Then, $\vert S_0\vert =\vert X_{n-1}^0\vert -\vert Y_0\vert -\vert Z_0\vert$ and $\vert S_1\vert =\vert X_{n-1}^1\vert -\vert Y_1\vert$. If $\vert S_1\vert <\vert S_0\vert$, then $\vert Z\vert<\vert Y_0\vert +\vert Z\vert <\vert Y_1\vert$, which is a contradiction. Therefore, $\vert S_1\vert \ge \vert S_0\vert$ and $\vert S\vert \ge 2\vert S_0\vert \ge (n-g)2^{g}$.

By the above discussion, we can conclude the $R_g$-conditional connectivity of $X_n$ is $\kappa ^{g}(X_{n})=(n-g)2^{g}$. $\square$

Lemma 8

For $G\!E\!X(s,t)$ with $3\le s\le t$ and $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$, the $R_g$-conditional connectivity of $G\!E\!X(s,t)$ is $\kappa ^{g}(G\!E\!X(s,t))\le (s-g+1)2^{g}$.

Proof

By Definition 2, it shows that $G\!E\!X(s,t)$ is composed of two disjoint subgraphs $\widetilde{L}$ and $\widetilde{R}$, where $\widetilde{L}$ (resp. $\widetilde{R}$) can be partitioned into $2^{t}$ (resp. $2^{s}$) subgraphs (clusters). Without loss of generality, suppose that there exists $A\subseteq V(\widetilde{L}_{1})$ such that $G\!E\!X(s,t)[A]\cong X_{g}$. By Definitions 1 and 2, we can get that $\vert A\vert =2^{g}$, $\widetilde{L}_{1}\cong X_s$ and $\vert N_{\widetilde{L}_{1}}(A)\vert =(s-g)2^{g}$. Moreover, each node in $V(\widetilde{L})$ has an unique neighbor in $V(\widetilde{R})$ by Definition 2. For distinct nodes in each $\widetilde{L}_{i}$, their neighbors of $\widetilde{R}$ locate in different $\widetilde{R}_{j}$, where $i\in [1,2^t]$ and $j\in [1,2^s]$. In addition, for any two different subgraphs $\widetilde{L}_{i}$ and $\widetilde{L}_{i^\prime }$ with $i\ne i^\prime$, the edge between them does not exist, so each node in $\widetilde{L}_{1}$ has only one neighbor in $G\!E\!X(s,t)-\widetilde{L}_{1}$. Then, we can deduce that $\vert N_{G\!E\!X(s,t)-\widetilde{L}_{1}}(A)\vert =\vert A\vert =2^{g}$. Thus, we have

$$\begin{aligned} \begin{array}{ll} \vert N_{G\!E\!X(s,t)}(A)\vert &= \ \vert N_{\widetilde{L}_{1}}(A)\vert +\vert N_{G\!E\!X(s,t)-\widetilde{L}_{1}}(A)\vert \\ &= \ (s-g)2^{g}+2^{g}\\ &= \ (s-g+1)2^{g}. \end{array} \end{aligned}$$

Since $\vert N_{G\!E\!X(s,t)}[A]\vert =(s-g+1)2^{g}+2^{g}=(s-g+2)2^{g}$ and $\vert V(G\!E\!X(s,t))\vert = 2^{s+t+1}> (s-g+2)2^{g}$, we can infer that $G\!E\!X(s,t)-N_{G\!E\!X(s,t)}(A)$ is disconnected and $N_{G\!E\!X(s,t)}(A)$ is a node cut of $G\!E\!X(s,t)$. It shows that $G\!E\!X(s,t)[A]\cong X_{g}$, and thus $\delta (G\!E\!X(s,t)[A])=g$. By Lemma 7, $N_{\widetilde{L}_{1}}(A)$ is an $R_g$-cut of $\widetilde{L}_{1}$ with $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$, thus $\delta (\widetilde{L}_{1}-N_{\widetilde{L}_{1}}[A])\ge g$. From $\delta (G\!E\!X(s,t))=s+1$ ($s\le t$) and Definition 2, we can deduce that $\delta (G\!E\!X(s,t)-\widetilde{L}_{1}-N_{G\!E\!X(s,t)-\widetilde{L}_{1}}(A))\ge s+1-1> g$ for any node in $G\!E\!X(s,t)-\widetilde{L}_{1}-N_{G\!E\!X(s,t)-\widetilde{L}_{1}}(A)$. Based on the above discussion, we have $\delta (G\!E\!X(s,t)-N_{G\!E\!X(s,t)}(A))\ge g$. By Definition 2, for distinct nodes in each $\widetilde{L}_{1}$, their neighbors of $\widetilde{R}$ locate in different $\widetilde{R}_{j}$. For any two different subgraphs $\widetilde{R}_{j}$ and $\widetilde{R}_{j'}$ with $j\ne j'$, there exists no edge between them. Hence, it shows that any node in $N_{G\!E\!X(s,t)-\widetilde{L}_{1}}(A)$ does not have neighbors in $N_{G\!E\!X(s,t)-\widetilde{L}_{1}}(A)$, but has at least s neighbors in $G\!E\!X(s,t)-N_{G\!E\!X(s,t)}(A)$. Since $N_{\widetilde{L}_{1}}(A)$ is an $R_g$-cut of $\widetilde{L}_{1}$, each node in $N_{\widetilde{L}_{1}}(A)$ has at least g neighbors in $\widetilde{L}_{1}-N_{\widetilde{L}_{1}}(A)$ and $N_{G\!E\!X(s,t)}(A)$ is an $R_g$-cut of $G\!E\!X(s,t)$. Hence, $\kappa ^{g}(G\!E\!X(s,t))\le (s-g+1)2^{g}$ with $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$ and $3\le s\le t$, the lemma holds. $\square$

Lemma 9

For $G\!E\!X(s,t)$ with $3\le s\le t$ and $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$, the $R_g$-conditional connectivity of $G\!E\!X(s,t)$ is $\kappa ^{g}(G\!E\!X(s,t))\ge (s-g+1)2^{g}$.

Proof

Assume that I is a minimum $R_g$-cut of $G\!E\!X(s,t)$. Let $I_{\widetilde{L}_{i}}=I\cap V(\widetilde{L}_{i})$ and $I_{\widetilde{R}_{j}}=I\cap V(\widetilde{R}_{j})$ for each $1\le i\le 2^{t}$ and $1\le j\le 2^{s}$. Then, we will prove that $\kappa ^{g}(G\!E\!X(s,t))=\vert I\vert \ge (s-g+1)2^{g}$ with $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$ and $s\ge 3$ by the following three cases.

Case 1: $\widetilde{L}_{i}-I_{\widetilde{L}_{i}}$ and $\widetilde{R}_{j}-I_{\widetilde{R}_{j}}$ are connected for each i and j.

We prove this case by contradiction. Suppose that $\vert I\vert \le (s-g+1)2^{g}-1$. Since I is a minimum $R_g$-cut of $G\!E\!X(s,t)$, it is no doubt that $G\!E\!X(s,t)-I$ is disconnected. Clearly, a component C necessarily traverses r clusters (i.e., subgraph $\widetilde{L}_{i}$ or $\widetilde{R}_{j}$), $r\ge 1$, say $B_1,B_2,\ldots ,B_r$. Let $I_{\alpha }=B_{\alpha }\cap I$ with $\alpha \in [1, r]$. Accordingly, $C=\bigcup _{\alpha =1}^{r}(B_{\alpha }-I_{\alpha })$. By Definition 2(2) and (3), we can deduce that at most $r-1$ cross edges between $B_{\alpha }-I_{\alpha }$ and $B_{\beta \setminus \{\alpha \}}$ exist, where $\beta =\{1,2,\ldots , r\}$. Moreover, there are at least $2^{s}-\vert I_{\alpha }\vert -(r-1)$ cross edges between $B_{\alpha }-I_{\alpha }$ and $\mathcal {W}$, where $\mathcal {W}=G\!E\!X(s,t)-\bigcup _{\alpha =1}^{r}B_{\alpha }$ and $s\le t$. Let $\mathcal {M}=I\setminus \bigcup _{\alpha =1}^{r}I_{\alpha }$. Since there is no edge between $B_{\alpha }-I_{\alpha }$ and $\mathcal {W}-\mathcal {M}$, $\vert \mathcal {M}\vert \ge \sum _{\alpha =1}^{r}[2^{s}-\vert I_{\alpha }\vert -(r-1)]$. Then, we have

$$\begin{aligned} \begin{array}{ll} \vert I\vert &= \ \vert I_{1}\vert +\vert I_{2}\vert +\cdots +\vert I_{r}\vert +\vert \mathcal {M}\vert \\ &\ge \ \vert I_{1}\vert +\vert I_{2}\vert +\cdots +\vert I_{r}\vert +\sum _{\alpha =1}^{r}[2^{s}- \vert I_{\alpha }\vert -(r-1)]\\ &= \ r(2^{s}-r+1). \end{array} \end{aligned}$$

Let the function $f(r)= r(2^{s}-r+1)$ with $r\ge 1$. We can obtain that $\frac{\partial f(r)}{\partial r}=2^{s}-2r+1> 0$ and f(r) is an increasing function. Thus, $f(r)\ge f(1)=2^{s}$ and $\vert I\vert \ge f(r)\ge 2^{s}$. Similarly, we suppose that $f(g)=2^{s}-[(s-g+1)2^{g}-1]$ with $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$. We can calculate that $\frac{\partial f(g)}{\partial g}=2^{g}[g\ln 2+1-(s+1)\ln 2]< 0$, which implies that f(g) is a decreasing function and $f(g)\ge f(\left\lfloor \frac{s}{2} \right\rfloor )> 0$. Clearly, $\vert I\vert \ge 2^{s}> (s-g+1)2^{g}-1$, which violates the assumption that $\vert I\vert \le (s-g+1)2^{g}-1$.

Case 2: Only one of $\widetilde{L}_{i}-I_{\widetilde{L}_{i}}$ and $\widetilde{R}_{j}-I_{\widetilde{R}_{j}}$ is disconnected.

Similarly, we also prove this case by contradiction. Suppose that $\vert I\vert \le (s-g+1)2^{g}-1$. Without loss of generality, we assume that $\widetilde{L}_{1}-I_{\widetilde{L}_{1}}$ is disconnected. Since I is an $R_g$-cut of $G\!E\!X(s,t)$, $\delta (\widetilde{L}_{1}-I_{\widetilde{L}_{1}})\ge g-1$ and $I_{\widetilde{L}_{1}}$ is an $R_{g-1}$-cut of $\widetilde{L}_{1}$. By Lemma 7, it shows that $\vert I_{\widetilde{L}_{1}}\vert \ge [s-(g-1)]2^{g-1}=(s-g+1)2^{g-1}$. Let $I_{1}=I_{\widetilde{L}_{1}}$ and $\mathcal {P} =I{\setminus } I_1$. Then, we can deduce that $\vert \mathcal {P}\vert \le (s-g+1)2^{g-1}-1$.

Moreover, we assume that $G\!E\!X(s,t)-\widetilde{L}_{1}-\mathcal {P}$ is disconnected. At this time, a component C must traverse r clusters with $r\ge 1$, that is, $B_2,B_3,\ldots ,B_{r+1}$. Let $I_{\alpha }=B_{\alpha }\cap I$ with $\alpha \in [2, r+1]$. Accordingly, $C=\bigcup _{\alpha =2}^{r+1}(B_{\alpha }-I_{\alpha })$. By Definition 2(2) and (3), we can deduce that at most r cross edges between $B_{\alpha }-I_{\alpha }$ and $B_{\beta \setminus \{\alpha \}}$ exist, where $\beta =\{1,2,\ldots , r+1\}$. Meanwhile, there are at least $2^{s}-\vert I_{\alpha }\vert -r$ cross edges between $B_{\alpha }-I_{\alpha }$ and $\mathcal {W}$, where $\mathcal {W}=G\!E\!X(s,t)-\bigcup _{\alpha =1}^{r+1}B_{\alpha }$ and $B_1\cong \widetilde{L}_{1}$. Let $\mathcal {M}=I\setminus \bigcup _{\alpha =1}^{r+1}I_{\alpha }$. Since there is no edge between $B_{\alpha }-I_{\alpha }$ and $\mathcal {W}-\mathcal {M}$, $\vert \mathcal {M}\vert \ge \sum _{\alpha =2}^{r+1}[2^{s}-\vert I_{\alpha }\vert -r]$. Figure 4 shows an illustration of this case. Then, we have

$$\begin{aligned} \begin{array}{ll} \vert \mathcal {P}\vert &= \ \vert I_{2}\vert +\cdots +\vert I_{r+1}\vert +\vert \mathcal {M}\vert \\ &\ge \ \vert I_{2}\vert +\cdots +\vert I_{r+1}\vert +\sum\limits_{\alpha =2}^{r+1}[2^{s}-\vert I_{\alpha }\vert -r]\\ &= \ r(2^{s}-r). \end{array} \end{aligned}$$

Fig. 4

An illustration of the proof of Case 2 in Lemma 9

Let $f(r)=r(2^{s}-r)$ with $r\ge 1$. We can obtain that $\frac{\partial f(r)}{\partial r}=2^{s}-2r> 0$ and f(r) is an increasing function. Hence, $f(r)\ge f(1)=2^{s}-1$ and $\vert \mathcal {P}\vert \ge f(r)\ge 2^{s}-1$. Similarly, we define the function $f(g)=2^{s}-1-[(s-g+1)2^{g-1}-1]$ with $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$ and $s\ge 3$. It shows that $\frac{\partial f(g)}{\partial g}=2^{g-1}[g\ln 2+1-(s+1)\ln 2]< 0$. Thus, f(g) is a decreasing function and $f(g)\ge f(\left\lfloor \frac{s}{2} \right\rfloor )> 0$. Then, $\vert \mathcal {P}\vert \ge 2^{s}-1> (s-g+1)2^{g-1}-1$, which results in a contradiction with $\vert \mathcal {P}\vert \le (s-g+1)2^{g-1}-1$. Therefore, $G\!E\!X(s,t)-\widetilde{L}_{1}-\mathcal {P}$ is connected.

Since $\widetilde{L}_{1}-I_{1}$ is disconnected, there must be a component U in $\widetilde{L}_{1}-I_{1}$ such that no edge between U and $G\!E\!X(s,t)-\widetilde{L}_{1}-\mathcal {P}$ exists. Then, $\vert \mathcal {P}\vert \ge \vert V(U)\vert$. Obviously, $N_{\widetilde{L}_{1}}(U)\subseteq I_{1}$, which means that $\vert I\vert =\vert I_{1}\vert +\vert \mathcal {P}\vert \ge \vert N_{\widetilde{L}_{1}}(U)\vert +\vert V(U)\vert =\vert N_{\widetilde{L}_{1}}[U]\vert$. Considering that I is an $R_g$-cut of $G\!E\!X(s,t)$, $\delta (U)\ge g$. By Lemma 3 and $\widetilde{L}_{1}\cong X_{s}$, we deduce that $\vert I\vert =\vert N_{\widetilde{L}_{1}}[U]\vert \ge (s-g+1)2^{g}$, which contradicts with $\vert I\vert \le (s-g+1)2^{g}-1$.

Case 3: At least two of $\widetilde{L}_{i}-I_{\widetilde{L}_{i}}$ and $\widetilde{R}_{j}-I_{\widetilde{R}_{j}}$ are disconnected.

Without loss of generality, suppose that $\widetilde{L}_{1}-I_{\widetilde{L}_{1}}$ and $\widetilde{L}_{2}-I_{\widetilde{L}_{2}}$ are disconnected. Since I is an $R_g$-cut of $G\!E\!X(s,t)$, we have that $\delta (\widetilde{L}_{1}-I_{\widetilde{L}_{1}})\ge g-1$ and $\delta (\widetilde{L}_{2}-I_{\widetilde{L}_{2}})\ge g-1$ by Definition 2. In addition, it is clear that every node in $\widetilde{L}_{1}$ (resp. $\widetilde{L}_{2}$) has at least $g-1$ neighbors in $\widetilde{L}_{1}-I_{\widetilde{L}_{1}}$ (resp. $\widetilde{L}_{2}-I_{\widetilde{L}_{2}})$. Thus, $I_{\widetilde{L}_{1}}$ (resp. $I_{\widetilde{L}_{2}}$) is an $R_{g-1}$-cut of $\widetilde{L}_{1}$ (resp. $\widetilde{L}_{2}$). By Lemma 7, $\vert I_{\widetilde{L}_{1}}\vert \ge (s-g+1)2^{g-1}$ and $\vert I_{\widetilde{L}_{2}}\vert \ge (s-g+1)2^{g-1}$. Then,

$$\begin{aligned} \begin{array}{ll} \vert I\vert &\ge \ \vert I_{\widetilde{L}_{1}}\vert +\vert I_{\widetilde{L}_{2}}\vert \\ &\ge \ (s-g+1)2^{g-1}+(s-g+1)2^{g-1}\\ &= \ (s-g+1)2^{g}. \end{array} \end{aligned}$$

As a result, based on the above discussion, we can conclude that $\kappa ^{g}(G\!E\!X(s,t))=\vert I\vert \ge (s-g+1)2^{g}$. $\square$

Thus, we combine Lemmas 8 and 9, and the following theorem holds.

Theorem 10

For $G\!E\!X(s,t)$ with $3\le s\le t$ and $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$, the $R_g$-conditional connectivity of $G\!E\!X(s,t)$ is $\kappa ^{g}(G\!E\!X(s,t))= (s-g+1)2^{g}$.

4 The $R_{g}$-conditional diagnosability of $G\!E\!X(s,t)$ under the PMC model

In this section, we will establish the upper and lower bounds of $R_g$-conditional diagnosability of $G\!E\!X(s,t)$.

Lemma 11

If H is a subgraph of $G\!E\!X(s,t)$ with $\vert V(H)\vert =g+1$ for $0\le g\le s-1$, $s\ge 2$, then $\vert N_{G\!E\!X(s,t)}(V(H))\vert \ge (g+1)s-\frac{g(g+1)}{2}+1$.

Proof

We shall prove the lemma by induction on $\vert V(H)\vert$. By Definition 2, it is clear that the result holds for $\vert V(H)\vert =1$. Suppose that the conclusion holds for all H with $\vert V(H)\vert \le g$, where $g\ge 1$. Then, we show the results are true for H with $\vert V(H)\vert =g+1\ge 2$ by the following two cases.

Case 1: V(H) is distributed in exactly one cluster.

Without loss of generality, we let $H\subset B_{\alpha }$, where $B_{\alpha }\cong X_{s}$ and a certain $\alpha \in [1,2^s+2^t]$. By Lemma 2, it is easy to deduce that $\vert N_{B_{\alpha }}(V(H))\vert \ge (g+1)s-\frac{g(g-1)}{2}-2\,g$. Since each node in $B_{\alpha }$ has only one neighbor in $V(G\!E\!X(s,t)-B_{\alpha })$, $\vert N_{G\!E\!X(s,t)}(V(H))\vert \ge (g+1)s-\frac{g(g-1)}{2}-2\,g+(g+1)=(g+1)s-\frac{g(g+1)}{2}+1.$

Case 2: V(H) is distributed in at least two different clusters.

Suppose that $H_{0}=H\cap B_{\alpha }$ and $H_{1}=H\cap (G\!E\!X(s,t)- B_{\alpha })$, where $\vert V(H_{0})\vert =x$, $\vert V(H_{1})\vert =g+1-x$ and $1\le x\le g$. By Lemma 2 and the induction hypothesis, we have

$$\begin{aligned} \begin{array}{ll} \vert N_{B_{\alpha }}(V(H_{0}))\vert &\ge \ xs-\frac{(x-1)(x-2)}{2}-2(x-1) \\ &= \ xs-\frac{x(x+1)}{2}+1, \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ll} \vert N_{G\!E\!X(s,t)}(V(H_{1}))\vert \ge (g+1-x)s-\frac{(g+1-x)(g-x)}{2}+1. \end{array} \end{aligned}$$

Since each node in $V(H_1)$ has at most one neighbor in $B_{\alpha }$, $\vert N_{B_{\alpha }}(V(H_{1}))\vert \le g+1-x$. Then,

$$\begin{aligned} \begin{array}{ll} \vert N_{G\!E\!X(s,t)- B_{\alpha }}(V(H_{1}))\vert &=\ \vert N_{G\!E\!X(s,t)}(V(H_{1}))\vert -\vert N_{{B_{\alpha }}}(V(H_{1}))\vert \\ &\ge \ [(g+1-x)s-\frac{(g+1-x)(g-x)}{2}+1]-(g+1-x). \end{array} \end{aligned}$$

Hence, we have

$$\begin{aligned} \begin{array}{ll} \vert N_{G\!E\!X(s,t)}(V(H))\vert &\ge \ \vert N_{B_{\alpha }}(V(H_{0}))\vert +\vert N_{G\!E\!X(s,t)- B_{\alpha }}(V(H_{1}))\vert \\ &\ge \ xs-\frac{x(x+1)}{2}+1+[(g+1-x)s-\frac{(g+1-x)(g-x)}{2}+1]\\ & \quad \ -(g+1-x) \\ &=\ (g+1)s-\frac{x(x+1)}{2}-\frac{(g-x)(g-x+3)}{2}+1. \end{array} \end{aligned}$$

Further, we deduce

$$\begin{aligned} \begin{array}{ll} \vert N_{G\!E\!X(s,t)}(V(H))\vert -[(g+1)s-&\frac{g(g+1)}{2}+1] \\ &\ge \ (g+1)s-\frac{x(x+1)}{2}-\frac{(g-x)(g-x+3)}{2}\\ &\quad \ +1-[(g+1)s-\frac{g(g+1)}{2}+1] \\ &=\ (g-x)(x-1)\\ &\ge \ 0. \end{array} \end{aligned}$$

Therefore, $\vert N_{G\!E\!X(s,t)}(V(H))\vert \ge (g+1)s-\frac{g(g+1)}{2}+1$. $\square$

Lemma 12

Suppose that H is a subgraph of $G\!E\!X(s,t)$ with $\delta (H)\ge g$ for $1\le s \le t$ and $1\le g \le s$, it shows that $\vert V(H)\vert \ge 2^g$.

Proof

We prove this lemma through the following two cases.

Case 1: V(H) is distributed in exactly one cluster.

At this time, it is easy to deduce that $\vert V(H)\vert \ge 2^g$ by Lemma 1.

Case 2: V(H) is distributed at least two different clusters.

We suppose that each $B_{\alpha }$ represents a cluster of $G\!E\!X(s,t)$ for $\alpha \in [1,2^s+2^t]$. Let $\mathcal {H}=\{H_1,H_2,\ldots , H_m\}$ with $m\ge 2$, where $H_{d}=H\cap B_{\alpha }$ for $d\in [1,m]$ and some $\alpha \in [1,2^s+2^t]$. By Definition 2, we can deduce that $\delta (H_{d})\ge g-1$. Thus, it is obvious that $\vert V(H_d)\vert \ge 2^{g-1}$ by Lemma 1. Then, we can conclude that $\vert V(H)\vert =\bigcup _{d=1}^{m}\vert V(H_d)\vert \ge 2^g$ because $m\ge 2$. Hence, this lemma holds. $\square$

Theorem 13

For $g \ge 1$ and $2^{2\,g}\le s \le t$, $t_{R_g}(G\!E\!X(s,t))\ge (2\,s-2^{2\,g}+3)2^{2\,g-2}+(s-g+1)2^{g-1}$ under the PMC model.

Proof

At first, we define the function $f(g)=(2s-2^{2g}+3)2^{2g-2}+(s-g+1)2^{g-1}$. Let $F_1$ and $F_2$ be two distinct $R_{g}$-conditional faulty sets with $\max \{\vert F_1\vert , \vert F_2\vert \}\le f(g)$. We prove this theorem by contradiction. Suppose that $F_1$ and $F_2$ are indistinguishable under the PMC model. We can deduce that $\vert V(G\!E\!X(s,t))\vert =2^{s+t+1}> 2f(g)\ge \vert F_1 \cup F_2\vert$, thus $\vert V(G\!E\!X(s,t))\setminus F_1 \cup F_2\vert \ge 1$. Since $F_1$ and $F_2$ are indistinguishable, and $F_1 \ne F_2$, $F_1 \cap F_2$ is an $R_g$-conditional faulty node cut set and $N_{G\!E\!X(s,t)}(F_1 \bigtriangleup F_2) \subseteq F_1 \cap F_2$. By Theorem 10, $\vert F_1 \cap F_2\vert \ge \kappa ^g(G\!E\!X(s,t)) = (s-g+1)2^{g}$. By Lemma 5 and Lemma 12, we have $\vert F_1 \bigtriangleup F_2\vert \ge 2^{2\,g}$.

Let Q be a component of $F_1 \bigtriangleup F_2$ with $\vert V(Q)\vert =2^{2\,g}$, and H be a subset of $\vert F_1 \cap F_2\vert$ with $\vert H\vert =(s-g+1)2^{g}$. By Lemma 11, $\vert N_{G\!E\!X(s,t)}(V(Q))\vert \ge 2^{2\,g}s- \frac{2^{2\,g}(2^{2\,g}-1)}{2} +1$. Thus, $\vert V(Q)\cup N_{G\!E\!X(s,t)}(V(Q))\vert \ge (s+1)2^{2\,g}- \frac{2^{2\,g}(2^{2\,g}-1)}{2} +1$. Since $V(Q)\cup N_{G\!E\!X(s,t)}(V(Q))\subseteq F_1 \cup F_2$ and $H\subseteq F_1 \cap F_2$, we have

$$\begin{aligned} \begin{array}{ll} \vert {F_1} \cup {F_2} \setminus H\vert &=\ \vert {F_1} \cup {F_2}\vert - \vert H\vert \\ &\ge \ \vert V(Q)\cup N_{G\!E\!X(s,t)}(V(Q))\vert - \vert H\vert \\ &\ge \ (s+1)2^{2g}- \frac{2^{2g}(2^{2g}-1)}{2} +1-(s-g+1)2^g\\ &=\ (s+1)2^{2g}- \frac{2^{2g}(2^{2g}-1)}{2}-(s-g+1)2^g +1\\ &=\ (2s-2^{2g}+3)2^{2g-1}-2^{g}(s-g+1)+1. \end{array} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{array}{ll} \max \{ \vert {F_1}\vert ,\vert {F_2}\vert \} &\ge \ \frac{{\vert {F_1} \cup {F_2}\vert + \vert {F_1} \cap {F_2}\vert }}{2}\\ &\ge \ \frac{{\vert {F_1} \cup {F_2}\vert + \vert H\vert }}{2}\\ &=\ \frac{{\vert {F_1} \cup {F_2} \setminus H\vert }}{2} + \vert H\vert \\ &\ge \ (2s-2^{2g}+3)2^{2g-2}-(s-g+1)2^{g-1}+ \frac{1}{2}+ (s-g+1)2^{g}\\ &=\ (2s-2^{2g}+3)2^{2g-2}+(s-g+1)2^{g-1}+\frac{1}{2}\\ &=\ f(g)+\frac{1}{2}\\ &>\ f(g). \end{array} \end{aligned}$$

This is a contradiction, which implies that $F_1$ and $F_2$ are distinguishable. Thus, $t_{R_g}(G\!E\!X(s,t))\ge (2\,s-2^{2\,g}+3)2^{2\,g-2}+(s-g+1)2^{g-1}$. $\square$

Theorem 14

For $4 \le s \le t$ and $1\le g \le \left\lfloor \frac{s}{3} \right\rfloor$, $t_{R_g}(G\!E\!X(s,t))\le 2^{2\,g-1}+2^{2\,g}(s+t+1-2\,g)-1$ under the PMC model.

Proof

By Definition 4, if there are two distinct and indistinguishable $R_{g}$-conditional faulty sets $F_1$ and $F_2$, where $\vert F_1\vert , \vert F_2\vert \le 2^{2\,g-1}+2^{2\,g}(s+t+1-2\,g)$, then $G\!E\!X(s,t)$ is not $R_g$-conditionally $2^{2g-1}+2^{2g}(s+t+1-2g)$-diagnosable with $t_{R_g}(G\!E\!X(s,t))\le 2^{2g-1}+2^{2g}(s+t+1-2g)-1$. As shown in Fig. 5, we have

$$\begin{aligned} \begin{array}{ll} F_1\setminus F_2 = & \{x_{s+t+1}x_{s+t}\cdots x_{s+t+1-g+1}\!\!\underbrace{0\cdots 0}_{s+t+1-2g}\!\!x_{g}\cdots x_{1}\vert x_{s+t+1}x_{s+t}\cdots x_{s+t+1-g+1} \\ & \text {have an even number of ``0''s}, x_{i}\in \{0,1\}\}, \end{array} \\ \begin{array}{ll} F_2 \setminus F_1 = & \{x_{s+t+1}x_{s+t}\cdots x_{s+t+1-g+1}\!\!\underbrace{0\cdots 0}_{s+t+1-2g}\!\!x_{g}\cdots x_{1}\vert x_{s+t+1}x_{s+t}\cdots x_{s+t+1-g+1} \\ & \text {have an odd number of ``0''s}, x_{i}\in \{0,1\}\}, \\ \\ F_1 \cap F_2 = & \{x_{s+t+1}x_{s+t}\cdots x_{s+t+1-g+1}x_{s+t+1-g}\cdots x_{g+1}\cdots x_{1}\vert x_{s+t+1-g}\cdots x_{g+1} \\ & \text {have exactly one ``1''}, x_{i}\in \{0,1\}\},\ \text {and} \end{array} \\ \begin{array}{ll} V(G\!E\!X(s,t))\setminus (F_1\cup F_2) = & \{x_{s+t+1}x_{s+t}\cdots x_{s+t+1-g+1} x_{s+t+1-g}\cdots x_{g+1}x_{g}\cdots x_{1} \\ & \vert x_{s+t+1-g}\cdots x_{g+1} \ \text {have at least two ``1''s},x_{i}\in \{0,1\}\}. \end{array} \end{aligned}$$

Fig. 5

An illustration of $F_1$ and $F_2$

Each node in $F_1 \bigtriangleup F_2$ has g neighbors in $F_1{\setminus } F_2$ and $F_2 {\setminus } F_1$, respectively. In addition, each node in $F_1 \cap F_2$ has at least $s-2g$ neighbors in $V(G\!E\!X(s,t)){\setminus } (F_1\cup F_2)$. Since $1\le g \le \left\lfloor \frac{s}{3} \right\rfloor$, we have $s-2\,g \ge g$. Each node in $V(G\!E\!X(s,t))\setminus (F_1\cup F_2)$ has at least 2g neighbors in $V(G\!E\!X(s,t))\setminus (F_1\cup F_2)$. At this time, there is no edge between $F_1 \bigtriangleup F_2$ and $V(G\!E\!X(s,t))\setminus (F_1\cup F_2)$. Hence, $F_1$ and $F_2$ are two distinct and indistinguishable $R_{g}$-conditional faulty sets.

Since $\vert F_2{\setminus } F_1\vert = \vert F_1 {\setminus } F_2\vert =2^{2\,g-1}$ and $\vert F_1 \cap F_2\vert =2^{2\,g}(s+t+1-2\,g)$, we have that $\vert F_1\vert = \vert F_1 {\setminus } F_2\vert +\vert F_1 \cap F_2\vert =2^{2\,g-1}+2^{2\,g}(s+t+1-2\,g)$ and $\vert F_2 \vert = \vert F_2 {\setminus } F_1\vert +\vert F_2 \cap F_1\vert =2^{2\,g-1}+2^{2\,g}(s+t+1-2\,g)$. Thus, $F_1$ and $F_2$ are two distinct and indistinguishable $R_{g}$-conditional faulty sets of $G\!E\!X(s,t)$, where $\vert F_1\vert \le 2^{2g-1}+2^{2g}(s+t+1-2g)$ and $\vert F_2\vert \le 2^{2g-1}+2^{2g}(s+t+1-2g)$. By Definition 4, $G\!E\!X(s,t)$ is not $R_{g}$-conditionally $2^{2g-1}+2^{2g}(s+t+1-2g)$-diagnosable. Therefore, the upper bound of $t_{R_g}(G\!E\!X(s,t))$ is $2^{2g-1}+2^{2g}(s+t+1-2g)-1$. $\square$

5 Applications to a family of famous networks

Based on Sects. 3 and 4, we obtain the $R_{g}$-conditional connectivity of $G\!E\!X(s,t)$ and determine the lower and upper bounds of $R_{g}$-conditional diagnosability of $G\!E\!X(s,t)$ under the PMC model. Applying the theorems of Sects. 3 and 4, we can directly establish the $R_{g}$-conditional connectivity and lower and upper bounds of $R_{g}$-conditional diagnosability of some generalized exchanged X-cubes, including generalized exchanged hypercubes, generalized exchanged crossed cubes, and locally generalized exchanged twisted cubes under the PMC model. In this section, we will give the applications to these networks.

5.1 The generalized exchanged hypercube

The exchanged hypercube $E\!H(s,t)$ was proposed by Loh et al. [35], which is a variant of hypercube obtained by removing some edges from a hypercube $Q_{s+t+1}$. We denote $\mathbb {I}_{n}=\{1,2,\cdots ,n\}$, where n is a given position integer. The definition of exchanged hypercubes is presented as follows.

Definition 5

(See [35]). For $s,t\ge 1$, the exchanged hypercube $E\!H(s,t)=(V, E)$ is an undirected graph with the node set $V=\{u_{s+t}\cdots u_{t+1}u_t\cdots u_1u_0\vert u_i\in \{0,1\} \ \text {for} \ i\in \{0\}\cup \mathbb {I}_{s+t}\}$, two nodes $u=u_{s+t}\cdots u_{t+1}u_{t}\cdots u_{1}u_{0}$ and $v=v_{s+t}\cdots v_{t+1}v_{t}\cdots v_{1}v_{0}$ are linked by an edge, called an r-dimensional edge, if and only if the following conditions are satisfied:

• (1) u and v differ exactly in the r-th bit for $r\in [0,s+t]$,

• (2) if $r\in \mathbb {I}_{t}$, then $u_{0}=v_{0}=1$,

• (3) if $r\in \mathbb {I}_{s+t}{\setminus } \mathbb {I}_{t}$, then $u_{0}=v_{0}=0$.

Later, Cheng et al. [23] further introduced the generalized exchange hypercube. The following is the formal definition of the generalized exchange hypercube $G\!E\!H(s,t,f)$.

Definition 6

(See [23]). For $s,t\ge 1$, $G\!E\!H(s,t,f)$ consists of two disjoint subgraphs $L^\prime$ and $R^\prime$, where $L^\prime$ contains $2^{t}$ subgraphs, denoted by the Class-0 clusters $L^\prime _i$ $(i\in [1,2^t])$ and $R^\prime$ contains $2^{s}$ subgraphs, denoted by the Class-1 clusters $R^\prime _j$ $(j\in [1,2^s])$. Class-0 and Class-1 clusters will be referred to as clusters of opposite classes of each other, same class otherwise, and collectively as clusters. In addition, $G\!E\!H(s,t,f)$ fulfills the following conditions:

• (1) for any $i\in [1,2^t]$ and $j\in [1,2^s]$, $L^\prime _i\cong Q_s$ and $R^\prime _j\cong Q_t$;

• (2) the function f is a bijection between nodes of Class-0 clusters and those of Class-1 clusters. If two nodes u and v are in the same cluster, then f(u) and f(v) belong to two different clusters, where the edge (u, f(u)) is called a cross edge.

Fig. 6

a $G\!E\!H(1,1)$; b $G\!E\!H(1,2)$

Furthermore, the bijection function f ensures the existence of perfect matching between nodes of Class-0 clusters and those in the Class-1 clusters but ignores the specifics of the perfect matching. For convenient, we simplify $G\!E\!H(s,t,f)$ as $G\!E\!H(s,t)$. According to the definition of generalized exchanged X-cubes $G\!E\!X(s,t)$ and the properties of generalized exchanged hypercube $G\!E\!H(s,t)$, we can deduce that $G\!E\!H(s,t)$ is a member of generalized exchanged X-cubes, where the X-cube is a hypercube. Figure 6 illustrates $G\!E\!H(1,1)$ and $G\!E\!H(1,2)$.

In particular, the dual-cube $D_{n}$ is a special case of the exchanged hypercube $E\!H(s,t)$ when $s=t$, that is, $E\!H(n,n)\cong D_{n}$, which was proposed by Li and Peng [36]. The dual-cube-like network $DC_{n}$ is a generalization of dual cubes and $DC_{n}\cong E\!H(n-1,n-1)$ [24]. Clearly, $DC_{n}$ is a special case of $G\!E\!H(n-1,n-1)$. Then, the following theorems hold obviously.

Theorem 15

The $R_g$-conditional connectivity of $G\!E\!H(s,t)$ and $DC_{n}$ are as follows:

(1) For any integers $3\le s\le t$ and $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$, $\kappa ^{g}(G\!E\!H(s,t))= (s-g+1)2^{g}$;

(2) For any integers $n\ge 4$ and $1\le g\le \left\lfloor \frac{n}{2} \right\rfloor$, $\kappa ^{g}(DC_{n})= (n-g)2^{g}$.

Theorem 16

The lower and upper bounds of $R_g$-conditional diagnosability of $G\!E\!H(s,t)$ under the PMC model are as follows:

(1) For any integers $g \ge 1$ and $2^{2\,g} \le s\le t$, $t_{R_g}(G\!E\!H(s,t))\ge (2\,s-2^{2\,g}+3)2^{2\,g-2}+(s-g+1)2^{g-1}$;

(2) For any integers $4\le s \le t$ and $1\le g \le \left\lfloor \frac{s}{3} \right\rfloor$, $t_{{R}_g}(G\!E\!H(s,t))\le 2^{2g-1}+2^{2g}(s+t+1-2g)-1$.

Theorem 17

The lower and upper bounds of $R_g$-conditional diagnosability of $DC_n$ under the PMC model are as follows:

(1) For any integers $g \ge 1$ and $2^{2\,g} \le n-1$, $t_{R_g}(DC_n)\ge (2n-2^{2g}+1)2^{2g-2}+(n-g)2^{g-1}$;

(2) For any integers $n \ge 5$ and $1\le g \le \left\lfloor \frac{n-1}{3} \right\rfloor$, $t_{R_g}(DC_n)\le 2^{2\,g-1}+2^{2\,g}(2n-2\,g+1)-1$.

5.2 The generalized exchanged crossed cube

Li et al. [37] proposed the exchanged crossed cube $E\!C\!Q(s,t)$, which is obtained by removing edges from a crossed cube $C\!Q_{s+t+1}$. In what follows, we review the definition of exchanged crossed cubes.

Definition 7

(See [37]). The (s, t)-dimensional exchanged crossed cube is defined as a graph $E\!C\!Q(s,t)\!=\!G(V, E)$ with $s,t\ge 1$, where the node set $V=\{a_{s-1}\cdots a_{0}$ $b_{t-1}\cdots b_{0}c\vert a_{i},b_{j},c\in \{0,1\}, i\in [0,s-1], j\in [0,t-1]\}$ and the edge set $E=\{(u,v)\vert (u,v)\in V\times V\}$. Especially, E is composed of three disjoint sets $E_{1}$, $E_{2}$, and $E_{3}$, as shown below:

• (1) $E_{1}: u[0]\ne v[0], u\oplus v=1$, where $\oplus$ is the exclusive-OR operator;

• (2) $E_{2}: u[0]=v[0]=1, u[s+t:t+1]=v[s+t:t+1]$, where $\lambda [x:y]$ denotes the bit pattern of the node $\lambda$ between dimensions y and x inclusive. Thus, u[t : 1] is denoted by $b=b_{t-1}\cdots b_{0}$ and v[t : 1] is denoted by $b^\prime =b^\prime _{t-1}\cdots b^\prime _{0}$, where u and v are adjacent by the following rule: for any $t\ge 1$, if and only if there is an $\ell$ $(1\le \ell \le t)$ such that $b_{t-1}\cdots b_{\ell }=b^\prime _{t-1}\cdots b^\prime _{\ell }$ and $b_{\ell -1}\ne b^\prime _{\ell -1}, b_{\ell -2}=b^\prime _{\ell -2}$ if $\ell$ is even, as well as $b_{2i+1}b_{2i}\sim b^\prime _{2i+1}b^\prime _{2i}$ with $0\le i< \lfloor (\ell -1)/2\rfloor$;

• (3) $E_{3}: u[0]=v[0]=0, u[t:1]=v[t:1]$, and $u[s+t:t+1]$ and $v[s+t:t+1]$ are denoted by $a=a_{s-1}\cdots a_{0}$ and $a^\prime =a^\prime _{t-1}\cdots a^\prime _{0}$, respectively. Then, u and v are adjacent by the following rule: for all $s\ge 1$, if and only if there exits an $\ell$ $(1\le \ell \le s)$ such that $a_{s-1}\cdots a_{\ell }=a^\prime _{s-1}\cdots a^\prime _{\ell }$ and $a_{\ell -1}\ne a^\prime _{\ell -1}, a_{\ell -2}=a^\prime _{\ell -2}$ if $\ell$ is even, as well as $a_{2i+1}a_{2i}\sim a^\prime _{2i+1}a^\prime _{2i}$ for $0\le i< \lfloor (\ell -1)/2\rfloor$.

Fig. 7

An exchanged crossed cube $G\!E\!C\!Q(1,3)$

The generalized exchanged crossed cube, denoted as $G\!E\!C\!Q(s,t,f)$ with $s,t\ge 1$, comprises two distinct classes of crossed cubes, known as the Class-0 clusters and the Class-1 clusters, respectively. The former contains $2^{t}$ $C\!Q_{s}$’s and the latter encompasses $2^{s}$ $C\!Q_{t}$’s. Class-0 clusters and Class-1 clusters are referred to as clusters of opposite classes of each other. The function f establishes a bijective relationship between the nodes of Class-0 clusters and Class-1 clusters. This bijection ensures that for any two nodes u and v within the same cluster, their corresponding values f(u) and f(v) reside in distinct clusters, with the edge (u, f(u)) (resp. (v, f(v))) representing a cross edge. The purpose of the bijection f is to ensure the existence of perfect matching between two nodes in different clusters, although the specific arrangement of this matching is not specified.

For the sake of convenience, the notation $G\!E\!C\!Q(s,t,f)$ is often abbreviated as $G\!E\!C\!Q(s,t)$. Based on the definition of generalized exchanged X-cubes and the properties of generalized exchanged crossed cube, it can be inferred that the generalized exchanged crossed cube $G\!E\!C\!Q(s,t)$ belongs to the family of generalized exchanged X-cubes, where the X-cube specifically represents a crossed cube (see $G\!E\!C\!Q(1,3)$ in Fig. 7). Then, the following theorems hold obviously.

Theorem 18

For any integers $s\ge 3$ and $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$, $\kappa ^{g}(G\!E\!C\!Q(s,t))= (s-g+1)2^{g}$.

Theorem 19

The lower and upper bounds of $R_g$-conditional diagnosability of $G\!E\!C\!Q(s,t)$ under the PMC model are as follows:

(1) For any integers $g \ge 1$ and $2^{2\,g} \le s\le t$, $t_{R_g}(G\!E\!C\!Q(s,t))\ge (2\,s-2^{2\,g}+3)2^{2\,g-2}+(s-g+1)2^{g-1}$;

(2) For any integers $4\le s \le t$ and $1\le g \le \left\lfloor \frac{s}{3} \right\rfloor$, $t_{R_g}(G\!E\!C\!Q(s,t))\le 2^{2\,g-1}+2^{2\,g}(s+t+1-2\,g)-1$.

5.3 The locally generalized exchanged twisted cube

The locally exchanged twisted cube $L\!ET\!Q(s,t)$ was proposed by Chang et al. [25], which is obtained by removing edges from a locally twisted cube $LT\!Q_{s+t+1}$. The definition of the locally exchanged twisted cube is introduced as follows.

Definition 8

(See [25]). The (s, t)-dimensional locally exchanged twisted cube $L\!ET\!Q(s,t)=(V, E)$ with $s,t\ge 1$, where the node set $V=\{x_{t+s}\cdots x_{t+1}x_{t}\cdots x_{1}$ $x_{0}\vert x_{i}\in \{0,1\}, i\in [0,s+t]\}$ and E is the edge set consisting of the following three types of disjoint sets $E_{1}$, $E_{2}$, and $E_{3}$.

• (1) $E_{1}=\{(x,y)\in V\times V: x\oplus y=2^{0}\}$,

• (2) $E_{2}=\{(x,y)\in V\times V: x_{0}=y_{0}=1, x_{1}=y_{1}=0$ and $x\oplus y =2^{k}$ for $k\in [3, t]\}\cup \{(x,y)\in V\times V:x_{0}=y_{0}=x_{1}=y_{1}=1$ and $x\oplus y=2^{k}+2^{k-1}$ for $k\in [3, t]\}\cup \{(x,y)\in V\times V: x_{0}=y_{0}=1$ and $x\oplus y\in \{2^{1},2^{2}\}\}$,

• (3) $E_{3}=\{(x,y)\in V\times V: x_{0}=y_{0}=x_{t+1}=y_{t+1}=0$ and $x\oplus y=2^{k}$ for $k\in [t+3, t+s]\}\cup \{(x,y)\in V\times V: x_{0}=y_{0}=0, x_{t+1}=y_{t+1}=1$ and $x\oplus y=2^{k}+2^{k-1}$ for $k\in [t+3, t+s]\}\cup \{(x,y)\in V\times V: x_{0}=y_{0}=0$ and $x\oplus y\in \{2^{t+1}, 2^{t+2}\}\}$.

Let $s,t\ge 1$, there are two classes of locally twisted cubes in the locally generalized exchanged twisted cube $L\!G\!ET\!Q(s,t,f)$: one class, referred to as the Class-0 clusters, contains $2^{t}$ $LT\!Q_{s}$’s; and the other, referred to as the Class-1 clusters, contains $2^{s}$ $LT\!Q_{t}$’s. They will be referred to as clusters of opposite classes of each other, same class otherwise. There exists a bijection function f between nodes of Class-0 clusters and those of Class-1 clusters. For two nodes u, v in the same cluster, f(u) and f(v) belong to two different ones, and the edge (u, f(u)) is a cross edge. The bijection f ensures the existence of perfect matching between nodes of Class-0 clusters and those in the Class-1 clusters, but the specifics of the perfect matching can be ignored. For convenient, $G\!E\!H(s,t,f)$ is denoted by $G\!E\!H(s,t)$. According to the definition of generalized exchanged X-cubes and the properties of locally generalized exchanged twisted cube, we can deduce that the locally generalized exchanged twisted cube $L\!G\!ET\!Q(s,t)$ is a member of generalized exchanged X-cubes, where the X-cube is a locally twisted cube (see $L\!G\!ET\!Q(1,3)$ in Fig. 8). Then, the following theorems hold obviously.

Fig. 8

A locally exchanged twisted cube $L\!G\!ET\!Q(1,3)$

Theorem 20

For any integers $s\ge 3$ and $1\le g\le \left\lfloor \frac{s}{2} \right\rfloor$, $\kappa ^{g}(L\!G\!ET\!Q(s,t))=(s-g+1)2^{g}.$

Theorem 21

The lower and upper bounds of $R_g$-conditional diagnosability of $L\!G\!ET\!Q(s,t)$ under the PMC model are as follows:

(1) For any integers $g \ge 1$ and $2^{2\,g} \le s\le t$, $t_{R_g}(L\!G\!ET\!Q(s,t))\ge (2s-2^{2g}+3)2^{2g-2}+(s-g+1)2^{g-1}$;

(2) For any integers $4\le s \le t$ and $1\le g \le \left\lfloor \frac{s}{3} \right\rfloor$, $t_{R_g}(L\!G\!ET\!Q(s,t))\le 2^{2g-1}+2^{2g}(s+t+1-2g)-1$.

6 Comparison results

In this section, we will demonstrate the superiority of our method by providing some comparative analysis with existing results. First, we focus on conducting comparisons and analyses pertaining to connectivity in Sect. 6.1. Following this, our emphasis will transition to conducting diagnosability analyses under the PMC and MM* models in Sect. 6.2.

6.1 Connectivity

In the following, we compare our results to the traditional connectivity, g-good-neighbor conditional connectivity, component connectivity, extra connectivity, and cyclic connectivity. We provide the definitions of these indicators as follows.

• The traditional connectivity of a graph G, denoted by $\kappa (G)$, is defined as the cardinality of a minimum node set F whose removal results in a disconnected or trivial graph.

• A node set F of a graph G is a g-good-neighbor node cut if and only if $G-F$ is disconnected and each remaining component has minimum degree at least g. The g-good-neighbor conditional connectivity of G, denoted by $\hat{\kappa }_g(G)$, is defined as the cardinality of a minimum g-good-neighbor node cut of G. Clearly, $\hat{\kappa }_0 (G)=\kappa (G)$.

• A node set F of a graph G is a g-component node cut if and only if $G-F$ is disconnected and has at least g components. The g-component connectivity of G, denoted by $\bar{\kappa }_{g}(G)$, is defined as the cardinality of a minimum g-component node cut of G. Clearly, $\bar{\kappa }_2 (G)=\kappa (G)$.

• A node set F of a graph G is a g-extra node cut if and only if $G-F$ is disconnected and every component of $G-F$ has at least g nodes. The g-extra connectivity of G, denoted by $\tilde{\kappa }_g (G)$, is defined as the cardinality of a minimum g-extra node cut of G. Obviously, $\tilde{\kappa }_1 (G)=\kappa (G)$.

• A node set F of a graph G is a cyclic node cut if and only if $G-F$ is disconnected and at least two components in $G-F$ contain a cycle. The cyclic connectivity of G, denoted by $\kappa ^\prime (G)$, is defined as the cardinality of a minimum cyclic node cut of G.

Fig. 9

The comparisons among traditional connectivity, g-good-neighbor conditional connectivity and $R_g$-conditional connectivity in $G\!E\!X(s,t)$

From Theorem 10, we have that the $R_g$-conditional connectivity of $G\!E\!X(s,t)$ is $\kappa ^g=(s-g+1)2^g$. It is clear that $\kappa (G\!E\!X(s,t))=s+1$ and $\hat{\kappa }_g(G\!E\!X(s,t))=(s-g+1)2^g$ [22]. As shown in Fig. 9, we can observe that the traditional connectivity significantly lags behind both $R_g$-conditional connectivity and g-good-neighbor conditional connectivity. Notably, the fault tolerance values for $R_g$-conditional connectivity and g-good-neighbor conditional connectivity remain identical. This uniformity stems from the sole distinction between the two being the constraints imposed on the faulty processor, a factor that does not impact the determination of connectivity.

As a subclass of $G\!E\!X(s,t)$, the generalized exchanged hypercube $G\!E\!H(s,t)$ has been the subject of extensive research, with Table 2 presenting a detailed compilation of the current results on the connectivity of $G\!E\!H(s,t)$.

Table 2 A brief summary of known results related to connectivity for $G\!E\!H(s,t)$

Fig. 10

The comparisons among $R_g$-conditional connectivity, g-component connectivity, g-extra connectivity and cyclic connectivity in $G\!E\!H(s,t)$

For $G\!E\!H(s,t)$, we compare our method with g-component connectivity, g-extra connectivity, and cyclic connectivity in Fig. 10. It is evident that each of these connectivity is monotonically increasing on s. Moreover, with a fixed value of s, the $R_g$-conditional connectivity asserts its dominance, exhibiting a significantly higher level than the other three connectivity. Figure 10b further illustrates that the parameter g exerts a more substantial influence on the $R_g$-conditional connectivity, in contrast to its negligible impact on the cyclic connectivity.

6.2 Diagnosability

In this subsection, we compare our results to the traditional diagnosability, g-good-neighbor conditional diagnosability, component diagnosability, and extra diagnosability under the PMC model or MM* model. Then, the definitions and results of these indicators are listed as follows.

• The traditional diagnosability of a graph G, denoted by t(G), is the maximum number of faulty processors that can be accurately identified.

• The g-good-neighbor conditional diagnosability of a graph G, denoted by $\hat{t}_g(G)$, is the maximum number of faulty processors that can be identified under the condition that every fault-free processor has at least g fault-free neighbors. In particular, $\hat{t}_0(G)=t(G)$.

• The g-component diagnosability of a graph G, denoted by $\bar{t}_g(G)$, is the maximum number of faulty processors that can be identified under the condition that the number of components in $G-F$ is at least g. Clearly, $\bar{t}_2 (G)=t(G)$.

• The g-extra diagnosability of a graph G, denoted by $\tilde{t}_g(G)$, is the maximum number of faulty processors that can be identified under the condition that each component in $G-F$ has at least g nodes. Obviously, $\tilde{t}_1 (G)=t(G)$.

Table 3 A brief summary of known results related to diagnosability for $G\!E\!X(s,t)$ and $G\!E\!H(s,t)$

By Lemma 4, the g-good-neighbor conditional diagnosability of $G\!E\!X(s,t)$ is $\hat{t}_g(G\!E\!X(s,t))=(s-g+2)2^g-1$ under the PMC model with $s\ge 3$ and $1 \le g \le s-2$ (resp. under the MM* model with $s\ge 4$ and $1\le g\le s-2$). Thus, we can deduce that $t(G\!E\!X(s,t))=s+1$ under the PMC model and MM* model. Furthermore, the lower (resp. upper) bound of $R_{g}$-conditional diagnosability of $G\!E\!X(s,t)$ is $(2s-2^{2g}+3)2^{2g-2}+(s-g+1)2^{g-1}$ (resp. $2^{2g-1}+2^{2g}(s+t+1-2g)-1$). It is evident that the upper bound of $R_{g}$-conditional diagnosability of $G\!E\!X(s,t)$ is larger than its lower bound by $(2s+4t+4-8g+2^{2g-1})2^{2g-2}+(s-g+1)2^{g-1}-1$ through calculation. Therefore, we compare the lower bound of $R_{g}$-conditional diagnosability of $G\!E\!X(s,t)$ with these other diagnosabilities. In Table 3, we show some outcomes based on these indicators and our methods for $G\!E\!X(s,t)$ and $G\!E\!H(s,t)$. We can observe that the traditional diagnosability (or g-good-neighbor conditional diagnosability) remains consistent, whether under the PMC model or the MM* model.

As shown in Fig. 11a, we can observe that each diagnosability of these increases with the value of s when g is fixed. This is not difficult to understand because when s increases, the size of $G\!E\!X(s,t)$ increases as well. Obviously, the $R_{g}$-conditional diagnosability of $G\!E\!X(s,t)$ is greater than its g-good-neighbor conditional diagnosability and traditional diagnosability under the PMC model. At the same time, Fig. 11b shows that if s is the same, as g increases, the value of the traditional diagnosability remains unchanged, but the rate of increase of the $R_{g}$-conditional diagnosability of $G\!E\!X(s,t)$ is much higher than that g-good-neighbor conditional diagnosability of $G\!E\!X(s,t)$ under the PMC model. Thus, $R_{g}$-conditional diagnosability can better improve the reliability of the interconnection network.

Fig. 11

The comparisons among traditional diagnosability, g-good-neighbor diagnosability and $R_g$-conditional diagnosability in $G\!E\!X(s,t)$ under the PMC model

Meanwhile, we delve into diagnosability results for $G\!E\!H(s,t)$ under the PMC model and MM* model, as detailed in Table 3. It is evident that for $G\!E\!H(s,t)$, g-component diagnosability ( resp. g-extra diagnosability) remains identical whether under the PMC model or the MM* model. Additionally, Fig. 12 reveals that, under the PMC model, the disparities between the values of g-component diagnosability and g-extra diagnosability are minimal. However, the reliability of $G\!E\!H(s,t)$ under the $R_g$ constraint consistently surpasses g-component diagnosability and g-extra diagnosability. Interestingly, when $s=6$, the $R_g$-conditional diagnosability is lower than the corresponding g-component diagnosability and g-extra diagnosability, highlighting the efficacy of $R_g$-conditional diagnosability in large-scale networks.

Fig. 12

The comparisons among $R_g$-conditional diagnosability, g-component diagnosability and g-extra diagnosability in $G\!E\!H(s,t)$ under the PMC model

7 Conclusion

The concepts of $R_{g}$-conditional connectivity and diagnosability hold immense importance in enhancing the reliability of multiprocessor systems. These properties help ensure seamless communication and connectivity within the system, minimizing potential failures and enhancing performance. Generalized exchanged X-cube is a promising solution for improving the performance of multiprocessor systems. These structures not only leverage the benefits of traditional X-cubes but also offer a reduction in interconnection complexity. This reduction allows for simpler and more efficient communication between nodes, thereby increasing the overall speed and reliability of the system.

In this paper, we first determine the $R_g$-conditional connectivity of generalized exchanged X-cubes. Further, we study the lower and upper bounds of $R_{g}$-conditional diagnosability of generalized exchanged X-cubes under the PMC model. As applications, the lower and upper bounds of $R_{g}$-conditional diagnosability of generalized exchanged hypercubes, generalized exchanged crossed cubes, and locally exchanged twisted cubes are established directly under the PMC model. The research results indicate that compared to the other existing results in terms of connectivity or diagnosability, $G\!E\!X(s,t)$ has showcased remarkable reliability under the $R_g$-conditional restriction. This significantly advances the exploration of network reliability, such as generalized exchanged hypercubes, generalized exchanged crossed cubes, and locally generalized exchanged twisted cubes.

Finally, we conclude this paper by proposing some directions worth exploring in future research:

• 1. We will attempt to study the $R_g$-conditional diagnosability of $G\!E\!X(s,t)$ under the MM* model.

• 2. We may extend the $R_g$-conditional restriction to edge faults, and study $R_g$-conditional edge connectivity/diagnosability.

• 3. We will try to apply $R_g$-conditional connectivity/diagnosability to real-world systems (e.g., data center networks and autonomous robots systems [41]) such that the systems can tolerate a range of node failures to keep operation effective.