1 Introduction

An interconnection network is a network composed of switching elements in a certain topology and control mode to achieve interconnection between multiple processors or functional components within a computer system. As the brain of interconnection networks, data centers have developed vigorously in recent years. With the increase in the number of processors in the interconnection networks, there will exist several almost inevitable errors that may result in communication interruption between some processors in the interconnection networks, and then lead to the communication delay of the whole network or even network paralysis. As a faulty processor will lose communication with other processors, these faulty links that disconnect the interconnection network are modeled as an edge-cut in the corresponding graph. Given a connected graph G, an edge subset \(F\subset E(G)\) is called an edge-cut of G if its deletion disconnects G. We call the numbers of vertices and edges in G as the order and size of G, respectively. The classical Menger’s edge-connectivity is the minimum cardinality of all edge-cuts of G, denoted as \(\lambda (G)\) [17]. In other words, edge-connectivity is the minimum number of faulty links that disconnect the network.

In a specific interconnection network, the processors and links that do not fail are called fault-free vertices and fault-free edges of the corresponding graph, respectively, which are collectively referred to as the fault-free set. Due to the different demands of fault-free sets in distinct connected graph G such as the number of components and the order of each component, we need to evaluate the reliability and fault tolerance of large-scale parallel and distributed systems using multiple parameters. Since the classical edge-connectivity does not exert any restriction on its surviving components, Harary proposed conditional edge-connectivity as a generalization of the classical edge-connectivity in 1983, denoted as \(\lambda (G,\mathcal {P} )\), where \(\mathcal {P}\) is the given properties of fault-free set in graph G [12]. There are two typical examples of conditional edge-connectivity, one is h-extra edge-connectivity and the other is r-component edge-connectivity. An edge subset of G, if any, is called an h-extra edge-cut if its deletion disconnects G, and each remaining component has at least h vertices. In 1996, Fàbrega and Fiol introduced h-extra edge-connectivity of the connected graph G which denoted as \(\lambda _h(G)\), is the minimum cardinality of any h-extra edge-cut of G [8]. Another well-known conditional edge-connectivity was introduced by Sampathkumar [19] in 1984 called r-component edge-connectivity. For a given positive integer r, an r-component edge-cut of a connected graph G, if any, is defined as an edge subset F of graph G, whose deletion yields a disconnected graph with at least r components. The r-component edge-connectivity of a connected graph G, denoted by \(c\lambda _r(G)\), is the minimum cardinality taken over all r-component edge-cuts of G. Some researches have obtained the r-component edge-connectivity of many special graphs with small r [4, 5]. In addition, let F be a minimum r-component edge-cut of connected graph G, then the extremal structure of \(G-F\) is usually composed of \(r-1\) isolated vertices and a giant component [11]. For some other researches on a variety of networks about conditional edge-connectivity, see [3, 7, 9, 10, 20, 21, 25, 27,28,29,30].

For an interconnection network with some faulty edges, in order to restrict the number of connected components and ensure the scale of normal working processors in each component, more recently, Li et al. [15] gave the definition of h-extra r-component connectivity by combining h-extra connectivity and r-component connectivity in 2021. In details, the h-extra r-component connectivity of connected graph G is the minimum cardinality of any vertex subset of G, whose removal disconnects G and then results in at least r components, and each component contains at least h vertices, denoted as \(c\kappa _{r}^{h} (G)\) [15]. In addition, they determined the h-extra r-component connectivity of n-dimensional hypercube \(Q_n\) that \(c\kappa _{r}^{2}(Q_n)=2(r-1)(n-r+1)\) for \(r\in \{ 2,3,4 \}\).

Motivated by the ideas of Fàbrega and Sampathkumar, as a generalization of [15], we consider the edge version of h-extra r-component connectivity to characterize the fault tolerance of interconnection networks and give the definition of h-extra r-component edge-connectivity as follows:

Definition 1

Given a connected graph \(G =(V,E)\), for two integers \(h\ge 1\) and \(r\ge 2\), a subset \(F\subset E\) is called an h-extra r-component edge-cut of G, if any, if there are at least r components in \(G-F\), and each component has at least h vertices. The h-extra r-component edge-connectivity of G, denoted as \(c\lambda _{r}^{h}(G)\), is the minimum cardinality of any h-extra r-component edge-cut of G.

Lemma 1

If F is a minimum h-extra r-component edge-cut of G, then \(G-F\) has exactly r components.

Proof

Suppose to the contrary that \(G-F\) has exactly p components as \(G_{1},G_{2},\dots ,G_{p}\) with \(p>r\) and \(|V(G_i)|\ge h\), \(1\le i\le p\). Since G is connected, then there exists an edge xy that \(x\in V(G_i)\) and \(y\in V(G_j)\) for some \(i,j\in \left\{ 1,2,\dots ,p \right\}\) and \(i\ne j\). Let \(F_1=F{\setminus }\{xy\}\). Note that \(G[V(G_i)\cup V(G_j)]\) is connected with at least \(2h>h\) vertices, then \(G-F_1\) has \(p-1\ge r\) components, and each component has at least h vertices. In other words, \(F_1\) is an h-extra r-component edge-cut of G with \(|F_1|<|F|\), which contradicts the minimality of F. Hence, \(G-F\) has exactly r components. \(\square\)

For the given connected graph G, let \(V_1,V_2,\ldots ,V_t\) be a partition of V(G). That is, \(V_i\subset V(G)\) for \(1\le i\le t\), \(\cup _{k=1}^tV_k=V(G)\), and \(V_i\cap V_j=\emptyset\) for \(1\le i<j\le t\). Let \([V_i,V_j]\) be the edges with one end-vertex in \(V_i\) and the other in \(V_j\) and \([V_1,V_2,\ldots ,V_k]=\cup _{1\le i<j\le k}[V_i,V_j]\). Define the function \(\xi _m(G)\) be the minimum cardinality of any edge-cut F of G such that \(G-F\) has one component with exactly m vertices [23, 24]. In other words, \(\xi _m(G)=\min \{|[V_0,\overline{V_0}]|:V_0\subset V(G),G[V_0]\) is connected, \(|V_0|=m \}\). In addition, we say that G is \(\lambda _h\)-optimal if \(\lambda _h(G)=\xi _h(G)\). As a generalization of \(\xi _m(G)\) denotes the minimum cardinality of any edge-cut F of connected graph G such that \(G-F\) has exactly \(r+1\) components with r components which have exactly m vertices as \(\xi _{m,r+1}(G)\). Let \(V_1,V_2,\ldots ,V_{r+1}\) be a partition of V(G). In detail, \(\xi _{m,r+1}(G)=\min \{|[V_1,V_2,\ldots ,V_{r+1}]|:|V_i|=m\le \lfloor |V(G)|/(r+1)\rfloor\) for \(1\le i\le r\), each \(G[V_j]\) is connected for \(1\le j\le r+1 \}\). Therefore, \(\lambda _h (G)=\min \{\xi _{m,2}(G):h\le m\le \lfloor |V(G)|/2 \rfloor \}\) by the definition of \(\lambda _h(G)\). Furthermore, if \(c\lambda _r^h(G)=\xi _{h,r}(G)\), we say that G is \(c\lambda _r^h\)-optimal; otherwise, G is not \(c\lambda _r^h\)-optimal. Motivated by the idea of introducing \(\xi _{m,2}(G)\) to solve \(\lambda _h(G)\), \(\xi _{m,r}(G)\) can be used to solve \(c\lambda _r^h(G)\), and whether G is \(c\lambda ^h_r\)-optimal or not similarly.

From the definition, it can be immediately obtained that the 1-extra 2-component edge-connectivity of G equals to the edge-connectivity of G as \(c\lambda _2^1(G)=\lambda (G)\), the 1-extra r-component edge-connectivity of G equals to the r-component edge-connectivity of G as \(c\lambda _r^1(G)=c\lambda _r(G)\), and the h-extra 2-component edge-connectivity of G equals to the h-extra edge-connectivity of G as \(c\lambda _2^h(G)=\lambda _h(G)\). In addition, let m be a positive integer, and \(ex_m(G)=\text {max}\{d(G[X]):X\subset V(G),~|X|=m\}\) be the maximum sum of the degrees of the subgraph induced by a vertex set with the given cardinality m in G, i.e., \(ex_m(G)/2\) is the maximum possible sizes of the subgraph induced by m vertices in G. If G is d-regular, then \(\xi _{m,2}(G)=dm-ex_m(G)\).

As an enhancement on hypercube, the augmented cube, introduced by Choudum and Sunitha in 2002 [6], not only reserves several of the advantages of the hypercube such as strong connectivity, small diameter, symmetry, recursive construction, relatively small degree, and regularity [1, 14], but also carries some embedding properties that the hypercube does not have [13, 18]. Due to its excellent topological properties, the augmented cube is often used for the underlying topological structure of parallel and distributed systems [26].

Definition 2

([6]) Let \(n \ge 1\) be an integer. The n-dimensional augmented cube, denoted by \(\text {AQ}_{n}\), is a vertex transitive and \((2n-1)\)-regular graph with \(2^{n}\) vertices, each labeled by an n-bit binary string \(x_{n} x_{n-1} \cdots x_2x_{1}\) where \(x_i\in \{0,1\},1\le i\le n\). Write \(V(\text {AQ}_n)\) as \(X_nX_{n-1}\cdots X_2X_1=\{x_{n}x_{n-1} \cdots x_2x_{1}:x_i\in \{0,1\},1\le i\le n\}\). Define \(\text {AQ}_{1}\) be the complete graph \(K_{2}\) with two vertices labeled by 0 and 1, respectively. As for \(n \ge 2\), \(\text {AQ}_n\) has recursive structure. That is, \(\text {AQ}_{n}\) consists of two copies of \((n-1)\)-dimensional augmented cubes, denoted by \(0\text {AQ}_{n-1}\) and \(1\text {AQ}_{n-1}\) that \(V(0\text {AQ}_{n-1})=0X_{n-1}\cdots X_2X_1\) and \(V\left( 1\text {AQ}_{n-1}\right) =1X_{n-1}\cdots X_2X_1\), and adding \(2^{n}\) edges (two perfect matchings of \(\text {AQ}_{n})\) between \(0\text {AQ}_{n-1}\) and \(1\text {AQ}_{n-1}\). The vertex \(a=0a_{n-1}\cdots a_2a_{1}\in V(0\text {AQ}_{n-1})\) is joined to the vertex \(b=1b_{n-1}\cdots b_2b_{1}\in V(1\text {AQ}_{n-1})\) if and only if,

  1. (i)

    \(a_{i}=b_{i}\) for \(1 \le i \le n-1\); or

  2. (ii)

    \(a_{i}=1-b_i\) for \(1 \le i \le n-1\).

From the definition, each vertex in \(V(0\text {AQ}_{n-1})\) has two neighbors in \(V(1\text {AQ}_{n-1})\) and vice versa. Hence, \(\text {AQ}_n\) can be written as \(0\text {AQ}_{n-1} \oplus 1\text {AQ}_{n-1}\) and \(E(\text {AQ}_n)\) can be partitioned into three disjoint edge subsets of \(\text {AQ}_n\) for \(n\ge 2\). Let \(u=u_nu_{n-1}\cdots u_2u_1\) and \(v=v_nv_{n-1}\cdots v_2v_1\) be any two adjacent vertices in \(\text {AQ}_n\). If \(uv\in E(0\text {AQ}_{n-1})\) or \(uv\in E(1\text {AQ}_{n-1})\), then uv is called an original edge (O-edge for short). Otherwise, uv is called a hypercube edge (H-edge for short) or a complement edge (C-edge for short) if uv satisfies the case (i) or the case (ii) in Definition 2, respectively. In detail, uv is an O-edge in \(\text {AQ}_n\) if and only if there exists an integer k with \(1\le k<n\) such that,

(i):

\(u_i=v_i\) for \(k+1\le i \le n\) and \(u_j=1-v_j\) for \(1\le j\le k\); or

(ii):

\(u_i=v_i\) for \(i\ne k\) and \(u_k=1-v_k\).

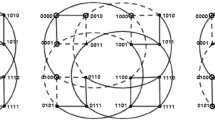
In other case, uv is an H-edge in \(\text {AQ}_n\) if and only if \(u_n=1-v_n\) and \(u_i=v_i\) for \(1\le i\le n-1\). Furthermore, uv is a C-edge in \(\text {AQ}_n\) if and only if \(u_i=1-v_i\) for \(1\le i\le n\). The n-dimensional augmented cubes for \(n=1,2,3\) are illustrated in Fig. 1. In addition, for \(n=2,3\), the O-edges, H-edges, and C-edges in \(\text {AQ}_n\) are marked in black, blue (dark gray in print), and red (light gray in print), respectively.

Fig. 1
figure 1

Illustration of \(\text {AQ}_n\)

Full size image

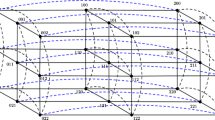
Let \(X^n\) and \(x^n\) denote \(X_nX_{n-1}\cdots X_2X_1\) and \(x_nx_{n-1}\cdots x_2x_1\), respectively. Denote the vertex set \(\{z_nz_{n-1}\cdots z_{k+1}x_kx_{k-1}\cdots x_1: x_i\in \{0,1\},1\le i\le k,z_j\) is fixed, \(k+1\le j\le n\}\) as \(z_nz_{n-1}\cdots z_{k+1}X^k\). It is obvious that \(\text {AQ}_n[z_nz_{n-1}\cdots z_{k+1}X^k]\) is a k-dimensional augmented subcube in \(\text {AQ}_n\). By this way, \(0\text {AQ}_{n-1}=\text {AQ}_n[0X^{n-1}]\) and \(1\text {AQ}_{n-1}=\text {AQ}_n[1X^{n-1}]\). We use \(z_nz_{n-1}\cdots z_{k+1}X^k\) to represent \(\text {AQ}_n[z_nz_{n-1}\cdots z_{k+1}X^k]\), if no confusion arises (Fig. 2).

Fig. 2
figure 2

\(\text {AQ}_4[0X^3]=0\text {AQ}_3\) and \(\text {AQ}_4[1X^3]=1\text {AQ}_3\)

Full size image

Let m and \(S_m\) be a positive integer with \(m\le 2^n\) and the set \(\{0,1,2,\ldots ,m-1\}\), respectively. Denote the corresponding set of \(S_m\) that is represented by n-binary strings as \(L_m^n\). Let \(m=\sum _{i=0}^{s} 2^{t_{i}}\) be the decomposition of m where \(t_{0}=\lfloor \log _{2} m\rfloor , t_{i}=\lfloor \log _{2}(m-\sum _{k=0}^{i-1} 2^{t_{k}})\rfloor\) for \(i\ge 1\). In 2014, Chien et al. showed that \(e x_{m}\left( \text {AQ}_{n}\right) =\sum _{i=0}^{s}(2 t_{i}-1) 2^{t_{i}}+\sum _{i=0}^{s} 4i \cdot 2^{t_{i}}\) [2], but this result is not true for m is odd. In 2021, Zhang et al. fixed it and obtained the value of \(ex_{m}(\text {AQ}_n)\) that \(e x_{m}\left( \text {AQ}_{n}\right) =\sum _{i=0}^{s}\left( 2 t_{i}-1\right) 2^{t_{i}}+\sum _{i=0}^{s} 4i \cdot 2^{t_{i}}+\delta\) where if m is even, then \(\delta =0\); if m is odd, then \(\delta =1\) [26]. It is noteworthy that they gave a lower bound of \(ex_{m}(\text {AQ}_{n})\) by showing that the vertex subset \(L_m^n\) in \(V(\text {AQ}_n)\) satisfies \(|L_m^n|=m\) and \(|E(\text {AQ}_n[L_m^n])|=\frac{1}{2}(\sum _{i=0}^{s}\left( 2 t_{i}-1\right) 2^{t_{i}}+\sum _{i=0}^{s} 4i \cdot 2^{t_{i}}+\delta )\).

For the given \(m={\textstyle \sum _{i=0}^{s}} 2^{t_i}\), take \(s+1\) \(t_i\)-dimensional augmented subcubes in an n-dimensional augmented cube for \(i=0,1,\dots ,s\) as follows:

\(A_m^{0}: 0 \ldots 0 \underbrace{X_{t_{0}} \ldots X_{1}}_{t_{0}}\)

(\(t_{0}\)-dimensional augmented cube)

\(A_m^{1}: 0 \ldots 01 \underbrace{0 \ldots 0 \underbrace{X_{t_{1}} \ldots X_{1}}_{t_{1}}}_{t_{0}}\)

(take a \(t_1\)-dimensional augmented cube from \(0\dots 01X_{t_0}\dots X_1\))

\(A_m^{2}: 0\dots 010\dots 01\underbrace{0\dots 0\underbrace{X_{t_2}\dots X_1}_{t_2}}_{t_1}\)

(take a \(t_2\)-dimensional augmented cube from \(0\dots 010\dots 01X_{t_1}\dots X_1\))

\(\dots\)

\(A_m^{s}: 0\dots 010\dots \dots 01\underbrace{0\dots 0\underbrace{X_{t_s}\dots X_1}_{t_s}}_{t_{s-1}}\)

(take a \(t_s\)-dimensional augmented cube from \(0\dots 010\dots \dots 01X_{t_{s-1}}\dots X_1\))

Note that \(L^n_m=V(A_m^{0}) \cup \cdots \cup V(A_m^{s})\) and \(A_m^0\) is fixed, \(A_m^i\) is taken from a \(t_{i-1}\)-dimensional augmented subcube which is obtained from \(A_m^{i-1}\) by changing the 0 of (\(t_{i-1}+1\))th-coordinate of \(A_m^{i-1}\) to 1 for \(i=1,\dots ,s\). Hence, \(V(A_m^i)\cap V(A_m^j)=\emptyset\) for \(i\ne j\), \(i,j\in \{0,\dots ,s\}\) and \(|V(A_m^{0}) \cup \cdots \cup V(A_m^{s})| = {\textstyle \sum _{i=0}^{s}} 2^{t_i}=|L^n_m|=m\). In [26], \(\text {AQ}_n-\text {AQ}_n[L_m^n]\) is connected and \(|E(AQ_n[L_m^n])|=\sum _{i=0}^{s-1}\left( 2 t_{i}-1\right) 2^{t_{i}-1}+\sum _{i=0}^{s} 2 i \cdot 2^{t_{i}}\) when \(t_s>0\); \(|E(\text {AQ}_n[L_m^n])|=\sum _{i=0}^{s}\left( 2t_{i}-1\right) 2^{t_{i}-1}+\sum _{i=0}^{s} 2i \cdot 2^{t_{i}}\) when \(t_s=0\) thus \(|E(\text {AQ}_n[L_m^n])|=\frac{1}{2}(\sum _{i=0}^{s}(2 t_{i}-1) 2^{t_{i}}+\sum _{i=0}^{s} 4i \cdot 2^{t_{i}}+\delta )\). The \(\text {AQ}_4[L^4_7]\) and \(\text {AQ}_4[L^4_{14}]\) are illustrated in Fig. 3.

Fig. 3
figure 3

The induced graphs \(\text {AQ}_4[L^4_7]\) and \(\text {AQ}_4[L^4_{14}]\)

Full size image

In 2021, Zhang et al. [26] showed that \(\text {AQ}_n\) is \(\lambda _h\)-optimal for \(n\ge 2\) and \(h\le 2^{\lfloor \frac{n}{2}\rfloor }\). In this paper, we determine the exact value of h-extra 3-component edge-connectivity of \(\text {AQ}_n\) and show that \(\text {AQ}_n\) is \(c\lambda _3^h\)-optimal for \(n\ge 4, h\le 2^{\left\lfloor \frac{n}{2} \right\rfloor -1 }\) and \(c\lambda _3^{2^c}(\text {AQ}_n)=\xi _{2^c,3}(\text {AQ}_n)=(2n-2c-1)2^{c+1}\) for \(n\ge 4\) and \(1\le c\le n-2\) as the following theorems.

Theorem 1

For \(n\ge 4\) and \(1\le h\le 2^{\left\lfloor \frac{n}{2} \right\rfloor -1 }\), \(c\lambda _3^h(\text {AQ}_n)=\xi _{h,3}(\text {AQ}_n)=(4n-4)h-2ex_h(\text {AQ}_n)+\delta\) where \(\delta =0\) if h is even, and \(\delta =1\) if h is odd.

Theorem 2

Given a positive integer \(n\ge 4\), then \(c\lambda _3^{2^c}(\text {AQ}_n)=\xi _{2^c,3}(\text {AQ}_n)=(2n-2c-1)2^{c+1}\) for \(1\le c\le n-2\).

The rest of this paper is organized as follows. In Sect. 2, we introduce some useful properties of \(\text {AQ}_n\). In Sect. 3, the proofs of Theorem 1 and Theorem 2 will be provided. In Sect. 4, we conclude this paper and propose some prospects.

2 Some properties and lemmas about \(\text {AQ}_n\)

As \(\text {AQ}_n\) is a \((2n-1)\)-regular connected graph, then \(\xi _{m,2}(\text {AQ}_n)=(2n-1)m-ex_m(\text {AQ}_n)\) and \(\lambda _h (\text {AQ}_n)=\min \{\xi _{m,2}(\text {AQ}_n):h\le m\le 2^{n-1}\}\) by the definition of \(\lambda _h(\text {AQ}_n)\). Basis on this, Zhang et al. [26] determined the exact value of \(\lambda _h(\text {AQ}_n)\) by showing that \(\lambda _h(AQ_n)=\xi _{h,2}(\text {AQ}_n)\) for \(n\ge 2\) and \(h\le 2^{\lfloor \frac{n}{2}\rfloor }\) in 2021. Motivated by the above, we can use \(\xi _{h,3}(\text {AQ}_n)\) to determine the exact value of \(c\lambda _3^h(\text {AQ}_n)\), and whether \(\text {AQ}_n\) is \(c\lambda _3^h\)-optimal or not. Let F be a minimum h-extra 3-component edge-cut of \(\text {AQ}_n\). Actually, \(|F|=c\lambda _3^h(\text {AQ}_n)\) and \(\text {AQ}_n-F\) have exactly three components. In Sect. 3, we will prove that two of the three components have exactly h vertices for \(n\ge 4\) and \(1\le h\le 2^{\lfloor \frac{n}{2}\rfloor -1}\) by the following lemmas. In other words, \(c\lambda _3^h(\text {AQ}_n)=\xi _{h,3}(\text {AQ}_n)\), i.e., \(\text {AQ}_n\) is \(c\lambda _3^h\)-optimal for \(n\ge 4\) and \(1\le h\le 2^{\lfloor \frac{n}{2}\rfloor -1}\).

Lemma 2

([26]) For two integers \(m_1\), \(m_2\) with \(m_1\le m_2\) and \(m_1+m_2>2\), \(ex_{m_1+m_2}(\text {AQ}_n)\ge ex_{m_1}(\text {AQ}_n)+ex_{m_2}(\text {AQ}_n)+4m_1\).

Lemma 3

([26]) For \(n\ge 4\) and \(1 \le h \le 2^{\left\lfloor \frac{n}{2} \right\rfloor }-1\), \(\lambda _h (\text {AQ}_n)=\xi _{h,2}(\text {AQ}_n)=(2n-1)h-ex_h(\text {AQ}_n)\) and \(\xi _{h,2}(\text {AQ}_n) \le \xi _{h+1,2}(\text {AQ}_n)\).

Lemma 4

([26]) For any three positive integers m, n, and b with \(1\le 2^b\le m\le 2^{n-1}\), \(\xi _{m,2}(\text {AQ}_n)\ge \xi _{2^b,2}(\text {AQ}_n)\).

Lemma 5

\(\text {AQ}_n[L_{2m}^n]\) contains two disjoint subgraphs that are both isomorphic to \(\text {AQ}_n[L_m^n]\) for \(n\ge 2\) and \(1\le m\le 2^{n-1}\).

Proof

Note that \(m\le 2^{n-1}\), then any vertex \(u\in L^n_m\) can be written as follows: \(u=0u_{n-1}u_{n-2}\cdots u_1\). Define two bijections \(\theta _1\): \(0u_{n-1}u_{n-2}\cdots u_1\rightarrow u_{n-1}u_{n-2}\cdots u_1u_1\) and \(\theta _2\): \(0u_{n-1}u_{n-2}\cdots u_1\rightarrow u_{n-1}u_{n-2}\cdots u_1\overline{u_1}\) where \(\overline{u_1}=1-u_1\). For any \(t\in S_m=\{0,1,\cdots ,m-1\}\), let \(0t_{n-1}t_{n-2}\cdots t_1\in L^n_m\) be the n-binary string corresponding to t. Denote \(\theta _1(t)\) and \(\theta _2(t)\) be the decimal representation of \(t_{n-1}t_{n-2}\cdots t_1t_1\) and \(t_{n-1}t_{n-2}\cdots t_1\overline{t_1}\), respectively. If \(t_1=0\), then \(\theta _1(t)=2t\), \(\theta _2(t)=2t+1\), and if \(t_1=1\), then \(\theta _1(t)=2t+1\), \(\theta _2(t)=2t\). Hence, \(\theta _i(t)\le 2m-1\) and \(\theta _i(0t_{n-1}t_{n-2}\cdots t_1)\in L^n_{2\,m}\), \(i=1,2\). Denote \(T_m^n=\{\theta _1(u):u\in L_m^n\}\) and \(H_m^n=\{\theta _2(u):u\in L_m^n\}\). Therefore, \(T_m^n\subset L^n_{2\,m}\) and \(H_m^n\subset L^n_{2\,m}\). Due to \(|T_m^n|=|H_m^n|=m\) and \(T_m^n\cap H_m^n=\emptyset\), \(L^n_{2\,m}\) can be partitioned into \(T^n_m\) and \(H^n_m\).

For any two vertices \(p=p_np_{n-1}\cdots p_2p_1\) and \(q=q_nq_{n-1}\cdots q_2q_1\) with \(p_n=q_n=0\) in \(L_m^n\), we prove that \(\text {AQ}_n[T^n_m]\) is isomorphic to \(\text {AQ}_n[L_m^n]\) by showing that \(pq\in E(\text {AQ}_n[L_m^n])\) if and only if \(\theta _1(p)\theta _1(q)\in E(\text {AQ}_n[T^n_m])\). Suppose that \(pq\in E(\text {AQ}_n[L_m^n])\), then pq is an O-edge in \(\text {AQ}_n\). Therefore, there exists an integer k with \(1\le k<n\) satisfying one of the following two cases.

Case 1. \(p_i=q_i\) for \(k+1\le i \le n\) and \(p_j=1-q_j\) for \(1\le j\le k\).

In this case, if \(k=n-1\), then \(p_i=1-q_i\) for \(1\le i\le n-1\). Note that \(\theta _1(p)=p_{n-1}p_{n-2}\cdots p_1p_1\) and \(\theta _1(q)=q_{n-1}q_{n-2}\cdots q_1q_1=\overline{p_{n-1}}~\overline{p_{n-2}}\cdots \overline{p_1}~\overline{p_1}\), \(\theta _1(p)\theta _1(q)\) is a C-edge in \(\text {AQ}_n\). Otherwise, \(1\le k\le n-2\). Considering \(p_i=q_i\) for \(i=n-1,n-2,\cdots ,k+1\) and \(p_j=1-p_j\) for \(j=k,k-1,\cdots ,1\), \(\theta _1(p)\theta _1(q)\) is an O-edge in \(AQ_n\).

Case 2. \(p_i=q_i\) for \(i\ne k\) and \(p_k=1-q_k\).

In this case, if \(k=n-1\), then \(p_{n-1}=1-q_{n-1}\) and \(p_i=q_i\) for \(1\le i\le n-2\). Hence, \(\theta _1(p)\theta _1(q)\) is an H-edge in \(\text {AQ}_n\). Otherwise, \(1\le k\le n-2\). Considering \(p_i=q_i\) for \(i=n-1,n-2,\cdots ,k+1,k-1,\cdots ,1\) and \(p_k=1-q_k\), \(\theta _1(p)\theta _1(q)\) is an O-edge in \(\text {AQ}_n\).

In a nutshell, if \(pq\in E(\text {AQ}_n[L_m^n])\), then \(\theta _1(p)\theta _1(q)\in E(\text {AQ}_n)\) and \(\theta _1(p)\theta _1(q)\in E(\text {AQ}_n[T_m^n])\) naturally. Conversely, let \(\theta _1(p)\theta _1(q)\in E(\text {AQ}_n[T_m^n])\). If \(\theta _1(p)\theta _1(q)\) is an O-edge in \(\text {AQ}_n\), then there exists an integer k with \(1\le k<n-1\) satisfying \(p_i=q_i\) for \(i=n-1, n-2,\cdots ,k+1\), \(p_j=1-q_j\) for \(j=k,k-1,\cdots ,2,1\), or \(p_i=q_i\) for \(i=n-1,n-2,\cdots ,k+1,k-1,\cdots ,1\), \(p_{k}=q_{k}\), respectively. Note that \(p=p_np_{n-1}\cdots p_2p_1\) and \(q=q_nq_{n-1}\cdots q_2q_1\) with \(p_n=q_n=0\), pq is an O-edge in \(\text {AQ}_n\). In other case, if \(\theta _1(p)\theta _1(q)\) is an H-edge in \(\text {AQ}_n\), then \(p_{n-1}=1-q_{n-1}\) and \(p_i=q_i\) for \(1\le i\le n-2\). Let \(k_1=n-1\). Since \(p_i=q_i\) for \(i\ne k_1\) and \(p_{k_1}=1-q_{k_1}\), pq is an O-edge in \(\text {AQ}_n\). In addition, if \(\theta _1(p)\theta _1(q)\) is a C-edge in \(\text {AQ}_n\), then \(p_i=1-q_i\) for \(1\le i\le n-1\). Let \(k_2=n-1\). Since \(p_i=q_i\) for \(k_2+1\le i \le n\) and \(p_j=1-q_j\) for \(1\le j\le k_2\), pq is an O-edge in \(\text {AQ}_n\). Briefly, if \(\theta _1(p)\theta _1(q)\in E(\text {AQ}_n[T_m^n])\), then \(pq\in E(\text {AQ}_n)\) and \(pq\in E(\text {AQ}_n[L_m^n])\) naturally. Summarize the above in one sentence, \(pq\in E(\text {AQ}_n[L_m^n])\) if and only if \(\theta _1(p)\theta _1(q)\in E(\text {AQ}_n[T^n_m])\). Hence, \(\text {AQ}_n[T^n_m]\) is isomorphic to \(\text {AQ}_n[L_m^n]\). Similarly, we can prove that \(AQ_n[H^n_m]\) is isomorphic to \(\text {AQ}_n[L_m^n]\) by showing that \(pq\in E(\text {AQ}_n[L_m^n])\) if and only if \(\theta _2(p)\theta _2(q)\in E(\text {AQ}_n[H^n_m])\). Thus, this lemma holds. \(\square\)

Incidentally, since \(ex_{2m}(\text {AQ}_n)=2ex_m(\text {AQ}_n)+4m-2\delta\), there are \(2m-\delta\) edges between \(\text {AQ}_n[T_m^n]\) and \(\text {AQ}_n[H_m^n]\) where \(\delta =0\) if m is even, \(\delta =1\) if m is odd. In Fig. 4, \(\text {AQ}_4[L_{14}^4]\) contains two disjoint connected subgraphs \(\text {AQ}_4[T_7^4]\) (marked in red, light gray in print) and \(\text {AQ}_n[H^4_7]\) (marked in blue, dark gray in print).

Fig. 4
figure 4

\(\text {AQ}_4[T_7^4]\) and \(\text {AQ}_4[H^4_7]\) are both isomorphic to \(\text {AQ}_4[L_7^4]\) and \(|[T_7^4,H^4_7]|=2\times 7-1\)

Full size image

Lemma 6

For \(n\ge 2\) and \(1\le m<2^{n-1}\), \(\xi _{m,3}(\text {AQ}_n)=(4n-4)m-2ex_m(\text {AQ}_n)+\delta\) where \(\delta =0\) if m is even, and \(\delta =1\) if m is odd.

Proof

We prove this lemma by giving an edge-cut F of \(\text {AQ}_n\) of size \((4n-4)m-2ex_m(\text {AQ}_n)+\delta\) such that \(G-F\) has exactly three components with two components which have exactly m vertices and showing that \((4n-4)m-2ex_m(\text {AQ}_n)+\delta\) is the lower bound of \(\xi _{m,3}(\text {AQ}_n)\).

As for \(\xi _{m,3}(\text {AQ}_n)\le (4n-4)m-2ex_m(\text {AQ}_n)+\delta\), given \(n\ge 2\) and \(1\le m < 2^{n-1}\), by Lemma 5, \(\text {AQ}_n[L_{2m}^n]\) contains two disjoint connected subgraphs with order m and size \(\frac{1}{2}ex_m(\text {AQ}_n)\) as \(M_1=\text {AQ}_n[T_m^n]\) and \(M_2=\text {AQ}_n[H_m^n]\). Let \(M_3=\text {AQ}_n[\overline{L_{2m}^n}]\). Note that \(M_1\), \(M_2\), and \(M_3\) are all connected and \(|T_m^n|=|H_m^n|=m\), then \(\xi _{m,3}(\text {AQ}_n)\le |[T_m^n,H_m^n,\overline{L_{2\,m}^n}]|=|[T_m^n,H_m^n]|+|[L_{2\,m}^n,\overline{L_{2\,m}^n}]|=2\,m-\delta +\xi _{2\,m,2}(\text {AQ}_n)=2\,m(2n-1)-(2ex_m(\text {AQ}_n)+4\,m-2\delta )+2\,m-\delta =(4n-4)m-2ex_m(\text {AQ}_n)+\delta.\)

Let F be any edge-cut of \(\text {AQ}_n\) that \(\text {AQ}_n-F\) has exactly three connected components \(A_1\), \(A_2\), and \(A_3\) with \(|V(A_1)|=|V(A_2)|=m\). Note that

$$\begin{aligned} 2|F|&=2|[V(A_1),V(A_2),V(A_3)]| \\ & =2(|[V(A_1),V(A_2)]|+|[V(A_2),V(A_3)]|+|[V(A_1),V(A_3)]|) \\ & \ge \xi_{m,2}(AQ_n)+\xi_{m,2}(AQ_n)+\xi_{2^n-2m,2}(AQ_n) \\ & =2\xi_{m,2}(AQ_n)+\xi_{2m,2}(AQ_n) \\ & =2(2n-1)m-2ex_m(AQ_n)+(2n-1)2m-ex_{2m}(AQ_n). \\ \end{aligned}$$

Since \(ex_{2m}(\text {AQ}_n)=2ex_m(\text {AQ}_n)+4m-2\delta\), we have \(|F|\ge (4n-4)m-2ex_m(\text {AQ}_n)+\delta\). By the generality of F, \(\xi _{m,3}(\text {AQ}_n)\ge (4n-4)m-2ex_m(\text {AQ}_n)+\delta\), this lemma holds. \(\square\)

3 The main proof of our results about h-extra r-component edge-connectivity of \(\text {AQ}_n\)

The proof of Theorem 1 for \(c\lambda _3^h(\text {AQ}_n)=\xi _{h,3}(\text {AQ}_n)\) for \(n\ge 4\) and \(1\le h\le 2^{\lfloor \frac{n}{2} \rfloor -1}\)

Proof

For \(n\ge 4\) and \(1\le h\le 2^{\lfloor \frac{n}{2} \rfloor -1}< \lfloor \frac{2^n}{3}\rfloor\), considering an upper bound for the exact value of general h-extra 3-component edge-connectivity of \(\text {AQ}_n\) is offered by Lemma 6 that \(c\lambda _3^h(\text {AQ}_n)\le \xi _{h,3}=(4n-4)h-2ex_h(\text {AQ}_n)+\delta\), we prove Theorem 1 by showing that \((4n-4)h-2ex_h(\text {AQ}_n)+\delta\) is the lower bound of \(c\lambda _3^h(\text {AQ}_n)\).

Let F be a minimum h-extra 3-component edge-cut of \(\text {AQ}_n\). By Lemma 1, \(\text {AQ}_n-F\) has exactly three components, denoted as \(C_1, C_2, C_3\) with \(|V(C_1)|\le |V(C_2)|\le |V(C_3)|\). As a general rule, two of the three components have small scales, and the other is a giant component as Fig. 5.

Fig. 5
figure 5

Illustration of \(\text {AQ}_n-F\)

Full size image

Let \(h_i=|V(C_i)|\) for \(i\in \{1,2,3\}\). Note that \(h\le h_1\le \lfloor \frac{2^n}{3} \rfloor\) and \(\Big \lceil \frac{2^n-h_1}{2} \Big \rceil \le h_3\le 2^n-2h_1\), then \(2\,h \le 2 h_{1} \le h_{1}+h_{2} \le 2^{n}-\Big \lceil \frac{2^{n}-h_{1}}{2}\Big \rceil\). For any \(1\le i\le 3\), we have \(|[V(C_{i}), \overline{V(C_{i})}]|=(2n-1)h_{i}-2| E(C_{i})| \ge \xi _{h_{i},2}(\text {AQ}_{n})=(2n-1)h_i-ex_{h_i}(\text {AQ}_n)\). By Lemma 2, it follows that

$$\begin{aligned} |F|\, & = \,|[V(C_{1} ),\overline{{V(C_{1} )}} ]| + |[V(C_{2} ),\overline{{V(C_{2} )}} ]| - |[V(C_{1} ),V(C_{2} )]| \\ & = (2n - 1)(h_{1} + h_{2} ) - 2|E(C_{1} )| - 2|E(C_{2} )| - (|E(C_{1} \cup C_{2} )| - |E(C_{1} )| - |E(C_{2} )|) \\ & \ge (2n - 1)\left( {h_{1} + h_{2} } \right) - \frac{1}{2}ex_{{h_{1} }} ({\text{AQ}}_{n} ) - \frac{1}{2}ex_{{h_{2} }} ({\text{AQ}}_{n} ) - \frac{1}{2}ex_{{h_{1} + h_{2} }} ({\text{AQ}}_{n} ) \\ & \ge (2n - 1)\left( {h_{1} + h_{2} } \right) - ex_{{h_{1} + h_{2} }} \left( {{\text{AQ}}_{n} } \right) + 2h_{1}. \\ \end{aligned}$$

Case 1. \(2h\le h_1+h_2\le 2^{ \lfloor \frac{n}{2} \rfloor }\).

By Lemma 3, we have \((2n-1)\left( h_{1}+h_{2}\right) -e x_{h_{1}+h_{2}}\left( \text {AQ}_{n}\right) +2h_{1}=\xi _{h_{1}+h_{2},2}\left( \text {AQ}_{n}\right) +2h_{1} \ge \xi _{2\,h,2}\left( \text {AQ}_{n}\right) +2h_1=(4n-2)h-ex_{2\,h}(\text {AQ}_n)+2h_1\). Therefore, \(|F| \ge (4n-2) h-e x_{2\,h}\left( \text {AQ}_{n}\right) +2\,h\) for \(1 \le h \le 2^{\lfloor \frac{n}{2}\rfloor -1}\) and \(n\ge 4\).

Case 2. \(2^{ \lfloor \frac{n}{2} \rfloor } \le h_1+h_2 \le 2^{n-1}\).

By Lemma 4, we have \((2n-1)\left( h_{1}+h_{2}\right) -e x_{h_{1}+h_{2}}(\text {AQ}_{n})+2h_{1}=\xi _{h_{1}+h_{2},2}\left( \text {AQ}_{n}\right) +2h_{1} \ge \xi _{2^{\left\lfloor \frac{n}{2} \right\rfloor },2}(\text {AQ}_n)+2h_1\). By Lemma 3, \(|F| \ge \xi _{2^{\left\lfloor \frac{n}{2} \right\rfloor },2}(\text {AQ}_n)+2h_{1} \ge \xi _{2\,h,2}\left( \text {AQ}_{n}\right) +2h_{1}=(4n-2)h-e x_{2\,h}\left( \text {AQ}_{n}\right) +2h_{1} \ge (4n-2) h-e x_{2\,h}\left( \text {AQ}_{n}\right) +2\,h\) for \(1 \le h \le 2^{\left\lfloor \frac{n}{2}\right\rfloor -1}\) and \(n\ge 4.\)

Case 3. \(2^{n-1} \le h_{1}+h_{2} \le 2^{n}-\Big \lceil \frac{2^{n}-h_{1}}{2}\Big \rceil\).

In this case, \(\Big \lceil \frac{2^{n}-h_{1}}{2}\Big \rceil \le 2^{n}-\left( h_{1}+h_{2}\right) \le 2^{n-1}\). Note that \(\xi _{2^{n}-(h_{1}+h_{2}),2}\left( \text {AQ}_{n}\right) =\xi _{h_{1}+h_{2},2}\left( \text {AQ}_{n}\right) =(2n-1)\left( h_{1}+h_{2}\right) -e x_{h_{1}+h_{2}}\left( \text {AQ}_{n}\right)\) and \(\Big \lceil \frac{2^{n}-h_{1}}{2}\Big \rceil >2^{\left\lfloor \frac{n}{2}\right\rfloor }\) for any \(1 \le h \le 2^{\left\lfloor \frac{n}{2}\right\rfloor -1}\) and \(h \le h_{1} \le \left\lfloor \frac{2^{n}}{3}\right\rfloor\). By Lemma 3 and Lemma 4, \(|F| \ge (2n-1)\left( h_{1}+h_{2}\right) -ex_{h_{1}+h_{2}}\left( \text {AQ}_{n} \right) +2h_{1}=\xi _{h_{1}+h_{2},2}\left( \text {AQ}_{n}\right) +2h_{1} >\xi _{2^{\lfloor \frac{n}{2}\rfloor },2}\left( \text {AQ}_{n}\right) +2h_{1} \ge \xi _{2\,h,2}\left( \text {AQ}_{n}\right) +2h_{1} \ge 2 n h-e x_{2\,h}\left( \text {AQ}_{n}\right) +2\,h\) for \(1 \le h \le 2^{\left\lfloor \frac{n}{2}\right\rfloor -1}\) and \(n \ge 4.\)

Thus, we have \(c\lambda _3^h(\text {AQ}_n)\ge (4n-2) h-e x_{2\,h}\left( \text {AQ}_{n}\right) +2\,h=(4n-2)h-(2ex_h(\text {AQ}_n)+4\,h-2\delta )+2\,h\ge (4n-4)h-2ex_h(\text {AQ}_n)+\delta.\) Combining with \(c\lambda _3^h(\text {AQ}_n)\le \xi _{h,3}(\text {AQ}_n)=(4n-4)h-2ex_h(\text {AQ}_n)+\delta\), we can obtain that \(c\lambda _3^h(\text {AQ}_n)=\xi _{h,3}(\text {AQ}_n)=(4n-4)h-2ex_h(\text {AQ}_n)+\delta\) for \(n\ge 4\) and \(1\le h\le 2^{\left\lfloor \frac{n}{2} \right\rfloor -1 }\). \(\square\)

The proof of Theorem 2 for \(c\lambda _3^{2^c}(\text {AQ}_n)=\xi _{2^c,3}(\text {AQ}_n)\) for \(n\ge 4\) and \(1\le c\le n-2\)

Proof

It is sufficient to show that \(c\lambda _3^{2^c}(\text {AQ}_n)\le (2n-2c-1)2^{c+1}\) by constructing a \(2^c\)-extra 3-component edge-cut of cardinality \((2n-2c-1)2^{c+1}\). For any \(1\le c\le n-2, n\ge 4\), note that \(\text {AQ}_n[L_{2^{c+1}}^n]\) can be divided into two c-dimensional augmented cubes as \(N_1=\text {AQ}_n[T_{2^c}^n]\) and \(N_2=\text {AQ}_n[H_{2^c}^n]\). Let \(N_3=\text {AQ}_n-\text {AQ}_n[L_{2^{c+1}}^n]\). Since \(N_1\), \(N_2\), and \(N_3\) are both connected and \(|V(N_3)|=2^n-2^{c+1}\ge 2^c\), \(F=[V(N_1),V(N_2),V(N_3)]\) is a \(2^c\)-extra 3-component edge-cut of \(\text {AQ}_n.\)Hence, \(c\lambda _3^{2^c}(\text {AQ}_n)\le |F|=2\xi _{2^c,2}(\text {AQ}_n)-2^{c+1}=(4n-2)2^c-(4c-2)2^c-2^{c+1}=(2n-2c-1)2^{c+1}.\)

As for \(c\lambda _3^{2^c}(\text {AQ}_n)\ge (2n-2c-1)2^{c+1}\), let F be a minimum \(2^c\)-extra 3-component edge-cut of \(\text {AQ}_n.\)By Lemma 1, \(\text {AQ}_n-F\) has exactly three components, denoted as \(W_1, W_2, W_3.\) Let \(2^c\le |V(W_1)|\le |V(W_2)|\le |V(W_3)|\) and \(|V(W_i)|=h_i\) for \(1\le i\le 3\). Note that \(\xi _{2^c,2}(\text {AQ}_n)=(2n-1)2^c-ex_{2^c}(\text {AQ}_n)=(2n-1)2^c-(2c-1)2^c=(2n-2c)2^c\), then

Case 1. \(1\le c\le \lfloor \frac{n}{2}\rfloor -1\).

By Theorem 1, we have \(|F|\ge (4n-2)2^c-2ex_{2^c}(\text {AQ}_n)-2^{c+1}=(4n-2)2^c-(2c-1)2^{c+1}-2^{c+1}=(2n-2c-1)2^{c+1}.\)

Case 2. \(\lfloor \frac{n}{2} \rfloor \le c \le n-3\).

If \(2^c\le h_1\le h_2\le h_3\le 2^{c+1}\le 2^{n-2}\), then \(h_1+h_2+h_3\le 3\cdot 2^{n-2}<2^n\), a contradiction. Hence, \(h_3>2^{c+1}.\) Since \(2|F|=|[V\left( W_{1}\right) , \overline{V\left( W_{1}\right) }]|+|[V\left( W_{2}\right) , \overline{V\left( W_{2}\right) }]|+|[V\left( W_{3}\right) , \overline{V\left( W_{3}\right) }]|\ge \xi _{h_1,2}(\text {AQ}_n)+\xi _{h_2,2}(\text {AQ}_n)+\xi _{h_3,2}(\text {AQ}_n)\), by Lemma 4, there is

    Subcase 1. \(2^{c+1}<h_3\le 2^{n-1}.\)

$$\begin{aligned} 2|F|\, & \ge \xi _{{h_{1} ,2}} ({\text{AQ}}_{n} ) + \xi _{{h_{2} ,2}} ({\text{AQ}}_{n} ) + \xi _{{h_{3} ,2}} ({\text{AQ}}_{n} ) \\ & \ge \xi _{{2^{c} ,2}} ({\text{AQ}}_{n} ) + \xi _{{2^{c} ,2}} ({\text{AQ}}_{n} ) + \xi _{{2^{{c + 1}} ,2}} ({\text{AQ}}_{n} ) \\ & = 2 \cdot (2n - 2c) \cdot 2^{c} + (2n - 2c - 2) \cdot 2^{{c + 1}} \\ & = (4n - 4c - 2) \cdot 2^{{c + 1}}. \\ \end{aligned}$$

    Subcase 2. \(h_3>2^{n-1}.\)

    As \(2^{c+1}\le h_1+h_2\le 2^{n-1}\), we have

$$\begin{aligned} 2|F|\, & \ge \xi _{{h_{1} ,2}} ({\text{AQ}}_{n} ) + \xi _{{h_{2} ,2}} ({\text{AQ}}_{n} ) + \xi _{{h_{3} ,2}} ({\text{AQ}}_{n} ) \\ & = \xi _{{h_{1} ,2}} ({\text{AQ}}_{n} ) + \xi _{{h_{2} ,2}} ({\text{AQ}}_{n} ) + \xi _{{h_{1} + h_{2} ,2}} ({\text{AQ}}_{n} ) \\ & \ge \xi _{{2^{c} ,2}} ({\text{AQ}}_{n} ) + \xi _{{2^{c} ,2}} ({\text{AQ}}_{n} ) + \xi _{{2^{{c + 1}} ,2}} ({\text{AQ}}_{n} ) \\ & = 2 \cdot (2n - 2c) \cdot 2^{c} + (2n - 2c - 2) \cdot 2^{{c + 1}} \\ & = (4n - 4c - 2) \cdot 2^{{c + 1}}. \\ \end{aligned}$$

Case 3. \(c=n-2.\)

In this case, there is \(2^{n-2}=2^c\le h_1\le h_2\le h_3\) and then \(h_1+h_2\ge 2^{n-1},~h_3\le 2^{n-1},\)

$$\begin{aligned} 2|F|\, & \ge \xi _{{h_{1} ,2}} ({\text{AQ}}_{n} ) + \xi _{{h_{2} ,2}} ({\text{AQ}}_{n} ) + \xi _{{h_{3} ,2}} ({\text{AQ}}_{n} ) \\ & \ge 3 \cdot \xi _{{2^{c} ,2}} ({\text{AQ}}_{n} ) \\ & = 3 \cdot (2n - 2c) \cdot 2^{c} \\ & = 3 \cdot (n - c) \cdot 2^{{c + 1}} \\ & = (4n - 4c - 2) \cdot 2^{{c + 1}}. \\ \end{aligned}$$

According to the discussion above, we have \(|F|\ge (2n-2c-1)\cdot 2^{c+1}\). Similar to the proof of Theorem 1, it can be obtained that \(c\lambda _3^{2^c}(\text {AQ}_n)=\xi _{2^c,3}(\text {AQ}_n)=(2n-2c-1)2^{c+1}\) for \(1\le c\le n-2\). The proof is completed. \(\square\)

4 Conclusions

In this paper, we combine Fàbrega and Sampathkumar’s concepts about the parameters of network fault tolerance as h-extra edge-connectivity and r-component edge-connectivity to introduce a more refined parameter for characterizing fault tolerance of interconnection networks as h-extra r-component edge-connectivity. Inspired by introducing \(\xi _{m,2}(G)\) to solve the exact value of \(\lambda _h(G)\) and whether G is \(\lambda _h\)-optimal or not, we introduce the concept of \(c\lambda _r^h\)-optimal and define the function \(\xi _{m,r}(G)\) to solve the exact value of \(c\lambda _r^h(G)\) and whether G is \(c\lambda _r^h\)-optimal or not. Basis on this, we determine the h-extra 3-component edge-connectivity of \(\text {AQ}_n\) and show that \(\text {AQ}_n\) is \(c\lambda _3^h\)-optimal for \(n\ge 4\) and \(1\le h\le 2^{\lfloor \frac{n}{2} \rfloor -1}\), that is, \(c\lambda _3^h(\text {AQ}_n)=\xi _{h,3}(\text {AQ}_n)=(4n-4)h-2ex_h(\text {AQ}_n)+\delta\). In addition, \(\text {AQ}_n\) is \(c\lambda _3^{2^c}\)-optimal for \(n\ge 4\) and \(1\le c\le n-2\), that is, \(c\lambda _3^{2^c}(\text {AQ}_n)=\xi _{2^c,3}(\text {AQ}_n)=(2n-2c-1)2^{c+1}\). In the future work, we would like to consider a more general case and get more results about \(c\lambda _r^h(\text {AQ}_n)\) and \(\xi _{h,r}(\text {AQ}_n)\) to discuss the \(c\lambda _r^h\)-optimality of \(\text {AQ}_n\) for \(r=3,2^{\lfloor \frac{n}{2}\rfloor -1}<h\le \lfloor 2^n/3\rfloor\) and \(r\ge 4\), respectively.