An O(log₂ N) algorithm for reliability assessment of augmented cubes based on h-extra edge-connectivity

Abstract

Reliability measure of multiprocessor systems is of great significant importance to the design and maintenance of multiprocessor systems. As a generalization of traditional edge-connectivity, extra edge-connectivity is one important parameter to evaluate the fault-tolerant capability of multiprocessor systems. Fast identifying the extra edge-connectivity of high order remains a scientific problem for many useful multiprocessor systems. In this paper, we determine the h-extra edge-connectivity of the n-dimensional augmented cube $AQ_n$ for $h \in [1, 2^{n-1}]$. Specifically, we divide the interval $[1, 2^{n-1}]$ into some subintervals and obtain the monotonicity of $\lambda _h(AQ_n)$ in these subintervals, and then deduce a recursive formula of $\lambda _h(AQ_n)$. Based on this formula, an efficient algorithm with complexity $O(\log _2 N)$ is designed to determine the exact values of h-extra edge-connectivity of $AQ_n$ for $h \in [1, 2^{n-1}]$ completely. Some previous results in Ma et al. (Inf Process Lett 106: 59-63, 2008) and Zhang et al. (J Parall Distrib Comput 147: 124-131, 2021) are extended.

1 Introduction

Due to the development of very large scale integration (VLSI) technology and software technology, multiprocessor systems with hundreds of thousands of processors are achievable. With the continuous increase in the size of multiprocessor systems, processor faults are inevitable. Hence, in the construction of multiprocessor systems, we have to consider the reliability of the multiprocessor systems. For convenience sake, a multiprocessor system can be usually enlightened as a simple connected graph, where each processor represents a vertex of the graph and each link between two processors represents an edge between two vertices in the graph. The graph is called the interconnection network of this multiprocessor system. The edge-connectivity of a graph G, denoted by $\lambda (G)$, is the minimum number of edges whose removal leaves the remaining graph disconnected. Edge-connectivity is an important parameter to measure the reliability and the fault tolerance of multiprocessor systems. The higher the edge-connectivity is, the more reliable a multiprocessor system is [24].

However, this parameter has some intrinsic shortcomings. Firstly, a lot of graphs with the same edge-connectivity behave quite differently in fault tolerance. Secondly, as explained by Xu [24], since edge-connectivity measures the worst-case failures, which seldom occur in the real world, the resilience of a network is drastically underestimated. To overcome such shortcomings, several new concepts on the edge-connectivity of graphs, called conditional edge-connectivity, were proposed by Harary [12]. One of them is the extra edge-connectivity. The extra edge-connectivity was introduced by Fàbrega and Foil [9]. For a given positive integer h, an h-extra edge-cut of a connected graph G is defined as a set of edges whose deletion yields a disconnected graph with all its components having at least h vertices. The h-extra edge-connectivity of a connected graph G, denoted by $\lambda _h(G)$, is the minimum cardinality taken over all h-extra edge-cuts of G. It is obvious that $\lambda _1(G) = \lambda (G)$. There are some results of the h-extra edge-connectivity for some classes of the interconnection networks. For example, Li and Yang [16] determined the h-extra edge-connectivity of the hypercube $Q_n$ for $1\le h\le 2^{\lceil \frac{n}{2}\rceil }$. Zhang et al. [30, 31] investigated the h-extra edge-connectivity of the folded hypercube $FQ_n$ for $1\le h\le 2^{\lceil \frac{n}{2}\rceil +1}$ and later designed an efficient $O(\log _2 N)$ algorithm to determine the h-extra edge-connectivity of the folded hypercube $FQ_n$ for each $1\le h \le 2^{n-1}$. Regarding the computational complexity of the problem, Esfahanian and Hakimi [8] presented a polynomial-time algorithm for the computation of $\lambda _2(G)$. Montejano and Sau [21] discussed the complexity of computing the h-extra edge-connectivity for general cases. Given a graph G with N vertices, they proved that the problem of determining that whether there exists an h-extra edge-cut or not for $1\le h \le \frac{N}{2}$ is NP-complete, even when the maximum degree of the G is at most 5. And for a given positive integer l, the problem of determining that whether the h-extra edge-connectivity of G is at most l is NP-hard. In addition, there are many interesting results related to the h-extra edge-connectivity, and others, one can refer [2, 7, 4, 10, 11, 14, 16, 17, 20, 22, 23, 25,26,27,28,29,30,31] and the references therein for the details. The focus of these results is either on some classes of graphs for several h or on some special graphs for linearly and even exponentially many values of h. However, seldom do the researchers pay their attentions on thoroughly solving this problem for some classes of networks for each $h \le \frac{|V(G)|}{2}$.

The hypercube is the most popular topology being used in interconnection networks, which possess many good properties such as strong connectivity, small diameter, symmetry, recursive construction, relatively small degree, and regularity [1, 15]. As an enhancement on the hypercube, the augmented cube, proposed by Choudum and Sunitha [6], not only retains some of the favorable properties of the hypercube, but also possesses some embedding properties that the hypercube does not have [13, 19].

Let n be a positive integer. The definition of the n-dimensional augmented cube is stated as follows.

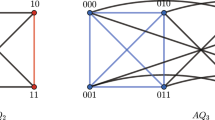
The n-dimensional augmented cube, denoted by $AQ_{n}$, has $2^{n}$ vertices, each labeled by an n-bit binary string and $V(AQ_{n})=\{x_nx_{n-1}\cdots x_2x_1:x_i=0 ~\text {or}~ 1\}$ where $x_i$ is called as the ith-coordinate of $AQ_{n}$ for $i=1, 2, \ldots ,n$. $AQ_1$ is a complete graph $K_2$ of two vertices labeled with 0 and 1, respectively. For $n\ge 2$, $AQ_{n}$ can be recursively constructed from two copies of $AQ_{n-1}$, denoted by $AQ_{n-1}^0$ and $AQ_{n-1}^1$, and by adding 2n edges between $AQ_{n-1}^0$ and $AQ_{n-1}^1$, where $V(AQ_{n-1}^{0})=\{0x_{n-1}\cdots x_2x_1:x_i=0 ~\text {or}~ 1\}$, $V(AQ_{n-1}^{1})=\{1x_{n-1}\cdots x_2x_1:x_i=0 ~\text {or}~ 1\}$. Vertex $u=0u_{n-1}\cdots u_2u_1\in V(AQ_{n-1}^{0})$ is adjacent to $v=1v_{n-1}\cdots v_2v_1\in V(AQ_{n-1}^{1})$, if and only if either

• (1) $u_i=v_i$ for $1\le i\le n-1$; or

• (2) $u_i={\overline{v}}_i$ for $1\le i\le n-1$, where ${\overline{v}}_i=1-v_i$.

From the definition, we can see that each vertex of $AQ_{n-1}^0$ has exactly two neighbors in $AQ_{n-1}^1$ and vice versa. In fact, $AQ_{n}$ can be obtained by adding two perfect matchings between $AQ_{n-1}^0$ and $AQ_{n-1}^1$. Hence, $AQ_{n}$ can be viewed as $AQ_{n-1}^{0} \oplus AQ_{n-1}^{1}$ briefly. Clearly, $AQ_{n}$ is $(2n-1)$-regular. Hence, $|E(AQ_n)|=(2n-1)2^{n-1}$. The augmented cubes $AQ_1$, $AQ_2$, and $AQ_3$ are illustrated in Fig. 1.

Fig. 1

Illusion of $AQ_{n}$

The exact values of the h-extra edge-connectivity of $AQ_n$ for some h are given in the several literatures. Ma et al. [18] proved that $\lambda _2(AQ_n)=4n-4$, $\lambda _3(AQ_n)=6n-9$. Zhang et al. [32] gave the exact values of $\lambda _h(AQ_n)$ for $1\le h\le 2^{\lfloor \frac{n}{2}\rfloor }$, $n\ge 2$.

Our work in this paper concerns the h-extra edge-connectivity of the n-dimensional augmented cube $AQ_n$ for $2^{\lfloor \frac{n}{2}\rfloor }\le h\le 2^{n-1}$, $n\ge 2$. We redivide the integer interval $[1, 2^{n-1}]$ into some subintervals, and each subinterval will be further divided, to obtain some properties of $\xi _h (AQ_n)$ for $h\in [1, 2^{n-1}]$. Furthermore, we deduce a recursive relation on $\lambda _h (AQ_n)$. This method is different from the existing methods in [18, 32]. Based on it, an efficient $O(\log _2 N)$ algorithm is designed to totally determine the exact values of $\lambda _h (AQ_n)$ for $h\in [1, 2^{n-1}]$. Some previous results in [18, 32] are extended.

The paper is organized as follows: In Sect. 2, some notations, definitions, and some known results are given. In Sect. 3, the main result about the h-extra edge-connectivity of $AQ_n$ is determined, from which we obtain an algorithm to calculate $\lambda _h (AQ_n)$. In Sect. 4, the paper is concluded.

2 Preliminaries

Let $G = (V(G), E(G))$ be a simple, undirected graph, where |V(G)| denotes the size of the vertex set and |E(G)| denotes the size of the edge set. We use $N_G(v)$ to denote all neighbors of v in G and use $d_G(v)$ to denote the order of $N_G(v)$. If $W \subseteq V(G)$ or if $W \subseteq E(G)$, then G[W] denotes the subgraph of G induced by W. For two disjoint subgraphs or vertex sets X, Y of G, we use [X, Y] the edges with one endpoint in X and the other in Y. Let

$\xi _m (G) = \text {min} \{|[X, {\overline{X}}]|: |X| = m \le \lfloor \frac{|V(G)|}{2}\rfloor , \ \text {and both}\ \ G[X]\ \text {and}\ G[{\overline{X}}]\ \text {are connected }\}.$

By the definition of $\lambda _h(G)$,

$$\begin{aligned} \lambda _h(G)=\text {min} \{\xi _m (G): h\le m\le \lfloor \frac{|V(G)|}{2}\rfloor \}. \end{aligned}$$

The $\lambda _h(Q_n^3)$ highly relies on the monotonic intervals and fractal-like structure of function $\xi _m (AQ_n)$. If $\lambda _h(G)=\xi _h (G)$, we say that G is $\lambda _h$-optimal.

Let $\frac{ex_m(G)}{2}$ denote the maximum number of edges of the subgraph induced by a vertex set with a given size m in G, i.e., $ex_m(G)$ is the maximum sum of degree of the subgraph induced by a vertex set with a given size m in G. For terminologies and notations undefined here, we follow [3].

For convenience, the vertex $x =x_1x_{2}\cdots x_n$ of the $AQ_n$ can be represented by decimal number $\sum _{i=1}^nx_i2^{n-i}$ in this paper.

For $1 \le m \le 2^n$, the subgraph induced by vertex set $\{0, 1, \ldots , m -1\}$ (under decimal representation) of $AQ_n$ is denoted by $L_m$, the subgraph induced by $\{2^n-1, 2^n-2, \ldots , 2^n-m \}$ is denoted $R_m$.

Lemma 2.3

[32] $L_m\cong R_m$ for $1 \le m \le 2^n$. If we delete the edges $[V(L_m), \overline{V(L_m)}]$, then both $L_m$ and $R_{2^n-m}$ are connected.

Lemma 2.4

[32]For $1 \le m \le 2^n$, $ex_m(AQ_n)=2|E(L_m)|$.

Lemma 2.5

[32] If $1\le m\le 2^t$ where $t\in \{0, 1, \ldots , n\}$, then $ex_m(AQ_n)\le (2t-1)m$.

In what follows, we denote $\begin{aligned} \delta (m)= \left\{ \begin{array}{ll} 0, \ m\ \text {is}\ \text {even};\\ 1, \ m\ \text {is}\ \text {odd}. \end{array} \right. \end{aligned}$

We define m be a positive integer and $m=\sum _{i=0}^{s}2^{t_i}$ be the decomposition of m such that $t_0=[\log _2m]$ and $t_i=[\log _2(m-\sum _{k=0}^{i-1}2^{t_k})]$ for $i\ge 1$. Let $f(m)=\sum _{i=0}^{s}(2t_i-1)2^{t_i}+\sum _{i=0}^{s}4\cdot i\cdot 2^{t_i}+\delta (m)$.

Lemma 2.6

[32] Let $m_1$ and $m_2$ be any positive integers such that $m_1\le m_2$. Then

$$\begin{aligned} ex_{m_1+m_2}(AQ_n)\ge ex_{m_1}(AQ_n)+ex_{m_2}(AQ_n)+ 4m_1. \end{aligned}$$

Lemma 2.7

[32] The following results hold.

• (i) $ex_m(AQ_n)=f(m)$;

• (ii) $ex_m (AQ_n) =ex_{m-2^{t_0}} (AQ_n)+ ex_{2^{t_0}} (AQ_n)+ 4(m-2^{t_0})$;

• (iii) $ex_{m+1}(AQ_n)-ex_m(AQ_n)=4(s+1)$ when m is even, and $ex_{m+1}(AQ_n)-ex_m(AQ_n)=4s+2$ when m is odd.

3 The h-extra edge-connectivity of $AQ_n$

By $(2n-1)$-regularity of the n-dimensional augmented cube $AQ_n$ [12] and Lemmas 2.3 and 2.4, it follows that

$$\begin{aligned} \xi _m(AQ_n)=(2n-1)m-ex_m(AQ_n). \end{aligned}$$

(1)

To deal with the integer interval $(2^{\lfloor \frac{n}{2}\rfloor }, 2^{n-1}]$, we divide the integer interval $(2^{\lfloor \frac{n}{2}\rfloor }, 2^{n-1}]$ into $\lceil \frac{n}{2}\rceil -1$ subintervals $(2^{\lfloor \frac{n}{2}\rfloor +r-1}, 2^{\lfloor \frac{n}{2}\rfloor +r}]$ for $r = 1, 2, \ldots , \lceil \frac{n}{2}\rceil -1$. Let

$$\begin{aligned} w_{r,j}=\sum _{i=0}^{j} 2^{\lfloor \frac{n}{2}\rfloor +r-1-i}, \end{aligned}$$

where $j = 0, 1, \ldots , \lceil \frac{n}{2}\rceil -r-1$. Thus, $w_{r,0} = 2^{\lfloor \frac{n}{2}\rfloor +r-1}$, $w_{r+1,0} = 2^{\lfloor \frac{n}{2}\rfloor +r}$, $w_{r,0}< w_{r,1}< \cdots< w_{r,j}< \cdots< w_{r, \lceil \frac{n}{2}\rceil -r-1}< w_{r+1,0}$, and $w_{r+1,0}-w_{r, \lceil \frac{n}{2}\rceil -r-1}=2^{2r-\delta (n)}$. Each interval of $(2^{\lfloor \frac{n}{2}\rfloor +r-1}, 2^{\lfloor \frac{n}{2}\rfloor +r}]$ for $r = 1, 2, \ldots , \lceil \frac{n}{2}\rceil -1$ is further divided into $\lceil \frac{n}{2}\rceil -r$ subintervals: $(w_{r,j}, w_{r,j+1}]$ with $j = 0, 1, \ldots , \lceil \frac{n}{2}\rceil -r-2$ and $(w_{r,\lceil \frac{n}{2}\rceil -r-1}, 2^{\lfloor \frac{n}{2}\rfloor +r}]$.

Lemma 3.1

[32] For any positive integer $h\in [1, 2^{\lfloor \frac{n}{2}\rfloor }]$, $n\ge 2$, $\lambda _{h}(AQ_n)=\xi _h(AQ_n)=(2n-1)h-ex_h(AQ_n)$.

The following properties of $\xi _{m}(AQ_n)$ play an extremely useful role.

Lemma 3.2

$\xi _{m}(AQ_n) \ge \xi _{2^{k}}(AQ_n)$ for $2^k \le m \le 2^{n-1}$, $k\in \{0,1,\ldots ,n-2\}$.

Proof

For $0\le k\le n-2$,

$$\begin{aligned} \xi _{2^{k+1}}(AQ_n)&-\xi _{2^k}(AQ_n)\\&=(2n-1)2^{k+1}-ex_{2^{k+1}}(AQ_n)-(2n-1)2^k+ex_{2^k}(AQ_n)\\&=(2n-1)2^{k}-(ex_{2^{k+1}}(AQ_n)-ex_{2^k}(AQ_n))\\&=(2n-1)2^{k}-((2k+1)2^{k+1}-(2k-1)2^{k})\\&=(n-k-2)2^{k+1}\ge 0. \end{aligned}$$

For $k\in \{0, \ldots , n-2 \}$, take any integer in $[2^k, 2^{k+1}]$, say m. Let $m'=m-2^k$. Then $m'\le 2^k$. By Lemmas 2.5 – 2.7, we have

$$\begin{aligned} \xi _m(AQ_n)&-\xi _{2^k}(AQ_n)\\&=(2n-1)m-ex_m(AQ_n)-((2n-1)2^k-ex_{2^k}(AQ_n))\\&=(2n-1)m'-(ex_{m'+2^k}(AQ_n)-ex_{2^k}(AQ_n))\\&=(2n-1)m'-4m'-ex_{m'}(AQ_n)\\&=(2n-5)m'-ex_{m'}(AQ_n)\\&\ge (2n-5)m'-(2k-1)m'\\&\ge 2(n-k-2)m'\ge 0. \end{aligned}$$

The lemma follows by the above inequalities. $\square$

Lemma 3.3

$$\begin{aligned} \begin{aligned} \xi _m(AQ_n) \left\{ \begin{array}{ll} > \xi _{2^{\lfloor \frac{n}{2}\rfloor +r}}(AQ_n), \ \text {if}~ w_{r, \lceil \frac{n}{2}\rceil -r-1}< m< 2^{\lfloor \frac{n}{2}\rfloor +r};\\ \\ =(\lfloor \frac{n}{2}\rfloor -r)2^{\lfloor \frac{n}{2}\rfloor +r+1}, \ \ \text {if}~ m=w_{r, \lceil \frac{n}{2}\rceil -r-1}, \ \text {or} \ m=2^{\lfloor \frac{n}{2}\rfloor +r}. \end{array} \right. \end{aligned} \end{aligned}$$

Proof

For $w_{r, \lceil \frac{n}{2}\rceil -r-1}< m< 2^{\lfloor \frac{n}{2}\rfloor +r}$, let $m = w_{r,\lceil \frac{n}{2}\rceil -r-1}+m'$. Then $0< m'< 2^{2r-\delta (n)}$, and so

$$\begin{aligned} \xi _{m}(AQ_n)&=\xi _{2^{\lfloor \frac{n}{2}\rfloor +r}-m'}(AQ_n)\\&=(2n-1)\cdot (2^{\lfloor \frac{n}{2}\rfloor +r}-m'0)\\&\quad -ex_{2^{\lfloor \frac{n}{2}\rfloor +r}-m'}(AQ_n)\\&=2(\lceil \frac{n}{2}\rceil -r)\cdot (2^{\lfloor \frac{n}{2}\rfloor +r}-m') +(2(\lfloor \frac{n}{2}\rfloor +r)-1)\cdot (2^{\lfloor \frac{n}{2}\rfloor +r}-m')\\&\quad -ex_{2^{[\frac{n}{2}]+r}-m'}(AQ_{[\frac{n}{2}]+r})\\&=2(\lceil \frac{n}{2}\rceil -r)\cdot (2^{\lfloor \frac{n}{2}\rfloor +r}-m')+(2(\lfloor \frac{n}{2}\rfloor +r)-1)\cdot m'-ex_{m'}(AQ_{\lfloor \frac{n}{2}\rfloor +r})\\&=\xi _{2^{\lfloor \frac{n}{2}\rfloor +r}}(AQ_n)+(2(2r-\delta (n))-1)\cdot m'-ex_{m'}(AQ_{\lfloor \frac{n}{2}\rfloor +r})\\&> \xi _{2^{\lfloor \frac{n}{2}\rfloor +r}}(AQ_n). \end{aligned}$$

The last inequality will hold, which is based on Lemma 2.5 that $2(2r-\delta (n))m'-ex_{m'}(AQ_{2^{\lfloor \frac{n}{2}\rfloor +r}})>0$ where $0< m'< 2^{2r-\delta (n)}$.

If $m=w_{r, \lceil \frac{n}{2}\rceil -r-1}$ or $m=2^{\lfloor \frac{n}{2}\rfloor +r}$, similar to the above discussion, we have

$$\begin{aligned} \xi _{w_{r,\lceil \frac{n}{2}\rceil -r-1}}(AQ_n)&=\xi _{2^{\lfloor \frac{n}{2}\rfloor +r}-2^{2r-\delta (n)}}(AQ_n)\\&=\xi _{2^{\lfloor \frac{n}{2}\rfloor +r}}(AQ_n)+(2(2r-\delta (n))-1) 2^{2r-\delta (n)}\\&\quad -ex_{2^{2r-\delta (n)}}(AQ_{\lfloor \frac{n}{2}\rfloor +r})\\&=\xi _{2^{\lfloor \frac{n}{2}\rfloor +r}}(AQ_n)=2(\lfloor \frac{n}{2}\rfloor -r)2^{\lfloor \frac{n}{2}\rfloor +r}. \end{aligned}$$

The proof is completed. $\square$

Lemma 3.4

$\xi _m(AQ_n)\ge \xi _{w_{r,j}}(AQ_n)$ for any $m \in [w_{r,j}, w_{r,\lceil \frac{n}{2}\rceil -r-1}]$ with $j = 0, 1, \ldots , \lceil \frac{n}{2}\rceil -r-2$ and $r = 1, 2, \ldots , \lceil \frac{n}{2}\rceil -1$.

Proof

Let $w_{r,j}\le h\le w_{r,j+1}$ and $h'=h-w_{r,j}$. Then $0\le h'\le 2^{{\lfloor \frac{n}{2}\rfloor }+r-2-j}$ and by Lemma 2.6, we have

$$\begin{aligned} \xi _{h}(AQ_n)&=\xi _{w_{r,j}+h'}(AQ_n)\nonumber \\&=(2n-1)(w_{r,j}+h')-ex_{w_{r,j}+h'}(AQ_n)\nonumber \\&=(2n-1)(w_{r,j}+h')-ex_{w_{r,j}}(AQ_n)-ex_{h'}(AQ_n)-4(j+1) h'\nonumber \\&=\xi _{w_{r,j}}(AQ_n)+(2(n-2j-2)-1)h'-ex_{h'}(AQ_{n-2j-2})\nonumber \\&=\xi _{w_{r,j}}(AQ_n)+\xi _{h'}(AQ_{n-2j-2}). \end{aligned}$$

(2)

Thus, $\xi _{w_{r,j+1}}(AQ_n)\ge \xi _{w_{r,j}}(AQ_n)$ and $\xi _{h}(AQ_n)\ge \xi _{w_{r,j}}(AQ_n)$. Based on these inequalities, the results hold. $\square$

Theorem 3.5

If $2^{\lfloor \frac{n}{2}\rfloor +r-1} < h \le 2^{\lfloor \frac{n}{2}\rfloor +r}$ for $r = 1, 2, \ldots , \lceil \frac{n}{2}\rceil -1$ ($n\ge 3$), then

$$\begin{aligned} \begin{aligned} \lambda _h (AQ_n) = \left\{ \begin{array}{ll} \xi _{2^{\lfloor \frac{n}{2}\rfloor +r}} (AQ_n)=(\lceil \frac{n}{2}\rceil -r)2^{\lfloor \frac{n}{2}\rfloor +r+1}, \ \ &{}\text {if}~w_{r, \lceil \frac{n}{2}\rceil -r-1}< h \le 2^{\lfloor \frac{n}{2}\rfloor +r}; \\ \\ \xi _{w_{r,j}} (AQ_n)+\lambda _{h-w_{r,j}}(AQ_{n-2j-2}),\ \ &{}\text {if}~ w_{r,j}< h \le w_{r,j+1}~ \\ &{} \text {where}~ j=0,1,\ldots ,\lceil \frac{n}{2}\rceil -r-2. \end{array} \right. \end{aligned} \end{aligned}$$

Proof

For $2^{\lfloor \frac{n}{2}\rfloor +r-1} < h \le 2^{\lfloor \frac{n}{2}\rfloor +r}$, there exists an integer j, such that $w_{r,j} < h \le w_{r,j+1}$, $j=0,1,\ldots ,\lceil \frac{n}{2}\rceil -r-2$, or $w_{r, \lceil \frac{n}{2}\rceil -r-1} < h \le 2^{\lfloor \frac{n}{2}\rfloor +r}$.

If $w_{r, \lceil \frac{n}{2}\rceil -r-1} < h\le 2^{\lfloor \frac{n}{2}\rfloor +r}$, then by Lemmas 3.1–3.3,

$$\begin{aligned} \lambda _h (AQ_n)&=\text {min}\{\xi _m(AQ_n) : h \le m \le 2^{n-1}\}\\&=\text {min}\{\xi _m(AQ_n) : h \le m \le 2^{\lfloor \frac{n}{2}\rfloor +r} \}\\&=\xi _{2^{\lfloor \frac{n}{2}\rfloor +r}} (AQ_n)\\&=(\lceil \frac{n}{2}\rceil -r)2^{\lfloor \frac{n}{2}\rfloor +r+1}. \end{aligned}$$

If $w_{r,j} < h \le w_{r,j+1}$ with $j = 0, 1, \ldots , \lceil \frac{n}{2}\rceil -r-2$, by (2), $\xi _h (AQ_n) = \xi _{w_{r, j}} (AQ_n) + \xi _{h-w_{r, j}} (AQ_{n-2j-2})$. Specially, $\xi _{w_{r, j+1}} (AQ_n) > \xi _{w_{r, j}} (AQ_n)$. By Lemma 3.4, $\xi _m(AQ_n ) \ge \xi _{w_{r, j}} (AQ_n )$, for any $w_{r,j}\le m \le w_{r,\lceil \frac{n}{2}\rceil -r-1}$ with $j = 0, 1, \ldots , \lceil \frac{n}{2}\rceil -r-2$ and $r = 1, 2, \ldots , \lceil \frac{n}{2}\rceil - 1$, we can deduce that min$\{\xi _m(AQ_n): w_{r,j+1} \le m \le w_{r,\lfloor \frac{n}{2}\rfloor -r-1} \} = \xi _{w_{r, j + 1}} (AQ_n )$. So for any $w_{r,j} \le h \le m \le w_{r,j+1}$, min$\{\xi _m(AQ_n): h \le m \le w_{r, \lceil \frac{n}{2}\rceil -r-1}\}$ = min$\{\xi _m(AQ_n): h \le m \le w_{r, j+1}\}$. Therefore, we have

$$\begin{aligned} \lambda _h (AQ_n)&=\text {min}\{\xi _m(AQ_n) : h \le m \le 2^{n-1}\}\\&=\text {min}\{\xi _m(AQ_n) : h \le m \le 2^{\lfloor \frac{n}{2}\rfloor +r} \}\\&=\text {min}\{\xi _m(AQ_n) : h \le m \le w_{r, j+1} \}\\&=\text {min}\{\xi _{w_{r, j}} (AQ_n)+\xi _{m-w_{r, j}} (AQ_{n-2j-2}) : h-w_{r,j} \\&\quad \le m-w_{r,j} \le 2^{\lfloor \frac{n}{2}\rfloor +r-j-2\rceil } \}\\&=\xi _{w_{r, j}} (AQ_n) + \text {min}\{\xi _{m-w_{r, j}} (AQ_{n-2j-2}) : h-w_{r,j}\\&\quad \le m-w_{r,j} \le 2^{\lfloor \frac{n}{2}\rfloor +r-j-2\rceil } \}\\&=\xi _{w_{r, j}} (AQ_n) +\lambda _{h-w_{r,j}}(AQ_{n-2j-2}). \end{aligned}$$

Hence, the proof of Theorem 3.5 is completed. $\square$

According to equation (2), Lemma 2.7, Lemmas 3.1–3.4, and Theorem 3.5, an $O(\log _2 N)$ ($N=|V(AQ_n)|=2^n$) algorithm to calculate $\xi _m(AQ_n)$ can be designed by the above formulas (Fig. 2).

Fig. 2

Flowchart on the algorithm of calculating $\lambda _h(AQ_n)$

Based on equation (2), Lemma 2.7, Lemmas 3.1–3.4, and Theorem 3.5, for given positive integers n and h with $n \ge 2$ and $h \le 2^{n-1}$, we can redesign an algorithm to determine the exact values of $\lambda _h (AQ_n)$ and to find an integer m such that $\lambda _h (AQ_n)=\xi _m (AQ_n)$ as follows.

Step 1: Let $m_0 = 0$.

Step 2: If $h \le 2^{\lfloor \frac{n}{2}\rfloor }$, then let $m = m_0 + h$, $\lambda _{h} (AQ_n) = \xi _{m} (AQ_n)$, and stop.

Step 3: If $w_{r, \lceil \frac{n}{2}\rceil -r-1} < h \le 2^{\lfloor \frac{n}{2}\rfloor +r}$ for some $r\in \{ 1, 2, \ldots , \lceil \frac{n}{2}\rceil -1 \}$, then let $m = m_0 + 2^{\lfloor \frac{n}{2}\rfloor +r}$, $\lambda _{h} (AQ_n) = \xi _{m} (AQ_n)$, and stop.

Step 4: If $w_{r,j} < h \le w_{r,j+1}$ for some integers $r\in \{1, 2, \ldots , \lceil \frac{n}{2}\rceil -1\}$ and $j\in \{0, 1, \ldots , \lceil \frac{n}{2}\rceil -r-2 \}$, let $m_0'= m_0+w_{r,j}$, $n'= n- 2j-2$, and $h' = h -w_{r,j}$ instead of $m_0$, n, and h, respectively. Then go to Step 2.

Steps 2 and 3 are based on Lemma 3.1, Lemma 3.3, and Theorem 3.5, respectively. And Step 4 can be deduced by Theorem 3.5. The process described above will be terminated on Steps 2 or 3, since in each Step 4, both n and h are strictly reduced, $n - 2j-2\ge \lceil \log _2 h'\rceil + 1 \ge 2$ and $2^{n-1} = 2^{\lfloor \frac{n}{2}\rfloor }$ if $n = 2$ or $n=3$. Specially, if the process terminates in Step 2, then $m=h$ and it is $\lambda _h$-optimal. Otherwise, it is not $\lambda _h$-optimal.

Combining with the equation to calculate $\xi _m(AQ_n)$ (see equation (2), Lemma 2.7 (i), Lemma 3.1 and Theorem 3.5), the flowchart of the algorithm is given in Fig. 4, where $\lambda _h (AQ_n) = \xi _m(AQ_n) = S$. The time complexity of the algorithm above is $O(n) = O(\log _2 2^n )$. In fact, the time complexity of algorithm is the same with the subprogram to find m such that $\lambda _h (AQ_n) = \xi _m(AQ_n)$ and also is the same with the subprogram to calculate $\xi _m(AQ_n)$. In the subprogram to find m such that $\lambda _h (AQ_n) = \xi _m(AQ_n)$, suppose that it needs t times to repeat the circulation. Then $t \le \lfloor \frac{n}{2}\rfloor -1$, $b_1 = \lceil \frac{n}{2}\rceil$, $r_1 = r \le \lfloor \frac{n}{2}\rfloor - 1$, and $j_1 = j \le b_1 - r_1$. For $i > 1$, in the ith time, the time complexity is at most $4 + 3j_i + 5$, where $b_i = b_{i-1} - j_{i-1}$, $r_i = r_{i-1} - i + 1$, and $j_i \le b_i -r_i$. Hence, $j_t \le b_1 - j_1 - \ldots - j_{t-1} - r_t$. Thus, $j_1 + j_2 + \ldots + j_t \le b_1 - r_t\le \lceil \frac{n}{2}\rceil$ and

$$\begin{aligned} \sum _{i=1}^t (4 + 3j_i + 5) \le 15 \lceil \frac{n}{2}\rceil . \end{aligned}$$

In the subprogram to calculate $\xi _m(AQ_n)$, the time complexity is at most 2n. Therefore, the time complexity of the algorithm is $O(\log _2 N)$, where $N = 2^n$. $\square$

Table 1 $\lambda _h(AQ_4)$ for $1\le h\le 8$

Table 2 Example of $\lambda _h(AQ_n)$ AND $\xi _h(AQ_n)$

4 Application

In parallel computing, the n-dimensional augmented cubes can be used as underlying topologies of several parallel systems. Moreover, the n-dimensional augmented cube has also been used in the construction of data center networks [5].

Our theoretical results offer a more refined quantitative analysis of indicators of the robustness of a n-dimensional augmented cube based on the multiprocessor system in the presence of failing links. For the n-dimensional augmented cube network with $N = 2^n$ processors, the h-extra edge-connectivity of $AQ_n$ is the minimum cardinality of set of links, whose removal disconnects the network with all its resulting components having at least h processors for each $1\le h \le \frac{N}{2}$. In other words, at least $\lambda _h(G)$ number of links must be deleted to disconnect this network, provided that the deletion of these links does not isolate any subnetwork with at most $h - 1$ processors.

By Lemma 3.1, Theorems 3.5, and equation (2), the values of the $\lambda _h(AQ_n)$ have close relationship with $\xi _m(AQ_n)$ for $1 \le m \le h \le 2^{n-1}$. Our algorithm is based on the fact that

$$\begin{aligned} \xi _m(AQ_n) = |[L_m, \overline{L_m}]| = (2n-1)m - \sum _{i=0}^{s}(2t_i-1)2^{t_i}-\sum _{i=0}^{s}4\cdot i\cdot 2^{t_i}-\delta (m), \end{aligned}$$

for $1\le m \le 2^{n-1}$.

For example, assume that $n = 4$ and $h = 4$. We have

$$\begin{aligned} S_4 = \{0, 1, 2, 3\}\ \text{ and }\ L_4 = \{0000, 0001, 0010, 0011\} \end{aligned}$$

. Since $4 = 2^2$, we have $t_0 = 2, s = 0$, and

$$\begin{aligned} \xi _4(AQ_n) = |[L_4, \overline{L_4}]|= (2\times 4-1)\times 4- ex_4(AQ_n) = 28- 3 \times 2^2-4\times 0\times 2^2=16. \end{aligned}$$

However, if

$$\begin{aligned}L_4^1 = \{0000, 0010, 0011, 0111\}\end{aligned}$$

and

$$\begin{aligned}L_4^2 = \{0000, 0001, 0010, 0100\},\end{aligned}$$

then both $[LT_4^1, \overline{L_4^1}]$ and $[L_4^2, \overline{L_4^2}]$ are four extra edge-cuts of $AQ_n$ with

$$\begin{aligned}|[L_4^1, \overline{L_4^1}]| = |[L_4^2, \overline{L_4^2}]| = 18 > 16 = |[L_4, \overline{L_4}]|.\end{aligned}$$

If

$$\begin{aligned}h = 7 = 2^2 +2^1+ 2^0,\end{aligned}$$

then

$$\begin{aligned}L_{7} = \{0000, 0001, 0010, 0011, 0100, 0101, 0110\}.\end{aligned}$$

We have $\xi _7(AQ_4) = |[L_7, \overline{L_7}]| = 30$. By our algorithm, the exact values of $\lambda _h(AQ_4)$ for each $1\le h \le 2^3$ are given in Table 1.

After processing Algorithm 1 for some small cases $1\le n \le 4$ and $1\le h \le 2^{n-1}$, the values of $\lambda _h (AQ_n)$ are presented in Table 2, where the values of $\lambda _h (AQ_n)$ not satisfying the equality $\lambda _h (AQ_n) = \xi _h (AQ_n)$ are marked in blue (bold in print version) and otherwise are marked in black. One can see that as the integer n increases, the number of h with $\lambda _h (AQ_n ) \ne \xi _h (AQ_n )$ also increases.

5 Concluding remarks

The h-extra edge-connectivity is the generalization of the traditional edge-connectivity. In this paper, we focus on the n-dimensional augmented cubes $AQ_{n}$. We investigate the h-extra edge-connectivity of this kind of interconnection networks. To determine the h-extra edge-connectivity of the n-dimensional augmented cubes $AQ_{n}$, we divide the interval $1 \le h \le 2^{n-1}$ into some subintervals and investigate some properties of $\xi _m(AQ_{n} )$ in these subintervals. A recurrence relation of $\lambda _h (AQ_{n} )$ is found. Based on them and some known results, an efficient $O(\log _2 N)$ algorithm to determine the exact values of $\lambda _h (AQ_{n} )$ is suggested. The problem on the h-extra edge-connectivity of the n-dimensional augmented cubes is completely solved.