1 Introduction

There are number of issues in quantum optics that are observed in the Jaynes Cummings (JC) model in interaction of a single mode and multimode radiation field with two or more-level atoms (Li et al. 1989; Xiao-shen and Nian-yu 1984; Abdel-Aty et al. 2013; Abo-Kahla et al. 2018; Abo-Kahla 2016a, 2020a; Enaki and Rosca 2012). This investigation is connected with multi-level system as q-bits in quantum computing and quantum processing information (Enaki and Eremeev 2005; Huang 2018; Abo-Kahla et al. 2021; Abo-Kahla and Farouk 2019; Abo-Kahla 2021, 2020b, 2016b; Abo-Kahla and Abdel-Aty 2015). Observations of revivals and collapses in a one atom maser lead to interest in researchers to moving from academia to experimental realm (Rempe et al. 1987). This allows us to investigate the potential of the model to produce other non-classical effects i.e. squeezing (Mahran 1992; Fakhri et al. 2021; Zou and Fang 2016), sub-Poissonian statistics (Zhang and Fan 1992; Failed 2006; Osad'ko 2005), antibunching (Ye et al. 2022; Hennrich et al. 2005; Kimble et al. 1977), revivals and collapse of Rabi oscillations (Alexanian 2022; Ozhigov et al. 2016) etc. theoretically as well as experimentally. Due to less quantum noise and large value of signal to noise ratio in one quadrature components (Failed 2022; Rani et al. 2007; Priyanka and S. 2021), such states have potential applications in gravitational wave detection (Chua et al. 2014; Caves 1981), optical communication systems (Yamamoto and Haus 1986) and quantum information (Fiurasek 2022). The concept of squeezed states has been extended to atoms (Wodkiewicz 1985) which was earlier investigated in radiation fields in nonlinear interaction processes. The atomic squeezing shown a great interest to generate squeezed states experimentally owing to their potential applications in high-resolution spectroscopy (Agarwal and Puri 1990; Kitagawa and Ueda 1993), high-precision atomic fountain clock (Sørensen and Mølmer 1999), high-precision spin polarization measurements (Sørensen et al. 1998), etc. Furthermore, squeezing has been experimentally realized for an interaction of field with atoms (Kuzmich et al. 1997; Takano et al. 2009; Muessel et al. 2014). Several authors have already investigated the squeezing in the Dicke model (Li et al. 1990; Seke 1995; Ramon et al. 1998; Saito and Ueda 1999). Li et al. (1990) studied normal and higher order squeezing in interaction of initial coherent light with multiple excited atoms in an optical cavity and found no analytic expression for quadrature variance and did not give the actual values of minimum value of squeezing parameter. Seke (1995) looked on same problem without using rotating wave approximation and found that there was no discernible change in non classical effect owing to rotating wave approximation. Ramon et al. (1998) studied the interaction of a single mode radiation field with two 2-level atoms in the ground, super radiant and excited states and conclude that the atoms in super radiant state experience the maximum squeezing. Further they used the factorization approaches valid for a strong field without any analytic expressions for excited and ground states. The squeezed atomic state was examined by Saito and Ueda (1999), who came to the conclusion that the non-classical effect might be exploited as a controllable source of squeezed radiation.

Sub-Poissonian photon statistics is an another nonclassical phenomenon (Zhang and Fan 1992; Ueda et al. 1996; Short and Mandel 1983) in which the variance of photons number is less than the average of photon number. Prakash and Chandra (1970) investigated that a nonlinear interaction with realistic light input can provide antibunching in the output light. They observed the two-photon attenuation of a laser beam with a noise component and found that antibunching can occur under specific situations. Theoretical predictions of photon antibunching in the resonance fluorescence have also been made (Carmichael and Walls 1976; Kimble and Mandel 1976). Joshi et al. (1990) and Agarwal et al. (1977) also showed the cooperative behavior of a two-atom system reduces antibunching significantly when compared to a single-atom example.

Hari Prakash et al. (2007) and some other authors (Kumar and Prakash 2010; Joshi and Puri 1989; Ficek et al. 1984; Eiselt and Risken 1991) investigated the squeezing of initially single mode radiation field caused by interactions with two identical 2-level atoms in different atomic states and reporting results for random coupling time. They have concluded that sub-Poissonian photon statistics had not been detected for the super radiant state. In the present work, we extended the results of authors (Prakash and Kumar 2007) to higher order squeezing for multi-mode radiation field with interaction of two 2-level atoms in different atomic states. It has been found that the squeezed light also show sub-Poissonian photon statistics in all the atomic states.

The present work is divided into the following sections. In Sect. 2, we obtain the unitary operator for the interaction of two 2-level atoms with multimode radiation field. Section 3 gives condition of higher order squeezing and in Sect. 4 we discuss the quantum noise with numerical value of squeezed parameter, when both the atoms in different atomic states. Sub-Poissonian photon statistics in all the atomic states has been discussed in Sect. 5. All the results are shown graphically.

2 The unitary operator for two 2-level atoms

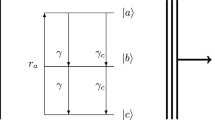
Consider a system of two 2-level atoms interacting with a multimode tuned resonant mode of radiation field which can be described by a parametric down conversion model.

Then, the Hamiltonian of the system for the proposed model is given as (Dicke 1954; Tavis and Cummings 1968).

\(H = H_{F} + H_{A} + H_{I}\) where \(H_{F} = \omega_{1} a^{\dag } a + \omega_{2} b^{\dag } b + \omega_{3} c^{\dag } c\), \(H_{A} = \omega_{a} S_{Z}\) and

$$ H_{I} = g(ab^{\dag } c^{\dag } S_{ + } + a^{\dag } bcS_{ - } ) $$
(1)

where \(H_{A} ,\,\,\,\,\,H_{F}\) and \(H_{I}\) are the atom, field and interaction Hamiltonian respectively, \(g\) is coupling constant and \(S_{Z, \pm }\) are the Dicke’s atomic operators (Dicke 1954). \(a\left( {a^{\dag } } \right)\), \(b\left( {b^{\dag } } \right)\), \(c\left( {c^{\dag } } \right)\) are the annihilation (creation) operators at frequency \(\omega_{1}\), \(\omega_{2}\) and \(\omega_{3}\), respectively. If \(\left| l \right\rangle_{k}\) and \(\left| u \right\rangle_{k}\) are the interacting lower and upper energy states of \(k^{th}\) (\(k = 1,2\)) two level atoms, then

$$ \begin{aligned} S_{ \pm } = & \sum\limits_{{k = 1,2}} {S_{{ \pm k}} } ,\quad S_{Z} = \sum\limits_{{k = 1,2}} {S_{{Zk}} } ,\quad S_{{ + k}} = \left| u \right\rangle _{{kk}} \langle l|,\quad S_{{ - k}} = \left| l \right\rangle _{{kk}} \langle u|\,{\text{and}}\, \\ S_{{Zk}} = & 1/2\left[ {\left| u \right\rangle _{{kk}} \langle u| - \left| l \right\rangle _{{kk}} \langle l|} \right] \\ \end{aligned} $$
(2)

These operators satisfy the uncertainty relation

$$ \left[ {S_{Z} ,S_{ \pm } } \right] = \pm S_{ \pm } $$
(3)
$$ S_{ \mp } \left| {j,m} \right\rangle = [(j \mp m)(j \mp m + 1)]^{\frac{1}{2}} \left| {j,m \mp 1} \right\rangle $$
(4)

where \(\left| {j,m} \right\rangle\) are the atomic states.

By solving Eq. (1) with \(\left[ {H_{0} ,H_{1} } \right] = 0\), then the unitary operator is given as

$$ U = U_{0} U_{I} \;{\text{where}}\;U_{0} = \exp ( - iH_{0} t)\;{\text{and}}\;U_{I} = \exp ( - iH_{I} t) $$
(5)

here \(U_{I}\) and \(U_{0}\) are the unitary operators in interaction picture. Representing matrices in the basis states \(\left| {1,1} \right\rangle\), \(\left| {1,0} \right\rangle\) and \(\left| {1, - 1} \right\rangle\), the interaction Hamiltonian is obtained as

$$ H_{I} = \sqrt 2 gY\,\,,\,\,\,\,\,\,Y = \left( {\begin{array}{*{20}c} 0 & {ab^{\dag } c^{\dag } } & 0 \\ {a^{\dag } bc} & 0 & {ab^{\dag } c^{\dag } } \\ 0 & {a^{\dag } bc} & 0 \\ \end{array} } \right) $$
(6)

whereas the exact expression for the unitary operator for the interacting system is given as

$$ U_{I} = \left( {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } \\ {a_{21} } & {a_{22} } & {a_{23} } \\ {a_{31} } & {a_{32} } & {a_{33} } \\ \end{array} } \right) $$
(7)

with

$$ a_{11} = 1 + (P_{na} + 1)P_{nb} P_{nc} \frac{{\{ \cos (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } ) - 1\} }}{{(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} }} $$
$$ a_{12} = - i\frac{{\{ \sin (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } )\} }}{{\sqrt {(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} } }}ab^{\dag } c^{\dag } $$
$$ a_{13} = \frac{{\{ \cos (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } ) - 1\} }}{{(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} }}a^{2} b^{\dag 2} c^{\dag 2} $$
$$ a_{21} = - ia^{\dag } bc\frac{{\{ \sin (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } )\} }}{{\sqrt {(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} } }} $$
$$ a_{22} = \cos (gt\sqrt {2(P_{na} + 1)P_{nb} P_{nc} + 2P_{na} (P_{nb} + 1)(P_{nc} + 1)} ) $$
$$ a_{23} = - i\frac{{\{ \sin (gt\sqrt {2(P_{na} + 1)(P_{nb} )(P_{nc} ) + 2(P_{na} )(P_{nb} + 1)(P_{nc} + 1)} )\} }}{{\sqrt {(P_{na} + 1)(P_{nb} )(P_{nc} ) + (P_{na} )(P_{nb} + 1)(P_{nc} + 1)} }}ab^{\dag } c^{\dag } $$
$$ a_{31} = a^{\dag 2} b^{2} c^{2} \frac{{\{ \cos (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } ) - 1\} }}{{(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} }} $$
$$ a_{32} = - ia^{\dag } bc\frac{{\{ \sin (gt\sqrt {2(P_{na} + 1)(P_{nb} )(P_{nc} ) + 2(P_{na} )(P_{nb} + 1)(P_{nc} + 1)} )\} }}{{\sqrt {(P_{na} + 1)(P_{nb} )(P_{nc} ) + (P_{na} )(P_{nb} + 1)(P_{nc} + 1)} }} $$
$$ a_{33} = 1 + P_{na} (P_{nb} + 1)(P_{nc} + 1)\frac{{\{ \cos (gt\sqrt {2(P_{na} )(P_{nb} + 1)(P_{nc} + 1) + 2(P_{na} - 1)(P_{nb} + 2)(P_{nc} + 2)} ) - 1\} }}{{(P_{na} )(P_{nb} + 1)(P_{nc} + 1) + (P_{na} - 1)(P_{nb} + 2)(P_{nc} + 2)}} $$

where \(P_{na} = a^{\dag } a\), \(P_{nb} = b^{\dag } b\) and \(P_{nc} = c^{\dag } c\) are the number of photons associated with frequencies \(\omega_{1}\), \(\omega_{2}\) and \(\omega_{3}\) respectively.

3 Condition of quantum noise squeezing during interaction of multi-mode radiation with two 2-level atoms

3.1 Condition for normal squeezing

For normal squeezing, we define the quadrature components in general only in the direction of \(\theta\) and \(\theta + \frac{\pi }{2}\) as (Prakash and Kumar 2007)

$$ \begin{aligned} X_{\theta } = & (1/\sqrt 2 )\left( {a\exp ( - i\theta ) + a^{\dag } \exp (i\theta )} \right)\;{\text{and}}\; \\ X_{{\theta + \frac{\pi }{2}}} = & (1/\sqrt 2 )\left( {a\exp ( - i(\theta + \frac{\pi }{2})) + a^{\dag } \exp (i(\theta + \frac{\pi }{2}))} \right) \\ \end{aligned} $$
(8)

Commutation relation of \(X_{\theta }\) and \(X_{{\theta + \frac{\pi }{2}}}\) is given as \(\left[ {X_{\theta } ,X_{{\theta + \frac{\pi }{2}}} } \right] = i\) and the uncertainty relation is given as

$$ \left\langle {\left( {\Delta X_{\theta } } \right)^{2} } \right\rangle \left\langle {\left( {\Delta X_{{\theta + \frac{\pi }{2}}} } \right)^{2} } \right\rangle \ge \frac{1}{4} $$
(9)

A state is squeezed in \(X_{\theta }\) variable if

$$ \left\langle {\left( {\Delta X_{\theta } } \right)^{2} } \right\rangle < \frac{1}{2} $$
(10)

Equation (8) leads to

$$ \left\langle {\left( {\Delta X_{\theta } } \right)^{2} } \right\rangle = 1/2\left[ {\left( {\left\langle {a^{\dag 2} } \right\rangle - \left\langle {a^{\dag } } \right\rangle^{2} } \right)\exp (2i\theta ) + \left( {\left\langle {a^{2} } \right\rangle - \left\langle a \right\rangle^{2} } \right)\exp ( - 2i\theta )} \right] + \left\langle {a^{\dag } a} \right\rangle - \left\langle {a^{\dag } } \right\rangle \left\langle a \right\rangle + 1/2 $$
(11)

3.2 Higher order squeezing

The operators \(Y_{\theta }\) and \(Y_{{\theta + \frac{\pi }{2}}}\) are used to define amplitude squared squeezing as (Prakash and Kumar 2007)

$$ \begin{gathered} Y_{\theta } = 1/2\left( {a^{\dag 2} \exp (i\theta ) + a^{2} \exp ( - i\theta )} \right)\;{\text{and}}\; \hfill \\ Y_{\theta } = 1/2\left( {a^{\dag 2} \exp (i(\theta + \frac{\pi }{2})) + a^{2} \exp ( - i(\theta + \frac{\pi }{2}))} \right) \hfill \\ \end{gathered} $$
(12)

The commutation relation is given as \(\left[ {Y_{\theta } ,Y_{{\theta + \frac{\pi }{2}}} } \right] = (2P_{na} + 1)\) where \(P_{na} = a^{\dag } a\).

Therefore, uncertainty relation leads to

$$ \left\langle {\left( {\Delta Y_{\theta } } \right)^{2} } \right\rangle \left\langle {\left( {\Delta Y_{{\theta + \frac{\pi }{2}}} } \right)^{2} } \right\rangle \ge \left( {P_{na} + 1/2} \right)^{2} $$
(13)

A state is squeezed in \(Y_{\theta }\) variable if

$$ \left\langle {\left( {\Delta Y_{\theta } } \right)^{2} } \right\rangle < \left( {P_{na} + 1/2} \right) $$
(14)

Equation (12) leads to

$$ \left\langle {\left( {\Delta Y_{\theta } } \right)^{2} } \right\rangle = 1/4\left[ {\left( {\left\langle {a^{\dag 4} } \right\rangle - \left\langle {a^{\dag 2} } \right\rangle^{2} } \right)\exp (2i\theta ) + \left( {\left\langle {a^{4} } \right\rangle - \left\langle {a^{2} } \right\rangle^{2} } \right)\exp ( - 2i\theta ) - 2\left\langle {a^{\dag 2} } \right\rangle \left\langle {a^{2} } \right\rangle + 2\left\langle {a^{\dag 2} a^{2} } \right\rangle } \right] + \left\langle {a^{\dag } a} \right\rangle + 1/2 $$
(15)

4 Discussion of squeezing in different atomic states

Here, we shall discuss the interaction of multimode radiation field with two 2-level atoms in three atomic states i.e. excited, ground and super radiant state.

4.1 Initially when both the atoms in excited state

At \(t = 0\), we assume that the two atoms and multimode field are in non interacting mode and the atoms are in excited state. After quantum interaction, the quantum state \(\left| \psi \right\rangle\) using Eq. (7) is represented as

$$ \begin{gathered} \left| \psi \right\rangle = \left[ {1 + (P_{na} + 1)P_{nb} P_{nc} \frac{{\{ \cos (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } ) - 1\} }}{{(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} }}} \right]\left| {1,1} \right\rangle \left| \alpha \right\rangle \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - ia^{\dag } bc\left[ {\frac{{\{ \sin (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } )\} }}{{\sqrt {(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} } }}} \right]\left| {1,0} \right\rangle \left| \alpha \right\rangle \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + a^{\dag 2} b^{2} c^{2} \left[ {\frac{{\{ \cos (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } ) - 1\} }}{{(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} }}} \right]\left| {1, - 1} \right\rangle \left| \alpha \right\rangle \hfill \\ \end{gathered} $$
(16)

We define the expectation values of annihilation and creation operators i.e. \(\left\langle a \right\rangle\) and \(\left\langle {a^{\dag } } \right\rangle\) using Eq. (16) as

$$ \left\langle a \right\rangle = \psi^{*} a\psi \;{\text{and}}\;\left\langle {a^{\dag } } \right\rangle = \psi^{*} a^{\dag } \psi $$
(17)

Therefore, we obtain

$$ \begin{aligned} \left\langle a \right\rangle = & B_{1} \exp (i\theta_{\alpha } ),\;\left\langle {a^{2} } \right\rangle = B_{2} \exp (2i\theta_{\alpha } ),\;\left\langle {a^{\dag } } \right\rangle = B_{3} \exp ( - i\theta_{\alpha } ),\;\left\langle {a^{\dag 2} } \right\rangle = B_{4} \exp ( - 2i\theta_{\alpha } ),\; \\ \left\langle {a^{\dag } a} \right\rangle = & B_{5} ,\;\left\langle {a^{\dag 2} a^{2} } \right\rangle = B_{6} ,\;\left\langle {a^{4} } \right\rangle = B_{7} \,\exp (4i\theta_{\alpha } ),\;\left\langle {a^{\dag 4} } \right\rangle = B_{8} \,\exp ( - 4i\theta_{\alpha } ) \\ \end{aligned} $$
(18)

The coefficients \(B_{1} ,\,\,B_{2} ,\,.........B_{8}\) are defined in Appendix from Eqs. (41–47)

After substituting the average values of \(\left\langle a \right\rangle\) and \(\left\langle {a^{\dag } } \right\rangle\) from Eq. (18) in Eq. (11) for normal squeezing, we get

$$ \left( {\Delta X_{\theta } } \right)^{2} = 1/2\left[ {(B_{4} - B_{3}^{2} )e^{{ - 2i(\theta_{\alpha } - \theta )}} + (B_{2} - B_{1}^{2} )e^{{2i(\theta_{\alpha } - \theta )}} } \right] - B_{3} B_{1} + B_{5} + 1/2 $$
(19)

Minima of \(\left( {\Delta X_{\theta } } \right)^{2}\) i.e. maximum squeezing occur at \(\theta = \theta_{\alpha }\).

Therefore, we get

$$ \left( {\Delta X_{\theta } } \right)^{2} - 1/2 = 1/2\left[ {(B_{4} - B_{3}^{2} ) + (B_{2} - B_{1}^{2} )} \right] - B_{3} B_{1} + B_{5} $$
(20)

Similarly, after substituting Eq. (18) in Eq. (15) of amplitude squared squeezing, we get

$$ \left( {\Delta Y_{\theta } } \right)^{2} = 1/4\left[ {(B_{8} - B_{4}^{2} )e^{{ - 2i(2\theta_{\alpha } - \theta )}} + (B_{7} - B_{2}^{2} )e^{{2i(2\theta_{\alpha } - \theta )}} - 2B_{4} B_{2} + 2B_{6} } \right] + B_{5} + 1/2 $$
(21)

Minima of \(\left( {\Delta Y_{\theta } } \right)^{2}\) i.e. maximum squeezing occurs at \(\theta = 2\theta_{\alpha }\).

Therefore, we get

$$ \left( {\Delta Y_{\theta } } \right)^{2} - (B_{5} + 1/2) = 1/4\left[ {(B_{8} - B_{4}^{2} ) + (B_{7} - B_{2}^{2} ) - 2B_{4} B_{2} + 2B_{6} } \right] $$
(22)

Figures 1 and 2 show the short time behavior of normal squeezing i.e.\(S_{E\,(X)} = \left( {\Delta X_{\theta } } \right)^{2} - 1/2\) as given in Eq. (20) and amplitude squared squeezing parameter i.e. \(S_{E\,(Y)} = \left( {\Delta Y_{\theta } } \right)^{2} - \left( {B_{5} + 1/2} \right)\) as given in Eq. (22) for different values of number of photons, respectively. It is clear from Figs. 1 and 2 that \(S_{E\,(X)}\) and \(S_{E\,(Y)}\) exhibit rapid and continuous oscillations whose amplitude increases and showing less noise with number of photons. For a large number of photons, the phenomenon of revivals and collapses is quite predictable. We have found that the minimum value of \(S_{E\,(X)}\) (i.e. maximum normal squeezing) in Fig. 1a and b are \(- 1.1 \times 10^{18}\) and \(- 6.19 \times 10^{20}\) at \(gt = 0.92\) and \(gt = 1.26\), respectively. Similarly the minimum value of \(S_{E\,(Y)}\)( i.e. maximum amplitude squared squeezing) in Fig. 2a and b are \(- 3.45 \times 10^{18}\) and \(- 1.90 \times 10^{21}\) at \(gt = 1.18\) and \(gt = 0.76\), respectively.

Fig. 1
figure 1

Variation of normal squeezing (\(S_{E(X)}\)) with coupling time (\(gt\)) for a \(P_{na} = 10,\,P_{nb} = 4,\,P_{nc} = 4\) b \(P_{na} = 10,\,P_{nb} = 6,\,P_{nc} = 6\)

Full size image
Fig. 2
figure 2

Variation of amplitude squared squeezing i.e. (\(S_{E(Y)}\)) with coupling time (\(gt\)) with a \(P_{na} = 10,\,P_{nb} = 4,\,P_{nc} = 4\); b \(P_{na} = 10,\,P_{nb} = 6,\,P_{nc} = 6\)

Full size image

4.2 When assembly of atoms in super radiant state

Now, we consider the case when both the atoms are in super radiant state. Then one can find the quantum state \(\left| \psi \right\rangle\) at \(t > 0\) using Eq. (7) as

$$ \begin{gathered} \left| \psi \right\rangle = \left[ { - i\left( {\frac{{\{ \sin (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } )\} }}{{\sqrt {(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} } }}} \right)ab^{\dag } c^{\dag } } \right]\left| {1,1} \right\rangle \left| \alpha \right\rangle \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + \left( {\cos (gt\sqrt {2(P_{na} + 1)P_{nb} P_{nc} + 2P_{na} (P_{nb} + 1)(P_{nc} + 1)} )} \right)\left| {1,0} \right\rangle \left| \alpha \right\rangle \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - ia^{\dag } bc\left[ {\frac{{\{ \sin (gt\sqrt {2(P_{na} + 1)(P_{nb} )(P_{nc} ) + 2(P_{na} )(P_{nb} + 1)(P_{nc} + 1)} )\} }}{{\sqrt {(P_{na} + 1)(P_{nb} )(P_{nc} ) + (P_{na} )(P_{nb} + 1)(P_{nc} + 1)} }}} \right]\left| {1, - 1} \right\rangle \left| \alpha \right\rangle \hfill \\ \end{gathered} $$
(23)

Using Eq. (23), we get average value of creation and annihilation operator as

$$ \begin{aligned} \left\langle a \right\rangle = & C_{1} \exp (i\theta_{\alpha } ),\,\left\langle {a^{2} } \right\rangle = C_{2} \exp (2i\theta_{\alpha } ),\,\left\langle {a^{\dag } } \right\rangle = C_{3} \exp ( - i\theta_{\alpha } ),\,\left\langle {a^{\dag 2} } \right\rangle = C_{4} \exp ( - 2i\theta_{\alpha } ),\, \\ \left\langle {a^{\dag } a} \right\rangle = & C_{5} ,\,\left\langle {a^{\dag 2} a^{2} } \right\rangle = C_{6} ,\,\left\langle {a^{4} } \right\rangle = C_{7} \,\exp (4i\theta_{\alpha } ),\,\left\langle {a^{\dag 4} } \right\rangle = C_{8} \,\exp ( - 4i\theta_{\alpha } ) \\ \end{aligned} $$
(24)

The coefficients \(C_{1} ,\,\,C_{2} ,\,.........C_{8}\) are given in Appendix from Eqs. (48–55).

Now, using Eq. (24) in Eq. (11) for normal squeezing, we get

$$ \left( {\Delta X_{\theta } } \right)^{2} = 1/2\left[ {(C_{4} - C_{3}^{2} )e^{{ - 2i(\theta_{\alpha } - \theta )}} + (C_{2} - C_{1}^{2} )e^{{2i(\theta_{\alpha } - \theta )}} } \right] - C_{3} C_{1} + C_{5} + 1/2 $$
(25)

Minima of \(\left( {\Delta X_{\theta } } \right)^{2}\) i.e. maximum squeezing occurs at \(\theta = \theta_{\alpha }\).

Therefore, we get

$$ \left( {\Delta X_{\theta } } \right)^{2} - 1/2 = 1/2\left[ {(C_{4} - C_{3}^{2} ) + (C_{2} - C_{1}^{2} )} \right] - C_{3} C_{1} + C_{5} $$
(26)

Now, using Eq. (23) in Eq. (15) of amplitude squared squeezing, we get

$$ \left( {\Delta Y_{\theta } } \right)^{2} = 1/4\left[ {(C_{8} - C_{4}^{2} )e^{{ - 2i(2\theta_{\alpha } - \theta )}} + (C_{7} - C_{2}^{2} )e^{{2i(2\theta_{\alpha } - \theta )}} - 2C_{4} C_{2} + 2C_{6} } \right] + C_{5} + 1/2 $$
(27)

Minima of \(\left( {\Delta Y_{\theta } } \right)^{2}\) i.e. maximum squeezing occurs at \(\theta = 2\theta_{\alpha }\).

Therefore, we get

$$ \left( {\Delta Y_{\theta } } \right)^{2} - (C_{5} + 1/2) = 1/4\left[ {(C_{8} - C_{4}^{2} ) + (C_{7} - C_{2}^{2} ) - 2C_{4} C_{2} + 2C_{6} } \right] $$
(28)

Here, we discuss the case when both the atoms in super radiant state, Figs. 3 and 4 show the short time behavior of normal squeezing i.e. \(S_{SR\,(X)} = \left( {\Delta X_{\theta } } \right)^{2} - 1/2\) as given in Eq. (26) and amplitude squared squeezing parameter i.e. \(S_{SR\,(Y)} = \left( {\Delta Y_{\theta } } \right)^{2} - \left( {C_{5} + 1/2} \right)\) as given in Eq. (28), respectively. In Figs. 3 and 4, we find that after a few periods, the amplitude of oscillations decay and \(S_{SR\,(X)}\) and \(S_{SR\,(Y)}\) become nearly constant. When neighboring revivals overlap, this decay is linked to a loss of regularity in the behavior of the atomic inversion. For all values of number of photons which we have taken into consideration, the minimum value of \(S_{SR\,(X)}\) (i.e. maximum normal squeezing) in Fig. 3a and b are \(- 3.87 \times 10^{18}\) and \(- 9.58 \times 10^{20}\) at \(gt = 0.06\) and \(0.04\), respectively and similarly minimum value of \(S_{SR\,(Y)}\)( i.e. maximum amplitude squared squeezing) in Fig. 4a and b are \(- 1.72 \times 10^{19}\) and \(- 4.31 \times 10^{21}\) at \(gt = 0.06\) and \(0.04\), respectively. We also found additional minima of \(S_{SR\,(X)}\) and \(S_{SR\,(Y)}\) parameters, but they are not so deep. It can also be seen from Figs. 3 and 4 that the decrease of minimum values of \(S_{SR\,(X)}\) and \(S_{SR\,(Y)}\) is linear fit and can be very much approximated by the empirical formula \(S_{SR} = f(n_{a} ,n_{b} ,n_{c} )(gt) + c\) where \(c\) is intercept on y axis when extrapolated.

Fig. 3
figure 3

Variation of normal squeezing i.e.\(S_{SR\,(X)}\) with coupling time (\(gt\)) with a \(P_{na} = 10,\,P_{nb} = 4,\,P_{nc} = 4\); b \(P_{na} = 10,\,P_{nb} = 6,\,P_{nc} = 6\)

Full size image
Fig. 4
figure 4

Variation of amplitude squared squeezing i.e. \(S_{SR\,(Y)}\) with coupling time (\(gt\)) with a \(P_{na} = 10,\,P_{nb} = 4,\,P_{nc} = 4\); b \(P_{na} = 10,\,P_{nb} = 6,\,P_{nc} = 6\)

Full size image

4.3 Initially when both the atoms in ground state

At \(t = 0\), we assume that the two atoms are in ground state and multimode fields are in non interacting mode. After quantum interaction, the quantum state \(\left| \psi \right\rangle\) using Eq. (7) is represented as

$$ \begin{gathered} \left| \psi \right\rangle = \left[ {\left( {\frac{{\{ \cos (gt\sqrt {2(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + 2(P_{na} + 1)P_{nb} P_{nc} } ) - 1\} }}{{(P_{na} + 2)(P_{nb} - 1)(P_{nc} - 1) + (P_{na} + 1)P_{nb} P_{nc} }}} \right)a^{2} b^{\dag 2} c^{\dag 2} } \right]\left| {1,1} \right\rangle \left| \alpha \right\rangle \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - i\left( {\frac{{\{ \sin (gt\sqrt {2(P_{na} + 1)(P_{nb} )(P_{nc} ) + 2(P_{na} )(P_{nb} + 1)(P_{nc} + 1)} )\} }}{{\sqrt {(P_{na} + 1)(P_{nb} )(P_{nc} ) + (P_{na} )(P_{nb} + 1)(P_{nc} + 1)} }}} \right)ab^{\dag } c^{\dag } \left| {1,0} \right\rangle \left| \alpha \right\rangle \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + \left[ {1 + P_{na} (P_{nb} + 1)(P_{nc} + 1)\frac{{\{ \cos (gt\sqrt {2(P_{na} )(P_{nb} + 1)(P_{nc} + 1) + 2(P_{na} - 1)(P_{nb} + 2)(P_{nc} + 2)} ) - 1\} }}{{(P_{na} )(P_{nb} + 1)(P_{nc} + 1) + (P_{na} - 1)(P_{nb} + 2)(P_{nc} + 2)}}} \right]\left| {1, - 1} \right\rangle \left| \alpha \right\rangle \hfill \\ \end{gathered} $$
(29)

Then straightforward calculations yields to

$$ \begin{aligned} \left\langle a \right\rangle = & D_{1} \exp (i\theta_{\alpha } ),\,\left\langle {a^{2} } \right\rangle = D_{2} \exp (2i\theta_{\alpha } ),\,\left\langle {a^{\dag } } \right\rangle = D_{3} \exp ( - i\theta_{\alpha } ),\,\left\langle {a^{\dag 2} } \right\rangle = D_{4} \exp ( - 2i\theta_{\alpha } ),\, \\ \left\langle {a^{\dag } a} \right\rangle = & D_{5} ,\,\left\langle {a^{\dag 2} a^{2} } \right\rangle = D_{6} ,\,\left\langle {a^{4} } \right\rangle = D_{7} \,\exp (4i\theta_{\alpha } ),\,\left\langle {a^{\dag 4} } \right\rangle = D_{8} \,\exp ( - 4i\theta_{\alpha } ) \\ \end{aligned} $$
(30)

The coefficients \(D_{1} ,\,\,D_{2} ,\,.........D_{8}\) are defined in Appendix from Eq. (56–63).

After substituting Eq. (30) in Eq. (11), we get

$$ \left( {\Delta X_{\theta } } \right)^{2} = 1/2\left[ {(D_{4} - D_{3}^{2} )e^{{ - 2i(\theta_{\alpha } - \theta )}} + (D_{2} - D_{1}^{2} )e^{{2i(\theta_{\alpha } - \theta )}} } \right] - D_{3} D_{1} + D_{5} + 1/2 $$
(31)

Minima of \(\left( {\Delta X_{\theta } } \right)^{2}\) i.e. maximum squeezing occurs at \(\theta = \theta_{\alpha }\).

Therefore, we get

$$ \left( {\Delta X_{\theta } } \right)^{2} - 1/2 = 1/2\left[ {(D_{4} - D_{3}^{2} ) + (D_{2} - D_{1}^{2} )} \right] - D_{3} D_{1} + D_{5} $$
(32)

Similarly, after substituting Eq. (30) in Eq. (15), we get

$$ \left( {\Delta Y_{\theta } } \right)^{2} = 1/4\left[ {(D_{8} - D_{4}^{2} )e^{{ - 2i(2\theta_{\alpha } - \theta )}} + (D_{7} - D_{2}^{2} )e^{{2i(2\theta_{\alpha } - \theta )}} - 2D_{4} D_{2} + 2D_{6} } \right] + D_{5} + 1/2 $$
(33)

Minima of \(\left( {\Delta Y_{\theta } } \right)^{2}\) i.e. maximum squeezing occur at \(\theta = 2\theta_{\alpha }\).

Therefore, we get

$$ \left( {\Delta Y_{\theta } } \right)^{2} - (D_{5} + 1/2) = 1/4\left[ {(D_{8} - D_{4}^{2} ) + (D_{7} - D_{2}^{2} ) - 2D_{4} D_{2} + 2D_{6} } \right] $$
(34)

In this case, the short time behavior of normal squeezing parameter i.e.\(S_{G\,(X)} = \left( {\Delta X_{\theta } } \right)^{2} - 1/2\) as shown in Eq. (32) and amplitude squared squeezing parameter i.e. \(S_{G\,(Y)} = \left( {\Delta Y_{\theta } } \right)^{2} - (D_{5} + 1/2)\) as shown in Eq. (34) are representing in Figs. 5 and 6.We found that the minimum value of squeezing parameter enhanced with increase in the coupling time. An interesting feature for this atomic state is that the minimum value of \(S_{G\,(X)}\) and \(S_{G\,(Y)}\) is achieved after a relatively large number of oscillations. We observed that the minimum value of \(S_{G\,(X)}\) (maximum normal squeezing) in Fig. 5a and b are \(- 5.09 \times 10^{10}\) and \(- 3.16 \times 10^{11}\) at \(gt = 1.46\) and \(1.6\), respectively and minimum value of \(S_{G\,(Y)}\) (maximum amplitude squared squeezing) in Fig. 6a and b are \(- 1.76 \times 10^{11}\) and \(- 1.07 \times 10^{11}\) at \(gt = 1.46\) and \(1.42\), respectively. It has also been observed from Figs. 5 and 6 that the increase in the minimum values of \(S_{G\,(X)}\) and \(S_{G\,(Y)}\) is also linear fit with slope negative (reverse to case II) and can be very much approximated by the empirical formula \(S_{G} = - f(n_{a} ,n_{b} ,n_{c} )(gt) + c\).

Fig. 5
figure 5

Variation of normal squeezing i.e. \(S_{G\,(X)}\) with coupling time (\(gt\)) with a \(P_{na} = 10,\,P_{nb} = 4,\,P_{nc} = 4\); b \(P_{na} = 10,\,P_{nb} = 6,\,P_{nc} = 6\)

Full size image
Fig. 6
figure 6

Variation of higher order squeezing i.e.\(S_{G\,(Y)}\) with coupling time (\(gt\)) with a \(P_{na} = 10,\,P_{nb} = 4,\,P_{nc} = 4\); b \(P_{na} = 10,\,P_{nb} = 6,\,P_{nc} = 6\)

Full size image

5 The Mandel’s Q parameter for both the atoms in different atomic states

The Q parameter is given as (Mandel 1979)

$$ Q = \frac{{\left\langle {\left( {\Delta P_{na} } \right)^{2} } \right\rangle - \left\langle {P_{na} } \right\rangle }}{{\left\langle {P_{na} } \right\rangle }} $$
(35)

where \(\left\langle {\left( {\Delta P_{na} } \right)^{2} } \right\rangle = \left\langle {P_{na}^{2} } \right\rangle - \left\langle {P_{na} } \right\rangle^{2}\), \(\left\langle {P_{na}^{2} } \right\rangle = \left\langle {a^{\dag } a} \right\rangle + \left\langle {a^{\dag 2} a^{2} } \right\rangle\) and \(P_{na} = a^{\dag } a\). After substituting all these values in above Eq. (35), we get

$$ Q = \frac{{\left\langle {a^{\dag 2} a^{2} } \right\rangle - \left\langle {a^{\dag } a} \right\rangle^{2} }}{{\left\langle {a^{\dag } a} \right\rangle }} $$
(36)

When \(Q < 0\), the photon statistics is called sub-Poissonian photon statistics.

5.1 When both the atoms are in excited state

Using Eq. (18) in Eq. (36), we get

$$ Q = \left[ {\frac{{\{ (B_{6} - (B_{5} )^{2} )\} }}{{B_{5} }}} \right] $$
(37)

5.2 Initially when both the atoms are in super-radiant state

Using Eq. (24) in Eq. (36), we get

$$ Q = \left[ {\frac{{\{ (C_{6} - (C_{5} )^{2} )\} }}{{C_{5} }}} \right] $$
(38)

5.3 When both the atoms are in ground state

After substituting Eq. (30) in Eq. (36), we get Q parameter as

$$ Q = \left[ {\frac{{\{ (D_{6} - (D_{5} )^{2} )\} }}{{D_{5} }}} \right] $$
(39)

Above Eqs. (37–39) show that the photon statistics for different atomic state.

Figure 7 shows the photon statistics using Mandel’s Q parameter from Eqs. (37–39) in all the atomic states. We found that as we increase the number of photons, Q parameter becomes more negative and we get more sub-Poissonian photon statistics behavior. It is evident from Fig. 7 that the curve is polynomial fit in all the atomic states.

Fig. 7
figure 7

Variation of Mandel’s Q parameter versus \(gt\) with different number of photons when both the atoms in different atomic states

Full size image

6 Conclusion

We have investigated that the two 2-level atoms interacting with multimode strong radiation field produce normal squeezing and amplitude squared squeezing. We found that normal and higher order quantum squeezing increase with increase of number of photons and coupling time. The results show the lowest limit to quantum noise for super radiant state among the other atomic states. Further, it is also found that resonant oscillations increase per period with coupling time and increase in sub-Poissonian photons statistics with increase of number of photons in all the atomic states. It is also found that the squeezing give more noise reduction than the models proposed in literature for the interaction of radiation field with atoms (Prakash and Kumar 2007; Kumar and Prakash 2010; Joshi and Puri 1989; Ficek et al. 1984; Eiselt and Risken 1991). This will help to improve the outputs of quantum information channels.