1 Introduction

Nanoparticles are any material in the nanoscale, which are used by the nanotechnology researchers to explore new applications of elements in this tiny form.

The quantum dot [1,2,3,4,5,6,7,8,9,10,11,12] is a nanoparticle made of any semiconducting material such as silicon, cadmium sulfide, cadmium selenide, or indium arsenide [13]. The quantum dots were discovered by Alexey I. Ekimov, in 1981 [14]. According to Alexey’s theory, the quantum dots are small nanoparticles whose color varies by their size and that their diameter ranges from 2 to 10 nm (nanometers) [1,2,3,4,5,6]. In general, their properties [15] are determined by size, shape, composition, and structure [16]. Because of their high extinction coefficient, which describes how fast the light passes through the material, the quantum dots have many potential contributions for the optical applications. They are particularly vital for the light-harvesting technologies, such as solar cells and photovoltaics. Also, due to their superior transport and optical properties, they have very promising uses in amplifiers, diode lasers, and biological sensors [17, 18].

Our study has focused on solving the master equation for the density matrix \(\rho \) of a single semiconductor quantum dot [1,2,3,4,5,6] excited by a pair of optical pulses. Although this problem has been handled in physics theoretically and experimentally [19,20,21,22], this vital area of research has not been handled mathematically in adequate way. Therefore, after reviewing previous studies, we believe the mathematical solution of this system will integrate with the physical treatments and represent a new perspective, from which we can investigate many equations for semiconductor quantum dot systems. Through our mathematical study of this system, some important observations are revealed. For example, long-lived quantum coherence in all the curves and a decay, in some of the curves, have been observed. They can be controlled over time through parameters.

Therefore, the mathematical study of our system can help a lot in laboratory experiments and in many applications in this field , such as LED lamps, medical imaging, quantum computing, transistors [23, 24], biology, and biochemistry.

Accordingly, as applications on the solution of this system, we have calculated the atomic occupation probabilities, \(\rho _{gg}(t)\), \(\rho _{mm}(t)\) and \(\rho _{ee}(t),\) the atomic population inversion \(\langle S_\mathrm{{z}}\rangle ,\) the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}}).\) The atomic population inversion \(\langle S_\mathrm{{z}}\rangle \) in the case of a two-level system is defined as “the difference between the probabilities of finding the atom in its excited state and the probabilities of finding it in its ground state.” In the case of a three-level system, it is defined as “the difference between the probability of finding the atom in its excited state and the probability of finding it in the lower states of energy (the exciton and ground states). Or, it is defined as “the difference between the total probability of an atom at the biexciton, exciton states and ground state.” In our system, a three-level semiconductor quantum dot, we have used the following formula for the atomic population inversion \(\langle S_\mathrm{{z}}\rangle \) [25, 26]:

$$\begin{aligned} \langle S_\mathrm{{z}}\rangle =\rho _{gg}(t)-\rho _{mm}(t)-\rho _{ee}(t), \end{aligned}$$
(1)

while the time evolution of the purity P(t)  is defined as follows [25]:

$$\begin{aligned} P(t)&= \mathrm{{Tr}}_\mathrm{{(Atom)}}(\rho _\mathrm{{Atom}}^{2}(t)) \\&= \rho _{gg}^{2}++\rho _{mm}^{2}+\rho _{ee}^{2}+2\big (\left| \rho _{gm}\right| ^{2}+\left| \rho _{ge}\right| ^{2}+\left| \rho _{me}\right| ^{2}\big ) \end{aligned}$$
(2)

where \(\rho _\mathrm{{(Atom)}}(t)\) is the reduced density matrix of the system which is defined by \(\rho _\mathrm{{(Atom)}}(t)= \mathrm{{Tr}}_{\mathrm{{(Field)}}}\) \(\rho (t)\). The purity P(t) is an indicator of the degree of effect of the field on the atom.

The range of their values is between \((1-1/\zeta )\) and 0, where \((1-1/\zeta )\) refers to a completely mixed state, 0 refers to a completely pure state, (here, \(\zeta \) is the dimension of the density matrix) [25]. For example, we have \(\zeta =2\) in case two-level atom, and \(\zeta =3\) in case three-level atom. On the other hand, entropy is a measure that determines the amount of lack of information about the system. It is also a measure of the degree of chaos in the system, resulting from the effect of the field or the surrounding environment on the system [27,28,29,30, 30,31,32]. There are many types of entropy, including differential entropy [33], approximate entropy, sample entropy [34], permutation entropy [35, 36] and multiscale entropy [37].

Also, there are three types of quantum interactions, which are atom–atom, field–field and atom–field interactions. These interactions have been studied in a huge number of works; see, for example, Refs. [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. Each of these interactions interprets a certain type of physical phenomena [55,56,57,58,59,60]. In our current study, we have focused on calculating information entropy \(H(\sigma _\mathrm{{z}})\) of the type of atom–field interaction.

The information entropy of the atomic operator \(\sigma _\mathrm{{z}}\) is defined as: [27,28,29]

$$\begin{aligned} H(\sigma _\mathrm{{z}})=-\sum _{r=1}^{\xi }P_{r}(\sigma _\mathrm{{z}})\ln P_{r}(\sigma _\mathrm{{z}}), \end{aligned}$$
(3)

where the probability distribution \(P_{r}(\sigma _\mathrm{{z}})\) for \(\xi \) possible outcomes of measurements for an arbitrary quantum state of an atomic operator \(\sigma _\mathrm{{z}}\) is

$$\begin{aligned} P_{r}(\sigma _\mathrm{{z}})=\left\langle \Psi _\mathrm{{zr}}\right| \rho \left| \Psi _\mathrm{{zr}}\right\rangle , \end{aligned}$$
(4)

\(\rho \) is the density operator of the total system, and \(\left| \Psi _\mathrm{{zr}}\right\rangle \) is eigenvector of the atomic operator \(\sigma _{\beta }\):

$$\begin{aligned} \sigma _\mathrm{{z}}\left| \Psi _\mathrm{{zr}}\right\rangle =\epsilon _\mathrm{{zr}}\left| \Psi _\mathrm{{zr}}\right\rangle ,\quad r=1,2,\ldots ,\xi , \end{aligned}$$
(5)

where \(\epsilon _\mathrm{{zr}}\) is the eigenvalue of the atomic operator \(\sigma _\mathrm{{z}}\) shown in Eq. (5).

For a two-level system, \(\xi =2\), and in case of a three-level system, \(\xi =3\), and so on. Here, we have calculated the information entropy \(H(\sigma _\mathrm{{z}})\) whose formula is as follows:

$$\begin{aligned} H(\sigma _\mathrm{{z}})=-\big (\rho _{gg}(t)\ln (\rho _{gg}(t)+\rho _{mm}(t)\ln (\rho _{mm}(t)+\rho _{ee}(t)\ln (\rho _{ee}(t)\big ). \end{aligned}$$
(6)

This paper has been organized as follows: in Sect. (2), we have obtained the analytical solution of a three-level semiconductor quantum dot. In Sect. (3), we have discussed the effects of the phenomenological damping parameters, the electromagnetic field amplitude \(E_{0}\) of the excitation pulse \(E(\omega )\), and the detuning parameters on the atomic occupation probabilities, \(\rho _{gg}(t)\), \(\rho _{mm}(t)\), and \(\rho _{ee}(t),\) the atomic population inversion \( \langle S_\mathrm{{z}}\rangle ,\) the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}})\). Finally, in Sect. (4), the conclusions and recommendations for further research have been presented.

2 The model

Here, We study a single semiconductor quantum dot (three-level atom) excited by a pair of optical pulses. The excitation of a single semiconductor quantum dot is in two stages.

The first stage (the first pulse) is done by populating the biexciton level \( \left| e\right\rangle \) by absorbing two photons, while the second stage (the second pulse) generates population in the exciton level \(\left| m\right\rangle \) via de-excitation from the biexciton level. The equation of motion for the density operator \(\rho \) representing our system is as follows:

$$\begin{aligned} \frac{\mathrm{{d}}\rho }{\mathrm{{d}}t}=-\frac{i}{\hslash }\left[ H_{T},\rho \right] -\frac{i}{ \hslash }\left[ H_{r},\rho \right] . \end{aligned}$$
(7)

where

$$\begin{aligned} H_{T}=H_{0}+H_{I}, \end{aligned}$$
(8)

the unperturbed Hamiltonian \(H_{0}\) for this system is defined as:

$$\begin{aligned} H_{0}=\left( \begin{array}{lll} \hslash \omega _{g} & 0 & 0 \\ 0 & \hslash \omega _{m} & 0 \\ 0 & 0 & \hslash \omega _{e} \end{array} \right) , \end{aligned}$$
(9)

where \(\hslash \omega _{g},\) \(\hslash \omega _{m}\), and \(\hslash \omega _{e}\) are the energy of the ground, exciton, and biexciton states, respectively. The transitions that are allowed are \(\left| e\right\rangle \longleftrightarrow \left| m\right\rangle \) and \( \left| m\right\rangle \longleftrightarrow \left| g\right\rangle \), while the transitions \(\left| e\right\rangle \longleftrightarrow \left| g\right\rangle \) are prohibited.

The interaction Hamiltonian \(H_{I}\) is defined as:

$$\begin{aligned} H_{I}=\left( \begin{array}{lll} 0 & -E_{0}\,\gamma _{gm} & 0 \\ -E_{0}^{*}\,\gamma _{mg} & 0 & -E_{0}^{*}\gamma _{me} \\ 0 & -E_{0}\,\gamma _{em} & 0 \end{array} \right) , \end{aligned}$$
(10)

where \(\gamma _{gm},\) \(\gamma _{mg},\) \(\gamma _{em}\), and \(\gamma _{me}\) are the elements of the transition dipole moment matrix operator, and \(E_{0}\) is the electromagnetic field amplitude of the excitation pulse \( E(\omega )\).

We take here \(E_{0}=E_{0}^{*},\) where \(E_{0}\) is the eigenvalue of Hermitian operator.

The relaxation Hamiltonian \(H_{r}\) is given by:

$$\begin{aligned} H_{r}=\left( \begin{array}{lll} \eta _{g} & 0 & 0 \\ 0 & \eta _{m} & 0 \\ 0 & 0 & \eta _{e} \end{array} \right) , \end{aligned}$$
(11)

where \(\eta _{g},\) \(\eta _{m}\), and \(\eta _{e}\) are the phenomenological damping parameters in the energy states \(\left| g\right\rangle \), \(\left| m\right\rangle \), and \(\left| e\right\rangle ,\) respectively.

We define the density matrix as the following:

$$\begin{aligned} \rho =\left( \begin{array}{lll} \rho _{gg} & \rho _{gm} & \rho _{ge} \\ \rho _{mg} & \rho _{mm} & \rho _{me} \\ \rho _{eg} & \rho _{em} & \rho _{ee} \end{array} \right) . \end{aligned}$$
(12)

In order to solve our system we follow the following procedures. By substituting from Eqs. (8), (9), (10), and (11) in Eq. (7), we can write the equation of motion (7) as the following:

$$\begin{aligned} i\frac{\mathrm{{d}}\rho }{\mathrm{{d}}t}=\Phi \rho , \end{aligned}$$
(13)

where \(\rho \) is a column matrix defined as:

$$\begin{aligned} \rho =(\rho _{gg}\,\rho _{gm}\,\rho _{ge}\,\rho _{mg} \,\rho _{mm}\,\rho _{me}\,\rho _{eg}\,\rho _{em}\,\rho _{ee})^{T}, \end{aligned}$$
(14)

and

$$\begin{aligned} \Phi&= \left( \begin{array}{llll} 0 & \lambda & 0 & -\lambda \\ \lambda & (\delta _{1}-i\Upsilon ^{-1}) & \mu & 0 \\ 0 & \mu & (\delta _{1}+\delta _{2}-i\Upsilon ^{-1}) & 0 \\ -\lambda & 0 & 0 & -(\delta _{1}+i\Upsilon ^{-1}) \\ 0 & -\lambda & 0 & \lambda \\ 0 & 0 & -\lambda & 0 \\ 0 & 0 & 0 & -\mu \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right. \\&\left. \begin{array}{lllll} 0 & 0 & 0 & 0 & 0 \\ -\lambda & 0 & 0 & 0 & 0 \\ 0 & -\lambda & 0 & 0 & 0 \\ \lambda & 0 & -\mu & 0 & 0 \\ 0 & \mu & 0 & -\mu & 0 \\ \mu & 0 & 0 & 0 & -\mu \\ 0 & 0 & -(\delta _{1}+\delta _{2}+i\Upsilon ^{-1}) & \lambda & 0 \\ -\mu & 0 & \lambda & -(\delta _{2}+i\Upsilon ^{-1}) & \mu \\ 0 & -\mu & 0 & \mu & 0 \end{array} \right) \end{aligned}$$
(15)

where

$$\begin{aligned} \delta _{1} =\omega -\omega _{gm},\;\delta _{2}=\omega -\omega _{me}, \end{aligned}$$
(16)
$$\begin{aligned} \omega _{gm}&=\omega _{m}-\omega _{g},\;\omega _{me}=\omega _{e}-\omega _{m},\\ \lambda&=\frac{\gamma _{gm}E_{0}}{2\hslash },\;\mu =\frac{\gamma _{me}E_{0}}{2\hslash },\\ \Upsilon ^{-1}&\sim \eta _{g}\sim \eta _{m}\sim \eta _{e},\\ \left| \gamma _{ij}\right|&=\left| \gamma _{ji}\right| =\gamma _{ij}. \end{aligned}$$

As shown in Eqs. (13), (14), and (15), it is necessary to solve a system of nine differential equations, where we see the matrix of coefficients consisting of \(9\times 9\) dimensions. It is difficult to solve this system of differential equations except by approximate methods, so the coefficients matrix must be reduced in order to get an analytical solution. The matrix of coefficients was previously reduced to \(8\times 8\) by using the concept of pseudospin. But, here, we reduce the coefficients matrix to \(6\times 6\) by the following procedure:

We define new elements by writing combinations of density matrix elements as follows [61, 62]:

$$\begin{aligned} M_{1}&=\rho _{gm}+\rho _{mg},\;M_{2}=-i(\rho _{gm}-\rho _{mg}), \;M_{3}=\rho _{gg}-\rho _{mm}, \\ M_{4}&=\rho _{me}+\rho _{em},\;M_{5}=-i(\rho _{me}-\rho _{em}), \;M_{6}=\rho _{mm}-\rho _{ee}. \end{aligned}$$
(17)

Hence, the equation of motion of the density matrix (13) is as follows:

$$\begin{aligned} i\frac{\mathrm{{d}}M}{\mathrm{{d}}t}=\Psi M, \end{aligned}$$
(18)

where

$$\begin{aligned} \Psi =\left( \begin{array}{cccccc} -\Upsilon ^{-1} & \delta _{1} & 0 & 0 & 0 & 0 \\ -\delta _{1} & -\Upsilon ^{-1} & -2\lambda & 0 & 0 & 0 \\ 0 & 2\lambda & 0 & 0 & -\mu & 0 \\ 0 & 0 & 0 & -\Upsilon ^{-1} & \delta _{2} & 0 \\ 0 & 0 & 0 & -\delta _{2} & -\Upsilon ^{-1} & -2\mu \\ 0 & -\lambda & 0 & 0 & 2\mu & 0 \end{array} \right) . \end{aligned}$$
(19)

Hence, we can solve the equation of motion (19) by using the Laplace transform. After long calculations, we get the following:

$$\begin{aligned} M_{1}&= -\lambda \delta _{1}\left( \sum _{k=1}^{6}\frac{2L_{k}}{\epsilon _{k} }\right) , \\ M_{2}&= -2\lambda \left( \sum _{k=1}^{6}\frac{L_{k}(\Upsilon +S_{k})}{ \epsilon _{k}}\right) , \\ M_{3}&= \sum _{k=1}^{6}\frac{L_{k}(\delta _{2}^{2}+(\Upsilon +S_{k})^{2})}{ \epsilon _{k}}, \\ M_{4}&= -4\lambda ^{2}\mu \delta _{2}\left( \sum _{k=1}^{6}\frac{ e^{tS_{k}}(\Upsilon +S_{k})}{\epsilon _{k}}\right) , \\ M_{5}&= -4\lambda ^{2}\mu \left( \sum _{k=1}^{6}\frac{e^{tS_{k}}(\Upsilon +S_{k})^{2}}{\epsilon _{k}}\right) , \\ M_{6}&= 2\lambda ^{2}\sum _{k=1}^{6}\frac{e^{tS_{k}}(\Upsilon +S_{k})(\delta _{2}^{2}+(\Upsilon +S_{k})^{2})}{\epsilon _{k}}, \\ \epsilon _{k}&= \prod _{\begin{array}{c} r=1 \\ r\ne k \end{array}}^{6}\left( S_{k}-S_{r}\right) . \end{aligned}$$
(20)

Since the calculations are so huge and complex, we write the remaining variables in case \(\lambda =\mu \) and \(\delta _{1}=\delta _{2}\) as follows:

$$\begin{aligned} L_{k}&=e^{tS_{k}}\big (4\lambda ^{2}\Upsilon +S_{k}(4\lambda ^{2}+\delta _{1}^{2}+(\Upsilon +S_{k})^{2}\big ),\end{aligned}$$
(21)
$$\begin{aligned} S_{1}&= \frac{-18\lambda ^{2}-3\delta _{1}^{2}+\big (\Upsilon -(A+3\sqrt{3}G)^{ \frac{1}{3}}\big )^{2}}{3(A+B)^{\frac{1}{3}}}, \\ S_{2}&= \frac{1}{12}\left( -8\Upsilon +\frac{2(1+i\sqrt{3})R}{(A+B)^{\frac{1 }{3}}}+2i(i+\sqrt{3})(A+B)^{\frac{1}{3}}\right) , \\ S_{3}&= \frac{1}{12}\left( -8\Upsilon +\frac{2(1-i\sqrt{3})R}{(A+B)^{\frac{1 }{3}}}-2i(i+\sqrt{3})(A+B)^{\frac{1}{3}}\right) , \\ S_{4}&= \frac{-6\lambda ^{2}-3\delta _{1}^{2}+(\Upsilon -(F+3\sqrt{3}J)^{ \frac{1}{3}})^{2}}{3(P+Q)^{\frac{1}{3}}}, \\ S_{5}&= \frac{1}{12}\left( -8\Upsilon +\frac{2(1+i\sqrt{3})F}{(P+Q)^{\frac{1 }{3}}}+2i(i+\sqrt{3})(P+Q)^{\frac{1}{3}}\right) , \\ S_{6}&= \frac{1}{12}\left( -8\Upsilon +\frac{2(1-i\sqrt{3})F}{(P+Q)^{\frac{1 }{3}}}-2i(i+\sqrt{3})(P+Q)^{\frac{1}{3}}\right) . \end{aligned}$$
(22)

And

$$\begin{aligned} A&= -27\lambda ^{2}\Upsilon ^{-1}+9\delta _{1}^{2}\Upsilon ^{-1}+(\Upsilon ^{-1})^{3} \\ B&= \sqrt{(18\lambda ^{2}+3\delta _{1}^{2}-(\Upsilon ^{-1})^{2})^{3}+(\Upsilon ^{-1})^{2}(-27\lambda ^{2}+9\delta _{1}^{2}+(\Upsilon ^{-1})^{2})^{2}} \\ R&= 18\lambda ^{2}+3\delta _{1}^{2}-(\Upsilon ^{-1})^{2} \\ Q&= \sqrt{(6\lambda ^{2}+3\delta _{1}^{2}-(\Upsilon ^{-1})^{2})^{3}+(\Upsilon ^{-1})^{2}(-9\lambda ^{2}+9\delta _{1}^{2}+(\Upsilon ^{-1})^{2})^{2}} \\ P&= -9\lambda ^{2}\Upsilon ^{-1}+9\delta _{1}^{2}\Upsilon ^{-1}+(\Upsilon ^{-1})^{3} \\ F&= 6\lambda ^{2}+3\delta _{1}^{2}-(\Upsilon ^{-1})^{2} \\ G&= \sqrt{216\lambda ^{6}+9\lambda ^{4}(12\delta _{1}^{2}-(\Upsilon ^{-1})^{2})+\delta _{1}^{2}(\delta _{1}^{2}+(\Upsilon ^{-1})^{2})^{2}+6\lambda ^{2}(3\delta _{1}^{4}-5\delta _{1}^{2}(\Upsilon ^{-1})^{2})} \\ J&= \sqrt{8\lambda ^{6}+\lambda ^{4}(12\delta _{1}^{2}-(\Upsilon ^{-1})^{2})+\delta _{1}^{2}(\delta _{1}^{2}+(\Upsilon ^{-1})^{2})^{2}+2\lambda ^{2}(3\delta _{1}^{4}-5\delta _{1}^{2}(\Upsilon ^{-1})^{2})}. \end{aligned}$$
(23)

So from Eqs. (17) and (20), we can get the density matrix elements, which satisfy the equation of motion (13), as follows:

$$\begin{aligned} \rho _{gg}&= \frac{1}{3}(1+2M_{3}+M_{6}) \\ \rho _{mm}&= \frac{1}{3}(1-M_{3}+M_{6}) \\ \rho _{ee}&= \frac{1}{3}(1-M_{3}-2M_{6}) \\ \rho _{gm}&= \frac{1}{2}(M_{1}+iM_{2}) \\ \rho _{mg}&= {\bar{\rho }}_{gm}\text { (the complex conjugate of }\rho _{gm}) \\ \rho _{me}&= \frac{1}{2}(M_{4}+iM_{5}) \\ \rho _{em}&= {\bar{\rho }}_{me}\text { (the complex conjugate of }\rho _{\rho _{me}}) \\ \rho _{ge}&= \rho _{eg}=0. \end{aligned}$$
(24)

As can be seen from the results in Eq. (25), that \(\rho _{ge}=\rho _{eg}=0\). This is consistent with what we said earlier, that there is no transitions between the ground state \(\left| g\right\rangle \) and biexciton state \(\left| e\right\rangle ,\) \(\left| m\right\rangle \nleftrightarrow \left| e\right\rangle \). That is, the solution is consistent with the nature of the system under study.

As applications on the previous solution of our system, we discuss the atomic occupation probabilities, \(\rho _{gg}(t)\), \(\rho _{mm}(t)\), and \(\rho _{ee}(t),\) the atomic population inversion \(\langle S_\mathrm{{z}}\rangle ,\) the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}})\) of the single semiconductor quantum dot.

3 Results and discussion

Based on the analytical solution of a three-level semiconductor quantum dot in the previous section, we investigate the evolution in time of the atomic occupation probabilities, \(\rho _{gg}(t)\), \(\rho _{mm}(t)\), and \(\rho _{ee}(t),\) the atomic population inversion, \(\langle S_\mathrm{{z}}\rangle ,\) the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}}).\)

In the numerical results, we consider the initial state \(\rho _{ee}(0)=1,\) \( \rho _{ij}(0)=0\) for every \(i\ne e,\) \(j\ne e\), (this means that initially our system will be in the excited state). In all figures, we can observe obviously the emergence of long-lived quantum coherence. This means that, the curve after a certain period time becomes fixed at a certain value, wherein the effect of the parameters fades away. In other words, the curve after some oscillations becomes fixed, without any effect of time. Now, We are going to analyze and study all figures in a simplified way, so that we can know the effect of different parameters on the behavior of our system.

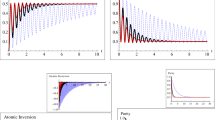
In Figs. 1 and 2, we investigate the effects of the phenomenological damping parameters (we take \(\Upsilon ^{-1}\sim \eta _{g}\sim \eta _{m}\sim \eta _{e})\) on the atomic occupation probabilities, \(\rho _{gg}(t)\), \(\rho _{mm}(t)\), and \(\rho _{ee}(t),\) the atomic population inversion \(\langle S_\mathrm{{z}}\rangle ,\) the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}})\) in case of the detuning parameters \(\delta _{1}=\delta _{2}=0.5\) and the parameters \(\lambda =\mu =0.3\) at \(\Upsilon ^{-1}=\eta _{g}=\eta _{m}=\eta _{e}=1,\) 5, and 10. The curves of the atomic occupation probability \(\rho _{gg}(t)\), the atomic population inversion \(\langle S_\mathrm{{z}}\rangle \), and the purity P(t) start from their maximum value at \(\rho _{gg}(t)=\langle S_\mathrm{{z}}\rangle =P(t)=1\) (the case of completely pure state), while the curves of the atomic occupation probabilities \(\rho _{mm}(t)\), \(\rho _{ee}(t)\), and the information entropy \(H(\sigma _\mathrm{{z}})\) start from their minimum value at \(\rho _{mm}(t)=\rho _{ee}(t)=H(\sigma _\mathrm{{z}})=0\). Thereafter, the atomic occupation probability \(\rho _{gg}(t)\), the atomic population inversion \( \langle S_\mathrm{{z}}\rangle \), and the purity P(t) gradually decay until they become fixed at a certain value after a period time (long-lived quantum coherence). As the damping parameter \(\Upsilon ^{-1}\) increases, the curves of \(\rho _{gg}(t),\) \(\langle S_\mathrm{{z}}\rangle \) and P(t) reach stability faster than before (the case of mixed state). The curves of the atomic occupation probabilities \(\rho _{mm}(t)\), \(\rho _{ee}(t)\), and \( H(\sigma _\mathrm{{z}})\) are increased suddenly until they reach their maximum value and settle at a certain value after a period time at a constant value (long-lived quantum coherence). Reaching the steady state becomes faster when the damping parameter increases, because the increase in the curves of \(\rho _{mm}(t)\), \(\rho _{ee}(t)\), and \(H(\sigma _\mathrm{{z}})\) resists the increase in the damping parameter. This, in turn, makes the curves of \(\rho _{mm}(t)\), \(\rho _{ee}(t)\), and \(H(\sigma _\mathrm{{z}})\) decay.

Fig. 1
figure 1

These Figures present the cases in which \(\delta _{1} =\delta _{2}=0.5\) and \(\lambda =\mu =0.3,\) where black solid, dot blue and red curves correspond, respectively, to \(\Upsilon ^{-1}=\eta _{g}=\eta _{m}=\eta _{e}=1, \) 5, and 10 (color figure online)

Full size image
Fig. 2
figure 2

Same as Fig. 1 (color figure online)

Full size image

We can observe that the behavior of \(\rho _{ee}(t)\) is opposite to the behavior of \(\rho _{gg}(t)\) because they are different in phase. In Figs. 3 and 4, we investigate the effects of the parameters \(\lambda \) and \(\mu \) on the atomic occupation probabilities, \(\rho _{gg}(t)\), \(\rho _{mm}(t)\), and \(\rho _{ee}(t),\) the atomic population inversion \(\langle S_\mathrm{{z}}\rangle ,\) the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}})\) in case of the detuning parameters \(\delta _{1}=\delta _{2}=0.5\) and the phenomenological damping parameters \(\Upsilon ^{-1}=\eta _{g}=\eta _{m}=\eta _{e}=1\) at \(\lambda =\mu =1,\) 0.5, and 0.3. We take \(\lambda =\mu =\frac{\gamma E_{0}}{2\hslash }.\) This means that the elements of the transition dipole moment matrix operator are equal, \(\gamma _{gm}=\gamma _{me}=\gamma \). Since the Dirac constant \(\hslash \) is a fixed value, if we stabilize the value of \(\gamma \), the effect here will be for the electromagnetic field amplitude \(E_{0}\) of the excitation pulse \(E(\omega )\) only. The curves of the atomic occupation probability \(\rho _{gg}(t)\) and the atomic population inversion \(\langle S_\mathrm{{z}}\rangle \) start from their maximum value at \(\rho _{gg}(t)=\langle S_\mathrm{{z}}\rangle =1\). At \(\lambda =\mu =1\), the curves \(\rho _{gg}(t)\) and \(\langle S_\mathrm{{z}}\rangle \) decrease significantly, and then increase until they become fixed at a certain value (long-lived quantum coherence). When the electromagnetic field amplitude \(E_{0}\) decreases, the curves \(\rho _{gg}(t)\) and \(\langle S_\mathrm{{z}}\rangle \) decrease without increasing again, until they become fixed after a specified period time. The curves of the atomic occupation probabilities \(\rho _{mm}(t)\) and \(\rho _{ee}(t)\) begin with their minimum value at \(\rho _{mm}(t)=\rho _{ee}(t)=0\). At \(\lambda =\mu =1,\) 0.5, the curve of \(\rho _{mm}(t)\) shows an ups and downs behavior making a simple oscillation until it becomes fixed at a certain value. But at \(\lambda =\mu =0.3\), the curve of \(\rho _{mm}(t)\) increases steadily until it reaches a steady state after a period time. As for the curve of the atomic occupation probability \(\rho _{ee}(t)\), at \(\lambda =\mu =1\), the curve of \(\rho _{ee}(t)\) increases and then decreases to become fixed. At \(\lambda =\mu =0.5,\) 0.3, the curve of \( \rho _{ee}(t)\) increases until it reaches its constant value. The purity curve P(t) starts from its maximum value at \(P(t)=1\) (the case of completely pure state), and decreases until it reaches its minimum value (the case of mixed state), which then becomes fixed. We note that the lower the value of the electromagnetic field amplitude \(E_{0}\) becomes, the higher the value of the curve of P(t) increases. So, we find that the pureness of the system decreases with the increase in \(E_{0}\) because there is a significant impact from the field on the system. On the other hand, the information entropy \(H(\sigma _\mathrm{{z}})\) starts from its minimum value at \(H(\sigma _\mathrm{{z}})=0\).

Fig. 3
figure 3

These Figures present the cases in which \(\delta _{1} =\delta _{2}=0.5\) and \(\Upsilon ^{-1}=\eta _{g}=\eta _{m}=\eta _{e}=1,\) where black solid, dot blue and red curves correspond, respectively, to \(\lambda =\mu =1,\) 0.5, and 0.3 (color figure online)

Full size image
Fig. 4
figure 4

Same as Fig. 3 (color figure online)

Full size image

When \(E_{0}\) decreases the information entropy \(H(\sigma _\mathrm{{z}})\) increases until it reaches a constant value after a specified period time (long-lived quantum coherence). But when \(E_{0} \) decreases, the information entropy \(H(\sigma _\mathrm{{z}})\) reaches stability faster, meaning that our information and knowledge of the system remain unchanged after a certain period time. In Figs. 5 and 6, we investigate the effects of the detuning parameters (we take \(\delta _{1}=\delta _{2})\) on the atomic occupation probabilities, \(\rho _{gg}(t)\), \(\rho _{mm}(t)\), and \(\rho _{ee}(t),\) the atomic population inversion \(\langle S_\mathrm{{z}}\rangle ,\) the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}})\) in case of the phenomenological damping parameters \(\Upsilon ^{-1}=\eta _{g}=\eta _{m}=\eta _{e}=0.5\) and the parameters \( \lambda =\mu =0.5\) at \(\delta _{1}=\delta _{2}=0.1,\) 0.5, and 1.

The curves of the atomic occupation probability \(\rho _{gg}(t)\) and the atomic population inversion \(\langle S_\mathrm{{z}}\rangle \) (the atomic occupation probabilities \(\rho _{mm}(t)\) and \(\rho _{ee}(t)\)) start from their maximum value (their minimum value) at \(\rho _{gg}(t)=\langle S_\mathrm{{z}}\rangle =1\) (at \(\rho _{mm}(t)=\rho _{ee}(t)=0)\), then the curves \(\rho _{gg}(t)\) and \(\langle S_\mathrm{{z}}\rangle \) (\(\rho _{mm}(t)\) and \(\rho _{ee}(t)\)) decrease (increase) significantly, then increase (decrease) until they reach their fixed state (long-lived quantum coherence). Also note that the curves \(\rho _{mm}(t)\) make oscillations in the beginning, but with the passing of time these oscillations gradually weaken until they become stable. We note that before the stability state, when the detuning parameter \(\delta _{1}=\delta _{2}\) increases, the values of the curve \(\rho _{gg}(t)\) increase, while the values of the curve \(\rho _{mm}(t)\) and \(\rho _{ee}(t)\) decrease. On the other hand, the curves of the purity P(t) (the information entropy \(H(\sigma _\mathrm{{z}})\)) start from their maximum value (minimum value) at \(P(t)=1\) (\(H(\sigma _\mathrm{{z}}=0\)), and then decreases (increases) until they reach their minimum values (maximum values) and then to the fixed state (long-lived quantum coherence). However, it should be noted that the effect of the detuning parameter \(\delta \) on the curves of the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}})\) is weak, as the curves are almost stacked on each other.

Fig. 5
figure 5

These Figures present the cases in which \(\Upsilon ^{-1}=\eta _{g}=\eta _{m}=\eta _{e}=0.5\) and \(\lambda =\mu =0.5,\) where black solid, dot blue and red curves correspond, respectively, to \(\delta _{1}=\delta _{2} =0.1,\) 0.5, and 1 (color figure online)

Full size image
Fig. 6
figure 6

Same as Fig. 5 (color figure online)

Full size image

4 Conclusion

In this paper, we have analytically solved the system of a three-level semiconductor quantum dot. We have discussed the effects of the phenomenological damping parameters, the electromagnetic field amplitude \(E_{0}\) of the excitation pulse \(E(\omega )\), and the detuning parameters on the atomic occupation probabilities, \(\rho _{gg}(t)\), \(\rho _{mm}(t)\), and \(\rho _{ee}(t),\) the atomic population inversion \(\langle S_\mathrm{{z}}\rangle ,\) the purity P(t), and the information entropy \(H(\sigma _\mathrm{{z}}).\) It has been observed that the curves of the atomic occupation probability \(\rho _{gg}(t),\) the atomic population inversion \(\langle S_\mathrm{{z}}\rangle \), and the purity P(t) have a decay over the passing of time. They are also decayed when the phenomenological damping parameters and the detuning parameters increase, and when the electromagnetic field amplitude \(E_{0}\) of the excitation pulse \(E(\omega )\) decreases. Besides, when the phenomenological damping parameters increase, the curves of the atomic occupation probabilities \(\rho _{mm}(t)\), \(\rho _{ee}(t)\), and the information entropy \(H(\sigma _\mathrm{{z}})\) quickly reach a stable state.

Since the increase in the curves resists the decay resulting from the damping parameters, so they settle at the fixed state. On the other hand, the effect of the detuning parameters on the curves of the purity P(t) and the information entropy \(H(\sigma _\mathrm{{z}})\) is very weak, So the curves have appeared as if they are stacked on each other without a significant change.

The purity P(t) of the atom is affected by the increase and decrease in the field, because of the effect from the field on the atom. The results have supported this fact, as the purity decreases when the field increases and vice versa. In addition, clearly in all figures, we can observe that the curve after a certain period time becomes fixed at a certain value, wherein the effect of the parameters vanishes. In other words, the curve after some oscillations becomes fixed, without any effect of time. This pinpoints the emergence of long-lived quantum coherence.

According to our results, the predictability of the long-lived quantum coherence has a significant importance. Since, by predicting the emergence of this phenomenon, we can identify the period time in which the field’s impact on the system remains constant and our information about the system can thereby be long-lasting [63].

Thus, our problem paves the way toward a versatile paradigm which potentiates many applications in, for example, quantum information processing and matter wave circuits for quantum sensing. Specifically speaking, the formalism presented in our problem can be materialized in the compound of gallium arsenide which has versatile applications. Our findings, therefore, could acquire more importance because they help us predict the period time in which our information about this highly sensitive system becomes stable. Accordingly, this should maintain the stability and enhance the controllability of the numerous applications in which GaAs is used as integral part, such as high-performance transistors [23, 24], microwave frequency integrated circuits , laser diodes, and solar cells. Finally, such kind of problems which tackle a semiconductor quantum dot is of crucial importance, as it is clearly shown in the relevance of the subject of semiconductor quantum dot to many sciences and interdisciplinary applications related to many fields, such as biology, medicine, industry, and others.

Therefore, we recommend further research and mathematical study along with experimental investigation of more complex problems of atoms with higher energy levels, in order to widen the scope of vision and unfold more ideas concerning this vital topic of research.