Quantum Squeezing of the Field of a Single-Atom Laser under Conditions of a Variable Coupling Constant

Abstract

A nonstationary regime of squeezed-light generation by a single-atom laser is investigated. Dependences of the quantum-squeezing parameter and radiation intensity on modulation frequency of the atom–field coupling constant are obtained. It is demonstrated that a resonance appears at the modulation frequency equal to twice the average coupling constant, which leads to a more efficient quantum squeezing in a nonstationary harmonic regime than in the case of a stationary regime for the same values of the relaxation and pump parameters.

INTRODUCTION

Light sources exhibiting nonclassical statistics are a trend in the development of quantum optics. Such sources have a wide range of applications, such as frequency standards [1, 2] and magnetometry [3, 4] in metrology, or writing and storing information, along with cryptography, in quantum-information applications [5–7]. The problem of generation of light characterized by a nonclassical statistics can be solved by different means. For example, it can be realized in lasers by using pumping exhibiting certain statistical properties [8–14] or/and utilizing multilevel pumping schemes [15, 16].

Isolated single emitters are also promising systems for obtaining nonclassical states of light due to the possibility of the photon antibunching effect in them. For example, laser action has been practically implemented in single atoms [17], ions [18], and quantum dots [19]. Sub-Poissonian statistics of radiation, along with suppression of amplitude fluctuations below quantum limit, were observed in the above experiments. It was demonstrated in theoretical works [20, 21] dealing with investigation of the fundamental model of a single-atom laser that such a laser can emit amplitude-squeezed light under certain relation between system parameters. Notably, an amplitude squeezing that is variable with time can be observed during a transient process. This circumstance suggests that the efficiency of quantum squeezing of the field of a single-atom laser can be increased by modulating the atom–field coupling constant.

The time dependence of the coupling constant can be realized by different means. One of them consists in using stimulated oscillations of the cavity mirrors. Qualitative estimation shows that a mirror-oscillation frequency lower than 10⁸ Hz should be sufficient for observation of the discussed effect. Such frequency can be achieved by means of, e.g., piezoelectric modulators. Another method consists in excitation of stimulated oscillations of a single emitter in an optical lattice the potential well of which is regulated by parameters of confining beams. A point emitter in a crystal lattice that can be described, with good approximation, as a two-level atom can experience thermal oscillations at a certain frequency, which results in the appearance of an additional noise. Thermal fluctuations of the cavity mirrors that were studied in detail in [22] can represent another source of noise. However, in the problem under consideration, we will assume that such fluctuations can be neglected and that the time dependence of the coupling constant is determined.

A MODEL OF A SINGLE-ATOM LASER WITH A MODULATED COUPLING CONSTANT

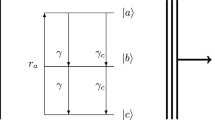
The simplest fundamental model of a single-atom laser represents a two-level atom that interacts with a single cavity mode with losses [23–28]. The system dynamics is governed by only four processes that determine the properties of the generated radiation, namely, incoherent pumping driving an atom from ground state $\left| a \right\rangle$ to excited state $\left| b \right\rangle$ with rate Γ, spontaneous decay of an atom from excited state $\left| b \right\rangle$ to ground state $\left| a \right\rangle$ that is characterized by rate γ, departure of photons from the cavity that is characterized by the cavity Q-factor or reciprocal lifetime of photons in the cavity κ, and interaction of an atom with the field mode characterized by coupling constant g.

The equation for an atom–field density operator of a single-atom laser with incoherent pumping has the form

$$\frac{{\partial \hat {\rho }}}{{\partial t}} = - \frac{i}{\hbar }[\hat {V},\hat {\rho }] + \frac{\kappa }{2}{\mathbf{\hat {{K}}}}\left\{ {\hat {\rho }} \right\} + \frac{\gamma }{2}{\mathbf{\hat {R}}}\left\{ {\hat {\rho }} \right\} + \frac{\Gamma }{2}{\mathbf{\hat {P}}}\left\{ {\hat {\rho }} \right\},$$

(1)

where the first term in the right-hand side describes interaction of the atom with the field mode, the second term describes field relaxation, the third term c-orresponds to spontaneous decay of the atom, and the fourth term describes incoherent pumping. An explicit form of interaction operator $\hat {V}$ and superoperators describing corresponding relaxation processes is given by

$$\hat {V} = i\hbar g({{\hat {a}}^{\dag }}\hat {\sigma } - {{\hat {\sigma }}^{\dag }}\hat {a}),$$

(2)

$${\mathbf{\hat {{K}}}}\left\{ {\hat {\rho }} \right\} = 2\hat {a}\hat {\rho }{{\hat {a}}^{\dag }} - {{\hat {a}}^{\dag }}\hat {a}\hat {\rho } - \hat {\rho }{{\hat {a}}^{\dag }}\hat {a},$$

(3)

$${\mathbf{\hat {R}}}\left\{ {\hat {\rho }} \right\} = 2\hat {\sigma }\hat {\rho }{{\hat {\sigma }}^{\dag }} - {{\hat {\sigma }}^{\dag }}\hat {\sigma }\hat {\rho } - \hat {\rho }{{\hat {\sigma }}^{\dag }}\hat {\sigma },$$

(4)

$${\mathbf{\hat {P}}}\left\{ {\hat {\rho }} \right\} = 2{{\hat {\sigma }}^{\dag }}\hat {\rho }\hat {\sigma } - \hat {\sigma }{{\hat {\sigma }}^{\dag }}\hat {\rho } - \hat {\rho }\hat {\sigma }{{\hat {\sigma }}^{\dag }}.$$

(5)

Here, $\hat {a}$ and ${{\hat {a}}^{\dag }}$ are the operators of photon annihilation and creation in the cavity mode, respectively, and $\hat {\sigma }$ and ${{\hat {\sigma }}^{\dag }}$ are operators of the dipole atomic transition. To investigate the solution to Eq. (1), let us recast the field operators in the basis of Fock states and recast atomic operators in the basis of stationary states of an unperturbed atom:

$$\hat {a} = \sum\limits_{n = 1}^\infty {\sqrt n \left| {n - 1} \right\rangle \left\langle n \right|} ,\quad \hat {\sigma } = \left| a \right\rangle \left\langle b \right|,$$

(6)

$${{\hat {a}}^{\dag }} = \sum\limits_{n = 0}^\infty {\sqrt {n + 1} \left| {n + 1} \right\rangle \left\langle n \right|} ,\quad {{\hat {\sigma }}^{\dag }} = \left| b \right\rangle \left\langle a \right|.$$

(7)

This representation of creation and annihilation operators is convenient for carrying out calculations, because it gives matrix elements of the operators in an explicit form. The equation governing density matrix $\rho _{{\alpha \beta }}^{{nm}}$ = $\left\langle {n,\alpha } \right|\hat {\rho }\left| {m,\beta } \right\rangle$ of a single-atom laser, where $\left| {n,\alpha } \right\rangle$ = $\left| n \right\rangle \left| \alpha \right\rangle$, $\alpha ,\beta = a,b$, $n = 0,1,2,...,\infty$, can be presented in the form of an infinite system of differential equations:

$$\begin{gathered} \frac{{\partial \rho _{{aa}}^{{nm}}}}{{\partial t}} = g(\sqrt n \rho _{{ba}}^{{n - 1,m}} + \sqrt m \rho _{{ab}}^{{n,m - 1}}) - \frac{\kappa }{2}(n + m)\rho _{{aa}}^{{nm}} \\ + \;\gamma \rho _{{bb}}^{{nm}} - \Gamma \rho _{{aa}}^{{nm}} + \kappa \sqrt {(n + 1)(m + 1)} \rho _{{aa}}^{{n + 1,m + 1}}, \\ \end{gathered} $$

(8)

$$\begin{gathered} \frac{{\partial \rho _{{bb}}^{{nm}}}}{{\partial t}} = - g(\sqrt {m + 1} \rho _{{ba}}^{{n,m + 1}} + \sqrt {n + 1} \rho _{{ab}}^{{n + 1,m}}) - \frac{\kappa }{2}(n + m)\rho _{{bb}}^{{nm}} \\ + \;\kappa \sqrt {(n + 1)(m + 1)} \rho _{{bb}}^{{n + 1,m + 1}} - \gamma \rho _{{bb}}^{{nm}} + \Gamma \rho _{{aa}}^{{nm}}, \\ \end{gathered} $$

(9)

$$\begin{gathered} \frac{{\partial \rho _{{ab}}^{{nm}}}}{{\partial t}} = g(\sqrt n \rho _{{bb}}^{{n - 1,m}} - \sqrt {m + 1} \rho _{{aa}}^{{n,m + 1}}) - \frac{\kappa }{2}(n + m)\rho _{{ab}}^{{nm}} \\ - \;\frac{{\gamma + \Gamma }}{2}\rho _{{ab}}^{{nm}} + \kappa \sqrt {(n + 1)(m + 1)} \rho _{{ab}}^{{n + 1,m + 1}}, \\ \end{gathered} $$

(10)

$$\begin{gathered} \frac{{\partial \rho _{{ba}}^{{nm}}}}{{\partial t}} = g(\sqrt m \rho _{{bb}}^{{n,m - 1}} - \sqrt {n + 1} \rho _{{aa}}^{{n + 1,m}}) - \frac{\kappa }{2}(n + m)\rho _{{ba}}^{{nm}} \\ - \;\frac{{\gamma + \Gamma }}{2}\rho _{{ba}}^{{nm}} + \kappa \sqrt {(n + 1)(m + 1)} \rho _{{ba}}^{{n + 1,m + 1}}. \\ \end{gathered} $$

(11)

To solve infinite system of differential equations (8)–(11), the basis of the field states was limited, similarly to in [21]. After that, the system was solved numerically. The steady-state regime of oscillation of a single-atom laser is most interesting from the practical point of view. In the case of constant parameters (Γ, γ, κ, g) of the quantum system, this regime is stationary. To characterize quantum statistics of the field after the end of the transient processes, we can find average number of photons in the cavity $\left\langle n \right\rangle$ and the degree of light squeezing in the stationary state that is described by the Mandel Q parameter:

$$\left\langle n \right\rangle = \sum\limits_{n = 0}^k {n(\rho _{{aa}}^{{nn}} + \rho _{{bb}}^{{nn}})} = \sum\limits_{n = 0}^k {n{{\rho }^{{nn}}}} ,$$

(12)

$$Q = \frac{{\left\langle {{{n}^{2}}} \right\rangle - {{{\left\langle n \right\rangle }}^{2}}}}{{\left\langle n \right\rangle }} - 1,$$

(13)

where k is the value of the filling factor at which the system of equations is artificially terminated and ρⁿⁿ is the diagonal element of the density matrix averaged over the two atomic states. The latter parameter characterizes the probability of finding n photons in the cavity field mode. When parameter Q becomes negative, light acquires nonclassical properties and is characterized by a sub-Poissonian quantum statistics.

Let us introduce the time dependence of the coupling constant corresponding to a harmonic function in Eqs. (8)–(11):

$$g = {{g}_{0}} + {{g}_{1}}\sin \left( {\Omega t + {{\varphi }_{1}}} \right).$$

(14)

Here, g₁ is the modulation amplitude, $\Omega$ is the coupling-constant modulation frequency, ${{\varphi }_{1}}$ is some constant phase, and g₀ is a time-independent part. Here, we assumed that function (14) obeys the inequality g₁/g₀$\ll$ 1.

The choice of a small modulation amplitude relative to the constant component of the coupling constant is dictated by the fact that we are interested in the deviation of the stationary regime of oscillation of a single-atom laser from the nonstationary regime in the first place. It is easier to analyze the nonstationary regime as a linear perturbation. Otherwise, large modulation amplitude g₁ can give rise to strong transient processes corresponding to system evolution from the stationary regime taking place at maximum value of the coupling constant g = g₀ + g₁ to the stationary state at minimum value g = g₀ – g₁. They do not contain any interesting information but substantially complicate the field dynamics in the cavity. The choice of harmonic function of the coupling constant (14) is explained by the fact that we are looking for resonance effects that can take place in the nonstationary regime of oscillation of a single-atom laser. Exactly determined initial phase ${{\varphi }_{1}}$ appearing in the argument of the sine function in (14) triggers the phase-synchronization mechanism and enables overcoming the decay of the squeezed state due to phase diffusion.

RESULTS

Preliminary analysis of dynamics of average photon number $\left\langle n \right\rangle$ and parameter Q at constant values of Γ, γ, κ, and g shows that the reciprocal time of the transient process can be estimated as being equal to the sum of rates Γ, γ, and κ of incoherent processes in the model, while the oscillation period of the diagonal elements of the atom-field density matrix during the transient process depends on the constant component of coupling constant g₀. To observe the resonance effect, modulation period g must be smaller or comparable to the time of the transient process. Otherwise, the dynamics will correspond to an adiabatic regime in which establishment of equilibrium occurs faster than the change in the system parameters. Therefore, when searching for the resonance effect, we chose parameters of a single-atom laser from [20] as initial ones:

$$\Gamma = 1.4{{g}_{0}},\quad \kappa = 1.4{{g}_{0}},\quad \gamma = 0.1{{g}_{0}}.$$

(15)

These parameters satisfy the above formulated requirements and lead to the highest degree of squeezing in the stationary regime, which makes them most promising from the point of view of expected results of the calculations.

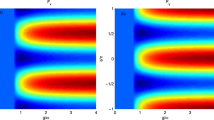
The dependences of the average photon number in the cavity and Mandel Q parameter on modulation frequency Ω for parameters of a single-atom laser specified in (15) are presented in Figs. 1 and 2. Since system of differential equations (8)–(11) does not have a stationary solution for a coupling constant given by (14), the results are presented by pairs of curves corresponding to maximum and minimum values of the studied quantity achieved during a modulation period in the steady-state dynamics. Indices min and max in the graphs denote maximum and minimum values of parameter Q or average photon number that are attained periodically in the nonstationary oscillation regime of a single-atom laser.

Fig. 1.

Average photon number as a function of the coupling-constant modulation frequency for two values of parameter g₁ in expression (14).

Fig. 2.

Mandel Q parameter as a function of coupling-constant modulation frequency for two values of parameter g₁ in expression (14).

The dependences of parameter Q on modulation frequency contain a characteristic extremum (Fig. 2) indicative of the presence of a parametric resonance in the model of a single-atom laser. The peak of the resonance curve is attained at modulation frequency $\Omega \approx 2{{g}_{0}}$, while its position on the axis of abscissas is nearly indistinguishable for different values of constants γ, κ, and Γ, which was verified by numerically solving system (8)–(11). The maximum on the frequency curve corresponding to average photon number $\left\langle n \right\rangle$ is less prominent than that in the curve corresponding to parameter Q (Fig. 1).

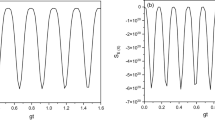
To observe the steady-state dynamics of the field state, we plotted the time dependences of the average photon number, parameter Q, and probabilities of several Fock states for a nonstationary oscillation regime (Figs. 3–5) in which parameter g is determined by expression (14). Note that the figures represent also additional dynamic curves corresponding to the stationary oscillation regime with largest (g_const = g₀ + g₁) and smallest (g_const = g₀ – g₁) values of coupling constant g attained during a modulation period.

Fig. 3.

Probability P_n of finding n photons in the cavity of a single-atom laser as a function of time: (1) P₀ in the stationary regime at g_const = 0.9g₀, (2) P₀ in the nonstationary regime (14) at g = g₀(1 + 0.1sin(2g₀t)), (3) P₀ in the stationary regime at g_const = 1.1g₀, (4) P₁ in the stationary regime at g_const = 0.9g₀, and (5) P₁ in nonstationary regime (14) at g = g₀(1 + 0.1sin(2g₀t)), (6) P₁ in the stationary regime at g_const = 1.1g₀; the three lower curves were plotted similarly to the upper ones.

Fig. 4.

Average photon number as a function of time for different values of the coupling constant corresponding to stationary and nonstationary regimes of oscillation. Constants g₁ and Ω are defined in (14): g₁ = 0.1g₀, Ω = 2g₀.

Fig. 5.

Mandel Q parameter as a function of time for different values of the coupling constant corresponding to stationary and nonstationary regimes of oscillation. Constants g₁ and Ω are defined in (14): g₁ = 0.1g₀, Ω = 2g₀.

That the difference in the value of parameter Q for the stationary regimes corresponding to the largest and the smallest values of coupling constant g are an order of magnitude smaller than variation of parameter Q over modulation period of the coupling constant in the same range but in the nonstationary oscillation regime (Fig. 5) was unexpected. Numerical values of the Mandel Q parameter corresponding to Fig. 5 are presented below:

$$Q_{{g = 0.9}}^{{(s)}} = - 0.132,\quad Q_{{g = 1.1}}^{{(s)}} = - 0.134,$$

(16)

$${{Q}_{{\min }}} = - 0.159,\quad {{Q}_{{\max }}} = - 0.111,$$

(17)

$$\frac{{\left| {{{Q}_{{\min }}} - {{Q}_{{\max }}}} \right|}}{{\left| {Q_{{g = 0.9}}^{{(s)}} - Q_{{g = 1.1}}^{{(s)}}} \right|}} = 2.25,$$

(18)

where $Q_{{g = 0.9}}^{{(s)}}$ and $Q_{{g = 1.1}}^{{(s)}}$ are the values of parameter Q for a single-atom laser in the stationary regime of oscillation at constant values of coupling parameter g = 0.9 and 1.1, respectively, and Q_min and Q_max are the maximum and the minimum values of parameter g = 0.9 and 1.1 in the nonstationary regime achieved during a modulation period of coupling constant (14) in the range between g = 0.9 and 1.1, respectively.

It should be noted that the time dependence of average photon number $\left\langle n \right\rangle$ does not exhibit such a property, i.e., the difference between the maximum and the minimum values for the two stationary regimes is approximately equal to the modulation amplitude in the case of the nonstationary oscillation regime (Fig. 4).

It follows from (16)–(18) that the nonstationary regime of oscillation cannot be considered to be an adiabatic dependence of the stationary regime on variable system parameters. Otherwise, the difference between the maximum and the minimum values of parameter Q would be close to each other for different modulation frequencies $\Omega$ of the coupling constant. This fact suggests the presence of a strong nonlinear resonance effect. We believe that it can be used for achieving a higher degree of squeezing of light generated in the cavity of a single-atom laser than in the stationary regime. Note that synchronous detection by means of a photoelectric element must be used for utilizing generation of squeezed light in the steady-state dynamic regime. Otherwise, statistics accumulated over a time interval long relative to the modulation period will be averaged over strong but frequent oscillations of the average photon number in the cavity.

CONCLUSIONS

The existence of a nonlinear resonance effect of squeezed-light generation in a cavity of a single-atom laser with a modulated coupling constant is predicted. The time dependence of the Mandel Q parameter and the average number of photons in the cavity at input parameters of a single-atom laser leading to maximum squeezing in the stationary regime of oscillation is obtained. The dependences of the maximum and minimum values of the Mandel Q parameter and average photon number $\left\langle n \right\rangle$ on modulation frequency of coupling constant g in the case of cavity characterized by low Q-factor are plotted based on the pattern of the steady-state dynamics. The effect of increase in the degree of light squeezing in the nonstationary regime of oscillation relative to the stationary regime of oscillation of a single-atom laser is predicted numerically.