1 Introduction

A system consisting of a single-mode quantized field corresponding to the harmonic oscillator interacting with an ensemble of two-level systems described by the spin-\(\frac{1}{2}\) operators was first considered by Dicke under a series of approximations [1]. The simplest case of this model is the interaction between an electromagnetic radiation field and a single two-level atom, which has nowadays attracted great attention in many areas of physical applications such as quantum optics, condensed matter, and quantum information. This model that was previously introduced by Rabi [2] in the rotating wave approximation is known as the one-photon Jaynes–Cummings model (JCM) [3]. The quantum effects in such systems with an optical field inside a cavity have been extensively studied both analytically and experimentally by many authors over the past decades (see, e.g., [4,5,6,7,8,9] and references therein). The JCM, which is an exactly solvable model, was first used to consider the classical effects of spontaneous emission and to follow traces of Rabi oscillations of the atomic population inversion [10]. Next, it was turned out that the Rabi oscillations collapse and revival repeatedly in a complicated pattern when the initial conditions are chosen appropriately [11,12,13,14]. This, in turn, provided a strong justification for the quantum behavior of radiation field excitation (the discreteness of photon). The results of the subsequent studies elucidated the other nonclassical properties of the JCM cavity field for which there is no classical counterpart such as vacuum Rabi oscillations [15], collapse and revival in the atomic excitation [16,17,18], entanglement between light and an optical atomic excitation (quantum correlation) in the course of time [19], sub-Poissonian statistics, squeezing of the radiation field [17, 18, 20,21,22] and the tendency of the photons to antibunch. One main reason for the high interest in studying the dynamics predicted by JCM is the fact that the interaction of the light wave with an atom can be realized and verified experimentally in the cavity-QED setups, optical lattices, laser-cooled trapped ions, and so on [23,24,25]. It must be emphasized that the temporal evolution of JCM is sensitive to the statistical properties of the initial state of the quantized radiation field. In other words, this model can be used as a scheme to produce the nonclassical states by considering appropriate initial states [26]. There exist a variety of extensions and generalizations of the original-JCM with alternative interactions between the field and atom, due to the importance of the nonclassical states in quantum optics and laser physics. The q-deformed, f-deformed and the parity \(\lambda \)-deformed one-photon JCMs are three different kinds of generalizations of the original-JCM with the cavity field operators replaced by the q-, f- and \(\lambda \)-deformed partners, respectively [27,28,29,30]. A quantum system consisting of a single two-level atom interacting with single-mode quantized cavity-field with two-photon coupling is the simplest extension of the original-JCM which has been studied in great detail during the past decades [31,32,33,34,35,36,37,38,39,40]. The boson annihilation and creation operators of this field represent the su(1, 1) Lie algebra with the Bargmann indices \(\frac{1}{4}\) and \(\frac{3}{4}\) for the even and odd parity states, respectively. For example, for the time evolution of the mean photon number and the variance of the field quadratures corresponding to a two-photon JCM (TPJCM) of a single two-level atom interacting with the squeezed vacuum one can refer to Ref. [34]. Furthermore, Jaynes–Cummings models with intensity-dependent coupling interacting with Holstein–Primakoff su(2) and su(1, 1) coherent states have been analyzed in [36, 38, 40] as other extensions of the original-JCM. Moreover, numerous other extensions have been suggested and investigated, such as multi-photon transitions [41], two- or three-cavity modes for three-level atoms [32], the Jaynes–Cummings-Hubbard model [42, 43], the Tavis-Cummings model [44] and driven Jaynes–Cummings model [45]. The aim of the present work is to consider the two-photon parity \(\lambda \)-deformed JCM of a single two-level atom interacting with a para-Bose oscillator cavity-field instead of the simple one. The para-Boson oscillator algebra, which has recently attracted considerable attention (see, for example, [46,47,48,49,50]), is a deformation of the harmonic oscillator algebra by the reflection operator in the context of integrability in the Calogero–Sutherland models [51,52,53].

The paper is organized as follows: Sect. 2 contains a brief review of para-Bose oscillator algebra of order \(p=2\lambda +1\) and its unitary lowest weight (Fock) representation. In Sect. 3 we introduce the parity \(\lambda \)-deformed version of two-photon Jaynes–Cummings Hamiltonian and obtain its eigenstates and energy levels. Time evolution of the atom-field states with the initial states of the even cat and excited for the field and atom is obtained in Sect. 4. Dynamics of the fidelity, atomic inversion, and cavity damping on the collapse and revival phenomena are studied in Sect. 5. Moreover, sub-Poissonian statistics, quadrature squeezing of the cavity field, and von Neumann entropy are investigated in Sect. 6. Finally, the results are summarized in Sect. 7.

2 The para-Bose oscillator algebra and its associated Lie algebra su(1, 1)

Let us fix the unital simple harmonic oscillator algebra by the annihilation and creation operators \(a=\frac{1}{\sqrt{2}}\left( x+\frac{d}{dx}\right) \) and \(a^{\dagger }=\frac{1}{\sqrt{2}}\left( x-\frac{d}{dx}\right) \) with the commutation relation \([a, a^{\dagger }]=1\). For the sake of simplicity, we have set the constant \(\hbar /m\omega \) to 1. Also, it has been assumed that x is non-zero and real. Suppose that \(\lambda \) is an arbitrary real parameter and R is the Hermitian and unitary parity operator, i.e. \({R^\dag }={R^{-1}}=R\). If we define the following annihilation and creation operators

$$\begin{aligned} \begin{array}{l} A \equiv a - \frac{\lambda }{{\sqrt{2} x}}R,\quad {A^\dag } \equiv {a^\dag } + \frac{\lambda }{{\sqrt{2} x}}R, \end{array} \end{aligned}$$
(2.1)

then we shall get the para-Bose (pseudo harmonic) oscillator algebra of order \(p=2\lambda +1\) as follows

$$\begin{aligned} \begin{array}{l} \left[ {A,{A^\dag }} \right] = 1 + 2\lambda R,\qquad \left\{ {R,A} \right\} = \left\{ {R,{A^\dag }} \right\} = 0. \end{array} \end{aligned}$$
(2.2)

This is a parity-deformed version of the simple harmonic oscillator algebra so that in the limit \(\lambda \rightarrow 0\) we lose the anti-commutation relations given in the last two equations of (2.2). The para-Bose oscillator algebra allocates itself a number self-adjoint operator as \(N \equiv {A^\dag }A+\lambda (1-R)\) subject to the commutation relations

$$\begin{aligned} \left[ N,A\right] =-A,\qquad [N,{A^\dag }]={A^\dag }, \qquad [N,R]=0. \end{aligned}$$
(2.3)

It is supposed that the generators of the algebra (2.2) are the linear operators on the infinite-dimensional Hilbert space \({\mathcal {H}}=\text{ Lin. } \text{ Span }\left\{ \left| n\right\rangle |\, n\in {{\mathbb {N}}}_0;\, \langle n|m\rangle =\delta _{n\,m},\, I\equiv \right. \left. \sum _{n=0}^{\infty }|n\rangle \langle n|\right\} \) with \(\langle .|.\rangle \) as a scalar product and I as the identity operator on that space. The space \({\mathcal {H}}\) can be split into a direct sum of two orthogonal infinite-dimensional Hilbert subspaces \({\mathcal {H}}^{e} =\mathrm {Lin.\,Span}\) \(\{\left| n\right\rangle _e \equiv |2n\rangle |n\in {\mathbb {N}}_0\}\) and \({\mathcal {H}}^o =\mathrm {Lin.\,Span}\,\{\left| n\right\rangle _o \equiv |2n+1\rangle |n\in {\mathbb {N}}_0\}\) with the positive and negative parities, respectively. According to the last relation of (2.3), the basis states of the Fock space \({\mathcal {H}}\) are the common eigenstates of parity operator, \(R\left| n\right\rangle ={(-1)^n}\left| n\right\rangle \), as well as number operator, \(N\left| n \right\rangle = n\left| n \right\rangle \). The irreducible Fock representation of the para-Bose oscillator algebra (2.2) with the lowest weight on \({\mathcal {H}}\) is given by

$$\begin{aligned}&A\left| 2n\right\rangle =\sqrt{2n}\,{\left| {2n-1} \right\rangle },\quad {A^\dag }{\left| 2n\right\rangle } = \sqrt{2n+2\lambda +1}\,{\left| 2n+1\right\rangle },\nonumber \\&A{\left| 2n+1\right\rangle }=\sqrt{2n+2\lambda +1}\,{\left| 2n\right\rangle }, \quad {A^\dag }{\left| 2n+1\right\rangle }=\sqrt{2n+2}\,{\left| {2n+2}\right\rangle }. \end{aligned}$$
(2.4)

The Fock vectors \(\left| 2n\right\rangle \) and \(\left| 2n+1\right\rangle \) in x-representation are expressed in terms of the associated Laguerre polynomials as (\(\lambda >\frac{-1}{2}\)) [54]

$$\begin{aligned}&\left\langle x|2n\right\rangle =(-1)^{n}\sqrt{\frac{n!}{\Gamma (n+\lambda +\frac{1}{2})}}\,|x|^{\lambda }e^{-\frac{x^2}{2}}L_{n}^{\lambda -\frac{1}{2}}(x^2),\nonumber \\&\left\langle x|2n+1\right\rangle =(-1)^{n}\sqrt{\frac{n!}{\Gamma (n+\lambda +\frac{3}{2})}}\,x|x|^{\lambda }e^{-\frac{x^2}{2}}L_{n}^{\lambda +\frac{1}{2}}(x^2). \end{aligned}$$
(2.5)

It is necessary to recall that the Hamiltonian for the parity \(\lambda \)-deformation of the harmonic oscillator is the so-called Calogero-Sutherland one:

$$\begin{aligned} H^{(\lambda )}=\frac{1}{2}\{A,A^{\dag }\}=\frac{1}{2}\left[ -\frac{d^2}{dx^2}+x^2+\frac{\lambda (\lambda -R)}{x^2}\right] . \end{aligned}$$
(2.6)

R is substituted by \(+1\) and \(-1\) depending on which of the Hilbert subspaces \({\mathcal {H}}^{e}\) and \({\mathcal {H}}^{o}\) is used to measure the energy value: \(\left\langle n\right| H^{(\lambda )}\left| n\right\rangle =n+\lambda +\frac{1}{2}\).

It is now straightforward to show that the su(1, 1) Lie algebra commutation relations, which are

$$\begin{aligned}{}[{K_+},{K_-}] =-2{K_0}, \qquad [{K_0},{K_ \pm }]=\pm {K_\pm }, \end{aligned}$$
(2.7)

are realized by the following operators

$$\begin{aligned} {K_+}\equiv \frac{1}{2}{A^{{\dag ^2}}}, \quad {K_-}\equiv \frac{1}{2}{A^2},\quad {K_0}\equiv \frac{1}{2}\left( N+\lambda (2R-1)+\frac{1}{2}\right) , \end{aligned}$$
(2.8)

in which, \(K_0\) is a self-adjoint operator, and the operators \(K_+\) and \(K_-\) are the Hermitian conjugate of each other with respect to the scalar product \(\langle .|.\rangle \). For a given positive real number \(\lambda \), it is straightforward to conclude that the Hilbert subspaces \({\mathcal {H}}^e\) and \({\mathcal {H}}^o\) form the irreducible positive discrete \((\frac{1}{4}+\frac{\lambda }{2})\)- and \((\frac{3}{4}+\frac{\lambda }{2})\)-representations of the su(1, 1) Lie algebra, respectively:

$$\begin{aligned}&K_+|n\rangle _{e(o)}=\sqrt{(n+1)(n+\lambda +1\mp \frac{1}{2})}|n+1\rangle _{e(o)},\nonumber \\&K_-|n+1\rangle _{e(o)}=\sqrt{(n+1)(n+\lambda +1\mp \frac{1}{2})}|n\rangle _{e(o)},\nonumber \\&K_0|n\rangle _{e(o)}=\frac{1}{2}(2n+\lambda +1\mp \frac{1}{2})|n\rangle _{e(o)}. \end{aligned}$$
(2.9)

The positive discrete series of su(1, 1) with the Bargmann indices 1/4 and 3/4 (see, for example, [55, 56]), as the limiting cases of the positive discrete \((\frac{1}{4}+\frac{\lambda }{2})\)- and \((\frac{3}{4}+\frac{\lambda }{2})\)-representations, are obtained by the limiting process \(\lambda \rightarrow 0\).

3 Two-photon Jaynes–Cummings model by a two-level atom interacting with the para-Bose field

We use the generators of su(1, 1) Lie algebra defined in (2.8) to generalize TPJCM Hamiltonian (assuming \(\hbar =1\)) by the parity operator as below

$$\begin{aligned} H^{(\lambda ,g)}\equiv 2\omega {K_0}+\frac{{{\omega _0}}}{2}{\sigma _3}+2g({K_+}{\sigma _-}+{K_-}{\sigma _+}). \end{aligned}$$
(3.1)

The two first and third term are the free and interaction parts of the Hamiltonian which are usually denoted by \(H_0\) and \(H_{{\mathop {\mathrm{int}}}}\) in the literature, respectively: \(H_0=2\omega {K_0}+\frac{{{\omega _0}}}{2}{\sigma _3}\) and \(H_{{\mathop {\mathrm{int}}}}=2g({K_+}{\sigma _-}+{K_-}{\sigma _+})\). The first term of \(H^{(\lambda ,g)}\) is the parity \(\lambda \)-deformed free-field Hamiltonian (without the zero-point energy term) that describes the energy of each photon by the parameter \(\omega \) and an infinite number of the states \(|n\rangle _{e}\) and \(|n\rangle _{o}\), introduced in the previous section. The second term is the free Hamiltonian corresponding to a two-level atom with \(\omega _0\) as the energy splitting between the ground and excited atomic states in the Hilbert space \({\mathcal {H}}^{\mathrm {atom}}=\mathrm {Lin. \,\,Span}\{|-\rangle , |+\rangle \}\). The atom is described by the three generators \(\sigma _{3}=|+\rangle \langle +|-|-\rangle \langle -|\) and \(\sigma _{\pm }=\sigma _1\pm i\sigma _2=|\pm \rangle \langle \mp |\) that obey the su(2) commutation relations \([\sigma _+,\sigma _-]=\sigma _3\) and \([\sigma _3,\sigma _{\pm }]=\pm 2\sigma _{\pm }\) (\(\sigma _1\), \(\sigma _2\) and \(\sigma _3\) are the well-known Pauli matrices). The third term of \(H^{(\lambda ,g)}\) refers to a parity \(\lambda \)-deformed version of the atom-field interaction with the coupling constant g. Using Eq. (2.1), the Hamiltonian \(H^{(\lambda ,g)}\) is written as

$$\begin{aligned} H^{(\lambda ,g)}=H_{TPJCM}^{(g)}+\left( \frac{\omega }{2}-g\right) \frac{\lambda ^2}{x^2}+\left( g\sigma _1-\omega \right) \frac{\lambda }{2x^2}R, \end{aligned}$$
(3.2)

in which

$$\begin{aligned} H_{TPJCM}^{(g)}=\frac{\omega }{2}\{a,{a^\dag }\}+\frac{{{\omega _0}}}{2}{\sigma _3} + g({a^2}{\sigma _+} +{a^\dag }^2{\sigma _-}) \end{aligned}$$
(3.3)

is the known Hamiltonian of the two-photon Jaynes–Cummings model [17, 18, 20, 57] obtained by the limiting processes \(\lambda \rightarrow 0\). The \(\lambda \)-dependent terms of the time-independent Hamiltonian (3.2) can be considered as the inversely quadratic potential and the radial external classical field, respectively. In continuation of our investigations, we will focus on the role of these terms via the deformation parameter \(\lambda \) in strengthening or weakening the nonclassical behaviors of the atom-field system. As it is known, the eigenstates of the Hamiltonian \(H_{TPJCM}^{(g)}\) are made by the even and odd subspaces of the unitary Fock representation space of the simple harmonic oscillator that themselves form the positive discrete series of su(1, 1) with the Bargmann indices 1/4 and 3/4, respectively. Here in this article, we are going to obtain the eigenstates of the Hamiltonian \(H^{(\lambda ,g)}\) by using the even and odd subspaces corresponding to the positive discrete \((\frac{1}{4}+\frac{\lambda }{2})\)- and \((\frac{3}{4}+\frac{\lambda }{2})\)-representations of su(1, 1). One can show that the free Hamiltonian (corresponding to \(g=0\)) is an integral of motion provided that the detuning parameter \(\Delta =2\omega -\omega _0\) between the radiation field and the atomic transition is zero, or, equivalently, the exact resonance condition holds.

Let us now use the positive discrete \((\frac{1}{4}+\frac{\lambda }{2})\)- and \((\frac{3}{4}+\frac{\lambda }{2})\)-representations of su(1, 1) and fix the bases \({\left| {n,\pm }\right\rangle _e}\equiv |n\rangle _e\otimes |\pm \rangle \) and \({\left| {n,\pm }\right\rangle _o}\equiv |n\rangle _o\otimes |\pm \rangle \) for the Hilbert space corresponding to \(\lambda \)-deformed TPJCM Hamiltonian \(H^{(\lambda ,g)}\), respectively. Its matrix representation with respect to an orthonormal basis ordered as \(\{\left| {n,+}\right\rangle _e, \left| {n+1,-}\right\rangle _e\}\) is given by

$$\begin{aligned} H_{n}^{(\lambda ,g)} = \left( {\begin{array}{*{20}{cc}} {\omega (2n + \lambda + \frac{1}{2}) + \frac{{{\omega _0}}}{2}}&{} &{}{2g\sqrt{(n + 1)(n + \lambda + \frac{1}{2})} }\\ &{} &{} \\ {2g\sqrt{(n + 1)(n + \lambda + \frac{1}{2})} }&{} &{}{\omega (2n + \lambda + \frac{5}{2}) - \frac{{{\omega _0}}}{2}} \end{array}} \right) . \end{aligned}$$
(3.4)

The energy eigenvalues of \(H_{n}^{(\lambda ,g)}\) are calculated as

$$\begin{aligned} E_{n,\pm }^{(\lambda ,g)}=\left( 2n + \lambda + \frac{3}{2}\right) \omega \pm \frac{{{\Omega _{n}^{(\lambda ,g)}}}}{2}, \end{aligned}$$
(3.5)

in correspondence with the eigenstates

$$\begin{aligned}&\left| E_{n,+}^{(\lambda ,g)} \right\rangle =\cos \theta _n{\left| {n,+} \right\rangle _e}+\sin \theta _n{\left| {n + 1,-} \right\rangle _e},\nonumber \\&\left| E_{n,-}^{(\lambda ,g)}\right\rangle =\sin \theta _n{\left| {n,+} \right\rangle _e}-\cos \theta _n{\left| {n + 1,-} \right\rangle _e}, \end{aligned}$$
(3.6)

respectively, with

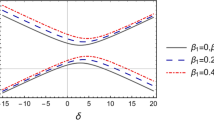
$$\begin{aligned} \sin \theta _n=\frac{{\Omega _{n}^{(\lambda ,g)}}+\Delta }{{\sqrt{{{({\Omega _{n}^{(\lambda ,g)}+\Delta })}^2}+8{g^2}(n + 1)(2n + 2\lambda +1)}}}. \end{aligned}$$
(3.7)

\(\Omega _{n}^{(\lambda ,g)}\) is the \(\lambda \)-generalization form of the quantum electrodynamics Rabi frequency [57], and its magnitude is given by \(\Omega _{n}^{(\lambda ,g)}={\left( {{\Delta }^2}+8{g^2}(n+1)(2n + 2\lambda + 1)\right) ^{1/2}}\). If there is no coupling between the photon and atom, that is, \(g=0\), then the energies \(E_{n,+}^{(\lambda ,0)}\) and \(E_{n,-}^{(\lambda ,0)}\) will be same for the case of exact resonance. Otherwise, for any nonvanishing value of g, it is straightforward to conclude that \(E_{n,+}^{(\lambda ,g)}>E_{n,-}^{(\lambda ,g)}\). Furthermore, by direct calculation, we find that \(E_{n,+}^{(\lambda _1,g)}>E_{n,+}^{(\lambda _2,g)}>0\) and \(\left| E_{n,+}^{(\lambda _1,g)}-E_{n,-}^{(\lambda _1,g)}\right| >\left| E_{n,+}^{(\lambda _2,g)}-E_{n,-}^{(\lambda _2,g)}\right| \) for \(\lambda _1>\lambda _2\). That is, not only the magnitude of the energy \(E_{n,+}^{(\lambda ,g)}\) but also the gap between energies \(E_{n,+}^{(\lambda ,g)}\) and \(E_{n,-}^{(\lambda ,g)}\) increase by increasing the deformation parameter \(\lambda \). Again, for \(\lambda _1>\lambda _2\), it is easy to show that \(E_{n,-}^{(\lambda _1,0)}>E_{n,-}^{(\lambda _2,0)}\). The Rabi frequency \(\Omega _{n}^{(\lambda ,g)}\) with \(g\ne 0\) suggests that the influence of the deformation parameter \(\lambda \) on \(E_{n,-}^{(\lambda ,g)}\) is more complex, it makes it possible to conclude that the nonzero \(\lambda \) causes the energy to be increased or decreased. Figure 1a, b respectively exhibit variations of the energies \(E_{n,-}^{(\lambda ,0.7 \omega _{0})}\) and \(E_{n,-}^{(\lambda ,0.8 \omega _{0})}\) in terms of the detuning parameter \(-5 \omega _{0}\le \Delta \le 5 \omega _{0}\) for \(\omega =0.5 \omega _{0}\), \(n=1, 2\) and \(\lambda =0,10\). As it is seen from the plots, for \(g=0.7 \omega _{0}\) and for both values 1 and 2 of the quantum number n the energy is increased by increasing the \(\lambda \)-deformation parameter from 0 to 10. Whilst, when g is \(0.8 \omega _{0}\), for \(n=1\) and \(n=2\), the energy is increased and decreased respectively by increasing \(\lambda \) from 0 to 10. One can directly use the ordered orthonormal basis \(\{\left| {n,+}\right\rangle _o, \left| {n+1,-}\right\rangle _o\}\) and get the energy levels \(E_{n,\pm }^{(\lambda +1)}\) for the Hamiltonian \(H^{(\lambda ,g)}\), which is only a shift in the deformation parameter \(\lambda \). For this reason, we do not consider the eigenvalues of \(H^{(\lambda ,g)}\) in the positive discrete \((\frac{3}{4}+\frac{\lambda }{2})\)-representations of su(1, 1) and will focus on the role of \(\lambda \) in the behaviors and properties of the solutions in terms of the basis \(\{\left| {n,+}\right\rangle _e, \left| {n+1,-}\right\rangle _e\}\), in what follows.

Fig. 1
figure 1

Variations of energies a \(E_{n,-}^{(\lambda ,0.7)}/\omega _{0}\) and b \(E_{n,-}^{(\lambda ,0.8)}/\omega _{0}\) versus detuning parameter \(-5 \omega _{0}\le \Delta \le 5 \omega _{0}\) for \(\omega =0.5 \omega _{0}\), \(n=1, 2\) and \(\lambda =0, 10\). The solid and dashed lines correspond to \(n=1\) and \(n=2\), respectively

Full size image

The even cat states that will be considered as initial ones of the field in the next section are superpositions of the kets of the even-photon numbers, the eigenstates for the Hamiltonian (2.6) with the eigenvalue \(+1\) instead of the parity operator R. The authors of Rodriguez-Lara [58, 59] have investigated the possibility of physical realization of the interaction of a single two-level atom with a single-mode cavity field in nonlinear two-photon transitions, a JCM that conserves parity symmetry. Therefore, we can propose the faithful realization propounded by them to reconstruct the mean value of quantum optics measurements, such as photon number and atomic excitation energy, from the intensity and from the field strength, such as von Neumann entropy and fidelity, at the output facet of the photonic lattices.

4 Time evolution of the atom-field states with the initial states of the even cat and excited for the field and atom

The dynamics of the \(\lambda \)-deformed two-photon Jaynes–Cummings system is achieved by transforming into the interaction picture with respect to the free Hamiltonian \(H_0\) as follows

$$\begin{aligned} {H_I}= & {} {e^{i{H_0}t}}{H_{{\mathop {\mathrm{int}}} }}{e^{ - i{H_0}t}}\nonumber \\= & {} 2g({e^{i\Delta t}}{\sigma _-}K_+ + {e^{-i\Delta t}}{\sigma _+}K_-), \end{aligned}$$
(4.1)

the so-called time-dependent interaction Hamiltonian. If we propose an infinite expansion as

$$\begin{aligned} {\left| {\psi (t)} \right\rangle _e} = \sum \limits _{n = 0}^\infty {\left( C_{n, + }^e(t){{\left| {n, + } \right\rangle }_e} + C_{n + 1, - }^e(t){{\left| {n + 1, - } \right\rangle }_e}\right) } \end{aligned}$$
(4.2)

for the solutions of the time-dependent Schrödinger equation \(i\frac{\partial }{{\partial t}}{\left| {\psi (t)} \right\rangle _e} = {H_I}{\left| {\psi (t)} \right\rangle _e}\), then we get two linear-coupled first-order differential equations as follows (dot is for derivative with respect to time)

$$\begin{aligned}&{\dot{C}}_{n,+}^e=-2ig\sqrt{(n+1)(n+\lambda +\frac{1}{2})}e^{-i\Delta t}C_{n+1,-}^e,\nonumber \\&{\dot{C}}_{n+1,-}^e=-2ig\sqrt{(n+1)(n+\lambda +\frac{1}{2})}e^{i\Delta t}C_{n,+}^e. \end{aligned}$$
(4.3)

The following two recursion relations are immediate:

$$\begin{aligned} C_{n, + }^e(t)= & {} {e^{ - i\frac{\Delta t}{2}}}\left\{ {C_{n, + }^e(0) \left( {\cos (\frac{{\Omega _{n}^{(\lambda ,g)} t}}{2}) + i(\frac{\Delta }{\Omega _{n}^{(\lambda ,g)}}) \sin (\frac{{\Omega _{n}^{(\lambda ,g)}t}}{2})} \right) } \right. \nonumber \\&\quad \left. {\,\,\, - C_{n + 1, - }^e(0)\left( {\frac{{4ig}}{\Omega _{n}^{(\lambda ,g)}}\sqrt{(n + 1)(n + \lambda + \frac{1}{2})} \sin (\frac{{\Omega _{n}^{(\lambda ,g)}t}}{2})} \right) } \right\} ,\nonumber \\ C_{n + 1, - }^e(t)= & {} {e^{i\frac{\Delta t}{2}}}\left\{ {C_{n + 1, - }^e(0) \left( {\cos (\frac{{\Omega _{n}^{(\lambda ,g)}t}}{2}) - i(\frac{\Delta }{\Omega _{n}^{(\lambda ,g)}}) \sin (\frac{{\Omega _{n}^{(\lambda ,g)}t}}{2})} \right) } \right. \nonumber \\&\quad \left. {\,\,\, - C_{n, + }^e(0)\left( {\frac{{4ig}}{\Omega _{n}^{(\lambda ,g)}} \sqrt{(n + 1)(n + \lambda + \frac{1}{2})} \sin (\frac{{\Omega _{n}^{(\lambda ,g)}t}}{2})} \right) } \right\} , \end{aligned}$$
(4.4)

where \(C_{n,+}^e(0)\) and \(C_{n+1,-}^e(0)\) are determined from the initial conditions of the system. In what follows, we assume that the field and atom are initially in a parity-deformed even cat state given in [54] as well as the excited state, respectively. Therefore, the initial state of the atom–field is

$$\begin{aligned} {\left| {\psi (0)}\right\rangle _e}\equiv {\left| z\right\rangle }_{\lambda ,e}\otimes \left| +\right\rangle = \sqrt{\frac{{{{\left( \frac{{|z|}}{{\sqrt{2} }}\right) }^{2\lambda - 1}}}}{{{\mathrm {I}_{\lambda - \frac{1}{2}}}(|z{|^2})}}} \sum \limits _{n = 0}^\infty {\frac{{{z^{2n}}}}{{\sqrt{{2^{2n}}\,n!\,\Gamma (n + \lambda + \frac{1}{2})} }}{{\left| n,+ \right\rangle }_e}}, \end{aligned}$$
(4.5)

in which, \(\mathrm {I}_{\lambda }(x)\) refers to the modified Bessel function of the first type [60] and z is an arbitrary complex variable with the polar form \(z=|z|e^{i\theta }\) so that \(0\le |z|<\infty \) and \(0\le \theta <2\pi \). The authors in Ref. [54] have shown that the even cat state \({\left| z\right\rangle }_{\lambda ,e}\) exhibit super-Poissonian statistics for any \(\lambda \ge 0\), except for the negative values of \(-\frac{1}{2}<\lambda < 0\) where a sub-Poissonian distribution appears for \(|z|>1\). Moreover, the even cat states \({\left| z\right\rangle }_{\lambda ,e}\) for \(\lambda >0\) and \(\theta =\frac{\pi }{2}\) exhibit squeezing effect in the position coordinate so that the degree of squeezing is enhanced by increasing \(\lambda \). Whilst, for \(-\frac{1}{2}<\lambda < 0\), squeezing disappears when we begin to increase the amount of |z| from small values to larger ones. Using the x-representation of the even cat states, namely \(\langle x|z\rangle _{\lambda ,e}\), we have evaluated the Wigner quasi probability distribution function \(W_{\lambda ,e}(x,p)\equiv \frac{1}{\pi }\int _{-\infty }^{\infty } \langle x+q|z\rangle _{\lambda ,e}\,_{\lambda ,e}\langle z|x-q\rangle e^{-2ip q}\,\mathrm{d}q\) and then plotted its changes in region \(-5\le x, p\le 5\) of the phase space for \(z=1\) in Fig. 2a–e for \(\lambda =0, 1, 2, 3, 4\), respectively. Indeed, Fig. 2a is for the even cat states corresponding to the undeformed harmonic oscillator, and Fig. 2b–e are for those of the parity \((\lambda =1, 2, 3, 4)\)-deformed harmonic oscillators to be compared and to show how the classical and quantum features of those states are influenced by the deformation parameter \(\lambda \). The Wigner functions of those states in Fig. 2 exhibit different features on both positive and negative probability distributions depending on the deformation parameter \(\lambda \). Contrary to the cases \(\lambda =1, 3\), for \(\lambda =2, 4\) just similar to \(\lambda =0\) (undeformed oscillator), the phase-space distributions of even cat states contribute the most positive probability precisely at the origin of the phase space. The number of positive humps increases by two units when \(\lambda \) changes from an even number to the next higher one, while it remains constant, equal to one, for the odd values of \(\lambda \). The width and height of the negative humps of the Wigner function, which make a detour from classical behavior, exhibit a quantum interference phenomenon. As it is seen from Fig. 2a–e, the interference patterns for \(\lambda =0, 2, 4\) are different from those of \(\lambda =1, 3\), the first items with the two negative humps and the latter items with the one negative hump. Despite the first cases, the positive and negative probability distributions of the second ones interchange under the parity operation \(x\rightarrow -x\). Furthermore, both negative and positive values of the Wigner functions of the first cases remain unchanged under the change in sign of both x and p. The initial state (4.5) leads to the initial probability amplitudes of the atom–field state being

$$\begin{aligned} C_{n,+}^e(0)=\frac{|z|^{\lambda -\frac{1}{2}}\,z^{2n}}{{\sqrt{2^{2n+\lambda -\frac{1}{2}}n!\,\Gamma \left( n+\lambda +\frac{1}{2}\right) {I_{\lambda -\frac{1}{2}}}(|z{|^2})}}}, \quad C_{n+1,-}^e(0)=0. \end{aligned}$$
(4.6)
Fig. 2
figure 2

Density (contour) plots of the Wigner quasi probability distribution function \(W_{\lambda ,e}(x,p)\) corresponding to the even cat state \({\left| z\right\rangle }_{\lambda ,e}\) with \(z=1\) for a \(\lambda =0\), b \(\lambda =1\), c \(\lambda =2\), d \(\lambda =3\) and e \(\lambda =4\)

Full size image

5 Time evolution of the fidelity, atomic inversion and level damping

Fidelity, which is here considered as a transition probability from the initial state of atom-field to another state in every next moment, indicates perfect and no overlap between the states when it takes the most and least values 1 and 0, respectively. Indeed, it is a criterion to measure the closeness and distance between the initial state and the dynamically evolved state, a characterization of distinguishability of two states. Therefore, the oscillating patterns in time for the fidelity denote how the atom-field state returns periodically to its initial state. In general, the trends of the changes in the fidelity and entropy of entanglement are not exactly opposite to each other which, in turn, implies that there exists a complicated relationship between entanglement and decoherence in the framework of quantum information theory. However, the high fidelity leads to the low entropy value that is associated with energy consumption. The fidelity (transition probability) between the initial state \({\left| {\psi (0)} \right\rangle _e}\) and the time evolved state \({\left| {\psi (t)} \right\rangle _e}\) is calculated as [61]

$$\begin{aligned} F\equiv |_e\langle \psi (0)|\psi (t)\rangle _e|^2=\left| \sum \limits _{n = 0}^\infty {| C_{n,+}^e(0){|^2}\left[ {\cos \left( \frac{{\Omega _{n}^{(\lambda ,g)} t}}{2}\right) +i\left( \frac{\Delta }{\Omega _{n}^{(\lambda ,g)}}\right) \sin \left( \frac{{\Omega _{n}^{(\lambda ,g)} t}}{2}\right) } \right] }\right| ^2.\nonumber \\ \end{aligned}$$
(5.1)

Figure 3a–c indicate fidelity as a function of gt in the range \(0\le gt\le 10\) for \(\Delta =0,\,0.05 \omega _{0},\,0.09 \omega _{0}\), respectively, with \(g=0.001 \omega _{0}\). Figure 3a, b have been plotted for \(|z|=\sqrt{30}\) and different three values \(\lambda =0, 10\) and 20 of the deformation parameter while Fig. 3c is for \(|z|=0.6\) and only one value of \(\lambda \), namely \(\lambda =20\). One can see that the larger peaks for fidelity are obtained from the larger \(\lambda \) in the case of off-resonance, and vice versa for the resonance case. This is confirmed by comparing the plots in Fig. 3a, b. Also, from the comparison of Fig. 3a–c, it is found that for \(\lambda =20\), the average of fidelity becomes stronger when \(\Delta \) is increased. Finally, Fig. 3a–c show that the amplitude and period of the fluctuations between the values 0 and 1 (the minimal and maximal closeness of the states) is dependent on the deformation parameter \(\lambda \).

Fig. 3
figure 3

Fidelity as a function of \(0\le gt\le 10\) for a \(\Delta =0\), b \(\Delta =0.05 \omega _{0}\) and c \(\Delta =0.09 \omega _{0}\) with \(g=0.001 \omega _{0}\) (Color figure online)

Full size image

At this stage, it is necessary to investigate the temporal evolution of the criterion for the population inversion of collective two-level atoms. Temporal evolution of the atomic inversion for the parity \(\lambda \)-deformed TPJCM with the initial condition (4.5) of the atom–field state is calculated as

$$\begin{aligned}&_e\left\langle \psi (t)| {{\sigma _3}} |\psi (t)\right\rangle _e=\sum \limits _{n = 0}^\infty \left[ {|C_{n, + }^e(t)|}^2-{|C_{n+1,-}^e(t)|}^2\right] \nonumber \\&\quad =\sum \limits _{n = 0}^\infty {|C_{n,+}^e(0){|^2} \left\{ {{\left( \frac{{\Delta }}{\Omega _{n}^{(\lambda ,g)}}\right) ^2}+ {\left( \frac{{4g}}{\Omega _{n}^{(\lambda ,g)}}\right) ^2}(n + 1) \left( n+\lambda +\frac{1}{2}\right) \cos (\Omega _{n}^{(\lambda ,g)} t)} \right\} }.\nonumber \\ \end{aligned}$$
(5.2)

The quasi-periodic collapse and revival phenomena in atomic population inversion of the parity \(\lambda \)-deformed TPJCM as a function of the scaled time \(0\le gt\le 6\) with \(|z|=\sqrt{30}\), \(g=0.001 \omega _{0}\) and \(\Delta =0,\,0.05 \omega _{0},\,0.09 \omega _{0}\) have been depicted in Fig. 4a, b for \(\lambda =0\) and 20, respectively. Figure 4a, b show that, as expected from formula (5.2), the amplitude of atomic population inversion decreases by increasing the detuning parameter \(\Delta \). These two figures also show that for the case of exact resonance, the partial revivals of the Rabi oscillations corresponding to nonzero deformation parameter \(\lambda \) (contrary to the value \(\lambda =0\) of the simple harmonic oscillator which is regular and complete) become less distinct as time increases. Furthermore, the partial revivals in the case of out-of-resonance for \(\lambda \)-deformed field become more periodic in comparison with the undeformed one. Moreover, the revivals of \(\lambda \)-deformed fields in the resonance and out-of-resonance cases become broader and narrower with respect to the undeformed field, respectively. Finally, the mean values of the atomic inversion increase by increasing the detuning parameter in both deformed and undeformed cases of the field.

Fig. 4
figure 4

Plots of the atomic inversion \(\,_e\langle \psi (t)|\sigma _3|\psi (t)\rangle _e\) for the parity \(\lambda \)-deformed TPJCM against the \(0\le gt\le 6\) for a \(\lambda =0\) and b \(\lambda =20\) with \(|z|=\sqrt{30}\) and \(g=0.001 \omega _{0}\)

Full size image

There are several phenomena such as spontaneous emission [62, 63], collisions [64] and scattering [65] which lead to decay in the populations of excited atomic levels. The finite level lifetimes are described by adding phenomenological decay terms to the equations of motion or, equivalently, the appropriate non-Hermitian terms to the Hamiltonian. Here, it is again assumed that the atom is initially in the excited state and thus the population inversion dynamics at time t is analyzed by adding decay term \(-i\frac{\gamma }{2}\left| + \right\rangle \left\langle +\right| \) to the Hamiltonian in order to consider dissipation phenomenon of energy into the environment. The real parameter \(\gamma \) is interpreted as the rate of energy dissipation. So, by this way, the damped Hamiltonian of the parity \(\lambda \)-deformed TPJCM is obtained as follows:

$$\begin{aligned} {H_{\mathrm{dam}}}= & {} {e^{i{H_0}t}}({H_{{\mathop {\mathrm{int}}} }}-i\frac{\gamma }{2}\left| + \right\rangle \left\langle +\right| ){e^{ - i{H_0}t}}\nonumber \\= & {} 2g({e^{i\Delta t}}{\sigma _-}K_+ + {e^{-i\Delta t}}{\sigma _+}K_-)-i\frac{\gamma }{2}\left| + \right\rangle \left\langle +\right| . \end{aligned}$$
(5.3)

For the solutions of the time-dependent Schrödinger equation \(i\frac{\partial }{{\partial t}}{\left| {\psi (t)} \right\rangle _e} = {H_{\mathrm{dam}}}{\left| {\psi (t)} \right\rangle _e}\) the second relation of (4.3) appears exactly as it is. Whilst, the first relation of that is converted to the following equation

$$\begin{aligned} {\dot{C}}_{n,+}^e(t)=-2ig\sqrt{(n+1)(n+\lambda +\frac{1}{2})}\,e^{-i\Delta t}C_{n+1,-}^e(t)-\frac{\gamma }{2}{C}_{n,+}^e(t). \end{aligned}$$
(5.4)

The second equation of (4.3) together with (5.4) have the following solutions:

$$\begin{aligned}&C_{n, + }^e(t)=C_{n,+}^e(0)\left[ {\cos (\frac{{\Theta _{n}^{(\lambda ,g)} t}}{2}) +(\frac{2i\Delta -\gamma }{2\Theta _{n}^{(\lambda ,g)}})\sin (\frac{{\Theta _{n}^{(\lambda ,g)} t}}{2})}\right] {e^{-\frac{2i\Delta +\gamma }{4}t}},\nonumber \\&C_{n+1,-}^e(t)=C_{n,+}^e(0)\frac{{-4ig}}{\Theta _{n}^{(\lambda ,g)}} \sqrt{(n+1)(n+\lambda +\frac{1}{2})} \sin (\frac{{\Theta _{n}^{(\lambda ,g)} t}}{2}){e^{\frac{2i\Delta -\gamma }{4}t}}, \end{aligned}$$
(5.5)

where \(\Theta _{n}^{(\lambda ,g)}={\left( {{(\Delta +i\frac{\gamma }{2})}^2}+8{g^2}(n+1)(2n + 2\lambda + 1)\right) ^{1/2}}\). For given values \(|z|=\sqrt{30}\), \(g=0.001 \omega _{0}\) and \(\Delta =0.05 \omega _{0}\), we have plotted the changes of the atomic inversion versus the scaled time in the interval \(0\le gt\le 6\), in Fig. 5a for \(\gamma =0\) and Fig. 5b for \(\gamma =0.001 \omega _{0}\) and both of them for \(\lambda =0\) (solid line) and \(\lambda =20\) (dotted line) as well as Fig. 5c for \(\gamma =0.05 \omega _{0}\), \(\lambda =0\) (solid line) and \(\lambda =1000\) (dotted line). When we compare Fig. 5a–c, we conclude that a nonzero value for \(\gamma \) in both undeformed and deformed cases causes the Rabi oscillations of the revivals to be destroyed in time. A comparison of Fig. 5b, c shows that the revivals will disappear sooner when \(\gamma \) is increased. For \(\gamma =0.05 \omega _{0}\), the close-up of Fig. 5c indicates that the oscillating behavior of revivals in atomic population inversion for the short time regime (just after \(t=0\)) intensifies by increasing the deformation parameter \(\lambda \).

Fig. 5
figure 5

Plots of the atomic inversion \(\,_e\langle \psi (t)|\sigma _3|\psi (t)\rangle _e\) for the parity \(\lambda \)-deformed TPJCM versus \(0\le gt\le 6\) for a \(\gamma =0\), b \(\gamma =0.001 \omega _{0}\) and c \(\gamma =0.05 \omega _{0}\) with \(|z|=\sqrt{30}\), \(g=0.001 \omega _{0}\) and \(\Delta =0.05 \omega _{0}\). The solid lines in any of the three figures are for \(\lambda =0\) (undeformed oscillator) and the dotted lines in a and b are for \(\lambda =20\) and in c for \(\lambda =1000\)

Full size image

6 Sub-Poissonian light, quadrature squeezing of the cavity field and von Neumann entropy

The relevant non-zero expectation values for the evaluation of nonclassical properties of the cavity field over the time-evolved atom-field state (4.2) with the expansion coefficients given by (4.4) and (4.6) are

$$\begin{aligned}&\,_e\langle \psi (t)| A^2|\psi (t) \rangle _e= 2\left( \eta _{\lambda }^{+}(t)+\eta _{\lambda }^{-}(t)\right) ,\nonumber \\&\,_e\langle \psi (t)|{{A^\dag }A}|\psi (t)\rangle _e=2\left( \xi _{\lambda }^{+}(t)+\xi _{\lambda }^{-}(t)\right) ,\nonumber \\&\,_e\langle \psi (t)|{{{({A^\dag }A)}^2}}|\psi (t)\rangle _e=4\left( \zeta _{\lambda }^{+}(t)+\zeta _{\lambda }^{-}(t)\right) , \end{aligned}$$
(6.1)

where

$$\begin{aligned}&\xi _{\lambda }^{\pm }(t)=\sum _{n=0}^{\infty }\left( n+\frac{1}{2}\mp \frac{1}{2}\right) |C_{n+\frac{1}{2}\mp \frac{1}{2},\pm }^e(t)|^2,\nonumber \\&\zeta _{\lambda }^{\pm }(t)=\sum _{n=0}^{\infty }\left( n+\frac{1}{2}\mp \frac{1}{2}\right) ^2|C_{n+\frac{1}{2}\mp \frac{1}{2},\pm }^e(t)|^2,\nonumber \\&\eta _{\lambda }^{\pm }(t)=\sum _{n=0}^{\infty }\sqrt{\left( n+1+\frac{1}{2}\mp \frac{1}{2}\right) \left( n+\lambda +1\mp \frac{1}{2}\right) } {C^*}^e_{n+\frac{1}{2}\mp \frac{1}{2},\pm }(t){C}^e_{n+1+\frac{1}{2}\mp \frac{1}{2},\pm }(t).\nonumber \\ \end{aligned}$$
(6.2)

It is clear that \(\,_e\langle \psi (t)|N|\psi (t) \rangle _e=\,_e\langle \psi (t)| {{A^\dag }A}|\psi (t)\rangle _e\) and \(\,_e\langle \psi (t)|{{N^2}}|\psi (t)\rangle _e=\,_e\langle \psi (t)| {{{({A^\dag }A)}^2}} |\psi (t)\rangle _e\).

The statistical features of the light field are characterized by evaluating the \(\lambda \)-deformed Mandel parameter for the normalized time-evolved atom-field state \(|\psi (t) \rangle _e\):

$$\begin{aligned} Q^{(\lambda ,g)}(t)\equiv & {} \frac{{\,_e\langle \psi (t)| {{N^2}} |\psi (t) \rangle _e- {{\,_e\langle \psi (t)| N|\psi (t) \rangle _e}^2}}}{{\,_e\langle \psi (t)| N |\psi (t) \rangle _e }}-1\nonumber \\= & {} 2\frac{\zeta _{\lambda }^{+}(t)+\zeta _{\lambda }^{-}(t) -\left( \xi _{\lambda }^{+}(t)+\xi _{\lambda }^{-}(t)\right) ^2}{\xi _{\lambda }^{+}(t)+\xi _{\lambda }^{-}(t)}-1. \end{aligned}$$
(6.3)

In order to consider the time evolution of the photon counting statistics, we have depicted quasi periodic plots of the \(\lambda \)-Mandel parameter \(Q^{(\lambda ,g)}(t)\) versus the scaled time \(0\le gt\le 3\) for \(\Delta =0\), \(\Delta =0.05 \omega _{0}\) and \(\Delta =0.09 \omega _{0}\) in Fig. 6a–c, respectively. Each of the parts (a), (b) and (c) involves three different curves corresponding to the deformation parameters \(\lambda =0, 1, 2\), respectively, with \(|z|=\sqrt{30}\) and \(g=0.001 \omega _{0}\). As it is seen from these figures, the fluctuations in the quasi-periodic plots are increased as detuning parameter \(\Delta \) and deformation parameter \(\lambda \) are allowed to increase. For both resonant and out-of-resonant cases, the sub-Poissonian statistics as a nonclassical behavior of the cavity field becomes weaker when the deformation parameter \(\lambda \) is increased from 0 to 2. Furthermore, the behavior of the states in the resonant case with respect to the off-resonant one becomes more nonclassical in both deformed and undeformed fields. Therefore, the model can be used as a source for generating the sub-Poissonian light when both the deformation parameter \(\lambda \) and detuning parameter \(\Delta \) are small enough.

In order to consider the squeezing of the cavity field, we introduce the two generalized quadrature operators as \(x=\frac{1}{\sqrt{2}}\left( A^{\dagger }+A\right) \) and \(p=\frac{i}{\sqrt{2}}\left( A^{\dagger }-A\right) \) with the commutation relation \([x,p]=i(1+2\lambda R)\). The squeezing of the quadratures of the field in any arbitrary moment t is rooted in Heisenberg–Weyl uncertainty inequality \(\sigma _{xx}^e(t) \sigma _{pp}^e(t) \ge \frac{1}{4}\left| \,_e\langle \psi (t)| [x,p]|\psi (t) \rangle _e\right| ^2\) with \(\sigma _{{{{\mathcal {O}}}}\mathcal{O}}^e(t)\equiv \,_e\langle \psi (t)|{{{\mathcal {O}}}}^2|\psi (t) \rangle _e-\,_e\langle \psi (t)|{{{\mathcal {O}}}}|\psi (t) \rangle _e^2\) for \({{{\mathcal {O}}}}=x, p \) as the variance of the position and momentum operators with respect to the time-evolved atom-field state (4.2). This means that the realization of squeezing in any of the quadratures, which is a purely quantum mechanical phenomenon, leads to the spreading in the other quadrature. Therefore, the degree of squeezing of the quadrature \({{{\mathcal {O}}}}\) on the state \(|\psi (t) \rangle _e\) is defined by the following parameter [38, 66]:

$$\begin{aligned} S_{{{\mathcal {O}}}}^{(\lambda ,g)}(t)\equiv \frac{2\sigma _{{{{\mathcal {O}}}}\mathcal{O}}^e(t)}{\left| \,_e\langle \psi (t)| [x,p]|\psi (t) \rangle _e\right| }-1, \end{aligned}$$
(6.4)

which for the most squeezing corresponds to the minimum value, i.e. \(-1\). We immediately derive the following results from Eq. (6.1):

$$\begin{aligned}&S_{x}^{(\lambda ,g)}(t)=\frac{4}{1+2\lambda }\left[ \left( \xi _{\lambda }^{+}(t)+\xi _{\lambda }^{-}(t)\right) +\mathrm {Re}\left( \eta _{\lambda }^{+}(t)+\eta _{\lambda }^{-}(t)\right) \right] ,\end{aligned}$$
(6.5)
$$\begin{aligned}&S_{p}^{(\lambda ,g)}(t)=\frac{4}{1+2\lambda }\left[ \left( \xi _{\lambda }^{+}(t)+\xi _{\lambda }^{-}(t)\right) -\mathrm {Re}\left( \eta _{\lambda }^{+}(t)+\eta _{\lambda }^{-}(t)\right) \right] . \end{aligned}$$
(6.6)

Evolution of the squeezing parameters of cavity field quadratures versus \(0\le gt\le 20\) with \(|z|=2\), \(\theta =0\), \(g=0.01 \omega _{0}\) and \(\Delta =0.09 \omega _{0}\) has been depicted in Fig. 7a–d for \(\lambda =0\) (undeformed oscillator), \(\lambda =2\), \(\lambda =5\) and \(\lambda =10\), respectively. As it is seen, the squeezing parameters of the quadratures x and p oscillate in completely opposite phases to each other but with the same amplitudes. Contrary to the undeformed oscillator case, parity \(\lambda \)-deformed atom-filed states exhibit a squeezing effect in the cavity field quadratures x and p and the largest magnitude of squeezing in both of them become weaker and happens over a long period of time when \(\lambda \) is increased.

Fig. 6
figure 6

Time evolution of the Mandel parameter \(Q^{(\lambda ,g)}\) versus the scaled time \(0\le gt\le 3\) for a \(\Delta =0\), b \(\Delta =0.05 \omega _{0}\) and (c) \(\Delta =0.09 \omega _{0}\) with \(|z|=\sqrt{30}\) and \(g=0.001 \omega _{0}\). Each of the parts a–c involves three different plots for \(\lambda =0, 1, 2\)

Full size image
Fig. 7
figure 7

Time evolution of the squeezing parameters of cavity field quadratures x and p in terms of the scaled time in the interval \(0\le gt\le 20\) with \(|z|=2\), \(\theta =0\), \(g=0.01 \omega _{0}\) and \(\Delta =0.09 \omega _{0}\) for a \(\lambda =0\), b \(\lambda =2\), c \(\lambda =5\) and d \(\lambda =10\), respectively

Full size image

Consider the density operator for the atom-field system as \(\rho _{_{AF}}(t)\) as well as the reduced density matrices of the atom and field as partial traces of \(\rho _{_{AF}}(t)\) over \({\mathcal {H}}^{\mathrm {atom}}\) and \({\mathcal {H}}\), respectively: \(\rho _{_{A}}(t)={\mathrm {tr}}_{_{F}}\rho _{_{AF}}(t)\) and \(\rho _{_{F}}(t)={\mathrm {tr}}_{_{A}}\rho _{_{AF}}(t)\). The dimensionless partial entropies of von Neumann for the atom and field in terms of their corresponding density matrices are given by

$$\begin{aligned} S_{_{A}}(t)=-{\mathrm {tr}}_{_{A}}(\rho _{_{A}}(t)\ln \rho _{_{A}}(t)), \quad S_{_{F}}(t)=-{\mathrm {tr}}_{_{F}}(\rho _{_{F}}(t)\ln \rho _{_{F}}(t)). \end{aligned}$$
(6.7)

The density matrix for the pure state (4.2) with the initial probability amplitudes (4.6) is \(\rho _{_{AF}}(t)=\left| \psi (t)\rangle _e\,_e \langle \psi (t)\right| \) which exhibits a disentangled state for the atom-field system at the initial moment. The real positive Schmidt weights \(\lambda _+=\sum \limits _{n = 0}^\infty \left| C_{n, + }^e(t)\right| ^2\) and \(\lambda _-=\sum \limits _{n = 0}^\infty \left| C_{n + 1, - }^e(t)\right| ^2\) are the common eigenvalues of the reduced density matrices \(\rho _{_{A}}(t)\) and \(\rho _{_{F}}(t)\) so that they obey \(\lambda _++\lambda _-=1\) which, in turn, shows that the Schmidt rank of the bipartite pure state \(\left| {\psi (t)} \right\rangle _e\) is 2 in any next time. Therefore, entanglement between the atom and field creates as time goes far away from the initial moment. The degree of entanglement can be characterized by the same entropy for the reduced density matrices of the atom and field:

$$\begin{aligned} S_{_A}(t)=S_{_F}(t)=-\lambda _+\ln \lambda _+-\lambda _-\ln \lambda _-. \end{aligned}$$
(6.8)

From (6.8), it is clear that \(S_{_A}(0)=0\) and the system of atom-field is separable at the initial moment, which is also verified by Fig. 8a, b. Figure 8a–c have been devoted to consider the entropy against the scaled time gt with \(g=0.001 \omega _{0}\). Figure 8a, b contain plots for \(|z|=\sqrt{30}\), \(0\le gt\le 6.5\) and three different values of detuning parameter \(\Delta =0,\,0.05 \omega _{0},\,0.09 \omega _{0}\) with the deformation parameters \(\lambda =0\) and \(\lambda =20\), respectively. Figure 8c contains only one plot for \(\lambda =20\), \(|z|=0.6\), \(6\le gt\le 6.5\) and \(\Delta =0.09 \omega _{0}\). As it is seen from Fig. 8a–c, the time evolution of atomic entropy has quasi-regular oscillatory behaviors in both resonant and off-resonant conditions as well as in both \(\lambda \)-deformed and undeformed cases. A comparison between Figs. 4a, b and 8a, b shows that the partial revivals and the partial entropies of the atom-field system have the same oscillation patterns and are modulated in the Rabi frequency. From the comparison of Fig. 8a with Fig. 8b, we conclude that the increase in \(\lambda \) causes, in a given time interval, the number of the peaks for the quasi-oscillations of the von Neumann entropies as well as their height to increase. This, in turn, implies that more entanglement occurs by increasing the deformation parameter \(\lambda \). Furthermore, Fig. 8c shows that entanglement between the two-level atom and para-Bose oscillator field disappears periodically in time when we take into account appropriate values for our parameters. For example, the entropy vanishes at \(gt=6.433\) where the fidelity is around 1 [see red lines in Fig. 3c and the close-up of Fig. 8c]. This result is exactly in line with what we have said earlier at the beginning of Sect. 5 regarding the relationship between fidelity and entropy.

Fig. 8
figure 8

Plots of the entropy versus gt with \(g=0.001 \omega _{0}\) for a \(\lambda =0\), \(|z|=\sqrt{30}\), b \(\lambda =20\), \(|z|=\sqrt{30}\) and c \(\lambda =20\), \(|z|=0.6\). The ranges of the scaled time for figures a–c are \(0\le gt\le 6.5\) and \(6\le gt\le 6.5\), respectively

Full size image

7 Concluding remarks and summary

In this work, we have studied TPJCM by using the para-Bose oscillator of order \(p=2\lambda +1\) for the cavity field mode interacting with a two-level atom. The energy levels and eigenstates of atom-field have been derived in terms of a \(\lambda \)-deformed version of the quantum electrodynamics Rabi frequencies \(\Omega _{n}^{(\lambda ,g)}\). The Rabi frequencies allocate themselves two different desired energy levels, and we have analyzed and compared them with each other, especially in a way that illustrates the role of the deformation parameter \(\lambda \). The dependence of one of these desired levels on \(\lambda \) is complex and its variations with the detuning parameter for \(\lambda =0\) and 10 have been depicted and compared in Fig. 1a, b. In continuation of our considerations, we have assumed that the cavity field and atom are initially in an even cat state and excited state, respectively, and have obtained a time-evolved atom-field state. In Fig. 2a–e, \(\lambda \)-dependency of the interference patterns of the initial light field has been investigated and cleared by evaluating the Wigner quasi probability distribution function. We have considered the fidelity for some special values of \(\lambda \) in Fig. 3a–c and shown that the minimal and maximal closeness of the states is dependent on the deformation parameter \(\lambda \). The height of the peaks in the quasi-oscillations of the fidelity in the case of off- and on-resonance increases and decreases by increasing \(\lambda \), respectively. We have compared the quasi-periodic collapse and revival features in atomic population inversion of the parity \(\lambda \)-deformed TPJCM in Fig. 4a, b for \(\lambda =0\) and 20. It has been shown that the partial revivals of the Rabi oscillations in the case of resonance for \(\lambda =20\) become less distinct with increasing the time, whilst those for the simple harmonic oscillator with \(\lambda =0\) are regular and complete. The partial revivals of out-of-resonance become thinner and more periodic in case that \(\lambda \) does not vanish. Figure 5a–c indicate that the evolution of atomic inversion for non-resonance case \(\Delta =0.05 \omega _{0}\) exhibit Rabi oscillations with quasi-periodicity of the population revivals in both undeformed and deformed models (\(\lambda =0, 20, 1000\)), while after a certain time period, the revivals completely disappear with growing the \(\gamma \)-parameter of the decay term in the interaction Hamiltonian. It has been found out that for a non-zero value of \(\gamma \) the oscillating behavior of revivals in atomic population inversion at the initial moments just after \(t=0\) resonates by increasing \(\lambda \). The quasi-periodic plots of the \((\lambda =0, 1, 2)\)-deformed Mandel parameters for the values \(\Delta =0\), \(\Delta =0.05 \omega _{0}\) and \(\Delta =0.09 \omega _{0}\) of the detuning parameter have been depicted respectively in Fig. 6a–c. It has been observed that the sub-Poissonian character of the cavity field decreases with increasing \(\lambda \) from 0 to 2 in both resonant and out-of-resonant cases. However, the statistics of the states become more sub-Poissonian in the first case for both deformed and undeformed fields. The time evolution of the squeezing parameters between cavity field quadratures x and p oscillate with opposite phases but the same amplitudes. This has been found out from Fig. 7a–d with the detuning parameter \(\Delta =0.09 \omega _{0}\) for \(\lambda =0, 2, 5, 10\), respectively. Plots in Fig. 8a–c demonstrate the time evolution of the atomic entropy for deformation parameters \(\lambda =0\) and \(\lambda =20\), with the values \(\Delta =0,\,0.05 \omega _{0},\,0.09 \omega _{0}\) as well as \(\Delta =0.09 \omega _{0}\) for detuning parameter in Fig. 8a–c, respectively, so that all of them have quasi-regular oscillatory behaviors. An important result is that the oscillation patterns are the same for both partial revivals and the partial entropies of the atom-field system, and are modulated in the Rabi frequency. Furthermore, the number of the peaks for the quasi-oscillations of the von Neumann entropies as well as their height is increased by increasing \(\lambda \), which, in turn, is an indication for more entanglement.