1 Introduction

In recent times, mathematical modeling of numerous complex nonlinear physical phenomena formulates nonlinear partial differential equations (NLPDEs). These intricate phenomena have a wide range of applications in several domains of sciences and their fields such as biology, solid-state physics, ocean dynamics, geochemistry, photonics, magnetized plasma, physics, optics, diffusion-reaction, plasma physics, shallow water waves, fiber optics, water optical metamaterials and so forth. Seek the exact solutions to these NLPDEs in nonlinear science, it is one of the critical problems. However, due to the intricacy of NLPDEs, giving all the exact solutions of an NLPDEs with a unified technique appears to be unfeasible. Diverse reliable techniques have been developed to construct exact solutions, such as the modified \(\exp (-\phi (\varpi ))\)-expansion function method (Rehman and Ahmad 2022a), the \((\frac{G^{'}}{G^{2}})\)-expansion function method (Owyed et al. 2022), the first integral method (Akinyemi et al. 2022c), the Hirota bilinear method (Rehman and Ahmad 2022b), new \(\varPhi ^{6}\)-model expansion function method (Seadawy et al. 2021b) and several others (Arafat et al. 2022c; Akram et al. 2021; Tariq et al. 2021; Bilal et al. 2021; Rabie and Ahmed 2022; Sulaiman et al. 2021; Rehman et al. 2022a, b; Raddadi et al. 2021; Aktar et al. 2022; Gomez et al. 2022; Rahman et al. 2021; Akinyemi et al. 2022a, b, d; Inan et al. 2022; Kumar et al. 2022; Mirzazadeh et al. 2022). Recently, different approaches are also considered for diverse lump solutions (Ma and Chen 2009; Ma and Lee 2009; Ma 2021, 2022a, b).

Optical solitons are one of the vital research frontiers of optics and optoelectronics due to their unique property of capability of propagation of waves without scattering over long distances i.e. they preserve their shape over long distances. The solitons in the fiber originated due to The delicate balance between nonlinearity and dispersion effects in the medium. In the recent era of science and technology, the theory of solitons has crafted innovative progress in the telecommunication industry and become the most sizzling domain of research over the past few decades and surmise as to the technology of future generations for high-speed communication systems. Therefore, the exploration and use of optical soliton in fiber expedite a new field of long-distance and demonstrated significant effects in the telecommunications engineering (Khater 2021; Pinar 2022; Sun 2021; Yusuf et al. 2021).

Several researchers in a variety of fields have recently organized a study on NLPDES with fractional order. Fractional nonlinear problems have great potential applications in the multiple areas of applied science particularly in the field of optics which can describe lots of physical nonlinear systems. These differential equations are generalizations of integer order to fractional order. These equations are used to model problems in fluid dynamics, biological and physical processes and systems. Compared Fractional derivative to the integer derivative, it is observed that fractional derivative not only describes the dependency process of function development and also has a global correlation. Fractional derivatives can better portray physical and engineering problems. It has not only very imperative theoretical value but also extensive application value. Different fractional derivatives have been investigated, such as Riemann–Liouville, Caputo, Atangana Baleanu, and conformable fractional derivatives, which are the most used ones to transform the NLPDEs problem with fractional-order into an ordinary differential equation with integer-order based on this characteristic. The fractional derivative model overwhelms the theoretical and practical inconsistencies of the classic integer derivative model, utilizes fewer parameters to achieve the desired result and gives more perfect mathematical and physical models. Nowadays fractional NLSE is one of the significant models and is extensively used in the region of quantum mechanics and optics which has so many applications in diverse domains of sciences, particularly in the field of optics, where the fractional order may be fractional diffraction effect. In an optical fiber, the NLSE is regarded as the elementary model to express soliton dynamics in optical fibers. in last two decades different schemes have been established to get the soliton solutions of different NLSE (Riaz et al. 2022; Seadawy et al. 2021a; Zulfiqar and Ahmad 2020, 2021; Rizvi et al. 2021; Jhangeer et al. 2021; Bilal et al. 2022; Younis et al. 2020; Khater et al. 2021; Rehman et al. 2021).

The fractional coupled nonlinear Schrödinger equation (FCNLSE) is written in underneath (Tang and Chen 2022; Wang et al. 2020)

$$\begin{aligned} \begin{aligned} i D_{t}^{\alpha } \varPhi _{1}+D_{x}^{2 \beta }\varPhi _{1}+\delta (|\varPhi _{1}|^{2}+ \gamma |\varPhi _{2}|^{2})\varPhi _{1}&=0,\\ i D_{t}^{\alpha } \varPhi _{2}+D_{x}^{2 \beta }\varPhi _{2}+\delta (|\varPhi _{1}|^{2}+ \gamma |\varPhi _{2}|^{2})\varPhi _{2}&=0, \end{aligned} \end{aligned}$$
(1)

where \(0<\alpha ,\beta \le 1\), \(\varPhi _{1}(x,t)\) and \(\varPhi _{2}(x,t)\) denotes the complex functions of x and t that represents the amplitudes of circularly-polarized waves in a nonlinear optical fiber. \(\gamma \) and \(\delta \) are non-zero real numbers.

After inspecting the published work, it is surveyed that the stated model is not solved yet by the proposed techniques. Keeping this idea in mind, the primary goal of this work is to retrieve optical and lump solutions of a given model by engaging two mechanisms, the modified generalized exponential rational function method (mGERFM) (Ghanbari 2021; Nonlaopon et al. 2022) and the Hirota bilinear method (HBM) along with different test functions (Alruwaili et al. 2022).

The layout of article is arranged as : In Sect. 2, basics of conformable derivative is presented. In Sect. 3, mGERFM is implemented. In Sect. 4, various lumps solutions are extracted. In Sect. 5, result and discussion is presented and at the end concluding remarks are revealed in Sect. 6.

2 Conformable derivative

This section covers the basics of the fractional derivatives. In recent times, fractional calculus is a unique topic and has gained prominence, therefore mathematician and researchers conduct a study on fractional calculus and derive some new fractional derivative operators such as the Caputo, the Riemann–Liouville, the Caputo–Fabrizio and the Atangana–Baleanu derivatives which have been manipulating in various fields because effects or memory can be better exemplified by fractional-order derivatives. Fractional order models representing certain real-life problems and have significant applications in sciences such as fluid mechanics, biochemistry, applied mathematics, viscoelastic materials, finance, polymers and several other subject areas. The conformable fractional operator overwhelms some restrictions of other fractional operators and its application is much easier and more proficient. This operator offers basic properties of classical calculus such as derivative of the quotient of two functions, the chain rule, the product of two functions, mean value theorem, Rolle’s theorem. Moreover, it permits us better grasp the dynamics of physical phenomena. The conformable derivatives can be defined as

Definition 1

Let \(g:[0,+\infty )\rightarrow R\), \(0<\alpha \le 1\) and \(\forall ~ t\ge 0\). The conformable derivative of g of order \(\alpha \) is

$$\begin{aligned} T_{\alpha }(g)(t)=\lim _ {\epsilon \rightarrow 0} \frac{g(t+\epsilon t^{1-\alpha })-g(t)}{\epsilon }, \end{aligned}$$
(2)

Theorem 1

Suppose \(g,h:(0,\infty )\rightarrow R\) and \(\alpha \) be differentiable functions, then chain rule holds

$$\begin{aligned} T_{\alpha }(g\circ h)(t)=t^{1-\alpha }h(t)^{\alpha -2}h^{'}(t)T_{\alpha }(g(t))|_{t=h(t)}. \end{aligned}$$
(3)

For more detail see references Ghanbari et al. (2019), Khalil et al. (2014).

3 Mathematical analysis

In this section the main focus is to gather multiple solutions of the given models. For the solutions of Eq. (1) substituting the following complex wave transformations:

$$\begin{aligned}&\varPhi _{1}(x,t)=\varOmega _{1} (\varsigma )e^{i\psi }, \end{aligned}$$
(4)
$$\begin{aligned}&\quad \varPhi _{2}(x,t)=\varOmega _{2} (\varsigma )e^{i\psi }, \end{aligned}$$
(5)

and

$$\begin{aligned} \varsigma =m\left( \frac{x^{\beta }}{\beta } -c \frac{t^{\alpha }}{\alpha }\right) , \psi = -\lambda \frac{x^{\beta }}{\beta }+\mu \frac{t^{\alpha }}{\alpha }+\theta _{0}, \end{aligned}$$

where m \(\lambda \) and \(\mu \) represents real constants while \(\theta _{0}\) denotes arbitrary constant. Substituting the following complex wave transformation (4) and (5) into Eq. (1) , we get the real and imaginary parts

$$\begin{aligned} {\left\{ \begin{array}{ll} m^{2}\varOmega _{1}^{''}+\delta \varOmega _{1}^{3}+\delta \gamma \varOmega _{2}^{2} \varOmega _{1}-(\lambda ^{2}+\mu )\varOmega _{1}=0,\\ m^{2}\varOmega _{2}^{''}+\delta \varOmega _{2}^{3}+\delta \gamma \varOmega _{1}^{2} \varOmega _{2}-(\lambda ^{2}+\mu )\varOmega _{2}=0, \end{array}\right. } \end{aligned}$$
(6)

and

$$\begin{aligned} c=-2 \lambda . \end{aligned}$$
(7)

Putting

$$\begin{aligned} \varOmega _{2}=k \varOmega _{1}. \end{aligned}$$
(8)

Then the Eq. (6) become

$$\begin{aligned} m^{2}\varOmega _{1}^{''}+(\delta +\delta \gamma k^{2})\varOmega _{1}^{3}-(\lambda ^{2}+\mu )\varOmega _{1}=0. \end{aligned}$$
(9)

3.1 mGERFM

Assume the trial solution of Eq. (9) as

$$\begin{aligned} \varOmega _{1}(\varsigma )=\chi _{0}+\sum _{j=1}^N \chi _j \bigg (\frac{\varpi ^{'}(\varsigma )}{\varpi (\varsigma )}\bigg )^{j}+\sum _{j=1}^N \varLambda _j \bigg (\frac{\varpi ^{'}(\varsigma )}{\varpi (\varsigma )}\bigg )^{-j},~~~~~~~ \end{aligned}$$
(10)

where

$$\begin{aligned} \varpi (\varsigma )=\frac{\varrho _1 e^{\gamma _1 \varsigma }+\varrho _2 e^{\gamma _2 \varsigma }}{\varrho _3 e^{\gamma _3 \varsigma }+\varrho _4 e^{\gamma _4 \varsigma }}. \end{aligned}$$
(11)

The values of unknown \(\chi _{0}\), \(\chi _{j}\), \(\varLambda _{j}\) \((1\le j \le N)\) and \(\varrho _{i}\), \(\gamma _{i}\) \((1\le i\le 4)\) are computed and the value of N will be calculated by utilizing homogeneous balance principle.

By balancing \(\varOmega _{1}''\) with \(\varOmega _{1}^{3}\) in Eq. (9), we get \(N=1\). So the Eq. (10) transform into

$$\begin{aligned} \varOmega _{1}(\varsigma )=\chi _{0}+\chi _{1}\bigg (\frac{\varpi ^{'}(\varsigma )}{\varpi (\varsigma )}\bigg )+\varLambda _{1}\bigg (\frac{\varpi ^{'}(\varsigma )}{\varpi (\varsigma )}\bigg )^{-1}. \end{aligned}$$
(12)

Family-1: On replacing \(\varrho _{1}=\varrho _{2}= \varrho _{3}=1, \varrho _{4}=0\) and \(\gamma _{1}=0, \gamma _{2}=-1, \gamma _{3}=\gamma _{4}=0\), the Eq. (11) converts into

$$\begin{aligned} \varpi (\varsigma )=1+e^{-\varsigma }. \end{aligned}$$
(13)

On inserting the Eqs. (12) along with (13) into Eq. (9), we earn a set of algebraic polynomials. On solving these polynomials through Mathematica we get following results.

Result-1:

$$\begin{aligned} \chi _0=\frac{m}{\sqrt{2} \sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~ \chi _{1}=\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~ \varLambda _{1}=0,~ \mu =-\lambda ^2-\frac{m^2}{2}. \end{aligned}$$

Corresponding to result-1, we secure following solutions.

$$\begin{aligned}&\varPhi _{1,1}(x,t)=\bigg [\frac{m \left( e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }-1\right) }{\sqrt{2} \sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+1\right) }\bigg ]\times e^{\left( i \left( \theta _0+\frac{\left( -\lambda ^2-\frac{m^2}{2}\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }.~~~~~~ \end{aligned}$$
(14)
$$\begin{aligned}&\quad \varPhi _{2,1}(x,t)=k\bigg [\frac{m \left( e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }-1\right) }{\sqrt{2} \sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+1\right) }\bigg ]\times e^{\left( i \left( \theta _0+\frac{\left( -\lambda ^2-\frac{m^2}{2}\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(15)

Result-2:

$$\begin{aligned} \chi _0=\chi _{0},~\chi _1= 2 \chi _{0} ,~\varLambda _{1}=0,~ \delta =-\frac{m^2}{2 r_0^2 \left( \gamma k^2+1\right) },~\lambda =-\sqrt{-\mu -\frac{m^2}{2}}a.~~ \end{aligned}$$

We attain following exponential solutions corresponding to result-2.

$$\begin{aligned}&\varPhi _{1,2}(x,t)=\bigg (\chi _0 \left( 1-\frac{2}{e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+1}\right) \bigg )\times e^{i \left( \theta _0+\frac{\sqrt{-\mu -\frac{m^2}{2}} x^{\beta }}{\beta }+\frac{\mu t^{\alpha }}{\alpha }\right) },~~~~ \end{aligned}$$
(16)
$$\begin{aligned}&\quad \varPhi _{2,2}(x,t)=k\bigg (\chi _0 \left( 1-\frac{2}{e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+1}\right) \bigg )\times e^{i \left( \theta _0+\frac{\sqrt{-\mu -\frac{m^2}{2}} x^{\beta }}{\beta }+\frac{\mu t^{\alpha }}{\alpha }\right) }.~~~~~~~~~~~~~~ \end{aligned}$$
(17)

Family-2: On replacing \(\varrho _{1}=i,\varrho _{2}=-i, \varrho _{3}=-2, \varrho _{4}=0\) and \(\gamma _{1}=i, \gamma _{2}=-i, \gamma _{3}=\gamma _{4}=0\), the Eq. (11) transform into

$$\begin{aligned} \varpi (\varsigma )=\frac{\sin (\varsigma )}{e^{\varsigma }}. \end{aligned}$$
(18)

Switching Eqs. (18) along with (12) into Eq. (9), we earn following results.

Result-1:

$$\begin{aligned} \chi _{0}=\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\chi _{1}=0,~\varLambda _{1}=\frac{2 \sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}, \mu =2 m^2-\lambda ^2 . ~~~~~~ \end{aligned}$$

We construct following periodic solutions corresponding to result-1.

$$\begin{aligned}&\varPhi _{1,3}(x,t)=\bigg (\frac{\sqrt{2} m \left( \cot \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +1\right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( \cot \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) -1\right) }\bigg ) \times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(19)
$$\begin{aligned}&\quad Phi_{2,3}(x,t)=k \bigg (\frac{\sqrt{2} m \left( \cot \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +1\right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( \cot \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) -1\right) }\bigg ) \times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(20)

Result-2:

$$\begin{aligned} \chi _{0}=-\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\chi _{1}=-\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\varLambda _{1}=0, \mu =\mu =2 m^2-\lambda ^2 . ~~~~~~ \end{aligned}$$

We construct trigonometric solutions corresponding to result-2.

$$\begin{aligned}&\varPhi _{1,4}(x,t)=\bigg (-\frac{\sqrt{2} m \cot \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg ) \times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(21)
$$\begin{aligned}&\quad \varPhi _{2,4}(x,t)=k \bigg (-\frac{\sqrt{2} m \cot \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg ) \times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(22)

Family-3: On replacing \(\varrho _{1}=\varrho _{2}=1, \varrho _{3}=2, \varrho _{4}=0\) and \(\gamma _{1}=i, \gamma _{2}=-i, \gamma _{3}=\gamma _{4}=0\), the Eq. (11) transform into

$$\begin{aligned} \varpi (\varsigma )=\cos (\varsigma ). \end{aligned}$$
(23)

Plugging Eqs. (12) together with (23) into (9), we derive the results.

Result-1:

$$\begin{aligned} \chi _{0}=0,~\chi _{1}=\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\varLambda _{1}=-\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\mu =8 m^2-\lambda ^2. \end{aligned}$$

Replacing these unknown in Eqs. (12) and (23) into Eq. (9), then we get

$$\begin{aligned}&\varPhi _{1,5}(x,t)=\bigg (\frac{2 \sqrt{2} m \cot \left( 2 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 8 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.\end{aligned}$$
(24)
$$\begin{aligned}&\quad \varPhi _{2,5}(x,t)=k\bigg (\frac{2 \sqrt{2} m \cot \left( 2 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 8 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.\end{aligned}$$
(25)

Result-2:

$$\begin{aligned} \chi _{0}=0,~\chi _{1}=\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\varLambda _{1}=0,~\mu =2 m^2-\lambda ^2. \end{aligned}$$

After putting these values of unknown in Eqs. (12) and (23) into Eq. (9), then we get

$$\begin{aligned}&\varPhi _{1,6}(x,t)=\bigg (-\frac{\sqrt{2} m \tan \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.~~~ \end{aligned}$$
(26)
$$\begin{aligned}&\quad \varPhi _{2,6}(x,t)=k\bigg (-\frac{\sqrt{2} m \tan \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.~~~~~~~~~ \end{aligned}$$
(27)

Family-4: On replacing \(\varrho _1=2, \varrho _2=0, \varrho _3=\varrho _4=1\) and \(\gamma _1=\gamma _2=0, \gamma _3=1, \gamma _4=-1\), the Eq. (11) modify as

$$\begin{aligned} \varpi (\varsigma )=\text {sech} (\varsigma ). \end{aligned}$$
(28)

Putting Eqs. (28) together with (12) into Eq. (9), we achieve

Result-1:

$$\begin{aligned} \chi _{0}=0,~\chi _{1}=\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\varLambda _{1}=0,~\mu =-\lambda ^2-2 m^2. \end{aligned}$$

We attain the dark solutions corresponding to result-1

$$\begin{aligned}&\varPhi _{1,7}(x,t)=\bigg (-\frac{\sqrt{2} m \tanh \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{\left( i \left( \theta _0+\frac{\left( -\lambda ^2-2 m^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(29)
$$\begin{aligned}&\quad \varPhi _{2,7}(x,t)=k\bigg (-\frac{\sqrt{2} m \tanh \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{\left( i \left( \theta _0+\frac{\left( -\lambda ^2-2 m^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(30)

Result-2:

$$\begin{aligned} \chi _{0}=0,~\chi _{1}=\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\varLambda _{1}=-\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\mu =4 m^2-\lambda ^2. \end{aligned}$$

According to result-2, we retrieve the following mixed solutions

$$\begin{aligned}&\varPhi _{1,8}(x,t)=\bigg (\frac{\sqrt{2} m \text {csch}\left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \text {sech}\left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 4 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.~~ \end{aligned}$$
(31)
$$\begin{aligned}&\quad \varPhi _{2,8}(x,t)=k\bigg (\frac{\sqrt{2} m \text {csch}\left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \text {sech}\left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 4 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(32)

Result-3:

$$\begin{aligned} \chi _{0}=0,~\chi _{1}=0,~\varLambda _{1}=-\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\mu =4 m^2-\lambda ^2. \end{aligned}$$

According to result-3, we formulate singular soliton solutions as

$$\begin{aligned}&\varPhi _{1,9}(x,t)=\bigg (\frac{\sqrt{2} m \coth \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 4 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.~~ \end{aligned}$$
(33)
$$\begin{aligned}&\quad \varPhi _{2,9}(x,t)=k\bigg (\frac{\sqrt{2} m \coth \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 4 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(34)

Family-5: On replacing \(\varrho _1=2,\varrho _2=0, \varrho _3=\varrho _4=1\) and \(\gamma _1=1, \gamma _2=0, \gamma _3=i, \gamma _4=-i\), the Eq. (11) becomes

$$\begin{aligned} \varpi (\varsigma )= \frac{e^{\varsigma }}{\cos (\varsigma )}. \end{aligned}$$
(35)

Imposing Eqs. (35) and (12) into Eq. (9), we acquire

Result-1:

$$\begin{aligned} \chi _{0}=-\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\chi _{1}=\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\varLambda _{1}=0,~\mu =2 m^2-\lambda ^2 . \end{aligned}$$

Periodic solutions correspond to result-1 can be compiled as

$$\begin{aligned}&\varPhi _{1,10}(x,t)=\bigg (-\frac{\sqrt{2} m \tan \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(36)
$$\begin{aligned}&\quad \varPhi _{2,10}(x,t)=k\bigg (-\frac{\sqrt{2} m \tan \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }}\bigg )\times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(37)

Family-6: On replacing \(\varrho _{1}=\varrho _{2}=\varrho _{3}=1, \varrho _{4}=0\) and \(\gamma _{1}=1, \gamma _{2}=0, \gamma _{3}=2, \gamma _{4}=0\), the Eq. (11) changes into

$$\begin{aligned} \varpi (\varsigma )=\frac{1+e^{\varsigma }}{e^{2\varsigma }}. \end{aligned}$$
(38)

Substituting Eqs. (38) and (12) into Eq. (9), we gain the following result

Result-1:

$$\begin{aligned} \chi _{0}=\frac{3 m}{\sqrt{2} \sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\chi _{1}=\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\varLambda _{1}=0,~\mu =-\lambda ^2-\frac{m^2}{2}. \end{aligned}$$

We get exponential function solution from result-1

$$\begin{aligned}\varPhi _{1,11}(x,t)&=\bigg (\frac{m \left( e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }-1\right) }{\sqrt{2} \sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+1\right) }\bigg )\nonumber \\&\quad \times e^{ \left( i \left( \theta _0+\frac{\left( -\lambda ^2-\frac{m^2}{2}\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. ~~~~ \end{aligned}$$
(39)
$$\begin{aligned}\quad \varPhi _{2,11}(x,t)&=k \bigg (\frac{m \left( e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }-1\right) }{\sqrt{2} \sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( e^{m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+1\right) }\bigg )\nonumber \\&\quad \times e^{ \left( i \left( \theta _0+\frac{\left( -\lambda ^2-\frac{m^2}{2}\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(40)

Family-7: On replacing \(\varrho _{1}=2,\varrho _{2}=0, \varrho _{3}=\varrho _{4}=1\) and \(\gamma _{1}=-2, \gamma _{2}=0, \gamma _{3}=1,\gamma _{4}=-1\), the Eq. (11) transform into

$$\begin{aligned} \chi (\varsigma )=\frac{e^{-2\varsigma }}{\cosh (\varsigma )}. \end{aligned}$$
(41)

Inserting Eqs. (41) and (12) into Eq.(9), we get

Result-1:

$$\begin{aligned} \chi _{0}=-\frac{2 \sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\chi _{1}=0,~\varLambda _{1}=-\frac{3 \sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\mu =-\lambda ^2-2 m^2. \end{aligned}$$

We attain dark soliton solutions correspond to result-1.

$$\begin{aligned}\varPhi _{1,12}(x,t)&=\bigg (-\frac{\sqrt{2} m \left( 2 \tanh \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +1\right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( \tanh \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +2\right) }\bigg )\nonumber \\&\quad \times e^{\left( i \left( \theta _0+\frac{\left( -\lambda ^2-2 m^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(42)
$$\begin{aligned}\quad \varPhi _{2,12}(x,t)&=k \bigg (-\frac{\sqrt{2} m \left( 2 \tanh \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +1\right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( \tanh \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +2\right) }\bigg )\nonumber \\&\quad \times e^{\left( i \left( \theta _0+\frac{\left( -\lambda ^2-2 m^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(43)

Family-8: On replacing \(\varrho _{1}=\varrho _{2}=1, \varrho _{3}=2,~\varrho _{4}=0\) and \(\gamma _{1}=i, \gamma _{2}=-i, \gamma _{3}=-1, \gamma _{4}=0\), the Eq. (11) takes the following form

$$\begin{aligned} \varpi (\varsigma )=e^{\varsigma } \cos (\varsigma ). \end{aligned}$$
(44)

Inserting Eqs. (44) and (12) into Eq. (9), we earn

Result-1:

$$\begin{aligned} \chi _{0}=-\frac{\sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\chi _{1}=0,~\varLambda _{1}=\frac{2 \sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\mu =2 m^2-\lambda ^2. \end{aligned}$$

After Insert these values in Eqs. (12) and (44), we get mixed periodic solutions as

$$\begin{aligned}\varPhi _{1,13}(x,t)&=\bigg (\frac{\sqrt{2} m \left( \sin \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +\cos \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( \cos \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) -\sin \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \right) }\bigg )\nonumber \\&\quad \times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.~ \end{aligned}$$
(45)
$$\begin{aligned}\quad \varPhi _{2,13}(x,t)&=k \bigg (\frac{\sqrt{2} m \left( \sin \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +\cos \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( \cos \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) -\sin \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \right) }\bigg )\nonumber \\&\quad \times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.~~~~~~~ \end{aligned}$$
(46)

Family-9: On replacing \(\varrho _{1}=2, \varrho _{2}=0, \varrho _{3}=\varrho _{4}=1\) and \(\gamma _{1}=1, \gamma _{2}=0, \gamma _{3}=1, \gamma _{4}=0\), then Eq. (11) can be written as

$$\begin{aligned} \varpi (\varsigma )=\frac{e^{\varsigma }}{\cos (\varsigma )}. \end{aligned}$$
(47)

On switching Eqs. (47) and (12) into Eq. (9), we secure

Result-1:

$$\begin{aligned} \chi _{0}=\frac{2 \sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\chi _{1}=0,~\varLambda _{1}=-\frac{5 \sqrt{2} m}{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) }},~\mu =2 m^2-\lambda ^2. \end{aligned}$$

Insert these values in Eqs. (12) and (47), we derive the trigonometric solutions as

$$\begin{aligned}\varPhi _{1,14}(x,t)&=\bigg (-\frac{\sqrt{2} m \left( 2 \sin \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +\cos \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( 2 \cos \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) -\sin \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \right) }\bigg )\nonumber \\&\quad \times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.~~~~~~~~~~ \end{aligned}$$
(48)
$$\begin{aligned} \varPhi _{2,14}(x,t)&=k\bigg (-\frac{\sqrt{2} m \left( 2 \sin \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) +\cos \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \right) }{\sqrt{\delta \left( -\left( \gamma k^2+1\right) \right) } \left( 2 \cos \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) -\sin \left( m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) \right) \right) }\bigg )\nonumber \\&\quad \times e^{i \left( \theta _0+\frac{\left( 2 m^2-\lambda ^2\right) t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }.~ \end{aligned}$$
(49)

4 Extraction of lump solutions

By the implementation of following logarithmic transformation,

$$\begin{aligned} \varOmega _{1}=2(\ln \Theta )_{\varsigma }. \end{aligned}$$
(50)

Equation (50) converts Eq. (9) into bilinear form as

$$\begin{aligned} 4 (\Theta _{\varsigma } )^3 \left( 2 \left( \delta +\gamma \delta k^2\right) +m^2\right) +2 \Theta ^{2} \left( m^2 \Theta _{\varsigma \varsigma \varsigma }-\left( \lambda ^2+\mu \right) \Theta _ {\varsigma }\right) -6 m^2 \Theta \Theta _{\varsigma } \Theta _{\varsigma \varsigma }=0. \end{aligned}$$
(51)

4.1 M-form solutions

To seek M-form rational solutions for Eq. (51), we implement the following test function

$$\begin{aligned} \Theta =\left( \varsigma \sigma _1+\sigma _2\right) {}^2+\left( \varsigma \sigma _3+\sigma _4\right) {}^2+\sigma _5, \end{aligned}$$
(52)

where \(\sigma _{1},\ldots ,\sigma _{5}\) are constants to be determined later. Switching Eq. (52) into Eq. (51) and equating all same power of \(\varsigma \) to zero, we attain the proper solutions sets as follows:

Set-1:

$$\begin{aligned} \sigma _1=i \sigma _3, \gamma =-\frac{2 \delta +m^2}{2 \delta k^2}, \mu =-\lambda ^2. \end{aligned}$$
(53)

Plugging Eq. (53) into (52), we earn,

$$\begin{aligned} \Theta =\frac{4 i \sigma _3 \left( \sigma _2-i \sigma _4\right) }{2 i \varsigma \sigma _3 \sigma _2+2 \varsigma \sigma _3 \sigma _4+\sigma _2^2+\sigma _4^2+\sigma _5}. \end{aligned}$$
(54)

Thus,

$$\begin{aligned} \varOmega _{1}=\frac{4 i \sigma _3 \left( \sigma _2-i \sigma _4\right) }{2 i \varsigma \sigma _3 \sigma _2+2 \varsigma \sigma _3 \sigma _4+\sigma _2^2+\sigma _4^2+\sigma _5}. \end{aligned}$$
(55)

By using Eq. (55), we obtain solutions of Eq. (1)

$$\begin{aligned}\varPhi _{1,15}(x,t)&=\bigg (\frac{4 i \sigma _3 \left( \sigma _2-i \sigma _4\right) }{2 i m \sigma _3 \sigma _2 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +2 m \sigma _3 \sigma _4 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _2^2+\sigma _4^2+\sigma _5}\bigg )\nonumber \\&\quad \times e^{i \left( \theta _0-\frac{\lambda ^2 t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(56)
$$\begin{aligned} \varPhi _{2,15}(x,t)&=k \bigg (\frac{4 i \sigma _3 \left( \sigma _2-i \sigma _4\right) }{2 i m \sigma _3 \sigma _2 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +2 m \sigma _3 \sigma _4 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _2^2+\sigma _4^2+\sigma _5}\bigg )\nonumber \\&\quad \times e^{i \left( \theta _0-\frac{\lambda ^2 t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(57)

Set-2:

$$\begin{aligned} \sigma _2=\frac{\sigma _1 \sigma _4}{\sigma _3},~\sigma _5=0,~\gamma =-\frac{8 \delta +m^2}{8 \delta k^2},~\mu =-\lambda ^2. \end{aligned}$$
(58)

Substitute the values of Eq. (58) into (52), we secure,

$$\begin{aligned} \Theta = \frac{\left( \sigma _1^2+\sigma _3^2\right) \left( \varsigma \sigma _3+\sigma _4\right) {}^2}{\sigma _3^2}. \end{aligned}$$
(59)

Thus,

$$\begin{aligned} \varOmega _{1}=\frac{4 \sigma _3}{\varsigma \sigma _3+\sigma _4}, \end{aligned}$$
(60)

By imposing Eq. (60), we earn the solution of Eq. (1)

$$\begin{aligned} \varPhi _{1,16}(x,t)=\bigg (\frac{4 \sigma _3 }{m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4}\bigg )\times e^{i \left( \theta _0+\frac{\mu t^{\alpha }}{\alpha }-\frac{\lambda ^{2} x^{\beta }}{\beta }\right) }. \end{aligned}$$
(61)
$$\begin{aligned} \varPhi _{2,16}(x,t)=k\bigg (\frac{4 \sigma _3 }{m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4}\bigg )\times e^{i \left( \theta _0+\frac{\mu t^{\alpha }}{\alpha }-\frac{\lambda ^{2} x^{\beta }}{\beta }\right) }. \end{aligned}$$
(62)

4.2 1-kink soliton

In order to find the 1-kink soliton of Eq. (1), we exercise following test function

$$\begin{aligned} \Theta =c \exp \left( \varsigma \sigma _5+\sigma _6\right) +\left( \varsigma \sigma _1+\sigma _2\right) {}^2+\left( \varsigma \sigma _3+\sigma _4\right) {}^2+\sigma _7, \end{aligned}$$
(63)

where \(\sigma _{1},\ldots ,\sigma _{7}\) are unknown to be computed. Plugging Eq. (63) into Eq. (51) and equating all coefficients of similar powers of \(\exp \) function and others to 0, we achieve the following solutions set:

Set-1

$$\begin{aligned} \sigma _1=i \sigma _3,~\sigma _4=-i \sigma _2,~\sigma _5=\frac{\sqrt{2} \sqrt{-\lambda ^2-\mu }}{m},~\sigma _7=0,~\gamma =-\frac{8 \delta +m^2}{8 \delta k^2}. \end{aligned}$$
(64)

Taking values of Eq. (64) into account in Eq. (63),we attain

$$\begin{aligned} \Theta =c e^{\frac{\sqrt{2} \varsigma \sqrt{-\lambda ^2-\mu }}{m}+\sigma _6}. \end{aligned}$$
(65)

So,

$$\begin{aligned} \varOmega _{1}=\frac{2 c \sigma _5 e^{\varsigma \sigma _5}}{c e^{\varsigma \sigma _5}+\sigma _6}. \end{aligned}$$
(66)

By inserting Eq. (66), we conceive

$$\begin{aligned} \varPhi _{1,17}(x,t)=\frac{2 c \sigma _5 \exp \left( m \sigma _5 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +i \left( \theta _0+\frac{\mu t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }{c e^{m \sigma _5 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+\sigma _6}. \end{aligned}$$
(67)
$$\begin{aligned} \varPhi _{2,17}(x,t)=k\bigg (\frac{2 c \sigma _5 \exp \left( m \sigma _5 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +i \left( \theta _0+\frac{\mu t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }{c e^{m \sigma _5 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+\sigma _6}\bigg ). \end{aligned}$$
(68)

4.3 Periodic waves

To derive the periodic solution of Eq. (1), we implement the following test function

$$\begin{aligned} \Theta =\left( \varsigma \sigma _1+\sigma _2\right) {}^2+\left( \varsigma \sigma _3+\sigma _4\right) {}^2+\cos \left( \varsigma \sigma _5+\sigma _6\right) +\sigma _7, \end{aligned}$$
(69)

where \(\sigma _{1},\ldots ,\sigma _{7}\) are unknown. Plugging Eq. (69) into Eq. (51) and equating all coefficients of similar powers of trigonometric function and others to 0, we achieve the following solutions set:

Set-1

$$\begin{aligned} \sigma _2=i \sigma _4, \sigma _3=-i \sigma _1, \sigma _7=0, \gamma =-\frac{2 \delta +m^2}{2 \delta k^2}, \mu =2 m^2 \sigma _5^2-\lambda ^2. \end{aligned}$$
(70)

Taking values of Eq. (70) into account in Eq. (69), we attain

$$\begin{aligned} \Theta =\cos \left( \varsigma \sigma _5+\sigma _6\right) . \end{aligned}$$
(71)

So,

$$\begin{aligned} \varOmega _{1}=-2 \sigma _5 \tan \left( \varsigma \sigma _5+\sigma _6\right) . \end{aligned}$$
(72)

By inserting Eq. (72), we conceive

$$\begin{aligned}&\varPhi _{1,18}(x,t)=\bigg (-2 \sigma _5 \tan \left( m \sigma _5 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _6\right) \bigg )\times e^{\left( i \left( \theta _0+\frac{t^{\alpha } \left( 2 m^2 \sigma _5^2-\lambda ^2\right) }{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(73)
$$\begin{aligned}&\quad \varPhi _{2,18}(x,t)=k\bigg (-2 \sigma _5 \tan \left( m \sigma _5 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _6\right) \bigg )\times e^{\left( i \left( \theta _0+\frac{t^{\alpha } \left( 2 m^2 \sigma _5^2-\lambda ^2\right) }{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(74)

4.4 Multiwave solutions

To retrieve the multiwave solutions of Eq. (1), we apply the following test function

$$\begin{aligned} \Theta =a_1 \cos \left( \varsigma \sigma _3+\sigma _4\right) +a_0 \cosh \left( \varsigma \sigma _1+\sigma _2\right) +a_2 \cosh \left( \varsigma \sigma _5+\sigma _6\right) , \end{aligned}$$
(75)

where \(\sigma _{1},\ldots ,\sigma _{6}\) are real unknown. Inserting Eq. (75) into Eq. (51) and equating all coefficients of same powers of trigonometric, hyperbolic and other functions to 0, we achieve the following solutions set:

Set-1

$$\begin{aligned} \sigma _1=-\sigma _5,~\sigma _3=i \sigma _5,~\gamma =\frac{\frac{\lambda ^2+\mu }{\delta \sigma _5^2}-4}{4 k^2},~m=\frac{\sqrt{-\lambda ^2-\mu }}{\sqrt{2} \sigma _5}. \end{aligned}$$
(76)

Taking values of Eq. (76) into account in Eq. (75), we construct

$$\begin{aligned} \Theta =a_1 \cos \left( \sigma _4+i \varsigma \sigma _5\right) +a_0 \cosh \left( \sigma _2-\varsigma \sigma _5\right) +a_2 \cosh \left( \varsigma \sigma _5+\sigma _6\right) . \end{aligned}$$
(77)

So,

$$\begin{aligned} \varOmega _{1}=\frac{2 \sigma _5 \left( -i a_1 \sin \left( \sigma _4+i \varsigma \sigma _5\right) +a_0 \left( -\sinh \left( \sigma _2-\varsigma \sigma _5\right) \right) +a_2 \sinh \left( \varsigma \sigma _5+\sigma _6\right) \right) }{a_1 \cos \left( \sigma _4+i \varsigma \sigma _5\right) +a_0 \cosh \left( \sigma _2-\varsigma \sigma _5\right) +a_2 \cosh \left( \varsigma \sigma _5+\sigma _6\right) }. \end{aligned}$$
(78)

By inserting Eq. (78), we conceive

$$\begin{aligned}\varPhi _{1,19}(x,t)&=\bigg (\frac{2 \sigma _5 \left( a_0 \sinh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}-\sigma _2\right) +a_1 \sinh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}-i \sigma _4\right) +a_2 \sinh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}+\sigma _6\right) \right) }{a_0 \cosh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}-\sigma _2\right) +a_1 \cosh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}-i \sigma _4\right) +a_2 \cosh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}+\sigma _6\right) }\bigg )\nonumber \\&\quad \times e^{i \left( \theta _0+\frac{\mu t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(79)
$$\begin{aligned} \varPhi _{2,19}(x,t)&=k\bigg (\frac{2 \sigma _5 \left( a_0 \sinh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}-\sigma _2\right) +a_1 \sinh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}-i \sigma _4\right) +a_2 \sinh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}+\sigma _6\right) \right) }{a_0 \cosh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}-\sigma _2\right) +a_1 \cosh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}-i \sigma _4\right) +a_2 \cosh \left( \frac{\sqrt{-\lambda ^2-\mu } \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }{\sqrt{2}}+\sigma _6\right) }\bigg )\nonumber \\&\quad \times e^{i \left( \theta _0+\frac{\mu t^{\alpha }}{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) }. \end{aligned}$$
(80)

4.5 Homoclinic breather approach

$$\begin{aligned} \Theta =e^{-p(\varsigma \sigma _{1}+\sigma _{2})}+b_{1}e^{p(\varsigma \sigma _{3}+\sigma _{4})}+b_{0}\cos (p_{1}(\varsigma \sigma _{5}+\sigma _{6})), \end{aligned}$$
(81)

where \(\sigma _{1},\ldots ,\sigma _{6}\) are unknown constants. Inserting Eq. (81) into Eq. (51) and equating all coefficients of same power of trigonometric and \(\exp \) functions to 0, we have the solutions sets as follows.

Set-1:

$$\begin{aligned} \sigma _1=\sigma _3,~\sigma _5=\frac{i \sigma _3 p}{p_1},~\gamma =-\frac{2 \delta +m^2}{2 \delta k^2},~\mu =-2 \sigma _3^2 m^2 p^2-\lambda ^2,~b_1=\frac{\lambda }{\sqrt{3} \sqrt{\sigma _3^2 \left( -m^2\right) p^2 \left( 2 \sigma _3 b_0 \lambda ^2 p+i\right) }}. \end{aligned}$$
(82)

By imposing Eq. (82) into Eq. (81), we secure

$$\begin{aligned} \Theta =\frac{\lambda e^{p \left( \sigma _3 \xi +\sigma _4\right) }}{\sqrt{3} \sqrt{\sigma _3^2 \left( -m^2\right) p^2 \left( 2 \sigma _3 b_0 \lambda ^2 p+i\right) }}+b_0 \cosh \left( \sigma _3 \xi p-i \sigma _6 p_1\right) +e^{-p \left( \sigma _3 \xi +\sigma _2\right) }. \end{aligned}$$
(83)

So,

$$\begin{aligned} \varOmega _{1}=\frac{2 \left( \frac{\sigma _3 \lambda p e^{p \left( \sigma _3 \xi +\sigma _4\right) }}{\sqrt{3} \sqrt{\sigma _3^2 \left( -m^2\right) p^2 \left( 2 \sigma _3 b_0 \lambda ^2 p+i\right) }}+\sigma _3 b_0 p \sinh \left( \sigma _3 \xi p-i \sigma _6 p_1\right) +\sigma _3 p \left( -e^{-p \left( \sigma _3 \xi +\sigma _2\right) }\right) \right) }{\frac{\lambda e^{p \left( \sigma _3 \xi +\sigma _4\right) }}{\sqrt{3} \sqrt{\sigma _3^2 \left( -m^2\right) p^2 \left( 2 \sigma _3 b_0 \lambda ^2 p+i\right) }}+b_0 \cosh \left( \sigma _3 \xi p-i \sigma _6 p_1\right) +e^{-p \left( \sigma _3 \xi +\sigma _2\right) }}. \end{aligned}$$
(84)

With the assistance of Eq. (84), we get the solution of Eq. (1) as

$$\begin{aligned}\varPhi _{1,20}(x,t)&=\bigg (\frac{a_3 p \left( \frac{\sqrt{3} \lambda e^{p \left( a_3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +a_4\right) }}{\sqrt{a_3^2 \left( -m^2\right) p^2 \left( 2 a_3 b_0 \lambda ^2 p+i\right) }}+3 b_0 \sinh \left( a_3 m p \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) -i a_6 p_1\right) -3 e^{-p \left( a_3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +a_2\right) }\right) }{3 \left( \frac{\lambda e^{p \left( a_3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +a_4\right) }}{\sqrt{3} \sqrt{a_3^2 \left( -m^2\right) p^2 \left( 2 a_3 b_0 \lambda ^2 p+i\right) }}+b_0 \cosh \left( a_3 m p \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) -i a_6 p_1\right) +e^{-p \left( a_3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +a_2\right) }\right) }\bigg )\nonumber \\&\quad \times e^{ \left( i \left( -\frac{t^{\alpha } \left( 2 \sigma _3^2 m^2 p^2+\lambda ^2\right) }{\alpha }+\theta _0-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(85)
$$\begin{aligned} \varPhi _{2,20}(x,t)&=k \bigg (\frac{a_3 p \left( \frac{\sqrt{3} \lambda e^{p \left( a_3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +a_4\right) }}{\sqrt{a_3^2 \left( -m^2\right) p^2 \left( 2 a_3 b_0 \lambda ^2 p+i\right) }}+3 b_0 \sinh \left( a_3 m p \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) -i a_6 p_1\right) -3 e^{-p \left( a_3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +a_2\right) }\right) }{3 \left( \frac{\lambda e^{p \left( a_3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +a_4\right) }}{\sqrt{3} \sqrt{a_3^2 \left( -m^2\right) p^2 \left( 2 a_3 b_0 \lambda ^2 p+i\right) }}+b_0 \cosh \left( a_3 m p \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) -i a_6 p_1\right) +e^{-p \left( a_3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +a_2\right) }\right) }\bigg )\nonumber \\&\quad \times e^{ \left( i \left( -\frac{t^{\alpha } \left( 2 \sigma _3^2 m^2 p^2+\lambda ^2\right) }{\alpha }+\theta _0-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(86)

4.6 Interaction via double exponential form

To obtain the interaction, using the following test function

$$\begin{aligned} \Theta =b_1 \exp \left( \sigma _1 \varsigma +\sigma _2\right) +b_2 \exp \left( \sigma _3 \varsigma +\sigma _4\right) , \end{aligned}$$
(87)

where \(\sigma _{1},\ldots ,\sigma _{4}\) are unknown to be calculated later. Employing Eq. (87) into Eq. (51) and equating all coefficients of similar powers of exp function to 0, we recover

$$\begin{aligned} \mu =-2 \sigma _3^2 m^2-\lambda ^2,~\sigma _1=-\sigma _3,~\gamma =-\frac{2 \delta +m^2}{2 \delta k^2}. \end{aligned}$$
(88)

By engaging Eq. (88) into Eq. (87), we acquire

$$\begin{aligned} \Theta =b_1 e^{\sigma _2-\sigma _3 \varsigma }+b_2 e^{\sigma _3 \varsigma +\sigma _4}. \end{aligned}$$
(89)

So,

$$\begin{aligned} \varOmega _{1}=\frac{2 \left( \sigma _3 b_2 e^{\sigma _3 \varsigma +\sigma _4}-\sigma _3 b_1 e^{\sigma _2-\sigma _3 \varsigma }\right) }{b_1 e^{\sigma _2-\sigma _3 \varsigma }+b_2 e^{\sigma _3 \varsigma +\sigma _4}}. \end{aligned}$$
(90)

By imposing Eq. (90), we gain the solution of Eq. (1) as

$$\begin{aligned}&\varPhi _{1,21}(x,t)=\bigg (-\frac{2 \sigma _3 \left( e^{\sigma _2} b_1-b_2 e^{2 \sigma _3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4}\right) }{b_2 e^{2 \sigma _3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4}+e^{\sigma _2} b_1}\bigg )\times e^{ \left( -i \left( \frac{t^{\alpha } \left( 2 \sigma _3^2 m^2+\lambda ^2\right) }{\alpha }-\theta _0+\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(91)
$$\begin{aligned}&\quad \varPhi _{2,21}(x,t)=k\bigg (-\frac{2 \sigma _3 \left( e^{\sigma _2} b_1-b_2 e^{2 \sigma _3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4}\right) }{b_2 e^{2 \sigma _3 m \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4}+e^{\sigma _2} b_1}\bigg )\times e^{ \left( -i \left( \frac{t^{\alpha } \left( 2 \sigma _3^2 m^2+\lambda ^2\right) }{\alpha }-\theta _0+\frac{\lambda x^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(92)

4.7 Periodic cross-kink wave solutions

To get the periodic cross-kink wave solution, using the following test function

$$\begin{aligned} \Theta =a_1 \exp \left( \varsigma \sigma _1+\sigma _2\right) +a_2 \cos \left( \varsigma \sigma _3+\sigma _4\right) +a_3 \cosh \left( \varsigma \sigma _5+\sigma _6\right) +\exp \left( -\left( \varsigma \sigma _1+\sigma _2\right) \right) +\sigma _7, \end{aligned}$$
(93)

where \(\sigma _{1},\ldots ,\sigma _{7}\) are unknown parameters to be calculated. Employing Eq. (93) into Eq. (51) and equating all coefficients of similar powers of \(\exp \), hyperbolic and trigonometric functions to zero, we recover

$$\begin{aligned} \delta =-\frac{m^2}{2 \gamma k^2+2},~\mu =2 m^2 \sigma _3^2-\lambda ^2,~\sigma _1=-i \sigma _3,~\sigma _5= -i \sigma _3,~\sigma _7=0. \end{aligned}$$
(94)

By engaging Eq. (94) into Eq. (93), we acquire

$$\begin{aligned} \Theta =a_1 e^{\sigma _2-i \varsigma \sigma _3}+a_2 \cos \left( \varsigma \sigma _3+\sigma _4\right) +a_3 \cosh \left( \varsigma \sigma _5+\sigma _6\right) +e^{-\sigma _2+i \varsigma \sigma _3}. \end{aligned}$$
(95)

So,

$$\begin{aligned} \varOmega _{1}=\frac{2 \left( a_3 \sigma _5 \sinh \left( \varsigma \sigma _5+\sigma _6\right) +\sigma _3 \left( -i a_1 e^{\sigma _2-i \varsigma \sigma _3}-a_2 \sin \left( \varsigma \sigma _3+\sigma _4\right) +i e^{-\sigma _2+i \varsigma \sigma _3}\right) \right) }{a_1 e^{\sigma _2-i \varsigma \sigma _3}+a_2 \cos \left( \varsigma \sigma _3+\sigma _4\right) +a_3 \cosh \left( \varsigma \sigma _5+\sigma _6\right) +e^{-\sigma _2+i \varsigma \sigma _3}}. \end{aligned}$$
(96)

By inserting Eq. (96), we gain the solution of Eq. (1) as

$$\begin{aligned}\varPhi _{1,22}(x,t)v=\bigg (\frac{2 \left( a_3 \sigma _5 \sinh \left( m \varDelta \right) +\sigma _3 \left( -i a_1 e^{\sigma _2-i m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }-a_2 \sin \left( m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4\right) +i e^{-\sigma _2+i m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }\right) \right) }{a_1 e^{\sigma _2-i m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+a_2 \cos \left( m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4\right) +a_3 \cosh \left( m \varDelta \right) +e^{-\sigma _2+i m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }}\bigg )\nonumber \\&\quad \times e^{ \left( i \left( \theta _0+\frac{t^{\alpha } \left( 2 m^2 \sigma _3^2-\lambda ^2\right) }{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }.~ \end{aligned}$$
(97)
$$\begin{aligned} \varPhi _{2,22}(x,t)&=k\bigg (\frac{2 \left( a_3 \sigma _5 \sinh \left( m \varDelta \right) +\sigma _3 \left( -i a_1 e^{\sigma _2-i m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }-a_2 \sin \left( m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4\right) +i e^{-\sigma _2+i m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }\right) \right) }{a_1 e^{\sigma _2-i m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }+a_2 \cos \left( m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _4\right) +a_3 \cosh \left( m \varDelta \right) +e^{-\sigma _2+i m \sigma _3 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) }}\bigg )\nonumber \\&\quad \times e^{ \left( i \left( \theta _0+\frac{t^{\alpha } \left( 2 m^2 \sigma _3^2-\lambda ^2\right) }{\alpha }-\frac{\lambda x^{\beta }}{\beta }\right) \right) }. ~~~~~~~ \end{aligned}$$
(98)

where \(\varDelta =\sigma _5 \left( \frac{x^{\beta }}{\beta }-\frac{c t^{\alpha }}{\alpha }\right) +\sigma _6\)

5 Results and discussion

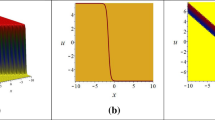
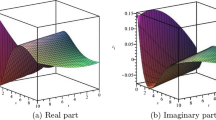
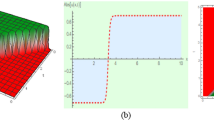
In this section, a detail comparison of acquired solutions is made with the previously evaluated results which reflects the novelty of this work. L. Tang and S. Chen constructed The classification of single traveling wave solutions by the virtue of the complete discriminant system method (Tang and Chen 2022). In Wang et al. (2020), B.H. Wang et al. computed Vector optical soliton and periodic solutions of the governing model by capitalizing two methods fractional Riccati method and fractional dual-function method. Our research manipulated this study to exercise two methods, modified generalized exponential rational function method (mGERFM) and the Hirota bilinear method (HBM). Comparing our outcomes with their outcomes display the novelty of our outcomes where it has not been gained in the previous published literature. The discovered results are novel and fresh and to the best of our knowledge these achievements have not been submitted to the literature beforehand. We observe that the retrieved solutions could be beneficial to understand the various physical behaviors. For Instance the hyperbolic sine function appears in the gravitational potential of a cylinder and the calculation of the Roche limit, the hyperbolic cosine function appears in the shape of a hanging cable (the so-called CATENARY), the hyperbolic tangent appears in the calculation of magnetic moment and special relativity rapidity, and the hyperbolic cotangent appears in the Langevin function for magnetic porosity (Weisstein 2002). The exponential functions are shown in Fig. 1. The Fig. 2 exhibit the periodic solutions. Singular bright solution is depicted in Fig. 3. The singular and dark solutions are exhibited in Figs. 4 and 5 respectively. The M-shape and 1-kink solutions are appeared in the Figs. 6 and 7. In Figs. 8 and 9, we present periodic waves and multiwaves solutions subsequently. Figures 10, 11, 12 and 13 indicate the homoclinic, interaction and periodic cross solutions, respectively.

Fig. 1
figure 1

Dynamics of Re and Im parts of Eq. (14) under parametric values \(m=1, \lambda =2, \theta _0=0.5, c=0.04, \mu =0.45, \delta =1.8, \alpha =0.96, \beta =0.9, \lambda =1, k=1.5, \gamma =2\)

Full size image
Fig. 2
figure 2

Dynamics of Re and Im parts of Eq. (19) under parametric values \(m=1.55, \lambda =1.5, \theta _0=0.45, c=0.09, \mu =0.55, \delta =1.8, \alpha =0.9, \beta =0.89, \lambda =0.99, k=1.5, \gamma =0.4\)

Full size image
Fig. 3
figure 3

Dynamics of Re and Im parts of Eq. (29) under parametric values \(m=0.65,~\lambda =2.35,~\theta _0=0.5,~c=0.05,~\mu =0.55,~\delta =1,~\alpha =0.85,~\beta =0.8,~\lambda =1.3,~k=1.3,~\gamma =0.85\)

Full size image
Fig. 4
figure 4

Dynamics of Re and Im parts of Eq. (31) under parametric values \(m=0.25,~\lambda =2.5,~\theta _0=0.5,~c=0.07,~\mu =0.58,~\delta =1.2,~\alpha =0.95,~\beta =0.93,~\lambda =1.3,~k=1.3,~\gamma =0.85\)

Full size image
Fig. 5
figure 5

Dynamics of Re and Im parts of Eq. (33) under parametric values \(m=0.002,~\lambda =0.04,~\theta _0=0.5,~c=0.08,~\mu =0.59,~\delta =1.2,~\alpha =0.93,~\beta =0.95,~\lambda =1.3,~k=1.3,~\gamma =0.86\)

Full size image
Fig. 6
figure 6

Dynamics of Re and Im parts of Eq. (42) under parametric values \(m=1.55,~\lambda =1.15,~\theta _0=0.8,~c=-0.04,~\mu =2.65,~\sigma _3=1.8,~\sigma _4=0.85,~\alpha =0.93,~\beta =0.9,~\sigma _2=1.75,~\sigma _5=0.95\)

Full size image
Fig. 7
figure 7

Dynamics of Re and Im parts of Eq. (56) under parametric values \(m=1.9,~\lambda =2.8,~\theta _0=2.08,~c=0.08,~\mu =2.65,~\sigma _3=1.8,~\sigma _4=0.85,~\alpha =0.96,~\beta =0.9,~\sigma _2=1.75,~\sigma _5=0.85,~\sigma _6=0.05\)

Full size image
Fig. 8
figure 8

Dynamics of Re and Im parts of Eq. (67) under parametric values \(m=1.35,~\lambda =0.88,~\theta _0=0.9,~c=-0.04,~\mu =2.55,~\sigma _3=1.8,~\sigma _4=0.75,~\alpha =0.99,~\beta =0.98,~\sigma _6=5,~\sigma _5=0.95\)

Full size image
Fig. 9
figure 9

Dynamics of Re and Im parts of Eq. (73) under parametric values \(\lambda =1,~\mu =3,~\alpha =0.93,~\beta =0.95,~c=1.5,~\sigma _2=-5,~\sigma _4=5,~\sigma _5=2,~a_0=-2,~a_1=1,~a_2=-2,~\sigma _6=3,~\theta _0=3\)

Full size image
Fig. 10
figure 10

Dynamics of Re and Im parts of Eq. (79) under parametric values \(m=1.8,~\lambda =2.98,~\theta _0=2.08,~c=0.04,~\mu =2.65,~\alpha =0.98,~\beta =0.99,~p=0.5,~\sigma _3=0.2,~\sigma _6=0.1,~b_0=0.3,~\sigma _2=0.5,~p_1=0.2,~\sigma _4=0.3\)

Full size image
Fig. 11
figure 11

Dynamics of Re and Im parts of Eq. (85) under parametric values \(m=0.75,~\lambda =0.55,~\theta _0=0.9,~c=-0.04,~\mu =2.55,~\sigma _3=1.8,~\sigma _4=0.75,~\alpha =0.99,~\beta =0.98,~\sigma _2=2,~\sigma _1=0.95,~b_1=0.25,~b_2=0.35\)

Full size image
Fig. 12
figure 12

Dynamics of Re and Im parts of Eq. (91) under parametric values \(m=0.45,~\lambda =1,~\mu =3,~\alpha =0.93,~\beta =0.95,~c=1.5,~\sigma _2=-5,~\sigma _4=5,~\sigma _5=2,~a_0=-2,~a_1=1,~a_2=-2,~\sigma _6=3,~\theta _0=3,~\sigma _3=2.5,~a_3=1.5\)

Full size image
Fig. 13
figure 13

Dynamics of Re and Im parts of Eq. (97) under parametric values \(m=0.45,~\lambda =1,~\mu =3,~\alpha =0.93,~\beta =0.95,~c=1.5,~\sigma _2=-5,~\sigma _4=5,~\sigma _5=2,~a_0=-2,~a_1=1,~a_2=-2,~\sigma _6=3,~\theta _0=3,~\sigma _3=2.5,~a_3=1.5\)

Full size image

6 Conclusion

In this work, two effective techniques namely, the modified generalized exponential rational function method (mGERFM) and Hirota bilinear method (HBM) along with different test functions are employed to construct to the fractional nonlinear Schrodinger equation which is an example of a universal nonlinear model that describes many physical nonlinear systems. The observed solutions are devised as exponential, dark, periodic and combo singular bright. Besides, rational, periodic, multiwaves, multi-kink with their interaction solution are also derived, which seems as far as we know, not available in the literature. To interpret the dynamics of some of these reported solutions, we provided supportive graphical depictions for the simulated numerical results of the governing model described pulse interactions in terms of the soliton parameters which set forth the reliability and well-productivity of the proposed methods. These computed results will expedite the analysis and optimization of the performance of the wave solutions in fiber optics.