1 Introduction

A variety of important phenomena that appear in the real live are described by means of nonlinear partial differential eauations (NLPDEs), and depending on its nature, are studied in several areas of the science, particularly in a variety of branchs of the physics, communications, finance, biology, and many others. On the solutions of that models have great relevance the solitons, due to, only with them its possible understand many phenomena and construct new technology used wydely oround of the world, so that, the solitons theory, is today one of the most important lines of investigation of the applied mathematics. All investigationes with new resuts are very important to improved and help to construc this new branch of the science. The study of NLPDEs can be made using analytic tools, computational methods, or from of point of view of numerical approximations. Actually, the analytic methods are used to prove existence of solutions, or obtain some characteristics of them, however, it must be complemented with computational methods to obtain exact solutions, or numerical methods to obtainn approximations on the respective solution. Each day, appear new models or appear new applications for the models analyzed previously and join with this fact, new thechniques are developed to handel those models, or in its defect, some methods used previously are improved. For example, many of the most classics models used in appplied mathematics, was construct with constant coeffcients, however, after some time, application of such models with variable coeffcicients have relevance today, see for instance the references (Nirmala et al. 1986), (Miura 1968), (Yang 2012), (Salas and Gómez 2009), (Gómez and Cesar 2020). Clearly, the use of variable coefficients, give us a generalization of the classical models, in the sense, the coefficient constants appear as a particular case. Moreover, solutions with new structure are derived, which can be help us to understand in a better way the dynamical of the phenomena described by the respective NLPDE. In the same direction, computational methods as the tanh-coth method (Wazwaz 2007), the Kudryashov method (Kudryashov 2012), was been implemented and use to obtain exact solutions for a variety of NLPDEs, however, the improved tanh-coth method was presented as a generaliztion of the two mentioned methods and has been used in a satisfactory way (Gómez and C. A., and Salas, A. H. 2008), (Salas 2010). We can mentined other additionally meethods such as the \(G'/G^2-\) method (Kaur and Wazwaz 2018), the Exp(\(-\phi (\xi )\)) method (Kaur and Wazwaz 2018; Hafez et al. 2015), the new extended auxiliary equation method (Zayed and Alurrfi 2016; Al-Ghafri et al. 2020; Bansal et al. 2018; Biswas et al. 2018), and many others computational methods used widely by many researches (Ghanbari 2021; Ghanbari et al. 2020; Ghanbari 2021; Srivastava et al. 2019; Akinyemi et al. 2021, 2021; Akinyemi 2021; Kumar 2021; Dhiman et al. 2021; Kumar and Rani 2021; Chen et al. 2021; Khodadad et al. 2021; Zafar et al. 2022; Hashemi 2018). Recently, the NLPDEs with fractional derivative are taking relevance in novel applications, so that, for this type of equations new computational and numerical methods have been implemented, in the following references, appear some fractional models and the respective method used to handle it: (Iqbal et al. 2021; Wang et al. 2022; Hajiseyedazizi et al. 2021; He et al. 2022; Rashid et al. 2022; Hasheimi and Baleanu 2020; Jin et al. 2022).

In this work, we will study, from of point of view of its exact solutions, the following perturbed Fokas-Lenells equation with variable coefficients

$$\begin{aligned} \imath q_t+A(t)q_{xx}+B(t)q_{xt}+C(t)|q|^2q+\imath D(t)|q|^2q_x=\imath [H(t)q_x+F(t)(|q|^{2m} q)_x+G(t)(|q|^{2m})_x q], \end{aligned}$$
(1)

where, \(q=q(x,t)\), and the coefficients in the equation are functions depending on t. In the case that that coefficients turn constant, the model reduce to classical perturbed Fokas-Lenells (PFL) equation (Al-Ghafri et al. 2020; Bansal et al. 2018). As was mentioned early, the solitons have many applications in the modern industry, specially in those that use optic fibre. Several models have used to modelling optical solutions: The Chen-Lee-Liu equation (Biswas et al. 2018), the nonlinear Schrödinger type equation (NLS) (Zayed and Alurrfi 2016), the Manakov system (Yıldırım 2019), the Gerdjikov-Ivanov equation (Gomez et al. 2021), the classical perturbed Fokas-Lenells equation (Al-Ghafri et al. 2020; Bansal et al. 2018) ,and many others. Many researches, from some year ago, was take the classical (PFL) as a important equation to modelling optical solitons and have used it to improved the technology that use optical fibres in the actuality: Internet, Facebook, email and many other fields of the industry of communications. The solutions obtained in this work, due to its variable coefficients, are clearly new in the literature, and therefore they are an important contribution to the solitons theory. Moreover, recently the study of nonlinear chirping for the NLS and generalizations of this equation, has become in a very important topic of study, due to widely applications in the industry of communications (Al-Ghafri et al. 2020). So that, from the results obtained here for the Fokas-Lenells equation, new chirped optical pulses ca be derived, and therefore, we are contributing to knowledge of this type of pulses, used widely in communications theory.

The paper is organized as follows: In Sect. 2, we use the tanh-coth method for solve Eq. (1), and we obtain exact solutions. In Sect. 3, we give a discussion on the results. Finally, some conclusions are given.

2 Exact solutions for (1) using the tanh-coth method

With the objective of find exact solutions for (1), we consider the wave transformation

$$\begin{aligned} {\left\{ \begin{array}{ll} q(x,t)=u(\xi )e^{\imath (\Phi (\xi )+\int \rho (t)dt+\xi _1)},\\ \xi =x+\int \lambda (t)dt+\xi _0, \end{array}\right. } \end{aligned}$$
(2)

which reduces (1), to following system where the first equation correspond to imaginary part, and the second to real part:

$$\begin{aligned} {\left\{ \begin{array}{ll} (\lambda +B\rho -H)u'(\xi )+(2A+2B \lambda )u'(\xi )\Phi '(\xi )+B\lambda u(\xi )\Phi ''(\xi )-(2m+1)Fu^{2m}(\xi )u'(\xi )-2mGu^{2m}(\xi )u'(\xi )=0,\\ (-H+\lambda +B\rho )u(\xi )\Phi '(\xi )-Fu^{2m}(\xi )\Phi '(\xi )+\rho u(\xi )-(A+B\lambda )u(\xi )(\Phi '(\xi ))^2-Cu^3(\xi )+Du^3(\xi )\Phi '(\xi )=0. \end{array}\right. } \end{aligned}$$
(3)

Here \("'"\) is the ordinary derivation respect to \(\xi \), and in (2), \(\xi _0,\,\xi _1\) are constant. All coefficients of the system (3), are depending on t, by simplicity we omit this notation in the follows.

2.1 Particular case

We take \(\Phi (\xi )=\xi \), \(\rho =0\) and \(m=1\), in (2), so that, (3), becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} (\lambda +2A+2B\lambda -H)u'(\xi )+(D-3F-2G)u^2(\xi )u'(\xi )=0,\\ (-\lambda -A-B\lambda +H)u(\xi )+(A+B\lambda )u''(\xi )+(C-D+F)u^3(\xi )=0. \end{array}\right. } \end{aligned}$$
(4)

With the restriction

$$\begin{aligned} D=3F+2G, \end{aligned}$$
(5)

we can take

$$\begin{aligned} \lambda =\frac{H-2A}{1+2B},\,\,B\ne -\frac{1}{2}, \end{aligned}$$
(6)

for reduce (4), to the equation

$$\begin{aligned} (-\lambda -A-B\lambda +H)u(\xi )+(A+B\lambda )u''(\xi )+(C-D+F)u^3(\xi )=0. \end{aligned}$$
(7)

In this step, we consider the solution for (7), in the following form:

$$\begin{aligned} u(\xi )=\sum ^{M}_{i=0}a_i(t)\phi (\xi )^{i}+\sum ^{2M}_{i=M+1}a_i(t)\phi (\xi )^{M-i}, \end{aligned}$$
(8)

where, \(\phi (\xi )\) satisfy the Riccati equation

$$\begin{aligned} \phi '(\xi )=\gamma (t) \phi ^2(\xi )+\beta (t) \phi (\xi )+\alpha (t). \end{aligned}$$
(9)

Substituting (8), into (7), and balancing \(u^3(\xi )\) with \(u''(\xi )\), we obtain \(M=1\). With this value, (8), converts to

$$\begin{aligned} u(\xi )=a_0+a_1\phi (\xi )+a_2\phi (\xi )^{-1}, \end{aligned}$$
(10)

where \(a_i=a_i(t),\,\,i=0,1,2\) are functions to be determinate latter. Now, replacing (10), into (7), and using (9), we obtain the algebraic system

$$\begin{aligned} {\left\{ \begin{array}{ll} 3 a_1 A \beta \gamma +6 a_0 a_1^2 B C-12 a_0 a_1^2 B F-12 a_0 a_1^2 B G+3 a_1 \beta B \gamma H+3 a_0 a_1^2 C-6 a_0 a_1^2 F-6 a_0 a_1^2 G=0,\\ 2 a_1 A \gamma ^2+2 a_1^3 B C-4 a_1^3 B F-4 a_1^3 B G+2 a_1 B \gamma ^2 H+a_1^3 C-2 a_1^3 F-2 a_1^3 G=0,\\ \alpha a_1 A \beta +a_2 A \beta \gamma +a_0 A+2 a_0^3 B C+12 a_1 a_2 a_0 B C-4 a_0^3 B F-24 a_1 a_2 a_0 B F-4 a_0^3 B G-24 a_1 a_2 a_0 B G+\\ \alpha a_1 \beta B H+a_2 \beta B \gamma H+a_0 B H+a_0^3 C+6 a_1 a_2 a_0 C-2 a_0^3 F-12 a_1 a_2 a_0 F-2 a_0^3 G-12 a_1 a_2 a_0 G=0,\\ 2 \alpha a_1 A \gamma +a_1 A \beta ^2+a_1 A+6 a_0^2 a_1 B C+6 a_1^2 a_2 B C-12 a_0^2 a_1 B F-12 a_1^2 a_2 B F-12 a_0^2 a_1 B G-12 a_1^2 a_2 B G+\\ 2 \alpha a_1 B \gamma H+a_1 \beta ^2 B H+a_1 B H+3 a_0^2 a_1 C+3 a_1^2 a_2 C-6 a_0^2 a_1 F-6 a_1^2 a_2 F-6 a_0^2 a_1 G-6 a_1^2 a_2 G=0,\\ 3 \alpha a_2 A \beta +6 a_0 a_2^2 B C-12 a_0 a_2^2 B F-12 a_0 a_2^2 B G+3 \alpha a_2 \beta B H+3 a_0 a_2^2 C-6 a_0 a_2^2 F-6 a_0 a_2^2 G=0,\\ 2 \alpha a_2 A \gamma +a_2 A \beta ^2+a_2 A+6 a_1 a_2^2 B C+6 a_0^2 a_2 B C-12 a_1 a_2^2 B F-12 a_0^2 a_2 B F-12 a_1 a_2^2 B G-12 a_0^2 a_2 B G+\\ 2 \alpha a_2 B \gamma H+a_2 \beta ^2 B H+a_2 B H+3 a_1 a_2^2 C+3 a_0^2 a_2 C-6 a_1 a_2^2 F-6 a_0^2 a_2 F-6 a_1 a_2^2 G-6 a_0^2 a_2 G=0,\\ 2 \alpha ^2 a_2 A+2 a_2^3 B C-4 a_2^3 B F-4 a_2^3 B G+2 \alpha ^2 a_2 B H+a_2^3 C-2 a_2^3 F-2 a_2^3 G=0. \end{array}\right. } \end{aligned}$$
(11)

Using Maple or Mathematica, the following solutions of previous system are obtained:

$$\begin{aligned}&{\left\{ \begin{array}{ll} \gamma =-\frac{i \left( a_0^2 (2 B+1) (C-2 (F+G))+A+B H\right) }{a_2 \sqrt{4 B+2} \sqrt{A+B H} \sqrt{C-2 (F+G)}},\\ \alpha =-\frac{i a_2 \sqrt{2 B+1} \sqrt{C-2 F-2 G}}{\sqrt{2} \sqrt{A+B H}},\\ \beta =-\frac{i \sqrt{2} a_0 \sqrt{2 B+1} \sqrt{C-2 F-2 G}}{\sqrt{A+B H}},\\ a_0=a_0,\,\,\,a_1=0,\,\,a_2=a_2. \end{array}\right. } \end{aligned}$$
(12)
$$\begin{aligned}&\quad {\left\{ \begin{array}{ll} \gamma =-\frac{i a_1 \sqrt{2 B+1} \sqrt{C-2 F-2 G}}{\sqrt{2} \sqrt{A+B H}},\\ \alpha =-\frac{i \left( a_0^2 (2 B+1) (C-2 (F+G))+A+B H\right) }{a_1 \sqrt{4 B+2} \sqrt{A+B H} \sqrt{C-2 (F+G)}},\\ \beta =-\frac{i \sqrt{2} a_0 \sqrt{2 B+1} \sqrt{C-2 F-2 G}}{\sqrt{A+B H}},\\ a_0=a_0,\,\,\,a_1=a_1,\,\,a_2=0. \end{array}\right. } \end{aligned}$$
(13)
$$\begin{aligned}&\quad {\left\{ \begin{array}{ll} \gamma =\frac{i \sqrt{2 A+2 B H}}{2 a_2 \sqrt{2 B+1} \sqrt{C-2 F-2 G}},\\ \alpha =\frac{i a_2 \sqrt{2 B+1} \sqrt{C-2 F-2 G}}{\sqrt{2 A+2 B H}},\\ \beta =0,\\ a_0=0,\,\,\,a_1=0,\,\,a_2=a_2. \end{array}\right. } \end{aligned}$$
(14)
$$\begin{aligned}&\quad {\left\{ \begin{array}{ll} \gamma =-\frac{i \sqrt{A+B H}}{4 a_2 \sqrt{4 B+2} \sqrt{C-2 (F+G)}},\\ \alpha =-\frac{i a_2 \sqrt{2 B+1} \sqrt{C-2 F-2 G}}{\sqrt{2 A+2 B H}},\\ \beta =0,\\ a_0=0,\,\,\,a_1=\frac{-A-B H}{4 a_2 (2 B+1) (C-2 F-2 G)},\,\,a_2=a_2. \end{array}\right. } \end{aligned}$$
(15)
$$\begin{aligned}&\quad {\left\{ \begin{array}{ll} \gamma =-\frac{i a_1 \sqrt{2 B+1} \sqrt{C-2 F-2 G}}{\sqrt{2 A+2 B H}},\\ \alpha =-\frac{i \sqrt{2 A+2 B H}}{2 a_1 \sqrt{2 B+1} \sqrt{C-2 F-2 G}},\\ \beta =0,\\ a_0=0,\,\,\,a_1=a_1,\,\,a_2=0. \end{array}\right. } \end{aligned}$$
(16)
$$\begin{aligned}&\quad {\left\{ \begin{array}{ll} \gamma =\frac{a_1 \sqrt{(2 B+1) (C-2 (F+G))}}{\sqrt{2} \sqrt{-A-B H}},\\ \alpha =0,\\ \beta =-\sqrt{2},\\ a_0=-\frac{\sqrt{-A-B H}}{\sqrt{2 B C-4 B F-4 B G+C-2 F-2 G}},\,\,\,a_1=a_1,\,\,a_2=0. \end{array}\right. } \end{aligned}$$
(17)

The general solution for (9), can be written as

$$\begin{aligned} \phi (\xi )=-\frac{\sqrt{\beta ^2(t)-4\alpha (t) \gamma (t)}\tanh [\frac{1}{2}\sqrt{\beta ^2(t)-4\alpha (t) \gamma (t)}\xi ]-\beta }{2\gamma },\,\,\,\beta ^2(t)-4\alpha (t) \gamma (t)>0, \end{aligned}$$
(18)

however, an explicit classification of the solutions for (8), can be find in the reference (Salas 2010). We obtain \(u(\xi )\), for the set of values given by (13), and (15): According with (13), (10), and (18), we have:

$$\begin{aligned} u(\xi )=-\frac{ \tanh \left( \frac{x}{\sqrt{2}}\right) \sqrt{-A-B H}}{\sqrt{2 B+1} \sqrt{C-2(F+G)}}. \end{aligned}$$
(19)

In the same way, for the values given by (15):

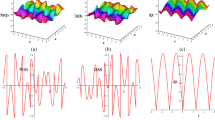
$$\begin{aligned} u(\xi )=-\frac{ \coth \left( \frac{x}{\sqrt{2}}\right) \sqrt{-A-B H}}{\sqrt{2 B+1} \sqrt{C-2 (F+G)}}. \end{aligned}$$
(20)

The following are the graphics, for \(u(\xi )\) given by (19), and given by (20), in the interval \((x,t)\in [-2,2]\times [0,3]\) (Fig. 1):

Fig. 1
figure 1

.

Full size image

The figures (\(u_1\)) and (\(u_3\)) correspond to (19) and (20) for the values: \(H=-3, B=1, C=5, F=1, G=1, A=1\). The figure (\(u_2\)) and (\(u_4\)) correspond to (19) and (20) for the values: \(H=-3t^2, B=t^2, C=5t, F=t^2, G=t, A=\frac{t^3}{2}\).

Finally, solutions for Eq. (1), in the particular case considered here, with the restriction (5), is given by:

$$\begin{aligned} {\left\{ \begin{array}{ll} q(x,t)= u(\xi )e^{\imath (\xi )}\\ \xi =x+\displaystyle \int \lambda \,dt+\xi _0,\\ \lambda =\frac{H-2A}{1+2B},\,\,B\ne -\frac{1}{2}, \end{array}\right. } \end{aligned}$$

where \(u(\xi )\), given as in (19), or (20). Using (12), (14), (16), and (17), can be construct more solutions for \(u(\xi )\) (and therefore for (1)), however, as it have the same structure of those showed here, we omit it.

2.2 General case

We consider the system (3). Multiplying the first equation by \(u'(\xi )\), and integrating the resultant equation with respect to \(\xi \), and taking the integration constant as zero, we obtain

$$\begin{aligned} \frac{\lambda +B\rho -H}{2}u^2(\xi )+(A+B\lambda )u^2(\xi )\Phi '(\xi )+\frac{D}{4}u^4(\xi )-\frac{(2m+1)F+2mG}{2m+2}u^{2m+2}(\xi )=0. \end{aligned}$$
(21)

We take \(m=1\). So that, (21), becomes

$$\begin{aligned} \Phi '(\xi )=\frac{H-\lambda -B\rho }{2(A+B\lambda )}+\frac{3F+2G-D}{4(A+B\lambda )}u^2(\xi ). \end{aligned}$$
(22)

Now, we replace (22), into second equation in the system (3). We have

$$\begin{aligned} \begin{array}{l} -4[H^2+\lambda ^2-2B\lambda \rho -2H(\lambda +B\rho )+\rho (-4A+B^2\rho )]u(\xi )\\ -8[2AC+FH+2BC\lambda -F\lambda -BF\rho +2D(-H+\lambda +B\rho )]u^3(\xi )\\ -[7D^2-22DF+3F^2-12DG-4FG-4G^2]u^5(\xi )\\ -16(A+B\lambda )^2u''(\xi )=0. \end{array} \end{aligned}$$
(23)

Multiplying (23), by \(u'(\xi )\), and Integrating respect to \(\xi \), setting the integration constant as zero, finally we have an equation of the form

$$\begin{aligned} u'(\xi )^2=r_2u^2(\xi )+r_4u^4(\xi )+r_6u^6(\xi ), \end{aligned}$$
(24)

where

$$\begin{aligned} \begin{array}{l} r_2(t)=-\frac{H^2+\lambda ^2-2B\lambda \rho -2H(\lambda +\beta |rho)+\rho (-4A+B^2\rho )}{4(A+B\lambda )^2}.\\ \\ r_4(t)=-\frac{2AC+FH+2BC\lambda -F\lambda -BF\rho +2D(-H+\lambda +B\rho )}{4(A+B\lambda )^2}\\ \\ r_6(t)=-\frac{7D^2-22DF+3F^2-12DG-4FG-4G^2}{48(A+B\lambda )^2} \end{array} \end{aligned}$$

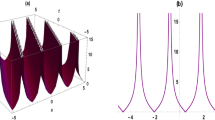
Solutions for equation \(u'(\xi )^2=r_2(t)u(\xi )^2+r_4(t)u(\xi )^4+r_6(t)u(\xi )^6\) can be expressed as:

$$\begin{aligned}&u(\xi )=\pm \sqrt{2} \sqrt{\frac{r_2 \left( r_4 \text {sech}^2\left( 2 \sqrt{r_2} \xi \right) +\sqrt{\left( r_4^2-4 r_2 r_6\right) \tanh ^2\left( 2 \sqrt{r_2} \xi \right) \left( -\text {sech}^2\left( 2 \sqrt{r_2} \xi \right) \right) }\right) }{4 r_2 r_6 \tanh ^2\left( 2 \sqrt{r_2} \xi \right) -r_4^2}}. \end{aligned}$$
(25)
$$\begin{aligned}&\quad u(\xi )=\pm \sqrt{2} \sqrt{\frac{r_2 \left( r_4 \text {sech}^2\left( 2 \sqrt{r_2} \xi \right) -\sqrt{\left( r_4^2-4 r_2 r_6\right) \tanh ^2\left( 2 \sqrt{r_2} \xi \right) \left( -\text {sech}^2\left( 2 \sqrt{r_2} \xi \right) \right) }\right) }{4 r_2 r_6 \tanh ^2\left( 2 \sqrt{r_2} \xi \right) -r_4^2}}. \end{aligned}$$
(26)

Here, \(r_i=r_i(t)\), \(r_2>0\). In this case, the solutions for (1), are determined by (2), with \(u(\xi )\) given by (25) or (26).

3 Results and Discussion

We have obtained exact solutions for the Fokas-Lenells equation with variable coefficients. The solution are new in the literature due to use of variable coefficients. Clearly, solutions for the standar model (constant coefficients) are derived as particular case. As was mentioned in the introduction, we have used the tanh-coth method due to several reasons: It is a generalization of the two classical methods, the tanh-coth method and the Kudriashov method; can be implemented computationally without the use of many resources; can be applied directly on a system, avoid in this way the reduction to only one equations as other methods; can be used to solve equations with variable coefficients. We have illustrate the type of solutions using some graphs: \(u_1\) and \(u_3\) illustrate the solutions (19), and (20), in the case of some constant coefficients. We can note that, the two solutions are plotted in the same interval, \(u_1\) a smooth wave, and \(u_3\) a solitary wave type dark soliton. In the same way, we have used variable coefficients in the same interval: \(u_2\) and \(u_4\). We note the two solutions are different, and compared with \(u_1\) and \(u_3\), the new waves are smooth and truncated. We note the use of variable coefficients, give us waves with new structures compared with the case of variable coefficient. Finally, we have solved (1), in a more general form, where we have used (24), from which, we obtain solutions that compared with those obtained in Al-Ghafri et al. (2020), are new, complementing in this way the results obtained by the authors in that reference. The generalization of a chirp pulse is defined as \(\delta w(x,t)=-\frac{\partial }{\partial x}[\Phi (\xi )-\displaystyle \int \rho (t)dt]=-\Phi '(\xi )\), (a definition is given by the authors in Al-Ghafri et al. (2020)), therefore, for each solution obtained here, the corresponding chirped pulse can be derived, complementing in this way the results obtained, for instance in Al-Ghafri et al. (2020).

4 Conclusions

A new generalized model with variable coefficients given by Eq. (1) is studied, from the point of view of its exact solutions. Two approximations to this task have been presented. First, we consider a particular case, where a condition (given by (5)) it necessary to construct the solutions. In this case, using the computational method (improved tanh-coth method) are derived soliton solutions, and some graphics corresponding to \(u(\xi )\) have been showed to illustrate the case in which the coefficients are constant or variable. Second, a more general approximation is considered, obtaining an equation which have special solutions, which we use to construct the solutions using the transformation (2). In this second case, all variables used are arbitrary, as well the function \(\Phi (\xi )\), taking into account that the coefficient given by \(r_2\), must by positive. As the coefficients are variable, those include the constants, so that, from the solutions presented here, solutions of the standard perturbed Fokas-Lenells equation can be obtain.