1 Introduction

Diverse complicated nonlinear physical characteristics may be signified in shape of nonlinear partial differential equations (NLPDEs). In recent years, NLPDEs have gained a remarkable attention in the realm of nonlinear sciences due to its wide range usage and applications. The NLPDEs perform a great role in plasma physics, ocean engineering, optical fibers, physics, biology, quantum physics, fluid mechanics, geochemistry and many other scientific areas to explain the dynamical and physical processes (Seadawy et al. 2019; Seadawy and Cheemaa 2020; Zhou 2014; Younis et al. 2018; Ozkan et al. 2020; Ahmad et al. 2020; Arshad et al. 2017b, c). In this advanced era of science and technology, the study of nonlinear phenomena has become attractive field for scientists and engineers. The NLPDEs explain the behaviour of waves in different fields. The exact solution of NPDEs plays major role to understand many physical phenomena in the various natural sciences. Due to this different kind of powerful and effective techniques are introduced to find exact and analytic solutions by using computational algebra as the discrete symmetry analysis of some classical and fractional differential equations; Lie symmetry analysis of conformable differential equations and Lie symmetry analysis and conservation laws for the time fractional Black-Scholes equation (Chatibi et al. 2019a, b, 2020). It is not possible to apply each method to all governing models because every method has its own shortcomings and criteria for the application to the governing model for discussing the exact solutions (Darvishi et al. 2018; Younis et al. 2020; Sulaiman et al. 2019; Ali et al. 2018; Zhang et al. 2011; Seadawy 2017a, b; Arshad et al. 2017a; Seadawy 2015, 2012). Particularly exact wave structures are presented in a quantum field and also in mathematical physics in the context of wave description of elementary systems. The study of quantum field theory is still booming, as the uses of its mechanism to many physical problems. In quantum field theory, the wave structures play an important role in the non-perturbative developments. It remains one of the most dynamic areas of theoretical physics today, providing a common language to several other branches of physics. Due to this different kind of powerful and effective techniques are introduced to find exact and analytic solutions by using computational algebra (Seadawy and Jun 2017; Younas et al. 2021; Ozkan et al. 2021; Seadawy et al. 2021a, b; Bilal et al. 2021a, b; Rizvi et al. 2021a, b). It is not possible to apply each method to all governing model because every method has its own shortcomings and criteria for the application to the governing model for discussing the exact solutions. Recently, the CNLSE has been analyzed by a number of effective approaches (Bulut et al. 2017; Abdul Al Woadud et al. 2019; Eslami 2016; Raza and Javid 2018; Ali et al. 2018; Dianchen et al. 2017; Johnpillai et al. 2012; Ali et al. 2017; Gianzo et al. 1999; Younis et al. 2016; Agrawal 2013; Seadawy 2017b) which yields fruitful results in diverse areas of nonlinear sciences.

The (1+1)-dimensional CNLSE is given by Nishino et al. (1998)

$$\begin{aligned} i \Theta _{t}+\Theta _{xx}-i\sigma (\Theta ^{*}\Theta _{x}-\Theta \Theta _{x}^{*})\Theta =0, \end{aligned}$$
(1)

where \(\Theta\) represents the complex function of x and t, while \(\sigma\) indicates nonlinear coupling constant and the \(*\) represents the complex conjugate.

However in this work, the key objective is to extract solitary wave solutions of (1+1)-dimensional CNLSE via extended rational sine–cosine/sinh–cosh techniques in quantum field theory. The (1+1)-dimensional CNLSE has been taken as model to demonstrate the efficiency of these proposed schemes.

This piece of article is discussed as sequence: in Sect. 2, overview of the methods. In Sect. 3, applications. In Sect. 4, modulation instability analysis. In Sect. 5, results and discussion and finally paper come to end with conclusions in Sect. 6.

2 Overview of the methods

We describe the first step of the extended rational methods for seeking the solutions of NLPDEs in this section.

Suppose that a NLPDE in its general form

$$\begin{aligned} F\left( {u,\frac{{\partial u}}{{\partial t}},\frac{{\partial u}}{{\partial x}},\frac{{\partial {u^2}}}{{\partial x}},\frac{{{\partial ^2}u}}{{\partial {x^2}}}, \cdots } \right) = 0, \end{aligned}$$
(2)

where F is a polynomial in u and its partial derivatives and \(u=u(x,t)\) is an unknown function. Suppose that

$$\begin{aligned} u(x, t) = u(\xi ),\quad \quad \xi = x + ct,~~ \end{aligned}$$
(3)

Then, by using (3), Eq. (2) can be turned into following ODE with respect to \(\xi\)

$$\begin{aligned} G\left( {u,u',u'', \cdots } \right) = 0. \end{aligned}$$
(4)

In next we discuss the exact solutions of Eq. (4) by using the extended rational techniques.

2.1 Extended rational sine–cosine method

We assume that Eq. (4) has following forms of solutions

$$\begin{aligned} u(\xi )&= \frac{{{a_0}\sin (\eta \xi )}}{{{a_2} + {a_1}\cos (\eta \xi )}},\quad \cos (\eta \xi ) \ne - \frac{{{a_2}}}{{{a_1}}},~~~~~~~~~~~ \end{aligned}$$
(5)
$$\begin{aligned} u(\xi )&= \frac{{{a_0}\cos (\eta \xi )}}{{{a_2} + {a_1}\sin (\eta \xi )}},\quad \sin (\eta \xi ) \ne - \frac{{{a_2}}}{{{a_1}}},~~~~~~~~~~~ \end{aligned}$$
(6)

where \(a_{0}\), \(a_{1}\) and \(a_{2}\) are parameters to be found in terms of the other parameters. The non-zero constant \(\eta\) is the wave number. The derivatives of the predicted solutions are

$$\begin{aligned} u'(\xi )&= \frac{{{a_0}\eta \left[ {\cos (\eta \xi ){a_2} + {a_1}} \right] }}{{{{\left[ {{a_2} + {a_1}\sin (\eta \xi )} \right] }^2}}}, \end{aligned}$$
(7)
$$\begin{aligned} ~u''(\xi )&= \frac{{{a_0}{\eta ^2}\sin (\eta \xi )\left[ {2a_1^2 + {a_1}\cos (\eta \xi ){a_2} - a_2^2} \right] }}{{{{\left[ {{a_2} + {a_1}\cos (\eta \xi )} \right] }^3}}},~~~~~ \end{aligned}$$
(8)

in the first form and

$$\begin{aligned} u'(\xi )&= - \frac{{{a_0}\eta \left[ {\sin (\eta \xi ){a_2} + {a_1}} \right] }}{{{{\left[ {{a_2} + {a_1}\sin (\eta \xi )} \right] }^2}}}, \end{aligned}$$
(9)
$$\begin{aligned} u''(\xi )&= \frac{{{a_0}{\eta ^2}\cos (\eta \xi )\left[ {2a_1^2 + {a_1}\sin (\eta \xi ){a_2} - a_2^2} \right] }}{{{{\left[ {{a_2} + {a_1}\sin (\eta \xi )} \right] }^3}}}.~~~~ \end{aligned}$$
(10)

in the second form. We substitute Eqs.(7) or (9) into the reduced form of the governing equation obtained above in Eq. (4). On collecting the same power coefficients of the \(\cos ^{m}(\eta \xi )\) or \(\sin ^{m}(\eta \xi )\) and equating to zero, we get a cluster of algebraic expression. The obtained algebraic polynomial produce the values of the coefficients involved. After determine \(a_{0}\), \(a_{1}\), \(a_{2}\), c and \(\eta\) in terms of other parameters and substitute into Eqs. (5) and (6), one gets solutions for Eq. (4) in rational sin-cos forms.

2.2 Extended rational sinh–cosh method

According to this method, which was introduced by Darvishi et al. (2018), we suppose that solutions of Eq. (4) can be written in the following forms

$$\begin{aligned} u(\xi )&= \frac{{{a_0}\sinh (\eta \xi )}}{{{a_2} + {a_1}\cosh (\eta \xi )}},\quad \cosh (\eta \xi ) \ne - \frac{{{a_2}}}{{{a_1}}},~~~~~~~~ \end{aligned}$$
(11)
$$\begin{aligned} u(\xi )&= \frac{{{a_0}\cosh (\eta \xi )}}{{{a_2} + {a_1}\sinh (\eta \xi )}},\quad \sinh (\eta \xi ) \ne - \frac{{{a_2}}}{{{a_1}}},~~~~~~~~ \end{aligned}$$
(12)

Where \(a_{0}\), \(a_{1}\) and \(a_{2}\) are parameters to be found in terms of the other parameters. The non-zero constant \(\eta\) is the wave number. The derivatives of the predicted solutions are

$$\begin{aligned} u'(\xi )&= \frac{{{a_0}\eta \left[ {\cosh (\eta \xi ){a_2} + {a_1}} \right] }}{{{{\left[ {{a_2} + {a_1}\sinh (\eta \xi )} \right] }^2}}}, \end{aligned}$$
(13)
$$\begin{aligned} ~~u''(\xi )&= - \frac{{{a_0}{\eta ^2}\sinh (\eta \xi )\left[ {2a_1^2 + {a_1}\cosh (\eta \xi ){a_2} - a_2^2} \right] }}{{{{\left[ {{a_2} + {a_1}\cosh (\eta \xi )} \right] }^3}}}, \end{aligned}$$
(14)

in the first form and

$$\begin{aligned} u'(\xi )&= \frac{{{a_0}\eta \left[ {\sinh (\eta \xi ){a_2} - {a_1}} \right] }}{{{{\left[ {{a_2} + {a_1}\sinh (\eta \xi )} \right] }^2}}},~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(15)
$$\begin{aligned} u''(\xi )&= \frac{{{a_0}{\eta ^2}\cosh (\eta \xi )\left[ {2a_1^2 - {a_1}\sinh (\eta \xi ){a_2} + a_2^2} \right] }}{{{{\left[ {{a_2} + {a_1}\sinh (\eta \xi )} \right] }^3}}}. \end{aligned}$$
(16)

in the second form. We substitute Eq. (13) or (15) into the reduced form of the governing equation obtained above in Eq. (4). On collecting the same power coefficients of the \(\cosh ^{m}(\eta \xi )\) or \(\sinh ^{m}(\eta \xi )\) and equating to zero, we achieve a cluster of algebraic expression. The obtained algebraic polynomial produce the values of the coefficients involved. After determine \(a_{0}\), \(a_{1}\), \(a_{2}\), c and \(\eta\) in terms of other parameters and substitute into Eqs. (11) and (12), one gets solutions for Eq. (4) in rational sinh–cosh forms.

3 Applications

For solving Eq. (1), we start with complex wave transformation \(\Theta (x,t)=\Psi (\tau )e^{i\Phi }, ~\text{ where }~\tau =c(x+\upsilon t), \Phi = k x +\omega t + \varphi .\) Here \(c, \nu , \varphi ,\omega\) and k are parameters, which represent the amplitude component of the soliton, velocity of soliton, phase constant, frequency and wave number respectively. Substitute transformation into Eq. (1), from the imaginary part we get the relation

$$\begin{aligned} \nu =-2k,~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(17)

and we obtain

$$\begin{aligned} c^{2}\Psi '' +2 k \sigma \Psi ^{3}-(\omega +k^{2})\Psi =0,~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(18)

from the real part. Using homogeneous balance principle, we yields, \(n = 1\).

3.1 Solutions via extended rational sine–cosine method

Assume that Eq. (18) possesses the solutions of the form

$$\begin{aligned} \Psi (\tau )=\frac{a_{0}\sin (\eta \tau )}{a_{2}+a_{1}\cos (\eta \tau )}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(19)

Inserting Eq. (19) and its derivative into Eq. (18) and the coefficients having same power of \(\cos (\eta \tau )^{m}\) equal to zero and resultantly, a bunch of equations is retrieved by using Mathematica:

$$\begin{aligned} \cos (\eta \tau )^{2} : a_1^2 k^2+2 a_0^2 k \sigma +a_1^2 \omega =0,\\ \cos (\eta \tau )^1 : a_1 a_2 c^2 \eta ^2-2 a_1 a_2 k^2-2 a_1 a_2 \omega =0,\\ \cos (\eta \tau )^{0} : 2 a_1^2 c^2 \eta ^2-a_2^2 c^2 \eta ^2-a_2^2 k^2+2 a_0^2 k \sigma -a_2^2 \omega =0. \end{aligned}$$

On solving above equations, we attain the following sets of solutions as:

Set-1

$$\begin{aligned} \eta =\pm \frac{\sqrt{k^2+\omega }}{\sqrt{2} c},~ a_{0}=\pm a_1 \sqrt{-\frac{k^2+\omega }{2 \hbox { k}\ \sigma }}~, a_{1}= a_{1} ~,a_{2}= 0 . \end{aligned}$$

Set-2

$$\begin{aligned} \eta =\pm \frac{\sqrt{2 \left( k^2+\omega \right) }}{c},~ a_{0}=\pm a_1 \sqrt{-\frac{k^2+\omega }{2 k \sigma }}~, a_{1}=a_{1} ~,a_{2}=\pm a_1 . \end{aligned}$$

For set 1, we express the solutions of Eq. (1) as:

$$\begin{aligned} \Theta _{1,1}(x,t)&= \sqrt{-\frac{k^2+\omega }{2 k \sigma }}\tan \bigg [\frac{\sqrt{k^{2}+\omega }}{\sqrt{2}} (x-2k t )\bigg ]\mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )} . \end{aligned}$$
(20)
$$\begin{aligned} \Theta _{1,2}(x,t)&= -\sqrt{-\frac{k^2+\omega }{2 k \sigma }}\tan \bigg [\frac{\sqrt{k^{2}+\omega }}{\sqrt{2}} (x-2k t ) \bigg ]\mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )}. \end{aligned}$$
(21)

Similarly, for set 2 we have the following solutions:

$$\begin{aligned} \Theta _{2,1}(x,t)&= \sqrt{-\frac{k^2+\omega }{2 k \sigma }}\frac{\sin \bigg [\sqrt{2(k^{2}+\omega )}(x-2k t )\bigg ]}{1+\cos \bigg [\sqrt{2(k^{2}+\omega )}(x-2k t )\bigg ]}\mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )}. ~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(22)
$$\begin{aligned} \Theta _{2,2}(x,t)&= -\sqrt{-\frac{k^2+\omega }{2 k \sigma }}\frac{\sin \bigg [\sqrt{2(k^{2}+\omega )}(x-2k t )\bigg ]}{1-\cos \bigg [\sqrt{2(k^{2}+\omega )}(x-2k t )\bigg ]}\mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )}.~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(23)
$$\begin{aligned} \Theta _{2,3}(x,t)&= -\sqrt{-\frac{k^2+\omega }{2 k \sigma }}\frac{\sin \bigg [\sqrt{2(k^{2}+\omega )}(x-2k t )\bigg ]}{1+\cos \bigg [\sqrt{2(k^{2}+\omega )}(x-2k t )\bigg ]}\mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )}.~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(24)
$$\begin{aligned} \Theta _{2,4}(x,t)&= \sqrt{-\frac{k^2+\omega }{2 k \sigma }}\frac{\sin \bigg [\sqrt{2(k^{2}+\omega )}(x-2k t )\bigg ]}{1-\cos \bigg [\sqrt{2(k^{2}+\omega )}(x-2k t )\bigg ]}\mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )}.~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(25)

OR

Consider the Eq.(18) has solutions in the form as

$$\begin{aligned} \Psi (\tau )=\frac{a_{0}\cos (\eta \tau )}{a_{2}+a_{1}\sin (\eta \tau )} \end{aligned}$$
(26)

Inserting Eq. (26) and its derivative into Eq. (18) and the coefficients having same power of \(\sin (\eta \tau )^{m}\) equal to zero and resultantly, a bunch of equations is retrieved by using Mathematica:

$$\begin{aligned}&\sin (\eta \tau )^{2} : -a_1^2 k^2-2 a_0^2 k \sigma -a_1^2 \omega =0,\\&\quad \sin (\eta \tau )^1 : a_1 a_2 c^2 \eta ^2-2 a_1 a_2 k^2-2 a_1 a_2 \qquad \omega =0,\\&\quad \sin (\eta \tau )^{0} : 2 a_1^2 c^2 \eta ^2-a_2^2 c^2 \eta ^2-a_2^2 k^2+2 a_0^2 k \sigma -a_2^2 \omega =0. \end{aligned}$$

On solving above equations, we attain the following sets of solutions as:

Set-3

$$\begin{aligned} \omega =2 c^2 \eta ^2-k^2,~ a_0=\pm a_1 c \eta \sqrt{-\frac{1}{\hbox { k}\ \sigma }} ~, a_{1}=a_{1} ~,a_{2}=0 . \end{aligned}$$

Set-4

$$\begin{aligned} \omega =\frac{1}{2} \left( c^2 \eta ^2-2 k^2\right) ,~ a_{0}=\pm a_{1}c \eta \sqrt{-\frac{1}{4 \hbox { k}\ \sigma }}~, a_{1}=a_{1} ~,a_{2}=\pm a_{1} . \end{aligned}$$

For set 3, we get the solutions of Eq. (1) in following form:

$$\begin{aligned} \Theta _{3,1}(x,t)&= c \eta \sqrt{-\frac{1}{ \text {k}\sigma }}\cot \bigg [\eta c(x-2k t)\bigg ]\mathrm {e}^{\mathrm {i}(kx+(2 c^2 \eta ^2-k^2) t+\varphi )}. \end{aligned}$$
(27)
$$\begin{aligned} \Theta _{3,2}(x,t)&= -c \eta \sqrt{-\frac{1}{ \text {k}\sigma }}\cot \bigg [\eta c(x-2k t)\bigg ]\mathrm {e}^{\mathrm {i}(k x+(2 c^2 \eta ^2-k^2) t+\varphi t)}. \end{aligned}$$
(28)

Similarly, for set 4, we have the following form of solutions:

$$\begin{aligned} \Theta _{4,1}(x,t)&= c \eta \sqrt{-\frac{1}{4 \text {k}\sigma }}\frac{\cos \bigg [\eta c(x-2k t)\bigg ]}{1+\sin \bigg [\eta c(x-2k t)\bigg ]}\mathrm e^{\mathrm {i}(kx+\frac{1}{2} \left( c^2 \eta ^2-2 k^2\right) t+\varphi )}. ~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(29)
$$\begin{aligned} \Theta _{4,2}(x,t)&= -c \eta \sqrt{-\frac{1}{4 \text {k}\sigma }}\frac{\cos \bigg [\eta c(x-2k t)\bigg ]}{1-\sin \bigg [\eta c(x-2k t)\bigg ]}\mathrm e^{\mathrm {i}(kx+\frac{1}{2} \left( c^2 \eta ^2-2 k^2\right) t+\varphi )}.~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(30)
$$\begin{aligned} \Theta _{4,3}(x,t)&= -c \eta \sqrt{-\frac{1}{4 \text {k}\sigma }}\frac{\cos \bigg [\eta c(x-2k t)\bigg ]}{1+\sin \bigg [\eta c(x-2k t)\bigg ]}\mathrm {e}^{\mathrm {i}(kx+\frac{1}{2} \left( c^2 \eta ^2-2 k^2\right) t+\varphi )}.~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(31)
$$\begin{aligned} \Theta _{4,4}(x,t)&= c \eta \sqrt{-\frac{1}{4 \text {k}\sigma }}\frac{\cos \bigg [\eta c(x-2k t)\bigg ]}{1-\sin \bigg [\eta c(x-2k t)\bigg ]}\mathrm e^{\mathrm {i}(kx+\frac{1}{2} \left( c^2 \eta ^2-2 k^2\right) t+\varphi )}.~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(32)

3.2 Solutions via extended rational sinh–cosh approach

Assume that the Eq.(18) has solutions of the form

$$\begin{aligned} \Psi (\tau )=\frac{a_{0}\sinh (\eta \tau )}{a_{2}+a_{1}\cosh (\eta \tau )} \end{aligned}$$
(33)

Inserting Eq. (33) and its derivative into Eq. (18) and the coefficients having same power of \(\cosh (\eta \tau )^{m}\) equal to zero and resultantly, a bunch of equations is retrieved by using Mathematica:

$$\begin{aligned}&\cosh (\eta \tau )^{2} : -a_1^2 k^2+2 a_0^2 k \sigma -a_1^2 \omega =0, \\&\quad \cosh (\eta \tau )^1 :-a_1 a_2 c^2 \eta ^2-2 a_1 a_2 k^2-2 a_1 a_2 \omega =0,\\&\quad \cosh (\eta \tau )^{0} : -2 a_1^2 c^2 \eta ^2+a_2^2 c^2 \eta ^2-a_2^2 k^2-2 a_0^2 k \sigma -a_2^2 \omega =0. \end{aligned}$$

On solving above equations, we attain the following sets of solutions as:

Set-5

$$\begin{aligned} ~~k=-\sqrt{-2 c^2 \eta ^2-\omega }, a_{0}=\pm a_{1}c \eta \root 4 \of {-2 c^2 \eta ^2-\omega } \sqrt{-\frac{1}{\sigma \left( 2 c^2 \eta ^2+\omega \right) }}~, a_{1}=a_{1} ~,a_{2}=0 . \end{aligned}$$

Set-6

$$\begin{aligned} k=\sqrt{-\frac{1}{2} \left( c^2 \eta ^2+2 \omega \right) }, a_{0}=\pm a_{1}\frac{c \eta \root 4 \of {-c^2 \eta ^2-2 \omega }}{2^{3/4} \sqrt{\sigma \left( c^2 \eta ^2+2 \omega \right) }}~, a_{1}=a_{1} ~,a_{2}= \pm a_{1} .~~~~~~~~~~ \end{aligned}$$

For set 5 the solutions of Eq. (1) can be written as:

$$\begin{aligned} \Theta _{5,1}(x,t)&= c \eta \root 4 \of {-2 c^2 \eta ^2-\omega } \sqrt{-\frac{1}{\sigma \left( 2 c^2 \eta ^2+\omega \right) }}\tanh \bigg [\eta c\left( x+2\left( \sqrt{-2 c^2 \eta ^2-\omega }\right) t\right) \bigg ]\nonumber ~~\\&\qquad \times \,\mathrm {e}^{\mathrm {i}\left( \left( -\sqrt{-2 c^2 \eta ^2-\omega }\right) x+\omega t+\varphi \right) }. \end{aligned}$$
(34)
$$\begin{aligned} ~\Theta _{5,2}(x,t)&= -c \eta \root 4 \of {-2 c^2 \eta ^2-\omega } \sqrt{-\frac{1}{\sigma \left( 2 c^2 \eta ^2+\omega \right) }}\tanh \bigg [\eta c\left( x+2\left( \sqrt{-2 c^2 \eta ^2-\omega }\right) t\right) \bigg ]\nonumber ~\\&\qquad \times \,\mathrm {e}^{\mathrm {i}\left( \left( -\sqrt{-2 c^2 \eta ^2-\omega }\right) x+\omega t+\varphi \right) } . \end{aligned}$$
(35)

Similarly, for set 6 the solutions of Eq. (1) can be written as:

$$\begin{aligned} \Theta _{6,1}(x,t)&= \frac{c \eta \root 4 \of {-c^2 \eta ^2-2 \omega }}{2^{3/4} \sqrt{\sigma \left( c^2 \eta ^2+2 \omega \right) }}\frac{\sinh \bigg [\eta c\left( x-\sqrt{-2 \left( c^2 \eta ^2+2 \omega \right) }~ t\right) \bigg ]}{1+\cosh \bigg [\eta c(x-\sqrt{-2 \left( c^2 \eta ^2+2 \omega \right) }~ t)\bigg ]}\nonumber \\&\qquad \times \,\mathrm {e}^{\mathrm {i}\left( \sqrt{-\frac{1}{2} \left( c^2 \eta ^2+2 \omega \right) }~x+\omega t+\varphi \right) }. \end{aligned}$$
(36)
$$\begin{aligned} \Theta _{6,2}(x,t)&= -\frac{c \eta \root 4 \of {-c^2 \eta ^2-2 \omega }}{2^{3/4} \sqrt{\sigma \left( c^2 \eta ^2+2 \omega \right) }}\frac{\sinh \bigg [\eta c\left( x-\sqrt{-2 \left( c^2 \eta ^2+2 \omega \right) }~ t\right) \bigg ]}{1-\cosh \bigg [\eta c(x-\sqrt{-2 \left( c^2 \eta ^2+2 \omega \right) } ~t)\bigg ]}\nonumber \\&\qquad \times \,\mathrm {e}^{\mathrm {i}\left( \sqrt{-\frac{1}{2} \left( c^2 \eta ^2+2 \omega \right) }~x+\omega t+\varphi \right) }. \end{aligned}$$
(37)
$$\begin{aligned} \Theta _{6,3}(x,t)&= -\frac{c \eta \root 4 \of {-c^2 \eta ^2-2 \omega }}{2^{3/4} \sqrt{\sigma \left( c^2 \eta ^2+2 \omega \right) }}\frac{\sinh \bigg [\eta c\left( x-\sqrt{-2 \left( c^2 \eta ^2+2 \omega \right) }~ t\right) \bigg ]}{1+\cosh \bigg [\eta c\left( x-\sqrt{-2 \left( c^2 \eta ^2+2 \omega \right) }~ t\right) \bigg ]}\nonumber \\&\qquad \times \,\mathrm {e}^{\mathrm {i}\left( \sqrt{-\frac{1}{2} \left( c^2 \eta ^2+2 \omega \right) }~x+\omega t+\varphi \right) }. \end{aligned}$$
(38)
$$\begin{aligned} \Theta _{6,4}(x,t)&= \frac{c \eta \root 4 \of {-c^2 \eta ^2-2 \omega }}{2^{3/4} \sqrt{\sigma \left( c^2 \eta ^2+2 \omega \right) }}\frac{\sinh \bigg [\eta c\left( x-\sqrt{-2 \left( c^2 \eta ^2+2 \omega \right) }~ t\right) \bigg ]}{1-\cosh \bigg [\eta c\left( x-\sqrt{-2 \left( c^2 \eta ^2+2 \omega \right) }~ t\right) \bigg ]}\nonumber \\&\qquad \times \,\mathrm {e}^{\mathrm {i}\left( \sqrt{-\frac{1}{2} \left( c^2 \eta ^2+2 \omega \right) }~x+\omega t+\varphi \right) }. \end{aligned}$$
(39)

OR

Consider the Eq.(18) has solutions in the form as

$$\begin{aligned} \Psi (\tau )=\frac{a_{0}\cosh (\eta \tau )}{a_{2}+a_{1}\sinh (\eta \tau )} \end{aligned}$$
(40)

Inserting Eq. (40) and its derivative into Eq. (18) and the coefficients having same power of \(\sinh (\eta \tau )^{m}\) equal to zero and resultantly, a bunch of equations is retrieved by using Mathematica:

$$\begin{aligned}&\sinh (\eta \tau )^{2} : -a_1^2 k^2+2 a_0^2 k \sigma -a_1^2 \omega =0,\\&\quad \sinh (\eta \tau )^1 : -a_1 a_2 c^2 \eta ^2-2 a_1 a_2 k^2-2 a_1 a_2 \omega =0,\\&\quad \sinh (\eta \tau )^{0} : 2 a_1^2 c^2 \eta ^2+a_2^2 c^2 \eta ^2-a_2^2 k^2+2 a_0^2 k \sigma -a_2^2 \omega =0. \end{aligned}$$

On solving above equations, we attain the following sets of solutions as:

Set-7

$$\begin{aligned} c= \pm \frac{\sqrt{-k^2-\omega }}{\sqrt{2} \eta } , a_{0}=\pm a_{1}\sqrt{\frac{k^2+\omega }{2 \hbox {k}\ \sigma }}~, a_{1}=a_{1} ~,a_{2}=0 . \end{aligned}$$

Set-8

$$\begin{aligned} c=\pm \frac{\sqrt{-2 \left( k^2+\omega \right) }}{\eta } , a_{0}=\pm a_{1}\sqrt{\frac{k^2+\omega }{2 \hbox { k}\ \sigma }}~, a_{1}= a_{1} ~,a_{2}=\pm \mathrm {i} a_{1}. \end{aligned}$$

For set 7, we get the solutions of Eq. (1) in the following form:

$$\begin{aligned} \Theta _{7,1}(x,t)&= \sqrt{\frac{k^{2}+\omega }{2k\sigma }}\coth \bigg [\sqrt{\frac{{-k^2-\omega }}{2}}(x-2k t)\bigg ]\mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )}. \end{aligned}$$
(41)
$$\begin{aligned} \Theta _{7,2}(x,t)&= -\sqrt{\frac{k^{2}+\omega }{2k\sigma }}\coth \bigg [\sqrt{\frac{{-k^2-\omega }}{2}}(x-2k t)\bigg ]\mathrm { e}^{\mathrm {i}(kx+\omega t+\varphi )} . \end{aligned}$$
(42)

Similarly, for set 8, we get the solutions as:

$$\begin{aligned} \Theta _{8,1}(x,t)&= \sqrt{\frac{k^{2}+\omega }{2k\sigma }}\frac{\cosh \bigg [\sqrt{-2 \left( k^2+\omega \right) }(x-2k t)\bigg ]}{\mathrm {i}+\sinh \bigg [\sqrt{-2 \left( k^2+\omega \right) }(x-2k t)\bigg ]}\mathrm e^{\mathrm {i}(kx+\omega t+\varphi )}. \end{aligned}$$
(43)
$$\begin{aligned} \Theta _{8,2}(x,t)&= -\sqrt{\frac{k^{2}+\omega }{2k\sigma }}\frac{\cosh \bigg [\sqrt{-2 \left( k^2+\omega \right) }(x-2k t)\bigg ]}{\mathrm {i}-\sinh \bigg [\sqrt{-2 \left( k^2+\omega \right) }(x-2k t)\bigg ]}\mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )}. \end{aligned}$$
(44)
$$\begin{aligned} \Theta _{8,3}(x,t)&= -\sqrt{\frac{k^{2}+\omega }{2k\sigma }}\frac{\cosh \bigg [\sqrt{-2 \left( k^2+\omega \right) }(x-2k t)\bigg ]}{\mathrm {i}+\sinh \bigg [\sqrt{-2 \left( k^2+\omega \right) }(x-2k t)\bigg ]} \mathrm {e}^{\mathrm {i}(kx+\omega t+\varphi )}. \end{aligned}$$
(45)
$$\begin{aligned} \Theta _{8,4}(x,t)&= \sqrt{\frac{k^{2}+\omega }{2k\sigma }}\frac{\cosh \bigg [\sqrt{-2 \left( k^2+\omega \right) }(x-2k t)\bigg ]}{\mathrm {i}-\sinh \bigg [\sqrt{-2 \left( k^2+\omega \right) }(x-2k t)\bigg ]}\mathrm e^{\mathrm {i}(kx+\omega t+\varphi )}. \end{aligned}$$
(46)

4 Modulation instability analysis

In this section, we analyze the modulation instability(MI) of the (1+1) dimensional CNLSE with the aid of the general concept of linear stability (Agrawal 2013; Seadawy 2017b; Ahmed et al. 2019).

Consider the steady-state solutions of the CNLSE to be of the form

$$\begin{aligned} \Theta (x, t)=\Big (\sqrt{k_{0}}+H(x, t)\Big )e^{ik_{0}t}, \end{aligned}$$
(47)

where \(k_{0}\) represents the normalized power.

Putting Eq. (47) into Eq. (1) and linearizing, provides

$$\begin{aligned} -k_{0}(H+H^{*})+i H_{t}+H_{xx} = 0, \end{aligned}$$
(48)

where H(x, t) is unknown complex function and * stands for the conjugate of H(x, t).

We assume that the solution of Eq. (48) to be in the following form

$$\begin{aligned} H (x, t)=b_{1}e^{i(l x-\varpi t)}+b_{2}e^{-i(l x -\varpi t)}, \end{aligned}$$
(49)

where l and \(\varpi\) denote the normalized wave number, and frequency of perturbation, respectively.

Putting Eq. (49) into Eq. (48), separate the coefficients of \(e^{i(l x-\varpi t)}\) and \(e^{-i(l x-\varpi t)}\), we attain the dispersion relation after solving the determinant of the coefficient matrix.

$$\begin{aligned} \begin{aligned} l^4+2 k_0 l^2-\varpi ^2=0. \end{aligned} \end{aligned}$$
(50)

Calculating the dispersion relation (50) for \(\varpi\), grants

$$\begin{aligned} \varpi =\sqrt{l^4+2 k_0 l^2}. \end{aligned}$$
(51)

The obtained dispersion relation reveals the steady-state stability. If the wave number \(\varpi\) is imaginary one then steady-state solution turn to unstable since the perturbation grows exponentially. Moreover if the wave number \(\varpi\) has real part then steady state turns to stable against small perturbations. Therefore, the steady-state solution is unstable if:

$$\begin{aligned} l^4+2 k_0 l^2<0. \end{aligned}$$

Finally, the MI gain spectrum G(l) is achieved as

$$\begin{aligned} G(l)=2Im(\varpi )=2Im \Bigg (\sqrt{l^4+2 k_0 l^2}\Bigg ). \end{aligned}$$
(52)
Fig. 1
figure 1

The dispersion relation between frequency \(\varpi\) and wave number l for distinct values of \(k_0=.6, .8, 1\)

Full size image

5 Results and discussion

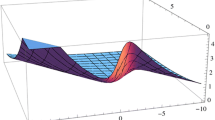
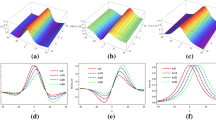
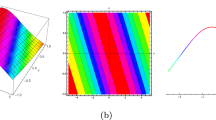
The graphical view of some reported result deals in this section. By applying proposed methods the exact wave solutions are extracted and graphically depicted into distinct physical structures in the form of multiple soliton solutions like, trigonometric, hyperbolic, periodic and singular wave functions. By the appropriate values of involved parameters, the real and absolute behaviors of some solutions are reported. Figure 2 for Eq. (20) and Fig. 3 for Eq. (28) represent wave solutions repeated periodically, while Figs 4 and 5 for the Eqs. (34) and (37) describe the dark soliton and exact wave solutions respectively. Moreover, Figes. 7 and 6 represent the singular soliton and exact wave solution for the equations Eqs. (43) and (41) respectively. These exact wave solutions have different physical behavior. For example, hyperbolic functions such as, the hyperbolic tangent appears in the calculation and rapidity of special relativity while, the hyperbolic cotangent arises in the Langevin function for magnetic polarization Weisstein (2002). Therefore, the result sake in this paper may be used to explain such relationship to the governing model.

Fig. 2
figure 2

The a, b and c show the 3D, 2D and contour physical behaviour of solution (20), respectively with the values \(k=-1\), \(\omega =3\), \(\sigma =2\), \(\varphi =0\)

Full size image
Fig. 3
figure 3

The a, b and c show the 3D, 2D and contour physical behaviour of solution (28), respectively with the values \(k=2\), \(\eta =2\), \(\sigma =-3\), \(\varphi =.3\), \(c=1\)

Full size image
Fig. 4
figure 4

The a, b and c show the 3D, 2D and contour physical behaviour of solution (34), respectively with the values \(\omega =-4\), \(\eta =-1\), \(\sigma =2\), \(\varphi =.3\), \(c=-1\)

Full size image
Fig. 5
figure 5

The a, b and c show the 3D, 2D and contour physical behaviour of solution (37), respectively under the parametric values of \(\omega =-3\), \(\eta =-2\), \(\sigma =1\), \(\varphi =.-1\), \(c=-1\)

Full size image
Fig. 6
figure 6

The a, b and c show the 3D, 2D and contour physical behaviour of solution (41), respectively under the parametric values of \(k=-2\) \(\omega =-3\), \(\eta =-1\), \(\sigma =-2\), \(\varphi =0\)

Full size image
Fig. 7
figure 7

The a, b and c show the 3D, 2D and contour physical behaviour of solution (43), respectively under the parametric values of \(\omega =-3\), \(\eta =-2\), \(\sigma =1\), \(\varphi =.-1\), \(c=-1\)

Full size image

6 Conclusions

In this research work, we have investigated diverse exact wave solutions are constructed in the form of trigonometric and hyperbolic solutions including dark soliton, kink type, singular soliton as well as periodic wave solutions to (1+1)-dimensional CNLSE via extended rational sine–cosine/sinh–cosh schemes. These various kinds of wave solutions are favourable for explaining diverse nonlinear physical phenomena. The MI analysis to the proposed model is also observed. Our acquired solutions exhibited that the proposed methods are powerful and can be used to extract exact wave solutions for various kinds of NLPDEs. Furthermore, we plot 3D, 2D and contour graphs of the some obtained solutions by setting appropriate values of involved parameters. It may be observed that wave behavior have reported their estimated wave propagation and distributions, physically, in Figs. 1, 2, 3, 4, 5 and 6. The results are new, interesting and have a great impact in the quantum field theory where the (1+1)-dimensional CNLSE will be used for the dynamics of exact wave solutions.