1 Introduction

Schrödinger equation is a famous equation in many fields of science, therefore, it attracts a lot of mathematicians trying to solve it in all forms. Recently, more attention were focusing on solving the variable coefficients nonlinear version of Schrödinger equation (vc-NLS) for different reasons, the first one, is that solving the vc-NLS equation is covering its constant coefficient version, the second reason, it is rely reflect the real physical situation more than the constant version. Moreover, the vc-NLS equation can cover many physical situations in different branches like optics, ocean dynamics and quantum mechanics ..etc.

In this paper, we are interested in studying and finding new solitary wave solutions for nonautonomous variable coefficients Schrödinger equation (Serkin et al. 2007)

$$\begin{aligned} i\Psi _{z}+\frac{\alpha (z)}{2}\Psi _{tt}+(\phi (z,t)-i\frac{\beta (z)}{2} )\Psi +\gamma (z)\left| \Psi \right| ^{2}\Psi =0, \end{aligned}$$
(1)

where \(\alpha (z)\) is the group-velocity dispersion, \(\phi (z,t)\) is the linear potential, \(\beta (z)\) is the gain/loss term and \(\gamma (z)\) is the nonlinearity term. Equation (1) describes self-similar waves which can be used for amplification and focusing of spatial solitons in nonlinear optics (Guo et al. 2011; Ponomarenko and Agrawal 2006; Tian et al. 2005; Yan 2010). Additionally, if \(\phi (z,t)\) is a function on z only, then the vc-NLS Eq. (1) represents many physical backgrounds in dusty plasma, nonlinear optics, ocean dynamics and arterial mechanics (El-Shiekh 2019; El-Shiekh and Al-Nowehy 2013; El-Shiekh and Gaballah 2020a, c; El-Shiekh 2019).

2 Direct similarity reduction

Recently, many new methods have been constructed to obtain new solutions for nonlinear partial differential equations like symmetry groups, tanh method, trial equation method, sin-Gordon equation method, etc. (Chen et al. 2019, 2020; Hua et al. 2019; Liu et al. 2019; Mao et al. 2019; Xia et al. 2020; Xu et al. 2020) (El-Sayed et al. 2015, 2014; El-Shiekh 2018, 2021, 2018a; El-Shiekh and Rehab 2018b; El-Shiekh 2017, 2015, 2013; El-Shiekh and Gaballah 2020b; Moatimid et al. 2013; Moussa et al. 2012; Moussa and El-Shiekh 2010, 2011; Moatimid and El Shikh 2008; Moussa and El Shikh 2006; Chen et al. 2021; He et al. 2021; Lü and Chen 2021; Lü et al. 2021; Lü and Ma 2016; Xia et al. 2020; Yin et al. 2020).

In the following we are going to apply one of the similarity techniques, the direct similarity reduction method (El-Shiekh 2019, 2017, 2015, 2013, 2018, 2018a; El-Shiekh and Gaballah 2020b; Moussa and El-Shiekh 2008, 2011), it used to transform the nonlinear partial differential equation into ordinary differential equation as follows:

Assume

$$\begin{aligned} \Psi (t,z)=U\left( \varsigma \left( z,t\right) \right) e^{i(\eta (z,t))}, \end{aligned}$$
(2)

where \(\varsigma (z,t)\) and \(\eta (z,t)\) are two arbitrary real functions and \(U(\varsigma )\) is a new dependent real variable.

Inserting (2) in (1), we get

$$\begin{aligned}&\left[ i\left( \frac{\partial \varsigma }{\partial z}U^{\prime }+i\frac{ \partial \eta }{\partial z}U\right) +\frac{\alpha (z)}{2}\left( \frac{ \partial ^{2}\varsigma }{\partial t^{2}}U^{\prime }+(\frac{\partial \varsigma }{\partial t})^{2}U^{\prime \prime }+i\frac{\partial ^{2}\eta }{ \partial t^{2}}U+2i\frac{\partial \varsigma }{\partial t}\frac{\partial \eta }{\partial t}U^{\prime }-(\frac{\partial \eta }{\partial t})^{2}U\right) \right. \nonumber \\&\quad \quad \quad\quad~~~~~~~~~\quad \left. +(\phi (z,t)-i\frac{\beta (z)}{2})U+\gamma (z)U^{3}\right] e^{i(\eta (z,t))}=0, \end{aligned}$$
(3)

where \(\prime\) denotes the derivative with respect to \(\varsigma .\) Collect the U coefficient and its derivatives, also, the real and imaginary parts together, assuming that \(e^{i(\eta (z,t))}\ne 0,\) we have

$$\begin{aligned}&\frac{\alpha (z)}{2}(\frac{\partial \varsigma }{\partial t})^{2}U^{\prime \prime }+\frac{\alpha (z)}{2}\frac{\partial ^{2}\varsigma }{\partial t^{2}} U^{\prime }+(\phi (z,t)-\frac{\partial \eta }{\partial z}-\frac{\alpha (z)}{2 }(\frac{\partial \eta }{\partial t})^{2})U+\gamma (z)U^{3} \nonumber \\&\quad \quad \quad \quad ~~~~~ +i\left( (\frac{\partial \varsigma }{\partial z}+\alpha (z)\frac{\partial \varsigma }{\partial t}\frac{\partial \eta }{\partial t})U^{\prime }+(\frac{ \alpha (z)}{2}\frac{\partial ^{2}\eta }{\partial t^{2}}-\frac{\beta (z)}{2} )U\right) =0. \end{aligned}$$
(4)

Assume that the imaginary part is finished, then we get

$$\begin{aligned}&\eta (z,t)=\frac{\beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z), \end{aligned}$$
(5)
$$\begin{aligned}&\quad \frac{\partial \varsigma }{\partial z}+\alpha (z)\frac{\partial \varsigma }{ \partial t}\frac{\partial \eta }{\partial t}=0, \end{aligned}$$
(6)

where \(h_{1}(z)\) and \(h_{2}(z)\) are two arbitrary functions in z. According to the direct similarity reduction method (El-Shiekh 2018a; He et al. 2021; Hua et al. 2019; Liu et al. 2019; Lü et al.2021; Moatimid et al. 2013; Moussa and El-Shiekh 2011, Moussa and El Shikh 2008, Moussa et al. 2012), the main target is to transform Eq. (2) into real nonlinear ordinary differential equation with constants coefficients in \(\varsigma\), therefore, by taking the dispersive term \(U^{\prime \prime }\) as a normalized coefficient . We get the following nonlinear system of partial differential equations

$$\begin{aligned} \frac{\alpha (z)}{2}\frac{\partial ^{2}\varsigma }{\partial t^{2}}= & {} \digamma _{1}(\varsigma )\frac{\alpha (z)}{2}(\frac{\partial \varsigma }{ \partial t})^{2}, \end{aligned}$$
(7)
$$\begin{aligned} (\phi (z,t)-\frac{\partial \eta }{\partial z}-\frac{\alpha (z)}{2}(\frac{ \partial \eta }{\partial t})^{2})= & {} \digamma _{2}(\varsigma )\frac{\alpha (z)}{2}(\frac{\partial \varsigma }{\partial t})^{2}, \end{aligned}$$
(8)
$$\begin{aligned} \gamma (z)= & {} \digamma _{3}(\varsigma )\frac{\alpha (z)}{2}(\frac{\partial \varsigma }{\partial t})^{2}, \end{aligned}$$
(9)

where \(\digamma _{1}(\varsigma ),\digamma _{2}(\varsigma )\) and \(\digamma _{3}(\varsigma )\) are three arbitrary real functions in \(\varsigma\) . By solving Eqs. (6)–(9) together using the direct reduction assumptions, we obtain

$$\begin{aligned} \varsigma= & {} k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) , \end{aligned}$$
(10)
$$\begin{aligned} \phi (z,t)= & {} \left( \frac{d}{dz}\left( \frac{\beta (z)}{2\alpha (z)}\right) +\frac{\beta ^{2}(z)}{2\alpha (z)}\right) t^{2}+\left( \frac{d}{dz} h_{1}(z)+\beta (z)h_{1}(z)\right) t \nonumber \\&+\frac{d}{dz}h_{2}(z)+\frac{\alpha (z)}{2}h_{1}^{2}\left( z\right) +\frac{ c_{2}k^{2}\alpha (z)}{2}e^{-2\int \beta (z)dz}, \end{aligned}$$
(11)
$$\begin{aligned} \gamma (z)= & {} \frac{c_{3}k^{2}\alpha (z)}{2}e^{-2\int \beta (z)dz}, \end{aligned}$$
(12)

where k is an integration constant and \(\digamma _{1}(\varsigma )=0,\digamma _{2}(\varsigma )=c_{2}\) and \(\digamma _{3}(\varsigma )=c_{3}\) with \(c_{2}\) and \(c_{3}\) as two arbitrary non-zero constants. Moreover, Eq. (4) transforms into the following nonlinear ordinary differential equation

$$\begin{aligned} U^{\prime \prime }+c_{2}U+c_{3}U^{3}=0. \end{aligned}$$
(13)

To solve Eq. (13) , integrate it firstly with respected to \(\varsigma\)

$$\begin{aligned} U^{^{\prime 2}}+c_{2}U^{2}+\frac{c_{3}}{2}U^{4}=c_{4} \end{aligned}$$
(14)

where \(c_{4}\) is an integration constant. Now, two cases arises for solutions of Eq. (14)

Case 1: If \(c_{2},c_{3}\) and \(c_{4}\) are nonzero constants, then Eq. (14) has many Jacobi elliptic wave solutions (El-Shiekh 2019), by using those solutions, many new Jacobi periodic wave solutions are obtained for the inhomogeneous nonlinear Schrödinger equation with variable coefficients as follows:

$$\begin{aligned} \Psi _{1}= & {} JacobiSN\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\left. \sqrt{-\frac{c_{3}}{2}}\right) e^{i(\frac{\beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \end{aligned}$$
(15)
$$\begin{aligned} \Psi _{2}= & {} JacobiCD\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{-\frac{c_{3}}{2}}\right) e^{i(\frac{\beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{2}= & {} \left( 1-\frac{c_{3}}{2}\right) {\text { for both }}\Psi _{1} {\text { and }}\Psi _{2}. \end{aligned}$$
(16)
$$\begin{aligned} \Psi _{3}= & {} JacobiCN\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{\frac{c_{3}}{2}}\right) e^{i(\frac{\beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{2}= & {} \left( 1-c_{3}\right) . \end{aligned}$$
(17)
$$\begin{aligned} \Psi _{4}= & {} JacobiDN\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{c_{2}+2}\right) e^{i(\frac{ \beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} 2. \end{aligned}$$
(18)
$$\begin{aligned} \Psi _{5}= & {} JacobiNS\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{c_{2}-1}\right) e^{i(\frac{ \beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}. \end{aligned}$$
(19)
$$\begin{aligned} \Psi _{6}= & {} JacobiDC\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{c_{2}-1}\right) e^{i(\frac{ \beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} -2{\text { for both }}\Psi _{5}{\text { and }}\Psi _{6}. \end{aligned}$$
(20)
$$\begin{aligned} \Psi _{7}= & {} JacobiNC\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{\frac{1}{2}(1-c_{2})} \right) e^{i(\frac{\beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} 1+c_{2}. \end{aligned}$$
(21)
$$\begin{aligned} \Psi _{8}= & {} JacobiND\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{2+c_{2}}\right) e^{i(\frac{ \beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} -2(1+c_{2}). \end{aligned}$$
(22)
$$\begin{aligned} \Psi _{9}= & {} JacobiSC\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{2+c_{2}}\right) e^{i(\frac{ \beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} 2(1+c_{2}). \end{aligned}$$
(23)
$$\begin{aligned} \Psi _{10}= & {} JacobiSD\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{\frac{1}{2}(1+c_{2})} \right) e^{i(\frac{\beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} \frac{1}{2}(1-c_{2}^{2}). \end{aligned}$$
(24)
$$\begin{aligned} \Psi _{11}= & {} JacobiCS\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{c_{2}+2}\right) e^{i(\frac{ \beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} -2,c_{2}\ge -2, \end{aligned}$$
(25)
$$\begin{aligned} \Psi _{12}= & {} JacobiDS\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) ,\right. \nonumber \\&\quad \left. \sqrt{\frac{1}{2}(1-c_{2})} \right) e^{i(\frac{\beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} -2. \end{aligned}$$
(26)
$$\begin{aligned} \Psi _{13}= & {} \left[ JacobiNS\left( \varsigma ,\sqrt{\frac{1}{2}(1+2c_{2})} \right) \pm JacobiCS\left( \varsigma ,\sqrt{\frac{1}{2}(1+2c_{2})}\right) \right] e^{i(\eta (z,t))}, \nonumber \\ {\text {where}} c_{3}= & {} -\frac{1}{2}, \end{aligned}$$
(27)
$$\begin{aligned} \Psi _{14}= & {} \left[ JacobiNC\left( \varsigma ,\sqrt{1+c_{3}}\right) \pm JacobiSC\left( \varsigma ,\sqrt{1+c_{3}}\right) \right] e^{i(\eta (z,t))},\nonumber \\ {\text {where }}c_{2}= & {} \frac{1}{2}(2+c_{3}), \end{aligned}$$
(28)
$$\begin{aligned} \Psi _{15}= & {} \left[ JacobiNS\left( \varsigma ,\sqrt{2(1+c_{2})}\right) \pm JacobiDS\left( \varsigma ,\sqrt{2(1+c_{2})}\right) \right] e^{i(\eta (z,t))}, \nonumber \\ {\text {where }}c_{3}= & {} -\frac{1}{2}, \end{aligned}$$
(29)

where the variables \(\eta\) and \(\varsigma\) given by Eqs. (5) and (10) respectively. The Jacobi elliptic wave solutions transformed to hyperbolic if the modulus of it becomes 1 and the following new solutions are given

$$\begin{aligned} \Psi _{16}= & {} \tanh \left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) \right) e^{i(\frac{\beta (z)}{ 2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text { where }}c_{2}= & {} 2,c_{3}=-2. \end{aligned}$$
(30)
$$\begin{aligned} \Psi _{17}= & {} sech\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) \right) e^{i(\frac{\beta (z)}{ 2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))},\nonumber \\ {\text {where }}c_{2}= & {} -1,c_{3}=2. \end{aligned}$$
(31)
$$\begin{aligned} \Psi _{18}= & {} \coth \left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) \right) e^{i(\frac{\beta (z)}{ 2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{2}= & {} 2,c_{3}=-2. \end{aligned}$$
(32)
$$\begin{aligned} \Psi _{19}= & {} csch\left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) \right) e^{i(\frac{\beta (z)}{ 2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{2}= & {} -1,c_{3}=-2. \end{aligned}$$
(33)
$$\begin{aligned} \Psi _{20}= & {} \left[ \coth \left( \varsigma \right) \pm csch\left( \varsigma \right) \right] e^{i(\eta (z,t))},{\text { where }}c_{2}=\frac{1}{2},c_{3}=- \frac{1}{2}, \end{aligned}$$
(34)

where the variables \(\eta\) and \(\varsigma\) given by Eqs. (5) and (10) respectively. If the modulus of the Jacobi functions on solutions (15–29) approch zero, the following new periodic wave solutions obtained

$$\begin{aligned} \Psi _{21}= & {} \csc \left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) \right) e^{i(\frac{\beta (z)}{ 2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} -2,c_{2}=1. \end{aligned}$$
(35)
$$\begin{aligned} \Psi _{22}= & {} \sec \left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) \right) e^{i(\frac{\beta (z)}{ 2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} -2,c_{2}=1. \end{aligned}$$
(36)
$$\begin{aligned} \Psi _{23}= & {} \tan \left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) \right) e^{i(\frac{\beta (z)}{ 2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ \text {where }c_{3}= & {} -2,c_{2}=-2. \end{aligned}$$
(37)
$$\begin{aligned} \Psi _{24}= & {} \cot \left( k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) \right) e^{i(\frac{\beta (z)}{ 2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}, \nonumber \\ {\text {where }}c_{3}= & {} -2,c_{2}=-2. \end{aligned}$$
(38)
$$\begin{aligned} \Psi _{20}= & {} \left[ \cot \left( \varsigma \right) \pm csc\left( \varsigma \right) \right] e^{i(\eta (z,t))},c_{2}=-\frac{1}{2},c_{3}=-\frac{1}{ 2}, \end{aligned}$$
(39)
$$\begin{aligned} \Psi _{21}= & {} \left[ \tan \left( \varsigma \right) \pm \sec \left( \varsigma \right) \right] e^{i(\eta (z,t))},c_{2}=-\frac{1}{2},c_{3}=-\frac{1}{ 2}, \end{aligned}$$
(40)

where the variables \(\eta\) and \(\varsigma\) given by Eqs. (5) and (10) respectively.

Case 2: If \(c_{2}=0\) and \(c_{4}=0\) but \(c_{3}\ne 0\), then Eq. (14) has the following rational solution

$$\begin{aligned} U\left( \varsigma \right) =\frac{\sqrt{\frac{-2}{c_{3}}}}{\varsigma }. \end{aligned}$$
(41)

By back substitution from (41) into (2) using Eqs. (5) and (10–12) we get the rational solution

$$\begin{aligned} \Psi _{22}=\frac{\sqrt{\frac{-2}{c_{3}}}}{k\left( e^{-\int \beta (z)dz}t-\int \alpha (z)h_{1}(z)e^{-\int \beta (z)dz}dz\right) }e^{i(\frac{ \beta (z)}{2\alpha (z)}t^{2}+h_{1}(z)t+h_{2}(z))}. \end{aligned}$$
(42)

3 Application in nonlinear optics

Yan (2010) defind ”the Rogon waves” as Rough waves if they reappear virtually unaffected in size or shape shortly after interactions therefore, we can say those waves appear in optics as optical rogon waves. In the following we are going to show the dynamical behavior of the intensity \(\left| \Psi \right| ^{2},\) by fixing the parameters \(h_{1}\left( z\right) =\frac{1}{z},\alpha \left( z\right) =z\), and \(k=\frac{1}{2}.\)

Fig. 1
figure 1

Gives the periodic rogon wave intensity \(\left| \Psi _{1}\right| ^{2}\)for two different values of the gain term \(\beta (z)\) as, tan(z) and \(\frac{-1}{z}\)respectively, where \(c_{3}\)is fixed as \(c_{3}=-0.5\)

Full size image
Fig. 2
figure 2

Shows the kink type rogon wave solution \(\left| \Psi _{16}\right| ^{2}\) for two different values of the gain term \(\beta (z)\) as, tan(z) and \(\frac{-1}{z}\)respectively

Full size image
Fig. 3
figure 3

Represents the rogon wave soliton solution \(\left| \Psi _{17}\right| ^{2}\) corresponding to the two different values of the gain term \(\beta (z)\) as, tan(z) and \(\frac{-1}{z}\)respectively

Full size image

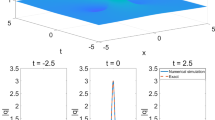
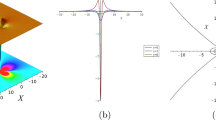
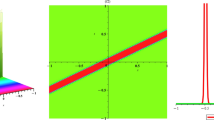
We can see that in Figs. 1, 2 and 3, two fixed values for the gain/loss term \(\beta (z)\) are given as tan(z) and \(\frac{-1}{z}\) chosen as positive and negative functions for the gain (+) and the loss (−) sign respectively. In Fig. 1, the rogon wave intensity propagation \(\left| \Psi _{1}\right| ^{2}\)effected with periodic jacobi sn wave and we could see it like a snake in figure (b). Moreover, in Fig. 2, the propagation of \(\left| \Psi _{16}\right| ^{2}\) was like a dark rogon wave in both figures (c) and (d) especially, in figure (d) it was so sharp and high. Finally, in Fig. 3, intensity propagation behavior \(\left| \Psi _{17}\right| ^{2}\) was as a bright rogon wave in both (e) and (f).

4 Conclusion

In this paper, the nonautonomous variable coefficients Schrödinger equation is reduced to nonlinear Riccati equation by using direct similarity reduction method. The Riccati equation has two cases for solution, the first case gives new Jacobi, hyperbolic, and periodic wave solutions. In other case, only rational solutions is obtained. From the obtained solutions we have the following concluding remarks:

  1. 1.

    The Direct similarity reduction method is an easy methodology for transforming nonlinear partial differential equations with variable coefficients to nonlinear ordinary differential equation with constant coefficients.

  2. 2.

    The obtained solutions cover other solutions obtained before in litrature (Serkin et al. 2007) additionaly, other new solutions were obtained.

  3. 3.

    Abundant novel exact travelling wave solutions including periodic Jacobi elliptic waves, solitons, kink, periodic and rational solutions have been found. These solutions might play important role in engineering and physics fields.

  4. 4.

    The obtained first Jacobi elliptic wave solution \(\left| \Psi _{1}\right| ^{2}\) was plotted in Fig. 1 and its limit solution when \(\hbox {m}-{>}1\), corresponding to kink wave solution \(\left| \Psi _{16}\right| ^{2}\) in Fig. 2 so we have shown that the Rogon wave shape was different in both figures. Moreover, for the soliton type orgon waves we take \(\left| \Psi _{17}\right| ^{2}\) and plot it in Fig. 3, finally we can see in all figures how the type of solution could affect the shape of the rogon wave propagation.