1 Introduction

Nonlinear integrable equations are often used to describe problems in the fields of mechanics, fluid mechanics, plasma, fiber optic communication and Bose–Einstein condensation [1,2,3,4,5]. Finding exact solutions of nonlinear integrable equations has become an important research topic [6,7,8,9,10,11,12,13], and a series of special methods have been proposed, such as inverse scattering method [14], Darboux transformation method [15], truncated Painlevé expansion method [16], Hirota’s bilinear method [17], \((G'/G)\)-expansion method [18], multi-exponential function method [19] and so on.

In recent years, lump-type solutions and lump–stripe mixed solutions have attracted many scholars’ attention. They can reveal very interesting dynamical properties [20,21,22,23,24,25,26,27,28,29,30,31,32]. The lump solution, also known as the rational solution, is an elastic collision in which the shape, amplitude and velocity remain unchanged after collision with the soliton solution. The mixed solution of lump–stripe mainly considers the interaction between lump solution and other soliton solutions. The research in this field is mainly based on Hirota’s bilinear method and symbolic computation. Many nonlinear integrable equations have lump formal solutions and lump–stripe mixed solutions. Some important results have been established. Gilson and Nimmo discussed the lump solution and properties of the B-type Kadomtsev–Petviashvili (KP) equation [33]. Li [34] and his collaborators considered the interaction between lump solution and \(\cosh \) function. Sun et al. [35] considered the interaction between lump solutions and exponential functions. Ma et al. [36] further considered the interaction between the lump solution and the trigonometric function and the bi-exponential function, which have more abundant dynamical properties and structures. With the development of lump formal solutions and lump–stripe mixed solutions, the dynamical properties of the solutions are discussed, which will help us to understand the physical background behind the nonlinear integrable equations.

The KP equation was first proposed in 1970 by Soviet physicists Kadomtsev and Petviashvili [37], which has been used to describe water waves of long wavelength with weakly nonlinear restoring forces and frequency dispersion, and waves in ferromagnetic media, as well as two-dimensional matter-wave pulses in Bose–Einstein condensates. The KP model has the wave dispersion changing significantly the nonlinear dynamics [38]. Nonlinear stability with infinite space and periodic boundary conditions and dynamics of solitary waves of KP-type equation have been discussed in many literatures [39,40,41].

In this paper, a (\(3+1\))-dimensional generalized KP equation with variable coefficients is presented as follows [42]:

$$\begin{aligned}&\vartheta _3(t) [\vartheta _5(t) u_y+u_{yt}]+u_x [3 \vartheta _2(t) u_{xy}+\vartheta _5(t)]\nonumber \\&\quad +3 \vartheta _2(t) u_y u_{xx} {+}\vartheta _1(t) u_{xxxy}{+}u_{xt}{-}\vartheta _4(t) u_{zz}=0,\nonumber \\ \end{aligned}$$
(1)

where \(u=u(x,y,z,t)\) is the wave amplitude function, which describes the long water waves and small-amplitude surface waves with weak nonlinearity, weak dispersion and weak perturbation in fluid mechanics. \(\vartheta _i(t)(i=1,2,3,4,5)\) are arbitrary differentiable functions. \(\vartheta _1(t)\) and \(\vartheta _2(t)\) represent the dispersion and nonlinearity, respectively. \(\vartheta _3(t)\) and \(\vartheta _5(t)\) are the functions representing the perturbed effects. \(\vartheta _4(t)\) represents the disturbed wave velocities along the z direction, and the subscripts represent the corresponding derivatives. When \(\vartheta _1=\vartheta _2=\vartheta _3=\vartheta _4=1\) and \(\vartheta _5=0\), Eq. (1) becomes the (\(3+1\))-dimensional generalized KP equation [43]. For Eq. (1), Wronskian and Grammian solutions were obtained with a constraint condition on the variable coefficients [44]. A couple of solutions have been studied by the extended transformed rational function method [45]. Pfaffian solutions were presented by the Pfaffianization procedure of Ohta and Hirota [42].

For the KP-type equations with constant coefficients, rational solutions and lump-type solutions have been obtained in many research works. However, as far as we know, rational solutions and lump-type solutions to the KP equation with the variable coefficients have not been found yet, which will become the primary work of our paper. Section 2 inquires the rational solutions and lump solutions by the Hirota’s bilinear form and a direct assumption with arbitrary functions; Sect. 3 describes the spatial structures of the lump waves in figures by choosing some suitable parameters; Sect. 4 gives the conclusion.

2 Rational solutions and lump solutions for Eq. (1)

Through the transformation \(u=\frac{2\,\vartheta _1(t)}{\vartheta _2(t)}\,[ln\xi (x,y,z,t)]_x\) and the constraint \(\vartheta _1(t)=\vartheta _0 \vartheta _2(t) e^{-\int \vartheta _5(t) \, \hbox {d}t}\), Hirota’s bilinear form of Eq. (1) can be presented as

$$\begin{aligned}&[D_t D_x+\vartheta _1(t) D_x^3 D_y+\vartheta _3(t) D_t\,D_y \nonumber \\&\quad -\vartheta _4(t) D_z^2] \xi \cdot \xi =0. \end{aligned}$$
(2)

This is equivalent to:

$$\begin{aligned}&-\xi _t \xi _x+\vartheta _4(t) \xi _z^2-\vartheta _3(t) \xi _t \xi _y+3 \vartheta _1(t) \xi _{xy} \xi _{xx}\nonumber \\&\quad -3 \vartheta _1(t) \xi _x \xi _{xxy}-\vartheta _1(t) \xi _y \xi _{xxx} +\xi [\xi _{xt} \nonumber \\&\quad -\vartheta _4(t) \xi _{zz}+\vartheta _3(t) \xi _{yt}+\vartheta _1(t) \xi _{xxxy}]=0. \end{aligned}$$
(3)

Considering the rational solutions and lump solutions for Eq. (1), we make the following assumption

$$\begin{aligned} \zeta= & {} x \alpha _1+y \alpha _2+z \alpha _3+\alpha _4(t),\nonumber \\ \varsigma= & {} x \alpha _5+y \alpha _6+z \alpha _7+\alpha _8(t),\nonumber \\ \xi= & {} \zeta ^2+\varsigma ^2+\alpha _9(t), \end{aligned}$$
(4)

where \(\alpha _1\), \(\alpha _2\), \(\alpha _3\), \(\alpha _5\), \(\alpha _6\) and \(\alpha _7\) are undefined constants. \(\alpha _4(t)\), \(\alpha _8(t)\), \(\alpha _9(t)\) are unknown differentiable function. Compared with those methods in Refs. [25,26,27,28,29,30,31,32], our assumption can be used for solving variable-coefficient nonlinear integrable equation. Substituting Eq. (4) into Eq. (3) with the Mathematica software, we have following results

$$\begin{aligned} (I): \alpha _2= & {} \alpha _6=0, \alpha _8(t)= \eta _1\nonumber \\&+\,\int _1^t \frac{\alpha _3^2 \alpha _1^2 \vartheta _4(t)+\alpha _3^2 \alpha _5^2 \vartheta _4(t)-\alpha _1^3 \alpha _4'(t)}{\alpha _1^2 \alpha _5} \, \hbox {d}t,\nonumber \\ \alpha _7= & {} \frac{\alpha _3 \alpha _5}{\alpha _1}, \alpha _9(t)=\eta _2\nonumber \\&+\,\int _1^t 2 [-\alpha _3^2 \alpha _1 \eta _1 \vartheta _4(t)+\alpha _1^2 \eta _1 \alpha _4'(t)\nonumber \\&+\,[\alpha _1^2 \alpha _4'(t)-\alpha _3^2 \alpha _1 \vartheta _4(t)]\nonumber \\&\times \, \int _1^t \frac{\alpha _3^2 \alpha _1^2 \vartheta _4(t)+\alpha _3^2 \alpha _5^2 \vartheta _4(t)-\alpha _1^3 \alpha _4'(t)}{\alpha _1^2 \alpha _5} \, \hbox {d}t\nonumber \\&+\,\alpha _3^2 \alpha _5 \alpha _4(t) \vartheta _4(t)-\alpha _5 \alpha _1 \alpha _4(t) \alpha _4'(t)]/(\alpha _1 \alpha _5) \, \hbox {d}t\nonumber \\ \end{aligned}$$
(5)

where \(\alpha _1 \alpha _5\ne 0\), \(\eta _1\) and \(\eta _2\) are integral constants. Substituting Eqs. (4), (5) and the constraint \(\vartheta _1(t)=\vartheta _0 \vartheta _2(t) e^{-\int \vartheta _5(t) \, \hbox {d}t}\) into the transformation \(u=\frac{2\,\vartheta _1(t)}{\vartheta _2(t)}\,[ln\xi (x,y,z,t)]_x\), the rational solutions for Eq. (1) can be expressed as follows:

$$\begin{aligned} u^{(I)}= & {} \left[ 2 \vartheta _0 e^{-\int \vartheta _5(t) \, \hbox {d}t}\right. \nonumber \\&\left. \left[ 2 \alpha _5 \left[ \eta _1 +\int _1^t \frac{\frac{\alpha _3^2 \left( \alpha _1^2+\alpha _5^2\right) \vartheta _4(t)}{\alpha _1^2}-\alpha _1 \alpha _4'(t)}{\alpha _5} \, \hbox {d}t \right. \right. \right. \nonumber \\&\left. \left. \left. +\alpha _5 \left( x+\frac{\alpha _3 z}{\alpha _1}\right) \right] +2 \alpha _1 \left( \alpha _4(t)+\alpha _1 x+\alpha _3 z\right) \right] \right] x\nonumber \\&/[\eta _2+\int _1^t \left[ 2 \left( \alpha _1 \alpha _4'(t)-\alpha _3^2 \vartheta _4(t)\right) \left[ \alpha _1 \left[ \eta _1 \right. \right. \right. \nonumber \\&\left. +\,\int _1^t \frac{\frac{\alpha _3^2 \left( \alpha _1^2+\alpha _5^2\right) \vartheta _4(t)}{\alpha _1^2}-\alpha _1 \alpha _4'(t)}{\alpha _5} \, \hbox {d}t\right] \nonumber \\&\left. \left. -\,\alpha _5 \alpha _4(t)\right] \right] /(\alpha _1 \alpha _5) \, \hbox {d}t+\left[ \eta _1\right. \nonumber \\&+\,\int _1^t \frac{\frac{\alpha _3^2 \left( \alpha _1^2+\alpha _5^2\right) \vartheta _4(t)}{\alpha _1^2}-\alpha _1 \alpha _4'(t)}{\alpha _5} \, \hbox {d}t\nonumber \\&\left. \left. +\,\alpha _5 \left( x+\frac{\alpha _3 z}{\alpha _1}\right) \right] {}^2+\left( \alpha _4(t)+\alpha _1 x+\alpha _3 z\right) {}^2\right] , \end{aligned}$$
(6)

where \(\vartheta _0\) is an arbitrary nonzero constant. In addition to the constraint (I), other parameters are arbitrary.

Fig. 1
figure 1

Rational solution \(u^{(I)}\) when \(z= -5\)a three-dimensional graph, b contour graph

Full size image

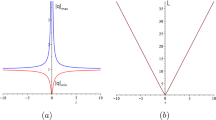
To describe the resulting rational solutions in Eq. (6), we select the two particular values for the parameters:

$$\begin{aligned}&\alpha _4(t)=\sin t,\quad \vartheta _3(t)=1,\quad \vartheta _4(t)=t,\quad \vartheta _5(t)=0,\nonumber \\&\quad \alpha _1=1, \alpha _3=2,\quad \alpha _5=-3,\quad \eta _1=\eta _2=\vartheta _0=1,\nonumber \\ \end{aligned}$$
(7)

and

$$\begin{aligned}&\alpha _4(t)=\sin t,\quad \vartheta _3(t)=1,\quad \vartheta _4(t)=t,\nonumber \\ \quad&\vartheta _5(t)=0,\quad \alpha _1=-5,\nonumber \\&\alpha _3=2,\quad \alpha _5=3,\quad \eta _1=\eta _2=\vartheta _0=1. \end{aligned}$$
(8)

Substituting Eq. (7) and Eq. (8) into solution \(u^{(I)}\), three-dimensional graphs and contour graphs at \(z=-5\) and \(x=-5\) are shown in Figs. 1 and 2, respectively.

Fig. 2
figure 2

Rational solution \(u^{(I)}\) when \(x= -5\)a three-dimensional graph, b contour graph

Full size image
Fig. 3
figure 3

Spatial structure of the bright–dark lump solution \(u^{(II)}\) when \(z= 0\)a three-dimensional graph, b contour plot

Full size image
Fig. 4
figure 4

Spatial structure of the bright–dark lump solution \(u^{(II)}\) when \(x= 0\)a three-dimensional graph, b contour plot

Full size image

Next, we will present the lump solutions for Eq. (1) and discuss their spatial structures as follows

$$\begin{aligned} (II): \vartheta _4(t)= & {} [3 (\alpha _1^2+\alpha _5^2) \left( \alpha _1 \alpha _2+\alpha _5 \alpha _6\right) \vartheta _1(t)\nonumber \\&\quad \left[ \alpha _1^2+\alpha _5^2+\left( \alpha _2^2+\alpha _6^2\right) \vartheta _3(t){}^2\right. \nonumber \\&\left. \left. +\,2 \left( \alpha _1 \alpha _2+\alpha _5 \alpha _6\right) \vartheta _3(t)\right] \right] \nonumber \\&/\left[ \alpha _9 [\alpha _7 \left( \alpha _1+\alpha _2 \vartheta _3(t)\right) -\alpha _3 [\alpha _5\right. \nonumber \\&+\,\alpha _6 \vartheta _3(t)]]{}^2], \alpha _9(t)=\alpha _9,\nonumber \\ \alpha _4(t)= & {} \eta _3+\int _1^t [3 \left( \alpha _1^2+\alpha _5^2\right) \left( \alpha _1 \alpha _2+\alpha _5 \alpha _6\right) \nonumber \\&\vartheta _1(t) \left[ 2 \alpha _3 \alpha _5 \alpha _7\right. \nonumber \\&+\,\alpha _1 \left( \alpha _3^2-\alpha _7^2\right) +\left[ 2 \alpha _3 \alpha _6 \alpha _7\right. \nonumber \\&\left. \left. \left. +\,\alpha _2 \left( \alpha _3^2-\alpha _7^2\right) \right] \vartheta _3(t)\right] \right] \nonumber \\&/[\alpha _9 \left[ \alpha _7 \left( \alpha _1+\alpha _2 \vartheta _3(t)\right) \right. \nonumber \\&-\,\alpha _3 \left( \alpha _5+\alpha _6 \vartheta _3(t)\right) ]{}^2] \, \hbox {d}t,\nonumber \\ \alpha _8(t)= & {} \eta _4+\int _1^t [3 \left( \alpha _1^2+\alpha _5^2\right) \left( \alpha _1 \alpha _2+\alpha _5 \alpha _6\right) \nonumber \\&\vartheta _1(t) [\alpha _3^2 [-[\alpha _5\nonumber \\&+\,\alpha _6 \vartheta _3(t)]]+2 \alpha _7 \alpha _3 \left( \alpha _1+\alpha _2 \vartheta _3(t)\right) \nonumber \\&+\,\alpha _7^2 \left( \alpha _5+\alpha _6 \vartheta _3(t)\right) ]]\nonumber \\&/[\alpha _9 [\alpha _7 \left( \alpha _1+\alpha _2 \vartheta _3(t)\right) \nonumber \\&-\,\alpha _3 \left( \alpha _5+\alpha _6 \vartheta _3(t)\right) ]{}^2] \, \hbox {d}t \end{aligned}$$
(9)

where \(\alpha _9 [\alpha _7 \left( \alpha _1+\alpha _2 \vartheta _3(t)\right) -\alpha _3 \left( \alpha _5+\alpha _6 \vartheta _3(t)\right) ]\ne 0\), \(\eta _3\) and \(\eta _4\) are integral constants. Substituting Eq. (4), Eq. (7) and the constraint \(\vartheta _1(t)=\vartheta _0 \vartheta _2(t) e^{-\int \vartheta _5(t) \, \hbox {d}t}\) into the transformation \(u=\frac{2\,\vartheta _1(t)}{\vartheta _2(t)}\,[ln\xi (x,y,z,t)]_x\), the lump solutions for Eq. (1) can be expressed as follows:

$$\begin{aligned} u^{(II)}= & {} \left[ 2 \vartheta _0 e^{-\int \vartheta _5(t) \, \hbox {d}t} [2 \alpha _1 (\alpha _4(t)+\alpha _1 x \right. \nonumber \\&\left. +\,\alpha _2 y+\alpha _3 z)+2 \alpha _5 (\alpha _8(t)+\alpha _5 x \right. \nonumber \\&\left. +\,\alpha _6 y+\alpha _7 z)]]/[\alpha _9+(\alpha _4(t)+\alpha _1 x \right. \nonumber \\&\left. +\,\alpha _2 y+\alpha _3 z){}^2 \right. \nonumber \\&\left. +\,\left( \alpha _8(t)+\alpha _5 x+\alpha _6 y+\alpha _7 z\right) {}^2\right] , \end{aligned}$$
(10)

where \(\vartheta _0\) is an arbitrary nonzero constant. In addition to the constraint (II), other parameters are arbitrary.

Fig. 5
figure 5

Spatial structure of the bright lump solution \(u^{(II)}\) when \(y= -5\) (a, d), \(y= 0\) (b, e) and \(y = 5\) (c, f)

Full size image
Fig. 6
figure 6

Periodic structure of the lump solution \(u^{(II)}\) when \(x= -5\) (a, d), \(x= 0\) (b, e) and \(x = 5\) (c, f)

Full size image

3 Spatial structures of lump solutions in Eq. (10)

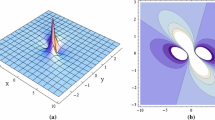
To demonstrate the spatial structures of lump solutions in Eq. (10), we select the three particular values for the parameters:

$$\begin{aligned} \vartheta _2(t)= & {} t,\quad \vartheta _3(t)=1,\quad \vartheta _5(t)=t=0,\quad \alpha _2=\alpha _9=2, \nonumber \\ \alpha _1= & {} \alpha _3=\alpha _6=\alpha _7=\eta _3=\eta _4=\vartheta _0=1,\quad \alpha _5=-3, \end{aligned}$$
(11)
$$\begin{aligned} \vartheta _2(t)= & {} t, \quad \vartheta _3(t)=1,\quad \vartheta _5(t)=x=0,\quad \alpha _2=\alpha _9=2, \nonumber \\ \alpha _1= & {} \alpha _3=\alpha _6=\alpha _7=\eta _3=\eta _4=\vartheta _0=1,\quad \alpha _5=-3, \end{aligned}$$
(12)

and

$$\begin{aligned}&\vartheta _2(t)=\sin t,\quad \vartheta _3(t)=1,\quad \vartheta _5(t)=y=0,\nonumber \\&\quad \alpha _2=\alpha _9=2, \alpha _1=\alpha _3=\alpha _6=\alpha _7=\eta _3\nonumber \\&\quad =\eta _4=\vartheta _0=1, \alpha _5=-3. \end{aligned}$$
(13)

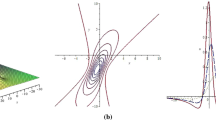
Substituting Eq. (11) into solution \(u^{(II)}\), three-dimensional graphs and contour plots at \(z=0\) and \(x=0\) are shown in Figs. 3 and 4, respectively. Substituting Eq. (12) and Eq. (13) into solution \(u^{(II)}\), three-dimensional graphs and contour plots at \(y=-5; 0; 5\) and \(x=-5; 0; 5\) are presented in Figs. 5 and 6, respectively.

Figures 3 and 4 demonstrate the spatial structure of the bright–dark lump solution because the height of the peak is competent for the depth of the valley bottom, which contains one peak and one valley. Their peak and valley are meristic. Figure 5 shows the spatial structure of the bright lump solution, which contains one peak and two valleys. Figure 6 shows the periodic structure of the lump solution.

4 Conclusion

In this work, by applying Hirota’s bilinear form and a direct assumption with arbitrary functions, we have obtained rational solutions and lump solutions to the (\(3+1\))-dimensional generalized KP equation with variable coefficients. Spatial structures of the bright lump solution and the bright–dark lump solution are shown by some three-dimensional graphs and contour plots.