Bäcklund transformation, Pfaffian, Wronskian and Grammian solutions to the $(3+1)$-dimensional generalized Kadomtsev–Petviashvili equation

Abstract

With the Hirota bilinear method and symbolic computation, we investigate the $(3+1)$-dimensional generalized Kadomtsev–Petviashvili equation. Based on its bilinear form, the bilinear Bäcklund transformation is constructed, which consists of four equations and five free parameters. The Pfaffian, Wronskian and Grammian form solutions are derived by using the properties of determinant. As an example, the one-, two- and three-soliton solutions are constructed in the context of the Pfaffian, Wronskian and Grammian forms. Moreover, the triangle function solutions are given based on the Pfaffian form solution. A few particular solutions are plotted by choosing the appropriate parameters.

1 Introduction

With the development of nonlinear science, nonlinear evolution equations (NLEEs) have become the frontier and hot topics of research, which are more and more closely connected with other disciplines [1,2,3,4]. In the history of the natural science, there are always unexpected surprises in interdisciplinary fields [5,6,7,8,9]. In physics, chemical reaction, microelectronics, biology and other fields, NLEEs are used to describe dynamic models [5,6,7, 10]. The study of NLEEs is helpful to solve many significant natural science and engineering technology problems [9].

It is very important to find the exact solutions to NLEEs. The Hirota method is a useful and direct method to construct the N-soliton solutions and Bäcklund transformation (BT) [2, 3, 5,6,7, 9] to NLEEs. NLEEs are firstly written in the Hirota bilinear form, and the perturbation method is then used to solve the bilinear equation for the exact solutions [3]. Recently, more and more types of solutions to NLEEs have been found [11,12,13,14]. In addition to soliton solutions, there are also lump solutions and interaction solutions, which can describe more different nonlinear phenomena [15, 16]. Based on the Hirota bilinear form, the lump solutions [17] and interaction solutions [18] can be directly obtained with symbolic computation.

If the N-soliton solutions are expressed as a Wronskian or Grammian determinant, then the soliton equation can be transformed into a determinant identity, which is a special case of Pfaffian identity, and the soliton equation can be cast into the simple Maya chart [3]. Some soliton equations have no determinant solution (here we refer to determinant solution as Wronskian or Grammian determinant solution), but have Pfaffian solution [1, 19]. For example, Kadomtsev–Petviashvili (KP) equation has the determinant solution of Wronskian and Grammian structure, while B-type Kadomtsev–Petviashvili (BKP) equation has the Pfaffian solution without the determinant solution [20].

In the process of constructing Wronskian and Grammian formulations, the Plücker relation and Jacobi identity for determinants are extremely critical [2, 3]. First of all, let us consider the product of the second-order determinant before introducing the Plücker relation

$$\begin{aligned} \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{0}&{}a_{1}\\ b_{0}&{}b_{1}\\ \end{array}\right| \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{2}&{}a_{3}\\ b_{2}&{}b_{3}\\ \end{array}\right| -\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{0}&{}a_{2}\\ b_{0}&{}b_{2}\\ \end{array}\right| \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{1}&{}a_{3}\\ b_{1}&{}b_{3}\\ \end{array}\right| +\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{0}&{}a_{3}\\ b_{0}&{}b_{3}\\ \end{array}\right| \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{1}&{}a_{2}\\ b_{1}&{}b_{2}\\ \end{array}\right| =0, \end{aligned}$$

where $a_{i}$ and $b_{i}$ ($i=0,1,2,3$) are arbitrary parameters. If each determinant is represented by its column vector in $c_{i}=(a_{i},b_{i})^T$, then we have

$$\begin{aligned} |c_{0}\;c_{1}|\;|c_{2}\;c_{3}|-|c_{2}\;c_{3}|\;|c_{1}\;c_{3}|+|c_{0}\;c_{3}|\;|c_{1}\;c_{2}|=0, \end{aligned}$$

(1)

which is the simplest case of the Plücker relation. It can be generalized to the general situation

$$\begin{aligned}&|f_{1}\;f_{2}\cdots f_{N}\;d_{0}\;d_{1}|\;|f_{1}\;f_{2}\cdots f_{N}\;d_{2}\;d_{3}|-|f_{1}\;f_{2}\cdots f_{N}\;d_{0}\;d_{2}|\;|f_{1}\;f_{2}\cdots f_{N}\;d_{1}\;d_{3}|\nonumber \\&\quad +|f_{1}\;f_{2}\cdots f_{N}\;d_{0}\;d_{3}|\;|f_{1}\;f_{2}\cdots f_{N}\;d_{1}\;d_{2}|=0, \end{aligned}$$

(2)

where $f_{i}$ ($i=1,2,\cdots ,N$) and $d_{j}$ ($j=0,1,2,3$) are N-dimensional column vectors. When the solutions to the soliton equations are expressed in Wronskian determinant, the bilinear equations are finally reduced to this identity. Secondly, we introduce the Jacobi identity for determinants

$$\begin{aligned} D\left[ \begin{array}{cccc} i\\ i\\ \end{array}\right] D\left[ \begin{array}{cccc} j\\ j\\ \end{array}\right] -D\left[ \begin{array}{cccc} i\\ j\\ \end{array}\right] D\left[ \begin{array}{cccc} j\\ i\\ \end{array}\right] =D\left[ \begin{array}{cccc} i&{}j\\ i&{}j\\ \end{array}\right] D, \end{aligned}$$

(3)

where $D\left[ \begin{array}{cccc} i&{}j\\ m&{}n\\ \end{array}\right]$ represents the $(n-2)$-order determinant obtained by removing row i, j and column m, n of n-order determinant D. When the solutions to the soliton equations are expressed in Grammian determinant, the bilinear equations are finally reduced to the Jacobi identity [3].

In this paper, we will study a $(3+1)$-dimensional generalized Kadomtsev–Petviashvili equation, which reads

$$\begin{aligned} u_{xxxy}+3u_{xx}u_{y}+3u_{x}u_{xy}+c_{1}u_{yt}+c_{2}u_{xz}=0, \end{aligned}$$

(4)

where $c_{i}\ne 0\,(i=1,2)$ are arbitrary real parameters and u is an analytic function of the variables x, y, z and t. As long as two arbitrary parameters in the equation are assigned, the equation can be rewritten into different equations and applied in different fields [1, 19, 27].

When $c_{1}=2$ and $c_{2}=-3$, Eq. (4) reduces to the $(3+1)$-dimensional Jimbo-Miwa equation [1]

$$\begin{aligned} u_{xxxy}+3u_{xx}u_{y}+3u_{x}u_{xy}+2u_{yt}-3u_{xz}=0, \end{aligned}$$

(5)

which is the second equation in the KP integrable hierarchies and often used to describe the propagation of three-dimensional nonlinear waves in physics. It is similar to KP equation with Wronskian solutions and Grammian solutions [3]. The $(3+1)$-dimensional Jimbo-Miwa equation has been studied by many methods, such as multiple exponential function method [21], Hirota bilinear method [1, 18, 22] and Bell polynomial method [2]. For example, BTs, Lax system, conservation laws and multi-soliton solutions to Jimbo-Miwa equation have been studied with Bell-polynomials [2].

When $c_{1}=-1$ and $c_{2}=-1$, Eq. (4) reduces to the $(3+1)$-dimensional generalized shallow water equation [19]

$$\begin{aligned} u_{xxxy}+3u_{xx}u_{y}+3u_{x}u_{xy}-u_{yt}-u_{xz}=0. \end{aligned}$$

(6)

Shallow water wave is a wave whose wavelength is more than ten times larger than that of deep water. The shallow water wave equation is often used to model the flow of fluids in the ocean and atmosphere [23,24,25]. This systematic model can predict the areas ultimately affected by pollution, coastal erosion and polar ice cap melting [26]. In Ref. [19], Grammian solutions, Wronski-type and Gramm-type solutions are given with the Hirota bilinear of Eq. (6).

When $c_{1}=-1$ and $c_{2}=-3$, Eq. (4) reduces to the $(3+1)$-dimensional nonlinear KP type equation [27]

$$\begin{aligned} u_{xxxy}+3u_{xx}u_{y}+3u_{x}u_{xy}-u_{yt}-3u_{xz}=0. \end{aligned}$$

(7)

The linear superposition principle is given, and a method to construct the Hirota bilinear equation with N-wave solutions is proposed [27]. Taking the nonlinear KP type Eq. (7) as an example, the feasibility of this method is fully illustrated.

In addition, Wronskian and Grammian solutions to another $(3+1)$-dimensional generalized KP equation are given [28], and the Pfaffianized systems for another KP equation is constructed [29], including Wronski-type Pfaffian and Gramm-type Pfaffian solutions. Moreover, the bilinear BT for another KP equation has been constructed [30], which consists of six bilinear equations and includes nine arbitrary parameters.

Under the Cole-Hopf transformation

$$\begin{aligned} u=2(\mathrm {ln}f)_{x}, \end{aligned}$$

(8)

the bilinear form of Eq. (4) is written as

$$\begin{aligned}&(D^{3}_{x}D_{y}+c_{1}D_{y}D_{t}+c_{2}D_{x}D_{z})f\cdot f \nonumber \\&\quad =(f_{xxxy}+c_{1}f_{yt}+c_{2}f_{xz})f-3f_{xxy}f_{x}+3f_{xy}f_{xx}\nonumber \\&\qquad -f_{y}f_{xxx}-c_{1}f_{y}f_{t}-c_{2}f_{x}f_{z}=0, \end{aligned}$$

(9)

where $D^{3}_{x}D_{y}$, $D_{y}D_{t}$ and $D_{x}D_{z}$ are the Hirota bilinear operators [3] defined by

$$\begin{aligned}&D_{x}^{\alpha }D_{y}^{\beta }D_{z}^{\delta }D_{t}^{\gamma }(f\cdot g)\\&\quad =\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^{\alpha }\left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\right) ^{\beta }\left( \frac{\partial }{\partial z}-\frac{\partial }{\partial z'}\right) ^{\delta }\left( \frac{\partial }{\partial t} -\frac{\partial }{\partial t'}\right) ^{\gamma }\\&\qquad \times f(x,y,z,t)g(x',y',z',t')\Big |_{x'=x,y'=y,z'=z,t'=t}. \end{aligned}$$

In this paper, we will construct a bilinear BT for Eq. (9) and give the Pfaffian, Wronskian and Grammian form solutions. In Sect. 2, by using the exchange formula, a bilinear BT will be constructed, which is composed of four equations and includes five arbitrary parameters. Based on the BT, the specific traveling wave solutions will be obtained. In Sect. 3, we will use Pfaffian technology to construct the N-soliton solutions, and prove that the bilinear equation is equivalent to Pfaffian identity. In Sect. 4, the Wronskian type N-soliton solutions will be derived, and it will be proved that bilinear Eq. (9) is equivalent to the Plücker relation. In Sect. 5, the Grammian type N-soliton solutions will be obtained, and it will be proved that the bilinear equation is equivalent to the Jacobi identity. Moreover, some specific solutions in each form will be plotted and analyzed.

2 Bilinear BT and exponential wave solutions

2.1 Bilinear BT

If one solution to Eq. (9) is given, another new solution can be obtained through a BT [31]. In order to obtain the bilinear BT of Eq. (9), we consider

$$\begin{aligned} \mathrm {P}&:=[(D^{3}_{x}D_{y}+c_{1}D_{y}D_{t}+c_{2}D_{x}D_{z})f'\cdot f']f^{2}\nonumber \\&\quad -f'^{2}[(D^{3}_{x}D_{y}+c_{1}D_{y}D_{t}+c_{2}D_{x}D_{z})f\cdot f], \end{aligned}$$

(10)

where it is supposed that $f'$ is another solution to Eq. (9). It can be observed that when $\mathrm {P} = 0$, f satisfies Eq. (9) if and only if $f'$ satisfies Eq. (9) too. In the following, we can derive a series of bilinear equations from $\mathrm {P} = 0$ with respect to the dependent variables f and $f'$, which will lead to a BT.

Based on the exchange formula, we have the following identities for Hiorta operators

$$\begin{aligned}&(D^{3}_{x}D_{y}f'\cdot f')f^{2}-(D^{3}_{x}D_{y}f\cdot f)f'^{2}=3D_{x}(D^{2}_{x}D_{y}f'\cdot f)\cdot ff'-D_{y}(D^{3}_{x}f'\cdot f)\nonumber \\&\quad \cdot ff'-3D_{y}(D^{2}_{x}f'\cdot f)\cdot (D_{x}f'\cdot f)-3D_{x}(D^{2}_{x}f'\cdot f)\cdot (D_{y}f'\cdot f), \end{aligned}$$

(11)

$$\begin{aligned} (D_{y}D_{t}f'\cdot f')f^{2}-(D_{y}D_{t}f\cdot f)f'^{2}&=2D_{y}(D_{t}f'\cdot f)\cdot ff' , \end{aligned}$$

(12)

$$\begin{aligned} (D_{x}D_{z}f'\cdot f')f^{2}-(D_{x}D_{z}f\cdot f)f'^{2}&=2D_{x}(D_{z}f'\cdot f)\cdot ff' . \end{aligned}$$

(13)

As a matter of fact, by applying the above three identities Eqs. (11),  (12) and  (13), Eq. (10) can be rewritten as

$$\begin{aligned} \mathrm {P}&= 3D_{x}(D^{2}_{x}D_{y}f'\cdot f)\cdot ff'-D_{y}(D^{3}_{x}f'\cdot f)\cdot ff'-3D_{y}(D^{2}_{x}f'\cdot f)\cdot (D_{x}f'\cdot f)\nonumber \\&\quad -3D_{x}(D^{2}_{x}f'\cdot f)\cdot (D_{y}f'\cdot f)+2c_{1}D_{y}(D_{t}f'\cdot f)\cdot ff'+2c_{2}D_{x}(D_{z}f'\cdot f)\cdot ff'\nonumber \\&=D_{x}[(3D^{2}_{x}D_{y}+2c_{2}D_{z}+2\lambda _{1}D_{y}+\lambda _{2})f'\cdot f]\cdot ff'\nonumber \\&\quad -D_{y}[(D^{3}_{x}-2c_{1}D_{t}+\lambda _{3})f'\cdot f]\cdot ff'\nonumber \\&\quad -3D_{y}[(D^{2}_{x}-\lambda _{1}+\lambda _{4}D_{x})f'\cdot f]\cdot (D_{x}f'\cdot f)\nonumber \\&\quad -3D_{x}[(D^{2}_{x}-\lambda _{1}+\lambda _{5}D_{y})f'\cdot f]\cdot (D_{y}f'\cdot f), \end{aligned}$$

(14)

where $\lambda _{i}(i=1,2,3,4,5)$ are some arbitrary parameters. It is concluded that a bilinear BT associated with Eq. (9) can be constructed as

$$\begin{aligned} \left\{ \begin{aligned} B_{1}f'\cdot f&=(3D^{2}_{x}D_{y}+2c_{2}D_{z}+2\lambda _{1}D_{y}+\lambda _{2})f'\cdot f=0,\\ B_{2}f'\cdot f&=(D^{3}_{x}-2c_{1}D_{t}+\lambda _{3})f'\cdot f=0,\\ B_{3}f'\cdot f&=(D^{2}_{x}-\lambda _{1}+\lambda _{4}D_{x})f'\cdot f=0,\\ B_{4}f'\cdot f&=(D^{2}_{x}-\lambda _{1}+\lambda _{5}D_{y})f'\cdot f. \end{aligned} \right. \end{aligned}$$

(15)

Obviously, through the above identities obtained from the exchange formula, a direct bilinear BT is constructed for Eq. (9). When $c_{1}=2$ and $c_{2}=-3$, Eq. (15) can be reduced to a bilinear BT of the $(3+1)$-dimensional Jimbo-Miwa equation, which is consistent with the result obtained by using Bell polynomial in Ref. [2].

2.2 Kink wave solutions

In order to obtain another new solution $f'$ through the BT, $f=1$ is taken as a solution to Eq. (9), which is corresponding to the solution $u=2(\mathrm {ln}f)_{x}=0$ to Eq. (4). The four bilinear equations of the BT reduce to the following partial differential equations

$$\begin{aligned} \left\{ \begin{aligned}&3f'_{xxy}+2c_{2}f'_{z}+2\lambda _{1}f'_{y}+\lambda _{2}f'=0,\\&f'_{xxx}-2c_{1}f'_{t}+\lambda _{3}f'=0,\\&f'_{xx}-\lambda _{1}f'+\lambda _{4}f'_{x}=0,\\&f'_{xx}-\lambda _{1}f'+\lambda _{5}f'_{y}=0. \end{aligned} \right. \end{aligned}$$

(16)

We take into account of a class of exponential wave solutions

$$\begin{aligned} f'=1+\varepsilon e^{kx+ly+mz-\omega t}, \end{aligned}$$

(17)

where $\varepsilon ,k,l,m$ and $\omega$ are all constants. Taking $\lambda _{1}=\lambda _{2}=\lambda _{3}=0$ in Eq. (16), we obtain

$$\begin{aligned} m =-\frac{3k^{2}l}{2c_{2}},\quad \omega =-\frac{k^{3}}{2c_{1}},\ \lambda _{4}=-k,\quad \lambda _{5}=-\frac{k^{2}}{l}. \end{aligned}$$

(18)

As a result, the exponential wave solution to the bilinear Eq. (9) is derived

$$\begin{aligned} f'=1+\varepsilon e^{\xi }, \end{aligned}$$

(19)

where $\xi =kx+ly-\frac{3k^{2}l}{2c_{2}}z+\frac{k^{3}}{2c_{1}}t$, and $\varepsilon$, k and l are all arbitrary constants. Further, the corresponding solution to Eq. (4) is

$$\begin{aligned} u=2(\mathrm {ln}f')_{x}=\frac{2\varepsilon k e^{\xi }}{1+\varepsilon e^{\xi }}, \end{aligned}$$

(20)

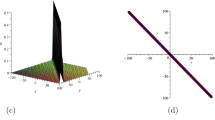
which is a kink wave solution. By selecting the appropriate parameters, this kink wave solution is plotted in Fig. 1.

Fig. 1

Plot of the kink wave solution via Eq. (20) with $c_{1}=c_{2}=-1$, $z=1$, $t=3$, $k=1$, $l=2$ and $\varepsilon =4$

3 Pfaffian solutions

In this section, we will use Pfaffian to express the soliton solutions to Eq. (9) and prove that the bilinear form is equivalent to the Pfaffian identity. The N-order Pfaffian $f_{N}$ associated with the N-soliton solutions can be expressed as

$$\begin{aligned} f_{N}=(1,2,\ldots ,2N), \end{aligned}$$

(21)

where the entries are defined by

$$\begin{aligned} (i,j)=c_{ij}+\int ^{x}D_{x}\phi _{i}\cdot \phi _{j}\, dx=c_{ij}+\int ^{x}\phi _{i,x}\phi _{j}-\phi _{i}\phi _{j,x}\, dx. \end{aligned}$$

(22)

It should be pointed out that each $c_{ij}$ ($1\leqslant i,j\leqslant 2N$) is constant and satisfies $c_{ij}=-c_{ji}$, and $\phi _{i}$’s are the functions of the scaled space coordinates x, y, z and time coordinate t, which satisfy the linear partial differential equations

$$\begin{aligned} \phi _{i,y}&=k\int ^{x} \phi _{i}\, dx,\quad \phi _{i,z}=-\frac{3}{c_{2}}k\;\phi _{i,x}-\frac{c_{1}}{c_{2}}kb\;\int ^{x}\phi _{i}\, dx,\nonumber \\ \phi _{i,t}&=-\frac{1}{c_{1}}\;\phi _{i,xxx}+b\;\phi _{i,x}, \end{aligned}$$

(23)

while $k\ne 0$ and b are arbitrary parameters. In addition, the lower limit of the above integral is $x=\pm \infty$, in order to make the value of the integrand converge to 0 when $x=+\infty$ or $x=-\infty$.

Theorem 1

If $\phi _{i}$’s satisfy the linear differential condition Eq. (23), then the Pfaffian $f_{N}$ defined by Eq. (21) solves Eq. (9), and the solution to Eq. (4) can be obtained as $u=2(\mathrm {ln}f_{N})_{x}$.

Proof

Based on the condition Eq. (23), the derivative of the entries (i, j) with respect to independent variables x, y, z and t can be easily calculated as

$$\begin{aligned} \frac{\partial }{\partial x}(i,j)&=\phi _{i,x}\phi _{j}-\phi _{i}\phi _{j,x}=(d_{0},d_{1},i,j),\\ \frac{\partial }{\partial y}(i,j)&=\int ^{x} \phi _{i,xy}\phi _{j}+\phi _{i,x}\phi _{j,y}-\phi _{i,y}\phi _{j,x}-\phi _{i}\phi _{j,xy}\, dx\nonumber \\&=k \left[ \phi _{i}\left( \int ^{x} \phi _{j}\, dx\right) -\left( \int ^{x} \phi _{i}\, dx\right) \phi _{j}\right] =k\;(d_{-1},d_{0},i,j),\\ \frac{\partial }{\partial z}(i,j)&=\int ^{x} \phi _{i,xz}\phi _{j}+\phi _{i,x}\phi _{j,z}-\phi _{i,z}\phi _{j,x}-\phi _{i}\phi _{j,xz}\, dx\\&=-\frac{3k}{c_2}(\phi _{i,x}\phi _{j}-\phi _{i}\phi _{j,x})-\frac{c_1}{c_2}kb\left[ \phi _{i}\left( \int ^{x} \phi _{j}\, dx\right) -\left( \int ^{x} \phi _{i}\, dx\right) \phi _{j}\right] \\&=-\frac{3k}{c_2}\;(d_{0},d_{1},i,j)-\frac{c_1}{c_2}kb\;(d_{-1},d_{0},i,j),\\ \frac{\partial }{\partial t}(i,j)&=\int ^{x} \phi _{i,xt}\phi _{j}+\phi _{i,x}\phi _{j,t}-\phi _{i,t}\phi _{j,x}-\phi _{i}\phi _{j,xt}\, dx\\&=-\frac{1}{c_1} \Big [\phi _{i,xxx}\phi _{j}-\phi _{i}\phi _{j,xxx}-2(\phi _{i,xx}\phi _{j,x}-\phi _{i,x}\phi _{j,xx})\Big ]\\&\quad +b\;(\phi _{i,x}\phi _{j}-\phi _{i}\phi _{j,x})\\ {}&=-\frac{1}{c_1}\;[(d_{0},d_{3},i,j) -2(d_{1},d_{2},i,j)]+b\;(d_{0},d_{1},i,j), \end{aligned}$$

where the new Pfaffian entries are defined by

$$\begin{aligned} (d_{-1},i)=\int ^{x} \phi _{i}\, dx,\quad (d_{n},i)= \frac{\partial ^{n}}{\partial x^{n}}\phi _{i},\quad (d_{m},d_{n})=0,\ (m,n=-1,0,1,2,3). \end{aligned}$$

(24)

For convenience, $f_{N}$ is abbreviated as $f_{N}=(1,2,\ldots ,2N)=(\bullet )$. Then by using differential rules for Pfaffian as in Ref. [3] and the derivative formula of Pfaffian entries (i, j), it is not difficult to get the derivative of $f_{N}$ as

$$\begin{aligned} f_{N,x}= & {} (d_{0},d_{1},\bullet ),\nonumber \\ f_{N,xx}= & {} (d_{0},d_{2},\bullet ),\nonumber \\ f_{N,xxx}= & {} (d_{1},d_{2},\bullet )+(d_{0},d_{3},\bullet ),\nonumber \\ f_{N,y}= & {} k\;(d_{-1},d_{0},\bullet ),\nonumber \\ f_{N,xy}= & {} k\;(d_{-1},d_{1},\bullet ),\nonumber \\ f_{N,xxy}= & {} k\;[(d_{0},d_{1},\bullet )+(d_{-1},d_{2},\bullet )],\nonumber \\ f_{N,xxxy}= & {} k\;[2(d_{0},d_{2},\bullet )+(d_{-1},d_{3},\bullet )+(d_{-1},d_{0},d_{1},d_{2},\bullet )],\nonumber \\ f_{N,z}= & {} -\frac{3k}{c_2}\;(d_{0},d_{1},\bullet )-\frac{c_2}{c_1}kb\;(d_{-1},d_{0},\bullet ),\nonumber \\ f_{N,xz}= & {} -\frac{3k}{c_2}\;(d_{0},d_{2},\bullet )-\frac{c_2}{c_1}kb\;(d_{-1},d_{1},\bullet ),\nonumber \\ f_{N,t}= & {} -\frac{1}{c_1}\;[(d_{0},d_{3},\bullet )-2(d_{1},d_{2},\bullet )]+b\;(d_{0},d_{1},\bullet ),\nonumber \\ f_{N,yt}= & {} -\frac{k}{c_1}\;[(d_{-1},d_{3},\bullet )-(d_{0},d_{2},\bullet )-2(d_{-1},d_{0},d_{1},d_{2},\bullet )]\nonumber \\&\quad + kb\;(d_{-1},d_{1},\bullet ). \end{aligned}$$

By means of the above results, we derive

$$\begin{aligned} \left\{ \begin{aligned}&(f_{xxxy}+c_{1}f_{yt}+c_{2}f_{xz})f=3k(d_{-1},d_{0},d_{1},d_{2},\bullet )(\bullet ),\nonumber \\&-3f_{xxy}f_{x}-f_{y}f_{xxx}-c_{1}f_{y}f_{t}-c_{2}f_{x}f_{z}=-3k(d_{-1},d_{0},\bullet )(d_{1},d_{2},\bullet )\\&\quad \qquad -3k(d_{0},d_{1},\bullet )(d_{-1},d_{2},\bullet ),\\&3f_{xy}f_{xx}=3k(d_{-1},d_{1},\bullet )(d_{0},d_{2},\bullet ), \end{aligned} \right. \end{aligned}$$

and further get

$$\begin{aligned}&(D^{3}_{x}D_{y}+c_{1}D_{y}D_{t}+c_{2}D_{x}D_{z})f_{N}\cdot f_{N}=3k[(d_{-1},d_{0},d_{1},d_{2},\bullet )(\bullet )\nonumber \\&\quad -(d_{-1},d_{0},\bullet )(d_{1},d_{2},\bullet )+(d_{-1},d_{1},\bullet )(d_{0},d_{2},\bullet )-(d_{0},d_{1},\bullet )(d_{-1},d_{2},\bullet )]=0. \end{aligned}$$

(25)

As a matter of fact, the equality is exactly the Pfaffian identity. Hence, it is evident that $f_{N}$ is the solution to Eq. (9), and the proof is completed. $\square$

Equivalently, the bilinear form of Eq. (9) can be represented by the following Maya chart

When b is taken as zero in Eq. (23), we derive the following differential system

$$\begin{aligned} \phi _{i,y}=k\int ^{x} \phi _{i}\, dx, \quad \phi _{i,z}=-\frac{3}{c_{2}}k\;\phi _{i,x}, \quad \phi _{i,t}=-\frac{1}{c_{1}}\;\phi _{i,xxx}. \end{aligned}$$

(26)

In this case, the bilinear form of Eq. (9) is still transformed into Pfaffian identity similarly.

Let us take into account of some special solutions to Eq. (9). We introduce the solution to the linear partial differential system Eq. (23) as follows

$$\begin{aligned} \phi _{i}=e^{\xi _{i}},\quad \xi _{i}=p_{i}x+kp_{i}^{-1}y-\frac{3}{c_{2}}kp_{i}z-\frac{1}{c_{1}}p_{i}^{3}t+\xi _{i}^{0},\quad i=1,2,\ldots ,2N, \end{aligned}$$

(27)

where $p_{i}$ and $\xi _{i}^{0}$ are free parameters. Three specific examples of soliton solutions to Eq. (4) will be given.

Case 1 Taking $N=1$ in Eq. (21), we can obtain the one-soliton solution. By choosing $c_{12}=1$, $\phi _{j}=e^{\xi _{j}}(j=1,2)$, and taking $\eta _{1}=\xi _{1}+\xi _{2}+\delta _{1}$ with $e^{\delta _{1}}=\frac{p_{1}-p_{2}}{p_{1}+p_{2}}$, we rewrite $f_{1}$ as

$$\begin{aligned} f_{1}=(1,2) =1+\frac{p_{1}-p_{2}}{p_{1}+p_{2}}e^{\xi _{1}+\xi _{2}}=1+e^{\eta _{1}}. \end{aligned}$$

Therefore, the one-soliton solution can be derived as

$$\begin{aligned} u&=2(\mathrm {ln}f_{1})_{x}=\frac{2(p_{1}+p_{2})e^{\eta _{1}}}{1+e^{\eta _{1}}}\nonumber \\&=(p_{1}+p_{2})+(p_{1}+p_{2})\tanh \Big (\frac{\eta _{1}}{2}\Big ). \end{aligned}$$

(28)

Case 2 Taking $N=2$ in Eq. (21), we can obtain the two-soliton solution. Choosing $c_{12}=c_{34}=1$, $c_{13}=c_{14}=c_{23}=c_{24}=0$ and $\phi _{j}=e^{\xi _{j}}(j=1,2,3,4)$, we have

$$\begin{aligned} f_{2}&=(1,2,3,4)=(1,2)(3,4)-(1,3)(2,4)+(1,4)(2,3) \\&=\left( 1+\frac{p_{1}-p_{2}}{p_{1}+p_{2}}e^{\xi _{1}+\xi _{2}}\right) \left( 1+\frac{p_{3}-p_{4}}{p_{3}+p_{4}}e^{\xi _{3}+\xi _{4}}\right) \\&\quad - \left( \frac{p_{1}-p_{3}}{p_{1}+p_{3}}e^{\xi _{1}+\xi _{3}}\right) \left( \frac{p_{2}-p_{4}}{p_{2}+p_{4}}e^{\xi _{2}+\xi _{4}}\right) \\&\quad +\left( \frac{p_{1}-p_{4}}{p_{1}+p_{4}}e^{\xi _{1}+\xi _{4}}\right) \left( \frac{p_{2}-p_{3}}{p_{2}+p_{3}}e^{\xi _{2}+\xi _{3}}\right) \\&=1+e^{\eta _{1}}+e^{\eta _{2}}+b_{12}e^{\eta _{1}+\eta _{2}}, \end{aligned}$$

where $\eta _{1}=\xi _{1}+\xi _{2}+\delta _{1}, \eta _{2}=\xi _{3}+\xi _{4}+\delta _{2}$, $e^{\delta _{1}}=\frac{p_{1}-p_{2}}{p_{1}+p_{2}}$, $e^{\delta _{2}}=\frac{p_{3}-p_{4}}{p_{3}+p_{4}}$, and

$$\begin{aligned} b_{12}=\frac{(p_{1}-p_{3})(p_{1}-p_{4})(p_{2}-p_{3})(p_{2}-p_{4})}{(p_{1}+p_{3})(p_{1}+p_{4})(p_{2}+p_{3})(p_{2}+p_{4})}. \end{aligned}$$

It is not difficult to find that the form of two-soliton solution is consistent with that obtained by perturbation method.

Case 3 Taking $N=3$ in Eq. (21), we can obtain the three-soliton solution. Choosing $c_{12}=c_{34}=c_{56}=1$, the rest of $c_{ij}=0 (i,j=1,2,\ldots ,6)$, and $\phi _{j}=e^{\xi _{j}}(j=1,2,\ldots ,6)$, we have

$$\begin{aligned} f_{3}&=(1,2,3,4,5,6) \\&=(1,2)(3,4,5,6)-(1,3)(2,4,5,6)+(1,4)(2,3,5,6)\\&\quad -(1,5)(2,3,4,6)+(1,6)(2,3,4,5) \\&=(1,2)(3,4)(5,6)-(1,2)(3,5)(4,6)+(1,2)(3,6)(4,5)\\&\quad -(1,3)(2,4)(5,6)+(1,3)(2,5)(4,6)\\&\quad -(1,3)(2,6)(4,5)+(1,4)(2,3)(5,6)\\&\quad -(1,4)(2,5)(3,6)+(1,4)(2,6)(3,5)\\&\quad -(1,5)(2,3)(4,6)+(1,5)(2,4)(3,6)\\&\quad -(1,5)(2,6)(3,4)+(1,6)(2,3)(4,5)\\&\quad -(1,6)(2,4)(3,5)+(1,6)(2,5)(3,4)\\&=1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{3}}+b_{12}e^{\eta _{1}+\eta _{2}}+b_{13}e^{\eta _{1}+\eta _{3}}\\&\quad +b_{23}e^{\eta _{2}+\eta _{3}}+b_{12}b_{13}b_{23}e^{\eta _{1}+\eta _{2}+\eta _{3}}, \end{aligned}$$

where

$$\begin{aligned} \eta _{3}&=\xi _{5}+\xi _{6}+\delta _{3},e^{\delta _{3}}=\frac{p_{5}-p_{6}}{p_{5}+p_{6}}, b_{13}=\frac{(p_{1}-p_{5})(p_{1}-p_{6})(p_{2}-p_{5})(p_{2}-p_{6})}{(p_{1}+p_{5})(p_{1}+p_{6})(p_{2}+p_{5}) (p_{2}+p_{6})},\\ b_{23}&=\frac{(p_{3}-p_{5})(p_{3}-p_{6})(p_{4}-p_{5})(p_{4}-p_{6})}{(p_{3}+p_{5})(p_{3}+p_{6})(p_{4}+p_{5})(p_{4}+p_{6})}. \end{aligned}$$

As an example, by selecting the appropriate parameters, the one-, two- and three-soliton solutions are plotted in Fig. 2.

Fig. 2

Soliton solutions to Eq. (4) with $c_{1}=c_{2}=-1$, $z=1$ and $t=1$ a one-soliton solution: $p_{1}= 2$, $p_{2}=1$, $\xi _{1}^{0}=\xi _{2}^{0}= 0$, $k=1$; b two-soliton solution: $p_{1}= 5$, $p_{2}=3$, $p_{3}=2$, $p_{4}=1$, $\xi _{1}^{0}=\xi _{2}^{0}=\xi _{3}^{0}=\xi _{4}^{0}= 0$, $k=1$; c three-soliton solution: $p_{1}= 5$, $p_{2}=3$, $p_{3}=2$, $p_{4}=1$, $p_{5}=3$, $p_{6}=2$, $\xi _{1}^{0}=\xi _{2}^{0}=\xi _{3}^{0}=\xi _{4}^{0}=\xi _{5}^{0}=\xi _{6}^{0}= 0$, $k=2$

The above solutions are also kink soliton solutions to Eq. (4). In Fig. 2a, the one-soliton can also be observed as a kink soliton. When $p_{1}+p_{2}$ is greater than zero, u is non-singular, and it is easy to see that the maximum value of u is $2(p_{1}+p_{2})$ and the minimum value is 0 via Eq. (28). In Fig. 2b and c, we also show two-soliton and three-soliton solutions. Not only all solitons have kink shapes, but also the interaction between solitons belongs to elastic collision, that is, the soliton shape and velocity are kept unchange before and after the collision.

It is worth noting that Pfaffian can not only express the soliton solutions, but also different types of solutions according to different assumptions of $\phi _{i}$ (29), such as the rational solution, hyperbola function solution and triangle function solution. Accordingly, we consider another solution in the Pfaffian that satisfies the linear partial differential system as follows

$$\begin{aligned} \phi _{i}=\cos {\theta _{i}},\quad \theta _{i}=p_{i}x-kp_{i}^{-1}y-\frac{3}{c_{2}}kp_{i}z+\frac{1}{c_{1}}p_{i}^{3}t+\theta _{i}^{0},\quad i=1,2,\ldots ,2N, \end{aligned}$$

(29)

where $p_{i}$ and $\theta _{i}^{0}$ are free parameters. The specific example of periodic solutions to Eq. (4) in the Pfaffian will be given. Taking $N=1$ in Eq. (21) and choosing $c_{12}=2$, $\phi _{1}=\cos {\theta _{1}},\phi _{2}=\cos {\theta _{2}}$, we have

$$\begin{aligned} f_{1}&=(1,2)=1+\int ^{x}\phi _{1,x}\phi _{2}-\phi _{1}\phi _{2,x}\, dx\\&\qquad =1+\frac{p_{1}-p_{2}}{2(p_{1}+p_{2})}\cos \left[ -(p_{1}+p_{2})x+\frac{p_{1}+p_{2}}{p_{1}p_{2}} ky+\frac{3}{c_{2}}k(p_{1}+p_{2})z\right. \\&\qquad \qquad \left. -\frac{1}{c_{1}}(p_{1}^{3}+p_{2}^{3})t+\theta _{1}^{0}\right] \\&\qquad \qquad +\frac{p_{1}+p_{2}}{2(p_{1}-p_{2})}\cos \left[ -(p_{1}+p_{2})x-\frac{p_{1}-p_{2}}{p_{1}p_{2}} ky+\frac{3}{c_{2}}k(p_{1}-p_{2})z\right. \\&\qquad \qquad \left. -\frac{1}{c_{1}}(p_{1}^{3}-p_{2}^{3})t+\theta _{2}^{0}\right] , \end{aligned}$$

which leads to periodic solutions to Eq. (4) via $u=2(\mathrm {ln}f_{1})_{x}$.

As an example, by selecting the appropriate parameters, the periodic solutions to Eq. (4) is plotted in Fig. 3. In Fig. 3, we can observe clearly that the solution f to Eq. (9) and the solution u to Eq. (4) are periodic waves, and their minimum positive period are both $2\pi$.

Fig. 3

The triangle function solution to Eq. (9) (a) and the periodic solutions to Eq. (4) (b) with $c_{1}=c_{2}=-1$, $k=1$, $p_{1}=2$, $p_{1}=1$, $t=1$ and $z=1$

4 Wronskian solutions

We firstly construct the Wronskian determinant solution to Eq. (9), and then prove that the bilinear form of Eq. (9) can be transformed into the Plücker relation (2). It is assumed that the N-soliton solutions are expressed in the form of N-order Wronskian determinant as

$$\begin{aligned} W(\phi _{1},\phi _{2},\ldots ,\phi _{N})= \left| \begin{array}{cccc} \phi _{1}^{(0)}&{}\quad \phi _{1}^{(1)}&{}\quad \cdots &{}\quad \phi _{1}^{(N-1)}\\ \phi _{2}^{(0)}&{}\quad \phi _{2}^{(1)}&{}\quad \cdots &{}\quad \phi _{2}^{(N-1)}\\ \vdots &{}\quad \quad \vdots &{}\quad \quad \ddots &{}\quad \quad \vdots \\ \phi _{N}^{(0)}&{}\quad \phi _{N}^{(1)}&{}\quad \cdots &{}\quad \phi _{N}^{(N-1)}\\ \end{array}\right| =|\widehat{N-1}|, \end{aligned}$$

(30)

where $\phi _{i}^{(m)}(i=1,2,\ldots ,N,\; m=0,1,\ldots ,N-1)$ are defined by

$$\begin{aligned} \phi _{i}^{(m)}=\frac{\partial ^{m}\phi _{i}}{\partial x^{m}}. \end{aligned}$$

(31)

The function $\phi _{i}$ satisfies the linear partial differential equations

$$\begin{aligned} \phi _{i,y}=\gamma \phi _{i,xx},\quad \phi _{i,z}=-\frac{3}{c_{2}}\gamma \;\phi _{i,xxxx},\quad \phi _{i,t}=\frac{2}{c_{1}}\;\phi _{i,xxx}, \end{aligned}$$

(32)

where $\gamma \ne 0$ is an arbitrary parameter.

According to the properties of the determinant, the derivative of $f_{N}$ to x is equal to the sum of N determinants that remain unchanged for the other columns. However, some determinants are zero because they have two identical columns. In the computation of the derivatives of $f_{N}$, only the number of derivatives in the column is changed, and the row is not affected. This is the advantage of using Wronskian determinant to express $f_{N}$.

Theorem 2

If $\phi _{i}$’s satisfy the linear differential conditions in Eq. (32), then the Wronskian determinant $f_{N}=|\widehat{N-1}|$ defined by Eq. (30) is the solution to Eq. (9) and the solution to Eq. (4) can be obtained as $u=2(\mathrm {ln}f_{N})_{x}$.

Proof

Based on the conditions in Eq. (32) and the properties of the determinant, the derivatives of $f_{N}$ with respect to the independent variables x, y, z, and t can be easily calculated as

$$\begin{aligned} f_{N,x}= & {} |\widehat{N-2},N|, \nonumber \\ f_{N,xx}= & {} |\widehat{N-2},N+1|+|\widehat{N-3},N-1,N|, \nonumber \\ f_{N,xxx}= & {} |\widehat{N-2},N+2|+2|\widehat{N-3},N-1,N+1|+|\widehat{N-4},N-2,N-1,N|,\nonumber \\ f_{N,y}= & {} \gamma (|\widehat{N-2},N+1|-|\widehat{N-3},N-1,N|),\nonumber \\ f_{N,xy}= & {} \gamma (|\widehat{N-2},N+2|-|\widehat{N-4},N-2,N-1,N|),\nonumber \\ f_{N,xxy}= & {} \gamma (|\widehat{N-2},N+3|+|\widehat{N-3},N-1,N+2|\nonumber \\&\quad -|\widehat{N-4},N-2,N-1,N+1|-|\widehat{N-5},N-3,N-2,N-1,N|),\nonumber \\ f_{N,xxxy}= & {} \gamma (|\widehat{N-2},N+4|+2|\widehat{N-3},N-1,N+3|+|\widehat{N-3},N,N+2|\nonumber \\&\quad -|\widehat{N-4},N-2,N,N+1|-2|\widehat{N-5},N-3,N-2,N-1,N+1|\nonumber \\&\quad -|\widehat{N-6},N-4,N-3,N-2,N-1,N|),\nonumber \\ f_{N,z}= & {} -\frac{3}{c_{2}}\gamma (|\widehat{N-2},N+3|-|\widehat{N-3},N-1,N+2|\nonumber \\&\quad +|\widehat{N-4},N-2,N-1,N+1|\nonumber \\&\quad -|\widehat{N-5},N-3,N-2,N-1,N|),\nonumber \\ f_{N,xz}= & {} -\frac{3}{c_{2}}\gamma (|\widehat{N-2},N+4|-|\widehat{N-3},N,N+2|+|\widehat{N-4},N-2,N,N+1|\nonumber \\&\quad -|\widehat{N-6},N-4,N-3,N-2,N-1,N|),\nonumber \\ f_{N,t}= & {} \frac{2}{c_{1}}(|\widehat{N-2},N+2|-|\widehat{N-3},N-1,N+1|+|\widehat{N-4},N-2,N-1,N|),\nonumber \\ f_{N,yt}= & {} -\frac{2}{c_{1}}\gamma (|\widehat{N-2},N+4|+|\widehat{N-3},N,N+2|-|\widehat{N-3},N-1,N+3|\nonumber \\&\quad -|\widehat{N-4},N-2,N,N+1|+|\widehat{N-5},N-3,N-2,N-1,N+1|\nonumber \\&\quad -|\widehat{N-6},N-4,N-3,N-2,N-1,N|). \end{aligned}$$

(33)

By means of the above results and substitute them into Eq. (9), we derive

$$\begin{aligned}&(f_{xxxy}+c_{1}f_{yt}+c_{2}f_{xz})f\\&\quad =6\gamma (|\widehat{N-3},N,N+2|-|\widehat{N-4},N-2,N,N+1|)|\widehat{N-1}|,\\&\qquad -3f_{xxy}f_{x}+3f_{xy}f_{xx}-f_{y}f_{xxx}-c_{1}f_{y}f_{t}-c_{2}f_{x}f_{z}\\&\quad =6\gamma (-|\widehat{N-2},N||\widehat{N-3},N-1,N+2|\\&\qquad +|\widehat{N-2},N||\widehat{N-4},N-2,N-1,N+1|\\&\qquad +|\widehat{N-2},N+2||\widehat{N-3},N-1,N|\\&\qquad -|\widehat{N-2},N+2||\widehat{N-4},N-2,N-1,N|), \end{aligned}$$

and further get

$$\begin{aligned} (D^{3}_{x}D_{y}+c_{1}D_{y}D_{t}+c_{2}D_{x}D_{z})f_{N}\cdot f_{N}=6\gamma (W_{1}+W_{2})=0, \end{aligned}$$

(34)

where

$$\begin{aligned} W_{1}&=|\widehat{N-3},N,N+2||\widehat{N-1}|-|\widehat{N-2},N||\widehat{N-3},N-1,N+2|\\&\quad +|\widehat{N-2},N+2||\widehat{N-3},N-1,N|,\\ W_{2}&=-|\widehat{N-4},N-2,N,N+1||\widehat{N-1}|\\&\quad +|\widehat{N-2},N||\widehat{N-4},N-2,N-1,N+1|\\&\quad -|\widehat{N-2},N+2||\widehat{N-4},N-2,N-1,N|. \end{aligned}$$

In fact, these two equalities are exactly the Plücker relation (2) of determinant and a special case of Pfaffian identity. Hence, it is evident that $f_{N}$ is the solution to Eq. (9). $\square$

$W_{1}$ and $W_{2}$ can be represented by the following Maya charts

The linear partial differential system in Eq. (32) enjoys the solution in the form

$$\begin{aligned} \phi _{i}&= e^{\xi _{i}}+e^{\zeta _{i}},\quad \xi _{i}=l_{i}x+\gamma l_{i}^{2}y-\frac{3}{c_{2}}\gamma l_{i}^{4}z+\frac{2}{c_{1}}l_{i}^{3}t+\xi _{i}^{0}, \zeta _{i}=k_{i}x+\gamma k_{i}^{2}y\nonumber \\&\quad -\frac{3}{c_{2}}\gamma k_{i}^{4}z+\frac{2}{c_{1}}k_{i}^{3}t+\zeta _{i}^{0}, \end{aligned}$$

(35)

where $l_{i},k_{i},\xi _{i}^{0}$ and $\zeta _{i}^{0}$ $(i=1,2,\ldots ,N)$ are free parameters. Some specific examples of solution to Eq. (4) will be given.

Case 1 Taking $N=1$ in Eq. (30), we can obtain the one-soliton solution. Let $\phi _{1}= e^{\xi _{1}}+e^{\zeta _{1}}$, we have

$$\begin{aligned} f_{1}=W(\phi _{1})=\phi _{1}= e^{\xi _{1}}+e^{\zeta _{1}}, \end{aligned}$$

which leads to the one-soliton solution to Eq. (4) as

$$\begin{aligned} u=2(\mathrm {ln}f_{1})_{x}=2\frac{l_{1}e^{\xi _{1}}+k_{1}e^{\zeta _{1}}}{e^{\xi _{1}}+e^{\zeta _{1}}}=(l_{1}+k_{1})+(l_{1}-k_{1})\tanh \frac{\xi _{1}-\zeta _{1}}{2}. \end{aligned}$$

(36)

Case 2 Taking $N=2$ in Eq. (30), we can obtain the two-soliton solution. Taking $\phi _{1}= e^{\xi _{1}}+e^{\zeta _{1}}$ and $\phi _{2}= e^{\xi _{2}}+e^{\zeta _{2}}$, we have

$$\begin{aligned} \begin{aligned} f_{2}&=W(\phi _{1},\phi _{2})=\left| \begin{array}{cc} \phi _{1}&{}\phi _{1,x}\\ \phi _{2}&{}\phi _{2,x}\\ \end{array}\right| \\&=(e^{\xi _{1}}+e^{\zeta _{1}})(l_{2}e^{\xi _{2}}+k_{2}e^{\zeta _{2}})-(l_{1}e^{\xi _{1}}+k_{1}e^{\zeta _{1}})(e^{\xi _{2}}+e^{\zeta _{2}})\\ {}&=(k_{2}-k_{1})e^{\zeta _{1}+\zeta _{2}}\left( 1+\frac{k_{2}-l_{1}}{k_{2}-k_{1}}e^{\xi _{1}-\zeta _{1}} +\frac{l_{2}-k_{1}}{k_{2}-k_{1}}e^{\xi _{2}-\zeta _{2}}+\frac{l_{2}-l_{1}}{k_{2}-k_{1}} e^{\xi _{1}+\xi _{2}-\zeta _{1}-\zeta _{2}}\right) , \end{aligned} \end{aligned}$$

which results in the two-soliton solution to Eq. (4) via $u=2(\mathrm {ln}f_{2})_{x}$.

Case 3 Taking $N=3$ in Eq. (30), we can obtain the three-soliton solution. Let $\phi _{1}= e^{\xi _{1}}+e^{\zeta _{1}}$, $\phi _{2}= e^{\xi _{2}}+e^{\zeta _{2}}$ and $\phi _{3}= e^{\xi _{3}}+e^{\zeta _{3}}$, then

$$\begin{aligned} f_{3}= & {} W(\phi _{1},\phi _{2},\phi _{3})=\left| \begin{array}{ccc} \phi _{1}&{}\quad \phi _{1,x}&{}\quad \phi _{1,xx}\\ \phi _{2}&{}\quad \phi _{2,x}&{}\quad \phi _{2,xx}\\ \phi _{3}&{}\quad \phi _{3,x}&{}\quad \phi _{3,xx}\\ \end{array}\right| \\= & {} (k_{1}-k_{2})(k_{3}-k_{2})(k_{1}-k_{3})e^{\zeta _{1}+\zeta _{2}+\zeta _{3}}\left[ 1+\frac{(k_{2}-l_{1})(k_{3}-l_{1})}{(k_{1}-k_{2})(k_{1}-k_{3})}e^{\xi _{1}-\zeta _{1}}\right. \\&\quad \left. +\frac{(k_{1}-l_{2})(k_{3}-l_{2})}{(k_{1}-k_{2})(k_{3}-k_{2})}e^{\xi _{2}-\zeta _{2}}+\frac{(l_{3}-k_{2})(k_{1}-l_{3})}{(k_{3}-k_{2})(k_{1}-k_{3})}e^{\xi _{3}-\zeta _{3}} \right. \\&\quad \left. +\frac{(l_{1}-l_{2})(k_{3}-l_{2})(l_{1}-k_{3})}{(k_{1}-k_{2})(k_{3}-k_{2})(k_{1}-k_{3})}e^{\xi _{1}+\xi _{2}-\zeta _{1}-\zeta _{2}}\right. \\&\quad \left. +\frac{(l_{1}-k_{2})(l_{3}-k_{2})(l_{1}-l_{3})}{(k_{1}-k_{2})(k_{3}-k_{2})(k_{1}-k_{3})}e^{\xi _{1}+\xi _{3}-\zeta _{1}-\zeta _{3}}\right. \\&\quad \left. +\frac{(k_{1}-l_{2})(l_{3}-l_{2})(k_{1}-l_{3})}{(k_{1}-k_{2})(k_{3}-k_{2})(k_{1}-k_{3})}e^{\xi _{2}+\xi _{3}-\zeta _{2}-\zeta _{3}}\right. \\&\quad \left. +\frac{(l_{1}-l_{2})(l_{3}-l_{2})(l_{1}-l_{3})}{(k_{1}-k_{2})(k_{3}-k_{2})(k_{1}-k_{3})} e^{\xi _{1}+\xi _{2}+\xi _{3}-\zeta _{1}-\zeta _{2}-\zeta _{3}}\right] , \end{aligned}$$

which gives rise to the three-soliton solution to Eq. (4) via $u=2(\mathrm {ln} f_{3})_{x}$.

Through taking $N=4$ in Eq. (30), the solution $f_{4}$ to Eq. (9) can be derived similarly, and further the four-soliton solution to Eq. (4) can be computed. As an example, by selecting the appropriate parameters, the one-, two-, three- and four-soliton solutions are plotted in Fig. 4.

Fig. 4

Soliton solutions to Eq. (4) with $c_{1}=c_{2}=-1$, $z=1$, $t=1$ and $\gamma =1$ a one-soliton solution: $l_{1}=2$, $k_{1}=1$, $\xi _{1}^{0}=\zeta _{1}^{0}=0$; b two-soliton solution: $l_{1}=2$, $l_{2}=3$, $k_{1}=1$, $k_{2}=2$, $\xi _{1}^{0}=\xi _{2}^{0}=\zeta _{1}^{0}=\zeta _{2}^{0}=0$; c three-soliton solution: $l_{1}=1$, $l_{2}=-1.2$, $l_{3}=0.2$, $k_{1}=1.6$, $k_{2}=-1.8$, $k_{3}=0.6$, $\xi _{1}^{0}=\xi _{2}^{0}=\xi _{3}^{0}=\zeta _{1}^{0}=\zeta _{2}^{0}=\zeta _{3}^{0}=0$; d four-soliton solution: $l_{1}=1$, $l_{2}=0.4$, $l_{3}=1.8$, $l_{4}=-1$, $k_{1}=1.5$, $k_{2}=-0.2$, $k_{3}=2$, $k_{4}=-1.5$, $\xi _{1}^{0}=\xi _{2}^{0}=\xi _{3}^{0}=\xi _{4}^{0}=\zeta _{1}^{0}=\zeta _{2}^{0}=\zeta _{3}^{0}=\zeta _{4}^{0}=0$

In Fig. 4a, the one-soliton can be observed to be also a kink soliton. It is easy to compute in Eq. (36) that the maximum value of u is $(l_{1}+k_{1})+|l_{1}-k_{1}|$ and the minimum value is $(l_{1}+k_{1})-|l_{1}-k_{1}|$. In Fig. 4, we also show two-, three- and four-soliton solutions, which can be seen in Fig. 4b–d, respectively. The two-soliton solution is two parallel kink solitons and the three-soliton and four-soliton solutions are the oblique kink solitons. The interaction between solitons belongs to elastic collision, that is, the soliton shape and velocity are kept unchange before and after the collision.

5 Grammian solutions

In the previous section, it has been proved that if the solution f is expressed as a Wronskian determinant, then the bilinear Eq. (9) becomes the Plücker relation. In this section, we will consider another type of representation of f, and prove that, in this case, the bilinear Eq. (9) can be transformed into another determinant identity, namely, Jacobi identity. It is assumed that the N-soliton solution is defined in the form of N-order Grammian determinant

$$\begin{aligned} f_{N}=\mathrm {det}(a_{ij})_{1\le i,j\le N}, \quad a_{ij}=c_{ij}+\int ^{x}\phi _{i}\psi _{j}\, dx, \end{aligned}$$

(37)

where $c_{ij}$ is constant, and $\phi _{i}$ and $\psi _{j}$ are the functions of the scaled space coordinate x, y, z and the time coordinate t satisfying the linear partial differential equations

$$\begin{aligned}&\phi _{i,y}=\gamma \phi _{i,xx},\quad \phi _{i,z}=-\frac{3}{c_{2}}\gamma \; \phi _{i,xxxx},\quad \phi _{i,t}=\frac{2}{c_{1}}\;\phi _{i,xxx},\nonumber \\&\psi _{i,y}=-\gamma \psi _{i,xx},\quad \psi _{i,z}=\frac{3}{c_{2}}\gamma \;\phi _{i,xxxx},\quad \psi _{i,t}=\frac{2}{c_{1}}\;\phi _{i,xxx}. \end{aligned}$$

(38)

Theorem 3

If $\phi _{i}$ and $\psi _{j}$ satisfy the linear differential conditions in Eq. (38), then the Grammian determinant $f_{N}=det(a_{ij})_{1\le i,j\le N}$ defined by Eq. (37) is the solution to Eq. (9), and $u=2(\mathrm {ln}f_{N})_{x}$ leads to the solution to Eq. (4).

Proof

In order to prove that $f_{N}$ satisfies Eq. (9), the derivatives of $f_{N}$ need to be calculated. First of all, we express $f_{N}$ as Pfaffian

$$\begin{aligned} f_{N}=(1,2,\ldots ,N,N^{*},\ldots ,2^{*},1^{*})=(\bullet ), \end{aligned}$$

(39)

where $(i,j^{*})=a_{ij}$ and $(i,j)=(i^{*},j^{*})=0$. To express the derivatives of the entries $(i,j^{*})$ with Pfaffian, the new Pfaffian entries are introduced

$$\begin{aligned} (d_{n},i^{*})&= \frac{\partial ^{n}}{\partial x^{n}}\phi _{i},\quad (d_{n}^{*},j)= \frac{\partial ^{n}}{\partial x^{n}}\psi _{j},\nonumber \\ (d_{m},d_{n}^{*})&=(d_{m}^{*},j^{*})=(d_{n},i)=0,\ (m,n=0,1,2,3,4). \end{aligned}$$

(40)

Based on the conditions in Eq. (38), it is not difficult to get

$$\begin{aligned} \frac{\partial }{\partial x}a_{ij}&=\phi _{i}\psi _{j}=(d_{0},d_{0}^{*},i,j^{*}),\\ \frac{\partial }{\partial y}a_{ij}&=\int ^{x} \phi _{i,y}\psi _{j}+\phi _{i}\psi _{j,y}\, dx\\&=\gamma (\phi _{i,x}\psi _{j}-\phi _{i}\psi _{j,x})=\gamma [(d_{0},d_{1}^{*},i,j^{*}) -(d_{1},d_{0}^{*},i,j^{*})],\\ \frac{\partial }{\partial z}a_{ij}&=\int ^{x} \phi _{i,z}\psi _{j}+\phi _{i}\psi _{j,z}\, dx\\&=-\frac{3}{c_{2}}\gamma (\phi _{i,xxx}\psi _{j}-\phi _{i}\psi _{j,xxx}-\phi _{i,xx}\psi _{j,x}+\phi _{i,x}\psi _{j,xx})\\&=-\frac{3}{c_{2}}\gamma [(d_{0},d_{3}^{*},i,j^{*})-(d_{3},d_{0}^{*},i,j^{*})-(d_{1},d_{2}^{*},i,j^{*})+(d_{2},d_{1}^{*},i,j^{*})],\\ \frac{\partial }{\partial t}a_{ij}&=\int ^{x} \phi _{i,t}\psi _{j}+\phi _{i}\psi _{j,t}\, dx\\&=\frac{2}{c_{1}}(\phi _{i,xx}\psi _{j}-\phi _{i,x}\psi _{j,x}+\phi _{i}\psi _{j,xx}) =\frac{2}{c_{1}}[(d_{0},d_{2}^{*},i,j^{*})\\&\quad -(d_{1},d_{1}^{*},i,j^{*})+(d_{2},d_{0}^{*},i,j^{*})]. \end{aligned}$$

Through using the properties of the Pfaffian, the derivatives of the $f_{N}$ with respect to independent variables x, y, z and t can be easily calculated as

$$\begin{aligned} f_{N,x}&=(d_{0},d_{0}^{*},\bullet ),\nonumber \\ f_{N,xx}&=(d_{1},d_{0}^{*},\bullet )+(d_{0},d_{1}^{*},\bullet ),\nonumber \\ f_{N,xxx}&=(d_{2},d_{0}^{*},\bullet )+2(d_{1},d_{1}^{*},\bullet )+(d_{0},d_{2}^{*},\bullet ),\nonumber \\ f_{N,y}&=\gamma [(d_{0},d_{1}^{*},\bullet )-(d_{1},d_{0}^{*},\bullet )],\nonumber \\ f_{N,xy}&=\gamma [(d_{0},d_{2}^{*},\bullet )-(d_{2},d_{0}^{*},\bullet )],\nonumber \\ f_{N,xxy}&=\gamma [(d_{1},d_{2}^{*},\bullet )+(d_{0},d_{3}^{*},\bullet )-(d_{3},d_{0}^{*},\bullet )-(d_{2},d_{1}^{*},\bullet )],\nonumber \\ f_{N,xxxy}&=\gamma [2(d_{1},d_{3}^{*},\bullet )+(d_{0},d_{4}^{*},\bullet )-(d_{4},d_{0}^{*},\bullet )-2(d_{3},d_{1}^{*},\bullet ) \nonumber \\&\quad +(d_{0},d_{0}^{*},d_{1},d_{2}^{*},\bullet )-(d_{0},d_{0}^{*},d_{2},d_{1}^{*},\bullet )],\nonumber \\ f_{N,z}&=-\frac{3}{c_{2}}\gamma [(d_{0},d_{3}^{*},\bullet )-(d_{3},d_{0}^{*},\bullet )-(d_{1},d_{2}^{*},\bullet )+(d_{2},d_{1}^{*},\bullet )],\nonumber \\ f_{N,xz}&=-\frac{3}{c_{2}}\gamma [(d_{0},d_{4}^{*},\bullet )-(d_{4},d_{0}^{*},\bullet ) -(d_{0},d_{0}^{*},d_{1},d_{2}^{*},\bullet )-(d_{0},d_{0}^{*},d_{2},d_{1}^{*},\bullet )],\nonumber \\ f_{N,t}&=\frac{2}{c_{1}}[(d_{0},d_{2}^{*},\bullet )-(d_{1},d_{1}^{*},\bullet )+(d_{2},d_{0}^{*},\bullet )],\nonumber \\ f_{N,yt}&=\frac{2}{c_{1}}\gamma [(d_{0},d_{4}^{*},\bullet )+(d_{3},d_{1}^{*},\bullet )-(d_{1},d_{3}^{*},\bullet )-(d_{4},d_{0}^{*},\bullet ) \nonumber \\&\quad +(d_{0},d_{0}^{*},d_{1},d_{2}^{*},\bullet )-(d_{0},d_{0}^{*},d_{2},d_{1}^{*},\bullet )]. \end{aligned}$$

(41)

By means of the above results, we derive

$$\begin{aligned}&(f_{xxxy}+c_{1}f_{yt}+c_{2}f_{xz})f=6\gamma [(d_{0},d_{0}^{*},d_{1},d_{2}^{*},\bullet )-(d_{0},d_{0}^{*},d_{2},d_{1}^{*},\bullet )](\bullet ),\\&\qquad -3f_{xxy}f_{x}+3f_{xy}f_{xx}-f_{y}f_{xxx}-c_{1}f_{y}f_{t}-c_{2}f_{x}f_{z}\\&\quad =6\gamma [-(d_{1},d_{2}^{*},\bullet )(d_{0},d_{0}^{*},\bullet )+(d_{2},d_{1}^{*},\bullet )(d_{0},d_{0}^{*},\bullet ) +(d_{0},d_{2}^{*},\bullet )(d_{1},d_{0}^{*},\bullet )\\&\qquad -(d_{2},d_{0}^{*},\bullet )(d_{0},d_{1}^{*},\bullet )], \end{aligned}$$

and further obtain

$$\begin{aligned} (D^{3}_{x}D_{y}+c_{1}D_{y}D_{t}+c_{2}D_{x}D_{z})f_{N}\cdot f_{N}=6\gamma (G_{1}+G_{2})=0, \end{aligned}$$

(42)

with

$$\begin{aligned} G_{1}&=(d_{0},d_{0}^{*},d_{1},d_{2}^{*},\bullet )(\bullet )-(d_{1},d_{2}^{*},\bullet )(d_{0},d_{0}^{*},\bullet ) +(d_{0},d_{2}^{*},\bullet )(d_{1},d_{0}^{*},\bullet )\\&=(d_{0},d_{0}^{*},d_{1},d_{2}^{*},\bullet )(\bullet )-(d_{0},d_{0}^{*},\bullet )(d_{1},d_{2}^{*},\bullet ) -(d_{0},d_{2}^{*},\bullet )(d_{0}^{*},d_{1},\bullet ),\\ G_{2}&=-(d_{0},d_{0}^{*},d_{2},d_{1}^{*},\bullet )(\bullet )+(d_{2},d_{1}^{*},\bullet )(d_{0},d_{0}^{*},\bullet ) -(d_{2},d_{0}^{*},\bullet )(d_{0},d_{1}^{*},\bullet )\\&=-(d_{0},d_{0}^{*},d_{2},d_{1}^{*},\bullet )(\bullet )+(d_{2},d_{1}^{*},\bullet )(d_{0},d_{0}^{*},\bullet ) +(d_{0},d_{1}^{*},\bullet )(d_{0}^{*},d_{2},\bullet ). \end{aligned}$$

As a matter of fact, these two equalities are exactly the Jacobi identity (3) of determinant and a special case of Pfaffian identity. Hence, it is evident that $f_{N}$ is the solution to Eq. (9). $\square$

$G_{1}$ and $G_{2}$ can be represented by the following Maya charts

The linear partial differential system in Eq. (38) have the solutions in the form

$$\begin{aligned} \phi _{i}&= e^{\xi _{i}},\quad \psi _{i}=e^{\zeta _{i}},\nonumber \\ \xi _{i}&=l_{i}x+\gamma l_{i}^{2}y-\frac{3}{c_{2}}\gamma l_{i}^{4}z+\frac{2}{c_{1}}l_{i}^{3}t+\xi _{i}^{0}, \nonumber \\ \zeta _{i}&=k_{i}x-\gamma k_{i}^{2}y+\frac{3}{c_{2}}\gamma k_{i}^{4}z+\frac{2}{c_{1}}k_{i}^{3}t+\zeta _{i}^{0}, \end{aligned}$$

(43)

where $l_{i},k_{i},\xi _{i}^{0}$ and $\zeta _{i}^{0}$ $(i=1,2,\ldots ,N)$ are free parameters. Some specific examples of soliton solutions to Eq. (4) will be given.

Case 1 Taking $N=1$ in Eq. (39), we can obtain the one-soliton solution. Choosing $c_{11}=1$, $\phi _{1}=e^{\xi _{1}}$ and $\psi _{1}=e^{\zeta _{1}}$, we have

$$\begin{aligned} f_{1}=(1,1^{*}) =1+\frac{1}{l_{1}+k_{1}}e^{\xi _{1}+\zeta _{1}}, \end{aligned}$$

(44)

which leads to the one-soliton solution to Eq. (4) as

$$\begin{aligned} u&=2(\mathrm {ln}f_{1})_{x}\nonumber \\&=\frac{2e^{\xi _{1}+\zeta _{1}}}{1+\frac{1}{l_{1}+k_{1}}e^{\xi _{1}+\zeta _{1}}}=(l_{1}+k_{1}) +(l_{1}+k_{1})\tanh \Big [\frac{1}{2}\Big (\xi _{1}+\zeta _{1} +\ln \frac{1}{l_{1}+k_{1}}\Big )\Big ]. \end{aligned}$$

(45)

Case 2 Taking $N=2$ in Eq. (39), we can obtain the two-soliton solution. Choosing $c_{11}=c_{22}=1$, $c_{12}=c_{21}=0$, $\phi _{j}=e^{\xi _{j}},\psi _{j}=e^{\zeta _{j}}(j=1,2)$, we have

$$\begin{aligned} \begin{aligned} f_{2}=(1,2,2^{*},1^{*})&=\left| \begin{array}{cc} 1+\frac{1}{l_{1}+k_{1}}e^{\xi _{1}+\zeta _{1}}&{}\frac{1}{l_{1}+k_{2}}e^{\xi _{1}+\zeta _{2}}\\ \frac{1}{l_{2}+k_{1}}e^{\xi _{2}+\zeta _{1}}&{}1+\frac{1}{l_{2}+k_{2}}e^{\xi _{2}+\zeta _{2}}\\ \end{array}\right| \\&=1+\frac{1}{l_{1}+k_{1}}e^{\xi _{1}+\zeta _{1}}+\frac{1}{l_{2}+k_{2}}e^{\xi _{2}+\zeta _{2}}\\&\quad +\frac{(l_{1}-l_{2})(k_{1}-k_{2})}{(l_{1}+k_{1})(l_{2}+k_{2})(l_{1}+k_{2})(l_{1}+k_{2})}e^{\xi _{1}+\zeta _{1} +\xi _{2}+\zeta _{2}}, \end{aligned} \end{aligned}$$

(46)

which results in the two-soliton solution to Eq. (4) via $u=2(\mathrm {ln}f_{2})_{x}$.

Fig. 5

Soliton solutions to Eq. (4) with $c_{1}=c_{2}=-1$, $z=1$, $t=1$ and $\gamma =1$ a one-soliton solution: $l_{1}= 2$, $l_{2}=3$, $k_{1}=1$, $k_{2}=2$, $\xi _{1}^{0}=\zeta _{1}^{0}= 0$; b two-soliton solution: $l_{1}= 2$, $l_{2}=3$, $k_{1}=1$, $k_{2}=2$, $\xi _{1}^{0}=\xi _{2}^{0}=\zeta _{1}^{0}=\zeta _{2}^{0}= 0$; c three-soliton solution: $l_{1}=1$, $l_{2}=-0.4$, $l_{3}=1.8$, $l_{4}=1.4$, $k_{1}=1.5$, $k_{2}=-0.6$, $k_{3}=2$, $k_{4}=1.2$, $\xi _{1}^{0}=\xi _{2}^{0}=\xi _{3}^{0}=\zeta _{1}^{0}=\zeta _{2}^{0}=\zeta _{3}^{0}= 0$; d four-soliton solution: $l_{1}=2$, $l_{2}=3$, $l_{3}=4$, $k_{1}=1$, $k_{2}=2$, $k_{3}=3$, $\xi _{1}^{0}=\xi _{2}^{0}=\xi _{3}^{0}=\xi _{4}^{0}=\zeta _{1}^{0}=\zeta _{2}^{0}=\zeta _{3}^{0}=\zeta _{4}^{0}= 0$

Case 3 Taking $N=3$ in Eq. (39), we can obtain the three-soliton solution. Choosing $c_{11}=c_{22}=c_{33}=1$, the rest of $c_{ij}=0 (i,j=1,2,3)$, and $\phi _{j}=e^{\xi _{j}}, \psi _{j}=e^{\zeta _{j}}(j=1,2,3)$, we have

$$\begin{aligned} \begin{aligned} f_{3}&=(1,2,3,3^{*},2^{*},1^{*})\\ {}&=\left| \begin{array}{ccc} 1+\frac{1}{l_{1}+k_{1}}e^{\xi _{1}+\zeta _{1}}&{}\frac{1}{l_{1}+k_{2}}e^{\xi _{1}+\zeta _{2}}&{}\frac{1}{l_{1}+k_{3}}e^{\xi _{1}+\zeta _{3}}\\ \frac{1}{l_{2}+k_{1}}e^{\xi _{2}+\zeta _{1}}&{}1+\frac{1}{l_{2}+k_{2}}e^{\xi _{2}+\zeta _{2}}&{}\frac{1}{l_{2}+k_{3}}e^{\xi _{2}+\zeta _{3}}\\ \frac{1}{l_{3}+k_{1}}e^{\xi _{3}+\zeta _{1}}&{}+\frac{1}{l_{3}+k_{2}}e^{\xi _{3}+\zeta _{2}}&{}1+\frac{1}{l_{3}+k_{3}}e^{\xi _{3}+\zeta _{3}}\\ \end{array}\right| \\&=1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{3}}+b_{12}e^{\eta _{1}+\eta _{2}}+b_{13}e^{\eta _{1}+\eta _{3}}\\&\quad +b_{23}e^{\eta _{2}+\eta _{3}}+b_{12}b_{13}b_{23}e^{\eta _{1}+\eta _{2}+\eta _{3}}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \eta _{1}&=\xi _{1}+\zeta _{1}+\delta _{1},\quad \eta _{2}=\xi _{2}+\zeta _{2}+\delta _{2},\quad \eta _{3}=\xi _{3}+\zeta _{3}+\delta _{3}, \quad e^{\delta _{i}}=\frac{1}{l_{i}+k_{i}}, \end{aligned}$$

and

$$\begin{aligned} b_{12}=\frac{(l_{1}-l_{2})(k_{1}-k_{2})}{(l_{1}+k_{2})(l_{2}+k_{1})},\quad b_{13}=\frac{(l_{1}-l_{3})(k_{1}-k_{3})}{(l_{1}+k_{3})(l_{3}+k_{1})} ,\quad b_{23}=\frac{(l_{2}-l_{3})(k_{2}-k_{3})}{(l_{2}+k_{3})(l_{3}+k_{2})}, \end{aligned}$$

which gives rise to the three-soliton solution to Eq. (4) via $u=2(\mathrm {ln}f_{3})_{x}$.

Through taking $N=4$ in Eq. (39), the solution $f_{4}$ to Eq. (9) can be derived similarly, and further the four-soliton solution to Eq. (4) can be computed. As an example, by selecting the appropriate parameters, the one-, two-, three- and four-soliton solutions are plotted in Fig. 5.

The above solutions in the Grammian form are also the kink solitons. In Fig. 5a, the one-soliton can be observed to be a kink soliton. When $l_{1}+k_{1}$ greater than zero, u in Eq. (45) is non-singular, and its maximum value is $2(l_{1}+k_{1})$, and the minimum value is 0. In Fig. 5, we also show two-, three- and four-soliton solutions, where the two- and three-soliton are both the parallel kink solitons, and the four-soliton is the oblique kink soliton. The interaction between solitons belongs to elastic collision, that is, the soliton shape and velocity are kept unchanged before and after the collision.

6 Conclusions

In this paper, we have investigated the $(3+1)$-dimensional generalized Kadomtsev–Petviashvili equation [see Eq. (4)], which contains two variable-coefficients $c_1$ and $c_2$. We can obtain the $(3+1)$-dimensional generalized shallow water wave equation and the $(3+1)$-dimensional Jimbo-Miwa equation through choosing the appropriate coefficients in Eq. (4). Based on the Hirota bilinear form, the bilinear BT has been constructed, which consists of four bilinear equations and five free parameters. In addition, a specific exponential wave solution has been given through the bilinear BT.

The N-soliton solutions to Eq. (4) have been obtained in the Pfaffian form, and reduced into Pfaffian identity. As a special case, the one-, two- and three-soliton solutions have been shown and analyzed in Fig. 2. It is worth noting that Pfaffian can not only give soliton solutions, but also solve different types of solutions according to different assumptions of $\phi _{i}$ (29), such as the rational solution, hyperbola function solution and triangle function solution. We have shown the solution in the form of triangle function solution in Pfaffian and plotted it in Fig. 3. From the properties of Pfaffian and determinant, we have derived the N-soliton solutions in Wronskian and Grammian forms, where bilinear Eq. (9) can be reduced into Jacobi and Plücker identities, respectively. One-, two-, three- and four-soliton solutions have been obtained and analyzed in Figs. 4  and 5.