A mass- and energy-conserved DG method for the Schrödinger-Poisson equation

Abstract

We construct, analyze, and numerically validate a class of conservative discontinuous Galerkin (DG) schemes for the Schrödinger-Poisson equation. The proposed schemes all shown to conserve both mass and energy. For the semi-discrete DG scheme the optimal L² error estimates are provided. Efficient iterative algorithms are also constructed to solve the second-order implicit time discretization. The presented numerical tests demonstrate the method’s accuracy and robustness, confirming that the conservation properties help to reproduce faithful solutions over long time simulation.

1 Introduction

Considered here is the following problem for the Schrödinger–Poisson (SP) equation:

$$ \begin{array}{@{}rcl@{}} {\mathbf{i}} u_{t} &=&-{\Delta} u + {\Phi} u,\quad t >0, x\in {\Omega}, \end{array} $$

(1.1a)

$$ \begin{array}{@{}rcl@{}} -{\Delta} {\Phi}&=&\mu(|u|^{2}-c), \quad x\in {\Omega}, \end{array} $$

(1.1b)

$$ \begin{array}{@{}rcl@{}} u(x, 0)&=& u_{0}(x), \quad \text{in} {\Omega}, \end{array} $$

(1.1c)

where u = u(x,t) is a complex-valued function of time t > 0 and spatial variable x ∈Ω, which is a bounded domain in $\mathbb {R}^{d}$, μ = ± 1 is a rescaled physical constant, which signifies the property of the underlying forcing, repulsive if μ > 0 and attractive if μ < 0. ${\mathbf {i}}=\sqrt {-1}$ stands for the imaginary unit, and c is a background charge. For the numerical purpose it is common to truncate the unbounded spatial domain to a sufficiently large finite domain and impose simple boundary conditions (see [1]). In this paper we consider both periodic and homogeneous Dirichlet boundary conditions (see Section 2), although most of our derivations can be carried out for other types of boundary conditions.

The Schrödinger–Poisson equation (also called Schrödinger-Newton equation or Schrödinger-Maxwell equation) describes many physical phenomena in quantum mechanical systems and in semiconductor modeling; we refer the readers to [14, 20, 23] and the references therein. It also appears as an approximate mean-field equation derived from the first principle model in a system of a large number of particles [7]. Mathematically, the Schrödinger–Poisson equation is a prototypical dispersive wave equation, its solution exhibits some intriguing properties. A great deal of interesting research has been devoted to the mathematical analysis for the Schrödinger-Poisson systems (see [10, 12, 19, 21, 34] and references therein). In particular, the equation preserves both the mass and the energy under appropriate boundary conditions. The quality of the numerical approximation hence hinges on how well the conserved integrals can be preserved at the discrete level. Numerical methods without this property may result in substantial phase and shape errors after long time integration. Indeed for some wave equations the invariant preserving high-order numerical methods have been shown more accurate than non-conservative methods after long-time numerical integration (see, e.g., [9, 28]).

The objective of this work is to develop and analyze conservative discontinuous Galerkin (DG henceforth ) schemes for the Schrödinger–Poisson equation, with particular attention on preservation of both mass and energy at the discrete level. In addition, we obtain sharp L² error estimates for the semi-discrete DG method (continuous in time) at the full nonlinear setting.

The DG method is a class of finite element approximations using discontinuous, piecewise polynomials as both the solution and test-function spaces (see [13] for a historical review). It combines advantages of both finite element and finite volume methods, including high-order accuracy, high parallel efficiency, flexibility for hp-adaptivity and straightforward implementation on arbitrary meshes in complex geometries. Particularly relevant for the present discussion is the fact that such schemes do not demand continuity at the spatial grid-points, and this allows a flexibility in making local refinements to an existing numerical grid not shared by continuous Galerkin methods. The DG method is also known to enjoy mathematically provable high-order accuracy and stability (see e.g., [17, 35, 36]).

The DG method was originally introduced in the context of hyperbolic conservation laws. Later, the method was extended to deal with derivatives of order higher than one. In recent years, the DG schemes have been actively designed and applied for the Schrödinger equation and its variants (see, e.g., [18, 22, 25, 29, 38, 39, 41,42,43] and references therein; see also works by spectral methods [5, 6]). One main effort is to preserve the mass by high-order spatial discretization. Within the DG-framework, especially relevant to our development is the body of work [25, 30, 40] on approximating solutions to Schrödinger type equations using the direct Discontinuous Galerkin method (DDG method) developed initially for the diffusion equation introduced by Liu and Yan [26, 27]. The idea of DDG methods is to directly force the weak solution formulation of the PDE into the DG function space for both the numerical solution and test functions. The main feature in the DDG schemes proposed in [26, 27] lies in numerical flux choices for the solution gradient, which involve higher order derivatives evaluated crossing cell interfaces. The parameter is often called method parameter or flux parameter due to its appearing in the choice of the numerical flux, or even penalty parameter when it is required to be large enough to ensure the scheme stability. In [30], a high-order mass-preserving DG (MPDG) method was introduced for the nonlinear Schrödinger equation, with the optimal L² error estimate obtained in one-dimensional setting. A key observation in [30] is that the conservation property and the optimal accuracy remains valid independent of the size of the flux parameter. An extension to multi-dimensional setting was further carried out in [25], in which the authors presented two different approaches to handle structured and unstructured meshes, respectively. For rectangular meshes, the error analysis is based-on tensor product of polynomials and a super-convergence result, the obtained result is sharp and valid with or without a flux parameter. For unstructured shape regular meshes, the optimal error analysis is based on a global projection and its approximation error [3, 24] when the flux parameter is large. This later approach was further extended to solve the nonlinear magnetic Schrödinger equation in [40]. Both mass and energy conservation are shown to hold for the semi-discrete DG scheme, with a proven optimal L² error estimate in nonlinear setting. For the time discretization a second-order Strang splitting is applied in [25, 30, 40].

In this paper, we extend the ideas in [25, 30, 40] to develop a mass- and energy-conserved DG method for the Schrödinger–Poisson equation. Our focus will be on constructing a spatially high-order conservative DG scheme with second-order time discretization so that two conserved quantities are preserved in the presence of a self-interaction electric field.

To our knowledge, there is as yet no rigorous convergence result in the literature for the DG method for the nonlinear Schrödinger-Poisson equation. We mention, however, the work by Lubich [33], where an error analysis was first given for a time-splitting method; and further works such as [4, 11] using the splitting method. The main conclusion of this paper is that both semi-discrete and fully discrete schemes can preserve both mass and energy independent of the size of the flux parameter. For time discretization we follow the recent work [16] in adopting a Crank-Nicolson type discretization, so that the resulting full-discrete scheme is second order in time. Furthermore, we establish the optimal L² error estimate for the semi-discrete scheme. Though the main analysis tool for nonlinear terms follows the line as in [40], it requires a careful handling of the coupling with the Poisson equation (see Lemma 3.2 and its proof).

This paper is organized as follows: In Section 2 we review some basic properties of the SP equation, and present semi-discrete DG schemes, which are shown to preserve both mass and energy for meshes of arbitrary size, for the nonlinear Schrödinger–Poisson equation. In Section 3 we carry out error estimates for the DG method, followed by an efficient iterative algorithm to solve the resulting nonlinear equations. In Section 4 we present numerical experiments to validate the theoretical results and to gauge the performance of the proposed schemes, especially the sharpness of the convergence rates. The paper is completed with some concluding remarks and comments given in Section 5.

Throughout this paper, we denote spatial variable $x=(x^{1}, \cdots , x^{d})\in \mathbb {R}^{d}$ and adopt standard notations for Sobolev spaces such as W^m,p(D) on sub-domain D ⊂Ω equipped with the norm ∥⋅∥_m,p,D and semi-norm |⋅|_m,p,D. When D = Ω, we omit the index D; and if p = 2, we set W^m,p(D) = H^m(D), ∥⋅∥_m,p,D = ∥⋅∥_m,D, and |⋅|_m,p,D = |⋅|_m,D. When m = 0, we simply use ∥⋅∥ to denote the usual L²-norm. We also denote ∂Ω the boundary of Ω. We use the notation $C\lesssim B$ to indicate that C can be bounded by B multiplied by a constant independent of the mesh size h. $C\sim B$ stands for $C\lesssim B$ and $B\lesssim C$. Also we use (⋅)⁺ to denote $\max \limits (\cdot , 0)$, and $(\cdot )^{-}=\min \limits (\cdot , 0)$.

2 The conservative DG method

Details of the numerical approximations are now set forth. This begins with a discussion of two conservation properties of the continuous problem, followed by the spatial discretization which leads directly to a semi-discrete approximation.

2.1 The Schrödinger-Poisson equation

For the model equation considered in this paper, we impose the homogeneous Dirichlet boundary condition

$$ (i) u=0, \quad \quad (ii) {\Phi}=0, \quad x\in \partial {\Omega}, t>0, $$

(2.1)

with which the weak formulation of the problem reads: find $u\in C^{0}([0, T), {H_{0}^{1}}({\Omega }))$ and ${\Phi }\in {H_{0}^{1}}({\Omega })$, such that

$$ \begin{array}{@{}rcl@{}} {\mathbf{i}} \langle u_{t}, v \rangle&=&\langle \nabla u, \nabla v\rangle+\langle{\Phi} u, v\rangle,\qquad \forall v\in {H_{0}^{1}}({\Omega}), \end{array} $$

(2.2)

$$ \begin{array}{@{}rcl@{}} (\nabla {\Phi}, \nabla w ) &=&\mu (|u|^{2}-c, w ),\qquad \forall w\in {H_{0}^{1}}({\Omega}). \end{array} $$

(2.3)

Here, 〈⋅,⋅〉 denotes the standard L² product for complex valued functions, i.e, $\langle u, v \rangle ={\int \limits }_{\Omega }u(x)\cdot v^{*}(x)dx$ with v^∗ denoting the complex conjugate of v, and (⋅,⋅) denotes the standard L² product for real valued functions, i.e, $(u, v)={\int \limits }_{\Omega }u(x)\cdot v(x)dx$.

One can verify that the problem (??) satisfies the conservation laws

$$ \begin{array}{@{}rcl@{}} \text{mass conservation} \qquad M(t)&=&{\int}_{\Omega}|u|^{2}dx=M(0), \end{array} $$

(2.4)

$$ \begin{array}{@{}rcl@{}} \text{energy conservation}\qquad E(t)&=&{\int}_{\Omega}\left( |\nabla u|^{2}+\frac{1}{2\mu}|\nabla {\Phi}|^{2}\right)dx=E(0). \end{array} $$

(2.5)

In fact, take v = u in (2.2), one has

$$ {\mathbf{i}} \langle u_{t}, u\rangle=\langle \nabla u, \nabla u\rangle+\langle{\Phi} u, u\rangle. $$

This upon subtraction of its conjugate gives (2.4).

Furthermore, taking v = u_t in (2.2) we have

$${\mathbf{i}} \langle u_{t}, u_{t}\rangle=\langle \nabla u, \nabla u_{t}\rangle+\langle {\Phi} u, u_{t}\rangle,$$

and

$${-\mathbf{i}}\langle u_{t}, u_{t}\rangle=\langle \nabla u_{t}, \nabla u\rangle+\langle{\Phi} u_{t}, u\rangle.$$

Thus,

$$ \frac{d}{dt}\|\nabla u\|^{2}+{\int}_{\Omega}{\Phi}\frac{d}{dt}|u|^{2}dx=\frac{d}{dt}\|\nabla u\|^{2}+{\int}_{\Omega}{\Phi}\frac{d}{dt}(|u|^{2}-c)dx=0. $$

The second term when using (2.3) reduces to

$$ \frac{1}{\mu}\int \nabla {\Phi}_t \cdot \nabla {\Phi} dx =\frac{1}{2\mu} \frac{d}{dt} \int |\nabla {\Phi}|^2 dx. $$

Hence $\frac {d}{dt} E(t)=0$, i.e., (2.5) holds. Note that these solution properties also hold true for periodic boundary conditions, for which we also present corresponding schemes as a comparison.

We shall design high-order DG schemes so that both mass and energy are also preserved at the discrete level.

2.2 Scheme formulation

Let the domain Ω be a Cartesian product

$$ {\Omega}= {\Pi}_{i=1}^d I^i, $$

where $I^{i}=\cup _{\alpha _{i}=1}^{N_{i}}I^{i}_{\alpha _{i}}$ with $I^{i}_{\alpha _{i}} =[x^{i}_{\alpha _{i}-1/2}, x^{i}_{\alpha _{i}+1/2}]$. We use rectangular meshes $\mathcal {T}_{h}=\{K_{\alpha }\}$, with $K_{\alpha }=I^{1}_{\alpha _{1}}\times {\cdots } \times I^{d}_{\alpha _{d}}$, where α = (α₁,⋯ ,α_d), N = (N₁,⋯ ,N_d). Denote by $h_{i} =\max \limits _{1\leq \alpha _{i}\leq N_{i}}|I^{i}_{\alpha _{i}}|$, with $h=\max \limits _{1\leq i\leq d} h_{i}$. In the following, we omit the subscript index α of K_α, for simplicity.

We define the discontinuous Galerkin (DG) space as follows

$$ {V_{h}=\{v: v\in Q_k(K),\quad \forall K\in \mathcal{T}_{h}\},} $$

where Q_k is the space of tensor products of one-dimensional polynomials of degree up to k. We also define another DG space ${V_{h}^{c}}$ as

$$ {{V_{h}^{c}}=\{v: v\in {Q_{k}^{c}}(K),\quad \forall K\in \mathcal{T}_{h}\},} $$

where ${Q_{k}^{c}}$ is the space of tensor products of one-dimensional complex polynomials of degree up to k. Note that the traces of functions are double-valued on ${{\Gamma }^{0}_{h}}:= {\Gamma }_{h}-\partial {\Omega }$ and single-valued on ${\Gamma }_{h}^{\partial }=\partial {\Omega }$, where ${\Gamma }_{h}={{\Gamma }_{h}^{0}}\cup {\Gamma }_{h}^{\partial }$ is the union of interior faces and boundary faces.

We also introduce some trace operators that will help us to define the interface terms. Let K¹ and K² be two neighboring cells with a common edge $e{\in {\Gamma }_{h}^{0}}$, and $w_{i}=w|_{\partial K^{i}} i=1, 2$, we define the average {w} and the jump [w] as follows:

$$ {\{w\}=\frac{1}{2}(w_1+w_2), \quad [w]=w_2-w_1 \quad \text{on} \quad e=\bar K_1\cap \bar K_2,} $$

where the jump is defined as a forward difference along the normal direction n, which is defined to be oriented from K¹ to K². For $e\in {\Gamma }_{h}^{\partial }$, w has a uniquely defined restriction on e, both average and jump need to be carefully defined in virtue of the specified boundary conditions.

A direct discretization of (2.2) and (2.3) leads to the DG method: find $(u_{h}, {\Phi }_{h})\in {V_{h}^{c}}\times V_{h}$, such that

$$ \begin{array}{@{}rcl@{}} {\mathbf{i}} \langle u_{ht}, v_{h}\rangle &=&A_{0}(u_{h}, v_{h})+\langle{\Phi}_{h}u_{h}, v_{h} \rangle,\qquad \forall v_{h}\in {V_{h}^{c}}, \end{array} $$

(2.6)

$$ \begin{array}{@{}rcl@{}} A_{1}({\Phi}_{h}, w_{h})&=&\mu(|u_{h}|^{2}-c, w_{h}),\qquad \forall w_{h}\in V_{h}. \end{array} $$

(2.7)

Here, $u_{ht}=\frac {\partial u_{h}(x, t)}{\partial t}$, the bilinear functional

$$ \begin{array}{@{}rcl@{}} A_{0}(u_{h}, v_{h}) & =& {A_{0}^{0}}(u_{h}, v_{h}) +{A_{0}^{b}}(u_{h}, v_{h})\\ {A_{0}^{0}}(u_{h}, v_{h}) & =&{\sum}_{K\in \mathcal{T}_{h}} \langle \nabla u_{h}, \nabla v_{h} \rangle_{K}+ {\sum}_{e\in {{\Gamma}_{h}^{0}}}\langle \widehat{\partial_{n} u_{h}}, [v_{h}] \rangle_{e} + \langle [u_{h}], \{\partial_{n} v_{h}\}\rangle_{e}, \end{array} $$

(2.8)

and

$$ \begin{aligned} A_{1}({\Phi}_{h}, w_{h}) =& {A_{1}^{0}}({\Phi}_{h}, w_{h}) +{A_{1}^{b}}({\Phi}_{h}, w_{h})\\ {A_{1}^{0}}({\Phi}_{h}, w_{h}) =& {\sum}_{K\in \mathcal{T}_{h}} (\nabla {\Phi}_{h}, \nabla w_{h})_{K}+ {\sum}_{e\in {{\Gamma}_{h}^{0}}} (\widehat{\partial_{n} {\Phi}_{h}}, [w_{h}] )_{e} + ([{\Phi}_{h}], \{\partial_{n} w_{h}\})_{e}, \end{aligned} $$

(2.9)

where boundary terms ${A_{1}^{b}}(u_{h}, v_{h})$ and ${A_{0}^{b}}({\Phi }_{h}, w_{h})$ are specified later accroding to the boundary conditions, the numerical fluxes are taken as

$$ \begin{array}{@{}rcl@{}} \widehat{\partial_{n} u_{h}}&:=&\beta h_{e}^{-1}[u_{h}]+\{\partial_{n} u_{h}\},\qquad \forall e\in {{\Gamma}_{h}^{0}}, \end{array} $$

(2.10)

$$ \begin{array}{@{}rcl@{}} \widehat{\partial_{n} {\Phi}_{h}}&:=&\beta_{0}h_{e}^{-1}[{\Phi}_{h}]+\{\partial_{n} {\Phi}_{h}\}+\beta_{1}h_{e}[{\partial_{n}^{2}}{\Phi}_{h}],\quad \forall e{\in{\Gamma}_{h}^{0}}, \end{array} $$

(2.11)

where n is the unit normal vector on the interface, ${\partial _{n}^{2}}$ denotes the second-order directional derivative in n, and β,β₀,β₁ are method parameters to be chosen. Boundary fluxes depend on the boundary conditions pre-specified, leading to the following formulations:

$$ \begin{array}{@{}rcl@{}} \text{for periodic case} &\qquad & {A^{b}_{0}}(u, v)=\frac{1}{2} {\int}_{{\Gamma}^{\partial} } \left( \{\partial_{n} u_{h}\}[v_{h}^{*}]+ [u_{h}]\{\partial_{n} v_{h}^{*}\} \right)ds, \end{array} $$

(2.12a)

$$ \begin{array}{@{}rcl@{}} \text{for periodic case} &\qquad & {A^{b}_{1}}({\Phi}, w_{h})=\frac{1}{2} {\int}_{{\Gamma}^{\partial} } \left( \{\partial_{n} {\Phi}_{h} \}[w_{h}]+ [{\Phi}_{h}]\{\partial_{n} w_{h}\} \right)ds, \end{array} $$

(2.12b)

$$ \begin{array}{@{}rcl@{}} \text{for (i) in (2.1)} &\qquad & {A^{b}_{0}}(u_{h}, v_{h})= {\int}_{{\Gamma}^{\partial}} ((\beta h_{e}^{-1}u_{h}-\partial_{n} u_{h})v_{h}^{*} - u_{h} \partial_{n} v_{h}^{*} )ds, \end{array} $$

(2.12c)

$$ \begin{array}{@{}rcl@{}} \text{for (ii) in (2.1)} &\qquad & {A^{b}_{1}}({\Phi}_{h}, w_{h})= {\int}_{{\Gamma}^{\partial}} ((\beta h_{e}^{-1}{\Phi}_{h}-\partial_{n} {\Phi}_{h})w_{h} - {\Phi}_{h} \partial_{n} w_{h} )ds. \end{array} $$

(2.12d)

Remark 2.1

Several remarks are in order:

• (i) For non-homogeneous boundary conditions, one needs only a slight change in boundary terms ${A_{i}^{b}} (i=0, 1)$.

• (ii) For periodic case the left boundary and the right boundary are considered as same, for which we use the factor 1/2 to avoid recounting.

• (iii) In the scheme formulation the choice of n on interior faces does not affect each product involved. Hence ∂_n is defined based on a fixed choice of n. However, on the boundary phase, n is taken as the usual outside normal unit to the domain boundary ∂Ω.

• (iv) Here on the interface with $x^{i}=x^{i}_{\alpha _{i}+1/2}$,

$$ h_e= \frac{1}{2}(|I^i_{\alpha_{i}}|+|I^i_{\alpha_{i+1}}|). $$

Note that for uniform meshes h_e = h_i.

The initial data for the semi-discrete DG scheme (2.6) can be defined by

$$ u_{h}(x, 0)={\Pi} u_0, $$

where π is the standard piecewise L² projection.

2.3 Conservation properties

In order to verify the conservation properties of the scheme (2.6)–(2.7), we prepare the following lemma.

Lemma 2.1

Let a,b be complex polynomials in ${V_{h}^{c}}$, then

$$ \begin{array}{@{}rcl@{}} A_{0}(a, b)= \overline{A_{0}(b, a)}. \end{array} $$

(2.13)

The proof of this identity requires only a direct verification. Then it is straightforward to show that the semi-discrete DG scheme (2.6)–(2.7) conserves both mass and energy.

Theorem 2.1

The semi-discrete DG scheme (2.6)–(2.7) for any $\beta \in \mathbb {R}$ satisfies discrete conservation laws for both mass and energy, respectively,

$$ \begin{array}{@{}rcl@{}} & &M_{h}(t):={\int}_{\Omega} |{u_{h}}|^{2}dx =M_{h}(0), \end{array} $$

(2.14)

$$ \begin{array}{@{}rcl@{}} && E_{h}(t): =A_{0}(u_{h}, u_{h}) + \frac{1}{2}{\int}_{\Omega} {\Phi}_{h}\left( |u_{h}|^{2}-c\right) dx =E_{h}(0) \end{array} $$

(2.15)

for all t ≥ 0 for which the solution exists.

Proof

Letting v_h = u_h in (2.6) leads to

$$ {\mathbf{i}} \langle u_{ht}, u_{h}\rangle =A_0(u_{h}, u_{h})+\langle{\Phi}_hu_{h}, u_{h} \rangle. $$

Then (2.14) follows at once from subtracting its conjugate.

Letting v_h = u_ht in (2.6) leads to

$$ {\mathbf{i}} \langle u_{ht}, u_{ht}\rangle=A_{0}(u_{h}, u_{ht})+\langle {\Phi}_{h} u_{h}, u_{ht}\rangle, $$

(2.16)

Taking its conjugate using (2.13) we obtain

$$ -{\mathbf{i}}\langle u_{ht}, u_{ht}\rangle=A_{0}(u_{ht}, u_{h})+\langle{\Phi}_{h} u_{ht}, u_{h}\rangle. $$

(2.17)

Adding (2.16) and (2.17) gives

$$ \frac{d}{dt}A_{0}(u_{h}, u_{h})+\left( {\Phi}_{h}, \partial_{t} |u_{h}|^{2}\right)=\frac{d}{dt}A_{0}(u_{h}, u_{h})+\left( {\Phi}_{h}, \partial_{t} (|u_{h}|^{2}-c)\right)=0. $$

That is

$$ \frac{d}{dt}\left[A_{0}(u_{h}, u_{h})+\left( {\Phi}_{h}, |u_{h}|^{2}-c\right)\right]=\left( {\Phi}_{ht}, |u_{h}|^{2}-c\right). $$

(2.18)

Taking w_h = Φ_ht in (2.7), we have

$$ (\nabla {\Phi}_{h}, \nabla {\Phi}_{ht})=\mu(|u_{h}|^{2}-c, {\Phi}_{ht}). $$

Take time derivative in (2.7) and choose w_h = Φ_h so that

$$ (\nabla {\Phi}_{ht}, \nabla {\Phi}_{h})=\mu\left( \partial_{t} (|u_{h}|^{2}-c), {\Phi}_{h}\right). $$

Then

$$(|u_{h}|^{2}-c, {\Phi}_{ht})=\left( \partial_{t} (|u_{h}|^{2}-c), {\Phi}_{h}\right).$$

From (2.18) we have

$$ \frac{d}{dt}\left[A_{0}(u_{h}, u_{h})+\left( {\Phi}_{h}, |u_{h}|^{2}-c\right)\right]=\left( \partial_{t} (|u_{h}|^{2}-c), {\Phi}_{h}\right)=\frac{1}{2}\frac{d}{dt}\left( |u_{h}|^{2}-c, {\Phi}_{h}\right). $$

Thus

$$\frac{d}{dt}E_{h}(t)=\frac{d}{dt}\left[A_{0}(u_{h}, u_{h})+\frac{1}{2}\left( {\Phi}_{h}, |u_{h}|^{2}-c\right)\right]=0.$$

This completes the proof. □

2.4 Time discretization

Not just any time-stepping method employed in a fully discrete scheme will preserve the conservation properties of the semi-discrete approximations. In this paper, we consider the Crank-Nicolson method for the time discretization so that the fully discrete DG scheme also conserves both mass and energy. Let 0 = t₀ < t₁ < ⋯ < t_K = T be a partition of the interval [0,T] with time step Δt = t_n+ 1 − t_n. Here uniform time step Δt is simply taken. The fully discrete second-order in time approximations are constructed using the midpoint rule in the following manner. We define

$$ D_t u_{h}^n=\frac{u_{h}^{n+1} -u_{h}^n}{\Delta t}, \quad u_{h}^{n+1/2}=\frac{u_{h}^{n+1}+u_{h}^n}{2}. $$

${\Phi }_{h}^{n+1/2}$ is defined analogously to $u_{h}^{n+1/2}$. Then the fully discrete DG method is to find

$$\left( u_{h}^{n+1}, {\Phi}_{h}^{n+1}\right)\in V_{h}^c\times V_{h} $$

such that

$$ \begin{array}{@{}rcl@{}} {\mathbf{i}} \langle D_{t} {u_{h}^{n}}, v_{h}\rangle &=&A_{0}(u_{h}^{n+1/2}, v_{h})+\langle{\Phi}_{h}^{n+1/2}u_{h}^{n+1/2}, v_{h} \rangle,\qquad \forall v_{h}\in {V_{h}^{c}}, \end{array} $$

(2.19a)

$$ \begin{array}{@{}rcl@{}} A_{1}({\Phi}_{h}^{n+1}, w_{h})&=&\mu(|u_{h}^{n+1}|^{2}-c, w_{h}),\qquad {\forall} w_{h}\in V_{h}, \end{array} $$

(2.19b)

with the initial data defined as follows:

$$ {u_{h}^{0}}={\Pi} u_{0}, \qquad A_{1}({{\Phi}_{h}^{0}}, w_{h})=\mu(|{u_{h}^{0}}|^{2}-c, w_{h}),\qquad {\forall} w_{h}\in V_{h}. $$

(2.20)

Theorem 2.2

The fully discrete DG scheme (??) for any $\beta \in \mathbb {R}$ and β₁ = 0 satisfies discrete conservation laws for both mass and energy, respectively,

$$ \begin{array}{@{}rcl@{}} & &{M_{h}^{n}}:={\int}_{\Omega} |{u_{h}^{n}}|^{2}dx ={M_{h}^{0}}, \end{array} $$

(2.21)

$$ \begin{array}{@{}rcl@{}} && {E_{h}^{n}}: =A_{0}({u_{h}^{n}}, {u_{h}^{n}}) + \frac{1}{2\mu}A_{1}({{\Phi}_{h}^{n}}, {{\Phi}_{h}^{n}}) ={E_{h}^{0}}, \end{array} $$

(2.22)

for any integer n > 0.

Proof

Letting $v_{h} = u_{h}^{n+1/2}$ in (2.19a) leads to

$$ {\mathbf{i}} \left\langle D_{t} {u_{h}^{n}}, \frac{u_{h}^{n+1}+{u_{h}^{n}}}{2}\right\rangle =A_{0}(u_{h}^{n+1/2}, u_{h}^{n+1/2})+\left\langle{\Phi}_{h}^{n+1/2}u_{h}^{n+1/2}, u_{h}^{n+1/2} \right\rangle. $$

(2.23)

Subtracting this from its conjugate and using (2.13) we obtain

$${\mathbf{i}} \left( \left\langle D_{t} {u_{h}^{n}}, \frac{u_{h}^{n+1}+{u_{h}^{n}}}{2}\right\rangle+\left\langle \frac{u_{h}^{n+1}+{u_{h}^{n}}}{2}, D_{t} {u_{h}^{n}}\right\rangle\right)=\frac{{\mathbf{i}}}{\Delta t}{\int}_{\Omega}|u_{h}^{n+1}|^{2}-|{u_{h}^{n}}|^{2}dx=0. $$

Thus $M_{h}^{n+1}={M_{h}^{n}}$.

Letting $v_{h}=D_{t}{u_{h}^{n}}$ in (2.19a) leads to

$$ {\mathbf{i}} \left\langle D_{t} {u_{h}^{n}}, D_{t} {u_{h}^{n}}\right\rangle =A_{0}\left( u_{h}^{n+1/2}, D_{t} {u_{h}^{n}}\right)+\left\langle{\Phi}_{h}^{n+1/2}u_{h}^{n+1/2}, D_{t} {u_{h}^{n}} \right\rangle. $$

Adding this upon its conjugate and using (2.13), after some algebraic manipulation, we obtain

$$\begin{aligned} &A_{0}\left( u_{h}^{n+1/2}, D_{t} {u_{h}^{n}}\right)+A_{0}\left( D_{t} {u_{h}^{n}}, u_{h}^{n+1/2}\right)\\ &\qquad\quad +\left\langle{\Phi}_{h}^{n+1/2}u_{h}^{n+1/2}, D_{t} {u_{h}^{n}} \right\rangle+\left\langle{\Phi}_{h}^{n+1/2}D_{t} {u_{h}^{n}}, u_{h}^{n+1/2} \right\rangle=0. \end{aligned} $$

Upon rewriting we obtain

$$ A_0\left( u_{h}^{n+1}, u_{h}^{n+1}\right)-A_0\left( u_{h}^{n}, u_{h}^{n}\right)+\left\langle{\Phi}_{h}^{n+1/2}u_{h}^{n+1}, u_{h}^{n+1}\right\rangle-\left\langle{\Phi}_{h}^{n+1/2}u_{h}^n, u_{h}^{n} \right\rangle =0. $$

Note that A₁(a,b) = A₁(b,a) if β₁ = 0, then

$$ \begin{array}{@{}rcl@{}} \left\langle{\Phi}_{h}^{n+1/2}u_{h}^{n+1}, u_{h}^{n+1}\right\rangle-\left\langle{\Phi}_{h}^{n+1/2}{u_{h}^{n}}, {u_{h}^{n}} \right\rangle &=&\sum\limits_{K\in\mathcal{T}_{h}}{\int}_{K}{\Phi}_{h}^{n+1/2}\left( |u_{h}^{n+1}|^{2}-c-\left( |{u_{h}^{n}}|^{2}-c\right)\right)dx\\ &=&\frac{1}{\mu}A_{1}({\Phi}_{h}^{n+1}, {\Phi}_{h}^{n+1/2})-\frac{1}{\mu}A_{1}({{\Phi}_{h}^{n}}, {\Phi}_{h}^{n+1/2})\\ &=&\frac{1}{2\mu} (A_{1}({\Phi}_{h}^{n+1}, {\Phi}_{h}^{n+1}) -A_{1}({{\Phi}_{h}^{n}}, {{\Phi}_{h}^{n}})). \end{array} $$

The energy conservation now follows from combining the above two relations. □

Finally, we introduce a simple iteration algorithm for solving the fully discrete DG scheme (??). From $({u_{h}^{n}}, {{\Phi }_{h}^{n}})$, we obtain $(u_{h}^{n+1}, {\Phi }_{h}^{n+1})$ as follows:

Set $(u_{h}^{n+1/2, m}, {\Phi }_{h}^{n+1, m})=({u_{h}^{n}}, {{\Phi }_{h}^{n}})$ for m = 0, we find

$$(u_{h}^{n+1/2, m+1}, {\Phi}_{h}^{n+1,m+1})\in V_{h}^c\times V_{h} $$

by iteratively solving

$$\begin{aligned} \left( {\mathbf{i}}-\frac{\Delta t}{4}({\Phi}_{h}^{n+1,m}+{{\Phi}_{h}^{n}})\right) \left\langle u_{h}^{n+1/2, m+1}, v_{h}\right\rangle-&\frac{\Delta t}{2}A_{0}(u_{h}^{n+1/2, m+1}, v_{h})={\mathbf{i}}\left\langle {u_{h}^{n}}, v_{h}\right\rangle,\qquad \forall v_{h}\in {V_{h}^{c}},\\ A_{1}({\Phi}_{h}^{n+1,m+1}, w_{h})=&\mu\left( |2u_{h}^{n+1/2, m+1}-{u_{h}^{n}}|^{2}-c, w_{h}\right),\qquad \forall w_{h}\in V_{h}, \end{aligned}$$

with m = 0,1,2,⋯ ,L, provided

$$\|u_{h}^{n+1/2, L+1}-u_{h}^{n+1/2, L}\|\leq \delta,$$

with some tolerance δ > 0 small, then let $u_{h}^{n+1}=2u_{h}^{n+1/2, L+1}-{u_{h}^{n}}$, and ${\Phi }_{h}^{n+1}={\Phi }_{h}^{n+1,L+1}$.

Remark 2.2

For the Schrödinger-Poisson equation of form

$$ \begin{aligned} \mathbf{i}u_{t}=&-{\Delta} u+{\Phi} u+V(x)u+|u|^{2}u, \quad t>0,\ x\in{\Omega},\\ -{\Delta} {\Phi}=&\mu(|u|^{2}-c), \quad x\in {\Omega},\\ u(x, 0)=&u_{0}(x),\quad x\in{\Omega}, \end{aligned} $$

(2.24)

both mass and energy of form

$$ \begin{array}{@{}rcl@{}} E(t)={\int}_{\Omega}\left( |\nabla u|^{2}+\frac{1}{2\mu}|\nabla {\Phi}|^{2}+V|u|^{2} +\frac{1}{2}|u|^{4}\right)dx \end{array} $$

(2.25)

are conserved. To deal with the additional nonlinear term |u|²u and still preserve total mass and energy at the discrete level, we adopt the relaxation-type scheme developed in [8]. As a consequence, the fully discrete DG scheme for (2.24) is formulated as follows: find

$$ ({\Psi}_{h}^{n+1/2}, u_{h}^{n+1}, {\Phi}_{h}^{n+1})\in V_{h}\times V_{h}^2\times V_{h}, $$

such that

$$ \begin{array}{@{}rcl@{}} & \left( \frac{{\Psi}_{h}^{n+1/2}+{\Psi}_{h}^{n-1/2}}{2}, w_{h}\right)=(|{u_{h}^{n}}|^{2}, w_{h}),\quad \forall w_{h}\in V_{h}, \end{array} $$

(2.26a)

$$ \begin{array}{@{}rcl@{}} &\mathbf{i}\left\langle D_{t} {u_{h}^{n}}, v_{h}\right\rangle=A_{0}\left( u_{h}^{n+1/2}, v_{h}\right) +\left\langle\left( {\Phi}_{h}^{n+1/2}+V+{\Psi}_{h}^{n+1/2}\right)u_{h}^{n+1/2}, v_{h}\right\rangle,\quad \forall v_{h}\in {V_{h}^{c}} \end{array} $$

(2.26b)

$$ \begin{array}{@{}rcl@{}} &A_{1}({\Phi}_{h}^{n+1}, w_{h})=\mu(|u_{h}^{n+1}|^{2}-c, w_{h}),\quad \forall w_{h}\in V_{h}, \end{array} $$

(2.26c)

subject to initial data u⁰(x) = u₀(x). With this time discretization, the discrete energy

$$ E_{h}^n: =A_0(u_{h}^n, u_{h}^n) + \frac{1}{2\mu}A_1({\Phi}_{h}^n, {\Phi}_{h}^n) +{\int}_{\Omega} \left( V(x)|u_{h}^n|^2 + \frac{1}{2} {\Psi}_{h}^{n+1/2}{\Psi}_{h}^{n-1/2} \right)dx $$

is indeed conserved. At each time step the discrete system can be solved by an iteration algorithm in the same manner. More precisely, set Ψ^− 1/2(x) = |u⁰(x)|² we update ${\Psi }_{h}^{n+1/2}$ by

$$ \left( {\Psi}_{h}^{n+1/2}, w_{h}\right)=(2|{u_{h}^{n}}|^{2}-{\Psi}_{h}^{n-1/2}, w_{h}),\quad \forall w_{h}\in V_{h}. $$

Then from $(u_{h}^{n+1/2, m}, {\Phi }_{h}^{n+1, m})=({u_{h}^{n}}, {{\Phi }_{h}^{n}})$ with m = 0, we find $(u_{h}^{n+1/2, m+1}, {\Phi }_{h}^{n+1,m+1})\in {V_{h}^{c}}\times V_{h}$ by iteratively solving

$$ \begin{aligned} \left( \mathbf{i}-\frac{\Delta t}{4}({\Phi}_{h}^{n+1,m}+{{\Phi}_{h}^{n}})\right) & \left\langle u_{h}^{n+1/2, m+1}, v_{h}\right\rangle-\frac{\Delta t}{2} A_{0}(u_{h}^{n+1/2, m+1}, v_{h})\\ &-\frac{\Delta t}{2} \left\langle (V+{\Psi}^{n+1/2})u_{h}^{n+1/2, m+1}, v_{h}\right\rangle=\mathbf{i}\left\langle {u_{h}^{n}}, v_{h}\right\rangle,\qquad \forall v_{h}\in {V_{h}^{c}},\\ &A_{1}({\Phi}_{h}^{n+1,m+1}, w_{h})=\mu\left( |2u_{h}^{n+1/2, m+1}-{u_{h}^{n}}|^{2}-c, w_{h}\right),\qquad \forall w_{h}\in V_{h}, \end{aligned} $$

with k = 0,1,2,⋯ ,L. Finally, let $u_{h}^{n+1}=2u_{h}^{n+1/2, L+1}-{u_{h}^{n}}$ and ${\Phi }_{h}^{n+1}={\Phi }_{h}^{n+1,L+1}$.

3 Optimal L ² error estimates for the semi-discrete scheme

In this section, we derive the optimal L² error estimates for the semi-discrete DG method proposed in Section 2.2. To be specific, we consider the periodic boundary condition for u and the homogeneous Dirichlet condition for Φ. Boundary terms are given by (??) and (??), respectively.

For $v\in V^{c}={V_{h}^{c}}+H^{2}({\Omega })$, we define the DG norm as

$$ |\!|\!|v|\!|\!|^2=\sum\limits_{K\in\mathcal{T}_{h}}\|\nabla v\|_{K}^2+\sum\limits_{K\in\mathcal{T}_{h}}h_K^2|v|_{2,K}^2+\sum\limits_{e\in {\Gamma}_{h}^0}h_e^{-1}|[v]|_{e}^2+\frac{1}{2}\sum\limits_{e\in {\Gamma}_{h}^{\partial}}h_e^{-1}|[v]|_{e}^2, $$

(3.1)

where h_e is the characteristic length of the edge e. One can verify that

$$ |A_0(w,v)|\leq {\Lambda}_0|\!|\!|w|\!|\!| \cdot|\!|\!|v|\!|\!|, \qquad \forall w,v\in V^c, $$

(3.2)

where Λ₀ is called the continuous constant. Furthermore, for $v\in {V_{h}^{c}}$, we have

$$ \|v\|_{E}^{2} \leq |\!|\!|v|\!|\!|^{2} \leq C_{0} \|v\|_{E}^{2} $$

(3.3)

for a constant C₀ > 1. Here the energy norm is given by

$$ \|v\|_{E}^{2}:= \sum\limits_{K\in\mathcal{T}_{h}}\|\nabla v\|_{K}^{2}+\sum\limits_{e{\in{\Gamma}_{h}^{0}}}h_{e}^{-1}|[v]|_{e}^{2} +\frac{1}{2}\sum\limits_{e\in {\Gamma}_{h}^{\partial}}h_{e}^{-1}|[v]|_{e}^{2}. $$

(3.4)

Similarly, for w ∈ V = V_h + H²(Ω), we have

$$ \begin{array}{@{}rcl@{}} |A_{1}(w,v)|\leq &{\Lambda}_{1}|\!|\!|w|\!|\!| \cdot|\!|\!|v|\!|\!|, \qquad \forall w,v\in V, \end{array} $$

(3.5)

$$ \begin{array}{@{}rcl@{}} \|v\|_{E}^{2} \leq &|\!|\!|v|\!|\!|^{2} \leq C_{1} \|v\|_{E}^{2},\qquad \forall v\in V_{h}. \end{array} $$

(3.6)

By abuse of notation, |[v_h]|² is meant to be |v_h|² in case of the homogeneous Dirichlet data on Γ^∂. Now we show that the bilinear operators A₀(⋅,⋅) and A₁(⋅,⋅) are coercive on DG spaces ${V_{h}^{c}}$ and V_h, respectively.

Lemma 3.1

For the bilinear forms A₀(⋅,⋅) and A₁(⋅,⋅) defined by (2.8) and (2.9), respectively, there exists Γ₁ > 0 and α ∈ (0,1) such that if β > Γ₁, then

$$ A_{0}(v, v) \geq \alpha \|v\|_{E}^{2}, \quad \forall v\in {V_{h}^{c}}, $$

(3.7)

and if the numerical flux (2.11) with (β₀,β₁) chosen so that β₀ > Γ₂(β₁) is suitably large, there exists γ > 0, such that

$$ A_{1}(w, w) \geq \gamma \|w\|_{E}^{2}, \qquad \forall w\in V_{h}. $$

(3.8)

The inequality (3.7) can be derived as in [40, Theorem 2.1], and the inequality (3.8) can be derived following [24, Lemma 3.1]. Details are hence omitted.

Remark 3.1

The conditions on the method parameters are only sufficient for the error estimate later. In our numerical tests β can be chosen as a small fixed number or zero, and the choice of (β₀,β₁) follows those known for the DDG method [24].

3.1 Projection and approximation properties

We first introduce a projection and then present its approximation properties. The specific form of the DG scheme led us to define the projection π₁ by

$$ \left\langle w-{\Pi}_{1} w, v\right\rangle + A_{0}(w- {\Pi}_{1} w,v)=0,\qquad \forall v\in {V_{h}^{c}}, $$

(3.9)

where this projection maps a function w into space ${V_{h}^{c}}$. This projection is uniquely defined; since for w = 0 with v = −π₁w we have

$$ 0=\|v\|^2 +A_0(v,v) \geq \|v\|^2+\alpha |\!|\!|v|\!|\!|^2, \quad\quad \forall v \in V_{h}^c, $$

where we have used the coercivity (3.7), hence v ≡ 0. This says that such projection is well-defined.

Theorem 3.1

For w ∈ H^k+ 1(Ω) and h suitably small, we have the following projection error:

$$ \| w-{\Pi}_{1} w\|\leq Ch^{k+1}|w|_{k+1} \text{and} |\!|\!|w-{\Pi}_{1} w|\!|\!| \leq Ch^{k}|w|_{k+1}, $$

(3.10)

where C depends on k, d, 1/α, and Λ₀.

This is a special case of that proved in [40].

We proceed to collect some basic inequalities, in which the bounding coefficients are easy to figure out in one dimension, yet often more involved in the case of several dimensions.

(1) Note that if w ∈ H³(K) and e is an edge of element K, we have [2, 2.4 & 2.5] the following trace inequalities

$$ \begin{array}{@{}rcl@{}} && \|v\|^{2}_{0, e}\leq C (h_{e}^{-1} \|v\|_{0, K}^{2} +h_{e} |v|^{2}_{1, K}), \end{array} $$

(3.11a)

$$ \begin{array}{@{}rcl@{}} && \| \partial_{n} v\|^{2}_{0, e}\leq C (h_{e}^{-1} |v|_{1, K}^{2} +h_{e} |v|^{2}_{2, K}), \end{array} $$

(3.11b)

$$ \begin{array}{@{}rcl@{}} && \| {\partial_{n}^{2}} v\|^{2}_{0, e}\leq C (h_{e}^{-1} |v|_{2, K}^{2} +h_{e} |v|^{2}_{3, K}), \end{array} $$

(3.11c)

where the constant C can depend on several geometric features of K, but it does not depend on the size of K and e.

(2) Inverse inequality. For a finite dimensional space, all norms are equivalent. For every polynomial of degree ≤ k, there exists C depending on k such that

$$ |v|_{s, K}^{2} \leq C h_{K}^{-2(s-m)}|v|_{m, K}^{2} \quad \text{for $s, m$ integers with $s > m$}. $$

(3.12)

Moreover, for any function v ∈ V_h, the following inverse inequalities hold

$$ \begin{array}{@{}rcl@{}} && \|v\|_{{\Gamma}_{h}} \leq Ch^{-1/2} \|v\|, \end{array} $$

(3.13a)

$$ \begin{array}{@{}rcl@{}} && \|v\|_{\infty} \leq Ch^{-d/2}\|v\|, \end{array} $$

(3.13b)

where d is the spatial dimension, and $\|v\|^{2}_{{\Gamma }_{h}}: ={\sum }_{e\in {\Gamma }_{h}}{\int \limits }_{e} v^{2} ds$. For more details of these inverse properties, we refer the reader to [15].

3.2 Error estimates

In order to obtain the error estimates for solutions to the semi-discrete DG scheme, we first verify that the DG scheme (2.6)–(2.7) is consistent in the sense that the exact solution (u,Φ) of (??) also satisfies (2.6)–(2.7), i.e.,

$$ \begin{array}{@{}rcl@{}} \mathbf{i} \langle u_{t}, v_{h}\rangle &=&A_{0}(u, v_{h})+\langle{\Phi} u, v_{h} \rangle,\qquad \forall v_{h}\in {V_{h}^{c}}, \end{array} $$

(3.14)

$$ \begin{array}{@{}rcl@{}} A_{1}({\Phi}, w_{h})&=&\mu(|u|^{2}-c, w_{h}),\qquad \forall w_{h}\in V_{h}. \end{array} $$

(3.15)

Substracting (2.6)–(2.7) from (3.14)–(3.15), respectively, leads to the error equation

$$ \begin{aligned} {\mathbf{i}}\left\langle u_{t}-u_{ht}, v_{h}\right\rangle=&A_0(u-u_{h}, v_{h})+H(v_{h}),\quad \forall v_{h}\in V_{h}^c,\\ A_1({\Phi}-{\Phi}_{h}, w_{h})=&\mu(|u|^2-|u_{h}|^2, w_{h}), \quad \forall w_{h}\in V_{h}. \end{aligned} $$

(3.16)

Here

$$ H(v_{h}):=\left\langle {\Phi} u-{\Phi}_{h}u_{h}, v_{h}\right\rangle. $$

To proceed we first prepare the following estimate.

Lemma 3.2

Given f ∈ L²(Ω). If

$$ \begin{array}{@{}rcl@{}} A_{1}(a, w_{h})=(f, w_{h}), \quad \forall w_{h}\in V_{h}, \end{array} $$

(3.17)

then there exists a constant C > 0 such that

$$ \begin{array}{@{}rcl@{}} \|a\|\leq C(\|f\| + h \min_{a_{h} \in V_{h}} |\!|\!|a_{h}-a|\!|\!|). \end{array} $$

(3.18)

Proof

This will be proved in two steps. Step 1. Let a_h ∈ V_h approximate a, then

$$ A_{1}(a_{h}, w_{h})=A_{1}(a_{h}-a, w_{h})+(f, w_{h}). $$

Taking w_h = a_h and using (3.8), then (3.6), we obtain

$$ C_{1}^{-1}\gamma|\!|\!|a_{h}|\!|\!|^{2} \leq \gamma\|a_{h}\|_{E}^{2}\leq {\Lambda}_{1} |\!|\!|a_{h}-a|\!|\!||\!|\!|a_{h}|\!|\!|+\|f\|\|a_{h}\|. $$

Note that ∥a_h∥≤ C| | |a_h| | |. Thus

$$ |\!|\!|a_{h}|\!|\!|\leq C(|\!|\!|a_{h}-a|\!|\!|+\|f\|).$$

This when combined the triangle inequality yields

$$ |\!|\!|a|\!|\!| \leq C(\min_{a_{h} \in V_{h}} |\!|\!|a_{h}-a|\!|\!|+\|f\|). $$

(3.19)

Step 2. We proceed to obtain ∥a∥ by coupling with a duality argument. Define the auxiliary function ψ as the solution of the elliptic problem

$$ \left\{\begin{aligned} -{\Delta} \psi =&a \quad \text{in} \ {\Omega},\\ \psi=&0 \quad \text{on}\ \partial{\Omega}. \end{aligned}\right. $$

(3.20)

This problem has a unique solution and admits the following regularity estimate for ψ ∈ H²(Ω),

$$ \|\psi\|_{2} \leq \|a\|. $$

(3.21)

We then have

$$ \begin{array}{@{}rcl@{}} \|a\|^2&= & \sum\limits_{K\in \mathcal{T}_{h}} {\int}_{K}a (-{\Delta} \psi)dx \\ &= & \sum\limits_{K\in \mathcal{T}_{h}}{\int}_K (\nabla a \cdot\nabla \psi ) dx +\sum\limits_{K\in\mathcal{T}_{h}} {\int}_{\partial K} \left( -a \frac{\partial \psi}{\partial n} \right)ds\\ &= & {\sum}_{K\in \mathcal{T}_{h}} (\nabla a, \nabla \psi)_K+ {\sum}_{e\in {\Gamma}_{h}^0} (\widehat{\partial_n a}, [\psi] )_e + ([a], \{\partial_n \psi\})_e+A_1^b(\psi, a)\\ &= & A_1(\psi, a)= A_1(a, \psi). \end{array} $$

(3.22)

For k ≥ 1, we take ψ_h ∈ V_h to be a piecewise linear interpolant of ψ so that

$$ \|\partial_x^m(\psi - \psi_{h})\|\leq Ch^{2-m} |\psi|_{2}, \quad m=0, 1, 2. $$

Using (3.17) with w_h = ψ_h, we obtain

$$ \begin{array}{@{}rcl@{}} \|a\|^{2}&=& A_{1}(a, \psi) = (f, \psi_{h})+ A_{1}(a, \psi-\psi_{h})\\ &\leq & \|f\| (\|\psi\|+\|\psi-\psi_{h}\|) + {\Lambda}|\!|\!|a|\!|\!| \cdot |\!|\!|\psi-\psi_{h}|\!|\!| \\ &\leq & C(1+h^{2})\|\psi\|_{2} \|f\|+ Ch\|\psi\|_{2} |\!|\!|a|\!|\!| \\ &\leq &C (\|f\| +h|\!|\!|a |\!|\!| )\|a\|, \end{array} $$

(3.23)

where we used (3.21). Hence

$$ \|a\| \leq C (\|f\| +h|\!|\!|a|\!|\!| ). $$

(3.24)

For h small, (3.24) with (3.19) yields

$$ \|a\| \leq C(\|f\| + h \min_{a_{h} \in V_{h}} |\!|\!|a_{h}-a|\!|\!|). $$

This is (3.18) as claimed. □

The groundwork has been laid for stating and proving the main convergence result for the semi-discrete approximation (2.6)–(2.7).

Theorem 3.2

Let u be the smooth solution of (??) subject to periodic boundary conditions for u and the Dirichlet condition for Φ. Let u_h be the solution to the semi-discrete DG scheme (2.6), (2.7) with β > Γ₁ and β₀ > Γ₂(β₁), and boundary terms (??) and (??), respectively. If h is suitably small, then we have the following error estimate

$$ \|u(\cdot, t)-u_{h}(\cdot, t)\| \leq Ch^{k+1},\qquad 0\leq t \leq T, $$

where C depends on |u|_k+ 1,|u_t|_k+ 1, $\|{\Phi }\|_{\infty }$, T, β, β₀, β₁, and ∥u₀∥_k+ 1, but is independent of h.

Proof

Applying the estimate (3.18) to the second error equation in (3.16) with a = Φ −Φ_h and f = μ(|u|² −|u_h|²), we obtain

$$ \begin{array}{@{}rcl@{}} \|{\Phi}-{\Phi}_{h}\|\lesssim &(\|f\|+h^{k+1}) \lesssim h^{k+1}+(\|u\|_{\infty} +\|u_{h}\|_{\infty})\|u-u_{h}\|. \end{array} $$

(3.25)

We now return to the first error equation. Set ξ = π₁u − u,η = π₁u − u_h, and v_h = η, we have

$$ {\mathbf{i}}{\int}_{\Omega}\eta_t\eta^{*}dx={\mathbf{i}}{\int}_{\Omega}\xi_t\eta^{*}dx+A_0(\eta, \eta)-A_0(\xi,\eta) +H(\eta). $$

Thus

$$ \frac{d}{dt}\|\eta\|^{2}=2\text{Re}\left( {\int}_{\Omega}\xi_{t}\eta^{*}dx\right) - 2\text{ Im}(A_{0}(\xi, \eta)) -2\text{Im} H(\eta). $$

(3.26)

Note that from (3.9) we have $A_{0}(\xi , \eta )=-{\int \limits }_{\Omega } \xi \eta ^{*} dx$. Thus the first two terms on the right are bounded from above by

$$ 2\|\xi_{t}\|\cdot\|\eta\| +2 \|\xi\|\cdot \|\eta\| \leq (2\|\xi_{t}\| +2 \|\xi\|) \|\eta\| \leq Ch^{k+1} \|\eta\|, $$

(3.27)

where C depends on |u|_k+ 1 and |u_t|_k+ 1. We proceed to estimate the nonlinear term as follows:

$$ \begin{array}{@{}rcl@{}} 2|H(\eta)|& =&2\left|\langle ({\Phi}-{\Phi}_{h})u_{h}+{\Phi}(u-u_{h}), \eta\rangle\right|\\ &\leq & 2\left( \|{\Phi}-{\Phi}_{h}\|\|u_{h}\|_{\infty}+\|u-u_{h}\|\|{\Phi}\|_{\infty}\right)\|\eta\|. \end{array} $$

Using the Sobolev embedding result we have for $k>\frac {d}{2}-1$,

$$ \|u\|_{\infty} \leq C \|u\|_{k+1}. $$

By the approximation results (3.10), we have for small h,

$$\begin{aligned} \|u-u_{h}\|=\|\xi -\eta\| \leq &\|\xi\| +\|\eta\| \lesssim h^{k+1}+\|\eta\|,\\ \|u-u_{h}\|_{\infty}=\|\xi -\eta\|_{\infty} \leq &\|\xi\|_{\infty} +\|\eta\|_{\infty} \lesssim h^{k}+h^{-d/2}\|\eta\|, \end{aligned}$$

where we used the following fact:

$$ \begin{array}{@{}rcl@{}} \|\xi\|_{\infty} & \leq \|u- u_{I}\|_{\infty} +\|u_{I}-{\Pi} u\|_{\infty} \\ & \lesssim h^{k} +h^{-1} \|u_{I}-{\Pi} u\| \leq C h^{k}, \end{array} $$

with u_I is a local interpolation polynomial to approximate u.

Substitution of the above estimates into (3.25) gives

$$ \|{\Phi}-{\Phi}_{h}\|\lesssim h^{k+1}+ \|\eta\|+h^{-d/2}\|\eta\|^{2}. $$

(3.28)

Hence (3.26) reduces to

$$ \begin{array}{@{}rcl@{}} \frac{d}{dt}\|\eta\| &\lesssim & h^{k+1} +\|{\Phi}-{\Phi}_{h}\|(\|u-u_{h}\|_{\infty}+\|u\|_{\infty})+\|u-u_{h}\|\|{\Phi}\|_{\infty}\\ &\lesssim &h^{k+1}+\|{\Phi}-{\Phi}_{h}\|(\|u\|_{k+1}+(h^{k}+h^{-d/2})\|\eta\|)+(h^{k+1}+\|\eta\|)\|{\Phi}\|_{\infty}\\ &\lesssim &h^{k+1}+\|\eta\|+h^{-d/2}\|\eta\|^{2}+h^{-d}\|\eta\|^{3}. \end{array} $$

For h < 1, we have

$$ \epsilon=h^{(k+1 - d/2)}<1. $$

Set $B = \frac {\|\eta \|}{h^{k+1}}$, so that

$$ \begin{array}{@{}rcl@{}} \frac{d}{dt} B \leq C (1+B+\epsilon B^{2}+\epsilon^{2} B^{3})\leq C (\epsilon B^{2}+1)(B+1). \end{array} $$

(3.29)

Note that at t = 0 we have

$$ \eta(x, 0) = {\Pi} u_0(x) -u_{h}(x,0)=\xi(x; 0) + u_0(x)-u_{h}(x, 0), $$

hence ∥η(⋅,0)∥² ≤ C₀h^2k+ 2 by (3.10) and the L²-projection error, with C₀ depending on ∥u₀∥_k+ 1. Thus B(0) = ∥η(⋅,0)∥/h^k+ 1 ≤ C₀.

Integration of (3.29) gives

$$ G(B(t)) \leq G(B(0)) +CT, \quad G(s):={\int}_1^s \frac{dz}{(\epsilon z^{2}+1)(z+1)} $$

for t ∈ [0,T]. If B(t) ≤ 1, then the proof is done. Otherwise for B(t) > 1, we bound G from below as follows:

$$ \begin{array}{@{}rcl@{}} G(B) & \geq& \frac{1}{2} {{\int}_{1}^{B}} \frac{dz}{z(1+\epsilon z^{2})} \\ & =&\frac{1}{2} {\int}_{\sqrt{\epsilon}}^{B\sqrt{\epsilon}} \frac{dy}{y(1+ y^{2})} \qquad(\text{set} \epsilon z^{2}=y^{2})\\ & =&-\frac{1}{4}\log\left( 1+\frac{1}{\epsilon B^{2}}\right) +\frac{1}{4}\log\left( 1+\frac{1}{\epsilon}\right). \end{array} $$

Hence

$$ \frac{1}{4}\log\left( 1+\frac{1}{\epsilon}\right)-\frac{1}{4}\log\left( 1+\frac{1}{\epsilon B^2}\right) \leq G(B(0)) +CT, $$

from which we are able to derive

$$ B(t) \leq \left[ \frac{e^a}{1-\epsilon (e^a-1)}\right]^{\frac{1}{2}}, \quad a=4(G(B_0)+CT). $$

It suffices to choose h suitably small so that $\epsilon \leq \frac {1}{2(e^{a}-1)}$, and as a result we have

$$ B(t) \leq [2e^a]^{\frac{1}{2}}=\sqrt{2}e^{2(G(B_0)+CT)}=C^{*}. $$

We thus conclude $B(t) \leq \max \limits \{1, C^{*}\}$. Hence $\|\eta (\cdot , t)\| \leq \max \limits \{1, C^{*}\}h^{k+1}$, which when combined with the triangle inequality ∥u(⋅,t) − u_h(⋅,t)∥≤∥η∥ + ∥ξ∥ leads to the desired error estimate. □

Remark 3.2

A sharp L² error estimate with homogeneous boundary condition also for u can be obtained as well. In such case, instead of projection (3.9) one can simply define π₁ by

$$ A_0(w- {\Pi}_1 w,v)=0,\qquad \forall v\in V_{h}^c. $$

The approximation result stated in Theorem 3. remains valid, as is already known from [3] in the non-complex setting.

Remark 3.3

Under some regularity assumptions on the exact solution, the convergence rates

$$ \max_{0\leq n \leq K}\|u\cdot, t_n)-u^n_{h}(\cdot)\|=O(h^{k+1} + ({\Delta} t)^2), $$

are expected for the fully discrete approximation. The arguments in a proof of these estimates are similar to those appearing already in [31, 32], yet more involved in handling nonlinear terms and stability of the time discretization, and so we leave it for future work.

4 Numerical examples

In this section, we present several numerical tests designed to gauge the performance of our conservative DG schemes. Interest is given particularly to validate our theoretical results, including a study of the convergence rates.

In all our numerical tests the L² error is measured in discrete norm by

$$ \|v-v_{h}\|:=\left( {\sum}_{\alpha=1}^N{\sum}_{i=1}^{Q} \omega_{i} (v(x_{\alpha}^{i}, t)-v_{h}(x_{\alpha}^{i}, t))^2|K_{\alpha}|\right)^{1/2},$$

where v = u^R or u^I, the real or imaginary part of u, and v_h is the corresponding part of the numerical solution. Here $x_{i}^{\alpha }$ is the i-th quadrature point associated with weight ω_i so that ${\sum }_{i=1}^Q\omega _{i}=1$. In our numerical tests, we take Q = 25 for all polynomial elements we tested. For the parameters β,β₀,β₁ in numerical fluxes (2.10) and (2.11), we take β = β₀ = 10 and $\beta _1=\frac {1}{12}$ for Q^k,k = 1,2 approximations.

Example 4.1

We consider the two-dimensional Schrödinger-Poisson problem:

$$ \begin{array}{@{}rcl@{}} {\mathbf{i}} u_{t}(x, y, t)&=&-\frac{1}{2}{\Delta} u(x, y, t)+{\Phi}(x, y, t) u(x, y, t), \quad (x, y)\in {\Omega}=[0, 5]^{2},\\ {\Delta} {\Phi}(x, y, t)&=&|u(x, y, t)|^{2}, \quad (x, y)\in {\Omega},\\ u(x, y, t)&=&0, \quad (x, y)\in \partial{\Omega},\\ {\Phi} (x, y, t)&=&0, \quad (x, y)\in \partial{\Omega},\\ u(x, y, 0)&=&u_{0}(x, y)=10e^{-10((x-2.5)^{2}+(y-2.5)^{2})}, \qquad (x, y)\in{\Omega}. \end{array} $$

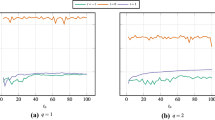
This problem was tested numerically in [4] by a second-order Strang splitting time discretization combined with a conforming finite element space discretization. We first test the accuracy and convergence rate using the Q^k polynomials with k = 1,2 on a uniform mesh with N × N cells. Without the exact solution, we calculate the error ∥u_N − u_2N∥ between the two level approximations with u_N denoting the numerical approximation on a mesh with N × N cells. Table 1 reports the L² errors and orders of accuracy. We observe that the DG method achieves the optimal k + 1 order for k = 1,2. We then test the conservation property of the scheme using Q² polynomials. Figure 1 plots the history of the relative mass and energy, respectively; we also compare the energy

$$E_{h}({u_{h}^{n}})={\int}_{\Omega}\left( |\nabla {u_{h}^{n}}|^{2}+\frac{1}{2\mu}|\nabla {{\Phi}_{h}^{n}}|^{2}\right)dx,$$

and the DG energy defined by

$$\tilde{E}_{h}({u_{h}^{n}})=A_{0}({u_{h}^{n}}, {u_{h}^{n}})+\frac{1}{2}{\int}_{\Omega} {{\Phi}_{h}^{n}}\left( |{u_{h}^{n}}|^{2}\right) dx. $$

It shows that the mass is well preserved, and the energy is asymptotically preserved as the discrete energy appears to evolve quite close to the initial energy. Figure 2 shows the wave function |u(x,y,t)| at time t = 0.1,0.2,2, and t = 10; using a 100 × 100 mesh and polynomial basis functions of degree 2.

Table 1 Errors for Example 4.1 when using Q^k,k = 1,2,3 polynomials on a uniform mesh. Final time is t = 0.1

Fig. 1

Example 4.1. Mass and energy history

Example 4.2

We consider the two-dimensional Schrödinger–Poisson equation in Ω = [− 8,8]² with nonlinear interaction:

$$ \begin{array}{@{}rcl@{}} {\mathbf{i}}u_{t}(x, y, t)&=&-\frac{1}{2}{\Delta} u(x, y, t)+{\Phi}(x, y, t) u(x, y, t)+V(x,y)u(x, y, t)+|u|^{2}u(x, y, t), \\ -{\Delta} {\Phi}(x, y, t)&=&|u(x, y, t)|^{2}-1, \quad (x, y)\in {\Omega},\\ u(x, y, t)&=&0, \quad (x, y)\in \partial{\Omega},\\ {\Phi} (x, y, t)&=&0, \quad (x, y)\in \partial{\Omega},\\ u(x, y, 0)&=&u_{0}(x, y)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}+y^{2}}{4}}(x+iy), \quad (x, y)\in{\Omega}. \end{array} $$

This problem has been tested numerically in [37] with the potential $V(x,y)=\frac {x^2+y^2}{2}$. We apply the fully discrete DG scheme (2.26a)–(2.26c) and the corresponding iteration algorithm for this problem. We carry out numerical tests with the potential $V(x,y)=\frac {x^2-y^2}{2}$ and $V(x,y)=\frac {-x^2+y^2}{2}$ on a 80 × 80 mesh and polynomial basis functions of degree 2. In Fig. 3 we plot the relative mass and energy history. During the simulation up to t = 10, the mass is preserved well, and the energy is asymptotically preserved. Figures 4, 5, 6 and 7 show the wave function |u(x,y,t)| at time t = 0,1,2 and t = 5,7.5,10, respectively. We can see clearly that the repulsive V enforces the dispersion in x or y direction.

Fig. 2

Example 4.1. Wave function |u(x,y,t)| at t = 0.1,0.2,2, and t = 10

Fig. 3

Example 4.2. Mass and energy history. Left: $V(x,y)=\frac {x^2-y^2}{2}$, Right: $V(x,y)=\frac {-x^2+y^2}{2}$

Fig. 4

Example 4.2, $V(x,y)=\frac {x^2-y^2}{2}$, numerical |u(x,y,t)| at t = 0,1,2. Left: 3D view of |u(x,y,t)|, Right: top view of |u(x,y,t)|

Fig. 5

Example 4.2, $V(x,y)=\frac {x^2-y^2}{2}$, numerical |u(x,y,t)| at t = 5,7.5,10. Left: 3D view of |u(x,y,t)|, Right: top view of |u(x,y,t)|

Fig. 6

Example 4.2, $V(x,y)=\frac {-x^2+y^2}{2}$, numerical |u(x,y,t)| at t = 0,1,2. Left: 3D view of |u(x,y,t)|, Right: top view of |u(x,y,t)|

Fig. 7

Example 4.2, $V(x,y)=\frac {-x^2+y^2}{2}$, numerical |u(x,y,t)| at t = 5,7.5,10. Left: 3D view of |u(x,y,t)|, Right: top view of |u(x,y,t)|

5 Concluding remarks

In this paper, we have constructed, analyzed and tested high-order conservative DG schemes for the nonlinear Schrödinger–Poisson equation. It is shown that both semi-discrete and fully discrete schemes preserve both mass and energy. For the semi-discrete DG scheme we obtained optimal L² error estimates in the full nonlinear setting. We presented a number of numerical tests to illustrate the performance of the proposed schemes and to validate the theoretical results of the paper. The numerical results confirm that the method is both accurate and robust, both mass and energy are well preserved over long time simulations. Therefore, the schemes can be considered as a competitive algorithm in the solution of the nonlinear Schrödinger–Poisson equation. A very interesting question is whether it is possible to improve these schemes into higher order (in time) schemes while still conserving both mass and (a modified) energy.