A New Multiscale Discontinuous Galerkin Method for the One-Dimensional Stationary Schrödinger Equation

Abstract

In this paper, we develop and analyze a new multiscale discontinuous Galerkin (DG) method for one-dimensional stationary Schrödinger equations with open boundary conditions which have highly oscillating solutions. Our method uses a smaller finite element space than the WKB local DG method proposed in Wang and Shu (J Comput Phys 218:295–323, 2006) while achieving the same order of accuracy with no resonance errors. We prove that the DG approximation converges optimally with respect to the mesh size $h$ in $L^2$ norm without the typical constraint that $h$ has to be smaller than the wave length. Numerical experiments were carried out to verify the second order optimal convergence rate of the method and to demonstrate its ability to capture oscillating solutions on coarse meshes in the applications to Schrödinger equations.

1 Introduction

In this paper, we propose a new multiscale discontinuous Galerkin (DG) method for the following one-dimensional second order elliptic equation

$$\begin{aligned} -\varepsilon ^2u''-f(x)u=0, \end{aligned}$$

(1.1)

where $\varepsilon >0$ is a small parameter and $f(x)$ is a real-valued smooth function independent of $\varepsilon$. The solution to this equation for positive $f$ is a wave function with the wave number $\frac{\sqrt{f(x)}}{\varepsilon }$.

One application of this type of equation is the stationary Schrödinger equation in the modeling of quantum transport in nanoscale semiconductors [5, 14, 18]

$$\begin{aligned} \left\{ \begin{array}{l} -\frac{\hbar ^2}{2m}\varphi ''(x)-qV(x)\varphi (x)=E\varphi (x)\quad \;\text{ on } \; [a,b]\\ \hbar \varphi '(a)+\varvec{i}p(a)\varphi _p(a)=2\varvec{i}p(a), \quad \hbar \varphi _p'(b)=\varvec{i}p(b)\varphi (b), \end{array} \right. \end{aligned}$$

(1.2)

with $\displaystyle \varepsilon =\frac{\hbar }{\sqrt{2mE}}$ and $\displaystyle f(x)=1+\frac{qV(x)}{E}$ in Eq. (1.1). Here $\hbar$ is the reduced Plank constant, $m$ is the effective mass (assumed to be constant), $q$ is the elementary positive charge of the electron, $V(x)$ is the total electrostatic potential in the device, $E$ is the injection energy, $p(x)=\sqrt{2m(E+qV(x))}$ is the momentum, and the solution $\varphi$ is a wave function. The quantum mechanical picture of the equation describes an electron injected from $x=a$ with an energy $E$, and partially transmitted or reflected by the potential $V$. The imposed open boundary conditions are the so-called quantum transmitting boundary conditions, see [13]. In the modeling of quantum transport, the Schrödinger equation is coupled with a Poisson equation in order to compute the self-consistent potential. In this paper, the total potential $V(x)$ is considered to be a known function as the coupling with the Poisson equation does not change our DG method for the Schrödinger equation.

When the electron has high energy $E$, i.e. $\varepsilon$ is very small, the solution to the Schrödinger equation will be highly oscillating. Standard numerical methods require very fine meshes to resolve such oscillations. As a result, the computational cost is tremendous in order to simulate quantum transport in nano devices since millions of Schrödinger equations need to be solved. The design of efficient multiscale numerical methods which produce accurate approximations of the solutions on coarse meshes is a formidable mathematical challenge. Note that when the energy $E$ is small, such that $E+qV<0$ (i.e. $f<0$), the solution is non-oscillatory. Thus we mainly focus on the challenging case of $f(x)\ge \tau >0$ and $0<\varepsilon \ll 1$.

A lot of work has been dedicated to the development of efficient methods for solving stationary Schrödinger equations, such as [3–5, 14–16, 18]. In [5], Ben Abdallah and Pinaud proposed a multiscale continuous finite element method for the one-dimensional Schrödinger equation (1.2). Using WKB asymptotics [6], they constructed continuous WKB basis functions, which can better approximate highly oscillating wave functions than the standard polynomial interpolation functions so that the computational cost is significantly reduced. This method was analyzed in [14] and second order convergence was shown independent of the wave length. One limitation of the method is that it is difficult to be generalized to general two-dimensional devices due to the difficulty in extending such continuous multiscale basis functions to two dimensions.

Different from continuous finite element methods, DG methods [2, 8, 9] do not enforce continuity at element interfaces, which makes them feasible to be extended to multidimensional devices. Multiscale DG methods with non-polynomial basis functions have been developed and studied in the literature, including [1, 7, 11, 12, 17–21]. In [18], Wang and Shu proposed a local DG method with WKB basis (WKB-LDG) for solving the one-dimensional stationary Schrödinger equation (1.2) in the simulation of resonant tunneling diode model. Numerical tests showed that the WKB-LDG method using piecewise exponential basis functions can resolve solutions on meshes that are coarser than what the standard DG with polynomial basis requires. However, no convergence analysis was done for this method.

In this paper, we propose and analyze a new multiscale DG method for the stationary Schrödinger equation. Our method is different from the WKB-LDG method in [18] in two aspects. First, we use a smaller finite element space than that of the WKB-LDG method to achieve the same order of convergence and reduce the resonance errors. Second, in the definition of the numerical traces we penalize the jumps using imaginary parameters, so our method is not an LDG method when the penalty parameters are nonzero.

The analysis of the multiscale DG method is challenging. Due to the strong indefiniteness of the Schrödinger equation with positive $f$, it is hard to establish stability estimates for finite element solutions. When an energy argument is used, one only gets a Gårding-type equality instead of the energy equality. Moreover, there is a typical mesh constraint $h\lesssim \varepsilon$ for numerically resolving highly oscillating solutions using finite element methods. In order to prove convergence results for both $h\gtrsim \varepsilon$ and $h\lesssim \varepsilon$ cases, special projection results and inverse inequalities are needed.

A novel and crucial part of our analysis is Theorem 3.1 for the $L^2$ projection onto the space of piecewise exponential functions. For general $H^1$ functions, the projection requires that the mesh size is small enough, at least comparable to the wave length, to have a second-order approximation. But for the oscillating solutions of the model problem and the corresponding dual problem, we show that the second-order approximation can be obtained even if the mesh size $h$ is larger than the wave length. Thanks to this projection result, we are able to derive error estimates without assuming $h\lesssim \varepsilon$. We first use an energy argument to get a Gårding type equality. The fact that the penalty parameters are imaginary allows us to estimate jumps of the errors at cell interfaces; similar idea has been used in [10]. Then we apply a duality argument to estimate the error in the interior of the mesh, and the error estimate at cell interfaces allows us to control the boundary terms without using inverse inequality and losing convergence orders.

The paper is organized as follows. In Sect. 2, we define our multiscale DG method for the stationary Schrödinger equation. In Sect. 3, we state and discuss the main results. The detailed proofs are given in Sect. 4. We display the numerical results in Sect. 5 to verify our error estimates and compare our method with the LDG method using piecewise linear and quadratic functions and the WKB-LDG method in [18]. Finally, we conclude in Sect. 6.

2 Multiscale DG Method: The Methodology

2.1 The DG Formulation

The model problem we investigate in this paper can be written as follows:

$$\begin{aligned} \left\{ \begin{array}{l} -\varepsilon ^2u''-f(x)u=0, \quad x\in [a,b],\\ u'(a)+\varvec{i}k(a) \, u(a)= 2\varvec{i}k(a), \quad u'(b)-\varvec{i}k(b)\, u(b)=0, \end{array} \right. \end{aligned}$$

(2.1)

where $\displaystyle k(x)=\frac{\sqrt{f(x)}}{\varepsilon }$ is the wave number.

In order to define a DG method for the elliptic Eq. (2.1), we rewrite it into a system of first order equations

$$\begin{aligned}&q-\varepsilon u'=0,\quad -\varepsilon q'-f(x)u=0 \end{aligned}$$

(2.2a)

with the boundary conditions

$$\begin{aligned}&q(a)+\varvec{i}\sqrt{f_a}\, u(a)=2\varvec{i}\sqrt{f_a},\quad q(b)-\varvec{i}\sqrt{f_b} \, u(b)=0, \end{aligned}$$

(2.2b)

where $f_a=f(a)$ and $f_b=f(b)$.

Let $I_j=(x_{j-\frac{1}{2}},x_{j + \frac{1}{2}}), j=1,\ldots ,N,$ be a partition of the domain, $x_j=\frac{1}{2}\left( x_{j-\frac{1}{2}}+x_{j+\frac{1}{2}}\right) , h_j=x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}}$ and $h =\max \limits _{j=1,\ldots , N} h_j$. Let ${\Omega _h}:=\{ I_j: j=1,\ldots ,N\}$ be the collection of all elements, ${\partial \Omega _h}:=\{ \partial I_j: j=1,\ldots ,N\}$ be the collection of the boundaries of all elements, ${{\fancyscript{E}}_h}:=\{x_{j+\frac{1}{2}}\}_{j=0}^N$ be the collection of all the cell interfaces, and ${{\fancyscript{E}}^i_h}:=\{x_{j+\frac{1}{2}}\}_{j=1}^{N-1}$ be the collection of all interior cell interfaces.

The weak formulation of a standard DG method for Eq. (2.2a) is to find approximate solutions $u_h$ and $q_h$ in a finite element space $V_h$ such that

$$\begin{aligned}&(q_h, w)_{\Omega _h}+ (\varepsilon u_h, w')_{\Omega _h}-\langle {\varepsilon }\widehat{u}_h,w\,\varvec{n}\rangle _{\partial \Omega _h}=0,\end{aligned}$$

(2.3a)

$$\begin{aligned}&(\varepsilon q_h, v')_{\Omega _h}-\langle {\varepsilon }\widehat{q}_h, v\,\varvec{n}\rangle _{\partial \Omega _h}-(f(x)u_h, v)_{\Omega _h}=0 \end{aligned}$$

(2.3b)

for all test functions $v_h, w_h \in V_h$. Here, we have used the notation

$$\begin{aligned} (\varphi , v)_{{\Omega _h}}:&=\sum _{j=1}^N (\varphi , v)_{I_j},\quad \langle \psi , w\,\varvec{n}\rangle _{{\partial \Omega _h}}:=\sum _{j=1}^N \langle \psi , w\,\varvec{n}\rangle _{\partial I_j}, \end{aligned}$$

where

$$\begin{aligned} (\varphi , v)_{I_j}&=\int _{I_j} \varphi (x)\overline{v}(x)\,dx,\\ \langle \psi , w\,\varvec{n}\rangle _{\partial I_j}&= \psi (x_{j+\frac{1}{2}})\overline{w}(x_{j+\frac{1}{2}}) -\psi (x_{j-\frac{1}{2}})\overline{w}(x_{j-\frac{1}{2}}), \end{aligned}$$

where $\overline{v}$ is the complex conjugate of $v$ and $\varvec{n}$ is the unit outward normal vector. For $I_j=\left( x_{j-\frac{1}{2}}, x_{j+\frac{1}{2}}\right)$, we assume $\varvec{n}(x_{j-\frac{1}{2}})=-1$ and $\varvec{n}(x_{j+\frac{1}{2}})=1$. The numerical traces $\widehat{u}_h$ and $\widehat{q}_h$ will be defined in the next subsection.

The finite element space $V_h$ contains functions which are discontinuous across cell interfaces. For standard DG methods, these functions are piecewise polynomials. For our proposed multiscale DG method, the basis functions are constructed to be non-polynomial functions which incorporate the small scales to better approximate the oscillating solutions, and we will give more details in Sect. 2.3. Since the functions in $V_h$ are allowed to have discontinuities at cell interfaces $x_{j+\frac{1}{2}}$, we use $v^-(x_{j+\frac{1}{2}})$ and $v^+(x_{j+\frac{1}{2}})$ to refer to the left and right limits of $v$ at $x_{j+\frac{1}{2}}$, respectively.

2.2 The Numerical Traces

The choices of numerical traces are essential for the definition of DG methods, and different numerical traces will lead to different DG methods [2]. In our scheme, the numerical traces $\widehat{u}_h$ and $\widehat{q}_h$ are defined in the following way. At the interior cell interfaces,

$$\begin{aligned} \widehat{u}_h=\,&u_h^- - \varvec{i}\,\beta \,[\![q_h]\!],\end{aligned}$$

(2.4a)

$$\begin{aligned} \widehat{q}_h=\,&q_h^+ + \varvec{i}\,\alpha \,[\![u_h]\!], \end{aligned}$$

(2.4b)

where $[\![\varphi ]\!]=\varphi ^--\varphi ^+$ represents the jump across the interface. In our error analysis, we assume that the penalty parameters $\beta$ and $\alpha$ are positive constants. Our numerical experiments show that the method is also well-defined for $\alpha =\beta =0$, which recovers the LDG method with alternating numerical fluxes.

At the two boundary points $\{a, b\}$,

$$\begin{aligned} \widehat{u}_h(a)&=(1-\gamma )u_h(a)+ \varvec{i}\frac{\gamma }{\sqrt{f_a}}\, q_h(a) + 2\gamma , \end{aligned}$$

(2.5a)

$$\begin{aligned} \widehat{q}_h(a)&=\gamma q_h(a)-\varvec{i}(1-\gamma )\sqrt{f_a}\, u_h(a)+2\varvec{i}\,(1-\gamma )\sqrt{f_a}, \end{aligned}$$

(2.5b)

$$\begin{aligned} \widehat{u}_h(b)&=(1-\gamma )u_h(b)- \varvec{i}\frac{\gamma }{\sqrt{f_b}}\, q_h(b), \end{aligned}$$

(2.5c)

$$\begin{aligned} \widehat{q}_h(b)&=\gamma q_h(b)+\varvec{i}(1-\gamma )\sqrt{f_b}\, u_h(b), \end{aligned}$$

(2.5d)

where $\gamma$ can be any real constant in $(0,1)$. The numerical traces at the boundary are defined in this way to match the boundary conditions in (2.2b). It is easy to see that

$$\begin{aligned} \widehat{q}_h(a)+\varvec{i}\sqrt{f_a} \widehat{u}_h(a)=2\varvec{i}\sqrt{f_a},\quad \widehat{q}_h(b)-\mathbf {i}\sqrt{f_b}\widehat{u}_h(b)=0. \end{aligned}$$

2.3 The Multiscale Approximation Space

For the Schrödinger equation (1.2), WKB asymptotic [6] states that if $E+qV>0$, when $\hbar \rightarrow 0$,

$$\begin{aligned} \varphi (x) \sim \frac{A}{\root 4 \of {2m(E+qV(x))}}e^{\varvec{i}S(x)}+\frac{B}{\root 4 \of {2m(E+qV(x))}}e^{-\varvec{i}S(x)}, \end{aligned}$$

(2.6)

where $A$ and $B$ are constants and $\displaystyle S(x)=\frac{\sqrt{2m}}{\hbar }\int ^x_{x_0}\sqrt{E+qV(s)}ds$ with integration constant $x_0$. Therefore, in [5], Ben Abdallah and Pinaud developed a continuous finite element method using WKB-interpolated basis function

$$\begin{aligned} \widetilde{\varphi }(x)=\frac{A_j}{\root 4 \of {2m(E+qV(x))}}e^{\varvec{i}S(x)}+ \frac{B_j}{\root 4 \of {2m(E+qV(x))}}e^{-\varvec{i}S(x)}, \quad x\in I_j. \end{aligned}$$

The constants $A_j$ and $B_j$ are determined by the nodal values at the cell boundaries.

Later, Wang and Shu in [18] developed a WKB-LDG method using the “constant form” of WKB basis functions. Their finite element space is defined as

$$\begin{aligned} E^2=\{ v_h : (v_h)|_{I_j} \in \text{ span }\{1, e^{\varvec{i}\frac{\sqrt{f(x_j)}}{\varepsilon }(x-x_j)}, e^{-\varvec{i}\frac{\sqrt{f(x_j)}}{\varepsilon }(x-x_j)}\}, \quad j=1,\ldots , N\}, \end{aligned}$$

where $\displaystyle \frac{\sqrt{f(x_j)}}{\varepsilon }=\frac{\sqrt{2m}}{\hbar }\sqrt{E+qV(x_j)}.$

In our new proposed multiscale DG method, we use a more compact approximation space by eliminating 1 in the previous $E^2$ space. The new finite element space in this paper is defined as

$$\begin{aligned} E^1=\big \{ v_h : (v_h)|_{I_j} \in \text{ span }\big \{e^{\varvec{i}\frac{\sqrt{f(x_j)}}{\varepsilon }(x-x_j)}, e^{-\varvec{i}\frac{\sqrt{f(x_j)}}{\varepsilon }(x-x_j)}\big \}, \quad j=1,\ldots , N\big \}. \end{aligned}$$

Therefore, our new proposed multiscale DG method is the DG formulation (2.3) in the multiscale finite element space $E^1$ with numerical traces defined in (2.4) and (2.4).

Remark 1

WKB asymptotic (2.6) is valid only for $E+qV>0$ and will break down close to turning points which are the points $x_j$ satisfying $E+qV(x_j)=0$.

Numerically, we require that $f(x_j)$ is not zero so that the basis functions are linearly independent. In implementation, we define a threshold $\tau >0$. When $|f(x)|<\tau$, we simply replace it by $\tau$ in the basis functions. Our numerical tests show that the proposed DG method works for any smooth $f\in W^{1,\infty }([a,b])$.

In our analysis, we assume that $f\in W^{1,\infty }(\Omega )$ and

$$\begin{aligned} f(x)\ge \tau >0\quad \text { for any }x\in {\Omega _h}. \end{aligned}$$

(2.7)

When $f$ is negative, the solution is non-oscillatory and the analysis is easier.

3 Error Estimates

In this section, we show error estimates of our multiscale DG method for the model problem (2.1).

First, let us introduce the following $L^2$ projection $\varvec{\Pi }$. For any $\omega \in H^1(I_j)$ where $I_j\in {\Omega _h}, \varvec{\Pi }\omega$ is a function in $E^1|_{I_j}$ which satisfies

$$\begin{aligned} (\omega -\varvec{\Pi }\omega , \varphi _1)_{I_j}=&0, \end{aligned}$$

(3.1a)

$$\begin{aligned} (\omega -\varvec{\Pi }\omega , \varphi _2)_{I_j}=&0, \end{aligned}$$

(3.1b)

where

$$\begin{aligned} \varphi _1=e^{\varvec{i}\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)} \quad \text { and }\quad \varphi _2=e^{-\varvec{i}\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)}, \end{aligned}$$

(3.2)

where $f_j=f(x_j)$.

In the rest of the paper, we use the notation $\delta _\omega =\omega -\varvec{\Pi }\omega$. The $H^s(D)$-norm is denoted by $\Vert \cdot \Vert _{s, D}$. We drop the first subindex if $s=0$, and the second if $D=\Omega$ or $\Omega _h$. The $L^\infty ({\Omega _h})$-norm and the $W^{1,\infty }({\Omega _h})$ semi-norm are denoted as $\Vert \cdot \Vert _\infty$ and $|\cdot |_{1,\infty }$, respectively. By default, $(\varphi , v)=(\varphi , v)_{\Omega _h}$ and $\langle \varphi , v\,\varvec{n}\rangle =\langle \varphi , v\,\varvec{n}\rangle _{{\partial \Omega _h}}$.

We show that the projection $\varvec{\Pi }$ has the following approximation properties.

Theorem 3.1

If a function $\varphi$ is the solution to the equation

$$\begin{aligned} -\varepsilon ^2 \varphi ''-f\varphi =\theta , \end{aligned}$$

(3.3)

where $\theta \in L^2({\Omega _h})$ and $f$ satisfies (2.7), and $\psi =\varepsilon \varphi '$, then on each $I_j\in {\Omega _h}$ we have

$$\begin{aligned} \Vert \delta _\varphi \Vert _{I_j} + \Vert \delta _\psi \Vert _{I_j} \le C \,\frac{h}{\varepsilon }\left( \Vert \theta \Vert _{I_j} +h|f|_{W^{1,\infty }(I_j)}\Vert \varphi \Vert _{I_j}\right) \end{aligned}$$

and

$$\begin{aligned} \Vert \delta _\varphi \Vert _{\partial I_j}+\Vert \delta _\psi \Vert _{\partial I_j}\le C\,\frac{h^{1/2}}{\varepsilon }\left( \Vert \theta \Vert _{I_j} +h|f|_{W^{1,\infty }(I_j)}\Vert \varphi \Vert _{I_j}\right) , \end{aligned}$$

where $C$ is independent of $\varepsilon$ and $h$.

The proofs of this Theorem and the remaining theorems in this section will be given in the next section.

Remark 2

Note that Theorem 3.1 holds only for functions which satisfy Eq. (3.3). For general smooth functions, the approximation result will require that $h$ is much smaller than the parameter $\varepsilon$. In our error analysis, we apply Theorem 3.1 to the solutions of the model problem (2.1) and its dual problem, and it is crucial for removing the typical mesh constraint $h\lesssim \varepsilon$ for resolving highly oscillating solutions.

Applying Theorem 3.1 to the solution of (2.1), we immediately get the following result.

Lemma 3.2

For the exact solution $u$ and $q$ to the Eq. (2.2a), we have

$$\begin{aligned} \Vert \delta _u\Vert + \Vert \delta _q\Vert \le C \,\frac{h^2}{\varepsilon }|f|_{W^{1,\infty }({\Omega _h})}\Vert u\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert \delta _u\Vert _{{\partial \Omega _h}}+\Vert \delta _q\Vert _{{\partial \Omega _h}}\le C\,\frac{h^{3/2}}{\varepsilon }|f|_{W^{1,\infty }({\Omega _h})}\Vert u\Vert . \end{aligned}$$

where $C$ is independent of $\varepsilon$ and $h$.

Note that when $f$ is constant, Lemma 3.2 implies that $\delta _u=\delta _q=0$. This is consistent with the fact that the solutions $u$ and $q$ are in the finite element space $E^1$ if $f$ is constant.

To state our main results, we need the following notation. Let $e_\omega =\omega -\omega _h$ and $\eta _\omega =\varvec{\Pi }\omega -\omega _h$. Then $e_\omega =\delta _\omega +\eta _\omega$. First we estimate the jumps of $\eta _u$ and $\eta _q$ at the cell interfaces.

Theorem 3.3

Assume that $\alpha$ and $\beta$ are positive constants and $0<\gamma <1$. For any mesh size $h>0$, we have

$$\begin{aligned} \Vert [\![\eta _u]\!] \Vert _{{{\fancyscript{E}}_h}} +\Vert [\![\eta _q]\!] \Vert _{{{\fancyscript{E}}_h}} \le&\, C|f|_{1,\infty }\,\frac{h^{3/2}}{\varepsilon }\left( \Vert \eta _u\Vert + \Vert u\Vert \right) , \end{aligned}$$

where $C$ is independent of $\varepsilon$ and $h$.

For the projection of error $\eta _u$ in the interior of the domain, we have the following result.

Theorem 3.4

Under the assumption of Theorem 3.3, we have

$$\begin{aligned} \Vert \eta _u\Vert \le C |f|_{1,\infty }\left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) \Vert u\Vert , \end{aligned}$$

where $C$ is independent of $\varepsilon$ and $h$.

Using the triangle inequality, Theorems 3.1 and 3.4, we now have our error estimate for the actual error $e_u=u-u_h$ as follows.

Theorem 3.5

Let $u$ be the solution of the problem (2.1) and $u_h\in E^1$ be the multiscale DG approximation defined by (2.3)–(2.5). Assume that $\alpha$ and $\beta$ are positive constants and $0<\gamma <1$. For any mesh size $h>0$, we have

$$\begin{aligned} \Vert u-u_h\Vert \le C |f|_{1,\infty }\left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) \Vert u\Vert , \end{aligned}$$

where $C$ is independent of $\varepsilon$ and $h$.

Theorem 3.5 shows that when $f$ is constant, the error of the multiscale DG method is zero. When $f$ is not constant, the method has a second order convergence rate, and the estimate holds even if $h\gtrsim \varepsilon$.

4 Proofs

In the section, we first prove the projection results in Theorem 3.1, which allow us to carry out error analysis without assuming that $h$ is smaller than $\varepsilon$. Then we use an energy argument to get the error estimate at cell interfaces in Theorem 3.3. Finally, we apply a duality argument to get the main result in Theorem 3.4. Let us begin by introducing some preliminaries.

4.1 Preliminaries

Note that the exact solution to Eq. () also satisfies the weak formulation (2.3). Using the orthogonality property of the projection $\varvec{\Pi }$ in (3.1), We get the following error equations

$$\begin{aligned} (\eta _q, w)+ (\varepsilon \eta _u, w')-\langle \varepsilon \widehat{e}_u,w\,\varvec{n}\rangle =0, \end{aligned}$$

(4.1a)

$$\begin{aligned} (\varepsilon \eta _q, v')-\langle \varepsilon \widehat{e}_q, v\,\varvec{n}\rangle -(f(x)\delta _u, v) -(f(x)\eta _u, v) =0, \end{aligned}$$

(4.1b)

for all test functions ${v, w} \in E^1$, where $\widehat{e}_u=u-\widehat{u}_h$ and $\widehat{e}_q=q-\widehat{q}_h$.

Before we prove our error estimates, let us gather some properties of the numerical traces. It is easy to check that the following two Lemmas hold for the numerical traces defined in (2.4) and (2.5).

Lemma 4.1

For the numerical traces defined in (2.4) at the interior cell interfaces, we have

$$\begin{aligned} \widehat{e}_u&=(\delta _u+\eta _u)^- -\varvec{i}\beta ([\![\delta _q]\!]+[\![\eta _q]\!]),\\ \widehat{e}_q&=(\delta _q+\eta _q)^+ +\varvec{i}\alpha ([\![\delta _u]\!]+[\![\eta _u]\!]). \end{aligned}$$

Lemma 4.2

For the numerical traces defined in (2.5) at the boundary points $\{a,b\}$, we have

$$\begin{aligned}&\widehat{e}_u=(1-\gamma )e_u- \varvec{i}\frac{\gamma }{\sqrt{f}} e_q\,\varvec{n},\\&\widehat{e}_q=\gamma e_q+\varvec{i}(1-\gamma )\sqrt{f} e_u\,\varvec{n}, \end{aligned}$$

which implies that

$$\begin{aligned}&\widehat{e}_q-\varvec{i}\sqrt{f} \widehat{e}_u\,\varvec{n}=0, \end{aligned}$$

where $\varvec{n}(a)=-1$ and $\varvec{n}(b)=1$.

4.2 Proof of Theorem 3.1

To prove the approximation property of the projection $\varvec{\Pi }$ in Theorem 3.1, first let us show the following inverse inequality.

Lemma 4.3

For any function $v\in E^1$ and $I_j\in {\Omega _h}$, we have

$$\begin{aligned} \Vert v\Vert _{\partial I_j}\le C h_j^{-1/2}\Vert v\Vert _{I_j}, \end{aligned}$$

where $C$ is a constant independent of $\varepsilon$ and $h_j$.

Proof

Suppose that $v=c_1\varphi _1+c_2\varphi _2$ on $I_j=(x_{j-\frac{1}{2}}, x_{j+\frac{1}{2}})$, where $\varphi _1$ and $\varphi _2$ are the basis functions of $E^1|_{I_j}$ defined in (3.2). Then we have

$$\begin{aligned} \Vert v\Vert ^2_{\partial I_j}=&|v(x_{j-\frac{1}{2}})|^2+|v(x_{j+\frac{1}{2}})|^2 = \left( \begin{array}{l@{\quad }l} c_1 &{} c_2 \\ \end{array} \right) A \left( \begin{array}{l} \overline{c}_1 \\ \overline{c}_2 \\ \end{array} \right) \\ \end{aligned}$$

and

$$\begin{aligned} \Vert v\Vert _{I_j}^2=&\left( \begin{array}{c@{\quad }c} c_1 &{} c_2 \\ \end{array} \right) \left( \begin{array}{c@{\quad }c} (\varphi _1,\varphi _1)_{I_j} &{} (\varphi _1,\varphi _2)_{I_j} \\ (\varphi _2,\varphi _1)_{I_j} &{} (\varphi _2,\varphi _2)_{I_j} \\ \end{array} \right) \left( \begin{array}{l} \overline{c}_1 \\ \overline{c}_2 \\ \end{array} \right) = \left( \begin{array}{l@{\quad }l} c_1 &{} c_2 \\ \end{array} \right) B \left( \begin{array}{l} \overline{c}_1 \\ \overline{c}_2 \\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} A= 2\left( \begin{array}{l@{\quad }l} 1 &{} \cos {\sigma } \\ \cos {\sigma } &{} 1 \\ \end{array} \right) \quad \text {and}\quad B= h_j\left( \begin{array}{cc} 1 &{} \frac{\sin {\sigma }}{\sigma } \\ \frac{\sin {\sigma }}{\sigma } &{} 1 \\ \end{array} \right) \end{aligned}$$

with $\sigma :=\frac{\sqrt{f_j}}{\varepsilon }h_j$. To find a constant $r>0$ so that $\Vert v\Vert ^2_{\partial I_j}\le r\Vert v\Vert _{I_j}^2$ for any $v\in E^1$, we need to find the largest eigenvalue of the generalized eigenvalue problem

$$\begin{aligned} A\mathbf {c}=\lambda B\mathbf {c}. \end{aligned}$$

This can be written as

$$\begin{aligned} B^{-1}A\mathbf {c}=\lambda \mathbf {c}, \end{aligned}$$

so we only need to find the largest eigenvalue of $B^{-1}A$. The two eigenvalues of $B^{-1}A$ are

$$\begin{aligned} \lambda _1=2h_j^{-1}\frac{1+\cos {\sigma }}{1+\frac{\sin {\sigma }}{\sigma }} \quad \text { and }\quad \lambda _2=2h_j^{-1}\frac{1-\cos {\sigma }}{1-\frac{\sin {\sigma }}{\sigma }}. \end{aligned}$$

Obviously,

$$\begin{aligned} |\lambda _1|\le Ch_j^{-1}\quad \text { for any } \sigma >0. \end{aligned}$$

Let us estimate $\lambda _2$. If $h_j>c_0 \frac{\varepsilon }{\sqrt{f_j}}$ for some $c_0\in (0,\frac{1}{2}]$, then $\sigma >c_0$. We get

$$\begin{aligned} \frac{\sin {\sigma }}{\sigma }<\frac{\sin {c_0}}{c_0}<1 \quad \text { and }\quad \frac{1}{1-\frac{\sin {\sigma }}{\sigma }} <\frac{1}{1-\frac{\sin {c_0}}{c_0}}, \end{aligned}$$

which implies that

$$\begin{aligned} |\lambda _2|\le Ch_j^{-1}. \end{aligned}$$

If $h_j<\frac{1}{2}\frac{\varepsilon }{\sqrt{f_j}}$, then $0 <\sigma <\frac{1}{2}$. We get $\frac{1-\cos {\sigma }}{1-\frac{\sin {\sigma }}{\sigma }}\le C,$ and then $|\lambda _2|\le Ch_j^{-1}.$ So we have

$$\begin{aligned} \max \{|\lambda _1|, |\lambda _2|\}\le Ch_j^{-1}, \end{aligned}$$

which implies

$$\begin{aligned} \Vert v\Vert ^2_{\partial I_j} \le Ch_j^{-1} \Vert v\Vert ^2_{I_j}. \end{aligned}$$

$\square$

Next, let us prove Theorem 3.1 by using Lemma 4.3 in four steps.

Proof

It is easy to check that

$$\begin{aligned} -\varepsilon ^2(\varvec{\Pi }\varphi )''-f_j\,\varvec{\Pi }\varphi =0\quad \text { on each }I_j, \; j=1, \ldots , N. \end{aligned}$$

Let $\delta _\varphi =\varphi -\varvec{\Pi }\varphi$. Then $\delta _\varphi$ satisfies the equation

$$\begin{aligned} -\varepsilon ^2\delta ''_{\varphi }-f_j\delta _\varphi =\theta +(f-f_j)\varphi , \end{aligned}$$

which is equivalent to

$$\begin{aligned} \delta ''_\varphi +\frac{f_j}{\varepsilon ^2}\delta _\varphi =g(x), \end{aligned}$$

(4.2)

where $g(x)=-(\theta +(f-f_j)\varphi )/\varepsilon ^2$. So we can assume

$$\begin{aligned} \delta _\varphi =c_1\varphi _1+c_2\varphi _2+Y(x), \end{aligned}$$

where $\varphi _1$ and $\varphi _2$ are the basis functions of $E^1|_{I_j}$ defined in (3.2), and $Y(x)$ is a particular solution to (4.2).

$(i)$ Let us compute and estimate $Y(x)$. Since $\varphi _1$ and $\varphi _2$ are two solutions to the homogeneous equation corresponding to (4.2), we use variation of parameters and get

$$\begin{aligned} Y=v_1(x)\varphi _1(x)+v_2(x)\varphi _2(x), \end{aligned}$$

where

$$\begin{aligned} v_1(x)=-\frac{\varvec{i}\varepsilon }{2\sqrt{f_j}}\int _{x_j}^x\varphi _2 g\,dx,\quad \text { and }\quad v_2(x)=\frac{\varvec{i}\varepsilon }{2\sqrt{f_j}}\int _{x_j}^x\varphi _1 g\,dx. \end{aligned}$$

It is easy to see that for any $x\in I_j\cup \partial I_j$,

$$\begin{aligned} |v_i(x)|\le&C\varepsilon \int _{x_j}^x|g|dx\le \frac{C}{\varepsilon }\left( h^{1/2}\Vert \theta \Vert _{I_j} +h^{3/2}|f|_{W^{1,\infty }(I_j)}\Vert \varphi \Vert _{I_j}\right) ,\quad i=1,2. \end{aligned}$$

(4.3)

Therefore,

$$\begin{aligned} \Vert Y\Vert _{I_j}\le \frac{C}{\varepsilon }(h\Vert \theta \Vert _{I_j}+h^2|f|_{W^{1,\infty }(I_j)} \Vert \varphi \Vert _{I_j}). \end{aligned}$$

(4.4)

$(ii)$ Let us compute and estimate the term $c_1\varphi _1+c_2\varphi _2$ in $\delta _\varphi$. By the definition of the projection $\varvec{\Pi }$, (3.1), we have

$$\begin{aligned} (\delta _\varphi , \varphi _1)_{I_j}=0,\quad (\delta _\varphi ,\varphi _2)_{I_j}=0. \end{aligned}$$

After some calculations, we can write the above linear system as

$$\begin{aligned} h_j \left( \begin{array}{l@{\quad }l} 1 &{} \frac{\sin {\sigma }}{\sigma } \\ \frac{\sin {\sigma }}{\sigma } &{} 1 \\ \end{array} \right) \left( \begin{array}{l} c_1 \\ c_2 \\ \end{array} \right) = -\left( \begin{array}{c} (Y,\varphi _1)_{I_j} \\ (Y,\varphi _2)_{I_j} \\ \end{array} \right) . \end{aligned}$$

The solution to the linear system is

$$\begin{aligned} c_1=D_1D_2\quad \text { and }\quad c_2=D_1 D_3, \end{aligned}$$

where

$$\begin{aligned} D_1=&-h_j^{-1}\left( 1-\frac{\sin ^2{\sigma }}{\sigma ^2}\right) ^{-1},\\ D_2=&\left( Y,\varphi _1-\frac{\sin {\sigma }}{\sigma }\varphi _2\right) _{I_j},\\ D_3=&\left( Y,\varphi _2-\frac{\sin {\sigma }}{\sigma }\varphi _1\right) _{I_j}. \end{aligned}$$

Note that

$$\begin{aligned} c_1\varphi _1+c_2\varphi _2&=D_1\left( (D_2+D_3)\cos {\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)} +\varvec{i}(D_2-D_3)\sin {\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)}\right) . \end{aligned}$$

Because

$$\begin{aligned} D_2+D_3&=2\left( 1-\frac{\sin {\sigma }}{\sigma }\right) \left( Y, \cos {\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)}\right) _{I_j}\\ \end{aligned}$$

and

$$\begin{aligned} D_2-D_3&=2\left( 1+\frac{\sin {\sigma }}{\sigma }\right) \left( Y, \varvec{i}\,\sin {\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)}\right) _{I_j}, \end{aligned}$$

we have

$$\begin{aligned} \Vert c_1\varphi _1+c_2\varphi _2\Vert _{I_j}&\le 2|D_1|\left( 1-\frac{\sin {\sigma }}{\sigma }\right) \Vert Y\Vert _{I_j} \Vert \cos {\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)}\Vert ^2_{I_j}\\&\quad + 2|D_1|\left( 1+\frac{\sin {\sigma }}{\sigma }\right) \Vert Y\Vert _{I_j} \Vert \sin {\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)}\Vert ^2_{I_j}. \end{aligned}$$

It is easy to check that

$$\begin{aligned} \Vert \sin {\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)}\Vert ^2_{I_j} =\frac{1}{2}h_j\left( 1-\frac{\sin {\sigma }}{\sigma }\right) \end{aligned}$$

and

$$\begin{aligned} \Vert \cos {\frac{\sqrt{f_j}}{\varepsilon }(x-x_j)}\Vert ^2_{I_j} =\frac{1}{2}h_j\left( 1+\frac{\sin {\sigma }}{\sigma }\right) . \end{aligned}$$

So we have

$$\begin{aligned} \Vert c_1\varphi _1+c_2\varphi _2\Vert _{I_j}\le 2\Vert Y\Vert _{I_j}\le C\,\frac{h}{\varepsilon }\left( \Vert \theta \Vert _{I_j}+h|f|_{W^{1,\infty }}\Vert \varphi \Vert _{I_j}\right) . \end{aligned}$$

(4.5)

$(iii)$ Now we estimate $\Vert \delta _\varphi \Vert _{I_j}$ and $\Vert \delta _\psi \Vert _{I_j}$. From (4.4) and (4.5), we immediately get

$$\begin{aligned} \Vert \delta _\varphi \Vert _{I_j}\le 3\Vert Y\Vert _{I_j}\le C\,\frac{h}{\varepsilon }\left( \Vert \theta \Vert _{I_j}+h|f|_{W^{1,\infty }}\Vert \varphi \Vert _{I_j}\right) . \end{aligned}$$

To estimate $\delta _\psi$, we let

$$\begin{aligned} v_\psi = \varepsilon (\varvec{\Pi }\varphi )'-2\varvec{i}\sqrt{f_j}\,c_2\varphi _2. \end{aligned}$$

Since $v_\psi \in E^1$, we have

$$\begin{aligned} \Vert \delta _\psi \Vert _{I_j} \le \Vert \psi -v_\psi \Vert _{I_j}. \end{aligned}$$

So we only need to estimate $\psi -v_\psi$. Note that

$$\begin{aligned} \psi -v_\psi&= \varepsilon \delta '_\varphi +2\varvec{i}\sqrt{f_j}\,c_2\,\varphi _2 =\varvec{i}\sqrt{f_j}(c_1\varphi _1+c_2\varphi _2)+\varepsilon Y'. \end{aligned}$$

(4.6)

Hence,

$$\begin{aligned} \Vert \psi -v_\psi \Vert _{I_j}\le \sqrt{f_j}\Vert c_1\varphi _1+c_2\varphi _2\Vert _{I_j}+\Vert \varepsilon Y'\Vert _{I_j}. \end{aligned}$$

It is easy to check that

$$\begin{aligned} Y'=v'_1\varphi _1+v_1\varphi '_1+v'_2\varphi _2+v_2\varphi '_2=v_1 \varphi '_1+v_2\varphi '_2. \end{aligned}$$

(4.7)

So

$$\begin{aligned} \Vert \varepsilon Y'\Vert _{I_j}&\le \Vert v_1\Vert _{L^\infty (I_j)}\Vert \varepsilon \varphi '_1\Vert _{I_j} +\Vert v_2\Vert _{L^\infty (I_j)}\Vert \varepsilon \varphi '_2\Vert _{I_j}\\&\le Ch_j^{1/2}\left( \Vert v_1\Vert _{L^\infty (I_j)}+\Vert v_2\Vert _{L^\infty (I_j)}\right) . \end{aligned}$$

Using (4.3), we have

$$\begin{aligned} \Vert \varepsilon Y'\Vert _{I_j}&\le C\frac{h}{\varepsilon }(\Vert \theta \Vert _{I_j} +h|f|_{W^{1,\infty }(I_j)}\Vert \varphi \Vert _{I_j}). \end{aligned}$$

Using the inequality above and (4.5), we get

$$\begin{aligned} \Vert \delta _\psi \Vert _{I_j}\le \Vert \psi -v_\psi \Vert _{I_j}\le C\frac{h}{\varepsilon }\left( \Vert \theta \Vert _{I_j}+h|f|_{W^{1,\infty }(I_j)}\Vert \varphi \Vert _{I_j}\right) . \end{aligned}$$

(4.8)

$(iv)$ Let us estimate $\Vert \delta _\varphi \Vert _{\partial I_j}$ and $\Vert \delta _\psi \Vert _{\partial I_j}$. Because $\delta _\varphi =c_1\varphi _1+c_2\varphi +Y$ and $c_1\varphi _1+c_2\varphi _2\in E^1$, by Lemma 4.3 we have

$$\begin{aligned} \Vert \delta _\varphi \Vert _{\partial I_j}\le Ch^{-1/2}\Vert c_1\varphi _1+c_2\varphi _2\Vert _{I_j}+\Vert Y\Vert _{\partial I_j}. \end{aligned}$$

Using the triangle inequality and (4.3), we get

$$\begin{aligned} \Vert Y\Vert _{\partial I_j}&\le \Vert v_1\Vert _{L^\infty (\partial I_j)}\Vert \varphi _1\Vert _{\partial I_j}+\Vert v_2\Vert _{L^\infty (\partial I_j)}\Vert \varphi _2\Vert _{\partial I_j}\\&\le \Vert v_1\Vert _{L^\infty (\partial I_j)}+\Vert v_2\Vert _{L^\infty (\partial I_j)}\\&\le \frac{C}{\varepsilon }\left( h^{1/2}\Vert \theta \Vert _{I_j} +h^{3/2}|f|_{W^{1,\infty }(I_j)}\Vert \varphi \Vert _{I_j}\right) . \end{aligned}$$

Using the last inequality and (4.5) we have

$$\begin{aligned} \Vert \delta _\varphi \Vert _{\partial I_j}\le C\frac{h^{1/2}}{\varepsilon }\left( \Vert \theta \Vert _{I_j}+h|f|_{W^{1,\infty } (I_j)}\Vert \varphi \Vert _{I_j}\right) . \end{aligned}$$

Next, we estimate $\Vert \delta _\psi \Vert _{\partial I_j}$. Using the triangle inequality and the expression of $\psi -v_\psi$, (4.6), we get

$$\begin{aligned} \Vert \delta _\psi \Vert _{\partial I_j}&\le \Vert \psi -v_\psi \Vert _{\partial I_j}+\Vert v_\psi -\varvec{\Pi }\psi \Vert _{\partial I_j}\\&\le C\Vert c_1\varphi _1+c_2\varphi _2\Vert _{\partial I_j}+\Vert \varepsilon Y'\Vert _{\partial I_j}+\Vert v_\psi -\varvec{\Pi }\psi \Vert _{\partial I_j}. \end{aligned}$$

Note that $c_1\varphi _1+c_2\varphi _2\in E^1$ and $v_\psi -\varvec{\Pi }\psi \in E^1$. By Lemma 4.3, we get

$$\begin{aligned} \Vert \delta _\psi \Vert _{\partial I_j}\le Ch^{-1/2}(\Vert c_1\varphi _1+c_2\varphi _2\Vert _{I_j}+ \Vert v_\psi -\varvec{\Pi }\psi \Vert _{I_j})+\Vert \varepsilon Y'\Vert _{\partial I_j}. \end{aligned}$$

(4.9)

From the Eq. (4.7), we obtain that

$$\begin{aligned} \Vert \varepsilon Y'\Vert _{\partial I_j}&\le \Vert v_1\Vert _{L^\infty (\partial I_j)}\Vert \varepsilon \varphi '_1\Vert _{\partial I_j}+\Vert v_2\Vert _{L^\infty (\partial I_j)}\Vert \varepsilon \varphi '_2\Vert _{\partial I_j}\\&\le C(\Vert v_1\Vert _{L^\infty (\partial I_j)}+\Vert v_2\Vert _{L^\infty (\partial I_j)}). \end{aligned}$$

Then by (4.3), we have

$$\begin{aligned} \Vert \varepsilon Y'\Vert _{\partial I_j} \le C\, \frac{h^{1/2}}{\varepsilon }\left( \Vert \theta \Vert _{I_j} +h|f|_{W^{1,\infty }(I_j)}\Vert \varphi \Vert _{I_j}\right) . \end{aligned}$$

(4.10)

Note that

$$\begin{aligned} \Vert v_\psi -\varvec{\Pi }\psi \Vert _{I_j}\le \Vert v_\psi -\psi \Vert _{I_j}+\Vert \psi -\varvec{\Pi }\psi \Vert _{I_j}\le 2\Vert v_\psi -\psi \Vert _{I_j}. \end{aligned}$$

Using (4.8), we get

$$\begin{aligned} \Vert v_\psi -\varvec{\Pi }\psi \Vert _{I_j}\le C\frac{h}{\varepsilon }\,(\Vert \theta \Vert _{I_j}+h|f|_{W^{1,\infty }(I_j)} \Vert \varphi \Vert _{I_j}). \end{aligned}$$

(4.11)

Applying (4.10), (4.11) and (4.5) to (4.9), we get

$$\begin{aligned} \Vert \delta _\psi \Vert _{\partial I_j}\le C\frac{h^{1/2}}{\varepsilon }(\Vert \theta \Vert _{I_j} +h|f|_{W^{1,\infty }(I_j)}\Vert \varphi \Vert _{I_j}). \end{aligned}$$

$\square$

4.3 Proof of Theorem 3.3

To prove Theorem 3.3, first we show the following Lemma by an energy argument.

Lemma 4.4

$$\begin{aligned} L=B_1+B_2, \end{aligned}$$

where

$$\begin{aligned} L=&\,\,\Vert \eta _q\Vert ^2-(f, |\eta _u|^2)+ \varvec{i}\beta \varepsilon \Vert [\![\eta _q]\!]\Vert ^2_{{{\fancyscript{E}}^i_h}} +\varvec{i}\alpha \varepsilon \Vert [\![\eta _u]\!]\Vert ^2_{{{\fancyscript{E}}^i_h}}\\&+\,\varvec{i}\gamma \varepsilon \left\langle \frac{1}{\sqrt{f}}, |\eta _q|^2\right\rangle _{\partial \Omega }+ \varvec{i}(1-\gamma )\varepsilon \langle |\eta _u|^2, \sqrt{f}\rangle _{\partial \Omega },\\ B_1=&\,\,(\eta _u, f\delta _u),\\ B_2=&\,\,\varepsilon \,\langle \delta _u^-,\, \eta _q\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}+\varepsilon \,\langle \eta _u, \,\delta _q^+\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}\\&-\,\varvec{i}\alpha \varepsilon \,\langle \eta _u,\, [\![\delta _u]\!]\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}-\varvec{i}\beta \varepsilon \, \langle [\![\delta _q]\!], \,\eta _q\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}\\&+\,\varepsilon \,\left\langle (1-\gamma )\delta _u-\varvec{i}\frac{\gamma }{\sqrt{f}}\delta _q\,\varvec{n}, \,\eta _q\,\varvec{n}\right\rangle _{\partial \Omega }+\varepsilon \,\left\langle \eta _u, \,\gamma \delta _q\,\varvec{n}+\varvec{i}(1-\gamma )\sqrt{f}\delta _u\right\rangle _{\partial \Omega }. \end{aligned}$$

Proof

Taking $w=\eta _q$ in the error Eq. (4.1a) and $v=\eta _u$ in the complex conjugate of (4.1b) and adding the equations together, we get

$$\begin{aligned} 0=&\,(\eta _q, \eta _q)+\varepsilon (\eta _u,\eta _q')-\varepsilon \langle \widehat{e}_u,\eta _q\,\varvec{n}\rangle \\&+\varepsilon ( \eta _u',\eta _q)-\varepsilon \langle \eta _u, \widehat{e}_q \, \varvec{n}\rangle -(\eta _u, f \,\eta _u)-(\eta _u, f\,\delta _u){.} \end{aligned}$$

Using integration by parts for the second term on the right hand side of the equation, we have

$$\begin{aligned} 0=\,\Vert \eta _q\Vert ^2-(\eta _u, f \,\eta _u)-(\eta _u, f\,\delta _u)+\Theta , \end{aligned}$$

(4.12)

where

$$\begin{aligned} \Theta =&\,\varepsilon \langle \eta _u,\eta _q\,\varvec{n}\rangle -\varepsilon \langle \widehat{e}_u,\eta _q\,\varvec{n}\rangle -\varepsilon \langle \eta _u, \widehat{e}_q\,\varvec{n}\rangle . \end{aligned}$$

Using Lemma 4.1 to rewrite $\widehat{e}_u$ and $\widehat{e}_q$ on interior cell interfaces, we get

$$\begin{aligned} \Theta =&\sum _{k=1}^4 A_k \end{aligned}$$

where

$$\begin{aligned} A_1&=\varepsilon \langle \eta _u,\eta _q\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }} -\varepsilon \langle \eta _u^-,\eta _q\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}-\varepsilon \langle \eta _u,\eta _q^+\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }},\\ A_2&=-\varepsilon \langle \delta _u^-, \eta _q\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}-\varepsilon \langle \eta _u, \delta _q^+\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }},\\ A_3&=\varvec{i}\beta \varepsilon \langle [\![\delta _q]\!]+[\![\eta _q]\!], \eta _q\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}+\varvec{i}\alpha \varepsilon \langle \eta _u, ([\![\delta _u]\!]+[\![\eta _u]\!])\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }},\\ A_4&=\varepsilon \langle \eta _u,\eta _q\,\varvec{n}\rangle _{\partial \Omega }-\varepsilon \langle \widehat{e}_u,\eta _q\,\varvec{n}\rangle _{\partial \Omega }-\varepsilon \langle \eta _u,\widehat{e}_q\, \varvec{n}\rangle _{\partial \Omega }. \end{aligned}$$

It is easy to see that

$$\begin{aligned} A_1=0, \end{aligned}$$

and

$$\begin{aligned} A_3=\varvec{i}\beta \varepsilon \Vert [\![\eta _q]\!]\Vert ^2_{{{\fancyscript{E}}^i_h}} +\varvec{i}\alpha \varepsilon \Vert [\![\eta _u]\!]\Vert ^2_{{{\fancyscript{E}}^i_h}}+\varvec{i}\beta \varepsilon \langle [\![\delta _q]\!], \eta _q\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}+\varvec{i}\alpha \varepsilon \langle \eta _u, [\![\delta _u]\!]\,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}. \end{aligned}$$

Using Lemma 4.2 and the fact that $e_\omega =\delta _\omega +\eta _\omega$ for $\omega =u, q$ to rewrite $\widehat{e}_u$ and $\widehat{e}_q$ on the domain boundary, we obtain

$$\begin{aligned} A_4=&\,\varvec{i}\gamma \varepsilon \,\langle \frac{1}{\sqrt{f}}\eta _q, \eta _q\rangle _{\partial \Omega }+ \varvec{i}(1-\gamma )\varepsilon \,\langle \eta _u, \sqrt{f}\eta _u\rangle _{\partial \Omega }\\&-\varepsilon \,\langle (1-\gamma )\delta _u-\varvec{i}\frac{\gamma }{\sqrt{f}}\delta _q\,\varvec{n}, \eta _q\,\varvec{n}\rangle _{\partial \Omega }-\varepsilon \,\langle \eta _u, \gamma \delta _q\,\varvec{n}+\varvec{i}(1-\gamma )\sqrt{f}\delta _u\rangle _{\partial \Omega }. \end{aligned}$$

Adding above expressions of $A_1, A_2, A_3 , A_4$ to get $\Theta$ and using it in (4.12), we get the conclusion. $\square$

Now let us prove Theorem 3.3 using Lemmas 4.4 and 3.2.

Proof

Taking the imaginary part of $L$ in Lemma 4.4, we get

$$\begin{aligned} \beta \varepsilon \Vert [\![\eta _q]\!]\Vert ^2_{{{\fancyscript{E}}^i_h}}+\alpha \varepsilon \Vert [\![\eta _u]\!]\Vert ^2_{{{\fancyscript{E}}^i_h}} +\gamma \varepsilon \langle \frac{1}{\sqrt{f}}, |\eta _q|^2\rangle _{\partial \Omega }+ (1-\gamma )\varepsilon \langle |\eta _u|^2, \sqrt{f}\rangle _{\partial \Omega }\le |B_1|+ |B_2|. \end{aligned}$$

Now we estimate $B_1$ and $B_2$. Let ${\mathbb {P}}^0$ be the $L^2$ projection onto constant functions on each element $I_j\in {\Omega _h}$. Using the orthogonality property of the projection $\varvec{\Pi }$, we have

$$\begin{aligned} |B_1|=|\big (\eta _u, (f-{\mathbb {P}}^0 f)\delta _u \big ) |\le Ch|f|_{1,\infty }\Vert \delta u\Vert \Vert \eta _u\Vert . \end{aligned}$$

Using the Cauchy inequality, we get

$$\begin{aligned} |B_2|&\le C\varepsilon \Vert [\![\eta _q]\!]\Vert _{{{\fancyscript{E}}^i_h}}(\Vert \delta _u\Vert _{{\partial \Omega _h}\setminus {\partial \Omega }} +\beta \Vert \delta _q\Vert _{{\partial \Omega _h}\setminus {\partial \Omega }})\\&\quad + C\varepsilon \Vert [\![\eta _u]\!]\Vert _{{{\fancyscript{E}}^i_h}}(\Vert \delta _q\Vert _{{\partial \Omega _h}\setminus {\partial \Omega }} +\alpha \Vert \delta _u\Vert _{{\partial \Omega _h}\setminus {\partial \Omega }})\\&\quad +C\varepsilon \Vert \eta _q\Vert _{{\partial \Omega }}\Big ( (1-\gamma )\Vert \delta _u\Vert _{{\partial \Omega }} +\gamma \Vert \delta _q\Vert _{{\partial \Omega }}\Big )\\&\quad +C\varepsilon \Vert \eta _u\Vert _{{\partial \Omega }}\Big (\gamma \Vert \delta _q\Vert _{{\partial \Omega }} +(1-\gamma )\Vert \delta _u\Vert _{{\partial \Omega }}\Big ) \end{aligned}$$

Because $\alpha ,\beta$ are positive constant and $0<\gamma <1$, we have

$$\begin{aligned} |B_2|&\le C\varepsilon (\Vert [\![\eta _q]\!]\Vert _{{{\fancyscript{E}}_h}} +\Vert [\![\eta _u]\!]\Vert _{{{\fancyscript{E}}_h}})(\Vert \delta _u\Vert _{{\partial \Omega _h}}+\Vert \delta _q\Vert _{{\partial \Omega _h}}). \end{aligned}$$

So

$$\begin{aligned}&\beta \Vert [\![\eta _q]\!]\Vert ^2_{{{\fancyscript{E}}^i_h}}+\alpha \Vert [\![\eta _u]\!]\Vert ^2_{{{\fancyscript{E}}^i_h}} +\gamma \langle \frac{1}{\sqrt{f}}, |\eta _q|^2\rangle _{\partial \Omega }+ (1-\gamma )\langle \sqrt{f}, |\eta _u|^2\rangle _{\partial \Omega }\\&\le \,\frac{1}{\varepsilon }\left( |B_1|+|B_2|\right) \\&\le \, C\frac{h}{\varepsilon }|f|_{1,\infty }\Vert \delta _u\Vert \Vert \eta _u\Vert + C\left( \Vert [\![\eta _q]\!]\Vert _{{{\fancyscript{E}}_h}}+\Vert [\![\eta _u]\!]\Vert _{{{\fancyscript{E}}_h}}\right) \left( \Vert \delta _u\Vert _{{\partial \Omega _h}} +\Vert \delta _q\Vert _{{\partial \Omega _h}}\right) , \end{aligned}$$

which implies that

$$\begin{aligned} \Vert [\![\eta _q]\!]\Vert ^2_{{{\fancyscript{E}}_h}}+\Vert [\![\eta _u]\!]\Vert ^2_{{{\fancyscript{E}}_h}}&\le C \frac{h}{\varepsilon }|f|_{1,\infty }\Vert \delta _u\Vert \Vert \eta _u\Vert + C\left( \Vert \delta _u\Vert ^2_{{\partial \Omega _h}}+\Vert \delta _q\Vert ^2_{{\partial \Omega _h}}\right) \\&\le C \frac{h^3}{\varepsilon ^2}|f|^2_{1,\infty } \Vert \eta _u\Vert ^2+\frac{C}{h}\Vert \delta _u\Vert ^2+ C\left( \Vert \delta _u\Vert ^2_{{\partial \Omega _h}}+\Vert \delta _q\Vert ^2_{{\partial \Omega _h}}\right) . \end{aligned}$$

Finally, applying the projection result in Lemma 3.2, we get

$$\begin{aligned} \Vert [\![\eta _q]\!]\Vert ^2_{{{\fancyscript{E}}_h}}+\Vert [\![\eta _u]\!]\Vert ^2_{{{\fancyscript{E}}_h}}\le&C\frac{h^3}{\varepsilon ^2}|f|^2_{1,\infty }\left( \Vert \eta _u\Vert ^2+\Vert u\Vert ^2\right) , \end{aligned}$$

which completes the proof. $\square$

4.4 Proof of Theorem 3.4

To obtain the error estimate for $u_h$ in Theorem 3.4, we use a duality argument. We first consider the following dual problem for any given $\theta \in L^2(\Omega )$

$$\begin{aligned}&\psi -\varepsilon \varphi '=0 \quad \text { in } \Omega , \end{aligned}$$

(4.13a)

$$\begin{aligned}&-\varepsilon \psi '-f \varphi =\theta \quad \text { in } \Omega , \end{aligned}$$

(4.13b)

$$\begin{aligned}&\psi (a)-\varvec{i}\sqrt{f}_a\,\varphi (a)=0, \end{aligned}$$

(4.13c)

$$\begin{aligned}&\psi (b)+\varvec{i}\sqrt{f}_b\,\varphi (b)=0. \end{aligned}$$

(4.13d)

For the dual problem, we have the following regularity result.

Lemma 4.5

Given $\theta \in L^2(\Omega )$, the solution $\varphi$ and $\psi$ of the dual problem (4.13) satisfy

$$\begin{aligned} \Vert \psi \Vert +\Vert \varphi \Vert \le C\varepsilon ^{-1}\Vert \theta \Vert , \end{aligned}$$

where $C$ is independent of $\varepsilon$.

Proof

From (4.13a) and (4.13b) we get

$$\begin{aligned} -\varepsilon ^2\varphi ''-f\varphi =\theta . \end{aligned}$$

(4.14)

First, we multiply the Eq. (4.14) by $\overline{\varphi }$ and integrate over $\Omega$ to get

$$\begin{aligned} -\varepsilon ^2(\varphi '',\varphi )_\Omega -(f, |\varphi |^2)_\Omega =(\theta ,\varphi )_\Omega . \end{aligned}$$

Using integration by parts and the boundary conditions (4.13c) and (4.13d), we get

$$\begin{aligned} \Vert \varepsilon \varphi '\Vert ^2-(f,|\varphi |^2)_\Omega +\varvec{i}\varepsilon \sqrt{f_b}\,|\varphi (b)|^2+\varvec{i}\varepsilon \sqrt{f_a}\,|\varphi (a)|^2 =(\theta ,\varphi )_\Omega . \end{aligned}$$

Taking the imaginary part of above equation, we get

$$\begin{aligned} |\varphi (b)|^2+|\varphi (a)|^2\le C\varepsilon ^{-1}\Vert \theta \Vert \Vert \varphi \Vert \end{aligned}$$

(4.15)

which implies that

$$\begin{aligned} |\varepsilon \varphi '(b)|^2+|\varepsilon \varphi '(a)|^2\le C\varepsilon ^{-1}\Vert \theta \Vert \Vert \varphi \Vert \end{aligned}$$

(4.16)

by using the boundary conditions (4.13c) and (4.13d).

Next, we multiply the Eq. (4.14) by $\overline{\varphi }'$ and get

$$\begin{aligned} -\varepsilon ^2\varphi ''\overline{\varphi }'-f\varphi \overline{\varphi }'=\theta \overline{\varphi }'. \end{aligned}$$

Taking the real part of the above equation, we have

$$\begin{aligned} -\frac{1}{2}\frac{d}{dx}|\varepsilon \varphi '|^2-\frac{1}{2}\frac{d}{dx} \left( f|\varphi |^2\right) =-\frac{1}{2} f'|\varphi |^2+\text {Re}(\theta \overline{\varphi }'), \end{aligned}$$

which implies

$$\begin{aligned} \frac{d}{dx}(|\varepsilon \varphi '|^2+f |\varphi |^2)&= f'|\varphi |^2-2\text {Re}(\theta \overline{\varphi }')\\&\le C|\varphi |^2+|\varepsilon \varphi '|^2+\frac{1}{\varepsilon ^2}|\theta |^2\\&\le C(|\varepsilon \varphi '|^2+f|\varphi |^2)+\frac{1}{\varepsilon ^2}|\theta |^2. \end{aligned}$$

Let $G(x)=|\varepsilon \varphi '|^2+f|\varphi |^2$. Then from above we have

$$\begin{aligned} G'(x)\le C G(x)+\frac{1}{\varepsilon ^2}|\theta (x)|^2. \end{aligned}$$

Using Gronwall’s inequality, we get

$$\begin{aligned} G(x)\le CG(a)+C\int _a^x \frac{1}{\varepsilon ^2}|\theta (x)|^2dx\le C\left( G(a)+\frac{1}{\varepsilon ^2}\Vert \theta \Vert ^2\right) . \end{aligned}$$

From (4.15) and (4.16), we have

$$\begin{aligned} G(a)=|\varepsilon \varphi '(a)|^2+f(a)|\varphi (a)|^2\le C\frac{1}{\varepsilon }\Vert \theta \Vert \Vert \varphi \Vert . \end{aligned}$$

So

$$\begin{aligned} G(x)\le C\frac{1}{\varepsilon }\Vert \theta \Vert \Vert \varphi \Vert +\frac{1}{\varepsilon ^2}\Vert \theta \Vert ^2. \end{aligned}$$

Now integrating $G(x)$ over $[a, b]$, we obtain

$$\begin{aligned} \Vert \varepsilon \varphi '\Vert ^2+\tau \Vert \varphi \Vert ^2\le&\int _a^b G(x)dx\le C\frac{1}{\varepsilon }\Vert \theta \Vert \Vert \varphi \Vert +C\frac{1}{\varepsilon ^2}\Vert \theta \Vert ^2\le C\frac{1}{\varepsilon ^2}\Vert \theta \Vert ^2+\frac{\tau }{2}\Vert \varphi \Vert ^2. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert \varepsilon \varphi '\Vert ^2+\Vert \varphi \Vert ^2\le C\frac{1}{\varepsilon ^2}\Vert \theta \Vert ^2. \end{aligned}$$

$\square$

Using the projection result in Theorem 3.1 and the regularity result in Lemma 4.5, we immediately get the following result.

Lemma 4.6

For the solution $\varphi$ and $\psi$ to the dual problem (4.13), we have

$$\begin{aligned} \Vert \delta _\varphi \Vert +\Vert \delta _\psi \Vert \le C\left( \frac{h}{\varepsilon }+\frac{h^2}{\varepsilon ^2}\right) \Vert \theta \Vert \end{aligned}$$

and

$$\begin{aligned} \Vert \delta _\varphi \Vert _{{\partial \Omega _h}}+\Vert \delta _\psi \Vert _{{\partial \Omega _h}}\le C\left( \frac{h^{1/2}}{\varepsilon }+\frac{h^{3/2}}{\varepsilon ^2}\right) \Vert \theta \Vert . \end{aligned}$$

We are now ready to prove Theorem 3.4.

Lemma 4.7

For any $\theta \in L^2({\Omega _h})$, we have

$$\begin{aligned} (\eta _u,\theta )_{\Omega _h}=S_1+S_2, \end{aligned}$$

where

$$\begin{aligned} S_1=&-\varepsilon \langle \eta _u, \delta _\psi \,\varvec{n}\rangle +\varepsilon \langle \eta _q,\delta _\varphi \, \varvec{n}\rangle -\varepsilon \langle \widehat{e}_q, \delta _\varphi \,\varvec{n}\rangle +\varepsilon \langle \widehat{e}_u, \delta \psi \,\varvec{n}\rangle ,\\ S_2=&\, ((f- {\mathbb {P}}^0f) \eta _u,\delta \varphi )+ ((f-{\mathbb {P}}^0 f)\delta _u, \varvec{\Pi }\varphi ). \end{aligned}$$

Proof

By the Eq. (4.13b) in the dual problem , we have

$$\begin{aligned} (\eta _u, {\theta }) =&-(\eta _u,\varepsilon {\psi '}) -(\eta _u, f{\varphi }) \\ =&-\varepsilon (\eta _u, \delta _\psi ') -\varepsilon (\eta _u, (\varvec{\Pi }\psi )')-(\eta _u,f\varphi ). \end{aligned}$$

Using integration by parts and the property of the projection $\varvec{\Pi }$ (3.1), we have

$$\begin{aligned} (\eta _u,\theta ) =&-\varepsilon \langle \eta _u, \delta _\psi \,\varvec{n}\rangle +\varepsilon (\eta _u', \delta _\psi ) -\varepsilon (\eta _u, (\varvec{\Pi }\psi )')-(\eta _u, f\varphi )\\ =&-\varepsilon \langle \eta _u, \delta _\psi \,\varvec{n}\rangle -\varepsilon (\eta _u, (\varvec{\Pi }\psi )')-(\eta _u, f\varphi ) \end{aligned}$$

Using the error Eq. (4.1a) with $\omega =\varvec{\Pi }\psi$, we get

$$\begin{aligned} (\eta _u,\theta )=&-\varepsilon \langle \eta _u, \delta _\psi \,\varvec{n}\rangle +(\eta _q, \varvec{\Pi }\psi )-\varepsilon \langle \widehat{e}_u, \varvec{\Pi }\psi \,\varvec{n}\rangle -(\eta _u, f\varphi ). \end{aligned}$$

For the second term on the right hand side of the equation, we use the definition of the projection $\varvec{\Pi }$ and then the equation (4.13b) to get

$$\begin{aligned} (\eta _q, \varvec{\Pi }\psi )=&(\eta _q, \psi )=(\eta _q, \varepsilon \varphi ')=\varepsilon (\eta _q,\delta _\varphi ')+\varepsilon (\eta _q, (\varvec{\Pi }\varphi )'). \end{aligned}$$

Using integration by parts and the definition of the projection $\varvec{\Pi }$, we have

$$\begin{aligned} (\eta _q, \varvec{\Pi }\psi )=&\varepsilon \langle \eta _q,\delta _\varphi \,\varvec{n}\rangle +\varepsilon (\eta _q, (\varvec{\Pi }\varphi )'). \end{aligned}$$

For the second term on the right hand side of the equation, we use the error Eq. (4.1b) with $v=\varvec{\Pi }\varphi$ and obtain

$$\begin{aligned} (\eta _q, \varvec{\Pi }\psi )=&\varepsilon \langle \eta _q,\delta _\varphi \,\varvec{n}\rangle +\varepsilon \langle \widehat{e}_q, \varvec{\Pi }\varphi \,\varvec{n}\rangle +(f \eta _u, \varvec{\Pi }\varphi )+(f\delta _u, \varvec{\Pi }\varphi ). \end{aligned}$$

So we have

$$\begin{aligned} (\eta _u,\theta )=&-\varepsilon \langle \eta _u, \delta _\psi \,\varvec{n}\rangle +\varepsilon \langle \eta _q,\delta _\varphi \, \varvec{n}\rangle +\varepsilon \langle \widehat{e}_q, \varvec{\Pi }\varphi \,\varvec{n}\rangle \\&-(f \eta _u, \delta \varphi )+(f\delta _u, \varvec{\Pi }\varphi ) -\varepsilon \langle \widehat{e}_u, \varvec{\Pi }\psi \,\varvec{n}\rangle . \end{aligned}$$

It is easy to check that $-\langle \widehat{e}_q, \varphi \,\varvec{n}\rangle +\langle \widehat{e}_u, \psi \,\varvec{n}\rangle =0$. So

$$\begin{aligned} (\eta _u,\theta )=&-\varepsilon \langle \eta _u, \delta _\psi \,\varvec{n}\rangle +\varepsilon \langle \eta _q,\delta _\varphi \, \varvec{n}\rangle -\varepsilon \langle \widehat{e}_q, \delta _\varphi \,\varvec{n}\rangle +\varepsilon \langle \widehat{e}_u, \delta \psi \,\varvec{n}\rangle \\&-(f \eta _u, \delta \varphi )+(f\delta _u, \varvec{\Pi }\varphi ). \end{aligned}$$

The Lemma follows by using the definition of the $L^2$ projection $\varvec{\Pi }$. $\square$

For single-valued functions $v$ and $w$ at ${{\fancyscript{E}}^i_h}$, let us introduce the notation

$$\begin{aligned} \langle v, \omega \rangle _{{{\fancyscript{E}}^i_h}}=\sum _{j=1}^{N-1} v(x_{j+\frac{1}{2}})w(x_{j+\frac{1}{2}}). \end{aligned}$$

Now we prove Theorem 3.4.

Proof

Taking $\theta =\eta _u$, we have

$$\begin{aligned} \Vert \eta _u\Vert ^2\le |S_1|+|S_2|. \end{aligned}$$

Let us estimate $S_1$ and $S_2$. Applying Lemma 4.1 and Lemma 4.2 to Lemma 4.7, we get

$$\begin{aligned} S_1=&-\varepsilon \langle \eta _u,\delta _\psi \,\varvec{n}\rangle +\varepsilon \langle \eta _q, \delta _\varphi \,\varvec{n}\rangle \\&+ \varepsilon \langle (\delta _u+\eta _u)^- -\varvec{i}\beta ([\![\delta _q]\!]+[\![\eta _q]\!]), \delta _\psi \,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}\\&-\varepsilon \langle (\delta _q+\eta _q)^+ +\varvec{i}\alpha ([\![\delta _u]\!]+[\![\eta _u]\!]), \delta _\varphi \,\varvec{n}\rangle _{{\partial \Omega _h}\setminus {\partial \Omega }}\\&+\varepsilon \langle (1-\gamma )(\delta _u+\eta _u)-\varvec{i}\frac{\gamma }{\sqrt{f}} (\delta _q+\eta _q)\,\varvec{n}, \delta _\psi \,\varvec{n}\rangle _{{\partial \Omega }}\\&-\varepsilon \langle \gamma (\delta _q+\eta _q)+\varvec{i}(1-\gamma )\sqrt{f}(\delta _u+\eta _u)\, \varvec{n},\delta _\varphi \,\varvec{n}\rangle _{{\partial \Omega }} \end{aligned}$$

After some algebraic manipulations, we have

$$\begin{aligned} S_1=&- \varepsilon \langle [\![\eta _u]\!], \delta _\psi ^+ -\varvec{i}\alpha [\![\delta _{\varphi }]\!]\rangle _{{{\fancyscript{E}}^i_h}}+\varepsilon \langle [\![\eta _q]\!], \delta _\varphi ^- +\varvec{i}\beta [\![\delta _\varphi ]\!]\rangle _{{{\fancyscript{E}}^i_h}}\\&-\varepsilon \langle \eta _u,(\gamma \delta _\psi -\varvec{i}(1-\gamma )\sqrt{f} \delta _\varphi )\, \varvec{n}\rangle _{{\partial \Omega }}+\varepsilon \langle \eta _q, \left( (1-\gamma )\delta _\varphi +\varvec{i}\frac{\gamma }{\sqrt{f}}\delta _{\psi }\right) \, \varvec{n}\rangle _{{\partial \Omega }}\\&+\,\varepsilon \left\langle \delta _u^--\varvec{i}\beta [\![\delta _q]\!], [\![\delta _\psi ]\!]\right\rangle _{{{\fancyscript{E}}^i_h}}-\varepsilon \left\langle \delta _q^++ \varvec{i}\alpha [\![\delta _u]\!], [\![\delta _\varphi ]\!]\right\rangle _{{{\fancyscript{E}}^i_h}}\\&+\,\varepsilon \langle (1-\gamma )\delta _u-\varvec{i}\frac{\gamma }{\sqrt{f}}\delta _q\, \varvec{n},\delta _\psi \,\varvec{n}\rangle _{{\partial \Omega }}-\varepsilon \langle \gamma \delta _q+ \varvec{i}(1-\gamma )\sqrt{f}\delta _u,\delta _\varphi \,\varvec{n}\rangle _{{\partial \Omega }}. \end{aligned}$$

Because $\alpha , \beta , \gamma , 1-\gamma$ are positive constants, using the Cauchy’s inequality, Lemma 3.2 and Lemma 4.6, we get

$$\begin{aligned} |S_1|&\le C \varepsilon (\Vert [\![\eta _u]\!]\Vert _{{{\fancyscript{E}}_h}}+\Vert [\![\eta _q]\!] \Vert _{{{\fancyscript{E}}_h}})(\Vert \delta _\varphi \Vert _{{\partial \Omega _h}}+\Vert \delta _\psi \Vert _{{\partial \Omega _h}})\\&\quad +C\varepsilon (\Vert \delta _u\Vert _{{\partial \Omega _h}}+\Vert \delta _q\Vert _{{\partial \Omega _h}})(\Vert \delta _\varphi \Vert _{{\partial \Omega _h}}+\Vert \delta _\psi \Vert _{{\partial \Omega _h}})\\&\le C \left( h^{1/2}+\frac{h^{3/2}}{\varepsilon }\right) (\Vert [\![\eta _u]\!] \Vert _{{{\fancyscript{E}}_h}}+\Vert [\![\eta _q]\!]\Vert _{{{\fancyscript{E}}_h}})\Vert \theta \Vert +C \left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) |f|_{1,\infty }\Vert u\Vert \Vert \theta \Vert . \end{aligned}$$

Then by Theorem 3.3, we have

$$\begin{aligned} |S_1| \le C\left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) |f|_{1,\infty } \Vert \eta _u\Vert \Vert \theta \Vert +C\left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) |f|_{1,\infty }\Vert u\Vert \Vert \theta \Vert . \end{aligned}$$

Similarly, we get

$$\begin{aligned} |S_2|\le&\Vert f- {\mathbb {P}}^0f\Vert _\infty \Vert \eta _u\Vert \Vert \delta \varphi \Vert + \Vert f-{\mathbb {P}}^0 f\Vert _\infty \Vert \delta _u\Vert \Vert \varvec{\Pi }\varphi \Vert \\ \le&\Vert f- {\mathbb {P}}^0f\Vert _\infty \Vert \eta _u\Vert \Vert \delta \varphi \Vert + \Vert f-{\mathbb {P}}^0 f\Vert _\infty \Vert \delta _u\Vert \Vert \varphi \Vert \\ \le&C \left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) |f|_{1,\infty }\Vert \eta _u\Vert \Vert \theta \Vert +C\frac{h^3}{\varepsilon ^2}|f|_{1,\infty }\Vert u\Vert \Vert \theta \Vert . \end{aligned}$$

So

$$\begin{aligned} \Vert \eta _u\Vert ^2 \le&C\left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) |f|_{1,\infty } \Vert \eta _u\Vert \Vert \theta \Vert +C\left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) |f|_{1,\infty }\Vert u\Vert \Vert \theta \Vert . \end{aligned}$$

If $\left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) |f|_{1,\infty }$ is sufficiently small, we have

$$\begin{aligned} \Vert \eta _u\Vert \le&C|f|_{1,\infty }\left( \frac{h^2}{\varepsilon }+\frac{h^3}{\varepsilon ^2}\right) \Vert u\Vert . \end{aligned}$$

$\square$

5 Numerical Results by the Multiscale DG

In this section, we will perform several numerical tests. The first example is to show the good approximation property of the multiscale bases $E^1$. The basis functions approximate the solution exactly when $f(x)$ is constant. The next example is to verify the second order convergence of our multiscale DG in the error estimates for a wide range of $\varepsilon$ from 1 to $10^{-4}$. In the last two examples, we apply the proposed scheme to the application of Schrödinger equation in the modeling of resonant tunneling diode (RTD).

For the proposed multiscale DG scheme, we use $\alpha =\beta =1$ and $\gamma =0.5$ in the tests. For other constants $\alpha ,\beta$ and $0<\gamma <1$, the numerical results are similar and thus we do not show them here. When $\alpha =\beta =\gamma =0$, the method becomes the minimal dissipation LDG (MD-LDG) method [8] with multiscale basis $E^1$. Although our analysis does not cover this case, numerically we see a similar second order convergence.

5.1 Constant $f$

Example 5.1

In the first example, we consider the simple case with constant function $f(x)$. When $f(x)$ is a constant, the exact solution of (2.1) is in the finite element space $E^1$. Thus the multiscale DG method can compute the solution exactly with only round-off errors. The $L^2$-errors of the multiscale DG with $\alpha =\beta =1$ and $\gamma =0.5$ for the case $f(x)=10$ are shown in Table 1. It is clear to see the round-off errors (in double precision) for $\varepsilon$ ranging from 1 to $10^{-4}$. We remark that when $\varepsilon$ is small, numerically integrating the exponential functions accumulates round-off errors. Thus the errors increase when $\varepsilon$ becomes small.

Table 1 Example 5.1: $L^2$-errors by multiscale DG with $\alpha =\beta =1, \gamma =0.5$

5.2 Accuracy Test

Example 5.2

In this example, we consider a smooth function $f(x)=\sin x+2$. Table 2 lists the $L^2$-errors and orders of accuracy by the proposed multiscale DG scheme with $\alpha =\beta =1, \gamma =0.5$ for $\varepsilon$ from 1 to $10^{-4}$. The reference solutions are computed by polynomial-based MD-LDG $P^3$ method with $N=50{,}000$ cells for $\varepsilon =1$ and with $N=500{,}000$ for $\varepsilon =10^{-2}, 10^{-3}, 10^{-4}$. Note that we stop refining the mesh when the errors are smaller than $10^{-8}$. We can see a clean second order convergence for both $h>\varepsilon$ and $h<\varepsilon$. For the same $h$, when $\varepsilon$ decreases by a factor of ten, the magnitude of the error increases by ten times. This verifies the convergence order is of $O(h^2/\varepsilon )$ in Theorem 3.4.

Table 2 Example 5.2: $L^2$-errors and orders of accuracy by multiscale DG with $\alpha =\beta =1, \gamma =0.5$

We also show the results by the multiscale MD-LDG method with $E^1$ space, i.e. the proposed multiscale DG method with $\alpha =\beta =\gamma =0$, in Table 3. Although our analysis is inconclusive in this case, we observe a second order convergence when $h>\varepsilon$ and a third order convergence when $h<\varepsilon$.

Table 3 Example 5.2: $L^2$-errors and orders of accuracy by multiscale DG with $\alpha =\beta =0, \gamma =0$

Next, we compare the results with the WKB-LDG method in [18] in Table 4. Note that WKB-LDG method is the multiscale MD-LDG method with $E^2$ space, which has one more basis function “1” than the $E^1$ space. Similar to the MD-LDG method with $E^1$ space, MD-LDG method with $E^2$ space also has a second order convergence when $h>\varepsilon$ and a third order convergence when $h<\varepsilon$. However, we observe a resonance error around $h=\varepsilon$ whereas our new proposed multiscale scheme does not have it. In Table 5, we show the condition numbers of the global matrices for the WKB-LDG method with $E^2$ space and our proposed DG method with $E^1$ space. Note that the condition numbers by using $E^2$ space become very large when $N=20$ for $\varepsilon =10^{-2}$ and when $N=160$ for $\varepsilon =10^{-3}$. Those are exactly where the resonance errors are observed in Table 4. In contrast, the condition numbers by using $E^1$ space only change slightly. This shows why removing the basis function “1” from the finite element basis will reduce the resonance errors.

Table 4 Example 5.2: $L^2$-errors and orders of accuracy by WKB-LDG in [18]

Table 5 Example 5.2: Condition numbers of the global matrices (in $L^{\infty }$ norm) by the proposed scheme with $E^1$ space and WKB-LDG with $E^2$ space

At the end of this section, we compare our multiscale DG with the MD-LDG using polynomials $P^1$ and $P^2$ in Table 6. Standard DG methods using polynomials do not have any order of convergence until the mesh is refined to $h<\varepsilon$. For example, for $\varepsilon =10^{-2}$, MD-LDG $P^1$ shows a second order starting from $N=160$ and MD-LDG $P^2$ shows a third order starting from $N=80$. When $\varepsilon$ becomes even smaller to $10^{-3}$, for both $P^1$ and $P^2$, there is no order of convergence till $N=640$. The multiscale DG method is convergent when $h$ is much larger than $\varepsilon$, and when $h<\varepsilon$, it also approximates the solution much more accurately than the standard DG. For example, when $\varepsilon =10^{-2}$ and $N=640$, the error is $O(10^{-3})$ by using $P^1, O(10^{-5})$ by $P^2$, and $O(10^{-7})$ by $E^1$. Therefore, the multiscale DG is more efficient and accurate than the standard DG methods for solving the stationary Schrödinger equation.

Table 6 Example 5.2: $L^2$-errors and orders of accuracy by standard MD-LDG $P^1$ and $P^2$

5.3 Applications to Schrödinger Equation

In this section, we apply our proposed multiscale DG method to solve the Schrödinger equation in the simulation of the resonant tunneling diode (RTD) model. RTD model is used to collect the electrons which have an energy extremely close to the resonant energy.

We consider the RTD model (see [5]) on the interval [0, 135 nm]. Its conduction band profile consists of two barriers of height $-0.3$ V located at $[60,65]$ and $[70, 75]$. A bias energy $\triangle v$ is applied between the source and the collector regions.

The wave function of the electrons injected at $x = 0$ with an energy $E > 0$ satisfies the stationary Schrödinger equation with open boundary conditions, (1.2), with $m=0.067\,m_e$. In our numerical simulations, we consider the total potential to be the external potential only. Figure 1 shows the external potential with the double barriers and an applied bias. These numerical tests were also performed in [5, 18].

Fig. 1

External voltage with double barriers of height $-0.3$ V located at $[60,65]$ and $[70, 75]$ and an applied bias of $0.8$ V

Example 5.3

In the first application example, we consider the energy $E=0.0895\,\hbox {eV}$ which is very close to the double-barrier resonant energy. For simplicity, no bias is applied to the external potential and the potential function $V(x)$ is a piecewise constant function

$$\begin{aligned} V(x)=\left\{ \begin{array}{ll} 0, &{} \quad x<60 \\ -0.3, &{} \quad 60 <x<65 \\ 0, &{} \quad 65 <x<70 \\ -0.3, &{} \quad 70 <x<75 \\ 0, &{} \quad x>75 \\ \end{array} \right. \end{aligned}$$

In this case, our proposed multiscale DG method can approximate the solution exactly with round off errors. We only use 23 cells for the proposed multiscale DG method with 6 cells each in $[0, 50], [85, 135]$, 2 cells each in $[50, 60], [60, 65], [70, 75]$ and $[75, 85]$, and 3 cells in $[65, 70]$.

Figure 2 shows the wave function modulus for the case of the resonance energy $E=0.0895$ eV. We see a big spike in the double barriers area [60, 75]. The proposed multiscale DG method is able to capture the resonance spike in only 23 cells. The standard polynomial-based DG methods will need a much more refined mesh to capture the resonance.

Fig. 2

Wavefunction modulus by multiscale DG for the resonance energy $E=0.0895$ eV. 23 cells are used in the multiscale DG method. In each cell, the solution is plotted as a function using 27 points

Example 5.4

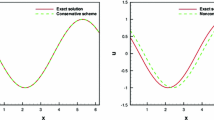
In the next example, a bias of $0.08$ V is added at the edges of the device. We compute in the case of a very high energy $E = 1.11 eV$ and the solution will be highly oscillating. The reference solution was obtained by the polynomial-based MD-LDG $P^3$ method of 13,500 cells. Figure 3 shows the wave function modulus computed by the multiscale DG with 23 cells. In each cell, the solution is plotted as a function using 27 points. We can see although the solution is highly oscillating, the proposed scheme matches the reference solution very well. The $L^2$-error is $1.49\times 10^{-5}$. The standard polynomial-based DG methods cannot well approximate the solution unless the mesh is very refined.

Fig. 3

Wavefunction modulus by the multiscale DG for a high energy $E=1.11\,\hbox {eV}$. 23 cells are used in the multiscale DG method. In each cell, the solution is plotted as a function using 27 points

6 Concluding Remarks

In this paper, we have developed a new multiscale discontinuous Galerkin method for a special second order elliptic equation with applications to one-dimensional stationary Schrödinger equations. The basis functions are constructed based on the WKB asymptotic and thus have good approximations to the solutions. The error estimate shows a second order convergent rate for both $h\gtrsim \varepsilon$ and $h\lesssim \varepsilon$. Numerical experiments confirmed the convergent rate and also demonstrated excellent accuracy on very coarse meshes when applied to Schrödinger equations. Compared with the continuous finite element based WKB method in [5], the multiscale DG method allows the full usage of the potential of this methodology in easy $h$-$p$ adaptivity and feasibility for the extension to two-dimensional case. Compared with the WKB-LDG method in [18], the new multiscale DG method uses a smaller finite element space and more importantly, it dose not have resonance errors. In future work, we will generalize our multiscale DG method to two-dimensional Schrödinger equations.