A Mixed Discontinuous Galerkin Method Without Interior Penalty for Time-Dependent Fourth Order Problems

Abstract

A novel discontinuous Galerkin (DG) method is developed to solve time-dependent bi-harmonic type equations involving fourth derivatives in one and multiple space dimensions. We present the spatial DG discretization based on a mixed formulation and central interface numerical fluxes so that the resulting semi-discrete schemes are $L^2$ stable even without interior penalty. For time discretization, we use Crank–Nicolson so that the resulting scheme is unconditionally stable and second order in time. We present the optimal $L^2$ error estimate of $O(h^{k+1})$ for polynomials of degree k for semi-discrete DG schemes, and the $L^2$ error of $O(h^{k+1} +(\Delta t)^2)$ for fully discrete DG schemes. Extensions to more general fourth order partial differential equations and cases with non-homogeneous boundary conditions are provided. Numerical results are presented to verify the stability and accuracy of the schemes. Finally, an application to the one-dimensional Swift–Hohenberg equation endowed with a decay free energy is presented.

1 Introduction

In this paper, we are interested in discontinuous Galerkin approximations to the fourth order partial differential equations (PDEs) of the form

$$\begin{aligned} u_t&= Lu \quad x\in \Omega \subset \mathbb {R}^d, \quad t>0,\end{aligned}$$

(1.1a)

$$\begin{aligned} u(x, 0)&=u_0(x), \quad x\in \Omega , \end{aligned}$$

(1.1b)

where $L=\sum _{m=0}^2a_m \Delta ^m$ is a linear differential operator of fourth order and $a_m (m=0,1,2)$ are constants with $a_2<0$, $\Omega$ is a bounded rectangular domain in $\mathbb {R}^d$, $u_0(x)$ is a given function. Our analysis is presented mostly for periodic boundary conditions, extensions to other non-homogeneous boundary conditions will then follow. The model could include a lower order term such as f(u, x, t), without additional difficulty.

The fourth order PDEs appear often in physical and engineering applications, such as the modeling of the thin beams and plates, strain gradient elasticity, thermal convection, and phase separation in binary mixtures. The special cases of (1.1) include the linear time-dependent biharmonic equation with

$$\begin{aligned} L=-\Delta ^2, \end{aligned}$$

and the linearized Cahn–Hilliard equation

$$\begin{aligned} L=-\Delta ^2 -\Delta . \end{aligned}$$

In the literature, various numerical methods have been developed to discretize fourth order partial differential equations, such as mixed finite element methods (see e.g. [1, 4, 10, 14, 16, 26]), and finite difference methods (see e.g. [18]). In this paper we will discuss discontinuous Galerkin methods, using a discontinuous Galerkin finite element approximation in the spatial variables coupled with a proper time discretization. It is well known that for equations containing higher order spatial derivatives, discontinuous Galerkin discretization cannot be directly applied. This is because the solution space, which consists of piecewise polynomials discontinuous at the element interfaces, is not regular enough to handle higher derivatives. This is a typical non-conforming case in finite elements.

One approach to resolve such difficulty is the local discontinuous Galerkin (LDG) method (see e.g., [12, 25, 33, 35] for fourth order problems). The idea is to suitably rewrite the higher order equation into a first order system and then discretize it by the DG method [11]. The local numerical fluxes without interior penalty can be designed to guarantee stability. The LDG method has been successful in handling equations with high-order derivatives, since it was first developed by Cockburn and Shu [11] for the second order convection diffusion equation. However, these schemes increase the number of unknowns in numerical solutions.

Another approach is to weakly impose the inter-element continuity conditions using interior penalties. In the context of finite element framework, $C^1$ conforming finite element methods for the biharmonic equation is known computationally intensive due to the imposition of $C^1$-continuity across the element interfaces, several non-conforming approaches such as $C^0$-interior penalty methods [3, 13] and interior penalty methods [2, 15, 27, 28, 31] have been proposed. These approaches use either continuous or discontinuous finite element solution spaces in which continuity conditions are weakly enforced through interior penalties. A related strategy is the direct DG discretization based on numerical fluxes which penalize jumps of derivatives when crossing element interfaces [7]. For DG schemes with interior penalties, the practical choice of penalty parameters is often a subtle matter.

In this work we reformulate the fourth order PDEs into a second order coupled system and discretize the system by a DG method without interior penalty. In the case $L=-\Delta ^2$, such reformulation

$$\begin{aligned} u_t= & {} \Delta q, \nonumber \\ q= & {} -\Delta u, \end{aligned}$$

(1.2)

is the usual mixed formulation [9], which has been used to design the mixed DG methods with interior penalties in [17, 34] for solving the biharmonic equation. Our DG method derives from a direct DG discretization of the mixed formulation (1.2). Instead of the standard DG ansatz analogous to the discretization of diffusion, the simplest form for numerical fluxes is used: the arithmetic mean of the solution gradient and the arithmetic mean of the solution. The resulting scheme is the most simple variant to date for the discretization of second order terms, i.e., without any interior penalty. This is in sharp contrast to the DDG methods introduced in [22, 23] for diffusion, where interface corrections are included to penalize jumps of both the numerical solution and its second order derivatives. With formulation (1.2), stability of the resulting DG scheme is naturally ensured due to the symmetric nature of the underlying bilinear operator. It is also parameter free, i.e. no particular choice of any penalty constant is necessary. This makes the scheme simple to implement for generic linear and non-linear problems.

It is known that for DG methods stability itself does not necessarily imply the optimal convergence. Obtaining optimal error estimates for DG methods has been a major subject of research. The a priori error estimate results for DG methods with interior penalties have been reported in [7, 17, 27, 28, 31, 34] for biharmonic type equations, in these works penalty parameters play a special role in both the stability analysis and the error estimates.

The main quest in this article is whether optimal convergence can still be achieved without interior penalty. We carry out the optimal $L^2$ error estimates for both semi-discrete and fully-discrete schemes with periodic boundary conditions, in both one and multi-dimensions. The crucial ingredient in the one-dimensional error analysis is a global projection P defined by $A(v-Pv,\phi )=0$ for any test function $\phi$ in the finite element space, and the corresponding projection error. Here $A(\cdot , \cdot )$ is the bilinear operator obtained by the penalty-free DG discretization of the operator $-\partial ^2_x$. In multi-dimensional case, we use the tensor product polynomials of degree at most k, and make use of the projection error obtained in [19] and the bilinear form estimate $|A(v-Pv,\phi )| \le Ch^{k+2}|v|_{k+2}\Vert \phi \Vert$ obtained in [20]. A related work is [5], in which the authors use the inf-sup strategy to prove the optimal $L^2$ convergence rates for the symmetric DG method without interior penalty using $P^k(k \ge 2)$ polynomials for one dimensional second order elliptic problems.

Extension to more general equations of form (1.1) is carried out by rewriting L as $L=- {\mathcal {L}}^2 +M$, where $M=a_0-\frac{a_1^2}{4a_2}$ and $\mathcal {L}=\sqrt{-a_2} \left( \Delta +\frac{a_1}{2a_2} \right)$ is a second order operator, and the optimal $L^2$ error estimate can also be obtained. For three typical non-homogeneous boundary conditions we present DG schemes with boundary corrections. Boundary penalty is needed in some cases to weakly enforce the given boundary data, as usually done for the weak formulation of elliptic problems [24]. In fact, imposing boundary conditions only weakly is one of the main advantages of the DG methods to boundary-value problems for higher order PDEs such as (1.1a).

The rest of the paper is organized as follows: in Sect. 2, we describe the mixed DG methods in one dimension and present the optimal error estimates for both semi-discrete and fully discrete schemes to time-dependent biharmonic problems. In Sect. 3, we formulate the DG scheme in multi-dimensions along with its stability and optimal error estimates using tensor product polynomials. In Sect. 4, we extend the DG schemes to more general fourth order time-dependent PDEs, cases with non-periodic boundary conditions, and the one-dimensional Swift–Hohenberg equation—a nonlinear problem with a decay free energy [32]. Several numerical results are presented in Sect. 5 to verify the stability and accuracy of the schemes. Finally, we give concluding remarks in Sect. 6 to summarize results in this paper and indicating future work.

2 The DG Scheme in One Dimension

In this section we consider the one dimensional time-dependent fourth order Eq. (1.1), i.e.,

$$\begin{aligned} u_t= - u_{xxxx} \quad x\in [a,b], \quad t>0, \end{aligned}$$

(2.1)

subject to initial data $u(x, 0)=u_0(x)$, and periodic boundary conditions.

We partition the interval [a, b] into computational cells $I_j=[x_{j-1/2},x_{j+1/2}]$, with $x_{1/2}=a$ and $x_{N+1/2}=b$, and mesh size $h_j=x_{j+1/2}-x_{j-1/2}$, with $h=\max _{1\le j \le N} h_j$. And we define the finite element space

$$\begin{aligned} V_h^k=\{ v \in L^2([a, b])\; : \; v |_{I_j} \in P^k(I_j), j=1,2, \cdots , N \}, \end{aligned}$$

where $P^k(I_j)$ denotes the set of all polynomials of degree at most k on $I_j$. At cell interfaces $x=x_{j+1/2}$ we use the notation

$$\begin{aligned} v^\pm =\lim _{\epsilon \rightarrow 0}v(x \pm \epsilon ), \quad \{v\}=\frac{v^-+v^+}{2}, \quad [v]=v^+-v^-. \end{aligned}$$

Based on its mixed formulation,

$$\begin{aligned} u_t = q_{xx}, \quad q = -u_{xx}, \end{aligned}$$

(2.2)

the DG scheme for (2.1) is to find $(u_h, q_h) \in V_h^k \times V_h^k$ such that for all $\phi , \ \psi \in V_h^k$ and $j =1, 2 \cdots , N$,

$$\begin{aligned} \int _{I_j} u_{ht} \phi dx&= - \int _{I_j} q_{hx} \phi _x dx+ \widehat{(q_{hx})} \phi |_{\partial I_j} + (q_h - \widehat{q_h})\phi _x|_{\partial I_j}, \end{aligned}$$

(2.3a)

$$\begin{aligned} \int _{I_j} q_h \psi dx&= \int _{I_j} u_{hx} \psi _x dx - \widehat{(u_{hx})} \psi |_{\partial I_j} -(u_h-\widehat{u_h})\psi _x|_{\partial I_j}, \end{aligned}$$

(2.3b)

where the notation $v|_{\partial I_j}=v^-_{j+1/2}-v^+_{j-1/2}$ is used, and on each cell interface $x_{j+1/2}, j=0, 1, 2, \ldots N$, the numerical fluxes are given by

$$\begin{aligned} \begin{aligned} \widehat{q_{hx}}&= \{q_{hx} \},\quad \widehat{q_h} = \{q_h \},\\ \widehat{u_{hx}}&= \{u_{hx} \}, \quad \widehat{u_h} = \{u_h \}, \end{aligned} \end{aligned}$$

(2.4)

where $\{v\}_{1/2}=\{v\}_{N+1/2}$ is understood as $\frac{1}{2}(v_{1/2}^+ + v_{N+1/2}^-)$ for $v=u_h, q_h, u_{hx}$ and $q_{hx}$. The initial data for $u_h$ is taken as the piecewise $L^2$ projection of $u_0(x)$, that is, $u_h(x, 0)\in V_h^k$ such that

$$\begin{aligned} \int _{I_j} (u_0(x)-u_h(x,0))\phi (x)dx=0, \quad \forall \phi \in P^k(I_j), \quad j=1, \ldots , N. \end{aligned}$$

(2.5)

Note that $q_h(x,0) \in V_h^k$ can be obtained from $u_h(x, 0)$ by solving (2.3b).

2.1 Stability and $L^2$ Error Estimate

We proceed to verify the $L^2$ stability of the above semi-discrete DG scheme and further obtain the optimal $L^2$ error estimate. To this end, we sum (2.3) over $j=1, \ldots , N$ to obtain

$$\begin{aligned} (u_{ht}, \phi )&= - A(q_h,\phi ), \end{aligned}$$

(2.6a)

$$\begin{aligned} (q_h, \psi )&= A(u_h,\psi ), \end{aligned}$$

(2.6b)

where $(\cdot , \cdot )$ denotes the inner product of two functions over [a, b], and the bilinear functional

$$\begin{aligned} A(w,v)=\sum _{j=1}^N \int _{I_j} w_x v_x dx + \sum _{j=1}^N \left( \{w_x\} [v] + [w]\{v_x\} \right) _{j+1/2}, \end{aligned}$$

(2.7)

where by $(\cdot )_{j+1/2}$ we mean evaluation of involved quantities at $x_{j+1/2}$. Note that $A(\cdot , \cdot )$ is symmetric, that is,

$$\begin{aligned} A(w,v)=A(v,w). \end{aligned}$$

(2.8)

For scheme (2.6) with (2.7) the following stability result holds.

Theorem 2.1

($L^2$-Stability) The numerical solution $u_h$ satisfies

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \int _a^b u_h^2dx=-\int _a^b q_h^2dx \le 0. \end{aligned}$$

(2.9)

Proof

Taking $\phi = u_h$ in (2.6a), and $\psi = q_h$ in (2.6b) respectively, we obtain

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \int _a^b u_h^2 dx = -A(q_h, u_h),\quad \Vert q_h\Vert ^2 =A(u_h, q_h), \end{aligned}$$

which when using (2.8) implies (2.9). $\square$

In order to estimate the $L^2$ error, we introduce a global projection: for a given piecewise smooth function $w \in L^2([a,b]), w|_{I_j} \in H^{s+1}(I_j), s\ge k \ge 1$, we define $P w \in V_h^k$ by

$$\begin{aligned}&\int _{I_j} \left( P w (x)-w(x) \right) v(x)dx=0, \quad \forall v \in P^{k-2}(I_j), \end{aligned}$$

(2.10a)

$$\begin{aligned}&\{ (P w)_x\}_{j+1/2}= \{w_x\}_{j+1/2}, \end{aligned}$$

(2.10b)

$$\begin{aligned}&\{P w\}_{j+1/2} := \{w\}_{j+1/2}, \end{aligned}$$

(2.10c)

for $j=1, \ldots , N$, where $\{v\}_{N+1/2}$ is understood as $\frac{1}{2}(v_{1/2}^+ + v_{N+1/2}^-)$. Note that for $k=1$, (2.10a) is redundant.

Lemma 2.1

For $k = 1$ with N odd, or any $k\ge 2$, there exists a unique projection P defined by (2.10). Moreover,

$$\begin{aligned} A(Pw-w, v)=0\quad \forall v\in V_h^k. \end{aligned}$$

(2.11)

Proof

• (i) From the more general result in [20, Lemma 2.1] it follows that such P is uniquely defined.

• (ii) Relation (2.11) can be derived from (2.7) using (2.10) and integration by parts once.

$\square$

Before going further we recall the following approximation result for projection P.

Lemma 2.2

[19] (Projection error) Assume that $w\in H^m$ with $m \ge k+1$. Then we have the following projection error

$$\begin{aligned} \Vert w-Pw\Vert \le C|w|_{k+1}h^{k+1}, \end{aligned}$$

(2.12)

where C is independent of h. Moreover,

$$\begin{aligned} Pv=v, \quad \forall v \in V_h^k. \end{aligned}$$

Theorem 2.2

Let $u_h$ be the numerical solution to (2.3) with (2.4), and u be the smooth solution to problem (2.1), then

$$\begin{aligned} \Vert u_h(\cdot , t)-u(\cdot , t) \Vert \le C h^{k+1}, \quad 0\le t\le T, \end{aligned}$$

(2.13)

where C depends on $\sup _{t \in [0,T]}|u_t(\cdot ,t)|_{k+1}$, $\sup _{t \in [0,T]}|u(\cdot ,t)|_{k+3}$ and linearly on T, but independent of h.

Proof

The consistency of the DG method (2.6) ensures that the exact solution u and q of (2.2) also satisfy

$$\begin{aligned} \begin{aligned} (u_t, \phi )&= - A(q,\phi ),\\ (q, \psi )&= A(u,\psi )\\ \end{aligned} \end{aligned}$$

(2.14)

for all $\phi \in V_h^k, \psi \in V_h^k$. Subtracting (2.6) from (2.14), we obtain the error system

$$\begin{aligned} \begin{aligned} ((u-u_h)_t, \phi )&= - A(q-q_h,\phi ),\\ (q-q_h, \psi )&= A(u-u_h,\psi ). \end{aligned} \end{aligned}$$

(2.15)

Denote

$$\begin{aligned} \begin{aligned} e_1&= Pu-u_h, \quad \epsilon _1= Pu-u, \\ e_2&= Pq-q_h, \quad \epsilon _2= Pq-q, \\ \end{aligned} \end{aligned}$$

and take $\phi =e_1, \psi =e_2$ in (2.15) respectively, we obtain

$$\begin{aligned} ( e_{1t}, e_1)&= (\epsilon _{1t}, e_1) + A(\epsilon _2, e_1) - A(e_2,e_1), \end{aligned}$$

(2.16a)

$$\begin{aligned} (e_2, e_2)&= (\epsilon _2, e_2)- A(\epsilon _1, e_2) + A(e_1,e_2). \end{aligned}$$

(2.16b)

Summation of (2.16a) and (2.16b) gives

$$\begin{aligned} \frac{1}{2} \frac{d}{dt}\Vert e_1\Vert ^2 + \Vert e_2\Vert ^2&= (\epsilon _{1t}, e_1) + (\epsilon _2, e_2) + A(\epsilon _2, e_1)- A(\epsilon _1, e_2)\\&=(\epsilon _{1t}, e_1) + (\epsilon _2, e_2), \end{aligned}$$

where property (2.11) of projection P has been used. This yields

$$\begin{aligned} \begin{aligned} \frac{1}{2} \frac{d}{dt}\Vert e_1\Vert ^2&\le \Vert \epsilon _{1t}\Vert \Vert e_1\Vert + \frac{1}{4} \Vert \epsilon _2\Vert ^2. \end{aligned} \end{aligned}$$

By property (2.12), the right hand side is dominated by $C |u_t|_{k+1}h^{k+1}\Vert e_1\Vert +\frac{1}{4}(C |u|_{k+3}h^{k+1})^2.$ Hence

$$\begin{aligned} \begin{aligned} \frac{1}{2} \frac{d}{dt}\Vert e_1\Vert ^2&\le C_1 h^{k+1} (\Vert e_1\Vert + h^{k+1}), \end{aligned} \end{aligned}$$

where $C_1=\max \{ C \sup _{t\in [0,T]}|u_t|_{k+1}, \frac{C^2}{4} \sup _{t\in [0,T]}|u|_{k+3}^2\}$. Set $B=\frac{\Vert e_1\Vert }{h^{k+1}}$, then

$$\begin{aligned} B\frac{dB}{dt} \le C_1 (B+1), \end{aligned}$$

which upon integration over [0, t] gives

$$\begin{aligned} G(B(t)) \le G(B(0)) + C_1 t, \end{aligned}$$

(2.17)

where $G(s)=s - \ln ( s+1)$ is an increasing and convex function on $[0, \infty )$. Note that $B(0)\le C_2$ for

$$\begin{aligned} \Vert e_1(\cdot , 0)\Vert \le \Vert Pu_0-u_0\Vert +\Vert u_0-u_h(\cdot , 0) \Vert \le C_2 h^{k+1}. \end{aligned}$$

(2.18)

It can be verified that $G^{-1}(s)/s$ is decreasing for $s>0$, note also that $G^{-1}(s)$ is increasing, hence

$$\begin{aligned} G^{-1}(s) \le \frac{G^{-1}(\delta )}{\delta } \max \{s, \delta \}. \end{aligned}$$

This with $\delta =G(C_2)$ when inserted into (2.17) gives

$$\begin{aligned} B(t) \le G^{-1}\left( C_1T+G(C_2)\right) \le C_2 +C T, \end{aligned}$$

with $C=\frac{C_1C_2}{G(C_2)}$. Thus,

$$\begin{aligned} \Vert e_1(\cdot , t)\Vert = B(t)h^{k+1} \le \left( C_2 +C T\right) h^{k+1}, \end{aligned}$$

which combined with the approximation result in Lemma 2.2 leads to (2.13) as desired. $\square$

2.2 Fully-Discrete DG Schemes

Let $(u^n_h, q_h^n)$ denote the approximation to $(u_h, q_h)(\cdot , t_n)$, where $t_n=n\Delta t$ with $\Delta t$ being the time step. We consider a class of time stepping methods indexed by a parameter $\theta \in [0, 1]$: find $(u_h^{n}, q_h^{n}) \in V_h^k \times V_h^k$ such that for all $\phi , \ \psi \in V_h^k$

$$\begin{aligned} \left( \frac{u^{n+1}_h - u^n_h}{\Delta t}, \phi \right)&= - A(q^{n+\theta }_h,\phi ),\end{aligned}$$

(2.19a)

$$\begin{aligned} (q^{n}_h, \psi )&= A(u^{n}_h,\psi ), \end{aligned}$$

(2.19b)

where $v^{n+\theta } = (1-\theta ) v^n + \theta v^{n+1}$. Note that when $\theta =0$, it is the forward Euler, $\theta =1$, it is backward Euler; and $\theta =1/2$, Crank–Nicolson.

To study the stability of the DG scheme (2.19), we first recall the following estimate.

Lemma 2.3

([21, Lemma 3.2]) The following inverse inequalities hold for all $v \in V_h^k$,

$$\begin{aligned} \begin{aligned} \sum _{j=1}^N \int _{I_j} (v_x)^2 dx&\le \frac{(k+1)^2k(k+2)}{h^2} \Vert v\Vert ^2, \\ \sum _{j=1}^N [v]^2_{j+1/2}&\le \frac{4(k+1)^2}{h} \Vert v\Vert ^2, \\ \sum _{j=1}^N \{v_x\}^2_{j+1/2}&\le \frac{k^3(k+1)^2(k+2) }{h^3} \Vert v\Vert ^2. \\ \end{aligned} \end{aligned}$$

Then, we have the following stability results.

Theorem 2.3

($L^2$-Stability) For $\frac{1}{2} \le \theta \le 1$, the fully discrete DG scheme (2.19) is unconditionally $L^2$ stable. Moreover,

$$\begin{aligned} \Vert u_h^{n+1}\Vert ^2 \le \Vert u_h^n\Vert ^2 -2 \Delta t \Vert (1-\theta )q^n_h +\theta q^{n+1}_h\Vert ^2 \end{aligned}$$

(2.20)

holds for any $\Delta t>0$. For $0 \le \theta < \frac{1}{2}$, (2.19) is $L^2$ stable, i.e., $\Vert u_h^{n+1}\Vert \le \Vert u_h^n\Vert ,$ provided

$$\begin{aligned} \Delta t < \frac{2h^4 }{(1-2\theta )\gamma ^2(k)}, \end{aligned}$$

(2.21)

where

$$\begin{aligned} \gamma (k) = (k+1)^2k(k+2)+ 4(k+1)^2k \sqrt{k(k+2)}. \end{aligned}$$

(2.22)

Proof

From (2.19b) it follows

$$\begin{aligned} \int _a^b q^{n+\theta }_h \psi dx = A(u^{n+\theta }_h,\psi ). \end{aligned}$$

This relation when added upon (2.19a) with $\phi = u^{n+\theta }_h, \; \psi = q^{n+\theta }_h$ gives

$$\begin{aligned} \int _a^b \frac{u^{n+1}_h - u_h^n}{\Delta t} u_h^{n+\theta } dx + \Vert q_h^{n+\theta }\Vert ^2 =0. \end{aligned}$$

(2.23)

Using the identity

$$\begin{aligned} u_h^{n+\theta }= \frac{1}{2}\left( u_h^{n+1}+u_h^n \right) + \left( \theta -\frac{1}{2} \right) \left( u_h^{n+1}-u_h^n \right) , \end{aligned}$$

we rewrite (2.23) as

$$\begin{aligned} \begin{aligned} \Vert u^{n+1}_h\Vert ^2-\Vert u_h^n\Vert ^2 + 2\Delta t \Vert q_h^{n+\theta }\Vert ^2 = (1-2\theta ) \Vert u_h^{n+1} - u_h^n\Vert ^2. \end{aligned} \end{aligned}$$

(2.24)

This implies (2.20) if $\frac{1}{2} \le \theta \le 1$. If $0 \le \theta < \frac{1}{2}$, we need to estimate the right hand side of (2.24). By taking $\phi =u^{n+1}_h - u_h^n$ in (2.19a) and using Lemma 2.3, we have

$$\begin{aligned} \begin{aligned} \frac{1}{\Delta t }\Vert u_h^{n+1} - u_h^n\Vert ^2&= - A(q_h^{n+\theta },u_h^{n+1} - u_h^n) \\&\le \left( \sum _{j=1}^N \int _{I_j} (q^{n+\theta }_{hx})^2 dx \right) ^\frac{1}{2} \left( \sum _{j=1}^N \int _{I_j} (u^{n+1}_{hx} - u^n_{hx})^2 dx \right) ^\frac{1}{2} \\&\quad + \left( \sum _{j=1}^N \{q^{n+\theta }_{hx}\}^2_{j+1/2} \right) ^\frac{1}{2} \left( \sum _{j=1}^N [u_h^{n+1} - u_h^n]^2_{j+1/2} \right) ^\frac{1}{2} \\&\quad + \left( \sum _{j=1}^N [q_h^{n+\theta }]^2_{j+1/2} \right) ^\frac{1}{2} \left( \sum _{j=1}^N \{(u^{n+1}_{hx} - u^n_{hx})_{j+1/2}\}^2 \right) ^\frac{1}{2} \\&\le \frac{(k+1)^2k(k+2)+4(k+1)^2k \sqrt{k(k+2)}}{h^2} \Vert q_h^{n+\theta }\Vert \Vert u_h^{n+1} - u_h^n\Vert \\&= \frac{\gamma (k) }{h^2} \Vert q_h^{n+\theta }\Vert \Vert u_h^{n+1} - u_h^n\Vert , \end{aligned} \end{aligned}$$

with $\gamma (k)$ defined in (2.22). Hence

$$\begin{aligned} \Vert u_h^{n+1} - u_h^n\Vert \le \frac{\Delta t \gamma (k) }{h^2} \Vert q_h^{n+\theta }\Vert . \end{aligned}$$

This upon insertion into (2.24) yields

$$\begin{aligned} \begin{aligned} \Vert u_h^{n+1}\Vert ^2 + \Delta t \left( 2-(1-2\theta ) \frac{\Delta t \gamma ^2(k)}{h^4} \right) \Vert q_h^{n+\theta }\Vert ^2 \le \Vert u_h^n\Vert ^2. \end{aligned} \end{aligned}$$

By (2.21) we therefore obtain the desired stability, i.e., $\Vert u_h^{n+1}\Vert \le \Vert u_h^n\Vert$. $\square$

The above results suggest that the semi-implicit time discretization with $\theta \in [1/2, 1]$ should be considered. To assist the error estimate for the fully-discrete DG scheme (2.19) with $\theta \in [1/2, 1]$, we prepare the following lemma.

Lemma 2.4

Let $\{a_n\}$ with $a_0>0$ be a non-negative sequence satisfying

$$\begin{aligned} \frac{a_{n+1}^2 - a_n^2}{\tau } \le \alpha (a_{n+1} +a_n+1), \end{aligned}$$

(2.25)

where $\tau >0$ and $\alpha >0$, then there exists $C=C(a_0, \alpha )$ such that

$$\begin{aligned} a_n \le a_0+C n\tau , \quad \forall n \ge 1. \end{aligned}$$

Proof

Define $A_n=\max _{0\le i\le n} a_i$, then (2.25) remains valid for $A_n$, i.e.,

$$\begin{aligned} \frac{A_{n+1}^2 - A_n^2}{\tau } \le \alpha (A_{n+1} +A_n+1). \end{aligned}$$

(2.26)

In fact, we have $a_n \le A_n, \forall n \ge 0,$ and

$$\begin{aligned} A_{n+1}=\max \{ a_{n+1}, A_n\}. \end{aligned}$$

If $A_{n+1}=A_n$, (2.26) is obvious; otherwise if $A_{n+1}=a_{n+1}$, it follows that

$$\begin{aligned} \frac{A_{n+1}^2 - A_n^2}{\tau } \le \frac{a_{n+1}^2 - a_n^2}{\tau } \le \alpha (a_{n+1} +a_n+1) \le \alpha (A_{n+1} +A_n+1). \end{aligned}$$

Rewriting (2.26) as

$$\begin{aligned} A_{n+1} -A_n -\frac{A_{n+1}-A_n}{A_{n+1}+A_{n}+1} \le \alpha \tau , \end{aligned}$$

and using

$$\begin{aligned} \int _{A_n}^{A_{n+1}} \frac{1}{2s+1}ds \ge \frac{A_{n+1}-A_n}{A_{n+1}+A_{n}+1}, \end{aligned}$$

we have

$$\begin{aligned} H(A_{n+1})-H(A_n) \le \alpha \tau , \end{aligned}$$

where $H(s)=s -\ln \sqrt{2s+1}$, and therefore

$$\begin{aligned} H(A_{n}) \le H(A_0) +\alpha n\tau . \end{aligned}$$

Note that H is increasing and convex over $[0, \infty )$, hence we have

$$\begin{aligned} A_n \le H^{-1} \left( H(A_0)+\alpha n\tau \right) = H^{-1} \left( H(a_0)+\alpha n\tau \right) . \end{aligned}$$

It can be verified that $H^{-1}(s)/s$ is decreasing for $s>0$. Thus,

$$\begin{aligned} A_n \le \frac{a_0}{H(a_0)}\left( H(a_0)+\alpha n\tau \right) = a_0 + C n\tau , \quad C=\frac{\alpha a_0}{H(a_0)}. \end{aligned}$$

Going back to $a_n \le A_n$ we prove the claimed estimate. $\square$

Theorem 2.4

Let $u^n_h$ be the numerical solution to the fully-discrete DG scheme (2.19) with $\frac{1}{2} \le \theta \le 1$, and u be the smooth solution to problem (2.1), then

$$\begin{aligned} \Vert u(\cdot ,t^n)-u^n_h(\cdot ) \Vert \le C \left( h^{k+1} + (\theta - 1/2) \Delta t + (\Delta t)^2 \right) , \end{aligned}$$

(2.27)

where C depends on $\sup _{t \in [0,T]}|u_t(\cdot ,t)|_{k+1}$, $\sup _{t \in [0,T]}|u(\cdot , t)|_{k+3}$, $\sup _{t\in [0,T]} \Vert u_{tt}(\cdot , t)\Vert$, $\sup _{t\in [0,T]} \Vert u_{ttt}(\cdot , t)\Vert$ and linearly on T, but independent of $h, \Delta t$.

Proof

Denote $u^n=u(x,t^n)$ and $q^n=q(x,t^n)$, then the consistency of the DG scheme, as given in (2.14), when evaluated at $t=t^{n+\theta }$ is

$$\begin{aligned} \begin{aligned} (u^{n+\theta }_t, \phi )&= - A(q^{n+\theta },\phi ),\\ (q^{n}, \psi )&= A(u^{n},\psi ),\\ \end{aligned} \end{aligned}$$

(2.28)

for all $\phi \in V_h^k, \psi \in V_h^k$, where $v^{n+\theta } = \theta v^{n+1}+(1-\theta ) v^n$ for $v=u, q$. To proceed, we first evaluate the term $u^{n+\theta }_t$. By Taylor’s expression, we have

$$\begin{aligned} \begin{aligned} u^n_t&= \frac{u^{n+1}-u^n}{\Delta t}-\frac{1}{2} u^n_{tt} \Delta t-\frac{1}{2\Delta t}\int _{t^n}^{t^{n+1}} (t^{n+1}-s)^2 u_{ttt}(x,s) ds, \\ u^{n+1}_t&= \frac{u^{n+1}-u^n}{\Delta t}+\frac{1}{2} u^{n+1}_{tt} \Delta t -\frac{1}{2\Delta t}\int _{t^n}^{t^{n+1}} (t^n-s)^2 u_{ttt}(x,s) ds, \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} u^{n+\theta }_t = \theta u^{n+1}_t + (1-\theta ) u^n_t = \frac{u^{n+1}-u^n}{\Delta t} + F(n,x,t,\theta ), \end{aligned}$$

where

$$\begin{aligned} F(n,x,t,\theta )&= u^n_{tt} \Delta t \left( \theta - \frac{1}{2}\right) - (1-\theta ) \left( \frac{1}{2\Delta t}\int _{t^n}^{t^{n+1}} (t^{n+1}-s)^2 u_{ttt}(x,s) ds \right) \\&\quad + \theta \left( \frac{1}{2} \Delta t \int _{t^n}^{t^{n+1}} u_{ttt}(x,s) ds -\frac{1}{2\Delta t}\int _{t^n}^{t^{n+1}} (t^n-s)^2 u_{ttt}(x,s) ds \right) . \end{aligned}$$

Then (2.28) becomes

$$\begin{aligned} \begin{aligned} \left( \frac{u^{n+1}-u^n}{\Delta t}, \phi \right)&= - A(q^{n+\theta },\phi ) - (F(n,x,t,\theta ), \phi ),\\ (q^{n}, \psi )&= A(u^{n},\psi ), \end{aligned} \end{aligned}$$

which together with (2.19) gives

$$\begin{aligned} \begin{aligned} \left( \frac{(u^{n+1}-u_h^{n+1})-(u^n-u_h^n)}{\Delta t}, \phi \right)&= - A(q^{n+\theta }-q_h^{n+\theta },\phi ) - (F(n,x,t,\theta ), \phi ),\\ (q^{n+\theta }-q_h^{n+\theta }, \psi )&= A(u^{n+\theta }-u_h^{n+\theta },\psi ). \end{aligned} \end{aligned}$$

(2.29)

Denote

$$\begin{aligned} \begin{aligned} e_1^n&= Pu^n - u^n_h, \quad \epsilon _1^n = Pu^n -u^n, \\ e_2^n&= Pq^n - q^n_h, \quad \epsilon _2^n = Pq^n -q^n, \end{aligned} \end{aligned}$$

and take $\phi = e_1^{n+\theta }, \ \psi = e_2^{n+\theta }$ in (2.29), upon summation and using (2.11), we obtain

$$\begin{aligned} \left( \frac{e_1^{n+1}-e_1^n}{\Delta t}, e_1^{n+\theta } \right) + \left( e_2^{n+\theta }, e_2^{n+\theta }\right)= & {} \left( \frac{\epsilon _1^{n+1}-\epsilon _1^n}{\Delta t}, e_1^{n+\theta } \right) + \left( \epsilon _2^{n+\theta }, e_2^{n+\theta }\right) \nonumber \\&-\,(F(n,x,t,\theta ), e_1^{n+\theta }). \end{aligned}$$

(2.30)

Applying

$$\begin{aligned} e_1^{n+\theta }= \frac{1}{2}\left( e_1^{n+1}+e_1^{n} \right) + \left( \theta -\frac{1}{2} \right) \left( e_1^{n+1}-e_1^{n} \right) , \end{aligned}$$

and the Cauchy–Schwarz inequality to (2.30), it follows that

$$\begin{aligned} \begin{aligned} \frac{\Vert e_1^{n+1}\Vert ^2-\Vert e_1^n\Vert ^2}{2\Delta t}&\le \left( \left\| \frac{\epsilon _1^{n+1}-\epsilon _1^n}{\Delta t} \right\| + \Vert F(n,\cdot ,t,\theta )\Vert \right) (\Vert e_1^{n+1}\Vert + \Vert e_1^n\Vert ) \\&\quad +\,\frac{1}{2}\left( \Vert \epsilon _2^{n+1}\Vert ^2 +\Vert \epsilon _2^{n}\Vert ^2\right) . \end{aligned} \end{aligned}$$

(2.31)

Recall the projection error estimate (2.12), we have

$$\begin{aligned} \begin{aligned} \Vert \epsilon _2^{n+i}\Vert&\le Ch^{k+1} | q(\cdot ,t^{n+i})|_{k+1} = C_1 h^{k+1} |u(\cdot ,t^{n+i})|_{k+3}, \end{aligned} \end{aligned}$$

(2.32)

for $i=0,1$, and along with the mean value theorem, we also have

$$\begin{aligned} \begin{aligned} \left\| \frac{\epsilon _1^{n+1}-\epsilon _1^n}{\Delta t} \right\| = \left\| P \left( \frac{u^{n+1}-u^n}{\Delta t} \right) - \frac{u^{n+1}-u^n}{\Delta t} \right\| \le C_2h^{k+1} |u_{t}(\cdot ,t^*)|_{k+1}, \end{aligned} \end{aligned}$$

(2.33)

where $t^* \in (t^n, t^{n+1})$. As for the term involving F, we have

$$\begin{aligned} \begin{aligned} | F(n,x,t,\theta ) |&\le \left| u^n_{tt} \right| \Delta t \left( \theta - \frac{1}{2}\right) + \frac{(1-\theta )}{2\Delta t}\int _{t^n}^{t^{n+1}} (t^{n+1}-s)^2 | u_{ttt}(x,s) | ds \\&\quad + \frac{\theta \Delta t }{2}\int _{t^n}^{t^{n+1}}\left| u_{ttt}(x,s) \right| ds + \frac{\theta }{2\Delta t}\int _{t^n}^{t^{n+1}} (t^n-s)^2 \left| u_{ttt}(x,s) \right| ds \\&\le \left( \theta - \frac{1}{2}\right) \Delta t \sup _{t\in [0,T]} | u_{tt}(x, t)|+\left( \frac{1}{6}+\frac{\theta }{2}\right) (\Delta t)^2 \sup _{t\in [0,T]} |u_{ttt}(x, t)|, \end{aligned} \end{aligned}$$

hence

$$\begin{aligned} \Vert F(n,\cdot ,t,\theta ) \Vert \le \left( \theta - \frac{1}{2}\right) \Delta t \sup _{t\in [0,T]} \Vert u_{tt}(\cdot , t)\Vert + (\Delta t)^2 \sup _{t\in [0,T]} \Vert u_{ttt}(\cdot , t)\Vert . \end{aligned}$$

(2.34)

Plugging (2.34), (2.33) and (2.32) into (2.31) leads to

$$\begin{aligned} \begin{aligned} \frac{\Vert e_1^{n+1}\Vert ^2-\Vert e_1^n\Vert ^2}{2\Delta t}&\le C \left( h^{k+1} + \left( \theta - 1/2\right) \Delta t + (\Delta t)^2 \right) (\Vert e_1^{n+1}\Vert + \Vert e_1^n\Vert ) + C h^{2(k+1)}, \end{aligned} \end{aligned}$$

where C depends on $\sup _{t\in [0,T]}|u_t(\cdot , t)|_{k+1}$, $\sup _{t\in [0,T]}|u(\cdot , t)|_{k+3}$, $\sup _{t\in [0,T]} \Vert u_{tt}(\cdot , t)\Vert$ and $\sup _{t\in [0,T]} \Vert u_{ttt}(\cdot , t)\Vert$.

Set $a_n=\frac{\Vert e_1^n\Vert }{ h^{k+1}}$, $\tau = 2\Delta t$, then $a_n$ satisfies (2.25) with

$$\begin{aligned} \alpha =Ch^{-(k+1)}\left( h^{k+1} + \left( \theta - 1/2\right) \Delta t + (\Delta t)^2 \right) . \end{aligned}$$

Note that $e_1^0= Pu_0-u_h^0$ and $\Vert e_1^0 \Vert \le \Vert Pu_0-u_0\Vert +\Vert u_0-u_h^0 \Vert \le C_0 h^{k+1},$ we thus take $a_0= C_0$. By Lemma 2.4 we have

$$\begin{aligned} \begin{aligned} \Vert e_1^n\Vert \le h^{k+1} \left( C_0 + \frac{C_0\alpha }{H(C_0)} n\tau \right) \le C(1+T) \left( h^{k+1} + \left( \theta - 1/2\right) \Delta t + (\Delta t)^2 \right) , \end{aligned} \end{aligned}$$

which combined with the projection error (2.12) leads to (2.27) as desired. $\square$

2.3 Algorithm

The details related to the implementation of scheme (2.19) with $\theta \in [1/2, 1]$ is summarized in the following algorithm.

• Step 1 (Initialization) from the given initial data $u_0(x)$,

  • (1) generate $u_h^0:=u_h(x,0) \in V_h^k$ from the piecewise $L^2$ projection (2.5), and

  • (2) further obtain $q_h^0$ from solving (2.19b).

• Step 2 (Evolution) obtain $u^{n+1}_h, \ q^{n+1}_h$ by solving (2.19) through the following form:

  $$\begin{aligned}&\frac{1}{\Delta t} (u^{n+1}_h, \phi ) + \theta A(q^{n+1}_h,\phi )= \frac{1}{\Delta t} ( u^{n}_h, \phi ) - (1-\theta ) A(q^{n}_h,\phi ), \end{aligned}$$

  (2.35a)
  $$\begin{aligned}&\theta A(u^{n+1}_h,\psi )- \theta ( q^{n+1}_h, \psi ) = 0. \end{aligned}$$

  (2.35b)

Remark 2.1

The advantage of using (2.35) is that its coefficient matrix is symmetric, hence more efficient linear system solvers, such as the ILU preconditioner + FGMRES (see e.g., [30]), ILU preconditioner + Bicgstab (see e.g., [6]). can be used.

3 The DG Scheme in Multi-dimensions

In this section we present DG schemes in multi-dimensional setting. Without loss of generality, we describe our DG scheme and prove the optimal error estimates in two dimension ($d=2$); The analysis depending on the tensor product of polynomials can be easily extended to higher dimensions. Hence, from now on we shall restrict ourselves mainly to the following two-dimensional problem

$$\begin{aligned} u_t&=-(\partial _x^2 +\partial _y^2)^2 u, \quad (x, y)\in \Omega , \quad t>0, \end{aligned}$$

(3.1a)

$$\begin{aligned} u(x, y, 0)&=u_0(x, y), \quad (x, y)\in \Omega \end{aligned}$$

(3.1b)

again with periodic boundary conditions.

We partition $\Omega$ by rectangular meshes

$$\begin{aligned} \Omega =\sum ^{N,M}_{i,j}I_{i,j}, \quad I_{i,j}=\left[ x_{i-\frac{1}{2}}, x_{j+\frac{1}{2}}\right] \times \left[ y_{j-\frac{1}{2}}, y_{j+\frac{1}{2}}\right] . \end{aligned}$$

For simplicity we assume we have a uniform rectangular mesh with $\Delta x=x_{i+1/2}-x_{i-1/2}, \Delta y=y_{j+1/2}-y_{j-1/2}$. Let

$$\begin{aligned} Q_h=\{v\in L^2(\Omega ): \quad v|_{I_{i,j}}\in Q^k(I_{i,j})\}, \end{aligned}$$

where $Q^k(K)$ denotes the space of tensor-product polynomials of degree at most k in each variable defined on K. No continuity is assumed across cell boundaries.

The semi-discrete DG approximations $(u_h, q_h) \in Q_h \times Q_h$ of (3.1) are defined through the reformulation of form (1.2) such that for all admissible test functions $\phi , \ \psi \in Q_h$ and all $I_{i,j}$

$$\begin{aligned} \begin{aligned} \iint _{I_{i, j}} u_{ht} \phi dxdy&= - \iint _{I_{i,j}} \nabla q_h \cdot \nabla \phi dxdy+ \int _{y_{j-1/2}}^{y_{j+1/2}} \left( \{q_{hx}\} \phi + (q_h - \{q_h\}) \phi _x \right) \Big |_{x_{i-1/2}}^{x_{i+1/2}} dy \\&\quad +\,\int _{x_{i-1/2}}^{x_{i+1/2}} \left( \{q_{hy}\} \phi + (q_h-\{q_h\})\phi _y\right) \Big |_{y_{j-1/2}}^{y_{j+1/2}} dx, \\ \iint _{I_{i,j}} q_h \psi dxdy&= \iint _{I_{i,j}} \nabla u_h \cdot \nabla \psi dxdy - \int _{y_{j-1/2}}^{y_{j+1/2}} \left( \{u_{hx}\} \psi + (u_h-\{u_h\})\psi _x \right) \Big |_{x_{i-1/2}}^{x_{i+1/2}} dy \\&\quad - \,\int _{x_{i-1/2}}^{x_{i+1/2}} \left( \{u_{hy}\} \psi + (u_h-\{u_h\})\psi _y \right) \Big |_{y_{j-1/2}}^{y_{j+1/2}} dx, \\ \end{aligned} \end{aligned}$$

(3.2)

where

$$\begin{aligned} \begin{aligned}&v\Big |_{x_{i-1/2}}^{x_{i+1/2}} =v(x_{i+1/2}^-, y) - v(x_{i-1/2}^+, y), \\&v\Big |_{y_{j-1/2}}^{y_{j+1/2}} =v(x, y_{j+1/2}^-) - v(x, y_{j-1/2}^+),\\&\{v\}\Big |_{x_{i+1/2}} = \frac{1}{2} \left( v(x_{i+1/2}^-, y) + v(x_{i+1/2}^+, y)\right) ,\\&\{v\}\Big |_{y_{j+1/2}}=\frac{1}{2} \left( v(x, y_{j+1/2}^-) +v(x, y_{j+1/2}^+)\right) . \end{aligned} \end{aligned}$$

The initial data for $u_h$ is also taken as the piecewise $L^2$ projection of $u_0$, that is $u_h(x, y, 0) \in Q_h$ such that

$$\begin{aligned} \iint _{\Omega } (u_0(x,y)-u_h(x, y, 0))\phi (x,y)dxdy=0, \quad \forall \phi \in Q_h. \end{aligned}$$

3.1 Stability and A Priori Error Estimates

In order to check the stability of the above scheme, we sum (3.2) over all computaitonal cells to obtain

$$\begin{aligned} (u_{ht}, \phi )&= - A(q_h,\phi ), \end{aligned}$$

(3.3a)

$$\begin{aligned} (q_h, \psi )&= A(u_h,\psi ), \end{aligned}$$

(3.3b)

where $(\cdot , \cdot )$ denotes the inner product of two functions over $\Omega$, and the bilinear functional

$$\begin{aligned} \begin{aligned} A(w,v)&= \sum _{i,j=1}^{N,M}\iint _{I_{i,j}} \nabla w \cdot \nabla v dxdy +\sum _{i, j=1}^{N, M} \int _{y_{j-1/2}}^{y_{j+1/2}} \left( \{w_{x}\} [v] + \{v_x\} [w] \right) _{x_{i+1/2}}dy \\&\quad +\,\sum _{i, j=1}^{N, M} \int _{x_{i-1/2}}^{x_{i+1/2}} \left( \{w_{y}\}[v] +\{v_y\}[w] \right) _{y_{j+1/2}}dx. \end{aligned} \end{aligned}$$

(3.4)

For scheme (3.2) the following stability result holds.

Theorem 3.1

($L^2$-Stability) The numerical solution $u_h$ to (3.3) satisfies

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \iint _{\Omega } |u_h|^2dxdy=-\iint _{\Omega } q_h^2dxdy \le 0. \end{aligned}$$

In order to obtain the error estimate for DG scheme (3.3) on rectangular meshes, we follow [19] extending the one-dimensional projection to multi-dimension by taking a tensor product of 2 one-dimensional projections as

$$\begin{aligned} \Pi w= P^{(x)} \otimes P^{(y)} w, \end{aligned}$$

where the superscripts indicate the application of one-dimensional projection operator.

We recall the following result established in [20].

Lemma 3.1

For $k \ge 1$ and $\eta \in Q_h$, the linear functional $w \rightarrow A(\Pi w-w, \eta )$ is continuous on $H^{k+2}(\Omega )$ and

$$\begin{aligned} |A(\Pi w-w, \eta )|&\le C h^{k+2}|w|_{k+2} \Vert \eta \Vert ,\\ \Vert \Pi w-w\Vert&\le Ch^{k+1}|w|_{k+1}, \end{aligned}$$

where C is a constant independent of h.

We are now ready to state the a priori error estimate result for the two-dimensional case.

Theorem 3.2

Let $u_h$ be the numerical solution to the DG scheme (3.2) and u be the smooth solution to problem (3.1), then

$$\begin{aligned} \Vert u(\cdot , t)-u_h(\cdot , t) \Vert \le Ch^{k+1}, \end{aligned}$$

(3.5)

for $0 \le t \le T$, where C depends on $\sup _{t\in [0, T]}\Vert u_t(\cdot , t)\Vert _{k+1}$, and linearly on T, but independent of h.

Proof

By consistency of the DG scheme (3.3), we have

$$\begin{aligned} \begin{aligned} (u_t, \phi )&= - A(q,\phi ), \quad \forall \phi \in Q_h,\\ (q, \psi )&= A(u,\psi ), \quad \forall \psi \in Q_h,\\ \end{aligned} \end{aligned}$$

where u is the exact solution to (3.1) with $q=-\Delta u$. Upon subtraction of this from (3.3), we have

$$\begin{aligned} \begin{aligned} ((u-u_h)_t, \phi )&= - A(q-q_h,\phi ),\\ (q-q_h, \psi )&= A(u-u_h,\psi ). \end{aligned} \end{aligned}$$

(3.6)

Denote

$$\begin{aligned} \begin{aligned} e_1&= \Pi u-u_h, \quad \epsilon _1= \Pi u-u, \\ e_2&= \Pi q-q_h, \quad \epsilon _2= \Pi q-q, \\ \end{aligned} \end{aligned}$$

take $\phi =e_1$ and $\psi =e_2$ in (3.6), to obtain

$$\begin{aligned} \begin{aligned} \frac{1}{2} \frac{d}{dt}\Vert e_1\Vert ^2 + \Vert e_2\Vert ^2 = ( \epsilon _{1t}, e_1) + (\epsilon _2, e_2) + A(\epsilon _2, e_1)- A(\epsilon _1, e_2). \end{aligned} \end{aligned}$$

By Schwartz’s inequality and Lemma 3.1 we have

$$\begin{aligned} \begin{aligned} \frac{1}{2} \frac{d}{dt}\Vert e_1\Vert ^2 + \Vert e_2\Vert ^2&\le \Vert \epsilon _{1t}\Vert \Vert e_1\Vert + \Vert \epsilon _2\Vert \Vert e_2\Vert +Ch^{k+2}\left( |q|_{k+2}\Vert e_1\Vert +|u|_{k+2}\Vert e_2\Vert \right) \\&\le C \left( |u_t|_{k+1}+|q|_{k+2}h \right) h^{k+1}\Vert e_1\Vert + C\left( |q|_{k+1} +|u|_{k+2}h\right) h^{k+1} \Vert e_2\Vert \\&\le C_1 h^{k+1} (\Vert e_1\Vert + h^{k+1}) + \Vert e_2\Vert ^2, \end{aligned} \end{aligned}$$

where $C_1=\max \{C\sup _{t\in [0,T]}\left( |u_t|_{k+1}+|q|_{k+2}h \right) , \frac{C^2}{4}\sup _{t\in [0,T]}\left( |q|_{k+1} +|u|_{k+2}h\right) ^2\}$. Following the same analysis as that in Theorem 2.2, we obtain the estimate for $\Vert e_1\Vert$, further (3.5) as desired. $\square$

3.2 Time Discretization

Let $(u^n_h, q_h^n)$ denote the approximation to $(u_h, q_h)(\cdot , t_n)$, where $t_n=n\Delta t$ with $\Delta t$ being the time step. We consider a class of time stepping methods in terms of a parameter $\theta \in [1/2, 1]$: find $(u_h^{n}, q_h^{n}) \in Q_h \times Q_h$ such that for all $\phi , \ \psi \in Q_h$,

$$\begin{aligned} \left( \frac{u_h^{n+1} - u^n_h}{\Delta t}, \phi \right)&= - A(q_h^{n+\theta },\phi ), \end{aligned}$$

(3.7a)

$$\begin{aligned} ( q_h^{n}, \psi )&= A(u_h^{n},\psi ), \end{aligned}$$

(3.7b)

where the notation $v^{n+\theta } := (1-\theta ) v^n + \theta v^{n+1}$ is used. Similar to the one-dimensional case, we have the following stability result.

Theorem 3.3

($L^2$-Stability) For $\frac{1}{2} \le \theta \le 1$, the fully discrete DG scheme (3.7) is unconditionally $L^2$ stable. Moreover,

$$\begin{aligned} \Vert u_h^{n+1}\Vert ^2 \le \Vert u_h^n\Vert ^2 -2\Delta t \Vert (1-\theta ) q^n_h + \theta q^{n+1}_h \Vert ^2 \end{aligned}$$

holds for any $\Delta t>0$.

In virtue of Lemma 3.1 and the techniques in Theorem 2.4, we can obtain the error estimates for the full DG scheme (3.7) on rectangular meshes without additional difficulty.

Theorem 3.4

Let $u^n_h$ be the numerical solution to the fully-discrete DG scheme (3.7) with $\frac{1}{2} \le \theta \le 1$, and u be the smooth solution to problem (3.1), then

$$\begin{aligned} \Vert u(x,t^n)-u^n_h \Vert \le C \left( h^{k+1} + \left( \theta - 1/2\right) \Delta t + (\Delta t)^2 \right) , \end{aligned}$$

where C depends on $\sup _{t \in [0,T]}\Vert u_t\Vert _{k+1}$, $\sup _{t\in [0,T]} \Vert u_{tt}(\cdot , t)\Vert$, $\sup _{t\in [0,T]} \Vert u_{ttt}(\cdot , t)\Vert$ and linearly on T, but independent of $h, \Delta t$.

4 Extensions

In this section, we discuss several extensions regarding the more general equation, non-homogeneous boundary conditions, and an application to a nonlinear problem.

4.1 General 4th Order Linear Operator

We consider the general 4th order time-dependent PDEs of form (1.1), with

$$\begin{aligned} Lu=\sum _{m=0}^2 a_m\partial _x^{2m}u. \end{aligned}$$

(4.1)

It is known that the initial boundary value problem with periodic boundary conditions is well-posed [18] if and only if there exists a constant K such that

$$\begin{aligned} a_0-a_1\xi ^2 +a_2 \xi ^4 \le M \end{aligned}$$

holds for any real number $\xi$. Hence, the problem is well-posed if $a_2<0$, accordingly we have $M=a_0-\frac{a_1^2}{4a_2}$ for $a_1 \le 0$ and $M=a_0$ for $a_1> 0$. The case of more interest is $a_1 \le 0$, and will be kept in mind in the following discussion, though the scheme can also be used for $a_1>0$.

We construct our DG scheme based on the following reformulation

$$\begin{aligned} \begin{aligned} u_t&= \sqrt{-a_2} \left( \partial _x^2 +\frac{a_{1}}{2a_2} \right) q +f,\\ q&= -\sqrt{-a_2} \left( \partial _x^2 +\frac{a_{1}}{2a_2} \right) u, \end{aligned} \end{aligned}$$

(4.2)

where

$$\begin{aligned} f =Mu, \quad M:=\left( a_0-\frac{a_{1}^2}{4a_2} \right) . \end{aligned}$$

The corresponding DG scheme may be given by

$$\begin{aligned} (u_{ht}, \phi )&= - \tilde{A}(q_h,\phi ) +M(u_h, \phi ), \end{aligned}$$

(4.3a)

$$\begin{aligned} (q_h, \psi )&= \tilde{A}(u_h,\psi ), \end{aligned}$$

(4.3b)

where

$$\begin{aligned} \tilde{A}(w,v)=\sqrt{-a_2} A(w, v)+\frac{a_1}{2\sqrt{-a_2}} (w, v) \end{aligned}$$

with $A(\cdot , \cdot )$ defined in (2.7). Such semi-discrete DG scheme can be shown $L^2$ stable, and optimally convergent. The result is summarized in the following.

Theorem 4.1

Let $u_h$ be the numerical solution to (4.3), then

$$\begin{aligned} \Vert u_h(\cdot , t)\Vert \le \Vert u_h(\cdot , 0)\Vert e^{Mt}, \quad M=a_0-\frac{a_1^2}{4a_2}. \end{aligned}$$

Assume that the exact solution u to problem (1.1) with operator L defined in (4.1) is smooth, then

$$\begin{aligned} \Vert u_h(\cdot , t)-u(\cdot , t) \Vert \le C h^{k+1}, \quad 0\le t\le T, \end{aligned}$$

(4.4)

where C depends on $\sup _{t \in [0,T]}|u_t(\cdot , t)|_{k+1}$, $\sup _{t \in [0,T]}|u(\cdot , t)|_{k+3}, \ \sup _{t\in [0,T]}|u(\cdot , t)|_{k+1}$ and T, but independent of h.

Proof

Firstly, the stability result follows from

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert u_h\Vert ^2 +\Vert q_h\Vert ^2 =M\Vert u_h\Vert ^2, \end{aligned}$$

which is obtained by adding two equations in (4.3) with $\phi =u_h$ and $\psi =q_h$. Here the terms involving $A(\cdot , \cdot )$ cancel out due to the symmetry property.

We proceed to carry out the error estimate. The consistency of the DG method (4.3) ensures that the exact solution u and q of (4.2) also satisfy

$$\begin{aligned} \begin{aligned} (u_t, \phi )&= -\tilde{A}(q,\phi )+M(u, \phi ),\\ (q, \psi )&= \tilde{A}(u,\psi ),\\ \end{aligned} \end{aligned}$$

(4.5)

for all $\phi \in V_h^k, \psi \in V_h^k$. Subtracting (4.3) from (4.5), we obtain the error system

$$\begin{aligned} \begin{aligned} ((u-u_h)_t, \phi )&= - \tilde{A}(q-q_h,\phi )+M(u-u_h, \phi ),\\ (q-q_h, \psi )&= \tilde{A}(u-u_h,\psi ). \end{aligned} \end{aligned}$$

(4.6)

Denote

$$\begin{aligned} \begin{aligned} e_1&= Pu-u_h, \quad \epsilon _1= Pu-u, \\ e_2&= Pq-q_h, \quad \epsilon _2= Pq-q, \\ \end{aligned} \end{aligned}$$

and take $\phi =e_1, \psi =e_2$ in (4.6), upon summation, we obtain

$$\begin{aligned} \begin{aligned} \frac{1}{2} \frac{d}{dt}\Vert e_1\Vert ^2 + \Vert e_2\Vert ^2&= M\Vert e_1\Vert ^2 -M(\epsilon _1, e_1)+ (\epsilon _{1t}, e_1) + (\epsilon _2, e_2) +\tilde{A}(\epsilon _2, e_1)- \tilde{A}(\epsilon _1, e_2). \end{aligned} \end{aligned}$$

(4.7)

By property (2.11) of the projection, we have

$$\begin{aligned} \begin{aligned} \tilde{A}(\epsilon _2, e_1)&= \sqrt{-a_2} A(\epsilon _2, e_1) +\frac{a_1}{2\sqrt{-a_2}}(\epsilon _2, e_1)=\frac{a_1}{2\sqrt{-a_2}}(\epsilon _2, e_1), \\ \tilde{A}(\epsilon _1, e_2)&= \sqrt{-a_2} A(\epsilon _1, e_2)+\frac{a_1}{2\sqrt{-a_2}}(\epsilon _1, e_2)=\frac{a_1}{2\sqrt{-a_2}}(\epsilon _1, e_2). \end{aligned} \end{aligned}$$

These when inserted into (4.7) upon further bounding terms on the right hand side gives

$$\begin{aligned} \begin{aligned} \frac{1}{2} \frac{d}{dt}\Vert e_1\Vert ^2&\le M\Vert e_1\Vert ^2+ \left( M\Vert \epsilon _1\Vert + \Vert \epsilon _{1t}\Vert +\frac{|a_1|}{2\sqrt{-a_2}}\Vert \epsilon _2\Vert \right) \Vert e_1\Vert \\&\quad + \,\frac{1}{4} \left( \Vert \epsilon _2\Vert +\frac{|a_1|}{2\sqrt{-a_2}}\Vert \epsilon _1\Vert \right) ^2 \\&\le C( \Vert e_1\Vert ^2+ h^{2(k+1)}), \end{aligned} \end{aligned}$$

where property (2.12) has been used, and C depends on M, $\sup _{t\in [0,T]}|u_t|_{k+1}$, $\sup _{0\le t\le T}|u|_{k+3}$, $\sup _{t\in [0,T]}|u|_{k+1}$, independent of h. By Grownwall’s inequality we have

$$\begin{aligned} \Vert e_1(\cdot , t)\Vert ^2 \le e^{2CT}(\Vert e_1(\cdot , 0)\Vert ^2+ h^{2k+2}), \quad 0\le t \le T, \end{aligned}$$

which together with the initial error $\Vert e_1(\cdot , 0)\Vert \le C h^{k+1}$ yields

$$\begin{aligned} \Vert e_1(\cdot , t)\Vert \le \sqrt{C^2+1} e^{CT} h^{k+1}, \quad 0\le t \le T. \end{aligned}$$

This when combined with the approximation result in Lemma 2.2 leads to (4.4) as desired. $\square$

In a similar fashion, we consider the 2D operator

$$\begin{aligned} Lu=\sum _{m=0}^2 a_m\Delta ^{m}u, \end{aligned}$$

(4.8)

with $a_2<0$, for which we have the following reformulation

$$\begin{aligned} \begin{aligned} u_t&= \sqrt{-a_2} \left( \Delta +\frac{a_1}{2a_2} \right) q +Mu,\\ q&= -\sqrt{-a_2} \left( \Delta +\frac{a_1}{2a_2} \right) u. \end{aligned} \end{aligned}$$

The corresponding DG scheme becomes

$$\begin{aligned} (u_{ht}, \phi )&= - \tilde{A}(q_h,\phi ) +(f(u_h), \phi ), \end{aligned}$$

(4.9a)

$$\begin{aligned} (q_h, \psi )&= \tilde{A}(u_h,\psi ), \end{aligned}$$

(4.9b)

where $f(u)=Mu$, and the bilinear functional for 2D rectangular meshes becomes

$$\begin{aligned} \tilde{A}(w,v)= \sqrt{-a_2} A(w, v)+\frac{a_1}{2\sqrt{-a_2}} (w, v), \end{aligned}$$

with $A(\cdot , \cdot )$ defined in (3.4). For DG scheme (4.9), we have the following result.

Theorem 4.2

Let $u_h$ be the numerical solution to (4.9), then

$$\begin{aligned} \Vert u_h(\cdot , t)\Vert \le \Vert u_h(\cdot , 0)\Vert e^{Mt}. \end{aligned}$$

Assume that the exact solution u to problem (1.1) with operator L defined in (4.8) is smooth, then

$$\begin{aligned} \Vert u_h(\cdot , t)-u(\cdot , t) \Vert \le C h^{k+1}, \quad 0\le t\le T, \end{aligned}$$

where C depends on $\sup _{t \in [0,T]}\Vert u_t(\cdot , t)\Vert _{k+1}$, $\sup _{t \in [0,T]}|u(\cdot , t)|_{k+3}, \ \sup _{t\in [0,T]}|u(\cdot , t)|_{k+1}$ and T, but independent of h.

4.2 Non-periodic Boundary Conditions

As is known if one of the following homogeneous boundary conditions is imposed,

$$\begin{aligned} u=\partial _\nu u=0; \quad u=\Delta u=0; \quad \partial _\nu u=\partial _\nu \Delta u=0, \quad x\in \partial \Omega , \end{aligned}$$

where $\nu$ stands for the outward normal direction to the boundary $\partial \Omega$, then the problem

$$\begin{aligned} u_t=-\Delta ^2 u, \quad u(x, 0)=u_0(x), x\in \Omega , \quad t>0 \end{aligned}$$

is also well-posed, and $\Vert u(\cdot , t)\Vert \le \Vert u_0(\cdot )\Vert$ holds for $t>0$. In practice, the boundary conditions are often non-homogeneous, for example, the above three types of boundary conditions can have the form

$$\begin{aligned} (i) \; u=g_1, \partial _\nu u=g_2; \quad (ii)\; u= g_1, \Delta u=g_3; \quad (iii)\; \partial _\nu u=g_2, \partial _\nu \Delta u=g_4, \quad x\in \partial \Omega , \end{aligned}$$

where $g_i$ are given, and can be different in these three cases. The first two may be called “generalized Dirichlet conditions” of the first and second kind, respectively, and the third one may be called “generalized Neumann condition”. There is no restriction to the use of mixed types of boundary conditions.

Let K be a computation cell such that $\partial \Omega \cap K$ is not empty, with $\nu$ still denoting the outward normal direction of $\partial \Omega \cap K$. We also denote the set of all boundary edges of $\partial \Omega \cap K$ by $\Gamma$, which is a union of all boundary edges in 2D case, and $\{x_{1/2}=a, b=x_{N+1/2}\}$ in one-dimensional case. We can then define the boundary fluxes for all edges $e \in \Gamma$ for case (i), (ii) and (iii), respectively:

$$\begin{aligned} \widehat{u_h}&= g_1, \quad \widehat{\partial _\nu u_h} = g_2, \end{aligned}$$

(4.10a)

$$\begin{aligned} \widehat{q_h}&= q_h, \quad \widehat{\partial _\nu q} = \frac{\beta _1}{h} (g_1-u_h)+ \partial _\nu q_h; \end{aligned}$$

(4.10b)

$$\begin{aligned} \widehat{u_h}&= g_1, \quad \widehat{\partial _\nu u_h} =\frac{\beta _0}{h} (g_1-u_h)+ \partial _\nu u_h, \end{aligned}$$

(4.11a)

$$\begin{aligned} \widehat{q_h}&= -g_3, \quad \widehat{\partial _\nu q} = \frac{\beta _0}{h} (-g_3-q_h) + \partial _\nu q_h; \end{aligned}$$

(4.11b)

$$\begin{aligned} \widehat{u_h}&= u_h, \quad \widehat{\partial _\nu u_h} = g_2, \end{aligned}$$

(4.12a)

$$\begin{aligned} \widehat{q_h}&= q_h, \quad \widehat{\partial _\nu q} =-g_4, \end{aligned}$$

(4.12b)

where the mesh size $h=diam\{K\}$. The flux parameters $\beta _{0}, \ \beta _{1}$ are used to ensure the numerical convergence. For these three types of boundary fluxes, the following stability results hold true.

Theorem 4.3

The DG scheme (2.6) or (3.3) subject to one of three types of boundary fluxes (4.10)–(4.12) is stable in the sense that

$$\begin{aligned} \Vert u_h - \widetilde{u}_h\Vert \le \Vert u_0-\widetilde{u}_0\Vert , \end{aligned}$$

(4.13)

provided (i) $\beta _1 \ge 0$, (ii) $\forall \beta _0$, and (iii) no flux parameter is needed. Here $u_h$ and $\widetilde{u}_h$ in (4.13) denote the corresponding numerical solutions that satisfy the same boundary conditions associated with the initial conditions $u_0$ and $\widetilde{u}_0$, respectively.

Proof

Let $A^0(\cdot , \cdot )$ be the bilinear operator defined in (2.6) or (3.3), yet without boundary terms. Then the sum of two global formulations yields the following

$$\begin{aligned} (u_{ht}, \phi ) +(q_h, \psi )=-A^0(q_h, \phi )+A^0(u_h, \psi )+B(u_h, q_h; \phi , \psi ), \end{aligned}$$

(4.14)

where

$$\begin{aligned} B=\int _\Gamma \left( \widehat{\partial _\nu q_h} \phi - \widehat{\partial _\nu u_h}\psi +(q_h-\widehat{q}_h)\partial _\nu \phi -(u_h-\widehat{u}_h)\partial _\nu \psi \right) ds. \end{aligned}$$

Upon careful calculation, B in each case is given as follows:

• (i)
  $$\begin{aligned} B=\int _{\Gamma } \left( \partial _\nu q_h \phi -u_h \partial _\nu \psi -\frac{\beta _1}{h} u_h \phi \right) ds +\int _\Gamma \left( g_1\partial _\nu \psi - g_2\psi +\frac{\beta _1}{h} g_1\phi \right) ds; \end{aligned}$$
• (ii)
  $$\begin{aligned} B&=\int _{\Gamma } \left( \partial _\nu q_h \phi + q_h \partial _\nu \phi -u_h \partial _\nu \psi -\partial _{\nu } u_h \psi \right) ds -\int _\Gamma \left( \frac{\beta _0}{h}(q_h\phi -u_h\psi )\right) ds \\&\quad +\int _\Gamma \left( \frac{\beta _0}{h} (-g_3\phi -g_1\psi )+g_1\partial _\nu \psi +g_3\partial _\nu \phi \right) ds; \text {and} \end{aligned}$$
• (iii)
  $$\begin{aligned} B=\int _{\Gamma } (-g_4\phi -g_2\psi )ds. \end{aligned}$$

Taking $\phi =u_h$ and $\psi =q_h$ in (4.14) we obtain

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \Vert u_{h}\Vert ^2+\Vert q_h\Vert ^2 =B(u_h, q_h; u_h, q_h), \end{aligned}$$

where such B reduces to

• (i) $B=-\frac{\beta _1}{h} \int _{\Gamma } u_h^2 ds +\int _\Gamma (g_1\partial _\nu q_h - g_2q_h+\frac{\beta _1}{h} g_1u_h)ds$,

• (ii) $B =\int _\Gamma (\frac{\beta _0}{h} (-g_3u_h -g_1q_h)+g_1\partial _\nu q_h +g_3\partial _\nu u_h)ds$, and

• (iii) $B=\int _{\Gamma } (-g_4u_h -g_2q_h)ds$.

Both the equation and the boundary conditions are linear, it suffices to show $\Vert u_h(\cdot , t)\Vert \le \Vert u_h(\cdot , 0)\Vert$ when boundary conditions are homogeneous, i.e., $g_i=0, \ i=1, \ldots , 4$. Indeed, in such cases we have (i) $B=-\frac{\beta _1}{h}\int _{\Gamma } u_h^2ds$, (ii) $B=0\quad \forall \beta _0$, and (iii) $B=0$. Thus, the conclusion follows. $\square$

Remark 4.1

If $\tilde{u}_h$ is an approximation to the steady solution of the corresponding time-independent problem, then (4.13) leads to

$$\begin{aligned} \Vert u_h \Vert \le \Vert u_0-\widetilde{u}_0\Vert +\Vert \widetilde{u}_h\Vert , \end{aligned}$$

which can be regarded as the priori bound in terms of both initial data and the boundary data.

The necessity of using $\beta _1$ in (4.10) and $\beta _0$ in (4.11) is illustrated numerically in Examples 5.4 and 5.5, respectively, by checking whether the optimal order of accuracy can be obtained. Extensive numerical tests including Examples 5.4 and 5.5 indicate that the choice of $\beta _0, \beta _1$ as shown in Table 1 is sufficient for achieving optimal convergence. In Table 1, $\delta >0$ can be a quite small number (see Fig. 1), and $C>0$ is a constant, say $C=3$ is a valid choice in our numerical examples on uniform meshes. It would be interesting to justify these sufficient conditions by establishing some optimal error estimates.

Table 1 The choice of $\beta _0, \beta _1$ in boundary fluxes (4.10) and (4.11)

4.3 Application to a Nonlinear Problem

We consider the initial-boundary value problem for the one-dimensional Swift–Hohenberg equation of the form,

$$\begin{aligned} \begin{aligned}&u_t=-D\kappa ^4 u-2D\kappa ^2 u_{xx} -D u_{xxxx}+f(u) \quad x \in [a,b], \quad t>0, \\&u=0 \quad \text {and} \; u_{xx}=0 \quad \text {at} \; x=a, b,\\&u(x,0)=u_0(x), \end{aligned} \end{aligned}$$

(4.15)

where $D>0, \ \kappa$ are constants and $f(u)= \varepsilon u+gu^2-u^3$ with non-negative constants $\varepsilon , \ g$. The Swift–Hohenberg equation introduced in [32] is noted for its pattern-forming behavior, and endowed with a gradient flow structure, $u_t= -\frac{\delta \mathcal {E}}{\delta u}$, for zero-flux boundary conditions. This equation relates the temporal evolution of the pattern to the spatial structure of the pattern, with $\epsilon$ measuring how far the temperature is above the minimum temperature difference required for convection, and g is the parameter controlling the strength of the quadratic nonlinearity.

The Swift–Hohenberg equation (4.15) can be rewritten as an equivalent system

$$\begin{aligned} \begin{aligned} u_t&= \sqrt{D}(\partial _x^2+\kappa ^2)q+f(u),\\ q&= -\sqrt{D}(\partial _x^2+\kappa ^2)u. \end{aligned} \end{aligned}$$

With this formulation the energy dissipation law becomes

$$\begin{aligned} \frac{d}{dt}\mathcal {E} = -\int _a^b|u_t|^2dx \le 0, \end{aligned}$$

where $\mathcal {E}=\int _a^b \Phi (u)+\frac{1}{2} |q|^2dx$ is a free-energy functional, and

$$\begin{aligned} \Phi (u) = -\frac{\varepsilon }{2}u^2-\frac{g}{3}u^3+\frac{1}{4}u^4= -\int _0^u f(\xi )d\xi . \end{aligned}$$

This is the fundamental stability property of the Swift–Hohenberg equation. The objective of this section is to illustrate that our DG discretization with proper time discretization inherits this property irrespectively of time step sizes.

The semi-discrete DG method for (4.15) may be given by

$$\begin{aligned} (u_{ht}, \phi )&= - A(q_h,\phi ) +(f(u_h), \phi ),\\ (q_h, \psi )&= A(u_h,\psi ), \end{aligned}$$

where

$$\begin{aligned} A(w,v)&= \sqrt{D} \left( A^0(w,v)-\kappa ^2(w, v)+\left( w^+v^+_x\right) _{1/2}-\left( w^-v^-_x\right) _{N+1/2} \right. \\&\quad \left. +\,\left( w_x^+v^+\right) _{1/2}-\left( w_x^-v^-\right) _{N+1/2}+\frac{\beta _{0}}{h}\left( w^+{v^+}\right) _{1/2} +\frac{\beta _{0}}{h}\left( w^-{v^-}\right) _{N+1/2} \right) , \end{aligned}$$

with parameter $\beta _0$ chosen as listed in Table 1. The DG scheme can be shown to preserve the energy dissipation law in the sense that

$$\begin{aligned} \frac{d}{dt}\mathcal {E}_h = -\int _a^b|u_{ht}|^2dx \le 0, \end{aligned}$$

where $\mathcal {E}_h=\int _a^b \Phi (u_h)+\frac{1}{2} |q_h|^2dx.$

Time discretization should be taken with care, here we want to preserve the energy dissipation law at each time step. A simple choice is to obtain $(u_h^{n+1}, q_h^{n+1}) \in V_h^k \times V_h^k$ from $(u_h^{n}, q_h^{n})$ by

$$\begin{aligned} \left( \frac{u_h^{n+1} - u_h^n}{\Delta t}, \phi \right)&= - A(q_h^{n+1/2},\phi )- \left( \frac{\Phi (u_h^{n+1})-\Phi (u^n)}{u_h^{n+1}-u_h^n},\phi \right) \end{aligned}$$

(4.16a)

$$\begin{aligned} (q_h^{n}, \psi )&= A(u_h^{n},\psi ) \end{aligned}$$

(4.16b)

for all $\phi , \ \psi \in V_h^k$, where $q_h^{n+1/2}=\frac{1}{2}(q^{n+1}_h+q_h^n)$. This fully discrete DG scheme does have the following property.

Theorem 4.4

The solution to (4.16) satisfies the energy dissipation law of the form

$$\begin{aligned} \mathcal {E}_h^{n+1} - \mathcal {E}_h^n = -\frac{\Vert u_h^{n+1}-u_h^{n}\Vert ^2}{\Delta t} , \end{aligned}$$

(4.17)

where

$$\begin{aligned} \mathcal {E}_h^n= \int _a^b \Phi (u_h^n) +\frac{1}{2}|q_h^n|^2dx. \end{aligned}$$

Proof

By taking the difference of (4.16b) at time level $n+1$ and n, we obtain

$$\begin{aligned} (q_h^{n+1}-q_h^{n}, \psi ) = A(u_h^{n+1}-u_h^{n},\psi ). \end{aligned}$$

(4.18)

Taking $\phi =u_h^{n+1} - u_h^n$ in (4.16a), $\psi =q_h^{n+1/2 }$ in (4.18), then plugging the resulting relation into (4.16a), we have

$$\begin{aligned} \begin{aligned} \frac{\Vert u_h^{n+1}-u_h^{n}\Vert ^2}{\Delta t}&= - \left( q_h^{n+1}-q_h^{n}, q_h^{n+1/2}\right) - \int _a^b (\Phi (u_h^{n+1})- \Phi (u_h^{n})) dx\\&= - \frac{1}{2}\left( \Vert q_h^{n+1}\Vert ^2-\Vert q_h^{n}\Vert ^2\right) -\int _a^b \Phi (u_h^{n+1})dx +\int _a^b \Phi (u_h^{n}) dx,\\ \end{aligned} \end{aligned}$$

which gives (4.17). $\square$

We next propose an iteration scheme to solve the nonlinear equation (4.16). Rewriting the nonlinear term in (4.16a) as

$$\begin{aligned} \frac{\Phi (u_h^{n+1})-\Phi (u_h^n)}{u_h^{n+1}-u_h^n} =G_1(u_h^{n+1},u_h^n)u_h^{n+1}+G_2(u_h^n), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} G_1(w,v)&= -\frac{\varepsilon }{2}-\frac{g}{3}(w+v)+\frac{1}{4}(w^2+wv+v^2), \\ G_2(v)&= -\frac{\varepsilon }{2}v-\frac{g}{3}v^2+\frac{1}{4}v^3, \end{aligned} \end{aligned}$$

with which we apply the idea in [8] to obtain the following iterative scheme,

$$\begin{aligned} \begin{aligned} \left( \frac{u_h^{n+1,l+1}-u_h^n}{\Delta t}, \phi \right) + \frac{1}{2}A(q_h^{n+1,l+1},\phi )&= -\frac{1}{2}A(q_h^{n},\phi )\\&\quad -\left( G_1(u_h^{n+1,l},u_h^n)u_h^{n+1,l+1}+G_2(u_h^n), \phi \right) ,\\ \frac{1}{2}A(u_h^{n+1,l+1},\psi ) -\frac{1}{2}(q_h^{n+1,l+1}, \psi )&= 0, \end{aligned} \end{aligned}$$

(4.19)

where $G_1(u_h^{n+1,0},u_h^n)=G_1(u_h^n,u_h^n)$, the iteration stops as $\Vert u_h^{n+1,l}-u_h^{n+1,l-1}\Vert < \delta$ for certain $l=L \ (L \ge 1)$. Then the last iteration gives the sought solution on the new time stage and we define

$$\begin{aligned} u_h^{n+1} =u_h^{n+1,L}. \end{aligned}$$

5 Numerical Examples

In this section we numerically validate our theoretical results, as well as the stated extension cases with one and two dimensional examples. The orders of convergence are calculated using

$$\begin{aligned} \log _2\frac{\Vert u-u_h\Vert _{L^2}}{\Vert u-u_{h/2}\Vert _{L^2}}, \quad \log _2\frac{\Vert u-u_h\Vert _{L^\infty }}{\Vert u-u_{h/2}\Vert _{L^\infty }}, \end{aligned}$$

respectively; where errors are given in the following way: for the one dimensional $L^2$ error, we use

$$\begin{aligned} \Vert u-u_h\Vert _{L^2} = \left( \sum _{j=1}^N \frac{h_j}{2} \sum _{\alpha =1}^{k+1} \omega _{\alpha } |u_h(\hat{x}^j_{\alpha },t)-u(\hat{x}^j_{\alpha },t)|^2 \right) ^{\frac{1}{2}}, \end{aligned}$$

where $\omega _{\alpha }>0$ are the weights, $\hat{x}^j_{\alpha }$ are the corresponding Gauss points in each cell $I_j$, and for the $L^\infty$ error,

$$\begin{aligned} \Vert u-u_h\Vert _{L^\infty } = \max _{1\le j \le N} \max _{1\le \alpha \le k+1} |u_h(\hat{x}^j_{\alpha },t)-u(\hat{x}^j_{\alpha },t)|. \end{aligned}$$

Example 5.1

(1D accuracy test) We consider the biharmonic equation

$$\begin{aligned} \begin{aligned}&u_t = -u_{xxxx} \quad (x,t) \in [0, 2\pi ]\times (0,T],\\&u(x,0) = \sin (x),\\ \end{aligned} \end{aligned}$$

with periodic boundary conditions. And the exact solution is given by

$$\begin{aligned} u(x,t) = e^{-t} \sin (x). \end{aligned}$$

We test this example using DG scheme (2.3) with the Crank–Nicolson time discretization, based on polynomials of degree k with $k=1, \ldots , 4$. Both errors and orders of accuracy at $T=1$ are reported in Table 2. These results show that $(k+1)$th order of accuracy in both $L^2$ and $L^{\infty }$ are obtained.

Table 2 1D $L^2, L^\infty$ errors for biharmonic equation at $T= 1$

Example 5.2

(2D accuracy test) We consider the 2D linear biharmonic equation

$$\begin{aligned} \begin{aligned} u_t + \Delta ^2 u&= 0 \quad (x,y,t) \in [0, 4\pi ]\times [0, 4\pi ]\times (0,T],\\ u(x,y,0)&= \sin (0.5x)\sin (0.5y),\\ \end{aligned} \end{aligned}$$

with periodic boundary conditions. And the exact solution is given by

$$\begin{aligned} u(x,t) = e^{-0.25t} \sin (0.5x)\sin (0.5y). \end{aligned}$$

We test this example by DG scheme (3.7) with $\theta =1/2$, based on tensor product of polynomials of degree k with $k=1, 2, 3$ on rectangular meshes. Both errors and orders of accuracy at $T=0.1$ are reported in Table 3. These results show that $(k+1)$th order of accuracy in both $L^2$ and $L^{\infty }$ are obtained.

Table 3 2D $L^2, L^\infty$ errors for biharmonic equation at $T= 0.1$

Example 5.3

(2D linearized Cahn–Hillard equation) We consider the 2D linearized Cahn–Hillard equation

$$\begin{aligned}&u_t + \Delta ^2 u + \Delta u = 0 \quad (x,y,t) \in [0, 2\pi /a]\times [0, 2\pi /a]\times (0,T],\\&u(x,y,0) = \sin (ax)\sin (ay), \end{aligned}$$

with periodic boundary conditions, where $a>0$ is a constant.

The exact solution is given by

$$\begin{aligned} u(x,t) = e^{-bt} \sin (ax)\sin (ay), \end{aligned}$$

where $b=4a^4-2a^2$.

We test this example using DG scheme (4.9) on rectangular meshes with the Crank–Nicolson time discretization, based on polynomials of degree k with $k=1, 2, 3$, by varying the interval length through a in three cases: (i) $a=1/2$; (ii) $a=\sqrt{2}/2$; and (iii) $a=\sqrt{3}/2$. They correspond to $b=-1/4, 0, 3/4$, while the solution in each case shows different growth/decay behavior in time.

Both errors and orders of accuracy at $T=0.1$ are reported in Tables 4, 5 and 6, respectively. These results show that $(k+1)$th order of accuracy in both $L^2$ and $L^{\infty }$ norms are obtained.

Table 4 2D $L^2, L^\infty$ errors for linearized Cahn–Hillard equation at $T= 0.1$, $\hbox {a}=1/2$

Table 5 2D $L^2, L^\infty$ errors for linearized Cahn–Hillard equation at $T = 0.1$, $a=\sqrt{2}/2$

Table 6 2D $L^2, L^\infty$ errors for linearized Cahn–Hillard equation at $T = 0.1$, $a=\sqrt{3}/2$

Example 5.4

(Dirichlet boundary condition of the first kind) We consider the following initial-boundary value problem

$$\begin{aligned} \begin{aligned}&u_t =-u_{xxxx},\quad (x, t)\in [0, 2\pi ]\times (0, T],\\&u(x, 0) =\sin x, \\&u(0, t) = u(2\pi ,t)=0,\\&u_x(0,t) = u_x(2\pi ,t)=e^{-t}, \end{aligned} \end{aligned}$$

which admits the exact solution $u(x,t) = e^{-t} \sin (x)$.

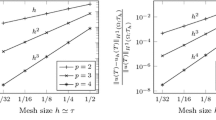
We test this example using DG scheme (2.3) with boundary fluxes (4.10). We pay special attention on the effects of the boundary flux parameter $\beta _1$. The comparison results in Fig. 1 show that the DG scheme with $\beta _1>0$ is optimally convergent, yet the scheme with $\beta _1=0$ only gives suboptimal orders of convergence for polynomials of degree k with $k \ge 2$. This test suggests that $\beta _1$ is necessary for $k\ge 2$ to weakly enforce the Dirichlet boundary data as formulated in (4.10), and $\beta _1=0$ is admissible for $k=1$. Here, the convergence orders shown in Fig. 1 are obtained based on total cell numbers $N=40, \ 80$ for $k \le 2$ and $N=20, \ 40$ for $k \ge 3$.

Fig. 1

The convergence orders with $P^k$ polynomials at $T=0.1$, Example 5.4

Fig. 2

The convergence order with $P^1$ polynomials at $T=0.1$, Example 5.5

Example 5.5

(Dirichlet boundary condition of the second kind) We consider the following initial-boundary value problem

$$\begin{aligned} \begin{aligned}&u_t =-u_{xxxx},\quad (x, t)\in [0, 3\pi ]\times (0, T],\\&u(x, 0) =\sin x, \\&u(0, t) = u(3\pi ,t)=0,\\&u_{xx}(0,t) = u_{xx}(3\pi ,t)=0. \end{aligned} \end{aligned}$$

We test this example using DG scheme (2.3) with boundary fluxes (4.11), with emphasis on the effects of the boundary flux parameters $\beta _0$. The numerical results are reported in Tables 7, 8 and Fig. 2. In Table 7 we test the DG scheme based on $P^1$ polynomials, and we observe that the DG scheme with $\beta _0=0$ only gives suboptimal order of accuracy, while the DG scheme with other values of $\beta _0$ give optimal order of convergence in both $L^2$ and $L^\infty$ norms. The comparison results in Table 7 show that $\beta _0$ is necessary for $k=1$ to weakly enforce the Dirichlet boundary data as formulated in (4.11). Convergence orders in Fig. 2, obtained based on $P^1$ polynomials and total cell numbers $N=40, \ 80$, indicate that $|\beta _0| \ge C$ for some constants C (e.g. $C=3$) is sufficient for the DG scheme to be optimally convergent. However, extensive numerical tests indicate that $\beta _0=0$ is sufficient for the DG scheme with $k\ge 2$ to be optimally convergent, see Table 8.

Table 7 1D $L^2, L^\infty$ errors at $T= 1$ based on $P^1$ polynomials

Table 8 1D $L^2, L^\infty$ errors at $T = 1$ with $k \ge 2$ and $\beta _0=0$

Example 5.6

(Pattern selection) For one-dimensional Swift–Hohenberg equation, we consider the following problem

$$\begin{aligned} \begin{aligned}&u_t=-u -2u_{xx} -u_{xxxx}+f(u) \quad (x,t) \in [0, L] \times (0,T], \\&u=0 \quad \text {and} \; u_{xx}=0 \quad \text {at} \; x=0, L, \; t>0,\\&u(x,0)=0.1\sin \left( \frac{\pi x}{L} \right) , \end{aligned} \end{aligned}$$

where $f(u) = \epsilon u - u^3$. The asymptotic solution behavior of this problem was studied in [29] with particular focus on the role of the parameter $\epsilon$ and the length L of the domain on the selection of the limiting profile. We test the case of $\epsilon =0.5$ with $L=4, 14$, respectively, and compare the results with those obtained in [29]. This problem is solved by DG scheme (4.19) based on polynomial $P^2$ with $\delta =10^{-12}$. The numerical solutions shown in Fig. 3 display the pattern dynamics, which is consistent with the analysis and numerical tests in [29]. The corresponding free energy dissipation is shown in Fig. 4.

Fig. 3

Evolution of patterns with a $L=4.0$, b $L=14.0$. The dashed curve is the initial pattern and the thick curve the final pattern. The other curves represent patterns at the intermediate times

Fig. 4

Energy evolution with a $\hbox {L}=4.0$, b $L=14.0$

6 Concluding Remarks

A novel discontinuous Galerkin (DG) method without interior penalty has been proposed to solve the time-dependent fourth order partial differential equations. For the biharmonic equation, the DG scheme is based on the mixed formulation of the original model. Both stability and optimal $L^2-$error estimates of the DG method are proved in both one-dimensional and multi-dimensional settings subject to periodic boundary conditions. Extensions to general fourth order equations and cases with three typical non-homogeneous boundary conditions are discussed, following by an application to solving the one-dimensional Swift–Hohenberg equation, which admits a decay free energy. Several numerical results are presented to verify the stability and accuracy of the schemes.