1 Introduction

Quantum plasmas are ubiquitous in micromechanical systems and ultrasmall electronic devices (Markowich et al. 1990; Sulem and Sulem 1999), in laser and microplasmas (Becker et al. 2006), in dense astrophysical environments (Opher et al. 2001) and in semiconductors (Markowich et al. 1990; Wang and Lu 2014).

Classical motion of charged particles can be described by kinetic equations (Vlasov or Boltzmann equation) coupled to Poisson equation for the electrostatic forces (see Ben 2000; Shukla and Stenflo 2006; Shukla and Eliasson 2006, 2007, and references therein). For ultrasmall electron devices, like nanostructures, quantum effects such as tunneling become important when the de Broglie length of the charge carriers is comparable to the dimension of the system. Such devices are well described by the Schrödinger–Poisson (SP) system (Shukla and Stenflo 2006). The SP system has been also used to model the dynamics of quantum plasma (Anderson 2002; Haas et al. 2000; Haas 2003; Manfredi and Haas 2001; Manfredi 2005) and was developed from the Vlasov equation coupled with the Poisson equation for the electric potential (Manfredi and Haas 2001; Shukla and Eliasson 2010; Shukla and Stenflo 2006). We also note that the SP system was originally derived by Hartree in the context of atomic physics for studying the self-consistent effect of atomic electrons on the Coulomb potential of the nucleus.

As far as we know, several kinds of numerical methods have been investigated on solving the SP system. Cheng et al. developed a novel fast-spectral element method for the self-consistent solution of the SP system in the simulation of semiconductor nanodevices (Cheng et al. 2004), where the field variables in SP equations are represented by high-order Legendre polynomials. Dong studied a simplified pseudospectral methods for computing ground state and dynamics of spherically symmetric Schrödinger–Poisson–Slater system (Dong 2011). Ehrhardt et al. presented a discrete transparent boundary condition for a Crank–Nicolson-type predictor–corrector scheme for solving the spherically symmetric SP system (Ehrhardt and Zisowsky 2006). Shaikh et al. performed three-dimensional nonlinear fluid simulations of electron fluid turbulence at nanoscales in an unmagnetized warm dense plasma by employing Fourier spectral method for solving the SP system (Shaikh and Shukla 2008). Combined with the Poisson solver, Mauser et al. proposed a backward Euler and a semi-implicit/leap-frog sine pseudospectral method in the computation of the ground state and dynamics of SP system (Mauser and Zhang 2014). Zheng investigated a perfectly matched layer approach for solving the nonlinear SP equations in unbounded domain (Zheng 2007). Lubich gave an error analysis of Strang-type splitting integrators for the SP equations with an \(H^4\)-regular solution and found a first-order error bound in the \(H^1\) norm and a second-order error bound in the \(L^2\) norm (Lubich 2008). Zhang presented optimal error estimates of compact finite difference discretizations for the SP system (Zhang 2013). We note that the SP system is sometimes called Schrödinger–Newton equations: the stationary spherical-symmetric case was investigated numerically in Harrison et al. (2003), Moroz et al. (1998) and Tan et al. (1990) and analytically in Tod and Moroz (1999).

For the mathematical analysis of the SP system, numerous research have been done (Bao et al. 2003; Castella 1997; Sulem and Sulem 1999). We name a few important works here: Ben Abdallah studied that the existence of weak solutions is shown for boundary value problems in the stationary and time-dependent regimes of Vlasov–Schrödinger–Poisson system (Ben 2000). Brezzi proved the existence of a unique, global classical solution of the quantum Vlasov–Poisson problem. The proof was based on a reformulation of the quantum Vlasov–Poisson problem as a system of countably many Schrödinger equations coupled to a Poisson equation for the potential (Brezzi and Markowich 1991). Castella studied existence, uniqueness, time behavior, and smoothing effects of the \(L^2\) solutions to the SP system (Castella 1997). Lange et al. showed the existence, uniqueness, and regularity of solutions of Wigner–Poisson problem and its associated SP system in various settings including periodic, stationary, and ‘mixed’ boundary value problems (Lange et al. 1995).

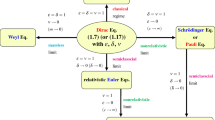
In this paper, we study the SP system numerically and propose a novel splitting Chebyshev collocation method for the time-dependant SP system. By means of splitting technique in time, the time-dependant SP system is first reduced to uncoupled linear Schrödinger and Poisson equations, respectively, at every time step. The space variables in the linear Schrödinger and Poisson equations are next represented by high-order Chebyshev polynomials and discretized by the spectral collocation method, and the resulting discretized system in one dimension, two dimensions and three dimensions can be solved efficiently by matrix diagonalization technique. The merits of the proposed method for the nonlinear SP system are that it is fast and unconditionally stable. Moreover the method is of spectral accuracy in space, and conserves the particle number and the energy of the system in the discretized level.

The paper is organized as follows. In Sect. 2, we review how to derive nonlinear Schrödinger–Poisson equations from the well-known Wigner–Poisson equation in quantum plasma and its dimensionless formulation. In Sect. 3, we propose a splitting Chebyshev collocation method for solving the time-dependent SP system. Detailed numerical algorithm for the Poisson equation and linear Schrödinger equation in one dimension (1D), two dimensions (2D) and three dimensions (3D) is provided in Sects. 4 and 5, respectively. Stability analysis for the proposed splitting Chebyshev collocation method has been provided in Sect. 7. Numerical results for the Poisson equation, linear Schrödinger equation, and the nonlinear SP system in 1D, 2D and 3D are presented in Sect. 8. Finally, some conclusions are drawn in final section.

2 Brief derivation of the nonlinear Schrödinger–Poisson system

Under the assumption of immobile ions, the Wigner–Poisson equations are often used to describe the collective electrostatic oscillations of electrons in quantum plasma (Haas et al. 2000; Manfredi and Haas 2001; Manfredi 2005; Shukla and Eliasson 2010; Shukla and Stenflo 2006; Shukla and Eliasson 2006, 2007; Wang and Lu 2014):

$$\begin{aligned} \frac{\partial f}{\partial t} + \mathbf{v}\cdot \nabla f= & {} - \frac{i em_e^3}{(2\pi )^3 \hbar ^4} \int \exp \left[ i \frac{m_e\lambda }{\hbar }(\mathbf{v}-\mathbf{v'}) \right] \left[ \phi \left( \mathbf{x}+\frac{{\varvec{\lambda }}}{2},t\right) \right. \nonumber \\&-\left. \phi \left( \mathbf{x}-\frac{{\varvec{\lambda }}}{2},t\right) \right] f(\mathbf{x},\mathbf{v'},t) {\text {d}}{{\varvec{\lambda }}} {\text {d}}{} \mathbf{v'} \end{aligned}$$
(2.1)

and

$$\begin{aligned} \triangle \phi = 4\pi e \left( \int f(\mathbf{x},\mathbf{v},t) {\text {d}}{} \mathbf{v}-n_0 \right) . \end{aligned}$$
(2.2)

The above Wigner–Poisson equations are integral-differential equations and quite complicated. In the following discussion, we follow the procedure provided by Shukla and Eliasson (2010) and briefly review how Wigner–Poisson equations can be reduced to SP System.

If we respectively denote the density \(n_e\), mean velocity \(\mathbf{u_e}\), and pressure tensor \(\mathbf{P_e}\) by:

$$\begin{aligned} n_e= & {} \int f(\mathbf{x} ,\mathbf{v},t){\text {d}}{} \mathbf{v}, \nonumber \\ n_e \mathbf{u_e}= & {} \int \mathbf{v} f(\mathbf{x} ,\mathbf{v},t){\text {d}}{} \mathbf{v}, \nonumber \\ \mathbf{P_e}= & {} \int \mathbf{(v-u_e)} \mathbf{(v-u_e)} f(\mathbf{x} ,\mathbf{v},t){\text {d}}{} \mathbf{v}, \end{aligned}$$

take the integral of Wigner equation (2.1) over \({\text {d}}{} \mathbf{v}\) (or multiply both sides of (2.1) by \(\mathbf{v}\) and the integral of the resulting equation over \({\text {d}}{} \mathbf{v}\) ) and assume the pressure \(\mathbf{P_e}\) is isotropic (=\(\mathbf{I} P_e \) with \(\mathbf{I}\) being the identity matrix), then we can get the quantum hydrodynamical equations [up to \(O(\hbar ^2)\)] as follows: the electron continuity equation

$$\begin{aligned} \frac{\partial n_e}{\partial t} + \nabla \cdot (n_e \mathbf{u_e})=0, \end{aligned}$$
(2.3)

and the electron momentum equation

$$\begin{aligned} m_e \left( \frac{\partial }{\partial t} + \mathbf{u_e} \cdot \nabla \right) \mathbf{u_e} = e\nabla \phi -\frac{1}{n_e} \nabla P_e + \mathbf{F}_Q. \end{aligned}$$
(2.4)

There are different expressions for \(P_e\), for the degenerate Fermi–Dirac-distributed plasma, the quantum statistical pressure for the electron applies:

$$\begin{aligned} P_e = \frac{m_eV_\mathrm{Fe}^2 n_0}{3} \left( \frac{n_e}{n_0}\right) ^{(d+2)/d}, \end{aligned}$$
(2.5)

where d is the number of degrees of freedom in the system. \(V_\mathrm{Fe}\) denotes the Fermi Velocity. While \(\mathbf{F}_Q\), the quantum force due to electron tunnelling is defined as

$$\begin{aligned} \mathbf{F}_Q=\frac{\hbar ^2}{2m_e} \nabla \left( \frac{ \triangle \sqrt{n_e}}{ \sqrt{n_e}}\right) . \end{aligned}$$

We introduce the wave function

$$\begin{aligned} \psi (\mathbf{x},t) = \sqrt{n_e(\mathbf{x},t)} \exp \left( i \frac{\varphi _e (\mathbf{x},t) }{\hbar }\right) , \end{aligned}$$
(2.6)

where the phase function \(\varphi _e (\mathbf{x},t)\) is defined according to

$$\begin{aligned}m_e \mathbf{u_e} =\nabla \varphi _e, \end{aligned}$$

and the density function \(n_e\) is defined as

$$\begin{aligned}n_e=|\psi |^2.\end{aligned}$$

It can be shown that the quantum hydrodynamical Eqs. (2.3)–(2.4) are equivalent to the following nonlinear SP system (Shukla and Eliasson 2010):

$$\begin{aligned} i \hbar \frac{\partial \psi }{\partial t} + \frac{\hbar ^2}{2m_e} \triangle \psi + e\phi \psi - \frac{m_e V_\mathrm{Fe}^2}{2n_0^2} |\psi |^{4/d}\psi =0, \end{aligned}$$
(2.7)

and

$$\begin{aligned} \triangle \phi = 4\pi e (|\psi |^2-n_0). \end{aligned}$$
(2.8)

Introducing parameters

$$\begin{aligned} t = \frac{\tilde{t}}{\hbar /T_{\text {F}}}, \; \mathbf{x} = \frac{\tilde{\mathbf{x} }}{\lambda _{\text {D}}}, \; \psi = \sqrt{n_0} \tilde{\psi }, \; \varphi = -\frac{T_{\text {F}}}{e} \tilde{\phi }, \end{aligned}$$
(2.9)

where \(\lambda _{\text {D}}=T_{\text {F}}/(4\pi n_0 e^2)^{1/2}\), \(T_{\text {F}}=C\hbar ^2 (n_0)^{2/3}/m_e\), \(C=\frac{(m_e)^2 V_\mathrm{Fe}^2}{2\hbar ^2} (n_0)^{5/3-2/d},\) and setting \(A= 4\pi m_e e^2/(\hbar ^2 n_0^{1/3})\), we get dimensionless SP equations after removing all \(\tilde{}\) :

$$\begin{aligned} i \frac{\partial \psi }{\partial t}= & {} \left( -A\triangle +\varphi +|\psi |^{4/d}\right) \psi , \end{aligned}$$
(2.10)
$$\begin{aligned} -\triangle \varphi= & {} |\psi |^2-1, \end{aligned}$$
(2.11)

where \(i^2=-1\), A is some constant.

System (2.10)–(2.11) has many conservation laws including:

the number of electrons

$$\begin{aligned} \int _{{\mathbb R}^d} |\psi (\mathbf{x} ,t)|^2\;{\text {d}} \mathbf{x} , \end{aligned}$$
(2.12)

the electron momentum

$$\begin{aligned} \mathbf{P}=-i\int _{{\mathbb R}^d} \psi ^*(\mathbf{x} ,t) \nabla \psi (\mathbf{x} ,t) \;{\text {d}} \mathbf{x} , \end{aligned}$$
(2.13)

and the total energy

$$\begin{aligned} E(\psi )= \int _{{\mathbb R}^d} \; \left[ A|\nabla \psi |^2 + \frac{|\nabla \varphi |^2}{2} + \frac{d}{2+d}|\psi |^{2+4/d} \right] {\text {d}}\mathbf{x} . \end{aligned}$$
(2.14)

3 A splitting Chebyshev collocation method

In this section, we present a splitting Chebyshev-collocation method for the SP system (2.10)–(2.11). In numerical computation, we truncate the problem into a bounded computational domain \(\Omega \) with homogeneous Dirichlet boundary conditions:

$$\begin{aligned} i \frac{\partial \psi }{\partial t}= & {} \left( -A\triangle +V+\varphi +|\psi |^{4/d}\right) \psi , \end{aligned}$$
(3.1)
$$\begin{aligned} -\triangle \varphi= & {} |\psi |^2-1, \end{aligned}$$
(3.2)
$$\begin{aligned} \psi (\mathbf{x} ,t)= & {} 0, \quad \varphi (\mathbf{x} ,t) =0 \quad \mathbf{x} \in \Gamma =\partial \Omega , \qquad t\ge 0, \end{aligned}$$
(3.3)
$$\begin{aligned} \psi ({\mathbf{x} },0)= & {} \psi _0({\mathbf{x} }), \quad {\mathbf{x} }\in \Omega . \end{aligned}$$
(3.4)

where \(\psi =\psi (\mathbf{x} ,t)\), \(\varphi =\varphi (\mathbf{x} ,t)\), \(\Omega =[a,b]\) in 1D, \(\Omega =[a,b]\times [c,d]\) in 2D, \(\Omega =[a,b]\times [c,d]\times [e,f]\) in 3D, with |a|, b, |c|, d, |e| and f sufficiently large. \(\partial \Omega \) is the boundary of \(\Omega \). \(V=V(\mathbf{x})\) is some given function that is added to account for more general setting.

We choose a time step size \(\tau =\Delta t>0\). For \(n=0,1,2,\ldots \), from time \(t=t_n=n\tau \) to \(t=t_{n+1}=t_n+\tau \), the system (3.1)–(3.2) may be solved by the following two splitting steps (Bao et al. 2003; Wang 2010):

Step 1 One solves first

$$\begin{aligned} i\;\partial _t\psi ({\mathbf{x} },t) = \mathscr {A} \psi (\mathbf{x} ,t) = V(\mathbf{x} )\psi (\mathbf{x} ,t)+ \varphi (\mathbf{x} ,t) \psi (\mathbf{x} ,t) + |\psi (\mathbf{x} ,t)|^{4/d}\psi (\mathbf{x} ,t) \end{aligned}$$
(3.5)

for the time step of length \(\Delta t\) [here \(\varphi (\mathbf{x} ,t)\) is defined in Eq. (3.2)];

Step 2 Followed by solving

$$\begin{aligned} i\;\partial _t\psi ({\mathbf{x} },t) = \mathscr {B} \psi (\mathbf{x} ,t) = -A\triangle \psi (\mathbf{x} ,t) \end{aligned}$$
(3.6)

for the same time step. Symbolically, the system (3.1)–(3.2) here is solved in the following way:

$$\begin{aligned} \psi (\mathbf{x} , t+\triangle t ) = e^{-i\mathscr {A} \triangle t} e^{-i\mathscr {B} \triangle t} \psi (\mathbf{x} , t). \end{aligned}$$
(3.7)

In Step 1, multiplying Eq. (3.5) by the conjugate of \(\psi \), i.e., \(\bar{\psi }\), we get

$$\begin{aligned} i\;\bar{\psi }\partial _t\psi ({\mathbf{x} },t) = [V(\mathbf{x} )+\varphi (\mathbf{x} ,t)] |\psi (\mathbf{x} ,t)|^2 + |\psi (\mathbf{x} ,t)|^{4/d+2}. \end{aligned}$$
(3.8)

Subtracting the conjugate of (3.8) from (3.8) and multiplying by \(-i\), one obtains

$$\begin{aligned} \frac{{\text {d}}}{{\text {d}}t} |\psi (\mathbf{x} ,t)|^2 = 0. \end{aligned}$$
(3.9)

Solving (3.9), we find

$$\begin{aligned} |\psi (\mathbf{x} ,t|^2 = |\psi (\mathbf{x} ,t_n|^2, \quad t_n\le t \le t_{n+1}. \end{aligned}$$
(3.10)

Noticing that \(\varphi (\mathbf{x} ,t)\) is obtained from Poisson Eq. (3.2). When \(t \in [t_n, t_{n+1}]\), from Poisson Eq. (3.2) we can find that

$$\begin{aligned} \varphi (\mathbf{x} ,t) = \varphi (\mathbf{x} ,t_n), \quad t_n\le t \le t_{n+1}. \end{aligned}$$
(3.11)

Thus, substituting both (3.10) and (3.11) into (3.5), we obtain

$$\begin{aligned} i\;\partial _t\psi ({\mathbf{x} },t) = [V(\mathbf{x} )+\varphi (\mathbf{x} ,t_n)] \psi (\mathbf{x} ,t) + |\psi (\mathbf{x} ,t_n|^{4/d+2} \psi (\mathbf{x} ,t), \end{aligned}$$
(3.12)

Integrating the Eq. (3.12) from \(t_n\) to \(t_{n+1}\), we find for \(\mathbf{x} \in \Omega \) and \(t_n\le t \le t_{n+1}\)

$$\begin{aligned} \psi (\mathbf{x} ,t)=e^{-i\left( V(\mathbf{x} )+\varphi (\mathbf{x} ,t_n)+|\psi (\mathbf{x} ,t_n)|^{4/d+2} \right) (t-t_n)}\; \psi (\mathbf{x} ,t_n). \end{aligned}$$
(3.13)

In Eq. (3.13), we note that \(\varphi (\mathbf{x} ,t_n)\) satisfies the following Poisson equation

$$\begin{aligned} -\triangle \varphi (\mathbf{x} , t_n) = |\psi (\mathbf{x} ,t_n)|^2-1. \end{aligned}$$
(3.14)

In Step 2, we first discretize the linear Schrödinger Eq. (3.6) with Chebyshev-collocation method, we then solve the resulting discretized system based on technique of matrix diagonalization.

In the next two sections, we show how to apply the Chebyshev-collocation method to solve Poisson Eq. (3.14) and linear Schrödinger Eq. (3.6), respectively. Once we have efficient solvers ready for Poisson equation and linear Schrödinger equation in hand, we can easily extend them to solve the SP system using the above splitting step (3.7).

We remark that the above splitting technique for the SP system (3.1)–(3.2) has only first-order accuracy in time. If we wish to solve the system (3.1)–(3.2) with second-order accuracy in time, we may solve it with the following second-order Strange splitting technique

$$\begin{aligned} \psi (\mathbf{x} , t+\triangle t ) = e^{-i\mathscr {A} \triangle t/2} e^{-i\mathscr {B} \triangle t} e^{-i\mathscr {A} \triangle t/2} \psi (\mathbf{x} , t). \end{aligned}$$
(3.15)

4 The Chebyshev collocation method for Poisson equation

In this section, we show how to use Chebyshev collocation method to discretize the Poisson equation with homogeneous boundary conditions in 1D, 2D and 3D, respectively. We pay attention to how to efficiently solve the resulting discretized system with technique of diagonalization of matrix. Detailed numerical algorithm are provided in 2D and 3D, respectively. We show that the matrix diagonalization procedure can reduce the usual computational cost greatly in 2D and 3D.

4.1 The Chebyshev collocation method

In general, an unknown function u(x) defined on [a, b] can be expanded by Chebyshev polynomials as follows:

$$\begin{aligned} u(x) \approx u_N(x)=\sum _{k=0}^N\hat{u}_k T_k\left( \frac{x-(a+b)/2}{(b-a)/2}\right) , \end{aligned}$$
(4.1)

However, based on Chebyshev collocation spectral methods, for collocation points \(\bar{x}_j=\frac{a+b}{2}+\frac{b-a}{2}x_j\) (with \( x_j=\cos \frac{\pi j}{N}\), \(j=0,\ldots ,N\)), the above expansion can be reformulated into (Canuto et al. 1987)

$$\begin{aligned} u(x) \approx u_N(x)=\sum _{j=0}^N u(\bar{x}_j) h_j\left( \frac{x-(a+b)/2}{(b-a)/2}\right) , \end{aligned}$$
(4.2)

where the polynomial \(h_j(x)\) is defined as

$$\begin{aligned} h_j(x)=\frac{(-1)^{j+1}(1-x^2)T'_N(x)}{\bar{c}_jN^2(x-x_j)}. \end{aligned}$$
(4.3)

From Eq.(4.2), we get the pth derivative

$$\begin{aligned} u_N^{(p)}(x)=\left( \frac{2}{b-a}\right) ^p\sum _{j=0}^N u(\bar{x}_j) h^{(p)}_j\left( \frac{x-(a+b)/2}{(b-a)/2}\right) . \end{aligned}$$
(4.4)

Therefore, the p-th derivative \(u_N(x)\) at grid points \(\bar{x}_i\) is evaluated as

$$\begin{aligned} u_N^{(p)}(\bar{x}_i)=\left( \frac{2}{b-a}\right) ^p \sum _{j=0}^N u(\bar{x}_j) h^{(p)}_j(x_i)=\left( \frac{2}{b-a}\right) ^p \sum _{j=0}^N u(\bar{x}_j) d_{ij}^{(p)}, \end{aligned}$$
(4.5)

for all \(i=0,1,\ldots ,N\). Here we define \(d_{i,j}^{(p)}=h^{(p)}_j(x_i)\). When \(p=2\), \(d_{ij}^{(2)}\) is defined as (Peyret 2002)

$$\begin{aligned} d_{i,j}^{(2)}= & {} \frac{(-1)^{i+j}}{\bar{c}_j}\frac{x^2_j+x_ix_j-2}{(1-x^2_i)(x_i-x_j)^2},1 \nonumber \\&\le i\le N-1,0\le j\le N,i\ne j, \nonumber \\ d_{i,i}^{(2)}= & {} -\frac{(N^2-1)(1-x^2_i)+3}{3(1-x^2_i)^2},1\le i\le N-1, \nonumber \\ d_{0,j}^{(2)}= & {} \frac{2}{3}\frac{(-1)^j}{\bar{c}_j}\frac{(2N^2+1)(1-x_j)-6}{(1-x_j)^2},1\le j\le N, \nonumber \\ d_{N,j}^{(2)}= & {} \frac{2}{3}\frac{(-1)^{j+N}}{\bar{c}_j}\frac{(2N^2+1)(1+x_j)-6}{(1+x_j)^2},1\le j\le N-1, \nonumber \\ d_{0,0}^{(2)}= & {} d_{N,N}^{(2)}=\frac{N^4-1}{15}, \end{aligned}$$
(4.6)

where \(x_j=\cos (\pi j/N)\) (\(0\le j\le N\)). \(\bar{c}_0=\bar{c}_N=2\), \(\bar{c}_j=1\) for \(1\le j\le N-1.\) Hereafter, for shortness, we denote the element of \((N+1)\times (N+1)\) matrix D as

$$\begin{aligned} d_{ij}\equiv d_{i,j}^{(2)},\quad 0\le i,j\le N. \end{aligned}$$
(4.7)

In the following subsection, we applied the Chebyshev-collocation method to solve Poisson equation in 1D, 2D and 3D, respectively.

4.2 Poisson equation in 1D

Let us consider the equation

$$\begin{aligned} -u''= & {} f,\quad a<x<b,\nonumber \\ u(a)= & {} 0, \quad u(b)=0. \end{aligned}$$
(4.8)

If we consider grid points:

$$\begin{aligned} \bar{x}_j=\frac{a+b}{2}+\frac{b-a}{2} \cos \frac{\pi j}{N}, \quad j=0,\ldots ,N, \end{aligned}$$

and assume that

$$\begin{aligned} u(x)\approx u_N(x)=\sum _{m=0}^{N} u(\bar{x}_m) h_m\left( \frac{x-\frac{a+b}{2}}{\frac{b-a}{2}}\right) . \end{aligned}$$
(4.9)

Then, we have

$$\begin{aligned} u''_N(x)=\sum _{m=0}^{N} u(\bar{x}_m) h''_m\left( \frac{x-\frac{a+b}{2}}{\frac{b-a}{2}}\right) . \end{aligned}$$
(4.10)

By setting Eq. (4.8) to be valid at the inner collocation points \(\bar{x}_j,j=1,\ldots ,N-1\), and by adding the boundary conditions, we obtain the collocation equations:

$$\begin{aligned} -u_N''(\bar{x}_j)= & {} f(\bar{x}_j),\quad j=1,\ldots ,N-1, \nonumber \\ u_N(\bar{x}_N)= & {} 0, \nonumber \\ u_N(\bar{x}_0)= & {} 0. \end{aligned}$$
(4.11)

They are equivalent to

$$\begin{aligned} -\gamma \sum _{m=1}^{N-1} u(\bar{x}_j) \left( d_{mj}\right) =f(\bar{x}_j),\; j=1,\ldots ,N-1 , \end{aligned}$$
(4.12)

where the constant \(\gamma =\frac{4}{(b-a)^2}\) and \( d_{mj}=h''_m\left( \frac{\bar{x}_j-\frac{a+b}{2}}{\frac{b-a}{2}}\right) \) (\( m,j=1,\ldots , N-1\)).

From the above system (4.12), we can rewrite it into matrix formulation

$$\begin{aligned} -\gamma DU=F, \end{aligned}$$
(4.13)

where \(U=(u(x_1),\ldots ,u(x_{N-1})^{\text {T}}\), I is the \((N-1)\times (N-1)\) identity matrix, and the \((N-1)\times (N-1)\) matrix \(D=\left( d_{mj}\right) \) (\(1\le m, j\le N-1 \)). From the linear system (4.13), we can easily get the approximation \(U=-(\gamma D)^{-1}F\).

4.3 Poisson equation in 2D

In this subsection, we will present the Chebyshev collocation approximation to the two-dimensional Poisson equation with Dirichlet boundary conditions:

$$\begin{aligned}&-\partial _{xx}u-\partial _{yy}u =f, \quad \mathrm{in} \quad \Omega ,\nonumber \\&u=0, \qquad \quad \mathrm{on} \quad \partial \Omega , \end{aligned}$$
(4.14)

where \(\Omega \) is the square \((a,b)\times (c,d)\). \(\Gamma =\partial \Omega \) is its boundary.

The Chebyshev collocation approximation to the problem makes use of the Gauss-Lobatto mesh \(\bar{\Omega }_N\) defined by

$$\begin{aligned} \bar{x}_j= & {} \frac{a+b}{2}+\frac{b-a}{2}\cos \frac{\pi j}{N_x}, \; j=0,\ldots ,N_x,\\ \bar{y}_k= & {} \frac{c+d}{2}+\frac{d-c}{2}\cos \frac{\pi k}{N_y}, \; k =0,\ldots ,N_y. \end{aligned}$$

Therefore, grid points are defined as (\(\bar{x}_{j},\bar{y}_{k}\)) where \( j=0,1,2,\ldots ,N_x\), \(k=0,1,2,\ldots ,N_y\). In addition, \(u_{jk}\) are denoted as approximation of u(x, y) at grid points, i.e., \(u_{jk}\approx u(\bar{x}_{j},\bar{y}_{k})\).

If we use the spectral collocation methods, then Eq. (4.14) can be approximated by

$$\begin{aligned}&-\left( \partial _{xx}u_N+\partial _{yy}u_N \right) |_{(x,y)=(\bar{x}_j,\bar{y}_k)}=f_{(x,y)=(\bar{x}_j,\bar{y}_k)}, \; 1\le j\le N_x\nonumber \\&\quad -1, 1\le k\le N_y-1, \end{aligned}$$
(4.15)

where

$$\begin{aligned} u_N(x,y)= & {} \sum _{m=0}^{N_x}\sum _{n=0}^{N_y} u(\bar{x}_m,\bar{y}_n) h_m\left( \frac{x-\frac{a+b}{2}}{\frac{b-a}{2}}\right) h_n\left( \frac{y-\frac{c+d}{2}}{\frac{d-c}{2}}\right) . \end{aligned}$$
(4.16)

Furthermore, Eq. (4.15) can be reduced to

$$\begin{aligned}&-\gamma _x \sum _{m=1}^{N_x-1}u_{mk}d^x_{mj}-\gamma _y\sum _{n=1}^{N_y-1}u_{jn}d^y_{nk} =f_{jk},\nonumber \\&\quad j =1,\ldots N_x-1, k=1,\ldots N_y-1. \end{aligned}$$
(4.17)

Here the constants \(\gamma _x=\frac{4}{(b-a)^2}\), \(\gamma _y=\frac{4}{(d-c)^2}\). In addition, let \(D_x=(d^x_{mj})\) and \(D_y=(d^y_{nk})\). They are the matrices of dimension \( ({N}_x-1)\times ({N}_x-1)\), \( ({N}_y-1)\times ({N}_y-1)\), respectively.

$$\begin{aligned} U=\left( \begin{array}{c} U_{11}, U_{12} , \ldots U_{1,N_y-1}, f_{21}, \ldots f_{2,N_y-1}, \ldots f_{N_x-1,1}, \ldots f_{N_x-1,N_y-1} \end{array} \right) ^{T} \end{aligned}$$
(4.18)

and

$$\begin{aligned} F=\left( \begin{array}{c} F_{11}, F_{12} , \ldots F_{1,N_y-1}, F_{21}, \ldots F_{2,N_y-1}, \ldots F_{N_x-1,1}, \ldots F_{N_x-1,N_y-1} \end{array} \right) ^{T}. \end{aligned}$$
(4.19)

By means of tensor product \(\bigotimes \), Eq. (4.17) can be reformulated into

$$\begin{aligned} - \left( \gamma _x D_x\bigotimes I_y + \gamma _y I_x \bigotimes D_y \right) U =F. \end{aligned}$$
(4.20)

where \(I_x\) and \(I_y\) are the identity matrices of dimension \( ({N}_x-1)\times ({N}_x-1)\), \( ({N}_y-1)\times ({N}_y-1)\), respectively.

However, the above linear system (4.20) becomes extremely large when grid numbers \(N_x\) and \(N_y\) grow large. In such case, one does not seek to solve the linear system (4.20) directly as the computation cost is unendurable. In the following, we first rewrite Eq. (4.17) into

$$\begin{aligned} -\gamma _x D_xU- \gamma _yUD_y^{\text {T}}=F, \end{aligned}$$
(4.21)

where U is the matrix of dimension \( ({N}_x-1)\times ({N}_y-1)\) made with the inner unknowns, that is,

$$\begin{aligned} U=\left( u(\bar{x}_j,\bar{y}_k)\right) ,\quad j=1,\ldots ,{N}_x-1, k=1,\ldots ,{N}_y-1. \end{aligned}$$
(4.22)

Here, using the technique of diagonalization of matrix, we can reduce the system (4.21) to a sequence of uncoupled equations. In fact, it is possible to rewrite \(D_x\) and \(D_y\) as

$$\begin{aligned} D_x=P\Lambda _xP^{-1},\quad D_y=Q\Lambda _yQ^{-1} \end{aligned}$$
(4.23)

where \(\Lambda _x,\Lambda _y\) are composed by the eigenvalues of \(D_x,D_y\) respectively; while P, Q are composed by the eigenvectors of \(D_x,D_y\), respectively. then we have

$$\begin{aligned} -\gamma _x\Lambda _x \tilde{U}-\gamma _y\tilde{U}D_y^{\text {T}}=\tilde{H}, \end{aligned}$$
(4.24)

where \(\tilde{U}=P^{-1}U, \tilde{H}=P^{-1}H\). we can also have if introduce \(\hat{U}=\tilde{U}(Q^{\text {T}})^{-1}\), \(\hat{H}=\tilde{H}(Q^{\text {T}})^{-1}\):

$$\begin{aligned} -\gamma _x\Lambda _x \hat{U}-\gamma _y\hat{U}\Lambda _y=\hat{H}. \end{aligned}$$
(4.25)

Therefore, if we define matrices \(\hat{U}=\left( \hat{u}_{j,k}\right) \), \(\hat{H}=\left( \hat{h}_{j,k}\right) \), \(\Lambda _x={\text {diag}}\) \((\lambda _{x,j}\), \(j=1,2\),\(\ldots , N_x-1)\), \(\Lambda _y={\text {diag}} \left( \lambda _{y,k},,k=1,2,\ldots , N_y-1\right) \), then Eq. (4.25) simply gives

$$\begin{aligned} \hat{u}_{j,k}=-\frac{\hat{h}_{j,k}}{\gamma _x\lambda _{x,j}+\gamma _y\lambda _{y,k}} \end{aligned}$$
(4.26)

for \(j=1,\ldots ,\bar{N}_x, k=1,\ldots ,\bar{N}_y\) (where \(\bar{N}_x={N}_x-1\),\(\bar{N}_y={N}_y-1\)). Finally, we can get the following algorithm for solving (4.14):

  1. (1)

    Do the factorization \(D_x=P\Lambda _xP^{-1}\), \(D_y=Q\Lambda _xQ^{-1}\);

  2. (2)

    Let \(H=\left( \begin{array}{llll} f(x_1,y_1) &{} f(x_1,y_2) &{} \cdots &{} f(x_1,y_{\bar{N}_y}) \\ f(x_2,y_1) &{} f(x_2,y_2) &{} \cdots &{} f(x_2,y_{\bar{N}_y}) \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ f(x_{\bar{N}_x},y_1) &{} f(x_{\bar{N}_x},y_2) &{} \cdots &{} f(x_{\bar{N}_x},y_{\bar{N}_y}) \end{array} \right) .\)

  3. (3)

    Compute \(\hat{H}=P^{-1}H(Q^{\text {T}})^{-1}\);

  4. (4)

    Calculate \(\hat{U}\) from Eq. (4.26);

  5. (5)

    Get the approximation \(U=P\hat{U}Q^{\text {T}}\).

In the case that \(N_x=N_y\equiv N\), the above algorithm will need \(O(N^3)\) operations, while solving the linear system (4.20) directly usually need \(O(N^4)\) operations.

4.4 Poisson equation in 3D

In this section, we will take the Chebyshev collocation approximation to the three-dimensional Poisson equation with Dirichlet boundary conditions:

$$\begin{aligned}&-\partial _{xx}u-\partial _{yy}u-\partial _{zz}u =f, \quad \mathrm{in} \quad \Omega , \end{aligned}$$
(4.27)
$$\begin{aligned}&u =0 \quad \mathrm{on} \quad \partial \Omega , \end{aligned}$$
(4.28)

where \(\Omega \) is the square \((a,b)\times (c,d)\times (e,f)\). \(\Gamma =\partial \Omega \) is its boundary.

The Chebyshev collocation approximation to the problem takes the Gauss–Lobatto mesh \(\bar{\Omega }_N\) defined by

$$\begin{aligned}&\bar{x}_j=\frac{a+b}{2}+\frac{b-a}{2}\cos \frac{\pi j}{N_x}, \quad j=0,\ldots ,N_x, \\&\bar{y}_k=\frac{c+d}{2}+\frac{d-c}{2}\cos \frac{\pi k}{N_y}, \quad k=0,\ldots ,N_y, \\&\bar{z}_l=\frac{e+f}{2}+\frac{f-e}{2}\cos \frac{\pi l}{N_z}, \quad l=0,\ldots ,N_z. \end{aligned}$$

As previously, we denote \(\Omega _N\) the open discretized domain. The inner grid points considered are \(\{\bar{x}_j,\bar{y}_k,\bar{z}_l|j=1,\ldots ,\bar{N}_x,k=1,\ldots ,\bar{N}_y,l=1,\ldots ,N_z \}\), where \(\bar{N}_x=N_x-1\), \(\bar{N}_y=N_y-1\), \(\bar{N}_z=N_z-1\).

The solution of (4.27)–(4.28) is approximated with the polynomial \(u_N(x,y,z)\) of degree at most equal to \(N_x\), \(N_y\), and \(N_z\), in the x-, y-, z-directions, respectively. If we use the spectral collocation methods, then Eq. (4.27) can be approximated by

$$\begin{aligned}&-\left( \partial _{xx}u_N+\partial _{yy}u_N+\partial _{zz}u_N \right) |_{(x,y,z)=(\bar{x}_j,\bar{y}_k,\bar{z}_l)}\nonumber \\&\quad =f_{(x,y,z) =(\bar{x}_j,\bar{y}_k,\bar{z}_l)}, 1\le j\le N_x-1, 1\le k\le N_y-1, 1\le l \le N_z-1, \end{aligned}$$
(4.29)

where

$$\begin{aligned}&u_N(x,y,z) \nonumber \\&\quad =\sum _{m=0}^{N_x}\sum _{n=0}^{N_y}\sum _{p=0}^{N_z} u(\bar{x}_m,\bar{y}_n,\bar{z}_p) h_m\left( \frac{x-\frac{a+b}{2}}{\frac{b-a}{2}}\right) h_n\left( \frac{x-\frac{c+d}{2}}{\frac{d-c}{2}}\right) h_p\left( \frac{z-\frac{e+f}{2}}{\frac{f-e}{2}}\right) . \end{aligned}$$

The derivatives are approximated with the usual expressions. First, the Eq. (4.27) are forced to be satisfied by the polynomial \(u_N(x,y,z)\) at every inner collocation point \((\bar{x}_j, \bar{y}_k, \bar{z}_l)\in \Omega _N \). The boundary condition (4.28) is prescribed to zero at every outer collocation points \((\bar{x}_j,\bar{y}_k,\bar{z}_l)\). We may also write the resulting algebraic system under the tensor product form:

$$\begin{aligned} -\left( \gamma _x I_z \bigotimes I_y \bigotimes D_x + \gamma _y I_z \bigotimes D_y \bigotimes I_x+ \gamma _z D_z \bigotimes I_y \bigotimes D_x \right) V=H\qquad \end{aligned}$$
(4.30)

where V is the column vector of inner unknowns ordered by row and horizontal section. More precisely, here, we first introduce the \(\bar{N}_x\)-component vector \(V_{j,k}\):

$$\begin{aligned} V_{k,l}=\left( u_N(\bar{x}_1,\bar{y}_k,\bar{z}_l),\ldots ,u_N(\bar{x}_{\bar{N}_x}, \bar{y}_k,\bar{z}_l)\right) ^{\text {T}}, \end{aligned}$$
(4.31)

for \(k=1,\ldots ,\bar{N}_y\), \(l=1,\ldots ,\bar{N}_z\). secondly we define the \(\bar{N}_x\bar{N}_y\)-component vector \(V_k\) by

$$\begin{aligned} V_l=(V_{1,l},\ldots ,V_{\bar{N}_y,l})^{\text {T}},\quad l=1,\ldots ,\bar{N}_z, \end{aligned}$$
(4.32)

and finally, V is the \(\bar{N}_x\bar{N}_y\bar{N}_z\)-component vector \(V_k\) by

$$\begin{aligned} V_l=(V_{1},\ldots ,V_{\bar{N}_z})^{\text {T}},\quad l=1,\ldots ,\bar{N}_z, \end{aligned}$$
(4.33)

\(D_x\), \(D_y\), \(D_z\) are square matrices of dimensions \(\bar{N}_x\times \bar{N}_x\),\(\bar{N}_y\times \bar{N}_y\), \(\bar{N}_z\times \bar{N}_z\), respectively, analogously to the matrix D defined in the one-dimension case; \(I_x\), \(I_y\), \(I_z\) are identity matrices in the x-, y- and z-directions having the same dimensions as \(D_x\), \(D_y\), \(D_z\). Lastly, H is the \(\bar{N}_x\bar{N}_y\bar{N}_z\)-component vector constructed in the same way as V, but with component \(h_{i,j,k}\) calculated from the inner values of function f and the values of function g.

As we can see from the resulting linear system (4.30), generally there will have a very large system \(AV=B\) to be solved. For the larger system, often direct solution methods will not be recommended when they are too costly, i.e., concerning computing time or memory requirements. Iterative procedures constitute an alternative to direct methods, especially in three-dimensional problems. Some usual iterative methods are discussed for the solution of linear algebraic systems arising from Chebyshev collocation approximations (Canuto et al. 1987).

We use the technique of diagonalization of matrix again to reduce the overall computation cost. In fact, Eq. (4.29) can be written as

$$\begin{aligned}&-\gamma _x\sum _{m=1}^{\bar{N}_x}u(x_m,y_k,z_l)d_{mj}-\gamma _y\sum _{n=1}^{\bar{N}_y}u(x_j,y_n,z_l)d_{nk}-\gamma _z\sum _{p=1}^{\bar{N}_z}u(x_j,y_k,z_p)d_{pl} \nonumber \\&\qquad =f_{jkl},\quad 1\le j \le \bar{N}_x, 1 \le k \le \bar{N}_y, 1\le l \le \bar{N}_z, \end{aligned}$$
(4.34)

where \(\gamma _z=\frac{4}{(f-e)^2}\).

For shortness, in the following, we assume that \(N_x=N_y=N_z=N\) and use repeated summation or Einstein summation (Shen 2006) and the above system can be reduced to

$$\begin{aligned} -\gamma _x u_{mkl}d_{mj}-\gamma _y u_{jnl}d_{nk}- \gamma _z u_{jkp}d_{pl}=f_{jkl}, \quad j,k,l=1,\ldots ,N-1, \end{aligned}$$
(4.35)

In addition, for \(D=(d_{mj}),j,m=1,\ldots ,N-1\), we have \(D=P\Lambda P^{-1}\) or \(DP=P\Lambda \) or \(d_{mj}e_{jq}=\lambda _qe_{jq}\) and \(e_{jq}e_{jp}=\delta _{qp}\). If setting

$$\begin{aligned} u_{mkl}= & {} e_{mq}v_{qkl}, \end{aligned}$$
(4.36)
$$\begin{aligned} f_{jkl}= & {} e_{jq}F_{qkl}, \end{aligned}$$
(4.37)

then we can obtain from Eq. (4.35)

$$\begin{aligned} \gamma _x e_{mq}v_{qkl}d_{mj}+\gamma _y e_{jq}v_{qnl}d_{nk}+\gamma _z e_{jq}v_{qkp}d_{pl}=e_{jq}F_{qkl}. \end{aligned}$$
(4.38)

Multiplying the above equation by \(e_{jq}\) gives

$$\begin{aligned}&-\gamma _x v_{qkl}\lambda _q - \gamma _y v_{qnp}d_{nk}- \gamma _z v_{qnp}d_{pl}={v}_{qkl},\quad i,j,k,q=1,\ldots ,N-1, \nonumber \\&\quad -\gamma _x\lambda _q v^q-\gamma _y v^qD-\gamma _z Dv^q=F^q, \end{aligned}$$
(4.39)

where \(v^q=(v_{qjk})\), \(F^q=(F_{qkl}),j,k=1,\ldots ,N-1. \)

For fixed q, the structure of Eq. (4.39) is similar to those of Eq. (4.21). Thus, we can get get an efficient solver. The full algorithm for the problem (4.27) is summarized as follows:

  1. (1)

    Do pre-processing, compute the eigenvalues and eigenvector of D and get \( D=P\Lambda P^{-1} \) with \(\Lambda =diag(\lambda _1,\lambda _2,\ldots ,\lambda _{N-1})\) and \(D=(e_{nl}) ,n,l=1,\ldots ,N-1 \);

  2. (2)

    Compute \(F_{qkl}=e_{jq}f_{qkl}\) for all \(j,k,l,q=1,\ldots ,N-1\);

  3. (3)

    Obtain \(v^q\) from Eq. (4.39);

  4. (4)

    Set \(u_{jkl}=e_{jq}v_{qkl}\) for all \(j,k,l,q=1,\ldots ,N-1.\)

In the case that \(N_x=N_y=N_z\equiv N\), we remark that the above algorithm takes about \(O(N^4)\) operations. In fact, in step (2), it takes about \(2N^4\) operations. The step (1) and (3) take \(2N^4\) operations. Moreover, in (4.39) we only need to solve \(N-1\) two-dimensional equations of the form [see Eq. (4.21) for reference]. However, solving the linear system (4.30) directly usually need \(O(N^6)\) operations.

5 The Chebyshev collocation method for linear Schrödinger equation

In this section, we present the detailed algorithm on the Chebyshev collocation method for solving the linear Schrödinger equation in 1D, 2D and 3D, respectively.

5.1 Schrödinger equation in 1D

In 1D, we are going to solve the following one-dimentional Schrödinger equation with the chebyshev-collocation method

$$\begin{aligned} i \frac{\partial \psi }{\partial t}=- \frac{1}{2} \frac{\partial ^2 \psi }{\partial x^2}, \quad a<x<b, t>0, \end{aligned}$$
(5.1)

along with homogeneous boundary conditions and given initial data. We assume the expansion

$$\begin{aligned} \psi \left( x,t \right) =\sum _{j=1}^{N-1}\psi \left( \bar{x}_j,t \right) h_j\left( \frac{x-\frac{a+b}{2}}{\frac{b-a}{2}}\right) . \end{aligned}$$
(5.2)

Plugging Eq. (5.2) into Eq. (5.1), we get

$$\begin{aligned} i \sum _{j=1}^{N-1} \psi _t(\bar{x}_j,t)h_j(x)=-\frac{1}{2}\sum _{j=1}^{N-1}\psi (\bar{x}_j,t)h''_j\left( \frac{x-\frac{a+b}{2}}{\frac{b-a}{2}}\right) . \end{aligned}$$
(5.3)

In Eq. (5.3), if we let Eq. (5.3) is exact at \(x=\bar{x}_k, k=1,\ldots ,N-1\), we obtain

$$\begin{aligned} i \psi _t(\bar{x}_k,t)=-\frac{\gamma }{2}\sum _{j=1}^{N-1}\psi (\bar{x}_j,t)h''_j\left( \frac{\bar{x}_k-\frac{a+b}{2}}{\frac{b-a}{2}}\right) ,\quad k=1,\ldots ,N-1. \end{aligned}$$
(5.4)

Equation (5.4) can be reformulated into the following matrix form

$$\begin{aligned} i \partial _t U=-\frac{\gamma }{2} D U, \end{aligned}$$
(5.5)

where we define \(U=U(t)=(\psi (x_1,t),\psi (x_2,t),\ldots ,\psi (x_{N-1},t))\) and D is defined in (4.7). Since D can be factorized into \(D=P \Lambda P^{-1}\), Eq. (5.5) can then be rewritten as

$$\begin{aligned} i\partial _tU= & {} -\frac{\gamma }{2}P\Lambda P^{-1}U,\\ i P^{-1}\partial _tU= & {} -\frac{\gamma }{2}\Lambda P^{-1} U,\\ i\partial _t{P^{-1}U}= & {} -\frac{\gamma }{2}\Lambda P^{-1} U. \end{aligned}$$

If we let \(\tilde{U}=P^{-1}U\), then we get

$$\begin{aligned} i\partial _t\tilde{U}=-\frac{\gamma }{2}\Lambda \tilde{U}. \end{aligned}$$
(5.6)

Noticing that the diagonal matrix \(\Lambda ={\text {diag}}(\lambda _1,\lambda _2,\ldots ,\lambda _{N-1})\), we find

$$\begin{aligned} i\partial _t\tilde{U}_j(t)=-\frac{\gamma }{2}\lambda _j\tilde{U}_j(t),\quad j=1,\ldots ,N-1, \end{aligned}$$
(5.7)

where \(\tilde{U}=P^{-1}U=(\tilde{U}_1(t),\tilde{U}_2(t),\ldots ,\tilde{U}_N(t))^{\text {T}}\).

Solving (5.7) gives us

$$\begin{aligned} \tilde{U}_j(t+\triangle t)=e^{i \frac{\gamma }{2}\lambda _j\triangle t}\tilde{U}_j(t),\quad j=1,\ldots ,N-1, \end{aligned}$$
(5.8)

So

$$\begin{aligned} \tilde{U}_j(t_{n+1})=e^{i \frac{\gamma }{2}\lambda _j\triangle t}\tilde{U}_j(t_n),\quad j=1,\ldots ,N-1, \end{aligned}$$
(5.9)

where \(t_n=n\triangle t, n=0,1,\ldots ,M\) with \(\triangle t =\frac{T}{M}\).

Then, we get the following algorithm for solving the Schrödinger equation (5.1):

  1. (1)

    Do the factorization \(D=P\Lambda P^{-1}\). Let \(n=0\);

  2. (2)

    Compute \(\tilde{U}(t_n)=P^{-1}U(t_n)\);

  3. (3)

    Calculate \(\tilde{U}_j(t_{n+1})=e^{i \frac{\gamma }{2}\lambda _j\triangle t}\tilde{U}_j(t_n),j=1,\ldots ,N-1\);

  4. (4)

    Get \(U(t_{n+1})=P\tilde{U}(t_{n+1})\);

  5. (5)

    Let \(n=n+1\) and repeat steps (2)–(4) until \(n=M\) ( the final time step).

5.2 Schrödinger equation in 2D

In 2D, we solve the following linear Schrödinger equation

$$\begin{aligned} i\frac{\partial \psi }{\partial t}=-\frac{1}{2}(\partial _{xx}+\partial _{yy}) \psi , \quad (x,y)\in \Omega , t>0. \end{aligned}$$
(5.10)

According to the Chebyshev-collocation method, we have the expansion

$$\begin{aligned} \psi (x,y,t)\approx \psi _N(x,y,t)=\sum _{m=0}^{N_x}\sum _{n=0}^{N_y} \psi (\bar{x}_m,\bar{y}_n,t) h_m\left( \frac{x-\frac{a+b}{2}}{\frac{b-a}{2}}\right) h_n\left( \frac{y-\frac{c+d}{2}}{\frac{d-c}{2}}\right) .\qquad \quad \end{aligned}$$
(5.11)

Then, Eq. (5.10) can be discretized as

$$\begin{aligned} \frac{\partial }{\partial t}U=-\frac{1}{2}\left( \gamma _x D_xU+\gamma _y UD_y^{\text {T}}\right) . \end{aligned}$$
(5.12)

Because we can do matrix factorization as follows:

$$\begin{aligned} D_x= & {} P\Lambda _xP^{-1},\\ D_y= & {} Q \Lambda _y Q^{-1}, \end{aligned}$$

we find

$$\begin{aligned} i\frac{\partial }{\partial t} U=-\frac{1}{2}[\gamma _x P\Lambda _xP^{-1}U+\gamma _y U(Q \Lambda _y Q^{-1})^{\text {T}}], \end{aligned}$$
(5.13)

where we define \((N_x-1)\times (N_y-1)\) matrix \(U=(u_{jk}(t))\). Multiplying the above equation with matrices \(P^{-1}\) and \((Q^{\text {T}})^{-1}\), we get

$$\begin{aligned} i\frac{\partial }{\partial t} \left( P^{-1}U(Q^{\text {T}})^{-1} \right) =-\frac{\gamma _x}{2}\Lambda _x(P^{-1}U(Q^{\text {T}})^{-1})-\frac{\gamma _y}{2} P^{-1}U(Q^{\text {T}})^{-1}\Lambda _y. \end{aligned}$$

If we define an \((N_x-1)\times (N_y-1)\) matrix \(\tilde{U}\) and let \(\tilde{U}=P^{-1}U(Q^{\text {T}})^{-1}\), then

$$\begin{aligned} i\frac{\partial }{\partial t}\tilde{U}= -\frac{1}{2}(\gamma _x\Lambda _x\tilde{U}+\gamma _y\tilde{U}\Lambda _y), \end{aligned}$$

i.e.,

$$\begin{aligned} i\frac{\partial }{\partial t}\tilde{u}_{jk}= -\frac{1}{2}(\gamma _x\lambda _{xj}+\gamma _y\lambda _{yk})\tilde{u}_{jk}, \end{aligned}$$
(5.14)

for all j, k. Solving the above equation over \([t_n,t_{n+1}\) gives us immediately

$$\begin{aligned} \tilde{u}_{jk}(t_{n+1})=e^{\frac{i}{2}(\gamma _x\lambda _{xj}+\gamma _y\lambda _{yk})\triangle t}\tilde{u}_{jk}(t_n). \end{aligned}$$
(5.15)

Finally, we get the following algorithm for solving Schrödinger equation (5.10):

  1. (1)

    Find matrices \(P,\Lambda _x, Q,\Lambda _y \) such that \(D_x=P\Lambda _xP^{-1}\), \(D_y=Q\Lambda _yQ^{-1}\). Starting \(n=0\);

  2. (2)

    Compute

    $$\begin{aligned} U(t_n)=\left( \begin{array}{llll} u(x_1,y_1,t_n) &{} u(x_1,y_2,t_n) &{} \cdots &{} u(x_1,y_{N_y-1},t_n) \\ u(x_2,y_1,t_n) &{} u(x_2,y_2,t_n) &{} \cdots &{} u(x_2,y_{N_y-1},t_n) \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ u(x_{N_x-1},y_1,t_n) &{} u(x_{N_x-1},y_2,t_n) &{} \cdots &{} u(x_{N_x-1},y_{N_y-1},t_n) \end{array} \right) ; \end{aligned}$$
  3. (3)

    Evaluate \(\tilde{U}(t_n)=P^{-1}U(t_n)(Q^{\text {T}})^{-1}\);

  4. (4)

    Calculate \(\tilde{u}_{jk}(t_{n+1})=e^{\frac{i}{2}(\gamma _x\lambda _{xj}+\gamma _y\lambda _{yk})\triangle t}\tilde{u}_{jk}(t_n)\), \(j=1,\ldots ,N_x-1\), \(k=1,\ldots ,N_y-1 \).

  5. (5)

    Compute \(U(t_{n+1})=P\tilde{U}(t_{n+1})Q^{\text {T}} \);

  6. (6)

    Let \(n=n+1\) and repeat steps (3)–(5) until \(n=M\) (the final time step).

5.3 Schrödinger equation in 3D

In 3D, we solve the following linear Schrödinger equation

$$\begin{aligned} i\frac{\partial \psi }{\partial t}=-\frac{1}{2}(\partial _{xx}+\partial _{yy}+\partial _{zz}) \psi , \quad (x,y,z)\in \Omega , t>0 . \end{aligned}$$
(5.16)

According to the Chebyshev-collocation method, we have the expansion

$$\begin{aligned} \psi (x,y,z,t)&\approx \psi _N(x,y,z,t) \sum _{m=0}^{N_x}\sum _{n=0}^{N_y}\sum _{p=0}^{N_z} h_m \psi (\bar{x}_m,\bar{y}_n,\bar{z}_p,t)\nonumber \\&\qquad \left( \frac{x-\frac{a+b}{2}}{\frac{b-a}{2}}\right) h_n\left( \frac{y-\frac{c+d}{2}}{\frac{d-c}{2}}\right) h_l\left( \frac{z-\frac{e+f}{2}}{\frac{f-e}{2}}\right) . \end{aligned}$$

Plugging the above equation into Eq. (5.16), we get

$$\begin{aligned} \partial _t \psi _{jkl}=-\frac{1}{2} \left( \gamma _x \psi _{mkl}d_{mj}+\gamma _y \psi _{jnl}d_{nk}+ \gamma _z \psi _{jkp}d_{pl}\right) , \end{aligned}$$
(5.17)

where repeated index is assumed and \(\psi _{jkl}=\psi _{jkl}(t)\) is defined as the approximation of \(\psi (x,y,z,t)\) at grid points \((\bar{x}_j,\bar{y}_k,\bar{z}_l,t)\). \(\psi ^n_{jkl}=\psi _{jkl}(t)\) is defined as the approximation of \(\psi (x,y,z,t)\) at grid points \((\bar{x}_j,\bar{y}_k,\bar{z}_l,t_n)\)

For shortness, we assume that \(N_x=N_y=N_z=N\) and use repeated summation in the following discussion. If we let

$$\begin{aligned} \psi _{mkl}=e_{mq}V_{qkl}, \end{aligned}$$
(5.18)

similarly we reduce Eq. (5.17) into

$$\begin{aligned} i \partial _t V^q=-\frac{1}{2}\left( \gamma _x\lambda _q v^q+\gamma _y v^qD+\gamma _z Dv^q \right) ,\quad q=1,2,\ldots ,N-1, \end{aligned}$$
(5.19)

where the matrix \(V^q=(\psi _{qkl})\). We are now faced with \(N_x-1\) decoupled equations whose structure is similar to Eq. (5.13). Thus, we again use the technique of matrix diagonalization which have been used to solve Eq. (5.13) efficiently. Finally, we can get a more efficient algorithm for the Eq. (5.16):

  1. (1)

    Starting from \(n=0\). Find matrices D and \(\Lambda \) such that \( D=P\Lambda P^{-1} \) with \(\Lambda ={\text {diag}}(\lambda _1,\lambda _2,\ldots ,\lambda _{N-1})\) and \(D=(e_{nl}) ,n,l=1,\ldots ,N-1. \)

  2. (2)

    Set \(V_{jkl}=(e_{jq}\psi ^n_{qkl})\) for all \(j,k,l=1,\ldots ,N-1\);

  3. (3)

    Obtain \(V^q(t_{n+1})\) from \(V^q(t_{n})\) by solving Eq. (5.19) using the similar algorithm provided in Sect. 5.2.

  4. (4)

    Compute \(\psi ^{n+1}_{jkl}=e_{jq}V^n_{qkl}\) for all \(j,k,l=1,\ldots ,N-1\);

  5. (5)

    Let \(n=n+1\) and repeat steps (2)–(4) until \(n=M\) (the final time step).

6 Stability analysis of the splitting Chebyshev-collocation method for the SP system

In Sect. 3, we gave the general idea of the first-order splitting method (3.7) on how to solve the SP system (2.10)–(2.11). In the numerical procedure, the key step to solve the SP system (2.10)–(2.11) from \(t_n\) to \(t_{n+1}\) is solving both Poisson equation and time-dependent linear Schrödinger equation. We now have efficient numerical algorithms ready for both the Poisson equation and the linear Schrödinger equation (presented in Sects. 4 and 5, respectively), thus it is easy for us to extend them to solve the SP system (2.10)–(2.11) numerically. We now give stability analysis of the presented splitting Chebyshev-collocation method in 1D, we note that stability analysis of the proposed method for the higher-dimensional SP system is similar.

Lemma 6.1

If we define the discrete weighted \(L^2\) norm at time \(t_n\) as \(||\Psi ^n||=\sqrt{\frac{(b-a)\pi }{2N} \sum _{j=1}^{N-1}|\psi (x_j,t_n)|^2}\), then we have

$$\begin{aligned} ||\Psi ^{n+1}|| = ||\Psi ^{n}||. \end{aligned}$$
(6.1)

Proof 6.1

Starting from the continuous weighted norm

$$\begin{aligned} ||\psi (t)||_w=\sqrt{\int _a^b |\psi (x,t)|^2 \omega (x) {\text {d}}x} \end{aligned}$$
(6.2)

where the weighted function \(\omega (x)=1/\sqrt{1-x^2}\) and discretizing it with the Chebyshev–Gauss–Lobatto quadrature, we get

$$\begin{aligned} ||\psi (t)||_w\approx & {} \sqrt{\frac{(b-a)\pi }{2N} \sum _{j=0}^{N}|\psi (x_j,t_n)|^2 w_j},\nonumber \\= & {} \sqrt{\frac{(b-a)\pi }{2N} \sum _{j=1}^{N-1}|\psi (x_j,t_n)|^2} \end{aligned}$$

where \(w_j=\left\{ \begin{array}{cc} \frac{\pi }{2N} &{} j=0\; \mathrm{or } \; N \\ \frac{\pi }{2N} &{} 1\le j \le N-1 \end{array} \right. \). The derivation gives us the reason why we define the discrete weighted \(L^2\) norm (6.2).

In the first step of splitting step (3.7), we solve the nonlinear equation exactly, i.e.,

$$\begin{aligned} \psi ^{n+1}_j = \psi ^{n}_je^{-i \triangle t(V(x_j)+\phi _j^n+\beta |\psi ^{n}_j|^2)}. \end{aligned}$$

It is obvious to see that \(||\psi ^{n+1}||_w\) is equal to \(||\psi ^{n}||_w\) in this step.

In the second step of splitting step (3.7), i.e., solving the linear Schrödinger equation with Chebyshev-collocation method, we need to solve from \(t_n\) to \(t_{n+1}\)

$$\begin{aligned} i \partial _t U = -\frac{\gamma }{2} D U. \end{aligned}$$

From which, we find \(U(t_{n+1})=P \Theta P^{-1} U(t_{n})\) where the diagonal matrix \(\Theta =diag\left( e^{-\frac{\gamma \lambda _1 \triangle t }{2}}, \ldots , e^{-\frac{\gamma \lambda _N \triangle t }{2}} \right) \).

Hence we get

$$\begin{aligned} \overline{U(t_{n+1})}^{\text {T}} U(t_{n+1})= & {} \overline{ P \Theta P^{-1} U(t_{n})}^{\text {T}} P \Theta P^{-1} U(t_{n})\nonumber \\= & {} \overline{ U(t_{n})}^{\text {T}} \overline{P^{-1}} \overline{ \Theta }^{\text {T}} \overline{P}^{\text {T}} P \Theta P^{-1} U(t_{n}) \nonumber \\= & {} \overline{ U(t_{n})}^{\text {T}} U(t_{n}) \end{aligned}$$
(6.3)

From Eq. (6.3) , we immediately get Eq. (6.1), which concludes our proof. \(\square \)

From this lemma, we find that the proposed method is unconditionally stable.

7 Numerical results

In this section, we first test numerical accuracy of the proposed Chebyshev collocation method for Poisson equation in 1D, 2D, and 3D, respectively. We next test numerical accuracy of the proposed Chebyshev-collocation method for the linear Schrödinger equation in 1D, 2D, and 3D, respectively. Finally, we apply the newly proposed splitting Chebyshev-collocation method to solve the SP system.

7.1 Numerical results for Poisson equation

We first consider

$$\begin{aligned} -\,u''(x)= & {} 2, \; x\in (-1,1), \nonumber \\ u(-1)= & {} u(1)=0, \end{aligned}$$

where the one-dimensional Poisson equation admits an exact solution \(u(x) = 1-x^2\). We solve the equation with our proposed algorithm presented in Sect. 4. Table 1 shows us the numerical accuracy test.

Table 1 Error analysis for the one-dimensional Poisson equation by Chebyshev-collocation method
Full size table

We next consider

$$\begin{aligned} -\,[u_{xx}+u_{yy}]&=2(-x^2+1)+2(-y^2+1), \; (x,y)\in \Omega \nonumber \\&=(-1,1)^2, u=0, \quad (x,y)\in \partial \Omega , \end{aligned}$$

where the two-dimensional Poisson equation admits an exact solution \(u(x,y)=(1-x^2)(1-y^2)\). We solve the equation with our proposed algorithm presented in Sect. 4. Table 2 shows us the numerical accuracy test.

Table 2 Error analysis for the two-dimensional Poisson equation by Chebyshev-collocation method
Full size table

We finally consider

$$\begin{aligned} -\,[u_{xx}+u_{yy}+u_{zz}]= & {} f(x,y,z), \; (x,y,z)\in \Omega \nonumber \\&=(-1,1)^3, u=0, \quad (x,y,z)\in \partial \Omega , \end{aligned}$$

where \(f(x,y,z)=-\,2[(1-y^2)(1-z^2)+(1-x^2)(1-z^2)+(1-x^2)(1-y^2)]\), the three-dimensional Poisson equation admits an exact solution \(u(x,y,z)=(1-x^2)(1-y^2)(1-z^2)\). We solve the equation with our proposed algorithm presented in Sect. 4. Table 3 shows us the numerical accuracy test.

Table 3 Error analysis for the three-dimensional Poisson equation by Chebyshev-collocation method
Full size table

Tables 1, 2 and 3 show us that the proposed Chebyshev-collocation method for Poisson equation has spectral accuracy.

7.2 Numerical results for the linear Schrödinger equation

In the first example, we consider one-dimensional problem with zero Dirichlet boundary conditions

$$\begin{aligned} \left\{ \begin{array}{ll} i \psi _t = -\frac{1}{2}\psi _{xx}, &{}\quad -12< x < 12, t>0 \\ \psi (-12,t)= \psi (12,t)=0, &{}\quad t\ge 0 . \end{array}\right. \end{aligned}$$

where the exact solution to problem is

$$\begin{aligned}\psi _{exact}(x,t)= (2.0/\pi )^{1/4}\sqrt{i/(-4t+i)} e^{(-2i x^2/(-4 t+i))}.\end{aligned}$$

Numerical result at time \(t=1\) is shown in Table 4.

Table 4 Error analysis for the Chebyshev-collocation method in solving the one-dimensional Schrödinger equation
Full size table

In the second example, we consider the two-dimensional problem with zero Dirichlet boundary conditions

$$\begin{aligned} \left\{ \begin{array}{ll} i \psi _t = -\frac{1}{2}\psi _{xx}-\frac{1}{2}\psi _{yy}, &{}\quad -12< x,y < 12, t>0 \\ \psi (-12,y,t)= \psi (12,y,t)=0, &{}\quad t\ge 0 ,\\ \psi (x,-12,t)= \psi (x,12,t)=0, &{}\quad t\ge 0 ,\end{array} \right. \end{aligned}$$

where the exact solution to this problem is

$$\begin{aligned}\psi _{\text {exact}}(x,y,t)=(2.0/\pi )^{1/2}i/(-4t+i) e^{(-2i (x^2+y^2)/(-4 t+i))}.\end{aligned}$$

Numerical result at time \(t=1\) is shown in Table 5.

Table 5 Error analysis for the Chebyshev-collocation method in solving the two-dimensional Schrödinger equation
Full size table

In the third example, we consider the three-dimensional problem with zero Dirichlet boundary conditions

$$\begin{aligned} \left\{ \begin{array}{ll} i \psi _t = -\frac{1}{2}\psi _{xx}-\frac{1}{2}\psi _{yy}-\frac{1}{2}\psi _{zz}, &{}\quad -6< x,y,z < 6, \; t>0 \\ \psi (-6,y,z,t)= \psi (6,y,z,t)=0,&{}\quad t\ge 0 , \\ \psi (x,-6,z,t)= \psi (x,6,z,t)=0,&{}\quad t\ge 0 \\ \psi (x,y,-6,t)= \psi (x,y,6,t)=0, &{}\quad t\ge 0, \end{array} \right. \end{aligned}$$

where the exact solution to this problem is

$$\begin{aligned}\psi _{{\text {exact}}}(x,y,z,t)=(2.0/\pi )^{3/4}(i/(-4t+i))^{3/2} e^{-2i (x^2+y^2+z^2)/(-4 t+i)}.\end{aligned}$$

Numerical result at time \(t=0.5\) is shown in Table 6.

Table 6 Error analysis for the Chebyshev-collocation method in solving the three-dimensional Schrödinger equation
Full size table
Fig. 1
figure 1

Time evolution of the norm N(t), moment P(t) and energy E(t)

Full size image
Fig. 2
figure 2

Density function \(|\psi (x,t)|\) at different times: a \(t=2.5\); b \(t=5\); c \(t=7.5\); d \(t=10\)

Full size image
Fig. 3
figure 3

Time evolution of the norm N(t), moment in x-direction \(P_x(t)\), moment in y-direction \(P_y(t)\) and energy E(t)

Full size image
Fig. 4
figure 4

Density function \(|\psi (x,y,t)|\) at different times: a \(t=2.5\); b \(t=5\); c \(t=7.5\); d \(t=10\)

Full size image
Fig. 5
figure 5

Time evolution of the norm N(t), moment in x-direction \(P_x(t)\), moment in y-direction \(P_y(t)\), moment in z-direction \(P_z(t)\) and energy E(t)

Full size image
Fig. 6
figure 6

Density function \(|\psi (0,y,z,t)|\) at different times: a \(t=5\), c \(t=10\); density function \(|\psi (x,y,0,t)|\) at different times: b \(t=5\), d \(t=10\)

Full size image

Tables 4, 5 and 6 show us that the proposed Chebyshev-collocation method for linear Schrödinger equation has spectral accuracy in space.

7.3 Numerical results for the Schrödinger–Poisson system

We now apply the newly proposed splitting Chebyshev collocation method presented in Sect. 3 to solve the SP system in 1D, 2D and 3D, respectively.

We first solve one-dimensional SP system (3.1)–(3.2) over [a, b], where \(a=-8,b=8,T=1\), \(V=V(x)=\frac{1}{2}x^2\), and the initial data \(\phi _{0}(x)=\frac{1}{(2\pi )^{\frac{1}{4}}}e^{\frac{-x^{2}}{4}}x\).

Figure 1 shows us the time evolution of the norm N(t), moment P(t) and energy E(t). From this figure, we find that the proposed splitting Chebyshev-collocation method keeps well the conservation laws of the SP system in 1D. Figure 2 shows us the density function \(|\psi (x,t)|\) at different times.

We next solve two-dimensional SP system (3.1)–(3.2) over \([a,b]\times [c,d]\), where \(a=c=-8, b=d=8\), \(V=V(x,y)=\frac{1}{2}(x^2+y^2)\) and the initial data \(\phi _{0}(x,y)=\frac{1}{\sqrt{2\pi }}e^{\frac{-(x^{2}+y^{2})}{4}}(x+iy)\).

Figure 3 gives us the time evolution of the norm N(t), moment in x-direction \(P_x(t)\), moment in y-direction \(P_y(t)\) and energy E(t). From this figure, we observe that the proposed splitting Chebyshev-collocation method keeps well the conservation laws of the SP system in 2D. Figure 4 shows us the density function \(|\psi (x,y,t)|\) at different times.

Finally, we solve three-dimensional SP system (3.1)–(3.2) over \([a,b]\times [c,d]\times [e,f]\), where \(a=c=e=-8, b=d=f=8\), \(V=V(x,y,z)=\frac{1}{2}(x^2+y^2+z^2)\) and the initial data \(\phi _{0}(x,y,z)=\frac{1}{(2\pi )^{3/4}}e^{\frac{-(x^{2}+y^{2}+z^2)}{4}}(x+iy)\).

Figure 5 gives us the time evolution of the norm N(t), moment in x-direction \(P_x(t)\), moment in y-direction \(P_y(t)\), moment in z-direction \(P_z(t)\) and energy E(t). From this figure, we observe that the proposed splitting Chebyshev-collocation method keeps well the conservation laws of the SP system in 3D. Figure 6 shows us the density function \(|\psi (x,0,z,t)|\) and \(|\psi (x,y,0,t)|\) at different times.

8 Conclusions

We proposed a splitting Chebyshev collocation method for the time-dependent Schrödigner–Poisson system. The method can be efficiently implemented by means of matrix diagonalization technique. Because of its flexibility, it could be extended to solve many other nonlinear Schrödigner equations with nonzero boundary conditions and variable coefficients. The newly proposed method not only achieve spectral accuracy in space but also significantly reducing the computer-memory requirements and lowering the computational time in comparison with conventional solver for the fully discretized system. Our numerical results on the effectiveness of the method show that it might be used to predict future experiments on the dynamics of quantum electron plasma.