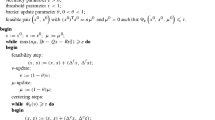A full-Newton step infeasible interior-point method based on a trigonometric kernel function without centering steps

Abstract

In this paper, a full-Newton step infeasible interior-point method for solving linear optimization problems is presented. In each iteration, the algorithm uses only one so-called feasibility step and computes the feasibility search directions by using a trigonometric kernel function with a double barrier term. Convergence of the algorithm is proved and it is shown that the complexity bound of the algorithm matches the currently best known iteration bound for infeasible interior-point methods. Finally, some numerical results are provided to illustrate the performance of the proposed algorithm.

1 Introduction

Among proposed approaches for solving linear optimization (LO) problems, interior-point methods (IPMs) gained more attention than others because they were successful in practice and theory. The primal-dual IPMs for LO problems was first suggested by Kojima et al. [17] and Megiddo [21]. Primal-dual IPMs can be classified into two categories: feasible IPMs and infeasible IPMs (IIPMs). The first category requires a strictly feasible starting point and maintains feasibility during the solution process. Usually such a starting point is not at hand. In that case the second category should be used which start with an arbitrary positive point and feasibility is reached as optimality is approached. The first IIPM was proposed for LO by Lustig [20]. Kojima et al. [16] gave the first theoretical results on IIPMs.

In 2006, Roos [23] introduced the first full-Newton step IIPM for LO and derived the currently best known iteration bound. Instead of using damped steps in the line search, the key feature of his method is that it uses only full-Newton steps at each iteration. Kheirfam and Mahdavi-Amiri [14] generalized the proposed algorithm in [23] to linear complementarity problems over symmetric cone (SCLCP) using Euclidean Jordan algebras. Some variants of Roos’ algorithm can be found in [5,6,7, 27].

El Ghami et al. [3] first introduced a trigonometric kernel function for primal-dual IPM for LO problems. Kheirfam [8] proposed a primal-dual IPM for semidefinite optimization (SDO) problems based a new trigonometric kernel function. Kheirfam [4] suggested a large update IPM with a new trigonometric kernel function for SCLCP problems and showed that the proposed algorithm enjoys the best-known iteration bound for such methods. Based on using a kernel function, Liu et al. [19] proposed a full-Newton step infeasible interior-point algorithm for LO problems and proved that the result complexity coincides with the best result for IIPMs. Recently, Kheirfam and Haghighi [13] presented a full-Newton step infeasible interior-point algorithm based on the trigonometric kernel function introduced in [15] for LO problems.

All the above-mentioned infeasible interior-point algorithms consisted of one so-called feasibility step and several centering steps to get an 𝜖-optimal solution of the underlying problem. Very recently, Roos [24] proposed an infeasible interior-point algorithm for LO so that his algorithm does not need centering steps and takes only one feasibility step in order to get a new iterate close enough to the central path. Kheirfam [9,10,11,12] respectively extended this algorithm to HLCP, the Cartesian P_∗(κ)-LCP, the convex quadratic symmetric cone optimization (CQSCO), and symmetric optimization (SO) problems.

Motivated by Roos [24], Kheirfam [9,10,11,12] and Kheirfam and Haghighi [13], we propose a full-Newton step infeasible interior-point algorithm for solving LO problems. Each iteration of algorithm consists of only one feasibility step and computes the search directions using the barrier function based on the trigonometric kernel function

$$ \phi(t)=\frac{(t-1)^{2}}{2}+\frac{(t-1)^{2}}{2t}+\frac{1}{8}\tan^{2}(h(t)),~~\text{where}~~h(t)=\frac{\pi(1-t)}{4t+2}. $$

Moreover, we prove that the proposed algorithm enjoys the best-known iteration complexity for IIPMs.

Let us consider the LO problem in the standard form

$$ \min \{c^{T}x:~Ax=b,~x\geq0\}, $$

(P)

where c, x ∈ Rⁿ, b ∈ R^m, and A ∈ R^m×n with rank(A) = m. The corresponding dual to (P) can be expressed as follows:

$$ \max \{b^{T}y:~ A^{T}y+s=c,~s\geq0\}, $$

(D)

where s ∈ Rⁿ and y ∈ R^m. Without loss of generality, we assume that both (P) and (D) satisfy interior-point condition (IPC). In accordance with the available results on infeasible IPMs (IIPMs), e.g., see [23], let (x^∗, y^∗, s^∗) be an optimal solution of the problem pair (P) and (D) that $\|x^{*}+s^{*}\|_{\infty }\leq \zeta$, and consider the starting point (x⁰, y⁰, s⁰) = (ζe,0, ζe) which satisfies x⁰s⁰ = μ⁰e with μ⁰ = ζ² and e is the all-one vector. It is worth noting that since x^∗, s^∗≥ 0, and (x^∗)^Ts^∗ = 0, $\|x^{*}+s^{*}\|_{\infty }\leq \zeta$ holds if and only if

$$ \begin{array}{@{}rcl@{}} 0\leq x^{*}\leq\zeta e,~~~ 0\leq s^{*}\leq\zeta e. \end{array} $$

(1)

The rest of the paper is structured as follows. Section 2 presents the infeasible full-Newton step IPM for solving LO problems. In Section 2.1, we recall the perturbed problem pair previously presented in [23]. Section 2.2 describes an iteration of our algorithm, and then we give new search directions in Section 2.3. In Section 2.4, a framework of the algorithm is presented. Section 3 is devoted to some technical results. Section 4 contains the analysis of the proposed algorithm. Section 4.1 gives an upper bound for the proximity measure after a main iteration of the algorithm. Section 4.2 serves to derive an upper bound for ω. In Section 4.3, we fix values for the parameters τ and 𝜃. In Section 4.4, we state that the algorithm is well defined for the chosen values of τ and 𝜃, provided that n ≥ 2. Some numerical results are presented in Section 5. Finally, we conclude the paper and outline some future research lines in Section 6.

2 Infeasible full-Newton step IPM

In the case of an infeasible method, we call the triple (x, y, s) an 𝜖-solution of (P) and (D) if the norm of the residual vectors do not exceed 𝜖, and also x^Ts ≤ 𝜖.

2.1 The perturbed problem

Let ${r^{0}_{b}}=b-Ax^{0}$ and ${r^{0}_{c}}=c-A^{T}y^{0}-s^{0}$ denote the initial residual vectors of (P) and (D), respectively. For any ν with 0 < ν ≤ 1, we consider the perturbed problem pair (P_ν) and (D_ν)

and

Note that (x, y, s) = (x⁰, y⁰, s⁰) yields a strictly feasible solution of the perturbed problem pair (P_ν) and (D_ν) when ν = 1. We conclude that if ν = 1, then the perturbed problem pair (P_ν) and (D_ν) satisfies the interior-point condition (IPC).

Lemma 1

([26, Theorem 5.13]) The problems (P) and (D) are feasible if and only if the perturbed problems (P_ν) and (D_ν) satisfy the IPC for every ν satisfying 0 < ν ≤ 1.

Due to Lemma 1, we conclude that the central path of the perturbed problem pair (P_ν) and (D_ν) exists. That is, the following system

$$ \begin{array}{@{}rcl@{}} b-Ax&=&\nu {r^{0}_{b}},~~ x\geq0, \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} c-A^{T}y-s&=&\nu {r^{0}_{c}},~~ s\geq0, \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} xs&=&\mu e, \end{array} $$

(4)

has a unique solution (x(μ, ν), y(μ, ν), s(μ, ν)) for every μ > 0 as the μ-center of the perturbed problem pair (P_ν) and (D_ν). In what follows, we assume that the parameters μ and ν always satisfy the relation μ = νμ⁰ and we denote (x(μ, ν), y(μ, ν), s(μ, ν)) = (x(ν), y(ν), s(ν)). We measure the distance of the iterate (x, y, s) to the μ-center of the perturbed pair (P_ν) and (D_ν) by the quantity

$$ \delta (x, s; \mu):=\delta (v):=\frac{1}{2}\|v^{-1}-v\|,~~\text{where}~~ v:=\sqrt{\frac{xs}{\mu}}. $$

(5)

As an immediate consequence, we have the following lemma.

Lemma 2

([25, Lemma II.62]) Let δ := δ(x, s;μ) and $\rho (\delta ):=\delta +\sqrt {1+\delta ^{2}}$. Then

$$\frac{1}{\rho(\delta)}\leq v_{i}\leq\rho(\delta),~~~i=1, \ldots, n.$$

2.2 An iteration of our algorithm

Here, we describe one (main) iteration of our algorithm. Suppose that for some μ ∈ (0, μ⁰], the algorithm starts from an arbitrary point (x, y, s) which satisfies the feasibility conditions (2) and (3) for $\nu =\frac {\mu }{\mu ^{0}}$ and such that δ(x, s;μ) ≤ τ, where τ is a threshold value. This is certainly true at the start of the first iteration. The algorithm finds a new iterate (x₊, y₊, s₊) that satisfies the feasibility conditions (2) and (3) with ν replaced by ν⁺ = (1 − 𝜃)ν with 𝜃 ∈ (0,1). Then μ is reduced to μ⁺ = (1 − 𝜃)μ and such that δ(x₊, s₊;μ⁺) ≤ τ.

To generate the feasibility solution (x₊, y₊, s₊) = (x + Δx, y + Δy, s + Δs), we need the displacement (Δx, Δy, Δs) which obtained by solving the following system

$$ \begin{array}{@{}rcl@{}} A{\varDelta} x&=&\theta\nu {r^{0}_{b}},\\ A^{T}{\varDelta} y+{\varDelta} s&=&\theta\nu {r^{0}_{c}},\\ s{\varDelta} x+x{\varDelta} s&=&\mu e-xs. \end{array} $$

(6)

2.3 New search directions

Defining the scaled search directions

$$ \begin{array}{@{}rcl@{}} d_{x}:=\frac{v{\varDelta} x}{x},~~ d_{s}:=\frac{v{\varDelta} s}{s}, \end{array} $$

(7)

where v is defined in (5), one can easily verify that the feasibility search direction system (6) can be written in terms of the scaled search directions d_x and d_s as follows:

$$ \begin{array}{@{}rcl@{}} \bar{A}d_{x}&=&\theta\nu {r^{0}_{b}},\\ \bar{A}^{T}\frac{{\varDelta} y}{\mu}+d_{s}&=&\theta\nu vs^{-1}{r^{0}_{c}},\\ d_{x}+d_{s}&=&v^{-1}-v, \end{array} $$

(8)

where $\bar A:=AV^{-1}X, V:=\text {diag}(v)$ and X := diag(x).

Definition 1

A twice differentiable function $\psi (t):(0, \infty )\rightarrow (0, \infty )$ is called a kernel function if

$$\psi(1)=\psi^{\prime}(1)=0,~~ \psi^{\prime\prime}(t)\geq0,~ \forall t>0.$$

Note that the right-hand side of the third equation in (8) is the negative gradient of the logarithmic barrier function ${\varPsi }(v)={\sum }_{i=1}^{n}\psi (v_{i})$ where $\psi (t)=\frac {t^{2}-1}{2}-\log t$. In this paper, the new search direction is obtained by the following system

$$ \begin{array}{@{}rcl@{}} \bar{A}d_{x}&=&\theta\nu {r^{0}_{b}},\\ \bar{A}^{T}\frac{{\varDelta} y}{\mu}+d_{s}&=&\theta\nu vs^{-1}{r^{0}_{c}},\\ d_{x}+d_{s}&=&-\nabla{\varPhi}(v), \end{array} $$

(9)

where the kernel function of ϕ(v) is

$$ \phi(t)=\frac{(t-1)^{2}}{2}+\frac{(t-1)^{2}}{2t}+\frac{1}{8}\tan^{2}(h(t)),~~~h(t)=\frac{\pi(1-t)}{4t+2}. $$

(10)

The above kernel function was first introduced in [18] for feasible IPMs based on the kernel functions. Since $\phi ^{\prime }(t)=\frac {2t^{3}-t^{2}-1}{2t^{2}}+\frac {1}{4}h^{\prime }(t)\tan (h(t))\left (1+\tan ^{2}(h(t))\right )$, the third equation of (9) can be written as

$$ \begin{array}{@{}rcl@{}} d_{x}+d_{s}=\frac{e+v^{2}-2v^{3}}{2v^{2}}-\frac{1}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v)). \end{array} $$

(11)

We define

$$ \sigma(x,s;\mu):=\sigma(v):=\left\|\nabla{\varPhi}(v)\right\| = \left\|\frac{e+v^{2}-2v^{3}}{2v^{2}}-\frac{1}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\|. $$

One easily verifies that

$$ \sigma(v)=0\Leftrightarrow \frac{e+v^2-2v^3}{2v^2}-\frac{1}{4}h^{\prime}(v)\tan(h(v))\sec^2(h(v))=0\Leftrightarrow v=e. $$

Thus σ(v) is a suitable proximity.

2.4 The algorithm

A more formal description of the algorithm is presented in Fig. 1.

Fig. 1

The algorithm

3 Technical results

In this section, we give some lemmas which are used in the analysis later.

Lemma 3

For t > 0, we have

$$\frac{1+t^{2}}{2t}-\frac{t}{4}h^{\prime}(t)\tan(h(t))\sec^{2}(h(t))>0.$$

Proof

Since $h^{\prime }(t)=\frac {-6\pi }{(2+4t)^{2}}$, for $f(t):=\tan (h(t))\sec ^{2}(h(t))$ we have

$$f^{\prime}(t)=\frac{-6\pi}{(2+4t)^{2}}\left[\sec^{4}(h(t))+2\tan^{2}(h(t))\sec^{2}(h(t))\right]<0.$$

That is, the function f(t) is monotonically decreasing with respect to t. So, it follows that

$$ \tan(h(t))\sec^{2}(h(t))>\lim_{t\to+\infty}\tan(h(t))\sec^{2}(h(t))=-2. $$

Hence, we obtain

$$ \begin{array}{@{}rcl@{}} \frac{1+t^{2}}{2t}-\frac{t}{4}h^{\prime}(t)\tan(h(t))\sec^{2}(h(t))&=&\frac{1+t^{2}}{2t}+\frac{3\pi t}{2(2+4t)^{2}}\tan(h(t))\sec^{2}(h(t))\\ &>&\frac{1+t^{2}}{2t}-\frac{3\pi t}{(2+4t)^{2}}\\ &=&\frac{16t^{4}+16t^{3} + (20 - 6\pi)t^{2}+16t+4}{2t(2+4t)^{2}}>0. \end{array} $$

The proof is complete. □

Lemma 4

For t > 0, we have

$$ \left\vert\frac{t h^{\prime}(t)}{4}\tan(h(t))\sec^2(h(t))\right\vert\leq\left\vert\frac{1}{8t}\left( t-\frac{1}{t}\right)\right\vert. $$

Proof

If 0 < t ≤ 1, then we have $h(t)\in [0, \frac {\pi }{2})$ and $\tan (h(t))>0$. Thus,

$$ \left\vert\frac{th^{\prime}(t)}{4}\tan(h(t))\sec^{2}(h(t))\right\vert=\frac{3\pi t}{2(2+4t)^{2}}\tan(h(t))\sec^{2}(h(t)). $$

(12)

Using $\cos \limits (x)\geq 1-\frac {2}{\pi }x$ and $\sin \limits (x)\leq \frac {4}{\pi }x-\frac {4}{\pi ^{2}}x^{2}$ for $x\in [0, \frac {\pi }{2}]$ [22], we get

$$ \cos(h(t))\geq\frac{6t}{2+4t},~~~~~~~\sin (h(t))\leq\frac{4(1-t)(1+5t)}{(2+4t)^{2}}. $$

Therefore,

$$ \begin{array}{@{}rcl@{}} \frac{1}{8t}\left( \frac{1}{t}-t\right)&-&\frac{3\pi t}{2(2+4t)^{2}}\tan(h(t))\sec^{2}(h(t))\\ &=&\frac{1}{8t}\left( \frac{1}{t}-t\right)-\frac{3\pi t\sin(h(t))}{2(2+4t)^{2}\cos^{3}(h(t))}\\ &\geq&\frac{1}{8t}\left( \frac{1}{t}-t\right)-\frac{\pi(1-t)(1+5t)}{36t^{2}(2+4t)} =\frac{1-t^{2}}{8t^{2}}-\frac{\pi(1-t)(1+5t)}{36t^{2}(2+4t)} \\ &=&\frac{(1-t)\left[(18-2\pi)+(54-10\pi)t+36 t^{2}\right]}{72 t^{2}(2+4t)}\geq0. \end{array} $$

The above inequality and (12) imply that

$$ \left\vert\frac{th^{\prime}(t)}{4}\tan(h(t))\sec^{2}(h(t))\right\vert\leq\frac{1}{8t}\left( \frac{1}{t}-t\right)=\left\vert\frac{1}{8t}\left( t-\frac{1}{t}\right)\right\vert. $$

If t > 1, then $h(t)\in (-\frac {\pi }{4},0]$ and $\tan (h(t))<0$. Therefore, we obtain

$$ \begin{array}{@{}rcl@{}} \left\vert\frac{th^{\prime}(t)}{4}\tan(h(t))\sec^{2}(h(t))\right\vert&=&\left\vert\frac{3\pi t}{2(2+4t)^{2}}\tan(h(t))\sec^{2}(h(t))\right\vert\\ &=&-\frac{3\pi t}{2(2+4t)^{2}}\tan(h(t))\sec^{2}(h(t)). \end{array} $$

(13)

From $\cos \limits (x)\geq 1-\frac {2}{\pi }x, x\in \left [0, \frac {\pi }{2}\right ]$ and $\tan (x)<\frac {\pi ^{2}x}{\pi ^{2}-4x^{2}}, x\in \left (0, \frac {\pi }{2}\right )$ [1], and the fact that $\cos \limits (-x)=\cos \limits (x)$ and $\tan (-x)=-\tan (x)$, we have

$$ \begin{array}{@{}rcl@{}} \cos(x)\geq1+\frac{2}{\pi}x,~~~x\in\left[-\frac{\pi}{2}, 0\right],~~\tan(x)>\frac{\pi^{2}x}{\pi^{2}-4x^{2}},~~~x\in\left( -\frac{\pi}{2}, 0\right). \end{array} $$

Thus, we get

$$ \cos(h(t))\geq\frac{2(2+t)}{2+4t},~~~~\tan(h(t))\geq\frac{\pi(1-t)(2+4t)}{12t(2+t)},~~t>1. $$

These two inequalities imply that

$$ \begin{array}{@{}rcl@{}} \tan(h(t))\sec^{2}(h(t))\geq\frac{-\pi(t-1)(2+4t)}{12t(2+t)\cos^{2}(h(t))}\geq\frac{-\pi(t-1)(2+4t)^{3}}{48t(t+2)^{3}}. \end{array} $$

(14)

Now, using (13) and (14) for t > 1, we obtain

$$ \begin{array}{@{}rcl@{}} \left\vert\frac{1}{8t}\left( t-\frac{1}{t}\right)\right\vert&-&\left\vert\frac{t h^{\prime}(t)}{4}\tan(h(t))\sec^{2}(h(t))\right\vert =\frac{1}{8t}\left( t-\frac{1}{t}\right)\\ &+&\frac{3\pi t}{2(2+4t)^{2}}\tan(h(t))\sec^{2}(h(t))\\ &\geq&\frac{t^{2}-1}{8t^{2}}-\frac{\pi^{2}(t-1)(2+4t)}{32(2+t)^{3}}\\ &=&\frac{t-1}{8}\left( \frac{t+1}{t^{2}}-\frac{\pi^{2}(2+4t)}{4(2+t)^{3}}\right)\\ &=&\frac{t-1}{8}\left( \frac{4t^{4}+(28-4\pi^{2})t^{3}+(72-2\pi^{2})t^{2}+80t+32}{4t^{2}(2+t)^{3}}\right)>0. \end{array} $$

This proves the lemma for t > 1. Therefore, the proof is complete. □

Lemma 5

For t > 0, we have

$$\left|\frac{1+t^{2}-2t^{3}}{2t^{2}}\right|\leq\left|\left( 1+\frac{1}{2t}\right)\left( t-\frac{1}{t}\right)\right|.$$

Proof

If 0 < t ≤ 1, then we have $\frac {1}{t}-t\geq 0$ and 1 + t² − 2t³ ≥ 0. Therefore, we get

$$ \begin{array}{@{}rcl@{}} \left( 1+\frac{1}{2t}\right)\left( \frac{1}{t}-t\right)-\frac{1+t^{2}-2t^{3}}{2t^{2}} =\frac{1-t}{t}\geq0. \end{array} $$

If t > 1, then $t-\frac {1}{t}>0$ and 1 + t² − 2t³ < 0. In this case, we have

$$ \begin{array}{@{}rcl@{}} \left( 1+\frac{1}{2t}\right)\left( t-\frac{1}{t}\right)+\frac{1+t^{2}-2t^{3}}{2t^{2}}=\frac{t-1}{t}\geq0. \end{array} $$

These two inequalities imply the desired result. □

4 Analysis of the algorithm

In this section, we investigate the proposed algorithm in Fig. 1 is well defined. The main part of our analysis is to find some values for the parameters τ and 𝜃 such that after a full-Newton step, the iterate (x₊, y₊, s₊) is strictly feasible for the perturbed problem pair ${\text (P_{\nu ^{+}})}$ and ${\text (D_{\nu ^{+}})}$, and also δ(x₊, s₊;μ⁺) ≤ τ.

4.1 Upper bound for δ(v⁺)

The following lemma guarantees the strict feasibility of the iterate (x₊, y₊, s₊) for the perturbed pair $(P_{\nu ^{+}})$ and $(D_{\nu ^{+}})$.

Lemma 6

The new iterate (x₊, y₊, s₊) is strictly feasible if

$$\frac{e+v^{2}}{2v}-\frac{v}{4}h^{\prime}(v)\tan (h(v))\sec^{2}(h(v))+d_{x}d_{s}>0.$$

Proof

Defining

$$ x(\alpha):=x+\alpha{\varDelta} x,~~~~ s(\alpha):=s+\alpha{\varDelta} s,~~~ \alpha\in[0, 1],$$

and using (7) and (11), we have

$$ \begin{array}{@{}rcl@{}} x(\alpha)s(\alpha) &=& (x+\alpha{\varDelta} x)(s+\alpha{\varDelta} s)=\mu(v+\alpha d_{x})(v+\alpha d_{s})\\ &=&\mu(v^{2}+\alpha v(d_{x}+d_{s})+\alpha^{2}d_{x}d_{s})\\ &=&\mu\left( v^{2}+\alpha v\!\left( \frac{e+v^{2}-2v^{3}}{2v^{2}} - \frac{1}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right) + \alpha^{2}d_{x}d_{s}\right)\\ &>&\mu\left( v^{2}+\alpha \left( \frac{e+v^{2}-2v^{3}}{2v}-\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right)\right.\\ &-&\left.\alpha^{2}\left( \frac{e+v^{2}}{2v}-\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right)\right)\\ &=&\mu\left( (1 - \alpha)v^{2}+\alpha(1 - \alpha)\!\left( \frac{e+v^{2}}{2v} - \frac{v}{4}h^{\prime}(v)\tan (h(v))\sec^{2}(h(v))\!\right)\!\right)\!\geq\!0, \end{array} $$

where the last inequality is due to Lemma 3 and v > 0. Hence, none of the entries of x(α) and s(α)vanishes for 0 ≤ α ≤ 1. Since x(0) = x > 0 and s(0) = s > 0 and x(α) and s(α) depend linearly on α, this implies that x(α) > 0 and s(α) > 0 for 0 ≤ α ≤ 1. Hence, x(1) = x₊ and s(1) = s₊ must be positive. This proves the lemma. □

In the sequel, we use the notation $\omega :=\frac {1}{2}(\Vert d_{x}\Vert ^{2} + \Vert d_{s}\Vert ^{2})$, and we have the following inequality:

$$ \Vert d_{x}d_{s}\Vert_{\infty}\leq\Vert d_{x}d_{s}\Vert\leq\Vert d_{x}\Vert\Vert d_{s}\Vert\leq\frac{1}{2}(\Vert d_{x}\Vert^{2}+\Vert d_{s}\Vert^{2})=\omega. $$

(15)

Lemma 7

If $\omega <\frac {1+\rho (\delta )^{2}}{2\rho (\delta )^{3}}-\frac {1}{4}\delta \rho (\delta )$, then the iterate (x₊, y₊, s₊) is strictly feasible.

Proof

By Lemma 6, the iterates (x₊, y₊, s₊) are strictly feasible if

$$\frac{e+v^{2}}{2v}-\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))+d_{x}d_{s}>0.$$

The last inequality certainly holds if

$$ \begin{array}{@{}rcl@{}} &&\min\left( \frac{e+v^{2}}{2v}-\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))+d_{x}d_{s}\right)\geq \frac{1+v_{\min}^{2}}{2v_{\max}}\\ &&\quad-\left\|\frac{v}{4}h^{\prime}(v)\tan h(v)\sec^{2}h(v)\right\|_{\infty}-\|d_{x}d_{s}\|_{\infty}>0. \end{array} $$

(16)

Using Lemma 4, Lemma 2, and the definition of δ, we obtain

$$ \begin{array}{@{}rcl@{}} \left\|\frac{v}{4}h^{\prime}(v)\tan h(v)\sec^{2}h(v)\right\|_{\infty}&\leq&\frac{1}{8}\left\|v^{-1}(v-v^{-1})\right\|_{\infty}~~~~~~~~~~~~~~~~~~~~~~~~~\\ &\leq&\frac{1}{8}\|v^{-1}\|_{\infty}\|v-v^{-1}\| \leq\frac{\delta}{4v_{\min}}\leq\frac{1}{4}\delta\rho(\delta). \end{array} $$

(17)

By Lemma 2, (17) and (15), we obtain

$$ \begin{array}{@{}rcl@{}} \frac{1+v_{\min}^{2}}{2v_{\max}}&-&\left\|\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\|_{\infty}-\|d_{x}d_{s}\|_{\infty}~~~~~~~~\\ &\geq&\frac{1+\rho(\delta)^{2}}{2\rho(\delta)^{3}}-\frac{1}{4}\delta\rho(\delta)-\omega>0. \end{array} $$

This means that (16) holds, and the proof is complete. □

Assuming v⁺ as the variance vector of the iterate (x₊, y₊, s₊) with respect to μ⁺, i.e., $v^{+}=\sqrt {\frac {x_{+}s_{+}}{\mu ^{+}}}$, the following lemma gives a lower bound for the components of v⁺.

Lemma 8

Let v⁺ be the variance vector related to the iterate (x₊, y₊, s₊) with respect to μ⁺, then

$$v^{+}_{\min}\geq\sqrt{\frac{1}{1-\theta}\left( \frac{1+\rho(\delta)^{2}}{2\rho(\delta)^{3}}-\frac{1}{4}\delta\rho(\delta)-\omega\right)}.$$

Proof

Using (7) and (11), we have

$$ \begin{array}{@{}rcl@{}} x_{+}s_{+}&=&(x+{\varDelta} x)(s+{\varDelta} s)=\mu\left( v^{2}+v(d_{x}+d_{s})+d_{x}d_{s}\right)~~\\ &=&\mu\left( \frac{e+v^{2}}{2v}-\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))+d_{x}d_{s}\right). \end{array} $$

Dividing both sides the above equality by μ⁺ = (1 − 𝜃)μ, we obtain

$$ (v^{+})^{2}=\frac{1}{1-\theta}\left( {\frac{e+v^{2}}{2v}-\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))+d_{x}d_{s}}\right), $$

(18)

which implies by Lemma 2, (15) and (17),

$$ \begin{array}{@{}rcl@{}} (v^{+}_{\min})^{2}&=&\frac{1}{1-\theta}\min\left( {\frac{e+v^{2}}{2v}-\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))+d_{x}d_{s}}\right)\\ &\geq&\frac{1}{1-\theta}\left( \frac{1+v^{2}_{\min}}{2v_{\max}}-\left\|\frac{v}{4}h^{\prime}(v)\tan(h(v)) \sec^{2}(h(v))\right\|_{\infty}-\left\|d_{x}d_{s}\right\|_{\infty}\right)\\ &\geq&\frac{1}{1-\theta}\left( \frac{1+\rho(\delta)^{2}}{2\rho(\delta)^{3}}-\frac{1}{4}\delta\rho(\delta)-\omega\right). \end{array} $$

Taking square roots gives the desired result. □

We proceed by deriving an upper bound for δ(x₊, s₊;μ⁺). By definition (5), we have

$$ \begin{array}{@{}rcl@{}} \delta(v^{+}):=\delta(x_{+}, s_{+}; \mu^{+}),~~\text{where}~~v^{+}=\sqrt{\frac{x_{+}s_{+}}{\mu^{+}}}. \end{array} $$

Lemma 9

If $\omega <\frac {1+\rho (\delta )^{2}}{2\rho (\delta )^{3}}-\frac {1}{4}\delta \rho (\delta )$, then

$$ \delta(v^{+})\leq\frac{\theta\sqrt{n}+2\rho(\delta)\delta^{2}+\frac{1}{4}\delta\rho(\delta) +\omega}{2\sqrt{(1-\theta)\left( \frac{1+\rho(\delta)^{2}}{2\rho(\delta)^{3}}-\frac{1}{4}\delta\rho(\delta)-\omega\right)}}. $$

Proof

Using (18) and the triangle inequality, we have

$$ \begin{array}{@{}rcl@{}} \delta(v^{+})&=&\frac{1}{2}\left\|(v^{+})^{-1}-v^{+}\right\|\leq\frac{1}{2v_{\min}^{+}}\left\|e-(v^{+})^{2}\right\|\\ &=&\frac{1}{2v_{\min}^{+}}\left\|e-\frac{1}{1-\theta}\left( {\frac{e+v^{2}}{2v}-\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))+d_{x}d_{s}}\right)\right\|\\ &=&\frac{1}{2(1-\theta)v^{+}_{\min}}\left\|(1-\theta)e-\frac{e+v^{2}}{2v} + \frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))-d_{x}d_{s}\right\|\\ &=&\frac{1}{2(1-\theta)v^{+}_{\min}}\left\|-\theta e-\frac{(e-v)^{2}}{2v}+\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))-d_{x}d_{s}\right\|\\ &\leq&\frac{1}{2(1-\theta)v^{+}_{\min}}\left( \theta\sqrt{n}+\left\|\frac{(e-v)^{2}}{2v}\right\|\right.\\ &&+\left.\left\|\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\|+\|d_{x}d_{s}\|\right)\\ &\leq&\frac{1}{2(1-\theta)v^{+}_{\min}}\left( \theta\sqrt{n}+\frac{1}{2}\|v^{-1}\|_{\infty}\|e-v\|^{2}\right.\\ &&+\left.\left\|\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\|+\omega\right), \end{array} $$

(19)

where the last inequality follows from (15).

To obtain an upper bound for $\frac {1}{2}\|v^{-1}\|_{\infty }\|e-v\|^{2}$, due to |1 − t|≤|t^− 1 − t|, for each t > 0, Lemma 2 and (5), we have

$$ \begin{array}{@{}rcl@{}} \frac{1}{2}\|v^{-1}\|_{\infty}\|e-v\|^{2}=\frac{1}{2v_{\min}}\|e-v\|^{2}\leq\frac{1}{2v_{\min}}\|v^{-1}-v\|^{2}\leq 2\rho(\delta)\delta^{2}. \end{array} $$

(20)

Using Lemma 4, we get

$$ \begin{array}{@{}rcl@{}} \left\|\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\|&\leq&\frac{1}{8}\left\|v^{-1}(v-v^{-1}\right\|~~~~~~~~~~~~~\\ &\leq&\frac{1}{8v_{\min}}\|v-v^{-1}\|\leq\frac{1}{4}\delta\rho(\delta). \end{array} $$

(21)

Substituting these two bounds into (19), and also using Lemma 8, we obtain the inequality in the lemma. □

4.2 Upper bound for ω

Let us denote the null space of the matrix $\bar {A}$ as ${\mathscr{L}}$. So

$$\mathcal{L}:=\{\xi\in\mathbb{R}^{n}: \bar{A}\xi=0\}.$$

Obviously, the affine space $\{\xi \in \mathbb {R}^{n}:\bar {A}\xi =\theta \nu {r_{b}^{0}}\}$ equals $d_{x}+{\mathscr{L}}$. The row space of $\bar {A}$ equals the orthogonal complement ${\mathscr{L}}^{\perp }$ of ${\mathscr{L}}$, and $d_{s}\in \theta \nu v s^{-1}{r_{c}^{0}}+{\mathscr{L}}^{\perp }$. Also note that ${\mathscr{L}}\cap {\mathscr{L}}^{\perp }=\{0\}$, and as a consequence the affine spaces $d_{x}+{\mathscr{L}}$ and $d_{s}+{\mathscr{L}}^{\perp }$ meet in a unique point q.

Lemma 10

Let q be the (unique) point in the intersection of the affine space $d_{x}+{\mathscr{L}}$and $d_{s}+{\mathscr{L}}^{\perp }$. Then

$$2\omega\leq\|q\|^{2}+\left( \|q\|+\sigma(v)\right)^{2}.$$

Proof

The proof of lemma is exactly the same as the proof of Lemma 3.4 in [24], except we make use of −∇Φ(v) instead of v^− 1 − v. □

Following the same argument as in Section 3.4 [24], we obtain

$$ \begin{array}{@{}rcl@{}} \|q\|\leq\theta\frac{\|x\|_{1}+\|s\|_{1}}{\zeta v_{\min}}\leq\frac{\theta(n+\|v\|^{2})}{v_{\min}}&\leq&\theta\rho(\delta)\left( n+n+2\delta^{2}+2\delta\sqrt{n+\delta^{2}}\right)\\ &=&n\theta\rho(\delta)\left( 1+\rho\left( \frac{\delta}{\sqrt{n}}\right)^{2}\right). \end{array} $$

(22)

The following lemma provides an upper bound for σ(v) in the terms of the measure proximity δ.

Lemma 11

One has

$$\sigma(v)\leq\left( 2+\rho(\delta)\right)\delta+\frac{1}{4}\delta\rho(\delta)^{2}.$$

Proof

Using the definition of σ(v), the triangle inequality, Lemma 5, and (21), we obtain

$$ \begin{array}{@{}rcl@{}} \sigma(v) &=&\left\|\frac{e+v^{2}-2v^{3}}{2v^{2}}-\frac{1}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\|\\ &\leq&\left\|\frac{e+v^{2}-2v^{3}}{2v^{2}}\left\Vert+\right\Vert\frac{v}{4v}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\Vert\\ &\leq&\left\Vert\left( e+\frac{v^{-1}}{2}\right)(v^{-1}-v)\right\Vert+\Vert v^{-1}\Vert_{\infty}\left\Vert\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\Vert\\ &\leq&T\left\Vert e+\frac{v^{-1}}{2}\right\Vert_{\infty}\left\Vert v^{-1}-v\right\Vert +\Vert v^{-1}\Vert_{\infty}\left\Vert\frac{v}{4}h^{\prime}(v)\tan(h(v))\sec^{2}(h(v))\right\Vert\\ &\leq&\left( 1+\frac{1}{2v_{\min}}\right)2\delta+\frac{1}{4v_{\min}}\delta\rho(\delta)\\ &\leq&\left( 2+\rho(\delta)\right)\delta+\frac{1}{4}\delta\rho(\delta)^{2}. \end{array} $$

The last inequality is due to Lemma 2. This completes the proof. □

Using Lemma 10, (22) and Lemma 11 we obtain an upper bound for ω.

$$ \begin{array}{@{}rcl@{}} \omega&\leq&\frac{1}{2}\left[n^{2}\theta^{2}\rho(\delta)^{2}\left( 1+\rho\left( \frac{\delta}{\sqrt{n}}\right)^{2}\right)^{2}\right.\\ &&+\left.\left( n\theta\rho(\delta)\left( 1+\rho\left( \frac{\delta}{\sqrt{n}}\right)^{2}\right)+\left( 2+\rho(\delta)\right)\delta +\frac{1}{4}\delta\rho(\delta)^{2}\right)^{2}\right]. \end{array} $$

(23)

4.3 Values for 𝜃 and τ

Our aim is to find a positive number τ such that if δ(v) ≤ τ holds, then δ(v⁺) ≤ τ. By Lemma 9, this is certainly true if

$$ \begin{array}{@{}rcl@{}} \omega<\frac{1+\rho(\delta)^{2}}{2\rho(\delta)^{3}}-\frac{1}{4}\delta\rho(\delta), \end{array} $$

(24)

$$ \begin{array}{@{}rcl@{}} \frac{\theta\sqrt{n}+2\rho(\delta)\delta^{2} +\frac{1}{4}\delta\rho(\delta)+\omega}{2\sqrt{(1-\theta)\left( \frac{1+\rho(\delta)^{2}} {2\rho(\delta)^{3}}-\frac{1}{4}\delta\rho(\delta)-\omega\right)}}\leq\tau. \end{array} $$

(25)

Using (23), the inequality (24) holds if

$$ \begin{array}{@{}rcl@{}} &&n^{2}\theta^{2}\rho(\delta)^{2}\left( 1+\rho\left( \frac{\delta}{\sqrt{n}}\right)^{2}\right)^{2} +\left( n\theta\rho(\delta)\left( 1+\rho\left( \frac{\delta}{\sqrt{n}}\right)^{2}\right)\right.\\ &&\quad+\left.\left( 2+\rho(\delta)\right)\delta +\frac{1}{4}\delta\rho(\delta)^{2}\right)^{2} <\frac{1+\rho(\delta)^{2}}{\rho(\delta)^{3}}-\frac{1}{2}\delta\rho(\delta). \end{array} $$

One easily verifies that the left-hand side expression in the above inequality is monotonically increasing with respect to δ, whereas the right-hand side expression is the monotonically decreasing. Hence, it suffices to have

$$ \begin{array}{@{}rcl@{}} &&n^{2}\theta^{2}\rho(\tau)^{2}\left( 1+\rho\left( \frac{\tau}{\sqrt{n}}\right)^{2}\right)^{2} +\left( n\theta\rho(\tau)\left( 1+\rho\left( \frac{\tau}{\sqrt{n}}\right)^{2}\right)\right.\\ &&\quad+\left.\left( 2+\rho(\tau)\right)\tau +\frac{1}{4}\tau\rho(\tau)^{2}\right)^{2} <\frac{1+\rho(\tau)^{2}}{\rho(\tau)^{3}}-\frac{1}{2}\tau\rho(\tau). \end{array} $$

(26)

One may easily check that the above inequality is satisfied if

$$ \tau=\frac{1}{16},~~~\theta=\frac{1}{22n}. $$

(27)

This means that the inequality (24) holds, i.e., the iterate (x₊, y₊, s₊) is strictly feasible, by Lemma 7. On the other hand, note that

$$ \begin{array}{@{}rcl@{}} g(n, \tau)&:=&\frac{\rho(\tau)^{2}}{968}\left( 1+\rho\left( \frac{\tau}{\sqrt{n}}\right)^{2}\right)^{2}\\ &&+\frac{1}{2}\left( \frac{\rho(\tau)}{22}\left( 1+\rho\left( \frac{\tau}{\sqrt{n}}\right)^{2}\right)+\left( 2+\rho(\tau)\right)\tau +\frac{1}{4}\tau\rho(\tau)^{2}\right)^{2} \end{array} $$

provides an upper bound for ω, by (23). Moreover, $g(n, \frac {1}{16})\leq g(2, \frac {1}{16})\leq 0.0533$. From Lemma 9, we have

$$ \begin{array}{@{}rcl@{}} \delta(v^{+})&\leq&\frac{\theta\sqrt{n}+2\rho(\delta)\delta^{2} +\frac{1}{4}\delta\rho(\delta)+\omega}{2\sqrt{(1-\theta)\left( \frac{1+\rho(\delta)^{2}} {2\rho(\delta)^{3}}-\frac{1}{4}\delta\rho(\delta)-\omega\right)}}\\ &\leq&\frac{\frac{1}{22\sqrt{n}}+2\rho(\tau)\tau^{2}+\frac{1}{4}\tau\rho(\tau) +g(2,\tau)}{2\sqrt{\left( 1-\frac{1}{22n}\right)\left( \frac{1+\rho(\tau)^{2}}{2\rho(\tau)^{3}}-\frac{1}{4}\tau\rho(\tau)-g(2,\tau)\right)}}\\ &\leq&\frac{\frac{1}{22\sqrt{2}}+2(1.0645)\frac{1}{256}+\frac{1}{64}(1.0645)+0.0533}{2\sqrt{\left( 1-\frac{1}{44}\right) \left( \frac{1+(1.0645)^{2}}{2(1.0645)^{3}}-\frac{1}{64}(1.0645)-0.0533\right)}}\\ &\leq&0.0619<0.0625=\tau. \end{array} $$

This means that the inequality (25) is true. That is, the algorithm is well defined in the sense that the property δ(x, s;μ) ≤ τ with τ and 𝜃 defined in (27) is maintained in all iterations.

4.4 Complexity analysis

In the previous sections, we have found that if n ≥ 2 and at the start of an iteration the iterates (x, y, s) satisfying δ(x, s;μ) ≤ τ, with τ and 𝜃 as defined in (27), then after the full-Newton step, the new iterate (x₊, y₊, s₊) is strictly feasible and δ(x₊, s₊;μ⁺) ≤ τ. This makes the algorithm well defined. After each iteration, the residuals and the duality gap are reduced by a factor 1 − 𝜃. Hence, using (x⁰)^Ts⁰ = nζ², the total number of main iterations is bounded above by

$$ \frac{1}{\theta}\log\frac{\max\{n\zeta^{2}, \|{r_{p}^{0}}\|, \|{r_{d}^{0}}\|\}}{\epsilon}. $$

Using $\theta =\frac {1}{22n}$, we have the following result.

Theorem 1

Let (P) and (D) be feasible and ζ > 0 such that $\|x^{*}+ s^{*}\|_{\infty }\leq \zeta$for some optimal solutions x^∗ of (P) and (y^∗, s^∗) of (D). Then after at most

$$ 22n\log\frac{\max\{n\zeta^{2},\|{r_{p}^{0}}\|, \|{r_{d}^{0}}\|\}}{\epsilon} $$

inner iterations the algorithm finds an 𝜖-solution of (P) and (D).

5 Numerical results

In this section, we report some computational results for the test problems given in Table 1 that are taken from the standard NETLIB test repository [2]. Numerical results were obtained by using MATLAB R2009a (version 7.8.0.347) on Windows XP Enterprize 32-bit operating system. The numerical results are summarized in Table 1, where “Iter.” denotes the required iteration numbers and “CPU” denotes the CPU time (in seconds) required to obtain an 𝜖-solution of the underlying problem. Moreover, in Table 1, “bound” and ”object. value” respectively denote the obtained bound in Theorem 1 and the objective function value. We set 𝜖 = 10^− 4 as the accuracy parameter and choose the initial starting point (x⁰, y⁰, s⁰) = (ζe,0, ζe) such that $\|x^{*}+s^{*}\|_{\infty }\leq \zeta$. Also, we set $\theta =\frac {1}{22 n}$ for the proposed algorithm and $\theta =\frac {1}{8n}$ for the algorithm in [24].

Table 1 Computational results for the test problems given

Note that the iteration bound in this paper is a worst-case bound, as is usual for theoretical bounds for IPMs (including IIPMs). When solving a particular problem, usually much smaller iteration numbers can be realized by taking 𝜃 larger than the value that is theoretically justified [24]. Now, we compare the proposed algorithm in this paper with the given algorithm in [13]. In order to, we again consider 𝜖 = 10^− 4,(x⁰, y⁰, s⁰) = (ζe,0, ζe) such that $\|x^{*}+s^{*}\|_{\infty }\leq \zeta$ and 𝜃 = 0.2. In Table 2, “C. Iter.” denotes the required centering iteration numbers. The numerical results are listed in Table 2.

Table 2 Numerical results

The obtained numerical results in Table 2 show that for each problem instance, the algorithm in [13] needs a number of inner iterations (C. Iter. ), while the proposed algorithm does not need to these iterations. Moreover, from the results in the Table 2, we find that the execution time of the proposed algorithm is almost one-third of the execution time of the algorithm in [13].

6 Concluding remarks

In this paper, we proposed a new infeasible interior-point algorithm for solving LO problems. In each iteration, the algorithm uses only one step as feasibility step and admits a trigonometric kernel function instead of the logarithmic kernel function in system of scaled search directions. Moreover, the new algorithm does not need the centering steps. The proposed algorithm uses only full steps and therefore no line-searches are needed for generating the new iterates. The complexity bound of the proposed algorithm coincides with the currently best known iteration bound of infeasible IPMs for LO problems. We presented some numerical results to illustrate the performance of the algorithm on NETLIB test problems.