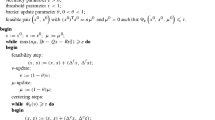An infeasible interior-point algorithm with full-Newton steps for $P_*(\kappa )$ horizontal linear complementarity problems based on a kernel function

Abstract

This paper contains an infeasible interior-point method for $P_*(\kappa )$ horizontal linear complementarity problem based on a kernel function. The kernel function is used to determine the search directions. These search directions differ from the usually used ones in some interior-point methods, and their analysis is more complicated. Main feature of our algorithm is that there is no calculation of the step size, i.e, we use full-Newton steps at each iteration. The algorithm constructs strictly feasible iterates for a sequence of perturbations of the given problem, close to its central path. Two types of full-Newton steps are used, feasibility steps and centering steps. The iteration bound matches the best-known iteration bound for these types of algorithms.

1 Introduction

In 1984, Karmarkar [9] introduced an interior-point method (IPM) for linear programming (LP). Karmarkar used the efficiency of the simplex method with the theoretical advantages of the ellipsoid method to create his efficient polynomial algorithm. This algorithm is based on projective transformations and the use of Karmarkar’s primal potential function. This new algorithm sparked much research, creating a new direction in optimization—the field of IPMs. Unlike the simplex method, which travels from vertex to vertex along the edges of the feasible region, IPMs follow approximately a central path in the interior of the feasible region and reaches the optimal solution only asymptotically. As a result of finding the optimal solution in this fashion, the analysis of the IPMs become substantially more complex than that of the simplex method. Since the first IPM was developed, many researchers have proposed and analyzed various IPMs for LP and a large amount of results have been reported [5, 7, 19]. IPMs have been very successful in solving wide classes of optimization problems such as linear complementarity problem (LCP) [10, 11, 15, 26], horizontal linear complementarity problem (HLCP) [2, 3, 8, 14, 22], semi-definite optimization (SDO) [16, 21] and convex quadratic programming (CQP) [20, 30].

Two interior-point approaches are proposed: feasible and infeasible interior-point methods (IIPMs). The above mentioned papers mostly focus on feasible methods. The most important class is the feasible path following method: the algorithm starts with a strictly feasible point neighbor the central path and generates a sequence of iterates which satisfy the same conditions. These conditions are an expensive process in general. Most existing codes make use of a starting point that satisfy strict positivity but not the equality condition. For this reason, the authors tried to develop algorithms which start with any strict positive point not necessarily feasible. More recently, algorithms that do not require feasible starting point have been the focus of active research [8, 15, 16, 23]. These algorithms are called IIPMs. Roos [23] introduced the first full-Newton step IIPM for LP. Mansouri et al. extended Roos’s algorithm to SDO, LCP and $P_*(\kappa )$-HLCP problems [3, 15, 16].

The majority of primal-dual IPMs, say the above mentioned ones, are based on the classical logarithmic barrier function, which leads to the usual Newton search directions. However, some authors, e.g Wang et al. [25] and Lee et al. [13], presented some different kernel function based IPMs for the $P_*(\kappa )-$HLCP, which reduce the gap between the practical behavior of the algorithms and their theoretical performance results. Darvay [6] presented a new technique for finding a class of search directions. The search direction of his algorithm which is called Darvay’ direction, was introduced by using an algebraic equivalent transformation (form) of the nonlinear equations which defined the central path and then applying Newton’s method for the new system of equations. Based on this direction, Darvay proposed a full-Newton step primal-dual path following IPM for LP. Later on, Achache [1], Wang and Bai [27–29] and Mansouri et al. [2, 18] extended Darvay’s algorithm for LP to CQP, SDO, second orde cone optimization (SOCO), symmetric cone optimization (SCO), monotone LCP and $P_*(\kappa )$-HLCPs, respectively.

In this paper, we use some different search directions from usual Newton directions and Darvay’s directions, to analyze the full-Newton step IIPM of Roos [23] for the $P_*(\kappa )$-HLCPs. These directions are based on a kernel function that used by Liu and Chen [12] for LP. The analysis of these directions is more complicated compared to the classical Newton directions and Darvay’s directions. This analysis shows the way of treatment with some directions which differ from the usually used directions in IPMs. We present a full-Newton step IIPM for HLCP based on the mentioned directions and prove that the number of iterations of our algorithm coincides with the best obtained bound for $P_*(\kappa )$-HLCPs.

The objective of the HLCP problem is to find a vector pair in a finite dimensional real vector space that satisfies a certain system of equations. More precisely, for a given vector $b\in {\mathbb {R}}^{n}$ and a pair of matrixes $Q,R\in {\mathbb {R}}^{n\times n}$, we want to find a vector pair $\left( x,\,s\right) \in {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}$ (or show that no such vector pair exists), such that the following inequalities and equations are satisfied:

Note that the linear complementarity problem (LCP) is obtained by taking $R = -I$. The HLCP is not an optimization problem. However, it is closely related to optimization problems, because Kurush–Kuhn–Tucker (KKT) optimality conditions for many optimization problems can be formulated as LCP. For example, KKT conditions of linear and quadratic optimization problems can be formulated as LCP and the HLCP provides a convenient general framework for the equivalent formulations of LCP [4].

In this paper, we are focusing on $P_*(\kappa )$-HLCP, in the sense that

$$\begin{aligned} Qu+Rv=0~\Rightarrow ~(1+4\kappa )\sum _{i\in {\mathcal {I}^+}}u_{i}v_{i} +\sum _{i\in {\mathcal {I}^-}}u_{i}v_{i}\ge 0~~~\forall u,v \in {\mathbb {R}}^n, \end{aligned}$$

(1)

where $\kappa$ is a nonnegative constant and ${\mathcal {I}^+}\!\!\!=\{i : u_iv_i>0\}$ and ${\mathcal {I}^-}\!\!\!=\{i : u_iv_i<0\}$. A $P_*(\kappa )$-HLCP is a general optimization problem, containing many aforementioned problems such as LP, $P_*(\kappa )$-LCP and CQP problems. Therefore dealing with this problem, remove the necessity of handling many of its subproblems, separately.

The paper is organized as follows. In Sect. 2, we introduce the central path of the $P_*(\kappa )$-HLCP as well as its perturbed problem. Moreover, we present two types of search directions. In Sect. 3, we give the new search directions for full-Newton step IIPMs, these directions can be interpreted as a kind of steepest descent direction of a separate function, which is constructed by using the kernel function on coordinates. The full-Newton step IIPM based on the new directions is also presented in this section. In Sect. 4, we investigate some useful tools that will be used in the analysis of the IIPM proposed in this paper. Section 5 is about the centering steps.

In Sect. 6, we analyze the feasibility step used in the algorithm.

We derive the complexity for the algorithm in Sect. 7; the complexity analysis shows that the complexity bound of the algorithm coincides with the best-known iteration complexity for IIPMs. Finally, some conclusions and remarks are given in Sect. 8.

Throughout the paper, we use the following notations. ${\mathbb {R}}^{n}_{ +}({\mathbb {R}}^{n}_{ ++})$ is the nonnegative (positive) orthant of ${\mathbb {R}}^n$. The 2-norm and the infinity norm are denoted by $\Vert \cdot \Vert _2$ and $\Vert \cdot \Vert _{\infty }$, respectively. If $x,s\in {\mathbb {R}}^n$, then $xs$ denotes the componentwise (or Hadamard) product of the vectors $x$ and $s$. $v_{\min }$ and $v_{\max }$ denote the minimal and maximal components of the vector $v$, respectively.

2 Preliminaries

2.1 The central path for $P_*(\kappa ){-}\hbox {HLCP}$

Solving $P_*(\kappa ){-}\hbox {HLCP}$ is equivalent with finding a solution of the following system of equations

$$\begin{aligned} \begin{aligned}&Qx+Rs=b,\,\quad x\ge 0,\,\\&xs=0,\,\quad s\ge 0. \end{aligned} \end{aligned}$$

(2)

The general idea is to solve (2) using Newton’s method. However, Newton’s method can “get stuck” at the complementarity equation $xs = 0$. Therefore, the main idea of IPMs is to replace the last equation in (2), the so called complementarity equation, with the parameterized equation $xs = \mu e$, with parameter $\mu > 0$. So we consider the following system

$$\begin{aligned} \begin{aligned}&Qx+Rs=b,\,\quad x\ge 0,\,\\&xs=\mu e,\,\quad s\ge 0. \end{aligned} \end{aligned}$$

(3)

Here $e$ is the all-one vector. In [24] is established that if HLCP satisfies the interior-point condition (IPC), i.e., there exists $(x,s)>0$ with $Qx+Rs=b$, then the above system has a unique solution for each $\mu >0$, that is denoted by $(x(\mu ),\,(s(\mu ))$ and is called the $\mu -$center of HLCP. We call the solution set $\{(x(\mu ), s(\mu )) | \mu > 0\}$ the central path of the HLCP. If $\mu \rightarrow 0$, then the limit of the central path exists [24] and since the limit point satisfies $xs=0$, the limit yields the optimal solution for HLCP.

2.2 The perturbed problem

Let $\left( x^{0},s^{0}\right) >0$ such that ${x^{0}}s^{0}=\mu ^{0} e$ for some (positive) number $\mu ^{0}$. We denote the initial value of the residual as $r^0$, as

$$\begin{aligned}&\displaystyle r^0=b-Qx^0-Rs^0. \end{aligned}$$

(4)

For any $\nu$ with $0<\nu \le 1$, we consider the perturbed problem $(P_{\nu })$, defined by

Note that if $\nu =1$ then $\left( x,\,s\right) =\left( x^{0},\,s^{0}\right)$ yields a strictly feasible solution of $\left( P_{\nu }\right)$. We conclude that if $\nu =1$ then $\left( P_{\nu }\right)$ satisfies the IPC.

Lemma 1

Let the original problem $\left( P\right)$ be feasible, then the perturbed problem $(P_{\nu })$ satisfies the IPC.

Proof

The proof is similar to the proof of Lemma 4.1 in [15]. $\square$

2.3 The central path of the perturbed problem

We assume that $(P)$ is feasible. Assuming $0<\nu \le 1$, Lemma 1 implies that the problem $P_{\nu }$ satisfies the IPC, and hence its central path exists. This means that the system

$$\begin{aligned} \begin{array}{c} \displaystyle b-Qx-Rs=\nu r^0,\,\quad x \ge 0,\,\quad s\ge 0,\,\\ \displaystyle xs=\mu e,\,\end{array} \end{aligned}$$

(5)

has a unique solution, for every $\mu >0$. In the sequel, this unique solution is denoted by $(x(\mu ,\nu ),\,s(\mu ,\nu ))$. It is the $\mu$-center of the perturbed problem $\left( P_{\nu }\right)$. Note that since $x^{0}s^{0}=\mu ^{0}e$, $(x^{0},\,s^{0})$ is the $\mu ^{0}$-center of the perturbed problem $\left( P_{1}\right)$. In other words, $\left( x\left( \mu ^{0},1\right) ,\,s\left( \mu ^{0},1\right) \right) =\left( x^{0},s^{0}\right)$. In the sequel the parameters $\mu$ and $\nu$ always satisfy the relation $\mu =\nu \mu ^{0}$.

2.4 Search directions

2.4.1 Centering search directions

We are given a positive feasible pair $(x,s)$ for $(P_{\nu })$ and some $\mu >0$. Our aim is to define centering search directions $\varDelta x,\varDelta s$ that move in the direction of the $\mu$-center $(x(\mu ,\nu ),\,s(\mu ,\nu ))$. In fact, we want the new iterates $x+\varDelta x,\,s+\varDelta s$ to satisfy system (5) and be positive with respect to $\mu$. After substitution, this yields the following conditions on $\varDelta x,\varDelta s$:

$$\begin{aligned} \begin{array}{c} \displaystyle b-Q(x+\varDelta x)-R(s+\varDelta s)=\nu r^{0},\,\,\,\,\left( x+\varDelta x,\,s+\varDelta s\right) >0,\,\\ \displaystyle (x+\varDelta x)(s+\varDelta s)=\mu e. \end{array} \end{aligned}$$

If we neglect for the moment the inequality constraints and ignore the quadratic term $\varDelta x\varDelta s$, since $b-Qx-Rs=\nu r^{0}$, this system can be rewritten as follows

$$\begin{aligned}&Q\varDelta x+R\varDelta s=0,\,\nonumber \\&s\varDelta x+x\varDelta s=\mu e-xs. \end{aligned}$$

(6)

In [11] is showed that If $(Q,R)$ is a $P_*(\kappa )$-pair, then the coefficient matrix in the above linear system is nonsingular. Hence this system uniquely defines the search directions $\varDelta x,\,\varDelta s$ for any $x > 0$ and $s > 0$. These directions follow the $\mu$-center $(x(\mu ,\nu ),\,s(\mu ,\nu ))$. We call them centering search directions. Let

$$\begin{aligned} v=\sqrt{\frac{xs}{\mu }},\,\quad d_x=\frac{v\varDelta x}{x},\quad d_s=\frac{v\varDelta s}{s}. \end{aligned}$$

(7)

Then system (6) can be expressed as

$$\begin{aligned} \begin{aligned}&\displaystyle \bar{Q}d_{x}+\bar{R}d_{s}=0,\,\\&\displaystyle d_{x}+d_{s}=v^{-1}-v,\,\end{aligned} \end{aligned}$$

(8)

where

$$\begin{aligned} \bar{Q}=QXV^{-1},~~~\bar{R}=RSV^{-1}, ~~~X=\,\hbox {diag}\,(x) ~~\text {and} ~~S=\,\hbox {diag}\,(s). \end{aligned}$$

(9)

2.4.2 Feasibility search directions

According to the definition of $P_{\nu }$, the feasibility equation for $\left( P_{\nu ^+}\right)$ is given by

$$\begin{aligned} b-Qx-Rs=\nu ^{+}r^{0},\,\,\,\,\left( x,\,s\right) \ge 0. \end{aligned}$$

(10)

To get iterates that are feasible for $\left( P_{\nu ^+}\right)$, we need search directions $\varDelta ^{f}x$ and $\varDelta ^{f}s$ such that

$$\begin{aligned} b-Q(x+\varDelta ^{f}x)-R(s+\varDelta ^{f}s)=\nu ^{+}r^{0},\,\,\,\,\left( x+\varDelta ^{f}x,\,s+\varDelta ^{f}s\right) >0. \end{aligned}$$

Let $\nu ^+=(1-\theta )\nu$, where $\theta$ is the barrier update parameter in the algorithm. Since $\left( x,\,s\right)$ is feasible for $(P_{\nu })$, it follows that $\varDelta ^{f}x$ and $\varDelta ^{f}s$ should satisfy

$$\begin{aligned} Q\varDelta ^{f}x+R\varDelta ^{f}s=\theta \nu r^{0}. \end{aligned}$$

Thus, if we neglect for the moment the inequality constraints and ignore the quadratic term $\varDelta ^f x\varDelta ^f s$, then $(\varDelta ^f x,\,\varDelta ^f s)$ can be defined by the following system

$$\begin{aligned} \begin{aligned}&Q\varDelta ^{f}x+R\varDelta ^{f}s =\theta \nu r^0,\,\\&s\varDelta ^{f}x+x\varDelta ^{f}s =\mu e-xs. \end{aligned} \end{aligned}$$

(11)

This system uniquely defines the search directions $\varDelta ^{f}x,\,\varDelta ^{f}s$ for any $x > 0$ and $s > 0$. Since these displacements are designed to find feasible iterates for $\left( P_{\nu ^+}\right)$, we call them feasibility search directions. Let

$$\begin{aligned} d^{f}_x = \frac{v\varDelta ^{f} x}{x},\quad d^{f}_s = \frac{v\varDelta ^{f} s}{s}, \end{aligned}$$

(12)

where $v$ is defined in (7), then the system (11) can be expressed as

$$\begin{aligned} \begin{aligned}&\bar{Q}d^{f}_{x}+\bar{R}d^{f}_{s}=\theta \nu r^{0},\,\\&d^{f}_{x}+d^{f}_{s}=v^{-1}-v, \end{aligned} \end{aligned}$$

(13)

where $\bar{Q}$ and $\bar{R}$ are as defined in (9).

3 The new search directions

Consider the kernel function $\psi (t):{\mathbb {R}}_{++}\rightarrow {\mathbb {R}}_{+}$ and its barrier function $\varPsi (v):{\mathbb {R}}^{n}_{++}\rightarrow {\mathbb {R}}_{+}$ as follows

$$\begin{aligned} \psi (t):=\frac{1}{2}\left( t-\frac{1}{t}\right) ^2,~~~\varPsi (v):=\sum _{i=1}^{n}\psi (v_i). \end{aligned}$$

Note that, this kernel function is a special case of the kernel function $\phi (t)$ as follows

$$\begin{aligned} \phi (t)=\frac{t^2-1}{2}+\frac{t^{1-q}-1}{q-1}, \end{aligned}$$

which is applied for linear and semidefinit programming by Peng et al. [21]. Noticing that $\psi '(t)=t-\frac{1}{t^3}$ and doing the transformation $d_x+d_s=-\bigtriangledown \varPsi (v)$ in (8), we obtain the following equivalent system of equations:

$$\begin{aligned} \begin{aligned}&\bar{Q}d_x+\bar{R}d_s = 0,\,\quad x\ge 0,\,\\&d_x+d_s = v^{-3}-v, \, s\ge 0. \end{aligned} \end{aligned}$$

(14)

By this transformation, we obtain the following equivalent system of equations for the centering search directions $\varDelta x,\varDelta s$:

(15)

Similarly, doing transformation $d_x^f+d_s^f=-\bigtriangledown \varPsi (v)$ in (13), we obtain the following equivalent system of equations for finding the scaled search directions $d^f_x$ and $d^f_s$:

$$\begin{aligned} \begin{aligned}&\bar{Q}d_{x}^{f}+\bar{R}d_{s}^{f}=\theta \nu r^0,\quad x\ge 0,\\&d^{f}_{x}+d^{f}_{s}=v^{-3}-v, \, x\ge 0. \end{aligned} \end{aligned}$$

(16)

We get the following system for the feasibility search directions $\varDelta ^f x$ and $\varDelta ^f s$:

(17)

3.1 Proximity function

We need a proximity measure to check how close we are to the $\mu$-center. So, to measure the quality of any approximation $(x, s)$ of $(x(\mu , \nu ), s(\mu ,\nu ))$, we introduce a norm-based proximity function as follows:

$$\begin{aligned} \delta (v):=\delta (x,s;\mu )=\Vert {v^{-2}-v^2}\Vert . \end{aligned}$$

(18)

Note that

$$\begin{aligned} v^2-v^{-2}=0\Leftrightarrow v=e. \end{aligned}$$

Therefore, this proximity function vanishes if and only if the pair $(x,\,s)$ coincides with the $\mu$-center $(x(\mu , \nu ), s(\mu ,\nu ))$.

3.2 Description of the full-Newton step IIPMs

Note that if $\nu =1$ and $\mu =\mu ^{0}$, then $\left( x,\,s\right) =\left( x^{0},\,s^{0}\right)$ is the $\mu$-center of the perturbed problem $P_{\nu }$. These are our initial iterates.

We measure proximity to the $\mu$-center of the perturbed problem $P_{\nu }$ by the quantity $\delta (v)$ as defined in (18). Initially we thus have $\delta (v)=0$. In the sequel we assume that at the start of each iteration, just before the $\mu$-update, $\delta (v)\le \tau$ for a (small) threshold value $\tau >0$. So this is certainly true at the start of the first iteration.

One (main) iteration of our algorithm works as follows. Suppose that for some $\mu \in \left( 0,\,\mu ^{0}\right)$ we have $\left( x,s\right)$ satisfying the feasibility condition (5) for $\nu =\frac{\mu }{\mu ^{0}}$, and $\delta (v)\le \tau$. We reduce $\mu$ to $\mu ^{+}=\left( 1-\theta \right) \mu$, with $\theta \in \left( 0,1\right)$, and find new iterates $\left( x^{+},\,s^{+}\right)$ that satisfy (5), with $\mu$ replaced by $\mu ^{+}$ and $\nu$ by $\nu ^{+}=\frac{\mu ^+}{\mu ^0}$, and such that $x^{T}s\le n\mu ^{+}$ and $\delta \left( x^{+},\,s^{+};\,\mu ^{+}\right) \le \tau$. Note that $\nu ^{+}=\left( 1-\theta \right) \nu$. For this mean we accomplish first one feasibility step and then a few centering steps. The feasibility step serves to get iterates $\left( x^{f},\,s^{f}\right)$ that are strictly feasible for $(P_{\nu ^{+}})$, and close to its $\mu$-center $\left( x\left( \mu ^{+},\nu ^{+}\right) ,\,s\left( \mu ^{+},\nu ^{+}\right) \right)$. Then the centering steps improve the closeness of $\left( x^{f},\,s^{f}\right)$ to the centeral path of $(P_{\nu ^{+}})$ and obtain a pair $(x,\,s)$ that satisfies the condition $\delta \left( x,\,s;\,\mu \right) \le \tau$.A more formal description of the algorithm is given in Fig. 1.

Fig. 1

Infeasible full-Newton-step algorithm

4 Some useful tools

Through the paper, we assume that $\delta :=\delta (v):=\delta \left( x,s;\mu \right)$. Our first lemma in this section provides a lower and an upper bound for the coordinates of $v$ in terms of $\delta$.

Lemma 2

Let $\delta :=\delta (v)$, as defined by (18). Then

$$\begin{aligned} \frac{1}{\sqrt{1+\delta }}\le v_{\min }\le v_{\max }\le \sqrt{1+\delta }. \end{aligned}$$

Proof

The lemma is trivial if $v_{\min }\ge 1$ and $v_{\max }\le 1$. Consider the case that $v_{\min } < 1$. From (18) we derive

$$\begin{aligned} \delta =\Vert v^{-2}-v^2\Vert \ge |v_{i}^{-2}-v_i^2|,~~~1\le i\le n, \end{aligned}$$

which implies

$$\begin{aligned} \delta \ge \frac{1}{v_{\min }^{2}}-v_{\min }^2\ge \frac{1}{v_{\min }^{2}}-1. \end{aligned}$$

On the other hand, if $v_{max} > 1$ then we find

$$\begin{aligned} \delta \ge v_{\max }^2-\frac{1}{v_{\max }^2}\ge v_{\max }^2-1. \end{aligned}$$

The lemma follows directly from the above inequalities. $\square$

By the lemma just made, it is clear that for $i=1,\,\ldots ,\,n$:

$$\begin{aligned} \frac{1}{\sqrt{1+\delta }}&\le v_i\le \sqrt{1+\delta },\end{aligned}$$

(19)

$$\begin{aligned} \frac{1}{\sqrt{1+\delta }}&\le v_i^{-1}\le \sqrt{1+\delta }. \end{aligned}$$

(20)

Using the next lemma we obtain some bounds for the unique solution of system (14).

Lemma 3

(Lemma 2 in [8]) Let $(Q, R)$ in the HLCP be a $P_*(\kappa )$-pair, then for any $(x,s)\in {\mathbb {R}}^{n}_{++}\times {\mathbb {R}}^{n}_{++}$ and any $a\in {\mathbb {R}}^n$ the unique solution $(u,v)$ of the linear system

$$\begin{aligned} \begin{aligned} su+xv&=a,\\ Qu+Rv&=0, \end{aligned} \end{aligned}$$

(21)

satisfies

$$\begin{aligned} \Vert Du\Vert ^2+\Vert D^{-1}v\Vert ^2\le \left( 1+2\kappa \right) \Vert \tilde{a}\Vert ^2, ~~~u^Tv\le \frac{1}{4}\Vert \tilde{a}\Vert ^2, \end{aligned}$$

where $D=X^{-\frac{1}{2}}S^{\frac{1}{2}}$ and $\tilde{a}=(xs)^{-\frac{1}{2}}~a.$

Corollary 1

The unique solution $(d_x,d_s)$ of the linear system (14) satisfies

$$\begin{aligned} \Vert d_x\Vert ^2+\Vert d_s\Vert ^2\le \left( 1+2\kappa \right) \left( 1+\delta \right) \delta ^2, ~~~\left( d_x\right) ^Td_s\le \frac{1}{4}\left( 1+\delta \right) \delta ^2. \end{aligned}$$

Proof

Comparing system (15) with (21) and let $a=\mu v\left( v^{-3}-v\right)$. Then we have $\tilde{a}=\frac{a}{\sqrt{\mu }~v}=\sqrt{\mu }\left( v^{-3}-v\right)$. So we may write

$$\begin{aligned} \Vert \tilde{a}\Vert ^2=\mu \Vert v^{-3}-v\Vert ^2=\mu \Vert v^{-1}\left( v^{-2}-v^2\right) \Vert ^2&\le \mu \Vert v^{-1}\Vert _{\infty }^2\Vert v^{-2}-v^2\Vert ^2 \\&\le \mu \left( 1+\delta \right) \delta ^2, \end{aligned}$$

where the last inequality follows from (20). Using Lemma 3 we derive that

$$\begin{aligned} \Vert D\varDelta x\Vert ^2+\Vert D^{-1}\varDelta s\Vert ^2\le \mu \left( 1+2\kappa \right) \left( 1+\delta \right) \delta ^2,~~~\left( \varDelta x\right) ^T\varDelta s\le \frac{\mu }{4}\left( 1+\delta \right) \delta ^2. \end{aligned}$$

Since $D\varDelta x=\sqrt{\mu }~d_x$, $D^{-1}\varDelta s=\sqrt{\mu }~d_s$ and $\left( \varDelta x\right) ^T\varDelta s=\mu \left( d_x\right) ^Td_s$, the corollary follows. $\square$

Let

$$\begin{aligned} \omega _i:=\omega _i(v): = \frac{1}{2}\sqrt{|d_{x_{i}}|^2+|d_{s_{i}}|^{2}}~,~~~~\omega :=\omega (v):=\Vert \left( \omega _1,\cdots ,\omega _n\right) \Vert . \end{aligned}$$

(22)

Then we have

$$\begin{aligned}&\displaystyle \left( d_x\right) ^Td_s\le \Vert d_x\Vert \Vert d_s\Vert \le \frac{1}{2}\left( \Vert d_x\Vert ^2+\Vert d_s\Vert ^2\right) =2\omega ^2, \end{aligned}$$

(23)

$$\begin{aligned}&\displaystyle |d_{x_{i}}d_{s_{i}}|=|d_{x_i}||d_{s_i}|\le \frac{1}{2}\left( |d_{x_{i}}|^2+|d_{s_{i}}|^2\right) =2\omega _i^{2}\le 2\omega ^2,~i=1,\cdots ,n.~~ \end{aligned}$$

(24)

Lemma 4

Let $\omega$ be as defined in (22). Then the following holds:

$$\begin{aligned} \omega ^2\le \frac{1+2\kappa }{4}\left( 1+\delta \right) \delta ^2. \end{aligned}$$

Proof

Using the definition of ${\omega }$ and corollary 1 , the lemma follows. $\square$

Lemma 5

(Lemma A.1 in [17]) Let $f_i={\mathbb {R}}_+\rightarrow {\mathbb {R}}, ~i=1,\cdots ,n$, be a convex function. Then for any nonzero vector $z\in {\mathbb {R}}^{n}_+$, the following inequality holds

$$\begin{aligned} \sum _{i=1}^n f_i(z_i)\le \frac{1}{e^Tz}\sum _{j=1}^n z_j\left( f_j\left( e^Tz\right) +\sum _{i\ne j}f_i(0)\right) . \end{aligned}$$

5 Analysis of the centering steps

We denote the result of the full-Newton step given by system (15) at $(x, s)$ by $(x^+ , s^+ )$, i.e.,

$$\begin{aligned} x^{+}=x+\varDelta x,\,~~~s^{+}=s+\varDelta s. \end{aligned}$$

5.1 The feasibility of the centering steps

Using (7) and system (15), we may write

$$\begin{aligned} x^+s^+\!\!=\!\!\left( x+\varDelta x\right) \left( s+\varDelta s\right) \!=\!xs+\left( s\varDelta x+x\varDelta s\right) +\varDelta x \varDelta s\!=\!\mu \left( v^{-2}+d_xd_s\right) .\nonumber \\ \end{aligned}$$

(25)

In the following lemma we state a feasibility condition for the centering steps.

Lemma 6

The iterates $\left( x^+,s^+\right)$ are strictly feasible if and only if $v^{-2}+d_xd_s>0$.

Proof

If $x^+$ and $s^+$ are positive, then the equality (25) makes it clear that $v^{-2}+d_xd_s>0$. For the prove of the converse implication, we introduce a step length $\alpha \in [0,1]$ and we define

$$\begin{aligned} x^{\alpha }=x+\alpha \varDelta x,~~~~s^{\alpha }=s+\alpha \varDelta s. \end{aligned}$$

Then we have $x^0 = x$, $x^1 = x^+$ and similar relations for s. Hence we obtain $x^0s^0 = xs > 0$. Using (25), we can write

$$\begin{aligned} x^{\alpha }s^{\alpha }&= xs+\alpha \left( s\varDelta x+x\varDelta s\right) +\alpha ^2\varDelta x\varDelta s\\&= \mu \left( v^2+\alpha \left( v^{-2}-v^2\right) +\alpha ^{2}d_xd_s\right) \\&> \mu \left( v^2+\alpha \left( v^{-2}-v^2\right) -\alpha ^{2}v^{-2}\right) \\&= \mu {(1-\alpha )v^2+\alpha \left( 1-\alpha \right) v^{-2}}\\&= \mu (1-\alpha )\left( v^2+\alpha v^{-2}\right) \ge 0 \end{aligned}$$

So $x^{\alpha }s^{\alpha } > 0$ for $\alpha \in [0,1]$. Thus, none of the entries of $x^{\alpha }$ and $s^{\alpha }$ vanishes for $\alpha \in [0,1]$. Since $x^0$ and $s^0$ are positive, and $x^{\alpha }$ and $s^{\alpha }$ are depend linearly on $\alpha$, this implies that $x^{\alpha }>0$ and $s^{\alpha }>0$ for $\alpha \in [0,1]$. Hence, $x^1$ and $s^1$ must be positive, which proves that $x^+$ and $s^+$ are positive. $\square$

Corollary 2

The iterates $(x^+, s^+)$ are strictly feasible if $\Vert d_xd_s\Vert _{\infty }<\frac{1}{1+\delta }$.

Proof

From (19) and Lemma 6, the corollary follows. $\square$

5.2 The effect of a full-Newton step on the proximity function

The following lemma investigates the effect of a full-Newton step on the proximity measure.

Lemma 7

Let $\delta \le \frac{1}{2\sqrt{1+2\kappa }}$. Then after a full-Newton step, we have

$$\begin{aligned} \delta ^+:=\delta \left( x^+,s^+;\mu \right) \le 5.4247\sqrt{1+2\kappa }~\delta . \end{aligned}$$

Proof

Let $v^+:=\sqrt{\frac{x^+s^+}{\mu }}$. Then from (25), we have $\left( v^+\right) ^2=v^{-2}+d_xd_s$. We may write

$$\begin{aligned} \left( \delta ^+\right) ^2&= \Vert \left( v^+\right) ^2-\left( v^+\right) ^{-2}\Vert ^2\\&= \sum _{i=1}^n\left( \left( v_i^+\right) ^4+\left( v_i^+\right) ^{-4}-2\right) \\&= \sum _{i=1}^n\left( \left( v_i^{-2}+d_{x_i}d_{s_i}\right) ^2+\frac{1}{\left( v_i^{-2}+d_{x_i}d_{s_i}\right) ^2}-2\right) \\&\le \sum _{i=1}^n\left( \left( v_i^{-2}+2\omega _i^2\right) ^2+\frac{1}{\left( v_i^{-2}-2\omega _i^2\right) ^2}-2\right) , \end{aligned}$$

where the inequality is due to (24). For each $i=1,\cdots ,n$, we define the function

$$\begin{aligned} f_i(z_i)=\left( v_i^{-2}+z_i\right) ^2+\frac{1}{\left( v_i^{-2}-z_i\right) ^2}-2. \end{aligned}$$

Note that this function is convex in $z_i$. Taking $z_i=2\omega _i^2$, using Lemma 5, we have

$$\begin{aligned} \left( \delta ^+\right) ^2&\le \sum _{i=1}^{n}f_i(2\omega _i^{2})\le \frac{1}{2\omega ^2}\sum _{j=1}^{n}2\omega _j^2\left( f_j(2\omega ^2)+\sum _{i\ne j}f_i(0)\right) \\&= \frac{1}{2\omega ^2}\sum _{j=1}^{n}2\omega _j^2\left( \left( v_j^{-2}+2\omega _j^2\right) ^2+\frac{1}{\left( v_j^{-2}\!-\!2\omega _j^2\right) ^2}\!-\!2\!+\!\sum _{i\ne j}\left( v_i^{-4}\!+\!\frac{1}{v_i^{-4}}\!-\!2\!\!\right) \!\!\right) \\&= \frac{1}{2\omega ^2}\sum _{j=1}^{n}2\omega _j^2\left( \left( v_j^{-2}+2\omega _j^2\right) ^2\!+\!\frac{1}{\left( v_j^{-2}\!-\!2\omega _j^2\right) ^2}-2\!+\!\delta ^2 \!-\!\left( v_j^{-4}\!+\! \frac{1}{v_j^{-4}}\!-\!2\!\right) \!\!\right) \\&= \frac{1}{2\omega ^2}\sum _{j=1}^{n}2\omega _j^2\left( 4\omega _j^4+4\omega _j^2v_j^{-2}+\frac{4\omega _j^2v_j^{-2}-4\omega _j^4}{v_j^{-8}+4\omega _j^4v_j^{-4} -4\omega _j^2v_j^{-6}}+\delta ^2\right) . \end{aligned}$$

Notice that if $\delta \le \frac{1}{2\sqrt{1+2\kappa }}$, then from (20) and Lemma 4, we may write for $1\le j\le n$:

$$\begin{aligned} v_j^{-2}-4\omega _j^2\ge v_j^{-2}-4\omega ^2\ge \frac{1}{1+\delta }-4\omega ^2\ge \frac{1}{1+\delta }-\left( 1+2\kappa \right) \left( 1+\delta \right) \delta ^2\ge 0. \end{aligned}$$

Therefore the above inequalities may continue as follows:

$$\begin{aligned} \left( \delta ^+\right) ^2&\le \frac{1}{2\omega ^2}\sum _{j=1}^{n}2\omega _j^2\left( 4\omega _j^4+4\omega _j^2v_j^{-2}+\frac{4\omega _j^2v_j^{-2}}{v_j^{-6} \left( v_j^{-2}-4\omega _j^2\right) } +\delta ^2\right) \\&\le \frac{1}{2\omega ^2}\sum _{j=1}^{n}2\omega _j^2\left( 4\omega ^4+4\omega ^2v_j^{-2}+\frac{4\omega ^2v_j^{-2}}{v_j^{-6}\left( v_j^{-2}-4\omega ^2\right) } +\delta ^2\right) \\&\le 4\omega ^4+4\omega ^2\left( 1+\delta \right) +\frac{4\omega ^2\left( 1+\delta \right) }{\frac{1}{\left( 1+\delta \right) ^3}\left( \frac{1}{1+\delta }-4\omega ^2\right) }+\delta ^2\\&\le \Bigg (\frac{\left( 1+2\kappa \right) ^2\left( 1+\delta \right) ^2\delta ^2}{4}+\left( 1+2\kappa \right) \left( 1+\delta \right) ^2 \\&+\frac{\left( 1+2\kappa \right) \left( 1+\delta \right) ^5}{\frac{1}{1+\delta }-\left( 1+2\kappa \right) \left( 1+\delta \right) \delta ^2} +1\Bigg )\delta ^2\\&\le 29.4263\left( 1+2\kappa \right) \delta ^2, \end{aligned}$$

where in the third and forth inequality, we used (20) and Lemma 4 respectively. The last inequality, is due to the assumption $\delta \le \frac{1}{2\sqrt{1+2\kappa }}$. $\square$

5.3 The value of $x^Ts$ after doing the step

The next lemma gives an upper bound for the quantity $x^Ts$ after each full-Newton step.

Lemma 8

One has

$$\begin{aligned} \left( x^+\right) ^Ts^+ \le \mu \left( 1+\delta \right) \left( n+\frac{\delta ^2}{4}\right) . \end{aligned}$$

Proof

From (25), (20) and Corollary 1 we derive:

$$\begin{aligned} \left( x^+\right) ^Ts^+=\mu e^T\left( v^+\right) ^2=\mu \left( e^Tv^{-2}+\left( d_x\right) ^Td_s\right) \le \mu \left( \left( 1+\delta \right) n+\frac{\left( 1+\delta \right) \delta ^2}{4}\right) , \end{aligned}$$

which proves the lemma. $\square$

6 Analysis of the feasibility step

We denote the resulting vectors of the feasibility step given by system (17) at $(x, s)$ by $(x^f , s^f )$, i.e.,

$$\begin{aligned} x^{f}=x+\varDelta ^f x,\,~~~s^{f}=s+\varDelta ^f s. \end{aligned}$$

6.1 The feasibility of the feasibility step

From (16) we may write

$$\begin{aligned} x^fs^f=\mu \left( v^{-2}+d_x^{f}d_s^{f}\right) . \end{aligned}$$

(26)

Lemma 9

The iterates $\left( x^f,s^f\right)$ are strictly feasible if and only if

$$\begin{aligned} v^{-2}+d_x^{f}d_s^{f}>0. \end{aligned}$$

Proof

The proof of this lemma is the same as that of Lemma 6.$\square$

Corollary 3

The iterates $(x^f, s^f)$ are strictly feasible if $\Vert d^f_xd^f_s\Vert _{\infty }<\frac{1}{1+\delta }$.

Proof

From (20) and Lemma 9 the corollary follows.$\square$

Let

$$\begin{aligned} \omega ^f_i:=\omega _i^f(v):=\frac{1}{2}\sqrt{|d^f_{x_{i}}|^2+|d^f_{s_{i}}|^2}~,~~~\omega ^f:=\omega ^f(v):=\left\| {\left( \omega ^f_1,\cdots ,\omega ^f_n\right) }\right\| .\nonumber \\ \end{aligned}$$

(27)

Then similar to (23) and (24), we have:

$$\begin{aligned}&\left( d_x^f\right) ^Td_s^f\le \Vert d^f_x\Vert \Vert d^f_s\Vert \le \frac{1}{2}\left( \Vert d^f_x\Vert ^2+\Vert d^f_s\Vert ^2\right) \!=\!2(\omega ^f)^2, \end{aligned}$$

(28)

$$\begin{aligned}&|d^f_{x_{i}}d^f_{s_{i}}|=|d^f_{x_i}||d^f_{s_i}|\!\le \!\frac{1}{2}\left( |d^f_{x_{i}}|^2+|d^f_{s_{i}}|^2\right) \!=\!2(\omega ^f_i)^{2}\le 2(\omega ^f)^2,~i=1,\ldots ,n.\qquad \quad \end{aligned}$$

(29)

Using this, in the next subsection we investigate the effect of the feasibility step on the proximity function.

6.2 An upper bound for proximity function after a feasibility step

Lemma 10

Let $\mu ^+=(1-\theta )\mu$, $v^f=\sqrt{\frac{x^fs^f}{\mu ^+}}$ and $\delta \le \frac{1}{2\sqrt{1+2\kappa }}$ , then we have

$$\begin{aligned}&\delta \left( v^f\right) ^2\le \left( 1-\theta \right) ^2\left( 4\left( \omega ^f\right) ^4+4\left( \omega ^f\right) ^2\left( 1+\delta \right) +\frac{4\left( \omega ^f\right) ^2\left( 1+\delta \right) ^4}{\frac{1}{1+\delta } -4\left( \omega ^f\right) ^2}+\delta ^2\right) \\&\quad +\left( \!\left( \frac{2\theta -\theta ^2}{1-\theta }\right) ^2+2\left( 2\theta -\theta ^2\right) \!\right) \left( \!\left( 1+\delta \right) ^2n+ 4\left( \omega ^f\right) ^4+4\left( 1+\delta \right) \left( \omega ^f\right) ^2\!\right) \\&\quad -2\left( 2\theta -\theta ^2\right) n. \end{aligned}$$

Proof

Let $u=v^{-2}+d^f_xd^f_s$. Using (26) we derive

$$\begin{aligned} \left( v^f\right) ^2=\frac{\mu \left( v^{-2}+d_x^{f}d_s^{f}\right) }{\mu ^+}=\frac{\left( v^{-2}+d_x^{f}d_s^{f}\right) }{1-\theta }=\frac{u}{1-\theta }, \end{aligned}$$

then, we may write

$$\begin{aligned} \delta \left( v^f\right) ^2&= \Vert \frac{u}{1-\theta }-\left( 1-\theta \right) u^{-1}\Vert ^2\\&= \Vert \left( 1-\theta \right) \left( u-u^{-1}\right) +\frac{2\theta -\theta ^2}{1-\theta }u\Vert ^2\\&= \left( 1-\theta \right) ^2\Vert u-u^{-1}\Vert ^2+ \left( \frac{2\theta -\theta ^2}{1-\theta }\right) ^2\Vert u\Vert ^2+2\left( 2\theta \!-\!\theta ^2\right) u^T\left( u-u^{-1}\right) \\&= \left( 1\!-\!\theta \right) ^2\Vert u\!-\!u^{-1}\Vert ^2\!+\left( \!\left( \frac{2\theta \!-\!\theta ^2}{1-\theta }\right) ^2+2\left( 2\theta \!-\!\theta ^2\right) \right) \Vert u\Vert ^2\!-\!2\left( 2\theta -\theta ^2\right) n. \end{aligned}$$

Note that, using (28) and (29), we have

$$\begin{aligned} \Vert u\Vert ^2=e^Tu^2&= e^Tv^{-4}+\Vert d_x^fd_s^f\Vert ^2+2\left( v^{-2}\right) ^Td_x^fd_s^f\\&\le \left( 1+\delta \right) ^2n+4\left( \omega ^f\right) ^4+4\left( 1+\delta \right) \left( \omega ^f\right) ^2. \end{aligned}$$

By the same way as in the proof of Lemma 7, we may derive

$$\begin{aligned} \Vert u-u^{-1}\Vert ^2=4\left( \omega ^f\right) ^4+4\left( \omega ^f\right) ^2\left( 1+\delta \right) +\frac{4\left( \omega ^f\right) ^2\left( 1+\delta \right) ^4}{\frac{1}{1+\delta }-4\left( \omega ^f\right) ^2}+\delta ^2. \end{aligned}$$

So the proof is completed. $\square$

Note that in the algorithm, for using the result of Lemma 7 after performing the feasibility step, we need the following condition be satisfied

$$\begin{aligned} \delta \left( x^f,s^f;\mu ^+\right) \le \frac{1}{2\sqrt{1+2\kappa }}. \end{aligned}$$

(30)

Using Lemma 10, this is certainly true, if

$$\begin{aligned}&\left( 1-\theta \right) ^2\left( 4\left( \omega ^f\right) ^4+4\left( \omega ^f\right) ^2\left( 1+\delta \right) +\frac{4\left( \omega ^f\right) ^2\left( 1+\delta \right) ^4}{\frac{1}{1+\delta }-4\left( \omega ^f\right) ^2}+\delta ^2\right) ~\nonumber \\&\quad \quad +\left( \left( \frac{2\theta -\theta ^2}{1-\theta }\right) ^2\!+\!2\left( 2\theta \!-\!\theta ^2\right) \right) \left( \left( 1+\delta \right) ^2n\!+\! 4\left( \omega ^f\right) ^4\!+\!4\left( 1+\delta \right) \left( \omega ^f\right) ^2\right) \nonumber \\&\quad \quad -2\left( 2\theta -\theta ^2\right) n\nonumber \\&\quad \le \frac{1}{4\left( 1+2\kappa \right) }. \end{aligned}$$

(31)

By some elementary calculations, we obtain that if

$$\begin{aligned} \omega ^f&\le \frac{1}{8\left( 1+2\kappa \right) },\end{aligned}$$

(32)

$$\begin{aligned} \delta&\le \tau \le \frac{1}{10\left( 1+2\kappa \right) },\end{aligned}$$

(33)

$$\begin{aligned} 0&\le \theta \le \frac{1}{20n(1+2\kappa )}, \end{aligned}$$

(34)

then the inequality (31) is satisfied.

6.3 An upper bound for $\omega ^f$

We start by finding some bounds for the unique solution of the linear system (17).

Lemma 11

(Lemma 3.3 in [8]) Let $(Q, R)$ in the HLCP be a $P_*(\kappa )$-pair, then the linear system

$$\begin{aligned} \begin{aligned} su+xv&=a,\\ Qu+Rv&=\tilde{b}, \end{aligned} \end{aligned}$$

(35)

has a unique solution $w=(u,v)$, for any $z=(x,s)\in R^{n}_{++}\times {\mathbb {R}}^{n}_{++}$ and any $a,\tilde{b}\in R^{n}$, such that the following inequality is satisfied:

$$\begin{aligned} \Vert w\Vert _z\le \sqrt{1+2\kappa }\Vert \tilde{a}\Vert +\left( 1+\sqrt{2+4\kappa }\right) \xi (z,\tilde{b}). \end{aligned}$$

Here

$$\begin{aligned} \Vert w\Vert _z^{2}&= \Vert (u,v)\Vert _z^2=\Vert Du\Vert ^2+\Vert D^{-1}v\Vert ^2,\\ \xi (z,\tilde{b})^{2}&= \min \{\Vert (\tilde{u},\tilde{v})\Vert _{z}^{2} :Q\tilde{u}+R\tilde{v}=\tilde{b}\}, \end{aligned}$$

and $\tilde{a}$ and $D$ are defined in Lemma 3.

Comparing system (35) with (17) and considering $w=(u,v)=(\varDelta ^{f}x,\varDelta ^{f}s)$, $a=\mu \left( v^{-2}-v^2\right)$, $\tilde{b}=\theta \nu r^0$, $z=(x,s)$ in system (35), we have

$$\begin{aligned}&\Vert D\varDelta ^{f}x\Vert ^2+\Vert D^{-1}\varDelta ^{f}s\Vert ^2\nonumber \\&\quad \le \left( \sqrt{1+2\kappa }\Vert (xs)^{-1/2}\left( \mu \left( v^{-2}-v^2\right) \right) \Vert + (1+\sqrt{2+4\kappa })\xi (z,\theta \nu r^0)\right) ^2.\qquad \end{aligned}$$

(36)

From (20) and the definition of $\delta$ in (18), we also have

$$\begin{aligned} \left\| {(xs)^{-\frac{1}{2}}\left( \mu \left( v^{-2}-v^2\right) \right) }\right\| =\left\| {\sqrt{\mu }v^{-1} \left( v^{-2}-v^2\right) }\right\|&\le \sqrt{\mu }\left\| {v^{-1}}\right\| _{\infty }\left\| {v^{-2}-v^2}\right\| \\&\le \sqrt{\mu \left( 1+\delta \right) }~\delta . \end{aligned}$$

Also by the definition of $\xi (z,\tilde{b})$, it is obvious that

$$\begin{aligned} \xi (z,\theta \nu r^0)=\theta \nu \xi (z,r^0). \end{aligned}$$

Furthermore, noticing the definitions of $\varDelta ^f x$ and $\varDelta ^f s$, we may write $D\varDelta ^f_x=\sqrt{\mu }~d^f_x$ and $D^{-1}\varDelta ^f_s=\sqrt{\mu }~d^f_s.$ Substituting the above equations in (36), we have

$$\begin{aligned} \left( \omega ^f\right) ^2\le \frac{1}{\mu }\left( \frac{1}{2}\sqrt{\mu \left( 1+\delta \right) (1+2\kappa )}~\delta +\frac{1}{2}\left( 1+\sqrt{2+4\kappa }\right) \theta \nu \xi (z, r^0)\right) ^2. \end{aligned}$$

(37)

Now we specify our initial iterates $\left( x^0,\,s^0\right)$. Assuming that $\rho _p$ and $\rho _d$ are such that

$$\begin{aligned} \Vert x^*\Vert \le \rho _p ,\,\quad \Vert s^*\Vert \le \rho _d,\, \end{aligned}$$

(38)

for some optimal solutions $\left( x^*,\,s^*\right)$ of $(P)$, as usual we start the algorithm with

$$\begin{aligned} x^0=\rho _p\,e,\,\quad s^0=\rho _d\,e,\,\quad \mu ^0=\rho _p\,\rho _d. \end{aligned}$$

(39)

The lemma below achieves a bound for the quantity $\xi (z,r^0)$ in (37).

Lemma 12

(Lemma 4.6 in [3]) Let $\xi (\cdot , \cdot )$ be as defined in Lemma 11. Then the following holds:

$$\begin{aligned} \xi (z,r^0)\le \sqrt{\frac{\rho _p^2}{\mu v_{\min }^2}\Vert s\Vert _{1}^{2}+\frac{\rho _d^2}{\mu v_{\min }^2}\Vert x\Vert _{1}^{2}}~. \end{aligned}$$

Thanks to the next Lemmas, we will obtain some upper bounds for $\Vert x\Vert _1$ and $\Vert s\Vert _1$.

Lemma 13

(Lemma 4.7 in [3]) Let $\left( x,\,s\right)$ be feasible for the perturbed problem $P_{\nu }$ and $\left( x^0,\,s^0\right)$ as defined in (39). Then for any optimal solution $\left( x^*,\,s^*\right)$, we have

$$\begin{aligned} \nu \left( x^Ts^0+s^Tx^0\right) \le (1+4\kappa )\left( \nu ^2n\mu ^0+\nu (1-\nu )\left( (x^*)^Ts^0+(x^0)^Ts^*\right) +x^Ts\right) . \end{aligned}$$

Lemma 14

Let $\left( x,\,s\right)$ be feasible for the perturbed problem $(P_{\nu })$ and $\left( x^0,\,s^0\right)$ as defined in (39). Then we have

$$\begin{aligned} \Vert x\Vert _1&\le (1+4\kappa )\left( 3n+n\delta \right) \rho _p,\,\end{aligned}$$

(40)

$$\begin{aligned} \Vert s\Vert _1&\le (1+4\kappa ) \left( 3n+n\delta \right) \rho _d. \end{aligned}$$

(41)

Proof

Since $x^0=\rho _p\,e,\,s^0=\rho _d\, e,\,\Vert x^*\Vert _\infty \le \rho _p$ and $\Vert s^*\Vert _\infty \le \rho _d$, we derive

$$\begin{aligned} \left( s^0\right) ^Tx^*+\left( x^0\right) ^Ts^*\le \rho _p\,\left( e^Ts^0\right) +\rho _d\, \left( e^Tx^0\right) =2\,n\,\rho _p\,\rho _d. \end{aligned}$$

Also $\left( x^0\right) ^Ts^0=n\,\rho _p\,\rho _d$. Substituting these values in Lemma 13 and noting that $\mu ^0=\rho _p\rho _d$, using (19), we have

$$\begin{aligned} x^Ts^0+s^Tx^0&\le (1+4\kappa )\left( \nu n\rho _p\rho _d+2(1-\nu )n\rho _p\rho _d+\frac{x^Ts}{\nu }\right) \\&= (1+4\kappa )\left( 2n\rho _p\rho _d-\nu n\rho _p\rho _d+\frac{x^Ts}{\nu }\right) \\&\le (1+4\kappa )\left( 2n\rho _p\rho _d+\frac{x^Ts}{\nu }\right) =(1+4\kappa )\left( 2n\rho _p\rho _d+\frac{\mu (e^Tv^2)}{\nu }\right) \\&= (1+4\kappa )\left( 2n\rho _p\rho _d+\rho _p\rho _d\Vert v\Vert ^2\right) \\&\le (1+4\kappa )\left( 2n\rho _p\rho _d+\rho _p\rho _d \left( 1+\delta \right) n\right) \\&= (1+4\kappa )\left( 3n+n\delta \right) \rho _p\rho _d. \end{aligned}$$

Since $x^0,\,s^0,\,x$ and $s$ are positive, we obtain

$$\begin{aligned} x^Ts^0&\le (1+4\kappa )\left( 3n+n\delta \right) \rho _p\rho _d ,\,\\ s^Tx^0&\le (1+4\kappa )\left( 3n+n\delta \right) \rho _p\rho _d. \end{aligned}$$

Due to $x^0=\rho _p\,e$ and $s^0=\rho _d\,e$, these statements follow the lemma. $\square$

Applying (40) and (41) in Lemma (12), using (19), we derive

$$\begin{aligned} \xi (z,r^0)&\le \sqrt{\frac{2\rho _p^2\rho _d^2}{\frac{\mu }{1+\delta }}(1+4\kappa )^2\left( 3n+n\delta \right) ^2}\nonumber \\&= \sqrt{\frac{2(1+\delta )}{\mu }}~\rho _p\rho _d(1+4\kappa )\left( 3n+n\delta \right) . \end{aligned}$$

(42)

Now substituting (42) in (37), we obtain

$$\begin{aligned} \left( \omega ^f\right) ^2&\le \Bigg (\frac{1}{2}\sqrt{(1+2\kappa )\left( 1+\delta \right) }~\delta + \theta \left( \frac{1}{\sqrt{2}}+ \sqrt{1+2\kappa }\right) \sqrt{1+\delta }\left( 1+4\kappa \right) \nonumber \\&\left( 3n+n\delta \right) \Bigg )^2. \end{aligned}$$

(43)

6.4 The values for $\theta$ and $\tau$

In this subsection, we specify some values for the algorithm’s parameters $\tau$ and $\theta$ such that our main targets are achieved. We have found that $\delta (x^f, s^f; \mu ^+)<\frac{1}{2\sqrt{1+2\kappa }}$ holds if the inequalities (32), (33) and (34) are satisfied. Then by (43), inequality (32) holds if

$$\begin{aligned}&\frac{1}{2}\sqrt{(1+2\kappa )\left( 1+\delta \right) }~\delta +\theta \left( \frac{1}{\sqrt{2}}+\sqrt{1+2\kappa }\right) \sqrt{1+\delta }\left( 1+4\kappa \right) \left( 3n+n\delta \right) \\&\quad \le \frac{1}{8\left( 1+2\kappa \right) }. \end{aligned}$$

Obviously, the left side of the above inequality is increasing in $\delta$. Using this, one may easily verify that the above inequality is satisfied if

$$\begin{aligned} \tau =\frac{1}{10(1+2\kappa )^2},\,\quad \theta =\frac{1}{20n\left( 1+\sqrt{1+2\kappa }\right) ^2(1+2\kappa )^2},\,\end{aligned}$$

(44)

which are in agreement with (32) and (33). Note that by Corollary 3, the feasibility step is strictly feasible if $\Vert d_x^fd_s^f\Vert _{\infty }<\frac{1}{1+\delta }$. From 29 we find that $\Vert d_x^fd_s^f\Vert _{\infty }\le 2(\omega ^f)^2$. Therefore $(x^f,s^f)$ are strictly feasible if $(\omega ^f)^2<\frac{1}{2(1+\delta )}$. Using (43), this inequality is certainly satisfied whenever

$$\begin{aligned}&\frac{1}{2}\sqrt{(1+2\kappa )\left( 1+\delta \right) }~\delta +\theta \left( \frac{1}{\sqrt{2}}+\sqrt{1+2\kappa }\right) \sqrt{1+\delta }\left( 1+4\kappa \right) \left( 3n+n\delta \right) \\&\quad < \frac{1}{\sqrt{2(1+\delta )}}. \end{aligned}$$

As is mentioned above, the left side of this inequality is monotonically increasing with respect to $\delta$ while the right side is monotonically decreasing. So substituiting $\delta$ by $\tau$ gives an upper bound for its left side and a lower bound for its right side. Consequently $(x^f,s^f)$ are strictly feasible if

$$\begin{aligned}&\frac{1}{2}\sqrt{(1+2\kappa )\left( 1+\tau \right) }~\tau +\theta \left( \frac{1}{\sqrt{2}}+\sqrt{1+2\kappa }\right) \sqrt{1+\tau }\left( 1+4\kappa \right) \left( 3n+n\tau \right) \nonumber \\&\quad <\frac{1}{\sqrt{2(1+\tau )}}. \end{aligned}$$

(45)

But with the values of $\tau$ and $\theta$ in (44), an upper bound for the left side of (45) is 0.1220 while a lower bound for its right side is 0.6742. Therefore (42) also guarantees the strict feasibility of the feasibility step.

7 Complexity analysis

Let $\delta \left( x^f,\,s^f;\,\mu ^+\right) \le \frac{1}{2\sqrt{1+2\kappa }}$. Starting at $(x^f,\,s^f)$ we repeatedly apply full-Newton steps until the $k-$iterate, denoted as $\left( x^+,\,s^+\right) :=(x^k,\,s^k)$, satisfies $\delta \left( x^k,\,s^k;\,\mu ^+\right) \le \tau$. We can estimate the required number of centering steps by using Lemma 7. Let $\delta (v^k)=\delta \left( x^k,s^k;\mu ^+\right)$, $\delta (v^0)=\delta \left( x^f,s^f;\mu ^+\right)$ and $\gamma =5.4247\sqrt{1+2\kappa }$. It then follows that

$$\begin{aligned} \delta \left( v^k\right) \le \left( \gamma \delta \left( v^{k-1}\right) \right) \le \left( \gamma \left( \gamma \delta \left( v^{k-2}\right) \right) \right) \le \cdots \le \gamma ^k\delta \left( v^0\right) . \end{aligned}$$

Using the definition of $\gamma$ and $\delta \left( v^0\right) \le \frac{1}{2\sqrt{1+2\kappa }}$, this gives

$$\begin{aligned} \delta \left( v^k\right) \le \left( 5.4247\sqrt{1+2\kappa }~\right) ^k\frac{1}{2\sqrt{1+2\kappa }}\le 2.7124\left( 5.4247\sqrt{1+2\kappa }\right) ^{k-1}. \end{aligned}$$

Hence we certainly have $\delta \left( x^+,s^+;\mu ^+\right) \le \tau$, if

$$\begin{aligned} 2.7124\left( 5.4247\sqrt{1+2\kappa }~\right) ^{k-1}\le \tau . \end{aligned}$$

(46)

Taking logarithms at both sides, this reduces to

$$\begin{aligned} \left( k-1\right) \log 5.4247\sqrt{1+2\kappa }\le \log \frac{\tau }{2.7124}. \end{aligned}$$

Thus we find that after no more than

$$\begin{aligned} 1+\left\lceil \frac{\log \frac{\tau }{2.7124}}{\log 5.4247\sqrt{1+2\kappa }}\right\rceil , \end{aligned}$$

(47)

centering steps, we have iterates $\left( x^+,s^+\right)$ that satisfy $\delta \left( x^+,\,s^+;\,\mu ^+\right) \le \tau$.

Substituting the value of $\tau$ from (44) in (47) implies that at most

$$\begin{aligned} 1+\left\lceil \frac{\log \frac{1}{27.124(1+2\kappa )^2}}{\log 5.4247\sqrt{1+2\kappa }}\right\rceil , \end{aligned}$$

centering steps are needed in our algorithm.

Note that in each main iteration of the algorithm, both the value of $x^Ts$ and the norm of the residual are reduced by the factor $1-\theta$. Hence, the total number of main iterations is bounded above by

$$\begin{aligned} \frac{1}{\theta }\log \frac{\max \left\{ \left( x^0\right) ^Ts^0,\,\Vert r^0\Vert \right\} }{\varepsilon }. \end{aligned}$$

Due to (44), we may state without further proof, the main result of the paper:

Theorem 1

If $(P)$ has an optimal solution $\left( x^*,\,s^*\right)$ such that $\Vert x^*\Vert \le \rho _p$ and $\Vert s^*\Vert \le \rho _d$, then after at most

$$\begin{aligned}&20n\left( 1+\sqrt{1+2\kappa }\right) ^2(1+2\kappa )^2\left( 1+\left\lceil \frac{\log \frac{1}{27.124(1+2\kappa )^2}}{\log 5.4247\sqrt{1+2\kappa }}\right\rceil \right) \\&\quad \log \frac{\max \left\{ \left( x^0\right) ^Ts^0,\,\Vert r^0\Vert \right\} }{\varepsilon }, \end{aligned}$$

iterations, the algorithm finds an $\varepsilon$-solution of $P_*(\kappa )-HLCP$.

8 Concluding remarks and further research

We generated the new search directions for full-Newton step IIPM based on a kernel function for $P_*(\kappa )$-HLCP. The complexity bound for the algorithm admits the best-known result for IIPMs. In general, the algorithm belongs to a kind of small-update IIPMs. According to the default value for $\theta$ in (44), for a $P_*(\kappa )$-HLCP with large data, one can not expect a good performance for the algorithm. Further research may focus on to design the kernel function based large-update IIPMs.