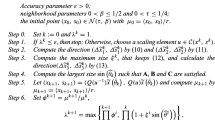A full step infeasible interior-point method for Cartesian $P_{*}(\kappa )$-SCLCP

Abstract

In this paper, a new full Nesterov–Todd step infeasible interior-point method for Cartesian $P_*(\kappa )$ linear complementarity problem over symmetric cone is considered. Our algorithm starts from a strictly feasible point of a perturbed problem, after a full Nesterov–Todd step for the new perturbed problem the obtained strictly feasible iterate is close to the central path of it, where closeness is measured by some merit function. Furthermore, the complexity bound of the algorithm is the best available for infeasible interior-point methods.

1 Introduction

The Cartesian $P_*(\kappa )$ linear complementarity problem over symmetric cone (Cartesian $P_*(\kappa )$-SCLCP), seeks vectors $x, s\in {\mathcal {J}}$ such that

$$\begin{aligned} x\in {\mathcal {K}}, s={\mathcal {A}}(x)+q\in {\mathcal {K}},\langle x, s \rangle =0, \end{aligned}$$

(1)

where $\langle x, s \rangle =\mathrm{tr}(x\circ s)$ denotes the Euclidean inner product, $\mathcal {J}=\mathcal {J}_1\times \cdots \times \mathcal {J}_N$ is the Cartesian product space with the corresponding cone of squares $\mathcal {K}=\mathcal {K}_1\times \cdots \times \mathcal {K}_N$ where each $\mathcal {J}_j$ is a Euclidean Jordan algebra with dimension $n_j$ and rank $r_j$ and each $\mathcal {K}_j$ is the corresponding cone of squares $\mathcal {J}_j$, $q\in \mathcal {J}$, and the linear transformation $\mathcal {A}: \mathcal {J} \rightarrow \mathcal {J}$ has the Cartesian $P_*(\kappa )$ property for some nonnegative constant $\kappa$, i.e.,

$$\begin{aligned} (1+4\kappa )\sum _{j\in I_+}\big \langle x^{(j)}, [\mathcal {A}(x)]^{(j)}\big \rangle +\sum _{j\in I_-}\big \langle x^{(j)}, [\mathcal {A}(x)]^{(j)}\big \rangle \ge 0,~\forall ~ ~ x\in \mathcal {J}, \end{aligned}$$

where $I_+=\big \{j: \big \langle x^{(j)}, [\mathcal {A}(x)]^{(j)}\big \rangle \ge 0\big \}$ and $I_-=\big \{j: \big \langle x^{(j)}, [\mathcal {A}(x)]^{(j)}\big \rangle <0\big \}.$ Note that the dimension of $\mathcal {J}$ is $n=\sum _{j=1}^Nn_j$ and the rank is $r=\sum _{j=1}^Nr_j$.

The concept of the Cartesian $P_*(\kappa )$-property was first introduced by Luo and Xiu [11] in the general Euclidean Jordan algebra. Factually, it is a straightforward extension of the $P_*(\kappa )$-matrix introduced by Kojima et al. [9], where they first proved the existence and uniqueness of the central path for the $P_{*}(\kappa )$-LCP and generalized the primal-dual interior-point algorithm for linear optimization (LO) to the $P_{*}(\kappa )$-LCP. The Cartesian $P_*(\kappa )$-SCLCP includes a wide class of problems, namely, $P_*(\kappa )$-LCP, Cartesian $P_*(\kappa )$ second-order cone linear complementarity problem (SOCLCP) and Cartesian $P_*(\kappa )$ semidefinite linear complementarity problem (SDLCP) as special cases. Luo and Xiu [11] extended the path-following interior-point algorithms for symmetric cone optimization (SCO) introduced by Schmieta and Alizadeh [16] to the Cartesian $P_*(\kappa )$-SCLCP. Wang and Bai [18] presented a class of polynomial interior-point algorithms for the Cartesian $P_*(\kappa )$-SCLCP based on a kernel function and obtained the currently best known iteration bounds with the addition of a factor $(1+2\kappa )$ for feasible IPMs.

The primal-dual full-Newton step feasible interior-point method (IPM) for LO was first introduced by Roos et al. [15], and the authors obtained the currently best known iteration bound for small-update methods, namely, $O(\sqrt{n}\log \frac{n}{\epsilon })$. Wang et al. [19, 21] and Wang and Lesaja [20] generalized the results for LO obtained by Roos et al. in [15] to SCO, convex quadratic symmetric cone optimization (CQSCO) and the Cartesian $P_*(\kappa )$-SCLCP, respectively. Based on a modified Nesterov–Todd (NT)-direction, Kheirfam and Mahdavi-Amiri [8] and Kheirfam [5] presented a feasible IPM for SCLCP and the Cartesian $P_*(\kappa )$-SCLCP. All methods mentioned so far are feasible IPM that can be started only if a strictly feasible point is known. Usually such a starting point is not at hand. In this case a so-called infeasible IPM (IIPM) should be used.

IIPMs start with an arbitrary positive point and feasibility is reached as optimality is approached. In 2006, Roos [13] proposed a full-Newton step IIPM for LO, which starts with a strictly feasible solution of a perturbed problem and generates iterates each of which is strictly feasible for a new perturbed problem. The author proved that the complexity of the algorithm coincides with the best-known iteration bound for IIPMs. Some variants of the method extended by Kheirfam and Mahdavi-Amiri [7] to SCLCP, Kheirfam [6] to horizontal LCP (HLCP), Gu et al. [4] to SCO and Liu and Sun [10] to LO. Recently, Roos [14] proposed a new method for LO by improving the full-Newton step IIPMs so that the centering steps not be needed, whereas the above-mentioned IIPMs require a few (at most three) centering steps in each main iteration. Motivated by Roos’ recent work, we present a new full-NT step IIPM for the Cartesian $P_*(\kappa )$-SCLCP which uses only one feasibility step in each iteration and the centering steps not to be required in this paper. In our algorithm, closeness to the central path is measured by a merit function introduced in [22] which makes a simple and interesting analysis. We derive the worst case iteration complexity, as is usual for theoretical iteration bounds for IIPMs.

The remainder of our work is organized as follows. In Sect. 2, we briefly recall some results from Euclidean Jordan algebra that we need in this paper. In Sect. 3, we introduce the perturbed problem and describe an iteration of our algorithm. We then present the algorithm. Section 4 contains the analysis of the algorithm. In Sect. 4.1, we derive an upper bound for the proximity measure after a full-NT step. Section 4.2 serves to derive an upper bound for $\omega (v)$. In Sect. 4.3, we fix values of the parameters $\theta$ and $\tau$ in the algorithm. As a result, we realize the algorithm to be well-defined for the chosen values of $\theta$ and $\tau$. We derive the iteration complexity of the algorithm in Sect. 4.4. Finally, Sect. 5 contains some concluding remarks.

2 Euclidean Jordan algebra

Here, we briefly outline some concepts, properties, and results from Euclidean Jordan algebras as needed. A comprehensive treatment of Euclidean Jordan algebra can be found in [1, 3, 17].

A Euclidean Jordan algebra is a triple $(\mathcal {J}, \circ , \langle \cdot , \cdot \rangle )$, where $(\mathcal {J}, \langle \cdot , \cdot \rangle )$ is an $n$-dimensional inner product space over $R$ and $\circ : (x, y)\rightarrow x\circ y$ is a bilinear mapping satisfying the following conditions for all $x, y, s\in \mathcal {J}$:

• (a) ${x}\circ {y}={y}\circ {x}$,

• (b) ${x}\circ ({x}^2\circ {y})={x}^2\circ ({ x}\circ {y})$, where ${x}^2={x}\circ {x},$

• (c) $\langle {x}\circ {y}, {s}\rangle =\langle {x}, {y}\circ {s}\rangle ,$ where the inner product $\langle \cdot , \cdot \rangle$ is defined by $\langle x, y\rangle =\mathrm{tr}(x\circ y)$ for any $x, y\in \mathcal {J}$.

We assume that there exists an element $e\in \mathcal {J}$, which called the identify element, such that $x\circ e=e\circ x=x$ for all $x\in \mathcal {J}$. Denote the corresponding cone of squares by $\mathcal {K}:=\{x^2: x\in \mathcal {J}\}$. Note that, by Theorem III.2.1 in [1], $\mathcal {K}$ is indeed a symmetric cone. Since $\mathcal {J}$ is finite-dimensional, given $x\in \mathcal {J}$, there exists a minimal positive integer $k$, which called the degree of $x$, such that the set $\{e, x, \ldots , x^k\}$ is linearly dependent. The rank of $\mathcal {J}$, denoted by $r$, is defined to be

$$\begin{aligned} r:=\max \{\mathrm{deg}(x): x\in \mathcal {J}\}, \end{aligned}$$

where $\mathrm{deg}(x)$ is the degree of $x$. An element $c\in {\mathcal {J}}$ is idempotent if $c\circ c=c\ne 0$, which is also primitive if it cannot be expressed as a sum of two idempotents. A set of primitive idempotents $\{{ c}_1, { c}_2, \ldots , { c}_k\}$ is called a Jordan frame if ${ c}_i\circ { c}_j=0$, for any $i\ne j\in \{1, 2, \ldots , k\}$, and $\sum _{i=1}^k{ c}_i={ e}.$ Let $({\mathcal {J}}, \circ , \langle \cdot ,\cdot \rangle )$ be a Euclidean Jordan algebra with $\mathrm{rank}({\mathcal {J}})=r$. Then, for any ${x}\in {\mathcal {J}}$, there exists a Jordan frame $\{{c}_1, {c}_2, \ldots , {c}_r\}$ and real numbers $\lambda _1({x}), \lambda _2({x}), \ldots , \lambda _r({x})$ such that ${x}=\sum _{i=1}^r\lambda _i({x}){ c}_i$ (spectral decomposition, Theorem III.1.2 in [1]). Every $\lambda _i({x})$ is called an eigenvalue of ${x}$. Since “$\circ$” is bilinear for every ${x}\in {\mathcal {J}}$, the Lyapunov transformation $L(x): \mathcal {J}\rightarrow \mathcal {J}$ is defined as $L(x)y=x\circ y$. For each ${x}\in {\mathcal {J}},$ define

$$\begin{aligned} P(x):=2L({x})^2-L({x}^2), \end{aligned}$$

where, $L({x})^2=L({x})L({x})$. The map $P({x})$ is called the quadratic representation of $x$ in ${\mathcal {J}}$, which is an essential concept in the theory of Jordan algebra and plays an important role in the analysis of interior-point algorithms. We say two elements $x, y$ of a Jordan algebra $\mathcal {J}$ operator commute if $L(x)L(y)=L(y)L(x)$. Two elements $x, y$ of a Jordan algebra $\mathcal {J}$ are called similar, denoted as $x\sim y$, if $x$ and $y$ share the same set of eigenvalues. In what follows, we generalize the definitions and properties stated so far in this section to the general case, when the cone underlying the given $P_{*}(\kappa )$-SCLCP is the Cartesian product of $N$ symmetric cones ${\mathcal {K}}_j,$ where $N>1$. For any $x=(x^{(1)}, x^{(2)}, \ldots , x^{(N)})\in {\mathcal {J}}$, where $x^{(j)}\in \mathcal {J}_j$, we have

$$\begin{aligned} \Vert x\Vert _F=\sqrt{\sum _{j=1}^N\Vert x^{(j)}\Vert ^2_F},\quad \mathrm{tr}(x)=\sum _{j=1}^N\mathrm{tr}\big (x^{(j)}\big ). \end{aligned}$$

For any $x, s\in \mathcal {J}$, we have

$$\begin{aligned} x\circ s=\Big (x^{(1)}\circ s^{(1)}, x^{(2)}\circ s^{(2)}, \ldots , x^{(N)}\circ s^{(N)}\Big ),\quad \langle x, s\rangle =\sum _{j=1}^N\Big \langle x^{(j)}, s^{(j)}\Big \rangle . \end{aligned}$$

Obviously, if $e^{(j)}\in {\mathcal {J}}_j$ is the identity element in the Jordan algebra for the $j$th cone, then the vector $e=(e^{(1)}, e^{(2)}, \ldots , e^{(N)})$ is the identify element in $({\mathcal {J}}, \circ )$. One can easily verify that $\mathrm{tr}(e)=r$. The Lyapunov transformation and the quadratic representation of ${\mathcal {J}}$ can be adjusted to

$$\begin{aligned} L(x)=\mathrm{diag}\Big (L(x^{(1)}), \ldots , L(x^{(N)})\Big ),\quad P(x)=\mathrm{diag}\Big (P(x^{(1)}), \ldots , P(x^{(N)})\Big ). \end{aligned}$$

3 Infeasible full-NT step IPM

In the case of an infeasible method, we call the pair $(x, s)$ an $\epsilon$-solution of (1) if the Frobenius norm of the residual vector $s-\mathcal {A}(x)-q$ does not exceed $\epsilon$, and also $\mathrm{tr}(x\circ s)\le \epsilon$.

3.1 The perturbed problem

We start with choosing arbitrarily $(x^0, s^0)\in \mathrm{int}\mathcal {K}\times \mathrm{int}\mathcal {K}$ such that $x^0\circ s^0=\mu ^0e$ for some positive number $\mu ^0$. For any $\nu$, with $0<\nu \le 1$, we consider the perturbed problem

$$\begin{aligned} s-\mathcal {A}(x)-q=\nu r_q^0,\quad (x, s)\in \mathcal {K}\times \mathcal {K}, \quad (SCLCP_{\nu }) \end{aligned}$$

where $r_q^0=s^0-\mathcal {A}(x^0)-q$. It is obvious that $(x, s)=(x^0, s^0)$ is a strictly feasible solution of $(SCLCP_{\nu })$, when $\nu =1$. We conclude that if $\nu =1$, then $(SCLCP_{\nu })$ satisfies the IPC, i.e., there exists $(x^0, s^0)\in \mathrm{int}\mathcal {K}\times \mathrm{int}\mathcal {K}$ such that $s^0-\mathcal {A}(x^0)-q=\nu r_q^0$, which then straightforwardly leads to the following result.

Lemma 1

Let (1) be feasible and $0<\nu \le 1$. Then, the perturbed problem $(SCLCP_{\nu })$ satisfies the IPC.

Proof

The proof is similar to the proof of the Theorem 3.1 in [7], and is therefore omitted.$\square$

3.2 The central path of the perturbed problem

Let (1) be feasible and $0<\nu \le 1$. Then, Lemma 1 implies that the problem $(\mathrm{SCLCP_{\nu }})$ satisfies the IPC, for $0<\nu \le 1$, and therefore its central path exists. This means that the system

$$\begin{aligned} s-\mathcal {A}(x)-q= & {} \nu r_q^0,\quad (x, s)\in {\mathcal {K}}\times {\mathcal {K}}, \nonumber \\ {x}\circ {s}= & {} \mu {e}, \end{aligned}$$

(2)

has a unique solution for any $\mu >0$, as the $\mu$-center of the perturbed problem $(\mathrm{SCLCP_{\nu }})$. The set of $\mu$-centers is called the central path. In the sequel, the parameters $\mu$ and $\nu$ will always be in a one-to-one correspondence, according to $\mu =\nu \mu ^0$.

3.3 An iteration of our algorithm

We just established that if $\nu =1$ and $\mu ={\mu }^{0}$, then $(x^{0}, s^{0})$ is the $\mu$-center of the perturbed problem $(SCLCP_{\nu })$. In accordance with the available results on IIPMs (e.g., see [7]), the initial iterates are given by

$$\begin{aligned} x^0=\rho _p e, \, s^0=\rho _d e, \, \mu ^0=\rho _p\rho _d,\, \nu =1, \end{aligned}$$

where $\rho _p>0$ and $\rho _d>0$ such that $\Vert x^*\Vert _{\infty }\le \rho _p$ and $\max \{\Vert s^*\Vert _{\infty }, \Vert \overline{\mathcal {A}}\Vert _F\rho _p\}\le \rho _d$ for some solution $(x^*, s^*)$ of (1). If the pair $(x, s)$ is feasible for the perturbed problem $(SCLCP_{\nu })$, and $\mu =\rho _p\rho _d\nu$, then we measure proximity to the $\mu$-center of this perturbed problem by the quantity

$$\begin{aligned} \delta (x, s; \mu ):=\delta (v):=\Vert e-v^2\Vert _F,\quad \mathrm{where}~v:=\frac{P(w^{\frac{1}{2}})s}{\sqrt{\mu }} \bigg [=\frac{P(w^{-\frac{1}{2}})x}{\sqrt{\mu }}\bigg ], \end{aligned}$$

(3)

and $w=P({x}^{\frac{1}{2}})\big (P({x}^{\frac{1}{2}}){ s}\big )^{-\frac{1}{2}} \big [= P({s}^{-\frac{1}{2}})\big (P({ s}^{\frac{1}{2}}){x}\big )^{\frac{1}{2}}\big ]$ is called the scaling point of $x$ and $s$ (Lemma 3.2 in [2]). This scaling point was first introduced by Nesterov and Todd [12] for self-scaled cones and then adapted by Faybusovich [3] for symmetric cones. As a consequence, we have the following lemma.

Lemma 2

(cf. Lemma 2.1 in [6]) If $\delta :=\delta (v)$, then

$$\begin{aligned} \sqrt{1-\delta }\le \lambda _i(v)\le \sqrt{1+\delta },~i=1, \ldots , r. \end{aligned}$$

Suppose that for some $\mu \in (0, \mu ^0]$ we have $x\in \mathcal {K}$ and $s\in \mathcal {K}$ satisfying the first equation in (2) for $\nu =\frac{\mu }{\mu ^0}$ and such that $\delta (x, s; \mu )\le \tau$. This certainly holds at the start of the first iteration, since $\delta (x^0, s^0; \mu ^0)=0<\tau$ and $s^0-\mathcal {A}(x^0)-q=\nu r_q^0$, when $\nu =1$. We reduce $\nu$ to $\nu ^+=(1-\theta )\nu$ and $\mu$ to $\mu ^+=(1-\theta )\mu$ with $\theta \in (0, 1)$, and find new iterate $(x^+, s^+)$ that is feasible for the perturbed problem $(SCLCP_{\nu ^+})$, and such that $\delta (x^+, s^+; \mu ^+)\le \tau .$

We proceed by deriving the search directions in the algorithm. For this purpose, we find displacements $\varDelta x$ and $\varDelta s$ such that

$$\begin{aligned} \mathcal {A}(\varDelta x)-{\varDelta s}= & {} \theta \nu r_q^0, \nonumber \\ s\circ \varDelta x+x\circ \varDelta s= & {} (1-\theta )\mu e-x\circ s. \end{aligned}$$

(4)

Due to the fact that $L(x)L(s)\ne L(s)L(x)$, in general, the above system does not always have a unique solution. This problem can be solved by replacing the second equation of the system (2) by $P(w^{-\frac{1}{2}})x\circ P(w^{\frac{1}{2}})s=\mu e$ (cf. Lemma 28 in [16]). Then the Newton system becomes

$$\begin{aligned}&\mathcal {A}(\varDelta x)-{\varDelta s}=\theta \nu r_q^0, \nonumber \\&P(w^{\frac{1}{2}}){ s}\circ P(w^{-\frac{1}{2}}){\varDelta { x}}+P(w^{-\frac{1}{2}}){ x}\circ P(w^{\frac{1}{2}}){\varDelta { s}}\nonumber \\&\quad =(1-\theta )\mu { e}-P(w^{-\frac{1}{2}}){ x}\circ P(w^{\frac{1}{2}}){ s}. \end{aligned}$$

(5)

It is easily seen that $x^+:=x+\varDelta x$ and $s^+:=s+\varDelta s$ satisfy $s-\mathcal {A}(x)-q=\nu ^+ r_q^0$. The main part of the analysis is to guarantee that $x^+\in \mathrm{int}\mathcal {K}$ and $s^+\in \mathrm{int}\mathcal {K}$ and satisfy $\delta (x^+, s^+; \mu ^+)\le \tau .$

3.4 The algorithm

A formal description of the algorithm is given in Fig. 1.

Fig. 1

The algorithm

4 Analysis of the algorithm

Let $(x, s)$ denote the iterate at the start of an iteration, and $\delta (x, s; \mu )\le \tau$.

4.1 Upper bound for $\delta (v^+)$

As established in Sect. 3.3, the full-NT step generates new iterates $(x^+, s^+)$ that satisfy the feasibility condition for $(SCLCP_{\nu ^+})$, except for possibly the constraints on the cone $\mathcal {K}$. A crucial element in the analysis is to show that, after the full-NT step, $\delta (x^+, s^+; \mu ^+)\le \tau$.

Defining

$$\begin{aligned} d_x:=\frac{P(w^{-\frac{1}{2}})\varDelta x}{\sqrt{\mu }},\quad d_s:=\frac{P(w^{\frac{1}{2}})\varDelta s}{\sqrt{\mu }}, \end{aligned}$$

(6)

where $w$ is the NT-scaling point of $x$ and $s$, we may easily check that the system (5), which defines the search directions $\varDelta x$ and $\varDelta s$, can be written in terms of the scaled directions $d_x$ and $d_s$ as follows:

$$\begin{aligned}&{\overline{\mathcal {A}}}(d_x)-d_s=\frac{P(w^{\frac{1}{2}})}{\sqrt{\mu }}\theta \nu r_q^0, \nonumber \\&d_x+d_s=(1-\theta )v^{-1}-v, \end{aligned}$$

(7)

where $\overline{\mathcal {A}}:=P(w^{\frac{1}{2}})\mathcal {A}P(w^{\frac{1}{2}}).$ Furthermore, using (3) and (6) we get

$$\begin{aligned} x^+=\sqrt{\mu }P(w^{\frac{1}{2}})(v+d_x), \quad s^+=\sqrt{\mu } P(w^{-\frac{1}{2}})(v+d_s). \end{aligned}$$

Since $P(w^{\frac{1}{2}})$ and $P(w^{-\frac{1}{2}})$ are automorphisms of $\mathrm{int}\mathcal {K}$ (Theorem III.2.1 in [1]), $x^+$ and $s^+$ belong to $\mathrm{int}\mathcal {K}$ if and only if $v+d_x$ and $v+d_s$ belong to $\mathrm{int}\mathcal {K}$. In this case, using the second equation of (7), we obtain

$$\begin{aligned} (v+d_x)\circ (v+d_s)=v^2+v\circ (d_x+d_s)+d_x\circ d_s=(1-\theta )e+d_x\circ d_s. \end{aligned}$$

(8)

Lemma 3

The iterate $(x^+, s^+)$ is strictly feasible if $(1-\theta )e+d_x\circ d_s\in \mathrm{int}\mathcal {K}$.

Proof

The proof is similar to the proof of Lemma 4.2 in [4], and is therefore omitted.$\square$

Corollary 1

The iterate $(x^+, s^+)$ is strictly feasible if $\Vert \lambda (d_x\circ d_s)\Vert _{\infty }<1-\theta .$

Proof

By Lemma 3, the iterate $(x^+, s^+)$ is strictly feasible if $(1-\theta )e+d_x\circ d_s\in \mathrm{int}\mathcal {K}$. If $\Vert \lambda (d_x\circ d_s)\Vert _{\infty }<1-\theta ,$ then we have $\theta -1<\lambda _i(d_x\circ d_s)<1-\theta$ for all $i=1, \ldots , r.$ Therefore,

$$\begin{aligned} \lambda _i((1-\theta )e+d_x\circ d_s)=1-\theta +\lambda _i(d_x\circ d_s)>0, \quad i=1, \ldots , r. \end{aligned}$$

The last inequalities mean that $(1-\theta )e+d_x\circ d_s\in \mathrm{int}\mathcal {K}$, and the corollary follows. $\square$

In the sequel, we denote

$$\begin{aligned} \omega (v):=\frac{1}{2}\big (\Vert d_x\Vert _F^2+\Vert d_s\Vert ^2_F\big ). \end{aligned}$$

(9)

It follows that

$$\begin{aligned} \Vert \lambda (d_x\circ d_s)\Vert _{\infty }\le \Vert d_x\circ d_s\Vert _F\le \frac{1}{2}(\Vert d_x\Vert _F^2+\Vert d_s\Vert _F^2)=\omega (v). \end{aligned}$$

(10)

Corollary 2

If $\omega (v)<1-\theta$, then the iterate $(x^+, s^+)$ is strictly feasible.

Proof

Due to (10), $\omega (v)<1-\theta$ implies $\Vert \lambda (d_x\circ d_s)\Vert _{\infty }<1-\theta$. By Corollary 1, the proof is complete.$\square$

Assuming $\omega (v)<1-\theta$, which guarantees strict feasibility of the iterates $(x^+, s^+)$, we proceed by deriving an upper bound for $\delta (x^+, s^+; \mu ^+)$. By definition, we have

$$\begin{aligned} \delta (x^+, s^+; \mu ^+)=\big \Vert e-(v^+)^2\big \Vert _F,~\mathrm{where}~ v^+=\frac{P((w^+)^{-\frac{1}{2}})x^+}{\sqrt{\mu ^+}}\big [=\frac{P((w^+)^{\frac{1}{2}})s^+}{\sqrt{\mu ^+}}\big ]. \end{aligned}$$

In what follows, we denote $\delta (x^+, s^+; \mu ^+)$ shortly by $\delta (v^+).$

Lemma 4

If $\omega (v)<1-\theta$, then

$$\begin{aligned} \delta (v^+)\le \frac{\omega (v)}{1-\theta }. \end{aligned}$$

Proof

Since $\omega (v)<1-\theta$, using Corollary 2, it follows that $x^+$ and $s^+$ are strictly feasible, hence $v+d_x, v+d_s$ and $(v+d_x)\circ (v+d_s)$ belong to $\mathrm{int}\mathcal {K}$. Similar to the proof of Lemma 3.3 in [7], we have

$$\begin{aligned} \sqrt{1-\theta } v^+\sim \big [P((v+d_x)^{\frac{1}{2}})(v+d_s)\big ]^{\frac{1}{2}}. \end{aligned}$$

(11)

Now, by using $\Vert P(x^{\frac{1}{2}})s-e\Vert _F\le \Vert x\circ s-e\Vert _F$ for any $x, s\in \mathrm{int}\mathcal {K}$ (cf. Lemma 30 in [16]), (11), (8) and (10), we may write

$$\begin{aligned} \delta (v^+)= & {} \big \Vert (v^+)^{2}-e\big \Vert _F=\Big \Vert P\Big (\frac{v+d_x}{\sqrt{1-\theta }}\Big )^{\frac{1}{2}} \Big (\frac{v+d_s}{\sqrt{1-\theta }}\Big )-e\Big \Vert _F\\\le & {} \Big \Vert \Big (\frac{v+d_x}{\sqrt{1-\theta }}\Big )\circ \Big (\frac{v+d_s}{\sqrt{1-\theta }}\Big )-e\Big \Vert _F\\= & {} \Big \Vert \frac{(1-\theta )e+d_x\circ d_s}{1-\theta }-e\Big \Vert _F=\frac{1}{1-\theta }\big \Vert d_x\circ d_s\big \Vert _F\le \frac{\omega (v)}{1-\theta }. \end{aligned}$$

This completes the proof.$\square$

4.2 Upper bound for $\omega (v)$

In this section, we obtain an upper bound for $\omega (v)$ which enable us to find a default value for $\theta$. For this purpose, the following two lemmas play an important role.

Lemma 5

If the linear transformation ${\overline{\mathcal {A}}}$ has the Cartesian $P_*(\kappa )$-property, then the solution $(d_x, d_s)$ of the linear system

$$\begin{aligned} {\overline{\mathcal {A}}}(d_x)-d_s= & {} 0, \nonumber \\ d_x+d_s= & {} h, \end{aligned}$$

(12)

satisfies

$$\begin{aligned} \Vert d_x\Vert _F^2+\Vert d_s\Vert _F^2\le (1+2\kappa )\Vert h\Vert _F^2. \end{aligned}$$

Proof

Since ${\overline{\mathcal {A}}}$ has the Cartesian $P_*(\kappa )$-property, we obtain

$$\begin{aligned} \big \langle d_x, d_s\big \rangle\ge & {} -4\kappa \sum _{j\in I_+}\big \langle d_x^{(j)}, d_s^{(j)}\big \rangle \ge -\kappa \sum _{j\in I_+}\big \Vert d_x^{(j)}+d_s^{(j)}\big \Vert _F^2\nonumber \\\ge & {} -\kappa \sum _{j=1}^N\big \Vert d_x^{(j)}+d_s^{(j)}\big \Vert _F^2=-\kappa \big \Vert d_x+d_s\big \Vert _F^2=-\kappa \Vert h\Vert _F^2. \end{aligned}$$

(13)

Therefore, using the above inequality, we get

$$\begin{aligned} \Vert d_x\Vert _F^2+\Vert d_s\Vert _F^2=\Vert d_x+d_s\Vert _F^2-2\langle d_x, d_s\rangle \le (1+2\kappa )\Vert h\Vert _F^2. \end{aligned}$$

This completes the proof.$\square$

Lemma 6

If the linear transformation ${\overline{\mathcal {A}}}$ has the Cartesian $P_*(\kappa )$-property, then the solution $(d_x, d_s)$ of the linear system

$$\begin{aligned} {\overline{\mathcal {A}}}(d_x)-d_s= & {} a, \nonumber \\ d_x+d_s= & {} b, \end{aligned}$$

(14)

satisfies

$$\begin{aligned} \Vert d_x\Vert _F^2+\Vert d_s\Vert _F^2\le 4(1+2\kappa )\big (\Vert a\Vert _F^2+\Vert b\Vert _F^2\big )+2\Vert a\Vert _F^2. \end{aligned}$$

Proof

It is easily seen that the system (14) can be written as

$$\begin{aligned} {\overline{\mathcal {A}}}(d_x)-\tilde{v}= & {} 0, \nonumber \\ d_x+\tilde{v}= & {} a+b, \end{aligned}$$

(15)

where $\tilde{v}=d_s+a$. Applying Lemma 5 to (15), it follows that

$$\begin{aligned} \Vert d_x\Vert ^2_F+\Vert \tilde{v}\Vert ^2_F\le (1+2\kappa )\Vert a+b\Vert _F^2\le 2(1+2\kappa )\big (\Vert a\Vert _F^2+\Vert b\Vert _F^2\big ). \end{aligned}$$

Therefore, using the above inequality, we get

$$\begin{aligned} \Vert d_x\Vert _F^2+\Vert d_s\Vert _F^2= & {} \Vert d_x\Vert _F^2+\Vert \tilde{v}-a\Vert _F^2\le 2\big (\Vert d_x\Vert _F^2+\Vert \tilde{v}\Vert _F^2\big )+2\Vert a\Vert _F^2\\\le & {} 4(1+2\kappa )\big (\Vert a\Vert _F^2+\Vert b\Vert _F^2\big )+2\Vert a\Vert _F^2. \end{aligned}$$

This completes the proof.$\square$

Comparing system (14) with the system (7) and considering $a=\frac{P(w^{\frac{1}{2}})}{\sqrt{\mu }}\theta \nu r^0_q$ and $b=(1-\theta )v^{-1}-v$, we get

$$\begin{aligned} \Vert d_x\Vert _F^2+\Vert d_s\Vert _F^2\le & {} 4(1+2\kappa )\Big (\Big \Vert \frac{\theta \nu }{\sqrt{\mu }} P(w^{\frac{1}{2}})r^0_q\Big \Vert ^2_F+\Vert (1-\theta )v^{-1}-v\Vert ^2_F\Big )\nonumber \\&+\,2\Big \Vert \frac{\theta \nu }{\sqrt{\mu }} P(w^{\frac{1}{2}})r^0_q\Big \Vert ^2_F. \end{aligned}$$

(16)

On the other hand, we have

$$\begin{aligned} \big \Vert P(w^{\frac{1}{2}})r^0_q\big \Vert ^2_F= & {} \big \langle P(w^{\frac{1}{2}})r^0_q, P(w^{\frac{1}{2}})r^0_q \big \rangle = \big \langle P(w)r^0_q, r^0_q\big \rangle \nonumber \\= & {} \big \langle P(w)r^0_q, 2\rho _de\big \rangle -\big \langle P(w)r^0_q, 2\rho _de-r^0_q\big \rangle \nonumber \\\le & {} \big \langle P(w)r^0_q, 2\rho _d e\big \rangle \nonumber \\= & {} \big \langle P(w)(2\rho _de), 2\rho _d e\big \rangle -\big \langle P(w)(2\rho _de-r^0_q), 2\rho _de\big \rangle \nonumber \\\le & {} \big \langle P(w)(2\rho _de), 2\rho _d e\big \rangle =4\rho _d^2\big \langle P(w)e, e\big \rangle \nonumber \\= & {} 4\rho _d^2{\mathrm{tr}(w^2)}\le {\frac{4\rho _d^2\mathrm{tr}(x^2)}{\mu \lambda _{\min }(v)^2}}\le {\frac{4\rho _d^2\mathrm{tr}(x)^2}{\mu \lambda _{\min }(v)^2}}, \end{aligned}$$

(17)

where the third inequality follows by Lemma 4.5 in [4] and the last inequality by $tr(x^2)\le tr(x)^2$.

Lemma 7

Let $(x, s)$ be feasible for the perturbed problem $(SCLCP_{\nu })$ and let $(x^0, s^0)=(\rho _p e, \rho _d e)$, $\langle x^*, s^*\rangle =0, \Vert s^*\Vert _{\infty }\le \rho _d$ and $\Vert x^*\Vert _{\infty }\le \rho _p$. Then, we have

$$\begin{aligned} {tr}(x)\le (1+4\kappa )r\rho _p\big (3+\delta \big ). \end{aligned}$$

(18)

Proof

It is easily seen that

$$\begin{aligned} \nu s^0+(1-\nu )s^*-s=\mathcal {A}(\nu x^0+(1-\nu )x^*-x). \end{aligned}$$

Since the linear transformation $\mathcal {A}$ has the Cartesian $P_*(\kappa )$-property, it follows that

$$\begin{aligned} \langle \nu x^0+(1-\nu )x^*- & {} x, \nu s^0+(1-\nu )s^*-s\rangle \\\ge & {} -4\kappa \Big (\nu ^2\langle x^0, s^0\rangle +\nu (1-\nu )\big (\langle x^0, s^*\rangle +\langle x^*, s^0\rangle \big )+\langle x, s\rangle \Big ). \end{aligned}$$

The above inequality, due to $\langle x^*, s\rangle +\langle x, s^*\rangle \ge 0$ and Lemma 2, implies that

$$\begin{aligned} \langle x^0, s\rangle +\langle x, s^0\rangle\le & {} (1+4\kappa )\Bigg (\nu \langle x^0, s^0\rangle +(1-\nu )\big (\langle x^0, s^*\rangle +\langle x^*, s^0\rangle \big )+\frac{1}{\nu }\langle x, s\rangle \Bigg )\\\le & {} (1+4\kappa )\Bigg (\nu r\rho _p\rho _d+2(1-\nu )r\rho _p\rho _d+\rho _p\rho _d\sum _{i=1}^r\lambda _i^2(v)\Bigg )\\\le & {} (1+4\kappa )r\rho _p\rho _d\big (3+\delta \big ). \end{aligned}$$

Therefore, $\langle x, s^0\rangle \le (1+4\kappa )r\rho _p\rho _d\big (3+\delta \big )$ which implies the result.$\square$

By substituting (18) and (17) into (16) and using (9) and the fact that $\mu =\nu \mu ^0=\nu \rho _p\rho _d$, we obtain

$$\begin{aligned} \omega (v)\le & {} 2(1+2\kappa )\left( \frac{4(1+4\kappa )^2\theta ^2 r^2(3+\delta )^2}{1-\delta }+\frac{(\delta +\theta \sqrt{r})^2}{1-\delta }\right) \nonumber \\&+\,\frac{4(1+4\kappa )^2\theta ^2 r^2(3+\delta )^2}{1-\delta }. \end{aligned}$$

(19)

4.3 Values for $\theta$ and $\tau$

Our aim is to find a positive number $\tau$ such that if $\delta \le \tau$, then $\delta (v^+)\le \tau$. By Lemma 4, this will hold if $\omega (v)<1-\theta$ and

$$\begin{aligned} \frac{\omega (v)}{1-\theta }\le \tau . \end{aligned}$$

(20)

In this stage, we choose

$$\begin{aligned} \tau =\frac{1}{8(1+2\kappa )},\quad \theta =\frac{1}{44(1+2\kappa )(1+4\kappa )r}. \end{aligned}$$

(21)

Using $\delta \le \tau$, it follows from (19), with the right-hand side of (19) being monotonically increasing with respect to $\delta$, that

$$\begin{aligned} \omega (v)\le & {} 2(1+2\kappa )\Big (\frac{4(1+4\kappa )^2\theta ^2 r^2(3+\tau )^2}{1-\tau }+\frac{(\tau +\theta \sqrt{r})^2}{1-\tau }\Big ) \nonumber \\&+\,\frac{4(1+4\kappa )^2\theta ^2 r^2(3+\tau )^2}{1-\tau }\nonumber \\= & {} \frac{1}{8(1+2\kappa )}\Bigg (\frac{8(25+48\kappa )^2}{1936(1+2\kappa )(7+16\kappa )} +\frac{128\big (\frac{1}{8}+\frac{1}{44(1+4\kappa )\sqrt{r}}\big )^2(1+2\kappa )}{7+16\kappa }\nonumber \\&+\,\frac{4(25+48\kappa )^2}{1936(1+2\kappa )^2(7+16\kappa )}\Bigg )\nonumber \\\le & {} \frac{1}{8(1+2\kappa )}(0.9525)<\frac{1}{8(1+2\kappa )}(0.9773)=(1-\theta )\tau . \end{aligned}$$

(22)

This implies that $\omega (v)<1-\theta$ with $\theta$ defined as in (21), and (20) holds. Therefore, the iterates generated by the algorithm are strictly feasible, and the algorithm is well-defined in the sense that the property $\delta (x, s; \mu )\le \tau$, with $\tau$ defined as in (21), is maintained in all iterations.

4.4 Complexity

We have found that if at the start of an iteration the iterates satisfy $\delta (x, s; \mu )\le \tau$, and $\tau$ and $\theta$ are defined as in (21), then after the full-NT step, the iterate is strictly feasible and satisfies $\delta (x^+, s^+; \mu ^+)\le \tau$. This establishes the algorithm to be well-defined.

In each main iteration, both the barrier parameter $\mu$ and the norm of the residual vector are reduced by the factor $1-\theta$. Hence, the total number of main iterations is bounded above by

$$\begin{aligned} \frac{1}{\theta }\log \frac{\max \{tr(x^0\circ s^0), \Vert r_q^0\Vert _F\}}{\epsilon }. \end{aligned}$$

Thus, we may state the main result of our work.

Theorem 1

If (1) has a solution $(x^*, s^*)$ such that $\Vert x^*\Vert _{\infty }\le \rho _p$ and $\Vert s^*\Vert _{\infty }\le \rho _d$, then after at most

$$\begin{aligned} 44 r(1+2\kappa )(1+4\kappa )\log \frac{\max \{tr(x^0\circ s^0), \Vert r_q^0\Vert _F\}}{\epsilon }, \end{aligned}$$

iterations the algorithm finds an $\epsilon$-solution of (1).

5 Conclusions

In this paper, we have presented a full-NT step IIPM for the Cartesian $P_*(\kappa )$-SCLCP. The method used in each iteration only a full step. The analysis is simpler and the closeness to central path is measured by some merit function. Finally, the iteration bound in this paper is a worst-case bound, as is usual for theoretical iteration bounds for IIPMs.