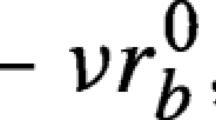1 Introduction

Linear optimization (LO) problem has increasingly been addressed in the literature, both from the theoretical and computational points of view. This model has been widely applied to modelize different problems in various areas such as economics, engineering and operations research.

The first modelisation of an economic problem in the form of a LO problem was made by the Russian mathematician Kantorovich (1939, [3]) and the general formulation was given later by the American mathematician G.B. Dantzig in his work [1].

In this paper, we study linear program in primal-dual standard form

$$\begin{aligned}&\left( P\right) \min c^{T}x \text { s.t. }Ax=b ,\;x\ge 0, \\&\left( D\right) \max b^{T}y\text { s.t. } A^{T}y+s=c ,\; s\ge 0, \end{aligned}$$

with \(A\in {\mathbb {R}}^{m\times n},\) \(x,s,c\in {\mathbb {R}}^n\) and \(b,y\in {\mathbb {R}}^m.\)

Several methods are used to find an optimal solution for this pair of problems. Interior-point methods (IPMs) are among the most popular methods. IPMs were first developed by Karmarkar [4] for LO. These methods are based on using Newton’s method in a careful and controlled manner.

Initially, IPAs that required a feasible starting point were studied [7, 13]. However, the feasible initial point is not given in general. Lustig [10] proposed a solution to this when he introduced the first infeasible-start algorithm. His approach was further improved in the predictor-corrector algorithm of Mehrotra [12]. After that, Roos [16] introduced a new infeasible IPA, which uses only full-Newton steps. Some extensions on LO were carried out by Liu and Sun [8], Liu et al. [9] and Mansouri and Roos [11].

Salahi et al. [18] presented a new IIPM for LO based on a specific self-regular KF. Recently, Kheirfam and Haghighi [5, 6] and Moslemi and Kheirfam [14] discussed the complexity of trigonometric proximity based IIPMs for different types of problems.

An alternative method to determine new search directions was introduced by Rigó and Darvay [15] where they presented a new method based on an algebraic equivalent transformation on the centering equation of the system which characterizes the central path.

In this paper, our main contribution is an infeasible-start IPM for LO that builds on the works of Roos [16] and Kheirfam and Haghighi [5, 6]. The algorithm avoids a big-M or a two-phase approach. Furthermore, under general conditions we guarantee that our algorithm will converge to an optimal solution.

We present some notations used throughout the paper. \(\Vert \cdot \Vert ,\) \(\Vert \cdot \Vert _1\) and \(\Vert \cdot \Vert _{\infty } \) denotes the Euclidean norm, the 1-norm and the infinity norm respectively. \({\mathbb {R}}^n_+\) and \({\mathbb {R}}^n_{++}\) denote the nonnegative and the positive orthants respectively. For given vectors \(x,s\in {\mathbb {R}}^n,\) \(X=\mathrm{{diag}}(x)\) denotes the \(n\times n\) diagonal matrix whose diagonal entries are the components of x,  and the vector xs indicate the component-wise product of x and s.

The remainder of this paper is organized as follows: In the next section we recall the basics of IIPMs. The complexity has been analyzed in Sect. 3. Our computational experiments are presented in Sect. 4. Finally, we give the conclusion in the last section.

2 Preliminaries

In this section, we briefly describe the basics of IIPMs for LO. We outline some concepts and basic tools required in IIPMs such as starting point, perturbed problem, central path and proximity measure quantity. We start by recalling the standard LO problem

$$\begin{aligned} \left( P\right) \left\{ \begin{array}{l} \min c^{T}x \\ Ax=b, \\ x\ge 0, \end{array} \right. \end{aligned}$$

and its dual problem

$$\begin{aligned} \left( D\right) \left\{ \begin{array}{l} \max b^{T}y \\ A^{T}y+s=c, \\ s\ge 0, \end{array} \right. \end{aligned}$$

where \(A\in {\mathbb {R}}^{m\times n}\) with rank\((A)=m\le n,\) \(c\in {\mathbb {R}}^n\) and \(b\in {\mathbb {R}}^m\) are given. Unlike feasible IPMs, in IIPMs, a triple (x, y, s) is called an \(\epsilon -\) solution of (P) and (D) if the norms of the residual vectors \(r_b=b-Ax\) and \(r_c=c-A^Ty-s\) do not exceed \(\epsilon ,\) and also \(x^Ts\le \epsilon .\)

Following the basics of IIPMs, we choose \(x^0>0\) and \(s^0>0\) such that \(x^0s^0=\mu ^0 e\) for some positive number \(\mu ^0,\) while \({r_b}^0\) and \({r_c}^0\) denote the initial residual vectors. In this work, we assume that

$$\begin{aligned} x^0=s^0=\xi e,\;\;y^0=0,\;\;\mu ^0=\xi ^2, \end{aligned}$$
(1)

with \(\mu ^0\) the initial duality gap and \(\xi \) satisfies the following inequality

$$\begin{aligned} \Vert x^*+s^*\Vert _{\infty }\le \xi ,\text {for some optimal solution}\,\, (x^*,y^*,s^*) \text { of } (P) \text { and } (D). \end{aligned}$$

For any \(\nu \) with \(0<\nu \le 1,\) we consider the perturbed problem pair \((P_\nu )\) and \((D_\nu )\)

$$\begin{aligned} \left( P_\nu \right) \left\{ \begin{array}{l} \min (c-\nu {r_c}^0)^{T}x \\ Ax=b-\nu {r_b}^0, \\ x\ge 0, \end{array} \right. \\ \left( D_\nu \right) \left\{ \begin{array}{l} \max (b-\nu {r_b}^0)^{T}y\\ A^{T}y+s=c-\nu {r_c}^0, \\ s\ge 0. \end{array} \right. \end{aligned}$$

Note that if \(\nu =1\) then \((P_\nu )\) and \((D_\nu )\) satisfy the interior-point condition (IPC), i.e., \((P_\nu )\) has a feasible solution \(x>0\) and \((D_\nu )\) has a solution (y, s) with \(s>0.\) This implies that the triple \((x,y,s)=(x^0,y^0,s^0)\) yields a strictly feasible solution of the pair of problems \((P_\nu )\) and \((D_\nu ).\)

Theorem 2.1

(Lemma 3.1 in [16]) The original problems (P) and (D) are feasible if and only if for each \(\nu \) satisfying \(0<\nu \le 1\) the perturbed problems \((P_\nu )\) and \((D_\nu )\) satisfy the IPC.

In what follows, we assume that (P) and (D) are feasible. Then Theorem 2.1 implies that for every \(0<\nu \le 1\) the system (2) has a unique solution

$$\begin{aligned} \left\{ \begin{array}{lllll} b-Ax= \nu {r_b}^0, x\ge 0, \\ c-A^{T}y-s=\nu {r_c}^0, s\ge 0, \\ xs = \mu e, \;\;\;\mu >0. \end{array} \right. \end{aligned}$$
(2)

This means that the central path exists and the set of unique solutions \(\{(x(\mu ,\nu ),y(\mu , \nu ),s(\mu ,\nu )): \mu >0,\;0<\nu \le 1\}\) forms the central path with \((x(\mu ,\nu ),y(\mu ,\nu ),s(\mu , \nu ))\) the \(\mu -\)centers of \((P_\nu )\) and \((D_\nu )\) and \(\mu =\nu \mu ^0.\) Furthermore, we denote \((x(\mu ,\nu ),y(\mu ,\nu ),s(\mu ,\nu ))=(x(\nu ),y(\nu ),s(\nu ))\) for simplicity purposes.

Now, we would like to compute an approximate solution of (2). Let (x, y, s) be a positive feasible triple of (2) and \(\mu >0.\) A direct application of Newton’s method produces the following system for the search direction \((\Delta x,\Delta y,\Delta s)\)

$$\begin{aligned} \left\{ \begin{array}{lll} A\Delta x = 0, \\ A^{T}\Delta y+\Delta s = 0, \\ s\Delta x+x\Delta s = \mu e-xs. \end{array} \right. \end{aligned}$$
(3)

Following this centrality step, the new point \((x^+,y^+,s^+)\) is then computed according to:

$$\begin{aligned} x^{+}=x+ \Delta x,\;y^{+}=y+ \Delta y,\;s^{+}=s+\Delta s. \end{aligned}$$

For convenience, we introduce the following scaled vector v and scaled search directions \(d_x\) and \(d_s\)

$$\begin{aligned} v=\sqrt{\frac{xs}{\mu }},\;\;d_x=\frac{v\Delta x}{x},\;\;d_s=\frac{v\Delta s}{s}. \end{aligned}$$
(4)

Using these notations, system (3) can be rewritten as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\overline{A}} d_{x}=0,\\ {\overline{A}}^{T}\frac{\Delta y}{\mu }+d_{s}=0,\\ d_{x}+d_{s}=v^{-1}-v, \end{array} \right. \end{aligned}$$
(5)

where \({\overline{A}}=AV^{-1}X,\;\;V=\mathrm{{diag}}(v)\) and \(X=\mathrm{{diag}}(x).\) The third equation in (5) is called the scaled centering equation.

Defining the proximity mesure \(\delta \) as follows:

$$\begin{aligned} \delta (x,s;\mu ):=\delta (v):=\frac{1}{2}\Vert v^{-1}-v\Vert . \end{aligned}$$
(6)

We use \(\delta \) to measure the distance between an iterate (x, y, s) and the \(\mu -\)center of the perturbed problem pair \((P_\nu )\) and \((D_\nu ).\)

We showcase the outline of one iteration of the algorithm. Starting by the initialization defined in (1), each main iteration consists of a so-called feasibility step, a \(\mu -\)update and a few centrality steps. The feasibility step provides iterates \((x^f,y^f,s^f)\) that are strictly feasible for \((P_{\nu ^+})\) and \((D_{\nu ^+}),\) with \(\nu ^+=(1-\theta )\nu \) and \(\theta \in ]0,1[.\) These iterates belong to the quadratic convergence region with respect to the \(\mu ^+-\)center of \((P_{\nu ^+})\) and \((D_{\nu ^+}),\) with \(\mu ^+=\xi ^2\nu ^+.\) After that, we apply a limited number of centering steps (at most 5 centering steps). These centering steps produces iterates \((x^+,y^+,s^+)\) that are strictly feasible for \((P_{\nu ^+})\) and \((D_{\nu ^+}),\) and such that \(\delta (x^+,s^+;\mu ^+)\le \tau .\)

To obtain iterates that are feasible for \((P_{\nu ^+})\) and \((D_{\nu ^+}),\) we need to solve the following system of equations

$$\begin{aligned} \left\{ \begin{array}{lll} A\Delta ^f x = \theta \nu {r}_b^0, \\ A^{T}\Delta ^f y+\Delta ^f s = \theta \nu {r}_c^0, \\ s\Delta ^f x+x\Delta ^f s = \mu e-xs, \end{array} \right. \end{aligned}$$
(7)

to compute the displacements \((\Delta ^f x,\Delta ^f y,\Delta ^f s).\) The feasible new iterates are then defined by

$$\begin{aligned} x^f=x+\Delta ^f x,\;\; y^f=y+\Delta ^f y,\;\; s^f=s+\Delta ^f s. \end{aligned}$$

Let the scaled search directions \({d}^f_x\) and \({d}^f_s\) be defined as follows:

$$\begin{aligned} {d}^f_x=\frac{v\Delta ^f x}{x},\;\;{d}^f_s=\frac{v\Delta ^f s}{s}. \end{aligned}$$

System (7) is then rewritten in the following form

$$\begin{aligned} \left\{ \begin{array}{l} {\overline{A}} {d}_{x}^f=\theta \nu {r}_b^0,\\ {\overline{A}}^{T}\frac{\Delta ^f y}{\mu }+d_{s}^f=\theta \nu v s^{-1}{r}_c^0,\\ d_{x}^f+d_{s}^f=v^{-1}-v, \end{array} \right. \end{aligned}$$
(8)

where \({\overline{A}}=AV^{-1}X,\;\;V=\mathrm{{diag}}(v),\;\;X=\mathrm{{diag}}(x).\)

Observe that the right-hand side in the last equation of (8) is equal to minus gradient of the classical logarithmic scaled barrier (proximity) function

$$\begin{aligned} \Psi (v)=\sum _{i=1}^n\psi _c(v_i), \end{aligned}$$

where

$$\begin{aligned} \psi _c(t)=\frac{t^2-1}{2}-\log t, \end{aligned}$$

is the so-called KF of the barrier function \(\Psi (v).\)

Coming back to system (8), we can convert it to

$$\begin{aligned} \left\{ \begin{array}{l} {\overline{A}} {d}_{x}^f=\theta \nu {r}_b^0,\\ {\overline{A}}^{T}\frac{\Delta ^f y}{\mu } +d_{s}^f=\theta \nu v s^{-1}{r}_c^0,\\ d_{x}^f+d_{s}^f=-\nabla \Psi (v). \end{array} \right. \end{aligned}$$
(9)

For a different KF, one gets a different search direction. In this context, we consider a new univariate KF \(\psi \) defined as follows:

$$\begin{aligned} \psi \left( t\right) =\frac{t^2-1}{4}-\int _{1}^{t}\frac{\sinh (1)}{2\sinh (y)}dy,\; \forall t>0. \end{aligned}$$
(10)

Based on our KF, let us define a new proximity mesure as follows:

$$\begin{aligned} \sigma (x,s;\mu )=\sigma (v)=\left\| d_{x}^f+d_{s}^f\right\| =\Vert \nabla \Psi (v)\Vert =\left\| \frac{\sinh (e)}{2\sinh (v)}-\frac{v}{2}\right\| . \end{aligned}$$
(11)

Note that

$$\begin{aligned} \sigma (v)=0\Leftrightarrow \nabla \Psi (v)=0\Leftrightarrow v=e, \end{aligned}$$

\(\sigma \) is thus a suitable proximity.

The generic primal-dual IIPM is summarized in Algorithm 1.

figure a

3 Analysis of the algorithm

In this section, we show that the IIPM based on the new KF is well defined. We first state some technical lemmas that we use in the complexity analysis of the algorithm. Then, we prove the strict feasibility of the iterates obtained after the feasibility step. After that, we derive an upper bound for the number of iterations required by the algorithm to obtain an optimal solution.

3.1 Technical lemmas

For conveniency, we give the first two derivatives of \(\psi \)

$$\begin{aligned}{} & {} \psi ^{\prime }(t) =\frac{t}{2}-\frac{\sinh (1)}{2\sinh (t)},\\{} & {} \psi ^{\prime \prime }(t)= \frac{1}{2}+\frac{\sinh (1)\cosh (t)}{2\sinh ^2(t)}> 0.\nonumber \end{aligned}$$
(12)

We can easily verify that \(\psi \) defined in (10) is indeed a KF.

Let \(\delta \) be the proximity defined previously in (6). For simplicity purposes, we put \(\delta (x,s,\mu )=\delta .\) Then, we can take advantage of the following well-known results.

Lemma 3.1

(Lemma \(\Pi .60\) in [17]) Let \(\rho (\delta ):=\delta +\sqrt{1+\delta ^2}.\) Then

$$\begin{aligned} \frac{1}{\rho (\delta )}\le v_i\le \rho (\delta ),\;i=1,\ldots ,n. \end{aligned}$$

Lemma 3.2

(Lemma \(\Pi .51\) in [17]) If \(\delta \le 1\), then the primal-dual Newton step is feasible, i.e. \(x^+\) and \(s^+\) are nonnegative and \((x^+)^Ts^+=n\mu .\) Moreover, if \(\delta <1,\) then

$$\begin{aligned} \delta (x^+,s^+;\mu )\le \frac{\delta ^2}{\sqrt{2(1-\delta ^4)}}. \end{aligned}$$

A direct consequence of this lemma is the following corollary.

Corollary 3.3

(Corollary 2.3 in [5]) If \(\delta \le \frac{1}{\root 4 \of {2}}\) then \(\delta (x^+,s^+;\mu )\le \delta ^2\) and

$$\begin{aligned} \delta (x^+,s^+;\mu ^+)\le {\left( \frac{1}{\root 4 \of {2}}\right) }^{2^k}. \end{aligned}$$

Remark 3.4

Using Corollary 3.3, we conclude that \(\delta (x^+,s^+;\mu ^+)\le \tau \) will hold after

$$\begin{aligned} 2+[\log _2(\log _2 \frac{1}{\tau })] \end{aligned}$$

centering steps.

The following lemma provides an important feature of the hyperbolic cotangent function that enables us to prove that the new KF is efficient.

Lemma 3.5

One has

$$\begin{aligned} t\coth (t)-1>0,\;\forall t>0. \end{aligned}$$
(13)

Proof

Let’s define the function l as follows:

$$\begin{aligned} l(t)=t\coth (t)-1,\;\forall t>0. \end{aligned}$$

Deriving l, we obtain

$$\begin{aligned} l^\prime (t)&=\coth (t)-\frac{t}{\sinh ^2(t)}\\&=\frac{\cosh (t)\sinh (t)-t}{\sinh ^2(t)}. \end{aligned}$$

Recall that

$$\begin{aligned} \sinh (2t)=2\cosh (t)\sinh (t),\;\forall t\in {\mathbb {R}}. \end{aligned}$$

Using this property of the hyperbolic functions, we can rewrite \(l^\prime \) as follows:

$$\begin{aligned} l^\prime (t)&=\frac{\sinh (2t)-2t}{2\sinh ^2(t)}. \end{aligned}$$

Moreover, the Taylor expansion of the hyperbolic sine function implies that

$$\begin{aligned} \sinh (t)\ge t,\;\forall t\ge 0. \end{aligned}$$

It follows that the function l is strictly increasing on the interval \(]0,+\infty [.\) Since

$$\begin{aligned} \lim _{t\rightarrow 0^{+}}l(t)=0\text { and }\lim _{t\rightarrow +\infty }l(t)=+\infty , \end{aligned}$$

we conclude that \(t\coth (t)-1>0,\;\forall t>0.\) \(\square \)

The following lemma plays an important role in the complexity analysis of our algorithm.

Lemma 3.6

One has

$$\begin{aligned} \left|\frac{t}{2}-\frac{\sinh (1)}{2\sinh (t)}\right|\le \left|t-\frac{1}{t}\right|,\;\forall t>0. \end{aligned}$$
(14)

Proof

It’s clear that (14) is satisfied for \(t=1.\) Let g be the function defined for \(t>0\) as follows:

$$\begin{aligned} g(t)&=\left|\frac{t}{2}-\frac{\sinh (1)}{2\sinh (t)}\right|- \left|t-\frac{1}{t}\right|\\&={\left\{ \begin{array}{ll} \dfrac{1}{t}-\dfrac{t}{2}-\dfrac{\sinh (1)}{2\sinh (t)},\;\forall t\ge 1,\\ \dfrac{t}{2}+\dfrac{\sinh (1)}{2\sinh (t)}-\dfrac{1}{t},\;\forall t\le 1. \end{array}\right. } \end{aligned}$$

For this function, we have

$$\begin{aligned} g^\prime (t)&={\left\{ \begin{array}{ll} \dfrac{\sinh (1)\coth (t)}{2\sinh (t)}-\left( \dfrac{1}{t^2}+\dfrac{1}{2}\right) ,\;\forall t> 1,\\ \left( \dfrac{1}{t^2}+\dfrac{1}{2}\right) -\dfrac{\sinh (1)\coth (t)}{2\sinh (t)},\;\forall t< 1.\\ \end{array}\right. } \end{aligned}$$

An important observation is that \(\lim \limits _{t\rightarrow 0^+}g(t)=\lim \limits _{t\rightarrow +\infty }g(t)=-\infty \) and \(g(1)=0.\) So, to prove the inequality (14), it suffices to verify that

$$\begin{aligned} g^\prime (t)>0,\;\forall 0<t< 1,\;\; \text {and}\;\; g^\prime (t)<0,\;\forall t> 1. \end{aligned}$$

We start by the case \(t> 1.\) Since the function \(t\mapsto \sinh (t)\) is monotonically increasing, this implies that

$$\begin{aligned} g^\prime (t)<\frac{t^2(\coth (t)-1)-2}{2 t^2}=:\frac{h(t)}{2 t^2}. \end{aligned}$$

By deriving h,  and using inequality (13), we can easily prove that \(h(t)<0,\;\forall t> 1.\)

Now, we move to the second case, i.e., \(t< 1.\) We rewrite \(g^\prime \) as follows:

$$\begin{aligned} g^\prime (t)=&\frac{(t^2+2)\sinh ^2(t)-\sinh (1)t^2\cosh (t)}{2t^2\sinh ^2(t)}\\&=\frac{t^2\sinh ^2(t)+\left( 2\sinh ^2(t)-\sinh (1)t^2\cosh (t)\right) }{2t^2\sinh ^2(t)}\\&>\frac{t^2\sinh ^2(t)+\left( 2\sinh ^2(t)-\sinh (1)\cosh (1)t^2\right) }{2t^2\sinh ^2(t)}\\&>\frac{t^2\sinh ^2(t)+2\left( \sinh ^2(t)-t^2\right) }{2t^2\sinh ^2(t)}>0, \end{aligned}$$

where the inequalities are obtained using the increase of the hyperbolic cosine function and the fact that \(\sinh (1)\cosh (1)<2.\) This completes the proof. \(\square \)

A direct consequence of this lemma is the following result which gives an upper bound for \(\sigma \) in terms of \(\delta .\)

Lemma 3.7

One has

$$\begin{aligned} \sigma (v)\le 2\delta (v). \end{aligned}$$

Proof

The proof is a direct consequence of Lemma 3.6 and definitions (11) and (6). \(\square \)

3.2 Analysis of the feasibility step

In this subsection, we show that after the feasibility step the new iterates are positive and within the region where the Newton process targeting at \(\mu ^+-\)centers of \((P_{\nu ^+})\) and \((D_{\nu ^+})\) is quadratically convergent, i.e.

$$\begin{aligned} \delta (x^f,s^f;\mu ^+)\le \frac{1}{\root 4 \of {2}}, \end{aligned}$$

with \(x^f,y^f\) and \(s^f\) denote the new iterates generated by the feasibility step such that the feasibility conditions of \((P_{\nu ^+})\) and \((D_{\nu ^+})\) are satisfied. Using (12) and the third equation of (9), we have

$$\begin{aligned} x^f s^f&=\frac{x s}{v^2}(v+d^f_x)(v+d^f_s)\nonumber \\&=\mu (v^2+v(d^f_x+d^f_s)+d^f_xd^f_s)\nonumber \\&=\mu \left( v^2+v\left( \frac{\sinh (e)}{2\sinh (v)}-\frac{v}{2}\right) +d^f_xd^f_s\right) \nonumber \\&=\mu \left( \frac{v^2}{2}+\frac{v\sinh (e)}{2\sinh (v)}+d^f_xd^f_s\right) . \end{aligned}$$
(15)

The next lemma reveals a sufficient condition for the strict feasibility of the feasibility step.

Lemma 3.8

The new iterates \((x^f,y^f,s^f)\) are strictly feasible if

$$\begin{aligned} \frac{v^2}{2}+\frac{v\sinh (e)}{2\sinh (v)}+d^f_xd^f_s>0. \end{aligned}$$
(16)

Proof

We first introduce a step length \(\alpha \in [0,1].\) Then, we define

$$\begin{aligned} x^\alpha =x+\alpha \Delta ^f x,\;\;y^\alpha =y+\alpha \Delta ^f y,\;\;s^\alpha =s+\alpha \Delta ^f s. \end{aligned}$$

Note that for \(\alpha =0\) (\(\alpha =1\)), \(x^0=x\) (\(x^1=x^f\)) respectively and \(x^0s^0>0.\) Hence, using notations (4) and inequality (16), we get

$$\begin{aligned} x^\alpha s^\alpha&=\mu (v+\alpha d^f_x)(v+\alpha d^f_s)\\&=\mu \left( v^2+\alpha v(d^f_x+d^f_s)+\alpha ^2d^f_x d^f_s\right) \\&=\mu \left( v^2+\alpha \left( \frac{v\sinh (e)}{2\sinh (v)}-\frac{v^2}{2}\right) +\alpha ^2d^f_x d^f_s\right) \\&>\mu \left( v^2+\alpha \left( \frac{v\sinh (e)}{2\sinh (v)}-\frac{v^2}{2}\right) +\alpha ^2\left( -\frac{v^2}{2}-\frac{v\sinh (e)}{2\sinh (v)}\right) \right) \\&>\mu \left( v^2+\alpha \frac{v\sinh (e)}{2\sinh (v)}-\alpha \frac{v^2}{2}-\alpha ^2\frac{v^2}{2}-\alpha ^2\frac{v\sinh (e)}{2\sinh (v)}\right) \\&>\mu \left( v^2+\alpha \frac{v\sinh (e)}{2\sinh (v)}-\alpha \frac{v^2}{2}-\alpha \frac{v^2}{2}-\alpha ^2\frac{v\sinh (e)}{2\sinh (v)}\right) \\&=\mu \left( (1-\alpha )v^2+\alpha (1-\alpha )\frac{v\sinh (e)}{2\sinh (v)}\right) . \end{aligned}$$

Obviously \(\left( (1-\alpha )v^2+\alpha (1-\alpha )\dfrac{v\sinh (e)}{2\sinh (v)}\right) \ge 0\) since \(\dfrac{v\sinh (e)}{2\sinh (v)}\ge 0,\;\forall v>0.\) Thus, for every \(\alpha \in [0,1],\) \(x^\alpha s^\alpha >0\) which implies that none of the components of \(x^\alpha \) and \(s^\alpha \) vanishes. Taking \(\alpha =1,\) we obtain \(x^f>0\) and \(s^f>0.\) This completes the proof. \(\square \)

In the sequel, we denote

$$\begin{aligned} \omega :=\Vert (\omega _1,...,\omega _n)\Vert , \text { where } \omega _i=\frac{1}{2}\sqrt{|{d^f_{x_i}}|^2+|{d^f_{s_i}}|^2}, \end{aligned}$$

and

$$\begin{aligned} \delta (x^f,s^f;\mu ^+):=\delta (v^f)=\frac{1}{2}\Vert (v^f)^{-1}-v^f\Vert ,\text { where } v^f=\sqrt{\frac{x^fs^f}{\mu ^+}}. \end{aligned}$$

Remark 3.9

Using the previous notations, it follows that

$$\begin{aligned} |{d^f_{x_i}}{d^f_{s_i}}|\le \frac{1}{2}\Big (|{d^f_{x_i}}|^2+|{d^f_{s_i}}|^2\Big )=2{\omega _i}^2\le 2\omega ^2,\; i=1,\ldots ,n. \end{aligned}$$

The following lemma gives an upper bound for the proximity function after the feasibility step.

Lemma 3.10

If \(\frac{v^2}{2}+\frac{v\sinh (e)}{2\sinh (v)}+d^f_xd^f_s>0,\) then

$$\begin{aligned} \delta (v^f)\le \frac{\theta \sqrt{n}+4\delta \rho (\delta )+2\omega ^2}{2\sqrt{(1-\theta )\left( \frac{1}{\rho (\delta )^2}-2\delta \rho (\delta )-2\omega ^2\right) }}. \end{aligned}$$

Proof

Definition (6) implies that

$$\begin{aligned} \delta (v^f)=\frac{1}{2}\Vert (v^f)^{-1}-v^f\Vert \le \dfrac{1}{2{v^f_{\min }}}\Vert e-(v^f)^2\Vert . \end{aligned}$$
(17)

Using (15) and Remark 3.9, we get

$$\begin{aligned} \Vert e-(v^f)^2\Vert \le&\frac{1}{1-\theta }\left\| (1-\theta )e-\frac{v^2}{2}-\frac{v\sinh (e)}{2\sinh (v)}-d^f_xd^f_s\right\| \nonumber \\ =&\frac{1}{1-\theta }\left\| (e-v^2)-\theta e+v\left( \frac{v}{2}-\frac{\sinh (e)}{2\sinh (v)}\right) -d^f_xd^f_s\right\| \nonumber \\ =&\frac{1}{1-\theta }\left\| v(v^{-1}-v)-\theta e+v\left( \frac{v}{2}-\frac{\sinh (e)}{2\sinh (v)}\right) -d^f_xd^f_s\right\| \nonumber \\ \le&\frac{1}{1-\theta }\left( \Vert v(v^{-1}-v)\Vert +\theta \sqrt{n}+\left\| v\left( \frac{v}{2}-\frac{\sinh (e)}{2\sinh (v)}\right) \right\| +2\omega ^2\right) . \end{aligned}$$
(18)

Moreover, using definition (6), Lemma 3.1 and Lemma 3.6 we obtain the following inequalities

$$\begin{aligned} \left\| v\left( \dfrac{1}{v}-v\right) \right\| ^2&=\sum _{i=1}^{n}\left|v_i\left( \dfrac{1}{v_i}-v_i\right) \right|^2\nonumber \\&\le \rho (\delta )^2\sum _{i=1}^{n}\left|\frac{1}{v_i}-v_i\right|^2\nonumber \\&= 4 \rho (\delta )^2\delta ^2, \end{aligned}$$
(19)

and

$$\begin{aligned} \left\| v\left( \dfrac{v}{2}-\dfrac{\sinh (e)}{2\sinh (v)}\right) \right\| ^2&=\sum _{i=1}^{n}\left|v_i\left( \dfrac{v_i}{2}-\dfrac{\sinh (1)}{2\sinh (v_i)}\right) \right|^2\nonumber \\&\le \rho (\delta )^2\sum _{i=1}^{n}\left|\frac{1}{v_i}-v_i\right|^2\nonumber \\&= 4\rho (\delta )^2\delta ^2. \end{aligned}$$
(20)

The substitution of inequalities (19) and (20) into (18) yields the following inequality

$$\begin{aligned} \left\| e-(v^f)^2\right\| \le \dfrac{1}{1-\theta }\left( 4\rho (\delta )\delta +\theta \sqrt{n}+2\omega ^2\right) . \end{aligned}$$
(21)

Using (15) and the definition of \(v^f,\) we have

$$\begin{aligned} ({v^f_{\min }})^2&=\min _{i}\dfrac{1}{1-\theta }\left( \dfrac{{v_i}^2}{2}+\dfrac{v_i\sinh (1)}{2\sinh (v_i)}+{d^f_{x_i}}{d^f_{s_i}}\right) \nonumber \\&=\min _{i}\dfrac{1}{1-\theta }\left( \dfrac{{v_i}^2}{2}+\dfrac{{v_i}^2}{2}-\frac{{v_i}^2}{2}+\dfrac{v_i\sinh (1)}{2\sinh (v_i)}+{d^f_{x_i}}{d^f_{s_i}}\right) \nonumber \\&=\min _{i}\dfrac{1}{1-\theta }\left( {v_i}^2-\left( \dfrac{{v_i}^2}{2}-\dfrac{v_i\sinh (1)}{2\sinh (v_i)}\right) +{d^f_{x_i}}{d^f_{s_i}}\right) \nonumber \\&\ge \dfrac{1}{1-\theta }\left( v_{\min }^2-\left\| \dfrac{{v}^2}{2}-\dfrac{v\sinh (e)}{2\sinh (v)}\right\| -2\omega ^2\right) \nonumber \\&\ge \dfrac{1}{1-\theta }\left( \dfrac{1}{\rho (\delta )^2}-2\rho (\delta )\delta -2\omega ^2\right) , \end{aligned}$$
(22)

where the last inequality is due to Lemma 3.1 and (20). The substitution of (21) and (22) in (17) yields the desired inequality. \(\square \)

Corollary 3.11

Let \(n\ge 2,\) \(\delta \le \tau .\) Choosing \(\tau =\dfrac{1}{16},\;\omega \le \dfrac{1}{2\sqrt{2}},\) and \(\theta =\dfrac{\alpha }{4\sqrt{n}}\) with \(\alpha \le 1,\) we have

  1. 1.

    the iterates \((x^f,y^f,s^f)\) obtained after feasibility step are strictly feasible, i.e., \(x^fs^f>0.\)

  2. 2.

    after the feasibility step, the new iterates \((x^f,y^f,s^f)\) are within the region where the Newton process targeting at the \(\mu ^+-\)centers of \((P_{\nu ^+})\) and \((D_{\nu ^+}),\) is quadratically convergent, i.e., \(\delta (v^f)\le \dfrac{1}{\root 4 \of {2}}.\)

Proof

For the first item, using (22), we obtain

$$\begin{aligned} \min _{i}\left( \dfrac{{v_i}^2}{2}+\dfrac{v_i\sinh (1)}{2\sinh (v_i)}+{d^f_{x_i}}{d^f_{s_i}}\right)&\ge \left( \dfrac{1}{\rho (\delta )^2}-2\rho (\delta )\delta -2\omega ^2\right) \\&\ge \left( \dfrac{1}{\rho (\tau )^2}-2\rho (\tau )\tau -2\omega ^2\right) \\&\simeq 0.4995>0, \end{aligned}$$

where the second inequality is due to the fact that \(\rho (\delta )\) is monotonically increasing with respect to \(\delta .\) The result derives then from Lemma 3.8. As for the second item, it’s clear that \(\dfrac{v^2}{2}+\dfrac{v\sinh (e)}{2\sinh (v)}+d^f_xd^f_s>0,\) from the proof of the first item. Therefore, using Lemma 3.10 we obtain

$$\begin{aligned} \delta (v^f)\le&\dfrac{\dfrac{1}{4}+\dfrac{1}{4}\left( \dfrac{1}{16}+\sqrt{1+\dfrac{1}{16^2}}\right) +\dfrac{1}{4}}{2\sqrt{\left( 1-\dfrac{1}{4\sqrt{2}}\right) \left( \dfrac{1}{\left( \dfrac{1}{16}+\sqrt{1+\dfrac{1}{16^2}}\right) ^2}-\dfrac{\left( \dfrac{1}{16}+\sqrt{1+\dfrac{1}{16^2}}\right) }{8}-\dfrac{1}{4}\right) }}\\&\le 0.5974, \end{aligned}$$

which implies that \(\delta (v^f)\le \dfrac{1}{\root 4 \of {2}}.\) This completes the proof. \(\square \)

In the rest of this section, we will assume that

$$\begin{aligned} \tau =\frac{1}{16},\;\omega \le \frac{1}{2\sqrt{2}}, \text { and } \theta =\frac{\alpha }{4\sqrt{n}} \text { with } \alpha \le 1. \end{aligned}$$

3.3 Upper bounds for \(\omega \) and \(\Vert q \Vert \)

In this subsection, we will follow the same procedure as in Section 4.3 in [16]. Let \({\mathcal {L}}\) be the null space of the matrix \({\bar{A}}.\) Note that the affine space

$$\begin{aligned} \{\xi \in {\mathbb {R}}^n: {\bar{A}}\xi =\theta \nu {r_b}^0\} \end{aligned}$$

equals \(d_x+{\mathcal {L}}.\) Furthermore, the row space \({\bar{A}}\) equals the orthogonal complement \({\mathcal {L}}^ \perp \) of \({\mathcal {L}}\) defined as follows:

$$\begin{aligned} {\mathcal {L}}^ \perp =\left\{ {\bar{A}}^Tz:z\in {\mathbb {R}}^m\right\} . \end{aligned}$$

An obvious observation is that \(d_s\in \theta \nu v s^{-1}{r_c}^0+{\mathcal {L}}^ \perp .\) In addition, \({\mathcal {L}}^ \perp \cap {\mathcal {L}}=\{0\}.\) As a consequence, the affine spaces \(d_x+{\mathcal {L}}\) and \(d_s+{\mathcal {L}}^ \perp \) meet in a unique point q,  i.e., q is the solution of the system

$$\begin{aligned} \left\{ \begin{array}{l} {\overline{A}} q=\theta \nu {r_b}^0,\\ {\overline{A}}^{T}z+q=\theta \nu v s^{-1}{r_c}^0. \end{array} \right. \end{aligned}$$
(23)

Lemma 3.12

Let q be the unique solution of (23). Then,

$$\begin{aligned} \omega \le \frac{1}{2}\sqrt{\Vert q\Vert ^2+(\Vert q\Vert +\sigma (v))^2}. \end{aligned}$$

Proof

The lemma is obtained using the same arguments as in Lemma 4.6 in [16] with \(r=-\nabla \Psi (v).\) \(\square \)

Lemma 3.13

(Lemma 4.7 in [16]) One has

$$\begin{aligned} \sqrt{\mu }\Vert q\Vert \le \theta \nu \xi \sqrt{e^T\left( \frac{x}{s}+\frac{s}{x}\right) }. \end{aligned}$$

Corollary 3.14

(Corollary 3.10 in [5]) Let \(\tau =\dfrac{1}{16}\) and \(\delta (v)\le \tau .\) Then

$$\begin{aligned} \sqrt{\frac{x}{s}}\le \sqrt{2}\frac{x(\mu ,\nu )}{\sqrt{\mu }},\;\sqrt{\frac{s}{x}}\le \sqrt{2}\frac{s(\mu ,\nu )}{\sqrt{\mu }}. \end{aligned}$$

Recall that \(\delta (v^f)\le \frac{1}{\root 4 \of {2}}\) holds if \(\omega \le \frac{1}{2\sqrt{2}}.\) Using Lemma 3.12 and Lemma 3.7, this will certainly hold if

$$\begin{aligned} \Vert q\Vert ^2+\left( \Vert q\Vert +2\delta \right) ^2\le \dfrac{1}{2}. \end{aligned}$$

Or from Lemma 3.13 and Corollary 3.14, it follows that

$$\begin{aligned} \mu \Vert q\Vert \le \theta \nu \xi \sqrt{2} \sqrt{\Vert x(\mu ,\nu )\Vert ^2+\Vert s(\mu ,\nu )\Vert ^2}. \end{aligned}$$

As in [16], using \(\mu =\mu ^0\nu =\nu \xi ^2\) and \(\theta =\frac{\alpha }{4\sqrt{n}}\), we obtain the following upper bound for the norm of q

$$\begin{aligned} \Vert q\Vert&\le \dfrac{\sqrt{2}\alpha }{4\xi \sqrt{n}}\sqrt{\Vert x(\mu ,\nu )\Vert ^2+\Vert s(\mu ,\nu )\Vert ^2}\\&=\dfrac{\alpha }{2\xi \sqrt{2n}}\sqrt{\Vert x(\mu ,\nu )\Vert ^2+\Vert s(\mu ,\nu )\Vert ^2}. \end{aligned}$$

Let us denote

$$\begin{aligned} \kappa (\xi ,\nu )=\dfrac{\sqrt{\Vert x(\mu ,\nu )\Vert ^2+\Vert s(\mu ,\nu )\Vert ^2}}{\xi \sqrt{2n}};\;0<\nu \le 1,\;\mu =\mu ^0\nu , \end{aligned}$$

and

$$\begin{aligned} {\bar{\kappa }}(\xi )=\max _{0<\nu \le 1}\kappa (\xi ,\nu ). \end{aligned}$$

We rewrite the upper bound for the norm of q as follows:

$$\begin{aligned} \Vert q\Vert \le \frac{1}{2}\alpha {\bar{\kappa }}(\xi ). \end{aligned}$$

After some calculations, we conclude that

$$\begin{aligned} \delta (v^f)\le \frac{1}{\root 4 \of {2}} \text { if } \Vert q\Vert \le 0.4336. \end{aligned}$$

Or since \(\Vert q\Vert \le \frac{1}{2}\alpha {\bar{\kappa }}(\xi ),\) the latter inequality will be satisfied if

$$\begin{aligned} \alpha :=\frac{ 0.8672}{{\bar{\kappa }}(\xi )}. \end{aligned}$$
(24)

The following result gives a range for the parameter \({\bar{\kappa }}(\xi ).\) We follow the technics from Section 4.6 of [16]. We skip some details of the proof since it doesn’t depend on the proposed KF.

Lemma 3.15

One has

$$\begin{aligned} 1\le {\bar{\kappa }}(\xi )\le \sqrt{2 n}. \end{aligned}$$

Proof

From initialization (1), we get \(\kappa (\xi )=1.\) This yields the left-hand side of the inequality. For the other side, let \(x^*\) be an optimal solution of (P) and \((y^*,s^*)\) an optimal solution of (D). For simplicity, we denote \(x=x(\mu ,\nu ),\) \(y=y(\mu ,\nu )\) and \(s=s(\mu ,\nu ).\) Hence, the triple (x, y, s) is the unique solution of the following system

$$\begin{aligned} \left\{ \begin{array}{lllll} A(x^*-x-\nu x^*+\nu \xi e)= 0, x\ge 0, \\ A^T(y^*-y-\nu y^*)=s-s^*+\nu s^*-\nu \xi e, s\ge 0, \\ xs = \nu \xi ^2 e, \;\;\;\mu >0. \end{array} \right. \end{aligned}$$

Using the fact that the row space of a matrix and its null space are orthogonal, we get

$$\begin{aligned} ((1-\nu )x^*-x+\nu \xi e)^T(s-(1-\nu )s^*-\nu \xi e)=0. \end{aligned}$$
(25)

Let us define

$$\begin{aligned} a_1&=(1-\nu )x^*+\nu \xi e\ge \nu \xi e,\\ a_2&=(1-\nu )s^*+\nu \xi e\ge \nu \xi e. \end{aligned}$$

From (25), we get

$$\begin{aligned} a^T_1a_2=a^T_1s+a_2^Tx. \end{aligned}$$
(26)

Therefore, since \({x^*}^Ts^*=0,\) and \(x^*+s^*\le \xi e\) we can obtain

$$\begin{aligned} a^T_1a_2+x^T s&=((1-\nu )x^*+\nu \xi e)^T ((1-\nu )s^*+\nu \xi e)+\nu \xi ^2 n\nonumber \\&\le 2\nu \xi ^2 n. \end{aligned}$$
(27)

In addition, we can easily verify that

$$\begin{aligned} a^T_1s+a^T_2 x&=((1-\nu )x^*+\nu \xi e)^T s+((1-\nu )s^*+\nu \xi e)^T x\nonumber \\&\ge \nu \xi e^T (x+s)=\nu \xi (\Vert x\Vert _1+\Vert s\Vert _1). \end{aligned}$$
(28)

Using (26), (27) and (28) it follows that

$$\begin{aligned} (\Vert x\Vert _1+\Vert s\Vert _1)\le 2\xi n. \end{aligned}$$

Using the equivalence between the Euclidean norm and the 1-norm, we get the final inequality. \(\square \)

3.4 Iteration bound

We arrive at the final result of this section which summarizes the complexity bound. As we found in the previous sections, starting from an iterate (x, y, s) satisfying \(\delta (x,s;\mu )\le \tau \) with \(\tau \) and \(\theta \) defined previously, the new iterate \((x^f,y^f,s^f)\) is strictly feasible and \(\delta (x^f,s^f;\mu ^+)\le \frac{1}{\root 4 \of {2}}.\) Moreover, according to Remark 3.4, the number of centrality steps needed to obtain iterates \((x^+,y^+,s^+)\) satisfying \(\delta (x^+,s^+;\mu ^+)\le \tau \) is at most 5. Therefore, the total number of main iterations is bounded by

$$\begin{aligned} \frac{1}{\theta }\log \frac{\max \{(x^0)^Ts^0,\Vert r^0_b\Vert ,\Vert r^0_c\Vert \}}{\epsilon }. \end{aligned}$$

Let us recall that \(\theta =\dfrac{\alpha }{4\sqrt{n}}.\) Thus, using (24) and the fact that \((x^0)^T s^0=n\xi ^2,\) we obtain the following upper bound for the total number of iterations

$$\begin{aligned} 25\sqrt{n} {\bar{\kappa }}(\xi )\log \frac{\max \{n\xi ^2,\Vert r^0_b\Vert ,\Vert r^0_c\Vert \}}{ \epsilon }. \end{aligned}$$

From Lemma 3.15, we can state the final result of this section which summarizes the complexity bound.

Theorem 3.16

Let (P) and (D) be feasible and \(\xi >0\) such that

$$\begin{aligned} \Vert x^*+s^*\Vert _{\infty }\le \xi , \end{aligned}$$

for some optimal solutions \(x^*\) of (P) and \((y^*,s^*)\) of (D). Then, the algorithm finds an \(\epsilon -\)solution of (P) and (D) after at most

$$\begin{aligned} 25\sqrt{2} n\log \frac{\max \{n\xi ^2,\Vert {r_b}^0\Vert ,\Vert {r_c}^0\Vert \}}{\epsilon } \end{aligned}$$

iterations.

4 Numerical tests

In this section, we showcase the performance of the proposed algorithm outlined in 1 by performing some preliminary numerical tests. Our experiments were directly implemented in MATLAB R2012b and performed on Supermicro dual\(-\)2.80 GHz Intel Core i5 server with 4.00 Go RAM.

We compare our algorithm (Alg. 1) with the SeDuMi solver using the average CPU time. The latter is the time needed to obtain an optimal solution. The comparison was done on a set of seven Netlib problems. While implementing our algorithm, we set \(\epsilon = 10^{-4},\) \( \tau =\dfrac{1}{16}\) and \((x^0,y^0,s^0)=(\xi e,0,\xi e),\) with \(\xi \) chosen such that \(\Vert x^*+s^*\Vert _{\infty }\le \xi .\) As for \(\theta ,\) we use fixed values, \(\theta \in \{0.4,0.5,0.6,0.7\}\) because they perform better than the theoretical value \(\theta =\dfrac{1}{5\sqrt{2}n}.\) The results are summarized in Table 1. For each example, we use bold font to highlight the best, i.e., the shortest CPU time.

Table 1 Average CPU time measured in seconds for seven Netlib problems
Full size table

From Table 1, it becomes clear that both our algorithm and SeDuMi solver take similar time to obtain an optimal solution.

5 Conclusions and remarks

This paper proposes a full-Newton step infeasible IPA with new search directions. The centrality step is derived using the classical search direction, while we used a KF with hyperbolic barrier term to induce the feasibility step. The complexity analysis for the primal-dual infeasible IPA based on this KF indicates that the proposed algorithm enjoys the favorable iteration bound for LO. Furthermore, numerical tests on a selected set of Netlib problems show that our algorithm seems promising in practice.