1 Introduction

Research on nonlinear dynamics of systems has become very prevalent in the past several decades, with applications ranging from structural design [1,2,3,4] to control systems [5, 6] to super-resolution sensors [7]. Vibro-contact dynamical systems, in particular, occur in many different engineering fields, ranging from large structures such as aircraft [8,9,10,11,12] and spacecraft [13] to small energy harvesters [1, 14]. These systems exhibit strongly nonlinear behaviors, and a variety of numerical methods are used to study these systems including finite element analysis (FEA) and reduced-order modeling. Reduced-order models (ROMs), in particular, have seen a lot of attention due to their combination of usually good fidelity and low computational costs compared to FEA or physical tests. Time-integration [8, 10] methods, and various forms of harmonic balance and modifications thereto [13, 15,16,17], are among the most common types of solution approaches used to study ROMs of contact systems.

Piecewise-smooth nonlinearities such as contact can induce strong, complex behavior and cause unique numerical difficulties due to their discontinuous and nonsmooth nature. For example, time integration methods suffer from accumulating roundoff error if the precise times and locations of contacts are not captured [8, 18, 19]. The improved accuracy from accurately capturing contacts requires a trade-off with computational cost. Harmonic balance methods (HBMs) also suffer because chaotic or otherwise aperiodic responses cannot be determined, and a very large number of harmonics may be required to obtain accurate periodic results [20]. Thus, an important consideration is how to adequately represent the contact forces in a piecewise-smooth nonlinear system’s equations of motion. Detroux et al. [13] utilized HBM to perform bifurcation tracking of Neimark–Sacker bifurcations in a spacecraft with mechanical stoppers. They used third-order polynomials to regularize the trilinear contact force "in the close vicinity of the clearances," in order to implement \({C}^{1}\) continuity and avoid numerical problems. Alcorta et al. [17] utilized a 15-mode HBM with continuation algorithms to perform bifurcation tracking of period-doubling (flip) bifurcations in a freeplay system and map out isolated resonance branches. In order to prevent their algorithms from failing, they had to represent the freeplay with an arctangent-based function that closely resembled the freeplay but was fully smooth and continuous.

Other continuous and fully smooth functions have been used to represent nonsmooth contact forces, such as absolute-value and polynomial functions [1, 21], the hyperbolic tangent function [8, 16], or combinations of similar functions. One advantage of replacing a nonsmooth contact force with a continuous representation is lower computational costs, but there are tradeoffs with new sources of error. The approximate contact force within a freeplay gap may be nonzero, for example, or the contact force outside the gap may be too large or too small. These errors may be significant or not depending on the particular representation used.

Kim et al. [15] tested four different representations (hyperbolic tangent, arctangent, hyperbolic cosine, and a quintic spline) on a single-degree-of-freedom torsional system. They found the first and second representations to be the best overall when used carefully, the third model performed worst due to singularity problems, and the fourth model was advantageous only for semianalytical methods like HBM. Vasconcellos et al. [8] studied an aeroelastic system with control-surface freeplay by comparing time-integration results obtained using three different models (piecewise, polynomial, and hyperbolic tangent) to past experimental data. They showed the hyperbolic tangent model could capture aperiodic responses well in conjunction with the exact discontinuous model, but the polynomial failed and only predicted periodic responses. More recently, Yoon et al. [16] compared three different representations (hyperbolic tangent, arctangent, and a proposed polynomial-based spline) for use with HBM to model a four-degree-of-freedom gear system with backlash. When properly converged, all three models produced good results but still suffered from numerical discrepancies.

These works indicate that some continuous representations are unable to capture all of the nonlinear behaviors that may be present in a dynamical system, whether using direct time integration or harmonic balance methods. This means that potentially dangerous responses, such as grazing and other discontinuity-induced bifurcations, may not be predicted. The goal of this work is to analyze the effectiveness of smooth and continuous contact-force representations at capturing the physics and nonlinear behavior of a general contact system. In particular, a single-degree-of-freedom forced Duffing oscillator with freeplay nonlinearity [22] is used as a test case. The different representations studied consist of (i) simple polynomial, (ii) rational polynomial, (iii) hyperbolic tangent, (iv) arctangent, and (v) logarithm-arctangent models. Numerical results using each representation and MATLAB ode45 time integration are compared to results using the exact piecewise-smooth contact force model, computed using ode45 with its Event Location capability for high accuracy [19]. The effectiveness of each representation is examined for numerical accuracy, including the ability to capture super- and subharmonic resonances, multiple solution branches, and chaotic responses, in addition to computation time. This work intends to expand on past studies by determining the limits of applicability for each representation and discussing under what conditions each representation may be used in lieu of the exact piecewise representation.

The remainder of this paper is structured as follows: Sect. 2 describes the nonlinear Duffing-freeplay system and the numerical method used. Section 3 discusses the representations to be analyzed and how well they can approximate the exact piecewise contact force. Section 4 is divided into two parts: Sect. 4.1 presents frequency–response curves and bifurcation diagrams obtained using each representation to determine how well each one can capture nonlinear behavior, and Sect. 4.2 compares computational costs and discusses the limits of applicability for each representation. The conclusions of the investigation are provided in Sect. 5.

2 Nonlinear system formulation and contact-force representations

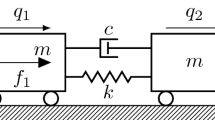
The nonlinear system used to compare the different contact-force representations studied here is a single degree-of-freedom forced Duffing oscillator with freeplay nonlinearity. A physical mockup of this spring-mass system was studied experimentally by deLangre et al. [22] and has the following equation of motion:

$$ \ddot{x}\left( t \right) + 2\zeta \omega_{n} \dot{x}\left( t \right) + \omega_{n}^{2} x\left( t \right) + \frac{\alpha }{m}x\left( t \right)^{3} + \frac{1}{m}F_{c} \left( x \right) = \frac{p}{m}\cos \left( {\omega t} \right), $$
(1a)
$$ F_{c} \left( x \right) = \left\{ {\begin{array}{*{20}c} {K_{c} \left( {x + j_{1} } \right),} \\ {0,} \\ {K_{c} \left( {x - j_{2} } \right),} \\ \end{array} } \right. - \begin{array}{*{20}c} {x < - j_{1} } \\ {j_{1} \le x \le j_{2} } \\ {x > j_{2} } \\ \end{array} ,\quad 0 < j_{1} < j_{2} $$
(1b)

where \(\zeta \) denotes the linear damping ratio, \({\omega }_{n}\) is the linear natural frequency, \(m\) represents the system mass (treated as a point mass), \(\alpha \) is the nonlinear cubic stiffness, \({F}_{c}\) is the force applied by two contact springs, \(p\) is the forcing magnitude, \(\omega \) represents the forcing frequency, \({K}_{c}\) is the contact-spring stiffness, and \({j}_{1},{j}_{2}\) denote the lower and upper gap boundaries, respectively, between the mass and the springs.

A spring is in contact with the mass only if the displacement exceeds \(x<-{j}_{1}\) or \(x>{j}_{2}\). This Duffing-freeplay model is represented in Fig. 1. This system has been shown to exhibit complex nonlinear behaviors, such as superharmonic and subharmonic resonances and chaos [17, 22]. The limit as \({K}_{c}\to \infty \) turns the contact into hard impact which generally enables contact systems to be more easily analyzed with analytical methods [23, 24]. The considered parameters in this study are given in Table 1.

Fig. 1
figure 1

a A schematic of a physical system and b a spring–mass–damper representation of the Duffing-freeplay system

Full size image
Table 1 Default variable values used for simulations
Full size table

Numerical simulations are performed in MATLAB® using the ode45 time integration solver. The Event Location feature is enabled to accurately capture the intermittent contact and discontinuous behavior [19]. It works by stopping and restarting time integration any time a user-defined “event” occurs (i.e., a contact between the mass and either of the contact springs). This forces a timestep at every location of contact so that the transitions from in-contact to out-of-contact are not abruptly crossed, which leads to accumulating roundoff error. Relative and absolute error tolerances are set to \({10}^{-4}\) and \({10}^{-7}\), respectively, for all simulations. All simulations are run until transient motions decayed out.

For reference, the frequency–response curves shown in later figures are generated by computing time histories to steady-state and plotting peak amplitude versus forcing frequency, with all time histories having the same initial conditions (ICs). This is repeated for different ICs. Bifurcation diagrams are similar but plot all the steady-state extrema (i.e., minima, maxima, and inflections) versus bifurcation parameter (usually the forcing frequency), and this is not repeated for multiple ICs. These two figures are similar but have different capabilities. A frequency–response curve will show the overall response of a system at different frequencies, will clearly reveal multiple solution branches (multistable behavior), and can imply the presence of chaos (or an otherwise aperiodic response), but periodic and aperiodic responses can be difficult to distinguish. On the other hand, a bifurcation diagram constructed as described above can distinguish aperiodic from periodic. A period-\(n\) response at a given forcing frequency will generally manifest as \(2n\) discrete points, whereas an aperiodic response will manifest as a coarse line of points. Other analyses can be performed to further guarantee a response is chaotic (such as Poincare map or Lyapunov exponent [25, 26], Melnikov function [27], etc.) if needed.

The contact-force representations that are studied and compared in this work are listed below and are taken from several different works [8, 10, 13, 15,16,17]. Those representations are modified as needed to represent an arbitrary symmetric freeplay function, since some works only studied or used a symmetric freeplay system. The different representations are as follows:

  1. 1.

    Simple polynomial model [8, 13]:

    $$ F_{c} = K_{c0} + K_{c1} x + K_{c2} x^{2} + K_{c3} x^{3} + \cdots + K_{cn} x^{n} $$
    (2)

    It should be noted that \({K}_{c0}\)represents the freeplay force at \(x=0\) and \({K}_{c1}\)the slope of the freeplay force at \(x=0.\) Intuitively, both would have values near zero for a symmetric freeplay system.

  2. 2.

    Rational polynomial model [10]:

    $$ F_{c} = \frac{{a_{n} x^{n} + a_{n - 1} x^{n - 1} + \cdots + a_{2} x^{2} + a_{1} x + a_{0} }}{{b_{m} x^{m} + b_{m - 1} x^{m - 1} + \cdots + b_{2} x^{2} + b_{1} x + b_{0} }} $$
    (3)
  3. 3.

    Hyperbolic tangent model [8, 15, 16]:

    $$ F_{c} = K_{c} \left( {\frac{1}{2}\left[ {1 - \tanh \left( {\varepsilon \left( {x + j_{1} } \right)} \right)} \right]\left( {x + j_{1} } \right) + \frac{1}{2}\left[ {1 + \tanh \left( {\varepsilon \left( {x - j_{2} } \right)} \right)} \right]\left( {x - j_{2} } \right) + P} \right) $$
    (4)

    Here, ε is a convergence parameter; increasing its value produces a more accurate representation of the piecewise-smooth function. Also, P denotes a preload that works to shift the entire force–displacement curve up or down. For a freeplay system, there is no contact force within the freeplay gap making ε = 0.

  4. 4.

    Arctangent model [15, 16]:

    $$ F_{c} = K_{c} \left( {\frac{1}{2}\left[ {1 - \frac{2}{\pi }\arctan \left( {\varepsilon \left( {x + j_{1} } \right)} \right)} \right]\left( {x + j_{1} } \right) + \frac{1}{2}\left[ {1 + \frac{2}{\pi }\arctan \left( {\varepsilon \left( {x - j_{2} } \right)} \right)} \right]\left( {x - j_{2} } \right)} \right) $$
    (5)

    Like before, ε is a convergence parameter and a larger value improves the model’s accuracy.

  5. 5.

    Logarithm-arctangent model [17]:

    $$ F_{c} \left( x \right) = K_{c} \left[ {x + \frac{1}{\pi }\left( {F^{ + } - F^{ - } + \frac{1}{2\gamma }F^{L} + A_{c} } \right)} \right], $$
    (6a)
    $$ F^{ + } \left( x \right) = \left( {x - j_{2} } \right)\tan^{ - 1} \left( {\gamma \left( {x - j_{2} } \right)} \right),F^{ - } \left( x \right) = \left( {x + j_{1} } \right)\tan^{ - 1} \left( {\gamma \left( {x + j_{1} } \right)} \right), $$
    (6b)
    $$ F^{L} \left( x \right) = \log \left[ {\frac{{1 + \left( {\gamma \left( {x + j_{1} } \right)} \right)^{2} }}{{1 + \left( {\gamma \left( {x - j_{2} } \right)} \right)^{2} }}} \right],\;A_{c} = F^{ - } \left( 0 \right) - F^{ + } \left( 0 \right) - \frac{1}{2\gamma }F^{L} \left( 0 \right) $$
    (6c)

The convergence parameter in this model is \(\gamma \). It should be mentioned that \(\lim_{\varepsilon \to \infty } \left( {x + j_{1} } \right)\tanh \left( {\varepsilon \left( {x + j_{1} } \right)} \right) = \left| {x + j_{1} } \right|\) and \(\lim_{\varepsilon ,\gamma \to \infty } \left( {x + j_{1} } \right)\arctan \left( {\varepsilon \left( {x + j_{1} } \right)} \right) = \frac{\pi }{2}\left| {x + j_{1} } \right|\). Thus, Eqs. (4–6) approach one another as their convergence parameters are increased. Kim et al. [15] studied the convergence properties of simpler forms of Eqs. (4) and (5) and found that the convergence parameter could be low enough to ensure the representation was smooth and would perform well in numerical codes, but also large enough to ensure the results were accurate to some tolerance.

3 Model accuracy considerations

The contact-force representations in Eqs. (2)–(6) are analyzed here for their ability to match the shape of the exact piecewise-smooth function in Eq. (1b). Starting with the polynomial model of Eq. (2), one might think to use a model of this type because of its simplicity and straightforward implementation into numerical solvers. Appropriate coefficients \({K}_{c0},{K}_{c1},\dots \) must be fit to the reference function before solving the numerical model, using either a simple least-squares regression or by manually selecting coefficients until the numerical results match a selection of experimental or numerical data. The latter method is avoided here because preliminary tests showed it to be very unreliable at capturing the proper system responses (results omitted for brevity). For the polynomial representation, regression is performed over the displacement range \(x\in \left[-4, 4\right] \mathrm{mm}\) as this encompassed the largest displacements present for the parameters in Table 1. MATLAB’s polyfit function is used to perform the actual regression.

Figure 2 presents the results of using polynomials to represent the piecewise freeplay force–displacement curve. Figure 2a is for symmetric and relatively soft contact, \({K}_{c}=1.4\times {10}^{4} \mathrm{N}/\mathrm{m},{j}_{1}={j}_{2}=0.4 \mathrm{mm}\), and shows polynomials of degree 3 through 21. It is clear that the polynomials match the piecewise behavior away from the freeplay gap better than the behavior near the gap. Within the gap itself, the freeplay force is over- or underestimated from zero, but this error decreases with higher degree. In Fig. 2b, the constant and linear terms \({K}_{c0},{K}_{c1}\) are removed from the regression to ensure zero position and slope at \(x = 0\), and it is clear that the polynomial function better captures the behavior in the freeplay gap but now oscillates outside the gap range. The polynomials for two other contact stiffnesses, very soft \({K}_{c}=1.4\times {10}^{3} \mathrm{N}/\mathrm{m}\) and hard \({K}_{c}=1.4\times {10}^{6} \mathrm{N}/\mathrm{m}\), and with the \({K}_{c0},{K}_{c1}\) terms added back to the regression, are shown in Fig. 2c. The polynomial representation matches the very soft contact but still fails to capture the transition at the freeplay boundaries. For hard contact, the match is poor even with 21 coefficients. In all cases, the polynomial representation converges slowly yet also suffers from being “badly conditioned” at higher degrees. More coefficients are required for harder contact stiffness beyond what was investigated here.

Fig. 2
figure 2

Polynomial representations using least-squares regression for small, symmetric freeplay gap \({j}_{1}={j}_{2}=0.4 \mathrm{mm}\)

Full size image

The rational polynomial is studied next in Fig. 3. Curves are denoted as \(n/m\), for \(n\)-degree numerator and \(m\)-degree denominator. A danger to consider with this type of polynomial function is the existence and locations of discontinuities caused by roots of the denominator polynomial. It should be ensured that all real roots are located outside the possible range of displacement. MATLAB’s cftool is used to perform curve fitting regression, but it is limited to numerator and denominator polynomials of degree 5 at most. In addition, the calculated curve fit can change every time a given numerator/denominator degree combination is selected and re-selected since the curve fitter depends on “random start points” to calculate a solution [28]. For curve fits that failed using cftool, an alternative curve fitting tool is employed instead [29]. In Fig. 3a, the soft contact freeplay is approximated by both a 3/2 and a 5/3 rational polynomial. Both curves match the behavior beyond the freeplay gap, and the 5/3 curve also fits more closely within the freeplay gap. The 3/2 curve is not rotationally symmetric about the origin and shows a negative force within most of the freeplay gap, unlike the 5/3 curve. Figure 3b, c shows rational polynomials for very soft contact \({K}_{c}=1.4\times {10}^{3} \mathrm{N}/\mathrm{m}\) and for hard contact \({K}_{c}=1.4\times {10}^{6} \mathrm{N}/\mathrm{m}\). For the softer contact, a larger range of rational polynomials can be used, ranging from 3/5 to 5/5, but as seen there is little advantage if any of using a particular combination of numerator and denominator degrees, as they are all very similar. Generally, up to a limit, harder contact stiffnesses are captured better with higher-degree numerator and denominator polynomials. For these reasons, convergence analysis is more difficult to perform than for simple polynomials.

Fig. 3
figure 3

Rational-polynomial representations for small symmetric freeplay gap \({j}_{1}={j}_{2}=0.4 \mathrm{mm}\)

Full size image

The three remaining representations for soft contact \({K}_{c}=1.4\times {10}^{4}\mathrm{N}/\mathrm{m}\), shown in Fig. 4, are the hyperbolic tangent, arctangent and logarithm-arctangent models. These functions do not require least-squares regression but instead employ the actual contact stiffness and freeplay gap boundary values explicitly, along with the convergence parameters \(\varepsilon \) and \(\gamma \) in Eqs. (4–6). In the limit as \(\varepsilon , \gamma \to \infty \), each of these representations approaches the exact piecewise model. As such, these models are simpler to use than either the polynomial or rational polynomial models. They also converge significantly faster and do not suffer from “poor conditioning” errors that can arise when using regression for the polynomial and rational polynomial representations. When one of these three representations is used, the convergence parameter should be sufficiently large to adequately capture freeplay behavior. However, in some situations the convergence parameter should not be too large because then the smoothness of the representation will be lost as it converges to the exact piecewise model. Following a recommendation from Yoon [16], particular care should go into determining an appropriate convergence parameter when using harmonic balance methods or any other numerical method that requires the contact force to have some level of smoothness.

Fig. 4
figure 4

Representations for soft contact \({K}_{c}=1.4\times {10}^{4} \mathrm{N}/\mathrm{m}\) based on hyperbolic tangent (solid lines), arctangent (dashed lines), and logarithm-arctangent (dotted-dashed lines) functions

Full size image

The final part of this section quantifies the accuracy of each representation. Figure 5 gives the root mean square error (RMSE) and \({R}^{2}\) best-fit factor for each representation with respect to the exact piecewise function, for the system with \({K}_{c}=1.4\times {10}^{4} \mathrm{N}/\mathrm{m},{j}_{1}={j}_{2}=0.4 \mathrm{mm}\). It can be seen that the polynomial slowly converges with higher degree, the convergence for rational polynomial is not straightforward, and the tangent-based models all converge quickly with hyperbolic tangent being the fastest and logarithm-arctangent the slowest.

Fig. 5
figure 5

RMS error and \({R}^{2}\) of the a polynomial, b rational polynomial, and c tangent-based (#3 hyperbolic tangent, #4 arctangent, and #5 logarithm-arctangent) representations as they are improved toward convergence

Full size image

4 Accuracy and limits of applicability of the continuous representations

4.1 Frequency–response and bifurcation analyses

Frequency–response and bifurcation characteristics of the nonlinear system in Eq. (1) are presented in this section to show the general accuracy of each representation at capturing the system’s nonlinear behaviors. For all results, the following representations are used: a 13th-degree polynomial, a 5/3 rational polynomial, and tangent-based models with \(\varepsilon ,\gamma ={10}^{4}\). This ensures each model has \(RMSE<0.5\) and \({R}^{2}>0.998\) for the symmetric-soft system \({K}_{c}=1.4\times {10}^{4} \mathrm{N}/\mathrm{m},{j}_{1}={j}_{2}=0.4 \mathrm{mm}\), according to Fig. 5, so the “quality” of each model can be compared. This also allows the success or failure at capturing nonlinear behavior to be observed for stronger or weaker contact with increased and decreased contact stiffness, respectively.

Figure 6 shows the frequency–response curves for the freeplay system with soft contact \(\left({K}_{c}=1.4\times {10}^{4} \mathrm{N}/\mathrm{m}\right)\) and three different freeplay-gap configurations. Figure 6a has the largest gap and therefore the weakest freeplay nonlinearity of the three. The only nonlinear behavior that is expected here is superharmonic resonance near \(\upomega =2 \mathrm{Hz}\), and every representation except the rational polynomial (RatPoly 5/3) agrees well with the exact piecewise representation. The RatPoly 5/3 predicts a larger region of superharmonic resonance and a region of subharmonic resonance near \(\omega =11-12 \mathrm{Hz}\), and for \(\omega >22 \mathrm{Hz}\) the peak amplitude is predicted to be negative. Further study omitted here showed that the resulting system responses in that region are low-amplitude steady-state sinusoidal, shifted down far enough that the entire response is below \(x<0\).

Fig. 6
figure 6

Frequency–response curves for soft contact \({K}_{c}=1.4\times {10}^{4} \mathrm{N}/\mathrm{m}\) and three different freeplay-gap configurations

Full size image

In Fig. 6b, all the representations are able to capture the region of superharmonic resonance to varying degrees, with the RatPoly 5/3, hyperbolic tangent (Tanh), and arctangent (Arctan) models appearing to capture the entire range of subharmonic resonance. The RatPoly 5/3, Tanh, and Arctan also have the best agreement to the primary resonance peak and to the jump to lower amplitude. The polynomial (Poly-13) and logarithm-arctangent (Log-Arctan) do not capture any of the subharmonic resonance near \(\omega =17-21 \mathrm{Hz}\), and the RatPoly 5/3 model predicts more subharmonic-resonance branches than the single one predicted by the exact piecewise model.

The plotted curves in Fig. 6c show weaker agreement for all models. The Poly-13 model shows excellent agreement up until the jump phenomenon, and afterwards captures none of the various chaotic, subharmonic-resonance, or periodic behaviors that occur beyond \(12 \mathrm{Hz}\). The RatPoly 5/3 operates similarly, except it does capture one section of periodic response between \(\omega =15-18 \mathrm{Hz}\) and section of subharmonic resonance between \(\omega =21-22 \mathrm{Hz}\). The Tanh and Arctan models have the best agreement to the piecewise results but still lose accuracy as forcing frequency increases. Finally, the Log-Arctan model has the weakest accuracy in the superharmonic-resonance region and also has poor accuracy in the chaotic region within \(\omega =13-15 \mathrm{Hz}\). It also fails to capture one branch of subharmonic resonance and underestimates the low-amplitude responses at higher frequencies.

The representations with better convergence are studied for the soft contact, asymmetric gap in Fig. 7. They consist of a 21-degree polynomial, 5/5 rational polynomial, and tangent-based models with \(\varepsilon ,\gamma ={10}^{6}\). All representations show excellent agreement in the superharmonic-resonance region and leading up to the primary resonance peak, but the Poly-21 and RatPoly 5/5 models begin to disagree with the reference model after the jump phenomenon. The tangent-based models are the most accurate, with Tanh and Arctan having similar accuracy and Log-Arctan having slightly less accuracy at higher forcing frequency.

Fig. 7
figure 7

Frequency–response curves for soft contact \({K}_{c}=1.4\times {10}^{4} \mathrm{N}/\mathrm{m}\) and small asymmetric gap \({j}_{1}=0,{j}_{2}=0.8 \mathrm{mm}\) for more converged representations

Full size image

The system’s bifurcation diagrams with respect to forcing frequency are presented next. These show how well the different representations can capture transitions in response type. Figure 8 presents 3D bifurcation diagrams of the dynamical system with symmetric freeplay gap \({j}_{1}={j}_{2}=0.4 \mathrm{mm}\) and very soft, soft, and hard contact stiffnesses. Note that the third axis is only used to expand the results of the different models in 3D for better visualization. All models are in excellent agreement for the very soft contact case of Fig. 8a. The exact piecewise representation indicates a region of superharmonic resonance is activated and the presence of “ringing” behavior as the system exceeds a freeplay boundary at very low frequencies, and all five representations capture both behaviors well. Figure 8b is the case for a harder intermediate contact stiffness and corresponds to the results of Fig. 6b. The Poly-13 model (red) is unable to capture the full frequency range of “ringing”, chaotic, or superharmonic resonance behaviors that all the other models are generally able to capture. The Arctan (gray) and Log-Arctan (yellow) models also fail to capture the narrow chaotic band near \(4-5 \mathrm{Hz}\). Only the Tanh model (blue) captures both the narrow transitions to superharmonic resonance near \(6 \mathrm{Hz}\) and \(7 \mathrm{Hz}\). At higher frequency, the Poly-13, Arctan, and Log-Arctan slightly overestimate the frequency value of the primary resonance peak. The RatPoly 5/3 (green) and Arctan models predict a region of nonlinear behavior shortly after the jump phenomenon and before the region of subharmonic resonance. The RatPoly 5/3, Tanh, and Arctan models all capture the subharmonic resonance behavior but predict a much larger frequency band, predict the correct-size band but shifted slightly down in frequency, and predict the correct-size band but shifted slightly up in frequency, respectively. Finally, Poly-13 and Log-Arctan do not capture any subharmonic resonance behavior.

Fig. 8
figure 8

Bifurcation diagrams for small, symmetric freeplay gap \({j}_{1}={j}_{2}=0.4 \mathrm{mm}\) and three different contact stiffnesses

Full size image

In Fig. 8c, with a contact stiffness two orders of magnitude harder than the soft case, all the representations seem to have failed altogether for their convergence quality. The Poly-13 and Log-Arctan predict very low-amplitude periodic solutions for the entire frequency range. The RatPoly 5/3 model predicts a low-amplitude periodic solution, with negative mean, for most of the frequency range before predicting higher amplitude periodic solutions above \(20 \mathrm{Hz}\). Tanh predicts a very low-amplitude periodic response with a high mean value, almost as if the system becomes trapped in a potential well away from the origin. Arctan also captures none of the correct system physics.

The final bifurcation analysis in Fig. 9 shows results using the representations with better convergence that were previously used for the data in Fig. 7. The freeplay system studied is the same as in Fig. 8c. The Tanh and Arctan models show the best agreement among all the models and capture the low-frequency chaos, the chaotic-to-periodic transitions, and the additional nonlinear behavior between \(\omega =10-12 \mathrm{Hz}\). Arctan captures more of the very narrow higher-period regions between \(12-20 \mathrm{Hz}\) than Tanh does. Log-Arctan is less accurate and does not capture the full range of chaotic responses well, and it also predicts a narrow region of behavior beyond \(20 \mathrm{Hz}\) that does not occur in the other models. Lastly, the Poly-21 and RatPoly 5/5 models are still unable to capture any of the system’s rich behavior.

Fig. 9
figure 9

Bifurcation diagrams for small, symmetric freeplay gap \({j}_{1}={j}_{2}=0.4 \mathrm{mm}\) and hard contact stiffnesses \({K}_{c}=1.4\times {10}^{6} \mathrm{N}/\mathrm{m}\) for more converged representations

Full size image

4.2 Computation time analysis and limits of applicability

In this section, the computational cost of using each representation is studied and the limits of applicability of each representation are discussed. Table 2 presents the total time to compute the bifurcation diagrams seen in Fig. 8b (case 1) and Fig. 9 (case 2). These simulations used representations with weaker and stronger convergences, respectively, and the color bars indicate slowest (darkest) to fastest (lightest) models. In both cases, the exact piecewise representation took either the first or second longest to run because it uses the event detection capability, which requires the simulation to stop and restart at every instance of contact. The rational polynomial model took the longest to run for case 2 and the second longest for case 1. The polynomial model was third slowest for both cases, but it was faster than the second slowest by a factor of about 1.5. The tangent-based representations were the fastest in both cases and differed by no more than half a second. These averaged about 6.5 times faster than the slowest model in both cases.

Table 2 Computation times for each representation in Figs. 8b and 9
Full size table

The final discussion in this study focuses on the limits of applicability of each representation and what models are appropriate for weak, medium, and strong nonlinearity. It is clear so far that the tangent-based representations are the most accurate and fastest for a given convergence accuracy. The rational-polynomial model is the most difficult to formulate and implement because the importance of the numerator and denominator degrees on the representation’s accuracy is unclear. Generally, the accuracy is good for soft contact stiffnesses as long as the degrees are “large enough” and the numerator degree is greater than the denominator degree, but these are not necessary conditions. As the contact stiffness increases, however, increasing the degrees does little to improve the representation accuracy and eventually leads to “badly conditioned” errors which can make the rational polynomial representation unusable. The polynomial was also challenging to utilize due to the often large number of coefficients required to get an accurate representation. A high contact stiffness may be represented by upwards of 20–45 coefficients and still have a poor accuracy. In addition, a small freeplay gap tends to produce a polynomial that behaves linearly over the entire displacement range without enough coefficients, rendering its use for capturing freeplay moot.

Even when a polynomial or rational polynomial can be found to model the freeplay force, the nonlinear behavior may not be captured entirely or at all and numerical problems may persist. A common problem that appeared is best explained by Figs. 2c and 9. If the freeplay representation has multiple roots within the freeplay gap and oscillates up and down (i.e. multiple zero-crossings due to overshoot), then the system response can become trapped at a higher amplitude and unable to return to the origin. This was a clear failure of the polynomial-based methods. A polynomial representation may offer better accuracy if a system’s contact force behaves like a quadratic or cubic curve, instead of linearly, but otherwise this method is unwieldy and converges too slowly to be accurate for anything but weak freeplay nonlinearities.

Unlike the polynomial-based representations, all three of the tangent-based representations were easy to implement and systematically evaluate convergence and also showed good to excellent agreement in all cases. For a given value of convergence parameter \(\varepsilon \) or \(\gamma \), the hyperbolic tangent model overall seemed to be the most accurate, with the arctangent model second and the logarithm-arctangent model third. Each of these models can also be applied for soft and hard contact stiffnesses and to large, small, and asymmetric freeplay gaps without problem since the accuracy depends only on the convergence parameter.

Some final studies are performed using the hyperbolic tangent representation to determine an upper limit to its accuracy. Figure 10 presents the bifurcation diagrams of the system for the case of hard contact and asymmetric freeplay: \({K}_{c}=1.4\times {10}^{6} \mathrm{N}/\mathrm{m},{j}_{1}=0,{j}_{2}=0.8 \mathrm{mm}\). Here, the hyperbolic tangent representation is used with two different large values of the convergence parameter, \(\varepsilon ={10}^{6}\) and \({10}^{9}\), and it is compared to the exact piecewise representation both without and with event detection. In theory, the hyperbolic tangent results would converge to the piecewise results without event detection as \(\upvarepsilon \to \infty \) but may not due to accumulating numerical errors. Comparing Fig. 10a, b, both hyperbolic tangent responses (blue, green, respectively) show excellent agreement with the piecewise no-event-detection response (pink). Any improvement gained from using the more converged representation is minimal. Comparing Fig. 10b, c shows that there are discrepancies between the result without and with event detection that do not resolve by increasing the convergence parameter. The narrow bands of periodic responses agree well in all cases, but the regions of chaos and other nonlinear behavior show less agreement.

Fig. 10
figure 10

Bifurcation diagrams of the hard contact, asymmetric freeplay case \({K}_{c}=1.4\times {10}^{6} \mathrm{N}/\mathrm{m},{j}_{1}=0,{j}_{2}=0.8 \mathrm{mm}\) comparing hyperbolic tangent with \(\varepsilon ={10}^{6}\) (blue) and \(\varepsilon ={10}^{9}\) (green) to the exact piecewise representation without (pink) and with event detection (black). Plot markers have different sizes to show overlap. (Color figure online)

Full size image

Two examples are given in Fig. 11, which show the time histories and frequency spectra at excitation frequencies \(\omega =11 \mathrm{Hz}\) and \(21.75 \mathrm{Hz}\). In Fig. 11a, b, the responses using hyperbolic tangent representation and the piecewise model without event detection scenario match well but differ significantly from the response using the piecewise model with event detection. A period-1 response with superharmonics should have been captured, but a period-3 response with both subharmonics and superharmonics is falsely detected instead. In the plotted curves in Fig. 11c, d, the overall behavior of the response is captured well, indicating a period-2 response with one subharmonic and many superharmonics. However, the results still differ on a small scale. The only way to remove these numerical issues at this point is to either refine the tolerances of the numerical solver itself (i.e., the relative and absolute tolerances within ode45) or to implement an event detection procedure such as the one used in this work based on ode45. Both options can be done together, but the accuracy improvement from using event detection by itself can be comparable to using finer ode45 tolerances.

Fig. 11
figure 11

Time histories and frequency spectra for the system in Fig. 10 at two different forcing frequencies

Full size image

The results of Figs. 10 and 11 show that, although the hyperbolic tangent model approaches the exact piecewise function as \(\varepsilon \to \infty \), the ability to accurately represent the freeplay contact force is only one aspect to accurately capturing contact behavior. The freeplay representation gives no provision for determining the precise times and locations of contacts, and it must be combined with the event detection procedure for the most accurate results. Despite the accuracy of the hyperbolic tangent model, an event detection procedure is needed to further improve accuracy and remove accumulating roundoff error. Otherwise, the numerical solver can predict significant errors and fail to capture important nonlinear behavior. Thus, the limit of applicability of the hyperbolic tangent model approaches that of the exact piecewise model without any event detection procedure. Thus, it would be valuable to ensure one’s numerical solver is adequately capturing contact times and locations, whether using a direct time integration method or a harmonic balance method.

5 Conclusions

In this work, different mathematical representations of the contact force in a forced Duffing oscillator with freeplay were studied for their effectiveness at capturing the physics and nonlinear behavior of the system. The representations studied consist of (i) polynomial, (ii) rational polynomial, (iii) hyperbolic tangent, (iv) arctangent, and (v) logarithm-arctangent models. The convergence behavior of each model was studied to assess their ability to actually resemble the piecewise-smooth force curve. Then, frequency–response and bifurcation analyses were performed and indicated the polynomial and rational polynomial representations performed the worst at accurately capturing system behavior and had the greatest computational costs of all the models studied. The tangent-based models generally had greater accuracy with lower, and nearly equal, computational costs. However, the accuracy of all representations is still limited when strong contact behavior is present; the precise times and locations of contact events must be captured to avoid additional numerical errors. If this is not a concern, the hyperbolic tangent representation is recommended based on the findings in this study. Overall, it was most effective at capturing both weak and strong contact nonlinearities, and it is easy to use and implement into a numerical solver code.

A future research path may be to expand this analysis to multiple-degree-of-freedom systems or continuous systems. The authors' preliminary thoughts are that similar conclusions as seen in this paper would be drawn: the tangent-based methods are accurate, and it is important to capture the precise moments of contact. This means another important avenue of work, which is already ongoing for a number of years now, is continuing the development or optimization of numerical solvers specifically for reduced-order nonsmooth systems. MATLAB's ode45, for example, is very common but suffers from significant overhead costs when it is used with its event location feature on a contact system. This is due to repeated stopping and restarting of ode45 to force a timestep at every contact “event.” If ode45 with event location could be modified to run without restarting, significant time savings could be obtained.