1 Introduction

Multi-degree-of-freedom nonlinear mechanical systems generally approach a steady-state response under periodic or quasi-periodic forcing. Determining this response is often the most important objective in analyzing nonlinear vibrations in engineering practice.

Despite the broad availability of effective numerical packages and powerful computers, identifying the steady-state response simply by numerically integrating the equations of motion is often a poor choice. First, modern engineering structures tend to be very lightly damped, resulting in exceedingly long integration times before the steady state is reached. Second, structural vibrations problems to be analyzed are often available as finite-element models for which repeated evaluations of the defining functions are costly. These evaluations are inherently not parallelizable, thus increasing the number of processors used in the simulation results in increased cross-communication times that slow down already slowly converging runs even further. As a result, even with today’s advances in computing, it may take days to reach a good approximation to a steady-state response in complex structural vibration problems (cf.  Avery et al. [1]).

To achieve feasible computation times for steady-state response in high-dimensional systems, reduced-order models (ROM) are often used to obtain a low-dimensional variant of the mechanical system. Various nonlinear normal modes (NNM) concepts have been used to describe such small-amplitude, nonlinear oscillations. Among these, the classic NNM definition of Rosenberg [2] targets periodic orbits in a two-dimensional subcenter-manifold [3] in the undamped limit of the oscillatory system. By contrast, Shaw and Pierre [4] define NNMs as the invariant manifolds tangent to modal subspaces at an equilibrium point (cf. Avramov and Mikhlin [5] for a review) allowing application to dissipative systems. Haller and Ponsioen [6] distinguish these two notions for dissipative systems under possible periodic/quasi-periodic forcing, by defining an NNM as a near-equilibrium trajectory with finitely many frequencies, and introducing a spectral submanifold (SSM) as the smoothest invariant manifold tangent to a spectral subbundle along such an NNM.

Alternatively, ROMs obtained using heuristic projection-based techniques are also used to approximate steady-state response of high-dimensional systems. These include sub-structuring methods such as the Craig–Bampton method [7] (cf. Theodosiou et al. [8]), proper orthogonal decomposition [9] (cf. Kerchen et al. [10]), reduction using natural modes (cf. Amabili [11], Touzé et al. [12]) and the modal-derivative method of Idelsohn  and Cardona [13] (cf. Sombroek et al. [14], Jain et al. [15]). A common feature of these methods is their local nature: they seek to approximate nonlinear steady-state response in the vicinity of an equilibrium. Thus, high-amplitude oscillations are generally missed by these approaches. The methods reviewed here are fundamentally heuristic as the relationship between the full system and its simplified approximation is generally unknown and has to be tested in each application. Though we focus on finite-dimensional dynamical systems in this work, the same limitations are shared by many truncation/approximation methods when applied to infinite-dimensional systems as well (cf. Malookani and van Horssen [16] for the case of Galerkin truncation applied to string vibrations).

On the analytic side, perturbation techniques relying on a small parameter have been widely used to approximate the steady-state response of nonlinear systems. Nayfeh et al. [17, 18] give a formal multiple-scales expansion applied to a system with small damping, small nonlinearities and small forcing. Their results are detailed amplitude equations to be worked out on a case-by-case basis. Mitropolskii and Van Dao [19] apply the method of averaging (cf. Bogoliubov and Mitropolsky [20] or, more recently, Sanders and Verhulst [21]) after a transformation to amplitude-phase coordinates in the case of small damping, nonlinearities and forcing. They consider single as well as multi-harmonic forcing of multi-degree of freedom systems and obtain the solution in terms of a multi-frequency Fourier expansion. Their formulas become involved even for a single oscillator, and thus, condensed formulas or algorithms are unavailable for general systems. As conceded by Mitroposkii and Van Dao [19], the series expansion is formal, as no attention is given to the actual existence of a periodic response. Existence is indeed a subtle question in this context, since the envisioned periodic orbits would perturb from a non-hyperbolic fixed point.

Vakakis [22] relaxes the small nonlinearity assumption and describes a perturbation approach for obtaining the periodic response of a single-degree-of-freedom Duffing oscillator subject to small forcing and small damping. A formal series expansion is performed around a conservative limit, where periodic solutions are explicitly known (elliptic Duffing oscillator). This approach only works for perturbations of integrable nonlinear systems.

Formally applicable without any small parameter assumption is the harmonic balance method. Introduced first by Kryloff and Bogoliuboff [23] for single-harmonic approximation of the forced response, the method has been gradually extended to include higher harmonics and quasi-periodic orbits (cf. Chua and Ushida [24] and Lau and Cheung [25]). In the harmonic balance procedure, the assumed steady-state solution is expanded in a Fourier series which, upon substitution, turns the original differential equations into a set of nonlinear algebraic equations for the unknown Fourier coefficients after truncation to finitely many harmonics. The error arising from this truncation, however, is not well understood. For the periodic case, Leipholz [26] and Bobylev et al. [27] show that the solution of the harmonic balance converges to the actual solution of the system if the periodic orbit exists and the number of harmonics considered tends to infinity. Explicit error bounds are only available as functions of the (a priori unknown) periodic orbit (cf. Bobylev et al. [27], Urabe [28], Stokes [29] and García-Saldaña and Gasull [30]). The quantities involved, however, generally require numerical integration to obtain. For quasi-periodic forcing, such error bounds remain unknown to the best of our knowledge.

The shooting method (cf. Keller [31], Peeters et al. [32] and Sracic and Allen [33]) is also broadly used to compute periodic orbits of nonlinear system. In this procedure, the periodicity of the sought orbit is used to formulate a two-point boundary value problem. The solutions are initial conditions on the periodic orbit. Starting from an initial guess, one corrects the initial conditions iteratively until the boundary value problem is solved up to a required precision. The iterated correction of the initial conditions, however, requires repeated numerical integration of the equation of variations along the current estimate of the periodic orbit, as well as numerical integration of the full system. Albeit the shooting method has moderate memory requirements relative to that of harmonic balance due to its smaller Jacobian, this advantage is useful only for very high-dimensional systems with memory constraints. In practice, shooting is limited by the capabilities of the time integrator used and can be unsuitable for solutions with large Floquet multipliers, as observed by Seydel [34]. Furthermore, the shooting method is only applicable to periodic steady-state solutions, not to quasi-periodic ones.

The shooting method uses a time-march-type integration, i.e., the solution at each time step is solved sequentially after the previous one. In contrast, collocation approaches solve for the solution at all time steps in the orbit simultaneously. Collocation schemes mitigate all the drawbacks of the shooting method but can be computationally expensive for large systems since all unknowns need to be solved together over the full orbit. Popular software packages, such as AUTO [35], MATCONT [36] and the po toolbox of coco [37], also use collocation schemes to continue periodic solutions of dynamical systems. Renson et al. [38] provide a thorough review of the commonly used methods for computation of periodic orbits in multi-degree-of-freedom mechanical systems.

Constructing particular solutions using integral equations is textbook material in physics or vibration courses for impulsive forcing the (system is at rest at the initial time, prior to which the forcing is zero). Solving this problem with a classic Duhamel integral will produce a particular solution that approaches the steady-state response asymptotically. This approach, therefore, suffers from the slow convergence we have already discussed for direct numerical integration.

In this paper, assuming either periodicity or quasi-periodicity for the external forcing, we derive an integral equation whose zeros are the steady-state responses of the mechanical system. Along with a phase condition to ensure uniqueness, the same integral equation can also be used to obtain the (quasi-) periodic response in conservative, autonomous mechanical systems.

While certain elements of the integral equations approach outlined here for periodic forcing have been already discussed outside the structural vibrations literature, our treatment of quasi-periodic forcing appears to be completely new. We do not set any conceptual bounds on the number of independent frequencies allowed in such a forcing, which enables one to apply the results to more complex excitations mimicking stochastic forcing.

First, we derive a Picard iteration approach with explicit convergence criteria to solve the integral equations for the steady-state response iteratively (Sect. 3.1). This fast iteration approach is particularly appealing for high-dimensional systems, since it does not require the construction and inversion of Jacobian matrices, and for non-smooth systems, as is does not rely on derivatives. At the same time, this Picard iteration will not converge near external resonances. Applying a Newton–Raphson scheme to the integral equation, however, we can achieve convergence of the iteration even for near-resonant forcing (Sect. 3.2). We additionally employ numerical continuation schemes to obtain forced response and backbone curves of nonlinear mechanical systems (Sect. J.1). Finally, we illustrate the performance gain from our newly proposed approach on several multi-degree-of-freedom mechanical examples (Sect. 4), using a MATLAB®-based implementation.Footnote 1

2 Setup

We consider a general nonlinear mechanical system of the form

$$\begin{aligned} {\mathbf {M}}\ddot{{\mathbf {x}}}+{\mathbf {C}} \dot{{\mathbf {x}}}+{\mathbf {Kx}} +{\mathbf {S}}({\mathbf {x}},\dot{{\mathbf {x}}})={\mathbf {f}}(t), \end{aligned}$$
(1)

where \({\mathbf {x}}(t)\in {\mathbb {R}}^{n}\) is the vector of generalized displacements; \({\mathbf {M}},{\mathbf {C}},{\mathbf {K}}\in {\mathbb {R}}^{n\times n}\) are the symmetric mass, stiffness and damping matrices; \({\mathbf {S}}\) is a nonlinear, Lipschitz continuous function such that \({\mathbf {S}}=\mathcal {O}\left( \left| {\mathbf {x}}\right| ^{2},\left| {\mathbf {x}}\right| \left| \dot{{\mathbf {x}}}\right| ,\left| \dot{{\mathbf {x}}}\right| ^{2}\right) \); \({\mathbf {f}}\) is a time-dependent, multi-frequency external forcing. Specifically, we assume that \({\mathbf {f}}(t)\) is quasi-periodic with a rationally incommensurate frequency basis \(\varvec{\Omega }\in {\mathbb {R}}^{k},\,k\ge 1\) which means

$$\begin{aligned} {\mathbf {f}}(t)=\tilde{{\mathbf {f}}}(\varvec{\Omega }t),\qquad \left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle \ne 0,\quad \varvec{\kappa }\in {\mathbb {Z}}^{k}-\{{\mathbf {0}}\}, \end{aligned}$$
(2)

for some continuous function \(\tilde{{\mathbf {f}}}:{\mathbb {T}}^{k}\rightarrow {\mathbb {R}}^{n}\), defined on a \(k-\)dimensional torus \({\mathbb {T}}^{k}\). For \(k=1\), \({\mathbf {f}}\) is periodic in t with period \(T=2\pi /\varvec{\Omega }\), while for \(k>1\), \({\mathbf {f}}\) describes a strictly quasi-periodic forcing. System (1) can be equivalently expressed in the first-order form as

$$\begin{aligned} {\mathbf {B}}\dot{{\mathbf {z}}} ={\mathbf {A}}{\mathbf {z}}-{\mathbf {R}} ({\mathbf {z}})+{\mathbf {F}}(t)\,, \end{aligned}$$
(3)

with

$$\begin{aligned}&{\mathbf {z}}=\left[ \begin{array}{l} \dot{{\mathbf {x}}}\\ {\mathbf {x}} \end{array}\right] ,\quad {\mathbf {B}}=\left[ \begin{array}{cc} {\mathbf {0}} &{} {\mathbf {M}}\\ {\mathbf {M}} &{} {\mathbf {C}} \end{array}\right] ,\quad {\mathbf {A}}=\left[ \begin{array}{cc} {\mathbf {M}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} -{\mathbf {K}} \end{array}\right] ,\\&{\mathbf {R}}({\mathbf {z}})=\left[ \begin{array}{c} {\mathbf {0}}\\ {\mathbf {S}}({\mathbf {x}},\dot{{\mathbf {x}}}) \end{array}\right] ,\quad {\mathbf {F}}(t)=\left[ \begin{array}{c} {\mathbf {0}}\\ {\mathbf {f}}(t) \end{array}\right] \,. \end{aligned}$$

The first-order form in (3) ensures that the coefficient matrices \({\mathbf {A}}\) and \({\mathbf {B}}\) are symmetric, if the matrices \({\mathbf {M}},{\mathbf {C}}\) and \({\mathbf {K}}\) are symmetric, as is usually the case in structural dynamics applications (cf. Gérardin and Rixen [39]). We assume that the coefficient matrix of the linear system

$$\begin{aligned} {\mathbf {B}}\dot{{\mathbf {z}}}={\mathbf {A}}{\mathbf {z}}+{\mathbf {F}}(t) \end{aligned}$$
(4)

can be diagonalized using the eigenvectors of the generalized eigenvalue problem

$$\begin{aligned} \left( {\mathbf {A}}-\lambda _{j}{\mathbf {B}}\right) {\mathbf {v}}_{j}={\mathbf {0}},\quad j=1,\dots ,2n, \end{aligned}$$
(5)

via the linear transformation \({\mathbf {z}}={\mathbf {V}}{\mathbf {w}}\), where \({\mathbf {w}}\in {\mathbb {C}}^{2n}\) represents the modal variables and \({\mathbf {V}}={\left[ {\mathbf {v}}_{1},\ldots ,\right. }\)\({\left. {\mathbf {v}}_{2n}\right] \in {\mathbb {C}}^{2n\times 2n}}\) is the modal transformation matrix containing the eigenvectors. The diagonalized linear version of (4) with forcing is given by

$$\begin{aligned} \dot{{\mathbf {w}}}&=\varvec{\Lambda }{\mathbf {w}}+\varvec{\psi }(t), \end{aligned}$$
(6)

where \({\varvec{\Lambda }}={\mathrm {diag}}\left( \lambda _{1},\ldots ,\lambda _{2n}\right) \), \(\psi _{j}(t)=\frac{\tilde{{\mathbf {v}}}_{j}{\mathbf {F}}(t)}{\tilde{{\mathbf {v}}}_{j}{\mathbf {B}}{\mathbf {v}}_{j}}\), where \(\tilde{{\mathbf {v}}}_{j}\) denotes the jth row of the matrix \({\mathbf {V}}^{-1}\). Furthermore, if the matrices \({\mathbf {A}}\) and \({\mathbf {B}}\) are symmetric, then \({\mathbf {V}}^{-1}={\mathbf {V}}^{\top }\).

Remark 1

We have assumed autonomous nonlinearities \({\mathbf {S}},{\mathbf {R}}\) in Eqs. (1) and (3) since this is relevant for structural dynamics systems, but the following treatment also allows for time dependence in \({\mathbf {S}}\) or \({\mathbf {R}}\). Specifically, all the following results hold for nonlinearities with explicit time dependence as long as the time dependence is quasi-periodic (cf. Eq. (2)) with the same frequency basis \(\varvec{\Omega }\) as that of the external forcing \({\mathbf {f}}(t)\).

2.1 Periodically forced system

We first review a classic result for periodic solutions in periodically forced linear systems (cf. Burd [40]).

Lemma 1

If the forcing \({\mathbf {F}}(t)\) is T-periodic, i.e., \({\mathbf {F}}(t+T)={\mathbf {F}}(t),\,t\in {\mathbb {R}},\) and the non-resonance conditions

$$\begin{aligned} \lambda _{j}\ne i\frac{2\pi }{T}\ell ,\qquad \ell \in {\mathbb {Z}}, \end{aligned}$$
(7)

are satisfied for all eigenvalues \(\lambda _{1},\dots ,\lambda _{2n}\) defined in (5), then there exists a unique T-periodic response to (4), given by

$$\begin{aligned} {\mathbf {z}}(t)&={\mathbf {V}}\int _{0}^{T}{\mathbf {G}}(t-s,T){\mathbf {V}}^{-1}{\mathbf {F}}(s)\,\mathrm{d}s, \end{aligned}$$
(8)

where \({\mathbf {G}}(t,T)\) is the diagonal matrix of periodic Green’s functions for the modal displacement variables, defined as

$$\begin{aligned}&{\mathbf {G}}(t,T) ={\mathrm {diag}} \left( G_{1}(t,T),\ldots ,G_{2n}(t,T)\right) \in {\mathbb {C}}^{2n\times 2n},\nonumber \\&G_{j}(t,T)=e^{\lambda _{j}t}\left( \frac{e^{\lambda _{j}T}}{1-e^{\lambda _{j}T}}+h(t)\right) ,\,\, j=1,\dots ,2n,\nonumber \\ \end{aligned}$$
(9)

with the Heaviside function h(t) given by

$$\begin{aligned} h(t):={\left\{ \begin{array}{ll} 1 &{} t\ge 0\\ 0 &{} t<0 \end{array}\right. }\,. \end{aligned}$$

Proof

We reproduce the proof for completeness in “Appendix A”. \(\square \)

Remark 2

The uniform-in-time sup norm of the Green’s function (9) can be bounded by the constant \(\varGamma (T)\) defined as

$$\begin{aligned} \varGamma (T):= & {} \max _{1\le j\le n}\frac{T\max (\left| e^{\lambda _{j}T}\right| ,1)}{\left| 1-e^{\lambda _{j}T}\right| }\nonumber \\\ge & {} \max _{0\le t<T}\left\| \int _{0}^{T}\left\| {\mathbf {G}}(t-s,T)\right\| _{0}\,\mathrm{d}s\right\| _{0}. \end{aligned}$$
(10)

We detail this estimate in “Appendix F”.

The Green’s functions defined in (9) turn out to play a key role in describing periodic solutions of the full, nonlinear system as well. We recall this in the following result (see eg. Bobylev et al. [27]).

Theorem 1

(i) If \({\mathbf {z}}(t)\) is a \(T-\)periodic solution of the nonlinear system (3), then \({\mathbf {z}}(t)\) must satisfy the integral equation

$$\begin{aligned} {\mathbf {z}}(t)={\mathbf {V}}\int _{0}^{T}{\mathbf {G}}(t-s,T){\mathbf {V}}^{-1}\left[ {\mathbf {F}}(s)-{\mathbf {R}}({\mathbf {z}}(s))\right] \,\mathrm{d}s. \end{aligned}$$
(11)

(ii) Furthermore, any continuous, \(T-\)periodic solution \({\mathbf {z}}(t)\) of (11) is a \(T-\)periodic solution of the nonlinear system (3).

Proof

We reproduce the proof for completeness in “Appendix B”. The term \( {\mathbf {V}}^{-1}\left[ {\mathbf {F}}(t)-{\mathbf {R}}({\mathbf {z}}(t))\right] \) is treated as a periodic forcing term in (6) for a T-periodic \( {\mathbf {z}}(t) \) and Lemma 1 is used to prove (i). Statement (ii) is then a direct consequence of the Leibniz rule. \(\square \)

2.2 Quasi-periodically forced systems

The above classic results on periodic steady-state solutions extend to quasi-periodic steady-state solutions under quasi-periodic forcing. This observation does not appear to be available in the literature, which prompts us to provide full detail.

Let the forcing \({\mathbf {F}}(t)\) be quasi-periodic with frequency basis \(\varvec{\Omega }\in {\mathbb {R}}{}^k{(k>1)}\), i.e.,

$$\begin{aligned} {\mathbf {F}}(t)=\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}{\mathbf {F}}_{\varvec{\kappa }}e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t}, \end{aligned}$$
(12)

where each member of this k-parameter summation represents a time-periodic forcing with frequency \(\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle \), i.e., forcing with period

$$\begin{aligned} T_{\varvec{\kappa }}=\frac{2\pi }{\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle }. \end{aligned}$$

Here, \(T_{{\mathbf {0}}}=\infty \) formally corresponds to the period of the mean \({\mathbf {F}}_{\varvec{0}}\) of \({\mathbf {F}}(t)\).

Lemma 2

If the forcing is quasi-periodic, as given by (12), then under the non-resonance conditions

$$\begin{aligned} \lambda _{j}\ne i\frac{2\pi }{T_{\varvec{\kappa }}}\ell ,\qquad \ell \in {\mathbb {Z}},\quad j\in \{1,\dots ,2n\},\quad \varvec{\kappa }\in {\mathbb {Z}}^{k}\,, \end{aligned}$$
(13)

there exists a unique quasi-periodic steady-state response to (4) with the same frequency basis \(\varvec{\Omega }\). This steady-state response is given by

$$\begin{aligned} {\mathbf {z}}(t)&={\mathbf {V}}\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}\int _{0}^{T_{\varvec{\kappa }}}{\mathbf {G}}(t-s,T_{\varvec{\kappa }}){\mathbf {V}}^{-1}{\mathbf {F}}(s)\,\mathrm{d}s. \end{aligned}$$
(14)

Furthermore, \( {\mathbf {z}}(t)\) is quasi-periodic with Fourier expansion

$$\begin{aligned} {\mathbf {z}}(t)={\mathbf {V}}\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}{\mathbf {H}}(T_{\varvec{\kappa }}){\mathbf {V}}^{-1}{\mathbf {F}}_{\varvec{\kappa }}e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t}\,, \end{aligned}$$
(15)

where \({\mathbf {H}}(T_{\varvec{\kappa }})\) is the diagonal matrix of the amplification factors, defined as

$$\begin{aligned}&{\mathbf {H}}(T_{\varvec{\kappa }})={\mathrm {diag}}\left( H_{1}(T_{\varvec{\kappa }}),\ldots ,H_{2n}(T_{\varvec{\kappa }})\right) \in {\mathbb {C}}^{2n\times 2n},\nonumber \\&H_{j}(t,T)=\frac{1}{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle -\lambda _{j}},\quad j=1,\dots ,2n\,. \end{aligned}$$
(16)

Proof

The proof is a consequence of the linearity of (4) along with Lemma 1, followed by the explicit evaluation of the integrals in (14). We give the details in “Appendix C”. \(\square \)

Remark 3

The maximum of \(H_{j}(T_{\varvec{\kappa }})\) can be bounded by the constant \(h_\mathrm{max}\), defined as

(17)

We note that the constant, \(h_\mathrm{max}\), increases as the real part of the minimal eigenvalue tends to zero (i.e., with decreasing damping values)

In analogy with Theorem 1, we present here an integral formulation for steady-state solutions of the nonlinear system (3) under quasi-periodic forcing.

Theorem 2

(i) If \({\mathbf {z}}(t)\) is a quasi-periodic solution of the nonlinear system (3) with frequency basis \(\varvec{\Omega }\), then the nonlinear function \({\mathbf {R}}({\mathbf {z}}(t))\) is also quasi-periodic with the same frequency basis \(\varvec{\Omega }\) and \({\mathbf {z}}(t)\) must satisfy the integral equation:

$$\begin{aligned} {\mathbf {z}}(t)&={\mathbf {V}}\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}\int _{0}^{T_{\varvec{\kappa }}}{\mathbf {G}}(t-s,T_{\varvec{\kappa }}){\mathbf {V}}^{-1}\nonumber \\&\quad \times \left[ {\mathbf {F}}(s)-{\mathbf {R}}({\mathbf {z}}(s))\right] \,\mathrm{d}s\,. \end{aligned}$$
(18)

(ii) Furthermore, any continuous, quasi-periodic solution \({\mathbf {z}}(t)\) of (18), with frequency basis \(\varvec{\Omega }\), is a quasi-periodic solution of the nonlinear system (3).

Proof

The proof is analogous to that for the periodic case (cf. Theorem 1). Again, the term \({{\mathbf {F}}(t)-{\mathbf {R}}({\mathbf {z}}(t))}\) is treated as a quasi-periodic forcing term. \(\square \)

Remark 4

With the Fourier expansion \( {\mathbf {z}}(t) = \sum _{\varvec{\kappa }\in {\mathbb {Z}}^k} {\mathbf {z}}_{\varvec{\kappa }} e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t} \), Eq. (18) can be equivalently written as

$$\begin{aligned} {\mathbf {z}}_{\varvec{\kappa }} ={\mathbf {V}}{\mathbf {H}}(T_{\varvec{\kappa }}){\mathbf {V}}^{-1}\left[ {\mathbf {F}}_{\varvec{\kappa }}-{\mathbf {R}}_{\varvec{\kappa }}\{{\mathbf {z}}\}\right] ,\qquad {\varvec{\kappa }\in {\mathbb {Z}}^{k}}\,, \end{aligned}$$
(19)

where \( {\mathbf {R}}_{\varvec{\kappa }}\{{\mathbf {z}}\} \) are the Fourier coefficients of the quasi-periodic function \( {\mathbf {R}}({\mathbf {z}}(t)) \), defined as

$$\begin{aligned} {\mathbf {R}}_{\varvec{\kappa }}\{{\mathbf {z}}\}:=\lim _{t\rightarrow \infty }\frac{1}{2t}\intop _{-t}^{t}{\mathbf {R}}({\mathbf {z}}(t))e^{-i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t}\mathrm{d}t. \end{aligned}$$
(20)

If we express the quasi-periodic solution using toroidal coordinates \( \varvec{\theta } \in {\mathbb {T}}^{k}\) such that \( {{\mathbf {z}}(t) = {\mathbf {u}}(\varvec{\Omega }t)} \), where \( {{\mathbf {u}}:{\mathbb {T}}^k\mapsto {\mathbb {R}}^{2n}} \) is the torus function, then we can express the Fourier coefficients as

$$\begin{aligned} {\mathbf {R}}_{\varvec{\kappa }}\{{\mathbf {u}}\}:=\frac{1}{(2\pi )^k}\int _{{\mathbb {T}}^k}{\mathbf {R}}({\mathbf {u}}(\varvec{\theta }))e^{-i\left\langle \varvec{\kappa },\varvec{\theta }\right\rangle t}\mathrm{d}\varvec{\theta }. \end{aligned}$$
(21)

This helps to avoid the infinite limit in the integral (20) that can pose numerical difficulties (cf. Schilder et al. [41], Mondelo González [42]. To this end, we have used the torus coordinates for the formulation of quasi-periodic oscillations in our supplementary MATLAB® code.

The present integral equation formulation (11), (18) assumes the knowledge of the eigenvectors and eigenvalues of the linearized system. These are usually computed numerically and may pose a computational challenge for very high-dimensional systems. Nonetheless, this computation needs to be performed only once for the full system (and not repeatedly for each forcing frequency). For this reason, it is expected that diagonalizing the system at the linear level forms only a fraction of the total computational cost for the forced response and backbone curves. The special case of proportional damping and purely position-dependent nonlinearities further alleviates these computational challenges by reducing the dimensionality to half, as we discuss in the following section.

2.3 Special case: structural damping and purely geometric nonlinearities

The results in Sects. 2.1 and 2.2 apply to general first-order systems of the form (3). The special case of second-order mechanical systems with proportional damping and purely geometric nonlinearities, however, is of significant interest to structural dynamicists (cf. Gérardin and Rixen [39]). These general results can be simplified for such systems, resulting in integral equations with half the dimensionality of Eqs. (11) and (18), as we discuss in this section.

We assume that the damping matrix \({\mathbf {C}}\) satisfies the proportional damping hypothesis, i.e., can be expressed as a linear combination of \({\mathbf {M}}\) and \({\mathbf {K}}\). We also assume that the nonlinearities depend on the positions only, i.e., we can simply write \({\mathbf {S}}({\mathbf {x}})\). The equations of motion are, therefore, given by

$$\begin{aligned} {\mathbf {M}}\ddot{{\mathbf {x}}}+{\mathbf {C}}\dot{{\mathbf {x}}}+{\mathbf {Kx}}+{\mathbf {S}}({\mathbf {x}})={\mathbf {f}}(t). \end{aligned}$$
(22)

Then, the real eigenvectors \({\mathbf {u}}_{j}\) of the undamped eigenvalue problem satisfy

$$\begin{aligned} \left( {\mathbf {K}}-\omega _{0,j}^{2}{\mathbf {M}}\right) {\mathbf {u}}_{j}={\mathbf {0}}\quad \left( j=1,2,\dots ,n\right) , \end{aligned}$$
(23)

where \(\omega _{0,j}\) is the eigenfrequency of the undamped vibration mode \({\mathbf {u}}_{j}\in {\mathbb {R}}^{n}\). These eigenvectors (or modes) can be used to diagonalize the linear part of (22) using the linear transformation \({{\mathbf {x}}={\mathbf {U}}{\mathbf {y}}}\), where \({{\mathbf {y}}\in {\mathbb {R}}^{n}}\) represents the modal variables and \({\mathbf {U}}=\left[ {\mathbf {u}}_{1},\ldots ,{\mathbf {u}}_{n}\right] \in {\mathbb {R}}^{n\times n}\) is the modal transformation matrix containing the vibration modes. Thus, the decoupled system of equations for the linear system,

$$\begin{aligned} {\mathbf {M}}\ddot{{\mathbf {x}}}+{\mathbf {C}}\dot{{\mathbf {x}}}+{\mathbf {Kx}}={\mathbf {f}}(t), \end{aligned}$$
(24)

is given by

$$\begin{aligned} {\mathbf {U}}^{\top }{\mathbf {MU}}\ddot{{\mathbf {y}}}+{\mathbf {U}}^{\top }\mathbf {CU}\dot{{\mathbf {y}}}+{\mathbf {U}}^{\top }\mathbf {KUy}={\mathbf {U}}^{\top }{\mathbf {f}}(t). \end{aligned}$$
(25)

Specifically, the jth mode \((y_{j})\) of equation (25) is customarily expressed in the vibrations literature as

$$\begin{aligned} \ddot{y}_{j}+2\zeta _{j}\omega _{0,j}\dot{y}_{j}+\omega _{0,j}^{2}y_{j}=\varphi _{j}(t),\quad j=1,\ldots ,n, \end{aligned}$$
(26)

where \(\omega _{0,j}=\sqrt{\frac{{\mathbf {u}}_{j}^{\top }{\mathbf {K}}{\mathbf {u}}_{j}}{{\mathbf {u}}_{j}^{\top }{\mathbf {M}}{\mathbf {u}}_{j}}}\) are the undamped natural frequencies; \(\zeta _{j}=\frac{1}{2\omega _{0,j}}\left( \frac{{\mathbf {u}}_{j}^{\top }{\mathbf {C}}{\mathbf {u}}_{j}}{{\mathbf {u}}_{j}^{\top }{\mathbf {M}}{\mathbf {u}}_{j}}\right) \) are the modal damping coefficients; and \(\varphi _{j}(t)=\left( \frac{{\mathbf {u}}_{j}^{\top }{\mathbf {F}}(t)}{{\mathbf {u}}_{j}^{\top }{\mathbf {M}}{\mathbf {u}}_{j}}\right) \) are the modal participation factors. The eigenvalues for the corresponding full system in phase space can be arranged as follows

$$\begin{aligned} \lambda _{2j-1,2j}&=\left( -\zeta _{j}\pm \sqrt{\zeta _{j}^{2}-1}\right) \omega _{0,j},\quad j=1,\dots ,n. \end{aligned}$$
(27)

With the constants

$$\begin{aligned}&\alpha _{j} :=\text {Re}(\lambda _{2j}),\quad \omega _{j}:=|\text {Im}(\lambda _{2j})|,\quad \beta _{j}:=\alpha _{j}+\omega _{j},\nonumber \\&\gamma _{j}:=\alpha _{j}-\omega _{j,}\quad j=1,\dots ,n, \end{aligned}$$
(28)

we can restate Lemma 1 specifically for linear systems with proportional damping as follows.

Lemma 3

For T-periodic forcing \({\mathbf {f}}(t)\), i.e., \({\mathbf {f}}(t+T)={\mathbf {f}}(t),\,t\in {\mathbb {R}},\,T>0\) and under the non-resonance conditions (7), there exists a unique T-periodic response for system (24), given by

$$\begin{aligned} {\mathbf {x}}(t)&={\mathbf {U}}\int _{0}^{T}{\mathbf {L}}(t-s,T){\mathbf {U}}^{\top }{\mathbf {f}}(s)\,\mathrm{d}s, \end{aligned}$$
(29)

where \({\mathbf {L}}(t,T)\) is the diagonal Green’s function matrix for the modal displacement variables defined as

$$\begin{aligned}&{\mathbf {L}}(t,T)={\mathrm {diag}}\left( L_{1}(t,T),\ldots ,L_{n}(t,T)\right) \in {\mathbb {R}}^{n\times n},\nonumber \\&L_{j}(t,T)\nonumber \\&\quad ={\left\{ \begin{array}{ll} \frac{e^{\alpha _{j}t}}{\omega _{j}}\left[ \frac{e^{\alpha _{j}T}\left[ \sin \omega _{j}(T+t)-e^{\alpha _{j}T}\sin \omega _{j}t\right] }{1+e^{2\alpha _{j}T}-2e^{\alpha _{j}T}\cos \omega _{j}T}+h(t)\sin \omega _{j}t\right] , &{} \zeta _{j}<1\\ \frac{e^{\alpha _{j}(T+t)}\left[ \left( 1-e^{\alpha _{j}T}\right) t+T\right] }{\left( 1-e^{\alpha _{j}T}\right) ^{2}}+h(t)te^{\alpha _{j}t}\,, &{} \zeta _{j}=1\\ \frac{1}{(\beta _{j}-\gamma _{j})}\left[ \frac{e^{\beta _{j}(T+t)}}{1-e^{\beta _{j}T}}-\frac{e^{\gamma _{j}(T+t)}}{1-e^{\gamma _{j}T}}+h(t)\left( e^{\beta _{j}t}-e^{\gamma _{j}t}\right) \right] , &{} \zeta _{j}>1 \end{array}\right. },\nonumber \\&\qquad j=1,\dots ,n \end{aligned}$$
(30)

and \(\varvec{\varphi }(s)=[\varphi _{1}(s),\dots ,\varphi _{n}(s)]^{\top }\) is the forcing vector in modal coordinates.

Proof

See “Appendix D”. \(\square \)

The periodic Green’s function \(L_{j}(t,T)\) for a single-degree-of-freedom, underdamped harmonic oscillator has already been derived in the controls literature (see, e.g., Kovaleva [43], p. 19., formula (1.40), or Babitsky [44] p. 90). They also note a simplification when the periodic forcing function has an odd symmetry with respect to half the period (e.g., sinusoidal forcing), in which case the integral can be taken over just half the period with another Green’s function. Kovaleva [43] also lists the Green function without damping for the case of a multi-degree-of-freedom system without damping, in transfer-function notation. In summary, formula (30) does not seem to appear in the vibrations literature, but earlier controls literature has simpler forms of it (single-degree-of-freedom modal form with damping, or multi-dimensional form without damping in modal coordinates), albeit for the underdamped case only.

Kovaleva [43] also observes for undamped multi-degree-of-freedom systems that an integral equation with this Green’s function can be written out for nonlinear systems, and then refers to Rosenwasser [45] for existence conditions and approximate solution methods. Chapter 4.2 of Babitsky and Krupenin [46] also discusses this material in the context of the response of linear discontinuous systems, citing Rosenwasser [45] for a similar formulation. We formalize and generalize these discussions as a theorem here:

Theorem 3

(i) If \({\mathbf {x}}(t)\) is a T-periodic solution of the nonlinear system (22), then \({\mathbf {x}}(t)\) must satisfy the integral equation

$$\begin{aligned} {\mathbf {x}}(t)={\mathbf {U}}\int _{0}^{T}{\mathbf {L}}(t-s,T){\mathbf {U}}^{\top }\left[ {\mathbf {f}}(s)-{\mathbf {S}}({\mathbf {x}}(s))\right] \,\mathrm{d}s\,, \end{aligned}$$
(31)

with \({\mathbf {L}}\) defined in (30).

(ii) Furthermore, any continuous, T-periodic solution of \({\mathbf {x}}(t)\) of (31) is a T-periodic solution of the nonlinear system (22).

Proof

This result is just a special case of Theorem 1, with the specific form of the Green’s function listed in (30). \(\square \)

Remark 5

Once a solution to (31) is obtained for the position variables \({\mathbf {x}}\) (cf. Sect. 3 for solution methods), the corresponding velocity \(\dot{{\mathbf {x}}}\) can be recovered as

$$\begin{aligned} \dot{{\mathbf {x}}}(t)={\mathbf {U}}\int _{0}^{T} {\mathbf {J}}(t-s,T){\mathbf {U}}^{\top }\left[ {\mathbf {f}}(s)-{\mathbf {S}}({\mathbf {x}}(s))\right] \,\mathrm{d}s, \end{aligned}$$

where \({\mathbf {J}}(t-s,T)={\mathrm {diag}}\left( J_{1}(t-s,T),\ldots ,J_{n}(t-s,T)\right) \in {\mathbb {R}}^{n\times n}\) is the diagonal Green’s matrix whose diagonal elements are given by

$$\begin{aligned} \begin{aligned}J_{j}(t,T)&={\left\{ \begin{array}{ll} \begin{array}{c} \frac{e^{\alpha _{j}t}}{\omega _{j}}\left[ \frac{e^{\alpha _{j}T}\left[ \omega _{j}\left( \cos \omega _{j}(T+t)-e^{\alpha _{j}T}\cos \omega _{j}t\right) +\alpha _{j}\left( \sin \omega _{j}(T+t)-e^{\alpha _{j}T}\sin \omega _{j}t\right) \right] }{1+e^{2\alpha _{j}T}-2e^{\alpha _{j}T}\cos \omega _{j}T}+\right. \\ \left. h(t)\left( \omega _{j}\cos \omega _{j}t+\alpha _{j}\sin \omega _{j}t,\right) \right] \end{array}\quad &{} \zeta _{j}<1\\ \frac{e^{\alpha _{j}(T+t)}\left[ \left( 1-e^{\alpha _{j}T}\right) \left( 1+\alpha _{j}t\right) +\alpha _{j}T\right] }{\left( 1-e^{\alpha _{j}T}\right) ^{2}}+h(t)\left( e^{\alpha _{j}t}+\alpha _{j}te^{\alpha _{j}t},\right) \, &{} \zeta _{j}=1\\ \frac{1}{(\beta _{j}-\gamma _{j})}\left[ \frac{\beta _{j}e^{\beta _{j}(T+t)}}{1-e^{\beta _{j}T}}-\frac{\gamma _{j}e^{\gamma _{j}(T+t)}}{1-e^{\gamma _{j}T}}+h(t)\left( \beta _{j}e^{\beta _{j}t}-\gamma _{j}e^{\gamma _{j}t}\right) \right] , &{} \zeta _{j}>1 \end{array}\right. }\end{aligned} \,, \end{aligned}$$
(32)

as shown in “Appendix D”.

Finally, the following result extends the integral equation formulation of Theorem 3 to quasi-periodic forcing.

Theorem 4

(i) If \({\mathbf {x}}(t)\) is a quasi-periodic solution of the nonlinear system (22) with frequency basis \(\varvec{\Omega }\), and the nonlinear function \({\mathbf {S}}({\mathbf {x}}(t))\) is also quasi-periodic with the same frequency basis \(\varvec{\Omega }\), then \({\mathbf {x}}(t)\) must satisfy the integral equation:

$$\begin{aligned} {\mathbf {x}}(t)&={\mathbf {U}}\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}\int _{0}^{T_{\varvec{\kappa }}}{\mathbf {L}}(t-s,T_{\varvec{\kappa }}){\mathbf {U}}^{\top }\left[ {\mathbf {f}}(s)-{\mathbf {S}}({\mathbf {x}}(s))\right] \,\mathrm{d}s \end{aligned}$$
(33)

(ii) Furthermore, any continuous quasi-periodic solution \({\mathbf {x}}(t)\) to (33), with frequency basis \(\varvec{\Omega }\), is a quasi-periodic solution of the nonlinear system (1).

Proof

This theorem is just a special case of Theorem 2.

\(\square \)

In analogy with Remark 4, we make the following remark for geometric nonlinearities and structural damping.

Remark 6

With the Fourier expansion \( {\mathbf {x}}(t) = \sum _{\varvec{\kappa }\in {\mathbb {Z}}^k} {\mathbf {x}}_{\varvec{\kappa }} e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t} \), Eq. (33) can be equivalently written as the system

$$\begin{aligned} {\mathbf {x}}_{\varvec{\kappa }}={\mathbf {U}} {\mathbf {Q}}(T_{\varvec{\kappa }}){\mathbf {U}}^{\top }\left[ {\mathbf {f}}_{\varvec{\kappa }}-{\mathbf {S}}_{\varvec{\kappa }}\{{\mathbf {x}}\}\right] ,\quad \varvec{\kappa }\in {\mathbb {Z}}^{k}\,, \end{aligned}$$
(34)

where

$$\begin{aligned} {\mathbf {Q}}(T_{\varvec{\kappa }})={\mathrm {diag}}\left( Q_{1}(T_{\varvec{\kappa }}),\ldots ,Q_{n}(T_{\varvec{\kappa }})\right) \in {\mathbb {C}}^{n\times n}, \end{aligned}$$

is the diagonal matrix of the amplification factors, which are explicitly given by

$$\begin{aligned}&Q_{j}(T_{\varvec{\kappa }})\nonumber \\&\quad :={\left\{ \begin{array}{ll} \frac{1}{(i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle -\alpha _{j})^{2}+\omega _{j}^{2}}, &{} \zeta _{j}<1\\ \frac{1}{(i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle -\alpha _{j})^{2}}, &{} \zeta _{j}=1,\quad j=1,\dots ,n,\\ \frac{1}{(\beta _{j}-i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle )(\gamma _{j}-i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle )}, &{} \zeta _{j}>1, \end{array}\right. } \nonumber \\ \end{aligned}$$
(35)

as derived in “Appendix I”.

Remark 7

The non-resonance conditions (7) and (13) are generically satisfied by dissipative systems as described in this section since none of the eigenvalues (27) are purely imaginary.

2.4 The unforced conservative case

In contrast to dissipative systems, which have isolated (quasi-) periodic solutions in response to (quasi-) periodic forcing, unforced conservative systems will generally exhibit families of periodic or quasi-periodic orbits (cf. Kelley [47] or Arnold [48]). The calculation of (quasi-) periodic orbits in an autonomous system such as

$$\begin{aligned} {\mathbf {B}}\dot{{\mathbf {z}}}={\mathbf {A}}{\mathbf {z}}+{\mathbf {R}}({\mathbf {z}})\,, \end{aligned}$$
(36)

is different from that in the forced case mainly due to two reasons:

  1. 1.

    The frequencies of such (quasi-) periodic oscillations are intrinsic to the system. This means that the time period T, or the base frequency vector \(\varvec{\Omega }\), of the response is a priori unknown.

  2. 2.

    Any given (quasi-) periodic solution \({\mathbf {z}}(t)\) to the autonomous system (36) is a part of a family of (quasi-) periodic solutions, with an arbitrary phase shift \(\theta \in {\mathbb {R}}\).

Nonetheless, Theorems 1–4 still hold for system (36) with the external forcing function set to zero. Special care needs to be taken, however, in the numerical implementation of these results for unforced mechanical systems, as we shall discuss in “Appendix J.1.1”.

3 Iterative solution of the integral equations

We would like to solve integral equations of the form (cf. Theorems 1 and 3)

$$\begin{aligned} {\mathbf {z}}(t)= & {} \int _{0}^{T}{\mathbf {V}}{\mathbf {G}}(t-s,T) {\mathbf {V}}^{-1}\left[ {\mathbf {F}}(s)\right. \nonumber \\&\left. -\,{\mathbf {R}}({\mathbf {z}}(s))\right] \,\mathrm{d}s,\quad t\in [0,T] \end{aligned}$$
(37)

to obtain periodic solutions, or integral equations of the form (cf. Theorem 2 and 4)

$$\begin{aligned} {\mathbf {z}}(t)={\mathbf {V}}\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}{\mathbf {H}}(T_{\kappa }){\mathbf {V}}^{-1}\left( {\mathbf {F}}_{\varvec{\kappa }}-{\mathbf {R}}_{\varvec{\kappa }}\{{\mathbf {z}}\}\right) e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t} \end{aligned}$$
(38)

to obtain quasi-periodic solutions of system (3). In the following, we propose iterative methods to solve these equations. First, we discuss a Picard iteration and then subsequently a Newton–Raphson scheme.

3.1 Picard iteration

Picard [49] proposed an iteration scheme to show local existence of solutions to ordinary differential equations, which is also used as practical iteration scheme to approximate the solutions to boundary value problems in numerical analysis (cf. Bailey et al. [50]). We derive explicit conditions on the convergence of the Picard iteration when applied to Eqs. (37), (38).

3.1.1 Periodic response

We define the right-hand side of the integral equation (11) as the mapping \(\varvec{\mathcal {G}}_{P}\) acting on the phase space vector \({\mathbf {z}}\), i.e.,

$$\begin{aligned} {\mathbf {z}}(t)= & {} {\varvec{\mathcal {G}}}_{P}({\mathbf {z}})\,(t) :=\int _{0}^{T} {\mathbf {V}}{\mathbf {G}}(t-s,T){\mathbf {V}}^{-1}\nonumber \\&\times \left[ {\mathbf {F}}(s)-{\mathbf {R}}({\mathbf {z}}(s))\right] \,\mathrm{d}s,\quad t\in [0,T]. \end{aligned}$$
(39)

Clearly, a fixed point of the mapping \({\varvec{\mathcal {G}}}_{P}\) in (39) corresponds to a periodic steady-state response of system (1) by Theorem 1. Starting with an initial guess \({\mathbf {z}}_{0}(t)\) for the periodic orbit, the Picard iteration applied to the mapping (37) is given by

$$\begin{aligned} {\mathbf {z}}_{\ell +1}={\varvec{\mathcal {G}}}_{P}({\mathbf {z}}_{\ell })\,,\quad \ell \in {\mathbb {N}}. \end{aligned}$$
(40)

To derive a convergence criterion for the Picard iteration, we define the sup norm \({\left\| \cdot \right\| _{0}=\max _{t\in [0,T]}\left| \cdot \right| }\) and consider a \(\delta -\)ball of \(C^{0}\)-continuous and T-periodic functions centered at \({\mathbf {z}}_{0}\):

$$\begin{aligned} C_{\delta }^{{\mathbf {z}}_{0}}[0,T]:= & {} \left\{ {\mathbf {z}}:[0,T]\rightarrow {\mathbb {R}}^{2n}\,\,\vert \quad {\mathbf {z}}\in C^{0}[0,T],\right. \nonumber \\&\left. {\mathbf {z}}(0)={\mathbf {z}}(T),\quad \left\| {\mathbf {z}}-{\mathbf {z}}_{0}\right\| _{0}\le \delta \right\} . \end{aligned}$$
(41)

We further define the first iterate under the map \( \varvec{\mathcal {G}}_{P} \) as

$$\begin{aligned} \varvec{\mathcal {E}}(t)= & {} \mathcal {\varvec{G}}_{P}({\mathbf {z}}_{0})(t) =\int _{0}^{T}{\mathbf {V}}{\mathbf {G}}(t-s,T){\mathbf {V}}^{-1}\nonumber \\&\times \left[ {\mathbf {F}}(s)-{\mathbf {R}}({\mathbf {z}}_{0}(s))\right] \,\mathrm{d}s,\quad t\in [0,T], \end{aligned}$$
(42)

and denote with \(L_{\delta }^{{\mathbf {z}}_{0}}\) a uniform-in-time Lipschitz constant for the nonlinearity \({\mathbf {R}}({\mathbf {z}})\) with respect to its argument \({\mathbf {z}}\) within \(C_{\delta }^{{\mathbf {z}}_{0}}[0,T]\). With that notation, we obtain the following theorem for the convergence of a Picard iteration performed on (37)

Theorem 5

If the conditions

$$\begin{aligned} L_{\delta }^{{\mathbf {z}}_{0}}< & {} \frac{1}{a\left\| {\mathbf {V}}\right\| \left\| {\mathbf {V}}^{-1}\right\| \varGamma (T)}\,, \end{aligned}$$
(43)
$$\begin{aligned} \delta\ge & {} \frac{\left\| \varvec{\mathcal {E}}\right\| _{0}}{1-\left\| {\mathbf {V}}\right\| \left\| {\mathbf {V}}^{-1}\right\| L_{\delta }^{{\mathbf {z}}_{0}}\varGamma (T)}\,, \end{aligned}$$
(44)

hold for some real number \(a\ge 1\), then the mapping \(\varvec{\mathcal {G}}_{P}\) defined in Eq. (37) has a unique fixed point in the space (41) and this fixed point can be found via the successive approximation

$$\begin{aligned} {\mathbf {z}}_{\ell +1}(t)= & {} {\varvec{\mathcal {G}}}_{P}({\mathbf {z}} _{\ell })\,(t) =\int _{0}^{T}{\mathbf {V}}{\mathbf {G}}(t-s,T){\mathbf {V}}^{-1}\nonumber \\&\times \left[ {\mathbf {F}}(s)-{\mathbf {R}}({\mathbf {z}}_{\ell }(s))\right] \,\mathrm{d}s,\quad \ell \in {\mathbb {N}} \end{aligned}$$
(45)

Proof

The proof relies on the Banach fixed point theorem. We establish that the mapping (37) is well defined on the space (41). Subsequently, we prove that under conditions (43), (44), the mapping (37) is a contraction. We detail all this in “Appendix G”. \(\square \)

Remark 8

If the nonlinearity \({\mathbf {R}}({\mathbf {z}})\) is not only Lipschitz but also of class \(C^{1}\) with respect to \({\mathbf {z}}\), then condition (43) can be more specifically written as

$$\begin{aligned} \max _{1\le j\le n\,\,\,}\max _{\left| {\mathbf {z}}-{\mathbf {z}}_{0}\right| \le \delta }\left| DR_{j}({\mathbf {z}})\right| <\frac{1}{a\varGamma (T)\left\| {\mathbf {V}}\right\| \left\| {\mathbf {V}}^{-1}\right\| }. \end{aligned}$$
(46)

Remark 9

In case of geometric (purely position dependent) nonlinearities and proportional damping (cf. Sect. 2.3), we can avoid iterating in the \(2n-\)dimensional phase space by defining the iteration as

$$\begin{aligned} {\mathbf {x}}_{\ell +1}(t)= & {} {\varvec{\mathcal {L}}}_{P}({\mathbf {x}}_{\ell }) \,(t) :=\int _{0}^{T}{\mathbf {U}}{\mathbf {L}}(t-s,T){\mathbf {U}}^{\top }\nonumber \\&\times \left[ {\mathbf {f}}(s)-{\mathbf {S}}({\mathbf {x}})\right] \,\mathrm{d}s,\quad t\in [0,T]. \end{aligned}$$
(47)

The existence of the steady-state solution and the convergence of the iteration (47) can be proven analogously.

Babistky [44] derives via transfer functions an iteration similar to (45) but without an explicit convergence proof. He asserts that the iteration is sensitive to the choice of the initial conditions \({\mathbf {z}}_{0}\). We can directly confirm this by examining condition (44). Indeed, the norm of the initial error \(\left\| \varvec{\mathcal {E}}\right\| _{0}\) is small for a good initial guess. Therefore, the \(\delta \)-ball in which the condition (43) on the Lipschitz constant needs to be satisfied can be selected small.

When no a priori information about the expected steady-state response is available, we can select \({\mathbf {z}}_{0}(t)\equiv {\mathbf {0}}\). Then, the term \(\varvec{\mathcal {E}}(0,t)\) is equal to the forced response of the linear system [cf. Eq. (42)]. In this case, the Lipschitz constant needs to be calculated for a \(\delta -\)ball centered at the origin.

The constant \(\varGamma (T)\) [cf. Eq. (10)] affects the convergence of the iteration (45). Larger damping (i.e., smaller \(e^{\mathrm{Re}(\lambda _{j})T})\), larger distance of the forcing frequency \(2\pi /T\) from the natural frequencies (i.e., larger \(|1-e^{\lambda _{j}T}|\)), and higher forcing frequencies (i.e., smaller T) all make the right-hand side of (43) larger and hence are beneficial to the convergence of the iteration. Likewise, a good initial guess (i.e., smaller \(\left\| \varvec{\mathcal {E}}\right\| _{0})\) and smaller nonlinearities (i.e., smaller \(\left| DS_{j}({\mathbf {x}})\right| \) ) all make the left-hand side of (43) smaller and hence are similarly beneficial to the convergence of the iteration. In the context of structural vibrations, higher frequencies, smaller forcing amplitudes, and forcing frequencies sufficiently separated from the natural frequencies of the system are realistic and affect the convergence positively. At the same time, low damping values in such systems are also typical and affect the convergence negatively.

An advantage of the Picard iteration approach we have discussed is that it converges monotonically, and hence, an upper estimate for the error after a finite number of iterations is readily available as the sup norm of the difference of the last two iterations. This can be exploited in numerical schemes to stop the iteration once the required precision is achieved.

3.1.2 Quasi-periodic response

We now consider the existence of a quasi-periodic solution under a Picard iteration of Eq. (18), which has apparently been completely absent in the literature. We rewrite the right-hand side of the integral equation (18) as the mapping

$$\begin{aligned} {\mathbf {z}}(t)= & {} \varvec{\mathcal {G}}_{Q}({\mathbf {z}})\,(t):={\mathbf {V}}\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}{\mathbf {H}}(T_{\kappa }){\mathbf {V}}^{-1}\nonumber \\&\times \left( {\mathbf {F}}_{\varvec{\kappa }}-{\mathbf {R}}_{\varvec{\kappa }}\{{\mathbf {z}}\}\right) e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t}, \end{aligned}$$
(48)

where we have made use of the Fourier expansion defined in Remark 4.

We consider a space of quasi-periodic functions with the frequency base \(\varvec{\Omega }\). Similarly to the periodic case (cf. Sect. 3.1.1), we restrict the iteration to a \(\delta -\)ball \(C_{\delta }^{{\mathbf {z}}_{0}}\left( \varvec{\Omega }\right) \) centered at the initial guess \({\mathbf {z}}_{0}\) with radius \(\delta \), i.e.,

$$\begin{aligned} C_{\delta }^{{\mathbf {z}}_{0}}\left( \varvec{\Omega }\right):= & {} \left\{ {\mathbf {z}}(\varvec{\theta }):\,{\mathbb {T}}^{k}\rightarrow {\mathbb {R}}^{2n}\;\vert \quad {\mathbf {z}}\in C^{0}, \right. \nonumber \\&\left. \left\| {\mathbf {z}}-{\mathbf {z}}_{0}\right\| _{0}\le \delta \right\} , \end{aligned}$$
(49)

where the sup norm \(\left\| \cdot \right\| _{0}=\max _{\varvec{\theta }\in {\mathbb {T}}^k}\left| \cdot \right| \) is the uniform supremum norm over the torus \( {\mathbb {T}}^k \). We then have the following theorem.

Theorem 6

If the conditions

$$\begin{aligned} L_{\delta }^{{\mathbf {z}}_{0}}< & {} \frac{1}{a\left\| {\mathbf {V}}\right\| \left\| {\mathbf {V}}^{-1}\right\| h_\mathrm{max}}\,, \end{aligned}$$
(50)
$$\begin{aligned} \delta\ge & {} \frac{\left\| \varvec{\mathcal {E}}\right\| _{0}}{1-2\left\| {\mathbf {V}}\right\| \left\| {\mathbf {V}}^{-1}\right\| L_{\delta }^{{\mathbf {z}}_{0}}h_\mathrm{max}}\,, \end{aligned}$$
(51)

hold for some real number \(a\ge 1\), then the mapping \(\varvec{\mathcal {G}}_{Q}\) defined in Eq. (48) has a unique fixed point in the space (49) and this fixed point can be found via the successive approximation

$$\begin{aligned} {\mathbf {z}}_{\ell +1}(t)=\varvec{\mathcal {G}}_{Q}({\mathbf {z}}_{\ell })\,(t),\quad \ell \in {\mathbb {N}}. \end{aligned}$$
(52)

Proof

The is analogous to the proof of Theorem 5. We first establish that the mapping (48) is well defined in the space (49). In “Appendix H”, we detail that the mapping (48) is a contraction under the conditions (50) and (51).

Remark 10

In case of geometric (position-dependent) nonlinearities and proportional damping, we can reduce the dimensionality of the iteration (52) by half, using (34). This results in the following, equivalent Picard iteration:

$$\begin{aligned} {\mathbf {x}}_{\ell +1}(t)= & {} \varvec{\mathcal {L}}_{Q} ({\mathbf {x}}_{\ell })\,(t) :={\mathbf {U}}\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}{\mathbf {Q}}(T_{\varvec{\kappa }}){\mathbf {U}}^{\top }\nonumber \\&\times \left[ {\mathbf {f}}_{\varvec{\kappa }}-{\mathbf {S}}_{\varvec{\kappa }}\{{\mathbf {x}}_{\ell }\}\right] e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t},\quad \ell \in {\mathbb {N}}. \end{aligned}$$
(53)

The existence of the steady-state solution and the convergence of the iteration (53) can be proven analogously.

As in the periodic case, the convergence of the iteration (52) depends on the quality of the initial guess and the constant \(h_\mathrm{max}\) [cf. Eq. (17)], which is the maximum amplification factor. Low damping results in a higher amplification factor [cf. Eq. (17)] and will therefore affect the iteration negatively, which is similar to the criterion derived in the periodic case.

3.1.3 Unforced conservative case

In the unforced conservative case, \({\mathbf {z}}(t)\equiv {\mathbf {0}}\) is the trivial fixed point of the maps \(\varvec{\mathcal {G}}_{P}\) and \(\varvec{\mathcal {G}}_{Q}\). Thus, by Theorems 5 and 6, the Picard iteration with an initial guess in the vicinity of the origin would make the iteration converge to the trivial fixed point. In practice, the simple Picard approach is found to be highly sensitive to the choice of initial guess for obtaining non-trivial solution in the case of unforced conservative systems. Thus, in such cases, more advanced iterative schemes equipped with continuation algorithms are desirable, such as the ones we describe next.

3.2 Newton–Raphson iteration

So far, we have described a fast iteration process and gave bounds on the expected convergence region of this iteration. We concluded that if the iteration converges, it leads to the unique (quasi-) periodic solution of the system (1). As discussed previously (cf. Sect. 3.1), our convergence criteria for the Picard iteration will not be satisfied for near-resonant forcing and low damping. However, even if the Picard iteration fails to converge, one or more periodic orbits may still exist.

A common alternative to the contraction mapping approach proposed above is the Newton–Raphson scheme (cf., e.g., Kelley [51] ). An advantage of this iteration is its quadratic convergence if the initial guess is close enough to the actual solution of the problem. This makes this procedure also appealing for a continuation setup. We first derive the Newton–Raphson scheme to periodically forced systems and afterward to quasi-periodically forced systems.

3.2.1 Periodic case

To set up a Newton–Raphson iteration, we reformulate the fixed point problem (37) with the help of a functional \(\varvec{\mathcal {F}}_{P}\) whose zeros need to be determined:

$$\begin{aligned} \varvec{\mathcal {F}}_{P}({\mathbf {z}}):= & {} {\mathbf {z}}-\varvec{\mathcal {G}}_{P}({\mathbf {z}}) ={\mathbf {z}}-\int _{0}^{T}{\mathbf {V}}{\mathbf {G}}(t-s,T){\mathbf {V}}^{-1}\nonumber \\&\times \left[ {\mathbf {F}}(s)-{\mathbf {R}}({\mathbf {z}}(s))\right] \,\mathrm{d}s={\mathbf {0}}. \end{aligned}$$
(54)

Starting with an initial solution guess \({\mathbf {z}}_{0}\), we formulate the iteration for the zero of the functional \(\varvec{\mathcal {F}}_{P}\) as

$$\begin{aligned} \begin{aligned}{\mathbf {z}}_{l+1}&={\mathbf {z}}_{l}+\varvec{\mu }_{l},\\ -\varvec{\mathcal {F}}_{P}({\mathbf {z}}_{l})&=D\varvec{\mathcal {F}}_{P}({\mathbf {z}}_{l})\varvec{\mu }_{l},\quad l\in {\mathbb {N}}\,, \end{aligned} \end{aligned}$$
(55)

where the second equation in (55) can be written using the Gateaux derivative of \( \varvec{\mathcal {F}}_{P} \) of

$$\begin{aligned}&-\varvec{\mathcal {F}}_{P}({\mathbf {z}}_{l}) =D\varvec{\mathcal {F}}_{P}({\mathbf {z}}_{l})\varvec{\mu }_{l}\nonumber \\&\quad =\left. \frac{d{\varvec{\mathcal {F}}}_{P}({\mathbf {z}}_{l} +s\varvec{\mu }_{l})}{ds}\right| _{s=0}\nonumber \\&\quad =\varvec{\mu }_{l}+\int _{0}^{T}{\mathbf {V}}{\mathbf {G}}(t-s,T){\mathbf {V}}^{-1}\left. D{\mathbf {R}}\left( {\mathbf {z}}(s)\right) \right| _{{\mathbf {z}}={\mathbf {z}}_{l}}\nonumber \\&\qquad \varvec{\mu }_{l}(s)ds. \end{aligned}$$
(56)

Equation (56) is a linear integral equation in \(\varvec{\mu }_{l}\), where \({\mathbf {z}}_{l}\) is the known approximation to the solution of (54) at the lth iteration step.

3.2.2 Quasi-periodic case

In the quasi-periodic case, the steady-state solution of system (1) is given by the zeros of the functional

$$\begin{aligned} {\varvec{\mathcal {F}}}_{Q}({\mathbf {z}}):= & {} {\mathbf {z}}-\varvec{\mathcal {G}}_{Q}({\mathbf {z}})={\mathbf {z}}-\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}{\mathbf {V}}{\mathbf {H}}(T_{\varvec{\kappa }}){\mathbf {V}}^{-1}\nonumber \\&\times \left( \mathbf {F_{\varvec{\kappa }}}-\mathbf {R_{\varvec{\kappa }}}\{{\mathbf {z}}_{l}\}\right) e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t}\,. \end{aligned}$$
(57)

Analogous to the periodic case, the Newton–Raphson scheme seeks to find a zero of \({\varvec{\mathcal {F}}}_{Q}\) via the iteration:

$$\begin{aligned} \begin{aligned}{\mathbf {z}}_{l+1}&={\mathbf {z}}_{l} +{\varvec{\nu }}_{l},\\ -\varvec{\mathcal {F}}_{Q}({\mathbf {z}}_{l})&=D\varvec{\mathcal {F}}_{Q}({\mathbf {z}}_{l}){\varvec{\nu }}_{l}. \end{aligned} \end{aligned}$$
(58)

To obtain the correction step \({\varvec{\nu }}_{l}\), the linear system of equations

$$\begin{aligned}&-\varvec{\mathcal {F}}_{Q}({\mathbf {z}}_{l}) =D\varvec{\mathcal {F}}_{Q}({\mathbf {z}}_{l}){\varvec{\nu }}_{l}\nonumber \\&\quad ={\varvec{\nu }}_{l}+{\mathbf {V}}\sum _{\varvec{\kappa }\in {\mathbb {Z}}^{k}}{\mathbf {H}}(T_{\varvec{\kappa }}){\mathbf {V}}^{-1}\left( \mathbf {F_{\varvec{\kappa }}}-\{D{\mathbf {R}}({\mathbf {z}}_{l}){\varvec{\nu }}_{l}\}_{\varvec{\kappa }}\right) e^{i\left\langle \varvec{\kappa },\varvec{\Omega }\right\rangle t}\nonumber \\ \end{aligned}$$
(59)

needs to be solved for \({\varvec{\nu }}_{l}\). The Fourier coefficients \(\{D{\mathbf {R}}({\mathbf {z}}_{l}){\varvec{\nu }}_{l}\}_{\varvec{\kappa }}\) in (59) are then given by the formula

$$\begin{aligned}&\{D{\mathbf {R}}({\mathbf {z}}_{l}(t)){\varvec{\nu }}_{l}\}_{\varvec{\kappa }}\\&\quad =\lim _{\tau \rightarrow \infty }\frac{1}{2\tau }\int _{-\tau }^{\tau }D{\mathbf {R}}({\mathbf {z}}(t))\varvec{\nu }_{l}(t)e^{-i\langle \varvec{\kappa },\varvec{\Omega }\rangle t}\mathrm{d}t\,. \end{aligned}$$

Remark 11

As noted in Introduction, the results in Sects. 3.1.2 and 3.2.2 hold without any restriction on the number of independent frequencies allowed in the forcing function \( {\mathbf {f}}(t) \). This enables us to compute the steady-state response for arbitrarily complicated forcing functions, as long as they are well approximated by a finite Fourier expansion. Thus, the treatment of random-like steady-state computations is possible with the methods proposed here.

3.3 Discussion of the iteration techniques and numerical solution

The Newton–Raphson iteration offers an alternative to the Picard iteration, especially when the system is forced near resonance, and hence, the convergence of the Picard iteration cannot be guaranteed. At the same time, the Newton–Raphson iteration is computationally more expensive than the Picard iteration for two reasons: First, the evaluation of the Gateaux derivatives (56) and (59) can be expensive, especially if the Jacobian of the nonlinearity is not directly available. Second, the correction step \(\varvec{\mu }_{l}\) or \(\varvec{\nu }_{l}\) at each iteration involves the inversion of the corresponding linear operator in Eq. (56) or (59), which is costly for large systems.

Regarding the first issue above, the tangent stiffness is often available in finite-element codes for structural vibration. Nonetheless, there are many quasi-Newton schemes in the literature that circumvent this issue by offering either a cost-effective but inaccurate approximation of the Jacobian (e.g., the Broyden’s method [52]), or avoid the calculation of the Jacobian altogether (cf. Kelley [51]).

For the second challenge above, one can opt for the iterative solution of the linear system (56) or (59), which would circumvent operator inversion when the system size is very large. A practical strategy for obtaining force response curves of high-dimensional systems would be to use the Picard iteration away from resonant forcing and switch toward the Newton–Raphson approach when the Picard iteration fails. Even though the Newton–Raphson approach has better rate of convergence (quadratic) as compared to the Picard approach (linear), the computational complexity of a single Picard iteration is an order of magnitude lower than that of Newton–Raphson method (simply because of the additional costs of Jacobian evaluation and inversion involved in the correction step). In our experience with high-dimensional systems, when the Picard iteration converges, it is significantly faster than the Newton–Raphson in terms of CPU time, even though it takes significantly more number of iterations to converge.

Both the Picard and the Newton–Raphson iteration are efficient solution techniques for specific forcing functions. However, to obtain the steady-state response as a function of forcing amplitudes and frequencies, numerical continuation (cf. Dankowicz and Schilder [37], Doedel et al. [35], Dhooge et al. [36]) is required. We discuss numerical continuation in the context of the proposed integral equations approach in “Appendix J.1”.

In the case of multiple coexisting equilibrium positions in the unforced-damped system, the persistence of these solutions as k-dimensional tori under small (quasi-) periodic forcing can be deduced by the general results of Haro and de la Llave [53]. Depending on the specific application, a selection of these solutions can be numerically continued with the described techniques. To explore bifurcation phenomena, such as merging of such solutions, advanced continuation techniques, such as those of Dankowicz and Schilder [37], Doedel et al. [35] and Dhooge et al. [36] are needed.

Furthermore, note that \({\mathbf {z}}(t)\) in Eqs. (37) and (38) is a continuous function of time that cannot generally be obtained in a closed form and, therefore, must be numerically approximated (cf. Kress [54], Zeyman [55], Atkinson [56]). We discuss the numerical solution procedure for such integral equations in “Appendix J”.

In the supplementary MATLAB® code, we have implemented a simple yet powerful collocation-based approach for the numerical approximation of the periodic solution, and a Galerkin projection approach using a Fourier basis for the quasi-periodic case. We have also implemented the Picard and the Newton–Raphson approaches for the iterative solution of the integral equations, as discussed above. While performing numerical continuation, we make use of both these techniques in the sense described above, i.e., we use the fast Picard approach away from resonance and switch to the use of the Newton–Raphson approach when the Picard approach fails. In our experience, this combination was found to be very effective in obtaining forced response curves/surfaces for periodic as well as quasi-periodic cases.

4 Numerical examples

To illustrate the power of our integral-equation-based approach in locating the steady-state response, we consider two numerical examples. The first one is a two-degree-of-freedom system with geometric nonlinearity. We apply our algorithms under periodic and quasi-periodic forcing, as well as to the autonomous system with no external forcing. We also treat a case of non-smooth nonlinearities. For periodic forcing, we compare the computational cost with algorithm implemented in the \(\texttt {po}\) toolbox of the state-of-the-art continuation software \(\textsc {coco}\) [37]. Subsequently, we perform similar computations for a higher-dimensional mechanical system.

Fig. 1
figure 1

Two-mass oscillator with the non-dimensional parameters m, k and c

Full size image

4.1 2-DOF example

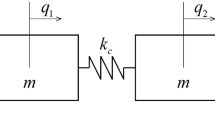
We consider a two-degree-of-freedom oscillator shown in Fig. 1. The nonlinearity \({\mathbf {S}}\) is confined to the first spring and depends on the displacement of the first mass only. The equations of motion are

$$\begin{aligned}&\left[ \begin{array}{cc} m &{} 0\\ 0 &{} m \end{array}\right] \ddot{{\mathbf {q}}}+\left[ \begin{array}{cc} 2c &{} -c\\ -c &{} 2c \end{array}\right] \dot{{\mathbf {q}}}+\left[ \begin{array}{cc} 2k &{} -k\\ -k &{} 2k \end{array}\right] {\mathbf {q}}+\left[ \begin{array}{c} S(q_{1})\\ 0 \end{array}\right] \nonumber \\&\quad =\left[ \begin{array}{c} f_{1}(t)\\ f_2(t) \end{array}\right] \,. \end{aligned}$$
(60)

This system is a generalization of the two-degree-of-freedom oscillator studied by Szalai et al. [57], which is a slight modification of the classic example of Shaw and Pierre [4]. Since the damping matrix \({\mathbf {C}}\) is proportional to the stiffness matrix \({\mathbf {K}}\), we can employ the Green’s function approach described in Sect. 2.3. The eigenfrequencies and modal damping of the linearized system at \(q_{1}=q_{2}=0\) are given by

$$\begin{aligned}&\omega _{0,1}=\sqrt{\frac{k}{m}},\qquad \omega _{0,2}=\sqrt{\frac{3k}{m}}, \qquad \zeta _{1}=\frac{cm}{2\omega _{0,1}},\\&\quad \zeta _{2}=\frac{cm}{2\omega _{0,2}}. \end{aligned}$$

With those constants, we can calculate the constants \(\alpha _{j}\) and \(\omega _{j}\) [cf. Eq. (28)] for the Green’s function \(L_{j}\) in Eq. (30). We will consider three different versions of system (60): smooth nonlinearity with periodic and subsequently quasi-periodic forcing; smooth nonlinearity without forcing; discontinuous nonlinearity without forcing.

4.1.1 Periodic forcing

First, we consider system (60) with harmonic forcing of the form

$$\begin{aligned} f_{1}=f_2(t)=A\sin (\varOmega t), \end{aligned}$$
(61)

and a smooth nonlinearity of the form

$$\begin{aligned} S(q_{1})=0.5q_{1}^{3}\,, \end{aligned}$$
(62)

which is the same nonlinearity considered by Szalai et al. [57]. The integral-equation-based steady-state response curves are shown in Fig. 2 for a full frequency sweep and for different forcing amplitudes. As expected, our Picard iteration scheme (blue) converges fast for all frequencies in case of low forcing amplitudes. For higher forcing amplitude, the method no longer converges in a growing neighborhood of the resonance. To improve the results close to the resonance, we employ the Newton–Raphson scheme of Sect. 3.2. We see that the latter iteration captures the periodic response even for larger amplitudes near resonances until a fold arises in the response curve. We need more sophisticated continuation algorithms to capture the response around such folds.

Fig. 2
figure 2

Nonlinear frequency response curves obtained using sequential continuation with the Picard iteration (blue) and Newton–Raphson iteration (red) on example (60) with the nonlinearity (62) and forcing (61). (Color figure online)

Full size image

Performance comparison between the integral equations and thepotoolbox ofcoco As shown in Table 1, the integral equation approach proposed in the present paper is substantially faster than the \(\texttt {po}\) toolbox for continuation of periodic orbits with the MATLAB®-based continuation package \(\textsc {coco}\) [37] for low enough amplitudes. However, as the frequency response starts developing complicated folds for higher amplitudes (cf. Fig. 3), a much higher number of continuation steps are required for the convergence of our simple implementation of the pseudo-arc-length continuation (cf. the third column in Table 1). Since \(\textsc {coco}\) is capable of performing continuation on general problems with advanced algorithms, we have implemented our integral equation approach in \(\textsc {coco}\) in order to overcome this limitation. As shown in Table 1, the integral equation approach, along with \(\textsc {coco}\)’s built-in continuation scheme, is much more efficient for high-amplitude loading than any other method we have considered.

Fig. 3
figure 3

Steady-state responses obtained for Example 1 [with nonlinearity (62) and forcing (61)] from different continuation techniques. Numerical continuation using coco or pseudo-arc-length technique is able to capture the fold appearing in the response curve for \( A=0.1 \) [cf. Fig. 3, Table 1]

Full size image
Table 1 Comparison of computational performance for different continuation approaches
Full size table
Fig. 4
figure 4

a Response curve for Example 1 with the nonlinearity (62) and the forcing (63), and the non-dimensional parameters \(m=1\), \(k=1\) and \(c=0.02\); b number of iterations needed on the construction of Fig. 4a. Red curves bound the a priori guaranteed region of convergence for the Picard iteration. The white region is the domain where this iteration fails, and we employ the Newton–Raphson scheme. (Color figure online)

Full size image

The integral-equation-based continuation was performed with \(n_{t}=50\) time steps to discretize the solution in the time domain. On the other hand, the \(\texttt {po}\) toolbox in \(\textsc {coco}\) performs collocation-based continuation of periodic orbits, whereby it is able to modify the time-step discretization in an adaptive manner to optimize performance. In principle, it is possible to build an integral-equation-based toolbox in \(\textsc {coco}\), which would allow for the adaptive selection of the discretization steps. This is expected to further increase the performance of integral equations approach, when equipped with \(\textsc {coco}\) for continuation.

4.1.2 Quasi-periodic forcing

Unlike the shooting technique reviewed earlier, our approach can also be applied to quasi-periodically forced systems (cf. Theorems 2 and 4). Therefore, we can also choose a quasi-periodic forcing of the form

$$\begin{aligned}&f_2(t) =0,\quad f_{1}=0.01(\sin (\varOmega _{1}t)+\sin (\varOmega _{2}t))\,,\nonumber \\&\quad \kappa _{1}\varOmega _{1}+\kappa _{2}\varOmega _{2}\ne 0\,,\kappa _{1},\kappa _{2}\in {\mathbb {Z}}-\{0\}, \end{aligned}$$
(63)

in Example 2, with the nonlinearity still given by Eq. (62). Choosing the first forcing frequency \(\varOmega _{1}\) close to the first eigenfrequency \(\omega _{1}\) and the second forcing frequency \(\varOmega _{2}\) close to \(\omega _{2}\), we obtain the results depicted in Fig. 4a. We show the maximal displacement as a function of the two forcing frequencies, which are always selected to be incommensurate; otherwise, the forcing would not be quasi-periodic. We nevertheless connect the resulting set of discrete points with a surface in Fig. 4a for better visibility.

Fig. 5
figure 5

a Graph of the non-smooth nonlinearity (64); b response curve for Example 1 with the nonlinearity (64) and the forcing (61); parameters: \(m=1\), \(k=1\) and \(c=0.02\), \( \alpha = \beta = 0.1\)

Full size image

To carry out the quasi-periodic Picard iteration (53), the infinite summation involved in the formula has to be truncated. We chose to truncate the Fourier expansion once its relative error is within \(10^{-3}\). If the iteration (53) did not converge, we switched to the Newton–Raphson scheme described in Sect. 3.2.2. In that case, we only kept the first three harmonics as Fourier basis.

Figure 4b shows the number of iterations needed to converge to a solution with this iteration procedure. Especially away from the resonances, a low number of iterations suffices for convergence to an accurate result. Also included in Fig. 4b are the conditions (50) and (51), which guarantee the convergence for the iteration to the steady-state solution of system (1). Outside the two red curves, both (50) and (51) are satisfied and, accordingly, the iteration is guaranteed to converge. Since these conditions are only sufficient for convergence, the iteration converges also for frequency pairs within the red curves. The number of iterations required increases gradually and within the white region bounded by green lines, the Picard iteration fails. In such cases, we proceed to employ the Newton– Raphson scheme (cf. Sect. 3.2.2).

4.1.3 Non-smooth nonlinearity

As noted earlier, our iteration schemes are also applicable to non-smooth system as long as they are still Lipschitz. We select the nonlinearity of the form

$$\begin{aligned} S(q_{1})={\left\{ \begin{array}{ll} \alpha \text {sign}(q_{1})(|q_{1}|-\beta ), &{} \text {for }|q_{1}|>\beta ,\\ 0, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$
(64)

which represents a hardening (\(\alpha >0\)) or softening (\(\alpha <0\)) spring with play \(\beta >0\). The spring coefficient is given by \(\tan ^{-1}(\alpha )\), as depicted in Fig. 5a.

If we apply the forcing

$$\begin{aligned} f_1(t) = 0.02 \sin (\varOmega t),\quad f_2(t) = 0 \end{aligned}$$

to system (60) with the nonlinearity (64), our iteration techniques yield the response curve depicted in Fig. 5b. The Picard iteration approach (47) converges for moderate amplitudes, also in the nonlinear regime (\(|q_{1}|>\beta \)). When the Picard iteration fails at higher amplitudes, we employ the Newton–Raphson iteration. These results match closely with the amplitudes obtained by numerical integration, as seen in Fig. 5b.

Fig. 6
figure 6

An n-mass oscillator chain with coupled nonlinearity. We select the non-dimensional parameters \(m=1\), \(k=1,\kappa =0.5\) and \(c=1\)

Full size image

4.2 Nonlinear oscillator chain

To illustrate the applicability of our results to higher-dimensional systems and more complex nonlinearities, we consider a modification of the oscillator chain studied by Breunung and Haller [58]. As shown in Fig. 6, the oscillator chain consists of n masses with linear and cubic nonlinear springs coupling every pair of adjacent masses. Thus, the nonlinear function \({\mathbf {S}}\) is given as:

$$\begin{aligned} {\mathbf {S}}({\mathbf {x}})=\kappa \left[ \begin{array}{c} x_{1}^{3}-\left( x_{2}-x_{1}\right) ^{3}\\ \left( x_{2}-x_{1}\right) ^{3}-\left( x_{3}-x_{2}\right) ^{3}\\ \left( x_{3}-x_{2}\right) ^{3}-\left( x_{4}-x_{3}\right) ^{3}\\ \vdots \\ \left( x_{n-1}-x_{n-2}\right) ^{3}-\left( x_{n}-x_{n-1}\right) ^{3}\\ \left( x_{2}-x_{1}\right) ^{3}+x_{n}^{3} \end{array}\right] . \end{aligned}$$

The frequency response curve obtained with the iteration described in Sect. 3.2 for harmonic forcing is shown in Fig. 7 for 20 degrees-of-freedom. We also include the frequency response obtained with the \(\texttt {po}\)-toolbox of \(\textsc {coco}\) [37] with default settings for comparison. The integral equations approach gives the same solution as the \(\texttt {po}\)-toolbox of coco, but the difference in run times is stunning: the po-toolbox of \(\textsc {coco}\) takes about 12 min and 59 s to generate this frequency response curve, whereas the integral equation approach with a naive sequential continuation strategy takes 13 s to generate the same curve. This underlines the power of the approaches proposed here for complex mechanical vibrations.

Fig. 7
figure 7

Comparison of frequency sweeps produced using different continuation techniques for a 20-DOF oscillator chain with coupled nonlinearity

Full size image

5 Conclusion

We have presented an integral equation approach for the fast computation of the steady-state response of nonlinear dynamical systems under external (quasi-) periodic forcing. Starting with a forced linear system, we derive integral equations that must be satisfied by the steady-state solutions of the full nonlinear system. The kernel of the integral equation is a Green’s function, which we calculate explicitly for general mechanical systems. Due to these explicit formulae, the convolution with the Green’s function can be performed with minimal effort, thereby making the solution of the equivalent integral equation significantly faster than full time integration of the dynamical system. We also show the applicability of the same equations to compute periodic orbits of unforced, conservative systems.

We employ a combination of Picard and the Newton–Raphson iterations to solve the integral equations for the steady-state response. Since the Picard iteration requires only a simple application of a nonlinear map (and no direct solution via operator inversion), it is especially appealing for high-dimensional system. Furthermore, the nonlinearity only needs to be Lipschitz continuous, therefore our approach also applies to non-smooth systems, as we demonstrated numerically in Sect. 4.1.3. We establish a rigorous a priori estimate for the convergence of the Picard iteration. From this estimate, we conclude that the convergence of the Picard iteration becomes problematic for high amplitudes and forcing frequencies near resonance with an eigenfrequency of the linearized system. This can also be observed numerically in Example 4.1.1, where the Picard iteration fails close to resonance.

To capture the steady-state response for a full frequency sweep (including high amplitudes and resonant frequencies), we deploy the Newton–Raphson iteration once the Picard iteration fails near resonance. The Newton–Raphson formulation can be computationally intensive as it requires a high-dimensional operator inversion, which would normally make this type of iteration potentially unfeasible for exceedingly high-dimensional systems. However, we circumvent this problem with the Newton–Raphson method using modifications discussed in Sect. 3.2.

We have further demonstrated that advanced numerical continuation is required to compute the (quasi-) periodic response when folds appear in solution branches. To this end, we formulated one such continuation scheme, i.e., the pseudo-arc-length scheme, in our integral equations setting to facilitate capturing response around such folds. We also demonstrated that the integral equations approach can be coupled with existing state-of-the-art continuation packages to obtain better performance (cf. Sect. 4.1.1).

Compared to well-established shooting-based techniques, our integral equation approach also calculates quasi-periodic responses of dynamical systems and avoids numerical time integration. The latter can be computationally expensive for high-dimensional or stiff systems. In the case of purely geometric (position-dependent) nonlinearities, we can reduce the dimensionality of the corresponding integral iteration by half, by iterating on the position vector only. For numerical examples, we show that our integral equation approach equipped with numerical continuation outperforms available continuation packages significantly. As opposed to the broadly used harmonic balance procedure (cf. Chua and Ushida [24] and Lau and Cheung [25]), our approach also gives a computable and rigorous existence criterion for the (quasi-) periodic response of the system.

Along with this work, we provide a MATLAB® code with a user-friendly implementation of the developed iterative schemes. This code implements the cheap and fast Picard iteration, as well as the robust Newton–Raphson iteration, along with sequential/pseudo-arc-length continuation. We have further tested our approach in combination with the MATLAB®-based continuation package \(\textsc {coco}\) [37] and obtained an improvement in performance. One could, therefore, further add an integral-equation-based toolbox to \(\textsc {coco}\) with adaptive time steps in the discretization to obtain better efficiency.