Abstract
Complex dynamic systems are described by differential dynamic equations, mostly nonlinear without closed form analytic solution. To solve them numerically, there are many methods such as Euler’s method, Taylor-series method and Runge-Kutta method, etc., each with advantages and disadvantages. In this chapter, a novel analytical and numerical methodology for the solutions of linear and nonlinear dynamical systems is introduced. The piecewise constant argument method combined with the Laplace transform, makes the new method called Piecewise constant argument-Laplace transform (PL). This method provides better reliability and efficiency for solving coupled dynamic systems. In addition, the numerical solutions of linear and nonlinear dynamic systems can be obtained smoothly and continuously on the entire time range from zero to t. The numerical results of the analytical solution of the method are given and compared with the results of the 4th-order Runge-Kutta (RK4) method, and the accuracy and reliability of the PL method are verified.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Complex dynamic systems
- Numerical solutions
- Argument-Laplace method
- Vehicle laziness
- Nonlinear differential equations
1 Introduction
Almost all the complex dynamic systems can be described by differential dynamic equations [1,2,3]. For exploring the dynamic characteristics of systems, obtaining accurate solutions of the dynamic equations is crucial in the engineering design. Of course, Euler’s method, Taylor series method, and Runge-Kutta method are relatively mature methods existing in numerical analysis for vibration systems [4, 5]. Euler’s method is the most traditional method to solve differential equations. However, the numerical accuracy of Euler’s method should be decreased as integral curve is replaced with approximated polyline in the calculation process [6]. To perfect numerical accuracy in computing principle, trapezoidal method employs trapezoid to match integral curve in calculation process, and so the solution precision of this method is much higher than Euler’s method [7,8,9]; but the computational efficiency is restricted on account of its own algorithm complexity and large calculating quantity. In order to improve the computation efficiency, Carl Runge and Martin Kutta proposed Runge-Kutta method, and the theoretical basis of this method is derived from Taylor’s expansion and slope approximation [10]; in the solving process, the weighted average of the slope of multiple points in an integrating interval is calculated; the accuracy of the Runge-Kutta method is depended on the number of points in the integrating interval: the more points, the more accurate the calculation, and the more time should be needed to be taken in the calculation [11]. Since almost all terms are linearized and discontinuous when solving equations with Runge-Kutta method, calculative deviation is inevitable, which has attracted much more attention of numerous researchers. Shampine and Watts proposed a local error estimator, which seems to be of broad applicability [12]; according to this estimator, an efficient computational code (Ode45) is compiled [13, 14], and comparing the results of traditional Runge-Kutta, solution accuracy of Runge-Kutta is defective as the obtained results are not continuous, and the inherent characteristics of the system are lost in the second step of the calculation by using the Runge-Kutta method [15].
In this chapter, a novel analytical and numerical methodology for the solutions of linear and nonlinear dynamical systems is further developed. According to the piecewise constant argument mentioned in “Nonlinear Dynamics of Piecewise Constant Systems and Implementation of Piecewise Constant Arguments,” combined with the Laplace transform, a method called piecewise constant argument-Laplace transform (PL) was established. On account of the characteristics of the Laplace transform, this method with better reliability and efficiency is for solving the coupled dynamic systems [16,17,18]. In addition, because of the continuity of solutions with the piecewise constant argument [Nt]/N and the corresponding recurrence relations, the numerical solutions of linear and nonlinear dynamic systems can be obtained smoothly. Unlike the discrete solutions produced by existing numerical methods, the solutions given by the PL method to be presented are actually continuous on the entire time range from zero to t. Formulae for numerical computation in solving various dynamic systems are to be provided and discussed in the present chapter. Meanwhile, the numerical results of the analytical solution of the method are given and compared with the results of the fourth-order Runge-Kutta (RK4) method [19, 20], and the accuracy and reliability of the PL method are verified.
With the development of science and technology, the study to the dynamics of low-dimensional nonlinear dynamic systems can hardly satisfy the requirements of actual engineering [21, 22]. To explore the exact dynamics in nonlinear systems, it is necessary to study the identification method of dynamic behavior for high-dimensional nonlinear systems. Nowadays, the principal method for identifying the dynamic behavior of the nonlinear system include Lyapunov exponent, Poincaré mapping method, and bifurcation theory. Lyapunov exponent is an important method for identifying chaotic signals of nonlinear dynamical systems [21, 23]. The important characteristic of the nonlinear dynamical systems is that the final value of the system is sensitively depended on the initial value; therefore, Lyapunov exponent represents the average exponential rates of divergence or convergence of closed orbits of the vibrating object in phase space of a dynamic system. The Lyapunov exponent is an efficient tool for estimating whether a dynamic system is periodic or chaotic. However, the Lyapunov exponent is not suitable for determining the dynamic behavior that is neither periodic nor chaotic. Poincaré mapping method can diagnose the dynamic characteristics of the nonlinear system based on the fixed points in the Poincaré section [24, 25]; however, it is unsuitable to determine the global dynamics and periodicity. Although global bifurcation and local bifurcation theory can discern the dynamic characteristics of higher-dimensional dynamical systems [26, 27], the prerequisite for this approach is BP normalization for the dynamic systems. Theoretically speaking, we can calculate the canonical form of any order from a given dynamical system. Actually, it is very difficult to calculate the high order normal form for the higher-dimensional dynamical system, because the process of the normalization computation is complex.
For the limitations of identifying characteristics of the dynamic system based on the methods above, Dai and Singh proposed a periodicity-ratio method to distinguish the dynamic characteristics of one-dimensional nonlinear dynamic system [25]. However, the identification method of the dynamic characteristics for high-dimensional nonlinear system is reported in the recent years. Mahmoud introduced a new theorem used to construct approximate analytical solutions for n-dimensional strongly nonlinear dynamical system, and then passive control method is also used to control n-dimensional chaotic complex nonlinear systems [28]. Here, considering the principle of Poincaré mapping, the periodicity-ratio (PR) method for diagnosing the dynamic characteristics of the high-dimensional nonlinear systems is proposed [29]. This method is employed to determine the dynamics and periodicity of the hull and Rössler system, respectively. The research findings will develop the evaluation method of dynamic characteristics for the high-dimensional nonlinear dynamic system.
2 Fundamental Theory
To develop the numerical solutions of the dynamic system in this chapter, the numerical approach named the piecewise constant argument method is used. By introducing a piecewise constant argument [Nt]/N, the original continuous governing equations are divided into many segments, denoted as N, and linearized in each time interval, i/N ≤ t < (i + 1)/N, in which a linear dynamic system is developed. In the expression, N is a parameter that controls the length of the time interval and the accuracy of the calculation. When N becomes large enough, the numerical solutions can be sufficiently accurate. To preferably utilize the PL and the PR method, some theorems must be understood.
2.1 Piecewise Constant Argument
Theorem 1.1
Suppose argument [Nt] is the integer-valued function of product of time t and parameter N, where N is a positive integer [29]. When N is approached to infinity, the value of the argument [Nt]/N tends to t, i.e.:
Theorem 1.2
Considering a vibrating system:
with initial conditions:
Then, in time interval i/N ≤ t < (i + 1)/N, Eq. (1.2) and Eq. (1.3) are converted to:
and:
where i = 0, 1, 2, …, [Nt].
2.2 Laplace Transformation and Residues Principle
The coupling system can be decoupled with the Laplace transformation. Some significant theorems should be stressed.
Theorem 1.3
Supposing functions \( {x}_i^{{\prime\prime} }(t) \), \( {x}_i^{\prime }(t) \), and x i(t) can be rewritten as Laplace style, i.e. [2, 30]:
where \( {x}_i^{{\prime\prime} }(t)=\frac{d^2{x}_i}{dt^2},{x}_i^{\prime }(t)=\frac{dx_i}{dt}. \)
Theorem 1.4
F(s) is assumed to the Laplace style in complex field. F(s) corresponding to time-domain solution can be determined with inverse Laplace transformation, i.e.:
Theorem 1.5
Through the definition of residues, the integral in Eq. (1.9) can be expressed by the summing of all the residuals in the definition domain, i.e.:
where s k represents value of the kth pole point of F(s). Here, considering F(s) to be a rational function, the fraction style of F(s) can be given by \( F(s)=\frac{A(s)}{B(s)}, \) where A(s) and B(s) are mutually irreducible, and the order of A(s) is lower than B(s) [30]. According to the exponent number of zero point in B(s), Res[F(s)e st, s k] can be calculated with following rules, i.e.:
-
A.
If s k is the first-order zero point of B(s), then \( \mathrm{Res}\left[\frac{A(s)}{B(s)}{e}^{st},{s}_k\right]={\left.\frac{A(s)}{B^{\prime }(s)}{e}^{st}\right|}_{s={s}_k} \).
-
B.
If s k is the n-order zero point of B(s), then \( \mathrm{Res}\left[\frac{A(s)}{B(s)}{e}^{st},{s}_k\right]\\=\frac{1}{\left(n-1\right)!}\underset{s\to {s}_k}{\lim}\frac{d^{n-1}}{ds^{n-1}}{\left(s-{s}_k\right)}^n\frac{A(s)}{B(s)}{e}^{st} \).
2.3 The Periodicity Ratio of Nonautonomous Systems
Consider the following second order of the n-dimensional nonautonomous system [31]:
Suppose that the system is subjected to an external excitation with period time T; meanwhile, x is the periodic solution of the differential system above, i.e., x = [x 1, x 2, …, x n]T. Usually, x is the solution of the harmonic vibration related to multiple period of T satisfying the following relationship:
where t 0 is the reference time and j is the number of period points of the system in the Poincaré section. For a completely periodic nonautonomous dynamic system, no matter how long the vibration is sustained, only j finite points appear in Poincaré section \( \mathbf{x}-\dot{\mathbf{x}}\left({x}_r-{\dot{x}}_r,\kern0.5em \left(r=1,2,\dots, n\right)\right) \). If the phase points are infinite in Poincaré section \( \mathbf{x}\hbox{---} \dot{\mathbf{x}} \), the n-dimensional nonautonomous system is aperiodic.
According to Eq. (1.12), the overlapping points in n Poincaré sections can describe the periodicity of n-dimensional nonautonomous dynamic system. The number of overlapping points in the rth Poincaré section can be determined by:
where k and i are integers: k ∈ [1, j], i ∈ [1, m]. Equation (1.13) represents the displacement difference between phase point i and k in the Poincaré section when the phase trajectories pass through the rth section. Equation (1.14) describes the velocity difference between phase point i and k in the Poincaré section when the phase trajectories pass through the rth section. m is the sum of the phase points in the Poincaré section, including the overlapping and nonoverlapping points. Therefore, the total number of phase points in the Poincaré section can be denoted as:
According to the above definition, the following conclusions are stressed:
-
1.
In the Poincaré section, the so-called overlapping phase points i \( \left({x}_i,{\dot{x}}_i\right) \) and j \( \left({x}_j,{\dot{x}}_j\right) \) represent x i = x j and \( {\dot{x}}_i={\dot{x}}_j \).
-
2.
According to the overlapping property of the phase points, the phase points of the nonlinear periodic system in the rth Poincaré section should satisfy the following condition:
-
3.
If the phase point in arbitrary Poincaré sections cannot satisfy Eq. (1.16), the phase points are nonoverlapping.
Applying Eq. (1.16), the total number ζ(k) of the kth overlapping phase pion in the rth Poincaré section can be expressed as follows:
where ζ r(k) is applied to calculate the number of all phase points overlapping to the kth phase point. Q and P are step functions as follows:
Considering Eq. (1.17), after the total number k of the overlapping phase points is determined, the number of the jth visible point corresponding to overlapping point can be calculated. Assign N r as overlapping points in the rth Poincaré section; thus, N r can be expressed by:
in which ∏ is the symbol for multiplication and P(⋅) is the step function as defined in Eq. (1.19). This equation ensures that the duplicate included in the calculations for N r or missing in any overlapping point is prevented. If the response of a dynamic system is completely periodic, all the points in the Poincaré map must be overlapping, and the corresponding N r can be simply expressed in the following form:
For periodicity of the nonlinear dynamic system, N r represents the overlapping phase points in the rth Poincaré section. Therefore, the total number of overlapping points and phase points in n-dimensional space can be independently denoted by:
where S r is the number of phase points in the rth Poincaré section. Therefore, the periodicity ratio of the nonlinear nonautonomous system with n-dimensional space can be denoted by:
It can be known that the number of the overlapping points is less than or equal to the all phase points, i.e., 0 ≤ S ≤ S a; in this case, 0 ≤ γ ≤ 1. If the dynamic responses of the nonlinear system are periodic, thus, all the phase points in the Poincaré section must be overlapping, and periodicity ratio γ is equal to 1. If the dynamic responses of the nonlinear system are chaotic, thus, all the phase points in the Poincaré section must be nonoverlapping, and periodicity ratio γ is equal to zero. Through the definition for the periodicity ratio γ of the nonlinear dynamic system, it is easy to find that periodicity ratio γ can describe the periodicity of the nonlinear dynamic system.
2.4 The Periodicity Ratio of Autonomous Systems
Consider the following second order of the n-dimensional autonomous system [32]:
As the system is an autonomous system without external excitation, the phase points in the Poincaré section cannot be determined by Eq. (1.12). For the n-dimensional nonlinear autonomous system, no matter how long the vibration of the system is sustained, only j finite phase points appeared in Poincaré section x r − 1 − x r(r = 2, 3, …, n). Therefore, the periodicity of the nonlinear system can be described by n–1 Poincaré sections. If there are infinite phase points in the n–1 Poincaré sections, the nonlinear dynamic system is nonperiodic.
If the vibration behavior of the autonomous system is periodic, period T 1 of x 1 can be estimated with the maximum method, as numerical solution of x 1 is a series of points related to time, i.e.,x 1(τ) = x 1(t τ), τ = 1, 2, 3…, ∞. Thus, the search procedure can be employed to determine the maximum value of x 1. If x 1(τ) satisfy the following condition:
thus x 1(τ) is the maximum point of x 1, and the point of x 2 corresponding to x 1(τ) in this time is x 2(τ). Thus, the phase point of the first Poincaré section is expressed by (x 1(τ), x 2(τ)). The amount of the overlapping phase points in the first Poincaré section is written by:
in which x 1(τ), kl = |x 1(τ), k − x 1(τ), l|. Therefore, the period ratio can be determined through the phase point in the first Poincaré section:
If γ 1 = 1, the period T of the system can be confirmed as the following:
-
1.
Assume that the number of the visible phase points in the first Poincaré section is j. Choosing the kth visible point of j, the number of the overlapping points is q, and so the span of average time between two arbitrary adjacent points can be expressed as:
where t k, q represents the time of the qth overlapping points in the kth visible points and t k, 1 represents the time of the qth overlapping points in the first visible points. If all the overlapping points are periodic, parameter η is equivalent to the vibration period of the dynamic system.
-
2.
To improve the accuracy and reliability for identifying the periodicity of the dynamic system, identification parameter ρ is defined as:
From the equation above, it follows that when the identifying parameter ρ = 0, the vibration behavior of the dynamic system is periodic. In this case, the period T 1 of the system can be expressed by:
Therefore, the number of overlapping points in the rth Poincaré section can be determined by:
where k and i are integers, k ∈ [1, j], i ∈ [1, m]. Equation (1.32) represents the displacement difference between phase points i and k. m is the number of the phase points in an arbitrary Poincaré sections. In this case, the total number of the phase points for the n-dimensional system can be denoted by:
According to the definition above, the following conclusions can be stressed:
-
1.
The so-called overlapping phase points represent x i = x j and x i + 1 = x j + 1.
-
2.
According to the characteristics of the overlapping points, the phase points of the periodic system satisfy the following condition:
-
3.
If Eq. (1.34) is not satisfied, these phase points cannot be overlapping.
Employing Eq. (1.34), the amount ζ(k) of the phase points overlapping with the kth phase point can be determined with:
According to Eq. (1.35), the overlapping points in the rth Poincaré sections can be defined by:
where ∏ is multiplication and P(⋅) is step function defined previously. If the responses of the nonlinear dynamic system are periodic, N r can be simply expressed by:
Therefore, the amount of the overlapping point and all the points in the Poincaré section can be represented by:
where S r represents the amount of the phase points in the rth Poincaré section. Therefore, the periodicity ratio of the n-dimensional nonlinear autonomous system is written by:
3 Analytical and Numerical Solutions of Stiffness Coupling Systems
To explore the PL method for solving the linear stiffness coupling system, consider the following research subjects: (1) stiffness coupling system, (2) stiffness and damping coupling system, and (3) stiffness and damping coupling system encountered with external excitation.
3.1 Stiffness Coupling System
A simple stiffness coupling system (SCS) is firstly shown in Fig. 1.1, where m n(n = 1, 2) is the mass of the vibrator, k n(n = 1, 2) represents the stiffness coefficient of the spring, and x n(n = 1, 2) denotes the displacement response of the vibrator. By applying an initial velocity and initial displacement to the vibrator, the response of the vibrator changes with time.
The stiffness coupling system
According to the physical model, the following differential equation can be established:
The simplified form of Eq. (1.41) can be expressed as:
where \( {\omega}_{1,1}=\sqrt{k_1/{m}_1},{\omega}_{1,2}=\sqrt{k_1/{m}_2},{\omega}_{2,2}=\sqrt{k_2/{m}_2} \). The initial value of the system can be assumed by:
Subsequently, the piecewise constant method should be employed to rearrange the continuous Eq. (1.42) as piecewise constant system. Replace terms x 1(t) and x 2(t) with piecewise constant functions \( {x}_{1,i}\left(\frac{i}{N}\right) \) and \( {x}_{2,i}\left(\frac{i}{N}\right) \) at arbitrary intervals of i/N ≤ t < (i + 1)/N (i = [Nt]), and it can be expressed as:
In this case, the initial conditions in Eq. (1.43) can be transformed into the following form:
It can be found from Eq. (1.44) that the piecewise style is coupled with respect to x 1, i and x 2, i. Therefore, the Laplace transformation can be used to separate the coupling variables, and the plural form of Eq. (1.44) in the interval i/N ≤ t < (i + 1)/N is calculated as:
Then, X 1, i(s) and X 2, i(s) can be expressed as:
In this situation, X 1, i(s) and X 2, i(s) are the plural form of x 1, i(t) and x 2, i(t) in interval i/N ≤ t < (i + 1)/N, respectively. Through using the reverse Laplace transformation, the expressions of x 1, i(t) and x 2, i(t) can be obtained by the replacement of i with [Nt]:
where:
-
\( {\displaystyle \begin{array}{c}{\mathbf{A}}_1=\left[1-\frac{1}{2}{\omega}_{1,1}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,t-\frac{\left[ Nt\right]}{N},\frac{1}{2}{\omega}_{1,1}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,0\right],\\ {}{\mathbf{A}}_2=\left[\frac{1}{2}{\omega}_{1,2}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,0,1-\frac{1}{2}{\omega}_{1,2}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2-\frac{1}{2}{\omega}_{2,2}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,t-\frac{\left[ Nt\right]}{N}\right],\end{array}} \)
-
v i = [d 1, i, v 1, i, d 2, i, v 2, i]T.
Therefore, the velocities \( {x}_{1,i}^{\prime }(t) \) and \( {x}_{2,i}^{\prime }(t) \) should be rewritten as follows:
As mentioned previously, the displacements (x 1, i(t), x 2, i(t)) and the velocities (\( {x}_{1,i}^{\prime }(t),{x}_{2,i}^{\prime }(t) \)) are continuous in t ∈ [0, +∞), which is physically implied that there is no jump (break) or discontinuity in the displacement and velocity over t ∈ [0, +∞). Thus, the displacement and velocity in two adjacent points must satisfy the following continuity condition:
According to the continuity condition in Eq. (1.53), the relation of displacement and velocity between the two adjacent truncation points can be represented as:
where v i = [d 1, i, v 1, i, d 2, i, v 2, i]T, v i − 1 = [d 1, i − 1, v 1, i − 1, d 2, i − 1, v 2, i − 1]T, p = [p ij]4 × 4(i = 1, …, 4, j = 1, …, 4), and the elements of the matrix p are shown as follows:
In light of Eq. (1.54), v i can be expressed via initial condition v 0 with iterative computations of i times, i.e.:
where v 0 = [d 1, 0, v 1, 0, d 2, 0, v 2, 0]T.
When the initial condition v 0 is determined, the displacement and velocity of the system at any time can be calculated by utilizing Eq. (1.55). The semi-analytical solution of the system in ith interval can be rewritten as the style of piecewise constant, i.e.:
The calculation program can be compiled by using the above expressions. The partial results of solving SCS for each method are obtained, as shown in Table 1.1.
With Table 1.1, take the results from RK4 with step 0.001 s as accurate values. By comparing the calculation results of each method with same step (0.01 s), the maximum relative errors of each method can be seen: Euler method, 15.28%; trapezoidal method, 9.54%; Ode45, 4.21%; RK4, 6.15%; and PL, 1.54%. Therefore, the most accurate method is the PL method, the second is ode45, the third is RK4, the fourth is the trapezoidal method, and the last is the Euler method. Figure 1.2 is the displacement responses of SCS. It also follows that the accuracy of numerical results calculated by the RK4 method is rougher than PL within time step 0.01 s; however, the PL solutions within time step 0.01 s are consistent with RK4 within time step 0.001 s. To evaluate the computational efficiency of the PL method, the CPU time for solving SCS with PL and RK4 methods in this same time domain is considered. As shown in Table 1.2, the CPU time spent by the PL method is approximately half of the RK4 method in time step 0.01 s, which reveals that the PL method is more efficient than RK4 in numerical calculation of SCS. Obviously, the same kind of computation method with short time step will take more time than long time step, but reliability result can be obtained with short time step.
Displacement response of SCS (ω 1, 1 = 22.361, ω 1, 2 = 20, ω 2, 2 = 17.321, \( {x}_1(0)=0.01,{x}_1^{\prime }(0)=0.1, \) x 2(0) = 0.02, \( {x}_2^{\prime }(0)=0.2. \))
3.2 Stiffness and Damping Coupling System
In actual engineering, damping usually existed in coupling dynamic system. Therefore, a dynamic system coupled with the terms of stiffness and damping (SDCS) is considered, as shown in Fig. 1.3,
The stiffness and damping coupling system
where m n(n = 1, 2) is the mass of the vibrator, k n(n = 1, 2) represents the stiffness coefficient of the spring, c n(n = 1, 2) is the damping coefficient of the damper, and x n(n = 1, 2) denotes the displacement response of the vibrator. Likewise, give the vibrator an initial velocity and initial displacement, and the analytical expression of the response of the vibrator can be obtained by the PL method.
Through this model, the following equation can be obtained:
The simplified form of Eq. (1.58) can be expressed as:
where \( {\omega}_{1,1}=\sqrt{k_1/{m}_1},{\omega}_{1,2}=\sqrt{k_1/{m}_2},{\omega}_{2,2}=\sqrt{k_2/{m}_2},{\xi}_{1,1}={c}_1/{m}_1,{\xi}_{1,2}={c}_1/{m}_2,{\xi}_{2,2}={c}_2/{m}_2. \)
In arbitrary interval i/N ≤ t < (i + 1)/N, Eq. (1.59) can be rearranged as a style of piecewise constant. Replace terms x 1(t), \( {x}_1^{\prime }(t) \), x 2(t), and \( {x}_2^{\prime }(t) \) with piecewise constant functions \( {x}_{1,i}\left(\frac{i}{N}\right) \), \( {x}_{1,i}^{\prime}\left(\frac{i}{N}\right) \), \( {x}_{2,i}\left(\frac{i}{N}\right) \), and \( {x}_{2,i}^{\prime}\left(\frac{i}{N}\right) \), and so Eq. (1.59) can expressed as:
The Laplace transformation can be used to separate the coupling variables, and the transformed plural form of Eq. (1.60) in the interval i/N ≤ t < (i + 1)/N is calculated as:
Then, X 1, i(s) and X 2, i(s) can be expressed as:
Through using the inverse Laplace transformation, the expressions of x 1, i(t) and x 2, i(t) can be obtained by the replacement of i with [Nt]:
where:
-
\( {\displaystyle \begin{array}{l}{\mathbf{v}}_i={\left[{d}_{1,i},{v}_{1,i},{d}_{2,i},{v}_{2,i}\right]}^T,\\ {}{\mathbf{B}}_1=\left[1-\frac{1}{2}{\omega}_{1,1}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,t-\frac{\left[ Nt\right]}{N}-\frac{1}{2}{\xi}_{1,1}{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,\frac{1}{2}{\omega}_{1,1}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,\frac{1}{2}{\xi}_{1,1}{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2\right],\\ {}{\mathbf{B}}_2=\left[\frac{1}{2}{\omega}_{1,2}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,\frac{1}{2}{\xi}_{1,2}{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2,1-\frac{1}{2}{\omega}_{1,2}^2{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2-\frac{1}{2}{\omega}_{2,2}^2{\left(t{-}\frac{\left[ Nt\right]}{N}\right)}^2,\left(t{-}\frac{\left[ Nt\right]}{N}\right){-}\frac{1}{2}{\xi}_{1,2}{\left(t{-}\frac{\left[ Nt\right]}{N}\right)}^2\right.\\\left.-\frac{1}{2}{\xi}_{2,2}{\left(t-\frac{\left[ Nt\right]}{N}\right)}^2\right].\end{array}} \)
Therefore, the velocities \( {x}_{1,i}^{\prime }(t) \) and \( {x}_{2,i}^{\prime }(t) \) should be rewritten as follows:
In the light of the continuity condition in Eq. (1.53), the relation of displacement and velocity between the two adjacent truncation points can be represented as:
where v i − 1 = [d 1, i − 1, v 1, i − 1, d 2, i − 1, v 2, i − 1]T, q = [q ij]4 × 4 (i = 1, …, 4, j = 1, …, 4), and the elements in matrix q are given by:
According to Eq. (1.68), v i can be expressed via initial condition v 0 with iterative computations of i times, i.e.:
where v 0 = [d 1, 0, v 1, 0, d 2, 0, v 2, 0]T.
When initial condition v 0 is determined, the displacement and velocity of the system at any time can be calculated by utilizing Eq. (1.69). The semi-analytical solution of the system in ith interval can be rewritten as the style of piecewise constant, i.e.:
The partial numerical results of solving SDCS for each method are shown in Table 1.3. Similarly, the maximum relative errors of each method can be seen: Euler method, 23.12%; trapezoidal method, 11.97%; Ode45, 6.78%; RK4, 10.18%; and PL, 1.52%. Likewise, the most accurate method is the PL method. As can be seen from the maximum relative error, compared to solving SCS, the relative error of each method has increased. This is due to the added damping term of the SDCS, which makes the calculation more complicated.
The displacement responses of SDCS are shown in Fig. 1.4, and it can be seen that the accuracy of numerical results calculated by RK4 is rougher than PL within time step 0.01 s; however, on account of continuity of the PL method, the numerical results within time step 0.01 s are coincident with the RK4 method within time step 0.001 s. The value of amplitude of the SDCS is gradually damped with the increase of time t. In order to evaluate the computational efficiency of the PL method, the CPU time for solving SDCS with PL and RK4 methods is considered. As shown in Table 1.4, the CPU time taken by the PL method is less than RK within the same time steps, which illustrates that PL calculating SDCS is faster than RK4 method. Comparing with Table 1.2, because of the existence of damping term, the CPU time taken by SDCS is longer than SCS.
Displacement response of SDCS (ω 1, 1 = 22.361, ω 1, 2 = 20, ω 2, 2 = 17.321, ξ 1, 1 = 10, ξ 1, 2 = 5, ξ 2, 2 = 2, x 1(0) = 0.01, \( {x}_1^{\prime }(0)=0.1, \) x 2(0) = 0.02, \( {x}_2^{\prime }(0)=0.2. \))
3.3 Stiffness and Damping Coupling System with External Excitation
In practical engineering, the stiffness and damping coupling system is encountered with external excitation. Consider a cosine force related to time t acted in the system (SDCSF), i.e. (Fig. 1.5):
The stiffness and damping coupling system with external excitation
where m n(n = 1, 2) is the mass of the vibrator, k n(n = 1, 2) represents the stiffness coefficient of the spring, c n(n = 1, 2) is the damping coefficient of the damper, F is the magnitude of the cosine force, ω represents the frequency of the cosine force, and x n(n = 1, 2) denotes the displacement response of the vibrator. When the external excitation acting on the vibrator changes periodically with time, the vibrator will respond accordingly.
According to the physical model, the following equation is established:
The simplified form of Eq. (1.72) can be expressed as:
where \( a=F/{m}_1,{\omega}_{1,1}=\sqrt{k_1/{m}_1},{\omega}_{1,2}=\sqrt{k_1/{m}_2},{\omega}_{2,2}=\sqrt{k_2/{m}_2},{\xi}_{1,1}={c}_1/{m}_1,{\xi}_{1,2}={c}_1/{m}_2,{\xi}_{2,2}={c}_2/{m}_2 \).
At time interval i/N ≤ t < (i + 1)/N, the piecewise constant method is employed to rearrange Eq. (1.73) as the style of piecewise constant. Replace terms \( {x}_1^{\prime }(t) \), \( {x}_2^{\prime }(t) \), and a cos (ωt) with the piecewise constant functions \( {x}_{1,i}^{\prime}\left(\frac{i}{N}\right) \), \( {x}_{2,i}^{\prime}\left(\frac{i}{N}\right) \), and \( a\;\cos \left(\omega \frac{i}{N}\right) \), respectively. Equation (1.73) can be expressed as:
The Laplace transformation can be used to separate the coupling variables, and the plural form of Eq. (1.74) in the interval i/N ≤ t < (i + 1)/N is calculated as:
Then, X 1, i(s) and X 2, i(s) can be decoupled and expressed as:
where \( Q={s}^2+{\omega}_{1,1}^2,W={s}^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2 \).
It is difficult to transform plural solution above into time-domain solution with the general inverse Laplace transformation. However, through Theorem 1.5 in Eq. (1.10), the expressions of x 1, i(t) and x 2, i(t) can be obtained by the replacement of i with [Nt]:
where \( {\mathbf{v}}_i={\left[{d}_{1,i},{v}_{1,i},{d}_{2,i},{v}_{2,i}\right]}^T,L={\omega}_{1,1}^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2, \)
-
\( {\mathbf{C}}_1={\left[\begin{array}{c}\sum \limits_{k=1}^4\frac{s_k^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2}{4{s}_k^2+2L}{e}^{s_k\left(t-\frac{i}{N}\right)}\\ {}\sum \limits_{k=1}^4\frac{s_k^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2}{4{s}_k^3+2{s}_kL}{e}^{s_k\left(t-\frac{i}{N}\right)}+\sum \limits_{k=1}^5\frac{\xi_{1,2}{\omega}_{1,1}^2-{\xi}_{1,1}\left({s}_k^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2\right)}{5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2}{e}^{s_k\left(t-\frac{i}{N}\right)}\\ {}\sum \limits_{k=1}^4\frac{\omega_{1,1}^2}{4{s}_k^2+2L}{e}^{s_k\left(t-\frac{i}{N}\right)}\\ {}\sum \limits_{k=1}^4\frac{\omega_{1,1}^2}{4{s}_k^3+2{s}_kL}{e}^{s_k\left(t-\frac{i}{N}\right)}+\sum \limits_{k=1}^5\frac{-{\xi}_{2,2}{\omega}_{1,1}^2-{\xi}_{1,2}{\omega}_{1,1}^2+{\xi}_{1,1}\left({s}_k^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2\right)}{5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2}{e}^{s_k\left(t-\frac{i}{N}\right)}\end{array}\right]}^{\mathrm{T}}, \)
-
\(\begin{array}{llll} {\mathbf{C}}_2={\left[\begin{array}{c}\sum \limits_{k=1}^4\frac{\omega_{1,2}^2}{2{s}_k^2+L}{e}^{s_k\left(t-\frac{i}{N}\right)}\\ {}\sum \limits_{k=5}^7\frac{\xi_{1,2}}{3{s}_k^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2}{e}^{s_k\left(t-\frac{i}{N}\right)}+\sum \limits_{k=1}^4\frac{\omega_{1,2}^2}{4{s}_k^3+2{s}_kL}{e}^{s_k\left(t-\frac{i}{N}\right)}-\sum \limits_{k=1}^5\frac{\xi_{1,1}{\omega}_{1,2}^2}{5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2}{e}^{s_k\left(t-\frac{i}{N}\right)}\\{}+\sum \limits_{k=1}^7\frac{\xi_{1,2}{\omega}_{1,1}^2{\omega}_{1,2}^2}{\begin{array}{c}7{s}_k^6+5{s}_k^4\left({\omega}_{1,1}^2+2{\omega}_{1,2}^2+2{\omega}_{2,2}^2\right)+3{s}_k^2\Big(2{\omega}_{1,1}^2{\omega}_{2,2}^2+{\omega}_{1,2}^4+{\omega}_{1,1}^2{\omega}_{1,2}^2\\ {}+2{\omega}_{1,2}^2{\omega}_{2,2}^2+{\omega}_{2,2}^4\Big)+\left({\omega}_{1,1}^2{\omega}_{1,2}^2{\omega}_{2,2}^2+{\omega}_{1,1}^2{\omega}_{2,2}^4\right)\end{array}}{e}^{s_k\left(t-\frac{i}{N}\right)}\\ {}\sum \limits_{k=5}^7\frac{1}{2}{e}^{s_k\left(t-\frac{i}{N}\right)}+\sum \limits_{k=1}^4\frac{\omega_{1,2}^2}{\begin{array}{c}6{s}_k^4+4{s}_k^2\left({\omega}_{1,1}^2+2{\omega}_{1,2}^2+2{\omega}_{2,2}^2\right)\\ {}+2\left(2{\omega}_{1,1}^2{\omega}_{2,2}^2+{\omega}_{1,2}^4+{\omega}_{1,1}^2{\omega}_{1,2}^2+2{\omega}_{1,2}^2{\omega}_{2,2}^2+{\omega}_{2,2}^4\right)\end{array}}{e}^{s_k\left(t-\frac{i}{N}\right)}\\{}+\sum \limits_{k=6}^7\frac{\omega_{1,1}^2{\omega}_{1,2}^2}{\begin{array}{c}6{s}_k^4+4{s}_k^2\left({\omega}_{1,1}^2+2{\omega}_{1,2}^2+2{\omega}_{2,2}^2\right)\\ {}+2\left(2{\omega}_{1,1}^2{\omega}_{2,2}^2+{\omega}_{1,2}^4+{\omega}_{1,1}^2{\omega}_{1,2}^2+2{\omega}_{1,2}^2{\omega}_{2,2}^2+{\omega}_{2,2}^4\right)\end{array}}{e}^{s_k\left(t-\frac{i}{N}\right)}\\ {}\begin{array}{l}\sum \limits_{k=5}^7\frac{1}{2{s}_k}{e}^{s_k\left(t-\frac{i}{N}\right)}-\sum \limits_{k=5}^7\frac{\xi_{1,2}+{\xi}_{2,2}}{3{s}_k^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2}{e}^{s_k\left(t-\frac{i}{N}\right)}+\sum \limits_{k=1}^5\frac{\xi_{1,1}{\omega}_{1,2}^2}{5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2}{e}^{s_k\left(t-\frac{i}{N}\right)}\\{}+\sum \limits_{k=1}^5\frac{\xi_{1,1}{\omega}_{1,2}^2}{\begin{array}{c}6{s}_k^5+4{s}_k^3\left({\omega}_{1,1}^2+2{\omega}_{1,2}^2+2{\omega}_{2,2}^2\right)\\ {}+2{s}_k\left(2{\omega}_{1,1}^2{\omega}_{2,2}^2+{\omega}_{1,2}^4+{\omega}_{1,1}^2{\omega}_{1,2}^2+2{\omega}_{1,2}^2{\omega}_{2,2}^2+{\omega}_{2,2}^4\right)\end{array}}{e}^{s_k\left(t-\frac{i}{N}\right)}\\ {}+\sum \limits_{k=6}^7\frac{\omega_{1,1}^2{\omega}_{1,2}^2}{\begin{array}{c}6{s}_k^5+4{s}_k^3\left({\omega}_{1,1}^2+2{\omega}_{1,2}^2+2{\omega}_{2,2}^2\right)\\ {}+2{s}_k\left(2{\omega}_{1,1}^2{\omega}_{2,2}^2+{\omega}_{1,2}^4+{\omega}_{1,1}^2{\omega}_{1,2}^2+2{\omega}_{1,2}^2{\omega}_{2,2}^2+{\omega}_{2,2}^4\right)\end{array}}{e}^{s_k\left(t-\frac{i}{N}\right)}\\{}-\sum \limits_{k=1}^7\frac{\xi_{1,2}{\omega}_{1,1}^2{\omega}_{1,2}^2+{\xi}_{2,2}{\omega}_{1,1}^2{\omega}_{1,2}^2}{\begin{array}{c}7{s}_k^6+5{s}_k^4\left({\omega}_{1,1}^2+2{\omega}_{1,2}^2+2{\omega}_{2,2}^2\right)+3{s}_k^2\Big(2{\omega}_{1,1}^2{\omega}_{2,2}^2+{\omega}_{1,2}^4+{\omega}_{1,1}^2{\omega}_{1,2}^2\\ {}+2{\omega}_{1,2}^2{\omega}_{2,2}^2+{\omega}_{2,2}^4\Big)+\left({\omega}_{1,1}^2{\omega}_{1,2}^2{\omega}_{2,2}^2+{\omega}_{1,1}^2{\omega}_{2,2}^4\right)\end{array}}{e}^{s_k\left(t-\frac{i}{N}\right)}\end{array}\end{array}\right]}^{\mathrm{T}}. \end{array}\)
Therefore, the velocities \( {x}_{1,i}^{\prime }(t) \) and \( {x}_{2,i}^{\prime }(t) \) should be rewritten as follows:
The first-order zero in expression \( 5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2 \) are shown below:
where \( M={\omega}_{1,1}^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2+2{\omega}_{1,1}^2{\omega}_{1,2}^2+2{\omega}_{1,2}^2{\omega}_{2,2}^2-2{\omega}_{1,1}^2{\omega}_{2,2}^2 \).
According to the continuity condition in Eq. (1.53), the relation of displacement and velocity between the two adjacent truncation points can be represented as:
where: \( \mathbf{g}={\left[\sum \limits_{k=1}^5\frac{s_k^2+{\omega}_{1,2}^2+{\omega}_{2,2}^2}{5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2}{e}^{s_kt},\right.\\{}\left.\sum \limits_{k=1}^5\frac{s_k^3+{\omega}_{1,2}^2{s}_k+{\omega}_{2,2}^2{s}_k}{5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2}{e}^{s_kt},\sum \limits_{k=1}^5\frac{\omega_{1,2}^2}{5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2}{e}^{s_kt},\sum \limits_{k=1}^5\frac{\omega_{1,2}^2{s}_k}{5{s}_k^4+3{s}_k^2L+{\omega}_{1,1}^2{\omega}_{2,2}^2}{e}^{s_kt}\right]}^{\mathrm{T}},\\{\mathbf{v}}_i={\left[{d}_{1,i},{v}_{1,i},{d}_{2,i},{v}_{2,i}\right]}^T, \) v i − 1 {=} [d 1, i − 1, v 1, i − 1, d 2, i − 1, v 2, i − 1]T, γ = [γ ij]4 × 4 (i = 1, …, 4, j = 1, …, 4). The elements of matrix γ are shown as follows:
According to Eq. (1.82), v i can be expressed via initial condition v 0 with iterative computations of i times, i.e.:
When the initial condition v 0 is determined, the displacement and velocity of the system at any time can be calculated by using Eq. (1.83). The approximate solution of the system in ith interval can be rewritten as the style of piecewise constant, i.e.:
The partial numerical results of solving SDCSF for each method are as shown in Table 1.5. The maximum relative errors of each method can be found: Euler method, 38.47%; trapezoidal method, 18.21%; Ode45, 8.75%; RK4, 16.44%; and PL, 3.41%. The PL method still has the highest accuracy. Compared to solving SDCS, the relative error of each method is increasing. This is due to the added external excitation related to time in SDCSF, which makes the calculation process more complicated and leads to a reduction in accuracy.
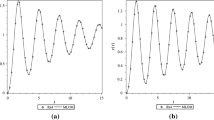
Figure 1.6 shows the displacement responses of the SDCSF. It follows that the accuracy of PL results is more accurate than RK4 within same time step; but PL solutions with time step 0.01 s are more approximately approached to RK4 with time step 0.001 s. As shown in Table 1.6, computational speed of the PL method is faster than RK4 when calculating SDCSF, and the CPU time required in solving the SDCSF is longer than that of SCS and SDCS in time step 0.01 s because of the presence of damping and external excitation.
Displacement response of SDCSF (ω 1, 1 = 15.811, ω 1, 2 = 17.321, ω 2, 2 = 20, ξ 1, 1 = 30, ξ 1, 2 = 20, ξ 2, 2 = 10, a = 50, ω = 160, x 1(0) = 0.01, \( {x}_1^{\prime }(0)=0.1, \) x 2(0) = 0.02, \( {x}_2^{\prime }(0)=0.2. \))
3.4 Convergence Analysis of the PL Method
The convergence of the PL method in calculating the above three systems is discussed, as illustrated in Figs. 1.7, 1.8 and 1.9. It can be seen that when N = 1000, the numerical results obtained by the PL method are deviated from the accurate value (AV). When N = 2000, the deviation of the numerical solution is reduced. Finally, when N = 20,000, the curve obtained by the PL method is coincident with that of AV. It is indicated that the numerical value obtained by the PL method is approached to the AV as the value of N is gradually increased. Obviously, parameter N is an important factor to control the precision of numerical results and speed of convergence. Therefore, when the value of N is increased, the calculation can converge faster and the precision of the PL method is improved. In order to obtain the high-precision results and faster convergence for solving the coupling dynamic systems, it is better to select a sufficiently large value of N.
Convergence of the solution of SCS by the PL method (ω 1, 1 = 22.361, ω 1, 2 = 20, ω 2, 2 = 17.321, x 1(0) = 0.01, \( {x}_1^{\prime }(0)=0.1, \) x 2(0) = 0.02, \( {x}_2^{\prime }(0)=0.2. \))
Convergence of the solution of SCDS by the PL method (ω 1, 1 = 22.361, ω 1, 2 = 20, ω 2, 2 = 17.321, ξ 1, 1 = 10, ξ 1, 2 = 5, ξ 2, 2 = 2, x 1(0) = 0.01, \( {x}_1^{\prime }(0)=0.1, \) x 2(0) = 0.02, \( {x}_2^{\prime }(0)=0.2. \))
Convergence of the solution of SCDSF by the PL method (ω 1, 1 = 15.811, ω 1, 2 = 17.321, ω 2, 2 = 20, ξ 1, 1 = 30, ξ 1, 2 = 20, ξ 2, 2 = 10, a = 50, ω = 160, x 1(0) = 0.01, \( {x}_1^{\prime }(0)=0.1, \) x 2(0) = 0.02, \( {x}_2^{\prime }(0)=0.2. \))
The above are the general processes of using PL method to solve the stiffness coupling systems, and some important conclusions should be stressed as the following:
-
1.
When solving the coupling system by using the traditional RK method, high order differential equations of dynamic system are usually descended into multiple first-order differential equations. In this way, crucial dynamic property of the original system may be neglected or simplified, which leads to the computational error when searching solution for dynamic model encountered in actual engineering. However, solving differential equations above with the PL method, the semi-analytical solution of systems is obtained directly through the derivation of equation. Therefore, the physical properties of systems are well preserved. In addition, the whole-time interval is divided into many tiny intervals by the PL method, and the solution is continuous on each interval. In this case, the accuracy of numerical solution of the PL method is better than the RK method, which is demonstrated by numerical analysis.
-
2.
The computed efficiency of the PL and RK methods are compared through statistics of operation time of CPU during computing process. The CPU time taken by the PL method is less than the RK method in the same time steps, which indicates that the PL method is more efficient than the RK method. The main reason is that value continuity of two adjacent truncation points is maintained by using the PL method, which simplifies the solving process and saves the calculated time, while the RK method combines iterative and averaged slope to search solutions, which makes the solution process more complicated.
-
3.
The numerical results of the PL method reflect the essence of dynamic system, since the PL method keeps the physical characteristics of dynamic system. The precision of the solution obtained by the PL method is related to the value of N. This article is an exploratory study for implementation of the PL method in coupling systems. Therefore, the classic two-degree freedom systems are considered, and whether the PL method is suitable to solve problems of multi-degree freedom system should be further verified in our next work.
4 Analytical and Numerical Solutions of Inertial Coupling Systems
There is no direct solution for the dynamic equations, which are fundamentally mutual coupling with inertia terms. Development of solutions for such equation is therefore unique in comparing with conventional dynamic equation. For purpose of simplification and demonstration of PL method, the solutions for the following equation of inertial coupling dynamic systems are primarily considered.
4.1 Undamped Inertial Coupling System
Consider an undamped inertial coupling equation such as:
where m i(i = 1, 2, 3, 4) is constant related to masses. x and y represent the displacement response in x and y directions, respectively. k x and k y represent the spring stiffness in x and y directions in the vibrating system, respectively.
The simplification style of the equation above can be expressed by:
where \( {\omega}_x=\sqrt{k_x/{m}_1},{\omega}_y=\sqrt{k_y/{m}_3},m={m}_2/{m}_1,n={m}_4/{m}_3 \). The initial condition for the system may be assumed as follows:
Then, the piecewise constant argument is applied to transform the continuous Eq. (1.87) into many piecewise constant systems. The system corresponding to that governed by Eq. (1.87) can be constructed by replacing the terms x(t) and y(t) with the piecewise constant function over an arbitrary time interval i/N ≤ t < (i + 1)/N (i = [Nt]/N). The corresponding equation of motion is expressible in the following form:
In this case, in arbitrary time interval i/N ≤ t < (i + 1)/N, the local initial conditions can be considered as:
With the consideration of the Laplace transformation, Eq. (1.89) in interval i/N ≤ t < (i + 1)/N can be expressed by plural form:
Then, X i and Y i can be solved by:
X i(s) and Y i(s) are pluralities corresponding to x i(t) and y i(t) in interval i/N ≤ t < (i + 1)/N, respectively. Based on inverse Laplace transformation and initial condition in Eq. (1.90), x i(t) and y i(t) is expressible in arbitrary time interval i/N ≤ t < (i + 1)/N with the substitution of i by [Nt]:
where:
Consequently, the velocities of the system in x- and y- directions can be expressed by:
As a rotational hypothesis of the actual response of a piecewise constant system in practice, there should be no jump or discontinuity of the displacements x i(t) and y i(t) and velocities \( {\dot{x}}_i(t) \) and \( {\dot{y}}_i(t) \) in the time of t ∈ [0, +∞). This implies the kinematic parameters x i(t), \( {\dot{x}}_i(t) \), y i(t), and \( {\dot{y}}_i(t) \) are continuous within time t. The following condition of continuity should therefore be satisfied for the solutions of piecewise constant system over all of time intervals, i.e.:
With the condition of continuity, a recursive relation is obtained with the consideration of Eqs. (1.94), (1.95), (1.96) and (1.97), such that:
where α = [α ij]4 × 4 (i = 1, …, 4, j = 1, …, 4), \( {\mathbf{v}}_{i-1}{=}{\left[\begin{array}{cccc}{d}_{i-1}& {v}_{i-1}& {\underset{\sim }{d}}_{i-1}& {\underset{\sim }{v}}_{i-1}\end{array}\right]}^{\mathrm{T}}. \) α is a fourth-order matrix, and the elements of the matrix are shown as the following:
Because of an iterative procedure, v i can be expressed by the initial displacements v 0 in the following form:
where \( {\mathbf{v}}_0={\left[\begin{array}{cccc}{d}_0& {v}_0& {\underset{\sim }{d}}_0& {\underset{\sim }{v}}_0\end{array}\right]}^{\mathrm{T}}. \)
One can see that the displacement and velocity of the system at any given point of time [Nt]/N can be calculated by using Eq. (1.100) on the condition that the initial values of displacement and velocity are known. Considering that ith time interval is arbitrarily chosen, the complete solution of the system is obtained by:
The calculation program can be compiled by using the above expressions. To express the difference of the RK4 method and the PL method for computing the solution of the dynamic system, the comparison of the two methods with different time step is treated under the same initial value. Figure 1.10 shows the difference of the computation results for the inertial coupling system with undamping term (ICSUT). By using longer time step (0.01 s) with the PL method, one can obtain the same accurate solution as classical fourth-order RK4 method with shorter time step (0.001 s). However, the numerical results of RK4 method within time step 0.01 s are less accurate than that of the PL method within time step 0.01 and that of the RK4 method within time step 0.001 s. This is mainly due to the cumulative error of iteration computation of the RK4 method in longer time step. Table 1.7 shows the computation values of the PL method and the RK4 method. It is indicated that the PL method is more accurate for solving the problem of dynamic system, because numerical solutions produced by the PL method are continuous everywhere in whole time history. Therefore, if a fixed accuracy of the numerical solution is required, the PL method with long time step can obtain the same or even more accuracy solution than the RK4 method. Table 1.8 shows the CPU time for solving ICSUT in the same time history. One can see that in the same time step, the PL method needs shorter CPU time to finish to the numerical computations than the RK4 method. This implies that the PL method is more efficient for computation of ICSUT than the RK4 method.
Comparison of the numerical results with the RK4 method and the PL method for Eq. (1.86) (x 0 = 0.1, \( {\dot{x}}_0=0.2, \) y 0 = 0, \( {\dot{y}}_0=0.1. \))
4.2 Damped Inertial Coupling System
In general, damping and resistance forces against motion may be existed in the inertia coupling system. For solving for the motion of a damped inertia coupling system, the dynamic equation in the following specific system is taken into consideration:
With simplification, the dynamic equation can be also rewritten as:
where \( {\omega}_x=\sqrt{k_x/{m}_1},{\omega}_y=\sqrt{k_y/{m}_3},m={m}_2/{m}_1,n={m}_4/{m}_3,{\xi}_x={f}_x/{m}_1,{\xi}_y={f}_y/{m}_3 \).
Then, the piecewise constant system corresponding to that governed by Eq. (1.104) can be constructed by replacing the terms \( \dot{x}(t) \) and \( \dot{y}(t) \) with piecewise constant function over an arbitrary time interval i/N ≤ t < (i + 1)/N. The corresponding equation of motion is expressible in the following form:
With the Laplace transformation, Eq. (1.105) can be also expressed as plural form:
Then, X i and Y i can be solved by:
Based on inverse Laplace transformation, x i(t) and y i(t) can be obtained in arbitrary time interval [Nt]/N ≤ t < ([Nt] + 1)/N:
with:
Then, the velocities of the system in x- and y- directions can be expressed by:
With the condition of continuity, the recursive relation is obtained by:
where β = [β ij]4 × 4 (i = 1, …, 4, j = 1, …, 4), and the elements of matrix β are shown as the following:
Because of the iterative procedure, \( {d}_i,{v}_i,{\underset{\sim }{d}}_i \) and \( {\underset{\sim }{v}}_i \) can be expressed by the initial displacements \( {d}_0,\kern0.5em {\underset{\sim }{d}}_0 \), and velocities \( {v}_0,{\underset{\sim }{v}}_0 \) in the following form:
The displacement and velocity of the system at any given point of time i/N(i = [Nt]) can be calculated by using Eq. (1.114). Considering that ith time interval is arbitrarily chosen, the complete solution is as follows:
For mastering the accuracy and efficiency of the PL method for computation of the inertial coupling system with damping term (ICSDT), the numerical results of displacements in x- and y- directions are shown in Fig. 1.11. Just like the numerical result of the ICSUT, the data points obtained by the PL method in time step 0.01 s are overlapped with that of the RK4 method in time step 0.001 s. On the contrary, one can see that the RK4 method in time step 0.01 s reduces the calculation accuracy of the ICSDT. Therefore, in the same time step, the numerical result of PL method for solving the ICSDT is more accurate than the RK4 method. The reason is that the solution of every piecewise system obtained with the PL method is continuous, unlike the RK4 method missing the physical characteristics of original system. In speaking of vibrating characteristics, the amplitude of the inertial coupling system is damping with time, and value of amplitudes will be stabilized at zero. Table 1.9 shows comparison of the numerical result for solving ICSDT with the two methods. One can see the numerical value with the PL method is approached to that of the RK4 method, although the time step of the former method is tenfold as the latter. Table 1.10 shows the CPU time for solving ICSDT in time history 50s. Comparing with Table 1.7, the CPU time of ICSDT needs longer than that of ICSUT as the existence of the damping terms. This implies that the PL method is more efficient for computation of dynamic systems than the ICSDT in the same time history.
Comparison of the numerical results with the RK4 method and the PL method for Eq. (1.103) ( ξ x = 1.36, ξ y = 1.52, x 0 = 0.05, \( {\dot{x}}_0=0.2, \) y 0 = 0.1, \( {\dot{y}}_0=0. \))
4.3 Forced and Damped Inertial Coupling System
In practical engineering, external forces always may be existed in the damped inertia coupling system. Suppose that the dynamic system is acted with a linear cosine force F cos ωt related to time t, therefore, the dynamic equation in the following specific system is undertaken:
Simplification of Eq. (1.117) can be written by:
where \( {\omega}_x=\sqrt{k_x/{m}_1},{\omega}_y=\sqrt{k_y/{m}_3},m={m}_2/{m}_1,n={m}_4/{m}_3,{\xi}_x={f}_x/{m}_1,\kern0.5em {\xi}_y={f}_y/{m}_3,A=F/{m}_1 \).
In this case, the piecewise constant system corresponding to that governed by Eq. (1.118) can be constructed by replacing damped terms \( \dot{x}(t) \) and \( \dot{y}(t) \) and external force A cos (ωt) with piecewise constant function over an arbitrary time interval i/N ≤ t < (i + 1)/N. The corresponding dynamics equation of the system is expressible in the following form:
With the Laplace transform, Eq. (1.119) can be also expressed as plural form:
Further separating variables, X i and Y i can be obtained by:
where \( \upsilon \left(\mathrm{s}\right)={s}^4-\sigma \left({\omega}_x^2+{\omega}_y^2\right){s}^2-{\sigma \omega}_x^2{\omega}_y^2,\kern0.6em \sigma ={\left( mn-1\right)}^{-1} \).
With the Theorem 1.5 in Eq. (1.10), substituting i with [Nt], displacement responses x i(t) and y i(t) in arbitrary time interval i/N ≤ t < (i + 1)/N can be expressed by:
with:
where s j and s k are zeros of function υ(s) shown as:
It should be noted that s j − s k = 1 in the whole process of the computations when j = k.
Then, the velocities of the system in x- and y- directions can be expressed by:
With the continuity condition, a recursive relation is obtained by combining Eqs. (1.123). (1.124), (1.125) and (1.126), such that:
where \( \mathbf{g}={\left[-\sum \limits_{i=1}^5\prod \limits_{j=1}^5\frac{\sigma {s}_i^2+{\sigma \omega}_y^2}{s_i-{s}_j}{e}^{\frac{s_i}{N}},-\sum \limits_{i=1}^5\prod \limits_{j=1}^5\frac{\sigma {s}_i^3+{\sigma \omega}_y^2{s}_i}{s_i-{s}_j}{e}^{\frac{s_i}{N}},-\sum \limits_{i=1}^4\prod \limits_{j=1}^4\frac{ns_i}{s_i-{s}_j}{e}^{\frac{s_i}{N}},\right.\\\left.-\sum \limits_{i=1}^4\prod \limits_{j=1}^4\frac{ns_i^2}{s_i-{s}_j}{e}^{\frac{s_i}{N}}\right]}^{\mathrm{T}} \), γ = [γ ij]4 × 4, and the elements of matrixes γ are shown as:
With the recursive relation in Eq. (1.127), the recursive relation with respect to initial conditions is obtained, such that:
The displacement responses of the system at any given point of time i/N can be calculated by using Eq. (1.128). Considering that ith time interval is arbitrarily chosen, thus, the complete solution is obtained by:
In the engineering application, the damping term and the external force term are considered. Finally, the numerical computation is implemented with the PL method and the RK4 method for computation of the inertial coupling system with damping and external force term (ICSDEFT). Figure 1.12 shows the displacement responses in x and y directions with the two method. It is also evident that the RK4 method for solving dynamic characteristics of the ICSDEFT is less accurate than the PL method in same time step 0.01 s. In summary, the solution process of RK4 method, employing the slope iteration related to an arithmetic mean value, damages the physical meaning contained in the original dynamic system and causes undesirable influence on the accuracy and reliability of numerical results. And the comparison of the numerical result for solving the ICSDEFT is shown in Table 1.11. In the speaking of computational efficiency, the computation time with the PL method is also shorter than the RK4 method in the ICSDEFT, as shown in Table 1.12. Because of the existence of the damping term and the external force term, the CPU time of the ICSDEFT needed is longer than that of the ICSUT and ICSDT in the same iterations.
Comparison of the numerical results with the RK4 method and the PL method for Eq. (1.117) ( ξ x = 1.36, ξ y = 1.52, A = 1.89, ω = 15, x 0 = 0.05, \( {\dot{x}}_0=0.2, \) y 0 = 0.1, \( {\dot{y}}_0=0. \))
4.4 Convergence Analysis of the PL Method
Taking undamped inertial coupling system in Eq. (1.86) as a sample, the convergence of the PL method is discussed. Starting with the initial state, Eq. (1.101) and Eq. (1.102) are used in a computer program to obtain solution in each interval. The numerical results obtained by the application equations are illustrated in Fig. 1.13. As shown in the figure, the error of the numerical results from the accurate value (AV) is already small as N is given a value of 10. The numerical results are getting closer and closer to the AV as the value of N increases. The parameter N obviously acts as a factor controlling the accuracy of the numerical solution, since it is directly related to the time interval i/N ≤ t ≤ (i + 1)/N. In order to have a numerical solution of high accuracy, one may choose a sufficiently large N.
Convergence of the solution of Eq. (1.59) (x 0 = 0.1, \( {\dot{x}}_0=0.2, \) y 0 = 0, \( {\dot{y}}_0=0.1. \))
With the finds for computations of the inertial coupling system, the following can be concluded:
-
1.
When applying the RK4 method to solve the inertial coupling system, the dynamic equations are primarily rewritten into the first-order differential equations, which leads to the loss of the essential characteristics of the dynamic system. In addition, the solution process of RK4 method, employing the slope iteration related to an arithmetic mean value, damages the physical meaning contained in the original dynamic system and causes undesirable influence on the accuracy and reliability of numerical results.
-
2.
The solutions of the PL method are directly obtained from the original dynamic system and continuous over the whole-time domain considered, which can obtain more accurate solution for solving the inertial coupling system than RK4 method in the fixed time step. And by using the PL method, the semi-analytical solutions of the system are determined, which is also verified with numerical computations.
-
3.
The PL method generates more accurate and reliable solutions in the comparison of RK4 method within shorter CPU time. The reason is that the solution of every piecewise system obtained with the PL method is continuous, unlike the RK4 method missing the physical characteristics of original system.
-
4.
The inertial coupling system presented in this section is linear. The computation results with PL method reflect the nature of the inertial coupling system and are close to the exact solution, since the PL method maintains the original physics characteristics of dynamic system. However, for solving the nonlinear dynamic system, the solutions are sensitive to the initial conditions and system parameters. Whether the PL method is suitable to handle the nonlinear dynamic system is our next work to purse.
5 Diagnosing Irregularities of Nonlinear Systems
5.1 Nonlinear Nonautonomous System
Here, the fourth-order Runge-Kutta method is employed to determine the periodicity ratio of the hull system, as shown in Eq. (1.131). This model is applied to describe the nonlinear coupling characteristics of the pitching and rolling of the hull.
Consider F and ω as control parameters, and the initial value of the system is assumed to be x 1(0) = 0.1, \( {\dot{x}}_1(0)=0.2 \), x 2(0) = 0.3, and \( {\dot{x}}_2(0)=0.4 \). The other parameters of the system are defined by μ 1 = 0.1, μ 2 = 0.1, α 1 = 0.5, ω 1 = 5.5, and ω 2 = 5.5. Figure 1.14 shows the periodicity ratio when the parameters of the system satisfy that α 2 = 1.0, α 2 = 1.5, α 2 = 2.0, and α 2 = 2.5. The red region in this figure represents that the dynamic characteristics of the system are periodic, i.e., γ = 1; the blue region denotes that the dynamic characteristics of the system are chaotic, i.e., γ = 0; and the other color region signifies that the dynamic characteristics of the system are neither periodic nor chaotic, i.e., 0 < γ < 1. The figure reveals the dynamic behavior of the system with the change of system parameters. As shown in this figure, when ω is located in region of (0, 2], the vibration behavior of the system is transferred from chaos to periodicity with the increase of the external excitations; when ω is located in region of (5.2, 5.8], the probability of nonperiodic vibration of the system is increased with the increase of coupling coefficient α 2; when ω is located in the other region, the vibration behavior of the system is periodic. It can be seen that the system is super near resonance, near resonance, sharp resonance, and far resonance when ω ∈ (0, 2], ω ∈ (2, 5.2], ω ∈ (5.2, 5.8], and ω ∈ (5.8, 10], respectively. It can be concluded that the dynamic characteristics are chaotic when the system is sharp resonance or super near resonance.
Periodicity of hull dynamic system. (a) α 2 = 1.0, (b) α 2 = 1.5, (c) α 2 = 2.0, (d) α 2 = 2.5
As shown in Fig. 1.14d, the system parameters are located in the blue region when ω = 0.2, α 2 = 2.5, and F = 0.9, and the vibration behavior is chaotic because of γ = 0; the system parameters are located in the red region when ω = 8, α 2 = 2.5, and F = 20, and the vibration behavior is chaotic because of γ = 1. The vibration characteristics of the hull are shown in Fig. 1.15 when ω = 0.2, α 2 = 2.5, and F = 0.9. Figure 1.15 (a) and (c) follow that the trajectory of the system is periodic in x 1-direction; and the trajectory is chaotic in x 2-direction as shown in Fig. 1.15b, d. Therefore, the vibration characteristics of the system are chaotic in the condition of ω = 0.2, α 2 = 2.5 and F = 0.9. As a result, the vibration characteristics of the system are chaotic in the condition of ω = 0.2, α 2 = 2.5 and F = 0.9. Figure 1.16 shows the vibration characteristics of the hull system considering ω = 8, α 2 = 2.5, and F = 20. It can be seen that the trajectory of the system is periodic in x 1- and x 2- directions. And so the vibration characteristics of the system are periodic in the condition of ω = 8,α 2 = 2.5, and F = 0.9. According to the analysis above, if the vibration characteristics in all dimensionality are periodic, the system is periodic or deterministic. Conversely, it is an uncertain system.
Vibration characteristics of hull dynamic system for ω = 0.2 α 2 = 2.5 F = 0.9. (a) Phase diagram in x 1- direction, (b) phase diagram in x 2- direction, (c) Poincaré map in x 1- direction, and (d) Poincaré map in x 2- direction
Vibration characteristics of hull dynamic system for ω = 8 α 2 = 2.5 F = 20. (a) Phase diagram in x 1- direction, (b) phase diagram in x 2- direction, (c) Poincaré map in x 1- direction, and (d) Poincaré map in x 2- direction
5.2 Nonlinear Autonomous System
Consider the famous Rössler system, shown in Eq. (1.132):
Assuming b and c to be control parameters, the periodicity of Rössler system can be determined with the periodicity-ratio method in Sect. 1.2.4. Considering the initial value of the system as x 1(0) = 0.1, x 2(0) = 0.1, and x 3(0) = 0.3, Fig. 1.17 shows the periodicity of Rössler system with different values of a. The red region in this figure represents that the dynamic characteristics of the system are periodic, i.e., γ = 1; the blue region denotes that the dynamic characteristics of the system are chaotic, i.e., γ = 0; and the other color region signifies that the dynamic characteristics of the system are neither periodic nor chaotic, i.e., 0 < γ < 1. The figure can intuitively determine the process of the dynamic behavior changed with parameters of the system. Because of the nonlinear characteristics of Rössler system, the dynamic characteristics of the system are sensitive to the system parameters.
Periodicity of Rössler dynamic system. (a) a = 0.05, (b) a = 0.10, (c) a = 0.15, (d) a = 0.20
As shown in Fig. 1.17d, the parameters are located in the red region when a = 0.20, b = 0.20, and c = 3.50; in this case, the vibration characteristics of the system are periodic; when a = 0.20, b = 0.20, and c = 5.50, the parameters are located in the blue region; in this case, the vibration characteristics of the system are chaotic. Figure 1.18 shows the periodic vibration of the Rössler system. It can be found that the phase trajectory is periodic when a = 0.20, b = 0.20, and c = 3.50, as shown in Fig. 1.18e, and the number of the visible points in the Poincaré sections of x 1–x 2 and x 2–x 3 is 2, respectively. However, the phase trajectory is chaotic when a = 0.20, b = 0.20, and c = 5.50; therefore, the number of the visible points in the sections of x 1–x 2 and x 2–x 3 is infinite, as shown in Fig. 1.19.
Vibration characteristics of Rössler dynamic system for a = 0.20, b = 0.20, and c = 3.50
Vibration characteristics of Rössler dynamic system for a = 0.20, b = 0.20, and c = 5.50
Through the discussions of theoretical research and numerical analysis, it can be found that periodicity ratio is an effective tool to identify the dynamic behavior of high-dimensional nonlinear systems. The conclusions of the study on the periodicity ratio are as follows:
-
1.
If the dynamic responses of the nonlinear system are periodic, the phase points in the Poincaré sections are overlapping. In this case, the value of the periodicity ratio is equal to 1.
-
2.
If the dynamic responses of the nonlinear system are chaotic, the phase points in the Poincaré sections are nonoverlapping. In this case, the value of the periodicity ratio is equal to 0.
-
3.
For a nonlinear dynamic system, there may exist an infinite number of nonperiodic solutions, which are neither periodic nor chaotic. For these nonperiodic solutions, the corresponding periodicity-ratio values are in the range of 0 < γ < 1. The larger value of the periodicity ratio represents the dynamic characteristics closed to periodic motion, and the smaller value of the periodicity ratio represents the dynamic characteristics closed to chaotic motion.
6 Conclusion
Using the traditional RK method for solving the dynamic system, high order differential equations of dynamic system are usually descended into multiple first-order differential equations. In this way, crucial dynamic property of the original system may be neglected or simplified, which leads to the computational error when searching solution for dynamic model encountered in actual engineering. However, solving differential equations above with the PL method proposed in the chapter, the semi-analytical solution of systems is obtained directly through the derivation of equation. Therefore, the physical properties of systems are well preserved. In addition, the whole-time interval is divided into many tiny intervals by the PL method, and the solution is continuous on each interval. In this case, the accuracy of numerical solution of the PL method is better than the RK method, which is demonstrated by numerical analysis. In addition, the computed efficiency of the PL and RK methods are compared through statistics of operation time of CPU during computing process. The CPU time taken by the PL method is less than the RK method in the same time steps, which indicates that the PL method is more efficient than the RK method. The main reason is that value continuity of two adjacent truncation points is maintained by using the PL method, which simplifies the solving process and saves the calculated time, while the RK method combines iterative and averaged slope to search solutions, which makes the solution process more complicated. Therefore, the numerical results of the PL method reflect the essence of dynamic system, since the PL method keeps the physical characteristics of dynamic system. The precision of the solution obtained by the PL method is related to the value of N. This article is an exploratory study for implementation of the PL method in coupling systems. Therefore, the classic two-degree freedom systems are considered, and whether the PL method is suitable to solve problems of multi-degree freedom system should be further verified in our next work. Based on the PL method, the periodicity ratio is proposed to explore the dynamic characteristics of the nonlinear system. If the dynamic responses of the nonlinear system are periodic, the phase points in the Poincaré sections are overlapping. In this case, the value of the periodicity ratio is equal to 1. If the dynamic responses of the nonlinear system are chaotic, the phase points in the Poincaré sections are nonoverlapping. In this case, the value of the periodicity ratio is equal to 0. For a nonlinear dynamic system, there may exist an infinite number of nonperiodic solutions, which are neither periodic nor chaotic. For these nonperiodic solutions, the corresponding periodicity-ratio values are in the range of 0 < γ < 1. The larger value of the periodicity ratio represents the dynamic characteristics closed to periodic motion, and the smaller value of the periodicity ratio represents the dynamic characteristics closed to chaotic motion.
References
Abukhaled MI, Allen EJ. A class of second-order Runge-Kutta methods for numerical solution of stochastic differential equations. Stochastic Analysis & Applications. 1998, 16(6):977–991.
Cai ZF, Kou KI. Laplace transform: a new approach in solving linear quaternion differential equations. Mathematical Methods in the Applied Sciences. 2018, 41(11):4033–48.
Chen Z, Qiu Z, Li J. Two-derivative Runge-Kutta-Nyström methods for second-order ordinary differential equations. 2015, 70(4):897–927.
Butcher, JC. Numerical Methods for Ordinary Differential Equations. Ussr Computational Mathematics & Mathematical Physics. 2010, 53:153–170.
Dai LM. Nonlinear Dynamics of Piecewise Constant Systems and Implementation of Piecewise Constant Arguments: World Scientific; 2008.
Iserles A, Ramaswami G and Mathematics M. Runge-Kutta methods for quadratic ordinary differential equations. Bit Numerical Mathematics. 1998, 38(2):315–46.
Hussain, Kasim A, Ismail F. Fourth-Order Improved Runge-Kutta Method for Directly Solving Special Third-Order Ordinary Differential Equations. Iranian journal of ence and technology. transaction a, 2017,41:429–437.
Ji XY, Zhou J. Solving High-Order Uncertain Differential Equations via Runge-Kutta Method. IEEE Transactions on Fuzzy Systems 2017:1–11.
Kanagarajan K, Suresh R, Mathematics A. Runge-Kutta method for solving fuzzy differential equations under generalized differentiability. 2016, 14(14):1–12.
Forcrand PD, Jäger B. Taylor expansion and the Cauchy Residue Theorem for finite-density QCD. The 36th Annual International Symposium on Lattice Field Theory. 2018.
Zingg DW, Chisholm TT. Runge-Kutta methods for linear ordinary differential equations. Applied Numerical Mathematics 1999, 31:227–238.
Zhang CY, Chen L. A symplectic partitioned Runge-Kutta method using the eighth-order NAD operator for solving the 2D elastic wave equation. Journal of Seismic Exploration. 2015, 24:205–230.
State Locus Drawing of RLC Circuit Based on Ode45 of MATLAB. China Science and Technology Information, 2008.
Immler, Fabian, Traut C. The Flow of ODEs: Formalization of Variational Equation and Poincaré Map. Journal of Automated Reasoning, 2019, 62(2):215–236.
Hartman, Philip. Ordinary differential equations. Mathematics of Computation.1982, 20:82–122.
Dai LM, Xia DD, Chen CP, An algorithm for diagnosing nonlinear characteristics of dynamic systems with the integrated periodicity ratio and lyapunov exponent methods, Communications in Nonlinear Science and Numerical Simulation, 2019, 73: 92–109.
Dai LM, Wang X, Chen C. Accuracy and Reliability of Piecewise-Constant Method in Studying the Responses of Nonlinear Dynamic Systems. Journal of Computational and Nonlinear Dynamics. 2015, 10(2):021009–10.
Dai LM, Singh MC, Structures. An analytical and numerical method for solving linear and nonlinear vibration problems. International Journal of Solids & Structures. 1997, 34(21):2709–2731.
Lu X, Sun J, Li G, Wang Q, Zhang D. Dynamic analysis of vibration stability in tandem cold rolling mill. Journal of Materials Processing Technology. 2019, 272:47–57.
Reyhanoglu M, van der Schaft A, Mcclamroch NH, Kolmanovsky I. Dynamics and control of a class of underactuated mechanical systems. IEEE Transactions on Automatic Control, 2017, 44(9):1663–1671.
Bryant P, Brown R, Abarbanel H. Lyapunov Exponents from Observed Time Series. Phys. rev. lett. 1990, 65(13):1523–1526.
Zhang W, Ye M. Local and global bifurcations of valve mechanism. Nonlinear Dynamics. 1994, 6(3):301–316.
Wolf A, Swift JB, Swinney HL, Vastano JA. Determining Lyapounov exponents from a time series. Springer Berlin Heidelberg. 1985, 16(3):285–317.
Jung C. Poincare map for scattering states. Journal of Physics A General Physics 19.8(1999):1345.
Dai, LM, Singh MC. Periodic, quasiperiodic and chaotic behavior of a driven Froude pendulum. International Journal of Nonlinear Mechanics. 1998, 33(6):947–965.
Ma H, Ho DWC, Lai YC, Lin W. Detection meeting control: Unstable steady states in high-dimensional nonlinear dynamical systems. Physical Review E. 2015.92.
Zhang W, Wang FX, Zu JW. Local bifurcations and codimension-3 degenerate bifurcations of a quintic nonlinear beam under parametric excitation. Chaos, Solitons & Fractals. 2005, 24(4):977–98.
Fang P, Dai LM, Hou YJ, Du MJ, Wang LY, Xi ZJ. Numerical Computation for the Inertial Coupling Vibration System Using PL Method. Journal of Vibration Engineering & Technologies, 2019, 7(2):139–148.
Dai L, Assessment of Solutions to Vibration Problems Involving Piecewise Constant Exertions, Symposium on Dynamics, Acoustic and Simulations (DAS2000) in ASME IMECE 2000, Orlando, 2000.
Arendt W, Batty CJ, Hieber M, Neubrander F. Vector-Valued Laplace Transforms and Cauchy Problems. Israel Journal of Mathematics. 1987, 59(3):327–352.
Fang P, Dai L, Hou Y, Du M, Wang L. The Study of Identification Method for Dynamic Behavior of High-Dimensional Nonlinear System. Shock and vibration. 2019.
Fang P, Hou YJ, Zhang LP, Du MJ, Zhang MY. Synchronous behavior of a rotor-pendulum system. Acta Physica Sinica. 2016, 65.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Pan, F., Liming, D., Kexin, W., Luyao, W. (2022). Improved Theoretical and Numerical Approaches for Solving Linear and Nonlinear Dynamic Systems. In: Dai, L., Jazar, R.N. (eds) Nonlinear Approaches in Engineering Application. Springer, Cham. https://doi.org/10.1007/978-3-030-82719-9_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-82719-9_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-82718-2
Online ISBN: 978-3-030-82719-9
eBook Packages: EngineeringEngineering (R0)