1 Introduction

Structural nonlinearities may occur in either a distributed or concentrated form. In general, distributed nonlinearity can only become significant when the amplitude of the response is large, while the concentrated nonlinearity may show a significant effect even for vibrations having small amplitude. The freeplay nonlinearity is one of the concentrated nonlinearities and is commonly encountered in mechanical engineering [2, 27]. For the present two degrees-of-freedom (DOF) airfoil model, the freeplay nonlinearity has been studied by several researchers. Yang and Zhao [34] carried out both experimental and theoretical analyses to investigate the limit cycle oscillations (LCOs) of the aeroelastic system, wherein the unsteady aerodynamic force and moment were expressed in terms of the Theodorsen function, and both bilinear and freeplay nonlinearities were studied. Hauenstein and Laurenson [16] conducted an experimental analysis of the airfoil with freeplay nonlinearity, and both LCOs and chaos were observed. Price et al. [28] studied the same model with a freeplay nonlinearity in pitch by the Houbolt’s finite difference method in conjunction with the RK4 method. They found that the critical flutter speed for the freeplay nonlinear model was well below the linear flutter speed. Liu et al. [24] proposed an analytical point transformation method to solve the two DOF model with freeplay nonlinearity. Although the point-transformation method can accurately detect the switching points of the freeplay, unfortunately, it is limited to the analysis of periodic motions due to its analytical nature. Abdelkefi et al. [3] investigated the response of the aeroelastic two DOF wing problem both experimentally and theoretically using numerical simulation methods. Vasconcellos et al. [31, 32] represented the freeplay nonlinearity by three different representations, namely, discontinuous based on Henon’s method, polynomial, and hyperbolic tangent. It was shown that the discontinuous and hyperbolic tangent representations are effective. Additionally, Chung et al. [7] and Liu et al. [22] employed the perturbation-incremental method and the incremental harmonic balance method, respectively, to study the bifurcation of this aeroelastic systems with hysteresis/freeplay nonlinearities. Nevertheless, these analytical methods are limited to the analysis of periodic motions.

In the aforementioned studies, either approximate analytical methods or numerical integration methods were adopted in theoretical analysis. Numerical integration methods, e.g., the RK4, are powerful in solving the nonlinear dynamical problems. In comparison with the approximate analytical methods such as the harmonic balance method [23], the perturbation method [26], and the time domain collocation method [9, 11, 35], the RK4 is much more straightforward and simpler to use. What is more, the RK4 can be applied to analyze the chaotic responses, while in contrast, the approximate analytical methods cannot work for chaotic analysis due to the periodicity feature of their trial functions. Unfortunately, the RK4 method works well only for systems with distributed nonlinearities. It may fail to produce accurate simulations when a discontinuous nonlinear system is encountered [8, 24]. The present system is essentially a combination of three distinct linear subsystems. Hence, it is crucial to accurately detect the switching points between subsystems. Failure to accurately identify the switching points would cause numerical inaccuracy in the analysis of LCOs and even more serious issues in the analysis of chaos.

Henon’s method [17] for integrating state-space equations to a prescribed value of a specified state coordinate was applied for the location of the switching points in the freeplay model by Conner et al. [8], Trickey et al. [29]. The method involves integrating the system until a change in linear subdomains occurs. At that moment, the distance the system has traveled into the new subdomain is known. Upon exchanging the dependent variable (the specified variable) and independent variable, viz. time, the ODE system can be integrated back to the exact discontinuous point in merely one step. Conner et al. [8] investigated the effect of the RK4Henon method on the accuracy of calculating periodic motions, by comparing with the RK4 method. It was found that the two methods were consistent with each other in the analysis of LCOs (see also Ref. [1]), except that the two methods may sometimes fall to different LCO attractors for the same set of initial conditions. The present work is a continuation of a previous paper, in which a numerical study of the chaotic motions of a two DOF airfoil with coupled cubic nonlinearities was conducted [10]. Also, as an extension to [8], in this study, the comparison of the RK4 and the RK4Henon methods is carried out, in the analyses of not only LCOs, but also chaos and chaotic transients. The importance of using the RK4Henon method rather than the classical RK4 method will be revealed, when chaotic motions are under consideration. More importantly, we will show that chaotic transients, which can be captured by the RK4Henon method, would be missed out by the RK4 method. The chaotic transients are observed in the present system for the first time.

An alternative strategy to handle the discontinuous nonlinearity is to use a proper rational polynomial (RP) to closely fit the discontinuous function. Alighanbari and Price [5] used a third-order RP function to fit the freeplay nonlinearity, and the resulting continuous system was applied in the analyses of both LCOs and chaos. Liu et al. [22] applied the same strategy to process the freeplay and hysteresis nonlinearities, and the resulting system was solved by an incremental harmonic balance method; this study was focused on the LCO analysis. Li et al. [21] demonstrated that the RP approximation method is highly accurate in the analysis of LCOs. However, whether the RP approximation method is suitable in the analyses of chaos and chaotic transients has not been answered until now. In this study, the comparison of the RP approximation method and the RK4Henon method will be carried out to answer this question.

Another objective of the present study is to introduce a simple method for predicting the existence of the long-lived chaotic transients. In general, if a very longtime chaotic transient exists before settling into a periodic motion, one would be apt to mistake it as a chaotic motion [15, 25]. Vasconcellos et al. [30] showed that this transition phenomenon is probably due to grazing bifurcations. A safe way to avoid this misunderstanding is to run a very long integration time and check the time response to see whether it settles into a periodic motion or not. Here, our method is based on viewing the evolution history of the largest Lyapunov exponent (LLE), that is, a decreasing LLE evolution curve implies the existence of chaotic transient. The present method is simpler and more efficient than the conventional method. Because in the case of chaotic transients, the LLE, if not convergent, will show a decreasing trend sooner than the periodicity begins to emerge in the time response. Finally, the effects of the freeplay nonlinearity, the damping level, and the frequency ratio \(\bar{\omega }\) on the aeroelastic response are analyzed by means of bifurcation diagrams.

2 Mathematical model

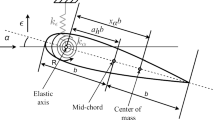
The mathematical model for the two DOF airfoil in subsonic flow was established by Fung [14]. Although only linear springs in pitch and plunge were considered, the structural nonlinearity can be readily introduced into Fung’s formulation. A sketch of the two DOF airfoil with freeplay nonlinearity in pitch is plotted in Fig. 1, in which the positive directions of the pitch angle \(\alpha \) and the plunge displacement \(h\) are defined.

Fig. 1
figure 1

Sketch of a typical airfoil section with freeplay nonlinearity in pitch

Full size image

Including the structural nonlinearity, the linear formulation of Fung [14] is modified into the following non-dimensional form [27]:

$$\begin{aligned}&\ddot{\xi }\!+\!x_\alpha \ddot{\alpha }+2\zeta _\xi \frac{\bar{\omega }}{U^*}\dot{\xi }\!+\!\left( \frac{\bar{\omega }}{U^*}\right) ^2G(\xi ) \!=\!-\frac{1}{\pi \mu }C_L(\tau ),\end{aligned}$$
(1a)
$$\begin{aligned}&\frac{x_\alpha }{r^2_\alpha }\ddot{\xi }\!+\!\ddot{\alpha }\!+\!2\zeta _\alpha \frac{1}{U^*}\dot{\alpha }\!+\!\left( \frac{1}{U^*}\right) ^2M(\alpha ) \!=\!\frac{2}{\pi \mu r^2_\alpha }C_M(\tau ),\nonumber \\ \end{aligned}$$
(1b)

where the related symbols are defined in “Appendix 1”.

In this study, the plunge spring is linear, and the pitch spring is freeplay nonlinear. Thus, the pitch and plunge stiffness terms \(M(\alpha )\) and \(G(\xi )\) are expressed as

$$\begin{aligned} M(\alpha )=\left\{ \begin{array}{ll} M_0+\alpha -\alpha _f,&{} \alpha <\alpha _f\\ M_0+M_f(\alpha -\alpha _f),&{} \alpha _f\le \alpha \le \alpha _f+\delta \\ M_0+\alpha -\alpha _f+\delta (M_f-1),&{} \alpha >\alpha _f+\delta \end{array}\right. \nonumber \\ \end{aligned}$$
(2)

and \(G(\xi )=\xi \), respectively. In fact, the nonlinearity expressed in Eq. (2) is generally referred to as a bilinear nonlinearity, a sketch for which is provided in Fig. 2a. Specifically, the bilinear nonlinearity can be reduced to a freeplay nonlinearity by fixing the stiffness of the freeplay range, viz. \(M_f\), to zero. In most cases, investigators also enforce the preload \(M_0=0\) and \(\alpha _f=-\frac{1}{2}\delta \), which results in a more special freeplay nonlinearity, as shown in Fig. 2b. In the present study, the general freeplay nonlinearity is analyzed, wherein only \(\alpha _f=-\frac{1}{2}\delta \) is fixed for the sake of freeplay symmetry. In numerical simulation, the variations of \(M_0\), \(M_f\) and \(\delta \) will be carried out to show their effects on the aeroelastic response of the present system.

Fig. 2
figure 2

Sketches of nonlinearity (a) bilinear nonlinearity (b) simple freeplay nonlinearity

Full size image

In addition to the structural nonlinearities, \(C_L(\tau )\) and \(C_M(\tau )\) accounting for linear aerodynamic force and aerodynamic moment are [14]

$$\begin{aligned} C_L(\tau )= & {} \pi (\ddot{\xi }-a_h\ddot{\alpha }+\dot{\alpha })\nonumber \\&\quad +\,2\pi \left[ \alpha (0)+\dot{\xi }(0)+\left( \frac{1}{2}-a_h\right) \dot{\alpha }(0)\right] \phi (\tau )\nonumber \\&\quad +\,2\pi \int ^\tau _0\phi (\tau -\sigma )[\dot{\alpha }(\sigma )+\ddot{\xi }(\sigma )\nonumber \\&\quad +\,\left( \frac{1}{2}-a_h\right) \ddot{\alpha }(\sigma )]d\sigma ,\end{aligned}$$
(3a)
$$\begin{aligned} C_M(\tau )= & {} \pi \left( \frac{1}{2}+a_h\right) \left[ \alpha (0)+\dot{\xi }(0)\right. \nonumber \\&\quad \left. +\,\left( \frac{1}{2}-a_h\right) \dot{\alpha }(0)\right] \phi (\tau )\nonumber \\&\quad +\,\frac{\pi }{2}(\ddot{\xi }-a_h\ddot{\alpha })-\frac{\pi }{16}\ddot{\alpha }-\left( \frac{1}{2}-a_h\right) \frac{\pi }{2}\dot{\alpha }\nonumber \\&\quad +\,\pi \left( \frac{1}{2}+a_h\right) \int ^\tau _0\phi (\tau -\sigma )\left[ \dot{\alpha }(\sigma )+\ddot{\xi }(\sigma )\right. \nonumber \\&\quad \left. +\,\left( \frac{1}{2}-a_h\right) \ddot{\alpha }(\sigma )\right] \hbox {d}\sigma , \end{aligned}$$
(3b)

where the Sears approximation to the Wagner function \(\phi (\tau )=1-\psi _1e^{-\epsilon _1\tau }-\psi _2e^{-\epsilon _2\tau }\) is [6]

$$\begin{aligned} \phi (\tau )=1-0.165e^{-0.0455\tau }-0.335e^{-0.3\tau }. \end{aligned}$$

System (1) is essentially a set of two integro-differential equations, which cannot be directly integrated. In this study, the original integro-differential equations are transformed into six first-order ODEs with the following two auxiliary variables introduced by Alighanbari and Hashemi [4]:

$$\begin{aligned} y_1= & {} \psi _1 e^{-\epsilon _1\tau }\left[ \dot{\xi }(0)+\left( \frac{1}{2}-a_h\right) \dot{\alpha }(0)+\alpha (0)\right] \nonumber \\&+\int ^\tau _0\psi _1e^{-\epsilon _1(\tau -\sigma )}\nonumber \\&\times \left[ \ddot{\xi }(\sigma )+\left( \frac{1}{2}-a_h\right) \ddot{\alpha }(\sigma )+\dot{\alpha }(\sigma )\right] d\sigma ,\end{aligned}$$
(4a)
$$\begin{aligned} y_2= & {} \psi _2 e^{-\epsilon _2\tau }\left[ \dot{\xi }(0)+\left( \frac{1}{2}-a_h\right) \dot{\alpha }(0)+\alpha (0)\right] \nonumber \\&+\,\int ^\tau _0\psi _2e^{-\epsilon _2(\tau -\sigma )}\nonumber \\&\times \left[ \ddot{\xi }(\sigma )+\left( \frac{1}{2}-a_h\right) \ddot{\alpha }(\sigma )+\dot{\alpha }(\sigma )\right] \hbox {d}\sigma . \end{aligned}$$
(4b)

The integral terms in the aerodynamic force can be suppressed by the introduced two auxiliary variables. Considering Eqs. (4), \(C_L(\tau )\) and \(C_M(\tau )\) can be rewritten as

$$\begin{aligned} C_L(\tau )= & {} \pi \left[ \ddot{\xi }-a_h \ddot{\alpha }+2\dot{\xi }+2\left( 1-a_h\right) \dot{\alpha }\right. \nonumber \\&\left. +\,2\alpha -2y_1-2y_2\right] , \end{aligned}$$

and

$$\begin{aligned} C_M(\tau )= & {} \frac{\pi }{2}\left[ a_h\ddot{\xi }-\left( \frac{1}{8}+a^2_h\right) \ddot{\alpha }+(1+2a_h)\dot{\xi }\right. \nonumber \\&\quad +\,\,a_h(1\!-\!2a_h)\dot{\alpha }\!+\!(1+2a_h)\alpha \!-\!(1+2a_h)y_1\nonumber \\&\left. \quad -\,\,(1+2a_h)y_2\right] . \end{aligned}$$

Consequently, Eqs. (1) are transformed into a couple of second-order ODEs. In the meanwhile, two additional variables \(y_1\) and \(y_2\) have been introduced into the system. For the system’s completeness, two supplemental equations should be constructed. Differentiating Eqs. (4a) and (4b) with respect to \(\tau \) yields

$$\begin{aligned} \dot{y}_1= & {} -\epsilon _1y_1+\psi _1\left[ \ddot{\xi }(\tau )+(\frac{1}{2}-a_h)\ddot{\alpha }(\tau )+\dot{\alpha }(\tau )\right] ,\end{aligned}$$
(5a)
$$\begin{aligned} \dot{y}_2= & {} -\epsilon _2y_2+\psi _2\left[ \ddot{\xi }(\tau )+(\frac{1}{2}-a_h)\ddot{\alpha }(\tau )+\dot{\alpha }(\tau )\right] .\nonumber \\ \end{aligned}$$
(5b)

Equations (5) are two supplemental first-order ODEs. Therefore, the complete system modeling the typical airfoil section consists of two second-order ODEs, plus two first-order ODEs. Upon introducing \(x_1=\alpha ,~x_2=\dot{\alpha },~x_3=\xi ,~x_4=\dot{\xi },~x_5=y_1\) and \(x_6=y_2\), the system can be written in a state-space form as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1=x_2,\\ \dot{x}_2=a_{21}x_1+a_{22}x_2+a_{23}x_3+a_{24}x_4+a_{25}x_5\\ ~~~~~~+a_{26}x_6+m_2M(x_1),\\ \dot{x}_3=x_4,\\ \dot{x}_4=a_{41}x_1+a_{42}x_2+a_{43}x_3+a_{44}x_4+a_{45}x_5\\ ~~~~~~+a_{46}x_6+m_4M(x_1),\\ \dot{x}_5=a_{51}x_1+a_{52}x_2+a_{53}x_3+a_{54}x_4+a_{55}x_5\\ ~~~~~~+a_{56}x_6+m_5M(x_1),\\ \dot{x}_6=a_{61}x_1+a_{62}x_2+a_{63}x_3+a_{64}x_4+a_{65}x_5\\ ~~~~~~+a_{66}x_6+m_6M(x_1), \end{array} \right. \nonumber \\ \end{aligned}$$
(6)

where the coefficients are given in “Appendix 2”.

In literature, most of the numerical studies have adopted an eight ODE system proposed by Lee’s model [18]. The present system (6) consisting of six first-order ODEs is expected to be computationally more efficient than Lee’s model. Dai et al. [12] compared the computational efficiency of employing the six ODE model (with cubic nonlinearity) and Lee’s model and found that using the six ODE model was approximately 20 % faster. In this study, the six ODE system (6) is applied in all computations.

3 Henon’s method

The presence of the discontinuous (or non-smooth) nonlinearity limits the range of application of the classical RK4 method to the analysis of periodic motions, due to the numerical inaccuracy induced by the crossover of the integration step, see Fig. 3.

Fig. 3
figure 3

Error mechanism of the traditional integration method

Full size image

Linear interpolation method is an intuitive technique to alleviate the numerical inaccuracy. Concretely, one is required to do a linear interpolation between the last two integration points which belong to two neighboring subdomains. Although simple to use, this method may produce an unacceptable error. High-order interpolation methods are available, but suffering from complex programming as well as the storage of a number of previous integration points.

The most effective method for accurately detecting a specified value of a state coordinate (herein \(x_1\)) is attributed to Henon [17], wherein Henon’s method was applied to construct Poincare maps. Henon’s method involves integrating the system until a change in linear subdomains is detected. At that time, the distance the system has traveled into the new subdomain is known. By exchanging the dependent variable of interest \(\alpha \) and independent variable \(\tau \), the system can be integrated from its current location back to the exact point of discontinuity within one step. Then, time is reverted to be the independent variable and the classical RK4 is then applied to integrate the new subsystem in the new subdomain with the initial conditions already known, until a next discontinuity is encountered.

System (6) can be written in state-space form as

$$\begin{aligned} \frac{d}{d\tau }\left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_6 \\ \end{array} \right) =\left( \begin{array}{c} f_1(\mathbf{x}) \\ f_2(\mathbf{x}) \\ \vdots \\ f_6(\mathbf{x}) \\ \end{array} \right) . \end{aligned}$$
(7)

Henon’s method involves exchanging the independent variable \(\tau \) and the identifying dependent variable \(x_1\), which is accomplished via, first dividing each of the equations in Eqs. (7) by \(dx_1/d\tau =f_1(\mathbf{x})\), and then replacing the first equation by \(d\tau /dx_1=1/f_1(\mathbf{x})\). Consequently, the new system with \(x_1\) being the independent variable is

$$\begin{aligned} \frac{d}{dx_1}\left( \begin{array}{c} \tau \\ x_2 \\ \vdots \\ x_6 \\ \end{array} \right) =\left( \begin{array}{c} 1/f_1(\mathbf{x}) \\ f_2(\mathbf{x})/f_1(\mathbf{x}) \\ \vdots \\ f_6(\mathbf{x})/f_1(\mathbf{x}) \\ \end{array} \right) . \end{aligned}$$
(8)

Note that the new system is used only for one integration step immediately after the identifying variable \(x_1\) crossed the specified value. The RK4Henon method is essentially a variable stepsize integration method, and the stepsize variation happens once the switching point has been crossed.

4 Results and discussions

Fig. 4
figure 4

Sketch of the freeplay nonlinearity with \(\alpha _f=-\frac{1}{2}\delta \)

Full size image

The sketch of the freeplay nonlinearity considered is plotted in Fig. 4, in which \(\alpha _f\) is fixed to be \(-0.5\delta \), which means the freeplay range is equally divided by the \(y\) axis. In general, the pattern of the freeplay nonlinearity is affected by three factors, namely, the freeplay magnitude \(\delta \), the preload \(M_0\), and the pitch stiffness in the freeplay region \(M_f\) (in the freeplay range, the stiffness is sometimes not exactly zero). The system parameters are given as Case 1 in Table 1, which are taken from Price et al. [27]. The corresponding linear flutter speed \(U^*_L\) is \(6.2851\).

Table 1 System parameters for Case 1, 2 and 3
Full size table
Fig. 5
figure 5

Bifurcation diagrams for the pitch motion with parameters of Case 1 in Table 1, with initial conditions \(\alpha (0)=3^\circ \) and the rest initial states are zero. The stepsize of the flow speed is \(0.01(U^*/U^*_L)\). For each flow speed, the number of integration steps is \(2\times 10^5\); the initial \(20\,\%\) data is dropped off to damp out transients

Full size image

Figure 5 shows the bifurcation diagram for the pitch motion, which is calculated by the RK4Henon method. It is consistent with the bifurcation diagram calculated by the combination of the finite difference method (FDM) and the classical RK4 method in Price et al. [27], which verifies the consistency of the present six ODE model and the FDM resulting model. However, the coarse comparison by means of the bifurcation diagrams is not sufficient to exhibit the significant difference between the RK4Henon and the classical RK4 methods. Thus, further investigations will be carried out to show the discrepancies between the RK4Henon method and the RK4 method, in the analyses of LCOs, chaos, and chaotic transients.

Fig. 6
figure 6

Comparisons of a time histories, and b phase plane portraits, for \(U^*/U^*_L=0.6\) using the present RK4Henon method and the RK4 method. The total number of integration steps (For the sake of rigor, we use “ the number of integration steps” instead of “integration time” due to the fact that the RK4Henon’s stepsize is variable) is \(2\times 10^5\).

Full size image

4.1 Limit cycle oscillations

The RK4 method can produce accurate solutions, provided that LCOs are under consideration [8, 24]. Figure 6 shows the comparisons of the time histories and phase portraits by using the RK4Henon and the RK4 at \(U^*/U^*_L=0.6\). This flow speed is selected, according to Fig. 5, to obtain LCOs. Unless otherwise specified, the integration step is \(\Delta \tau =0.1\) throughout the paper. It can be seen that the results by the two methods are in good agreement. However, a partial enlargement in Fig. 6b illustrates that the RK4 phase trajectory contains numerous loops in a limited band, while the RK4Henon trajectory falls exactly in a single loop at current resolution. This indicates that the RK4Henon method is numerically more stable and accurate than the RK4 method. Liu et al. [24] applied both the point transformation method and the RK4 to examine the airfoil section with freeplay nonlinearity. The numerical results were used as the benchmark solutions to evaluate the results via the point transformation method. However, as stated earlier, the integration time step \(\Delta \tau \) has to be very small in order to yield an accurate result. In addition, \(\Delta \tau \) can only be selected numerically when the solution computed by \(\Delta \tau \) is essentially the same as those obtained using \(\Delta \tau /2\) [24], which is a tedious procedure. For the chaotic response, this procedure fails to work.

4.2 Chaotic motions

Having compared the performance of the RK4Henon and the RK4 methods for analyzing LCOs, we turn our attention to their performance in chaotic analysis. Before comparison, we introduce several descriptors of chaos. Normally, time series and phase plane portraits are straightforward hints of chaos. But sometimes, they may not be sufficient to distinguish long-term periodic motions, quasi-periodic motions, and chaos [13].

The Poincare map is a useful tool to identify chaos. For an autonomous system, its Poincare map is plotted by recording the phase plane points at discrete times when a prescribed “event” occurs. Here, the event is defined as being the passage of a specified coordinate through zero. As suggested by Moon [25], more than 4000 points should be plotted in a Poincare map so as to ensure the integration time is long enough to rule out the possibility of chaotic transients.

A quantitative means to identify chaos is to calculate the largest Lyapunov exponent (LLE) of a time series. A positive LLE indicates that the motion is chaotic, while a nonpositive LLE implies a regular motion. In the present computations, the LLE is calculated based on the algorithms of Wolf et al. [33]. All involved parameters during the calculation of LLE are provided in Table 2. Base-\(2\) instead of base-\(e\) is used.

Table 2 Parameters used during the calculation of LLE
Full size table
Fig. 7
figure 7

a Poincare map, b amplitude spectrum, and c evolution history of LLE for \(U^*/U^*_L=0.27\)

Full size image

Figure 7 shows the Poincare map, the amplitude spectrum, and the evolution of the LLE for \(U^*/U^*_L=0.27\). As shown in Fig. 7a, the Poincare map is neither a finite set of points (means periodic) nor a closed orbit (means quasi-periodic), which implies that the motion may be chaotic. The amplitude frequency spectrum in Fig. 7b shows a broadband, which is consistent with chaos. To add a further evidence, the LLE has also been calculated. The terminal time for calculating the LLE is different case by case to ensure the convergence of the LLE (if it can converge). As can be seen from Fig. 7c, the LLE converges to approximately \(0.009\), which indicates mild chaos.

Shown in Fig. 8 are the time histories for \(U^*/U^*_L=0.27\) by the RK4Henon method and the RK4 method with different integration stepsizes. The time series in Fig. 8 are short segments cut out from long chaotic time series. Although they appear to be rather periodic in this short time range, they are definitely chaotic motions as demonstrated in Fig. 7. It can be seen from Fig. 8 that the RK4 method with a smaller integration step can produce a result closer to the RK4Henon result. Also, it is known that the RK4 with a smaller integration step would generate a more accurate result. That is, the result via RK4 method with \(\Delta \tau =0.001\) is better than that with \(\Delta \tau =0.01\), and similarly result with \(\Delta \tau =0.01\) is better than that with \(\Delta \tau =0.1\). In addition, Fig. 8c shows that RK4 with \(\Delta \tau =0.001\) agrees very well with the RK4Henon. Thus, it can be concluded that the RK4Henon with \(\Delta \tau =0.1\) produces a more accurate result than the RK4 with \(\Delta \tau =0.1\) and RK4 with \(\Delta \tau =0.01\). A further comparison between RK4 with \(\Delta \tau =0.0001\) and the RK4Henon with \(\Delta \tau =0.1\) shows an even closer agreement (not reported in figure), which indicates that the RK4Henon with \(\Delta \tau =0.1\) is better than the RK4 with \(\Delta \tau =0.001\). This demonstrates the accuracy and efficiency of the RK4Henon method over the classical RK4 method. In computations, we also tried the RK4Henon method with \(\Delta t=0.05\) and \(0.02\) for comparison purpose. We found that deceasing the integration step \(\Delta t\) can increase the accuracy. However, due to the fact that the RK4Henon with \(\Delta t=0.1\) already has a relatively high accuracy, the improvement of using a smaller step is not prominent. Besides, a smaller size step may cause a longer computing time. Therefore, the results of RK4Henon with \(\Delta t=0.05\) and \(0.02\) are not reported.

Fig. 8
figure 8

Comparison of the time series for \(U^*/U^*_L=0.27\) calculated by the RK4Henon, \(\Delta \tau =0.1\) with that calculated by a the RK4, \(\Delta \tau =0.1\), b the RK4, \(\Delta \tau =0.01\), and c the RK4, \(\Delta \tau =0.001\)

Full size image

It should be emphasized that in the analysis of chaos, even a slight numerical inaccuracy may lead to entirely different solutions after a longtime. Therefore, the RK4Henon method would be the only choice for the chaotic analyses considering (1) its computational economy compared to the classical RK4 method (RK4 requires a much smaller integration stepsize) and (2) its high accuracy (RK4Henon overcomes the numerical instability arising from the crossover during integrations, while RK4 suffers from this).

Fig. 9
figure 9

a Time history and b phase portrait for \(U^*/U^*_L=0.27\) using RK4Henon with \(\Delta \tau =0.01,~0.1,~0.2,~0.4\)

Full size image

Shown in Fig. 9 are the time histories and phase portraits computed by RK4Henon with \(\Delta \tau =0.01\), \(0.1, 0.2,~0.4\). The result by RK4Henon with \(\Delta \tau =0.01\) serves as the benchmark. It can be seen that (1) decreasing the integration step can increase the accuracy of RK4Henon method; (2) \(\Delta \tau =0.1\) is sufficient for the present chaotic study; and (3) globally speaking, \(\Delta \tau =0.01,~0.1,~0.2,~0.4\) yield similar results, see Fig. 9b.

In addition, the order of convergence, \(p\), of the RK4Henon method has been evaluated by \(p=\log _2\frac{E_{02\sim 04}}{E_{01\sim 02}}\), where \(E_{02\sim 04}\) is the maximum absolute distance of the plunge responses between \(\Delta \tau =~0.2\) and \(0.4\). In the present case, \(p\approx 2.1\).

Fig. 10
figure 10

Comparisons of a phase portraits, b Poincare maps, and c amplitude spectra for \(U^*/U^*_L=0.3\) through using the classical RK4 and the RK4Henon methods

Full size image

4.3 Chaotic transients

We move our attention to the chaotic transients in this section. Shown in Fig. 10 are the phase portraits, the Poincare maps, and the amplitude spectra for \(U^*/U^*_L=0.3\) by the RK4 and the RK4Henon methods. All three subfigures show that the results by the two methods are qualitatively in very good agreement. In particular, Fig. 10a shows two phase trajectories which spread out the phase plane, implying chaos. Figure 10b shows Poincare maps with many points in a well-organized structure, and Fig. 10c shows two spectra with broadbands. All of these descriptors imply a chaotic motion. However, by careful observation, there seems to be sometime abnormal in Fig. 10b. That is, the structure of the Poincare map by the RK4Henon appears to be much sparser than that by the RK4. Bear in mind that the two methods run the same number of integration steps (\(2\times 10^6\) integration steps), the RK4Henon’s Poincare map should not be so sparse. It implies that a large number of points must be hitting at one or some points, repeatedly.

Fig. 11
figure 11

Time series of the pitch motion for \(U^*/U^*_L=0.3\) via a and b: the RK4 method, and c and d: the RK4Henon method. Note that b and d are cut out from a and c, respectively

Full size image
Fig. 12
figure 12

a Phase plane portrait and b Poincare map via RK4Henon method after completely damping out transients for \(U^*/U^*_L=0.3\)

Full size image

Now, we turn to the time response curve for help. Figure 11 shows the time histories of the pitch motion for \(U^*/U^*_L=0.3\) by the two methods. We can see that the time series via RK4 corresponds to a chaotic motion, while that via RK4Henon seems to settle to a periodic motion after a longtime (approximately \(1.12\times 10^4s\)) chaotic transient. The phase plane portrait and the Poincare map are replotted in Fig. 12, in which the initial \(1.5\times 10^4\,\hbox {s}\) response has been dropped out before plotting, such that the chaotic transient can be completely damped out. Both the phase trajectory of Fig. 12a and the Poincare map of Fig. 12b show that the response is a period-2 LCO.

Previous studies show that the chaotic transients are difficult to detect. One must always be careful before identifying a random-like motion in a deterministic system to be chaos. Moon [25] suggested that a sufficient longtime must be run before one can safely determine chaos. By his suggestion, the simulation time should be so long such that more than \(4000\) points have been plotted in the Poincare map. Of course, this time length is not necessary for some short chaotic transients and might be insufficient for some super long-lived chaotic transients. Although simple, this method is not robust and sometimes computationally expensive.

Fig. 13
figure 13

LLE evolution curves for \(U^*/U^*_L=0.3\) calculated by the RK4Henon method, dropping out the initial \(3\times 10^4\) integration steps before calculation

Full size image

Now, we propose a more robust and economic method for researchers to distinguish chaos and chaotic transients based on the trend of the LLE evolution curve. Figure 13 provides the evolution history of the LLE for the pitch motion calculated by the RK4Henon method for \(U^*/U^*_L=0.3\). It can be seen that the LLE evolution curve has a decreasing trend. In addition, we have already known from Fig. 11c, d that the present motion is a long- term chaotic transient followed by a periodic motion. So, it seems that the decreasing LLE evolution curve implies the existence of chaotic transient.

In a previous study [10], the present authors analyzed a two DOF airfoil with a cubic structural nonlinearity. The chaotic transient was detected, and its corresponding LLE evolution curve also showed a decreasing trend. Furthermore, this finding has also been verified in a totally different dynamical system. In an ongoing study, a cantilevered three-dimensional fluttering panel has been analyzed, in which a decreasing LLE evolution curve was also found to be associated with the chaotic transient. Therefore, it is reasonable to conclude that a decreasing LLE evolution curve implies the existence of chaotic transient prior to settling into a periodic motion. This finding provides a simple but efficient tool to determine whether a random-like motion is chaos or chaotic transient.

5 RK4Henon method versus RP approximation method

In this section, we compare the performance of the Rational Polynomial (RP) approximation method and the present RK4Henon method. The RP approximation method consists of first approximating the discontinuous nonlinearity \(M(\alpha )\) by a well-fitted rational polynomial and then integrating the resulting continuously dynamical system via the classical RK4. In contrast, the present method directly integrates the original discontinuous system via the highly accurate RK4Henon method. The comparison is carried out in the analyses of LCOs, chaos, and chaotic transients.

5.1 Limit cycle oscillations

The RP approximation is essentially a modification of the dynamical model via smoothing the discontinuous nonlinearity. This technique has been used in many studies, e.g., [5, 19, 20], however, its validity has not been verified thoroughly. Li et al. [20] applied the RP approximation method to analyze an airfoil with either freeplay or hysteresis nonlinearity. The accuracy of the RP approximation method was proved only in the LCO analysis.

In accordance with [20], we take the system parameters of Case 2 in Table 1. Note that \(\delta \) in the present study is twice that in [20]. According to Eq. (2), the freeplay nonlinearity is

$$\begin{aligned} M(\alpha )=\left\{ \begin{array}{ll} \alpha +0.25^\circ ,&{}~~\alpha <0.25^\circ \\ 0,&{}~~0.25^\circ \le \alpha \le 0.25^\circ \\ \alpha -0.25^\circ ,&{}~~\alpha >0.25^\circ \end{array}\right. \end{aligned}$$
(9)

In implementing the RP approximation method, the freeplay nonlinearity is then represented by a rational polynomial using a curve fitting tool in Matlab [20]:

$$\begin{aligned}&M_{RP}(\alpha )\\&\quad =\frac{0.00002747-0.01702\alpha -11.94 \alpha ^2+5462\alpha ^3}{0.4556-12.36\alpha +5732\alpha ^2}. \end{aligned}$$
Fig. 14
figure 14

a Time history and b phase portrait for pitch motion; c time history and d phase portrait for plunge motion for \(U^*/U^*_L=0.35\) (LCO)

Full size image

Figure 14 shows the time histories and the phase portraits for \(U^*/U^*_L=0.35\) by using the RP approximation method and the RK4Henon method. The initial conditions for the numerical simulation are \(\alpha =3^\circ \) and the rest being zero. The phase portraits are plotted after a sufficient longtime has been run to remove transients. Figure 14 indicates that the response is LCO. It can be seen from Fig. 14a, c that the results by the RP approximation are in agreement with those by the RK4Henon in the first 300 seconds. Then, discrepancy occurs between them. The phase portraits in Fig. 14b, d show that the results by the two different methods are different. However, by numerical verification, we confirm that the portraits by the two methods are exactly symmetric about the origin. Thus, the RP approximation method can be used in the analysis of LCOs. This conclusion is consistent with Li et al. [20].

Fig. 15
figure 15

a Time histories, b phase portraits, c Poincare maps, and d amplitude spectra for the pitch motion for \(U^*/U^*_L=0.26\) (chaos) by using the RP approximation method and the RK4Henon method

Full size image

5.2 Chaotic motions

Next, we will show whether the RP approximation method is capable of analyzing the chaotic motions. Figure 15 shows the time histories, phase portraits, Poincare maps, and amplitude spectra for \(U^*/U^*_L=0.26\), where the corresponding response is chaos. It can be seen from the four subfigures that the results by the two different methods are qualitatively in good agreement. However, the inset in Fig. 15a shows that the two results are in excellent agreement in the first 200 seconds, after which the two begin to deviate. The pattern of the phase trajectories in Fig. 15b can ensure that the discrepancy of the time histories in Fig. 15a is not caused by the responses’ symmetry, but by the accuracy of the two numerical schemes. Overall, the RP approximation method can be applied in the analysis of chaotic motions to capture the primary feature of chaos.

Fig. 16
figure 16

a Time history, b phase portrait and c Poincare map for the pitch motion for \(U^*/U^*_L=0.27\) (chaotic transient)

Full size image

5.3 Chaotic transients

Furthermore, the chaotic transients will be analyzed in this part. Shown in Fig. 16 are the time histories, phase portraits, and Poincare maps for \(U^*/U^*_L=0.27\) by the two methods. We can see from Fig. 16a that the two responses agree well until roughly \(0.8\times 10^4\,s\), after which they differ from each other qualitatively. Very interestingly, the inset shows that the time history calculated by the RK4Henon method settles into a periodic motion after a long-lived chaotic transient, while that by the RP approximation method keeps being chaotic. The lifetime of the chaotic transient is up to \(3.77\times 10^4\,s\). Figure 16b, c shows the phase portraits and the Poincare maps, respectively; these figures are constructed after the long-lived chaotic transients have been dropped out. Figure 16b indicates that the response by RK4Henon is indeed periodic (after a very long chaotic transient). Although the two motions are essentially different types, the symmetry of the two trajectories, which was discussed in the LCO case, can be noticed in Fig. 16b. Figure 16c shows the Poincare maps by the two methods. The Poincare map by the RK4Henon contains two adjacent points, which indicates a period-2 motion, while that by the RP approximation method shows a well-organized structure indicating chaos. In sum, the RP approximation method cannot be applied to capture the long-lived chaotic transient followed by a periodic motion.

6 Parametric variations

The effects of the various parameters on the aeroelastic response will be explored in this part. In the following computations, the reference system parameters are provided as Case 3 in Table 1. In the course of investigating a specified parameter, only the one under consideration is varied with the rest being fixed. Except that when \(\delta \) is varied, the \(\alpha _f\) is varied correspondingly. The linear flutter speed \(U^*_L\) remains to be 6.2851, and \(U^*_L\) keeps unchanged during parametric variations.

6.1 Effect of freeplay nonlinearity

The freeplay nonlinearity is affected by three factors: (1) the freeplay magnitude \(\delta \), (2) the preload \(M_0\), and (3) the stiffness in the freeplay range \(M_f\). We will investigate their effect one by one, by means of bifurcation diagrams. In plotting the bifurcation diagrams, the stepsize of the flow speed is \(0.01(U^*/U^*_L)\).

Fig. 17
figure 17

Bifurcation diagrams plotting \(\alpha \) for \(\dot{\alpha }=0\) as a function of \(U^*/U^*_L\) for various values of \(\delta \): a \(\delta =0.25\), b \(\delta =0.5\), c \(\delta =0.75\); and (d), phase portrait for \(U^*/U^*_L=0.48\) for the case with \(\delta =0.75\)

Full size image

6.1.1 Effect of \(\delta \)

Figure 17 shows the bifurcation diagrams for the pitch motion for various values of freeplay \(\delta \). It is seen that as the freeplay \(\delta \) increases the peak amplitude of the response becomes larger. In particular, the peak amplitudes for \(\delta =0.25,~0.5\) and \(0.75\) are \(0.54,~1.1\) and \(1.6\), respectively, for \(U^*/U^*_L=0.8\). On the other hand, the critical flutter speeds for the three cases are almost the same (approximately at \(U^*/U^*_L=0.14\)), which means that the magnitude of the freeplay does not alter the critical flutter speed (here, flutter means LCO occurs).

The “flip-over” phenomenon, e.g., around \(U^*/U^*_L \!=\! 0.6\) in Fig. 17a, is pervasive in bifurcation diagrams. If a parameter marching procedure is employed, “flip-over” can be avoided. Figure 17d shows the phase portrait of the pitch motion for \(U^*/U^*_L=0.48\) in Fig. 17c. Its chaos-like appearance explains the densely plotted vertical line at \(U^*/U^*_L=0.48\) in Fig. 17c. Moreover, we note that the response, prior to the flutter speed, is statically stable with a constant pitch angle. The statically stable response is not the present concern in the present study.

Fig. 18
figure 18

Bifurcation diagrams plotting \(\alpha \) for \(\dot{\alpha }=0\) as a function of \(U^*/U^*_L\) for various values of \(M_0\): a \(M_0=-0.0025\), b \(M_0=0.0025\), c \(M_0=0.01\)

Full size image

6.1.2 Effect of \(M_0\)

Shown in Fig. 18 are the bifurcation diagrams for different values of preload \(M_0\). Overall, the magnitude of the preload does not significantly influence the amplitude of the motions. Specifically, the first two diagrams with \(M_0=-0.0025\) and \(0.0025\) are similar, except that prior to \(U^*/U^*_L=0.55\), the two responses are symmetric. This symmetric feature can be explained by the solutions’ dependance on initial conditions. The comparison between the last two diagrams indicates that increasing the magnitude of the preload may increase the flutter speed.

Fig. 19
figure 19

Bifurcation diagrams plotting \(\alpha \) for \(\dot{\alpha }=0\) as a function of \(U^*/U^*_L\) for various values of \(M_f\): a \(M_f=0.01\), b \(M_f=0.02\), c \(M_f=0.03\)

Full size image

6.1.3 Effect of \(M_f\)

Similarly, the effect of \(M_f\) is also investigated. In practice, \(M_f\) is much smaller than the linear stiffness, viz. \(1\). Here, the bifurcation diagrams for \(M_f=0.001,~0.02\), and \(0.03\) are plotted in Fig. 19. Generally speaking, \(M_f\) does not significantly influence the response of the aeroelastic system, which can be intuitively understood by the facts that (1) \(M_f\) exists only within the freeplay and (2) \(M_f\) has a very small value compared with unity. In detail, we can see from Fig. 19 that a larger value of \(M_f\) slightly increases the onset of flutter. In the limiting situation, if the \(M_f\) is increased to \(1\), the present system with freeplay nonlinearity degenerates to a linear system. In this special case, the critical flutter speed is equal to the linear flutter speed \(U^*_L\).

Fig. 20
figure 20

Bifurcation diagrams plotting \(\alpha \) for \(\dot{\alpha }=0\) as a function of \(U^*/U^*_L\) for various levels of damping: a \(\zeta _\alpha =\zeta _\xi =0.02\), b \(\zeta _\alpha =\zeta _\xi =0.04\), c \(\zeta _\alpha =\zeta _\xi =0.1\)

Full size image
Fig. 21
figure 21

Bifurcation diagrams plotting \(\alpha \) for \(\dot{\alpha }=0\) as a function of \(U^*/U^*_L\) for different values of \(\bar{\omega }\): a \(\bar{\omega }=0.22\), b \(\bar{\omega }=0.25\), c \(\bar{\omega }=0.3\)

Full size image

6.2 Effect of damping level

Figure 20 provides three bifurcation diagrams for three different levels of damping. As shown in Fig. 20a, when the damping is relatively weak, viz. \(\zeta _\alpha =\zeta _\xi =0.02\), the bifurcation diagram has a chaotic region approximately from \(0.25\) to \(0.57\). Increasing the damping to \(\zeta _\alpha =\zeta _\xi =0.04\), the chaotic range will be reduced significantly, see Fig. 20b. Further increasing the damping to \(\zeta _\alpha =\zeta _\xi =0.1\), the chaotic response has been completely removed, see Fig. 20c. So, it can be concluded that a reasonably large damping can suppress the presence of chaos, which is consistent with the report of Price et al. [27]. On the other hand, it can be seen by comparing the diagrams in Fig. 20 that the damping can slightly affect the critical flutter speed. Specifically, the critical values for \(\zeta _\alpha =\zeta _\xi =0.02,~0.04\) and \(0.1\) are \(U^*/U^*_L=1.14,~1.16\) and \(2.11\), respectively, which indicates that the damping also has the effect of stabilizing the aeroelastic airfoil. Besides, the damping level does not influence the amplitude of motions.

6.3 Effect of frequency ratio

The bifurcation diagrams for different values of \(\bar{\omega }\) are given in Fig. 21. We can see that the response amplitude increases with the increase of \(\bar{\omega }\), especially for a relatively large flow speed. For instance, when \(U^*/U^*_L=0.8\), the maximum pitch amplitudes for \(\bar{\omega }=0.22,~0.25\) and 0.3 are 1.13, 1.28, and 1.75, respectively. Additionally, the critical flutter speeds for different values of \(\bar{\omega }\) are also different. Specifically, flutter speeds for \(\bar{\omega }=0.22,~0.25\) and 0.3 are 0.14, 1.16 and 0.21, respectively. It means that increasing the frequency ratio \(\bar{\omega }\) can raise the flutter speed of the present two DOF airfoil system. Moreover, it can be seen that the increase in the frequency ratio has an effect of suppressing the occurrence of chaos. Concretely, when \(\bar{\omega }=0.22\), the diagram has a range of chaos. Increasing \(\bar{\omega }\) to 0.25, the diagram only exhibits periodic motions. Further increasing \(\bar{\omega }\) to 0.3, the diagram shows a much simpler period-1 response.

7 Concluding remarks

A numerical study of the two DOF airfoil with freeplay nonlinearity was carried out. The comparison of the classical RK4 method and the RK4Henon method was conducted in the analyses of LCOs, chaos, and chaotic transients. Some conclusions were drawn. First, the RK4 method can be used to generate a relatively good result in the analysis of LCOs, although there exists an inherent numerical instability due to the crossover of the discontinuous points. Second, the RK4 method cannot capture the chaotic response to a long- term, as in contrast to the RK4Henon method. Even applying a very small integration stepsize, the RK4 method cannot match with the present RK4Henon method. Third and most importantly, the RK4Henon method can capture the long-lived chaotic transient followed by a periodic motion, while the RK4 method cannot. In sum, the RK4Henon method is a better choice when analyzing periodic motions and (perhaps) the only choice for analyzing chaos and chaotic transients. Moreover, the comparison of the RP approximation method and the RK4Henon method has been conducted. It showed that the RP approximation method was suitable for analyzing LCOs, and chaos, but not for chaotic transients.

In addition, a useful tool for identifying chaotic transients, based on viewing the evolution history of the LLE of a time series, was proposed. It was demonstrated that a decreasing LLE history implies the existence of chaotic transient. This finding provides researchers in the dynamics community with an efficient tool to distinguish chaos and long-lived chaotic transients. This method is believed to be more effective than the normally used method, that is, running a very longtime numerical integration to see whether the time history finally settles to a periodic attractor.

Finally, the effects of freeplay, damping level, and frequency ratio on the aeroelastic response were analyzed. For the freeplay nonlinearity, (1) increasing the freeplay magnitude raises the amplitude of the response, but does not change the flutter speed; (2) conversely, increasing the preload of the freeplay nonlinearity increases the flutter speed, but the response amplitude keeps unchanged; and (3) the magnitude of \(M_f\) only slightly affects the critical flutter speed. For the effect of damping, we come to two conclusions: (1) increasing the damping level may increase the flutter speed; and (2) the damping has an effect of suppressing the occurrence of chaos. Moreover, the increase in the frequency ratio \(\bar{\omega }\) enhances both the response amplitude and the flutter speed.