Hyperchaos in constrained Hamiltonian system and its control

Abstract

This paper first formulates a Hamiltonian system with hyperchaotic phenomena and investigates the equilibrium point and double Hopf bifurcation of the system. We obtain the result that the Hamiltonian system has hyperchaotic behaviors when any system parameter varies. The influences of holonomic constraint and nonholonomic constraint on the equilibrium points, invariance and the hyperchaotic state of the Hamiltonian system are then studied. Finally, we achieve the hyperchaotic control of the Hamiltonian system by introducing the constraint method. The studies indicate that the constraint can not only change the Hamiltonian system from hyperchaotic state to periodic state or chaotic state, but also make the Hamiltonian system become globally asymptotically stable. Numerical simulations, including Lyapunov exponents, bifurcation diagrams, Poincaré maps and phase portraits for systems, exhibit the complex dynamical behaviors.

1 Introduction

The Hamiltonian system is a very important dynamical system in physics, mechanics, life sciences and engineering applications, where many Hamiltonian dynamical models have emerged in recent years [1,2,3,4,5]. Since many systems can be written in a Hamiltonian form easily, the Hamiltonian systems have been investigated widely in mechanics, mathematics and engineering applications and many remarkable research results are obtained, such as Refs. [6,7,8,9,10]. Recently, the chaotic behaviors of Hamiltonian systems have attracted many scientists and have been introduced to almost every field of natural science [11,12,13,14]. Chaos is a universal phenomenon of nature. Study on chaos is in the front field of nonlinear systems. Nowadays, we can observe a growing interest in the higher-dimensional dynamical systems as a result of extensive studies of the chaotic systems. Any system containing at least one positive Lyapunov exponent is defined to be hyperchaotic [15]. The Lyapunov exponents are the average exponential rates of divergence or convergence of nearby trajectories in the phase space. It means that hyperchaotic systems generate much more complex dynamical behaviors compared with chaotic systems [16]. Chaos has two sides in practice. On the one hand, the chaos is useful in image encryption scheme [17], secure key distribution [18] and secure communications [19]. On the other hand, the chaos is harmful in vehicles vibration [20], permanent magnet synchronous machine [21] and complex networks with disturbances [22]. Therefore, it is necessary to control chaos according to the actual needs of different disciplines and fields. Based on different strategies, various methods of chaos control are proposed, such as parameter switching algorithm for the Hastings-Pouwll system [23], the decreasing-impulse-induced chaos-controlling scenario in starlike networks [24] and the state feedback control strategy and pole-placement technique for a modified Nicholson-Bailey model [25].

Compared to a chaotic system, the hyperchaotic system has better application prospects when the chaos is useful in practical application. For instance, the application of hyperchaotic system can make the information more secure [26,27,28]. In recent years, it has become a hot spot to formulate and investigate the hyperchaotic system because of its useful applications, and various hyperchaotic systems were discovered and studied. For example, Ma and his cooperators [29] proposed a time-varying hyperchaotic system by introducing changeable electric power source into circuit. Jajarmi et al. [30] constructed a hyperchaotic financial system by adding a new state variable into a three-dimensional chaotic economic model. Based on the four-dimensional Rabinovich differential system [31], He et al. formulated a fractional-order hyperchaotic Rabinovich system and discussed the hyperchaos control of the system by using the linear feedback control and the active control method [32]. In this paper, we will propose a hyperchaotic Hamiltonian system through the Hamiltonian function and discuss the influences of holonomic constraint and nonholonomic constraint on the Hamiltonian system behaviors. Furthermore, we will achieve the hyperchaotic control of the Hamiltonian system by introducing the constraint method, which is different from the methods in Refs. [23,24,25, 32].

The organization of this paper is as follows. In Sect. 2, we formulate a hyperchaotic Hamiltonian system. The invariance, the type of equilibrium points, double Hopf bifurcation and hyperchaotic behaviors of the system changing with any system parameter are analyzed. In Sect. 3, we present a holonomic constrained system and a nonholonomic constrained system, respectively. By using the methods of Ref. [33] and Lagrange multiplier, the explicit equations for constrained systems are obtained. The influences of constrained parameters on the equilibrium points, symmetry and the hyperchaotic behaviors of the Hamiltonian system are investigated. In Sect. 4, by introducing the constraint method, how to control the hyperchaotic behavior of the Hamiltonian system is studied. The conclusions are summarized in Sect. 5.

2 Hyperchaotic Hamiltonian system

2.1 Model

In general, the dynamics of Hamiltonian system with s degrees of freedom is described by a Hamiltonian function $H({{{\varvec{{q}}}},\mathbf{p } },t)$, where ${{{\varvec{q}}}}=(q_{1},q_{2},\ldots ,q_{s})$ is the generalized coordinate, ${{{\varvec{p}}}}=(p_{1},p_{2},\ldots ,p_{s})$ is the canonical momentum and t denotes time. The unconstrained Hamilton’s equations are

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{i}=\frac{\partial H({{{\varvec{q}}}},{{{\varvec{p}}}},t)}{\partial p_{i}}, \\ \dot{p}_{i}=-\frac{\partial H({{{\varvec{q}}}},{{{\varvec{p}}}},t)}{\partial q_{i}},\\ \end{array} \right. \end{aligned}$$

(1)

here $i=1,2,\ldots ,s$. Because of its clear structure and convenience of use, the Hamiltonian function has been widely used to represent physical processes and physical phenomena, such as the dynamical motion of Rydberg atoms in the crossed magnetic and electric fields [34], the motion of the Foucault pendulum and Lagrange top [35] and the nonlinear vibration of the damped and unloaded cylindrical shells [36].

In this subsection, we assume that the Hamiltonian system is described by a function

$$\begin{aligned} H({{{\varvec{q}}}},{{{\varvec{p}}}},t)= & {} \frac{p_{1}^2+p_{2}^2-\theta q_{1}^2-\theta q_{2}^2}{2}\\&+\,\frac{\beta (q_{1}^4+q_{2}^4)}{4}+\eta q_{1}\left( q_{2}-\frac{\eta q_{1}}{2}\right) . \end{aligned}$$

Then, according to (1), the Hamiltonian system can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{1}=p_{1},\\ \dot{q}_{2}=p_{2},\\ \dot{p}_{1}=\theta q_{1}-\beta q_{1}^3-\eta q_{2}+\eta ^2q_{1},\\ \dot{p}_{2}=\theta q_{2}-\beta q_{2}^{3}-\eta q_{1},\\ \end{array} \right. \end{aligned}$$

(2)

where $\theta$, $\beta$, $\eta$ are positive parameters. The dot expresses the derivative with respect to t.

Obviously, system (2) is invariant for the coordinate transformation

$$\begin{aligned} (q_{1},q_{2},p_{1},p_{2})\rightarrow (-q_{1},-q_{2},-p_{1},-p_{2}). \end{aligned}$$

It is easy to visualize that system (2) always has the equilibrium point ${{{\varvec{E}}}_{0}}=(0,0,0,0)$. The Jacobian matrix at ${{{\varvec{E}}}_{0}}$ is

$$\begin{aligned} {{{\varvec{J}}}}({{{\varvec{E}}}_{0}}) =\left( \begin{array}{cccc} 0 &{}0 &{}1 &{} 0\\ 0 &{} 0 &{}0 &{} 1\\ \theta +\eta ^2 &{}-\eta &{} 0 &{}0\\ -\eta &{}\theta &{}0&{} 0 \end{array} \right) . \end{aligned}$$

The characteristic equation of ${{{\varvec{J}}}}({{{\varvec{E}}}_{0}})$ is

$$\begin{aligned} \lambda ^4-(2\theta +\eta ^2)\lambda ^2+\theta ^2+\theta \eta ^2-\eta ^2=0. \end{aligned}$$

Based on computation results, the roots of the characteristic equation are

$$\begin{aligned}&\lambda _{1,2}=\pm \sqrt{\frac{2\theta +\eta ^2+\eta \sqrt{\eta ^2+4}}{2}}, \\&(\lambda _{3,4})^2=\frac{2\theta +\eta ^2-\eta \sqrt{\eta ^2+4}}{2}. \end{aligned}$$

Thus, ${{{\varvec{E}}}_{0}}$ is an unstable equilibrium point. In addition, ${{{\varvec{E}}}_{0}}$ is a saddle point when $\frac{2\theta +\eta ^2}{\eta \sqrt{\eta ^2+4}}>1$, and a saddle-center point when $\frac{2\theta +\eta ^2}{\eta \sqrt{\eta ^2+4}}<1$. System (2) also has equilibria ${{{\varvec{E}}}_{j}}$ $=(q_{j1},q_{j2},0,0)$ , when

$$\begin{aligned} \left( \frac{\theta }{\eta ^2}+1-\frac{\beta q_{j1}^2}{\eta ^2}\right) \left( \theta -\beta q_{j2}^2\right) =1. \end{aligned}$$

It can be seen that there are multiple equilibrium points; those points meet the condition. For the equilibria ${{{\varvec{E}}}_{j}}$, the Jacobian matrix is

$$\begin{aligned} {{{\varvec{J}}}}({{{\varvec{E}}}_{j}}) =\left( \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ \theta -3\beta q_{j1}^2+\eta ^2 &{} -\eta &{} 0 &{} 0\\ -\eta &{} \theta -3\beta q_{j2}^2 &{} 0&{} 0 \end{array} \right) . \end{aligned}$$

By using $|\lambda {{{\varvec{I}}}}-{{{\varvec{J}}}}({{{\varvec{E}}}_{j}})|=0$, the characteristic equation of ${{{\varvec{J}}}}({{{\varvec{E}}}_{j}})$ is obtained as follows:

$$\begin{aligned} f(\lambda )=\lambda ^4+a_{2}\lambda ^2+a_{0}, \end{aligned}$$

where

$$\begin{aligned} a_{2}= & {} 3\beta q_{j1}^2+3\beta q_{j2}^2-2\theta -\eta ^2,\\ a_{0}= & {} 6\beta ^2 q_{j1}^2q_{j2}^2+2\eta ^2-2\theta (\theta +\eta ^2). \end{aligned}$$

Thus,

$$\begin{aligned} \lambda ^2=\frac{2\theta +\eta ^2-3\beta q_{j1}^2-3\beta q_{j2}^2\pm \sqrt{\delta }}{2}, \end{aligned}$$

where

$$\begin{aligned} \delta =4\eta ^2+\left( \eta ^2-3\beta \left( q_{j1}^2-q_{j2}^2\right) \right) ^2. \end{aligned}$$

For the equilibrium point ${{{\varvec{E}}}_{j}}$, by analysis and calculation, we obtain

(I) ${{{\varvec{E}}}_{j}}$ is a saddle-center point, when $\frac{6\beta ^2q_{j1}^2q_{j2}^2}{2\theta (\theta +\eta ^2)}<1$,

(II) ${{{\varvec{E}}}_{j}}$ is a saddle point, when $\frac{6\beta ^2q_{j1}^2q_{j2}^2}{2\theta (\theta +\eta ^2)}>1$ and $\frac{3\beta (q_{j1}^2+q_{j2}^2)}{2\theta +\eta ^2}<1$,

(III) the double Hopf bifurcation will occur at ${{{\varvec{E}}}_{j}}$ of system (2), when $\frac{6\beta ^2q_{j1}^2q_{j2}^2}{2\theta (\theta +\eta ^2)}>1$ and $\frac{3\beta (q_{j1}^2+q_{j2}^2)}{2\theta +\eta ^2}>1$.

Thus, ${{{\varvec{E}}}_{j}}$ is unstable in the case of (I), (II) and the system exhibits equilibrium center. In the case of (III), $f(\lambda )$ has two paris of conjugate purely imaginary roots

$$\begin{aligned} \lambda _{1,2}= & {} \pm \sqrt{\frac{-2\theta -\eta ^2+3\beta (q_{j1}^2+q_{j2}^2)+\sqrt{\delta }}{2}}i,\\ \lambda _{3,4}= & {} \pm \sqrt{\frac{-2\theta -\eta ^2+3\beta (q_{j1}^2+q_{j2}^2)-\sqrt{\delta }}{2}}i. \end{aligned}$$

From the above analyses, we can see that system (2) may have many equilibria and they almost are unstable. In chaos theory, the equilibrium points of the system are of great importance to understand its nonlinear dynamics [37]. It has been long supposed that the existence of chaotic behavior in the microscopic motions is responsible for their equilibrium and non-equilibrium properties [38]. Meanwhile, the double Hopf bifurcation indicates the possible existence of a chaotic attractor [39]. Therefore, it is necessary to further analyze the complex behaviors of the Hamiltonian system.

2.2 Hyperchaos and simulation

Because there is large difficulty in theory analysis of hyperchaotic phenomena [40], we give some simulations to study system (2). In this subsection, we compute the Lyapunov spectrum and bifurcation diagram to explore the complex dynamics of system (2) using MATLAB. In order to show hyperchaotic phenomenon of system (2), by taking the parameters

$$\begin{aligned} \theta =1, ~\eta =0.01,~\beta \in (0.1,10), \end{aligned}$$

and initial values

$$\begin{aligned} (q_{10},q_{20},p_{10},p_{20})=(1,0.1,0.01,0.001). \end{aligned}$$

In this case, eigenvalues of ${{{\varvec{J}}}}({{{\varvec{E}}}_{0}})$ are

$$\begin{aligned} \lambda _{1,2}=\pm \,0.9913271003,~~\lambda _{3,4}=\pm \,1.008647897. \end{aligned}$$

${{{\varvec{E}}}}_{0}$ is an unstable equilibrium point. According to the discussion of nonzero equilibrium point in Sect. 2.1, $q_{j1}$, $q_{j2}$ and $\beta$ satisfy $F(q_{j1},q_{j2},\beta )=0$, where

$$\begin{aligned} F(q_{j1},q_{j2},\beta )=\beta q_{j1}^2q_{j2}^2-q_{j1}^2-1.0001\beta q_{j2}^2+1. \end{aligned}$$

To more directly illustrate the relationship between $q_{j1}$, $q_{j2}$ and $\beta$, the $(q_{j1},q_{j2})$ of rest equilibrium points with different $\beta$ are on the surface in Fig. 1. It shows the distribution of $q_{j1}$, $q_{j2}$ under different parameter $\beta$.

Fig. 1

Surface of $(q_{j1},q_{j2},\beta )$

To study equilibria ${{{\varvec{E}}}_{j}}$, we transform the last two equations of (2) into

$$\begin{aligned} \beta q_{j1}^2=\theta +\eta ^2-\eta \frac{q_{j2}}{q_{j1}},~~\beta q_{j2}^2=\theta -\eta \frac{q_{j1}}{q_{j2}}, \end{aligned}$$

then

$$\begin{aligned} a_{2}= & {} 4\theta +2\eta ^2-3\eta \left( y+\frac{1}{y}\right) ,\\ a_{0}= & {} 6\left( \theta +\eta ^2-\frac{\eta }{y}\right) (\theta -\eta y)+2\eta ^2-2\theta (\theta +\eta ^2), \end{aligned}$$

where $y=\frac{q_{j1}}{q_{j2}}$ and satisfies

$$\begin{aligned} \eta y^4-\theta y^3+\left( \theta +\eta ^2\right) y-\eta =0. \end{aligned}$$

When $\theta =1$, $\eta =0.01$, the results of the direct calculations are as follows:

$$\begin{aligned} y_{1}= & {} 0.0099999999,~~a_{2}=0.99989997,~~a_{0}=-\,1.9994;\\ y_{2}= & {} 1.000051019,~~a_{2}=3.9402,~~a_{0}=3.881193999;\\ y_{3}= & {} 99.989998,~~a_{2}=1.00020003,~~a_{0}=-\,1.99939988;\\ y_{4}= & {} -\,1.000049018,~~a_{2}=4.0602,~~a_{0}=4.121206. \end{aligned}$$

Hence, there are saddle-center equilibrium points and double Hopf bifurcations in system (2) under certain conditions of $\beta$. For example, if $\beta =1.131$, then

$$\begin{aligned}&(-\,0.9403048916,-\,0.9403989503,0,0),\\&(0.9403048916,0.9403989503,0,0),\\&(-\,0.00940257,-\,0.9402578799,0,0),\\&(0.00940257,0.9402578799,0,0) \end{aligned}$$

are saddle-center equilibrium points, and the system occurs double Hopf bifurcations at

$$\begin{aligned}&(-\,0.93563905,-\,0.9355913178,0,0),\\&(0.93563905,0.9355913178,0,0),\\&(-\,0.94504128,0.9449949547,0,0),\\&(0.94504128,-\,0.9449949547,0,0). \end{aligned}$$

In the same way, system (2) still has the equilibrium points which satisfy the one of (I), (II) and (III) under certain conditions of $\theta$ or $\eta$.

Fig. 2

Lyapunov exponents of (2) by adjusting $\beta$

Fig. 3

Bifurcation diagram of (2) by adjusting $\beta$

Any system with more than two positive Lyapunov exponents is defined to be hyperchaotic [15, 41]. The Lyapunov exponents of system (2) with different parameters $\beta$ are displayed in Fig. 2. It is shown that the unconstrained Hamiltonian system has two positive Lyapunov exponents, which exhibits the hyperchaotic behavior. From Fig. 2, we can see that two Lyapunov exponents are positive and negative variations when parameter $\beta$ varies in (0.1, 1.735). In particular, the system has three positive Lyapunov exponents when $\beta$ varies in (1.131, 1.735). The Lyapunov exponents and the bifurcation diagram match very well. The bifurcation diagram of system (2) by adjusting parameter $\beta$ is shown in Fig. 3, which also indicates the change of dynamic behaviors of Hamiltonian system (2) with different parameters $\beta$.

Figures 4 and 5 show that the Hamiltonian system (2) is hyperchaotic when the parameters

$$\begin{aligned} \beta =1,~~\eta =0.01,~~\theta \in (0.1,10), \end{aligned}$$

and $\theta =1$, $\beta =1$, $\eta \in (0.001,1)$, respectively. It indicates that in system (2), three Lyapunov exponents and positive and negative variations of Lyapunov exponents in a certain interval of parameter $\theta$ or $\eta$ also occur. Based on above analysis, we can see that the Hamiltonian system is hyperchaotic when any system parameter varies, and the Hamiltonian system has rich hyperchaotic behaviors when the system parameter varies in certain interval.

Fig. 4

Lyapunov exponents of (2) by adjusting $\theta$

Fig. 5

Lyapunov exponents of (2) by adjusting $\eta$

3 Constrained Hamiltonian system

The constrained Hamiltonian systems have many applications, for instance in multi-body dynamics, electrical circuits, molecular dynamics, chemistry and statistical mechanics [42,43,44,45,46,47,48]. In the following, we mainly investigate the hyperchaotic phenomenon in system (2) under constraint condition.

3.1 Holonomic constraint

Assume the constraint on Hamiltonian system (2) is

$$\begin{aligned} q_{1}^2+q_{2}^2=L^2. \end{aligned}$$

(3)

Here, we use the three-step approach of Ref. [33] for obtaining the explicit equations which are equivalent to the equations of holonomic Hamiltonian system (2), (3). Differentiating Eq. (3) with respect to time, we get

$$\begin{aligned} \phi ({{{\varvec{q}}}},{{{\varvec{p}}}}): ={{{\varvec{q}}}}{{{\varvec{p}}}}^\mathrm{T}=0. \end{aligned}$$

(4)

Differentiating Eq. (4) with respect to time, we obtain

$$\begin{aligned} {{{{\varvec{A}}}}}_{p}\dot{{{{\varvec{p}}}}}^\mathrm{T}={{{{\varvec{b}}}}}_{p}, \end{aligned}$$

where

$$\begin{aligned} {{{{\varvec{A}}}}}_{p}={{{\varvec{q}}}}, {{{{\varvec{b}}}}}_{p}=-{{{\varvec{p}}}}{{{\varvec{p}}}}^\mathrm{T}. \end{aligned}$$

The matrix

$$\begin{aligned} H_{{{{\varvec{p}}}}{{{\varvec{p}}}}}^{-1}=\left( \frac{\partial ^2H}{\partial {{{{\varvec{p}}}}}^2}\right) ^{-1}={{{\varvec{I}}}}_{2}. \end{aligned}$$

The Hamiltonian system (2) is subjected to the single constraint $\phi ({{{\varvec{q}}}},{{{\varvec{p}}}})=0$, and the holonomic Hamiltonian system (2), (3) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \dot{{{\varvec{q}}}}=\frac{\partial H}{\partial {{{\varvec{p}}}}},\\ \dot{{{\varvec{p}}}}=-\frac{\partial H}{\partial {{{\varvec{q}}}}}+ C({{{\varvec{q}}}},{{{\varvec{p}}}}),\\ \end{array} \right. \end{aligned}$$

(5)

where

$$\begin{aligned} C({{{\varvec{q}}}},{{{\varvec{p}}}})^\mathrm{T}= & {} ({{{\varvec{I}}}}_{2})^{-1}{{{\varvec{q}}}}^\mathrm{T} ({{{\varvec{q}}}}{{{{\varvec{I}}}}_{2}}^{-1}{{{\varvec{q}}}}^\mathrm{T})^{-1}\\&\times \left( -{{{\varvec{p}}}} {{{\varvec{p}}}}^\mathrm{T}+\frac{\partial H}{\partial {{{\varvec{q}}}}}{{{\varvec{q}}}}^\mathrm{T}\right) . \end{aligned}$$

Then,

$$\begin{aligned} C({{{\varvec{q}}}},{{{\varvec{p}}}})^\mathrm{T}= & {} {{{\varvec{I}}}}_{2} \left( \begin{array}{c} q_{1}\\ q_{2} \end{array} \right) (q_{1}^2+q_{2}^2)^{-1}\left( -p_{1}^2-p_{2}^2\right. \\&\left. +\, \frac{\partial {H}}{\partial {{{\varvec{q}}}}}\left( \begin{array}{c} q_{1}\\ q_{2} \end{array} \right) \right) =\frac{1}{L^2} \left( \begin{array}{c} q_{1}\\ q_{2} \end{array} \right) C_{1}({{{\varvec{q}}}},{{{\varvec{p}}}}), \end{aligned}$$

where

$$\begin{aligned} C_{1}({{{\varvec{q}}}},{{{\varvec{p}}}})= & {} -p_{1}^2-p_{2}^2-\theta L^2+\beta L^4-2\beta q_{1}^2q_{2}^2\\&+\,2\eta q_{1}q_{2}-\eta ^2q_{1}^2. \end{aligned}$$

Thus, the holonomic Hamiltonian system is transformed into

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{1}=p_{1},\\ \dot{q}_{2}=p_{2},\\ \dot{p}_{1}=\beta L^2q_{1}+\eta ^2q_{1}-\eta q_{2}-P_{1h}({{{\varvec{q}}}},{{{\varvec{p}}}}),\\ \dot{p}_{2}=\beta L^2q_{2}-\eta q_{1}-P_{2h}({{{\varvec{q}}}},{{{\varvec{p}}}}),\\ \end{array} \right. \end{aligned}$$

(6)

where

$$\begin{aligned}&{P_{1h}({{{\varvec{q}}}},{{{\varvec{p}}}})}=\beta q_{1}^3 \\&\quad +\,\frac{\eta ^2 q_{1}^3-2\eta q_{1}^2q_{2}+p_{1}^2q_{1}+p_{2}^2q_{1}+2\beta q_{1}^3q_{2}^2}{L^2},\\&{P_{2h}({{{\varvec{q}}}},{{{\varvec{p}}}})}=\beta q_{2}^3\\&\quad +\,\frac{\eta ^2q_{1}^2q_{2}-2\eta q_{1}q_{2}^2+p_{1}^2q_{2}+p_{2}^2q_{2}+2\beta q_{1}^2q_{2}^3}{L^2}. \end{aligned}$$

It can be seen from (6) that the system is also invariant for the coordinate transformation

$$\begin{aligned} (q_{1},q_{2},p_{1},p_{2})\rightarrow (-q_{1},-q_{2},-p_{1},-p_{2}). \end{aligned}$$

The Jacobian matrix ${{{\varvec{J}}}}({{{\varvec{E}}}}_{0})$ is

$$\begin{aligned} \left( \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ \beta L^2+\eta ^2 &{} -\eta &{} 0 &{} 0\\ -\eta &{} \beta L^2 &{} 0&{} 0 \end{array} \right) . \end{aligned}$$

The eigenvalues of ${{{\varvec{J}}}}({{{\varvec{E}}}}_{0})$ are

$$\begin{aligned} \lambda _{1,2}=\pm \sqrt{\frac{2\beta L^2+\eta ^2+\eta \sqrt{\eta ^2+4}}{2}} \end{aligned}$$

and

$$\begin{aligned} (\lambda _{3,4})^2=\frac{2\beta L^2+\eta ^2-\eta \sqrt{\eta ^2+4}}{2}. \end{aligned}$$

${{{\varvec{E}}}}_{0}$ is also an unstable equilibrium point. In addition, ${{{\varvec{E}}}}_{0}$ is a saddle point when

$$\begin{aligned} \frac{2\beta L^2+\eta ^2}{\eta \sqrt{\eta ^2+4}}>1, \end{aligned}$$

and a saddle-center point when

$$\begin{aligned} \frac{2\beta L^2+\eta ^2}{\eta \sqrt{\eta ^2+4}}<1. \end{aligned}$$

Similarly, system (6) exhibits equilibria ${{{\varvec{E}}}}_{j}=(q_{j1},q_{j2},0,0)$, when

$$\begin{aligned}&\frac{(2\eta q_{j2}^2{-}L^2\eta {+}2\beta q_{j1}^3q_{j2})(2\eta q_{j1}^2-L^2\eta {+}2\beta q_{j1}q_{j2}^3)}{(\beta ^2L^4{-}\eta ^4)q_{j1}^2q_{j2}^2}=1. \end{aligned}$$

Let

$$\begin{aligned}&P_{11}(q_{1},q_{2})\\&\quad =-\frac{-(\beta L^4+L^2\eta ^2)q_{1}+L^2\eta q_{2}+(\beta L^2+\eta ^2)q_{1}^3-2\zeta _{10}}{L^2},\\&P_{12}(q_{1},q_{2})\\&\quad =-\frac{-\beta L^4q_{2}+L^2\eta q_{1}+\beta L^2q_{2}^3+\eta ^2 q_{1}^2q_{2}-2\eta q_{j}q_{2}^2+2\zeta _{20}}{L^2}.\\&\zeta _{10}=(\eta -\beta q_{1}q_{2}) q_{1}^2q_{2}, \zeta _{20}=\beta q_{1}^2q_{2}^3, \end{aligned}$$

the Jacobian matrix ${{{\varvec{J}}}}({{{\varvec{E}}}}_{j})$ is

$$\begin{aligned} \left( \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ \frac{\partial P_{11}}{\partial q_{1}}|_{(q_{j1},q_{j2})} &{} \frac{\partial P_{11}}{\partial q_{2}}|_{(q_{j1},q_{j2})}&{} 0 &{} 0\\ \frac{\partial P_{12}}{\partial q_{1}}|_{(q_{j1},q_{j2})} &{} \frac{\partial P_{12}}{\partial q_{2}}|_{(q_{j1},q_{j2})} &{} 0&{} 0 \end{array} \right) . \end{aligned}$$

The characteristic equation can be obtained as follows:

$$\begin{aligned}&\lambda ^4-\left( \frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})}+\frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}\right) \lambda ^2\\&\quad +\, \frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})}\right. \\&\quad \left. \times \frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}-\frac{\partial P_{11}}{\partial q_{2}}\left| _{(q_{j1},q_{j2})}\frac{\partial P_{12}}{\partial q_{1}}\right| _{(q_{j1},q_{j2})}=0. \end{aligned}$$

Then,

$$\begin{aligned} 2\lambda ^2= & {} \frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})}+\frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}\\&\pm \sqrt{\left( \frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})}+\frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}\right) ^2+4\epsilon },\\ \epsilon= & {} \frac{\partial P_{11}}{\partial q_{2}}\left| _{(q_{j1},q_{j2})}\frac{\partial P_{12}}{\partial q_{1}}\right| _{(q_{j1},q_{j2})}\\&-\frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})} \times \frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}. \end{aligned}$$

Obviously, for the equilibrium point ${{{\varvec{E}}}_{j}}$ of constraint system (6), we can obtain the conclusions:

(I) ${{\varvec{E}}}_{j}$ is a saddle-center point, when $\epsilon >0$,

(II) ${{\varvec{E}}}_{j}$ is a saddle point, when

$$\begin{aligned} \epsilon <0, \frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})}+\frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}>0, \end{aligned}$$

(III) the double Hopf bifurcation occurs at ${{{\varvec{E}}}_{j}}$ of (6), when

$$\begin{aligned} \epsilon<0, \frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})}+\frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}<0 \end{aligned}$$

and

$$\begin{aligned} \left( \frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})}+\frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}\right) ^2+4\epsilon >0, \end{aligned}$$

(IV) when

$$\begin{aligned} \left( \frac{\partial P_{11}}{\partial q_{1}}\left| _{(q_{j1},q_{j2})}+\frac{\partial P_{12}}{\partial q_{2}}\right| _{(q_{j1},q_{j2})}\right) ^2+4\epsilon <0, \end{aligned}$$

the focus point will occur in system (6).

Thus, it can be seen that the equilibrium points and their characteristics of (2) have changed because of constraint (3). Furthermore, based on the Helmholtz’s theorem [49], the energy function $H_{L}({{{\varvec{q}}}},{{{\varvec{p}}}})$ satisfies

$$\begin{aligned} \frac{\mathrm{d}H_{L}}{\mathrm{d}t}=-\frac{q_{1}p_{1}^2\frac{\partial H_{L}}{\partial p_{1}}+q_{2}p_{2}^2\frac{\partial H_{L}}{\partial p_{2}}}{L^2}. \end{aligned}$$

So, the energy of (6) is changed over time. In conclusion, the constrained system (6) has different complex dynamical behaviors from system (2).

System (6) may be of hyperchaos under some conditions according to the conclusions of Refs. [34, 35] and the results of Sect. 2. In order to find the effect of the constraint parameter L on the hyperchaotic system (2) and to study the complex dynamic behaviors of system (6), the parameters are fixed $\eta =0.01$, $L=1$, $\beta \in [0.1,10]$, and the same initial values as given in Sect. 2. Using the same method in previous section, the $(q_{j1},q_{j2})$ of rest equilibrium points with different $\beta$ is shown in Fig. 6. It shows the relationship between $(q_{j1},q_{j2})$ and $\beta$ when the constraint parameter $L=1$.

Fig. 6

Surface of $(q_{j1},q_{j2},\beta )$

The Lyapunov exponents of system (6) by adjusting parameter $\beta$ are given in Fig. 7, which indicates that the system has at least two positive Lyapunov exponents and has three positive Lyapunov exponents in the several values of parameter $\beta$. Therefore, system (2) is still hyperchaotic under the nonholonomic constraint ${{{\varvec{q}}}}{{{\varvec{q}}}}^\mathrm{T}=1$ when $\beta$ varies in [0.1, 10]. We can see from $\dot{p}_{1}$, $\dot{p}_{2}$ of (6) that the constant coefficient $\theta$ of $q_{1}$, $q_{2}$, $q_{2}^3$ of (2) has turned into $\beta L^2$. From the comparison, we know that the variation trend of the Lyapunov exponents of system (6) with $\beta$ varying in [0.1, 10] is similar to that of the hyperchaotic system (2) with $\theta$ varying in [0.1, 10], which is shown in Fig. 4. But what is different is that the hyperchaotic degree of system (6) is weakened because of the constraint.

Fig. 7

Lyapunov exponents of (6) by adjusting $\beta$

Fig. 8 shows that the system (6) is also hyperchaotic when $\beta =1$, $L=1$, $\eta \in [0.001,1]$, and that indicates the rich dynamic behaviors of the holonomic system. As can be seen from the illustration, there exists a Lyapunov exponent undulating between positive and negative value and three positive Lyapunov exponents occur when $\eta \in [0.295,0.413]$ and $\eta \in [0.687,1]$. Compared with Fig. 5, the illustration shows that Hamiltonian system (2) has more complicated dynamic behavior under constraint $\phi ({{{\varvec{q}}}},{{{\varvec{p}}}})=0$, such as stronger hyperchaotic phenomena. In the above studies, the constraint parameter $L=1$, that is, we have selected the constraint ${{{\varvec{q}}}}{{{\varvec{q}}}}^\mathrm{T}=1$ on Hamiltonian system (2) and have found the hyperchaotic phenomena of holonomic system. In fact, system (6) has different hyperchaotic behaviors with different constraint parameters. Figure 9 illustrates that system (6) has at least two positive Lyapunov exponents and has three positive Lyapunov exponents in the several values of parameter L; here, we fix the parameter $\beta =1$, $\eta =0.01$, and the constraint parameter L varies in [1, 10]. As shown in Fig. 9, there are three positive Lyapunov exponents in system (6) when the constraint parameter L is 1.359, 1.963, 2.052, 2.617, 3.093, etc. Table 1 shows the partial results of the three positive Lyapunov exponents values for (6) under different constraint parameters L; here, $LE_{1}$, $LE_{2}$ and $LE_{3}$ denote the corresponding Lyapunov exponent values of the points on the green curve, magenta curve and blue curve, respectively. Thus, (2) still is hyperchaotic under the holonomic constraint (3).

Fig. 8

Lyapunov exponents of (6) by adjusting $\eta$

Fig. 9

Lyapunov exponents of (6) by adjusting L

Table 1 Three positive Lyapunov exponents for (6) under different constrained parameters L

In order to further investigate the influence of constraint $\phi ({{{\varvec{q}}}}$, ${{{\varvec{p}}}})=0$ on the hyperchaotic character of the Hamiltonian system (2), we give the hyperchaotic attractor in phase space and Poincaré maps with different parameters. Here, we fix the parameters

$$\begin{aligned} \theta =1,~~\beta =1,~~\eta =0.7 \end{aligned}$$

and the initial values are

$$\begin{aligned} (q_{10},q_{20},p_{10},p_{20})=(1,0.1,0.01,0.001). \end{aligned}$$

For system (2), we obtain that (0, 0, 0, 0) is a saddle point, and

$$\begin{aligned}&(0.4224087642, 0.7914557371,0,0),\\&(-\,0.4224087642, -\,0.7914557371,0,0) \end{aligned}$$

are saddle-center points, and double Hopf bifurcations occur at $(-\,1.458779774, 1.329653647,0,0)$ and

$$\begin{aligned} (1.458779774, -\,1.329653647,0,0). \end{aligned}$$

For system (6), we obtain the results as follows:

(I) (0, 0, 0, 0) is a saddle point,

$$\begin{aligned}&(0.4347738172, 0.900539687,0,0),\\&(-\,0.4347738172,-\,0.900539687,0,0) \end{aligned}$$

are saddle-center points, and double Hopf bifurcations occur at

$$\begin{aligned}&(0.7751444429,-\,0.6317840553,0,0),\\&(-\,0.7751444429,0.6317840553,0,0), \end{aligned}$$

where $L=1$.

(II) (0, 0, 0, 0) is a saddle point,

$$\begin{aligned}&(0.3139420099,1.975206423,0,0),\\&(-\,0.3139420099,-\,1.975206423,0,0),\\&(1.956888096,0.413024187,0,0),\\&(-\,1.956888096,-\,0.413024187,0,0) \end{aligned}$$

are saddle-center points, and double Hopf bifurcations occur at

$$\begin{aligned}&(1.476918143, -\,1.348596604,0,0),\\&(-\,1.476918143, 1.348596604,0,0),\\&(1.542965390,1.272500611,0,0),\\&(-\,1.542965390,-\,1.272500611,0,0), \end{aligned}$$

where $L=2$. The next simulations show the influence of L on the dynamic behaviors of (2).

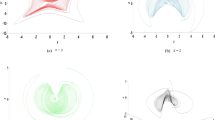
Figure 10 shows the hyperchaotic attractor and Poincar$\acute{e}$ map in $q_{1}-p_{1}$ plane of Hamiltonian system without constraint, respectively, and indicates the complex dynamic behavior. The hyperchaotic attractor and Poincar$\acute{e}$ map in $q_{1}-p_{1}$ plane of Hamiltonian system with constraint parameter $L=1$ and $L=2$ are given in Fig. 11. By comparison with Fig. 10, we can see that the constraint $\phi ({{\varvec{q}}},{{\varvec{p}}})=0$ can change the status of the Hamiltonian system and different constraint parameters will result in different dynamic behaviors. Figure 11 shows that the hyperchaotic attractor and Poincar$\acute{e}$ map of Hamiltonian system (2) have obviously changed due to the constraint $\phi ({{{\varvec{q}}}},{{{\varvec{p}}}})=0$ and Hamiltonian system (2) becomes different hyperchaotic system with the constraint parameter $L=1$ and $L=2$.

Fig. 10

i Hyperchaotic attractor in $q_{1}-p_{1}$ plane of Hamiltonian system (2). ii The Poincaré map in $q_{1}-p_{1}$ plane of Hamiltonian system (2)

Fig. 11

(1) Hyperchaotic attractor (a) and the Poincaré map (b) in $q_{1}-p_{1}$ plane of (6) with $L=1$. (2) The hyperchaotic attractor (a) and the Poincaré map (b) in $q_{1}-p_{1}$ plane of (6) with $L=2$

It shows that the constraint parameter L influences the dynamic behaviors of (2), including equilibrium points and their characteristics, energy and the periodic orbits from the double Hopf bifurcations; then, (6) exhibits different hyperchaotic attractors under different L.

3.2 Nonholonomic constraint

Assume the constraint on Hamiltonian system (2) is

$$\begin{aligned} \dot{q}_{1}^2+\dot{q}_{2}^2=l^2. \end{aligned}$$

(7)

For the system (2) with nonholonomic constraint

$$\begin{aligned} \varphi (q_{s},\dot{q}_{s},t):=\dot{q}_{1}^2+\dot{q}_{2}^2-l^2=0, \end{aligned}$$

The Lagrange multiplier method is used to reduce the variational equation to a system

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial T}{\partial \dot{q}_{i}}\right) -\frac{\partial T}{\partial q_{i}}=F_{i}+\lambda \frac{\partial \varphi (q_{i},\dot{q}_{i},t)}{\partial \dot{q}_{i}} (\hbox {i}=1,2), \end{aligned}$$

where

$$\begin{aligned} F_{1}= & {} \theta q_{1}-\beta q_{1}^3-\eta q_{2}+\eta ^2q_{1},\\ F_{2}= & {} \theta q_{2}-\beta q_{2}^{3}-\eta q_{1}. \end{aligned}$$

$T=\frac{\dot{q}_{1}^2+\dot{q}_{2}^2}{2}$ denotes the kinetic energy of the system. $\lambda$ is the Lagrange multiplier.

Then, the nonholonomic system (2), (7) can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{q}_{1}=\theta q_{1}-\beta q_{1}^3-\eta q_{2}+\eta ^2q_{1}+2\lambda \dot{q}_{1},\\ \ddot{q}_{2}=\theta q_{2}-\beta q_{2}^{3}-\eta q_{1}+2 \lambda \dot{q}_{2}.\\ \end{array} \right. \end{aligned}$$

(8)

Differentiating $\varphi (q_{s},\dot{q}_{s},t)$ with respect to time, we have

$$\begin{aligned} \dot{q}_{1}\ddot{q}_{1}+\dot{q}_{2}\ddot{q}_{2}=0. \end{aligned}$$

(9)

Substituting (9) into (8), we obtain

$$\begin{aligned} 2\lambda= & {} [(\beta q_{1}^3+\eta q_{2}) \dot{q}_{1}+(\beta q_{2}^3+\eta q_{1})\dot{q}_{2}\\&-\,(\theta +\eta ^2)q_{1}\dot{q}_{1}-\theta q_{2}\dot{q}_{2}]/l^2 \end{aligned}$$

The nonholonomic system becomes

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{1}=p_{1},\\ \dot{q}_{2}=p_{2},\\ \dot{p}_{1}=\theta q_{1}-\beta q_{1}^3-\eta q_{2}+\eta ^2q_{1}+\frac{P_{1n}}{l^2},\\ \dot{p}_{2}=\theta q_{2}-\beta q_{2}^{3}-\eta q_{1}+\frac{P_{2n}}{l^2},\\ \end{array} \right. \end{aligned}$$

(10)

where

$$\begin{aligned} P_{1n}= & {} [(\beta q_{1}^3+\eta q_{2}) p_{1}+(\beta q_{2}^3+\eta q_{1})p_{2}\\&-\,(\theta +\eta ^2)q_{1}\dot{q}_{1}-\theta q_{2}p_{2}]p_{1},\\ P_{2n}= & {} [(\beta q_{1}^3+\eta q_{2}) p_{1}+(\beta q_{2}^3+\eta q_{1})p_{2}\\&-\,(\theta +\eta ^2)q_{1}\dot{q}_{1}-\theta q_{2}p_{2}]p_{2}. \end{aligned}$$

It can be seen from (10) that the system is also invariant under the coordinate transformation

$$\begin{aligned} (q_{1},q_{2},p_{1},p_{2})\rightarrow (-q_{1},-q_{2},-p_{1},-p_{2}). \end{aligned}$$

It follows that the holonomic constraint $\phi ({{{\varvec{q}}}},{{{\varvec{p}}}})=0$ and the nonholonomic constraint $\varphi (q_{s},\dot{q}_{s},t)=0$ do not affect the symmetric invariant of the system. By computations, we obtain that system (10) and the Hamiltonian system (2) have the same equilibria and their stability. Therefore, the Hamiltonian system (2) may have hyperchaotic phenomena under the nonholonomic constraint $\varphi (q_{s},\dot{q}_{s},t)=0$. For illustration, we fix the parameters

$$\begin{aligned} \theta =1,~~\eta =1,~~l=10, \end{aligned}$$

and initial values

$$\begin{aligned} (q_{10},q_{20},p_{10},p_{20})=(1,0.1,0.01,0.001), \end{aligned}$$

and the parameter $\beta$ varies in the interval [0.1, 10]. Figure 12 shows that the nonholonomic system has two positive Lyapunov exponents when $\beta$ varies in [0.1, 4.901) and has three positive Lyapunov exponents when $\beta$ varies in [4.901, 10]. Compared with Fig. 2, under the nonholonomic constraint $\varphi (q_{s},\dot{q}_{s},t)=0$, the hyperchaotic degree of the system is becoming stronger and exhibits abundant hyperchaotic phenomena with the increase of parameter $\beta$.

Fig. 12

Lyapunov exponents of (10) by adjusting $\beta$

Next, we investigate the effect of the parameters $\theta$ and $\eta$ on the nonholonomic system (10) with the same initial values and constraint parameter l. Figure 13 shows that system (10) is hyperchaotic when $\beta =1, \eta =0.01$ and $\theta$ varies in [0.1, 10]. Compared with Fig. 4, the variation of the largest Lyapunov exponent value is smaller, but there exists an exponential curve changing between positive and negative when $\theta$ varies in [5.233, 10].

Fig. 13

Lyapunov exponents of (10) by adjusting $\theta$

It can be seen from Fig. 14 that system (10) also is hyperchaotic when $\beta =1, \theta =1$ and $\eta$ varies in [0.001, 1]. Compared with Fig. 5, the variation of the largest Lyapunov exponent value is larger, and there exists an exponential curve changing between positive and negative when $\eta$ varies in [0.577, 1]. These results indicate the richer hyperchaotic behaviors of the nonholonomic system.

Fig. 14

Lyapunov exponents of (10) by adjusting $\eta$

The Lyapunov exponents by adjusting l are given in Fig. 15. It shows that system (10) is hyperchaotic when $\theta =1, \beta =1,\eta =1$, initial values

$$\begin{aligned} (q_{10},q_{20},p_{10},p_{20})=(1,0.1,0.01,0.001) \end{aligned}$$

and l varies in [1, 10]. Therefore, the Hamiltonian system (2) is still hyperchaotic under the nonholonomic constraint $\varphi (q_{s},\dot{q}_{s},t)=0$. As well as system (6), the nonholonomic constraint $\varphi (q_{s},\dot{q}_{s},t)=0$ will cause new hyperchaotic phenomena in system (10). To illustrate this, the hyperchaotic attractor and Poincaré map are given in Fig. 16, where $\theta =1$, $\beta =1$, $\eta =0.7$, $l=10$.

Fig. 15

Lyapunov exponents of (10) by adjusting l

Fig. 16

i Hyperchaotic attractor in $q_{1}-p_{1}$ plane of system (10). ii The Poincaré map in $q_{1}-p_{1}$ plane of system (10)

Comparing Figs. 16 with 10, we can see that in both system (6) and system (2), double Hopf bifurcations occur at the same points

$$\begin{aligned}&(-\,1.458779774, 1.329653647,0,0),\\&(1.458779774, -\,1.329653647,0,0), \end{aligned}$$

but the periodic orbits from the double Hopf bifurcations are different. Thus, there are different hyperchaotic attractors between the Hamiltonian system (2) and constrained system (10). To further illustrate the influence of constraint parameter l on (2), we use the energy function to analytically evaluate the energy variation of system (10) and system (2). Based on Helmholtz’s theorem [49], we obtain that the energy function of both (10) and (2) is

$$\begin{aligned}&H_{l}(q_{1},q_{2},p_{1},p_{2})=\frac{p_{1}^2+p_{2}^2-\theta q_{1}^2-\theta q_{2}^2}{2}\\&\quad +\,\frac{\beta (q_{1}^4+q_{2}^4)}{4}+\eta q_{1}\left( q_{2}-\frac{\eta q_{1}}{2}\right) . \end{aligned}$$

Thus, $\frac{\mathrm{d}H_{l}}{\mathrm{d}t}=0$ for system (2), and for system (10)

$$\begin{aligned}&\frac{\mathrm{d}H_{l}}{\mathrm{d}t}{=}\nonumber \\&\quad \frac{(-\eta ^2 p_{1}q_{1}{+}\eta q_{1}p_{2}{+}\eta p_{1}q_{2}{+}\beta p_{1}q_{1}^3{-}\theta p_{1}q_{1}{+}\beta p_{2}q_{2}^3-\theta p_{2}q_{2})}{l^2}. \end{aligned}$$

The energy evolution of system (10) is shown in Fig. 17, which shows the energy in the constrained system changes disorderly. It indicates that the Hamiltonian system has complex hyperchaotic behavior under constraint $\varphi (q_{s},\dot{q}_{s},t)=0$.

Fig. 17

Evolution process of $\frac{H_{l}}{dt}$ versus t

4 Hyperchaos control

In some cases, since chaos can be harmful in several contexts, the complex behavior should be controlled [50]. The chaos control has received much attention, and many valuable methods have been appeared to effectively control the chaotic phenomena [51,52,53,54,55]. From the above discussion, we can see that constraints (3) and (7) have changed the status of the hyperchaotic system, but these constraints cannot make the hyperchaos disappear. So, a method of finding the constraint under which the hyperchaotic behaviors of the Hamiltonian system disappear is given as follows.

To achieve hyperchaos control, we propose a method of introducing constraint to reduce the dimension of the hyperchaotic system, because the dimension of the hyperchaotic system is at least four. We assume that the Hamiltonian system (2) is subjected to the constraint $\psi ({{{\varvec{q}}}},{{{\varvec{p}}}},t)=0$; then, the system becomes [33]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{1}=p_{1},\\ \dot{q}_{2}=p_{2},\\ \dot{p}_{1}=A_{1}+\frac{\frac{\partial \psi }{\partial p_{1}}}{\frac{\partial \psi }{\partial {{{\varvec{p}}}}}\left( \frac{\partial \psi }{\partial {{{\varvec{p}}}}}\right) ^\mathrm{T}}\left( -\frac{\partial \psi }{\partial {{{\varvec{q}}}}} {{{\varvec{p}}}}^\mathrm{T}-\frac{\partial \psi }{\partial t}-\frac{\partial \psi }{\partial {{{\varvec{p}}}}}{{{\varvec{A}}}}^\mathrm{T}\right) ,\\ \dot{p}_{2}=A_{2}+\frac{\frac{\partial \psi }{\partial p_{2}}}{\frac{\partial \psi }{\partial {{{\varvec{p}}}}}\left( \frac{\partial \psi }{\partial {{{\varvec{p}}}}}\right) ^\mathrm{T}}\left( -\frac{\partial \psi }{\partial {{{\varvec{q}}}}} {{{\varvec{p}}}}^\mathrm{T}-\frac{\partial \psi }{\partial t}-\frac{\partial \psi }{\partial {{{\varvec{p}}}}}{{{\varvec{A}}}}^\mathrm{T}\right) ,\\ \end{array} \right. \end{aligned}$$

(11)

where

$$\begin{aligned} A_{1}= & {} \theta q_{1}-\beta q_{1}^3-\eta q_{2}+\eta ^2q_{1},\\ A_{2}= & {} \theta q_{2}-\beta q_{2}^{3}-\eta q_{1},\\ {{{\varvec{A}}}}= & {} (A_{1} \quad A_{2}). \end{aligned}$$

Here, we assume

$$\begin{aligned} \frac{\partial \psi ({{{\varvec{q}}}},{{{\varvec{p}}}},t)}{\partial {{{\varvec{p}}}}}=(\mu _{1},\mu _{2}), \quad \rho =-\frac{\partial \psi }{\partial {{{{\varvec{q}}}}}}{{{{\varvec{p}}}}}^\mathrm{T}-\frac{\partial \psi }{\partial t}. \end{aligned}$$

(12)

Substituting (12) into (11), we have

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{1}=p_{1},\\ \dot{q}_{2}=p_{2},\\ \dot{p}_{1}=\frac{\mu _{1}\rho +\mu _{2}^2A_{1}-\mu _{1}\mu _{2}A_{2}}{\mu _{1}^2+\mu _{2}^2},\\ \dot{p}_{2}=\frac{\mu _{2}\rho +\mu _{1}^2A_{2}-\mu _{1}\mu _{2}A_{1}}{\mu _{1}^2+\mu _{2}^2}.\\ \end{array} \right. \end{aligned}$$

(13)

For simplicity, we further assume $\mu _{1}=0,\quad \mu _{2}=1$; then, $\dot{p}_{1}=A_{1}$ and $\dot{p}_{2}=-p_{1}\frac{\partial \psi }{\partial q_{1}}-p_{2}\frac{\partial \psi }{\partial q_{2}}-\frac{\partial \psi }{\partial t}$. Therefore, when $\frac{\partial \psi }{\partial q_{1}}=\frac{\partial \psi }{\partial t}=0$ and $\frac{\partial \psi }{\partial q_{2}}=\theta$, we obtain the constraint $\psi _{1}({{{\varvec{q}}}},{{{\varvec{p}}}},t):=\theta q_{2}+p_{2}=0$ which can reduce the dimension of the hyperchaotic system. So under the constraint $\psi _{1}({{{\varvec{q}}}},{{{\varvec{p}}}},t)=0$, the four-dimensional system is equivalent to a three-dimensional system, which is described by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{1}=p_{1},\\ \dot{q}_{2}=-\theta q_{2}, \\ \dot{p}_{1}=(\theta +\eta ^2)q_{1}-\beta q_{1}^3-\eta q_{2}.\\ \end{array} \right. \end{aligned}$$

(14)

Obviously, the three-dimensional system (14) has not shown hyperchaotic phenomena [15]. It shows that system (14) has three equilibrium points ${{{\varvec{E}}}}_{o}=(0,0,0)$ and ${{{{\varvec{E}}}}}_{1,2}=(\pm \sqrt{\frac{\theta +\eta ^2}{\beta }},0,0)$ by computing. The Jacobian matrix at ${{{{\varvec{E}}}}}_{o}$ is

$$\begin{aligned} {{{\varvec{J}}}}({{{\varvec{E}}}}_{o}) =\left( \begin{array}{ccc} 0 &{} 0 &{} 1\\ 0 &{} -\theta &{} 0\\ \theta +\eta ^2 &{} -\eta &{} 0\\ \end{array} \right) . \end{aligned}$$

By using $\left| \lambda {{{\varvec{I}}}}-{{{\varvec{J}}}}({{{\varvec{E}}}}_{o})\right| =0$, we can obtain

$$\begin{aligned} \lambda _{1}=-\theta , \lambda _{2,3}=\pm \sqrt{\theta +\eta ^2}, \end{aligned}$$

${{{\varvec{E}}}}_{o}$ is a saddle point. The Jacobian matrix at ${{{\varvec{E}}}}_{1,2}$ is

$$\begin{aligned} {{{\varvec{J}}}}({{{\varvec{E}}}}_{1,2}) =\left( \begin{array}{ccc} 0 &{} 0 &{} 1\\ 0 &{} -\theta &{} 0\\ -2\theta -2\eta ^2 &{} -\eta &{} 0\\ \end{array} \right) . \end{aligned}$$

The eigenvalues of ${{{\varvec{J}}}}({{{\varvec{E}}}}_{1,2})$ are

$$\begin{aligned} \lambda _{1}=-\theta , \quad \lambda _{2,3}=\pm \sqrt{2\theta +2\eta ^2}i. \end{aligned}$$

For ${{{\varvec{E}}}_{1}}$, define

$$\begin{aligned} {{{\varvec{M}}}} =\left( \begin{array}{ccc} 1 &{} 1 &{} 1\\ \sqrt{2(\theta +\eta ^2)} &{} -\sqrt{2(\theta +\eta ^2)} &{}\quad -\theta \\ 0 &{} 0 &{} -\frac{\theta ^2+2\theta +2\eta ^2}{\eta }\\ \end{array} \right) , \end{aligned}$$

and let

$$\begin{aligned} \left( \begin{array}{c} q_{1}-\sqrt{\frac{\theta +\eta ^2}{\beta }}\\ p_{1}\\ q_{2}\\ \end{array} \right) ={{\varvec{M}}} \left( \begin{array}{c} x_{1}\\ x_{2}\\ x_{3}\\ \end{array} \right) . \end{aligned}$$

Then, system (14) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{1}=-\sqrt{2(\theta +\eta ^2)}x_{2},\\ \dot{x}_{2}=\sqrt{2(\theta +\eta ^2)}x_{1}+F(x_{1},x_{2},x_{3}), \\ \dot{x}_{3}=-\,\theta x_{3},\\ \end{array} \right. \end{aligned}$$

(15)

where

$$\begin{aligned}&F(x_{1},x_{2},x_{3})\\&\quad =\frac{\sqrt{2}(x_{1}+x_{2}+x_{3})^2(\beta (x_{1}+x_{2}+x_{3})+3\sqrt{\beta (\theta +\eta ^2)})}{4\sqrt{\theta +\eta ^2}}. \end{aligned}$$

According to the procedures proposed by Hassard et al. [56], we have

$$\begin{aligned} g_{11}= & {} \frac{3\sqrt{2}\sqrt{\beta (\theta +\eta ^2)}i}{4\sqrt{\theta +\eta ^2}},~~ g_{02}=-\frac{3\sqrt{2}\sqrt{\beta (\theta +\eta ^2)}}{4\sqrt{\theta +\eta ^2}},\\ g_{20}= & {} \frac{3\sqrt{2}\sqrt{\beta (\theta +\eta ^2)}}{4\sqrt{\theta +\eta ^2}},\\g_{21}= & {} \frac{3\sqrt{2}\beta i}{8\sqrt{\theta +\eta ^2}}-\frac{3\sqrt{2}\beta }{16\sqrt{\theta +\eta ^2}}. \end{aligned}$$

Therefore,

$$\begin{aligned} \hbox {2Re}(c_{1}(0))= & {} 2\hbox {Re}\left( \frac{g_{20}g_{11}-2\left| g_{11}\right| ^2-\frac{1}{3}\left| g_{02}\right| ^2}{2\sqrt{2(\theta +\eta ^2)}}+\frac{g_{21}}{2}\right) \\= & {} -\frac{4\beta }{3\sqrt{2(\theta +\eta ^2)}}<0. \end{aligned}$$

Because system (14) is invariant for the coordinate transformation $(q_{1},q_{2},p_{1})\rightarrow (-q_{1},-q_{2},-p_{1})$, the system has the same dynamical behavior at ${{{\varvec{E}}}}_{2}$ and ${{{\varvec{E}}}}_{1}$. Then, in the system, Hopf bifurcation can occur at ${{{\varvec{E}}}}_{1,2}$ and the bifurcating periodic solutions on the center manifold are unstable, which indicates that two equilibrium points undergo Hopf bifurcations in system (14).

Fig. 18

Lyapunov exponents of (14) by adjusting $\eta$

Fig. 19

$q_{1}-p_{1}$ plane with different values of $\eta$

Fig. 20

Poincaré map with different values of $\eta$

To numerical simulations, we take the parameter values $\theta =1,\beta =1$, $\eta \in [0.01,10]$, $(q_{10},q_{20},p_{10})=(1,0.1,0.01)$. Figure 18 shows that in system (14) chaotic attractor exists when $\eta \in (1.909,10]$ and periodic solutions and chaos state coexist when $\eta \in (1.234,1.909]$. The phase diagrams on $q_{1}-p_{1}$ plane under different parameters $\eta$ are shown in Fig. 19. The corresponding Poincaré maps with different values of $\eta$ are shown in Fig. 20. This illustrates that the constraint $\psi _{1}({{{\varvec{q}}}},{{{\varvec{p}}}},t)=0$ can transform the Hamiltonian system from hyperchaotic state into periodic state or chaotic state.

In order to make the chaos disappear and achieve the global stability of system, we further introduce the constraint

$$\begin{aligned} \psi _{2}({{{\varvec{q}}}},{{{\varvec{p}}}},t):=(\theta +\eta ^2)q_{1}-\beta q_{1}^3+p_{1}=0; \end{aligned}$$

therefore, $\dot{p}_{1}$ becomes $-\eta q_{2}-p_{1}$, the expressions of both $\dot{p}_{1}$ and $\dot{q}_{2}$ do not include $q_{1}$ and the system (14) is translated into the equivalent system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{2}=-\theta q_{2},\\ \dot{p}_{1}=-\eta q_{2}-p_{1}.\\ \end{array} \right. \end{aligned}$$

(16)

It can be seen that there is only one equilibrium point ${{{\varvec{E}}}}_{00}=(0,0)$ in system (16). To study the stability of ${{{\varvec{E}}}}_{00}$, we formulate the Lyapunov function

$$\begin{aligned} V(q_{2},p_{1})=\frac{\left( p_{1}-\frac{\eta q_{2}}{\theta }\right) ^2}{2}+\frac{\eta ^2q_{2}^2}{4\theta ^3}, \end{aligned}$$

and the derivative of the function satisfies

$$\begin{aligned} \dot{V}(q_{2},p_{1})=-\left( p_{1}-\frac{\eta q_{2}}{2\theta }\right) ^2\le 0. \end{aligned}$$

According to the asymptotic stability theorem [57], ${{{\varvec{E}}}}_{00}$ is globally asymptotically stable. Figure 21 shows the time series of $q_{2}$ and $p_{1}$ of system (16) with $\theta =1$ and $\eta =0.7$. It shows that system (16) is globally asymptotically stable at ${{{\varvec{E}}}}_{00}$.

Fig. 21

Time series of $q_{2}$ and $p_{1}$, respectively

Table 2 Performance analysis of chaos control methods

5 Conclusions

In this paper, a hyperchaotic Hamiltonian system is formulated, and then the existence of equilibrium point and double Hopf bifurcation and the type of equilibrium point are investigated. The results show that the Hamiltonian system is always hyperchaotic with any system parameter varying, which is not the same as other Refs. [40, 58]. It also indicates that the system exhibits not only chaotic attractor [39] but also hyperchaotic attractor when the double Hopf bifurcations occur. Then, the influences of holonomic constraint and nonholonomic constraint on the dynamic behaviors of (2) are studied. Comparing with (2), the energies of the constrained Hamiltonian systems are changed over time; hence, the state variable trajectories of the system have changed accordingly. The multiple equilibrium points and double Hopf bifurcation still exist in the constrained Hamiltonian system. Moreover, the holonomic constraint can influence the number and characteristic of the equilibrium point and the double Hopf bifurcation of the Hamiltonian system. Thus, the Hamiltonian system also exhibits hyperchaotic behaviors with the system parameter varying under the constraint conditions. From the analysis results, it is shown that the constraint parameters can influence the hyperchaotic state of the Hamiltonian system in different degrees. Furthermore, the results indicate that the constraints can not only enhance or diminish the hyperchaotic state of (2), but also generate new hyperchaotic systems with different constraint parameters. In addition, the constraints can achieve hyperchaos control and make the hyperchaotic behavior change into chaotic state, periodic state, even globally stable state. In order to determine the constraint of hyperchaos control, we firstly obtain the explicit equations for the constrained Hamiltonian system using the method in Ref. [33]. Next, the suitable constraint is selected to make hyperchaos disappear and the Hopf bifurcation and chaotic attractor occur in the constrained system. Then, the chaotic state is transformed into global asymptotic stable state by introducing constraint. The results illustrate that the hyperchaotic Hamiltonian system can be controlled to a chaotic system and then to a globally stable system by selecting specific constraints. In the future, we will investigate the constraints in general form which make hyperchaotic attractor become chaotic attractor and globally asymptotically stable point, respectively. The proposed method is different from the methods in Refs [23,24,25, 32]. The introducing constraint method can be used for hyperchaos control in any Hamiltonian systems. The new hyperchaotic attractor, chaotic attractor and globally stable point can be generated by applying the method. For comparison, the performance analysis of these methods is shown in Table 2.