Bifurcations and chaos in the semi-passive bipedal dynamic walking model under a modified OGY-based control approach

Abstract

This paper aims at investigating the semi-passive dynamic walking of a torso-driven biped robot under the Ott–Grebogi–Yorke (OGY) control approach as it goes down inclined planes. For the control, we used the desired torso angle as the accessible control parameter. Compared with our work in Gritli et al. (Nonlinear Dyn 79(2):1363–1384, 2015), a modified design of the OGY-based controller is proposed in this paper. Such controller is obtained by linearizing the impulsive hybrid nonlinear dynamics of the biped robot around a desired one-periodic hybrid limit cycle. Both the differential equation and the algebraic equation are linearized. As a result, we develop a simple mathematical expression of a controlled hybrid Poincaré map. Determination of its fixed point and its Jacobian matrix requires only the knowledge of the nominal impact instant. We show efficiency of the designed OGY controller for the control of chaos in the impulsive hybrid nonlinear dynamics for some desired nominal values of the slope, and the desired torso angle. Furthermore, we analyzed via bifurcation diagrams the displayed behaviors in the controlled semi-passive biped robot as the slope parameter varies. We show the appearance of a Neimark–Sacker bifurcation and a cyclic-fold bifurcation, and also the exhibition of chaos. Our analysis of the controlled semi-passive gait is achieved also by means of the spectrum of Lyapunov exponents. Such study is realized via the controlled hybrid Poincaré map where a reduction of its dimension is achieved.

1 Introduction

It is well known nowadays that passive dynamic walking of biped robots descending inclined planes exhibits chaos and several types of bifurcations. Iqbal et al. presented in [14] a review on studies realized on analysis of bifurcations and chaos in passive dynamic walking. Such walking mode displays the conventional scenario of period-doubling bifurcations as route to chaos, the cyclic-fold bifurcation, the type-I intermittency and the interior crisis as two novel routes to chaos, the boundary crisis causing the sudden death of the bipedal chaos [3, 5, 6, 8–10, 12, 16–18, 24, 27, 29].

It has been known that the spectrum of Lyapunov exponents has been investigated as one of the most important and precise dynamical diagnostics to quantify and provide characteristics of attractors of dynamical systems [19–21]. Moreover, the sign of the largest Lyapunov exponent can infer the stability of systems and can rigorously prove the stability of the nonlinear system under control [26]. In [6], we analyzed order/chaos by means of the spectrum of Lyapunov exponents and the fractal Lyapunov dimension in order to distinguish between different displayed periodic/chaotic attractors displayed in the passive dynamic walking of the compass-gait model and the semi-passive dynamic walking of the torso-driven biped model. The numerical procedure used for calculating the spectrum of Lyapunov exponents is presented in [6]. Such numerical calculation was based mainly on the Gram–Schmit Reorthonormalization procedure [21].

Furthermore, we showed recently in [4] that the semi-passive dynamic walking of a torso-driven biped robot exhibits a novel type of local bifurcation, namely the torus (secondary-Hopf or Neimark–Sacker) bifurcation. It is known that the Neimark–Sacker (secondary-Hopf) bifurcation and the torus bifurcation are the same from dynamics point-of-view when dealing with the Poincaré map of a limit cycle of the corresponding ODE [15]. Furthermore, the Neimark–Sacker bifurcation is characterized by the birth in the Poincaré section of a closed invariant curve from a fixed point, when the fixed point loses its stability via a pair of complex-conjugate eigenvalues with unit modulus. Thus, the Neimark–Sacker bifurcation generates an invariant two-dimensional torus in the corresponding ODE [15].

On the other hand, the issue of chaos control in passive dynamic walking was not much treated (see [7, 11, 14] and references therein). Recently, we employed the OGY-based control approach in order to control chaos for the passive dynamic walking of the compass-gait biped robot [11] and for the semi-passive dynamic walking of the torso-driven biped robot [7]. In [11] we used the hip torque as the controller input. However, in [7], we used the desired torso angle as the available control parameter. The walking model of such biped robots is modeled by an impulsive hybrid nonlinear dynamics composed of a nonlinear differential equation describing the dynamics during the swing phase and a nonlinear algebraic equation representing the impulsive dynamics during the instantaneous impact phase. The OGY control method is based mainly on the linearization of the controlled Poincaré map [1]. Thus, the essential key in the design of the OGY control is the determination of an analytical expression of the controlled Poincaré map. Then, in order to overcome such design problem, our methodology was based chiefly on the linearization of the nonlinear differential equation around a nominal one-periodic limit cycle (only the flow during the swing phase). Thus, we obtained a linear differential equation. However, the algebraic equation was kept nonlinear in [7, 11]. Accordingly, we formulated an impulsive hybrid linear dynamics, which generates features fairly close to those of the original impulsive nonlinear dynamics. Then, we developed an analytical expression of a controlled hybrid (constrained) nonlinear Poincaré map. Thus, we designed an OGY control law (a state-feedback controller) to stabilize the one-periodic fixed point of such Poincaré map.

We note that the design method of an OGY-based control for a nonlinear dynamics using an accessible control parameter offers two strategies for the linearization process. The first strategy is to linearize the nonlinear dynamics around a desired one-period limit cycle without taking into account the accessible parameter as the control input. Then, after linearization, we will obtain an expression of the linear model and hence of the Poincaré map where the control parameter (as a control input) is expressed within the different matrices of the linear model. Such linearization method was realized in [7]. In contrast, the second offered strategy is to linearize the nonlinear system by considering from the start that the available control parameter will be used as the control input. Then, the linearized dynamics will be expressed linearly in terms of the control parameter as the control input similar to that obtained in [11]. Thus, one obtains a Poincaré map linearly defined with respect to the control parameter. In this paper, in Sect. 2, we use this linearization method in order to design a controlled hybrid linear Poincaré map completely different to that developed by us in [7]. Moreover, the algebraic equation of the impulsive hybrid nonlinear dynamics is also linearized in this paper. We show that such Poincaré map is simple enough to be amendable to both theoretical and numerical analyses. We demonstrate that the identification of the fixed point of the hybrid linear Poincaré map requires the resolution of only one scalar function contrary to our results in [7].

We demonstrated recently in [4], based on bifurcation diagrams, Floquet multipliers and Poincaré sections, that the semi-passive dynamics of the torso-driven biped robot under the OGY control exhibits the classical period-doubling route to chaos and also the torus (Neimark–Sacker) bifurcation as the slope parameter varies. In this paper, in Sect. 3, we analyze chaos and bifurcations exhibited in the impulsive hybrid nonlinear dynamics of the torso-driven biped robot under the modified OGY control method by means of bifurcation diagrams. We show that the parameters of the designed OGY control are almost identical to that calculated in [4, 7]. Nevertheless, this slight difference will provoke an important and dramatic change in the behavior of the controlled semi-passive gaits of the biped robot as the slope parameter varies. Furthermore, we show that the Neimark–Sacker bifurcation still exists. Moreover, an analysis of the attractors in the 2D Poincaré section raised through the Neimark–Sacker bifurcation is also presented. We show the transformation of the closed invariant cycle born just after the Neimark–Sacker bifurcation into the chaotic attractor as the bifurcation parameter varies.

In addition, in this paper and in [4], we encountered some problems and difficulties in the development of the variational equation in order to provide characteristics of the displayed attractors by means of the spectrum of Lyapunov exponents using the impulsive hybrid nonlinear dynamics with the OGY control law. These difficulties arise not because the nonlinear dynamics is hybrid, but because of the presence of the OGY controller. Then, in order to overcome such problems, which is the second objective of this paper, we used the controlled hybrid linear Poincaré map (with the OGY control) for the evaluation of the spectrum of Lyapunov exponents in Sect. 4. This tool will be employed to analyze and quantify chaos and order in the semi-passive bipedal dynamic walking of the torso-driven biped robot under the OGY control based on the designed controlled hybrid linear Poincaré map. In order to calculate adequately the spectrum of Lyapunov exponents, a reduction of the dimension of such hybrid map is realized also in this section. Section 5 provides a discussion on the obtained results and the performance/drawback of the OGY-based control approach. The conclusion and some future works are presented in Sect. 6.

Fig. 1

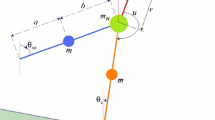
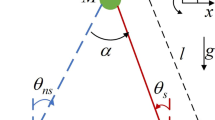
Semi-passive torso-driven biped robot on an inclined surface of slope angle $\varphi$. Here, $\theta _{s}$, $\theta _{ns}$ and $\theta _{t}$ denote the stance (supporting) angle, the swing (nonsupporting) angle and the torso angle. Values of important simulation parameters for the semi-passive walking dynamics of the biped robot are given in [7]

2 Modified OGY control method for the semi-passive torso-driven biped robot

2.1 The semi-passive torso-driven biped robot

The torso-driven biped robot is illustrated in Fig. 1 [5–7, 9]. Such biped is composed of two identical legs: a stance leg and a swing leg, a frictionless hip connecting the two legs, and a torso as an upper-body. We introduced only one torque u between the torso and the stance leg, whereas the swing leg is non-actuated. The controller u is employed in order to stabilize the torso at some desired position (desired torso angle $\theta ^{d}_{t}$) and hence in order to achieve a semi-passive dynamic walking down an inclined plane. We designed such controller in [6, 7, 9], which is named the semi-passive control law. We reported in [9] that the torso can be used as a mechanism for controlling chaos. In [7], the desired torso angle $\theta ^{d}_{t}$ was used as the accessible control parameter for chaos control subject based on the OGY approach.

2.2 Impulsive hybrid nonlinear dynamics of the semi-passive torso-driven biped robot

Under some basic modeling hypotheses [7], the semi-passive dynamic walking of the torso-driven biped robot is composed of two alternating phases, namely the swing phase and the impact phase. The swing phase is modeled by a nonlinear differential equation, whereas the impact phase is described by a nonlinear algebraic equation. Under the semi-passive control law u, these equations define then the impulsive hybrid nonlinear dynamics, which reveals the semi-passive dynamic walking of the torso-driven biped robot. According to [7], the impulsive hybrid nonlinear dynamics is expressed in terms of the desired torso angle $\theta ^{d}_{t}$ as follows:

$$\begin{aligned}&\dot{{\varvec{x}}} = {\varvec{f}}({\varvec{x}})+{\varvec{g}}({\varvec{x}})\theta ^{d}_{t} \quad \text {as long as}\quad {\varvec{x}}\in {\varOmega }, \end{aligned}$$

(1a)

$$\begin{aligned}&{\varvec{x}}^{+} = {{\varvec{h}}}\left( {\varvec{x}}^{-}\right) \quad \text {whenever} \quad {\varvec{x}}^{-}\in {\varGamma }, \end{aligned}$$

(1b)

where

$$\begin{aligned} {\varOmega }= & {} \left\{ {\varvec{x}}\in \mathfrak {R}^{6}\ :\ {{\mathcal {L}}}_{1}\left( {\varvec{x}}\right) >0\right\} , \end{aligned}$$

(2a)

$$\begin{aligned} {\varGamma }= & {} \left\{ {\varvec{x}}\in \mathfrak {R}^{6} : \ {{\mathcal {L}}}_{1}\left( {\varvec{x}}\right) = 0, \ {{\mathcal {L}}}_{2}\left( {\varvec{x}}\right) < 0,\right. \ \nonumber \\&\left. {{\mathcal {L}}}_{3}\left( {\varvec{x}}\right) > 0 \right\} , \end{aligned}$$

(2b)

and superscripts $+$ and − denotes the value of the state vector ${\varvec{x}}$ just after and just before the impact phase, respectively. “Appendix 1” describes, using the Lagrangian formalism, the mathematical model of the torso-driven biped robot and the corresponding state representation where expressions of all terms ${\varvec{f}}({\varvec{x}})$, ${\varvec{g}}({\varvec{x}})$ and ${\varvec{h}}({\varvec{x}})$ in (1) are given. Moreover, the developed expression of the semi-passive control law u is presented also in this Appendix. Readers can refer to [9, 13] for further details about the method for determining the algebraic equations (1b).

We note that the nonlinear differential equation (1a) models the motion of the biped robot during the swing phase, whereas the nonlinear algebraic equation (1b) translates the impulsive dynamics during the impact phase. The set ${\varGamma }$ defines the unilateral rigid constraints of the biped robot as it walks down the slope. However, the set ${\varOmega }$ describes the constraint on the movement of the biped robot during the swing phase.

We stress that the two constrains ${{\mathcal {L}}}_{1}\left( {\varvec{x}}\right) = 0$ and ${{\mathcal {L}}}_{2}\left( {\varvec{x}}\right) < 0$ in (2b) are expressed as follows:

$$\begin{aligned} {{\mathcal {L}}}_{1}\left( {\varvec{x}}\right)= & {} \varvec{{\mathcal {C}}}{\varvec{x}} + 2\varphi = 0, \end{aligned}$$

(3a)

$$\begin{aligned} {{\mathcal {L}}}_{2}\left( {\varvec{x}}\right)= & {} \frac{\partial {{\mathcal {L}}}_{1}\left( {\varvec{x}}\right) }{\partial {\varvec{x}}}\dot{{\varvec{x}}} < 0. \end{aligned}$$

(3b)

where $\varvec{{\mathcal {C}}}=\left[ \begin{array}{cccccc} 1&\;1&\;0&\;0&\;0&\;0 \end{array}\right]$. In fact, according to the expression of ${{\mathcal {L}}}_{1}(\varvec{\theta })=0$ (or ${{\mathcal {L}}}_{1}({\varvec{x}})=0$) in (21b), it is easy to demonstrate that the condition $l\left( cos(\theta _{s}+\varphi )-cos(\theta _{ns}+\varphi )\right) =0$ can be recast as $\theta _{ns} + \theta _{s} + 2\varphi = 0$. Then, we will obtain expression (3a).

2.3 Modified OGY-based control of the semi-passive bipedal dynamic walking

In this section, we describe the modified OGY-based control method for the semi-passive dynamic walking of the torso-driven biped robot compared with that developed in [7]. We recall that our methodology for designing the OGY controller was realized according to the following steps:

• 1. Linearization of only the nonlinear differential equation (1a) around a desired one-period flow revealing the motion of the biped only during the swing phase. The algebraic equation (1b) was not linearized.

• 2. Determination of a reduced impulsive hybrid linear dynamics with a nonlinear algebraic equation different to (1b).

• 3. Determination of an explicit expression of a controlled hybrid Poincaré map, which is nonlinear with respect to the state vector and also with respect to the control input (the desired torso angle).

• 4. Identification of the one-periodic fixed point of the controlled hybrid nonlinear Poincaré map,

• 5. Linearization of the controlled hybrid nonlinear Poincaré map around the identified one-periodic fixed point by considering here the accessible control parameter $\theta ^{d}_{t}$ as the control input for the stabilization subject.

• 6. Stabilization of the linearized Poincaré map with a classical state-feedback control law.

We stress that in [7], the accessible control parameter $\theta ^{d}_{t}$ was taken into account as the control input only in the 5th step. In this paper, the OGY control approach will be based also almost on these six steps. However, some improvements on our design strategy will be performed. Firstly, we will consider from the beginning that the accessible control parameter $\theta ^{d}_{t}$ is the control input in the impulsive hybrid nonlinear dynamics (1). Secondly, we will linearize the whole impulsive hybrid nonlinear dynamics [the nonlinear differential equation (1a) together with the nonlinear algebraic equation (1b)] around a desired one-periodic hybrid limit cycle. Such linearization strategy will give us a reduced impulsive hybrid linear dynamics with a linear algebraic equation. As a result, we will obtain an analytical expression of a controlled hybrid linear Poincaré map, which will be found to be simpler than that developed in [7] and to be simple enough to be amendable for analysis.

2.3.1 Linearization of the impulsive hybrid nonlinear dynamics around a desired one-periodic hybrid limit cycle

Consider first, for some desired nominal slope $\varphi _{n}$ and for some nominal desired torso angle $\theta ^{d}_{tn}$, the desired one-periodic flow ${\varvec{x}}_{d}(t)=\varvec{\phi }_{d}\left( t,{\varvec{x}}_{d}^{-},\varphi _{n},\theta ^{d}_{tn}\right)$ describing a desired one-periodic hybrid limit cycle in the state space of the impulsive hybrid nonlinear dynamics defined by (1). Moreover, we consider ${\varvec{x}}_{d}^{-}$ the desired one-periodic fixed point of the desired hybrid limit cycle. For this desired fixed point, it corresponds a desired step period (desired impact instant) $\tau _{d}$.

The first step lies in the linearization of the nonlinear differential equation (1a) around n points $\varvec{\chi }_{i}$, for $i=1,2,\ldots ,n$, of the desired one-periodic flow, such that $\varvec{\chi }_{i}={\varvec{x}}_{d}\left( \frac{t_{i}+t_{\left( i-1\right) }}{2}\right) ={\varvec{x}}_{d}\left( \frac{2i-1}{2n}\tau _{d}\right)$ where $t_{i}=\frac{i}{n}\tau _{d}$. Then, around each point $\varvec{\chi }_{i}$, we define a linear submodel $M_{i}$ valid during a well-defined time interval: $\left[ \begin{array}{cc} t_{\left( i-1\right) }&\, t_{i} \end{array} \right]$ (see [7] for more details). Hence, by considering the desired torso angle $\theta ^{d}_{t}$ as the control input in the nonlinear differential equations (1a), each linear submodel $M_{i}$, for $i=1,2,\ldots ,n$, around the point defined by the pair $\left( \varvec{\chi }_{i},\ \theta ^{d}_{tn}\right)$ is formulated as follows:

$$\begin{aligned} \dot{{\varvec{x}}}= & {} \varvec{{\mathcal {A}}}_{i}{{\varvec{x}}} + \varvec{{\mathcal {D}}}_{i} + \varvec{{\mathcal {B}}}_{i}\theta ^{d}_{t} \quad \text {for} \quad t_{\left( i-1\right) } \le t \le t_{i}, \end{aligned}$$

(4)

with $\varvec{{\mathcal {A}}}_{i}={\varvec{f}}_{x}\left( \varvec{\chi }_{i}\right) +{\varvec{g}}_{x}\left( \varvec{\chi }_{i}\right) \theta ^{d}_{tn}$, $\varvec{{\mathcal {B}}}_{i}={\varvec{g}}\left( \varvec{\chi }_{i}\right)$, and $\varvec{{\mathcal {D}}}_{i}={\varvec{f}}\left( \varvec{\chi }_{i}\right) -\varvec{{\mathcal {A}}}_{i}\varvec{\chi }_{i}$, where ${\varvec{f}}_{x}=\frac{\partial {\varvec{f}}\left( {\varvec{x}}\right) }{\partial {\varvec{x}}}$ and ${\varvec{g}}_{x}=\frac{\partial {\varvec{g}}\left( {\varvec{x}}\right) }{\partial {\varvec{x}}}$.

This expression of the differential equation of the linear submodel (4) is different to that developed in [7] and that not contains the term $\varvec{{\mathcal {B}}}_{i}\theta ^{d}_{t}$. Moreover, in [7], the control input $\theta ^{d}_{t}$ is expressed into the two matrices $\varvec{{\mathcal {A}}}_{i}$ and $\varvec{{\mathcal {D}}}_{i}$ (see “Appendix 2” for the linear submodel derived in [7]).

The second step in the linearization process of the impulsive hybrid nonlinear dynamics (1) is to linearize the nonlinear algebraic equation (1b) around the desired one-periodic fixed point ${\varvec{x}}_{d}^{-}$ of the hybrid limit cycle. Thus, we obtain the following linear algebraic equation:

$$\begin{aligned} {\varvec{x}}^{+} = \varvec{{\mathcal {M}}}{\varvec{x}}^{-} + \varvec{{\mathcal {N}}} \quad \text {for} \quad t = \tau _{d}, \end{aligned}$$

(5)

with $\varvec{{\mathcal {M}}} = {\varvec{h}}_{{\varvec{x}}}\left( {\varvec{x}}_{d}^{-}\right)$ and $\varvec{{\mathcal {N}}} = {\varvec{h}}\left( {\varvec{x}}_{d}^{-}\right) - \varvec{{\mathcal {M}}}{\varvec{x}}_{d}^{-}$, where ${\varvec{h}}_{{\varvec{x}}}=\frac{\partial {\varvec{h}}\left( {\varvec{x}}\right) }{\partial {\varvec{x}}}$.

2.3.2 Determination of a reduced impulsive hybrid linear dynamics

According to [7], by solving the linear differential equations of only the first $\left( n-1\right)$ submodel $M_{i}$, the linearization procedure around the desired one-periodic hybrid limit cycle will give us the following formulation of a reduced impulsive hybrid linear model:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{{\varvec{x}}} &{}=&{} \varvec{{\mathcal {A}}}_{n}{{\varvec{x}}} + \varvec{{\mathcal {D}}}_{n} + \varvec{{\mathcal {B}}}_{n}\theta ^{d}_{t}, \quad \text {as long as} \quad {\varvec{x}}\in {\varOmega }\\ {\varvec{x}}^{+} &{}=&{} \varvec{{\mathcal {J}}}_{1}{\varvec{x}}^{-} + \varvec{{\mathcal {H}}}_{1} + \varvec{{\mathcal {G}}}_{1}\theta ^{d}_{t} \quad \text {whenever} \quad {\varvec{x}}^{-}\in {\varGamma } \end{array} \right. ,\nonumber \\ \end{aligned}$$

(6)

with $\varvec{{\mathcal {J}}}_{1}=\left( \prod _{i=1}^{n-1}e^{\frac{\tau _{d}}{n}\varvec{{\mathcal {A}}}_{i}}\right) \varvec{{\mathcal {M}}}$, $\varvec{{\mathcal {G}}}_{1}=\sum _{i=1}^{n-1}\left( \prod _{j=i+1}^{n-1}\right. \left. e^{\frac{\tau _{d}}{n}\varvec{{\mathcal {A}}}_{j}}\right) \left( e^{\frac{\tau _{d}}{n}\varvec{{\mathcal {A}}}_{i}}-\varvec{{\mathcal {I}}}\right) \varvec{{\mathcal {A}}}_{i}^{-1}\varvec{{\mathcal {B}}}_{i}$, and $\varvec{{\mathcal {H}}}_{1}=\left( \prod _{i=1}^{n-1}\right. \left. e^{\frac{\tau _{d}}{n}\varvec{{\mathcal {A}}}_{i}}\right) \varvec{{\mathcal {N}}} + \sum _{i=1}^{n-1}\left( \prod _{j=i+1}^{n-1}e^{\frac{\tau _{d}}{n}\varvec{{\mathcal {A}}}_{j}}\right) \left( e^{\frac{\tau _{d}}{n}\varvec{{\mathcal {A}}}_{i}}-\varvec{{\mathcal {I}}}\right) \varvec{{\mathcal {A}}}_{i}^{-1}\varvec{{\mathcal {D}}}_{i}$. Here and in the sequel of this paper, $\varvec{{\mathcal {I}}}$ is the identity matrix with appropriate dimension.

We stress that the linear differential equation in (6) describes the last step in the swing phase of the biped robot. Then, we emphasize that the two constrains ${{\mathcal {L}}}_{2}\left( {\varvec{x}}\right) < 0$ and ${{\mathcal {L}}}_{3}\left( {\varvec{x}}\right) > 0$ describing the set ${\varGamma }$ for the impact conditions are always satisfied with the reduced impulsive hybrid linear model (6). Then, for simplicity, these two constraints will not be considered in the sequel.

2.3.3 Development of the explicit expression of the controlled hybrid Poincaré map

Let us define first the following notations:

• ${\varvec{x}}_{k}^{-}$ is the initial state just before the impact for the kth cycle,

• $\tau _{k}$ is the impact instant for the kth cycle,

• $\theta ^{d}_{tk}$ is the desired torso angle applied during the kth cycle, and

• ${\varvec{x}}_{k+1}^{-}$ is the initial state for the $\left( k+1\right)$th cycle.

Relying on our work in [7], the resolution of the linear differential equation in (6) and the use of the linear algebraic equation will give us an analytical expression of a controlled hybrid linear Poincaré map defined as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{x}}_{k+1}^{-} = \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) \\ \text {s.t.}\\ {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) = 0\\ \end{array} \right. , \end{aligned}$$

(7)

with

$$\begin{aligned} \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk} \right)= & {} \varvec{{\mathcal {J}}}\left( \tau _{k}\right) {\varvec{x}}^{-}_{k}\nonumber \\&+\, \varvec{{\mathcal {H}}}\left( \tau _{k}\right) + \varvec{{\mathcal {G}}}\left( \tau _{k}\right) \theta ^{d}_{tk}, \end{aligned}$$

(8a)

$$\begin{aligned} {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)= & {} \varvec{{\mathcal {J}}}_{0}\left( \tau _{k}\right) {\varvec{x}}^{-}_{k}\nonumber \\&+\, \varvec{{\mathcal {H}}}_{0}\left( \tau _{k}\right) + \varvec{{\mathcal {G}}}_{0}\left( \tau _{k}\right) \theta ^{d}_{tk}, \end{aligned}$$

(8b)

where $\varvec{{\mathcal {J}}}\left( \tau _{k}\right) =\varvec{{\mathcal {J}}}_{2}\left( \tau _{k}\right) \varvec{{\mathcal {J}}}_{1}$, $\varvec{{\mathcal {H}}}\left( \tau _{k}\right) =\varvec{{\mathcal {J}}}_{2}\left( \tau _{k}\right) \varvec{{\mathcal {H}}}_{1}+\varvec{{\mathcal {H}}}_{2}\left( \tau _{k}\right)$, $\varvec{{\mathcal {G}}}\left( \tau _{k}\right) =\varvec{{\mathcal {J}}}_{2}\left( \tau _{k}\right) \varvec{{\mathcal {G}}}_{1}+\varvec{{\mathcal {G}}}_{2}\left( \tau _{k}\right)$, $\varvec{{\mathcal {J}}}_{0}\left( \tau _{k}\right) =\varvec{{\mathcal {C}}}\varvec{{\mathcal {J}}}\left( \tau _{k}\right)$, $\varvec{{\mathcal {H}}}_{0}\left( \tau _{k}\right) =\varvec{{\mathcal {C}}}\varvec{{\mathcal {H}}}\left( \tau _{k}\right) +2\varphi$, and $\varvec{{\mathcal {G}}}_{0}\left( \tau _{k}\right) =\varvec{{\mathcal {C}}}\varvec{{\mathcal {G}}}\left( \tau _{k}\right)$, with $\varvec{{\mathcal {J}}}_{2}\left( \tau _{k}\right) =e^{\tau _{k}\varvec{{\mathcal {A}}}_{n}}$, $\varvec{{\mathcal {H}}}_{2}\left( \tau _{k}\right) =\left( \varvec{{\mathcal {J}}}_{2}\left( \tau _{k}\right) \right. \left. - \varvec{{\mathcal {I}}}\right) \varvec{{\mathcal {A}}}_{n}^{-1}\varvec{{\mathcal {D}}}_{n}$, and $\varvec{{\mathcal {G}}}_{2}\left( \tau _{k}\right) =\left( \varvec{{\mathcal {J}}}_{2}\left( \tau _{k}\right) - \varvec{{\mathcal {I}}}\right) \varvec{{\mathcal {A}}}_{n}^{-1}\varvec{{\mathcal {B}}}_{n}$.

It is obvious that the controlled hybrid Poincaré map (7) is linear in terms of the state vector ${\varvec{x}}_{k}^{-}$ and also the control parameter $\theta ^{d}_{tk}$ contrary to that developed in [7] where the Poincaré map is fully nonlinear.

2.3.4 Determination of the one-periodic fixed point of the controlled hybrid Poincaré map

This section is dedicated for the determination of the relations allowing us to calculate the one-periodic fixed point of the controlled hybrid Poincaré map (7) for the nominal desired torso angle $\theta ^{d}_{t*}=\theta ^{d}_{tn}$. Let ${\varvec{x}}_{*}^{-}$ be the one-periodic fixed point of the controlled hybrid Poincaré map. For this fixed point, it corresponds a nominal impact instant $\tau _{*}$. The fixed point can be obtained by enforcing the periodicity ${\varvec{x}}_{k+1}^{-}={\varvec{x}}_{k}^{-}={\varvec{x}}_{*}^{-}$. Hence, the one-periodic fixed point ${\varvec{x}}_{*}^{-}$ together with $\theta ^{d}_{t*}$ and $\tau _{*}$ must verify the following expressions:

$$\begin{aligned}&\varvec{{\mathcal {P}}}\left( {\varvec{x}}_{*}^{-}, \tau _{*},\theta ^{d}_{t*}\right) - {\varvec{x}}_{*}^{-} = {\varvec{0}}, \end{aligned}$$

(9a)

$$\begin{aligned}&{{\mathcal {Q}}}\left( {\varvec{x}}_{*}^{-}, \tau _{*},\theta ^{d}_{t*}\right) = 0. \end{aligned}$$

(9b)

Relying on expressions (8a) and (8b), we can show that the nominal impact instant $\tau _{*}$ is the solution of the following scalar function:

$$\begin{aligned}&\varvec{{\mathcal {C}}}\left( \varvec{{\mathcal {J}}}\left( \tau _{*}\right) \left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}+\varvec{{\mathcal {I}}}\right) \nonumber \\&\quad \left( \varvec{{\mathcal {H}}}\left( \tau _{*}\right) +\varvec{{\mathcal {G}}}\left( \tau _{*}\right) \theta ^{d}_{t*}\right) +2\varphi =0 . \end{aligned}$$

(10)

Using the following relation:

$$\begin{aligned} \varvec{{\mathcal {J}}}\left( \tau _{*}\right) \left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}+\varvec{{\mathcal {I}}}=\left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}, \end{aligned}$$

(11)

then expression (10) will be simplified as follows:

$$\begin{aligned} \varvec{{\mathcal {C}}}\left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}\left( \varvec{{\mathcal {H}}}\left( \tau _{*}\right) +\varvec{{\mathcal {G}}}\left( \tau _{*}\right) \theta ^{d}_{t*}\right) +2\varphi =0.\nonumber \\ \end{aligned}$$

(12)

We stress that function (12) is nonlinear with respect to the unknown variable $\tau _{*}$. Hence, the only possible way to solve it is numerically.

Once the impact time $\tau _{*}$ is calculated numerically, the fixed point ${\varvec{x}}_{*}^{-}$ will be evaluated according to the following expression:

$$\begin{aligned} {\varvec{x}}_{*}^{-}=\left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}\left( \varvec{{\mathcal {H}}}\left( \tau _{*}\right) +\varvec{{\mathcal {G}}}\left( \tau _{*}\right) \theta ^{d}_{t*}\right) . \end{aligned}$$

(13)

It is obvious that the identification of the fixed point ${\varvec{x}}_{*}^{-}$ needs only the resolution of the scalar function (12) contrary to our designed method in [7] where the fixed point ${\varvec{x}}_{*}^{-}$ and the impact time $\tau _{*}$ must be computed numerically together.

2.3.5 Linearization of the controlled hybrid Poincaré map around its one-periodic fixed point

Let us consider first the following notations: ${\Delta } {\varvec{x}}_{k+1}^{-} = {\varvec{x}}_{k+1}^{-} - {\varvec{x}}_{*}^{-}$, ${\Delta } {\varvec{x}}_{k}^{-} = {\varvec{x}}_{k}^{-} - {\varvec{x}}_{*}^{-}$, and ${\varDelta } \theta ^{d}_{tk} = \theta ^{d}_{tk} - \theta ^{d}_{t*}$. Relying on the expression of the controlled hybrid Poincaré map (7) and the relation (9a), the linearization of the controlled hybrid Poincaré map around the one-periodic fixed point ${\varvec{x}}_{*}^{-}$ yields:

$$\begin{aligned} {\varDelta } {\varvec{x}}_{k+1}^{-} = {{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{*}^{-}}{\varDelta } {\varvec{x}}_{k}^{-} + {{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{t*}}{\varDelta } \theta ^{d}_{tk}, \end{aligned}$$

(14)

with ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{*}^{-}}={{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{k}^{-}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) _{\left| \left( {\varvec{x}}_{*}^{-}, \tau _{*}, \theta ^{d}_{t*}\right) \right. }$ is the Jacobian matrix, and ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{t*}}={{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{tk}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) _{\left| \left( {\varvec{x}}_{*}^{-}, \tau _{*}, \theta ^{d}_{t*}\right) \right. }$ is the derivative of the controlled hybrid Poincaré map with respect to the control parameter $\theta ^{d}_{tk}$. “Appendix 3” provides the method for establishing expressions of the two matrices ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{k}^{-}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)$ and ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{tk}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)$ using expression of the controlled hybrid Poincaré map (7) with relations in (8).

Based on expression (13) of the one-periodic fixed point ${\varvec{x}}_{*}^{-}$ and expressions in (27), the two matrices ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{*}^{-}}$ and ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{t*}}$ in the linearized controlled Poincaré map (14) are expressed like so:

$$\begin{aligned} {{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{*}^{-}}= & {} \left[ \varvec{{\mathcal {I}}} - \frac{\varvec{{\mathcal {A}}}_{n}\left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}\left( \varvec{{\mathcal {H}}}\left( \tau _{*}\right) +\varvec{{\mathcal {G}}}\left( \tau _{*}\right) \theta ^{d}_{t*}\right) \varvec{{\mathcal {C}}}+\left( \varvec{{\mathcal {D}}}_{n}+\varvec{{\mathcal {B}}}_{n}\theta ^{d}_{t*}\right) \varvec{{\mathcal {C}}}}{\varvec{{\mathcal {C}}}\varvec{{\mathcal {A}}}_{n}\left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}\left( \varvec{{\mathcal {H}}}\left( \tau _{*}\right) +\varvec{{\mathcal {G}}}\left( \tau _{*}\right) \theta ^{d}_{t*}\right) +\varvec{{\mathcal {C}}}\left( \varvec{{\mathcal {D}}}_{n}+\varvec{{\mathcal {B}}}_{n}\theta ^{d}_{t*}\right) }\right] \varvec{{\mathcal {J}}}\left( \tau _{*}\right) , \end{aligned}$$

(15a)

$$\begin{aligned} {{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{t*}}= & {} \left[ \varvec{{\mathcal {I}}} - \frac{\varvec{{\mathcal {A}}}_{n}\left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}\left( \varvec{{\mathcal {H}}}\left( \tau _{*}\right) +\varvec{{\mathcal {G}}}\left( \tau _{*}\right) \theta ^{d}_{t*}\right) \varvec{{\mathcal {C}}}+\left( \varvec{{\mathcal {D}}}_{n}+\varvec{{\mathcal {B}}}_{n}\theta ^{d}_{t*}\right) \varvec{{\mathcal {C}}}}{\varvec{{\mathcal {C}}}\varvec{{\mathcal {A}}}_{n}\left( \varvec{{\mathcal {I}}}-\varvec{{\mathcal {J}}}\left( \tau _{*}\right) \right) ^{-1}\left( \varvec{{\mathcal {H}}}\left( \tau _{*}\right) +\varvec{{\mathcal {G}}}\left( \tau _{*}\right) \theta ^{d}_{t*}\right) +\varvec{{\mathcal {C}}}\left( \varvec{{\mathcal {D}}}_{n}+\varvec{{\mathcal {B}}}_{n}\theta ^{d}_{t*}\right) }\right] \varvec{{\mathcal {G}}}\left( \tau _{*}\right) . \end{aligned}$$

(15b)

It is worth noting that the state matrix ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{*}^{-}}$ and the input matrix ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{t*}}$ depend only upon the nominal impact instant $\tau _{*}$. Expressions of these two matrices are simpler than those presented in [7].

2.3.6 Stabilization of the one-periodic fixed point

According to [7], stabilization of the discrete linear system (14) is achieved with a classical state-feedback controller ${\varDelta } \theta ^{d}_{tk}=\varvec{{\mathcal {K}}}{\varDelta } {\varvec{x}}_{k}^{-}$. Hence, stabilization of the one-periodic fixed point ${\varvec{x}}_{*}^{-}$ of the controlled hybrid Poincaré map (7) is realized with the following OGY-based control law:

$$\begin{aligned} \theta ^{d}_{tk} = \theta ^{d}_{t*} + \varvec{{\mathcal {K}}}\left( {\varvec{x}}_{k}^{-} - {\varvec{x}}_{*}^{-}\right) . \end{aligned}$$

(16)

The research for the matrix gain $\varvec{{\mathcal {K}}}$ of the control law is subject to the resolution of a linear matrix inequality [7].

2.3.7 Application of the OGY control into the impulsive hybrid nonlinear dynamics

We have chosen first the same nominal values as in [7], i.e., a desired nominal slope $\varphi _{n}=5$ and a nominal desired torso angle $\theta ^{d}_{tn}=0$. For these nominal values, the semi-passive gait of the torso-driven biped robot is chaotic [5, 7]. Relying on the previous subsections, the parameters of the OGY control (16) are:

${\varvec{x}}_{*}^{-} = [16.2245 \ -26.2245 \ -0.0510 \ -118.8042 -95.8755 \ \ 0.2238]^{T}$ and $\varvec{{\mathcal {K}}}=[5.2077 \ -0.9356 \ 1.1625 -0.0516\ 1.0082 \ 0.3042 ]$. For such fixed point ${\varvec{x}}_{*}^{-}$, it corresponds the nominal impact instant $\tau _{*}=0.1173$ (or $\tau _{*}=0.8230$ after scaling according to [7]). We stress that these results are fairly close to that identified in [7] with a slight difference in the value of the gain matrix $\varvec{{\mathcal {K}}}$. Application of the OGY control law to the impulsive hybrid nonlinear dynamics of the torso-driven biped robot has controlled chaos as seen in Fig. 2. Figure 2a shows the variation of the step period of the controlled semi-passive dynamic walking of the biped robot, whereas Fig. 2b reveals the variation of the desired torso angle or the OGY control law at each walking step. Here, the departure point of the controlled semi-passive gait is chosen to be the fixed point ${\varvec{x}}_{*}^{-}$ itself of the desired one-periodic hybrid limit cycle. Although chaos is controlled, nevertheless the one-periodic fixed point at which the controlled semi-passive gait converges is completely different to the desired fixed point ${\varvec{x}}_{*}^{-}$ and hence the desired step period $\tau _{*}$ where the nominal desired torso angle is $\theta ^{d}_{tn}=0\$. The controlled step period stabilizes at the value 0.8197 and the desired torso angle is found to converge to the value $-2.1691$. Moreover, such stabilization needs almost 100 steps of the biped robot. We note that this unexpected result is completely different to that found in [7], where the semi-passive gait converges nearly to the desired one-period cyclic motion.

Fig. 2

Controlled step period (a) and controlled desired torso angle (OGY control law) (b) for the nominal values $\varphi _{n}=5$ and $\theta ^{d}_{tn}=0$

Fig. 3

Controlled step period (a) and controlled desired torso angle (OGY control law) (b) for the nominal values $\varphi _{n}=5$ and $\theta ^{d}_{tn}=20$

In addition, we have chosen another value of the nominal desired torso angle $\theta ^{d}_{tn}=20$ and we kept the same nominal slope $\varphi _{n}=5$. We stress that the uncontrolled semi-passive gait of the torso-driven biped robot is also chaotic [5, 7]. Numerical calculation of the one-periodic fixed point of the hybrid Poincaré map and the gain matrix gave the following results:

${\varvec{x}}_{*}^{-} = [10.2346 \ -20.2346 \ 20.0004 \ -121.4976 -66.5838 \ -0.0016 ]^{T}, \varvec{{\mathcal {K}}}=[ 5.1745 \ -0.8128 \ 1.0744 -0.0563 \ 1.1977 \ 0.3255 ]$, and $\tau _{*}=0.1234$ (or $\tau _{*}=0.8687$ after scaling). With these values of the OGY control law (16), the chaotic semi-passive gait is well controlled as seen in Fig. 3. Here, the departure point of the semi-passive gait is chosen arbitrary to be different to the identified fixed point ${\varvec{x}}_{*}^{-}$. The step period converges to the value 0.8699 and the desired torso angle converges to 20.1624. These results are almost identical to the desired ones. Compared to the previous case, the chaotic semi-passive gait needs about 20 steps in order to be controlled. In the present case, results obtained from the OGY control of the impulsive hybrid nonlinear dynamics are more convincing (Fig. 3).

Fig. 4

Bifurcation diagrams (a and c: step period, b and d: desired torso angle, i.e., the OGY control) revealing the displayed behaviors of the semi-passive dynamic walking of the torso-driven biped robot under the OGY control as the slope parameter $\varphi$ varies for the nominal slope $\varphi _{n}=5$ and for two different nominal desired torso angles: a and b for $\theta ^{d}_{tn}=0$, and c and d for $\theta ^{d}_{tn}=20$

3 Analysis of the controlled impulsive hybrid nonlinear dynamics via bifurcation diagrams

In this section, we aim at investigating mainly by means of bifurcation diagrams the displayed behaviors in the impulsive hybrid nonlinear dynamics of the torso-driven biped robot under the OGY control designed in the previous section. In addition, these behaviors will be compared with those identified in [4] in order to highlight the difference between the linearization method of the impulsive hybrid nonlinear dynamics developed in this paper and that achieved in [7]. Then, we have chosen the desired nominal slope $\varphi _{n}=5$ and the two nominal values of the desired torso angle: $\theta ^{d}_{tn}=0$ (as in [4]) and $\theta ^{d}_{tn}=20$. Thus, using the calculated parameters of the OGY control law in the previous section, we vary gradually the slope angle $\varphi$ (chosen to be the bifurcation parameter) in order to show the influence/performance of the OGY control on the behavior of the controlled semi-passive dynamic walking of the biped robot under variation of the slope parameter.

Fig. 5

Transformation of the closed invariant circle born via the Neimark–Sacker bifurcation (for the case $\varphi _{n}=5$ and $\theta ^{d}_{tn}=0$) into a chaotic attractor in the 2D Poincaré section as the slope parameter decreases: a $\varphi =4.18$, b $\varphi =4.01$, c $\varphi =3.98$ and d $\varphi =3.93$

Figure 4 shows the different bifurcation diagrams revealing the controlled step period as well as the desired torso angle (the OGY control law) of the controlled semi-passive gait of the biped robot under the OGY control. It is obvious that, as the bifurcation parameter $\varphi$ is swept from left to right from the nominal value $\varphi _{n}=5$, the controlled impulsive hybrid nonlinear dynamics exhibits only one-periodic motions in a very narrow interval of slopes. The one-periodic behavior is terminated at $\varphi =5.011$ (resp. $\varphi =5.075$) for $\theta ^{d}_{tn}=0$ (resp. $\theta ^{d}_{tn}=20$) through a cyclic-fold bifurcation (indicated by CFB) leading hence to the abrupt fall of the biped robot. However, when the bifurcation parameter is swept in the opposite direction, the controlled semi-passive dynamics displays a Neimark–Sacker bifurcation (marked NSB in Fig. 4) (a secondary-Hopf bifurcation or a torus bifurcation) as in [4] giving rise hence to the generation of a quasi-periodic behavior. This Neimark–Sacker bifurcation occurs at the parameter $\varphi =4.185$ (resp. $\varphi =4.635$) for $\theta ^{d}_{tn}=0$ (resp. $\theta ^{d}_{tn}=20$). On further decreasing the parameter $\varphi$, the controlled impulsive hybrid nonlinear dynamics experiences the formation of chaos and as a result the sudden death of the bipedal chaos at $\varphi =3.928$ (resp. $\varphi =4.435$) for $\theta ^{d}_{tn}=0$ (resp. $\theta ^{d}_{tn}=20$) by means of a boundary crisis [5].

Fig. 6

Numerical simulation of the one-periodic gait (a) and the chaotic gait (b) for $\varphi =4.4$ and $\varphi =3.93$, respectively

Figure 5 shows different attractors in the 2D projected Poincaré section (${\dot{\theta }}_{ns}^{-}$ versus $\theta _{ns}^{-}$). These attractors are plotted for different values of the slope parameter $\varphi$ beyond the Neimark–Sacker bifurcation and for the nominal slope $\varphi _{n}=5$ and the nominal desired torso angle $\theta ^{d}_{tn}=0$. Figure 5a depicts the 2D torus (or equivalently the 2D closed invariant circle) for the slope parameter $\varphi =4.18$. The transient dynamics is shown inside the invariant circle in Fig. 5a. By moving slightly the bifurcation parameter $\varphi$, the closed invariant circle loses progressively its own shape, as seen in Fig. 5b for $\varphi =4.01$ and Fig. 5c for $\varphi =3.98$. For these two parameters, the controlled dynamics of the biped robot under consideration is also quasi-periodic, but the form of the 2D closed invariant curve becomes more complex as the slope parameter $\varphi$ decreases. Figure 5c reveals a chaotic attractor in the 2D projected Poincaré section for $\varphi =3.93$.

Fig. 7

Bifurcation diagrams: step period (a, c) and desired torso angle (OGY controller) (b, d) as the bifurcation parameter $\varphi$ varies, for the nominal slope $\varphi _{n}=5$ and for two different values of the nominal desired torso angle: a and b $\theta ^{d}_{tn}=0$, c and d $\theta ^{d}_{tn}=20$. Here, we plot the behavior of semi-passive gait under the OGY control designed in this paper (attractor $A_{2}$) and that observed in [4] using the OGY control method developed in [7]

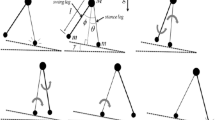
In order to better understand the behavior of the torso-driven biped robot under control as it goes down an inclined surface, we have captured both the one-periodic gait for the slope angle $\varphi =4.4$ and the chaotic gait for $\varphi =3.93$, as seen in Fig. 6. Figure 6a shows some typical steps of the one-periodic gait, whereas Fig. 6b reveals 12 steps of the chaotic gait. In these two pictures, the values under the slope indicate the period of each step. It is obvious that the step period keeps the same value for $\varphi =4.4$, but it is erratic for $\varphi =3.93$. Moreover, it is clear from Fig. 6b that at each step, the torso of the biped robot reaches a new desired position. Nevertheless, such desired position of the torso varies also in a chaotic manner as observed in the bifurcation diagram in Fig. 5b. Thus, the torso can be stabilized either in the backward position or in the forward position as the biped robot walks down the slope.

Figure 7 shows the previous displayed nonlinear phenomena in Fig. 4 (indicated by $A_{2}$) and those (indicated by $A_{1}$) identified in [4]. We emphasize that only the case for $\varphi _{n}=5$ and $\theta ^{d}_{tn}=0$ was investigated by us in [4]. The other case ($\varphi _{n}=5$ and $\theta ^{d}_{tn}=20$) is investigated for the first time in this paper. It is obvious from Fig. 7 that the displayed behaviors in the impulsive hybrid nonlinear dynamics under the two OGY controllers are completely different. For the attractor $A_{1}$, the impulsive hybrid nonlinear dynamics under the OGY control experiences a period-doubling route to chaos from the critical point $\varphi =6.33$ (resp. $\varphi =5.954$) for $\theta ^{d}_{tn}=0$ (resp. $\theta ^{d}_{tn}=20$) giving then rise to an interval of slopes for an efficient controlled one-periodic semi-passive gait larger than that of the attractor $A_{2}$. In addition, we emphasize that the attractor $A_{1}$ was found to exhibit also the Neimark–Sacker bifurcation [4]. We stress that the displayed behaviors for the two controlled semi-passive walking dynamics for slopes inferior to $\varphi _{n}=5$ have almost the same shape. In addition, it is worth noting that for all slopes, the attractor $A_{2}$ is developed in a very small interval of slopes compared with the attractor $A_{1}$.

4 Calculation of the spectrum of Lyapunov exponents via the controlled hybrid Poincaré map

In this section, we aim at computing the spectrum of Lyapunov exponents in the impulsive hybrid nonlinear dynamics (1) under the OGY controller (16) in order to investigate further periodic, quasi-periodic and chaotic gaits. However, morbid problems have been encountered in which we are unable to calculate the Jacobian matrix of the continuous dynamics (1) under the OGY control and hence we are unable to compute numerically the fundamental solution matrix. We note that in [6], we calculated the spectrum of the Lyapunov exponents in the impulsive hybrid nonlinear dynamics but without control (the desire torso angle $\theta ^{d}_{t}$ was kept constant). Then, in order to prevent the computation problem of Lyapunov exponents, our main idea is to use the controlled hybrid Poincaré map (7) under the OGY control (16).

Furthermore, the second problem in the calculation of the spectrum of Lyapunov exponents via the controlled hybrid Poincaré map lies in its dimension. Indeed, we note first that the dimension of the impulsive hybrid nonlinear dynamics (1) is 6. Then, we have 6 Lyapunov exponents: $\lambda _{0}$, $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, $\lambda _{4}$ and $\lambda _{5}$, where $\lambda _{0}$ is always zero [6, 21]. Moreover, the controlled hybrid Poincaré map (7) is also 6-dimensional. However, the Poincaré map must be 5-dimensional. Then, using expression (7) to calculate the spectrum of Lyapunov exponents makes the numerical computation results unreliable. Therefore, to prevent also this problem, a dimension reduction of the hybrid Poincaré map will be achieved. As a result, the five Lyapunov exponents calculated using the reduced-dimension Poincaré map will be approximately: $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, $\lambda _{4}$ and $\lambda _{5}$.

4.1 Dimension reduction of the controlled hybrid Poincaré map

Using expression of the control law (16), the controlled hybrid Poincaré map (7) in closed loop becomes:

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{x}}_{k+1}^{-} = \varvec{\hat{{\mathcal {P}}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}\right) = \varvec{\hat{{\mathcal {J}}}}\left( \tau _{k}\right) {\varvec{x}}^{-}_{k} + \varvec{\hat{{\mathcal {H}}}}\left( \tau _{k}\right) \\ \text {s.t.}\\ \hat{{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}\right) = \varvec{\hat{{\mathcal {J}}}}_{0}\left( \tau _{k}\right) {\varvec{x}}^{-}_{k} + \varvec{\hat{{\mathcal {H}}}}_{0}\left( \tau _{k}\right) = 0\\ \end{array} \right. , \end{aligned}$$

(17)

where $\varvec{\hat{{\mathcal {J}}}}\left( \tau _{k}\right) =\varvec{{\mathcal {J}}}\left( \tau _{k}\right) +\varvec{{\mathcal {G}}}\left( \tau _{k}\right) \varvec{{\mathcal {K}}}$, $\varvec{\hat{{\mathcal {H}}}}\left( \tau _{k}\right) =\varvec{{\mathcal {H}}}\left( \tau _{k}\right) +\varvec{{\mathcal {G}}}\left( \tau _{k}\right) \left( \theta ^{d}_{t*}-\varvec{{\mathcal {K}}}{\varvec{x}}_{*}^{-}\right)$, $\varvec{\hat{{\mathcal {J}}}}_{0}\left( \tau _{k}\right) =\varvec{{\mathcal {C}}}\varvec{\hat{{\mathcal {J}}}}\left( \tau _{k}\right)$, and $\varvec{\hat{{\mathcal {H}}}}_{0}\left( \tau _{k}\right) =\varvec{{\mathcal {C}}}\varvec{\hat{{\mathcal {H}}}}\left( \tau _{k}\right) +2\varphi$.

We note that in (3), $\varvec{{\mathcal {C}}}=\left[ \begin{array}{cc} 1&\;\varvec{\hat{{\mathcal {C}}}} \end{array}\right]$, where $\varvec{\hat{{\mathcal {C}}}}=\left[ \begin{array}{ccccc} 1&\;0&\;0&\;0&\;0 \end{array}\right]$. Posing ${\varvec{x}}_{k}^{-}=\left[ \begin{array}{c} x_{1,k}^{-} \\ {\varvec{z}}_{k}^{-} \end{array}\right]$, where $x_{1,k}^{-}\in {\mathbb {R}}$ and ${\varvec{z}}_{k}^{-}\in {\mathbb {R}}^{5\times 1}$. Then, using expression (3a), we can write the following relations lying ${\varvec{z}}_{k}^{-}$ and ${\varvec{x}}_{k}^{-}$:

$$\begin{aligned} {\varvec{x}}_{k}^{-}= & {} \varvec{{\varPhi }}{\varvec{z}}_{k}^{-} + \varvec{{\varTheta }}, \end{aligned}$$

(18a)

$$\begin{aligned} {\varvec{z}}_{k}^{-}= & {} \varvec{{\varPsi }}{\varvec{x}}_{k}^{-}, \end{aligned}$$

(18b)

where $\varvec{{\varPhi }}=\left[ \begin{array}{c} -\varvec{\hat{{\mathcal {C}}}} \\ \varvec{{\mathcal {I}}}_{5\times 5} \end{array}\right]$, $\varvec{{\varTheta }}=\left[ \begin{array}{c} -2\varphi \\ \varvec{{\mathcal {O}}}_{5\times 1} \end{array}\right]$, and $\varvec{{\varPsi }}=\left[ \begin{array}{cc} \varvec{{\mathcal {O}}}_{5\times 1}&\; \varvec{{\mathcal {I}}}_{5\times 5} \end{array}\right]$, with $\varvec{{\mathcal {O}}}$ is the zero matrix.

Then, relying on relations in (18), expressions in (17) are reformulated as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{z}}_{k+1}^{-} = \varvec{\check{{\mathcal {P}}}}\left( {\varvec{z}}_{k}^{-}, \tau _{k}\right) = \varvec{\check{{\mathcal {J}}}}\left( \tau _{k}\right) {\varvec{z}}^{-}_{k} + \varvec{\check{{\mathcal {H}}}}\left( \tau _{k}\right) \\ \text {s.t.}\\ \check{{\mathcal {Q}}}\left( {\varvec{z}}_{k}^{-}, \tau _{k}\right) = \varvec{\check{{\mathcal {J}}}}_{0}\left( \tau _{k}\right) {\varvec{z}}^{-}_{k} + \varvec{\check{{\mathcal {H}}}}_{0}\left( \tau _{k}\right) = 0\\ \end{array} \right. , \end{aligned}$$

(19)

where $\varvec{\check{{\mathcal {J}}}}\left( \tau _{k}\right) =\varvec{{\varPsi }}\varvec{\hat{{\mathcal {J}}}}\left( \tau _{k}\right) \varvec{{\varPhi }}$, $\varvec{\check{{\mathcal {H}}}}\left( \tau _{k}\right) =\varvec{{\varPsi }}\varvec{\hat{{\mathcal {J}}}}\left( \tau _{k}\right) \varvec{{\varTheta }}+\varvec{{\varPsi }}\varvec{\hat{{\mathcal {H}}}}\left( \tau _{k}\right)$, $\varvec{\check{{\mathcal {J}}}}_{0}\left( \tau _{k}\right) =\varvec{\hat{{\mathcal {J}}}}_{0}\left( \tau _{k}\right) \varvec{{\varPhi }}$, and $\varvec{\check{{\mathcal {H}}}}_{0}\left( \tau _{k}\right) =\varvec{\hat{{\mathcal {J}}}}_{0}\left( \tau _{k}\right) \varvec{{\varTheta }}+\varvec{\hat{{\mathcal {H}}}}_{0}\left( \tau _{k}\right)$.

Hence, expression (19) reveals the reduced-dimension controlled hybrid Poincaré map in the closed loop.

4.2 Analysis of order/chaos with the spectrum of Lyapunov exponents

We emphasize that the numerical computation of the spectrum of Lyapunov exponents via the controlled hybrid Poincaré map (19) was achieved by means of its Jacobian matrix ${{\mathcal {D}}}\varvec{\check{{\mathcal {P}}}}\left( {\varvec{z}}_{k}^{-}, \tau _{k}\right)$ [21]. “Appendix 4” presents the method for determining expression of such Jacobian matrix.

In order to classify approximately the observed (periodic and chaotic) attractors in the bifurcation diagrams in the previous Sect. 3, the bifurcation diagram of the controlled hybrid Poincaré map system (19) for the case $\varphi _{n}=5$ and $\theta ^{d}_{tn}=0$, and the corresponding Lyapunov exponents diagram are given in Fig. 8a, b, respectively. Figure 8c, d are an enlargement of Fig. 8a, b, respectively. In Fig. 8d, we plotted only the two largest Lyapunov exponents $\lambda _{1}$ and $\lambda _{2}$ in order to show the variation of the largest Lyapunov exponent $\lambda _{1}$.

Fig. 8

a The bifurcation diagram of the controlled hybrid Poincaré map (19) with respect to the slope parameter $\varphi$ and b variation of the Lyapunov exponents with respect to the slope parameter $\varphi$. c and d are a blow-up view of a and b, respectively

It is obvious that the regions where all Lyapunov exponents are negative correspond to periodic attractors and that with a positive Lyapunov exponent (i.e., $\lambda _{1}>0$) correspond to chaotic attractors. Furthermore, when $\lambda _{1}=0$, then the controlled behavior of the bipedal gait is quasi-periodic, as depicted in Fig. 8d. Moreover, it is worth noting that when the periodic solution meets the Neimark–Sacker bifurcation and also the cyclic-fold bifurcation, the two largest Lyapunov exponents $\lambda _{1}$ and $\lambda _{2}$ tends to zero, as shown in Fig. 8b. The diagram of Lyapunov exponents in Fig. 8b (resp. (d)) is in good agreement with the bifurcation diagram in Fig. 8a (resp. (c)).

5 Discussion

We have seen that chaos and bifurcations were displayed in the OGY-based controlled hybrid Poincaré map and also in the impulsive hybrid nonlinear dynamics of the torso-driven biped robot under the OGY control as the slope parameter $\varphi$ varies. Then, we can stress that the OGY control, since it was developed using the Poincaré map’s concept and via its linearization around the one-periodic fixed point and for some nominal value $\varphi _{n}$ of the slope, its effect was remarkable only around such nominal value. Then, as $\varphi$ varies away of its nominal value, the OGY control loses progressively its performance and hence the torso-driven biped robot under the OGY control will generate some unexpected behaviors, i.e., the cyclic-fold bifurcation, the Neimark–Sacker bifurcation and chaos. Such nonlinear phenomena can be observed also using other control methods such as the damping method, which was used by Goswami et al. [2].

On the other hand, we can emphasize that the major drawback of the OGY-based control approach was due to the (long) waiting time until the system trajectory (the flow) enters with the Poincaré section (here the walking surface ${\varGamma }$ in (2b)) a close neighborhood of the target one-periodic limit cycle. In fact, in literature, several papers have showed the drawbacks of the OGY method in some dynamic systems (see for example [1, 25, 28]). It has been shown that the dynamics of the controlled system under the OGY method can change and accordingly exhibits different nonlinear behaviors and generally the period-doubling route to chaos was generated.

6 Conclusion and future works

In this work, we analyzed bifurcations and chaos in the semi-passive dynamic walking of the torso-driven biped robot under an OGY-based controller where the desired torso angle was the accessible control parameter. Such controller was designed firstly by linearizing the impulsive hybrid nonlinear dynamics of the semi-passive biped robot around a desired one-period hybrid limit cycle, and secondly by developing an analytical expression of a controlled hybrid Poincaré map. We linearized both the differential equation and the algebraic equation of the semi-passive walking model. Hence, the Poincaré map was found to be linear in terms of the state vector and also in terms of the control input, the desired torso angle. We demonstrated that identification of the one-periodic fixed point of the hybrid Poincaré map and calculation of its Jacobian matrix depend only upon the impact instant. We showed that application of the designed controller into the impulsive hybrid nonlinear dynamics has controlled chaos.

In addition, we analyzed the performance of the OGY-based controller on the behavior of the semi-passive biped robot as the slope parameter varies. We showed through bifurcation diagrams that, for some nominal values of the slope and the desired torso angle, the controlled semi-passive dynamic walking of the biped robot exhibits a cyclic-fold (resp. Neimark–Sacker) bifurcation for slopes higher than (inferior to) the nominal slope. Moreover, we showed that, on further decreasing the slope parameter, chaos was developed. In addition, we analyzed the closed invariant circle and its deformation to a chaotic attractor in the 2D Poincaré section as the bifurcation parameter varies.

Furthermore, our investigation on chaos and bifurcations in the semi-passive walking dynamics under the OGY-based control approach was achieved by means of the spectrum of Lyapunov exponents. In fact, in order to overcome the calculation problem of the spectrum of Lyapunov exponents via the continuous-time impulsive hybrid nonlinear dynamics, such study was done via the controlled hybrid Poincaré map. To achieve this objective, we reduced the dimension of the hybrid Poincaré map (under the OGY controller) and we determined expression of the Jacobian matrix.

Our proposed strategy for the building of an analytical expression of the controlled hybrid Poincaré map from the impulsive hybrid nonlinear dynamics for the OGY-based controller design can be applied for several model of biped robots with a more complicated morphology, such as the passive biped robot with knees (and with torso), the compass-gait biped robot with semicircular feet (with knees and/or torso), etc. Moreover, developing a controller using the designed controlled hybrid Poincaré map without linearizing it should be considered as future works.

Furthermore, as chaos and bifurcations were displayed in the hybrid Poincaré map under the OGY control, we can use the multiparameter control method [22] or the semi-continuous method [23] in order to improve the response of the torso-driven biped robot while walking down the inclined surface.

Appendices

Appendix 1

In this appendix, we describe the impulsive hybrid nonlinear dynamics (1)–(2) of the torso-driven biped robot based on the Lagrangian formulation [6, 7].

1.1 Lagrangian representation

As $\varvec{\theta }=\left[ \begin{array}{ccc} \theta _{ns}&\,\theta _{s}&\,\theta _{t} \end{array} \right] ^T$ is the vector of generalized coordinates of the torso-driven biped robot, the impulsive hybrid nonlinear dynamics of its dynamic walking is modeled as follows [7]:

$$\begin{aligned}&\varvec{{{\mathcal {J}}}}(\varvec{\theta })\varvec{{\ddot{\theta }}}+\varvec{{{\mathcal {H}}}}(\varvec{\theta },\varvec{{\dot{\theta }}})+\varvec{{{\mathcal {G}}}}(\varvec{\theta }) =\varvec{{{\mathcal {B}}}}u \quad \text {as long as}\quad \varvec{\theta }\in {\varOmega }, \end{aligned}$$

(20a)

$$\begin{aligned}&\left\{ \begin{array}{rcl} \varvec{\theta }^{+} &{}=&{} \varvec{{{\mathcal {R}}}}_{e}\varvec{\theta }^{-}\\ \dot{\varvec{\theta }}^{+} &{}=&{} \varvec{{{\mathcal {S}}}}_{e}\dot{\varvec{\theta }}^{-} \end{array} \right. \quad \begin{array}{rl} \text {whenever}&\left\{ \varvec{\theta },\varvec{{\dot{\theta }}}\right\} \in {\varGamma } \end{array}, \end{aligned}$$

(20b)

where subscribes $^{+}$ and $^{-}$ mean just after and just before the impulsive impact phase, respectively. In (20), $\varvec{{\mathcal {J}}}$ is the inertia matrix, $\varvec{{\mathcal {H}}}$ includes Coriolis and centrifugal terms, $\varvec{{\mathcal {G}}}$ includes gravity forces, $\varvec{{\mathcal {B}}}$ is the input matrix, $\varvec{{{\mathcal {R}}}_{e}}$ is the position renaming matrix, and $\varvec{{{\mathcal {S}}}_{e}}$ is the velocity reset matrix. These matrices are expressed like so:

$$\begin{aligned} {\varvec{{\mathcal {J}}}}(\varvec{\theta })= & {} \left[ \begin{array}{ccc} mb^2 &{} -mlbcos(\theta _{s}-\theta _{ns}) &{} 0\\ -mlbcos(\theta _{s}-\theta _{ns}) \,\,\,\,\, &{} ma^2+(m+m_{H}+m_{T})l^2 \,\,\,\,\, &{} m_{T}rlcos(\theta _{s}-\theta _{t})\\ 0 &{} m_{T}rlcos(\theta _{s}-\theta _{t}) &{} m_{T}r^2 \end{array} \right] ,\\ {\varvec{{\mathcal {H}}}}(\varvec{\theta },\dot{\varvec{\theta }})= & {} \left[ \begin{array}{c} mlb{\dot{\theta }}_{s}^2sin(\theta _{s}-\theta _{ns})\\ -mlb{\dot{\theta }}_{ns}^2sin(\theta _{s}-\theta _{ns})+m_{T}rl{\dot{\theta }}_{t}^2sin(\theta _{s}-\theta _{t})\\ -m_{T}rl{\dot{\theta }}_{s}^2sin(\theta _{s}-\theta _{t}) \end{array} \right] ,\\ {\varvec{{\mathcal {G}}}}(\varvec{\theta })= & {} g\left[ \begin{array}{c} mbsin(\theta _{ns})\\ -(ma+(m+m_{H}+m_{T})l)sin(\theta _{s})\\ -m_{T}rsin(\theta _{t}) \end{array} \right] ,\nonumber \\ {\varvec{{\mathcal {B}}}}= & {} \left[ \begin{array}{c} 0\\ 1\\ -1 \end{array} \right] ,\ {\varvec{{\mathcal {R}}}}_{e}=\left[ \begin{array}{ccc} 0 &{}\;\; 1 &{}\;\; 0\\ 1 &{}\;\; 0 &{}\;\; 0\\ 0 &{}\;\; 0 &{}\;\; 1 \end{array} \right] ,\\ \varvec{{{\mathcal {S}}}}_{e}= & {} \varvec{{{\mathcal {R}}}}_{e} - \varvec{{{\mathcal {R}}}}_{e}\varvec{{{\mathcal {M}}}}_{e}^{-1}\varvec{{{\mathcal {N}}}}_{e}\left( \varvec{{{\mathcal {D}}}}_{e}^{-1} + \varvec{{{\mathcal {N}}}}_{e}^{T}\varvec{{{\mathcal {M}}}}_{e}^{-1}\varvec{{{\mathcal {N}}}}_{e}\right) ^{-1}\varvec{{{\mathcal {Q}}}}_{e},\nonumber \\ \ \varvec{{{\mathcal {N}}}}_{e}= & {} \varvec{{\mathcal {Q}}}_{e}^{T} - \varvec{{{\mathcal {C}}}}_{e}\varvec{{{\mathcal {D}}}}_{e}^{-1},\ \varvec{{{\mathcal {M}}}}_{e} = \varvec{{{\mathcal {J}}}}-\varvec{{{\mathcal {C}}}}_{e}\varvec{{{\mathcal {D}}}}_{e}^{-1}\varvec{{{\mathcal {C}}}}_{e}^{T},\nonumber \\\ {\varvec{{\mathcal {D}}}}_{e}= & {} \left( 2m+m_{H}+m_{T}\right) \varvec{{\mathcal {I}}}_{2},\nonumber \\ \ {\varvec{{\mathcal {Q}}}}_{e}= & {} \left[ \begin{array}{ccc} lcos(\theta _{ns}) \,\,\,\,\, &{} -lcos(\theta _{s}) \,\,\,\,\, &{} 0\\ lsin(\theta _{ns}) \,\,\,\,\, &{} -lsin(\theta _{s}) \,\,\,\,\, &{} 0 \end{array} \right] ,\hbox { and}\\ {\varvec{{\mathcal {C}}}}_{e}= & {} \left[ \begin{array}{cc} mbcos(\theta _{ns}) &{} mbsin(\theta _{ns})\\ -\left( ma+\left( m+m_{H}+m_{T}\right) l\right) cos(\theta _{s}) \,\,\,\,\, &{} -\left( ma+\left( m+m_{H}+m_{T}\right) l\right) sin(\theta _{s})\\ -m_{T}rcos(\theta _{t}) &{} -m_{T}rsin(\theta _{t}) \end{array} \right] . \end{aligned}$$

In (20), the two sets ${\varOmega }$ and ${\varGamma }$ are described as follows:

$$\begin{aligned} {\varOmega }= & {} \left\{ \varvec{\theta }\in \mathfrak {R}^{3}\ :\ {{\mathcal {L}}}_{1}(\varvec{\theta })=l\left( cos(\theta _{s}+\varphi )-cos(\theta _{ns}+\varphi )\right) >0\right\} \nonumber \\\end{aligned}$$

(21a)

$$\begin{aligned} {\varGamma }= & {} \left\{ \begin{array}{rl} {{\mathcal {L}}}_{1}(\varvec{\theta }) &{}=l\left( cos(\theta _{s}+\varphi )-cos(\theta _{ns}+\varphi )\right) =0\\ {{\mathcal {L}}}_{2}(\varvec{\theta },\varvec{{\dot{\theta }}}) &{}=l\left( sin(\theta _{ns}+\varphi ){\dot{\theta }}_{ns}-sin(\theta _{s}+\varphi ){\dot{\theta }}_{s}\right) <0\\ {{\mathcal {L}}}_{3}(\varvec{\theta }) &{}= l\left( sin(\theta _{ns})-sin(\theta _{s})\right) >0 \end{array} \right\} \nonumber \\ \end{aligned}$$

(21b)

1.2 Semi-passive control law

As described in [6, 7], the main role of the control law u is to stabilize the torso of the biped robot at some desired position (or systematically at some desired torso angle $\theta ^{d}_{t}$) in order to achieve a semi-passive dynamic walking. Then, according to [7], the designed semi-passive control input u is expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} u = \left( \varvec{{\mathcal {C}}}\varvec{{{\mathcal {N}}}}(\varvec{\theta })\right) ^{-1}\left( v-\varvec{{\mathcal {C}}}\varvec{{\mathcal {M}}}(\varvec{\theta },\dot{\varvec{\theta }})\right) \\ v = -{{\mathcal {K}}}_{d}{\dot{\theta }}_{t}+{{\mathcal {K}}}_{p}(\theta ^{d}_{t}-\theta _{t}) \end{array} \right. \end{aligned}$$

(22)

where ${{\mathcal {K}}}_{p}$ and ${{\mathcal {K}}}_{d}$ are two gains of the semi-passive control law u, $\varvec{{\mathcal {C}}}=\left[ \begin{array}{c c c} 0&0&1 \end{array}\right]$,

$\varvec{{{\mathcal {M}}}}(\varvec{\theta },\dot{\varvec{\theta }})=-\varvec{{{\mathcal {J}}}}(\varvec{\theta })^{-1}\left( \varvec{{{\mathcal {H}}}}(\varvec{\theta },\dot{\varvec{\theta }})+\varvec{{{\mathcal {G}}}}(\varvec{\theta })\right)$, and $\varvec{{{\mathcal {N}}}}(\varvec{\theta })=\varvec{{{\mathcal {J}}}}(\varvec{\theta })^{-1}\varvec{{{\mathcal {B}}}}$.

1.3 State representation of the semi-passive walking dynamics

Using expression of the semi-passive control law (22), the impulsive hybrid nonlinear dynamics defined by (20) and (21) is reformulated hence with the state representation (1) and (2).

In (1), ${\varvec{f}}({\varvec{x}})=\left[ \begin{array}{c} \dot{\varvec{\theta }} \\ \left( \varvec{{\mathcal {I}}}_{3}-\frac{\varvec{{\mathcal {N}}}(\varvec{\theta })\varvec{{\mathcal {C}}}}{\varvec{{\mathcal {C}}}\varvec{{\mathcal {N}}}(\varvec{\theta })}\right) \varvec{{\mathcal {M}}}(\varvec{\theta },\dot{\varvec{\theta }})-\frac{\varvec{{\mathcal {N}}}(\varvec{\theta })\varvec{{\mathcal {C}}}}{\varvec{{\mathcal {C}}}\varvec{{\mathcal {N}}}(\varvec{\theta })}\left( {{\mathcal {K}}}_{p}\varvec{\theta } + {{\mathcal {K}}}_{d}\dot{\varvec{\theta }}\right) \end{array} \right]$, ${\varvec{g}}({\varvec{x}})=\left[ \begin{array}{c} {\varvec{0}}_{3 \times 3} \\ \frac{\varvec{{\mathcal {N}}}(\varvec{\theta })}{\varvec{{\mathcal {C}}}\varvec{{\mathcal {N}}}(\varvec{\theta })}{{\mathcal {K}}}_{p} \end{array} \right]$, ${{\varvec{h}}}\left( {\varvec{x}}\right) =\left[ \begin{array}{cc} \varvec{{{\mathcal {R}}}}_{e} &{}\, \varvec{{0}}_{3\times 3}\\ \varvec{{0}}_{3\times 3} &{}\, \varvec{{{\mathcal {S}}}}_{e} \end{array} \right] {\varvec{x}}$, and $\varvec{{\mathcal {I}}}_{3}$ is the three-dimensional identity matrix.

Appendix 2

According to [7], linearization of the nonlinear dynamics (1a) around a desired one-periodic flow is achieved without considering that the desired torso angle $\theta ^{d}_{t}$ is effectively the control input. Then, each linear submodel $M_{i}$, for all $i=1,2,\ldots ,n$, around the point $\varvec{\chi }_{i}$ is defined as follows:

$$\begin{aligned} \dot{{\varvec{x}}}=\varvec{{\mathcal {A}}}_{i}{{\varvec{x}}} + \varvec{{\mathcal {D}}}_{i} \quad \text {for} \quad t_{\left( i-1\right) } \le t \le t_{i}, \end{aligned}$$

with $\varvec{{\mathcal {A}}}_{i}={\varvec{f}}_{{\varvec{x}}}(\varvec{\chi }_{i}) + {\varvec{g}}_{{\varvec{x}}}(\varvec{\chi }_{i})\theta ^{d}_{t}$, and $\varvec{{\mathcal {D}}}_{i}=\left( {\varvec{f}}(\varvec{\chi }_{i})\right. \left. -{\varvec{f}}_{{\varvec{x}}}(\varvec{\chi }_{i})\varvec{\chi }_{i}\right) + \left( {\varvec{g}}(\varvec{\chi }_{i}) - {\varvec{g}}_{{\varvec{x}}}(\varvec{\chi }_{i})\varvec{\chi }_{i}\right) \theta ^{d}_{t}$, where ${\varvec{f}}_{{\varvec{x}}}({\varvec{x}}) = \frac{\partial {\varvec{f}}({\varvec{x}})}{\partial {\varvec{x}}}$, and ${\varvec{g}}_{{\varvec{x}}}({\varvec{x}}) = \frac{\partial {\varvec{g}}({\varvec{x}})}{\partial {\varvec{x}}}$.

Appendix 3

In this section, we define expressions of the Jacobian matrix ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{k}^{-}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)$ and the matrix ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{tk}}\left( {\varvec{x}}_{k}^{-},\right. \left. \tau _{k}, \theta ^{d}_{tk}\right)$, which are introduced in the linearized controlled Poincaré map (14). According to [11], these two matrices are defined like so:

$$\begin{aligned} {{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{k}^{-}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)= & {} \frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial {\varvec{x}}_{k}^{-}} \nonumber \\&+\;\frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\frac{\partial \tau _{k}}{\partial {\varvec{x}}_{k}^{-}}, \nonumber \\ \end{aligned}$$

(23a)

$$\begin{aligned} {{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{tk}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)= & {} \frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \theta ^{d}_{tk}} \nonumber \\&+ \;\frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\frac{\partial \tau _{k}}{\partial \theta ^{d}_{tk}}. \nonumber \\ \end{aligned}$$

(23b)

Based on expression (8a), we have in (23): $\frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial {\varvec{x}}_{k}^{-}}=\varvec{{\mathcal {J}}}\left( \tau _{k}\right)$, and $\frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \theta ^{d}_{tk}}=\varvec{{\mathcal {G}}}\left( \tau _{k}\right)$. Moreover, according to [7], we can demonstrate that: $\frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}=\varvec{{\mathcal {A}}}_{n}\varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) + \varvec{{\mathcal {D}}}_{n} + \varvec{{\mathcal {B}}}_{n}\theta ^{d}_{tk}$. Furthermore, we emphasize that determination of expression of the two quantities $\frac{\partial \tau _{k}}{\partial {\varvec{x}}_{k}^{-}}$ and $\frac{\partial \tau _{k}}{\partial \theta ^{d}_{tk}}$ in (23) needs the derivation of the relation (8b). Then, the derivative of the function ${{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) =0$ with respect to ${\varvec{x}}_{k}^{-}$ and $\theta ^{d}_{tk}$ yields respectively:

$$\begin{aligned} \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial {\varvec{x}}_{k}^{-}} + \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\frac{\partial \tau _{k}}{\partial {\varvec{x}}_{k}^{-}}= & {} 0, \end{aligned}$$

(24a)

$$\begin{aligned} \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \theta ^{d}_{tk}} + \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\frac{\partial \tau _{k}}{\partial \theta ^{d}_{tk}}= & {} 0. \end{aligned}$$

(24b)

Relying on expression (8b), we have: $\frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial {\varvec{x}}_{k}^{-}}=\varvec{{\mathcal {J}}}_{0}\left( \tau _{k}\right)$, and $\frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \theta ^{d}_{tk}}=\varvec{{\mathcal {G}}}_{0}\left( \tau _{k}\right)$. In addition, based on (3b), we can write: $\frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}=\frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }\frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}<0$, and $\frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }=\varvec{{\mathcal {C}}}$.

From relations in (24), the two quantities $\frac{\partial \tau _{k}}{\partial {\varvec{x}}_{k}^{-}}$ and $\frac{\partial \tau _{k}}{\partial \theta ^{d}_{tk}}$ are expressed like so:

$$\begin{aligned} \frac{\partial \tau _{k}}{\partial {\varvec{x}}_{k}^{-}}= & {} - \left( \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\right) ^{-1}\nonumber \\&\times \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial {\varvec{x}}_{k}^{-}}, \end{aligned}$$

(25a)

$$\begin{aligned} \frac{\partial \tau _{k}}{\partial \theta ^{d}_{tk}}= & {} - \left( \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\right) ^{-1}\nonumber \\&\times \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \theta ^{d}_{tk}}. \end{aligned}$$

(25b)

Substitution of (25a) and (25b) into (23a) and (23b) gives then the following expressions:

$$\begin{aligned} {{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{k}^{-}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)= & {} \frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial {\varvec{x}}_{k}^{-}} \nonumber \\&- \frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\nonumber \\&\times \left( \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\right) ^{-1}\nonumber \\&\times \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial {\varvec{x}}_{k}^{-}}, \end{aligned}$$

(26a)

$$\begin{aligned} {{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{tk}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)= & {} \frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \theta ^{d}_{tk}} \nonumber \\&- \frac{\partial \varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\nonumber \\&\times \left( \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \tau _{k}}\right) ^{-1}\nonumber \\&\times \frac{\partial {{\mathcal {Q}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) }{\partial \theta ^{d}_{tk}}. \end{aligned}$$

(26b)

Hence, since $\varvec{{\mathcal {J}}}_{0}\left( \tau _{k}\right) =\varvec{{\mathcal {C}}}\varvec{{\mathcal {J}}}\left( \tau _{k}\right)$ and $\varvec{{\mathcal {G}}}_{0}\left( \tau _{k}\right) =\varvec{{\mathcal {C}}}\varvec{{\mathcal {G}}}\left( \tau _{k}\right)$, the two expressions in (26) can be recast as follows:

$$\begin{aligned}&{{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{k}^{-}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) \nonumber \\&\quad = \left[ \varvec{{\mathcal {I}}} - \frac{\left( \varvec{{\mathcal {A}}}_{n}\varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) + \varvec{{\mathcal {D}}}_{n} + \varvec{{\mathcal {B}}}_{n}\theta ^{d}_{tk}\right) \varvec{{\mathcal {C}}}}{\varvec{{\mathcal {C}}}\left( \varvec{{\mathcal {A}}}_{n}\varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) + \varvec{{\mathcal {D}}}_{n} + \varvec{{\mathcal {B}}}_{n}\theta ^{d}_{tk}\right) }\right] \varvec{{\mathcal {J}}}\left( \tau _{k}\right) , \end{aligned}$$

(27a)

$$\begin{aligned}&{{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{tk}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) \nonumber \\&\quad = \left[ \varvec{{\mathcal {I}}} - \frac{\left( \varvec{{\mathcal {A}}}_{n}\varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) + \varvec{{\mathcal {D}}}_{n} + \varvec{{\mathcal {B}}}_{n}\theta ^{d}_{tk}\right) \varvec{{\mathcal {C}}}}{\varvec{{\mathcal {C}}}\left( \varvec{{\mathcal {A}}}_{n}\varvec{{\mathcal {P}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) + \varvec{{\mathcal {D}}}_{n} + \varvec{{\mathcal {B}}}_{n}\theta ^{d}_{tk}\right) }\right] \varvec{{\mathcal {G}}}\left( \tau _{k}\right) .\nonumber \\ \end{aligned}$$

(27b)

Appendix 4

In this Appendix, we present the method for determining expression of the Jacobian matrix $\varvec{{\mathcal {D}}}\varvec{\check{{\mathcal {P}}}}$ of the reduced-dimension controlled hybrid Poincaré map (19) in order to calculate the spectrum of Lyapunov exponents.

The Jacobian matrix $\varvec{{\mathcal {D}}}\varvec{\check{{\mathcal {P}}}}$ is expressed like so:

$$\begin{aligned} {{\mathcal {D}}}\varvec{\check{{\mathcal {P}}}}\left( {\varvec{z}}_{k}^{-}, \tau _{k}\right)= & {} \frac{\mathrm{d} \varvec{\check{{\mathcal {P}}}}\left( {\varvec{z}}_{k}^{-}, \tau _{k}\right) }{\mathrm{d} \varvec{\hat{{\mathcal {P}}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}\right) }\nonumber \\&\times \frac{\mathrm{d} \varvec{\hat{{\mathcal {P}}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}\right) }{\mathrm{d} {\varvec{x}}_{k}^{-}} \times \frac{\mathrm{d} {\varvec{x}}_{k}^{-}}{\mathrm{d} {\varvec{z}}_{k}^{-}}. \end{aligned}$$

(28)

As $\varvec{\check{{\mathcal {P}}}}\left( {\varvec{z}}_{k}^{-}, \tau _{k}\right) ={\varvec{z}}_{k+1}^{-}$ and $\varvec{\hat{{\mathcal {P}}}}\left( {\varvec{z}}_{k}^{-}, \tau _{k}\right) ={\varvec{x}}_{k+1}^{-}$, then according to expressions in (18) it is easy to demonstrate that $\frac{\mathrm{d} \varvec{\check{{\mathcal {P}}}}\left( {\varvec{z}}_{k}^{-}, \tau _{k}\right) }{\mathrm{d} \varvec{\hat{{\mathcal {P}}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}\right) }=\varvec{{\varPsi }}$ and $\frac{\mathrm{d} {\varvec{x}}_{k}^{-}}{\mathrm{d} {\varvec{z}}_{k}^{-}}=\varvec{{\varPhi }}$. Moreover, $\frac{\mathrm{d} \varvec{\hat{{\mathcal {P}}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}\right) }{\mathrm{d} {\varvec{x}}_{k}^{-}}$ is the Jacobian matrix of the controlled hybrid Poincaré map with non-reduced dimension (17). According to Sect. 2.3.5, we have: $\frac{\mathrm{d} \varvec{\hat{{\mathcal {P}}}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}\right) }{\mathrm{d} {\varvec{x}}_{k}^{-}}={{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{k}^{-}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) +{{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{tk}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right) \varvec{{\mathcal {K}}}$, where expression of ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{{\varvec{x}}_{k}^{-}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)$ and that of ${{\mathcal {D}}}\varvec{{\mathcal {P}}}_{\theta ^{d}_{tk}}\left( {\varvec{x}}_{k}^{-}, \tau _{k}, \theta ^{d}_{tk}\right)$ are defined in (26), and $\theta ^{d}_{tk}$ is the control law expressed by (16).

Hence, we emphasize that computation of the Jacobian matrix of the reduced-dimension controlled hybrid Poincaré map (19) is based mainly on the Jacobian matrix of the controlled hybrid Poincaré map (17).