Dynamics and control in a novel hyperchaotic system

Abstract

In this work, a novel hyperchaotic system is introduced. The system consists of four coupled continuous-time ordinary differential equations with three quadratic nonlinearities. Based on the center manifold and local bifurcation theorems, the existence of pitchfork bifurcation is proved at the origin equilibrium point of the proposed system. Also, the existence of Hopf bifurcation near all the equilibrium points of the system is shown. Moreover, stability analysis of the resulting periodic solutions is analyzed using Kuznetsov’s theory which determines the analytical conditions for the occurrence of supercritical (subcritical) Hopf bifurcation’s type. Numerical verifications such as Lyapunov exponents’ spectrum, Lyapunov dimension, bifurcation diagrams and the continuation software MATCONT are used to show the rich dynamics of the proposed system and to confirm the analytical results. Finally, the hyperchaotic behaviors in this system are suppressed to its three equilibrium points using a novel control method based on Lyapunov stability approach.

1 Introduction

Recently, studying dynamical behaviors and applications in hyperchaotic systems has attracted increasing attention of scientists and engineers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29], since the birth of Rössler’s hyperchaotic attractors [1, 2]. A regular chaotic dynamical system has no more than one Lyapunov exponent (LE), however a hyperchaotic system possesses at least two positive Lyapunov exponents (LEs), which reflect the complex dynamics and abundant behaviors that make its implementation is useful to various potential applications including encryption algorithms [30,31,32,33], backtracking search optimization algorithms [34], secure communications [35,36,37] and circuit design [3, 4, 25, 33, 38, 39]. Moreover, hyperchaotic systems have useful applications in lasers and secure optical communications [40, 41] due to their high capacity, high security and high efficiency. In dissipative hyperchaotic systems, all LEs have sum less than zero. In [42], it is found that every trajectory which does not approach at a fixed point must have at least one zero LE. Hence, the hyperchaotic case most probably exists in four-dimensional dynamical systems because they have four LEs. So, an explicit criterion for investigating hyperchaotic attractors in a dissipative autonomous system is described as

• (i) The system may have at least four-dimensional phase space.

• (ii) The system may have at least two nonlinear equations to increase its instability.

• (iii) The system possesses at least two positive LEs ($\Lambda _1>0, \Lambda _2 >0)$, or equivalently; the Lyapunov dimension $D_L$ is a fraction greater than three, where $D_L =j+\frac{\sum \nolimits _{i=1}^{i=j} {\Lambda _i } }{\left| {\Lambda _{j+1} } \right| }$, j is the largest integer that makes $\sum \limits _{i=1}^{i=j} {\Lambda _i } >0$.

Indeed, the pioneering Rössler’s hyperchaotic system has a single quadratic nonlinearity. Afterwards, some hyperchaotic systems with two quadratic nonlinearities had been introduced such as Lü hyperchaotic system [43] and Lorenz-Stenflo hyperchaotic system [44]. Recently, a Lü hyperchaotic system with parameter uncertainty is investigated in [45]. Moreover, hyperchaotic systems with three quadratic nonlinearities had recently been appeared such as the Chen’s hyperchaotic system [35], the hyperchaotic Lü system generated via state feedback control [9] and the hyperchaotic system given by El-Sayed et al. [25]. In Khan and Bhat [7], introduced a new hyperchaotic system with four quadratic nonlinearities. In Tripathi et al. [46] investigated the dynamical behaviors in a new hyperchaotic system with four cubic nonlinearities. In Singh and Roy [47] developed a new simple 4-D system with a single quadratic nonlinearity that has no equilibrium point and has hidden attractors. On the other hand, hyperchaotic behaviors were shown to be existed in a three-dimensional nonautonomous system with cubic nonlinearity [13].

Due to the fact that the three quadratic nonlinearities increase the instability of the system in more than two dimensions, a new hyperchaotic system with three differential nonlinear equations with each equation involves a quadratic nonlinearity, is proposed. The fourth differential equation is linear state equation to make its variable w act as feedback state variable, since the linear equation is designed to make w decay or increase as the time increases. So by decaying w, we may faster the occurrence of hyperchaotic attractor since in dissipative hyperchaotic system, contraction must outweigh expansion. Also, another state variable x in the system is commonly existed in all the nonlinear terms and acts as a nonlinear feedback. The resulting system has three equilibrium points which enrich the variety of dynamical behaviors in the system. Motivated by this discussion, the proposed system is candidate to be implemented in real world applications used to generate hyperchaotic behaviors. Therefore, the new hyperchaotic system can easily be used to show some novel behaviors in addition that it has a simple form of nonlinearities which match the criteria for publication a new chaotic/hyperchaotic system [48, 49].

On the other hand, the occurrence of Hopf bifurcation in a continuous-time dynamical system is considered to be one of the most fascinating dynamical behaviors. It is characterized by the existence of a closed invariant curve, namely a limit cycle, in the phase plane which means that the limit set of solution trajectory of the system is an isolated closed periodic orbit. At the critical parameter value of Hopf bifurcation, two purely imaginary eigenvalues of the equilibrium point exist. Thus, as the Hopf bifurcation occurs, the system switches its stability and a periodic solution arises. A supercritical Hopf bifurcation takes place when a stable equilibrium is replaced by a stable periodic orbit as the dynamical parameter passes through the critical Hopf bifurcation’s value. Otherwise, when the bifurcation orbit is unstable, Hopf bifurcation is said to be subcritical which is always more dramatic, and potentially dangerous in engineering applications. Therefore, these two types of Hopf bifurcations are important in experimental work, because they explain the important phenomenon of the created periodic orbits. Recently, the analytical study of Hopf bifurcation in three-dimensional chaotic systems has received increasing attention [50,51,52,53,54,55], however more detailed investigations of Hopf bifurcation is required in the case of four-dimensional hyperchaotic systems.

In real world applications there are many practical situations where chaos must be controlled, such as suppressing chaotic behavior of power electronics, improving the performance of a dynamical system, eliminating drag in flow systems and suppressing complicated circuit oscillations. Moreover, the appearance of chaos is not favorable situation in economy. So, if chaos is controlled then companies can plan for the future.

Motivated by the previous discussion, the objective of this work is to investigate bifurcations, chaos, hyperchaos and control in a novel hyperchaotic system consists of four coupled continuous-time ordinary differential equations with three quadratic nonlinearities. The existence of pitchfork bifurcation in this system is proved using the center manifold and local bifurcation theorems [56]. Also, the existence of Hopf bifurcations near all the equilibrium points of the system is shown. Conditions for supercritical and subcritical Hopf bifurcations are also derived using the criterion given by Kuznetsov [57]. The LEs of the system are calculated to investigate the existence of chaos and hyperchaos, using the efficient algorithm given by Wolf et al. [58]. Moreover, the corresponding fractal dimension $D_L$ is calculated using Kaplan and Yorke method [59]. Finally, hyperchaos control is achieved in this system using a novel simple linear feedback control criterion based on the Lyapunov stability theory.

2 The proposed system

The system under study is introduced by the following set of ordinary differential equations (known here as Matouk’s hyperchaotic system):

$$\begin{aligned} \dot{x}= & {} a(w-y)+hx-xw, \nonumber \\ \dot{y}= & {} bx-xz+w, \nonumber \\ \dot{z}= & {} -\,cz+x^{2}, \nonumber \\ \dot{w}= & {} dw. \end{aligned}$$

(1)

The system has three equilibrium points defined as

$$\begin{aligned} E_0= & {} (0,0,0,0), E_1 =(\sqrt{bc},h\sqrt{bc}/a,b,0), \\ E_2= & {} (-\sqrt{bc},-h\sqrt{bc}/a,b,0), \end{aligned}$$

where a, b, c, d, h are real valued parameters and the condition $a\ne 0, bc>0$ must be satisfied to ensure the existence of the equilibrium points $E_1$ and $E_2 .$ Also, the system (1) is dissipative if it satisfies the condition $\nabla .V=\frac{\partial \dot{x}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial \dot{z}}{\partial z}+\frac{\partial \dot{w}}{\partial w}<0,$ which implies that the flow with initial volume $V_0$ is contracted into $V_0 e^{-(w+c-h-d)t}$ at time t.

3 Some stability conditions in the proposed system

In this Section, some stability conditions for system (1) are derived. The system has the following the Jacobian matrix:

$$\begin{aligned} J=\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {-w+h}&{} {-a}&{} 0&{} {a-x} \\ {b-z}&{} 0&{} {-x}&{} 1 \\ {2x}&{} 0&{} {-c}&{} 0 \\ 0&{} 0&{} 0&{} d \\ \end{array} }} \right) . \end{aligned}$$

(2)

In the case of the origin equilibrium point, the characteristic equation of the Jacobian matrix (2) has the eigenvalues:

$$\begin{aligned} \lambda _1= & {} d, \lambda _2 =-\,c, \\ \lambda _3= & {} \frac{h-\sqrt{h^{2}-4ab}}{2}, \\ \lambda _4= & {} \frac{h+\sqrt{h^{2}-4ab}}{2}. \end{aligned}$$

So, $E_0$ is locally asymptotically stable if and only if $Re(\lambda _i )<0, i=1,2,3,4$, where $\lambda _i$ is an eigenvalue of the Jacobian matrix (2) evaluated at $E_0$. So, $E_0$ is locally asymptotically stable iff

$$\begin{aligned} d<0, c>0, h<0, ab>0. \end{aligned}$$

(3)

The other equilibrium points $E_1 , E_2$ have the same characteristic equation

$$\begin{aligned}&\lambda ^{4}+(c-d-h)\lambda ^{3}+(hd-hc-cd)\lambda ^{2} \\&\quad +(hcd-2abc)\lambda +2abcd=0. \end{aligned}$$

It is also clear that $\lambda =d$ is a root of this eigenvalue equation. So for $\lambda \ne d,$ the characterstic equation of $E_1 , E_2$ is reduced to

$$\begin{aligned} \lambda ^{3}+(c-h)\lambda ^{2}-hc\lambda -2abc=0. \end{aligned}$$

Hence based on the Routh–Hurwitz stability criterion, the equilibrium points $E_1 =(\sqrt{bc},h\sqrt{bc}/a,b,0), \quad E_2 =(-\sqrt{bc},-h\sqrt{bc}/a,b,0)$ are locally asymptotically stable iff at least one of the following statements holds true:

• (i) $c>\max \{0,h\}, b>0, h<h_1 , a<0, d<0$,

• (ii) $c>\max \{0,h\}, b>0, h>h_2 , a<0, d<0$,

• (iii) $h<c<0, b<0, h_1<h<h_2 , a<0, d<0$,

where

$$\begin{aligned} h_1= & {} 0.5c-\sqrt{0.25c^{2}-2ab}, \\ h_2= & {} 0.5c+\sqrt{0.25c^{2}-2ab}. \end{aligned}$$

Remark 1

According to the classical Routh–Hurwitz stability criterion, it is easy to verify that the necessary conditions for the equilibrium points $E_0$ and $E_{1,2}$ to be locally asymptotically stable, are $abcd<0$ and $2abcd>0,$ respectively.

4 Pitchfork bifurcation analysis in the system

In this Section, the parameter b is selected as a dynamical parameter of the novel hyperchaotic system. So, the critical parameter’s value at which pitchfork bifurcation takes place is denoted by $b_c$. At this critical value of the parameter b,  the Jacobian matrix evaluated at the origin equilibrium point $E_0$ is given as

$$\begin{aligned} J(E_0 )=\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} h&{} {-a}&{} 0&{} a \\ {b_c }&{} 0&{} 0&{} 1 \\ 0&{} 0&{} {-c}&{} 0 \\ 0&{} 0&{} 0&{} d \\ \end{array} }} \right) . \end{aligned}$$

(4)

When $b_c =0$, the equilibrium point $E_0$ is not hyperbolic and has the following eigenvalues:

$$\begin{aligned} \lambda _1 =0, \lambda _2 =-c, \lambda _3 =d, \lambda _4 =h. \end{aligned}$$

Hence, the center manifold Theorem [56] can be used to investigate the dynamics near the origin equilibrium point $E_0 .$ By utilizing the following transformation:

$$\begin{aligned} \begin{array}{l} \left( {{\begin{array}{l} x \\ y \\ z \\ w \\ \end{array} }} \right) =\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1&{} 0&{} 1&{} 1 \\ {h/a}&{} 0&{} {-\sigma }&{} 0 \\ 0&{} 1&{} 0&{} 0 \\ 0&{} 0&{} {-d\sigma }&{} 0 \\ \end{array} }} \right) \left( {{\begin{array}{l} {x_1 } \\ {x_2 } \\ {x_3 } \\ {x_4 } \\ \end{array} }} \right) , \\ \sigma =(h-d)/(a[d-1]), \\ \end{array} \end{aligned}$$

system (1) is transformed as follows

$$\begin{aligned} \left( {{\begin{array}{l} {\dot{x}_1 } \\ {\dot{x}_2 } \\ {\dot{x}_3 } \\ {\dot{x}_4 } \\ \end{array} }} \right) =\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 0&{} 0&{} 0&{} 0 \\ 0&{} {-c}&{} 0&{} 0 \\ 0&{} 0&{} d&{} 0 \\ 0&{} 0&{} 0&{} h \\ \end{array} }} \right) \left( {{\begin{array}{l} {x_1} \\ {x_2} \\ {x_3} \\ {x_4} \\ \end{array}}} \right) +\left( {{\begin{array}{l} {\Phi _1} \\ {\Phi _2} \\ {\Phi _3} \\ {\Phi _4} \\ \end{array}}} \right) , \end{aligned}$$

(5)

where

$$\begin{aligned}&\Phi _1 =a(\mu x_1 +\mu x_3 +\mu x_4 -x_1 x_2 -x_2 x_3 -x_2 x_4 )/h, \\&\Phi _2 =(x_1 +x_3 +x_4 )^{2}, \\&\Phi _3 =0, \\&\Phi _4 =a((1-d)\sigma x_3 -hx_1 /a) \\&\ \quad +\,d\sigma x_3 (x_1 +x_3 +x_4 ) \\&\ \quad +\,h(x_1 +x_3 )-d^{2}(h-1)x_3 /(hd-h) \\&\ \quad -\,a((\mu -x_2 )(x_1 +x_3 +x_4 )-d\sigma x_3 )/h, \end{aligned}$$

and $\mu =b-b_c$ is considered to be the bifurcation parameter of the transformed system. Then, the dimensions of the system are reduced using the center manifold Theorem [56] which ensures the existence of a center manifold for system (5):

$$\begin{aligned}&W^{c}(0)= \left\{ \left. {(x_1 ,x_2 ,x_3 ,x_4 ,\mu )\in R^{5}} \right| x_2 =h_1 (x_1 ,\mu ), \right. \nonumber \\&x_3 =h_2 (x_1 ,\mu ), x_4 =h_3 (x_1 ,\mu ), \left| {x_1 } \right|<\varepsilon , \nonumber \\&\quad \left. \left| \mu \right| <\bar{{\varepsilon }}, h_i (0,0)=0, Dh_i (0,0)=0, i=1,2,3 \right\} , \end{aligned}$$

(6)

for sufficiently small constants $\varepsilon$ and $\bar{{\varepsilon }}$. The center manifold $W^{c}(0)$ must satisfy

$$\begin{aligned}&\Theta (\mathrm{H}(\hat{{x}},\rho ))\cong D_{\hat{{x}}} \mathrm{H}(\hat{{x}},\rho ) \nonumber \\&[\Lambda \hat{{x}}+f(\hat{{x}},\mathrm{H}(\hat{{x}},\rho ),\rho )] \nonumber \\&\quad -\mathrm{B}\mathrm{H}(\hat{{x}},\rho )-\Phi (\hat{{x}},\mathrm{H}(\hat{{x}},\rho ),\rho )=0, \end{aligned}$$

(7)

where

$$\begin{aligned}&\hat{{x}}\equiv x_1 , \rho \equiv \mu , \Lambda =0, f=\Phi _1 , \\&\mathrm{B}=\left( {{\begin{array}{l@{\quad }l@{\quad }l} {-c}&{} 0&{} 0 \\ 0&{} d&{} 0 \\ 0&{} 0&{} h \\ \end{array} }} \right) , \Phi =\left( {{\begin{array}{l} {\Phi _2 } \\ {\Phi _3 } \\ {\Phi _4 } \\ \end{array}}} \right) , \mathrm{H}=\left( {{\begin{array}{l} {\mathrm{H}_1 } \\ {\mathrm{H}_2 } \\ {\mathrm{H}_3 } \\ \end{array} }} \right) , \end{aligned}$$

$$\begin{aligned}&\mathrm{H}_1 (x_1 ,\mu )=a_1 x_1^2 +a_2 x_1 \mu +a_3 \mu ^{2}+\cdots , \\&\mathrm{H}_2 (x_1 ,\mu )=b_1 x_1^2 +b_2 x_1 \mu +b_3 \mu ^{2}+\cdots , \\&\mathrm{H}_3 (x_1 ,\mu )=c_1 x_1^2 +c_2 x_1 \mu +c_3 \mu ^{2}+\cdots . \end{aligned}$$

Equating terms of like powers in Eq. (7) to zero yields

$$\begin{aligned} a_1= & {} \frac{1}{c}, a_2 =a_3 =0, \\ b_1= & {} b_2 =b_3 =0, \\ c_1= & {} c_3 =0, c_2 =\frac{a}{h^{2}}, \end{aligned}$$

provided that $a\ne 0, c\ne 0, h\ne 0, d\notin \{0,1\}.$ Therefore

$$\begin{aligned} x_2= & {} \mathrm{H}_1 (x_1 ,\mu )=\frac{1}{c}x_1^2 +0.x_1 \mu +0.\mu ^{2}+\cdots , \nonumber \\ x_3= & {} \mathrm{H}_2 (x_1 ,\mu )=0.x_1^2 +0.x_1 \mu +0.\mu ^{2}+\cdots , \nonumber \\ x_4= & {} \mathrm{H}_3 (x_1 ,\mu )=0.x_1^2 +\frac{a}{h^{2}}x_1 \mu +0.\mu ^{2}+\cdots . \end{aligned}$$

(8)

Thus, the reduced vector field is obtained as follows

$$\begin{aligned} \dot{x}_1= & {} \frac{a}{h}\left( {\mu x_1 +\frac{a}{h^{2}}\mu ^{2}x_1 -\frac{1}{c}x_1^3 -\frac{a}{ch^{2}}\mu x_1^3 } \right) +\cdots , \nonumber \\&\dot{\mu }=0. \end{aligned}$$

(9)

Now, it is clear that $G(x_1 ,\mu )=\frac{a}{h}(\mu x_1 +\frac{a}{h^{2}}\mu ^{2}x_1 -\frac{1}{c}x_1^3 -\frac{a}{ch^{2}}\mu x_1^3 )$ satisfy the following conditions:

$$\begin{aligned}&G(0,0)=0, \left. {\frac{\partial G}{\partial x_1 }} \right| _{(0,0)} =0, \left. {\frac{\partial G}{\partial \mu }} \right| _{(0,0)} =0, \left. {\frac{\partial ^{2}G}{\partial x_1^2 }} \right| _{(0,0)} =0, \\&\left. {\frac{\partial ^{2}G}{\partial x_1 \partial \mu }} \right| _{(0,0)} =\frac{a}{h}\ne 0, \left. {\frac{\partial ^{3}G}{\partial x_1^3 }} \right| _{(0,0)} =-\frac{6a}{ch}\ne 0. \end{aligned}$$

Consequently, pitchfork bifurcation occurs at the origin equilibrium point of system (9).

Thus, the following theorem has been proved:

Theorem 1

For $a\ne 0, c\ne 0, h\ne 0, d\notin \{0,1\}$, system (1) exhibits a pitchfork bifurcation at the origin equilibrium point when the parameter b passes through the critical value $b_c =0$. Furthermore, for some parameters $a<0, c\in R^{+}, d<0, h<0$ and $b<b_c$, the unique origin equilibrium point is locally asymptotically stable. However, when $b>b_c$, the origin equilibrium point becomes unstable and two other equilibrium points $E_1 =(\sqrt{bc},h\sqrt{bc}/a,b,0)$ and $E_2 =(-\sqrt{bc},-h\sqrt{bc}/a,b,0)$ appear, and they are locally asymptotically stable for some parameters $a<0, c\in R^{+}, d<0, h<0$.

5 Existence of Hopf bifurcation in the system

In this Section, the existence of Hopf bifurcation in system (1) will be shown using the first Lyapunov coefficient technique by Kuznetsov [57]. This method can be summarized as follows:

Consider the following n-dimensional system

$$\begin{aligned} \dot{X}=F(X,\mu ), X\in R^{n}, \mu \in R. \end{aligned}$$

(10)

Assume that system (10) is written as

$$\begin{aligned} \dot{X}=A(\mu )X+\mathrm{N}(X,\mu ), \end{aligned}$$

(11)

where A is the Jacobian matrix of system (10) and $\mathrm{N}(X)$ is a smooth function of order $\left\| X \right\| ^{3}.$ Then, $\mathrm{N}(X)$ is written as

$$\begin{aligned} \mathrm{N}(X)=\frac{U(X,X)}{2!}+\frac{V(X,X,X)}{3!}+O(\left\| X \right\| ^{4}), \end{aligned}$$

(12)

where

$$\begin{aligned} U_i (X,Y)= & {} \left. {\sum _{j,k=1}^n {\frac{\partial ^{2}\mathrm{N}_i (\xi )}{\partial \xi _j \partial \xi _k }} } \right| _{\xi =0} x_j y_k , V_i (X,Y,Z) \\= & {} \left. {\sum _{j,k,m=1}^n {\frac{\partial ^{3}\mathrm{N}_i (\xi )}{\partial \xi _j \partial \xi _k \partial \xi _m }} } \right| _{\xi =0} x_j y_k z_m , i=1, \ldots , n. \end{aligned}$$

If the equilibrium point X = 0 of system (10) exhibits a nondegenerate Hopf bifurcation, the Jacobian matrix $A(\mu _c )$ has a simple pair of eigenvalues $\lambda _{1,2} =\pm i\omega _0 , i=\sqrt{-1}, \omega _0 =\omega (\mu _c )>0,$with no other eigenvalue with zero real part and the first Lyapunov coefficient $l_1$ is not vanished, where

$$\begin{aligned}&l_1 (0)=\frac{1}{2\omega _0 }Re\left[ \left\langle {p,V(q,q,\bar{{q}})} \right\rangle \right. \nonumber \\&\quad -2\left\langle {p,U(q,A^{-1}U(q,\bar{{q}}))} \right\rangle \nonumber \\&\quad \left. +\left\langle {p,U(\bar{{q}},(2i\omega _0 I_n -A)^{-1}U(q,q))} \right\rangle \right] , \end{aligned}$$

(13)

and $I_n$ is the identity matrix of order n. The complex vectors p and q in Eq. (13) satisfy the following properties:

$$\begin{aligned}&A(\mu _c )q=i\omega _0 q, A(\mu _c )\bar{{q}}=-i\omega _0 \bar{{q}}, \nonumber \\&A^{T}(\mu _c )p=-i\omega _0 p, \nonumber \\&A^{T}(\mu _c )\bar{{p}}=i\omega _0 \bar{{p}}, \nonumber \\&\left\langle {p,q} \right\rangle =\bar{{p}}^{T}q=1, \end{aligned}$$

(14)

where $q,p\in C^{n}$.

The Hopf bifurcation is supercritical (subcritical) when $l_1 (0)$ is negative (positive) respectively.

5.1 Hopf bifurcation of the origin equilibrium point $E_0$

The Jacobian matrix $J(E_0 )$ of system (1) has the following eigenvalues:

$$\begin{aligned} \lambda _1 =d, \lambda _2 =-\,c, \lambda _{3,4} =(h\pm \sqrt{h^{2}-4ab})/2. \end{aligned}$$

(15)

So, the origin equilibrium point of system (1) possesses two purely complex conjugate eigenvalues if $h=h_c =0, ab=\omega _0^2 >0.$ Thus, based on conditions (3), the following lemma is proved.

Lemma 1

The origin equilibrium point $E_0$ of system (1) is locally asymptotically stable iff

$$\begin{aligned} h<h_c , c>0, d<0, ab>0. \end{aligned}$$

(16)

Now, the vectors p and q given by the relations (14) can be chosen as

$$\begin{aligned} q= & {} \left( {{\begin{array}{l} {i\sqrt{ab}/b} \\ 1 \\ 0 \\ 0 \\ \end{array} }} \right) , \nonumber \\ p= & {} \left( {{\begin{array}{l} {i\sqrt{ab}(1+ab)/(2a(1+a))} \\ {1/2} \\ 0 \\ {(-ab-d+i\sqrt{ab}(1-d))/(2(ab+d^{2}))} \\ \end{array} }} \right) . \end{aligned}$$

(17)

The vector functions $U(\xi ,\eta ), V(\xi ,\eta ,\zeta )$ defined in (12) are given by

$$\begin{aligned}&U(\xi ,\eta )=(-\xi _1 \eta _4 -\xi _4 \eta _1 , -\xi _1 \eta _3 -\xi _3 \eta _1 , 2\xi _1 \eta _1 , 0)^{T}, \nonumber \\&V(\xi ,\eta ,\zeta )=(0,0,0,0)^{T}. \end{aligned}$$

(18)

Consequently, the following quantities can be obtained using straightforward calculations:

$$\begin{aligned} U(q,q)=\left( {{\begin{array}{l} 0 \\ 0 \\ {-2a/b} \\ 0 \\ \end{array} }} \right) , U(q,\bar{{q}})=\left( {{\begin{array}{l} 0 \\ 0 \\ {2a/b} \\ 0 \\ \end{array} }} \right) . \end{aligned}$$

(19)

Thus, using (19), we get

$$\begin{aligned} \begin{array}{l} J^{-1}U(q,\bar{{q}})=\frac{-2a}{bc}\left( {{\begin{array}{l} 0 \\ 0 \\ 1 \\ 0 \\ \end{array} }} \right) , \\ U(q,J^{-1}U(q,\bar{{q}}))=\frac{2a\sqrt{ab}}{b^{2}c}\left( {{\begin{array}{l} 0 \\ i \\ 0 \\ 0 \\ \end{array} }} \right) , \\ \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{l} (2i\omega _0 I_4 -J)^{-1}U(q,q) \\ =\frac{-2a}{b}\left( {{\begin{array}{l} 0 \\ 0 \\ {\frac{2i\sqrt{ab}-d}{-4ab-cd+2i\sqrt{ab}(c-d)}} \\ 0 \\ \end{array} }} \right) , \\ U(\bar{{q}},(2i\omega _0 I_4 -J)^{-1}U(q,q)) \\ =\frac{-2a\sqrt{ab}}{b^{2}}\left( {{\begin{array}{l} 0 \\ {\frac{2\sqrt{ab}+ic}{c^{2}+4ab}} \\ 0 \\ 0 \\ \end{array} }} \right) , V(q,q,\bar{{q}})=0. \\ \end{array} \end{aligned}$$

Substituting the previous quantities into Eq. (13) yields

$$\begin{aligned} l_1 (0)=-\,\frac{a\sqrt{ab}}{b^{2}(c^{2}+4ab)}. \end{aligned}$$

(20)

It is assumed that $ab>0,$ so the direction of Hopf bifurcation is determined by the sign of the parameter a. Thus, the following theorem has been proved:

Theorem 2

System (1) undergoes a Hopf bifurcation at the origin equilibrium point $E_0$ for given parameters $a, b, c, d, h, ab>0,$ in the neighborhood of $h=h_c .$ Moreover, the Hopf bifurcation is nondegenerate and supercritical when $a>0;$ However when $a<0$, the Hopf bifurcation is nondegenerate and subcritical.

5.2 Hopf bifurcation of the equilibrium points $E_1$ and $E_2$

Firstly, the conditions of Hopf bifurcation will be shown near the equilibrium point $E_1$. Since $E_1$ is not the origin, it is required to translate this point to the origin of coordinates

$$\begin{aligned} X(t)= & {} x(t)-\sqrt{bc}, Y(t) \nonumber \\= & {} y(t)-h\sqrt{bc}/a, Z(t) \nonumber \\= & {} z(t)-b, W(t)=w(t), \end{aligned}$$

(21)

where b and c must have the same sign. So, the system (1) is reduced to

$$\begin{aligned} \dot{X}= & {} hX-aY+(a-\sqrt{bc})W-XW, \nonumber \\ \dot{Y}= & {} (b-1)X-\sqrt{bc}Z+W-XZ, \nonumber \\ \dot{Z}= & {} -cZ+2\sqrt{bc}X+X^{2}, \nonumber \\ \dot{W}= & {} dW. \end{aligned}$$

(22)

The characterestic equation of system (22) is given by

$$\begin{aligned}&\lambda ^{4}+(c-d-h)\lambda ^{3}+(hd-hc-cd)\lambda ^{2} \nonumber \\&\quad +(hcd-2abc)\lambda +2abcd=0. \end{aligned}$$

(23)

Remark 2

The two equilibrium points $E_1$ and $E_2$ have the same characterestic equation, so the conditions of Hopf bifurcation in each of the two points are the same.

According to the stability analysis of the equilibrium points $E_1$ and $E_2$, the following lemma is obtained:

Lemma 2

The origin equilibrium point of system (22) is locally asymptotically stable if and only if at least one of the stability conditions (i)–(iii) holds true.

For $a<0, b>0, h=h_1 ,$ the characterestic Eq. (23) has the eigenvalues

$$\begin{aligned} \lambda _1= & {} d, \lambda _2 =4ab/(\sqrt{c^{2}-8ab}-c), \nonumber \\ \lambda _{3,4}= & {} \pm \omega _0 i, \omega _0 \nonumber \\= & {} \sqrt{-0.5c^{2}+0.5c\sqrt{c^{2}-8ab}}>0. \end{aligned}$$

(24)

Then, the vectors p and q given by the relations (14) are selected as

$$\begin{aligned} q=\left( {{\begin{array}{l} {\omega _0 (\omega _0 -ic)/2bc} \\ 1 \\ {-i\gamma _1 } \\ 0 \\ \end{array} }} \right) , p=\beta _0 \left( {{\begin{array}{l} 1 \\ {\beta _1 } \\ {\beta _2 } \\ {\beta _3 } \\ \end{array} }} \right) , \gamma _1 =\frac{\omega _0 }{\sqrt{bc}},\nonumber \\ \end{aligned}$$

(25)

where $\beta _0 , \beta _1 , \beta _2 , \beta _3 \in C^{1}$ and defined as

$$\begin{aligned}&\beta _0 =-2bc\beta _1 \beta _2 /(-2\left| {\beta _1 } \right| ^{2}\beta _2 (bc)-\beta _1 \beta _2 \omega _0^2 \\&\qquad +\,\omega _0 \beta _1 i(2\sqrt{bc}\left| {\beta _2 } \right| ^{2}+c\beta _2 )\bar{)}, \\&\beta _1 =\frac{i\gamma _0 \gamma _2 }{8bc}, \beta _2 =\frac{\gamma _3 +i\gamma _0 }{-4\sqrt{bc}}, \\&\beta _3 =\frac{8bc(a-\sqrt{bc})+i\gamma _0 \gamma _2 }{-4bc(2d+i\gamma _0 )}, \\&\gamma _0 =2\omega _0 , \gamma _2 =c+\sqrt{c^{2}-8ab}, \\&\gamma _3 =c-\sqrt{c^{2}-8ab}, \end{aligned}$$

and $(.\bar{{)}}$ stands for the conjugate of a complex number.

In this case the vector functions $U(\xi ,\eta ), V(\xi ,\eta ,\zeta )$ are also given by Eq. (18). Therefore, the quantities U(q, q) and $U(q,\bar{{q}})$ are given as

$$\begin{aligned}&U(q,q)=\left( {{\begin{array}{c} 0 \\ 2\gamma _1 iZ_1 \\ 2Z_1^2 \\ 0 \\ \end{array} }} \right) , \nonumber \\&U(q,\bar{{q}})=\left( {{\begin{array}{c} 0 \\ 0 \\ {\left( \omega _0^4 +\omega _0^2 c^{2}\right) /2b^{2}c^{2}} \\ 0 \\ \end{array} }} \right) , \nonumber \\&Z_1 =\frac{\omega _0^2 -ic\omega _0 }{2bc}. \end{aligned}$$

(26)

Furthermore

$$\begin{aligned}&J^{-1}U(q,\bar{{q}})=\frac{\sqrt{bc}(\omega _0^4 +\omega _0^2 c^{2})}{4b^{3}c^{3}} \\&\qquad \times \left( {{\begin{array}{l} 1 \\ {\left( c-\sqrt{c^{2}-8ab}\right) /2a} \\ 0 \\ 0 \\ \end{array} }} \right) , \\&U(q,J^{-1}U(q,\bar{{q}})) \\&\quad =\frac{\sqrt{bc}\left( \omega _0^4 +\omega _0^2 c^{2}\right) }{4b^{3}c^{3}}\left( {{\begin{array}{l} 0 \\ {i\gamma _1 } \\ {2Z_1 } \\ 0 \\ \end{array} }} \right) , \end{aligned}$$

$$\begin{aligned}&(2i\omega _0 I_4 -J)^{-1}U(q,q) \\&\quad =\frac{(d-2i\omega _0 )Z_1 }{Z_2 } \\&\qquad \times \left( {{\begin{array}{l} {aZ_3 } \\ {(h_1 -2i\omega _0 )Z_3 } \\ {2i(a\gamma _1 \sqrt{bc}+\omega _0 Z_1 (h_1 -2i\omega _0 ))} \\ 0 \\ \end{array} }} \right) , \end{aligned}$$

Fig. 1

The bifurcation plots of system (1) using MATCONT with the parameter values $a=1, b=2, c=0.4,\,d=-\,2, h=0$, show that Hopf bifurcation (H) exists at $E_0 =(0,0,0,0)$

$$\begin{aligned}&U\left( \bar{{q}},(2i\omega _0 I_4 -J)^{-1}U(q,q)\right) \\&\quad =\frac{(d-2i\omega _0 )Z_1 }{Z_2 } \\&\qquad \times \left( {{\begin{array}{l} 0 \\ {-2i\bar{{Z}}_1 \left( a\gamma _1 \sqrt{bc}+\omega _0 Z_1 (h_1 -2i\omega _0 )\right) -ia\gamma _1 Z_3 } \\ {2a\bar{{Z}}_1 Z_3 } \\ 0 \\ \end{array} }} \right) , \end{aligned}$$

$$\begin{aligned} V(q,q,\bar{{q}})=0, \\ \end{aligned}$$

where

$$\begin{aligned}&Z_2 =8\omega _0^4 +2cd\omega _0^2 -2dh_1 \omega _0^2 +2ch_1 \omega _0^2 +abcd \\&\quad +i(4d\omega _0^3 -4c\omega _0^3 +4h_1 \omega _0^3 +cdh_1 \omega _0 -2abc\omega _0 ), \\&Z_3 =(-2\omega _0 +ic)\gamma _1 -\sqrt{bc}Z_1. \end{aligned}$$

Fig. 2

A stable limit cycle of system (1) exists when $a=1, b=2, c=0.4, d=-\,2, h=0.001$

Fig. 3

The bifurcation plots of system (1) using MATCONT with the parameter values $a=-\,1, b=2, c=0.4,\,d=-\,2, h=-\,1.809975$, show that Hopf bifurcation (H) exists at $E_1$ and $E_2 .$ BP is a branching point

Substituting the previous quantities into Eq. (13) yields

$$\begin{aligned}&l_1 (0)=-\frac{\omega _0 }{2}Re(\vartheta ), \nonumber \\&\vartheta =\left[ i\omega _0^4 \left| {\beta _1 } \right| ^{2}\beta _2 \gamma _1^2 Z_2 \right. \nonumber \\&\quad +\,ic^{2}\omega _0^2 \left| {\beta _1 } \right| ^{2}\beta _2 \gamma _1^2 Z_2 \nonumber \\&\quad +\,2\omega _0^4 \left| {\beta _2 } \right| ^{2}\beta _1 \gamma _1 Z_1 Z_2 \nonumber \\&\quad +\,2c^{2}\omega _0^2 \left| {\beta _2 } \right| ^{2}\beta _1 \gamma _1 Z_1 Z_2 \nonumber \\&\quad +\,8ab^{3}c^{3}\omega _0 \left| {\beta _1^2 Z_1^2 } \right| \beta _2 \gamma _1^2 \nonumber \\&\quad -\,16ib^{2}c^{2}\sqrt{bc}\omega _0^3 \left| {\beta _1^2 Z_1^2 } \right| \beta _2 \gamma _1 Z_1 \nonumber \\&\quad +\,8b^{2}c^{2}\sqrt{bc}h_1 \omega _0^2 \left| {\beta _1^2 Z_1^2 } \right| \beta _2 \gamma _1 Z_1 \nonumber \\&\quad +\,4iadb^{3}c^{3}\left| {\beta _1^2 Z_1^2 } \right| \beta _2 \gamma _1^2 \nonumber \\&\quad +\,8b^{2}c^{2}d\sqrt{bc}\omega _0^2 \left| {\beta _1^2 Z_1^2 } \right| \beta _2 \gamma _1 Z_1 \nonumber \\&\quad +\,4ib^{2}c^{2}d\sqrt{bc}h_1 \omega _0 \left| {\beta _1^2 Z_1^2 } \right| \beta _2 \gamma _1 Z_1 \nonumber \\&\quad +\,4ab^{2}c^{2}\sqrt{bc}\omega _0 \left| {\beta _1^2 \gamma _1^2 } \right| \beta _2 Z_1 Z_3 \nonumber \\&\quad +\,2iab^{2}c^{2}d\sqrt{bc}\left| {\beta _1^2 \gamma _1^2 } \right| \beta _2 Z_1 Z_3 \nonumber \\&\quad +\,8iab^{2}c^{2}\sqrt{bc}\omega _0 \left| {\beta _2^2 Z_1^2 } \right| \beta _1 \gamma _1 Z_3 \nonumber \\&\quad \left. -\,4ab^{2}c^{2}d\sqrt{bc}\left| {\beta _2^2 Z_1^2 } \right| \beta _1 \gamma _1 Z_3 \right] /\Big \{bc\gamma _1 Z_2 \nonumber \\&\quad \times \left( 2bc\sqrt{bc}\left| {\beta _1 } \right| ^{2}\beta _2 -2ibc\omega _0 \left| {\beta _2 } \right| ^{2}\beta _1 \right. \nonumber \\&\quad \left. \left. +\,\sqrt{bc}\omega _0^2 \beta _1 \beta _2 -ic\sqrt{bc}\omega _0 \beta _1 \beta _2 \right) \right\} . \end{aligned}$$

(27)

Therefore, the following theorem has been proved:

Theorem 3

System (1) undergoes a Hopf bifurcation at the equilibrium points $E_1 (E_2 )$ for given parameters $a<0, b>0, c>0, d, h$, in the neighborhood of $h=h_1 .$ Moreover, the Hopf bifurcation is nondegenerate and supercritical when $Re(\vartheta )>0$. While if $Re(\vartheta )<0$, Hopf bifurcation is nondegenerate and subcritical.

6 Numerical simulations

In the following, simulation results are carried out to verify the above theoretical results. Using the parameter values $a=1, b=2, c=0.4, d=-\,2$ and $h_c =0,$ the system (1) exhibits Hopf bifurcation around the equilibrium point $E_0$. The bifurcation is supercritical since the first Lyapunov coefficient $l_1 (0)=-\,0.0433<0$ [as determined by Eq. (20)]. In other words, as the parameter h changes its sign from negative to positive, the stable equilibrium point $E_0$ changes its stability according to Lemma 1 and a stable periodic solution emanating from $E_0$ appears based on Theorem 2. The software MATCONT confirms this result as shown in Fig. 1. Also, the limit cycle resulting from this Hopf bifurcation is shown using the previous parameter values and h above $h_c =0$ (see Fig. 2). Moreover, system (1) exhibits Hopf bifurcation around the equilibrium points $E_1$ and $E_2$ at the critical value $h_1 =-\,1.809975$ and when the other parameter values are fixed at $a=-\,1, b=2, c=0.4, d=-\,2$. The bifurcation is supercritical since the first Lyapunov coefficient $l_1 (0)=-\,0.005363099<0$ [as determined by Eq. (27)] i.e., as the parameter h is increased above the critical value $h_1$, the stable equilibrium point $E_1 (E_2 )$ changes its stability according to Lemma 2 and a stable periodic solution emanating from $E_1 (E_2 )$ appears based on Theorem 3. The numerical verification of Hopf bifurcation via MATCONT and the appearance of corresponding limit cycle are shown in Figs. 3 and 4, respectively. Furthermore, the software MATCONT is used to produce Fig. 5 in order to show the existence of Hopf bifurcation around the equilibrium points $E_1$ and $E_2$ when using the parameter values $a=-\,1, b=2, c=40,\, d=-\,2, h_1 =-\,0.099751.$ Also, in this case the bifurcation is supercritical (since $l_1 (0)=-\,0.0002415323<0)$, therefore a stable limit cycle appears above $h_1$ as shown in Fig. 6.

On the other hand, Lyapunov exponents (LEs) of system (1) are calculated with the parameter values $a=-\,3, b=15, c=0.6, d=-\,0.001, h=-\,1.5$ using the Wolf’s algorithm [58]. They are given as follow

$$\begin{aligned} \Lambda _1 =0.57, \Lambda _2 =0.02, \Lambda _3 =0.00, \Lambda _4 =-\,2.69. \end{aligned}$$

(28)

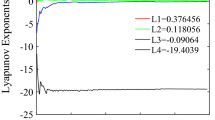
Hence, they confirm the existence of hyperchaos in system (1). Moreover, the corresponding hyperchaotic attractors of system (1) are depicted in Fig. 7. Furthermore, the Lyapunov exponents’ spectrum of system (1) is calculated by setting the parameter values $b=15, c=0.5, d=-\,1, h=-\,2$ and varying the parameter a. The results are depicted in Fig. 8 which illustrates the chaotic dynamics of the system (1). Also, Fig. 9 shows the corresponding chaotic attractors using the specific choice of the parameters; $a=-\,15, b=15, c=0.5, d=-\,1, h=-\,2.$ The Lyapunov dimension related to (28) is also calculated by means of Kaplan and Yorke [59]. It is found that $D_L$ approximately equals 3.22. In addition, the bifurcation diagram is also a vital numerical tool that shows the rich variety of dynamical behaviors in a dynamical system. Therefore, the bifurcation diagrams corresponding to system (1) are calculated and depicted in Fig. 10.

Fig. 4

A stable limit cycle of system (1) exists when $a=-\,1, b=2, c=0.4, d=-\,2, h=-\,1.808$

Fig. 5

The bifurcation plots of system (1) using MATCONT with the parameter values $a=-\,1, b=2, c=40,d=-\,2, h=-\,0.099751$, show that Hopf bifurcation (H) exists at $E_1$ and $E_2$. BP is a branching point

7 Controlling hyperchaos in the system

Assume that $E^{*}=(x^{*},y^{*},z^{*},w^{*})$ refers to any equilibrium point of system (1) and $k_1 , k_2 , k_3 , k_4$ are the positive feedback control gains (FCG’s). Then, a controlled form of system (1) is given as

$$\begin{aligned} \dot{x}= & {} a(w-y)+hx-xw-k_1 (x-x^{*}), \nonumber \\ \dot{y}= & {} bx-xz+w-k_2 (y-y^{*}), \nonumber \\ \dot{z}= & {} -cz+x^{2}-k_3 (z-z^{*}), \nonumber \\ \dot{w}= & {} dw-k_4 (w-w^{*}). \end{aligned}$$

(29)

In case of $E^{*}=E_0$, the following lemma is obtained:

Fig. 6

A stable limit cycle of system (1) appears when $a=-\,1, b=2, c=40, d=-\,2, h=-\,0.084$

Lemma 3

The hyperchaos in system (29) is suppressed to its origin equilibrium point if the following inequalities hold:

$$\begin{aligned}&k_3>-c, k_4>d, \nonumber \\&k_2>\frac{1}{4(k_4 -d)}, \nonumber \\&k_1 >\frac{1}{k_2 (k_4 -d)-\frac{1}{4}} \nonumber \\&\left\{ \frac{a+b}{4}\left[ (k_4 -d)(a+b)+\frac{a}{2}\right] +\frac{a}{4}\left[ \frac{a+b}{2}+ak_2 \right] \right. \nonumber \\&\left. +\,\frac{\sigma _y^2 }{4(k_3 +c)} \left[ k_2 (k_4 -d)-\frac{1}{4}\right] \right\} \nonumber \\&+\,h+\sigma _z +\sigma _w , \end{aligned}$$

(30)

where $\sigma _y>\left| y \right| , \sigma _z>\left| z \right| , \sigma _w >\left| w \right|$.

Fig. 7

3-D views of hyperchaotic attractors of system (1) using the parameter values $a=-\,3, b=15, c=0.6, d=-\,0.001, h=-\,1.5$

Fig. 8

Lyapunov exponents’ spectrum of system (1) versus the dynamical parameter a, using the parameter values $b=15, c=0.5, d=-\,1, h=-\,2$

Proof

The Lyapunov function is selected for system (29) as follows

$$\begin{aligned} V(x,y,z,w)=0.5(x^{2}+y^{2}+z^{2}+w^{2}). \end{aligned}$$

(31)

Then, the time derivative of V is given as

$$\begin{aligned}&\dot{V}=x\dot{x}+y\dot{y}+z\dot{z}+w\dot{w} \nonumber \\&\quad =(z+h-w-k_1 )x^{2} -k_2 y^{2}-(c+k_3 )z^{2} \nonumber \\&\qquad +\,(d-k_4 )w^{2}+(b-a)xy -xyz+axw+yw \nonumber \\&\quad <(\sigma _z +\sigma _w +h-k_1 )\left| x \right| ^{2} -k_2 \left| y \right| ^{2}-(c+k_3 )\left| z \right| ^{2} \nonumber \\&\qquad +\,(d-k_4 )\left| w \right| ^{2}+(b+a)\left| x \right| \left| y \right| \nonumber \\&\qquad +\,\sigma _y \left| x \right| \left| z \right| +a\left| x \right| \left| w \right| +\left| y \right| \left| w \right| =-\mathrm{X}^{T}P\mathrm{X}, \end{aligned}$$

(32)

where

$$\begin{aligned}&\mathrm{X}=\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {\left| x \right| }&{} {\left| y \right| }&{} {\left| z \right| }&{} {\left| w \right| } \\ \end{array} }} \right] ^{T}, \\&P=\left( {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {-(h-k_1 +\sigma _z +\sigma _w )}&{} {-0.5(a+b)}&{} {-0.5\sigma _y }&{} {-0.5a} \\ {-0.5(a+b)}&{} {k_2 }&{} 0&{} {-0.5} \\ {-0.5\sigma _y }&{} 0&{} {c+k_3 }&{} 0 \\ {-0.5a}&{} {-0.5}&{} 0&{} {k_4 -d} \\ \end{array} }} \right) . \end{aligned}$$

The matrix P is positive definite if the inequalities (30) hold. So, the origin equilibrium point of system (29) is globally asymptotically stable. Therefore, the trajectories of the controlled hyperchaotic system (29) are stabilized to its origin equilibrium point. $\square$

The controlled hyperchaotic system (29) is numerically integrated using the parameters $a=-\,3, b=15, c=0.6, d=-\,0.001, h=-\,1.5,$ at which the equilibrium points $E_0$, $E_1 (E_2 )$ are unstable according to the conditions (3) and (i)–(iii), respectively. So, our objective is to stabilize the trajectories of the controlled system (29) to one of its unstable equilibrium points $E_0$, $E_1$ and $E_2$ via the proposed linear feedback control technique. From Fig. 1, the upper bounds $\sigma _y , \sigma _z , \sigma _w$ can be selected as $\sigma _y =60, \sigma _z =70, \sigma _w =0.01$. Now according to the inequalities (30), the FCG’s can be selected as $k_1 =700, k_2 =1, k_3 =1, k_4 =1$. The results are summarized in Fig. 11.

Fig. 9

Chaotic attractors of system (1) using the parameter values $a=-\,15, b=15, c=0.5, d=-\,1$, $h=-\,2:$a xyz view, b xyw view

Fig. 10

Bifurcation diagrams of system (1) as: a varying a and setting $b=15, c=0.5, d=-\,1$, $h=-\,2,$b varying b and setting $a=-\,2, c=1, d=-\,0.2, h=-\,2$, c varying c and setting $a=-\,2$, $b=15, d=-\,0.2, h=-\,2,$d varying h and setting $a=-\,2, b=15, c=0.5, d=-\,0.2,$in which Xstands for y(t)

Fig. 11

The states of controlled hyperchaotic system (29) tend to the origin equilibrium point as using the parameters $a=-\,3, b=15, c=0.6, d=-\,0.001, h=-\,1.5$ and FCG’s $k_1 =700, k_2 =1, k_3 =1, k_4 =1$

Fig. 12

The states of controlled hyperchaotic system (29) tend to the point $E_1 =(\sqrt{bc},h\sqrt{bc}/a,b,0)$ as using the parameters $a=-\,3, b=15, c=0.6, d=-\,0.001, h=-\,1.5$ and FCG’s $k_1 =700, k_2 =1, k_3 =1, k_4 =1$

Fig. 13

The states of controlled hyperchaotic system (29) tend to the point $E_2 =(-\sqrt{bc},-h\sqrt{bc}/a,b,0)$ as using the parameters $a=-\,3, b=15, c=0.6, d=-\,0.001, h=-\,1.5$ and FCG’s $k_1 =700, k_2 =1, k_3 =1, k_4 =1$

Similarly, the controlled hyperchaotic system (29) can be controlled to the equilibrium points $E_1 =(\sqrt{bc},h\sqrt{bc}/ab,0)$ and $E_2 =(-\sqrt{bc},-h\sqrt{bc}/a,b,0)$. The transformation ${X}'=X-E^{*}$can be used to translate the points $E_1 =(\sqrt{bc},h\sqrt{bc}/a,b,0)$ and $E_2 =(-\sqrt{bc},-h\sqrt{bc}/a,b,0)$ to the origin of coordinates. Hence, Lemma 3 can also be applied to control the states of system (29) to these equilibrium points. The results are also depicted in Figs. 12 and 13.

8 Conclusion

In this paper, a new hyperchaotic system consists of four coupled continuous-time ordinary differential equations with three quadratic nonlinearities has been introduced. The existence of pitchfork bifurcation in the system has been proved using the center manifold and local bifurcation theorems. The conditions of Hopf bifurcation around all the three equilibrium points of the system have also been obtained. Furthermore, the Kuznetsov’s first Lyapunov coefficient theory has been used to determine the supercritical and subcritical types of Hopf bifurcation in this system. Various numerical tools such as Lyapunov exponents’ spectrum, Lyapunov dimension, bifurcation diagrams and the continuation software MATCONT have been utilized to verify the occurrence of variety of complex dynamics in this system and also to confirm the correctness of the theoretical analysis. Furthermore, the hyperchaotic behaviors in this system have been suppressed to its three equilibrium points using a novel control method based on Lyapunov stability theory. Finally, the new hyperchaotic system has promising applications in encryption algorithms, circuit design and secure communications because of its high resistance to dynamics reconstruction.