1 Introduction

The use of long articulated vehicles is economically attractive due to lower fuel and driver costs per ton of cargo. Unlike automobiles, the transport productivity and efficiency are generally prioritized for heavy vehicles, particularly the directional and roll dynamic performance [1–3]. The ride properties of heavy vehicles concern the preservation of health, safety and comfort of the drivers and/or passengers, and protection of the cargoes, while the suspension design is subject to the constraints imposed by requirements on productivity and functional efficiency [1]. The dynamic characteristics of heavy vehicle systems are therefore considerably different from those of the passenger cars. Suspension design of road vehicles necessities a complex compromise among different performance measures related to ride and handling qualities. The road-friendliness and road-damaging potential of an articulated vehicle have been two of the important design and regulation objectives. They are influenced by interactions between the vehicle units, which are strongly coupled by their respective bounce and pitch motions.

When the heavy articulated vehicle is running on the road, changes in the road surface profile can be led to undesirable oscillations. A portion of those vibrations can be absorbed by the wheels, but the most should be absorbed by the suspension system between the tires and sprung masses. The heavy articulated vehicle suspension system is necessary equipment, which can reduce the vibration generated by the road surface irregularities and isolate the sprung masses from road-induced disturbances. Conventional passive suspension systems in heavy vehicles typically consist of springs, dampers and anti-roll bars and can only dissipate energy. Some studies have been investigated passive suspensions in heavy vehicles [4–8]. Recently, there has been a significant research activity in a new class of so-called advanced suspension systems. Advanced suspensions can be divided into three categories: fully active, slow active and semi-active. Fully active and slow active suspension systems are attractive because they allow more design flexibility than passive suspension systems for specifying the transfer functions that govern the handling, ride and roll performance of a vehicle [9]. Semi-active suspensions consist of controllable dampers and conventional springs. Such systems can only dissipate energy, by contrast with fully active and slow active systems, which can supply energy.

In recent years, numerous researches have focused on the semi-active and active suspensions with magnetorheological (MR) damper in vehicles [10–17]. Magnetorheological damper fluid is a kind of smart materials, which is made by mixing fine particles into a liquid with low viscosity. The important feature of MR fluids is their ability to reversibly change states from a viscous fluid to a semisolid or even solid with controlled yielding strength, which it is subjected to controlled magnetic field. The application of MR dampers in vibration control of heavy vehicle’s suspension system was investigated by many researchers. Extended groundhook control logic was investigated by Valasek et al. [18] in order to reduce the dynamic tire forces. Hendrick and Yi [19] studied the effect of alternative heavy truck suspensions on flexible pavement response, and Yi and Song [20] developed a novel control model that called road detection algorithm (RDA). The aim of this algorithm was to combine the advantages of the skyhook damping and the tire deflection feedback. Liao and Wang [21] and Lau and Liao [22] designed a MR fluid damper that is suitable for a semi-active train suspension. Their results showed that the semi-active suspension with the developed MR dampers can substantially improve the ride quality of the passengers. A unique MR fluid bypass damper for heavy vehicle controllable suspension systems was designed, fabricated, and tested by Shahin et al. [23]. Their results showed that the MR fluid damper could achieve better performance for protection from the vehicle rollover and estimated that the roll angle can be reduced by 45% compared to the regular original equipment manufacturer passive dampers. Tsampardoukas et al. [24] investigated a truck with semi-active suspension and presented a hybrid balance algorithm based on dynamic tire force tracking to reduce road damage and to investigate the performance of a heavy articulated vehicle compared to one with passive viscous dampers. Yu et al. [25] proposed two extended versions of Time-To-Rollover (TTR) metrics for heavy-duty vehicle rollover detection. Based on the TTR rollover detection module, a prototype active roll control (ARC) system is designed. The results show that a heavy-duty vehicle’s roll stability is considerably improved with the rollover detection and active roll control systems proposed. Also, some other active control methods [26–29] are applied to vehicle systems.

Because of nonlinear properties of MR dampers as well as other components such as springs and wheels, a heavy vehicle must be regarded as a nonlinear system. There are some contradictions between experimental results and obtained results from linear models. The nonlinear characteristics of vehicle components can be the source of these contradictions. Owing to the existence of the nonlinear factors and especially multi-valued and non-smooth hysteresis of MR dampers, the vehicle exhibits complex phenomena such as jumps, bifurcation, quasi-periodic vibration and chaotic vibration when it is running on a bumpy road. Quasi-periodic and chaotic vibration may cause shock vibration due to road surface that can influence the life time of vehicle components, safety of driving, protection of the cargoes and driver’s comfort.

Fig. 1
figure 1

Schematic diagram of a nonlinear half-truck oscillatory model

Full size image

Many studies have been conducted by researchers in order to introduce the benefits of MR dampers in vehicle suspension, while the nonlinear characteristics of these dampers can result in irregular behaviours (chaotic or quasi-periodic) in vehicle suspension system. In heavy vehicle systems, some parts can be more critical against unwanted vibrations. One of these sections is articulation point, which connects the tractor to the trailer, and its unwanted displacements and vibrations can result in failure; therefore, it should be avoided. However, without appropriate controlling action, using MR dampers is doubtful. So, there is need to a compromise between the advantage and disadvantage in utilizing these dampers. Up to now, no work has been reported on the control of chaotic behaviours of heavy vehicle with MR damper suspension system.

In this paper, the nonlinear dynamic behaviour of a half-truck oscillatory system is studied by using the bifurcation diagrams and Poincaré maps. After detecting irregular (chaotic and quasi-periodic) sections, the appropriate controller is proposed to return the system’s vibrations to desired region. The control law is derived based on the backstepping method, and the stability of the controller is proved based on Lyapunov theorem. Then, an optimal backstepping controller is proposed such that error norm is minimized during motion. The validity of the proposed method is verified by some simulation experiments. The results analysis shows the vehicle tracks desired periodic motion in spite of the chaos motion conditions. The main contributions of this paper are summarized as: considering the nonlinear features of MR dampers and their influences on dynamic behaviour of the heavy articulated vehicle and optimal backstepping control design for eliminating the chaotic behaviours.

The rest of this paper is arranged as follows. In Sect. 2, the dynamic model of a half-truck oscillatory system is presented. Chaotic vibration analysis is explained in Sect. 3. Controller design and stability analysis of motion is addressed in Sect. 4. Simulation results and discussions are given in Sect. 5, and finally some concluding remarks are presented in Sect. 6.

2 Dynamic modelling

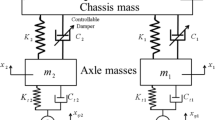
Figure 1 shows the schematic diagram of a nonlinear half-truck oscillatory system which has carried out as a heavy articulated vehicle model. The notations in Fig. 1 are given in “Appendix”. Both vehicle units are represented by massive rigid cuboids, sprung masses, and the axles are shown by massive blocks, unsprung masses [24].

The half-truck is presented as a seven degree-of-freedom system including the bounce and pitch motions of tractor and trailer; and three bounce motions of the centre of gravity of unsprung masses. The vehicle’s yaw roll motions are neglected due to the small effects.

The suspension system between the sprung masses and the unsprung masses is modelled as spring and damper elements. Suspension’s spring units of the heavy articulated vehicle have linear mechanical characteristics [24], and the articulation connection is also modelled as a high linear stiffness spring and damper. Suspension’s dampers are both passive viscous damper and MR damper which are considered as nonlinear units. All of the truck’s axles are equipped with MR dampers.

Before analysing the dynamic behaviour of the system, the differential equations of motion corresponding to the oscillatory model, shown in Fig. 1, should be derived. By applying Newton–Euler laws and taking the above assumptions into account, the differential equations of motion are obtained in compact form as follows:

$$\begin{aligned} {{{\varvec{M}}}}\ddot{{{{\varvec{q}}}}}={{\varvec{h}}}({{\varvec{q}}},{\dot{{{\varvec{q}}}}}) \end{aligned}$$
(1)

where \({{{\varvec{q}}}}=\left[ {X_C ,\theta _C ,X_T ,\theta _T ,X_{\text {UF}} ,X_{\text {UR}} ,X_{\text {UT}} } \right] ^{T}\) is the generalized coordinates vector and the inertia matrix \({{{\varvec{M}}}}\) is defined as:

$$\begin{aligned} {{{\varvec{M}}}}=\left[ {{\begin{array}{lllllll} {M_C +2m}&{} {m(L_2 -L_1 )\cos q_2 }&{} 0&{} 0&{} {-m}&{} {-m}&{} 0 \\ {m(L_2 -L_1 )}&{} {I_C +m(L_1^2 +L_2^2 )\cos q_2 }&{} 0&{} 0&{} {mL_1 }&{} {mL_2 }&{} 0 \\ 0&{} 0&{} {M_T +m}&{} {mL_5 \cos q_4 }&{} 0&{} 0&{} {-m} \\ 0&{} 0&{} {mL_5 }&{} {I_T +mL_5^2 \cos q_4 }&{} 0&{} 0&{} {-mL_5 } \\ {-m}&{} {mL_1 \cos q_2 }&{} 0&{} 0&{} {M_{\text {UF}} +m}&{} 0&{} 0 \\ {-m}&{} {-mL_2 \cos q_2 }&{} 0&{} 0&{} 0&{} {M_{\text {UR}} +m}&{} 0 \\ 0&{} 0&{} {-m}&{} {-mL_5 \cos q_4 }&{} 0&{} 0&{} {M_{\text {UT}} +m} \end{array} }} \right] \end{aligned}$$
(2)

where m is MR damper mass. The force vector \({{{\varvec{h}}}({{\varvec{q}}},{\dot{{{{\varvec{q}}}}}},\ddot{{{\varvec{q}}}})}\) contains all of springs and dampers forces. These forces are as functions of relative displacements and velocities between the sprung and unsprung masses. The relative displacements and velocities vectors are given by

$$\begin{aligned}&{{\varvec{X(q)}}}=\left[ {{\begin{array}{l} {q_1 -L_1 \sin q_2 -q_5 } \\ {q_1 +L_2 \sin q_2 -q_6 } \\ {q_3 +L_5 \sin q_4 -q_7 } \\ {q_3 -q_1 -L_3 \sin q_2 -L_4 \sin q_4 } \\ {q_5 -X_{\text {WF}} } \\ {q_6 -X_{\text {WR}} } \\ {q_7 -X_{\text {WT}} } \\ \end{array} }} \right] ,\nonumber \\&\dot{{{{\varvec{X}}}}}({{\varvec{q}}})=\left[ {{\begin{array}{l} {{\dot{q}}_1 -L_1 {\dot{q}}_2 \cos q_2 -{\dot{q}}_5 } \\ {{\dot{q}}_1 +L_2 {\dot{q}}_2 \cos q_2 -{\dot{q}}_6 } \\ {{\dot{q}}_3 +L_5 {\dot{q}}_4 \cos q_4 -{\dot{q}}_7 } \\ {{\dot{q}}_3 -{\dot{q}}_1 -L_3 {\dot{q}}_2 \cos q_2 -L_4 {\dot{q}}_4 \cos q_4 } \\ {{\dot{q}}_5 -\dot{X}_{\text {WF}} } \\ {{\dot{q}}_6 -\dot{X}_{\text {WR}} } \\ {{\dot{q}}_7 -\dot{X}_{\text {WT}} } \end{array} }} \right] \end{aligned}$$
(3)

where the \(X_{\text {WF}}\), \(X_{\text {WR}}\) and \(X_{\text {WT}}\) are the road roughness on the tractor front and rear wheels and on the trailer wheel, respectively, which are defined as:

$$\begin{aligned} X_{\text {WF}}= & {} \xi (t) \end{aligned}$$
(4)
$$\begin{aligned} X_{\text {WR}}= & {} \xi (t-t_1 ) \end{aligned}$$
(5)
$$\begin{aligned} X_{\text {WT}}= & {} \xi (t-t_2 ) \end{aligned}$$
(6)

where \( t_{1}\) and \(t_{2 }\) are time delays of the tractor drive axle and trailer axle, respectively. The sinusoid forcing function [24, 25] is used to describe the excitations caused by road surface. Thus, the forcing functions for three axles are approximated by:

$$\begin{aligned}&\xi (t)=b\sin (\omega t) \end{aligned}$$
(7)
$$\begin{aligned}&\xi (t-t_1 )=b\sin \omega (t-t_1 ) \end{aligned}$$
(8)
$$\begin{aligned}&\xi (t-t_2 )=b\sin \omega (t-t_2 ) \end{aligned}$$
(9)

where b and \(\omega \) are harmonic excitation amplitude and frequency, respectively. Also, the excitation frequency is defined as \(\omega =2\pi (v/\lambda )\) where v is the velocity of the vehicle and \(\lambda \) is the wavelength of the harmonic excitation. Hence, the truck goes through a series of consecutive harmonic excitation with speed v, so \(t_1 =(L_1 +L_2 )/v\) and \(t_2 =(L_1 +L_3 +L_4 +L_5 )/v\).

The mathematical model of the passive viscous damper is described by

$$\begin{aligned} F_{d-F} =\left\{ \begin{array}{ll} C_b \dot{X}_j &{} \quad \dot{X}_j \ge 0 \\ C_r \dot{X}_j &{} \quad \dot{X}_j <0 \\ \end{array}\right. \end{aligned}$$
(10)

where the damping coefficients are different for the bound and rebound strokes.

Lau and Liao [22] designed and modelled a prototype MR damper for a train suspension. Here, the same model of the MR damper is used. Such a damper develops forces of the same order of magnitude as those required in a truck application, and in this respect it could be potentially suitable for heavy vehicle applications as well. It is a Bouc–Wen model [21, 22, 24] that includes a set of differential equations for describing the hysteretic characteristic of the damper force/velocity response. This model is given as follows:

$$\begin{aligned} \dot{z}= & {} -\gamma \left| {\dot{X}_j } \right| \left| z \right| ^{n-1}z-\beta \dot{X}_j \left| z \right| ^{n}\nonumber \\&+A\dot{X}_j \quad ( j=1,2,3) \end{aligned}$$
(11)
$$\begin{aligned} C=a_1 \exp \left[ {-\left| {a_2 \dot{X}_j } \right| ^{p}} \right] \quad (j=1,2,3) \end{aligned}$$
(12)
$$\begin{aligned} F_{MR-i}= & {} az+kX_j +C\dot{X}_j +m\ddot{X}_j\nonumber \\&+F_0 \quad (i=F,R,T \quad j=1,2,3) \end{aligned}$$
(13)

where z is the evolutionary variable and the parameters \(\beta \),\(\gamma \), A and n define the shape of the hysteresis loop. The numerical values of the MR damper parameters are given in Tables 1 and 2.

Table 1 Constant parameters for MR damper [22]
Full size table
Table 2 Current-dependent parameters of MR damper [22]
Full size table

Having the springs and dampers force, the vector \({{{\varvec{h}}}}({{{\varvec{q}}}},{\dot{{{\varvec{q}}}}},\ddot{{{\varvec{q}}}})\) can be obtained as:

$$\begin{aligned} {{{\varvec{h}}}}({{{\varvec{q}}}},{\dot{{{\varvec{q}}}}},\ddot{{{\varvec{q}}}})=\left[ {{\begin{array}{l} -K_F X_1 -F_{\text {MR}-F} -K_R X_2 \\ \quad -F_{\text {MR}-R} -K_4 X_4 -C_4 \dot{X}_4 \\ L_1 (K_F X_1 +F_{\text {MR}-F} )\\ \quad -L_2 (K_R X_2 +F_{\text {MR}-R} )\\ \quad +L_3 (K_4 X_4 +C_4 \dot{X}_4 ) \\ -K_T X_3 -F_{\text {MR}-T} -K_4 X_4 -C_4 \dot{X}_4 \\ -L_5 (K_T X_3 +F_{\text {MR}-T} )\\ \quad +L_4 (K_4 X_4 +C_4 \dot{X}_4 ) \\ K_F X_1 +F_{\text {MR}-F} -K_{\text {UF}} X_5 -C_F \dot{X}_5 \\ K_R X_2 +F_{\text {MR}-R} -K_{\text {UR}} X_6 -C_R \dot{X}_6 \\ K_T X_3 +F_{\text {MR}-T} -K_{\text {UT}} X_7 -C_T \dot{X}_7 \\ \end{array} }} \right] \end{aligned}$$
(14)

where the \(F_{\text {MR}-F}\), \(F_{\text {MR}-R}\) and \(F_{\text {MR}-T} \) are tractor steering axle, tractor drive axle and trailer axle MR dampers forces, respectively. These forces are functions of relative displacements, velocities and accelerations. Also, they have nonlinear nature, Eqs. (11)–(13); so the relation (14) is nonlinear.

3 Chaotic vibration analysis

In this section, the chaotic behaviour analysis of the vehicle is carried out by the numerical analysis of Eq. (1) with variable step continuous solver based on the forth-order Runge–Kutta method. In order to guarantee that the data being used are in a steady state, the first few hundred time series data of the integration were neglected. The results of the next few hundred time series were retained to carry out the analysis. The numerical values of the half-truck’s parameters which were used in this study are given in Tables 3, 4 and 5 [24].

Table 3 Geometric parameters of the half-truck
Full size table
Table 4 Mass parameters of the half-truck
Full size table
Table 5 Oscillatory parameters of the half-truck
Full size table

The bifurcation diagrams are one of the main tools to analyse the nonlinear dynamic behaviour of the systems. These diagrams can be useful in detecting the irregular regions of the system’s behaviour as a function of some controlling parameters. The bifurcation diagram of the amplitude versus the excitation frequency in vehicle dynamic is typically used to analyse the response of system. For the vehicle that encounters road roughness, the speed is more significant parameter; so it can be taken as a control parameter instead of frequency in bifurcation diagrams. To generate the bifurcation diagram, the speed of vehicle is as a control parameter that varies with fixed steps, and the state variables at the end of each step are used as initial conditions for the next step. These data points are then plotted versus the speed of vehicle. If the motion is regular, periodic, at the specific vehicle’s speed, the bifurcation diagram should contain a finite number of separate points. When the motion is irregular, quasi-periodic or chaotic, the data points in the bifurcation diagram are distributed along a vertical line. As mentioned previously, the articulation point between the trailer and tractor and its displacements can be more serious [30, 31]. So, the bifurcation diagram of the articulation point displacement is depicted to analyse the system behaviour. The bifurcation diagrams of the system are obtained when the vehicle speed is slowly changed in region \(0.01<v<8\)  m/s and the step size of the speed is 0.01 m/s. The amplitude of the road excitation used in the computation is \(b= 0.05\) m, and the initial conditions for all variables set to zero. Figures 2, 3 and 4 show the bifurcation diagrams of the heave, pitch and articulation point displacements.

Fig. 2
figure 2

Bifurcation diagrams of a tractor heave motion b trailer heave motion

Full size image
Fig. 3
figure 3

Bifurcation diagrams of a tractor pitch motion b trailer pitch motion

Full size image
Fig. 4
figure 4

Bifurcation diagram of the articulation point

Full size image

These figures show at the speed regions \(v\in [2.4\sim 3]\), \(v\in [3.83\sim 5.95]\) and \(v\in [6.43\sim 6.73]\), the irregular motion, quasi-periodic or chaotic, can be detected in the system dynamic behaviour. However, the chaotic behaviour has an oscillatory nature with unpredictable amplitudes that can lead to cyclic stresses and a reduction in life of the vehicle components, safety of driving, protection of the cargoes and driver’s comfort. The aim is to detect the chaotic regions and then to apply the active control action to this behaviour. For more detailed analyses of system behaviour and confirmation of the chaotic responses, other identifying techniques are necessary. One of the main techniques is Poincaré map. In non-autonomous systems, a point on the Poincaré section is referred to as the return point of the time series at the constant interval T, where T is the driving period of the exciting force. The projection of the Poincaré section on the phase plane is referred to as the Poincaré map. If there have been k discrete return points, the corresponding motion will be periodic with the period kT. For a quasi-periodic motion, the return points form a closed curve. For a chaotic motion, the return points on the Poincaré map form a geometrically fractal structure [32].

Figures 5 and 6 show the Poincaré map of the heave and pitch displacements of tractor and trailer. At speed \(v=4.6 \,{\mathrm{m/s}}\), all displacements show the chaotic behaviour, but at \(v=5.9\, {\mathrm{m/s}}\) the tractor’s irregular behaviour is chaotic and the trailer’s irregular behaviour is quasi-periodic. However, the irregular motions have variable nature with relatively high amplitude that is not desirable.

Fig. 5
figure 5

Poincaré maps of a heave displacement of tractor, b pitch displacement of tractor, c heave displacement of trailer, d pitch displacement of trailer at \(v=4.6 \,{\mathrm{m/s}}\)

Full size image
Fig. 6
figure 6

Poincaré maps of a heave displacement of tractor, b pitch displacement of tractor, c heave displacement of trailer, d pitch displacement of trailer, at \(v=5.9\, {\mathrm{m/s}}\)

Full size image

However, the obtained results show the nonlinear terms in the MR dampers lead to chaotic motions in the trailer system. The displacement of articulation point is a function of the heave and pitch displacements of trailer and tractor. Here, first we show that the chaotic behaviour of the above-mentioned displacements results in chaotic vibrations of the articulation point. Then, the active control of the chaotic behaviour is proposed in the next section. As shown in Fig. 5, Poincaré maps consist of a pile of points in the phase space or have a fractal structures for all of vehicle displacements at \(v=4.6 \,{\mathrm{m/s}}\), which confirm that the irregular motions in the respective bifurcation diagrams, Figs. 2, 3 and 4, are chaotic motions. Thus, in the next section we intend to apply active control on the chaotic behaviour at \(v=4.6\,{\mathrm{m/s}}\).

4 Controller design

In this section, an active chaos control system is designed to control the appeared chaotic vibrations in the vehicle. In Sect.  3, it was shown that the vehicle has chaotic behaviour at \(v=4.6\,{\mathrm{m/s}}\). The control objective is to force the heavy vehicle’s state to follow a periodic motion in spite of its chaotic situation. To this end, the variables of the heave motions of tractor and trailer and the pitch motion of tractor are controlled such that they follow periodic desired trajectories during the motion. Here, it is assumed that the dynamic model of the vehicle is known and a control law is designed based on the backstepping method.

To apply the active control, the equations of motion, Eq. (1), should be written as

$$\begin{aligned} {{{{\varvec{M}}}}\ddot{{{\varvec{q}}}}-{{{\varvec{{{\varvec{h}}}}}}}({{{\varvec{q}}}},{\dot{{{\varvec{q}}}}})={{{\varvec{{{\varvec{Bu}}}}}}}+{{{\varvec{f}}}}}_d \end{aligned}$$
(15)

where \({{{\varvec{u}}}}=\left[ {u_F ,u_R ,u_T } \right] ^{T}\) is controller input vector and matrix \({{{\varvec{B}}}}\) is defined the number of controller as

$$\begin{aligned} {{{\varvec{B}}}}=\left[ {{\begin{array}{lll} {-1}&{} {-1}&{} 0 \\ {L_1 }&{} {-L_2 }&{} 0 \\ 0&{} 0&{} {-1} \\ 0&{} 0&{} {-L_5 } \\ 1&{} 0&{} 0 \\ 0&{} 1&{} 0 \\ 0&{} 0&{} 1 \\ \end{array} }} \right] \end{aligned}$$
(16)

and \( {{{\varvec{f}}}}_d\) is external disturbance forces vector. It is assumed that the external disturbances are bounded.

In this paper, the backstepping method is used for stabilizing and trajectory tracking of the vehicle. The backstepping control is a nonlinear control method based on the Lyapunov theorem. The design flexibility of backstepping method is its advantage compared with other control methods. This flexibility is due to recursive Lyapunov functions which are used in the backstepping method. The backstepping control is derived step-by-step as follows:

Step 1 The tracking error of the heave motion of tractor is defined as

$$\begin{aligned} e_1 =X_C^d -X_C \end{aligned}$$
(17)

where the superscript d in \(X_C^d \) denotes its desired state. Considering the first Lyapunov function as \(V_1 =\frac{1}{2}e_1^2 \), the time derivation of \(V_1 \) is given as

$$\begin{aligned} \dot{V}_1 =e_1 \dot{e}_1 =e_1 (\dot{X}_C^d -\dot{X}_C ) \end{aligned}$$
(18)

\(\dot{X}_C \) can be used as a virtual input. To this end, based on the desired value of virtual control, a stabilizing function is defined as follows:

$$\begin{aligned} \eta _1 =\dot{X}_C^d +k_1 e_1 \end{aligned}$$
(19)

where \(k_1 \) is a positive constant. By considering (19), Eq. (18) yields

$$\begin{aligned} \dot{V}_1 =-k_1 e_1^2 +e_1 (\eta _1 -\dot{X}_C ) \end{aligned}$$
(20)

Step 2 Considering the error of the virtual control as

$$\begin{aligned} e_2 =\eta _1 -\dot{X}_C \end{aligned}$$
(21)

The second Lyapunov function is chosen as follows:

$$\begin{aligned} V_2 =V_1 +\frac{1}{2}e_2^2 \end{aligned}$$
(22)

The time derivation of \(V_2 \) yields

$$\begin{aligned} \dot{V}_2 =-k_1 e_1^2 +k_1 e_2^2 +e_1 e_2 -k_1^2 e_1 e_2 +e_2 \ddot{X}_C^d -e_2 \ddot{X}_C \end{aligned}$$
(23)

Step 3 In this step, the tracking error of the tractor pitch motion is considered as

$$\begin{aligned} e_3 =\theta _C^d -\theta _C \end{aligned}$$
(24)

and the Lyapunov function is modified as follows:

$$\begin{aligned} V_3 =V_2 +\frac{1}{2}e_3^2 . \end{aligned}$$
(25)

Differentiating \(V_3 \) with respect time yields

$$\begin{aligned} \dot{V}_3 =\dot{V}_2 +e_3 (\dot{\theta }_C^{ d} -\dot{\theta }_C ) \end{aligned}$$
(26)

Now, the stabilizing function is chosen as

$$\begin{aligned} \eta _2 =\dot{\theta }_4^{ d} +k_2 e_3 \end{aligned}$$
(27)

where \(k_2 \) is a positive constant. By considering (27), Eq. (26) gives

$$\begin{aligned} \dot{V}_3 =\dot{V}_2 -k_2 e_3^2 +e_3 (\eta _2 -\dot{\theta }_C ) \end{aligned}$$
(28)

Step 4 Defining the error \(e_4 \) as

$$\begin{aligned} e_4 =\eta _2 -\dot{\theta }_4 \end{aligned}$$
(29)

The Lyapunov function is updated as follows:

$$\begin{aligned} V_4 =V_3 +\frac{1}{2}e_4^2 \end{aligned}$$
(30)

The time derivation of \(V_4 \) is given as

$$\begin{aligned} \dot{V}_4 =\dot{V}_2 -k_2 e_3^2 +k_2 e_4^2 +e_3 e_4 -k_2^2 e_3 e_4 +e_2 {\ddot{\theta }}_4^{ d} -e_4 {\ddot{\theta }}_4 \end{aligned}$$
(31)

Step 5 Now, the tracking error of the trailer heave motion is considered as

$$\begin{aligned} e_5 =X_T^d -X_T \end{aligned}$$
(32)

and the Lyapunov function is chosen as

$$\begin{aligned} V_5 =V_4 +\frac{1}{2}e_5^2 \end{aligned}$$
(33)

The time derivative of (33) is given as

$$\begin{aligned} \dot{V}_5 =\dot{V}_4 +e_5 (\dot{X}_T^d -\dot{X}_T ) \end{aligned}$$
(34)

By considering the stabilizing function

$$\begin{aligned} \eta _3 =\dot{X}_T^d +k_3 e_5 \end{aligned}$$
(35)

where \(k_3 \) is a positive constant, Eq. (34) is rewritten as

$$\begin{aligned} \dot{V}_5 =\dot{V}_4 -k_3 e_5^2 +e_5 (\eta _3 -\dot{X}_T ) \end{aligned}$$
(36)

Step 6 The error \(e_6 \) is considered as

$$\begin{aligned} e_6 =\eta _3 -\dot{X}_T \end{aligned}$$
(37)

The Lyapunov function is modified as follows:

$$\begin{aligned} V_6 =V_5 +\frac{1}{2}e_6^2 \end{aligned}$$
(38)

The time derivative of (38) yields

$$\begin{aligned} \dot{V}_6 =\dot{V}_4 -k_3 e_5^2 +k_3 e_6^2 +e_5 e_6 -k_3^2 e_5 e_6 +e_6 \ddot{X}_T^d -e_6 \ddot{X}_T \end{aligned}$$
(39)

Substituting Eqs. (23) and (32) in Eq. (39) gives

$$\begin{aligned} \dot{V}_6= & {} -k_1 e_1^2 -k_2 e_3^2 -k_3 e_5^2 +e_1 e_2 +e_3 e_4 +e_5 e_6\nonumber \\&+\,k_1 e_2^2 +k_2 e_4^2 +k_3 e_6^2\nonumber \\&-\,k_1^2 e_1 e_2 -k_2^2 e_3 e_4 -k_3^2 e_5 e_6\nonumber \\&+\,e_2 (\ddot{X}_C^d -\ddot{X}_C )+e_4 ({\ddot{\theta }}_C^{ d} -{\ddot{\theta }}_C )+e_6 (\ddot{X}_T^d -\ddot{X}_T )\nonumber \\ \end{aligned}$$
(40)

Now, the accelerations \(\ddot{X}_C , {\ddot{\theta }}_C \) and \(\ddot{X}_T \) are obtained from equations of motion, Eq. (15), as follows:

$$\begin{aligned}&\ddot{X}_C =\alpha _1 ({{{\varvec{q}}}},{\dot{{{{\varvec{q}}}}}})+{{{\varvec{P}}}}_1^T {{{\varvec{u}}}}+\delta _1 \nonumber \\&{\ddot{\theta }}_C =\alpha _2 ({{{\varvec{q}}}},{\dot{{{{\varvec{q}}}}}})+{{{\varvec{P}}}}_2^T {{{\varvec{u}}}}+\delta _2 \nonumber \\&\ddot{X}_T =\alpha _3 ({ {{\varvec{q}}}},{\dot{{{{\varvec{q}}}}}})+{{{\varvec{P}}}}_3^T {{{\varvec{u}}}}+\delta _3 \end{aligned}$$
(41)

where \({{{\varvec{P}}}}_i (i=1,2,3)\) is \(i\mathrm{th}\) row of matrix \({{{\varvec{M}}}}^{-1}{{{\varvec{B}}}}\); \(\alpha _i \) (\(i=1,2,3\)) is \(i\mathrm{th}\) elements of vector \({{{\varvec{M}}}}^{-1}{{{\varvec{h}}}}\) and \(\delta _i \) (\(i=1,2,3\)) is the acceleration due to the external disturbances. It is assumed that \(\left\| {{{{\varvec{f}}}}_d } \right\| \le \beta \) where \(\beta \) is a positive constant. Therefore, \(\delta _i \) (\(i=1,2,3\)) is bounded. Substituting the accelerations presented in (41) into Eq. (40) leads to

$$\begin{aligned} \dot{V}_6= & {} -k_1 e_1^2 -k_2 e_3^2 -k_3 e_5^2 +e_1 e_2 +e_3 e_4 +e_5 e_6 \nonumber \\&+\,k_1 e_2^2 +k_2 e_4^2 +k_3 e_6^2 -k_1^2 e_1 e_2\nonumber \\&-\,k_2^2 e_3 e_4 -k_3^2 e_5 e_6 \nonumber \\&+\,e_2 (\ddot{X}_C^d -\alpha _1 -\delta _1 -{{{\varvec{P}}}}_1^{T} {{{\varvec{u}}}})\nonumber \\&+\,e_4 ({\ddot{\theta }}_C^{ d} -\alpha _2 -\delta _2 -{{{\varvec{P}}}}_2^T {{{\varvec{u}}}})\nonumber \\&+\,e_6 (\ddot{X}_T^d -\alpha _3 -\delta _3 -{{{\varvec{P}}}}_3^T {{{\varvec{u}}}}) \end{aligned}$$
(42)

By considering the following relations:

$$\begin{aligned} {{{{\varvec{P}}}}_1 {{{\varvec{u}}}}=\ddot{X}_C^d -\alpha _1 +k_4 e_2 }\nonumber \\ {{{{\varvec{P}}}}_2 {{{\varvec{u}}}}={\ddot{\theta }}_C^{ d} -\alpha _2 +k_5 e_4 }\nonumber \\ {{{{\varvec{P}}}}_3 {{{\varvec{u}}}}=\ddot{X}_T^d -\alpha _3 +k_6 e_6 } \end{aligned}$$
(43)

the control law is proposed as

$$\begin{aligned} {{{\varvec{u}}}}={{{\varvec{P}}}}^{-1}(\ddot{{{\varvec{q}}}}_{c}^{ d} {{{-{\varvec{\alpha }}}}} +{{{\varvec{k}}}}{\tilde{{\varvec{e}}}}) \end{aligned}$$
(44)

with

$$\begin{aligned} \begin{array}{l} {{{\varvec{P}}}}=\left[ {{\begin{array}{lll} {{{{\varvec{P}}}}_1 ^{T}}&{} {{{{\varvec{P}}}}_2 ^{T}}&{} {{{{\varvec{P}}}}_3 ^{T}} \\ \end{array} }} \right] ^{T} , \ddot{{{\varvec{q}}}}^{d}_c =\left[ {{\begin{array}{lll} {\ddot{X}_C^d }&{} {{\ddot{\theta }}_C^{ d} }&{} {\ddot{X}_T^d } \\ \end{array} }} \right] ^{T} \\ {\varvec{\alpha }} =\left[ {{\begin{array}{lll} {\alpha _1 }&{} {\alpha _2 }&{} {\alpha _3 } \\ \end{array} }} \right] ^{T} , {{{\varvec{k}}}}=\mathrm{diag}(k_4 ,k_5 ,k_6 ) , \tilde{{{\varvec{e}}}}=\left[ {{\begin{array}{lll} {e_2 }&{} {e_4 }&{} {e_6 } \\ \end{array} }} \right] ^{T} \\ \end{array} \end{aligned}$$

Based on Eq. (44), to control the articulation point, three controllers are required. The above results can be summarized in the following theorem for the chaos control of heavy articulated vehicles.

Fig. 7
figure 7

Tracking performance on heave displacement of tractor

Full size image
Fig. 8
figure 8

Tracking performance on heave displacement of trailer

Full size image
Fig. 9
figure 9

Tracking performance on pitch displacement of the tractor

Full size image
Fig. 10
figure 10

Tracking performance on pitch displacement of the trailer

Full size image
Fig. 11
figure 11

Tracking performance on articulation point

Full size image

Theorem 1

Consider the heavy articulated vehicle with magnetorheological dampers represented by (15) with the bounded external disturbances. If the inputs are chosen by (44), the vehicle can follow the desired periodic motion and the tracking errors can be made bounded by choosing properly gains \(k_i \) (\(i=1,{\ldots },6\)).

Proof

The Lyapunov stability theorem is used in the proof. To this end, the Lyapunov candidate function is considered as (40). Considering the control law (44), Eq. (39) can be written as follows:

$$\begin{aligned} \dot{V}_6\le & {} -k_1 e_1^2 -k_2 e_3^2 -k_3 e_5^2\nonumber \\&+\frac{\left( {1+k_1^2 } \right) }{2}\left( {\frac{e_1^2 }{\rho _1 }+\rho _1 e_2^2 } \right) \nonumber \\&+\frac{\left( {1+k_2^2 } \right) }{2}\left( {\frac{e_3^2 }{\rho _2 }+\rho _2 e_4^2 } \right) \nonumber \\&+\frac{\left( {1+k_3^2 } \right) }{2}\left( {\frac{e_5^2 }{\rho _3 }+\rho _3 e_6^2 } \right) \nonumber \\&+\frac{1}{2}\left( {\frac{\delta _{1m}^2 }{\rho _4 }+\rho _4 e_2^2 } \right) \nonumber \\&+\frac{1}{2}\left( {\frac{\delta _{2m}^2 }{\rho _5 }+\rho _5 e_4^2 } \right) \nonumber \\&+\frac{1}{2}\left( {\frac{\delta _{3m}^2 }{\rho _6 }+\rho _6 e_6^2 } \right) \nonumber \\&+\,k_1 e_2^2 +k_2 e_4^2 +k_3 e_6^2 -k_4 e_2^2 -k_5 e_4^2 -k_6 e_6^2\nonumber \\ \end{aligned}$$
(45)

where Young’s inequality, i.e. \(ab\le \frac{1}{2}\left( {\frac{a^2 }{\rho }+\rho b^2 } \right) \) with \((a,b)\in R^{2}\) and \(\rho >0\), has been used in (45). \(\rho _i \) (\(i=1,{\ldots },6\)) are positive constants, and \(\delta _{\text {i m}}S\) (\(i=1,2,3\)) is the maximum of \(\delta _{i }\).

$$\begin{aligned} \dot{V}_6\le & {} -\left[ {k_1 -\frac{\left( {1+k_1^2 } \right) }{2\rho _1 }} \right] e_1^2\nonumber \\&-\left[ {k_4 -k_1 -\frac{\left( {1+k_1^2 } \right) \rho _1 }{2}-\frac{\rho _4 }{2}} \right] e_2^2\nonumber \\&-\left[ {k_2 -\frac{\left( {1+k_2^2 } \right) }{2\rho _2 }} \right] e_3^2\nonumber \\&-\left[ {k_5 -k_2 -\frac{\left( {1+k_2^2 } \right) \rho _2 }{2}-\frac{\rho _5 }{2}} \right] e_4^2\nonumber \\&-\left[ {k_3 -\frac{\left( {1+k_3^2 } \right) }{2\rho _3 }} \right] e_5^2\nonumber \\&-\left[ {k_6 -k_3 -\frac{\left( {1+k_3^2 } \right) \rho _3 }{2}-\frac{\rho _6 }{2}} \right] e_6^2 +\lambda \end{aligned}$$
(46)

where \(\lambda =\frac{1}{2}\left( {\frac{\delta _{1m}^2 }{\rho _4 }+\frac{\delta _{2m}^2 }{\rho _5 }+\frac{\delta _{3m}^2 }{\rho _6 }} \right) \) is positive constant. Now, the following coefficients are defined:

$$\begin{aligned} \mu _1= & {} \left[ {k_1 -\frac{\left( {1+k_1^2 } \right) }{2\rho _1 }} \right] \nonumber \\ \mu _2= & {} \left[ {k_4 -k_1 -\frac{\left( {1+k_1^2 } \right) \rho _1 }{2}-\frac{\rho _4 }{2}} \right] \nonumber \\ \mu _3= & {} \left[ {k_2 -\frac{\left( {1+k_2^2 } \right) }{2\rho _2 }} \right] \nonumber \\ \mu _4= & {} \left[ {k_5 -k_2 -\frac{\left( {1+k_2^2 } \right) \rho _2 }{2}-\frac{\rho _5 }{2}} \right] \nonumber \\ \mu _5= & {} \left[ {k_3 -\frac{\left( {1+k_3^2 } \right) }{2\rho _3 }} \right] \nonumber \\ \mu _6= & {} \left[ {k_6 -k_3 -\frac{\left( {1+k_3^2 } \right) \rho _3 }{2}-\frac{\rho _6 }{2}} \right] \end{aligned}$$
(47)

Coefficients \(k_i \) (\(i=1,{\ldots },6\)) and \(\rho _i \) (\(i=1,{\ldots },6\)) are chosen such that \(\mu _i >0\) (\(i=1,{\ldots },6\)). Equation (46) is rewritten as

$$\begin{aligned} \dot{V}_6 \le -\mu _1 e_1^2 -\mu _2 e_2^2 -\mu _3 e_3^2 -\mu _4 e_4^2 -\mu _5 e_5^2 -\mu _6 e_6^2 +\lambda \end{aligned}$$
(48)

Defining \(\mu =\min \left\{ {\mu _1 , . . . , \mu _6 } \right\} \), Eq. (48) gives

$$\begin{aligned} \dot{V}_6 \le -2\mu V_6 +\lambda \end{aligned}$$
(49)

Solving inequality (49) yields

$$\begin{aligned} \dot{V}_6 \le V_6 (0)e^{-2\mu t}+\frac{\lambda }{2\mu } , \quad \forall t>0 \end{aligned}$$
(50)

This shows the Lyapunov function \(V_6 \) is bounded by \(\lambda /2\mu \). Therefore, all the errors are bounded during the motion. By properly regulating the values of \(k_i \) (\(i=1,\ldots ,6\)) and \(\rho _i \) (\(i=1,\ldots ,6\)), the value of \(\lambda /2\mu \) can be made arbitrarily small. Therefore, the tracking error can be made small arbitrarily and the proof is completed.

Table 6 Optimization parameters values
Full size table
Fig. 12
figure 12

Fitness function values during optimization

Full size image
Fig. 13
figure 13

Tracking performance on heave displacement of tractor by COBC

Full size image
Fig. 14
figure 14

Tracking performance on heave displacement of trailer by COBC

Full size image
Fig. 15
figure 15

Tracking performance on pitch displacement of the tractor by COBC

Full size image
Fig. 16
figure 16

Tracking performance on pitch displacement of the trailer by COBC

Full size image
Fig. 17
figure 17

Tracking performance on articulation point by COBC

Full size image

5 Simulation results

In this section, simulation results of the vehicle motion are presented. Choosing the controller gains, inputs (44) are applied to the vehicle equations. The simulations are performed in two cases: designed inputs based on the backstepping method (44) and designed inputs based on the optimal backstepping method. In the following, these two cases are presented.

Fig. 18
figure 18

Tracking performance on heave displacement of tractor

Full size image
Fig. 19
figure 19

Tracking performance on heave displacement of trailer

Full size image
Fig. 20
figure 20

Tracking performance on pitch displacement of the tractor

Full size image
Fig. 21
figure 21

Tracking performance on pitch displacement of the trailer

Full size image
Fig. 22
figure 22

Tracking performance on articulation point

Full size image
Fig. 23
figure 23

Norm of the disturbance forces

Full size image

5.1 Chaos backstepping control

Here, the presented backstepping control in (44) is applied to the vehicle to control the appeared chaos in the vehicle behaviour. As it is shown in Figs. 5 and 6, the vehicle response is chaotic at \(v=4.6\,{\mathrm{m/s}}\). Therefore, the chaos control is carried out for when the vehicle moves in this velocity. The desired periodic motion is planned based on \(v=0.5\, {\mathrm{m/s}}\) in where the vehicle response is periodic (see Figs. 2, 3, 4). In other to show better the effectiveness of the controller, it is assumed that the vehicle moves with \(v=4.6\, {\mathrm{m/s}}\) and the controller is applied at \(t=50\,\mathrm{s}\). The controller gains are chosen \(k_1 = k_2 =k_3 =k_4 =k_5 =k_6 =2\). The simulation results for the phase plane portrait and time history of the heave displacements of tractor and trailer are depicted in Figs. 7 and 8. These figures show the chaotic motion converges to the desired periodic motion after applying the backstepping controller (44).

Also, Figs. 9 and 10 illustrate the phase plane portrait and time history of the pitch displacements of tractor and trailer. As depicted, these displacements reach the desired periodic trajectories and follow it after applying the controller.

Figure 11 shows the displacement of the articulation point. As shown, its motion is periodic after applying the chaos control. As the results of the phase planes, Figs. 7, 8, 9 and 10, show, the vehicle motion is periodic by designed controller in (44). Therefore, designed inputs in (44) can remove the chaos from the vehicle motion and derive towards the periodic motion.

5.2 Chaos optimal backstepping control

In the backstepping method, the controller gains are generally chosen by trial and error. Although the gains values are fairly exact, they are not optimal. So, there is needed to optimize the gain values. In this section, the controller gain coefficients are designed by optimizing and the effects of those values on simulation results are investigated. Here, the optimization problem is defined as

$$\begin{aligned} \hbox {Minimize} \quad {{{\varvec{J}}}}\left( {k_i } \right) ={{\int }}_{t_1 }^{t_2 } {\left\| {{{\varvec{e}}}} \right\| } \text {d}t\nonumber \\ \hbox {such}\,{\hbox {that}} \nonumber \\ k_i >0 , i=1,. . . ,6 \end{aligned}$$
(51)

where \({{{\varvec{e}}}}=[{\begin{array}{llllll} {e_1 }&{} {e_2 }&{} {e_3 }&{} {e_4 }&{} {e_5 }&{} {e_6 } \\ \end{array} }]^{T}\) and is obtained from Sect. 4. Therefore, the controller gain values are obtained such that the error norm is minimized in interval \(t_1 \)–\(t_2 \). Here, for solving the optimization problem (51), genetic algorithm (GA) is used. The GA method is widely used in optimization problems [33–35].

An implantation of GA begins with a population of chromosomes randomly. Each chromosome is evaluated by using the objective function called fitness function. In order to apply the GA reproductive operations, two individuals as parents are randomly selected. By exchanging some of bits between parents, if its probability reaches, applying the crossover operation will result in produce two children. Also, a mutation is the second operator which is applied on the single children by inverting its bit if the probability reaches. Then, it can be obtained two populations: parents and children, the individual who has a good solution is preserved [36]. The optimization problem (51) is solved by MATLAB software with given parameters values in Table 6.

The fitness function during optimization is shown in Fig. 12. After optimization, the controller optimal gains are obtained as \(k_1 =9.8995\), \(k_2 =13.228\), \(k_3 =6.8823\), \(k_4 =15.3121\), \(k_5 =16.9461\), \(k_6 =12.9362\), and the best fitness value is 0.00622 in iteration number 75.

Now, the chaos backstepping control (44) with the optimized gains is applied to the vehicle and its response is analysed. The simulation results of the chaos optimal backstepping control (COBC) are presented in Figs. 13, 14, 15, 16 and 17.

Figures 13 and 14 show the phase plane portrait and time history of the heave displacements of tractor and trailer, respectively. It can be seen that the behaviour is chaotic up to \(t=50\,\mathrm s\), and afterwards the trajectories follow the desired path and the time history gets to periodic motion. Also, Figs. 15 and 16 reveal the effectiveness of proposed controller for controlling the pitch motions of tractor and trailer. Figure 17 indicates the time history of articulation point. As shown, the response is chaotic before \(t=50 \,\mathrm{s}\). When the controller is applied, the displacement converges to periodic motion with very small amplitude. This goal is not achievable only by the MR dampers, but due to the nonlinear nature of these dampers, the vehicle dynamic behaviour goes to chaotic vibration which is undesirable. These results show for reaching the desired periodic behaviour, it is needed that the active controller is accompanied with MR dampers.

5.3 Robustness of COBC

In this section, the robustness of the proposed COBC is studied. In the worst case, the random disturbance force is applied as an arbitrary excitation force during a time interval \([52 \,53 ]\). The COBC is applied with the same previous gains and the same initial conditions. The simulation results are shown in Figs. 18, 19, 20, 21 and 22. In these figures, the tracking performance of the vehicle is depicted. It can be seen that the vehicle’s responses converge to the desired trajectory despite the existing disturbance. Therefore, the proposed controlling system has good robustness in tracking performance. Also, the control action on articulation point shows the appropriate robustness encountering the external disturbance. Figure 23 shows the disturbance force norm in the presence of external disturbances. Therefore, these results depict the control approach proposed in this paper is robust against the external disturbances.

6 Conclusion

In this paper, the active chaos control of a heavy articulated vehicle equipped with MR dampers was studied. MR dampers are used to semi-active control of the vehicle vibration. These dampers can reduce the amplitude of the free oscillations and dynamic tire forces, and improve the ride quality of the passengers [22, 24]. However, nonlinear features of these dampers can lead to the chaotic behaviour of the vehicle. In this paper, firstly the nonlinear dynamic behaviour of half-truck model was studied. The irregular regions were detected by utilizing the bifurcation diagrams and Poincaré maps. Then, the active controller was proposed to control the chaotic behaviours. The control law was derived based on the backstepping method. The simulation results showed the chaotic motion of the vehicle reaches to the periodic desired motion and follows it by the proposed controller. In order to minimize the error norm, chaos optimal backstepping control was proposed and the optimal gains were obtained by the genetic algorithm. The main contributions of this paper are summarized as: considering the nonlinear features of MR dampers and their influences on dynamic behaviour of the heavy articulated vehicle and optimal backstepping control design for eliminating the chaotic behaviours. The obtained results showed, by using the optimal gain values, the controller performance was extremely enhanced. Also, the simulation results of the robustness showed the vehicle body displacements converge to periodic desired motion in spite of the existing external disturbance. Therefore, the proposed controller removed the chaos from the vehicle motion and forced it to move towards the periodic motion.