1 Introduction

We know that nonlinearities and time-delays, which are non-ignorable features of various engineering systems, might result in terrible deterioration of stability and control effectiveness of many real processes. Over the past few decades, the researches on such dynamical systems with nonlinearities and time-delays have been extensively given attention in control science and engineering field. Many results have been arrived at in this studied issue, see, for instance, [1,2,3] and the relevant references. Recalling these results related to nonlinear dynamics, Takagi–Sugeno fuzzy (TSF) models [4] have received considerable attention. We always use TSF model to represent the local linear relations related to the input–output terms of some nonlinear dynamics. By the fuzzy membership functions, the relevant TSF model gives a feasible framework to express the nonlinear plant by a series of local linear submodels. Many research results of nonlinear systems modeled by TSF representation have been studied on stability, robust stabilization, controller synthesis and state estimation, see [5,6,7,8,9] and the relevant references.

As a kind of important stochastic hybrid systems, Markovian jumping systems (MJSs) is one of the hot research topics in the past three decades. MJSs contains two factors. The first one is the modes represented by a Markov stochastic process; the second one is the states described by the time-domain differential (or difference) equations. Many results related to the stochastic stability (i.e., almost surely stability), controllability and robust filtering problems of MJSs have been widely studied, see for example, [10,11,12,13,14,15,16,17] and the relevant references. When we study MJSs or use MJSs to model some dynamics, we need to consider the time-delays owing to the inherent features. In most research of MJSs, the delays are mode-independent or the delayed modes are assumed to be the same as the system modes. In fact, some time-delays are mode-dependent. In this case, the delay modes might not be the same as the system modes, and the mode-dependent delays might not cause abrupt changes. When MJSs exist as mode-dependent time-delays, the research will be more interesting and challenging in theory and practice aspects.

On another research from line, the fault detection (FD) problem has regained a hot attention in recent years due to the high reliability and high safety demands of modern industrial process. Among the fault detection methods, model-based fault detection [18, 19] is an active one. In the model-based fault detection process, we can design a parameter/state estimator to generate residual signals and to construct a evaluation function of the residual signals. Then we can set a preset threshold of the residual evaluation function and the residual signals. In fault detection process, an alarm of fault will generate if the evaluated function response exceeds the given threshold. In this paper, we considered the \(H_{\infty }\) filtering-based model fault detection scheme. In the \(H_{\infty }\) filtering formulation, the given \(H_{\infty }\)-norm from external disturbances to residual signals is used to estimate the influence of disturbance inputs and the system sensitivity to faults. Motivated by these, the \(H_{\infty }\) filtering formulations have been proposed to detect the faults for uncertain systems [20, 21], nonlinear systems [22, 23], time-delayed systems [24, 25] and MJSs [26,27,28,29,30,31,32,33,34], etc. In [26, 27], the observer-based robust fault detection method and the \(H_{\infty }\)-filtering formulation were, respectively, constructed to obtain the fault detection filter (FDF) for linear MJSs. Considering the \(H_{\infty }/H_{-}\) setting methods, the robust FDF design problem of stochastic uncertain nonlinear time-delayed MJSs was studied [28]. Based on the \(H_{\infty }\) filtering-based fault detection formulation, the FDF design problems were, respectively, studied for discrete-time MJSs [29] and mode-dependent time-delayed MJSs [30]. For more results on the FDF design of MJSs, we refer interested readers to [31,32,33,34] and the relevant references.

This paper considered the FDF design problem of time-delayed TSF-MJSs. The delays are considered to be time-varying and mode-dependent. By selecting an appropriate weighting matrix function, the jumping fuzzy FDF systems and the \(H_{\infty }\)-filtering formulation residual generator are constructed. We aim to find a suitable FDF which derives a minimal difference between the ideal solution of the reference model and the real result of the designed FDF. A sufficient condition related to the designed FDF is obtained to guarantee the stochastic stability of the resulting TSF-MJSs and satisfy the given \(H_{\infty }\) index to against external disturbances, nonlinearities and time-delays. The design scheme is proposed and proved in terms of linear matrix inequalities (LMIs) algorithms and a simulation example is derived to demonstrate the feasibility of the presented methods.

In this paper, the states are driven by the random process \(\left\{ {r_t ,t\ge 0} \right\} \) which are taking values on the finite set \(\varUpsilon _1 =\left\{ {1,2,\ldots ,N_1 } \right\} \). The time-delays are varying and mode-dependent and are driven by the random process \(\left\{ {l_t ,t\ge 0} \right\} \) which are taking values on the finite set \(\varUpsilon _2 =\left\{ {1,2,\ldots ,N_2 } \right\} \). In the process, these two random processes are mutually independent. In fact, if the delays are mode-dependent, the modes of delays are always different with the modes of systems. For convenience, some published results assume that the delay modes are the same as the system modes, see for example, [35, 36] and the references therein. It is obviously difficult to conduct the FDF design research on MJSs with varying and mode-dependent delays. When we design the fuzzy FDF, we choose the Lyapunov–Krasovskii functional (LKF) candidate as mode-dependent case, which is driven by the random processes \(\left\{ {r_t ,t\ge 0} \right\} \) and \(\left\{ {l_t ,t\ge 0} \right\} \). By choosing an appropriate LKF, a mode-dependent sufficient condition is derived to prove that the resulting TSF-MJSs is stochastically stable (SS) and satisfy the given \(H_{\infty }\) index formulation. The designed algorithms and the numerical example also illustrate the contribution of the designed results.

Notations In this paper, \(\mathfrak {R}^{n}\) represents the n-dimensional Euclidean space; \(\mathfrak {R}^{n\times m}\) represents the \(n\times m\)-dimensional matrices; \(A^{-1}\) and \(A^{\mathrm {T}}\), respectively, represent the inverse and the transpose of matrix A; \(\hbox {diag}\{A_1 ,A_2 \}\) denotes the block-diagonal matrix of \(A_1 \) and \(A_2 \); \(\sigma _{\min } (A)\) and \(\sigma _{\max } (A)\), respectively, denote the minimal and maximal eigenvalues of A; \(\left\| {*} \right\| \) represents the vectors’ Euclidean norm; \(\mathbf{E }\left\{ {*} \right\} \) denotes the expectation of the relevant stochastic process or vector; \(\Vert {x( t )} \Vert _{2,\mathbf{E }} \) denotes the mean square norm, where \(\Vert {x( t )}\Vert _{2,\mathbf{E }} =\sqrt{\mathbf{E }\int _0^\infty x^{\mathrm{T}}( t )x( t )\hbox {d}t }\); \(P>0\) (\(P<0)\) denotes a negative (or positive)-definite matrix; I and 0, respectively, denote a unit matrix and a zero matrix with appropriate dimensions; “\({*}\)” denotes the symmetric matrix.

2 Problem formulation

To obtain a Takagi and Sugeno [4] fuzzy dynamic, the principal methods are used to linearize the system trajectories through different operating points and the optimization methods are used to minimize the relevant identification errors. In this paper, the linear model is derived by the so-called IF-THEN rules and then used to design the FDF for a class of TFS-MJSs. Given a probability space \(\left( {\varPsi ,\varGamma ,{P}_r } \right) \), where \(\varPsi \) represents the sample space, \(\varGamma \) represents the algebra of events and \({P}_r \) represents the measure probability defined on \(\varGamma \). Consider a class of TFS-MJSs defined in \(\left( {\varPsi ,\varGamma ,{P}_r } \right) \) which is described by:

System Rule r:

IF \(\alpha _1 (t)\) is \(F_1^r \), \(\alpha _2 (t)\) is \(F_2^r \), and ..., \(\alpha _K (t)\) is \(F_K^r \), THEN:

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{x}}(t)=A_r (m_t )x(t)+A_{\tau r} (m_t )x[t-\tau (i_t )]\\ \quad \; \qquad +\,B_r (m_t )u(t)+B_{dr} (m_t )d(t)+B_{fr} (m_t )f(t) \\ y(t)=C_r (m_t )x(t)+C_{\tau r} (m_t )x[t-\tau (i_t )]\\ \quad \;\qquad +\,D_{dr} (m_t )d(t)+D_{fr} (m_t )f(t) \\ \;x(t)=a_1 (t),\quad m_t =a_2 (t),\quad i_t =a_3 (t),\\ \qquad \quad \; t\in \left[ {\begin{array}{cc} {-\tau _1 }&{} \quad 0 \\ \end{array} }\right] ,\quad r=1,2,\ldots ,S. \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(1)

where \(x(t)\in \mathfrak {R}^{n}\) represents the state, \(y(t)\in \mathfrak {R}^{m}\) represents the measured output, \(u(t)\in \mathfrak {R}^{l}\) represents the controlled input, \(d(t)\in L_2^p \left[ {{\begin{array}{cc} 0&{} \quad +\infty \\ \end{array} }} \right) \) represents the external disturbance, \(f(t)\in \mathfrak {R}^{q}\) represents the detected fault. \(\alpha _1 \left( t \right) ,\alpha _2 \left( t \right) ,\ldots ,\alpha _g \left( t \right) \) represent the premise variables which can be available. \(F_k^r \), \(r=1,2,\ldots ,L\), \(k=1,2,\ldots ,K\) represent the fuzzy sets, L represents the numbers of the fuzzy rules. \(A_r (m_t )\), \(A_{\tau r} (m_t )\), \(B_r (m_t )\), \(B_{dr} (m_t )\), \(B_{fr} (m_t )\), \(C_r (m_t )\), \(C_{\tau r} (m_t )\), \(D_{dr} (m_t )\), \(D_{fr} (m_t )\) are known compatible matrices. \(a_1 (t)\) is the initial vector-valued condition which is defined on \([{\begin{array}{cc} {-\tau _1 }&{}\quad 0 \\ \end{array} }]\), where \(\tau _1 =\max \left\{ {\tau _{1i} ,i_t \in \varUpsilon _2 =\left\{ {1,2,\ldots ,S_2 } \right\} } \right\} \); \(a_2 (t)\) and \(a_3 (t)\) are, respectively, the dependent initial modes. \(\tau (i_t )\) is the time-varying and mode-dependent delay satisfying:

$$\begin{aligned} 0\le \tau _{2i} \le \tau (i_t )\le \tau _{1i}<\infty , \quad {\dot{\tau }}(i_t )\le \tau _{3i} <1. \end{aligned}$$
(2)

Define the stochastic processes \(\left\{ {m_t ,t\ge 0} \right\} \) and \(\left\{ {i_t ,t\ge 0} \right\} \) as two continuous-time and discrete-state Markov processes which take values on two finite sets \(\varUpsilon _1 =\left\{ {1,2,\ldots ,S_1 } \right\} \) and \(\varUpsilon _2 =\left\{ {1,2,\ldots ,S_2 } \right\} \). The relevant transition rate matrices are \(\varLambda _1 =\left\{ {\pi _{mn} } \right\} \), \(m,n\in \varUpsilon _1 \) and \(\varLambda _2 =\left\{ {\pi _{ij} } \right\} \), \(i,j\in \varUpsilon _2 \), respectively. We assume that \(\left\{ {m_t ,t\ge 0} \right\} \) and \(\left\{ {i_t ,t\ge 0} \right\} \) are mutually independent. In this paper, we obtain the transition probability of stochastic Markov process \(\left\{ {m_t ,t\ge 0} \right\} \) from mode m at time t to mode n at time \(t+\Delta t\) as:

$$\begin{aligned} {P}_m= & {} {P}_m \left\{ {r_{t+\Delta t} =n|r_t =m} \right\} \nonumber \\= & {} \left\{ {{\begin{array}{ll} {\pi _{mn} \Delta t+o\left( {\Delta t} \right) ,}&{}\quad {\hbox {if } m\ne n} \\ {1+\pi _{mm} \Delta t+o\left( {\Delta t} \right) ,}&{}\quad {\hbox {if } m=n} \\ \end{array} }} \right. \end{aligned}$$
(3)

and similarly we can get the transition probability of stochastic Markov process \(\left\{ {i_t ,t\ge 0} \right\} \) as:

$$\begin{aligned} P_i= & {} P_i \left\{ {r_{t+\Delta t} =j|r_t =i} \right\} \nonumber \\= & {} \left\{ {{\begin{array}{ll} {\pi _{ij} \Delta t+o\left( {\Delta t} \right) ,}&{}\quad {\hbox {if } i\ne j} \\ {1+\pi _{ii} \Delta t+o\left( {\Delta t} \right) ,}&{} \quad {\hbox {if }i=j} \\ \end{array} }} \right. \end{aligned}$$
(4)

where \(\Delta t>0\) and \(\mathop {\hbox {lim}}\limits _{\Delta t\rightarrow 0} \frac{o\left( {\Delta t} \right) }{\Delta t}=0. \quad \pi _{mn} \ge 0\) (or \(\pi _{ij} \ge 0)\) represents the transition probability rates from mode m (or i) at time t to mode n (or j) at time \(t+\Delta t\). Then we have \(\mathop \sum \limits _{n=1,n\ne m}^{S_1 } {\pi _{mn} } =-\pi _{mm} \) and \(\mathop \sum \nolimits _{j=1,j\ne i}^{S_2 } {\pi _{ij} } =-\pi _{ii} \).

For convenience, \(A_r (m_t )\), \(A_{\tau r} (m_t )\), \(B_r (m_t )\), \(B_{dr} (m_t )\), \(B_{fr} (m_t )\), \(C_r (m_t )\), \(C_{\tau r} (m_t )\), \(D_{dr} (m_t )\), \(D_{fr} (m_t )\), \(x[t-\tau (i_t )]\) are denoted as \(A_r (m)\), \(A_{\tau r} (m)\), \(B_r (m)\), \(B_{dr} (m)\), \(B_{fr} (m)\), \(C_r (m)\), \(C_{\tau r} (m)\), \(D_{dr} (m)\), \(D_{fr} (m)\), \(x[t-\tau (i)]\) respectively.

We let \(\alpha (t)=[{\begin{array}{cccc} {\alpha _1 (t)}&{}\quad {\alpha _2 (t)}&{}\quad \cdots &{}\quad {\alpha _S (t)} \\ \end{array} }]\) and assume that the available variables only depend on the states. Applying the standard fuzzy singleton inference approach, i.e., a singleton fuzzifier to derive a fuzzy inference and weighted center-average defuzzifier [4, 5, 7,8,9, 23, 25, 28, 37,38,39,40,41], we have the TSF-MJSs as:

$$\begin{aligned} \left\{ {\begin{array}{rll} {\dot{x}}(t)&{}=\mathop \sum \limits _{r=1}^L {h_r [\alpha (t)]} \left\{ A_r (m)x(t)\right. \\ &{}\quad +\,A_{\tau r} (m)x(t-\tau (i)) +B_r (m)u(t)\\ &{}\left. \quad +\,B_{dr} (m)d(t)+\,B_{fr} (m)f(t) \right\} \\ y(t)&{}=\mathop \sum \limits _{r=1}^L {h_r [\alpha (t)]} \left\{ C_r (m)x(t) \right. \\ &{}\left. \quad +\,C_{\tau r} (m)x(t-\tau (i)) +D_{dr} (m)d(t)\right. \\ &{}\left. \quad +\,D_{fr} (m)f(t) \right\} \\ \;x(t)&{}=a_1 (t), \quad m_t =a_2 (t),\\ \;i_t &{}=a_3 (t),\quad t\in [{\begin{array}{cc} {-\tau _1 }&{}\quad 0 \\ \end{array} }],\\ r&{}=1,2,\ldots ,L. \\ \end{array}} \right. \end{aligned}$$
(5)

where

$$\begin{aligned} \left\{ {\begin{array}{ccccc} h_r [\alpha (t)]=\frac{\upsilon _r [\alpha (t)]}{\mathop \sum \nolimits _{r=1}^L {\upsilon _r [\alpha (t)]} } \\ \upsilon _r [\alpha (t)]=\mathop \Pi \limits _{k=1}^g F_k^r [\alpha _k (t)] \\ \end{array}} \right. \end{aligned}$$
(6)

and \(F_k^r [\alpha _k (t)]\) represents the membership grade of \(\alpha _k (t)\) with \(\upsilon _r [\alpha (t)]\ge 0\) and \(\mathop \sum \nolimits _{r=1}^L {\upsilon _r [\alpha (t)]} >0\). Then, it is always assumed that:

$$\begin{aligned} \left\{ {\begin{array}{lcccc} \mathop \sum \limits _{r=1}^L {h_r [\alpha (t)]} =1, \\ 0\le h_r [\alpha (t)]\le 1,\quad r=1,2,\ldots ,L. \\ \end{array}} \right. \end{aligned}$$
(7)

In order to detect f(t), we aim to design a suitable FDF of the TSF-MJSs (5). Before designing the FDF, we need the following definitions.

Definition 1

The TSF-MJSs (1) (letting \(u(t)=0\), \(d(t)=0\), \(f(t)=0)\) is SS if, for \(x(t)=a_1 (t)\),\(m_t =a_2 (t)\), \(i_t =a_3 (t)\), we have:

$$\begin{aligned} \mathop {\lim }\limits _{T\rightarrow \infty } \mathbf{E }\left\{ {\left. {\int _0^T {\left\| {x\left[ {t,m_t ,i_t } \right] } \right\| ^{2}\hbox {d}t} } \right| x(t)=a_1 (t)} \right\} <\infty .\nonumber \\ \end{aligned}$$
(8)

Definition 2

[10] In Euclidean space \(\{ \mathfrak {R}^{n}\times \varUpsilon _1 \times \varUpsilon _2 \times \mathfrak {R}_+ \}\), we select a positive stochastic functional as \(V\left[ {x(t),m_t =m,i_t =i,t>0} \right] \) and we can define the relevant weak infinitesimal operator of \(V\left[ {x(t),m,i} \right] \) as:

$$\begin{aligned}&\mathfrak {I}V\left[ {x(t),m,i} \right] \nonumber \\&\quad =\mathop {\lim }\limits _{\Delta t\rightarrow 0} \frac{1}{\Delta t} \Big [ \left. \mathbf{E }\left\{ V {(x(t+\Delta t),m_{t+\Delta t} ,i_{t+\Delta t} )} \right| x(t),\right. \nonumber \\&\qquad \left. m_t =m,i_t =i \right\} -V(x(t),m,i) \Big ]. \end{aligned}$$
(9)

In the following, we construct the jumping fuzzy FDF as:

Filter Rule r:

IF \(\alpha _1 (t)\) is \(F_1^r \), \(\alpha _2 (t)\) is \(F_2^r \), and ..., \(\alpha _K (t)\) is \(F_K^r \), THEN:

$$\begin{aligned} \left\{ {\begin{array}{lcccc} {\dot{x}}_F (t)=A_{Fr} (m,i)x_F (t)+B_{Fr} (m,i)y(t) \\ g_F (t)=C_{Fr} (m,i)x_F (t)+D_{Fr} (m,i)y(t) \\ x_F (t)=0. \\ \end{array}} \right. \end{aligned}$$
(10)

Then, the relevant fuzzy FDF dynamic model is derived as:

$$\begin{aligned} \left\{ {\begin{array}{lcccc} {\dot{x}}_F (t)=\mathop \sum \limits _{r=1}^L {h_r [\alpha (t)]} \left[ A_{Fr} (m,i)x_F (t)\right. \\ \qquad \qquad \left. +\,B_{Fr} (m,i)y(t) \right] \\ g_F (t)=\mathop \sum \limits _{r=1}^L {h_r [\alpha (t)]} \left[ C_{Fr} (m,i)x_F (t)\right. \\ \left. \qquad \qquad +\,D_{Fr} (m,i)y(t) \right] \\ x_F (t)=0. \\ \end{array}} \right. \end{aligned}$$
(11)

where \(x_F (t)\in \mathfrak {R}^{n}\) represents the filter state, \(g_F (t)\in \mathfrak {R}^{m}\) represents the filter output, \(A_{Fr} (m,i)\), \(B_{Fr} (m,i)\), \(C_{Fr} (m,i)\), \(D_{Fr} (m,i)\) are the designed filtering parameters for each value \(m\in \varUpsilon _1 \), \(i\in \varUpsilon _2 \).

To detect the faults, we introduce a suitable stable weighting matrix function \(W_f (s)\) to improve the performance and to identify the detected faults. We set \(W_f (s)\) as a full rank, diagonal or identity matrix. In some published results [21, 26], we always give the reference residual model with the following form:

$$\begin{aligned} g_f (s)=W_f (s)f(s). \end{aligned}$$
(12)

We can get the minimal realization of \(W_f (s)\) as:

$$\begin{aligned} \left\{ {\begin{array}{ccccc} {\dot{x}}_f (t)=A_W x_f (t)+B_W f(t) \\ g_f (t)=C_W x_f (t)+D_W f(t). \\ \end{array}} \right. \end{aligned}$$
(13)

Denote \(h_r \left[ {\alpha (t)} \right] \) as \(h_r \), and define \(e(t)=x(t)-x_F (t)\), \(g(t)=g_F (t)-g_f (t)\). The resulting TSF-MJSs are given as:

$$\begin{aligned} \left\{ {\begin{array}{ccccc} \dot{{\tilde{x}}}(t)=\hat{{A}}_{rk} (m,i){\tilde{x}}(t)+\hat{{A}}_{\tau rk} (m,i){\tilde{x}}\left[ {t-\tau (i)} \right] \\ \quad \qquad \;+\,\hat{{B}}_{rk} (m,i)w(t) \\ g(t)=\hat{{C}}_{rk} (m,i){\tilde{x}}(t)+\hat{{C}}_{\tau rk} (m,i){\tilde{x}}\left[ {t-\tau (i)} \right] \\ \quad \qquad \;+\,\hat{{D}}_{rk} (m,i)w(t) \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(14)

where \({\tilde{x}}(t)=\left[ {{\begin{array}{c} {x(t)} \\ {e(t)} \\ {x_f (t)} \\ \end{array} }} \right] \), \(w(t)=\left[ {{\begin{array}{c} {u(t)} \\ {d(t)} \\ {f(t)} \\ \end{array} }} \right] \),

$$\begin{aligned} \hat{{A}}_{rk} (m,i)= & {} \mathop \sum \limits _{r=1}^L {h_r } \sum _{k=1}^L {h_k }\\&\times \left[ {{\begin{array}{ccc} {A_r (m)}&{}0&{}0 \\ A_r (m)-A_{Fr} (m,i)-B_{Fr} (m,i)C_k (m)&{}{A_{Fr} (m,i)}&{}0 \\ 0&{}0&{}{A_W } \\ \end{array} }} \right] , \\ \hat{{A}}_{\tau rk} (m,i)= & {} \mathop \sum \limits _{r=1}^L {h_r } \sum _{k=1}^L {h_k }\left[ {{\begin{array}{ccc} {A_{\tau r} (m)}&{}0&{}0 \\ {-B_{Fr} (m,i)C_{\tau k} (m)}&{}0&{}0 \\ 0&{}0&{}0 \\ \end{array} }} \right] , \\ \hat{{B}}_{rk} (m,i)= & {} \mathop \sum \limits _{r=1}^L {h_r } \sum _{k=1}^L {h_k }\\&\times \left[ {{\begin{array}{ccc} {B_r (m)}&{}{B_{dr} (m)}&{}{B_{fr} (m)} \\ 0&{}{-B_{Fr} (m,i)D_{dk} (m)}&{}{-B_{Fr} (m,i)D_{fk} (m)} \\ 0&{}0&{}{B_W } \\ \end{array} }} \right] , \\ \hat{{C}}_{rk} (m,i)= & {} \mathop \sum \limits _{r=1}^L {h_r } \sum _{k=1}^L {h_k } \\&\times \left[ {C_{Fr} (m,i)+D_{Fr} (m,i)C_k (m)}{-\,C_{Fr} (m,i)} {C_W } \right] , \\ \hat{{C}}_{\tau rk} (m,i)= & {} \mathop \sum \limits _{r=1}^L {h_r } \sum _{k=1}^L {h_k } \left[ {{\begin{array}{ccc} {D_{Fr} (m,i)C_{\tau k} (m)}&{}0&{}0 \\ \end{array} }} \right] , \\ \hat{{D}}_{rk} (m,i)= & {} \mathop \sum \limits _{r=1}^L {h_r } \sum _{k=1}^L {h_k }\\&\times \left[ {{\begin{array}{ccc} 0&{}{D_{Fr} (m,i)D_{dk} (m)}&{}{D_{Fr} (m,i)D_{fk} (m)-D_W } \\ \end{array}}} \right] . \end{aligned}$$

Remark 1

The weighting matrix function \(W_f (s)\) is introduced to limit the interval of frequency. By the weighting matrix function, the faults can be identified and the relevant performance of the detected systems can be improved. By introducing the reference residual dynamic \(g_f (s)\), the optimization criterion of the fuzzy FDF dynamic (11) is the worst case distance between the real solution (i.e., the generated residual) and the ideal solution (i.e., the reference residual signal). Meanwhile, the minimization of the worst case distance with respect to \(H_{\infty }\) norm provides robustness by the designed FDF.

Throughput analysis, the design problem of the fuzzy FDF dynamic (11) is derived as an \(H_{\infty }\)index formulation and model matching problem, i.e., find suitable filtering parameters \(A_{Fr} (m,i)\), \(B_{Fr} (m,i)\), \(C_{Fr} (m,i)\), \(D_{Fr} (m,i)\), satisfying the following two objectives:

  1. (a)

    The resulting TSF-MJSs (14) should be stochastically stable, i.e., almost asymptotically stable;

  2. (b)

    Given a scalar \(\gamma >0\), the index formulation J(w) is made small:

    $$\begin{aligned} J(w)=\mathop {\sup }\limits _{w(t)\in L_2 ,w(t)\ne 0} \frac{\left\| {g(t)} \right\| _{2,\mathbf{E }} }{\left\| {w(t)} \right\| _2 }\le \gamma \end{aligned}$$
    (15)

    where \(\left\| {g(t)} \right\| _{2,\mathbf{E }} =\sqrt{E\left[ {\int _0^\infty {g^{\mathrm{T}}(t)g(t)\hbox {d}t} } \right] }\), \(\left\| {w(t)} \right\| _2 =\sqrt{\int _0^\infty {w^{\mathrm{T}}(t)w(t)\hbox {d}t} }\).

According to the above two objectives, the design problem of the fuzzy FDF can be derived as the \(H_{\infty }\) filtering formulation, i.e., design the fuzzy FDF dynamic (11) with parameters \(A_{Fr} (m,i)\), \(B_{Fr} (m,i)\), \(C_{Fr} (m,i)\), \(D_{Fr} (m,i)\), \(m\in \varUpsilon _1 \), \(i\in \varUpsilon _2 \), such that the resulting TSF-MJSs (14) with \(w(t)\in L_2 \) is SS and satisfy the\( H_{\infty }\) index formulation with \(\left\| {g(t)} \right\| _{2,\mathbf{E }} \le \gamma \left\| {w(t)} \right\| _2 \).

To design the fuzzy FDF dynamic (11), we should determine the appropriate threshold and residual evaluation function. Considering the norm bounded external disturbance d(t), that is, \(d(t)\in L_2^p \left[ {{\begin{array}{cc} 0&{}\quad {+\infty } \\ \end{array} }} \right) \), we can determine the following fault detection threshold \(J_{th} \):

$$\begin{aligned} J_{th} =\mathop {\sup }\limits _{d(t)\in L_2 ,f(t)=0} \mathbf{E }\left\{ {\int _{T_1 }^{T_2 } {g^{\mathrm{T}}(t)g(t)} \hbox {d}t} \right\} \end{aligned}$$
(16)

where \(\left[ {{\begin{array}{cc} {T_1 }&{}\quad {T_2 } \\ \end{array} }} \right] \) is the detection finite-time interval with \(T_1 <T_2 \); \(T_f =T_2 -T_1 \) represents the initial fault estimated time. In general, the fault estimated time \(T_f \) is always finite because the residual evaluation over an infinite-time range is not the fact.

Then, we can determine the following evaluation function f(g):

$$\begin{aligned} f(g)=\mathbf{E }\left\{ {\int _{T_1 }^{T_2 } {g^{\mathrm{T}}(t)g(t)} \hbox {d}t} \right\} . \end{aligned}$$
(17)

In the following, we can make a decision logic to detect the faults:

$$\begin{aligned} \left\{ {\begin{array}{ll} f(g)>J_{th} \Rightarrow \hbox {having}\,\hbox {faults}\left( \hbox {fault-alarm} \right) \\ f(g)\le J_{th} \Rightarrow \hbox {without}\,\hbox {faults}\left( \hbox {fault-free} \right) \\ \end{array}} \right. . \end{aligned}$$
(18)

3 Main results

Theorem 1

The resulting TSF-MJSs (14) is SS, if there exist mode-dependent matrix \({\tilde{P}}(m,i)>0\), matrix \({\tilde{Q}}>0\) and scalars \(\tau _1 >0\), \(\tau _2 >0\) and \(\tau _{3i} >0\), satisfying the following (19) for \(m,n\in \varUpsilon _1 \), \(i,j\in \varUpsilon _2 \),

$$\begin{aligned} \Xi (m,i)=\left[ {{\begin{array}{cc} {\Xi _{rk} (m,i)}&{}\quad {{\tilde{P}}(m,i)\hat{{A}}_{\tau rk} (m)} \\ {*}&{}\quad {-\,\left( {1-\tau _{3i} } \right) {\tilde{Q}}} \\ \end{array} }} \right] <0 \end{aligned}$$
(19)

where

$$\begin{aligned} \Xi _{rk} (m,i)= & {} {\tilde{P}}(m,i)\hat{{A}}_{rk} (m)+\hat{{A}}_{rk}^\mathrm{T} (m){\tilde{P}}(m,i)\\&+\,\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] {\tilde{Q}}\\&+\,\sum _{j=1}^{S_2 } {\pi _{ij} {\tilde{P}}(m,j)} +\sum _{n=1}^{S_1 } {\pi _{mn} {\tilde{P}}(n,i)} , \\ \pi= & {} \max \left\{ \left| {\pi _{mm} } \right| , \right. \left. m\in \varUpsilon _1 \right\} ,\\ \tau _2= & {} \min \left\{ {\tau _{1i} ,i\in \varUpsilon _2 } \right\} . \end{aligned}$$

Proof

Select a LKF candidate as:

$$\begin{aligned} V\left[ {{\tilde{x}}(t),m,i} \right]= & {} V_1 \left[ {{\tilde{x}}(t),m,i} \right] +V_2 \left[ {{\tilde{x}}(t),m,i} \right] \\&+\,V_3 \left[ {{\tilde{x}}(t),m,i} \right] , \end{aligned}$$

where

$$\begin{aligned} V_1 \left[ {{\tilde{x}}(t),m,i} \right]= & {} {\tilde{x}}^{\mathrm{T}}(t){\tilde{P}}(m,i){\tilde{x}}(t),\\ V_2 \left[ {{\tilde{x}}(t),m,i} \right]= & {} \int _{t-\tau (i)}^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )}\hbox {d} \rho ,\\ V_3 \left[ {{\tilde{x}}(t),m,i} \right]= & {} \pi \int _{-\tau _1 }^{-\tau _2 } {\int _{t+\nu }^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } } \hbox {d}\nu . \end{aligned}$$

Recalling to Definition 2, we can get the weak infinitesimal operator of \(V\left[ {{\tilde{x}}(t),m,i} \right] \):

$$\begin{aligned}&\mathfrak {I}V_1 \left[ {{\tilde{x}}(t),m,i} \right] \\&\quad =\mathop {\lim }\limits _{\varDelta \rightarrow 0} \frac{1}{\varDelta }\mathbf{E }\left\{ {\tilde{x}}^{\mathrm{T}} (t+\varDelta ){\tilde{P}}(m_{t+\varDelta } ,i_{t+\varDelta } ){\tilde{x}}(t+\varDelta )\right. \\&\qquad \left. -\,\,{\tilde{x}}^{\mathrm{T}}(t){\tilde{P}}(m,i){\tilde{x}}(t) \right\} \\&\quad =\mathop {\lim }\limits _{\varDelta \rightarrow 0} \frac{1}{\varDelta }\left\{ {\tilde{x}}^{\mathrm{T}}(t+\varDelta )\left[ \left[ 1+\pi _{mm} \varDelta +o(\varDelta ) \right] \right. \right. \\&\qquad \left[ 1+\pi _{ii} \varDelta +o(\varDelta )\right] {\tilde{P}}(m,i) +\left( 1+\pi _{mm} \varDelta \right. \\&\qquad \left. +\,\,o(\varDelta ) \right) \left( \sum _{j=1}^{S_2 } \left[ 1+\pi _{ij} \varDelta +o(\varDelta ) \right] \right) {\tilde{P}}\left( {m,j} \right) \\&\qquad +\,\,\left( 1+\pi _{ii} \varDelta +o(\varDelta ) \right) \left( {\sum _{n=1}^{S_1 } {\left[ {1+\pi _{mn} \varDelta +o(\varDelta )} \right] } } \right) {\tilde{P}}(n,i) \\&\qquad \left. +\,\,\left( \sum _{j=1}^{S_2 } \left[ 1+\pi _{ij} \varDelta +o(\varDelta ) \right] \right) \left( \sum _{n=1}^{S_2 } \left[ 1+\pi _{mn} \varDelta \right. \right. \right. \\&\quad \left. \left. \left. \left. \left. \left. +\,\,o(\varDelta ) \right] \right) {\tilde{P}}(n,j) \right] {\tilde{x}}(t+\varDelta )\right. \right. -{\tilde{x}}^{\mathrm{T}}(t){\tilde{P}}(n,i){\tilde{x}}(t) \right\} \\&\quad =2{\tilde{x}}^{\mathrm{T}}(t){\tilde{P}}(m,i)\dot{{\tilde{x}}}(t)\\&\qquad +\,\,{\tilde{x}}^{\mathrm{T}}(t)\left[ \sum _{j=1}^{S_2 } {\pi _{ij} {\tilde{P}}(m,j)}+\sum _{n=1}^{S_1 } {\pi _{mn} {\tilde{P}}(n,i)} \right] {\tilde{x}}(t) \\&\quad =2{\tilde{x}}^{\mathrm{T}}(t){\tilde{P}}(m,i)\left[ \hat{{A}}(m){\tilde{x}}(t)\right. \\&\qquad \left. +\,\,\hat{{A}}_\tau (m){\tilde{x}}(t-\tau (i))+\hat{{B}}_d (m)d(t) \right] \\&\qquad +\,\,{\tilde{x}}^{\mathrm{T}}(t)\left[ \sum _{j=1}^{S_2 } {\pi _{ij} {\tilde{P}}(m,j)}+\sum _{n=1}^{S_1 } {\pi _{mn} {\tilde{P}}(n,i)} \right] {\tilde{x}}(t), \end{aligned}$$
$$\begin{aligned}&\mathfrak {I}V_2 \left[ {{\tilde{x}}(t),m,i} \right] \\&\quad =\mathop {\lim }\limits _{\Delta \rightarrow 0} \frac{1}{\varDelta }\mathbf{E }\left\{ \int _{t+\varDelta -\tau \left( {t+\varDelta ,i_{t+\varDelta } } \right) }^{t+\varDelta } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \right. \\&\qquad \left. -\,\,\int _{t-\tau (i)}^{t+\Delta } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \right\} \\&\quad =\mathop {\lim }\limits _{\varDelta \rightarrow 0} \frac{1}{\varDelta }\left[ \int _{t+\varDelta -\tau (i)}^{t+\varDelta } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho }\right. \\&\qquad \left. +\,\,\sum _{j=1}^{L_2 } {\left( {\pi _{ij} \varDelta +o(\varDelta )} \right) \int _{t+\varDelta -\tau (j)}^{t+\varDelta } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } } \right. \\&\qquad \left. -\,\,\int _{t-\tau (i)}^{t+\varDelta } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \right] \\&\quad =\mathop {\lim }\limits _{\varDelta \rightarrow 0} \frac{1}{\varDelta }\left[ \int _{t+\varDelta -\tau (i)}^{t-\tau (i)} {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho }\right. \\&\qquad \left. +\,\,\int _t^{t+\varDelta } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \right] \\&\qquad +\,\sum _{j=1}^{S_2 } {\pi _{ij} \int _{t-\tau (j)}^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } } \\&\quad ={\tilde{x}}^{\mathrm{T}}(t){\tilde{Q}}{\tilde{x}}(t)\\&\qquad -\,\,\left[ {1-{\dot{\tau }}(i)} \right] {\tilde{x}}^{\mathrm{T}}\left[ {t-\tau (i)} \right] {\tilde{Q}}{\tilde{x}}\left[ {t-\tau (i)} \right] \\&\qquad +\,\,\sum _{j=1}^{S_2 } {\pi _{ij} \int _{t-\tau (j)}^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } } ,\\&\mathfrak {I}V_3 \left[ {{\tilde{x}}(t),m,i} \right] =\pi \left( {\tau _1 -\tau _2 } \right) {\tilde{x}}^{\mathrm{T}}(t){\tilde{Q}}{\tilde{x}}(t)\\&\qquad -\,\,\pi \int _{t-\tau _1 }^{t-\tau _2 } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } . \end{aligned}$$

Considering that \(\pi _{ij} \ge 0\) for \(i\ne j\), and \(\pi _{ii} \le 0\), we have:

$$\begin{aligned} \begin{array}{llll} &{}&{}\mathop \sum \limits _{j=1}^{L_2 } {\pi _{ij} \int _{t-\tau (j)}^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } }\\ &{}&{}\quad =\mathop \sum \limits _{i\ne j} {\pi _{ij} \int _{t-\tau (j)}^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } }\\ &{}&{}\qquad +\,\pi _{ii} \int _{t-\tau (i)}^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \\ &{}&{}\quad \le \sum _{i\ne j} {\pi _{ij} \int _{t-\tau _1 }^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } }\\ &{}&{}\qquad +\,\pi _{ii} \int _{t-\tau _2 }^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \\ &{}&{}\quad =-\,\pi _{ii} \int _{t-\tau _1 }^t {\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho \\ &{}&{}\qquad +\,\pi _{ii} \int _{t-\tau _2 }^t {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \\ &{}&{}\quad =-\,\pi _{ii} \int _{t-\tau _1 }^{t-\tau _2 } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \\ &{}&{}\quad \le \pi \int _{t-\tau _1 }^{t-\tau _2 } {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } \\ \end{array}. \end{aligned}$$

Letting \(d(t)\equiv 0\), we know that \(\mathfrak {I}V\left[ {{\tilde{x}}(t),m,i} \right] <0\) can be derived by:

$$\begin{aligned} \mathfrak {I}V\left[ {{\tilde{x}}(t),m,i} \right] \le \eta ^{\mathrm{T}}(t)\Xi (m,i)\eta (t)<0, \end{aligned}$$

which leads to \(\Xi (m,i)<0\) with \(\eta (t)=\left[ {{\begin{array}{lllll} {{\tilde{x}}^{\mathrm{T}}(t)}&{} {{\tilde{x}}^{\mathrm{T}}(t-\tau (i))} \\ \end{array} }} \right] ^{\mathrm{T}}\).

And there will exist a mode-dependent matrix \(\Delta _{rk} (m,i)>0\), and

$$\begin{aligned} \mathbf{E }\left\{ {\mathfrak {I}V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} \le -\eta ^{\mathrm{T}}(t)\Delta _{rk} (m,i)\eta (t). \end{aligned}$$
(20)

Considering \(\mathfrak {I}V\left[ {{\tilde{x}}(t),m,i} \right] <0\), it yields:

$$\begin{aligned} \begin{array}{lll} \mathbf{E }\left\{ {V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} &{}<\mathbf{E }\left\{ {\left. {V\left[ {{\tilde{x}}(0),m_0 ,i_0 } \right] } \right| _{t=0} } \right\} \\ {} &{}={\tilde{x}}^{\mathrm{T}}(0){\tilde{P}}(m,i){\tilde{x}}(0) \\ &{}\quad +\,\int _{-\tau (i)}^0 {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )}\hbox {d} \rho \\ &{}\quad +\,\pi \int _{-\tau _1 }^{-\tau _2 } {\int _\nu ^0 {{\tilde{x}}^{\mathrm{T}}(\rho ){\tilde{Q}}{\tilde{x}}(\rho )\hbox {d}\rho } } d\nu \\ \end{array}. \end{aligned}$$
(21)

Combining the above relations, we can get:

$$\begin{aligned} \frac{\mathbf{E }\left\{ {\mathfrak {I}V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} }{\mathbf{E }\left\{ {V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} }<\frac{-\eta ^{\mathrm{T}}(t)\Delta _{rk} (m,i)\eta (t)}{\mathbf{E }\left\{ {V\left[ {{\tilde{x}}(0),m_0 ,i_0 } \right] } \right\} }. \end{aligned}$$
(22)

Defining \(\eta _1 =\mathbf{E }\left\| {\eta (t)} \right\| ^{2}\), \(\eta _2 =\mathop {\sup }\nolimits _{\tau _1 \le t\le 0} \mathbf{E }\left\| {{\tilde{x}}(t)} \right\| ^{2}\), \(\lambda _1 =\mathop {\min }\nolimits _{m\in \varUpsilon _1 ,i\in \varUpsilon _2 } \lambda _{\min } \left[ {\varGamma _{rk} (m,i)} \right] \), \(\lambda _2 =\mathop {\max }\nolimits _{m\in \varUpsilon _1 ,i\in \varUpsilon _2 } \lambda _{\max } \left[ {\varGamma _{rk} (m,i)} \right] \), \(\lambda _3 =\lambda _{\max } ({\tilde{Q}})\), it concludes that

$$\begin{aligned}&\eta ^{\mathrm{T}}(t)\Delta _{rk} (m,i)\eta (t)\ge \lambda _1 \eta _1 , \end{aligned}$$
(23)
$$\begin{aligned}&\mathbf{E }\left\{ {V\left[ {{\tilde{x}}(t), m,i} \right] } \right\} <\mathbf{E }\left\{ {\left. {V\left[ {\tilde{x}}(0), m_0 ,i_0 \right] } \right| _{t=0} } \right\} \nonumber \\&\quad \le \left[ {\lambda _2 +\tau _1 \lambda _3 +\pi \left( {\tau _1 -\tau _2 } \right) \lambda _3 } \right] \eta _2 . \end{aligned}$$
(24)

Therefore, there must exist a sufficient small scalar \(\lambda >0\) which satisfies:

$$\begin{aligned}&\frac{\mathbf{E }\left\{ {\mathfrak {I}V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} }{\mathbf{E }\left\{ {V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} } <\frac{-\xi ^{\mathrm{T}}(t)\Delta _{rk} (m,i)\xi (t)}{\mathbf{E }\left\{ {V\left[ {{\tilde{x}}(0),m_0 ,i_0 } \right] } \right\} }\nonumber \\&\quad \le \frac{-\lambda _1 \eta _1 }{\left[ {\lambda _2 +\tau _1 \lambda _3 +\pi \left( {\tau _1 -\tau _2 } \right) \lambda _3 } \right] \eta _2 }\nonumber \\&\quad =-\lambda . \end{aligned}$$
(25)

Since \(\eta _1 >0\), \(\eta _2 >0\), \(\lambda _1>0,\lambda _2>0,\lambda _3>0,\lambda >0\), we can get:

$$\begin{aligned} \mathbf{E }\left\{ {\mathfrak {I}V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} <-\lambda \mathbf{E }\left\{ {V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} . \end{aligned}$$
(26)

Then we have

$$\begin{aligned} \mathbf{E }\left\{ {V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} <-\hbox {e}^{\lambda t}\mathbf{E }\left\{ {V\left[ {{\tilde{x}}(0),m_0 ,i_0 } \right] } \right\} . \end{aligned}$$
(27)

Defining \(\sigma =\left[ {\lambda _2 +\tau _1 \lambda _3 +\pi \left( {\tau _1 -\tau _2 } \right) \lambda _3 } \right] \eta _2 \), \(\lambda _4 =\mathop {\min }\limits _{m\in \varUpsilon _1 ,i\in \varUpsilon _2 } \lambda _{\min } \left[ {{\tilde{P}}(m,i)} \right] \), we obtain:

$$\begin{aligned} \lambda _4 \mathbf{E }\left\{ {{\tilde{x}}^{\mathrm{T}}(t){\tilde{x}}(t)} \right\} \le \mathbf{E }\left\{ {V\left[ {{\tilde{x}}(t),m,i} \right] } \right\} \le \sigma \hbox {e}^{-\lambda t}. \end{aligned}$$
(28)

Taking limit as \(T\rightarrow \infty \), it concludes that:

$$\begin{aligned}&\mathop {\lim }\limits _{T\rightarrow \infty } \mathbf{E }\left\{ {\int _0^T {\left. {{\tilde{x}}^{\mathrm{T}}(t){\tilde{x}}(t)\hbox {d}t} \right| {\tilde{x}}(0),m_0 ,i_0 } } \right\} \nonumber \\&\quad \le \mathop {\lim }\limits _{T\rightarrow \infty } \frac{\sigma }{\lambda \cdot \lambda _4 }\left( {1-\hbox {e}^{-\lambda T}} \right) =\frac{\sigma }{\lambda \cdot \lambda _4 }<\infty . \end{aligned}$$
(29)

Back to Definition 1, we get that the resulting TSF-MJSs (14) is SS. We can also derive that it is almost asymptotically stable by the main results of Feng et al. [11]. This completes the proof. \(\square \)

To obtain the FDF, the main problem can be considered to design the fuzzy filter \(A_{Fr} (m,i)\), \(B_{Fr} (m,i)\), \(C_{Fr} (m,i)\), \(D_{Fr} (m,i)\), \(m\in \varUpsilon _1 \), \(i\in \varUpsilon _2 \), such that the resulting TSF-MJSs (14) with \(w(t)\in L_2 \) is stochastically stable (i.e., almost surely stable) and satisfies a prescribed \(H_{\infty }\) index with \(\left\| {g(t)} \right\| _{2,\mathbf{E }} \le \gamma \left\| {w(t)} \right\| _2 \) under zero-initial conditions.

Theorem 2

The resulting TSF-MJSs (14) is SS, i.e., almost asymptotically stable and satisfies the given \(H_{\infty }\) index level with \(\gamma >0\), if there exist \(P(m,i)>0\), matrices \(Q_{11} >0\), \(Q_{22} >0\), \(Q_{33} >0\), matrices \(X_r (m,i)\), \(Y_r (m,i)\),\(C_{Fr} (m,i)\), \(D_{Fr} (m,i)\), \(Q_{12} \), \(Q_{13} \), \(Q_{23} \), and scalars \(\tau _1 >0\), \(\tau _2 >0\) and \(\tau _{3i} >0\), LMIs (30)–(31) hold for all \(m,n\in \varUpsilon _1 \), \(i,j\in \varUpsilon _2 \), and \(r,k=1,2,\ldots ,L\),

$$\begin{aligned}&\Omega _{rr} (m,i)<0,r=1,2,\ldots ,L \end{aligned}$$
(30)
$$\begin{aligned}&\Omega _{rk} (m,i)+\Omega _{kr} (m,i)<0,r<k,r,k=1,2,\ldots ,L\nonumber \\ \end{aligned}$$
(31)

where \(\Omega _{rk} (m,i)=\left[ {\Omega _{rk} (m,i)} \right] _{10\times 10} \), with

$$\begin{aligned} \Omega _{11rk}= & {} A_r^\mathrm{T} (m)P(m,i)+P(m,i)A_r (m)\\&+\,\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{11} \\&+\,\sum _{n=1}^{S_1 } {\pi _{mn} P(n,i)} +\sum _{j=1}^{S_2 } {\pi _{ij} P(m,j)} , \\ \Omega _{21rk}= & {} P(m,i)A_r (m)-X_r (m,i)\\&-\,Y_r (m,i)C_k (m)+\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{21} , \\ \Omega _{13rk}= & {} \left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{13} ,\\ \Omega _{14rk}= & {} P(m,i)A_{\tau r} (m), \\ \Omega _{17rk}= & {} P(m,i)B_r (m),\\ \Omega _{18rk}= & {} P(m,i)B_{dr} (m),\\ \Omega _{19rk}= & {} P(m,i)B_{fr} (m),\\ \Omega _{110rk}= & {} C_{Fr}^\mathrm{T} (m,i)+C_k^\mathrm{T} (m,i)D_{Fr}^\mathrm{T} (m,i),\\ \Omega _{22rk}= & {} X_r^\mathrm{T} (m,i)+X_r (m,i)\\&+\,\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{22}\\&+\,\sum _{n=1}^{S_1 } {\pi _{mn} P(n,i)} +\sum _{j=1}^{S_2 } {\pi _{ij} P(m,j)} , \end{aligned}$$
$$\begin{aligned} \Omega _{23rk}= & {} \left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{23} ,\\ \Omega _{24rk}= & {} -Y_r (m,i)C_{\tau k} (m),\\ \Omega _{28rk}= & {} -Y_r (m,i)D_{dk} (m),\\ \Omega _{29rk}= & {} -Y_r (m,i)D_{fk} (m),\\ \Omega _{210rk}= & {} -C_{Fr}^\mathrm{T} (m,i),\\ \Omega _{33rk}= & {} P(m,i)A_W +A_W^\mathrm{T} P(m,i)\\&+\,\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{33}\\&+\sum _{n=1}^{S_1 } {\pi _{mn} P(n,i)} +\sum _{j=1}^{S_2 } {\pi _{ij}P(m,j)} ,\\ \Omega _{39rk}= & {} P(m,i)B_W ,\\ \Omega _{310rk}= & {} C_W^\mathrm{T} ,\\ \Omega _{44rk}= & {} -\left( {1-\tau _{3i} } \right) Q_{11} ,\\ \Omega _{45rk}= & {} -\left( {1-\tau _{3i} } \right) Q_{12} ,\\ \Omega _{46rk}= & {} -\left( {1-\tau _{3i} } \right) Q_{13} ,\\ \Omega _{410rk}= & {} C_{\tau k}^\mathrm{T} (m,i)D_{Fr}^\mathrm{T} (m,i),\\ \Omega _{55rk}= & {} -\left( {1-\tau _{3i} } \right) Q_{22} ,\\ \Omega _{56rk}= & {} -\left( {1-\tau _{3i} } \right) Q_{23} ,\\ \Omega _{66rk}= & {} -\left( {1-\tau _{3i} } \right) Q_{33} ,\\ \Omega _{77rk}= & {} -\gamma ^{2}I,\\ \Omega _{88rk}= & {} -\gamma ^{2}I,\\ \Omega _{99rk}= & {} -\gamma ^{2}I,\\ \Omega _{810rk}= & {} D_{dk}^\mathrm{T} (m,i)D_{Fr}^\mathrm{T} (m,i),\\ \Omega _{910rk}= & {} D_{fk}^\mathrm{T} (m,i)D_{Fr}^\mathrm{T} (m,i)-D_W^\mathrm{T} ,\\ \Omega _{1010rk}= & {} -I.\\&\pi =\max \left\{ {\left| {\pi _{mm} } \right| ,m\in \varUpsilon _1 }\right\} ,\\&\tau _2 =\min \left\{ {\tau _{2i} ,i\in \varUpsilon _2 } \right\} , \quad \tau _1 =\max \left\{ {\tau _{2i} ,i\in \varUpsilon _2 } \right\} . \end{aligned}$$

Moreover, the fuzzy FDF parameters can be obtained by:

$$\begin{aligned} \left\{ {\begin{array}{l} A_{Fr} (m,i)=P^{-1}(m,i)X_r (m,i),\\ B_{Fr} (m,i)=P^{-1}(m,i)Y_r (m,i), \\ C_{Fr} (m,i)=C_{Fr} (m,i),D_{Fr} (m,i)=D_{Fr} (m,i). \end{array}} \right. \end{aligned}$$
(32)

Proof

We set the following performance index for \(T>0\):

$$\begin{aligned} J(T)=\mathbf{E }\left\{ {\int _0^T {g^{\mathrm{T}}(t)g(t)dt} -\gamma ^{2}\int _0^T {w(t)w(t)\hbox {d}t} } \right\} . \end{aligned}$$

Under the zero-initial condition, we have:

$$\begin{aligned} \begin{array}{llllll} J(T)&{}=&{}\mathbf{E }\left\{ \int _0^T {\left[ {g^{\mathrm{T}}(t)g(t)-\gamma ^{2}w(t)w(t)} \right] } \hbox {d}t\right. \\ &{}&{}\left. +\,V\left[ {{\tilde{x}}(t),m,i} \right] \right\} -EV\left[ {{\tilde{x}}(t),m,i} \right] \\ &{}=&{}\mathbf{E }\Big \{ \int _0^T \Big [ g^{\mathrm{T}}(t)g(t)-\gamma ^{2}w(t)w(t)\\ &{}&{}+\,\mathfrak {I}V\Big [ {{\tilde{x}}(t),m,i} \Big ] \Big ] \hbox {d}t \Big \}-EV\Big [ {{\tilde{x}}(t),m,i} \Big ] \\ &{}<&{}\mathbf{E }\left\{ {\int _0^T {\beta ^{\mathrm{T}}(t)\left[ {X_{rk} (m,i)+Y_{kr} (m,i)} \right] \beta (t)\hbox {d}t} } \right\} \\ \end{array}. \end{aligned}$$

where,

$$\begin{aligned}&\beta (t)=\left[ {{\begin{array}{lllll} {{\tilde{x}}(t)} \\ {{\tilde{x}}_\tau (t-\tau (i))} \\ {w(t)} \\ \end{array} }} \right] , \\&X_{rk} (m,i)=\left[ {{\begin{array}{lllll} {\Xi _{rk} (m,i)}&{}\quad {{\tilde{P}}(m,i)\hat{{A}}_{\tau rk} (m)}&{}\quad {{\tilde{P}}(m,i)\hat{{B}}_{rk} (m)} \\ {*}&{}\quad {-\left( {1-\tau _{3i} } \right) {\tilde{Q}}}&{}\quad 0 \\ {*}&{}\quad {*}&{}\quad {-\gamma ^{2}I} \\ \end{array} }} \right] , \\&Y_{rk} (m,i)=\left[ {{\begin{array}{lllll} {\hat{{C}}_{rk}^\mathrm{T} (m)} \\ {\hat{{C}}_{\tau rk}^\mathrm{T} (m)} \\ {\hat{{D}}_{rk}^\mathrm{T} (m)} \\ \end{array} }} \right] \left[ {{\begin{array}{lllll} {\hat{{C}}_{rk} (m)}&{}\quad {\hat{{C}}_{\tau rk} (m)}&{}\quad {\hat{{D}}_{rk} (m)} \\ \end{array} }} \right] . \end{aligned}$$

As \(T\rightarrow \infty \), we know that \(J(T)<0\) if \(X_{rk} (m,i)+Y_{rk} (m,i)<0\) holds. According to Schur complements, \(X_{rk} (m,i)+Y_{rk} (m,i)<0\) equals to:

$$\begin{aligned} \Sigma (m,i)=\left[ {{\begin{array}{lllll} {\Xi _{rk} (m,i)}&{}\quad {{\tilde{P}}(m,i)\hat{{A}}_{\tau rk} (m)}&{}\quad {{\tilde{P}}(m,i)\hat{{B}}_{rk} (m)}&{}\quad {\hat{{C}}_{rk}^\mathrm{T} (m)} \\ {*}&{} \quad {-\left( {1-\tau _{3i} } \right) {\tilde{Q}}}&{}\quad 0&{}\quad {\hat{{C}}_{\tau rk}^\mathrm{T} (m)} \\ {*}&{}\quad {*}&{}\quad {-\gamma ^{2}I}&{}\quad {\hat{{D}}_{rk}^\mathrm{T} (m)} \\ {*}&{}\quad {*}&{}\quad {*}&{}\quad {-I} \\ \end{array} }} \right] <0.\nonumber \\ \end{aligned}$$
(33)

We can choose , \({\tilde{Q}}=\left[ {{\begin{array}{lll} {Q_{11} }&{}\quad {Q_{12} }&{}\quad {Q_{13} } \\ {*}&{}\quad {Q_{22} }&{}\quad {Q_{23} } \\ *&{}\quad *&{} \quad {Q_{33} } \\ \end{array} }} \right] \). Then, we obtain the following relation by inequality (33):

$$\begin{aligned} \sum \limits _{r=1}^L {h_r } \sum \limits _{k=1}^L {h_k} \varPsi (m,i)<0 \end{aligned}$$
(34)

where

$$\begin{aligned}&\varPsi (m,i)=\left[ {{\begin{array}{lll} {\varPsi _{1rk} (m,i)}&{}\quad {\varPsi _{2rk} (m,i)}&{}\quad {\varPsi _{3rk} (m,i)} \\ *&{}\quad {\varPsi _{4rk} (m,i)}&{}\quad {\varPsi _{5rk} (m,i)} \\ *&{}\quad *&{}\quad {\varPsi _{6rk} (m,i)} \\ \end{array} }} \right] , \\&\varPsi _{1rk} (m,i)=\left[ {{\begin{array}{lll} {\Omega _{11rk} }&{}\quad *&{}\quad {\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{13} } \\ {\varPsi _{21rk} }&{}\quad {\varPsi _{22rk} }&{}\quad {\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{23} } \\ *&{}\quad *&{}\quad {\Omega _{33rk} } \\ \end{array} }} \right] , \\&\varPsi _{2rk} (m,i)=\left[ {{\begin{array}{lll} {P(m,i)A_{\tau r} (m)}&{}\quad 0&{}\quad 0 \\ {-P(m,i)B_{Fr} (m,i)C_{\tau k} (m)}&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] , \end{aligned}$$
$$\begin{aligned} \varPsi _{3rk} (m,i)= & {} \left[ {{\begin{array}{llll} {P(m,i)B_r (m)}&{}\quad {P(m,i)B_{dr} (m)}&{}\quad {P(m,i)B_{fr} (m)}&{}\quad {C_{Fr}^\mathrm{T} (m,i)+C_k^\mathrm{T} (m,i)D_{Fr}^\mathrm{T} (m,i)} \\ 0&{}\quad {-P(m,i)B_{Fr} (m,i)D_{dk} (m)}&{}\quad {-P(m,i)B_{Fr} (m,i)D_{fk} (m)}&{}\quad {-C_{Fr}^\mathrm{T} (m,i)} \\ 0&{}\quad 0&{}\quad {P(m,i)B_W }&{}\quad {C_W^\mathrm{T} } \\ \end{array} }} \right] ,\\ \varPsi _{4rk} (m,i)= & {} -\left( {1-\tau _{3i} } \right) \left[ {{\begin{array}{lll} {Q_{11} }&{}\quad {Q_{12} }&{}\quad {Q_{13} } \\ {*}&{}\quad {Q_{22} }&{}\quad {Q_{23} } \\ *&{}\quad *&{}\quad {Q_{33} } \\ \end{array} }} \right] , \\ \varPsi _{5rk} (m,i)= & {} \left[ {\mathrm{O}_{3\times 3} \vdots {\begin{array}{c} {C_{\tau k}^\mathrm{T} (m,i)D_{Fr}^\mathrm{T} (m,i)} \\ 0 \\ 0 \\ \end{array} }} \right] , \\ \varPsi _{6rk} (m,i)= & {} \left[ {{\begin{array}{lllll} {-\gamma ^{2}I}&{}\quad 0&{}\quad 0&{}\quad 0 \\ {*}&{}\quad {-\gamma ^{2}I}&{}\quad 0&{}\quad {D_{dk}^\mathrm{T} (m,i)D_{Fr}^\mathrm{T} (m,i)} \\ {*}&{}\quad {*}&{}\quad {-\gamma ^{2}I}&{}\quad {D_{fk}^\mathrm{T} (m,i)D_{Fr}^\mathrm{T} (m,i)-D_W^\mathrm{T} } \\ {*}&{}\quad {*}&{}\quad {*}&{}\quad {-I} \\ \end{array} }} \right] , \end{aligned}$$

with

$$\begin{aligned} \varPsi _{21rk}= & {} P(m,i)A_r (m)-P(m,i)A_{Fr} (m,i)\\&-\,P(m,i)B_{Fr} (m,i)C_k (m)\\&+\,\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{21} , \\ \varPsi _{22rk}= & {} A_{Fr}^\mathrm{T} (m,i)P(m,i)+P(m,i)A_{Fr} (m,i)\\&+\,\left[ {1+\pi \left( {\tau _1 -\tau _2 } \right) } \right] Q_{22}\\&+\,\sum _{n=1}^{S_1 } {\pi _{mn} P(n,i)} +\sum _{j=1}^{S_2 } {\pi _{ij} P(m,j)} . \end{aligned}$$

Using Schur complements and letting \(X_r (m,i)=P(m,i)A_{Fr} (m,i)\), \(Y_r (m,i)=P(m,i)B_{Fr} (m,i)\), we know that inequality (34) is equivalent to the relation as follows:

$$\begin{aligned}&\mathop \sum \limits _{r=1}^L {h_r^2 } \Omega _{ii} (m,i)\nonumber \\&\quad +\,\mathop \sum \limits _{r=1}^L {h_r } \left\{ {\sum _{k=1}^L {h_k } \left[ {\Omega _{rk} (m,i)+\Omega _{kr} (m,i)} \right] } \right\} \nonumber \\&\quad <0. \end{aligned}$$
(35)

It easily leads to LMIs (30)–(31). By Theorem 1, it is derived that the resulting TSF-MJSs (14) is SS and satisfies \(\left\| {g(t)} \right\| _{2,\mathbf{E }} <\gamma \left\| {w(t)} \right\| _2 \). This completes the proof. \(\square \)

Remark 2

By selecting an appropriate LKF, we get the mode-dependent sufficient conditions in Theorems 1 and 2. According to LMIs (29)–(31), we should determine \(\tau _1 =\max \left\{ {\tau _{1i} } \right\} \), \(\tau _2 =\min \left\{ {\tau _{2i} } \right\} \) and \(\tau _{3i} \), where \(i=i_t \in \varUpsilon _2 =\left\{ {1,2,\ldots ,L_2 } \right\} \). The values \(\tau _1 \), \(\tau _2 \) and \(\tau _{3i} \) are related to the mode-dependent delay \(i_t \). Meanwhile, we also choose the positive-definite matrix P(m, i) and the fuzzy FDF gains \(X_r (m,i)\), \(Y_r (m,i)\), \(C_{Fr} (m,i)\), \(D_{Fr} (m,i)\) as mode-dependent, which are driven by the random processes \(\left\{ {m_t ,t\ge 0} \right\} \) and \(\left\{ {i_t ,t\ge 0} \right\} \).

Corollary 1

To obtain an optimization fuzzy FDF formulation against external disturbance, time-varying delays, nonlinearities and faults, the attenuation index \(\gamma \) can be derived to the following optimization problem satisfying LMIs (30)–(31):

$$\begin{aligned} \begin{array}{l} \mathop {\mathrm{min}}\limits _{P(m,i),X_r (m,i),Y_r (m,i),C_{Fr} (m,i),D_{Fr} (m,i),Q,\chi } \chi \\ \mathrm{s.t.\;LMIs\;(30){-}(31)\;with\;}\chi =\gamma ^{2} \\ \end{array}. \end{aligned}$$
(36)

To describe the efficiency of the designed approach, we give a two-dimension and two-mode stochastic MJSs with varying and mode-dependent time-delays. Recalling to the main results in LMIs (30)–(31), we should choose the initial values. Applying MATLAB LMI Toolbox, we can straightforwardly solve LMIs (30)–(31). To prove the feasibility of the designed approaches, we give a simulation example in the next Section.

4 Numeral example

Considering a two-dimension and two-mode TSF-MJSs with parameters described by:

$$\begin{aligned}&A_1 \left( 1 \right) =\left[ {{\begin{array}{cc} {-\,0.3}&{}\quad {0.2} \\ {0.1}&{}\quad {-\,0.4} \\ \end{array} }} \right] , \\&A_{\tau 1} \left( 1 \right) =\left[ {{\begin{array}{cc} {-\,0.1}&{}\quad {-\,0.1} \\ 0&{}\quad {-\,0.1} \\ \end{array} }} \right] , \\&A_2 \left( 1 \right) =\left[ {{\begin{array}{cc} {-\,0.3}&{}\quad {0.5} \\ {0.1}&{}\quad {-\,1} \\ \end{array} }} \right] , \\&A_{\tau 2} \left( 1 \right) =\left[ {{\begin{array}{cc} {-0.05}&{}\quad {-0.1} \\ 0&{}\quad {0.05} \\ \end{array} }} \right] , \\&A_1 \left( 2 \right) =\left[ {{\begin{array}{cc} {-\,0.3}&{}\quad {-\,0.4} \\ {-\,0.1}&{}\quad {-\,1} \\ \end{array} }} \right] , \\&A_{\tau 1} \left( 2 \right) =\left[ {{\begin{array}{cc} 0&{}\quad {-0.1} \\ {0.1}&{}\quad 0 \\ \end{array} }} \right] , \\&A_2 \left( 2 \right) =\left[ {{\begin{array}{cc} {-\,0.1}&{}\quad {10} \\ {-\,1}&{}\quad {-\,10} \\ \end{array} }} \right] ,\\&A_{\tau 2} \left( 1 \right) =\left[ {{\begin{array}{cc} {0.05}&{} \quad {-\,0.1} \\ 0&{}\quad {0.1} \\ \end{array} }} \right] , \\&B_{r} (m)=\left[ {{\begin{array}{c} {0.8} \\ {1.2} \\ \end{array} }} \right] , \\&B_{dr} (m)=\left[ {{\begin{array}{c} {0.1} \\ {0.1} \\ \end{array} }} \right] , \\&B_{fr} (m)=\left[ {{\begin{array}{c} {-0.2} \\ {0.1} \\ \end{array} }} \right] , \\&C_r (m)=\left[ {{\begin{array}{cc} {0.2}&{}\quad {0.1} \\ \end{array} }} \right] , \\&C_{\tau r} (m)=\left[ {{\begin{array}{cc} {-0.1}&{} \quad {0.1} \\ \end{array} }} \right] , \\&D_{dr} (m)=0.5, \\&D_{fr} (m)=1.5. \end{aligned}$$

The transition rate matrices related to the two operation modes are shown as \(\varLambda _1 =\left[ {{\begin{array}{cc} {-0.3}&{} \quad {0.3} \\ {0.2}&{}\quad {-0.2} \\ \end{array} }} \right] \) and \(\varLambda _2 =\left[ {{\begin{array}{cc} {-0.4}&{} \quad {0.4} \\ {0.6}&{} \quad {-0.6} \\ \end{array} }} \right] \). Give the following state-space realization of the weighting function \(W_f (s)\) as:

$$\begin{aligned} A_W= & {} \left[ {{\begin{array}{cc} {-0.8}&{} \quad 0 \\ 0&{}\quad {-0.6} \\ \end{array} }} \right] , \\ B_W= & {} \left[ {{\begin{array}{c} {0.1} \\ {0.2} \\ \end{array} }} \right] , \\ C_W= & {} \left[ {{\begin{array}{cc} {0.4}&{} \quad {0.3} \\ \end{array} }} \right] , \\ D_W= & {} 0.2. \end{aligned}$$
Fig. 1
figure 1

Bound-limited random noise d(t)

Full size image
Fig. 2
figure 2

Residual signal g(t)

Full size image
Fig. 3
figure 3

Residual evaluation response f(g)

Full size image

In this simulation, we give the initial values as \(\tau _1 =0.8\), \(\tau _2 =0.3\), \(\tau _{31} =0.4\), \(\tau _{32} =0.7\). Solving LMIs (30, 31), the optimization level can be derived as \(\gamma _{\min } =1.4749\). The relevant TSF-FDF dynamic is obtained as follows:

$$\begin{aligned} A_{F1} (1,1)= & {} \left[ {{\begin{array}{cc} {-\,0.4706}&{}\quad {0.0764} \\ {0.0596}&{}\quad {-\,0.4434} \\ \end{array} }} \right] , \\ B_{F1} (1,1)= & {} \left[ {{\begin{array}{c} {0.7040} \\ {0.1833} \\ \end{array} }} \right] , \\ C_{F1} (1,1)= & {} \left[ {{\begin{array}{cc} {-\,0.0106}&{} \quad {-0.0076} \\ \end{array} }} \right] , \\ D_{F1} (1,1)= & {} 0.0401; \\ A_{F1} (1,2)= & {} \left[ {{\begin{array}{cc} {-\,0.4270}&{}\quad {0.0883} \\ {0.0175}&{}\quad {-\,0.4957} \\ \end{array} }} \right] , \\ B_{F1} (1,2)= & {} \left[ {{\begin{array}{c} {0.4259} \\ {0.2978} \\ \end{array} }} \right] , \\ C_{F1} (1,2)= & {} \left[ {{\begin{array}{cc} {-\,0.0086}&{} \quad {-0.0073} \\ \end{array} }} \right] , \\ D_{F1} (1,2)= & {} 0.0256; \\ A_{F1} (2,1)= & {} \left[ {{\begin{array}{cc} {-0.3658}&{}\quad {-0.6126} \\ {-0.5791}&{}\quad {-2.7647} \\ \end{array} }} \right] , \\ B_{F1} (2,1)= & {} \left[ {{\begin{array}{c} {0.0286} \\ {-\,0.0920} \\ \end{array} }} \right] , \\ C_{F1} (2,1)= & {} \left[ {{\begin{array}{cc} {-\,0.0038}&{}\quad {0.0020} \\ \end{array} }} \right] , \\ D_{F1} (2,1)= & {} 0.0278; \\ A_{F1} (2,2)= & {} \left[ {{\begin{array}{cc} {-0.8038}&{}\quad {-\,0.5018} \\ {0.1618}&{}\quad {-\,2.3777} \\ \end{array} }} \right] , \\ B_{F1} (2,2)= & {} \left[ {{\begin{array}{c} {2.6915} \\ {-\,3.0573} \\ \end{array} }} \right] , \\ C_{F1} (2,2)= & {} \left[ {{\begin{array}{cc} {-0.0118}&{}\quad {0.0028} \\ \end{array} }} \right] , \\ D_{F1} (2,2)= & {} 0.0840; \end{aligned}$$
$$\begin{aligned} A_{F2} (1,1)= & {} \left[ {{\begin{array}{cc} {-\,0.3996}&{}\quad {1.1487} \\ {0.0184}&{}\quad {-\,2.3124} \\ \end{array} }} \right] , \\ B_{F2} (1,1)= & {} \left[ {{\begin{array}{c} {0.5656} \\ {0.0601} \\ \end{array} }} \right] , \\ C_{F2} (1,1)= & {} \left[ {{\begin{array}{cc} {-0.0042}&{}\quad {-0.0021} \\ \end{array} }} \right] , \\ D_{F2} (1,1)= & {} 0.0182; \\ A_{F2} (1,2)= & {} \left[ {{\begin{array}{cc} {-\,0.4086}&{} \quad {1.1841} \\ {0.0402}&{} \quad {-\,2.3695} \\ \end{array} }} \right] , \\ B_{F2} (1,2)= & {} \left[ {{\begin{array}{c} {0.2500} \\ {0.1375} \\ \end{array} }} \right] , \\ C_{F2} (1,2)= & {} \left[ {{\begin{array}{cc} {-\,0.0054}&{} \quad {-\,0.0039} \\ \end{array} }} \right] , \\ D_{F2} (1,2)= & {} 0.0256; \\ A_{F2} (2,1)= & {} \left[ {{\begin{array}{cc} {-\,1.1645}&{} \quad {16.8291} \\ {-\,0.5676}&{} \quad {-\,20.5278} \\ \end{array} }} \right] , \\ B_{F2} (2,1)= & {} \left[ {{\begin{array}{c} {0.2020} \\ {0.0757} \\ \end{array} }} \right] , \\ C_{F2} (2,1)= & {} \left[ {{\begin{array}{cc} {-\,0.0060}&{} \quad {-\,0.0051} \\ \end{array} }} \right] , \\ D_{F2} (2,1)= & {} 0.0330; \\ A_{F2} (2,2)= & {} \left[ {{\begin{array}{cc} {-\,1.2270}&{} \quad {20.2688} \\ {0.8656}&{} \quad {-\,27.2868} \\ \end{array} }} \right] , \\ B_{F2} (2,2)= & {} \left[ {{\begin{array}{c} {-\,1.0432} \\ {2.0936} \\ \end{array} }} \right] , \\ C_{F2} (2,2)= & {} \left[ {{\begin{array}{cc} {-\,0.0066}&{} \quad {-\,0.0116} \\ \end{array} }} \right] , \\ D_{F2} (2,2)= & {} 0.0450. \end{aligned}$$

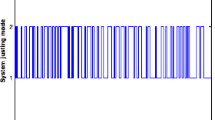
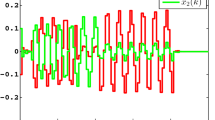
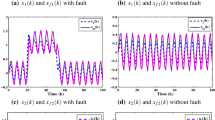
To show the feasibility of the designed TSF-FDF, we suppose that the external disturbance d(t) is a \([-0.5 0.5]\)-bound-limited random noise. The fault f(t) is chosen as a step square wave which occurs from 9s to 15s with positive unit amplitude. The external disturbance d(t), the residual response g(t) and the residual evaluation response f(g) are illustrated in Figs. 1, 2 and 3.

Figure 3 shows the residual evaluation response f(g) with respect to fault case and fault-free case. From the residual evaluation response, we select the threshold as \(J_{th} =\mathop {\sup }\nolimits _{d(t)\in L_2 ,f(t)=0} \mathbf{E }\left\{ {\int _0^{20} {g^{\mathrm{T}}(t)g(t)\hbox {d}t} } \right\} =2.42\). It is shown from Fig. 3 that \(f(g)=\mathbf{E }\left\{ {\int _0^{9.96} {g^{\mathrm{T}}(t)g(t){d}t} } \right\} =2.44>J_{th} \). Therefore, we can detect the appeared fault within 1.0s after its occurrence.

Remark 3

To prove the efficiency of the designed approach, we give a two-dimension and two-mode MJSs with varying and mode-dependent time-delays. Recalling to the main results in LMIs (29)–(31), we choose the values \(\tau _1 , \tau _2 \) and \(\tau _{3i} \) related to the mode-dependent delay \(i_t \) as \(\tau _1 =0.8, \tau _2 =0.3,\tau _{31} =0.4, \tau _{32} =0.7\). For the MJSs containing mode-independent time-delays, the interested readers can see [28, 29, 33, 42].

Remark 4

It is observed that the novelty in our study relates to nonlinearities and mode-dependent time-delays existing in MJSs. By using the designed algorithms, it is seen that the appeared faults can be detected within 1.0s by the designed fuzzy FDF. By means of \(H_{\infty }\)-filtering formulation and LMIs techniques, Zhong et. al. [21, 26], respectively, studied the FDF design problems for uncertain LTI systems and linear MJSs. The main results in our study show more applicable advantages in time-varying and mode-dependent delayed systems. Moreover, it will be an important improvement in the research of TSF systems. It should point out that if the time-delays are constant or without delays, the main conclusions in this paper can be derived to the general results published in [21, 26, 29, 33].

5 Conclusion

The \(H_{\infty }\) filtering-based FDF designed problems for nonlinear MJSs with varying and mode-dependent time-delays have been researched. Applying the LKF techniques and LMIs algorithms, sufficient conditions are obtained such that the resulting TSF-MJSs is SS and the derived fuzzy FDF are presented and proved. A simulation example has been obtained to show the feasibility of the presented methods.