Fault Detection Finite-Time Filter Design for T–S Fuzzy Markovian Jump System with Missing Measurements

Abstract

The primary purpose of this work was to address the problem of finite-time fault detection filtering for a class of discrete-time Takagi–Sugeno (T–S) fuzzy Markovian jump systems subject to randomly occurring uncertainties, time-varying delay, missing measurements and partly unknown transition probability matrices. Precisely the missing measurement phenomenon in the network environment satisfies the Bernoulli distributed white noise sequences. Firstly a fuzzy rule-dependent filter is constructed for estimating the unmeasured states of the system and the corresponding fault detection problem. Further, based on the filtering problem, the error between residual and fault is minimized with the prescribed strict $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipativity performance. Secondly, the sufficient criteria are derived to ensure the filtering error system to be finite-time stochastic bounded. Finally, the applicability and usefulness of the proposed filter design through two numerical examples are verified.

1 Introduction

Markovian jump systems (MJSs) are a special kind of hybrid and stochastic systems which describe many practical systems such as networked control systems, aerospace systems, communication systems, electrical systems [16, 21, 39, 40, 42]. Precisely, MJSs form a class of multi-model systems, and the Markov process governs the transition probability among the modes. In general, the transition probability of MJSs can be described by time-dependent polytope set when the transition rates are not exactly known. Many beneficial works on control and filtering for MJSs are available in the recent literature [3, 17, 19, 24, 29, 31]. In [24], the authors investigated the asynchronous sliding mode control problem for a class of discrete-time MJSs with time-varying delays based on partly accessible mode detection probabilities. In many practical applications, the system of state variables is not always accessible by direct measurements, so it is necessary to estimate the states of a dynamical system through available measurements. For instance, the class of discrete time-varying systems addresses the effects of missing measurements, signal quantization and non-Gaussian disturbances in [29]. Recently, numerous results for the filtering problem of MJSs have been investigated, for example, [1, 2, 8, 12, 15, 20, 33,34,35,36, 44]. In [8], the mode-dependent filtering has been studied for a class of nonhomogeneous MJSs with dual-layer operation modes.

In another research direction, a T–S fuzzy model is a useful tool for describing nonlinear dynamical systems having any degree of accuracy. Significantly, the T–S fuzzy-based model estimates a nonlinear system wherein IF-THEN rules denote the input–output relationship of the system. As a result, most of the literature illustrates the importance of T–S fuzzy systems [4, 5, 14, 22, 28, 30, 38, 43]. The authors in [38] obtained sufficient conditions in terms of linear matrix inequalities (LMIs) to ensure the exponential stability of the discrete-time T–S fuzzy switched systems with time-varying delay and packet dropouts. In [43], for a class of switched T–S fuzzy systems, the mixed $H_\infty$ and passivity-based filtering problem has been studied with average dwell time approach. Although T–S fuzzy systems with Markovian jumping parameters have great potential applications in a variety of areas, there has been almost no existing literature on the fault-detection filtering problem for T–S fuzzy MJSs with missing measurements, and the purpose of this paper is to fill the gap.

On the other hand, in many real-time systems, faults may occur due to parameter shifting, component failures, sudden environmental changes, etc. The presence of faults may often lead to poor performance degradation or even loss of stability. To ensure higher performance and reliability of systems and maintain higher safety, the faults need to be detected and identified as quickly as possible. Based on this circumstance, many significant results have been reported regarding fault detection filter design problem [7, 9, 13, 27, 32, 41]. In [7], for nonhomogeneous MJSs, the fault detection filtering problem is addressed via T–S fuzzy techniques. However, most of the works mentioned above regarding the fault detection filtering problem of T–S fuzzy MJSs have focused only on the behavior over an infinite time interval. Based on this phenomenon, for various discrete-time systems, a huge number of results on finite-time fault detection filtering problem have been proposed; for instance; see [6, 10, 11, 18, 23, 25, 26, 37, 45]. In [10], for discrete-time interconnected systems, the finite-time fault detection filter design with average dwell time is investigated. To the best of our observation, however, the finite-time fault detection filtering problem for a class of discrete-time T–S fuzzy-based MJSs is not yet completely examined.

Inspired by the above discussion, in this paper, we focus on the finite-time fault detection filtering problem for a class of discrete-time T–S fuzzy MJSs subject to missing measurements, time-varying delay and randomly occurring uncertainties. By constructing Lyapunov–Krasovskii functional and Jensen’s inequality, some sufficient conditions are developed to obtain the finite-time fault detection filter design for the above-mentioned T–S fuzzy MJSs. The main contributions of this paper are presented as follows:

• 1. The problem of finite-time fault detection filter design for T–S fuzzy MJSs with randomly occurring uncertainties, time-varying delay and missing measurements is considered.

• 2. The proposed fuzzy rule-dependent non-fragile filter design is easy to implement since it has a significant amount of parameters that can be easily tuned via a simple algebraic structure.

• 3. The fault detection filtering problem is solved by using a residual signal approach. By comparing the outputs of the filter and fault signal, a residual is generated from which the fault is detected when the obtained residual signal exceeds the threshold value.

Finally, two numerical examples including mass–spring damper model are given to validate the usefulness of the proposed filter design technique.

Notations Throughout this paper, the following notations are used: The subscripts T and $(-1)$ represent the matrix transpose and matrix inverse, respectively. $\mathbf {R}^n$ denotes the n- dimensional Euclidean space. I and 0 stand for the identity and zero matrices respectively. A block-diagonal matrix is notated as $diag\{\cdots \}$. In symmetric block matrix expressions, we use asterisk $(*)$ to specify the terms that are induced by symmetry. Further, $\mathbf {E}\{\centerdot \}$ expresses the mathematical expectation.

2 Problem Formulation and Preliminaries

Let $\{r(k),k\in {\mathscr {Z}}^+\}$ be a Markov chain taking the value in a state-space ${\mathscr {S}}=\{1,2,\ldots ,{\mathscr {M}}\}$ with transition probabilities defined by $\Phi (k)={\phi _{mn}(k)}, \ m,n\in {\mathscr {S}}$, where $\Pr \{r(k+1)=n|r(k)=m\}=\phi _{mn}$ is the transition probabilities from mode m to n at time k and $k+1$ respectively and $\phi _{mn}(k)\ge 0$, $\sum \nolimits _{n=1}^{{\mathscr {M}}}\phi _{mn}(k)=1$ should be satisfied.

Consider a class of discrete-time T–S fuzzy MJSs with randomly occurring uncertainties, time-varying transition probabilities and missing measurements over a probability space $(\Omega ,{\mathscr {F}},\Pr )$ and its dynamics are given as follows:

Plant Rule $\upsilon$: IF $\Theta _1(k)$ is $\mathbb {M}_{\upsilon 1}$, $\Theta _2(k)$ is $\mathbb {M}_{\upsilon 2}, \ldots$, and $\Theta _p(k)$ is $\mathbb {M}_{\upsilon p}$, Then

$$\begin{aligned}&x(k+1)={\mathscr {A}}_{r(k)}^{\upsilon }x(k)+{\mathscr {A}}_{dr(k)}^{\upsilon }x(k-d(k)) +{\mathscr {B}}_{r(k)}^\upsilon u(k) +{\mathscr {E}}_{r(k)}^\upsilon w(k)+ {\mathscr {F}}_{r(k)}^\upsilon f(k), \nonumber \\&y(k)=\rho (k){\mathscr {C}}_{r(k)}^\upsilon x(k)+{\mathscr {C}}_{d r(k)}^\upsilon x(k-d(k)) +{\mathscr {D}}_{r(k)}^\upsilon u(k) +{\mathscr {G}}_{r(k)}^\upsilon w(k)+{\mathscr {H}}_{r(k)}^\upsilon f(k), \end{aligned}$$

(1)

where $\upsilon =1,2,\ldots ,t$, ${\mathscr {A}}_{r(k)}^{\upsilon }=A_{r(k)}^\upsilon +\lambda _1(k) \Delta A_{r(k)}^\upsilon$; ${\mathscr {A}}_{dr(k)}^{\upsilon }=A_{d r(k)}^\upsilon +\lambda _2(k) \Delta A_{d r(k)}^\upsilon (k)$; $x(k)\in \mathbf {R}^n$ is a state vector; $u(k)\in \mathbf {R}^m$ is the control input; $w(k)\in \mathbf {R}^q$ denotes the disturbance input which belongs to $\ell _2[0,\infty );$ $y(k)\in \mathbf {R}^p$ is the measured output; $f(k)\in \mathbf {R}^l$ is a fault to be detected; d(k) is the time-varying function satisfying $1\le d_1\le d(k)\le d_2$, where $d_1$ and $d_2$ are the lower and upper bounds of time-varying delay, respectively. $A_{r(k)}^\upsilon$, $A_{dr(k)}^\upsilon$, ${\mathscr {B}}_{r(k)}^\upsilon$, ${\mathscr {E}}_{r(k)}^\upsilon$, ${\mathscr {F}}_{r(k)}^\upsilon$, ${\mathscr {C}}_{r(k)}^\upsilon$, ${\mathscr {D}}_{r(k)}^\upsilon$, ${\mathscr {G}}_{r(k)}^\upsilon$ and ${\mathscr {H}}_{r(k)}^\upsilon$ are known constant matrices with appropriate dimensions. The uncertainties $\Delta A_{r(k)}^\upsilon (k)$ and $\Delta A_{d r(k)}^\upsilon (k)$ are defined as $[\Delta A_{r(k)}^\upsilon (k) \ \Delta A_{d r(k)}^\upsilon (k) ]=M_{r(k)} F_{r(k)}(k)[N_{r(k)}\ N_{d r(k)}]$, where $M_{r(k)}$, $N_{r(k)}$ and $N_{dr(k)}$ are the known appropriate dimensional matrices; $F_{r(k)}(k)$ is the unknown time-varying matrix function satisfying $F_{r(k)}^T(k)F_{r(k)}(k)\le I$. The stochastic variables $\rho (k)$ and $\lambda _z(k)\ (z=1,2)$ are Bernoulli distributed white noise sequences with $\mathbf{{\Pr }} \{\rho (k)=1\} = \bar{\rho }$ and $\Pr \{\lambda _z(k)=1\}=\bar{\lambda }_z$, where $\bar{\rho }$, $\bar{\lambda }_1$, $\bar{\lambda }_2\in [0,1]$ are known constants. For the sake of convenience, we denote $r(k)=m$.

The stochastic variable $\rho (k)$ is used to represent the phenomena of missing measurements, when $\rho (k)=1$, there is no packet dropout. If $\rho (k)=0$, then the loss of packet dropout may have occurred and it is taken as $\mathbf{E} \{\rho (k)-\bar{\rho }\}=0$, $\mathbf{E}\{|\rho (k)-\bar{\rho }|^2\}=\bar{\rho }(1-\bar{\rho })$. Let $\mathbb {M}_{\upsilon \rho }$ be the fuzzy sets with t number of IF–THEN rules. The premise variable vector is $\Theta (k) = [\Theta _1(k),\Theta _2(k),\ldots ,\ \Theta _{p}(k)]$. The given $\beta _{\upsilon }(\Theta (k))=\frac{\prod _{\rho =1}^{p}\mathbb {M}_{\upsilon \rho }(\Theta _{\upsilon }(k))}{\sum _{\upsilon =1}^{t}\prod _{\rho =1}^{p}\mathbb {M}_{\upsilon \rho }(\Theta _{\upsilon }(k))}\ge 0$ is the fuzzy basis functions with $\mathbb {M}_{\upsilon \rho }(\Theta _{\upsilon }(k))$ representing the grade of membership of $\Theta _{\upsilon }(k)$ in $\mathbb {M}_{\upsilon \rho }\ (\upsilon =1,2,\ldots ,t;\, \rho =1,2,\ldots ,p)$. Moreover we have $\beta _{\upsilon }(\Theta (k))\ge 0$ and $\sum \limits _{\upsilon =1}^{t}\beta _{\upsilon }(\Theta (k))=1$ for all k.

The T–S fuzzy MJSs with missing measurement (1) are formulated as

$$\begin{aligned}&x(k+1)=\sum \limits _{\upsilon =1}^{t} \beta _{\upsilon }(\Theta (k))\bigg [{\mathscr {A}}_{m} ^{\upsilon }x(k)+{\mathscr {A}}^{\upsilon }_{d m}x(k-d(k))+{\mathscr {B}}^{\upsilon }_{m}u(k) +{\mathscr {E}}^{\upsilon }_{m}w(k)+{\mathscr {F}}^{\upsilon }_{m}f(k)\bigg ],\nonumber \\&y(k) =\sum \limits _{\upsilon =1}^{t} \beta _{\upsilon }(\Theta (k))\bigg [\rho (k){\mathscr {C}}_{m}^{\upsilon }x(k)+{\mathscr {C}}_{d m}^{\upsilon }x(k-d(k))+{\mathscr {D}}_{m}^{\upsilon }u(k) +{\mathscr {G}}_{m}^{\upsilon }w(k)+{\mathscr {H}}_{m}^{\upsilon }f(k)\bigg ]. \end{aligned}$$

(2)

Further for the T–S fuzzy MJSs (2), we design a fuzzy-rule-dependent non-fragile filter as given below:

Rule $\rho$: IF $\Theta _1(k)$ is $\mathbb {M}_{\rho 1}$, $\Theta _2(k)$ is $\mathbb {M}_{\rho 2}, \ldots$ and $\Theta _p(k)$ is $\mathbb {M}_{\rho p},$ THEN

$$\begin{aligned} x_{f}(k+1)&=\sum \limits _{\rho =1}^{p}\beta _{\rho }(\Theta (k))\big [{\mathscr {A}}_{f m}^{\rho }x_f(k)+{\mathscr {B}}_{f m}^{\rho }y(k)\big ],\nonumber \\ \mu (k)&=\sum \limits _{\rho =1}^{p}\beta _{\rho }(\Theta (k))\big [{\mathscr {C}}_{fm}^{\rho }x_{f}(k)\big ], \end{aligned}$$

(3)

where ${\mathscr {A}}_{fm}^{\rho }=A_{fm}^{\rho }+\Delta A_{f m}^{\rho }(k)$; ${\mathscr {B}}_{fm}^{\rho }=B_{fm}^{\rho }+\Delta B_{f m}^{\rho }(k)$; $x_f(k)\in \mathbf {R}^s$ denotes the state vector of the filter; $\mu (k)\in \mathbf {R}^l$ is the residual signal; $A_{f m}^{\rho }, B_{f m}^{\rho }$ and ${\mathscr {C}}_{fm}^{\rho }$ are the filter parameters to be designed; The matrices $\Delta A_{fm}^{\rho }(k)$ and $\Delta B_{fm}^{\rho }(k)$ are the non-fragile terms in the filter gain matrices and they are taken as $[\Delta A_{fm}^\rho (k) \ \Delta B_{fm}^\rho (k)]=M_{1m} F_{m}(k)[N_{am}\ N_{bm}]$, where $M_{1m} ,\ N_{am}$ and $N_{bm}$ are the known matrices; $F_{m}(k)$ is the unknown time-varying matrix function satisfying $F_{m}(k)^TF_{m}(k)\le I$.

Now a weighting matrix functional is considered, which is combined with the fault f(k). The main purpose of introducing the weighting matrix functional is to increase the performances of the fault detection system, that is, $f_w(z)=W(z)f(z)$ can be interpreted into the state-space model as follows:

$$\begin{aligned} x_{w}(k+1)&=A_wx_w(k)+B_wf(k),\nonumber \\ f_w(k)&=C_wx_w(k), \end{aligned}$$

(4)

where $x_w(k)\in {\mathscr {R}}^k$ is the state vector; $A_w,$ $B_w,$ and $C_w$ are known matrices with appropriate dimensions. Let $e(k)=\mu (k)-f_w(k)$ be the estimation error and it can be represented by the augmented filtering error system by

$$\begin{aligned} \eta (k+1)&=\sum \limits _{\upsilon =1}^{t}\sum \limits _{\rho =1}^{p}\bigg [(\bar{\mathbb {A}}^{\upsilon \rho }_{m}+\bar{\rho }\tilde{\mathbb {A}}^{\upsilon \rho }_{m})\eta (k)+\bar{\mathbb {A}}^{\upsilon \rho }_{dm}\eta (k-d(k))+\bar{\mathbb {B}}^{\upsilon \rho }_{m}\vartheta (k)\bigg ],\nonumber \\ e(k)&=\sum \limits _{\upsilon =1}^{t}\sum \limits _{\rho =1}^{p}\bar{\mathbb {C}}^{\upsilon \rho }_{m}\eta (k), \end{aligned}$$

(5)

where

$$\begin{aligned} \eta (k)&=\begin{bmatrix} x^T(k)&\quad x^T_f(k)&\quad x^T_w(k) \end{bmatrix}^T,\ \vartheta (k)=\begin{bmatrix} u^T(k)&\quad w^T(k)&\quad f^T(k) \end{bmatrix}^T,\\ \bar{\mathbb {A}}_{m}^{\upsilon \rho }&=\begin{bmatrix} {\mathscr {A}}_{m}^{\upsilon }&{} \quad 0&{} \quad 0\\ \bar{\rho }{\mathscr {B}}_{fm}^{\rho }{\mathscr {C}}_{m}^{\upsilon }&{} \quad {\mathscr {A}}_{fm}^{\rho }&{} \quad 0\\ 0&{} \quad 0&{} \quad A_w \end{bmatrix},\ \tilde{\mathbb {A}}_{m}^{\upsilon \rho }=\begin{bmatrix} 0&{} \quad 0&{} \quad 0\\ {\mathscr {B}}_{fm}^{\rho }{\mathscr {C}}_{m}^{\upsilon }&{} \quad 0&{} \quad 0\\ 0&{} \quad 0&{} \quad 0 \end{bmatrix}, \\ \bar{\mathbb {A}}_{dm}^{\upsilon \rho }&=\begin{bmatrix} {\mathscr {A}}_{dm}^{\upsilon }&{} \quad 0&{} \quad 0\\ {\mathscr {B}}_{fm}^{\rho }{\mathscr {C}}_{dm}^{\upsilon }&{} \quad 0&{} \quad 0\\ 0&{} \quad 0&{} \quad 0 \end{bmatrix},\\ \bar{\mathbb {B}}_{m}^{\upsilon \rho }&=\begin{bmatrix} {\mathscr {B}}_{m}^{\upsilon }&{} \quad {\mathscr {E}}_{m}^{\upsilon }&{} \quad {\mathscr {F}}_{m}^{\upsilon }\\ {\mathscr {B}}_{fm}^{\rho }{\mathscr {D}}_{m}^{\upsilon }&{} \quad {\mathscr {B}}_{fm}^{\rho }{\mathscr {G}}_{m}^{\upsilon }&{} \quad {\mathscr {B}}_{fm}^{\rho }{\mathscr {H}}_{m}^{\upsilon }\\ 0&{} \quad 0&{} \quad B_w \end{bmatrix},\ \bar{\mathbb {C}}_{m}^{\upsilon \rho }=\begin{bmatrix} 0\\ {\mathscr {C}}_{fm}^{\rho } \\ -C_w \end{bmatrix}^T. \end{aligned}$$

Remark 1

While taking the transition probability matrix $\Phi (k)$, two important things are noted for the MJSs; (i) A comparable T–S fuzzy MJSs (1) obeys the homogeneous Markov chain, when $\Phi (k)$ is a constant matrix. (ii) If the matrix $\Phi (k)$ is time-variant, then the system (1) follows the non-homogeneous Markov chain. More precisely the time-varying transition probability matrix is studied throughout this paper. Specifically, the difference of transition probability can be expressed in a polytope which is given as

$$\begin{aligned} \Phi (k)=\sum _{s=1}^{\mathbb {L}}\alpha _{s}(k)\Phi ^s, \end{aligned}$$

where $\Phi ^s=\{\phi _{mn}^s\}, s=1,2,\ldots ,\mathbb {L}$, are the matrices denoting the vertices in the polytope $\alpha _s(k)$. Further $\alpha _s(k) \in [0 \ 1]$ and also satisfies $\sum _{s=1}^\mathbb {L}\alpha _s(k)=1$.

Throughout this paper, the fault detection is measured by choosing the residual evaluation which includes an evaluation function $\mathsf {J}_{\mu }(k)$ and a threshold $\mathsf {J}_{th}$ denoted in the form $\mathsf {J}_{\mu }(k)=\sqrt{\sum \limits _{k=k_0}^{k_0+\mathsf {L}}\mu ^T(k)\mu (k),}$ and $\mathsf {J}_{th}=\sup \limits _{w\ne 0,\ u\ne 0,\ f=0}\mathsf {J}_{\mu }(k)$ respectively, where $\mathsf {L}$ denotes the finite evaluation time length. Thus the fault can be detected by comparing an evaluation function and threshold according to the following rule:

$$\begin{aligned}&\mathsf {J}_{\mu }(k)>\mathsf {J}_{th}\Longrightarrow \text {with-fault},\\&\mathsf {J}_{\mu }(k)\le \mathsf {J}_{th}\Longrightarrow \text {without-fault}. \end{aligned}$$

The following assumption and definitions will be useful in providing our main results in Sect. 3.

Assumption 1

The disturbance input vector ${\vartheta (k)}$ is time-varying and satisfies $\sum \nolimits _{k=0}^{\mathbb {H}}{\vartheta }^T(k){\vartheta }(k)\le \tilde{\delta },$ where $\tilde{\delta }>0$.

Definition 1

[18] Let ${\mathscr {F}}_m \ (m\in {\mathscr {S}})$ be symmetric positive matrices and $0<\Sigma _1<\Sigma _2$. Then the augmented filtering error system (5) is finite-time stochastic bounded with respect to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta })$, if

$$\begin{aligned} E \{\eta ^T(k_1){\mathscr {F}}_m\eta (k_1)\}\le \Sigma _1\Longrightarrow E \{\eta ^T(k){\mathscr {F}}_m\eta (k)\}< \Sigma _2, \end{aligned}$$

$\forall k_1\in \{-d_2,d_2+1,\ldots ,0\}$ and $k\in \{0,1,2,\ldots ,\mathbb {H}\}$ holds for any nonzero ${\vartheta }(k)$ satisfying Assumption (1).

Definition 2

[26] The augmented filtering error system (5) is finite-time stochastic bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipative subject to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta },\gamma )$, where ${\mathscr {F}}_m$ is a positive definite matrix, $0<\Sigma _1<\Sigma _2$, if the system is finite-time stochastic bounded with respect to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta })$ and under zero initial condition, the estimation error e(k) satisfies

$$\begin{aligned} E\bigg \{\sum \limits ^{\mathbb {H}}_{k=0}[e^T(k)\mathsf {Q}e(k)+2e^T(k)\mathsf {S}\vartheta (k)+\vartheta ^T(k)\mathsf {R}\vartheta (k)]\bigg \}\ge \gamma E\bigg \{\sum \limits _{k=0}^{\mathbb {H}}\vartheta ^T(k)\vartheta (k)\bigg \}, \end{aligned}$$

for any nonzero ${\vartheta }(k)$ satisfying Assumption (1), where $\mathsf {Q}$, $\mathsf {S}$ and $\mathsf {R}$ are real constant matrices with symmetric $\mathsf {Q}$ and $\mathsf {R}$.

3 Main Results

In this section, our main attention is to derive sufficient conditions for the finite-time stochastic boundedness and strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipativity of the augmented filtering error system (5) with missing measurement and randomly occurring uncertainties. For this purpose, first we prove the finite-time stochastic boundedness with known filter gain matrices for the augmented filtering error system (5). Secondly, the finite-time stochastic bounded strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipative performance of the filtering system (5) is investigated. Finally, by considering the parameter uncertainties and filter gain fluctuations, we get the proposed finite-time fault detection filter for the augmented filtering error system (5). Further a corollary deals with the considered model (5) in the absence of Markovian jump process to ensure the finite-time stochastic boundedness with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipativity subject to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta },\gamma )$.

Theorem 1

Consider the augmented filtering error system (5) with Assumption 1. For given positive scalars $d_1$, $d_2$, $\tilde{\mu },\ \tilde{\mu }^{-k}$, $\Sigma _1$, $\mathbb {H}$, $\tilde{\delta }$, $\bar{\rho },\bar{\lambda }_1,\bar{\lambda }_2$ and let ${\mathscr {F}}_m \ (m\in {\mathscr {S}})$ be positive definite matrices, the augmented filtering error system (5) with $\Delta A_m^{\upsilon }=0$, $\Delta A_{dm}^{\upsilon }=0$ is finite-time stochastic bounded with respect to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta })$ if there exist $\Sigma _2>0$ and positive definite matrices ${\mathscr {P}}_m^{s},\ P_{m}^{s}\ (m\in {\mathscr {S}},\ s=1,2,\ldots ,{\mathscr {M}})$, $Q_a \ (a=1,2,3)$ such that the following inequalities hold for all $\upsilon ,\rho =1,2,\ldots ,t$:

$$\begin{aligned}&[\Xi _{m}^{\upsilon \upsilon }]<0, \quad \upsilon =\rho , \end{aligned}$$

(6)

$$\begin{aligned}&[\Xi _{m}^{\upsilon \rho }]+[\Xi _{m}^{\rho \upsilon }]<0, \quad \upsilon <\rho , \end{aligned}$$

(7)

$$\begin{aligned}&\tilde{\psi }\Sigma _1+\tilde{\theta }_{{\mathscr {W}}}\tilde{\delta }<\tilde{\theta }_{\hat{P}_m^s}\Sigma _2\tilde{\mu }^{-k}, \end{aligned}$$

(8)

$$\begin{aligned}&\tilde{\theta }^{\hat{P}_m^s}\le P_m^s\le \tilde{\theta }_{\hat{P}_m^S},\quad 0<Q_1<\tilde{\theta }_{\hat{Q}_1},\quad 0<Q_2<\tilde{\theta }_{\hat{Q}_2},\quad 0<Q_3<\tilde{\theta }_{\hat{Q}_3}, \end{aligned}$$

(9)

where

$$\begin{aligned}&\Xi _{m}^{\upsilon \rho }=\begin{bmatrix} [\hat{\Xi }_m^{\upsilon \rho }]_{5\times 5}&{} \quad {\tilde{\Xi }_m^{\upsilon \rho T}}{\mathscr {P}}_{ms}^{l}\\ *&{} \quad -{\mathscr {P}}_{ms}^{l} \end{bmatrix},\quad [\hat{\Xi }_m^{\upsilon \rho }]_{1,1}=-\tilde{\mu }{\mathscr {P}}_m^{s}+(1+d_M)Q_1+Q_2+Q_3, \\&[\hat{\Xi }_m^{\upsilon \rho }]_{2,2}=-Q_2,\quad [\hat{\Xi }_m^{\upsilon \rho }]_{3,3}=-Q_1,\quad [\hat{\Xi }_m^{\upsilon \rho }]_{4,4}=-Q_3,\quad [\hat{\Xi }_m^{\upsilon \rho }]_{5,5}=-{\mathscr {W}},\\&\tilde{\Xi }_m^{\upsilon \rho }=\begin{bmatrix} {\mathscr {P}}^{lT}_{ms}(\bar{\mathbb {A}}^{\upsilon }_{m}+\bar{\rho }\tilde{\mathbb {A}}^{\upsilon }_{m})&\quad 0&\quad {\mathscr {P}}^{lT}_{ms}\bar{\mathbb {B}}^{\upsilon }_{m}&\quad 0&\quad {\mathscr {P}}^{lT}_{ms}\bar{\mathbb {A}}_{dm} \end{bmatrix}^T,\\&\beta _l(k)=\alpha _s(k+1),\quad {\mathscr {P}}_{ms}^{l}=\sum \limits _{n=1}^\mathbb {L}\sum \limits _{s=1}^\mathbb {L}\sum \limits _{l=1}^\mathbb {L}\alpha _{s}(k)\beta _{l}(k)\phi _{mn}^sP_n^{l},\quad {\mathscr {P}}_{m}^s=\sum \limits _{s=1}^{\mathbb {L}}\alpha _s(k)P_m^{s},\\&\tilde{\psi }=\tilde{\theta }_{\hat{P}_m^s}+d_1\tilde{\theta }_{\hat{Q}_2}+d_2\tilde{\theta }_{\hat{Q}_3}+d_2\tilde{\theta }_{\hat{Q}_1}+\tilde{\theta }_{\hat{Q}_1}\frac{(d_2-d_1)(d_2+d_1-1)}{2}. \end{aligned}$$

Proof

The Lyapunov–Krasovskii functional is considered for the augmented filtering error system (5) in the following form

$$\begin{aligned} {\mathscr {V}}(k)={\mathscr {V}}_1(k)+{\mathscr {V}}_2(k)+{\mathscr {V}}_3(k), \end{aligned}$$

(10)

where

$$\begin{aligned}&{\mathscr {V}}_{1}(k)=\eta ^T(k)\left( \sum \limits _{s=1}^{\mathbb {L}}\alpha _{s}(k)P_{m}^{s}\right) \eta (k),\\&{\mathscr {V}}_{2}(k)=\sum \limits _{g=k-d(k)}^{k-1}\eta ^T(g)Q_1\eta (g)+ \sum \limits _{g=k-d_1}^{k-1}\eta ^T(g)Q_2\eta (g)+\sum \limits _{g=k-d_2}^{k-1}\eta ^T(g)Q_3\eta (g),\\&{\mathscr {V}}_{3}(k)=\sum \limits _{i=-d_2+1}^{-d_1}\sum \limits _{g=k+i}^{k-1}\eta ^T(g)Q_1\eta (g). \end{aligned}$$

By considering the forward difference of ${\mathscr {V}}(k)$ together with the trajectories of proposed augmented system (5) and taking the mathematical expectation, we obtain

$$\begin{aligned} E \{\Delta {\mathscr {V}}_1(k)\}&=E\bigg \{\eta ^T(k+1)\bigg (\sum \limits _{s=1}^{\mathbb {L}}\alpha _s(k)\alpha (k+1)\sum \limits _{n=1}^{\mathbb {L}}\Phi _{mn}P_n^s\bigg )\eta (k+1)\nonumber \\&\ \quad -\eta ^T(k)\bigg ( \sum \limits _{s=1}^{\mathbb {L}}\alpha _s(k)P_m^s\bigg )\eta (k)\bigg \},\nonumber \\&= E \bigg \{\eta ^T(k+1)\bigg [\sum \limits _{s=1}^\mathbb {L}\sum \limits _{n=1}^{\mathbb {L}}\sum \limits _{l=1}^{\mathbb {L}}\alpha _s(k)\beta _l(k)\Phi _{mn}P_n^l\bigg ]\eta (k+1)\nonumber \\&\ \quad -\eta ^T(k)\bigg (\sum \limits _{s=1}^{\mathbb {L}}\alpha _s(k)P_m^s\bigg )\eta (k)\bigg \},\nonumber \\&= E \bigg \{\big [\big (\bar{\mathbb {A}}^{\upsilon \rho }_{m}+\bar{\rho }\tilde{\mathbb {A}}^{\upsilon \rho }_{m}\big )\eta (k)\big ]^T{\mathscr {P}}^{l}_{ms}\big [\big (\bar{\mathbb {A}}^{\upsilon \rho }_{m}+\bar{\rho }\tilde{\mathbb {A}}^{\upsilon \rho }_{m}\big )\eta (k)\big ]\nonumber \\&\quad \ +[\bar{\mathbb {A}}^{\upsilon \rho }_{dm}\eta (k-d(k))]^T{\mathscr {P}}^{l}_{ms}\nonumber \\&\quad \ \ [\bar{\mathbb {A}}^{\upsilon \rho }_{dm}\eta (k-d(k))]+\bar{\mathbb {B}}^{\upsilon \rho T}_{m} {\mathscr {P}}^{l}_{ms} {\bar{\mathbb {B}}^{\upsilon \rho }_{m}}-\eta ^T(k)P_m^s\eta (k)\bigg \},\end{aligned}$$

(11)

$$\begin{aligned} E \{\Delta {\mathscr {V}}_2(k)\}&= E \bigg \{\eta ^T(k)Q_1\eta (k)+\eta ^T(k)Q_2\eta (k)+\eta ^T(k)Q_3\eta (k)\ \nonumber \\&\quad -\eta ^T(k-d(k))Q_1\eta (k-d(k))-\eta ^T(k-d_1)Q_2\eta (k-d_1)\nonumber \\&\quad -\eta ^T(k-d_2)Q_3\eta (k-d_2)+\sum \limits _{g=k-d_2+1}^{k-1}\eta ^T(g)Q_1\eta (k)\bigg \}, \end{aligned}$$

(12)

$$\begin{aligned} E \{\Delta {\mathscr {V}}_3(k)\}&= E \bigg \{(d_2-d_1)\eta ^T(k)Q_1\eta (k)-\sum \limits _{g=k-d_2+1}^{k-1}\eta (g)Q_1\eta (g).\bigg \} \end{aligned}$$

(13)

Then, from (11)–(13), it follows that

$$\begin{aligned} E \{\Delta {\mathscr {V}}(k)-\vartheta ^T(k){\mathscr {W}}\vartheta (k)\}&\le E \{\zeta ^T(k)\big [[\Xi _m^{\upsilon \rho }]_{5\times 5}+{\Xi _m^{\upsilon \rho T}}{\mathscr {P}}_{ms}^l\Xi _m^{\upsilon \rho }]\zeta (k)\}, \end{aligned}$$

(14)

where $\zeta (k)=[\eta (k)\quad \eta (k-d_1)\quad \eta (k-d(k)) \quad \eta (k-d_2) \quad \vartheta (k)]$ and the elements of $[\Xi _m^{\upsilon \rho }]_{5\times 5}$, $\Xi _m^{\upsilon \rho }$ and ${\mathscr {P}}_{ms}^{l}$ are defined as in the Theorem statement.

Now the elements in Theorem 1 are obtained from (14) by implementing Lemma 2.3 in [18]. Thus, if the LMIs in (6) and (7) hold, it is obvious that

$$\begin{aligned} E \{{\mathscr {V}}(k+1)\}<\tilde{\mu } E \{{\mathscr {V}}(k)\}+\tilde{\theta }_{{\mathscr {W}}} E \{\vartheta ^T(k)\vartheta (k)\}, \end{aligned}$$

(15)

where $\tilde{\theta }_{{\mathscr {W}}}=\tilde{\theta }_{max}{\mathscr {W}}$. Furthermore, if $\tilde{\mu }\ge 1$, then from Assumption 1, we can obtain the following inequality

$$\begin{aligned} E \{{\mathscr {V}}(k)\}\le \tilde{\mu }^ke\{{\mathscr {V}}(0)\}+\tilde{\mu }^k\tilde{\theta }_{{\mathscr {W}}}\tilde{\delta }. \end{aligned}$$

(16)

Let $\hat{P}_{m}^s={\mathscr {F}}^{-1/2}P_m^s{\mathscr {F}}^{-1/2}$, $\hat{Q}_1={\mathscr {F}}^{-1/2}Q_1{\mathscr {F}}^{-1/2}$, $\hat{Q}_2={\mathscr {F}}^{-1/2}Q_2{\mathscr {F}}^{-1/2}$ and $\hat{Q}_3={\mathscr {F}}^{-1/2}Q_3{\mathscr {F}}^{-1/2}$. Then it follows from constraints (10) and $0\le k\le \mathbb {H}$ that

$$\begin{aligned} E \{{\mathscr {V}}(0)\}&= E \bigg \{\eta ^T(0){\mathscr {F}}^{1/2}P_{m}^s{\mathscr {F}}^{1/2}\eta (0)\bigg \}+E\bigg \{\sum \limits _{g=-d(0)}^{-1}\eta ^T(0){\mathscr {F}}^{1/2}Q_1{\mathscr {F}}^{1/2}\eta (0)\bigg \}\nonumber \\&\quad +E\bigg \{\sum \limits _{g=-d_1}^{-1}\eta ^T(0){\mathscr {F}}^{1/2}Q_2{\mathscr {F}}^{1/2}\eta (0)\bigg \}\nonumber \\&\quad + E \bigg \{\sum \limits _{g=-d_2}^{-1}\eta ^T(0){\mathscr {F}}^{1/2}Q_3{\mathscr {F}}^{1/2}\eta (0)\bigg \}\nonumber \\&\quad + E \bigg \{\sum \limits _{i=-d_2+1}^{-d_1}\sum \limits _{g=i}^{-1}\eta ^T(0){\mathscr {F}}^{1/2}Q_1{\mathscr {F}}^{1/2}\eta (0)\bigg \},\nonumber \\&\le \tilde{\psi }\Sigma _1, \end{aligned}$$

(17)

where $\tilde{\psi }$ is defined in theorem statement.

On the other hand, from (10), we can have

$$\begin{aligned} E \{{\mathscr {V}}(k)\}\ge E \{\eta ^T(k)P_m^s\eta (k)\} \ge \tilde{\theta }^{\hat{P}_{m}^s} E \{\eta ^T(k){\mathscr {F}}_m\eta (k)\}. \end{aligned}$$

(18)

Now, by combining the inequalities (17) and (18), we have

$$\begin{aligned} E \{\eta ^T(k){\mathscr {F}}_m\eta (k)\}&\le (1/ \tilde{\theta }_{\hat{P}_m^{s}}(\tilde{\psi }\Sigma _1+\tilde{\theta }_{{\mathscr {W}}}\tilde{\delta }))\tilde{\mu }^k<\Sigma _2. \end{aligned}$$

(19)

It is obvious to see that the inequality (19) is the same as that in (8) which is the desired condition. Thus it is concluded that the augmented filtering error system (5) is finite-time stochastic bounded with respect to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta })$, which completes the proof. $\square$

By considering that the dissipative performance index is taken into account, sufficient conditions for proving the finite-time stochastic boundedness with strict $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipativity of the augmented filtering error system (5) is given in the following theorem.

Theorem 2

Let $d_1$, $d_2$, $\tilde{\mu }$, $\tilde{\mu }^{-k}$, $\Sigma _1$, $\mathbb {H}$, $\tilde{\delta }$, $\gamma$, $\bar{\rho },\bar{\lambda }_1,\bar{\lambda }_2$ be given positive scalars and ${\mathscr {F}}_m\ (m\in {\mathscr {S}})$ be the positive symmetric matrices. Further, the augmented filtering error system (5) is finite-time stochastic bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipativity subject to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta },\gamma )$, if there exist positive definite matrices ${\mathscr {P}}_m^{s},\ {\mathscr {P}}_{ms}^{l}\ (m\in {\mathscr {S}})$, $Q_{a}\ (a=1,2,3)$, $\mathsf {Q}$, $\mathsf {S}$, $\mathsf {R}_{q}=\mathsf {R}_q^T$ and a scalar $\Sigma _2>0$ such that the following LMIs hold for $\upsilon ,\rho =1,2,\ldots ,t$:

$$\begin{aligned}{}[\tilde{\Xi }_{1m}^{\upsilon \upsilon }]&<0,\qquad \qquad \upsilon =\rho , \end{aligned}$$

(20)

$$\begin{aligned} +[\tilde{\Xi }_{1m}^{\rho \upsilon }]&<0,\qquad \qquad \upsilon <\rho , \end{aligned}$$

(21)

$$\begin{aligned} \tilde{\psi }\Sigma _1+ \tilde{\theta }_{{\mathscr {W}}} \tilde{\delta }&<\tilde{\theta }_{\hat{P}_m^s}\Sigma _2\tilde{\mu }^{-k},\ m\in {\mathscr {S}}, \end{aligned}$$

(22)

where

$$\begin{aligned} \tilde{\Xi }_{1m}^{\upsilon \rho }&= \begin{bmatrix} [\tilde{\Xi }_m^{\upsilon \rho }]_{5\times 5}&{} \quad \tilde{\Xi }_m^{\upsilon \rho T}{\mathscr {P}}_{ms}^l&{} \quad \bar{{{\mathscr {C}}}_m^{\upsilon }}^T\sqrt{\mathsf {Q}}\\ *&{} \quad -{\mathscr {P}}_{ms}^l&{} \quad 0\\ *&{} \quad *&{} \quad -I \end{bmatrix},\quad \\&\quad [\tilde{\Xi }_m^{\upsilon \rho }]_{1,5}=-\bar{{{\mathscr {C}}}_m^{\upsilon }}^T\mathsf {S},\quad [\tilde{\Xi }_m^{\upsilon \rho }]_{5,5}=\mathsf {R}-\gamma I, \end{aligned}$$

and the other elements of $[\tilde{\Xi }_m^{\upsilon \rho }]_{5\times 5}$ and $\tilde{\Xi }_m^{\upsilon \rho }$ are same as in Theorem 1.

Proof

To determine the strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipativity of the augmented filtering error system (5), we consider the performance index as follows :

$$\begin{aligned} J(k)= E \bigg \{\sum \limits ^{\mathbb {H}}_{k=0}\big ([e^T(k)\mathsf {Q}e(k)+2e^T(k)\mathsf {S}\vartheta (k)+\vartheta ^T(k)\mathsf {R}\vartheta (k)]-\gamma \vartheta ^T(k)\vartheta (k)\big )\bigg \}. \end{aligned}$$

(23)

By following similar steps in the proof of Theorem 1, it is obvious that $E \{\Delta {\mathscr {V}}(k)-(\tilde{\mu }-1){\mathscr {V}}(k)-J(k)\}\le 0$. Thus we get $E \{{\mathscr {V}}(k+1)\}<E\big \{\tilde{\mu }{\mathscr {V}}(k)+e^T(k)\mathsf {Q}e(k)+2e^T(k)\mathsf {S}\vartheta (k)+\vartheta ^T(k)[\mathsf {R}-\gamma I]\vartheta (k)\big \}$.

In addition, $\tilde{\mu }\ge 1$, then it follows that

$$\begin{aligned} E \{{\mathscr {V}}(k)\}&\le E \left\{ \tilde{\mu }^k{\mathscr {V}}(0)+\sum \limits _{a=0}^{k-1}\tilde{\mu }^{k-a-1}e^T(k)\mathsf {Q}e(k)+2\sum \limits _{a=0}^{k-1}\tilde{\mu }^{k-a-1}e^T(k)\mathsf {S}\vartheta (k)\right. \\&\left. \quad +\sum \limits _{a=0}^{k-1}\tilde{\mu }^{k-a-1}\vartheta ^T(k)[\mathsf {R}-\gamma I]\vartheta (k)\right\} . \end{aligned}$$

On the other hand ${\mathscr {V}}(k)\ge 0\ \forall k=1,2\ldots ,\mathbb {H}$ and under zero initial condition, we have

$$\begin{aligned}&E \bigg \{\gamma \sum \limits _{a=0}^{k-1}\tilde{\mu }^{k-a-1}\vartheta ^T(k)\vartheta (k)\bigg \}\\&\quad \le E \bigg \{\sum \limits _{a=0}^{k-1}\tilde{\mu }^{k-a-1}e^T(k)\mathsf {Q}e(k)+2\sum \limits _{a=0}^{k-1}\tilde{\mu }^{k-a-1}e^T(k)\mathsf {S}\vartheta (k)\\&\quad \quad +\sum \limits _{a=0}^{k-1}\tilde{\mu }^{k-a-1}\vartheta ^T(k)\mathsf {R}\vartheta (k)\bigg \}. \end{aligned}$$

This implies that

$$\begin{aligned} J(k)= E \bigg \{\gamma \sum \limits _{k=0}^{\mathbb {H}}\vartheta ^T(k)\vartheta (k)\bigg \}&\le E \bigg \{\sum \limits _{k=0}^{\mathbb {H}}e^T(k)\mathsf {Q}e(k)+2\sum \limits _{k=0}^{\mathbb {H}}e^T(k)\mathsf {S}\vartheta (k)\\&\quad +\sum \limits _{k=0}^{\mathbb {H}}\vartheta ^T(k)\mathsf {R}\vartheta (k)\bigg \}. \end{aligned}$$

Moreover, if LMIs (20)–(22) hold, then $J(k)<0$. Thus, by Definition 2, it is concluded that the augmented filtering error system (5) is finite-time stochastic bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipativity subject to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta },\gamma )$. Hence the proof is complete. $\square$

Next we design the filtering error system (5) with the presence of randomly occurring uncertainties which is denoted as ${\mathscr {A}}_{m}^{\upsilon }=A_m^{\upsilon }+\bar{\lambda }_1\Delta A_{m}^\upsilon (k)$ and ${\mathscr {A}}_{dm}^{\upsilon }=A_{dm}^{\upsilon }+\bar{\lambda }_2\Delta A_{dm}^\upsilon (k)$.

Theorem 3

Let $d_1$, $d_2$, $\tilde{\mu }$, $\tilde{\mu }^{-k}$, $\Sigma _1$, $\mathbb {H}$, $\tilde{\delta }$, $\gamma$, $\bar{\rho },\bar{\lambda }_1,\bar{\lambda }_2$ be given positive scalars and ${\mathscr {F}}_m\ (m\in {\mathscr {S}})$ be the known positive matrices. Moreover the augmented filtering error system (5) is finite-time bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipative subject to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta },\gamma )$ if there exist positive definite matrices $\mathsf {P}_{111}$, $\mathsf {P}_{112}$, $\mathsf {P}_{12}$, $U_1$, $U_3$, V, $Q_{111}$, $Q_{112}$, $Q_{12}$, $Q_{211}$, $Q_{212}$, $Q_{22}$, $Q_{311}$, $Q_{312}$, $Q_{32}$, any appropriate dimensioned matrices $\mathbb {U}$, $\mathbb {V}$, $\mathsf {A}_{Fm}^{\upsilon }$, $\mathsf {B}_{Fm}^{\upsilon }$, $C_{Fm}^{\upsilon }$ and positive scalars $\Sigma _{2}$, $\tilde{\varepsilon _1}$, $\tilde{\varepsilon _2}$ such that the following LMIs together with (22) hold for all $\upsilon ,\rho =1,2,\ldots ,t$:

$$\begin{aligned}{}[\Psi _{m}^{\upsilon \upsilon }]&<0,\quad \upsilon =\rho , \end{aligned}$$

(24)

$$\begin{aligned} +[\Psi _{m}^{\rho \upsilon }]&<0,\quad \upsilon <\rho , \end{aligned}$$

(25)

$$\begin{aligned} \begin{bmatrix} \mathbb {U}&{} \quad \mathbb {V}\\ *&{} \quad \mathbb {V} \end{bmatrix}&>0, \end{aligned}$$

(26)

where $\Psi _m^{\upsilon \rho }=\begin{bmatrix} [\tilde{\Psi }_m^{\upsilon \rho }]_{19\times 19}&{} \quad \tilde{\varepsilon _1}\Gamma _1&{} \quad \Gamma _2&{} \quad \tilde{\varepsilon _2}\Gamma _3&{} \quad \Gamma _4\\ *&{} \quad -\tilde{\varepsilon _1}&{} \quad 0&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad -\tilde{\varepsilon _1}&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -\tilde{\varepsilon _2}&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\tilde{\varepsilon _2}\\ \end{bmatrix}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{1,1}=-\tilde{\mu }\mathsf {P}_{11}+(1+d_M)Q_{111}+Q_{211}+Q_{311}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{1,16}=A_{m}^{\upsilon T}\mathbb {U}+\bar{\rho }{C}_{m}^{\upsilon T}{B}_{Fm}^{\upsilon \rho T}+{\mathscr {C}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{1,17}=A_{m}^{\upsilon T}\mathbb {V}+\bar{\rho }{\mathscr {C}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}+{\mathscr {C}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{2,2}= -\tilde{\mu }\mathsf {P}_{12}+Q_{112}+d_MQ_{112}+Q_{212}+Q_{312}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{2,14}= -C_{Fm}^{\upsilon \rho T}\mathsf {S}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{2,16}= \mathsf {A}_{Fm}^{\upsilon \rho T}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{2,17}= \mathsf {A}_{Fm}^{\upsilon \rho T}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{2,19}=C_{Fm}^{\upsilon \rho T} \sqrt{-\mathsf {Q}}$,    $[\tilde{\Psi }^{\upsilon \rho }_m]_{3,3}=-\tilde{\mu }\mathsf {P}_{2}+Q_{12}+d_MQ_{12}+Q_{22}+Q_{32}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{3,15}= {C}_{w}^{\upsilon T}\mathsf {S}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{3,18}={A}_w^TV$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{3,19}=-C_{w}^T \sqrt{-\mathsf {Q}}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{4,4}= -Q_{211}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{5,5}=-Q_{212}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{6,6}=-Q_{22}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{7,7}=-Q_{111}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{7,16}= A_{dm}^{\upsilon T}\mathbb {U}+{\mathscr {C}}_{dm}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,    $[\tilde{\Psi }^{\upsilon \rho }_m]_{8,8}=-Q_{112}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{9,9}=-Q_{12}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{10,10}=-Q_{311}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{11,11}=-Q_{312}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{12,12}=-Q_{32}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{13,13}=\mathsf {R}_1-\gamma I$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{13,16}={\mathscr {B}}_{m}^{\upsilon T}\mathbb {U}+{\mathscr {D}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{13,17}={\mathscr {B}}_{m}^{\upsilon T}\mathbb {V}+{\mathscr {D}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{14,14}=\mathsf {R}_2-\gamma I$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{14,16}= {\mathscr {E}}_{m}^{\upsilon T}\mathbb {U}+{\mathscr {G}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{14,17}={\mathscr {E}}_{m}^{\upsilon T}\mathbb {V}+{\mathscr {G}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{15,15}= \mathsf {R}_3-\gamma I$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{15,16}= {\mathscr {F}}_{m}^{\upsilon T}\mathbb {U}+{\mathscr {H}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{15,17}= {\mathscr {F}}_{m}^{\upsilon T}\mathbb {V}+{\mathscr {H}}_{m}^{\upsilon T}\mathsf {B}_{Fm}^{\upsilon \rho T}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{15,18}= \mathbb {V}^TB_{w}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{16,16}=-\mathbb {V}$,

$[\tilde{\Psi }^{\upsilon \rho }_m]_{17,17}=-\mathbb {V}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{18,18}=-\mathbb {V}$,   $[\tilde{\Psi }^{\upsilon \rho }_m]_{19,19}=-I$,

$\Gamma _1=[\lambda _1\mathsf {N}_{m}^{\upsilon }\quad \underbrace{0\cdots 0}_{5}\quad \lambda _2\mathsf {N}_{m}^{\upsilon }\ \underbrace{0\cdots 0}_{12}]^T$,   $\Gamma _2=[\underbrace{0\cdots 0}_{15}\quad \mathsf {M}_{m}^{\upsilon T}\mathbb {U}\quad \mathsf {M}_{m}^{\upsilon T}\mathbb {V}\quad 0\quad 0]^T$,

$\Gamma _3=[0\quad \mathsf {N}_m^{\rho }\ \underbrace{0\cdots 0}_{10}\quad \mathsf {N}_{m}^{\rho } {\mathscr {D}}_{m}^{\upsilon }\quad \mathsf {N}_{m}^{\rho } G_{m}^{\upsilon }\quad \mathsf {N}_{m}^{\rho } {\mathscr {H}}_{m}^{\upsilon }\quad \underbrace{0\cdots 0}_{4} ]^T$,

$\Gamma _4=[\underbrace{0\cdots 0}_{15} \quad {M_{1m}^{\rho T}}\quad {M_{1m}^{\rho T}}\quad 0 \quad 0]^T$ and the rest of the elements are zero. Then there exists a desired fault detection filter in the form of (3) such that the augmented filtering error system (5) is finite-time stochastic bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipative. Moreover, if the matrix inequalities (24)–(26) are feasible, then the matrices for a desired filtering error system in the form of (5) are constructed as

$$\begin{aligned} \begin{bmatrix} A_{fm}^{\rho } &{} \quad B_{fm}^{\rho }\\ C_{fm}^{\rho }&{} \quad \quad 0 \end{bmatrix}=\begin{bmatrix} \mathbb {V}^{-1}&{} \quad 0\\ 0&{} \quad I \end{bmatrix} \begin{bmatrix} \mathsf {A}_{Fm}^{\rho }&{} \quad \mathsf {B}_{Fm}^{\rho }\\ C_{Fm}^{\rho }&{} \quad 0 \end{bmatrix}. \end{aligned}$$

(27)

Proof

From Theorem 2, we partition some matrices in (21) which are given by ${\mathscr {P}}_{ms}^l=diag\{U,V\}$, ${\mathscr {P}}_{m}^{s}=diag\{\mathsf {P}_1,\mathsf {P}_2\}$, $Q_1=diag\{Q_{11},Q_{12}\}$, $Q_2=diag\{Q_{21},Q_{22}\}$, $Q_3=diag\{Q_{31},Q_{32}\}$, where $U,\mathsf {P}_1\in \mathbb {R}^{2n}\times \mathbb {R}^{2n}$ and $V,\mathsf {P}_2\in \mathbb {R}^{k}\times \mathbb {R}^{k}$. Now the augmented filtering error system (5) is finite-time stochastic bounded with strict $(\mathsf {Q},\mathsf {S},\mathsf {R})-\gamma$ dissipativity if the above-defined partition matrices exist such that the following LMIs hold:

$$\begin{aligned}{}[\widehat{\Xi }_m^{\upsilon \upsilon }]&<0,\quad \upsilon =\rho , \end{aligned}$$

(28)

$$\begin{aligned} +[\widehat{\Xi }_m^{\rho \upsilon }]&<0,\quad \upsilon <\rho , \end{aligned}$$

(29)

where

$$\begin{aligned}&\widehat{\Xi }_m^{\upsilon \rho }=\begin{bmatrix} [\widehat{\Xi }_m^{\upsilon \rho }]_{9\times 9}&{} \quad \widehat{\Xi }_{m}^{\upsilon \rho }U&{} \quad \widehat{\Xi }_{w}V&{} \quad \widehat{\Xi }_{C}^{\rho }\\ *&{} \quad -U&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad -V&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -I \end{bmatrix} \end{aligned}$$

with

$$\begin{aligned}&[\widehat{\Xi }_m^{\upsilon \rho }]_{1,1}=-\tilde{\mu }\mathsf {P}_1+(1+d_M)Q_{11}+Q_{21}+Q_{31},\ [\widehat{\Xi }_m^{\upsilon \rho }]_{1,9}=-\hat{{\mathscr {C}}}_{fm}^{\rho T},\\&[\widehat{\Xi }_m^{\upsilon \rho }]_{2,2}=-\tilde{\mu }\mathsf {P}_2+(1+d_M)Q_{12}+Q_{22}+Q_{32},\\&\quad [\widehat{\Xi }_m^{\upsilon \rho }]_{2,9}=C_w^TS,\ [\widehat{\Xi }_m^{\upsilon \rho }]_{3,3}=-Q_{21},\\&[\widehat{\Xi }_m^{\upsilon \rho }]_{4,4}=-Q_{22},\ [\widehat{\Xi }_m^{\upsilon \rho }]_{5,5}=-Q_{11},\ [\widehat{\Xi }_m^{\upsilon \rho }]_{6,6}=-Q_{12},\ [\widehat{\Xi }_m^{\upsilon \rho }]_{7,7}=-Q_{31},\\&[\widehat{\Xi }_m^{\upsilon \rho }]_{8,8}=-Q_{32},\ [\widehat{\Xi }_m^{\upsilon \rho }]_{9,9}=\mathsf {R}-\gamma I,\\&\widehat{\Xi }_{m}^{\upsilon \rho }=[ \hat{\mathbb {A}}_{1m}^{\upsilon }+\hat{\mathbb {A}}_{2m}^{\upsilon }\quad 0 \quad 0 \quad 0\quad \hat{\mathbb {A}}_{dm}^{\upsilon }\quad 0\quad 0\quad 0\quad \hat{{\mathscr {B}}}_{m}^{\upsilon \rho }]^T,\\&\widehat{\Xi }_{w}= [0\quad A_{w}\quad \underbrace{0\cdots 0}_{6}\quad \hat{B}_w]^T,\ \widehat{\Xi }_{C}^{\rho }=[\sqrt{\mathsf {Q}}^T\hat{{\mathscr {C}}}_{fm}^{\rho }\quad -\sqrt{\mathsf {Q}}^T C_{w}\quad \underbrace{0\cdots 0}_{7}]^T,\\&\hat{\mathbb {A}}_{1m}^{\upsilon \rho }=\begin{bmatrix} {\mathscr {A}}_{m}^{\upsilon }&{}0\\ \bar{\rho }{\mathscr {B}}_{fm}^{\rho }{\mathscr {C}}_{m}^{\upsilon }&{}{\mathscr {A}}_{fm}^{\rho } \end{bmatrix}^T, \ \hat{\mathbb {A}}_{2m}^{\upsilon \rho }=\begin{bmatrix} 0&{}0\\ {\mathscr {B}}_{fm}^{\rho }{\mathscr {C}}_{m}^{\upsilon }&{}0 \end{bmatrix}^T,\\&\hat{{\mathscr {B}}}_{m}^{\upsilon \rho }= \begin{bmatrix} {\mathscr {B}}_{m}^{\upsilon }&{} \quad {\mathscr {E}}_{m}^{\upsilon }&{} \quad {\mathscr {F}}_{m}^{\upsilon }\\ {\mathscr {B}}_{fm}^{\rho }{\mathscr {D}}_{m}^{\upsilon }&{} \quad {\mathscr {B}}_{fm}^{\rho }{\mathscr {G}}_{m}^{\upsilon }&{} \quad {\mathscr {B}}_{fm}^{\rho }{\mathscr {H}}_{m}^{\upsilon } \end{bmatrix}^T,\ \hat{{\mathscr {C}}}_{fm}^{\rho }=[0\quad {\mathscr {C}}_{fm}^{\rho }],\quad \hat{B}_{w}=[0\quad 0\quad B_w]. \end{aligned}$$

Now partition matrices $\mathsf {P}_{11},\ Q_{11},\ Q_{21},\ Q_{31}$ are defined as $\mathsf {P}_{11}=diag\{\mathsf {P}_{111}, \mathsf {P}_{112}\}, Q_{11}=diag\{Q_{111},\ Q_{112}\}, Q_{21}=diag\{Q_{211},\ Q_{112}\},\ Q_{31}=diag\{Q_{311},\ Q_{312}\}$ and also partition $U=\begin{bmatrix} U_1&{} \quad U_2\\ *&{} \quad U_3 \end{bmatrix}>0$, where $U_1,\ U_2,\ U_3\in \mathbb {R}^{n\times n}$. If $U_2$ is square, it is accepted as a nonsingular matrix without affecting generality. Moreover, define the nonsingular matrices as follows:

$$\begin{aligned} \digamma \triangleq \begin{bmatrix} I&{} \quad 0\\ 0&{} \quad U_3^{-1}U_2^T \end{bmatrix},\quad \mathbb {V}\triangleq U_2U_3^{-1}U_2^T,\quad \mathbb {U}\triangleq U_1. \end{aligned}$$

(30)

On the other hand, the filter gain parameters are modified as

$$\begin{aligned} \begin{bmatrix} \mathsf {A}_{Fm}^{\rho }&{} \quad \mathsf {B}_{Fm}^{\rho }\\ C_{Fm}^{\rho }&{} \quad 0 \end{bmatrix}\triangleq \begin{bmatrix} U_2&{} \quad 0\\ 0&{} \quad I \end{bmatrix} \begin{bmatrix} A_{Fm}^{\rho } &{} \quad {B}_{fm}^{\rho }\\ {C}_{fm}^{\rho }&{} \quad 0 \end{bmatrix} \begin{bmatrix} U_3^{-1}U_2^T&{} \quad 0\\ 0&{} \quad I \end{bmatrix}. \end{aligned}$$

(31)

Further, by performing a congruence transformation to (28) and (29) by $\Lambda =diag\{I_{9\times 9},\digamma ,I,I\}$, we obtain

$$\begin{aligned} \Lambda ^T\widehat{\Xi }_m^{\upsilon \upsilon }\Lambda&<0, \end{aligned}$$

(32)

$$\begin{aligned} \Lambda ^T\widehat{\Xi }_m^{\upsilon \rho }\Lambda +\Lambda ^T\widehat{\Xi }_m^{\rho \upsilon }\Lambda&<0. \end{aligned}$$

(33)

Considering (30)–(31), we have

$$\begin{aligned} \begin{array}{lll} &{}{\mathbb {A}_{1m}^{\upsilon \rho T}}U\digamma =\begin{bmatrix} {{\mathscr {A}}_{m}^{\upsilon T}}\mathbb {U}+\bar{\rho }{{\mathscr {C}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}}&{} \quad {{\mathscr {A}}_{m}^{\upsilon T}}\mathbb {V}+\bar{\rho }{{\mathscr {C}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}}\\ {\mathsf {A}_{Fm}^{\rho T}}&{} \quad {\mathsf {A}_{Fm}^{\rho T}} \end{bmatrix},\\ &{}{\mathbb {A}_{2m}^{\upsilon \rho T}}U\digamma =\begin{bmatrix} {{\mathscr {C}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}}&{} \quad {{\mathscr {C}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}}\\ 0&{} \quad 0 \end{bmatrix},\\ &{}{\mathbb {A}_{dm}^{\upsilon T}}U\digamma =\begin{bmatrix} {{\mathscr {A}}_{dm}^{\upsilon \rho T}}\mathbb {U}+\bar{\rho }{{\mathscr {C}}_{dm}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}}&{} \quad {{\mathscr {A}}_{dm}^{\upsilon T}}\mathbb {V}+\bar{\rho }{{\mathscr {C}}_{dm}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}}\\ 0&{} \quad 0 \end{bmatrix},\\ &{}{\mathbb {B}_{m}^{\upsilon \rho T}}U\digamma =\begin{bmatrix} {{\mathscr {B}}_{m}^{\upsilon T}}\mathbb {U}+{{\mathscr {D}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}}&{} \quad {{\mathscr {B}}_{m}^{\upsilon T}}\mathbb {V}+{{\mathscr {D}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}}\\ {{\mathscr {E}}_{m}^{\upsilon T}}\mathbb {V}+{{\mathscr {G}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}} &{} \quad {{\mathscr {E}}_{m}^{\upsilon T}}\mathbb {U}+{{\mathscr {G}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho }}^T\\ {{\mathscr {F}}_{m}^{\upsilon T}}\mathbb {U}+{{\mathscr {H}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}} &{} \quad {{\mathscr {F}}_{m}^{\upsilon T}}\mathbb {V}+{{\mathscr {H}}_{m}^{\upsilon T}}{\mathsf {B}_{Fm}^{\rho T}} \end{bmatrix}. \end{array} \end{aligned}$$

Now (31) can be expressed as

$$\begin{aligned} \begin{bmatrix} {A}_{fm}^{\rho }&{} \quad {B}_{fm}^{\rho }\\ {C}_{fm}^{\rho }&{} \quad 0 \end{bmatrix}=\begin{bmatrix} U_2^{-T}U_3^{-1}\mathbb {V}^{-1}&{} \quad 0\\ 0&{} \quad I \end{bmatrix} \begin{bmatrix} \mathsf {A}_{Fm}^{\rho }&{} \quad \mathsf {B}_{Fm}^{\rho }\\ C_{Fm}^{\rho } &{} \quad 0 \end{bmatrix}\begin{bmatrix} U_2^{-T}U_3&{} \quad 0\\ 0&{} \quad I \end{bmatrix}. \end{aligned}$$

(34)

Note that the filter gain parameters ${A}_{fm}^{\rho }$, ${B}_{fm}^{\rho }$ and ${C}_{fm}^{\rho }$ in (3) can be modified as (34) which involve $U_2^{-T}U_3$ as similarity transformation on the state-space realization of the filter. Without loss of generality, we may assume that $U_2^{-T}U_3=I$, thus we obtain (27). Furthermore, by considering (32)–(34) together with Lemma 2.1 in [18], we can get the LMIs (24) and (25). Thus the considered augmented filtering error system (5) is finite-time stochastic bounded with strict $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipative subject to $(\Sigma _1,\Sigma _2,{\mathscr {F}}_m,\mathbb {H},\tilde{\delta },\gamma )$, only if the LMIs (24) and (25) hold together with (22). Hence the proof of this Theorem is complete. $\square$

Next we consider the augmented filtering error system (5) with the absence of the Markovian jump parameters in the following form

$$\begin{aligned} \eta (k+1)&=(\bar{\mathbb {A}}^{\upsilon \rho }+\bar{\rho }\tilde{\mathbb {A}}^{\upsilon })\eta (k)+\bar{\mathbb {A}}^{\upsilon \rho }_{d}\eta (k-d(k))+\bar{\mathbb {B}}^{\upsilon \rho }\vartheta (k),\nonumber \\ e(k)&=\bar{\mathbb {C}}^{\upsilon \rho }\eta (k), \end{aligned}$$

(35)

where

$$\begin{aligned}&\bar{\mathbb {A}}^{\upsilon \rho }=\begin{bmatrix} {\mathscr {A}}^{\upsilon }&{} \quad 0&{} \quad 0\\ \bar{\rho }{\mathscr {B}}_{f}^{\rho }{\mathscr {C}}^{\upsilon }&{} \quad {\mathscr {A}}_{f}^{\rho }&{} \quad 0\\ 0&{} \quad 0&{} \quad A_w \end{bmatrix},\quad \tilde{\mathbb {A}}^{\upsilon \rho }=\begin{bmatrix} 0&{}0&{}0\\ {\mathscr {B}}_{f}^{\rho }{\mathscr {C}}^{\upsilon }&{} \quad 0&{} \quad 0\\ 0&{} \quad 0&{} \quad 0 \end{bmatrix},\quad \\&\bar{\mathbb {A}}_{d}^{\upsilon \rho }=\begin{bmatrix} {\mathscr {A}}_{d}^{\upsilon }&{} \quad 0&{} \quad 0\\ {\mathscr {B}}_{f}^{\rho }{\mathscr {C}}_{d}^{\upsilon }&{} \quad 0&{} \quad 0\\ 0&{} \quad 0&{} \quad 0 \end{bmatrix},\\&\bar{\mathbb {B}}^{\upsilon \rho }=\begin{bmatrix} {\mathscr {B}}^{\upsilon }&{} \quad {\mathscr {E}}^{\upsilon }&{} \quad {\mathscr {F}}^{\upsilon }\\ {\mathscr {B}}_{f}^{\rho }{\mathscr {D}}^{\upsilon }&{} \quad {\mathscr {B}}_{f}^{\rho }{\mathscr {G}}^{\upsilon }&{} \quad {\mathscr {B}}_{f}^{\rho }{\mathscr {H}}^{\upsilon }\\ 0&{} \quad 0&{} \quad B_w \end{bmatrix}\quad \text{ and }\quad \bar{\mathbb {C}}^{\upsilon \rho }=\begin{bmatrix} 0&\quad {\mathscr {C}}_{f}^{\rho }&\quad -C_w \end{bmatrix}. \end{aligned}$$

Corollary 1

Under the Assumption 1, for given positive scalars $d_1$, $d_2$, $\tilde{\mu }$, $\tilde{\mu }^{-k}$, $\Sigma _1$, $\mathbb {H}$, $\tilde{\delta }$, $\gamma$, $\bar{\rho },\bar{\lambda }_1,\bar{\lambda }_2$ and positive definite matrix ${\mathscr {F}}$, the considered augmented system (35) is finite-time stochastic bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$, dissipative subject to $(\Sigma _1,\Sigma _2,{\mathscr {F}},\mathbb {H},\tilde{\delta },\gamma )$ if there exist positive definite matrices $\mathsf {P}_{111}$, $\mathsf {P}_{112}$, $\mathsf {P}_{12}$, $U_1$, $U_3$, V, $Q_{111}$, $Q_{112}$, $Q_{12}$, $Q_{211}$, $Q_{212}$, $Q_{22}$, $Q_{311}$, $Q_{312}$, $Q_{32}$, any appropriate dimensioned matrices $\mathbb {U}$, $\mathbb {V}$, $\mathsf {A}_{F}^{\upsilon }$, $\mathsf {B}_{F}^{\upsilon }$, $\Sigma _{F}^{\upsilon }$ and positive scalars $\Sigma _{2}$, $\tilde{\varepsilon _3}$, $\tilde{\varepsilon _4}$ such that the following LMIs together with (22) hold:

$$\begin{aligned}{}[\Psi ^{\upsilon \upsilon }]&<0,\quad \upsilon =\rho , \end{aligned}$$

(36)

$$\begin{aligned} +[\Psi ^{\rho \upsilon }]&<0,\quad \upsilon <\rho , \end{aligned}$$

(37)

where $\Psi ^{\upsilon \rho }=\begin{bmatrix} [\hat{\Psi }^{\upsilon \rho }]_{19\times 19}&{} \quad \tilde{\varepsilon _3}\Gamma _5^T&{} \quad \Gamma _6&{}\tilde{\varepsilon _4}\Gamma _7^T&{} \quad \Gamma _8\\ *&{} \quad -\tilde{\varepsilon _3}&{} \quad 0&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad -\tilde{\varepsilon _3}&{} \quad 0&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -\tilde{\varepsilon _4}&{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\tilde{\varepsilon _4} \end{bmatrix}$,

$[\hat{\Psi }^{\upsilon \rho }]_{1,1}=-\tilde{\mu }\mathsf {P}_{11}+(1+d_M)Q_{111}+Q_{211}+Q_{311}$,

$[\hat{\Psi }^{\upsilon \rho }]_{1,16}=A^{\upsilon T}\mathbb {U}+\bar{\rho }{C}^{\upsilon T}{B}_{F}^{\upsilon \rho T}+{\mathscr {C}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$,

$[\hat{\Psi }^{\upsilon \rho }]_{1,17}=A^{\upsilon T}\mathbb {V}+\bar{\rho }{\mathscr {C}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}+{\mathscr {C}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$,

$[\hat{\Psi }^{\upsilon \rho }]_{2,2}=-\hat{\mu }\mathsf {P}_{12}+Q_{112}+d_MQ_{112}+Q_{212}+Q_{312}$,

$[\hat{\Psi }^{\upsilon \rho }]_{2,14}= -C_{F}^{\upsilon \rho T}\mathsf {S}$, $[\hat{\Psi }^{\upsilon \rho }]_{2,16}= \mathsf {A}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{2,17}= \mathsf {A}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{2,19}=C_{F}^{\upsilon \rho T} \sqrt{-\mathsf {Q}}$, $[\hat{\Psi }^{\upsilon \rho }]_{3,3}=-\tilde{\mu }\mathsf {P}_{2}+Q_{12}+d_MQ_{12}+Q_{22}+Q_{32}$, $[\hat{\Psi }^{\upsilon \rho }]_{3,15}= {C}_{w}^{\upsilon T}\mathsf {S}$, $[\hat{\Psi }^{\upsilon \rho }]_{3,18}={A}_w^TV$, $[\hat{\Psi }^{\upsilon \rho }]_{3,19}=-C_{w}^T \sqrt{-\mathsf {Q}}$, $[\hat{\Psi }^{\upsilon \rho }]_{4,4}= -Q_{211}$, $[\hat{\Psi }^{\upsilon \rho }]_{5,5}=-Q_{212}$, $[\hat{\Psi }^{\upsilon \rho }]_{6,6}=-Q_{22}$, $[\hat{\Psi }^{\upsilon \rho }]_{7,7}=-Q_{111}$, $[\hat{\Psi }^{\upsilon \rho }]_{7,16}= A_{d}^{\upsilon T}\mathbb {U}+{\mathscr {C}}_{d}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{8,8}=-Q_{112}$, $[\hat{\Psi }^{\upsilon \rho }]_{9,9}=-Q_{12}$, $[\hat{\Psi }^{\upsilon \rho }]_{10,10}=-Q_{311}$, $[\hat{\Psi }^{\upsilon \rho }]_{11,11}=-Q_{312}$, $[\hat{\Psi }^{\upsilon \rho }]_{12,12}=-Q_{32}$, $[\hat{\Psi }^{\upsilon \rho }]_{13,13}=\mathsf {R}_1-\gamma I$, $[\hat{\Psi }^{\upsilon \rho }]_{13,16}={\mathscr {B}}^{\upsilon T}\mathbb {U}+{\mathscr {D}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{13,17}={\mathscr {B}}^{\upsilon T}\mathbb {V}+{\mathscr {D}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{14,14}=\mathsf {R}_2-\gamma I$, $[\hat{\Psi }^{\upsilon \rho }]_{14,16}= {\mathscr {E}}^{\upsilon T}\mathbb {U}+{\mathscr {G}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{14,17}={\mathscr {E}}^{\upsilon T}\mathbb {V}+{\mathscr {G}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{15,15}= \mathsf {R}_3-\gamma I$, $[\hat{\Psi }^{\upsilon \rho }]_{15,16}= {\mathscr {F}}^{\upsilon T}\mathbb {U}+{\mathscr {H}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{15,17}= {\mathscr {F}}^{\upsilon T}\mathbb {V}+{\mathscr {H}}^{\upsilon T}\mathsf {B}_{F}^{\upsilon \rho T}$, $[\hat{\Psi }^{\upsilon \rho }]_{15,18}= \mathbb {V}^TB_{w}$, $[\hat{\Psi }^{\upsilon \rho }]_{16,16}=-\mathbb {V}$, $[\hat{\Psi }^{\upsilon \rho }]_{17,17}=-\mathbb {V}$, $[\hat{\Psi }^{\upsilon \rho }]_{18,18}=-\mathbb {V}$, $[\hat{\Psi }^{\upsilon \rho }]_{19,19}=-I$, $\Gamma _1=[\tilde{\varepsilon _1}\lambda _1\mathsf {N}^{\upsilon }\quad \underbrace{0\cdots 0}_{5}\quad \tilde{\varepsilon _1}\lambda _2\mathsf {N}_{d}^{\upsilon }\quad \underbrace{0\cdots 0}_{12}]^T$, $\Gamma _2=[\underbrace{0\cdots 0}_{15}\quad M^{\upsilon T}\mathbb {U}\quad M^{\upsilon T}\mathbb {V}\quad 0\quad 0]^T$, $\Gamma _3=[0\quad \tilde{\varepsilon _2}\mathsf {N}_a^{\rho }\quad \underbrace{0\cdots 0}_{10}\quad \tilde{\varepsilon _2}\mathsf {N}_{b}^{\rho } {\mathscr {D}}^{\upsilon }\quad \tilde{\varepsilon _2}\mathsf {N}_{b}^{\rho } G^{\upsilon }\quad \tilde{\varepsilon _2}\mathsf {N}_{b}^{\rho } {\mathscr {H}}^{\upsilon }\quad \underbrace{0\cdots 0}_{4} ]^T$, $\Gamma _4=[\underbrace{0\cdots 0}_{15} \quad {M_{1}^{\rho }}^T\quad {M_{1}^{\rho }}^T\quad 0 \quad 0]^T$ and the remaining elements are zero. Then there exists a desired fault detection filter in the form of (3) such that the augmented filtering error system (5) is finite-time stochastic bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipative. Moreover, the parameters of the filtering error system in the form of (35) are taken by

$$\begin{aligned} \begin{bmatrix} A_{f}^{\upsilon } &{} \quad B_{f}^{\upsilon }\\ C_{f}^{\upsilon }&{} \quad 0 \end{bmatrix}=\begin{bmatrix} \mathbb {V}^{-1}&{} \quad 0\\ 0&{} \quad I \end{bmatrix} \begin{bmatrix} \mathsf {A}_{F}^{\upsilon }&{} \quad \mathsf {B}_{F}^{\upsilon }\\ C_{F}^{\upsilon }&{} \quad 0 \end{bmatrix}. \end{aligned}$$

(38)

Proof

The proof of this corollary is similar to that of Theorem 3, and hence it is neglected. $\square$

Remark 2

The system under consideration and results derived in this paper can effectively reflect the nature of practical systems since it involves random parameter uncertainties, time-varying delays and missing measurements. Thus, it is worthy of mentioning that the consideration of all the unavoidable factors in a single framework makes the system to be more appropriate and significant. In [7, 8, 33, 34], various filters are developed for discrete-time Markovian jump systems. So far in the works mentioned above, the finite-time results have not yet been discussed. However, from the practical point of view, finite-time stability and boundedness are the most appropriate concepts to employ in real-world systems. On the other hand, parameter uncertainty is significant complexity in system modeling due to environmental disturbances. Further, the parameter uncertainties occur in a probabilistic way due to sudden environmental changes. Also, the transition probabilities among the modes are not always exactly available, and hence, they are assumed to be partly known. Based on this scenario, in this paper, the problem of finite-time fault detection filtering for a class of discrete-time T–S fuzzy Markovian jump system subject to randomly occurring parameter uncertainties, time-varying delay, external disturbances and missing measurements is addressed which makes the present work different from the existing works.

4 Numerical Examples

In this section, we provide two numerical examples, including mass–spring–damper model and their simulation results to display the validity of the proposed filter design scheme.

Example 1

Consider the T–S fuzzy MJSs (1) with two-mode and two-plant rule given as follows:

Rule 1 and mode = 1, 2

$$\begin{aligned}&A_{1}^{1}=\begin{bmatrix} -0.04 &{} \quad -0.015\\ 0.012 &{} \quad -0.035 \end{bmatrix},\ A_{2}^{1}=\begin{bmatrix} -0.006 &{} \quad -0.039\\ 0.046 &{} \quad -0.79 \end{bmatrix},\ A_{d1}^{1}=\begin{bmatrix} -0.055 &{} \quad 0.034\\ 0.067 &{} \quad -0.035 \end{bmatrix},\\&A_{d2}^{1}=\begin{bmatrix} -0.0025 &{} \quad 0.0015\\ 0 &{} \quad -0.0025 \end{bmatrix},\ B_{1}^{1}=[-0.003 \quad -0.035]^T,\ B_{2}^{1}=[-0.008 \quad -0.02]^T,\\&C_{1}^{1}=[-0.036 \quad -0.09],\ C_{2}^{1}=[-0.035 \quad -0.04],\ C_{d1}^{1}=[-0.001 \quad 0.06],\\&C_{d2}^{1}=[0.002 \quad -0.03],\ E_{1}^{1}=E_{2}^{1}=[-0.08\quad 0.02]^T,\ F_{1}^{1}=[0.04 \quad -0.05]^T,\\&F_{2}^{1}=[0.06\quad 0.02]^T,\ H_{1}^{1}= G_{2}^{1}=0.02,\ H_{2}^{1}=D_{1}^{1}=0.04,\ D_{2}^{1}=0.09,\ G_{1}^{1}=-0.03. \end{aligned}$$

The parametric uncertainties for plant rule:1 are chosen as follows

$$\begin{aligned}&M_{1}^{1}=M_{11}^{1}=[0.1\quad 0.02]^T,\ M_{2}^{1}=M_{12}^{1}=[0.1\quad 0.14]^T,\ N_{1}^{1}=[0.01\quad 0.01],\\&N_{2}^{1}=[0.06 \quad 0.02],\ N_{d1}^{1}=[0.04\quad 0.12],\ N_{d2}^{1}=[0.08\quad 0.11],\ N_{a1}^{1}=[0.01\quad 0.12],\\&N_{a2}^{1}=[0.03\quad 0.02],\ N_{b1}^{1}=0.01,\ N_{b2}^{1}=0.03. \end{aligned}$$

Rule 2 and mode = 1, 2

$$\begin{aligned}&A_{1}^{2}=\begin{bmatrix} -0.024 &{} \quad 0.05\\ 0.022 &{} \quad -0.05 \end{bmatrix},\ A_{2}^{2}=\begin{bmatrix} -0.016 &{} \quad -0.05\\ 0.006 &{} \quad -0.043 \end{bmatrix},\ A_{d1}^{2}=\begin{bmatrix} -0.0025 &{} \quad 0.011\\ 0 &{} \quad 0.02 \end{bmatrix},\\&A_{d2}^{2}=\begin{bmatrix} -0.003 &{} \quad 0.01\\ 0 &{} \quad -0.03 \end{bmatrix},\ B_{1}^{2}=[-0.001 \quad -0.030]^T,\ B_{2}^{2}=[-0.005 \quad -0.022]^T,\\&C_{1}^{2}=[-0.025 \quad -0.06]^T,\ C_{2}^{2}=[-0.018 \quad -0.03],\ C_{d1}^{2}=[-0.05 \quad -0.03],\\&C_{d2}^{2}=[-0.003 \quad -0.08],\ E_{1}^{2}=[-0.004 \quad 0.039]^T,\ E_{2}^{2}=[-0.005 \quad 0.022]^T,\\&F_{1}^{2}=[0.02\quad -0.03]^T,\ F_{2}^{2}=[0.03\quad 0.08]^T,\ H_{1}^{2}=-0.03,\ H_{2}^{2}=0.02,\ D_{1}^{2}=0.08,\\&D_{2}^{2}=0.05,\ G_{1}^{2}=0.07,\ G_{2}^{2}=0.09. \end{aligned}$$

The parametric uncertainties for plant rule:2 are taken as

$$\begin{aligned}&M_{1}^{2}=M_{11}^{2}=[0.1 \quad 0.03]^T,\ M_{2}^{2}=M_{12}^{2}=[0.1\quad 0.32]^T,\ N_{1}^{2}=[0.05\quad 0.11],\\&N_{2}^{2}=[0.03\quad 0.04],\ N_{d1}^{2}=[0.06\quad 0.04],\ N_{d2}^{2}=[0.01\quad 0.01],\ N_{a1}^{2}=[0.02\quad 0.01],\\&N_{a2}^{2}=[0.04\quad 0.05],\ N_{b1}^{2}=0.02,\ N_{b2}^{2}=0.04. \end{aligned}$$

Further the fault weighting matrices are taken as $A_w=\begin{bmatrix} 0.65 &{} \quad 0.22\\ 0.45 &{} \quad 0.07 \end{bmatrix}, B_w=[0.05\quad 0.09]^T$ and $C_w=[-0.02\quad 0.05]$. Furthermore we choose the parameters as $\bar{\lambda }_1=0.1$, $\bar{\lambda }_2=0.53$, $\bar{\rho }=0.04$, $\tilde{\mu }=0.2$, $\gamma =2.5789$ and assume that the time-varying delay bound lies between 1 to 5. By solving the LMIs in Theorem (3) together with the aforementioned parameter values, we obtain the filter gain matrices as

$$\begin{aligned}&A_{f11}=\begin{bmatrix} -0.0104 &{} \quad -0.1247\\ 0.0090 &{} \quad 0.1085 \end{bmatrix},\quad A_{f12}=\begin{bmatrix} -0.1223 &{} \quad -0.1800\\ 0.1023 &{} \quad 0.1489 \end{bmatrix},\\&A_{f21}=\begin{bmatrix} -0.0312 &{} \quad -0.0207\\ -0.0072 &{} \quad -0.0044 \end{bmatrix},\quad A_{f22}=\begin{bmatrix} -0.1101 &{} \quad -0.1799\\ 0.1855 &{} \quad 0.2090 \end{bmatrix},\\&B_{f11}=\begin{bmatrix} 0.2019&\quad -0.1741 \end{bmatrix}^T,\ B_{f12}=\begin{bmatrix} 0.2134\&-0.1818 \end{bmatrix}^T,\\&B_{f21}=\begin{bmatrix} 0.1230&\quad 0.0874 \end{bmatrix}^T,\ B_{f22}=\begin{bmatrix} 0.0800&\quad 0.0449 \end{bmatrix}^T,\ C_{f11}=\begin{bmatrix} 0.1483&\quad 1.7831 \end{bmatrix},\\&C_{f12}=\begin{bmatrix} 0.2706&\quad 0.5276 \end{bmatrix},\ C_{f21}=\begin{bmatrix} 0.9557&\quad 0.6339 \end{bmatrix}\ \text{ and }\ C_{f22}=\begin{bmatrix} 1.0656&\quad 0.9983 \end{bmatrix}. \end{aligned}$$

Fig. 1

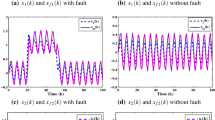
State responses of the system (2)

Fig. 2

Trajectory of $x_1(k)$ and $x_{f1}(k)$

Fig. 3

Trajectory of $x_2(k)$ and $x_{f2}(k)$

Fig. 4

State responses of the filter system (3)

Fig. 5

Filtering error

Fig. 6

Residual signal

Fig. 7

Residual evaluation function

Fig. 8

Jumping mode

Fig. 9

Evolution of $x^T(k){\mathscr {F}}_mx(k)$

For the simulation purposes, we have selected the following time-varying transition probability matrices as

$$\begin{aligned} \Pi _1=\begin{bmatrix}0.2 &{}0.8\\ ? &{}0.65 \end{bmatrix},\quad \Pi _2=\begin{bmatrix}? &{} \quad 0.45\\ 0.48 &{} \quad ? \end{bmatrix},\quad \Pi _3=\begin{bmatrix}0.6 &{} \quad 0.4\\ 0.3 &{}0.7 \end{bmatrix},\quad \Pi _4=\begin{bmatrix}? &{} \quad 0.8\\ ? &{} \quad 0.1 \end{bmatrix}. \end{aligned}$$

Moreover the control inputs the external disturbances, the fault signals and the membership functions are chosen as $u(k)=0.0065$, $w(k)=\left\{ \begin{array}{rcl}4\sin (k), &{}5\le k\le 50,\\ 0,&{}\text{ elsewhere }.\end{array}\right.$, $f(k)=\left\{ \begin{array}{ccl} 2.5\sin (k), &{}30\le k\le 80,\\ 0, &{}\text{ elsewhere }. \end{array}\right.$, $h_1(x_1(k))=\frac{1-\frac{\sin ^2k}{0.2}}{2}$ and $h_2(x_2(k))=\frac{1+\frac{\sin ^2k}{0.2}}{2}$ respectively. Under the initial conditions $x(0)=x_f(0)=[0.1\quad 0.1]^T$together with the above mentioned gain values, the corresponding simulation results are plotted in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. The state response curves are depicted in Fig. 1. Specifically Figs. 2 and 3 expose the original state and the proposed filter state responses respectively. Moreover the corresponding filter state responses, the error state responses and the residual signal are shown in Figs. 4, 5 and 6, respectively. In Fig. 7, the evaluation function is given for the fault and fault-free cases. Meanwhile, the selected threshold value is $\mathsf {J}_{th}=\sup \limits _{w\ne 0,u\ne 0,f=0}\sqrt{\sum \limits _{0}^{150}\mu (k)^T\mu (k)}=0.0797$. Then we obtain the evaluation function $\mathsf {J}_{\mu }=\sum \limits _{0}^{35}\mu ^T(k)\mu (k)=0.0798$ and it is evident that the evaluation function $J_{\mu }$ is greater than the threshold $\mathsf {J}_{th}$. In this way, the fault is detected in five time steps within the fault range. Further the jumping mode is given in Fig. 8. Moreover within the $\Sigma _2$ bound the time evolution of $x^T(k){\mathscr {F}}_mx(k)\ (m\in {\mathscr {S}})$ is shown in Fig. 9. It is examined from Fig. 9 that the trajectories of the augmented filtering error system are under the prescribed bounded $\Sigma _2=0.1957$, which means that the considered system (2) is finite-time stochastic bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipative subject to (0.1, 0.1957, I, 100, 0.3, 2.5789). Hence, it can be concluded from the simulations that the designed filter algorithm effectively works for the augmented filtering error system (5) even in the presence of uncertainties and missing measurements.

Example 2

The mass–spring damper mechanical system from [45] is described as follows:

$$\begin{aligned} x(k+1)&=(A^{\upsilon }+\bar{\lambda }_1\Delta A^{\upsilon }(k))x(k)+(A_{d}^{\upsilon }+\bar{\lambda }_2\Delta A_d^{\upsilon }(k))x(k-d(k)) +B^\upsilon u(k) +E^\upsilon w(k)\nonumber \\&\quad + F^\upsilon f(k), \nonumber \\ y(k)&=\rho (k)C^\upsilon x(k)+C_{d}^\upsilon x(k-d(k)) +D^\upsilon u(k) +G^\upsilon w(k)+H^\upsilon f(k), \end{aligned}$$

(39)

Rule 1

$$\begin{aligned}&A^{1}=\begin{bmatrix} 0.3 &{} \quad 0.2\\ -0.0012 &{} \quad 0.5\end{bmatrix},\ A_d^{1}=\begin{bmatrix}0.2 &{} \quad 0\\ -0.0028 &{} \quad 0.1\end{bmatrix},\ B^{1}=\begin{bmatrix}0 \\ 0.2\end{bmatrix},\ E^{1}=\begin{bmatrix}0.02 \\ -0.01\end{bmatrix},\\&F^{1}=\begin{bmatrix}0.3\\ 0.5\end{bmatrix},\ C^{1}=\begin{bmatrix}0.2&\quad 0.9\end{bmatrix},\ Cd^{1}=\begin{bmatrix}0&\quad -0.1\end{bmatrix},\ D^{1}=0.4,\ G^{1}=0.2,\ H^{1}=-1.2. \end{aligned}$$

We choose the uncertain parameters as

$$\begin{aligned} M^{1}&=[0.1\ 0.02]^T,\ N^{1}=[0.01\ 0.2],\ N_d^{1}=[0.04\ 0.12],\\ N_a^{1}&=[0.01\ 0.1],\ N_b^{1}=0.01. \end{aligned}$$

Rule 2

$$\begin{aligned}&A^{2}=\begin{bmatrix} 0.3 &{} \quad 0.2\\ -0.0048 &{} \quad 0.5\end{bmatrix},\ A_d^{2}=\begin{bmatrix}0.2 &{} \quad 0\\ -0.0113 &{} \quad 0.1\end{bmatrix},\ B^{2}=\begin{bmatrix}0&\quad 0.2\end{bmatrix}^T,\ E^{2}=\begin{bmatrix}-0.09 \\ 0.03\end{bmatrix},\\&F^{2}=\begin{bmatrix}-0.4\\ 0.6\end{bmatrix},\ C^{2}=\begin{bmatrix}0.1&\quad 0.3\end{bmatrix},\ Cd^{2}=\begin{bmatrix}0.6&\quad -0.3\end{bmatrix},\ D^{2}=0.3,\ G^{2}=-0.2. \end{aligned}$$

We consider the uncertain parameters as $M^{2}=[0.1\quad 0.14]^T$, $N^{2}=[0.06 \quad 0.1]$, $N_d^{2}=[0.06\quad 0.04]$, $N_a^{2}=[0.03\quad 0.1]$ and $N_b^{2}=0.03.$

Fig. 10

State responses of the system (2)

Fig. 11

Trajectory of $x_1(k)$ and $x_{f1}(k)$

Fig. 12

Trajectory of $x_2(k)$ and $x_{f2}(k)$

Fig. 13

State responses of the filter system (35)

Fig. 14

Response of estimation error

Fig. 15

Response of residual signal

Fig. 16

Residual evaluation function

Fig. 17

Evaluation of $x^T(k){\mathscr {F}}x(k)$

Further, we set the remaining parameters to be the same as in Example 1. Then, by solving the LMIs in Corollary (1) along with the parameter values as mentioned above, we obtain the filter gain matrices as

$$\begin{aligned}&A_{f1} =\begin{bmatrix}-0.0574 &{} \quad -0.5744\\ 0.0518 &{} \quad 0.5177\end{bmatrix},\ A_{f2}=\begin{bmatrix}0.2145&{} \quad 0.0270\\ 0.0270&{} \quad 0.2805\end{bmatrix},\ B_{f1}=\begin{bmatrix}-0.5146&\quad -0.1038\end{bmatrix},\\&B_{f2}=\begin{bmatrix}-0.4445&\quad 0.0959\end{bmatrix},\quad C_{f1}=\begin{bmatrix}0.0460&\quad 0.4591\end{bmatrix},\quad C_{f2}=\begin{bmatrix}0.0736&\quad 0.3497\end{bmatrix}. \end{aligned}$$

For simulation purposes, we consider the control input, disturbances input and fault signals are $w(k)=\left\{ \begin{array}{cl} 1.5\sin (k) &{}15\le k\le 30\\ 0 &{} \text {otherwise}, \end{array}\right.$ $f(k)=\left\{ \begin{array}{cl} 0.8\sin (k)&{} 20\le k\le 40\\ 0 &{} \text {otherwise} \end{array} \right. \$, $u(k)=0.0045$, $h_1(x_1(k))=1-\frac{(0.3x(k)+0.7x(k))^2}{0.09}$ and $h_2(x_2(k))=\frac{(0.3x(k)+0.7x(k))^2}{0.09}$. Moreover, under the initial conditions $x(0)=[0.1\quad 0.1]^T$ and $x_f(0)=[ 0.1\quad 0.3]^T$, the corresponding simulation results are plotted in Figs. 10, 11, 12, 13, 14, 15, 16, and 17. The state trajectory is displayed in Fig. 10.The actual states and their estimations are shown in Figs. 11 and 12. Moreover, the corresponding filter state responses, the error state responses and the residual signal are depicted in Figs. 13, 14 and 15, respectively. The evaluation function $\mathsf {J}_{th}$ is illustrated for fault and fault-free cases in Fig. 16. Furthermore, the selected threshold values are $\mathsf {J}_{th}$ $=\sup \limits _{u\ne 0,\ w\ne 0,f=0}\bigg (\sum _{k=0}^{150}\mu '(k)\mu (k)\bigg )^{1/2}=0.1679$. Then we have the evaluation function $\mathsf {J}_{\mu }(k)=\sqrt{\bigg (\sum _{k=0}^{24}\mu '(k)\mu (k)\bigg )^{1/2}}=0.1682$ and it is clear that the evaluation function $\mathsf {J}_{\mu }$ is greater than the threshold $\mathsf {J}_{th}$; thus the fault can be detected after four time steps within the fault range. In addition to obtain the finite-time stability, the time history of $x^T(k){\mathscr {F}}x(k)$ is displayed in Fig. 17. It is easy to observe that the state responses of the filter state lies within the optimum bound $\Sigma _2$ which is clearly shown in Fig. 17. Hence, from these simulation results, it is concluded that the considered mechanical system (39) is finite-time bounded with strictly $(\mathsf {Q},\mathsf {S},\mathsf {R})$-$\gamma$ dissipative subject to (0.07, 0.5017, I, 100, 0.1, 1.512) through the proposed filter design approach.

5 Conclusion

In this paper, we have studied the robust finite-time fault detection filtering problem for a class of T–S fuzzy MJSs with randomly occurring uncertainties, time-varying delay and missing measurements. In particular, we have considered the non-homogeneous Markov process, which takes the transition probability as partly unknown. Besides, the system uncertainties are described through stochastic variables satisfying the Bernoulli distribution. By employing the Lyapunov stability theory and some discrete-time type Jensen’s inequality technique, we developed a finite-time boundedness criterion with the prescribed performance index. Moreover, a filter design algorithm is presented in the form of LMI constraints to ensure the finite-time stochastic stabilization of the addressed systems. Finally, we have provided two numerical examples to verify the developed theoretical results.