Finite-Time Fault Detection Filter Design for T–S Fuzzy Markovian Jump Systems with Distributed Delays and Incomplete Measurements

Abstract

This paper is concerned with the problem of fault detection filter design for a class of nonlinear Markovian jump systems with incomplete measurements and distributed delay. A unified model is proposed to address the phenomena such as packet losses, signal quantization and sensor saturation. The objective is to design a finite-time dissipative-based fault detection filter such that for all unknown disturbances, the estimation error between the residual signal and the fault is minimized and also to guarantee the stochastic finite-time boundedness of the augmented filtering error system with a prespecified dissipative performance level. By using Lyapunov stability theory along with stochastic analysis techniques, a set of sufficient criterion is established for the existence of desired fault detection filter. Further, the filter gain parameters are obtained by solving the linear matrix inequality-based constraints. Two numerical examples including an inverted pendulum model are presented to illustrate the effectiveness of the proposed filter design algorithm.

1 Introduction

The actual operation process of many physical systems may be subject to abrupt changes in the structure or parameters of the system due to unexpected variations in the environment, component failures, random delays and sudden changes in subsystem interconnections. Markovian jump systems (MJSs) provide an efficient framework for the analysis and synthesis of such a class of dynamic systems and have received considerable research attention. Over the past decades, many significant issues have been deeply investigated for MJSs and number of important results have been proposed [2, 7, 8, 13, 20, 28]. For instance, in [13] an observer-based fault detection filter is constructed for a class of nonlinear Markovian jump systems subject to unreliable communication channels. The authors in [28] designed a robust fault detection filter for Markovian jump linear systems by considering the effects of missing measurements and signal quantization. A fault detection filtering problem for Markovian jump systems subject to randomly varying nonlinearities and sensor saturations is addressed in [7], wherein the transition probabilities are assumed to be partly known.

The fuzzy model-based filtering technique has attracted prominent attention from the researchers since it has been regarded as a powerful and conceptually simple tool to deal with complex nonlinear systems. It should be mentioned that the Takagi–Sugeno (T–S) fuzzy model is characterized by a set of fuzzy IF-THEN rules which represent the local input-output relations of the nonlinear system. In general, the comprehensive model is obtained by combining the linear models via nonlinear fuzzy membership functions. In recent years many fruitful results have been developed for T–S fuzzy systems [1, 4, 5, 11, 25, 30]. For example, In [1], a sufficient condition through a novel Lyapunov function that depends on the hidden mode and the observed mode with the elapsed time is developed in terms of LMIs to ensure the stability and $H_{\infty }$ performance of the closed-loop system via T–S fuzzy model. The authors in [5] studied the fault estimation problem for T–S fuzzy systems with a finite frequency $H_\infty$ performance index. In [4], a fault detection filter is developed for discrete-time T–S fuzzy systems in finite frequency domain. An asynchronous $l_2 - l_\infty$ filtering problem for fuzzy Markovian jump systems in the presence of sensor nonlinearity and packet dropouts is investigated in [25].

Due to the increased demands of higher performance, reliability and safety on the complex systems, the fault detection filtering techniques have been investigated extensively. The main purpose of fault detection is to accurately detect the fault signal whenever it appears. In order to achieve this, a residual signal is generated to indicate the inconsistency between the nominal and faulty system operation. The generated residual signal is then compared with a pre-defined threshold. If the residual exceeds the threshold, then it can be concluded that the fault has occurred. Based on this technique, great number of important results have been proposed in the literature regarding fault detection filtering for T–S fuzzy systems [3, 14,15,16, 29]. On another research front, the distributed fault detection has been an active research field since in a spatially distributed system, the information of an individual node is not only from its own measurement but also from its neighboring nodes measurements according to the given topology (see [9, 10, 33] and references therein).

The existence of time delay is inevitable in most of the physical processes such as communication systems, biological systems, flight control systems, chemical processes. Further, the presence of delay significantly deteriorates the system performance or instantaneously leads to instability. When the number of summands in a system equation is increased and the differences between neighboring argument values are decreased, then systems with distributed delays will arise. Therefore, distributed delay systems have received much attention in the past years. It should be mentioned that distributed delay has gained remarkable research interest since signal transmission is distributed among parallel transmission lines [6, 12, 17, 21, 27, 31]. However, insertion of communication networks introduces some unavoidable technological imperfections such as sensor saturations, quantization effects, packet losses due to the unreliability of communication channels. It should be mentioned that sensors cannot always provide unlimited signals due to physical and technological constraints which results in sensor saturations. The saturation in sensors instantaneously brings unexpected variations that result in nonlinear characteristics of sensors or even instability of the overall system [19, 22, 34].

It is worth mentioning that dissipative theory plays an important role in the study of system stability. Moreover, compared with $H_\infty$ and passivity performances, dissipativity is a more general criterion. Also, it provides a less conservative and more flexible filter design since it manages a better trade-off between the gain and phase performances. However, there are only few results that have been proposed regarding the dissipative-based fault detection filtering [23, 26, 32]. Most of the existing results in the literature regarding fault detection filters focus on the Lyapunov asymptotic stability defined over an infinite time interval. However, in practical applications, analyzing the behavior within a finite time is significant and meaningful. Finite-time stability and boundedness admit that the states of the system do not exceed a certain bound during a finite-time interval. In recent years, many results on finite-time stability or boundedness are obtained [18, 24].

From the practical point of view, the fault detection technique is a powerful tool to detect the fault signal which is common in nature and often reduces the performance of the system. In practical engineering, due to communication channel inconstancy, some inevitable technological defect, namely incomplete measurement, may occur and critically affect the measurement of the system information. Moreover, infinite distributed delays cannot be ignored since they may do serious harm to the stability of practical systems. On the other hand, in practical applications, it is significant and interesting to analyze the behavior of systems within a finite period. Therefore, it is sensible and noteworthy to design a finite-time distributed fault detection filtering for nonlinear Markovian jump systems subject to distributed delays, packet losses, signal quantization and sensor saturation.

Based on the above discussions, this paper concerns the fault detection filtering problem for nonlinear Markovian jump systems with incomplete measurements and distributed delays. The main concerns of this paper are as follows:

• 1. A dissipative-based distributed fault detection filtering problem is investigated for a class of nonlinear Markovian jump systems with incomplete measurements and distributed delays.

• 2. A unified system model is proposed to describe the phenomena of incomplete measurements, namely packet losses, signal quantization and sensor saturation.

• 3. By using Lyapunov stability theory together with stochastic system analysis, a new set of sufficient conditions is established for the existence of desired fault detection filter.

Finally, the feasibility and effectiveness of the developed distributed fault detection filter design methodology are illustrated by using numerical examples including an inverted pendulum model.

Notations: ${\mathbb {R}}^{n}$ and ${\mathbb {R}}^{n\times n}$ denote the $n-$dimensional Euclidean space and set of all $n\times n$ real-valued matrices, respectively; a positive definite matrix ${\mathscr {P}}$ is denoted ${\mathscr {P}}>0$; the superscripts T and $(-1)$ stand for matrix transposition and matrix inverse, respectively. In symmetric block matrix expressions, we use an asterisk $*$ to represent the term induced by symmetry; ${\mathrm{diag}}\{\cdot \}$ indicates a block diagonal matrix; $l_{2}[0,\infty )$ refers to space that are square summable sequence; the symbol ${\mathbb {Q}}^{i}(\cdot )$ denoted the quantization effects of the ith sensor; ${\mathbb {E}}\{\cdot \}$ represents the mathematical expectation operator.

2 Problem Formulation and Preliminaries

It is assumed that the sensor network considered in this paper has n number of sensor nodes that are distributed according to a specific interconnection topology described by a directed graph ${\mathsf {G}}=({\mathsf {V}},{\mathsf {E}},{\mathsf {A}})$, where ${\mathsf {V}}=\{1,2,\ldots ,n\}$ is the set of sensors; ${\mathsf {E}}$ is the set of edges contained in sensors mapping set; and ${\mathsf {A}}=(a_{ij})_{n\times n}$ is the nonnegative adjacency matrix correlated with the edges of the directed graph, i.e., $a_{ij}>0$ implies edge $(i,j)\in {\mathsf {E}}$, which means the jth sensor node transfers the information to the ith sensor node and also jth node is called as neighbor of ith node. Furthermore, it is assumed that the sensors are self-connected, i.e., $a_{ii}=1$ for all $i\in {\mathsf {V}}$. Finally, for all $j\in {\mathsf {V}}$, ${\mathscr {N}}_i=\{i\in {\mathsf {V}}:(i,j)\in {\mathsf {E}}\}$ means that the sensor node i can receive the information from its neighboring sensor node j according to the prescribed network topology.

Let $\{\nu (k),k\in {\mathscr {Z}}^+\}$ is a Markov chain taking the values in a state-space ${\mathscr {S}}=\{1,2,\ldots ,{\mathscr {M}}\}$ with transition probabilities defined as $\chi ={\phi _{mn}(k)}, \ m,n\in {\mathscr {S}}$, where $\Pr \{\nu (k+1)=n|\nu (k)=m\}=\phi _{mn}$ be the transition probabilities from mode m to n at time k and $k+1$, respectively, and $\phi _{mn}(k)\ge 0$, $\sum \limits _{n=1}^{{\mathscr {M}}}\phi _{mn}(k)=1$ should be satisfied and for notational convenience let us denote $\nu (k)=m$.

The plant is a nonlinear system with Markovian jumping parameters, which can be approximated by the following fuzzy rule:

Plant Rule s: IF $\phi _1(k)$ is ${\mathsf {M}}_{s1}$ and $\phi _2(k)$ is ${\mathsf {M}}_{s2}$ $\cdots$ and $\phi _g(k)$ is ${\mathsf {M}}_{sg}$, THEN

$$\begin{aligned} x(k+1)=&A_{s}^{m}x(k)+A_{\tau s}^{m}\sum \limits _{b=1}^{h}x(k-\tau _{b}(k))+B_{s}^{m}w(k)+E_{s}^{m}f(k),\nonumber \\ s=&1,2,\ldots ,l, \end{aligned}$$

(1)

where $x(k)\in {\mathbb {R}}^{n_1}$ is the state of the plant; $w(k)\in {\mathbb {R}}^{n_2}$ is the disturbance vector belonging to $l_2[0,\infty )$ ; $f(k)\in {\mathbb {R}}^{n_f}$ is the fault signal. $A_s^{m}$, $A_{\tau s}^{m}$, $B_s^{m}$ and $E_s^{m}$ are known constant matrices with appropriate dimensions. The distributed time-varying delay is denoted as $\sum \limits _{b=1}^{h}x(k-\tau _{b}(k))$ in which $\tau _b(k), \ b=1,2,\ldots ,h$ are the communication time-varying delays satisfying the condition $\tau _1\le \tau _b(k)\le \tau _2$, where $\tau _1$ and $\tau _2$ are the positive scalars representing the minimum and maximum delays, respectively. Let $\phi (k)=[\phi _1(k),\phi _2(k),\ldots ,\phi _g(k)]$ be the premise variable vector; ${\mathsf {M}}_{st}$ is the fuzzy set; l is the number of IF-THEN rules. The fuzzy basis function is given by

$$\begin{aligned} h_s(\phi )=\frac{\Pi _{t=1}^{q}{\mathsf {M}}_{st}(\phi _t)}{\sum _{s=1}^{l}\Pi _{t=1}^{q}{\mathsf {M}}_{st}(\phi _t)}, \end{aligned}$$

(2)

where ${\mathsf {M}}_{st}(\phi _s)$ represents the grade of membership of $\phi _s$ in ${\mathsf {M}}_{st}$. Therefore, for all k we have $h_s(\phi )\ge 0,$ $s=1,2,\ldots ,l$ and $\sum _{s=1}^{l}h_s(\phi )=1$. Then, by fuzzy blending system (1) can be rewritten as follows:

$$\begin{aligned} x(k+1)=\sum \limits _{s=1}^{l}h_s(\phi )[A_{s}^{m}x(k)+A_{\tau s}^{m}\sum \limits _{b=1}^{h}x(k-\tau _{b}(k))+B_{s}^{m}w(k)+E_{s}^{m}f(k)]. \end{aligned}$$

(3)

For the purpose of estimation, the local measurement of ith sensor node is described as follows

$$\begin{aligned} {y}_{i}(k)=C_{is}x(k), \end{aligned}$$

(4)

where $y_{i}(k)\in {\mathbb {R}}^{n_{4i}}$ is the ith sensor measurement and $C_{is}$ be the known constant matrix.

The sensor saturation phenomenon frequently appears in practical systems due to some physical limitations of the sensor nodes. The estimation performance is extremely distressed since the sensor saturation eventually results in nonlinear characteristics of sensors. Here, we have considered the sensor saturation for the distributed filtering system. We first assume that the sensor saturation function $\theta _i(\cdot )$ which belongs to $[{\mathscr {S}}_1,{\mathscr {S}}_2]$. Let ${\mathscr {S}}_1\in {\mathbb {R}}^{n_{4i}\times n_{4i}}$ and ${\mathscr {S}}_2\in {\mathbb {R}}^{n_{4i}\times n_{4i}}$ be any known diagonal matrices, where ${\mathscr {S}}_1,\ {\mathscr {S}}_2\ge 0$ and ${\mathscr {S}}_2>{\mathscr {S}}_1$. The sensor saturation function $\theta _i(\cdot )$ satisfies the inequality:

$$\begin{aligned}{}[\theta _i(y_i(k))-{\mathscr {S}}_1y_i(k)]^T[\theta _i(y_i(k))-{\mathscr {S}}_2y_i(k)]\le 0,\quad \forall \ y_i(k)\in {\mathbb {R}}^{n_{4i}}. \end{aligned}$$

(5)

By (5), the sensor saturation function $\theta _i(y_i(k))$ can be separated into a linear and nonlinear part as

$$\begin{aligned} \theta _i(y_i(k))={\bar{\theta }}_i(y_i(k))+{\mathscr {S}}_1y_i(k), \end{aligned}$$

(6)

where ${\bar{\theta }}_i(y_i(k))$ is a nonlinear function belonging to $\Theta =\big \{ {\bar{\theta }}:{\bar{\theta }}_i(y_i(k))^T({\bar{\theta }}_i(y_i(k))-\mathcal {V}y_i(k))\le 0\big \}$, ${\mathbb {S}}={\mathscr {S}}_{2}-{\mathscr {S}}_{1}>0.$

Further, a logarithmic quantizer is utilized for the purpose of packet size reduction. The quantizer is static and it is assumed to be symmetric, i.e., ${\mathbb {Q}}^{i}(-v_i)=-{\mathbb {Q}}^{i}(-v_i)$. The quantization level set can be described as

$$\begin{aligned} { U_i = {\pm \kappa ^{i}_{\iota },\kappa ^{i}_{\iota }=\phi _{\iota }^{i}\kappa _0^{i},\iota =0,\pm 1,\pm 2,\ldots ,c}\cup \{\pm \kappa _0^{i}\}\cup {0},\quad 0<\phi ^{i}<1,\quad \kappa _0^{i}>0.} \end{aligned}$$

(7)

The output of the quantizer is given by

$$\begin{aligned} {\mathbb {Q}}^{i}(v_i)=\left\{ \begin{array}{ll} \kappa _{\iota }^{i}, &{}\text {if}\ \frac{1}{1+\varrho ^{i}\kappa _{\iota }^{i}}<v_i<\frac{1}{1-\varrho ^{i}\kappa _{\iota }^{i}}, v_i>0,\\ 0, &{}\text {if} \ v_i=0,\\ -{\mathbb {Q}}^{i}(-v_i), &{}\text {if} \ v_i<0, \end{array}\right. \end{aligned}$$

where $\varsigma _{i}=\frac{1-\varpi _{i}}{1+\varpi _{i}}<1$ with $0<\varpi _{i}<1$ is the quantization density and it is taken as ${\mathbb {Q}}(v_i)=(I+\varDelta _i)v_i,$ where $\Vert \varDelta _i\Vert \le \varsigma _{i}.$

Due to communication constraints, the transmitted packet may be lost or delayed and it is not crucial to find bounds of the time-varying delay. So, the communication delay d(k) is assumed to satisfy $d_1\le d(k)\le d_2$, where $d_1$ and $d_2$ are positive scalars. The effectiveness of these network uncertainties quite included toward the measurement model is as follows:

$$\begin{aligned} {\tilde{y}}_{i}(k)=&\beta _{1i}(k)y_{i}(k)+\beta _{2i}(k)\theta _i (y_{i}(k))+\beta _{3i}(k){\mathbb {Q}}(y_{i}(k))+\beta _{4i}(k)y_i(k-d(k))\nonumber \\&+D_{is}w(k), \end{aligned}$$

(8)

where $D_{is}$ is known constant; w(k) is the disturbance in communication channel; and $\beta _{zi}\ (z=1,2,3,4)$ are stochastic variables satisfying the Bernoulli distribution: $\beta _{zi}(k)\in [0,1]$, ${\mathbb {E}}\{\beta _{zi}(k)=1\}={\bar{\beta }}_{zi}$ and ${\mathbb {E}}\{\beta _{zi}(k)=0\}=1-{\bar{\beta }}_{zi}$. To determine the distributed filter design problem it is assumed that the packet dropout rates, quantization density and bounds of communication delay are granted to be known.

From local measurement (8), it is clear that the size of ${\tilde{y}}_{i}(k)$ is $n_{4i}$. So, the transmission takes place in multiple packet mechanism which is essential to propose the result. A matrix operator is considered in this paper for scheduling the transmission. In the view of above analysis, the final measurement is expressed as

$$\begin{aligned} {\bar{y}}_{i}(k)=\Pi _{\rho _{i}(k)}{\tilde{y}}_{i}(k), \end{aligned}$$

(9)

where ${\bar{y}}_{i}(k)$ is the measurement; $\Pi _{\rho _{i}(k)}$ is the structured matrix. Here, we choose only one element for transmission which is the most energy efficient case. Then $\rho _{i}(k)$ is the switching signal which belongs to $\chi _i=\{1,2,\ldots ,n_{4i}\}$. By defining a mapping from $\rho _{i}(k)$ to $\rho (k)$, only one switching signal can be used to describe all the cases and for all the sensors.

It should be noticed that in the distributed filter design for sensor networks, the sensor node i will blend the available information from both self-node and the neighboring nodes. In this paper, we take the premise variables of the filter are as same as that of the plant. The following distributed fuzzy-dependent filter is proposed for fault detection purpose as

Filter rule t: IF $\phi _1(k)$ is ${\mathsf {M}}_{t2}$ and $\phi _2(k)$ is ${\mathsf {M}}_{t2}$ $\ldots$ and $\phi _g(k)$ is ${\mathsf {M}}_{tl}$, THEN

$$\begin{aligned} {\bar{x}}_i(k+1)=&\sum \limits _{t=1}^{l}h_t(\phi )\bigg [\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {K}}^m_{ijt}{\bar{x}}_{j}(k)+\sum \limits _{j \in {\mathscr {N}}_{i}}{a}_{ij}{\mathscr {H}}^m_{ijt}{\bar{y}}_{j}(k)\bigg ],\nonumber \\ \vartheta (k)=&\sum \limits _{t=1}^{l}h_t(\phi ){\mathscr {L}}^m_{iit}{\bar{x}}_{i}(k), \end{aligned}$$

(10)

where $a_{ij}$ is the adjacency scalar, ${\bar{x}}_j(k)\in {\mathscr {R}}^{n_x}$ is the filter state vector; $\vartheta (k)\in {\mathscr {R}}^{n_\vartheta }$ are the residual signal; ${\mathscr {K}}^m_{ijt}\in {\mathscr {R}}^{{n_x}\times {n_x}},\ {\mathscr {H}}^m_{ijt}\in {\mathscr {R}}^{{n_x}\times {n_y}},\ {\mathscr {L}}^m_{iit}{\mathscr {R}}^{{n_\vartheta }\times {n_x}}$ are the filter gain parameters to be determined for sensor node i. Further, for the sensor node $i\in \{1,2,\ldots ,n\}$, the initial condition is taken as ${\hat{x}}_i(0)=0_{n_x\times 1}$. Let us define ${\tilde{x}}_{i}(k)=x(k)-{\bar{x}}_i(k)$, then we have,

$$\begin{aligned} {\tilde{x}}_i(k+1)=&\sum \limits _{s=1}^{l}h_s(\phi )\sum _{t=1}^lh_t(\phi )\bigg \{\bigg (A_{s}^{m}-\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {K}}^m_{ijt}-\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {H}}^m_{ijt}\Pi _{\rho _i(k)}\nonumber \\&\beta _ {1j}(k){C}_{jt}^m\nonumber \\&-\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {H}}^m_{ijt}\Pi _{\rho _i(k)}\beta _{3j}(k){C}_{jt}^m -\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {H}}^m_{ijt}\Pi _{\rho _i(k)}\beta _{3j}(k)\varDelta (k){C}_{jt}^m\nonumber \\&-\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {H}}^m_{ijt}\Pi _{\rho _i(k)}\beta _{2j}(k){\mathscr {S}}_1C_{jt}^m\bigg ){x}(k)-\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {K}}^m_{ijt}{\tilde{x}}_i(k)\nonumber \\&+A_{\tau s}^{m}\sum \limits _{b=1}^{h} x(k-\tau _{b}(k))-\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {H}}^m_{ijt}\Pi _{\rho _i(k)}\beta _{2j}(k){\bar{\theta }}_j(C _{jt}^mx(k))\nonumber \\&-\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {H}}^m_{ijt}\Pi _{\rho _i(k)}\beta _{4j}(k) C_{jt}^mx(k-d(k)) +E_{s}^mf(k)+\big (B_s^m\nonumber \\&-\sum \limits _{j\in {\mathscr {N}}_{i}} {a}_{ij}{\mathscr {H}}^m_{ijt}\Pi _{\rho _i(k)}D_{jt}^m\big )w(k) \bigg \}. \end{aligned}$$

(11)

For notational simplicity, we denote

$$\begin{aligned}&S_s=\sum \limits _{s=1}^{l}h_s(\phi ),\ T_t=\sum _{t=1}^lh_t(\phi ),\ \pi _{zi}=\sqrt{\beta _{zi}(1+2\beta _{zi})},\ {\hat{A}}_s^m={\mathrm{diag}}\{{A}_s^m,\ldots ,{A}_s^m\},\\&{\widehat{A}}_{\tau _b s}^m={\mathrm{diag}}\{{A}_{\tau _b s},{A}_{\tau _b s},\ldots ,{A}_{\tau _b s}\}\ (b=1,2,\ldots ,h),\ {\widehat{B}}_s^m=[{B}_s^m,\ldots ,{B}_s^m]^T,\\&{\widehat{D}}_s^m=[{D}_s^m,\ldots ,{D}_s^m]^T,\quad {\widehat{F}}_s^m=[{F}_s^m,\ldots ,{F}_s^m]^T,\quad {\widehat{C}}_s^m={\mathrm{diag}}\{{C}_{1s}^m,\ldots ,{C}_{ns}^m\},\\&\Pi _{{\bar{\rho }}}={\mathrm{diag}}\{\Pi _{\rho _{1k}},\ldots ,\Pi _{\rho _{nk}}\},\quad \Lambda _{\beta _z}={\mathrm{diag}}\{\beta _{{z1}}I,\ldots ,\beta _{zn}I\} (z=1,2,3,4),\\&{\hat{L}}_s^m={\mathrm{diag}}\{{\hat{L}}_s^m,\ldots ,{\hat{L}}_s^m\},\quad {\widehat{x}}(k)=[x^T(k),\ldots ,x^T(k)]^T,\quad \\&\quad \sigma _{i}={\mathrm{diag}}\{0,\ldots ,1,\ldots ,0\},\\&{{\hat{x}}}(k)=[{\tilde{x}}_1^T(k),\ldots ,{\tilde{x}}_s^T(k)]^T,\quad \hat{{\mathscr {K}}}_{t}^m=\left\{ \begin{array}{ll}a_{ij}{K}^m_{ijt}&{}i\in {\mathsf {V}},\ j\in {\mathscr {N}}_i\\ 0, &{}i\in {\mathsf {V}},j\notin {\mathscr {N}}_{i} \end{array}\right. \quad \text {and}\quad \\&{\hat{\mathscr {H}}}_{t}^m=\left\{ \begin{array}{ll}a_{ij}{H}^m_{ijt}&{}i\in {\mathsf {V}},\ j\in {\mathscr {N}}_i\\ 0, &{}i\in {\mathsf {V}},j\notin {\mathscr {N}}_{i} \end{array}\right. . \end{aligned}$$

Now, we can rewrite (11) in the following form:

$$\begin{aligned} \breve{x}(k+1)=&\sum \limits _{s=1}^{l}h_s(\phi )\sum _{t=1}^lh_t(\phi )\bigg ({\hat{A}}_{s}^{m}-\hat{{\mathscr {K}}}^m_{t}-{\hat{\mathscr {H}}}^m_{t}\Pi _{{\bar{\rho }}}\Lambda _{\beta _ {1}}{\widehat{C}}_{t}^m-{\hat{\mathscr {H}}}^m_{t}\Pi _{{\bar{\rho }}}\Lambda _{\beta _{3}}{\widehat{C}}_{t}^m\nonumber \\&-{\hat{\mathscr {H}}}^m_{t}\Pi _{{\bar{\rho }}}\Lambda _{\beta _{3}}\varDelta (k){\widehat{C}}_{t}^m-{\hat{\mathscr {H}}}^m_{t}\Pi _{\rho _i(k)}\Lambda _{\beta _{2}}{\mathscr {S}}_1{\widehat{C}}_{t}^m\bigg ){\widehat{x}}(k)-\hat{{\mathscr {K}}}^m_{t}{\hat{x}}(k)\nonumber \\&+\sum \limits _{b=1}^{h}{\widehat{A}}_{\tau _b s}^{m}{\hat{x}}(k-\tau _{b}(k))-{\hat{\mathscr {H}}}^m_{t}\Pi _{{\bar{\rho }}}\Lambda _{\beta _{2}}{\bar{\theta }}_j({\widehat{C}} _{t}^mx(k))\nonumber \\&-{\hat{\mathscr {H}}}^m_{t}\Pi _{{\bar{\rho }}}\Lambda _{\beta _{4}}{\widehat{C}}_{t}^m{\hat{x}}(k-d(k))+{\widehat{E}}_{s}^mf(k)+\big ({\widehat{B}}_s^m-{\hat{\mathscr {H}}}^m_{t}\Pi _{{\bar{\rho }}}{\widehat{D}}_{t}^m\big )w(k). \end{aligned}$$

(12)

Then for each $\rho (k)=r\in \chi$, the augmented fault detection filter system and the error system are obtained in the following form:

$$\begin{aligned} \Xi (k+1)=&S_sT_t\bigg \{\big ({\hat{A}}_{{\bar{\rho }},s}^{m} +{\hat{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t}\big )\Xi (k) +{\hat{E}}_{{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))\nonumber \\&+\sum \limits _{b=1}^h{\hat{A}}_{\tau _{b},s}^{m}{\hat{I}}\Xi (k-\tau _b(k))\nonumber \\&+{\hat{A}}_{{\bar{\rho }},s}^{dm}{\hat{I}}\Xi (k-d(k))+{\hat{B}}_{{\bar{\rho }},s}^mw(k) +{\hat{F}}_s^{m}f(k) +{\hat{A}}_{1{\bar{\rho }},s}^{m}\Xi (k)\nonumber \\&+{\hat{A}}_{2{\bar{\rho }},s}^{m}\Xi (k)\nonumber \\&+\big ({\hat{A}}_{3{\bar{\rho }},s}^{m} +{\tilde{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t}\big )\Xi (k)+{\hat{A}}_{4{\bar{\rho }},s}^{dm}{\hat{I}}\Xi (k-d(k))\nonumber \\&+{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))\bigg \},\nonumber \\ e(k)=&{\hat{L}}_t\Xi (k)-f(k), \end{aligned}$$

(13)

where

$$\begin{aligned}&\Xi (k)=[{\widehat{x}}(k) \ {\hat{x}}(k)]^T,\quad e(k)=\vartheta (k)-f(k),\quad {\hat{\beta }}_{zi}=\beta _{zi}(k)-{\bar{\beta }}_{zi}\ (z=1,2,3,4),\quad \\ {}&{\hat{A}}_{1{\bar{\rho }},s}^m=\sum \limits _{i=1}^{q}{\hat{\beta }}_{1i}(k){\hat{A}}_{1{\bar{\rho }},si}^{m1},\quad {\hat{A}}_{2{\bar{\rho }},s}^m=\sum \limits _{i=1}^{q}{\hat{\beta }}_{2i}(k){\hat{A}}_{2{\bar{\rho }},si}^{m2},\quad {\hat{A}}_{3{\bar{\rho }},s}^m=\sum \limits _{i=1}^{q}{\hat{\beta }}_{1i}(k){\hat{A}}_{1{\bar{\rho }},si}^{m1},\nonumber \\&{\hat{A}}_{4{\bar{\rho }},s}^m=\sum \limits _{i=1}^{q}{\hat{\beta }}_{4i}(k){\hat{A}}_{3{\bar{\rho }},si}^{m4},\quad {\hat{E}}_{1{\bar{\rho }},s}=\sum \limits _{i=1}^{q}{\hat{\beta }}_{2i}(k){\hat{E}}_{1{\bar{\rho }},si}^{m2},{\tilde{M}}_{{\bar{\rho }},s}^m=\sum \limits _{i=1}^{q}{\hat{\beta }}_{3i}(k){\tilde{M}}_{{\bar{\rho }},si}^{m3},\nonumber \\&{\hat{A}}_{{\bar{\rho }},s}^{m}=\begin{bmatrix}{\hat{A}}_s^m&{}0\\ \omega &{}\hat{{\mathscr {K}}}_t^m \end{bmatrix}, \quad {\hat{M}}_{{\bar{\rho }},si}^{m3}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t^m\Pi _{\beta _3}\Lambda _{{\bar{\rho }}} \end{bmatrix},\quad {\hat{E}}_{{\bar{\rho }},s}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t^m\Lambda _{\beta 2}\Pi _{{\bar{\rho }}} \end{bmatrix},\quad \\&{\hat{A}}_{\tau _{b},s}^{m}=\begin{bmatrix} {\widehat{A}}_{\tau _{b}s}^m\\ {\widehat{A}}_{\tau _{b}s}^m \end{bmatrix}, \quad {\hat{A}}_{{\bar{\rho }},s}^{dm}=\begin{bmatrix}0\\ -{\hat{\mathscr {H}}}_t^m\Lambda _{\beta 4}\Pi _{{\bar{\rho }}}{\widehat{C}}_t^m\end{bmatrix},\quad {\hat{B}}_{{\bar{\rho }},s}^m=\begin{bmatrix} {\widehat{B}}_s^m\\ {\widehat{B}}_s^m-{\hat{\mathscr {H}}}_t^m\Pi _{{\bar{\rho }}}{\widehat{D}}_t^m \end{bmatrix},\nonumber \\&{\hat{F}}_s^m=\begin{bmatrix}{\widehat{F}}_s^m\\ {\widehat{F}}_s^m \end{bmatrix}, \quad {\hat{A}}_{1{\bar{\rho }},si}^{m1}=\begin{bmatrix}0&{}0\\ -{\hat{\mathscr {H}}}_t^m\sigma _i\Lambda _{{\bar{\rho }}}{\widehat{C}}_t^m&{}0\end{bmatrix} ,\quad {\hat{A}}_{2{\bar{\rho }},si}^{m2}=\begin{bmatrix}0&{}0\\ -{\hat{\mathscr {H}}}_t^m\sigma _i\Lambda _{{\bar{\rho }}}{\mathscr {S}}_1{\widehat{C}}_t^m&{}0\end{bmatrix},\quad \nonumber \\&{\hat{A}}_{3{\bar{\rho }},si}^{m4}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t^m\sigma _i\Lambda _{{\bar{\rho }}}{\widehat{C}}_t^m \end{bmatrix},\quad {\tilde{M}}_{{\bar{\rho }},si}^{m3}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t^m\sigma _{i}\Lambda _{{\bar{\rho }}} \end{bmatrix},\quad {\hat{E}}_{1{\bar{\rho }},si}^{m2}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t^m\sigma _i\Lambda _{{\bar{\rho }}} \end{bmatrix},\quad \nonumber \\&{\hat{C}}_t=[{\widehat{C}}_t^m\ 0], \quad {\hat{L}}_t=[L_t^m\ -L_t^m],\quad {\hat{I}}=[0\ 1],\quad \\&\omega ={\hat{A}}_s^m-\hat{{\mathscr {K}}}_t^m-{\hat{\mathscr {H}}}_t^m(\Lambda _{\beta 1}+\Lambda _{\beta 3})\Pi _{{\bar{\rho }}}{\widehat{C}}_t^m-{\hat{\mathscr {H}}}_t^m\Lambda _{\beta 2}\Pi _{{\bar{\rho }}}{\mathscr {S}}_1{\widehat{C}}_t^m. \end{aligned}$$

The following assumption and definition will be useful to prove the required results.

Assumption 1

The disturbance input vector w(k) is time-varying and satisfies $\sum \limits _{k=0}^{{N}}w^T(k)w(k)\le \varepsilon ,$ where $\varepsilon >0$.

Definition 1

[24] Considered system (1) subject to disturbance input w(k) satisfying Assumption 1, is stochastically finite-time bounded with respect to $({\mathscr {C}}_1,{\mathscr {C}}_2,{\mathscr {G}}_m,N,\varepsilon )$, where ${\mathscr {G}}_m$ is a positive definite matrix and $0\le {\mathscr {C}}_1<{\mathscr {C}}_2$, if $\Xi ^T(0){\mathscr {G}}_m\Xi (0)\le {\mathscr {C}}_1\Longrightarrow \Xi ^T(k){\mathscr {G}}_m\Xi (k)<{\mathscr {C}}_2$ for all $k=1,2,\ldots ,N.$

3 Main Results

In this section, a set of sufficient conditions that guarantees the finite-time boundedness of augmented fault detection filter system (13) with strictly $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipative index will be derived. Moreover, the desired distributed filter will be designed in the form of (10) such that augmented fault detection filter system (13) in the presence of distributed delays and incomplete measurements is stochastically finite-time bounded.

The following theorem proves the stochastic finite-time boundedness and strict $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipativity of considered system (3) when the filter gain parameters are known.

Theorem 1

Let Assumption 1 holds. $\beta _{zi}$, $\upsilon$, ${\mathscr {C}}_1$, $\alpha$ be known scalars and ${\mathscr {Q}}\le 0$, ${\mathscr {S}}$, ${\mathscr {R}}={\mathscr {R}}^T$, $\mathcal {V}$ be known matrices and ${\mathscr {G}}_m$ be the symmetric matrix. If there exist positive definite matrices ${\mathscr {P}}_r^m$, ${\mathscr {Q}}_r$, ${\mathscr {R}}_{br}(b=1,2,\ldots ,h)$ and positive scalars $\lambda _{\tilde{{\mathscr {P}}}^m},\lambda ^{\tilde{{\mathscr {P}}}^m},\lambda _{\tilde{{\mathscr {Q}}}}$, $\lambda _{\tilde{{\mathscr {R}}}_{b}} \ (b=1,2,\ldots ,h)$ such that the following inequalities hold for all $s,t=1,2,\cdots ,l:$

$$\begin{aligned}{}[\Upsilon _{ss}]&<0,\quad s=t, \end{aligned}$$

(14)

$$\begin{aligned} +[\Upsilon _{ts}]&<0,\quad s\ne t, \end{aligned}$$

(15)

$$\begin{aligned} {\upsilon ^N}\alpha ^{\frac{N}{\tau _a}}(\widetilde{\lambda }{\mathscr {C}}_1+\varepsilon \mu _{{\mathscr {W}}})&<{\mathscr {C}}_2\lambda ^{\tilde{{\mathscr {P}}}^m} \end{aligned}$$

(16)

$$\begin{aligned} \lambda ^{\tilde{{\mathscr {P}}}^m}I\le \tilde{{\mathscr {P}}}^m\le \lambda _{\tilde{{\mathscr {P}}}^m}I,\&0\le {\tilde{\mathscr {Q}}}\le \lambda _{\tilde{{\mathscr {Q}}}}I,\ 0\le \tilde{{\mathscr {R}}}_b\le \lambda _{\tilde{{\mathscr {R}}}_b}I \end{aligned}$$

(17)

and the switching signal $\rho (k)$ satisfies the average dwell time (ADT) condition

$$\begin{aligned} \tau _a>\tau _a^{*}=\frac{In\alpha }{ In{\mathscr {C}}_2\lambda ^{\tilde{{\mathscr {P}}}^m_r}-In\mu _{{\mathscr {W}}}\varepsilon \upsilon ^N}, \end{aligned}$$

(18)

where

$$\begin{aligned}&\Upsilon _{st}=\begin{bmatrix} [{\bar{\Upsilon }}]_{6\times 6}&{}\Upsilon _{1,2}&{}\Upsilon _{1,3}&{}\Upsilon _{1,4}&{}{{\hat{\Upsilon }}}_{1,3}&{}\Upsilon _{1,5}&{}{\hat{L}}_t^T\sqrt{-{\mathscr {Q}}}\\ *&{}-({\bar{{\mathscr {P}}}^{m}_{r}})^{-1}&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}\hat{{\mathscr {P}}}_r^m&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}\hat{{\mathscr {P}}}_r^m&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}\hat{{\mathscr {P}}}_r^m&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}\hat{{\mathscr {P}}}_r^m&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}-I \end{bmatrix},\\&{\bar{\Upsilon }}_{1,1}=-\upsilon \bar{{\mathscr {P}}}_r^m+{\mathscr {Q}}_{r}+d{\mathscr {Q}}+{\mathscr {R}}_{br}+\tau {\mathscr {R}}_{br},\ {\bar{\Upsilon }}_{1,2}={\hat{C}}_t^T \mathcal {V}^T,\ {\bar{\Upsilon }}_{1,5}=-{\hat{L}}_{t}^T{\mathscr {S}},\\&{\bar{\Upsilon }}_{1,6}={\hat{L}}_{t}^T{\mathscr {R}},\\&{\bar{\Upsilon }}_{2,2}=-2I,\ {\bar{\Upsilon }}_{3,3}=-\upsilon ^{d_2}{\mathscr {Q}}_r,\ {\bar{\Upsilon }}_{4,4}=-\upsilon ^{\tau _2}{\mathscr {R}}_{br},\ {\bar{\Upsilon }}_{5,5}=-I-{\mathscr {S}},\\&{\bar{\Upsilon }}_{6,6}=-{\mathscr {R}}+\gamma I,\\&\Upsilon _{1,2}=[{\hat{A}}_{{\bar{\rho }},s}^{m} +{\hat{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t}\quad {\hat{E}}_{{\bar{\rho }},s}\ {\hat{A}}_{{\bar{\rho }},s}^{dm}\quad {\hat{A}}_{\tau _{b},s}^{m}\ {\hat{F}}_{{\bar{\rho }},s}^{m}\quad {\hat{B}}_{{\bar{\rho }},s}^m]^T,\\&\Upsilon _{1,3}=[\pi _{1i}^2\big ({\hat{A}}_{1{\bar{\rho }},si}^{m1}\big )\ \underbrace{0\cdots 0}_{5}]^T,\\&\Upsilon _{1,4}=[\pi _{2i}^3\big ({\hat{A}}_{2{\bar{\rho }},si}^{m2}\big )\quad \pi _{2i}^2\big ({\hat{E}}_{1{\bar{\rho }},si}^{m2}\big )\quad \underbrace{0\cdots 0}_{5}]^T,\\&{\hat{\Upsilon }}_{1,3}=[\pi _{3i}^2\big ({\hat{A}}_{1{\bar{\rho }},si}^{m1}+{\tilde{M}}_{{\bar{\rho }},si}^{m3}\varDelta (k){\hat{C}}_{t}\big )\quad \underbrace{0\cdots 0}_{5}]^T,\\&\Upsilon _{1,5}=[\underbrace{0\cdots 0}_{5}\quad \pi _{4i}^2({\hat{A}}_{3{\bar{\rho }},si}^{m3})]^T,\ \hat{{\mathscr {P}}}_{r}^{m}={\mathrm{diag}}\{(\bar{{\mathscr {P}}}^{m}_{r})^{-1},(\bar{{\mathscr {P}}}^{m}_{r})^{-1},\ldots ,\\&\quad (\bar{{\mathscr {P}}}^{m}_{r})^{-1}\}\ \text {and}\ \\&\bar{{\mathscr {P}}}^m_r=\sum \limits _{q=1}^{{\mathscr {M}}}\phi _{mn}(k){\mathscr {P}}_{r}^{n}, \end{aligned}$$

then augmented fault detection filter system (13) is stochastically finite-time bounded and strictly $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipative with respect to $({\mathscr {C}}_1,{\mathscr {C}}_2,{\mathscr {G}},N,\varepsilon )$.

Proof

Let us first define the Lyapunov–Krasovskii functional to prove the required results as follows:

$$\begin{aligned} {\mathbb {V}}_r(k)=\sum \limits _{p=1}^{3}{\mathbb {V}}_{p}(k), \end{aligned}$$

(19)

where

$$\begin{aligned}&{\mathbb {V}}_{1r}(k)=\Xi ^T(k){\mathscr {P}}_{r}^{m}\Xi (k),&\\&{\mathbb {V}}_{2r}(k)=\sum \limits _{g=k-d(k)}^{k-1}\upsilon ^{k-g-1}\Xi ^T(g){\mathscr {Q}}_{r}\Xi (g)+\sum \limits _{{\tilde{g}}=-d_2+1}^{-d_1}\sum \limits _{{\bar{g}}=k+{\tilde{g}}}^{k-1}\upsilon ^{k-{\tilde{g}}-1}\Xi ^{T}({\bar{g}}){\mathscr {Q}}_{r}\Xi ({\bar{g}}),&\\&{\mathbb {V}}_{3r}(k)=\sum \limits _{b=1}^{h}\sum \limits _{c=k-\tau _{b}(k)}^{k-1}\upsilon ^{k-c-1}\Xi ^T(c){\mathscr {R}}_{br}\Xi (c)&\\&\quad \qquad +\sum \limits _{b=1}^{h}\sum \limits _{{\bar{c}}=-\tau _2+1}^{-\tau _1}\sum \limits _{{\tilde{c}}=k+{\bar{c}}}^{k-1}\upsilon ^{k-{\tilde{c}}-1}\Xi ^{T}({\tilde{c}}){\mathscr {R}}_{br}\Xi ({\tilde{c}}).&\end{aligned}$$

Then, by calculating the differences of ${\mathbb {V}}_r(k)$ along the trajectories of augmented system (13) and taking the mathematical expectation, we obtain

$$\begin{aligned}&{\mathbb {E}}\{\varDelta {\mathbb {V}}_{1r}(k)-(\upsilon -1){\mathbb {V}}_{1r}(k)\}={\mathbb {E}}\bigg \{\Xi ^T(k+1)(\sum \limits _{q=1}^{{\mathscr {M}}}\phi _{mn}(k){\mathscr {P}}_{r}^{n})\Xi (k+1) \nonumber \\&\qquad -\upsilon \Xi ^T(k){\mathscr {P}}_{r}^m\Xi (k)\bigg \}, \nonumber \\&\quad \le {\mathbb {E}}\bigg \{S_sT_t[({\hat{A}}_{{\bar{\rho }},s}^{m} +{\hat{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k) +{\hat{E}}_{{\bar{\rho }},s}\theta ({\hat{C}}\Xi (k)) \nonumber \\&\qquad +\sum \limits _{b=1}^h{\hat{A}}_{\tau _{b},s}^{m}I\Xi (k-\tau _b(k)) +{\hat{A}}_{{\bar{\rho }},s}^{dm}I\Xi (k-d(k))+{\hat{B}}_{{\bar{\rho }},s}^m\nonumber \\&\qquad \times w(k) +{\hat{F}}_{{\bar{\rho }},s}^{m}f(k) +{\hat{A}}_{1{\bar{\rho }},s}^{m}\Xi (k) +{\hat{A}}_{2{\bar{\rho }},s}^{m}\Xi (k)+({\hat{A}}_{3{\bar{\rho }},s}^{m}\nonumber \\&\qquad +{\tilde{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k)+{\hat{A}}_{4{\bar{\rho }},s}^{dm}{\hat{I}}\Xi (k-d(k))\nonumber \\&\qquad +{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))]^T\bar{{\mathscr {P}}}_{r}^m[({\hat{A}}_{{\bar{\rho }},s}^{m}+{\hat{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k) \nonumber \\&\qquad +{\hat{E}}_{{\bar{\rho }},s}\theta ({\hat{C}}\Xi (k)) +\sum \limits _{b=1}^h{\hat{A}}_{\tau _{b},s}^{m}I\Xi (k-\tau _b(k))+{\hat{A}}_{{\bar{\rho }},s}^{dm}I \nonumber \\&\qquad \times \Xi (k-d(k))+{\hat{B}}_{{\bar{\rho }},s}^mw(k) +{\hat{F}}_{{\bar{\rho }},s}^{m}f(k) +{\hat{A}}_{1{\bar{\rho }},s}^{m}\Xi (k)\nonumber \\&\qquad +{\hat{A}}_{2{\bar{\rho }},s}^{m}\Xi (k) +({\hat{A}}_{3{\bar{\rho }},s}^{m} +{\tilde{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k)\nonumber \\&\qquad +{\hat{A}}_{4{\bar{\rho }},s}^{dm}{\hat{I}}\Xi (k-d(k))+{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))]\nonumber \\&\qquad -\upsilon \Xi ^T(k){\mathscr {P}}_{r}^m\Xi (k)]\bigg \}. \end{aligned}$$

(20)

$$\begin{aligned}&\quad {\mathbb {E}}\{\varDelta {\mathbb {V}}_{2r}(k)-(\upsilon -1){\mathbb {V}}_{2r}(k)\}\le {\mathbb {E}}\bigg \{\Xi ^T(k){\mathscr {Q}}_{r}\Xi (k)-\upsilon ^{d_2}\Xi ^T(k-d(k)){\mathscr {Q}}_{r}\nonumber \\&\qquad \Xi (k-d(k))\nonumber \\&\qquad +(d_2-d_1)\Xi ^T(k){\mathscr {Q}}_{r}\Xi (k)\bigg \}. \end{aligned}$$

(21)

$$\begin{aligned}&{\mathbb {E}}\{\varDelta {\mathbb {V}}_{3r}(k)-(\upsilon -1){\mathbb {V}}_{3r}(k)\}\le {\mathbb {E}}\bigg \{\sum \limits _{b=1}^{h}\big [\Xi ^T(k){\mathscr {R}}_{br}\Xi (k)-\upsilon ^{\tau _2}\Xi ^T(k-\tau _b(k)){\mathscr {R}}_{br}\nonumber \\&\quad \times \Xi (k-\tau _b(k))+(\tau _{2}-\tau _1)\Xi ^T(k){\mathscr {R}}_{br}\big ]\bigg \}. \end{aligned}$$

(22)

From saturation nonlinearity we have

$$\begin{aligned} -2{\bar{\theta }}_i(y_i(k))^T{\bar{\theta }}_i(y_i(k))+2{\bar{\theta }}_i(y_i(k))^T\mathcal {V}y_i(k)\ge 0, \end{aligned}$$

which implies that

$$\begin{aligned} -2{\bar{\theta }}_i(y_i(k))^T{\bar{\theta }}_i(y_i(k))+2{\bar{\theta }}_i(y_i(k))^T\mathcal {V}C_{is}(k)\Xi (k)\ge 0. \end{aligned}$$

(23)

By combining from (20)–(23), we can get

$$\begin{aligned}&{\mathbb {E}}\{\varDelta {\mathbb {V}}_r(k)-(\upsilon -1){\mathbb {V}}_r(k)\} \le [({\hat{A}}_{{\bar{\rho }},s}^{m}+{\hat{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k)+{\hat{E}}_{{\bar{\rho }},s}\theta ({\hat{C}}\Xi (k))\nonumber \\&\quad +{\hat{A}}_{{\bar{\rho }},s}^{dm}\Xi (k-d(k))+\sum \limits _{b=1}^h{\hat{A}}_{\tau _{b},s}^{m}\Xi (k-\tau _b(k))+{\hat{B}}_{{\bar{\rho }},s}^mw(k)\nonumber \\&\quad +{\hat{F}}_{{\bar{\rho }},s}^{m}f(k)]^T\bar{{\mathscr {P}}}_{r}^{m}[({\hat{A}}_{{\bar{\rho }},s}^{m}+{\hat{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k)+{\hat{E}}_{{\bar{\rho }},s}\nonumber \\&\quad \times \theta ({\hat{C}}\Xi (k))+{\hat{A}}_{{\bar{\rho }},s}^{dm}\Xi (k-d(k))+\sum \limits _{b=1}^h{\hat{A}}_{\tau _{b},s}^{m}\Xi (k-\tau _b(k))\nonumber \\&\quad +{\hat{B}}_{{\bar{\rho }},s}^mw(k)+{\hat{F}}_{{\bar{\rho }},s}^{m}f(k)]+\sum \limits _{i=1}^{n}\pi _{1i}^2[{\hat{A}}_{1{\bar{\rho }},s}^{mz}\Xi (k)]^T\bar{{\mathscr {P}}}_{r}^m\nonumber \\&\quad \times [{\hat{A}}_{1{\bar{\rho }},s}^{mz}\Xi (k)]+\sum \limits _{i=1}^{n}\pi _{2i}^2[{\hat{A}}_{2{\bar{\rho }},s}^{mz}+{\hat{E}}_{1{\bar{\rho }},s}^{mz}\theta ({\hat{C}}_t\Xi (k))]^T\nonumber \\&\quad \times \bar{{\mathscr {P}}}_{r}^m[{\hat{A}}_{2{\bar{\rho }},s}^{mz}+{\hat{E}}_{1{\bar{\rho }},s}^{mz}\theta ({\hat{C}}_t\Xi (k))] + \sum \limits _{i=1}^{n}\pi _{3i}^2[({\hat{A}}_{1{\bar{\rho }},s}^{mz}+{\tilde{M}}_{{\bar{\rho }},s}^{mz}\nonumber \\&\quad \times \varDelta (k){\hat{C}}_{t})\Xi (k)]^T\bar{{\mathscr {P}}}_{r}^{m}[({\hat{A}}_{3{\bar{\rho }},s}^{mz} +{\tilde{M}}_{3{\bar{\rho }},s}^{mz}\varDelta (k){\hat{C}}_{t})\Xi (k)]\nonumber \\&\quad +\sum \limits _{i=1}^n\pi _{4i}^2[{\hat{A}}_{3{\bar{\rho }},s}^{mz}{\hat{I}}\Xi (k-d(k))]^T\bar{{\mathscr {P}}}_r^m[{\hat{A}}_{3{\bar{\rho }},s}^{mz}{\hat{I}}\Xi (k-d(k))]\nonumber \\&\quad +\sum \limits _{z=1}^{6}{\mathscr {H}}_z. \end{aligned}$$

(24)

where

$$\begin{aligned} {\mathscr {H}}_1= & {} 2[{\hat{A}}_{1}{{\bar{\rho }},s}^{m}\Xi (k)]^T\bar{{\mathscr {P}}}_r^m [{\hat{A}}_{2{\bar{\rho }},s}^{m}\Xi (k)+{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))],\\ {\mathscr {H}}_2= & {} 2[{\hat{A}}_{1}{{\bar{\rho }},s}^{m}\Xi (k)]^T\bar{{\mathscr {P}}}_r^m[({\hat{A}}_{3{\bar{\rho }},s}^{m}+{\tilde{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k)],\\ {\mathscr {H}}_3= & {} 2[{\hat{A}}_{1}{{\bar{\rho }},s}^{m}\Xi (k)]^T\bar{{\mathscr {P}}}_r^m[{\hat{A}}_{4{\bar{\rho }},s}^{dm}{\hat{I}}\Xi (k-d(k))],\\ {\mathscr {H}}_4= & {} 2[{\hat{A}}_{2{\bar{\rho }},s}^{m}\Xi (k) +{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))]^T\bar{{\mathscr {P}}}_r^m[({\hat{A}}_{3{\bar{\rho }},s}^{m}+{\tilde{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k)],\\ {\mathscr {H}}_5= & {} 2[{\hat{A}}_{2{\bar{\rho }},s}^{m}\Xi (k) +{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))]^T\bar{{\mathscr {P}}}_r^m[{\hat{A}}_{4{\bar{\rho }},s}^{dm}{\hat{I}}\Xi (k-d(k))],\\ {\mathscr {H}}_6= & {} 2[({\hat{A}}_{3{\bar{\rho }},s}^{m}+{\tilde{M}}_{{\bar{\rho }},s}^m\varDelta (k){\hat{C}}_{t})\Xi (k)]\bar{{\mathscr {P}}}_r^m [{\hat{A}}_{4{\bar{\rho }},s}^{dm}{\hat{I}}\Xi (k-d(k))]. \end{aligned}$$

By the inequality $\pm 2ab\le a^2+b^2$, it is clear that

$$\begin{aligned} {\mathscr {H}}_1\le&[{\hat{A}}_{1}{{\bar{\rho }},s}^{m}\Xi (k)]^T\bar{{\mathscr {P}}}_r^m[{\hat{A}}_{1}{{\bar{\rho }},s}^{m}\Xi (k)]+[{\hat{A}}_{2{\bar{\rho }},s}^{m}\Xi (k)+{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))]^T\bar{{\mathscr {P}}}_{r}^m\\&[{\hat{A}}_{2{\bar{\rho }},s}^{m}\Xi (k)+{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))]. \end{aligned}$$

By using the similar evaluation for $\sum \limits _{z=2}^{6}{\mathscr {H}}_z$, we obtain

$$\begin{aligned} {\mathbb {E}}\{\varDelta {\mathbb {V}}_r(k)-(\upsilon -1){\mathbb {V}}_r(k)\}\le S_sT_t \zeta ^T(k)\Upsilon \zeta (k), \end{aligned}$$

(25)

where $\zeta (k)=[\Xi ^T\quad \theta ({\hat{C}}_t\Xi (k))^T\quad x(k-d(k))^T\quad {\widehat{x}}_b(k-\tau _b(k))^T\quad f(k)^T], {\widehat{x}}_b(k-\tau _b(k))=[{\widehat{x}}_1(k-\tau _1(k))\quad {\widehat{x}}_2(k-\tau _2(k))\quad \ldots ,{\widehat{x}}_h(k-\tau _h(k))]$, $\Upsilon ={\bar{\Upsilon }}+\Upsilon _2^T\bar{{\mathscr {P}}}_r^m\Upsilon _2+\sum \limits _{i=1}^n\Upsilon _3^T\bar{{\mathscr {P}}}_r^m\Upsilon _3+\sum \limits _{i=1}^n\Upsilon _4^T\bar{{\mathscr {P}}}_r^m\Upsilon _4+\sum \limits _{i=1}^n{\hat{\Upsilon }}_3^T\bar{{\mathscr {P}}}_r^m{\hat{\Upsilon }}_3+\sum \limits _{i=1}^n\Upsilon _5^T\bar{{\mathscr {P}}}_r^m\Upsilon _5$ and the elements of ${\bar{\Upsilon }}$ and $\Upsilon$ are as given in theorem statement.

Then by applying Schur complement lemma to (25), we can obtain LMIs (14) and (15). Hence, it is obvious that

$$\begin{aligned} {\mathbb {E}}\{\varDelta {\mathbb {V}}_r(k)-(\upsilon -1){\mathbb {V}}_r(k)- w^T(k){\mathbb {W}}w(k)\}&\le 0,\\ {\mathbb {E}}\{{\mathbb {V}}_r(k+1)-\upsilon {\mathbb {V}}_r(k)\}&\le {\mathbb {E}}\{ w^T(k){\mathbb {W}}w(k)\},\\ {\mathbb {E}}\{{\mathbb {V}}_r(k+1)\}&\le \upsilon {\mathbb {E}}\{{\mathbb {V}}_r(k)\}+{\mathbb {E}}\{w^T(k){\mathbb {W}}w(k)\}\\ {\mathbb {E}}\{{\mathbb {V}}_ {\rho (k_l)}(k)\}&\le \upsilon ^{k-k_l}{\mathbb {E}}\{{\mathbb {V}}_{\rho (k_l)}(k_l)\}\\&\quad +\mu _{{\mathscr {W}}}{\mathbb {E}}\{\sum _{g=k_l}^{k_l-1}\upsilon ^{k-g-1}w^T(k){\mathbb {W}}w(k)\}. \end{aligned}$$

Note that ${\mathbb {E}}\{{\mathbb {V}}_{\rho (k_l)}(k_l)\}\le \alpha {\mathbb {E}}\{{\mathbb {V}}_{\rho (k_{l-1})}(k_{l-1})\}$ and ${\mathbb {E}}\{{\mathbb {V}}_{\rho (k_{l-1})}(k_{l-1})\}\le \upsilon ^{k_l-k_{l-1}} {\mathbb {E}}\{{\mathbb {V}}_{k_{l-1}}(k_{l-1})\}+\sum \limits _{g=k_{l-1}}^{k_{l-1}}\upsilon ^{k_{l}-g-1}\mu _{{\mathscr {W}}}w^T(g)w(g).$ From the above inequalities, we can obtain

$$\begin{aligned} {\mathbb {E}}\{{\mathbb {V}}_{\rho _{(k_l)}}(k)\}\le&\upsilon ^{k-k_{l}}{\mathbb {E}}\{{\mathbb {V}}_{\rho _{k_{l}}}(k_{l})\}+\mu _{{\mathscr {W}}}\sum \limits _{g=k_{l}}^{k-1}\upsilon ^{k-g-1}w^T(g)w(g),\nonumber \\ \le&\alpha \upsilon ^{k-k_{l-1}}{\mathbb {E}}\{{\mathbb {V}}(\rho _{k_{l-1}})(k_{l-1})\}+\alpha \mu _{{\mathscr {W}}}\upsilon ^{k-k_l}\sum \limits _{g=k_{l-1}}^{k_l-1}\upsilon ^{k_l-s-1}w^T(g)w(k)\nonumber \\&+\mu _{{\mathscr {W}}}\sum \limits _{g=k_{l}}^{k-1}\upsilon ^{k-g-1}w^T(g)w(g). \end{aligned}$$

(26)

Letting $k=N,\ k_0=0$ we can get,

$$\begin{aligned} {\mathbb {E}}\{{\mathbb {V}}_{\rho (k)}(k)\}\le&\upsilon ^N\alpha ^{N_\rho (0,\ N)}{\mathbb {E}}\{{\mathbb {V}}_{\rho (0)}(0)\}\}+\upsilon ^N\mu _{{\mathscr {W}}}\alpha ^{N_{\rho }(0,N)}\sum \limits _{g=0}^{N-1}w^T(g)w(g),\nonumber \\ \le&\upsilon ^N\alpha ^{N_\rho (0,\ N)}{\mathbb {E}}\{{\mathbb {V}}_{\rho (0)}(0)\}+\upsilon ^N\mu _{{\mathscr {W}}}\alpha ^{N_{\rho }(0,N)}\varepsilon . \end{aligned}$$

(27)

From considered Lyapunov–Krasovskii functional (19), we have

$$\begin{aligned} {\mathbb {E}}\{{\mathbb {V}}_{\rho (0)}(0)\}=&\Xi ^T(0){\mathscr {P}}_{\rho (0)}^{m}\Xi (0) +\sum \limits _{g=k-d(0)}^{-1}\varrho ^{-g-1}\Xi ^T(g){\mathscr {Q}}_{\rho (0)}\Xi (g)\\ {}&+\sum \limits _{{\tilde{g}}=-d_2+1}^{-d_1}\sum \limits _{{\bar{g}}={\tilde{g}}}^{-1}\varrho ^{-{\bar{g}}-1}\Xi ^{T}({\bar{g}}){\mathscr {Q}}_{\rho (0)}\Xi ({\bar{g}})+\sum \limits _{b=1}^{h}\sum \limits _{c=-\tau _{b}(0)}^{-1}\varrho ^{-c-1}\\&\times \Xi ^T(c){\mathscr {R}}_{b\rho (0)}\Xi (c)+\sum \limits _{b=1}^{h}\sum \limits _{{\bar{c}}=-\tau _2+1}^{-\tau _1}\sum \limits _{{\tilde{g}}={\bar{g}}}^{-1}\varrho ^{-{\tilde{g}}-1}\Xi ^{T}({\tilde{g}}){\mathscr {R}}_{b\rho (0)}\Xi ({\bar{g}}). \end{aligned}$$

Defining $\tilde{{\mathscr {P}}}^m={\mathscr {G}}^{-1/2}{\mathscr {P}}^m{\mathscr {G}}^{-1/2}$, $\tilde{{\mathscr {Q}}}={\mathscr {G}}^{-1/2}{\mathscr {Q}}{\mathscr {G}}^{-1/2}$ and $\tilde{{\mathscr {R}}}_{b}={\mathscr {G}}^{-1/2}{\mathscr {R}}_{b}{\mathscr {G}}^{-1/2}$ $(b=1,2,\ldots ,h)$, we obtain

$$\begin{aligned} {\mathbb {E}}\{{\mathbb {V}}_{\rho (0)}(0)\}=&\lambda _{\tilde{{\mathscr {P}}}^m} \Xi ^T(0){\mathscr {G}}\Xi (0) +\lambda _{\tilde{{\mathscr {Q}}}}\sum \limits _{g=k-d(0)}^{-1}\varrho ^{-g-1}\Xi ^T(g){\mathscr {G}}\Xi (g)\nonumber \\&+\lambda _{\tilde{{\mathscr {Q}}}}\sum \limits _{{\tilde{g}}=-d_2+1}^{-d_1}\sum \limits _{{\bar{g}}={\tilde{g}}}^{-1}\varrho ^{-{\bar{g}}-1}\Xi ^{T}({\tilde{g}}){\mathscr {G}}\Xi ({\tilde{g}})+\lambda _{\tilde{{\mathscr {R}}}}\sum \limits _{b=1}^{h}\sum \limits _{c=-\tau _{b}(0)}^{-1}\varrho ^{-c-1}\nonumber \\&\times \Xi ^T(c){\mathscr {G}}\Xi (c)+\lambda _{\tilde{{\mathscr {R}}}}\sum \limits _{b=1}^{h}\sum \limits _{{\bar{c}}=-\tau _2+1}^{-\tau _1}\sum \limits _{{\tilde{c}}={\bar{c}}}^{-1}\varrho ^{-{\tilde{c}}-1}\Xi ^{T}({\tilde{c}}){\mathscr {G}}\Xi ({\tilde{c}}),\nonumber \\ \le&\bigg \{\lambda _{\tilde{{\mathscr {P}}}^m}+d_2\upsilon ^{d_2-1}\lambda _{\tilde{{\mathscr {Q}}}}+ \upsilon ^{d_2}\frac{(d_2-d_1)(d_1+d_2-1)}{2}\lambda _{\tilde{{\mathscr {Q}}}} +\tau _2\upsilon ^{\tau _2-1}\lambda _{\tilde{{\mathscr {R}}}_{b}}\nonumber \\&+\upsilon ^{\tau _2}\frac{(\tau _2-\tau _1)(\tau _1+\tau _2-1)}{2}\lambda _{\tilde{{\mathscr {R}}_b}}\bigg \}{\mathscr {C}}_2, \le \widetilde{\lambda }{\mathscr {C}}_2, \end{aligned}$$

(28)

where $\widetilde{\lambda }=\lambda _{\tilde{{\mathscr {P}}}^m}+d_2\upsilon ^{d_2-1}\lambda _{\tilde{{\mathscr {Q}}}}+ \upsilon ^{d_2}\frac{(d_2-d_1)(d_1+d_2-1)}{2}\lambda _{\tilde{{\mathscr {Q}}}} +\tau _2\upsilon ^{\tau _2-1}\lambda _{\tilde{{\mathscr {R}}}_{b}}+ \upsilon ^{\tau _2}\frac{(\tau _2-\tau _1)(\tau _1+\tau _2-1)}{2}\lambda _{\tilde{{\mathscr {R}}_b}}$. Further, if inequality (17) holds, then we have

$$\begin{aligned} {\mathbb {E}}\{{\mathbb {V}}_{\rho (k)}(k)\}\le&\upsilon ^N\alpha ^{N_\rho (0,\ N)}\widetilde{\lambda }{\mathscr {C}}_1+\upsilon ^N\mu _{{\mathscr {W}}}\alpha ^{N_{\rho }(0,N)}\varepsilon .\nonumber \\ \le&\upsilon ^N\alpha ^{\frac{N}{\tau _a}}(\widetilde{\lambda }{\mathscr {C}}_1+\varepsilon \mu _{{\mathscr {W}}}). \end{aligned}$$

(29)

On the other hand, we get ${\mathbb {E}}\{{\mathbb {V}}_{\rho (k)}(k)\}\ge {\mathbb {E}}\{\Xi ^T(k){\mathscr {P}}_{\rho (k)}^m\Xi (k)\ge {\mathscr {E}}\{\Xi ^T(k){\mathscr {G}}^{1/2}\tilde{{\mathscr {P}}}_{\rho (0)}^m{\mathscr {G}}^{1/2}\}\ge \lambda ^{\tilde{{\mathscr {P}}}^m_r}.$ From (28)–(29), we can deduce that $\Xi ^T(k){\mathscr {G}}\Xi (k) \le \frac{\upsilon ^N}{\lambda ^{\tilde{{\mathscr {P}}}^m_r}}\alpha ^{\frac{N}{\tau _a}}(\widetilde{\lambda }{\mathscr {C}}_1+\varepsilon \mu _{{\mathscr {W}}}).$

Then, it is clear from (16) that $\Xi ^T(k){\mathscr {G}}\Xi (k)<{\mathscr {C}}_2.$ Thus, considered augmented filtering system (13) is finite-time bounded subject to $(0,{\mathscr {C}}_2,{\mathscr {G}},N,\varepsilon )$. Next, we will show the strictly $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipativity of augmented filtering error system (13), by considering the performance index as follows:

$$\begin{aligned} J(k)={\mathbb {E}}\bigg \{\sum \limits ^{N}_{k=0}[e^T(k){\mathscr {Q}}e(k)+2e^T(k){\mathscr {S}}\varphi (k)+\varphi ^T(k){\mathscr {R}}\varphi (k)]-\beta \sum \limits _{k=0}^{N}\varphi ^T(k)\varphi (k)\bigg \}. \end{aligned}$$

(30)

Hence, it is obvious that ${\mathbb {E}}\{\varDelta {\mathbb {V}}_r(k)-(\upsilon -1){\mathbb {V}}_r(k)-J(k)\}\le 0$. Thus, we get

${\mathbb {E}}\{{\mathbb {V}}_r(k+1)\}<{\mathbb {E}}\big \{\upsilon {\mathbb {V}}_r(k)+e^T(k){\mathscr {Q}}e(k)+2e^T(k){\mathscr {S}}\varphi (k)+\varphi ^T(k)[{\mathscr {R}}-\beta I]\varphi (k)\big \}$.

In addition, for any scalar $\upsilon \ge 1$ it follows that

$$\begin{aligned} {\mathbb {E}}\{{\mathbb {V}}_r(k)\}\le&{\mathbb {E}}\big \{\upsilon ^k{\mathbb {V}}_r(0)+\sum \limits _{a=0}^{k-1}\upsilon ^{k-a-1}e^T(k){\mathscr {Q}}e(k)+2\sum \limits _{a=0}^{k-1}\upsilon ^{k-a-1}e^T(k){\mathscr {S}}\varphi (k)\\&+\sum \limits _{a=0}^{k-1}\upsilon ^{k-a-1}\varphi ^T(k)[{\mathscr {R}}-\beta I]\varphi (k)\big \}. \end{aligned}$$

On the other hand ${\mathbb {V}}_r(k)\ge 0\ \forall k=1,2\ldots ,N$ and under zero initial conditions, we have

$$\begin{aligned} {\mathbb {E}}\bigg \{\beta \sum \limits _{a=0}^{k-1}\upsilon ^{k-a-1}\varphi ^T(k)\varphi (k)\bigg \}\le&{\mathbb {E}}\bigg \{\sum \limits _{a=0}^{k-1}\upsilon ^{k-a-1}e^T(k){\mathscr {Q}}e(k)\\&+2\sum \limits _{a=0}^{k-1}\upsilon ^{k-a-1}e^T(k){\mathscr {S}}\varphi (k)\\&+\sum \limits _{a=0}^{k-1}\upsilon ^{k-a-1}\varphi ^T(k){\mathscr {R}}\varphi (k)\bigg \}. \end{aligned}$$

This implies that

$$\begin{aligned} J(k)={\mathbb {E}}\bigg \{\beta \sum \limits _{k=0}^{N}\varphi ^T(k)\varphi (k)\bigg \}\le&{\mathbb {E}}\bigg \{\sum \limits _{k=0}^{N}e^T(k){\mathscr {Q}}e(k)+2\sum \limits _{k=0}^{N}e^T(k){\mathscr {S}}\varphi (k)\nonumber \\ {}&+\sum \limits _{k=0}^{N}\varphi ^T(k){\mathscr {R}}\varphi (k)\bigg \}. \end{aligned}$$

(31)

Moreover, from (31) the inequality of Definition 2 in [26] can be easily obtained. Thus, it is concluded that augmented filtering error system (13) is stochastically finite-time bounded with strict $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipative performance subject to $({\mathscr {C}}_1,{\mathscr {C}}_2,{\mathscr {G}},N,\varepsilon )$. Hence, the proof is completed. $\square$

The following theorem proves the stochastically finite-time boundedness with strictly $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})-\beta$ dissipative of augmented fault detection filter system (13) when the filter gain parameters are unknown.

Theorem 2

Let Assumption 1 holds. $\beta _{zi}$, $\upsilon$, ${\mathscr {C}}_1$, $\alpha$, $\epsilon _1$ be known scalars. ${\mathscr {Q}}\le 0$, ${\mathscr {S}}$, ${\mathscr {R}}={\mathscr {R}}^T$ and $\mathcal {V}$ are known matrices. If there exist positive definite matrices ${\mathscr {P}}_r^m$, ${\mathscr {Q}}$, ${\mathscr {Q}}_r$, ${\mathscr {R}}_{br}(b=1,2,\ldots ,h)$, positive scalars $\lambda _{\tilde{{\mathscr {P}}}^m}$, $\lambda ^{\tilde{{\mathscr {P}}}^m}$, $\lambda _{\tilde{{\mathscr {Q}}}}$, $\lambda _{\tilde{{\mathscr {Q}}_r}}$, $\lambda _{\tilde{{\mathscr {R}}}_{b}} \ (b=1,2,\ldots ,h)$ and any matrices Y, $\tilde{{\mathscr {K}}}_t^m$, $\tilde{{\mathscr {H}}}_t^m$, $\tilde{{\mathscr {L}}}_t^m$ such that the following inequalities hold together with (16)–(18) for all $s,t=1,2,\ldots ,l:$

$$\begin{aligned}&[{\tilde{\Upsilon }}_{ss}]<0,\quad s=t, \end{aligned}$$

(32)

$$\begin{aligned}&[{\tilde{\Upsilon }}_{st}]+[{\tilde{\Upsilon }}_{ts}]<0,\quad s\ne t, \end{aligned}$$

(33)

where

$$\begin{aligned}&\widetilde{\Upsilon }_{st}=\begin{bmatrix} [{\bar{\Upsilon }}]_{6\times 6}&{}\widetilde{\Upsilon }_{1,2}&{}\widetilde{\Upsilon }_{1,3}&{}\widetilde{\Upsilon }_{1,4}&{}\breve{\Upsilon }_{1,3}&{}\widetilde{\Upsilon }_{1,5}&{}{\hat{L}}_t^T\sqrt{-{\mathscr {Q}}}&{}\epsilon _1{N_{\tau }}^T&{}0\\ *&{}{\bar{{\mathscr {P}}}^{m}_{r}}-Y^T-Y&{}0&{}0&{}0&{}0&{}0&{}0&{}M_{\tau }\\ *&{}*&{}\breve{{\mathscr {P}}}_r^m&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}\breve{{\mathscr {P}}}_r^m&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}\breve{{\mathscr {P}}}_r^m&{}0&{}0&{}0&{}M_{\tau }\\ *&{}*&{}*&{}*&{}*&{}\breve{{\mathscr {P}}}_r^m&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}-I&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}-\epsilon _1 I&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}*&{}-\epsilon _1 I \end{bmatrix},\\&Y=\begin{bmatrix} Y_{1}&{}Y_2\\ Y_2^T&{}Y_3 \end{bmatrix},\ \bar{{\mathscr {P}}}_{r}^{m}=\begin{bmatrix} \bar{{\mathscr {P}}}_{1r}^{m}&{}\bar{{\mathscr {P}}}_{2r}^{m}\\ \bar{{\mathscr {P}}}_{2r}^{mT}&{}\bar{{\mathscr {P}}}_{3r}^{m} \end{bmatrix},\ {\mathscr {R}}_{r\tau }=\begin{bmatrix} {\mathscr {R}}_{1r\tau }&{}{\mathscr {R}}_{2r\tau }\\ {\mathscr {R}}_{2r\tau }^T&{}{\mathscr {R}}_{3r\tau } \end{bmatrix},\ {\mathscr {Q}}=\begin{bmatrix} {\mathscr {Q}}_{1}&{}{\mathscr {Q}}_2\\ {\mathscr {Q}}_2^T&{}{\mathscr {Q}}_3 \end{bmatrix},\\ {}&{\mathscr {Q}}_r=\begin{bmatrix} {\mathscr {Q}}_{1r}&{}{\mathscr {Q}}_{2r}\\ {\mathscr {Q}}_{2r}^T&{}{\mathscr {Q}}_{3r} \end{bmatrix},\ {\bar{\Upsilon }}_{1,1}=-\upsilon \bar{{\mathscr {P}}}_r^m+{\mathscr {Q}}_{r}+d{\mathscr {Q}}+{\mathscr {R}}_{br}+\tau {\mathscr {R}}_{br},\ {\bar{\Upsilon }}_{1,2}={\hat{C}}_t^T\mathcal {V}^T,\\ {}&{\bar{\Upsilon }}_{1,5}=-{\hat{L}}_{t}^T{\mathscr {S}},\ {\bar{\Upsilon }}_{1,6}={\hat{L}}_{t}^T{\mathscr {R}},\ {\bar{\Upsilon }}_{2,2}=-2I,\ {\bar{\Upsilon }}_{3,3}=-\upsilon ^{d_2}{\mathscr {Q}}_r,\ {\bar{\Upsilon }}_{4,4}=-\upsilon ^{\tau _2}{\mathscr {R}}_{br},\\ {}&{\bar{\Upsilon }}_{5,5}=-I-{\mathscr {S}},\ {\bar{\Upsilon }}_{6,6}=-{\mathscr {R}}+\gamma ,\ \tilde{\Upsilon }_{1,3}=[\pi _{1i}^2{\hat{A}}_{1{\bar{\rho }},si}^{m1}Y^T\quad 0\quad 0\quad 0\quad 0\quad 0]^T,\\&\tilde{\Upsilon }_{1,2}=[{\hat{A}}_{{\bar{\rho }},s}^{m} Y^T\quad {\hat{E}}_{{\bar{\rho }},s}Y^T\quad {\hat{A}}_{{\bar{\rho }},s}^{dm}Y^T\quad {\hat{A}}_{\tau _{b},s}^{m}Y^T\quad {\hat{F}}_{{\bar{\rho }},s}^{m}Y^T\quad {\hat{B}}_{{\bar{\rho }},s}^{m}Y^T]^T,\\ {}&\tilde{\Upsilon }_{1,4}=[\pi _{2i}^3{\hat{A}}_{2{\bar{\rho }},si}^{m2}Y^T\quad \pi _{2i}^2{\hat{E}}_{1{\bar{\rho }},si}^{m2}Y^T\quad \underbrace{0 \ldots 0}_{4}]^T,\ {\hat{\Upsilon }}_{1,3}=[\pi _{3i}^2{\hat{A}}_{1{\bar{\rho }},si}^{m1}Y^T\quad \underbrace{0 \ldots 0}_{5}]^T,\\ {}&\tilde{\Upsilon }_{1,5}=[\underbrace{0 \ldots 0}_{5}\quad \pi _{4i}^2{\hat{A}}_{3{\bar{\rho }},si}^{m4}Y^T]^T,\ N_{\tau }^T=[ N_m({\hat{M}}_{{\bar{\rho }},s}^m+{\tilde{M}}_{{\bar{\rho }},si}^{m3})\quad \underbrace{0 \ldots 0}_{5} ]^T,\\&{M}_{\tau }={\hat{C}}_{t}M,\ \hat{{\mathscr {P}}}_{r}^{m}={\mathrm{diag}}\{{\bar{{\mathscr {P}}}^{m}_{r}}-Y^T-Y,{\bar{{\mathscr {P}}}^{m}_{r}}-Y^T-Y,\ldots ,{\bar{{\mathscr {P}}}^{m}_{r}}-Y^T-Y\}, \end{aligned}$$

then there exists distributed fuzzy-dependent filter (10) for addressed system (1) such that augmented fault detection filter system (13) is stochastically finite-time bounded and strictly $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipative with respect to $({\mathscr {C}}_1,{\mathscr {C}}_2,{\mathscr {G}},N,\varepsilon )$. Moreover, the filter gain parameters in (10) can be obtained by ${\mathscr {K}}_t^m=Y_2^{-1}\tilde{{\mathscr {K}}}_t^m$, ${\mathscr {H}}_t^m=Y_2^{-1}\tilde{{\mathscr {H}}}_t^m$ and $\hat{{\mathscr {L}}}_t^m=\tilde{{\mathscr {L}}}_t^m$.

Proof

To prove the theorem, left and right multiplying (14) and (15) by ${\mathrm{diag}}\{\underbrace{I,\ldots I}_6,Y^T,Y^T,Y^T,Y^T,Y^T,I\}$ and its transpose, respectively, and then using the inequality $-Y^T(\bar{{\mathscr {P}}}_r^m)^{-1}Y\le (\bar{{\mathscr {P}}}_r^m)^{-1}-Y-Y^T$, we have

$$\begin{aligned} \tilde{\Upsilon }_{12\times 12}+sym({N_{\tau }}\varDelta {\mathsf {F}}(k){M_{\tau }})<0, \end{aligned}$$

(34)

where $\tilde{\Upsilon }_{12\times 12}$, $\bar{{\mathscr {P}}}_r^m,\ Y,$ $N_{\tau }$ and $M_{\tau }$ are defined as in the statement of Theorem 2.

By applying Lemma 1 in [31], there exist positive scalars $\epsilon _1$ and $\epsilon _2$ such that (34) can be rewritten as

$$\begin{aligned} \tilde{\Upsilon }_{12\times 12}+\epsilon _1{N_{\tau }}^T\varpi _{N_{\tau }}+\epsilon _1^{-1}{M_{\tau }}{M_{\tau }}^T<0. \end{aligned}$$

(35)

Inequality (35) can be precisely observed as the matrix terms in (32). Hence, if LMIs (32) and (33) together with (16)–(18) hold, considered system (1) with fault detection distributed filter (10) is stochastically finite-time bounded with strict $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipative subject to $({\mathscr {C}}_1,{\mathscr {C}}_2,{\mathscr {G}},N,\varepsilon )$. Hence the proof of this theorem is completed. $\square$

Suppose that there is no distributed time-varying delay and Markovian jump in discrete-time system (1), then augmented fault detection filtering system (13) can be rewritten as

$$\begin{aligned} \Xi (k+1)=&S_sT_t\bigg \{\big ({\hat{A}}_{{\bar{\rho }},s} +{\hat{M}}_{{\bar{\rho }},s}\varDelta (k){\hat{C}}_{t}\big )\Xi (k) +{\hat{E}}_{{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k)) +{\hat{A}}_{{\bar{\rho }},s}^{d}{\hat{I}}\Xi (k-d(k))\nonumber \\&+{\hat{B}}_{{\bar{\rho }},s}w(k) +{\hat{F}}_sf(k) +{\hat{A}}_{1{\bar{\rho }},s}\Xi (k) +{\hat{A}}_{2{\bar{\rho }},s}\Xi (k)\nonumber \\&+\big ({\hat{A}}_{3{\bar{\rho }},s} +{\tilde{M}}_{{\bar{\rho }},s}\varDelta (k){\hat{C}}_{t}\big )\Xi (k)\nonumber \\&+{\hat{A}}_{4{\bar{\rho }},s}^{d}{\hat{I}}\Xi (k-d(k)) +{\hat{E}}_{1{\bar{\rho }},s}\theta ({\hat{C}}_t\Xi (k))\bigg \},\nonumber \\ e(k)=&{\hat{L}}_t\Xi (k)-f(k), \end{aligned}$$

(36)

where

$$\begin{aligned}&{\hat{A}}_{1{\bar{\rho }},s}=\sum \limits _{i=1}^{q}{\hat{\beta }}_{1i}(k){\hat{A}}_{1{\bar{\rho }},si}^{1},\ {\hat{A}}_{2{\bar{\rho }},s}=\sum \limits _{i=1}^{q}{\hat{\beta }}_{2i}(k){\hat{A}}_{2{\bar{\rho }},si}^{2},\ {\hat{A}}_{3{\bar{\rho }},s}=\sum \limits _{i=1}^{q}{\hat{\beta }}_{1i}(k){\hat{A}}_{1{\bar{\rho }},si}^{1},\\&{\hat{A}}_{4{\bar{\rho }},s}=\sum \limits _{i=1}^{q}{\hat{\beta }}_{4i}(k){\hat{A}}_{3{\bar{\rho }},si}^{4},\ {\hat{E}}_{1{\bar{\rho }},s}=\sum \limits _{i=1}^{q}{\hat{\beta }}_{2i}(k){\hat{E}}_{1{\bar{\rho }},si}^{2},\ {\tilde{M}}_{{\bar{\rho }},s}=\sum \limits _{i=1}^{q}{\hat{\beta }}_{3i}(k){\tilde{M}}_{{\bar{\rho }},si}^{3},\\&{\hat{A}}_{{\bar{\rho }},s}=\begin{bmatrix}{\hat{A}}_s&{}0\\ \omega &{}\hat{{\mathscr {K}}}_t \end{bmatrix}, \ {\hat{M}}_{{\bar{\rho }},si}^{3}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t\Pi _{\beta _3}\Lambda _{{\bar{\rho }}} \end{bmatrix},\ {\hat{E}}_{{\bar{\rho }},s}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t\Lambda _{\beta 2}\Pi _{{\bar{\rho }}} \end{bmatrix},\\&{\hat{A}}_{\tau _{b},s}=\begin{bmatrix} {\widehat{A}}_{\tau _{b}s}\\ {\widehat{A}}_{\tau _{b}s} \end{bmatrix}, \\&{\hat{A}}_{{\bar{\rho }},s}^{d}=\begin{bmatrix}0\\ -{\hat{\mathscr {H}}}_t\Lambda _{\beta 4}\Pi _{{\bar{\rho }}}{\widehat{C}}_t\end{bmatrix},\ {\hat{B}}_{{\bar{\rho }},s}=\begin{bmatrix} {\widehat{B}}_s\\ {\widehat{B}}_s-{\hat{\mathscr {H}}}_t\Pi _{{\bar{\rho }}}{\widehat{D}}_t \end{bmatrix},\ {\hat{F}}_s=\begin{bmatrix}{\widehat{F}}_s\\ {\widehat{F}}_s\end{bmatrix},\\&{\hat{A}}_{3{\bar{\rho }},si}^{4}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t\sigma _i\Lambda _{{\bar{\rho }}}{\widehat{C}}_t \end{bmatrix},\\&{\hat{A}}_{1{\bar{\rho }},si}^{1}=\begin{bmatrix}0&{}0\\ -{\hat{\mathscr {H}}}_t\sigma _i\Lambda _{{\bar{\rho }}}{\widehat{C}}_t&{}0\end{bmatrix}, \ {\hat{A}}_{2{\bar{\rho }},si}^{2}=\begin{bmatrix}0&{}0\\ -{\hat{\mathscr {H}}}_t\sigma _i\Lambda _{{\bar{\rho }}}{\mathscr {S}}_1{\widehat{C}}_t&{}0\end{bmatrix},\ {\tilde{M}}_{{\bar{\rho }},si}^{3}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t\sigma _{i}\Lambda _{{\bar{\rho }}} \end{bmatrix},\\&{\hat{E}}_{1{\bar{\rho }},si}^{2}=\begin{bmatrix} 0\\ -{\hat{\mathscr {H}}}_t\sigma _i\Lambda _{{\bar{\rho }}} \end{bmatrix},\ {\hat{C}}_t=[{\widehat{C}}_t\ 0], \ {\hat{L}}_t=[L_t\ -L_t],\quad {\hat{I}}=[0\ 1],\ \omega ={\hat{A}}_s-\hat{{\mathscr {K}}}_t-\\&\quad {\hat{\mathscr {H}}}_t(\Lambda _{\beta 1}+\Lambda _{\beta 3})\Pi _{{\bar{\rho }}}{\hat{C}}_t-{\hat{\mathscr {H}}}_t\Lambda _{\beta 2}\Pi _{{\bar{\rho }}}{\mathscr {S}}_1{\hat{C}}_t. \end{aligned}$$

Corollary 1

Let Assumption 1 holds and $\beta _{zi}$, $\upsilon$, ${\mathscr {C}}_1$, $\alpha$, $\epsilon _2$ are known scalars. ${\mathscr {Q}}\le 0$, ${\mathscr {S}}$, ${\mathscr {R}}={\mathscr {R}}^T$ and $\mathcal {V}$ be known matrices. If there exist positive definite matrices ${\mathscr {P}}_r^m$, ${\mathscr {Q}}$, ${\mathscr {Q}}_r$, positive scalars $\lambda _{\tilde{{\mathscr {P}}}^m}$, $\lambda _{\tilde{{\mathscr {Q}}}}$, $\lambda ^{\tilde{{\mathscr {P}}}^m}$, $\lambda _{\tilde{{\mathscr {Q}}_r}}$ and any matrices Y, $\tilde{{\mathscr {K}}}_t$, $\tilde{{\mathscr {H}}}_t$, $\tilde{{\mathscr {L}}}_t$ such that the following inequalities hold together with (16)–(18) for all $s,t=1,2,\ldots ,l:$

$$\begin{aligned}{}[{\tilde{\Omega }}_{ss}]<0,\quad s=t, \end{aligned}$$

(37)

$$\begin{aligned} +[{\tilde{\Omega }}_{ts}]<0,\quad s\ne t, \end{aligned}$$

(38)

where

$$\begin{aligned}&\widetilde{\Omega }_{st}=\begin{bmatrix} \big [{\bar{\Omega }}\big ]_{5\times 5}&{}\widetilde{\Omega }_{1,2}&{}\widetilde{\Omega }_{1,3}&{}\widetilde{\Omega }_{1,4}&{}\breve{\Omega }_{1,3}&{}\widetilde{\Omega }_{1,5}&{}{\hat{L}}_t^T\sqrt{-{\mathscr {Q}}}&{}\epsilon _2{{\bar{N}}}^T&{}0\\ *&{}{\bar{{\mathscr {P}}}_{r}}-Y^T-Y&{}0&{}0&{}0&{}0&{}0&{}0&{}{\bar{M}}\\ *&{}*&{}\breve{{\mathscr {P}}}_r&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}\breve{{\mathscr {P}}}_r&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}\breve{{\mathscr {P}}}_r&{}0&{}0&{}0&{}{\bar{M}}\\ *&{}*&{}*&{}*&{}*&{}\breve{{\mathscr {P}}}_r&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}-I&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}-\epsilon _2 I&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}*&{}-\epsilon _2 I \end{bmatrix},\\&Y=\begin{bmatrix} Y_{1}&{}Y_2\\ Y_2^T&{}Y_3 \end{bmatrix},\ \bar{{\mathscr {P}}}_{r}=\begin{bmatrix} \bar{{\mathscr {P}}}_{1r}&{}\bar{{\mathscr {P}}}_{2r}\\ \bar{{\mathscr {P}}}_{2r}^{T}&{}\bar{{\mathscr {P}}}_{3r} \end{bmatrix},\ {\mathscr {Q}}=\begin{bmatrix} {\mathscr {Q}}_{1}&{}{\mathscr {Q}}_2\\ {\mathscr {Q}}_2^T&{}{\mathscr {Q}}_3 \end{bmatrix},\ {\mathscr {Q}}_r=\begin{bmatrix} {\mathscr {Q}}_{1r}&{}{\mathscr {Q}}_{2r}\\ {\mathscr {Q}}_{2r}^T&{}{\mathscr {Q}}_{3r} \end{bmatrix},\ \\&{\bar{\Omega }}_{1,1}=-\upsilon \bar{{\mathscr {P}}}_r+{\mathscr {Q}}_{r} +d{\mathscr {Q}},\ {\bar{\Omega }}_{1,5}=-{\hat{L}}_{t}^T{\mathscr {S}},\ {\bar{\Omega }}_{1,6}={\hat{L}}_{t}^T{\mathscr {R}},\ {\bar{\Omega }}_{2,2}=-2I,\\&{\bar{\Omega }}_{4,4}=-I-{\mathscr {S}},\ {\bar{\Omega }}_{5,5}=-{\mathscr {R}}+\gamma I,\\&\tilde{\Omega }_{1,2}=\big [{\hat{A}}_{{\bar{\rho }},s} Y^T\ {\hat{E}}_{{\bar{\rho }},s}Y^T\ {\hat{A}}_{{\bar{\rho }},s}^{d}Y^T\ {\hat{F}}_{{\bar{\rho }},s}Y^T\ {\hat{B}}_{{\bar{\rho }},s}Y^T\big ]^T,\\&\tilde{\Omega }_{1,3}=\big [\pi _{1i}^2{\hat{A}}_{1{\bar{\rho }},si}^{1}Y^T\ \underbrace{0\cdots 0}_{4}\big ]^T,\ \tilde{\Omega }_{1,4}=\big [\pi _{2i}^3{\hat{A}}_{2{\bar{\rho }},si}^{2}Y^T\ \pi _{2i}^2{\hat{E}}_{1{\bar{\rho }},si}^{2}Y^T\ \underbrace{0\cdots 0}_{3}\big ]^T,\ \\ {}&\breve{\Omega }_{1,3}=\big [\pi _{3i}^2{\hat{A}}_{1{\bar{\rho }},si}^{1}Y^T\ \underbrace{0\cdots 0}_{4}\big ]^T,\ \tilde{\Omega }_{1,5}=\big [\underbrace{0\cdots 0}_{4}\quad \pi _{4i}^2{\hat{A}}_{3{\bar{\rho }},si}^{4}Y^T\big ]^T,\ {\bar{\Omega }}_{1,2}={\hat{C}}_t^TV_i^T, \\ {}&{\bar{N}}^T=\big [N({\hat{M}}_{{\bar{\rho }},s}+{\tilde{M}}_{{\bar{\rho }},si}^{3})\quad \underbrace{0\cdots 0}_{4}\big ]^T,\ {\bar{\Omega }}_{3,3}=-\upsilon ^{d_2}{\mathscr {Q}}_r,\ {\bar{M}}={\hat{C}}_{t}M,\\ {}&\breve{{\mathscr {P}}}_{r}={\mathrm{diag}}\{{{{\mathscr {P}}}_{r}}-Y^T-Y,{{{\mathscr {P}}}_{r}}-Y^T-Y,\ldots ,{{{\mathscr {P}}}_{r}}-Y^T-Y\}, \end{aligned}$$

then there exists distributed fuzzy-dependent filter (10) such that augmented fault detection filter system (36) is stochastically finite-time bounded and strict $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipative with respect to $({\mathscr {C}}_1,{\mathscr {C}}_2,{\mathscr {G}},N,\varepsilon )$. Moreover, the filter gain parameters in (10) can be obtained by ${\mathscr {K}}_t=Y_2^{-1}\tilde{{\mathscr {K}}}_t$, ${\mathscr {H}}_t=Y_2^{-1}\tilde{{\mathscr {H}}}_t$ and $\hat{{\mathscr {L}}}_t=\tilde{{\mathscr {L}}}_t$.

Proof

The proof of this corollary is similar to Theorem 2 and hence it is neglected. $\square$

4 Numerical Examples

In this section, we have given two numerical examples including inverted pendulum model to demonstrate the efficiency of the proposed distributed filter design technique.

Example 1

In this example, the sensor network is presented in terms of directed graph ${\mathsf {G}}=({\mathsf {V}},{\mathsf {E}},{\mathsf {A}})$, with ${\mathsf {V}}=\{1,2\}$ and ${\mathsf {E}}=\{(1,1),(1,2),(2,2)\}$, where ${\mathsf {V}}$ and ${\mathsf {E}}$ are the set of nodes and edges of the graph, respectively. Moreover, we consider the adjacency matrix as

$$\begin{aligned} {\mathsf {A}}=\begin{bmatrix} 1&{}1\\ 0&{}1 \end{bmatrix}. \end{aligned}$$

Next, we consider nonlinear discrete-time Markovian jump system (1) with two operation modes and two plant rules as follows:

Fuzzy Rule 1:

$$\begin{aligned}&A_{1}^{1}=\begin{bmatrix} -0.2925 &{}0.0895&{}0.02130\\ 0.2075&{}-0.07216 &{}0.0045\\ 0.1783 &{}0.1160 &{}-0.2325 \end{bmatrix},\ A_{1}^{2}=\begin{bmatrix} -0.3716 &{}0.085&{}0.3300\\ 0.2275&{}-0.0722 &{}0.0445\\ 0.2783 &{}0.1260 &{}-0.2495 \end{bmatrix},\\&A_{1,1}^{1}=\begin{bmatrix} -0.0028 &{}0.0189&{}0.0023\\ 0.0064&{}-0.09116 &{}0.0055\\ 0.0913 &{}0.0216 &{}-0.0125 \end{bmatrix},\ A_{1,1}^{2}=\begin{bmatrix} -0.0027 &{}0.0895&{}0.0013\\ 0.0545&{}-0.0822 &{}0.0045\\ 0.0883 &{}0.0161 &{}-0.0025 \end{bmatrix},\\&A_{2,1}^{1}=\begin{bmatrix} -0.0573 &{}0.0833&{}0.0345\\ 0.03&{}-0.0584 &{}0.0035\\ 0.0476 &{}0.0839 &{}-0.0466 \end{bmatrix},\ A_{2,1}^{2}=\begin{bmatrix} -0.0027 &{}0.0895&{}0.0013\\ 0.0545&{}-0.0822 &{}0.0045\\ 0.0883 &{}0.0161 &{}-0.0025 \end{bmatrix},\\&E_{1}^{1}=\begin{bmatrix} 0.5&0.3&0.1 \end{bmatrix}^T,\ E_{1}^{2}=\begin{bmatrix} 0.6&0.5&0.1 \end{bmatrix}^T. \end{aligned}$$

Fuzzy Rule 2:

$$\begin{aligned}&A_{2}^{1}=\begin{bmatrix} -0.2917 &{}0.0833&{}0.0220\\ 0.1430&{}-0.0583 &{}0.0026\\ 0.1366 &{}0.1519 &{}-0.2501 \end{bmatrix},\ A_{2}^{2}=\begin{bmatrix} -0.2356 &{}0.083&{}0.3300\\ 0.2275&{}-0.0722 &{}0.220\\ 0.103 &{}0.1260 &{}-0.0583 \end{bmatrix},\\&A_{1,2}^{1}=\begin{bmatrix} -0.0357 &{}0.0833&{}0.023\\ 0.0075&{}-0.0832 &{}0.0055\\ 0.0983 &{}0.026 &{}-0.0184 \end{bmatrix},\ A_{1,2}^{2}=\begin{bmatrix} -0.0036 &{}0.0089&{}0.0023\\ 0.0745&{}-0.0816 &{}0.0054\\ 0.0983 &{}0.0264 &{}-0.0034 \end{bmatrix},\\&A_{2,2}^{1}=\begin{bmatrix} -0.077 &{}0.0191&{}0.0456\\ 0.055&{}-0.0523 &{}0.0354\\ 0.0586 &{}0.0722 &{}-0.0207 \end{bmatrix},\ A_{2,2}^{2}=\begin{bmatrix} -0.0657 &{}0.0911&{}0.0362\\ 0.0450&{}-0.0613 &{}0.0275\\ 0.0465 &{}0.0521 &{}-0.0106 \end{bmatrix},\\&E_{2}^{1}=\begin{bmatrix} 0.3&0.2&0.2 \end{bmatrix}^T,\ E_{2}^{2}=\begin{bmatrix} 0.4&0.3&0.2 \end{bmatrix}^T. \end{aligned}$$

The transition probability matrix is taken as $\chi =\begin{bmatrix} 0.2 &{}0.8\\ 0.6 &{}0.4 \end{bmatrix}.$ The measurement output of the $i^{th}\$ sensor node with $s,m,i=1,2$ is described in (8), and the parameter values are chosen as,

$$\begin{aligned}&C_{1,1}^{1}=\begin{bmatrix} 0.1 &{}0.2 &{}0.3\\ 0.2 &{}0.3 &{}0.1 \end{bmatrix},\ C_{1,2}^{1}=\begin{bmatrix} 0.1 &{}0.1 &{}0.2\\ 0.1 &{}0.2 &{}0.1 \end{bmatrix},\ C_{1,1}^{2}=\begin{bmatrix} 0.2 &{}0.3 &{}0.4\\ 0.3 &{}0.3 &{}0.2 \end{bmatrix},\\&C_{1,2}^{2}=\begin{bmatrix} 0.1 &{}0.2 &{}0.1\\ 0.2 &{}0.2 &{}0.2 \end{bmatrix},\\&C_{2,1}^{1}=\begin{bmatrix} 0.1&0.2&0.2 \end{bmatrix},\ C_{2,2}^{1}=\begin{bmatrix} 0.1&0.2&0.1 \end{bmatrix},\ C_{2,1}^{2}=\begin{bmatrix} 0.1&0.4&0.3 \end{bmatrix},\\&C_{2,2}^{2}=\begin{bmatrix} 0.1&0.2&0.2 \end{bmatrix},\\&D_{1,1}^{1}=\begin{bmatrix} 0.2&0.4 \end{bmatrix}^T,\ D_{1,2}^{1}=\begin{bmatrix} 0.15&0.35 \end{bmatrix}^T,\ D_{1,1}^{2}=\begin{bmatrix} 0.2&0.3 \end{bmatrix}^T,\ D_{1,2}^{2}=\begin{bmatrix} 0.1&0.2 \end{bmatrix}^T,\\&D_{2,1}^{1}=0.33 ,\ D_{2,2}^{1}=0.21 ,\ D_{2,1}^{2}=0.29\ \text {and}\ D_{2,2}^{2}=0.22. \end{aligned}$$

Further, we assume that the distributed time delay satisfies $1\le \tau _b(k)\le 4$, where $b=1,2$ with $\tau _1(k)=1.4+0.22\sin (k)$ and $\tau _2(k)=1.3+0.2\cos (k)$. Further, the communication delay bound satisfies $1\le d(k)\le 3$ which occurs stochastically. The saturation value for ${\mathscr {S}}_1$ and ${\mathscr {S}}_2$ is taken as ${\mathrm{diag}}\{0.6,0.6,0.6\}$ and ${\mathrm{diag}}\{0.7,0.7,0.7\}$, respectively. Let $\varpi _1=0.7$ and $\varpi _2=0.5$ be the quantization densities. The occurrence probabilities of saturation nonlinearity, packet losses, communication delay and quantization densities are taken for each sensor nodes. For the first sensor node, we choose ${\bar{\beta }}_{11}=0.7$, ${\bar{\beta }}_{21}=0.1$, ${\bar{\beta }}_{31}=0.05$ and ${\bar{\beta }}_{41}=0.15$ and for the second sensor node, we have ${\bar{\beta }}_{12}=0.6$, ${\bar{\beta }}_{22}=0.15$, ${\bar{\beta }}_{32}=0.05$, ${\bar{\beta }}_{42}=0.15$. The other parameters are chosen as $\upsilon =1.01$, ${\mathscr {Q}}=-0.4$, ${\mathscr {S}}=0.7$ and ${\mathscr {R}}=2.1$. By solving the LMI constraints derived in Theorem 2 together with the above given parameters, we obtain the minimum $\beta =0.897$. Due to page limitations, the filter gain parameters are not presented here.

Fig. 1

Trajectories of $x_l(k)$ and $x_{fl}(k)\ (l=1,2,3)$ with and without fault

Fig. 2

Responses of error system

Fig. 3

Responses of residual signal

Fig. 4

Evaluation function with and without fault

Fig. 5

Sensor node

Fig. 6

Distributed delay $\tau _1(k)$ and $\tau _2(k)$

Fig. 7

Evolution of ${\tilde{x}}^T(k){\mathscr {G}}_m{\tilde{x}}(k)$

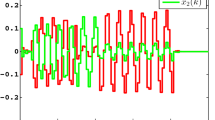
Let us set the initial conditions as $x(0)=x_f(k)=[0\ 0\ 0]^T$ for the system and filter states. The simulation results for augmented fault detection filter system (13) are presented in Figs. 1–7. The responses of the state $x_{l}(k)$ and its estimate $x_{fl}(k)\ (l=1,2,3)$ with and without fault are plotted in Fig. 1. Moreover, Fig. 2 shows the responses of error system. To be more specific, Fig. 2 clearly displays the impact of fault signal f(k). In Fig. 3 the residual signal is depicted. Further, the residual evaluation function is calculated as $J_{\vartheta }(k)=\sqrt{\sum \nolimits _{k=0}^{20} \vartheta ^T(k)\vartheta (k)}=0.0917$ and the selected threshold value is $J_{\mathrm{th}}=0.0911$. It is obvious from Fig. 4 that the value of $J_{\vartheta }$ exceeds the selected threshold $J_{{\mathrm{th}}}$ in one time step. The sensor node that is active at each time instant is displayed in Fig. 5. Finally, the distributed time-varying delay $\tau _q(k)\ (q=1,2)$ and time history of ${\tilde{x}}^T(k){\mathscr {G}}_m{\tilde{x}}(k)$ are presented in Figs. 6 and 7, respectively. Thus, augmented fault detection filter system (13) is stochastically finite-time bounded with prescribed strict $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipative performance index subject to (0, 22.8235, I, 100, 0.78) in the presence of distributed delays and incomplete measurements.

Example 2

In this example, the effectiveness of the proposed distributed filter design is examined for a nonlinear inverted pendulum model as in [31]. The parameter values are taken as in [31], which are given as follows:

$$\begin{aligned}&A_{1}=\begin{bmatrix} 1.0157 &{} 0.0895 &{} 0.0030\\ 0.0745 &{}0.7216 &{}0.0445\\ 14.7832 &{} 5.1604 &{} 0.0250 \end{bmatrix},\ B_{1}=\begin{bmatrix} 0.0047\\ 0.0895\\ 0.3246 \end{bmatrix},\\&A_{2}=\begin{bmatrix} 0.9573 &{}0.0833&{}0.0022\\ 1.0300 &{} 0.5834 &{}0.0259\\ 12.3656 &{}5.5189 &{}0.1056 \end{bmatrix},\ B_{2}=\begin{bmatrix} 0.0045 \\ 0.0833\\ 0.4166 \end{bmatrix}. \end{aligned}$$

Further, the other parameter values for addressed system (1) are taken as $E_1=\begin{bmatrix} 0.55&0.39&0.9 \end{bmatrix}^T$ and $E_2=\begin{bmatrix} 0.32&0.25&0.5 \end{bmatrix}^T.$ Here, we have taken the sensor network with two sensors and the local measurements are $y_1(k)=C_{1s}x(k)$ and $y_2(k)=C_{2s}x(k),$ where

$$\begin{aligned} C_{1s}=\begin{bmatrix} 1&{}0&{}0\\ 0&{}0&{}1 \end{bmatrix} \ \text {and} \ C_{2s}=\begin{bmatrix} 1&0&0 \end{bmatrix},\ s=1,2. \end{aligned}$$

Moreover, the disturbance distribution matrices $D_{1s}$ and $D_{2s}$ in (8) are taken as 0.2 and $[0.1 \ \ 0.2]^T$, respectively. Due to the physical limitations of the sensor nodes, the measurements may be saturated and the values of the saturation function can be taken as ${\mathscr {S}}_1={\mathrm{diag}}\{0.6,0.6,0.6\}$ and ${\mathscr {S}}_2={\mathrm{diag}}\{0.9,0.9,0.9\}$. Here, the values for quantization densities are assumed to be $\varpi _{1}=0.9,\ \varpi _{2}=0.88$. Furthermore, the lower and upper bounds of the randomly occurring communication delay d(k) are taken as 1 and 3, respectively. Moreover, the occurrence probabilities of the quantization, sensor saturation, packet losses and random delay are selected to be $70\%$, $10\%$, $10\%$, $10\%$ and $75\%$, $5\%$, $5\%$, $15\%$ for the first and second sensor, respectively. In this regard, we have ${\bar{\beta }}_{11}=0.7$, ${\bar{\beta }}_{21}=0.1$, ${\bar{\beta }}_{31}=0.1$, ${\bar{\beta }}_{41}=0.1$, ${\bar{\beta }}_{12}=0.75$, ${\bar{\beta }}_{22}=0.05$, ${\bar{\beta }}_{32}=0.05$, ${\bar{\beta }}_{42}=0.15$.

Fig. 8

Responses of the states $x_z(k)$ and its estimates $x_{fz}(k)\ (z=1,2,3)$ with and without fault

Fig. 9

Response of error system

Fig. 10

Responses of residual signal

Notice that the first sensor has two elements and more transmission power and bandwidth may be consumed if such a measurement is directly transmitted. Further, the second sensor transmits only one element from the local measurement. Now, we have $\Pi _{\rho _{1}(k)}\in \{[1\ 0],\ [0\ 1]\}$ and $\Pi _{\rho _{2}(k)}=1$. Moreover, we consider periodic signals for the switching purpose of two sensors as

$$\begin{aligned} \rho (k)=\left\{ \begin{array}{ll}1, \quad 1\le k\le 6 \\ 2, \quad 6< k<11. \end{array}\right. \end{aligned}$$

The other parameters are chosen as $\upsilon =1.01$, ${\mathscr {Q}}=-0.6$, ${\mathscr {S}}=1.9$ and ${\mathscr {R}}=2.9$. Now, using the aforementioned parameters and solving the LMIs in Corollary 1, the dissipative performance level is obtained as $\beta =2.1937$. Next, we set the initial conditions as $x(0)=x_f(0)=[0\ 0\ 0]^T$ for the state and filter system. Moreover, the fault signal and disturbance input are taken as

$$\begin{aligned} f(k)=\left\{ \begin{array}{ll} 0.45sin(k), \quad 10\le k\le 25,\\ 0.05sin(k),\quad 55\le k\le 75, \end{array}\right. \quad \text {and} \ w(k)=\left\{ \begin{array}{cl} -0.8sin(k), \quad 10\le k\le 30,\\ 0, \quad \quad \quad \quad otherwise. \end{array}\right. \end{aligned}$$

Fig. 11

Evaluation function and threshold

Fig. 12

Channel switching

Fig. 13

Evolution of ${\tilde{x}}^T(k){\mathscr {G}}{\tilde{x}}(k)$

The corresponding simulation results are presented in Figs.  89, 10, 11 and 12. Specifically, Fig. 8 displays the state trajectories of the system and fault detection filter with and without fault signal. The responses of error system can be viewed in Fig. 9. Further, the response of residual signal $\vartheta (k)$ is plotted in Fig. 10. It is clear from Fig. 11 that the residual evaluation function $J_{\vartheta }(k)=\sqrt{\sum \nolimits _{k=0}^{16}\vartheta ^T(k)\vartheta (k)}=0.2648$ exceeds the selected threshold $J_{{\mathrm{th}}}=0.2568$ within six time steps, wherein the efficiency of the proposed fault detection is clearly revealed. Moreover, active sensor node at each time instant is shown in Fig. 12. Finally, the evolution of ${\tilde{x}}^T(k){\mathscr {G}}{\tilde{x}}(k)$ is shown in Fig. 13. From this figure, it is obvious that the trajectories of the augmented fault detection filtering error system do not exceed the bound ${\mathscr {C}}_2$. Thus from these simulation results, it can be concluded that fault detection filtering error system (36) is stochastically finite-time bounded with strict $({\mathscr {Q}},{\mathscr {S}},{\mathscr {R}})$-$\beta$ dissipative performance index subject to (0, 50.4043, I, 100, 0.9) under the proposed distributed fault detection filter design even in the presence of incomplete measurements.

5 Conclusion

The finite-time fault detection filter design problem for a class of T–S fuzzy Markovian jump systems with distributed delay and incomplete measurements has been investigated. The issues such as packet losses, sensor saturation and signal quantization are considered simultaneously in a single framework. Lyapunov stability theory and stochastic analysis techniques are used to establish the sufficient conditions for the existence of fault detection filter that ensures the stochastic finite-time boundedness of the resulting augmented filtering error system with a prescribed dissipative performance level. Further, the fault detection filter gain parameters have been obtained by solving the linear matrix inequality-based constraints. Two numerical examples including an inverted pendulum model have been presented to establish the efficiency and applicability of the proposed finite-time fault detection filter design technique.