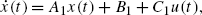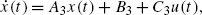1 Introduction

The synchronization of chaotic systems has been investigated since its introduction in the paper [1] by Pecora and Carrol in 1990. For instance, chaotic dynamics can be found in various real-life processes, for instance in weather, turbulences in liquids, human heart beating, brain activities, financial markets, population explosion, among many others. For that reason, synchronization of chaotic systems is an interesting topic that, has caught the attention of the nonlinear science community [2–4]. Two research directions have been already conformed in synchronizing chaos: (i) analysis and (ii) synthesis. Analysis problem comprises: (a) the classification of synchronization phenomena [5], (b) the construction of a general framework for unifying chaotic synchronization [6], and (c) the comprehension of the synchronization properties, for instance, robustness [7] or geometry [8]. On the other hand, synthesis of synchronization systems concerns the problem of finding the control force such that two chaotic systems share time evolution in some sense. Both analysis and synthesis directions are active research areas and one of the current challenges is to achieve and explain synchronization of a chaotic system with a different model. In fact, the study of the chaotic synchronization with different models makes sense in several systems, (see for details, [9–17], and references therein).

Further, geophysicists have long been puzzled by one striking aspect of the earth’s geomagnetic field. The dipole has reversed its polarity many times over geological history. The average interval between geomagnetic polarity reversals is about 7×105 years. However, the time series of reversals is highly irregular: There have been intervals as long as 3×107 years when the polarity apparently remained unchanged. One model which attempts to explain the reversal of the earth’s magnetic field is the Rikitake system [18]. Among the studied topics related with the Rikitake system, we are recalling a few of them together with a partial list of references, namely: shape and dynamics [19, 20], the chaotic behavior [21–23], time delay [24], passivity [25], secure communications [26–29], parameter estimation [28–30] and many others.

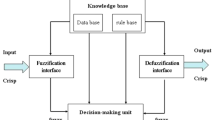
On the other hand, recently fuzzy control has been proved to be a powerful method for the control problem of complex nonlinear systems. For many real-life systems, which are highly complex and inherently nonlinear, conventional approaches to modeling often cannot be applied whereas the fuzzy approach might be the only appropriate alternative. In particular, the control technique based on the so-called Takagi–Sugeno (T-S) fuzzy model [31] has attracted a great deal of attention. The main purpose of the T-S fuzzy model is to represent or approximate a complex nonlinear system. The T-S fuzzy model approach will provide a powerful method for analysis of nonlinear systems [32–34]. There are two model-based approaches to construct theoretically a T-S fuzzy system of a nonlinear system. One is from local linear approximation, which generates linear consequence with a constant term included in each rule, called an affine T-S fuzzy system [35]. The other is via a sector nonlinearity concept, in general, results in constant free linear consequence for each rule, called a linear T-S fuzzy system [32]. Both fuzzy systems are demonstrated to be universal approximations to any smooth nonlinear system [32, 35]. However, it is impractical to describe a theoretical conversion of a mathematical model into a T-S fuzzy model if the nonlinear system is too complex. Subsequently, this fuzzy control was successfully applied in many areas such as servo control design [35], industries [36], medicine [37], speed wind turbine [38], energy resource systems [39], etc. Furthermore, chaos synchronization based on the T-S fuzzy control approach has been widely discussed in many applications [40–46].

For more general nonlinear systems, it may be difficult to formulate the chaos synchronization based on T-S fuzzy control techniques in terms of linear matrix inequalities (LMIs). Since the Rikitake system is a nonlinear system, the synchronization scheme based on T-S fuzzy control techniques can be established in terms of LMIs. For instance, LMI techniques [47] have been used in [32], which help to design fuzzy controllers capable of regulating chaotic systems based on their T-S fuzzy representation. In this paper, new criterion for T-S fuzzy Rikitake system and synchronization results for two identical Rikitake systems are developed in terms of LMIs, which can be efficiently solved by resorting to some standard algorithms [47] and different from the existing literature [23, 25–29], based on Lyapunov stability theory and fuzzy state-feedback controllers. Finally, numerical results are provided to show the effectiveness of the obtained results.

The detailed arrangement is as follows. Section 2 briefs the concepts of identical synchronization; Sect. 3 describes the Rikitake system; In Sect. 4, the Rikitake system and its fuzzy modeling theory are introduced. In Sect. 5, a chaotic synchronization scheme for the Rikitake system based on T-S fuzzy control techniques are given. In Sect. 6, robust chaotic synchronization scheme for an uncertain Rikitake system based on T-S fuzzy control techniques are given, and numerical simulations to verify the results are shown in Sect. 7. Section 8 draws some conclusions.

2 Description of identical synchronization

Chaotic systems present high sensitivity to initial conditions. Nevertheless, it is possible to synchronize these kinds of complex systems, to drive them to evolve on the same chaotic trajectory. Synchronization of identical chaotic systems can be seen as an asymptotic equality of the state variables while both of the systems evolve in time. This type of synchronization is known as identical synchronization, conventional synchronization, or complete synchronization. Consider the following chaotic systems with controller u:

$$\dot{x}(t) = f\bigl(x(t)\bigr) \quad \textrm{as the drive system} $$

and

$$\dot{y}(t) = \hat{f}\bigl(y(t),x(t),u(t)\bigr) \quad \textmd{as the response system}. $$

The existence of identical synchronization implies that lim t→∞∥e(t)∥=0, where e(t)=x(t)−y(t) is the synchronizing error.

3 Description of Rikitake system

The Rikitake system is a simple mechanical model used to study the reversals of the magnetic field of the Earth, idealized by the Japanese geophysicist Rikitake [18], and consists of two identical single Faraday-disk dynamos of the Bullard type coupled together. The Rikitake two-disk dynamo system is depicted in Fig. 1, and consists of two Bullard dynamos coupled together such that the wire of one disk is wrapped around the other, which was described by the four-dimensional nonlinear ordinary differential equations:

$$ \begin{array}{@{}l} L_{1}\dot{I}_{1} = - R_{1}I_{1} + \varOmega_{1}G_{1}I_{2}, \\ \noalign {\vspace {4pt}} L_{2}\dot{I}_{2} = - R_{2}I_{2} + \varOmega_{2}G_{2}I_{1}, \\ \noalign {\vspace {4pt}} \mathcal{I}_{1}\dot{\varOmega}_{1} = \tau_{1}-G_{1}I_{1}I_{2}, \\ \noalign {\vspace {4pt}} \mathcal{I}_{2}\dot{\varOmega}_{2} = \tau_{2}-G_{2}I_{1}I_{2}, \end{array} $$
(1)

where the quantities that apply to the first disk are denoted with a subscript 1, and the quantities pertinent to the second disk have a subscript 2. Further, Ω 1 and Ω 2 are angular velocity of the disks; I 1 and I 2 are the current running through the system; G 1 and G 2 are the mutual inductance of the disks; R 1 and R 2 are the resistance of the disks; \(\mathcal{I}_{1}\) and \(\mathcal{I}_{2}\) are the rotational inertia of the disks; L 1 and L 2 are the self inductance of the wires; τ 1 and τ 2 is the externally applied torque driving the disks. System (1) can be cast into the following three-dimensional nonlinear ordinary differential equation form:

(2)

where the parameters μ and a have some physical meaning when they are positive. For a physical meaning of the states x 1, x 2, and x 3, one can see [18]. However, the states x 1 and x 2 are directly related to the currents through each disc of the dynamo system, and x 3 is related to the angular velocity of one of the discs. The choice of the parameters a>0 and μ>0 reflects a physical meaning in the Rikitake model. This system displays a chaotic behavior which is shown in Fig. 2 for the parameters values in a neighborhood {μ=2, a=5} and for a large enough set of initial conditions. It is interesting to note that Eq. (2) looks similar to the Lorenz equations. But there are a few differences, the most important of which is the fact that there is a constant in the last equation.

Fig. 1
figure 1

Rikitake’s system of coupled disks

Full size image
Fig. 2
figure 2

Rikitake system chaotic attractor in (x 1,x 2,x 3)-space

Full size image

4 T-S fuzzy modeling of the Rikitake system

For the general nonlinear Rikitake system (2), it is not convenient to find an appropriate Lyapunov function V such that the conditions for synchronization is satisfied. The approach assumes that the chaotic systems can be represented by means of T-S fuzzy models, which allows the controllers to be designed on the basis of linear techniques. Moreover, fuzzy models have a natural capability of describing, or at least of approximating, the dynamics of very complex nonlinear systems. For that reason, they have been used as an important tool to solve problems involving chaotic systems including synchronization. Hence, the T-S fuzzy control logic has also been potential tool for approximating the nonlinear Rikitake systems, which yields an easy way to use Lyapunov stability theory [32], in terms of LMIs.

For convenience, the system (2) can be written in the state-space matrix form as

$$ \dot{x}(t)=Ax(t)+B, $$
(3)

where

For the nonlinear terms, define z 1(t)=x 3(t) and z 2(t)=x 1(t), then we have

Next, calculate the minimum and maximum values of z 1(t) and z 2(t) under x 3(t)∈[−1,1] and x 1(t)∈[−1,1], respectively, then we get the following:

From the maximum and minimum values, z 1(t) and z 2(t) can be represented by

where

Therefore, the membership functions can be calculated as

Figures 3(a), (b) show the membership functions. By using \(M_{1}^{1}\), \(M_{1}^{2}\), \(M_{2}^{1}\), and \(M_{2}^{2}\), the controlled nonlinear Rikitake system (3) with control input u(t) can be expressed by the following T-S fuzzy models:

Plant Rule 1::

IF z 1(t) is \(M_{1}^{1}\) and z 2(t) is \(M_{2}^{1}\) THEN

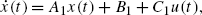
Plant Rule 2::

IF z 1(t) is \(M_{1}^{1}\) and z 2(t) is \(M_{2}^{2}\) THEN

Plant Rule 3::

IF z 1(t) is \(M_{1}^{2}\) and z 2(t) is \(M_{2}^{1}\) THEN

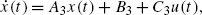
Plant Rule 4::

IF z 1(t) is \(M_{1}^{2}\) and z 2(t) is \(M_{2}^{2}\) THEN

Here,

By using center average defuzzifier method, the dynamical model of the Rikitake system (3) can be reformulated as

(4)

where

This fuzzy model exactly represents the nonlinear Rikitake system (3) in the region [−1,1]×[−1,1] on the x 3 x 1 plane.

Fig. 3
figure 3

(a) Membership functions \(M_{1}^{1}(z_{1}(t))\) and \(M_{1}^{2}(z_{1}(t))\); (b) Membership functions \(M_{2}^{1}(z_{2}(t))\) and \(M_{2}^{2}(z_{2}(t))\)

Full size image

As discussed in Sect. 2 and by using drive-response concept, the system (4) of T-S fuzzy Rikitake system (master system) is given as

(5)

Then the controlled response system (slave system) is given by

(6)

where y(t)=[y 1(t),y 2(t),y 3(t)]T∈R 3 is the state vector, u(t) is the control input, and C i is the known constant matrix. For chaotic systems, the premise variables in the T-S fuzzy models are used as outputs [40, 42]. Therefore, it is straightforward that the premise variables in the slave system are measurable and same as the master. In other words, we set \(h_{i}(\hat{z}(t))=h_{i}(z(t))\).

Hence, the synchronization error system is written as

(7)

where the synchronization error e(t)=y(t)−x(t).

Lemma 1

[33]

If the following conditions hold,

then the following inequality holds:

where h i , 1≤i≤r satisfy 0≤h i ≤1, \(\sum_{i=1}^{r} h_{i}=1\); and r denotes the number of IF-THEN rules.

5 Conditions for chaotic synchronization of the Rikitake system

Next, the LMI problem for achieving the synchronization for two identical Rikitake system is presented. Now by using the T-S fuzzy control technique, we can obtain the following sufficient conditions for synchronization of nonlinear Rikitake system using fuzzy state feedback controllers.

Theorem 1

If there exist symmetric positive definite matrix X and symmetric matrices Y j , (j=1,2,3,4) such that

(8)

and

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l} \frac{1}{r-1} \varTheta_{ii} + \frac{1}{2} \varTheta_{ij} + \frac{1}{2} \varTheta_{ji} <0, \quad \textmd{for} \ 1 \leq \ i \neq j \leq r, \\ \noalign {\vspace {-10pt}} \end{array} $$
(9)

where

then the synchronization error system (7), under the control input u(t) is given by K j =Y j X −1 e(t), is globally asymptotically stable. Here, r is the number of IF-THEN rules.

Proof

The closed-loop error system with the control input \(u(t)=\sum_{j=1}^{4} h_{j}(z(t))K_{j}e(t)\), where K j ∈R n×n is the gain matrix of the control input u(t), can be written as

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l} \dot{e}(t)=\sum_{i=1}^{4} \sum_{j=1}^{4} h_{i}\bigl(z(t)\bigr) h_{j}\bigl(z(t)\bigr) \bigl\{[A_{i}+C_{i}K_{j}]e(t) \bigr\}. \\ \noalign {\vspace {-12pt}} \end{array} $$
(10)

Consider the following Lyapunov function:

The time derivative of V(e(t)) along the trajectory of (10) is

If the following matrix inequality is satisfied,

(11)

then we have

(12)

By using Lemma 1 and Schur complement lemma [48], the matrix inequality (11) is equivalent to

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l} PA_{i}+A_{i}^{T}P+PC_{i}K_{i}+K_{i}^{T}C_{i}^{T}P < 0, \\ \noalign {\vspace {4pt}} \quad \textmd{for} \ 1 \leq i \leq r, \end{array} $$
(13)

and

(14)

Pre- and Post- multiplying by P −1 and introducing change of variables X=P −1, Y j =K j P −1, matrix inequalities (13) and (14) are equivalent to LMIs (8) and (9) respectively. Then, the gain matrix of the control input u(t) is given by K j =Y j X −1. This completes the proof of Theorem 1. □

Remark 1

Comparing with the past works [23, 25, 28], and [29], the main contributions of our method can be summarized as follows: (i) In the existing literature, it seems that there are no results on the T-S fuzzy model for Rikitake system. This work mainly focuses on the synchronizing error for Rikitake system based on T-S fuzzy modelling representation; (ii) Since all the derived criteria are formulated in terms of LMIs, the synchronization error analyzing for the considered systems are readily achieved by any available LMI solvers; (iii) The superiority and practicability of the derived approach are demonstrated by a Rikitake nonlinear system.

Remark 2

Among various fuzzy modeling themes, the T-S model [31] has been one of the most popular modelling frameworks. A general T-S model employs an affine model with a constant term in the consequent part for each rule. This is often referred as an affine T-S model [35, 40], and [41]. On the other hand, the special type of T-S fuzzy model in which the consequent part for each rule is represented by a linear model without a constant term [32, 34]. This type of T-S fuzzy model is often referred as T-S fuzzy model with linear rule consequence, or simply a linear T-S model. The master system (5) and slave system (6) considered in this paper are in the form of an affine T-S fuzzy model, whereas the synchronization error system (7) is a simple linear T-S fuzzy model.

6 Conditions for robust chaotic synchronization of the Rikitake system

Meanwhile, parameter uncertainties frequently appear in practical systems due to the modeling inaccuracies and/or changes in the environment. It is thus of great importance to take parameter uncertainties into account in the master-slave synchronization scheme [7, 11, 16, 28]. Motivated by the above, in this section we intend to design a robust state feedback control law for an uncertain model of the Rikitake system (master system). The uncertain model of the Rikitake system is in the form

(15)

where

in which E i and H i are constant matrices with appropriate dimensions, and unknown time-varying matrices F i (t) satisfying

It is assumed that all the elements of F i (t) are Lebesgue measurable. Further, the controlled response system (slave system) is given by

$$ \everymath{\displaystyle }\begin{array}[b]{rcl} \dot {y}(t) &=&\sum_{i=1}^{4} h_{i}\bigl(\hat{z}(t)\bigr) \bigl\{\bigl(A_{i}+\varDelta A_{i}(t)\bigr)y(t)\\ \noalign {\vspace {5pt}} &&{}+B_{i} +C_{i}u(t) \bigr\},\\ \end{array} $$
(16)

where y(t)=[y 1(t),y 2(t),y 3(t)]T∈R 3 is the state vector, u(t) is the control input, and C i is the known constant matrix. Hence, the robust synchronization error system is written as

$$ \everymath{\displaystyle }\begin{array}[b]{rcl} \dot{e}(t)&=&\sum_{i=1}^{4} h_{i}\bigl(z(t)\bigr) \bigl\{\bigl(A_{i}+\varDelta A_{i}(t)\bigr) e(t)+C_{i}u(t) \bigr\}. \\ \noalign {\vspace {-14pt}} \end{array} $$
(17)

where the synchronization error e(t)=y(t)−x(t).

Theorem 2

If there exist symmetric positive definite matrix X, symmetric matrices Y j , (j=1,2,3,4), and scalars ϵ i >0, (i=1,2,3,4) such that

(18)

and

(19)

where

then the robust synchronization error system (17), under the control input u(t) is given by K j =Y j X −1 e(t), is globally robustly asymptotically stable. Here, r is the number of IF-THEN rules.

Proof

The proof is similar to those in Theorem 1, and thus are omitted here. □

Remark 3

In this paper, we have presented the T-S fuzzy model representation for the chaotic Rikitake system. Further, synchronization control schemes are based on linear state feedback control methods. At present, sliding-mode control has become an important embranchment of control theory. Sliding-mode control is strongly robust to parameter uncertainties and external noise disturbances of the controlled system, and has been successfully applied in controlling chaos [27, 44]. On the other hand, in practical systems, some unknown parameters and disturbances always exist that may cause instability and poor performance. In this regard, the H ∞ synchronization concept has been introduced in [6, 13] to reduce the effect of the disturbance for chaotic synchronization problem of a class of chaotic systems via state output feedback control scheme based on Lyapunov theory and LMI framework. In the future, we will combine the novel sliding-mode control and H ∞ control to design a sliding mode H ∞ controller along with the fuzzy modeling techniques, in order to improve further the control performance of Rikitake system. Also, we will consider the uncertain model of the Rikitake system and design a robust sliding mode H ∞ controller. These works will appear in near future.

7 Numerical results

Example 1

(Synchronization of the Rikitake system without uncertain parameters)

In this example, to verify and demonstrate the effectiveness and the feasibility of the presented fuzzy control method, the simulation results have been performed. The parameters of the Rikitake system are selected as in Sect. 3. From Theorem 1, by using the MATLAB LMI Solver, the following feasible solutions are obtained.

The initial conditions of the drive and response system are chosen to be (x 1(0),x 2(0),x 3(0))=(1,−1,1) and (y 1(0),y 2(0),y 3(0))=(2,−1,−2), respectively. Figures 4(a)–(c) display that the trajectories of drive system and response system with time length 200 seconds whereas the trajectories of drive system and response system with time length 25 seconds is depicted in Figs. 5(a)–(c). Chaotic attractor of Rikitake system (both master and slave) in different planes are given in Figs. 6(a)–(f). Synchronization errors of the Rikitake system with fuzzy control law u(t) are shown in Fig. 7. In Fig. 7, we can see that the synchronization error system (7) asymptotically converges to zero. That is, the slave system follows almost perfectly the master system. Control input u(t) of the Rikitake system is shown in Fig. 8.

Fig. 4
figure 4

Synchronization between master system and slave systems with time length 200 seconds

Full size image
Fig. 5
figure 5

Synchronization between master system and slave systems with time length 25 seconds

Full size image
Fig. 6
figure 6

Projections of the Rikitake attractor into the plane (a) x 1 x 2; (b) x 1 x 3; (c) x 2 x 3; (d) y 1 y 2; (e) y 1 y 3; (f) y 2 y 3

Full size image
Fig. 7
figure 7

Synchronization errors e(t)

Full size image
Fig. 8
figure 8

Control input u(t)

Full size image

Example 2

(Synchronization of the Rikitake system with uncertain parameters)

In this example, the synchronization of an uncertain Rikitake system and their numerical simulation results have been performed. The parameters of the Rikitake system are selected as in Sect. 3. The uncertain matrix parameters E i and H i are given by

and let

From Theorem 2, by using the MATLAB LMI Solver, the following feasible solutions are obtained:

The initial conditions of the drive and response system are chosen to be (x 1(0),x 2(0),x 3(0))=(1,−1,1) and (y 1(0),y 2(0),y 3(0))=(2,−1,−2), respectively. Figures 9(a)–(c) display that the trajectories of uncertain drive system and uncertain response system with time length 200 seconds. The chaotic attractor of the uncertain Rikitake system (both master and slave) in different planes are given in Figs. 10(a)–(f). Synchronization errors of the Rikitake system with uncertain parameters and fuzzy control law u(t) are shown in Fig. 11. In Fig. 11, we can see that the synchronization of an uncertain error system (17) robustly asymptotically converges to zero. That is, the uncertain slave system follows almost perfectly the uncertain master system.

Fig. 9
figure 9

Synchronization between uncertain master system and uncertain slave systems with time length 200 seconds

Full size image
Fig. 10
figure 10

Projections of the uncertain Rikitake attractor into the plane (a) x 1 x 2; (b) x 1 x 3; (c) x 2 x 3; (d) y 1 y 2; (e) y 1 y 3; (f) y 2 y 3

Full size image
Fig. 11
figure 11

Synchronization errors e(t) with uncertain parameters

Full size image

Remark 4

The simulation results imply that the two identical Rikitake system are synchronized with each other, and validate the effectiveness of the derived results. In the numerical simulations, the Euler method is employed to solve the systems of differential equations with step size 0.01 and time length 200 seconds.

8 Conclusion

In this paper, the chaos synchronization problem has been investigated for nonlinear Rikitake systems based on T-S fuzzy control approach. By choosing the Lyapunov function and designing a fuzzy state-feedback controller, the sufficient conditions have been established to ensure the synchronization of the Rikitake system, which are given in terms of LMIs that can be solved using any available LMI solvers. Simulations results have been provided to show the merits of the obtained results.