1 Introduction

In recent years, traffic jams have attracted much attention because of its complex mechanism. Many traffic flow models have been developed to investigate the traffic jams [1,2,3,4,5,6,7,8,9,10,11], such as car-following models [12,13,14,15,16,17,18], cellular automation models [19,20,21,22], gas kinetic models [23,24,25], and hydrodynamic lattice models [26,27,28].

The optimal velocity model (for short OVM) proposed firstly by Bando [29] was further researched [30, 35], which has successfully revealed the dynamic evolution of traffic jam in a simple way. Subsequently, Helbing and Tilch [36] developed a generalized force model (for short GFM) by considering negative velocity difference on the basis of OVM. It overcome the shortcomings of high acceleration and unrealistic deceleration occurring in the OVM. In 2001, by introducing positive relative velocity into the GFM, Jiang [37] developed the full velocity difference model (FVDM). Jiang’s expanded study [10, 11] shows that the FVDM is in agreement with the field data better than OVM and GFM. Ge [38] proposed the two-velocity difference model (for short, TVDM) by considering the ITS application. Nakayama [18] presented the additional energy consumption with respect to the stable statue for all vehicles.

The aforementioned models can describe many complex traffic phenomena. However, these models cannot be employed to study the optimal velocity difference and a two-velocity difference of the leading car and the current car, because they did not consider two factor simultaneously [39]. In fact, the optimal speed difference and the two speed difference reflect the whole traffic situation. A leading car can send the velocity changes signal command to the follower, and the following car can obtain the leading car’s running state information to control its speed. By considering the optimal velocity difference term, not only the stability of traffic flow can be improved, but also the disadvantage of collision and unrealistic deceleration can be avoided. In view of this, the improved car-following model is presented to investigate the traffic flow.

Real traffic is affected by many complicated factors such as passerby, capability, driver’s sensitivity and so on [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. These factors on the traffic flow are treated as disturbance to cause change of vehicle velocity. These changes of velocity result in the additional consumption of energy compared to the case of no disturbance. By comparison of energy consumption in order to reduce air pollution.

Based on the optimal speed and the two speed difference, this paper investigated an improved car-following model. In Sect. 2, the model is presented with considering the two-velocity difference and the optimal velocity difference. The model is analyzed by using linear stability theory. In Sect. 3, our model is analyzed by the nonlinear analysis near the critical point, and the TDGL equation and its corresponding solution are obtained. In Sect. 4, the mKdV equation is derived. In Sect. 5, numerical simulation is given. In Sect. 6, the conclusions are drawn.

2 The car-following model and linear stability analysis

According to the above mentioned idea, we derived an improved car-following model considering the optimal velocity difference and a two-velocity difference. The motion equation is given as follows:

$$\begin{aligned} \frac{dv_{n}[t]}{dt}= & {} a\left[ V(\Delta {x_{n}[t]})+k(V(\Delta {x_{n+1}[t]})\right. \nonumber \\&\left. -V[\Delta {x_{n}(t)}])-v_{n}(t)\right] +\lambda \left[ p\Delta {v_{n}[t]}\right. \nonumber \\&\left. +(1-p)\Delta {v_{n+1}[t]}\right] \end{aligned}$$
(1)

where a is the sensitivity which corresponds to the inverse of the delay time, k is the optimal velocity difference parameter and \(\lambda \) is the two-velocity difference parameter. The optimal velocity function is proposed

$$\begin{aligned} V(\Delta x_{n}[t])=\frac{v_{max}}{2}[\tanh (\Delta x_{n}(t)-h_{c})+\tanh (h_{c})]\nonumber \\ \end{aligned}$$
(2)

where \(v_{max}\) is the maximal velocity. The function V(.) is a monotonically increasing function with an upper bound(maximal velocity) and has a turning point \(\Delta x_{n}=h_{c}:V{}''(h_{c})=0\). Therefore, we can derive the TDGL equation from Eq. (1), which could describe traffic jam. For convenience of linear analysis, Eq. (1) can be rewritten:

$$\begin{aligned} \frac{d^{2}x_{n}(t)}{dt^{2}}= & {} a \left[ V(\Delta x_{n}[t])+k(V(\Delta x_{n+1}[t])\right. \nonumber \\&\left. -V[\Delta x_{n}(t)])-\frac{dx_{n}(t)}{dt}\right] +\lambda \left[ p\left( \frac{dx_{n+1}(t)}{dt}\right. \right. \nonumber \\&\left. \left. -\frac{dx_{n}(t)}{dt}\right) +(1-p)\left( \frac{dx_{_{n+2}(t)}}{dt}-\frac{dx_{n+1 }(t)}{dt}\right) \right] \nonumber \\ \end{aligned}$$
(3)

Furthermore, Eq. (3) can be rewritten in terms of the headway:

$$\begin{aligned} \frac{d^{2}\Delta x_{n}(t)}{dt^{2}}= & {} a\left[ V(\Delta x_{n+1}[t])-V(\Delta x_{n}[t])+k(V(\Delta x_{n+2}[t])\right. \nonumber \\&\left. -2V(\Delta x_{n+1}[t])+V[\Delta x_{n}(t)])-\frac{d\Delta x_{n}(t)}{dt}\right] \nonumber \\&+\lambda \left[ p\left( \frac{dx_{n+2}(t)}{dt}-2\frac{dx_{n+1}(t)}{dt}+\frac{d_{n}(t)}{dt}\right) \right. \nonumber \\&\left. +(1-p)\left( \frac{dx_{n+3}(t)}{dt}-2\frac{dx_{n+2}}{dt}+\frac{dx_{n+1}(t)}{dt}\right) \right] \nonumber \\ \end{aligned}$$
(4)

The change in energy \(\Delta E_{n}\) for the vehicle n between the two successive time step in defined as:

$$\begin{aligned} \Delta E_{n}=\frac{1}{2}\left[ v_{n}^{2}(t)-v_{n}^{2}(t-1)\right] \end{aligned}$$
(5)

where \(v_{n}(t)\) and \(v_{n}(t-1)\) are the velocity of vehicle n in the two successive time step.

Fig. 1
figure 1

The phase diagram of the model according to different values of parameter k and \(\lambda \)

Full size image

Then, linear stability analysis can be conducted. It is obvious that the traffic flow can reach the steady state when the vehicle run with constant headway h and constant velocity V(h). Therefore, the steady-state solution is given as

$$\begin{aligned} x_{n}^{0}(t)=hn+V(h)t, h=\frac{L}{N} \end{aligned}$$
(6)

where N is the total vehicle number and L is the road length. Suppose \(y_{n}(t)\) is a small deviation from the steady state \(x_{0}^{n}(t):x_{n}(t)=x_{0}^{n}(t)+y_{n}(t)\). Substitute it into Eq. (3) and linearize it which yields

$$\begin{aligned} \frac{dy{_{n}}^{2}(t)}{dt^{2}}= & {} a\left[ V{}'(h)\Delta y_{n}(t)+k(V{}'(h)\Delta y_{n+1}(t)\right. \nonumber \\&\left. -V{}'(h)\Delta y_{n}[t])-\frac{dy_{n}(t)}{dt}\right] \nonumber \\&+\lambda \left[ p\left( \frac{dy_{n+1}(t)}{dt}-\frac{dy_{n}(t)}{dt}\right) \right. \nonumber \\&\left. +(1-p)\left( \frac{dy_{n+2}(t)}{dt}-\frac{dy_{n+1}(t)}{dt}\right) \right] \end{aligned}$$
(7)
Table 1 The coefficients \(m_{j}\) of the model
Full size table

where \(\Delta y_{n}(t)=y_{n+1}(t)-y_{n}(t)\) and \({V}'(h)=dV(\Delta x_{n})dt|\Delta x_{n}=h\). Expanding \(y_{n}(t)=exp(ikn+zt)\), it reads

$$\begin{aligned} z^{2}= & {} a[{V}'(e^{ik}-1)+kV{}'(e^{ik}-1)^{2}-z]\nonumber \\&+\,\lambda z[p(e^{ik}-1)+(1-p)(e^{2ik}-e^{ik})] \end{aligned}$$
(8)

where \({V}'={V}'(h)\). Let \(z=z_{1}(ik)+z_{2}(ik)^{2}+\cdots \), then the first-and second-order terms of ik are:

$$\begin{aligned} z_{1}={V}'(h), z_{2}=\frac{{V}'}{2}+kV{}'+\frac{\lambda z_{1}-z_{1}^{2}}{a} \end{aligned}$$
(9)

For small disturbance with long wavelengths, the uniform traffic flow is instable in the condition that

$$\begin{aligned} a< \frac{2(V{}'-\lambda )}{1+2k} \end{aligned}$$
(10)

The stability condition is given:

$$\begin{aligned} a= \frac{2(V{}'-\lambda )}{1+2k} \end{aligned}$$
(11)

The result is relevant with the parameter k. \((v_{max}=2,h_{c}=4)\)

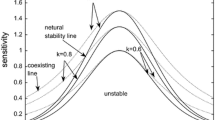
Figure 1 shows the phase diagram in the (h, a)-plane where h is the headway and a is sensitivity. The solid lines show the results of the neutral stability curves with different \(\lambda \) and k. It shows the stable region and the critical points increase with increasing the value of the parameter \(\lambda \) and k.

From the pattern (a) of Fig. 1 with \(\lambda =0\) and \(k=0\), the neutral stability line and the critical point are consistent with these in OVM which proposed by Bando et al. It is very unstable.

From the pattern (a), (b) and (c) of Fig. 1, we use the fixed k. With the increase of \(\lambda \) \(\lambda =0, 0.1, 0.3\), the stable region gradually increase. As can be seen from the pattern (a), (b) and (c) of Fig. 1, the stable region gradually increases with the increase of k (\(k=0, 0.3, 0.5\)) and the fixed \(\lambda \). The traffic flow is more stable.

Obviously, we can see that our model is more stable than OVM. Especially, from the pattern (d) of Fig. 1, the stable region reaches the best range when the values are selected as \(\lambda =0.3\), \(k=0.5\).

3 TDGL equation

In car-following models, by deriving the nonlinear wave equation, we depicted the propagation behavior of traffic jam. Equation is derived by using the long wavelength mode for describing the traffic flow on coarse-grained scale. The slowly vary behavior at long waves near the critical point is analyzed. The slow scales for space variable j and time variable t are introduced, and the slow variable X and T is defined as follows:

$$\begin{aligned} X=\varepsilon (j+bt),T=\varepsilon ^{3}t,0< \varepsilon \ll 1 \end{aligned}$$
(12)

The headway \(\Delta x_{n}(t)=h_{c}+\varepsilon R(X,T) \) is set as:

$$\begin{aligned} \Delta x_{n}(t)=h_{c}+\varepsilon R(X,T) \end{aligned}$$
(13)

By bringing Eqs. (12)–(13) into (4), and expanding to the fifth-order of \(\varepsilon \). We obtain the following expression:

$$\begin{aligned}&\varepsilon ^{2}m_{1}\partial _{X}R+\varepsilon ^{3}m_{2}\partial ^{2}_{X}R+\varepsilon ^{4}[m_{3}\partial ^{3}_{X}R+m_{4}\partial _{X}R^{3}-\partial _{T}R]\nonumber \\&\qquad +\,\varepsilon ^{5}[m_{5}\partial _{X}^{4}R+m_{6}\partial _{X}^{2}R^{3}+m_{7}\partial _{X}\partial _{T}R]=0 \end{aligned}$$
(14)

Here, the coefficients \(m_{j}\) are given in Table 1. Now, we consider the traffic flow near critical point \(\tau =(1+\varepsilon ^{2})\tau _{c} \). By taking \( b=V{}'\), the second-order and third-order terms of \(\varepsilon \) is eliminated from Eq. (14), which leads to the simplified equation as follows:

$$\begin{aligned} \varepsilon ^{4}\partial _{T}R= & {} \varepsilon ^{4}\left( \frac{1}{6}V{}'+kV{}'+\frac{3\lambda \tau V{}'(1-p)}{2}\right) \partial _{X}^{3}R \nonumber \\&+\,\varepsilon ^{4}\frac{1}{12}V{}'''\partial _{X}R^{3}-\varepsilon ^{3}\left( \lambda V{}'-\frac{1}{2}V{}'-\lambda V{}'\tau \right) \partial _{X}^{2}R\nonumber \\&+\,\varepsilon ^{5}\left[ \frac{1}{24}V{}'+\frac{7}{12}V{}'k+\lambda V{}'\tau \left( \frac{7}{6}-p\right) \right. \nonumber \\&+\,(\lambda (2p-1)-2b)\left. \left( \frac{1}{6}V{}'+kV{}'+\frac{3}{2}\lambda V{}'\tau (1-p)\right) \right] \partial _{X}^{4}R\nonumber \\&+\,\varepsilon ^{5}\left( \frac{1}{12}V{}'''+\frac{5}{6}V{}'''k\right) \partial _{X}^{2}R^{3} \end{aligned}$$
(15)
Table 2 The coefficients \(j_{i} \) of the model
Full size table

By transforming variable X and T into variable \( x= \varepsilon ^{-1}X \) and \( t=\varepsilon ^{-3}T \), and taking \( S(x,t)=\varepsilon R(X,T)\), Eq. (15) is rewritten as follows:

$$\begin{aligned} \partial _{t}R= & {} \left( \frac{1}{6}V{}'+kV{}'+\frac{3\lambda V{}'\tau (1-p)}{2}\right) \partial _{x}^{3}R \nonumber \\&+\frac{1}{12}V{}'''\partial _{x}R^{3}-\left( \lambda V{}'-\frac{1}{2}V{}'-\lambda V{}'\tau \right) \partial _{x}^{2}R\nonumber \\&+\left[ \frac{1}{24}V{}'+\frac{7}{12}V{}'k+\lambda V{}'\tau \left( \frac{7}{6}-p\right) \right. \nonumber \\&+(\lambda (2p-1)-2b)\left. \left( \frac{1}{6}V{}'+kV{}'+\frac{3}{2}\tau \lambda b(1-p)\right) \right] \partial _{x}^{4}R\nonumber \\&+\left( \frac{1}{12}V{}'''+\frac{5}{6}V{}'''k\right) \partial _{x}^{2}R^{3} \end{aligned}$$
(16)

By adding term \( \frac{2V{}'(\lambda V{}'\tau +\frac{1}{2}V{}'-\lambda V{}')}{\frac{1}{12}V{}'+\frac{5}{6}V{}'''k}\partial _{x}S \) on both left and right sides of Eq. (16) and performing \( t_{1}=t \) and \( x _{1}=x-\frac{2V{}'(\lambda V{}'\tau +\frac{1}{2}V{}'-\lambda V{}')}{\frac{1}{12}V{}'+\frac{5}{6}V{}'''k} \) for Eq. (16), we get

$$\begin{aligned} \partial _{t_{1}}S= & {} \left( \partial _{x_{1}}-\frac{2V{}'\left( \lambda V{}'\tau +\frac{1}{2}V{}'-\lambda V{}'\right) }{\frac{1}{12}V{}'-\frac{5}{6}V{}'''k}\partial _{x_{1}}^{2}\right) \left[ \left( \frac{1}{6}V'\right. \right. \nonumber \\&\left. +\,kV{}'\frac{3\lambda V{}'\tau (1-p)}{2}\right) \partial _{x_{1}}^{2}S +\frac{\frac{1}{12}V'+\frac{5}{6}V{}'''k}{2V{}'''}S\nonumber \\&\left. +\,\frac{1}{2V{}'\left( \lambda V{}'\tau +\frac{1}{2}V'-\lambda V'\right) }S^{3}\right] \end{aligned}$$
(17)

We define the thermodynamic potentials:

$$\begin{aligned} \phi (S)= & {} \frac{\frac{1}{12}V{}'+\frac{5}{6}V{}'''k}{4V{}'''}S^{2}\nonumber \\&+\frac{1}{8V{}'(\lambda V{}'\tau +\,\frac{1}{2}V{}'-\lambda V{}')}S^{4} \end{aligned}$$
(18)

By rewritten Eqs. (17) with (18), the TDGL equation is derived

$$\begin{aligned} \partial _{t_{1}}S= & {} -\left( \partial _{x_{1}}+\frac{2V{}'\left( \lambda V{}'\tau +\frac{1}{2}V{}'-\lambda V{}'\right) }{\frac{1}{12}V{}'+\frac{5}{6}V{}'''k}\partial ^{2} _{x_{1}}\right) \frac{\delta \Phi (S)}{\delta S} \end{aligned}$$
(19)
$$\begin{aligned} \Phi (S)= & {} \int dx_{1}\left[ \frac{1}{2}\left( \frac{1}{6}V{}'+kV{}'+\frac{3\lambda V{}'\tau (1-p)}{2}\right) (dx_{1}S)^{2}+\phi (S)\right] \nonumber \\ \end{aligned}$$
(20)

where \( \delta \Phi (S)/\delta S\) indicates the function derivative. The TDGL Eq. (19) has two steady-state solutions except trivial solution \(S=0\): one is the uniform solution

$$\begin{aligned} S(x_{1},t_{1})=\pm \left[ \frac{V{}'+10V{}'''k}{4V{}'''}{}S^{2}\right] ^{\frac{1}{2}} \end{aligned}$$
(21)

And the other is the kink solution

$$\begin{aligned} S(x_{1},t_{1})= & {} \pm \left[ \frac{V{}'+10V{}'''k}{4V{}'''}{}S^{2}\right] ^{\frac{1}{2}}\nonumber \\&\times \tanh \left\{ \left( \frac{C}{A+B}\right) ^{\frac{1}{2}}\times \left( x_{1}-x_{0}\right) \right\} \end{aligned}$$
(22)

where \( x_{0} \) is constant. \(A=\frac{1}{24}V{}'+\frac{7}{12}V{}'k+\lambda V{}'\tau (\frac{7}{6}-p)\), \(B=(\lambda (2p-1)-2b)(\frac{1}{6}V{}'+kV{}'+\frac{3}{2}\tau \lambda b(1-p))\), \(C=(\frac{1}{2}V{}'+\lambda V{}'\tau -\lambda V{}')\). Equation (22) represents the coexisting phase. By the condition

$$\begin{aligned} \partial \phi /\partial S=0,\partial ^{2}\phi /\partial S^{2}> 0 \end{aligned}$$
(23)

We obtain the coexisting curve from Eq. (18) in terms of the original parameters

$$\begin{aligned} (\Delta x)_{co}=h_{c}\pm \left[ \frac{V{}'+10V{}'''k}{4V{}'''}{}S^{2}\right] ^{\frac{1}{2}} \end{aligned}$$
(24)

The spinodal line is given by the condition

$$\begin{aligned} \partial ^{2}\phi /\partial S^{2}=0 \end{aligned}$$
(25)

From Eq. (23), we obtain the spinodal line described by the following equation

$$\begin{aligned} (\Delta x)_{co}= & {} h_{c}\pm \left\{ \frac{3(V{}'-\lambda )}{(2\gamma \tau _{0}V{}'-1)V{}'''}\right. \nonumber \\&\left. \left[ (2b\gamma \tau _{0}-1)-\frac{2(\tau \lambda b-\tau b)}{V{}'}\right] \right\} ^{\frac{1}{2}} \end{aligned}$$
(26)

The critical point is given by the condition \( \partial \phi /\partial S=0\) and Eq. (25)

$$\begin{aligned} (\Delta x)_{c}=h_{c},a_{c}=\frac{2(V{}'-\lambda )}{2\gamma \tau _{0}V{}'-1} \end{aligned}$$
(27)

4 mKdV Equation

Similarly with the derivation of the TDGL equation, we study the slowly varying behavior at long wavelengths near the critical point. We extract slow scale for space variable n and time variable t. By inserting \( a_{c}=\frac{2(V{}'-\lambda )}{1+2k}\), \( a=(1+\varepsilon ^{2})a_{c}\) into Eq. (14), one obtains:

$$\begin{aligned}&\varepsilon ^{4}(j_{1}\partial _{X}^{3}R+j_{2}\partial _{X}R^{3}-\partial _{T}R)\nonumber \\&\qquad +\varepsilon ^{5}(j_{3}\partial _{X}^{4}R+j_{4}\partial _{X}^{2}R^{3}+j_{5}\partial _{X}^{2})=0 \end{aligned}$$
(28)
Fig. 2
figure 2

Space-time evolution of the headway after \(t=10,000\)

Full size image
Fig. 3
figure 3

The headway profile at \(t=10,000\) under the different value of k and \(\lambda \)

Full size image

Here, the coefficients \(j_{i}\) are given in Table 2.

In the table \({V}'=dV(\Delta x_{n})/d\Delta x_{n}|\Delta x_{n}=h_{c}\), \( {V}'''=d^{3}V(\Delta x_{n})/d\Delta x_{n}^{3}|\Delta x_{n}=h_{c}\).

In order to derive the regularized equation, we make the following transformation:

$$\begin{aligned} T=\frac{1}{j_{1}}T{}',R=\sqrt{\frac{j_{1}}{j_{2}}} \end{aligned}$$
(29)

So the standard mKdV equation with an \(O(\xi )\) correction term is obtained as follows:

$$\begin{aligned} \partial _{T{}'}R{}'= & {} \partial _{X}^{3}R{}'-\partial _{X}R{}'^{3}-\varepsilon \left[ \frac{j_{3}}{j_{1}}\partial _{X}^{2}R{}'\right. \nonumber \\&\left. +\frac{j_{4}}{j_{1}}\partial _{X}^{4}R{}'+\frac{j_{5}}{j_{2}}\partial _{X}^{2}R{}'^{3}\right] \end{aligned}$$
(30)

If we ignore the \(O(\varepsilon )\), they are just the mKdV equations with a kink solution as the desired solution:

$$\begin{aligned} R{}'_{o}(X,T{}')=\sqrt{c}tanh\sqrt{\frac{c}{2}}(X-cT{}') \end{aligned}$$
(31)

Then, assuming that \( R{}'(X,T{}')=R_{o}{}'(X,T{}')+\varepsilon R_{1}{}'(X,T{}')\), we take into account the \(O(\varepsilon )\) correction. For the purpose of determining the selected value of the velocity c for the kink solution, it is necessary to satisfy the solvability condition. As \((R_{o}{}',M[R_{o}{}']\equiv \int _{-\infty }^{+\infty }dX{}'R_{o}{}'M[R_{}{}'])\), where \( M [R_{o}{}']=\frac{j_{3}}{j_{1}}\partial _{X}^{2}R{}'+\frac{j_{4}}{j_{1}}\partial _{X}^{4}R{}'+\frac{j_{5}}{j_{2}}\partial _{X}^{2}R{}'^{3}\). We get the general velocity c:

$$\begin{aligned} c=\frac{5j_{2}j_{3}}{2j_{2}j_{4}-3j_{1}j_{5}} \end{aligned}$$
(32)

Hence, the general kink–antikink soliton solution of the headway, from the mKdV equation is obtained:

$$\begin{aligned} \Delta x_{n}(t)= & {} h_{c}\pm \sqrt{\frac{j_{1}c}{j_{2}}(\frac{\tau }{\tau _{c}}-1)}\times tanh\sqrt{\frac{c}{2}\left( \frac{\tau }{\tau _{c}}-1\right) }\nonumber \\&\times \left[ n+(1-cj_{1})\left( \frac{\tau }{\tau _{c}}-1\right) t\right] \end{aligned}$$
(33)

where \(V{}'''< 0\), this kink soliton solution also represents the coexisting phase, and the kink solution (33) agrees with the solution (22) obtained from the TDGL equation. Thus, the jamming transition can be described by both the TDGL equation with a nontravelling solution and the mKdV equation with a propagating solution.

5 Numerical simulation

In this section, we test the validity of the theoretical results by numerical simulation. With the periodic boundary condition, the initial conditions are given as follows:

\( \Delta x_{j}(0)=\Delta x_{0}=4.0,\Delta x_{j}(1)=\Delta x_{0}=4.0, \) for \(j\ne 50,51 \), \(\Delta x_{j}(1)=4.0-0.5\), for \( j=50,\Delta x_{j}(1)=4.0+0.5\), for \( j=51\).

We choose the total number of cars and the sensitivity as \(N=100\) and \(a=1.05\).

Figure 2 shows the space-time evolution of the headway after \( t=10^{4}\) time steps under the different parameter k and \(\lambda \). It can exhibit the kink–antikink solutions propagating backwards. It can be seen that the traffic flow becomes more stable with the k and \(\lambda \). From pattern (a) with \(k=0\) and \(\lambda =0\), it corresponds to the OVM model. It is obviously that the traffic flow are very unstable. When a small disturbance is added into the uniform traffic flow, the propagating backward stop-and-go traffic jam appears which is very similar to the mKdV solution. The traffic jams diminish gradually from pattern (a) to pattern (b) with \(k=0.3\) and \(\lambda =0 \) to pattern (c) with \(k=0.5\) and \(\lambda =0 \). Pattern (d) with \(k=0 , \lambda =0.1 \) and pattern (e) with \(k=0 \), \(\lambda =0.3\), the traffic congestion is more stable than in pattern (a). Pattern (f) with \(k=0.5, \lambda =0.3\), the traffic flow is very stability. It is found that the new consideration plays the positive function on stabilization of traffic flow. It is obvious that the amplitude of the kink–antikink soliton weakens gradually with increasing the parameter k and the parameter \(\lambda \). Furthermore, it demonstrates that the new consideration is enough to suppress the traffic congestion efficiently.

Figure 3 shows the headway profile obtained at \(t =10,000\) corresponding to panels in Fig. 2; the similar results are obtained from Fig. 2. So, the simulation results are in agreement with the theoretical analysis

Figure 4 shows the distribution of energy consumption for the different parameters k and \(\lambda \). The change in the profile of kinetic energy in each model is loop. They divided into two regions with \(\Delta E_{n}>0\) and \(\Delta E_{n}<0\). \(\Delta E_{n}>0\) indicates that the vehicles will leave the congestion region in the state of acceleration process. \(\Delta E_{n}<0\) indicates that the vehicles will enter the congestion region in the state of deceleration process. The area of the parameter with \(k=0, \lambda =0\) model is the largest and those of the parameter with \(k=0.5, \lambda =0.3\) model is the minimal of all. The parameter with \(k=0, \lambda =0\) model is the most unstable and the stability of the parameter with \(k=0.5, \lambda =0.3\) model is the best of all. The stability of the parameter with \(k=0.3, \lambda =0.1\) model is better than OVM. As a result, the smaller loop of the kinetic energy change , the more stable traffic flow is.

Fig. 4
figure 4

Profile of energy consumption of each vehicle in different k and \(\lambda \)

Full size image

6 Conclusion

In this paper, an improved car-following model of traffic flow is put forward to describe traffic behaviors. The above analysis confirms that the optimal velocity difference and a two-velocity difference effect did improve the stability of traffic flow. We obtain the neutral stability line and the critical point through the linear stability analysis. The TDGL equation has been derived to describe traffic behavior near the critical point by applying the reductive perturbation method. Furthermore, the mKdV equation has been derived and showed the connection between the TDGL and the mKdV equations. When the optimal velocity difference and a two-velocity difference are considered in our model, it is enough to enhance the stability of traffic flow and reduce the energy consumption. Also, numerical simulation results confirm that the stable region grows increasingly large with the optimal velocity difference and a two-velocity difference effect. The preceding analytical results show that the optimal velocity difference and a two-velocity difference effect should be taken into account.