1 Introduction

Although urbanization provides modern science and technologies, modern civilization and convenient way of life for human beings, it also forms some problems such as public security, air pollution and energy crisis. Traffic flow is a topical issue in social problems; the congested traffic flow not only causes much inconvenience, but also results in security risks for drivers. Due to the importance of traffic, traffic flow has attracted considerable attention in the field of physical science [1–5]. In order to make a better understanding of traffic flow, there is a demand for realistic and quantitative models that can predict traffic flux and travel times for a given infrastructure and duplicate the phenomena observed in a real situation. To achieve this goal, various traffic flow models including the car-following models, the hydrodynamic models, the cellular automaton models and gas kinetic models were proposed by many scholars with different backgrounds. A series of experiments had been done for investigating the mechanism of traffic flow and identifying the influencing factors. Many interesting non-equilibrium phenomena such as phase transition, density waves, stop-and-go flows, local clusters and ghost jams had been observed. See Refs. [6–37] for details.

Among these models, Nagatani firstly proposed a lattice hydrodynamic model for traffic flow in Ref. [20]. By using the linear stability theory and nonlinear analysis method, Nagatani found the neutral stability line and the modified Korteweg–de Vries (MKdV) equation successfully and derived the solutions of kink density wave in the MKdV. Based on the model proposed by Nagatani, many researchers had proposed many extended versions with the consideration of different factors like backward effect, lateral effect, density difference effect, lane changing effect and anticipation effect [24, 25, 29–32, 37, 38]. Considering two-dimensional traffic flow, Nagatani extended his work to two-dimensional lattice hydrodynamic model in Ref. [22]. All the above works and unmentioned in this paper undoubtedly enrich the traffic flow theory and make lattice hydrodynamic models more realistic.

From the process of deducing the one-dimensional lattice hydrodynamic model in Ref. [20], it can be seen that the proposed model in Ref. [20] is based on the car-following models and the continuum models. And one assumption of car-following theory is that the vehicles should travel in the middle of a straight road. But in real traffic environment, not every traffic road is straight, it may be a curved road. And when turning a corner, the track of vehicles is curved line. Considering the road situation, Zhu and Zhang [39] proposed a lattice model considering the effect of gradient. In Refs. [19, 40], by using car-following model and lattice model, Zhu and Zhang, Cao and Shi, respectively, investigated the effects of friction coefficient and radius of curvature upon traffic flow on curved road.

But, as we know, traffic flow on curved road may be affected by the length of curved road. Usually, when the length of curved road is long, traffic flow will become unstable; otherwise, traffic flow will become stable. In the other words, traffic flow on curved road may be affected by radian of curved road. Moreover, traffic flow on curved road is affected by the angle going into curved road. And these two factors have not been considered in lattice hydrodynamic models. Lattice hydrodynamic models have the merit that the linear stability analysis and the nonlinear analysis can be applied. In this paper, taking the effects of radian, friction coefficient and curvature radius of curved road into account, an extended lattice hydrodynamic model for traffic flow is proposed.

The paper is organized as follows. In Sect. 2, the model is formulated by considering radian, friction coefficient and curvature radius. The stability analysis is obtained by using linear stability analysis in Sect. 3. We can see the stability condition varies with radian, friction coefficient and curvature radius. In Sect. 4, the Burgers, Korteweg–de Vries (KdV) and MKdV equations are derived in three types of traffic flow regions by using nonlinear analysis. The simulations are given in Sect. 5. Section 6 is the conclusion.

2 Model

In Ref. [20], Nagatani proposed a lattice hydrodynamic model to describe the jam transition in traffic flow. By the use of the proposed model, Nagatani successfully derived the MKdV equation to describe traffic congestion as the kink density wave. The model is

$$\begin{aligned} \partial _{t}\rho (j,t)+\rho _{0}\partial _{j}\rho (j,t)v(j,t)=0, \end{aligned}$$
(1)

where \(\rho _{0}\) is the total average density, and it is the reciprocal of average headway \(\delta \), that is \(\rho _{0}=1/\delta \). \(\rho (j,t), v(j,t)\) denote the density and velocity at site j at time t, respectively.

In terms of Nagatani’s idea [20], the traffic flux \(\rho v\) at site j is determined by the total optimal current at site \(j+1\) with delay time \(\tau \), that is

$$\begin{aligned} \rho (j,t+\tau )v(j,t+\tau )=\rho _{0}V(\rho (j+1,t)), \end{aligned}$$
(2)

\(V(\rho (j,t))\) is the optimal velocity function. In Ref. [22], Nagatani proposed the optimal velocity function as follows

$$\begin{aligned} V(\rho (j,t))&{=}\left[ \tanh \left( \frac{2}{\rho _{0}}{-}\frac{\rho (j,t)}{\rho _{0}^{2}}-\frac{1}{\rho _\mathrm{c}}\right) {+}\tanh \left( \frac{1}{\rho _\mathrm{c}}\right) \right] .\nonumber \\ \end{aligned}$$
(3)

where \(\rho _\mathrm{c}\) is the critical density and it is equal to the inverse of the safety distance [26].

The model (1)–(2) is a very abstract model. When the road is horizontal, the model (1)–(2) can be rewritten as

$$\begin{aligned} \partial _{t}\rho (x,t)+\partial _{x}\rho (x,t)v(x,t)=0, \end{aligned}$$
(4)

and

$$\begin{aligned} \rho (x,t+\tau )v(x,t+\tau )=\rho _{0}V(\rho (x+\delta ,t)) \end{aligned}$$
(5)

by using the following formulas, that is

$$\begin{aligned} j=x/\delta , \rho _{0}=1/\delta , \end{aligned}$$

then

$$\begin{aligned} \rho _{0}\partial _{j}\rho (j,t)v(j,t)=\partial _{x}\rho (x,t)v(x,t), \end{aligned}$$
(6)

and Eqs. (4) and (5) can be deduced. The process is similar as in Ref. [20].

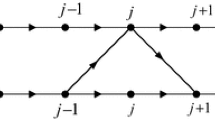
Now, we consider the vehicles running on curved road. Figure  1 is the illustration of vehicles running on curved road. And Fig. 2 is an abstract illustration of Fig. 1. We denote the curved road as \(y=\sqrt{R^2-(x-R)^2}\), where R represents the curvature radius of the curved road. The length between site j and \(j-1\) is

$$\begin{aligned} \int ^{x}_{x-x_0}\sqrt{1+y'^2}d x\approx \frac{x_0}{\sin \theta _j}, \end{aligned}$$

where \(\theta _j\) represents the radian at site j of the curved road. This formula shows the relationship between average headway on straight road and the one on curved road.

Fig. 1
figure 1

The illustration of vehicles running on curved road

Full size image
Fig. 2
figure 2

The abstract illustration of Fig. 1

Full size image

Now, considering the curved road, we modify the lattice hydrodynamic model as follows

$$\begin{aligned} \partial _{t}\rho (j,t)+\frac{\rho _{0}}{\sin \theta _j}\partial _{j}\rho (j,t)v(j,t)=0, \end{aligned}$$
(7)

and

$$\begin{aligned} \rho (j,t+\tau )v(j,t+\tau )=\frac{\rho _{0}}{\sin \theta _j}V(\rho (j+1,t)). \end{aligned}$$
(8)

Here, compared with Eqs. (1) and (2), \(\frac{1}{\sin \theta _j}\) in Eqs. (7) and (8) is a new factor which represents the difference between traffic flow on curved road and traffic flow on straight road.

As we know, objects running on curved road are affected by the centripetal force, and the maximal linear velocity \(v_\mathrm{{max}}\) can be represented as \(v_\mathrm{{max}}=\sqrt{\mu gR}\), where \(\mu \) is the friction coefficient, R is the radius of curved road, g is gravity acceleration. Taking the situation of curved road into account, we use a modified optimal velocity function [40] which is similar as the one in Ref. [22], that is

$$\begin{aligned} \begin{aligned} V\left( \rho (j,t)\right)&= k\frac{\sqrt{\mu g R}}{2}\left[ \tanh \left( \frac{2}{\rho _{0}}{-}\frac{\rho (j,t)}{\rho _{0}^{2}}{-}\frac{1}{\rho _\mathrm{c}}\right) \right. \\&\left. \quad +\,\tanh \left( \frac{1}{\rho _\mathrm{c}}\right) \right] , \end{aligned} \end{aligned}$$
(9)

where k is the control parameter of \(v_\mathrm{{max}}\). Because when running on curved road, drivers always slow down with the consideration of safety. The velocity is far less than the maximal velocity. Here, based on the characteristic of vehicles running on curved road, we introduce the new factor \(\frac{\sqrt{\mu gR}}{2}\) for addressing the difference between traffic flow on curved road and traffic flow on straight road.

By inserting Eq. (8) into Eq. (7), and when site j is sufficiently close to site \(j-1\), then \(\theta _j\approx \theta _{j-1}\). And the total density equation is obtained as

$$\begin{aligned} \begin{aligned}&\rho (j,t+2\tau )-\rho (j,t+\tau )\\&\quad +\,\frac{\tau \rho _0^2}{\sin ^2\theta _j}\left[ V(\rho (j+1,t))-V(\rho (j,t))\right] =0. \end{aligned} \end{aligned}$$
(10)

Here, \(\frac{1}{\sin ^2\theta _j}\) in Eq. (10) is a new factor which reflects the effect of curved road upon traffic flow. And the total density equation (10) is different from the previous work in Refs. [20, 40].

3 Linear stability analysis

We apply the linear stability theory to analyze the traffic flow model described by Eq. (10). Supposing the vehicles running on curved road with the uniform density \(\rho _{0}\) and optimal velocity \(V(\rho _{0})\), then we get the uniform steady-state solution \(\rho (j,t)\) for Eq. (10)

$$\begin{aligned} \rho (j,t)=\rho _{0}, v(j,t)=V(\rho _{0}). \end{aligned}$$
(11)

Assuming y(j, t) be a small deviation from the uniform steady solution, that is

$$\begin{aligned} \rho (j,t)=\rho _{0}+y(j,t). \end{aligned}$$
(12)

Inserting it and Eq. (11) into Eq. (10), then the linearized equation for y(j, t) is obtained from Eq. (10)

$$\begin{aligned} \begin{aligned}&y(j,t+2\tau )-y(j,t+\tau ) \\&\quad +\,\frac{\tau \rho _0^2}{\sin ^2\theta _j}V'(\rho _{0})\left[ y(j+1,t)-y(j,t)\right] =0, \end{aligned} \end{aligned}$$
(13)

where \(V'(\rho _{0})\) is the derivative of optimal velocity function \(V(\rho )\) at point \(\rho =\rho _{0}\). Expand \(y(j,t)\propto \exp [ikj+zt]\) resulting in the following equation of z

$$\begin{aligned} \begin{aligned}&e ^{2z\tau }-e ^{z\tau }+\frac{\tau \rho _0^2}{\sin ^2\theta _j}V'(\rho _{0})(e ^{ik}-1)=0, \end{aligned} \end{aligned}$$
(14)

where \(z = z_{1}(ik)+z_{2}(ik)^{2} +\cdots \), and inserting it into Eq. (14), the first- and second-order terms of ik are obtained

$$\begin{aligned} z_{1} = - \frac{\rho _0^2}{\sin ^2\theta _j}V'(\rho _{0}), \end{aligned}$$
(15)
$$\begin{aligned} z_{2} = -\frac{3\tau \rho _{0}^4V'^{2}(\rho _{0})}{2\sin ^4\theta _j}-\frac{\rho _{0}^2V'(\rho _{0})}{2\sin ^2\theta _j}. \end{aligned}$$
(16)

If \(z_{2}>0\), the uniform steady state becomes stable, while the uniform steady state becomes unstable if \(z_{2}<0\). Then the stable condition for traffic flow is

$$\begin{aligned} \tau < \frac{-\sin ^2\theta _j}{3\rho _{0}^2V'(\rho _{0})}. \end{aligned}$$
(17)

Moreover, for small disturbances of long wavelength, the neutral stability condition is given by

$$\begin{aligned} \tau _{s}=\frac{-\sin ^2\theta _j}{3\rho _{0}^2V'(\rho _{0})}. \end{aligned}$$
(18)

When \(\theta _j=\pi /2\), the results are agreed with the ones in Ref. [20].

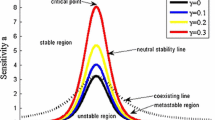
The coexisting curves (dash lines) and neutral stability lines (solid lines) in the space \((\rho ,a)\) (\(a=1/\tau \)) for different values of \(\theta \) with \(\rho _{0}=\rho _\mathrm{c}=0.2, \mu =0.3, R=20, k=0.14\) are shown in Fig. 3. The coexisting curve and the neutral stability line are similar to the conventional gas–liquid phase transition. Three regions in traffic flow are distinguished: the unstable region which is within the neutral stability line, the metastable region which is between the neutral stability line and the coexisting curve and the stable region which is out of the coexisting curve. The apex of each curve represents the critical point \((\rho _\mathrm{c},a_\mathrm{c})\). From Fig. 3, it is shown that traffic flow becomes stable with the increasing radian \(\theta _j\).

Fig. 3
figure 3

Phase diagram in the \((\rho ,a)\) space with \(\rho _0=\rho _\mathrm{c}=0.2, \mu =0.3, R=20, k=0.14\) for different \(\theta _j\)

Full size image

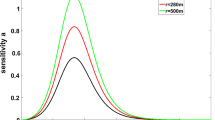
Figure 4 shows the phase diagram in the space \((\rho ,a)\) for different values of R with \(\rho _{0}=\rho _\mathrm{c}=0.2, \mu =0.3, \theta _j=\pi /4, k=0.14\). From Fig. 4, we can see that the critical sensitivity \(a_\mathrm{c}\) increases with the increase in R which means traffic flow becomes more and more unstable with the increasing curvature radius. The results are agreed with the ones in Refs. [19, 40]. And the results also mean that traffic flow will become unstable with the increase in length of curved road.

Fig. 4
figure 4

Phase diagram in the \((\rho ,a)\) space with \(\rho _0=\rho _\mathrm{c}=0.2, \theta =\pi /6, \mu =0.3, k=0.14\) for different R

Full size image

Figure 5 shows the phase diagram in the space \((\rho ,a)\) for different values of \(\mu \) with \(\rho _{0}=\rho _\mathrm{c}=0.2, R=20, \theta _j=\pi /4\). From Fig. 5, we can see that the critical sensitivity \(a_\mathrm{c}\) increases with the increase in \(\mu \) which means traffic flow becomes more and more unstable with the increase in friction coefficient. The results are agreed with the ones in Refs. [19, 40].

Figure 6 shows the plot of \(a_\mathrm{c}\) against \(\theta _j\) with \(\rho _\mathrm{c}^{2}V_{0}'(\rho _\mathrm{c})=-1, R=20, \mu =0.3, k=0.14\). From Fig. 6, the critical sensitivity \(a_\mathrm{c}\) decreases with the increase in \(\theta _j\). Compared with straight road, the result also shows that curved road will make traffic flow become unstable.

Fig. 5
figure 5

Phase diagram in the \((\rho ,a)\) space with \(\rho _0=\rho _\mathrm{c}=0.2, \theta =\pi /6, R=20, k=0.14\) for different \(\mu \)

Full size image
Fig. 6
figure 6

Plot of \(a_\mathrm{c}\) with \(\rho _0^2V'(\rho _0)|_{\rho _0=\rho _\mathrm{c}}=-1, R=20, \mu =0.3, k=0.14\) against \(\theta _j\)

Full size image

4 Nonlinear analysis

In this section, we study the nonlinear behavior in the stable, metastable and unstable regions, respectively. Note that the Eq. (10) is a nonlinear partial differential equation, and it is difficult to get the exact and analytical solution for Eq. (10). To overcome this difficulty, we apply the reductive perturbation method introduced in Ref. [32] to solve Eq. (10) and derive the corresponding Burgers, KdV and MKdV equations in the stable, metastable and unstable regions, respectively. These three equations are solvable equations. And we get the approximate solutions of the models with the help of exact and analytical solutions of the above three solvable equations. We introduce slow scales for space variable j, m and time variable t and define slow variables X and T for \( 0 <\varepsilon \ll 1\) [38]

$$\begin{aligned} X =\varepsilon (j+bt),\quad T =\varepsilon ^{s}t \end{aligned}$$
(19)

where b is a constant to be determined. Assume

$$\begin{aligned} \rho (j,t) = \rho _{0} +\varepsilon ^{l} R(X,T). \end{aligned}$$
(20)

The values of the index s, l represent different phases of the traffic flow. Three groups of values \(s = 2,l = 1\); \(s = 3,l = 2\); \(s = 3,l = 1\) are corresponding to the stable traffic flow region, metastable traffic flow region and unstable traffic flow, respectively.

By substituting Eqs. (19)–(20) into Eq. (10) and expanding to the \(s+l+1\) order of \(\varepsilon \), we obtain the following nonlinear partial differential equation

$$\begin{aligned}&\varepsilon ^{l+1}\left( b+\frac{\rho _{0}^2V'(\rho _{0})}{\sin ^2\theta _j}\right) \partial _{X}R +\varepsilon ^{l+2}\nonumber \\&\quad \times \,\left( \frac{3b^{2}\tau }{2}+\frac{\rho _{0}^2V'(\rho _{0})}{2\sin ^2\theta _j}\right) \partial _{X}^{2}R\nonumber \\&\quad +\,\varepsilon ^{l+3}\left( \frac{7b^{3}\tau ^{2}}{6}+\frac{\rho _{0}^2V'(\rho _{0})}{6\sin ^2\theta _j}\right) \partial _{X}^{3}R\nonumber \\&\quad +\,\varepsilon ^{l+4}\left( \frac{5b^{4}\tau ^{3}}{8}+\frac{\rho _{0}^2V'(\rho _{0})}{24\sin ^2\theta _j}\right) \partial _{X}^{4}R\nonumber \\&\quad +\,\varepsilon ^{2l+1}\frac{\rho _{0}^2V''(\rho _{0})}{2\sin ^2\theta _j}\partial _{X}R^{2} +\varepsilon ^{2l+2}\frac{\rho _{0}^2V''(\rho _{0})}{4\sin ^2\theta _j}\partial _{X}^{2}R^{2}\nonumber \\&\quad +\,\varepsilon ^{3l+1}\frac{\rho _{0}^2V'''(\rho _{0})}{6\sin ^2\theta _j}\partial _{X}R^{3} +\varepsilon ^{3l+2}\frac{\rho _{0}^2V'''(\rho _{0})}{12\sin ^2\theta _j}\partial _{X}^{2}R^{3}\nonumber \\&\quad +\,\varepsilon ^{s+l}\partial _{T}R +\varepsilon ^{s+l+1}(3b\tau )\partial _{X}\partial _{T}R=0. \end{aligned}$$
(21)

Firstly, we discuss the triangular shock waves of traffic flow in the stable region. The nonlinear partial differential equation is obtained from Eq. (21) for \(s= 2,l = 1\).

$$\begin{aligned} \begin{aligned}&\varepsilon ^{2}\left( b+\frac{\rho _{0}^2V'(\rho _{0})}{\sin ^2\theta _j}\right) \partial _{X}R +\,\varepsilon ^{3}\\&\quad \times \,\left[ \partial _{T}R+\frac{\rho _{0}^2V''(\rho _{0})}{2\sin ^2\theta _j}\partial _{X}R^{2}\right. \\&\left. \quad +\,\left( \frac{3b^{2}\tau }{2}+\frac{\rho _{0}^2V'(\rho _{0})}{2\sin ^2\theta _j}\right) \partial _{X}^{2}R\right] =0. \end{aligned} \end{aligned}$$
(22)

Taking \(b = -\frac{\rho _{0}^2V'(\rho _{0})}{\sin ^2\theta _j}\), the second-order term of \(\varepsilon \) is eliminated in Eq. (22). We obtain the following partial differential equation

$$\begin{aligned} \begin{aligned}&\partial _{T}R+\frac{\rho _{0}^2V''(\rho _{0})}{\sin ^2\theta _j}R\partial _{X}R\\&\quad =\frac{-\sin ^2\theta _j-3\rho _{0}^2V'(\rho _{0})\tau }{2\sin ^4\theta _j}\rho _{0}^2V'(\rho _{0})\partial _{X}^{2}R. \end{aligned} \end{aligned}$$
(23)

In accordance with criterion equation (18), the coefficient of the second derivative of Eq. (23) is positive in the stable region. Therefore, in the stable region, Eq. (23) is just the Burgers equation. If R(X, 0) is of compact support, then the solution R(X, T) of Eq. (23) is

$$\begin{aligned} \begin{aligned}&R(X,T)= \frac{\sin ^2\theta _j}{|\rho _{0}^2V''(\rho _{0})|T}\left[ X-\frac{\eta _{n+1}+\eta _{n}}{2}\right] \\&\quad -\,\frac{\sin ^2\theta _j(\eta _{n+1}{-}\eta _{n})}{2|\rho _{0}^2V''(\rho _{0})|T} \tanh \bigg [\frac{{-}\sin ^2\theta _j-3\rho _{0}^2V'(\rho _{0})\tau }{2\sin ^2\theta _j}\\&\quad \times \,\rho _{0}^2V_{0}'(\rho _{0})\frac{(\eta _{n+1}-\eta _{n})(X-\xi _{n})}{4|\rho _{0}^2V''(\rho _{0})|T}\bigg ]. \end{aligned}\nonumber \\ \end{aligned}$$
(24)

where \(\xi _{n}\) are the coordinates of the shock fronts and \(\eta _{n}\) are the coordinates of the intersections of the slopes with the x-axis \((n = 1,2,\ldots ,N)\). As \(O(\frac{1}{T})\), R(X, T) decays to 0 when \(T\rightarrow +\infty \). That means any shock wave expressed by Eq. (24) in stable traffic flow region will evolve to a uniform flow when time is sufficiently large.

Secondly, we discuss the soliton waves of traffic flow in the metastable region. The nonlinear partial differential equation is obtained from Eq. (21) for \(s = 3,l = 2\).

$$\begin{aligned} \begin{aligned}&\varepsilon ^{3}\left( b+\frac{\rho _{0}^2V'(\rho _{0})}{\sin ^2\theta _j}\right) \partial _{X}R \\&\quad +\varepsilon ^{4}\left( \frac{3b^{2}\tau }{2}+\frac{\rho _{0}^2V'(\rho _{0})}{2\sin ^2\theta _j}\right) \partial _{X}^{2}R\\&\quad +\,\varepsilon ^{5}\left[ \partial _{T}R+\frac{\rho _{0}^2V''(\rho _{0})}{2\sin ^2\theta _j}\partial _{X}R^{2}\right. \\&\left. \quad +\,\left( \frac{\rho _{0}^2V'(\rho _{0})}{6\sin ^2\theta _j}+\frac{7b^{3}\tau ^{2}}{6}\right) \partial _{X}^{3}R\right] \\&\quad +\,\varepsilon ^{6}\left[ \frac{\rho _{0}^2V''(\rho _{0})}{4\sin ^2\theta _j}\partial _{X}^{2}R^{2} +(3b\tau )\partial _{X}\partial _{T}R\right. \\&\left. \quad +\,\left( \frac{5b^{4}\tau ^{3}}{8}+\frac{\rho _{0}^2V'(\rho _{0})}{24\sin ^2\theta _j}\right) \partial _{X}^{4}R\right] =0. \end{aligned} \end{aligned}$$
(25)

Near the neutral stability line in the unstable region, let

$$\begin{aligned} \frac{\tau }{\tau _{s}}=1-\varepsilon ^{2}. \end{aligned}$$
(26)

By taking \(b=-\frac{\rho _{0}^2V'(\rho _{0})}{\sin ^2\theta _j}\), and then \(\tau = \frac{1-\varepsilon ^2}{3b}\), the third- and fourth-order terms of \(\varepsilon \) are eliminated from Eq. (25), and Eq. (25) can be rewritten as

$$\begin{aligned} \begin{aligned}&\varepsilon ^{5}\left[ \partial _{T}R-f_{1}\partial ^{3}_{X}R-f_{2}R\partial _{X}R\right] \\&\quad +\varepsilon ^{6}\left[ -f_{3}\partial ^{2}_{X}R+f_{4}\partial ^{2}_{X}R^{2}+f_{5}\partial ^{4}_{X}R\right] =0 \end{aligned} \end{aligned}$$
(27)

where

$$\begin{aligned}&f_{1}=-\frac{\rho _{0}^2V'(\rho _{0})}{27\sin ^2\theta _j},\; f_{2}=-\frac{\rho _{0}^2V''(\rho _{0})}{2\sin ^2\theta _j},\\&f_{3}=-\frac{\rho _{0}^2V'(\rho _{0})}{2\sin ^2\theta _j},\\&f_{4}=-\frac{\rho _{0}^2V''(\rho _{0})}{4\sin ^2\theta _j},\; f_{5}=-\frac{\rho _{0}^2V'(\rho _{0})}{54\sin ^2\theta _j}. \end{aligned}$$

In order to derive the standard KdV equation with higher-order correction, we make the following transformation in Eq. (27)

$$\begin{aligned} T = \sqrt{f_{1}}T_{k}, \qquad X = - \sqrt{f_{1}}X_{k},\qquad R = \frac{1}{f_{2}} R_{k}. \end{aligned}$$
(28)

By using Eq. (28), we obtain the standard KdV equation with higher-order correction term

$$\begin{aligned}&\partial _{T_{k}}R_{k}+\partial ^{3}_{X_{k}}R_{k}+R_{k}\partial _{X_{k}}R_{k}\nonumber \\&\quad +\frac{\varepsilon }{\sqrt{f_{1}}}\left[ -f_{3}\partial ^{2}_{X_{k}}R_{k}+\frac{f_{4}}{f_{2}}\partial ^{2}_{X_{k}}R_{k}^{2}+\frac{f_{5}}{f_{1}}\partial ^{4}_{X_{k}}R_{k}\right] =0.\nonumber \\ \end{aligned}$$
(29)

Next, we assume that \(R_{k}(X_{k},T_{k}) = R_{0}(X_{k},T_{k})+\varepsilon R_{1}(X_{k},T_{k})\) to consider the \(O(\varepsilon )\) correction in Eq. (29). If we ignore the \(O(\varepsilon )\) term in Eq. (29), it is just the KdV equation with soliton solutions

$$\begin{aligned} R_{0}(X_{k},T_{k}) = A {\text {sech}}^{2} \left[ \sqrt{\frac{A}{12}}\left( X_{k}-\frac{A}{3}T_{k}\right) \right] , \end{aligned}$$
(30)

where A is a free parameter. It is the amplitude of soliton solutions of the KdV equation. The perturbation term in Eq. (29) gives the condition of selecting a unique member from the continuous family of KdV solitons. In order to obtain the value of A, the solvability condition [10, 41, 42] is

$$\begin{aligned} \left( R_{0},M[R_{0}]\right) \equiv \int ^{\infty } _{-\infty }d X_{k}R_{0}M[R_{0}]= 0 \end{aligned}$$
(31)

that must be satisfied, here \(M[R_{0}]\) is the \(O(\varepsilon )\) term in Eq. (29). By computing the integration in Eq. (31), we obtain the value of amplitude A

$$\begin{aligned} A = \frac{21f_{1}f_{2}f_{3}}{24f_{1}f_{4} -5f_{2}f_{5}}. \end{aligned}$$
(32)

Substituting the values of \(f_{1}\)-\(f_{5}\) into Eq. (32), we get the value of A. Substituting each variable by the original one, we obtain soliton solutions of the density

$$\begin{aligned} \begin{aligned} \rho (j,t)&= \rho _{0} +\frac{A}{f_{2}}\left( \frac{\tau }{\tau _{s}}-1\right) {\text {sech}}^{2}\\&\left[ \sqrt{\frac{A}{12f_{1}} \left( \frac{\tau }{\tau _{s}}-1\right) }\right. \\&\left. \quad \times \,\left( j+\rho _{0}^2V'(\rho _{0})t +\frac{A}{3}\left( \frac{\tau }{\tau _{s}}-1\right) t\right) \right] . \end{aligned} \end{aligned}$$
(33)

Now, we have derived the soliton density wave described by the KdV equation near the neutral stability line.

Finally, we discuss the kink–antikink waves of traffic flow in the unstable region. The nonlinear partial differential equation is obtained from Eq. (21) for \(s= 3,l = 1\).

$$\begin{aligned} \begin{aligned}&\varepsilon ^{2}\left( b+\frac{\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}{\sin ^2\theta _j}\right) \partial _{X}R \\&\quad +\varepsilon ^{3}\left( \frac{3b^{2}\tau }{2}+\frac{\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}{2\sin ^2\theta _j}\right) \partial _{X}^{2}R\\&\quad +\,\varepsilon ^{4}\left[ \left( \frac{\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}{6\sin ^2\theta _j}+\frac{7b^{3}\tau ^{2}}{6} \right) \partial _{X}^{3}R\right. \\&\left. \quad +\,\frac{\rho _\mathrm{c}^2V'''(\rho _\mathrm{c})}{6\sin ^2\theta _j}\partial _{X}R^{3}+\partial _{T}R\right] \\&\quad +\,\varepsilon ^{5}\left[ \left( \frac{5b^{4}\tau ^{3}}{8}+\frac{\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}{24\sin ^2\theta _j}\right) \partial _{X}^{4}R\right. \\&\left. \quad +\,\frac{\rho _\mathrm{c}^2V'''(\rho _\mathrm{c})}{12\sin ^2\theta _j}\partial _{X}^{2}R^{3}+3b\tau \partial _{X}\partial _{T}R\right] =0. \end{aligned} \end{aligned}$$
(34)

Supposing

$$\begin{aligned} \frac{\tau }{\tau _\mathrm{c}}=1+\varepsilon ^{2} \end{aligned}$$
(35)

for \(\tau \) near the critical point \((h_\mathrm{c},1/\tau _\mathrm{c})\), where \(\tau _\mathrm{c}=\frac{-\sin ^2\theta _j}{3\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}\). Let \(b = -\frac{\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}{\sin ^2\theta _j}\), and then \(\tau = \frac{1+\varepsilon ^2}{3b}\), the second- and third-order terms of \(\varepsilon \) can be eliminated from Eq. (34). Then Eq. (34) can be rewritten as

$$\begin{aligned} \begin{aligned}&\varepsilon ^{4}\left[ \partial _{T}R-g_{1}\partial ^{3}_{X}R+g_{2}\partial _{X}R^{3}\right] \\&\quad +\,\varepsilon ^{5}\left[ g_{3}\partial ^{2}_{X}R+g_{4}\partial ^{2}_{X}R^{3}+g_{5}\partial ^{4}_{X}R\right] =0 \end{aligned} \end{aligned}$$
(36)

where

$$\begin{aligned}&g_{1}=-\frac{\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}{27\sin ^2\theta _j},\; g_{2}=\frac{\rho _\mathrm{c}^2V'''(\rho _\mathrm{c})}{6\sin ^2\theta _j},\;\\&g_{3}=-\frac{\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}{2\sin ^2\theta _j},\\&g_{4}=-\frac{\rho _\mathrm{c}^2V'''(\rho _\mathrm{c})}{12\sin ^2\theta _j},\; g_{5}=-\frac{\rho _\mathrm{c}^2V'(\rho _\mathrm{c})}{54\sin ^2\theta _j}. \end{aligned}$$

In order to derive the standard MKdV equation with higher-order correction, we make the following transformation in Eq. (36)

$$\begin{aligned} T = \frac{1}{g_{1}}T_{m}, \qquad R = \sqrt{\frac{g_{1}}{g_{2}}} R_{m}. \end{aligned}$$
(37)

Then we obtain the standard MKdV equation with higher-order correction term

$$\begin{aligned} \begin{aligned}&\partial _{T_{m}}R_{m}-\partial ^{3}_{X}R_{m}+\partial _{X}R_{m}^{3}\\&\quad +\frac{\varepsilon }{g_{1}}\left[ g_{3}\partial ^{2}_{X}R_{m}{+}\frac{g_{1}g_{4}}{g_{2}}\partial ^{2}_{X}R_{m}^{3}{+}g_{5}\partial ^{4}_{X}R_{m}\right] =0. \end{aligned} \end{aligned}$$
(38)

If we ignore the \(O(\varepsilon )\) term in Eq. (37), it is just the MKdV equation with the kink–antikink solution

$$\begin{aligned} R_{m0}(X,T_{m}) = \sqrt{B}\tanh \sqrt{\frac{B}{2}}(X -BT_{m}). \end{aligned}$$
(39)

Similar to the process of deriving the amplitude A for KdV equation, we obtain the value of propagation velocity B for the kink–antikink solution as follows

$$\begin{aligned} B=\frac{5g_{2}g_{3}}{2g_{2}g_{5} -3g_{1}g_{4}}. \end{aligned}$$
(40)

Inserting Eq. (37) into Eq. (39), we get the solution of the MKdV equation

$$\begin{aligned} R(X,T) = \sqrt{\frac{g_{1}B}{g_{2}}}\tanh \sqrt{\frac{B}{2}}(X -Bg_{1}T). \end{aligned}$$
(41)

Then we gain the kink–antikink solution of the density

$$\begin{aligned}&\rho (j,t) = \rho _\mathrm{c} + \sqrt{\frac{g_{1}B}{g_{2}}\left( \frac{\tau }{\tau _\mathrm{c}}-1\right) }{\text {tanh}} \left[ \sqrt{\frac{B}{2}\left( \frac{\tau }{\tau _\mathrm{c}}-1\right) }\right. \nonumber \\&\left. \quad \times \,\left( j+\rho _\mathrm{c}^2V'(\rho _\mathrm{c})t-Bg_{1}\left( \frac{\tau }{\tau _\mathrm{c}}-1\right) t\right) \right] . \end{aligned}$$
(42)

And the amplitude C of the kink–antikink solution equation (42) is given by

$$\begin{aligned} C =\sqrt{\frac{g_{1}B}{g_{2}}\left( \frac{\tau }{\tau _\mathrm{c}}-1\right) }. \end{aligned}$$

The kink solution represents the coexisting phase, which consists of the freely moving phase with low density and the congested phase with high density. The coexisting curve can be described by \(\rho = \rho _\mathrm{c} \pm C \). Therefore, we get the coexisting curve in the \((\rho ,a)\) plane (see Fig. 3).

5 Simulation

In order to check the theoretical results, we carry out numerical simulations in this section. The initial conditions of the numerical simulation are as follows: There are \(N =100\) lattices in the system, and the periodical boundary condition is applied. The initial perturbations are adopted as follows: \(\rho (j,0) = \rho _0=\rho _\mathrm{c}= 0.2\). The local densities \(\rho (N/2, 1)\) and \(\rho (N/2-1, 1)\) at sites N / 2 and \(N/2-1\) at time \(t = 1\) are set as 0.15 and 0.25, \(k=0.14\).

In order to check the effect of the angle going into curved road upon traffic flow, we carry out corresponding simulations. The results are shown in Figs. 7, 8, 9, 10, 11, 12 and 13. We denote the angle going into curved road as \(\theta _0\), and the increment of the angle \({\varDelta }\theta \) is same in different patterns. Here we select \({\varDelta }\theta =\pi /12\) for \(a=3\).

Fig. 7
figure 7

The traffic patterns from time \(t = 99{,}000\) to \(t = 100{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, {\varDelta }\theta =\pi /12\) for \(\theta _0=\pi /12, \pi /6, \pi /4\), respectively

Full size image
Fig. 8
figure 8

The density profiles \(\rho (j,t)\) at time \(t = 90{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, {\varDelta }\theta =\pi /12\) for \(\theta _0=\pi /12, \pi /6, \pi /4\), respectively

Full size image
Fig. 9
figure 9

The density profiles \(\rho (20,t)\) from time \(t = 99{,}900\) to \(t = 100{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, {\varDelta }\theta =\pi /12\) for \(\theta _0=\pi /12, \pi /6, \pi /4\), respectively

Full size image
Fig. 10
figure 10

The density profiles \(\rho (60,t)\) from time \(t = 99{,}900\) to \(t = 100{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, {\varDelta }\theta =\pi /12\) for \(\theta _0=\pi /12, \pi /6, \pi /4\), respectively

Full size image
Fig. 11
figure 11

The phase space plot at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, {\varDelta }\theta =\pi /12\) for \(\theta _0=\pi /12, \pi /6, \pi /4\), respectively

Full size image
Fig. 12
figure 12

The hysteresis loop of flux at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, {\varDelta }\theta =\pi /12\) for \(\theta _0=\pi /12, \pi /6, \pi /4\), respectively

Full size image
Fig. 13
figure 13

The hysteresis loop of velocity at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, {\varDelta }\theta =\pi /12\) for \(\theta _0=\pi /12, \pi /6, \pi /4\), respectively

Full size image

Figure 7 shows the traffic patterns after a sufficiently long time \(t = 100{,}000\) with different \(\theta _0\) for \(\mu =0.3, R=20\). In Fig. 7, the patterns (a), (b), (c) exhibit the time evolution of the density \(\rho (j,t)\) for \(\theta _0= \pi /12, \pi /6, \pi /4\). The initial disturbance leads to the kink–antikink density waves as shown in patterns (a) and (b). This small amplitude disturbance grows into congested flow as the stability condition is not satisfied. When the stability condition is satisfied, the small amplitude disturbance will dissipate, and traffic flow becomes uniform which is shown in pattern (c). The results show that with the increase in \(\theta _0\), traffic flow will become more and more stable. It also means that the angle going into curved road has a great effect upon the stability of traffic flow.

Figure 8 shows the density profile obtained at \(t=90{,}000\) corresponding to Fig. 7. And it makes us see the evolution of the density with the small disturbances more clearly. From pattern (a), we can see that the congested flow easily occurs at the entrance of curved road.

Figures 9 and 10 show the density profile obtained for \(t=99{,}900{-}100{,}000\) at site \(j=20, 60\) corresponding to Fig. 7, respectively. The radian at site \(j=60\) is larger than the one at site \(j=20\). From the figures, it is shown that traffic flow will become stable with the increase in the radian of curved road.

Figure 11 represents the phase space plot of density difference \(\rho (j,t)-\rho (j,t-1)\) against \(\rho (t)\) at site \(j=60\) for \(t = 60{,}000{-}70{,}000\,\mathrm{s}\), corresponding to Fig. 7. The patterns (a) and (b) exhibit the characteristic of periodicity in the form of limit cycle, and the nodes on the right sides as well as on the left sides are corresponding to the traffic states within and out of the kink traffic jam. For pattern (c) with \(\theta _0=\pi /4\), the limit cycle leads to a single point which represents the uniform flow in the stable region. When \(a = 3\), the jamming transition occurs among freely moving phase, the coexisting phase with kink–antikink density wave and the uniformly congested phase with an increase in the value of \(\theta _0\).

Figures 12 and 13 show the hysteresis loop of the flux and velocity for different \(\theta _0\) at site \(j=60\) for \(t = 60{,}000{-}70{,}000\,\hbox {s}\) corresponding to Fig. 7, respectively. From Figs. 12, it shows that with the increase in the value of \(\theta _0\), the size of loops will shrink and the maximal flux decreases. When \(\theta _0= \pi /4 \) in Fig. 12c, the stability condition is held, the traffic flow is stable, and the hysteresis loop will not be generated, and in phase space, there will be only a point on the optimal current curve instead. From Fig. 13, it shows that with the increase in the value of \(\theta _0\), the size of loops will shrink and the maximal velocity decreases. When \(\theta _0= \pi /4 \) in Fig. 13c, the stability condition is held, the traffic flow is stable, and the hysteresis loop will not be generated, and in phase space, there will be only a point on the optimal velocity curve instead. Furthermore, from Figs. 12 and 13, we can see that the maximal theoretical flux and velocity, which are represented by the curves in Figs. 12 and 13, decrease with the increase in \(\theta _0\). Therefore, the above results furthermore verify that the angle going into curved road has an important effect upon traffic flow.

Next, we do the corresponding simulations to verify the effect of the increment of the angle \({\varDelta }\theta \) upon traffic flow. Here, we keep \(\theta _0=\pi /6\) as a constant, \({\varDelta }\theta =\pi /12, \pi /6, \pi /3\) with \(a= 2.5\), respectively. The results are shown in Figs. 14, 15, 16, 17, 18, 19 and 20. From Figs. 14, 15, 16, 17, 18, 19 and 20, we can see traffic flow becomes stable with the increase in the increment of the angle \({\varDelta }\theta \). Furthermore, from Figs. 19 and 20, we can see that the maximal theoretical flux and velocity, which are represented by the curves in Figs. 19 and 20, decrease with the increase in \({\varDelta }\theta \). Through the process, we can deduce that when the angle leaving out the curved road \(\theta _N\) is fixed, the increase in the increment of the angle \({\varDelta }\theta \) will make traffic flow become unstable, but the maximal theoretical flux and velocity increase. In real traffic situation, the angle leaving out the curved road is always fixed, so the traffic flow will become unstable with the increase in the length of curved road which means the increase in the increment of the angle \({\varDelta }\theta \) when the radius R is fixed.

Fig. 14
figure 14

The traffic patterns from time \(t = 99{,}000\) to \(t = 100{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, \theta _0=\pi /6\) for \({\varDelta }\theta =\pi /12, \pi /6, \pi /3\), respectively

Full size image
Fig. 15
figure 15

The density profiles \(\rho (j,t)\) at time \(t = 90{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, \theta _0=\pi /6\) for \({\varDelta }\theta =\pi /12, \pi /6, \pi /3\), respectively

Full size image
Fig. 16
figure 16

The density profiles \(\rho (20,t)\) from time \(t = 99{,}900\) to \(t = 100{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, \theta _0=\pi /6\) for \({\varDelta }\theta =\pi /12, \pi /6, \pi /3\), respectively

Full size image
Fig. 17
figure 17

The density profiles \(\rho (60,t)\) from time \(t = 99{,}900\) to \(t = 100{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, \theta _0=\pi /6\) for \({\varDelta }\theta =\pi /12, \pi /6, \pi /3\), respectively

Full size image
Fig. 18
figure 18

The phase space plot at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, \theta _0=\pi /6\) for \({\varDelta }\theta =\pi /12, \pi /6, \pi /3\), respectively

Full size image
Fig. 19
figure 19

The hysteresis loop of flux at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, \theta _0=\pi /6\) for \({\varDelta }\theta =\pi /12, \pi /6, \pi /3\), respectively

Full size image
Fig. 20
figure 20

The hysteresis loop of velocity at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, \mu =0.3, k=0.14, \theta _0=\pi /6\) for \({\varDelta }\theta =\pi /12, \pi /6, \pi /3\), respectively

Full size image

We also carry out the corresponding simulation to show the effect of radius of curved road on traffic flow. Here we select \(a=2.5, \theta _0=\pi /4, {\varDelta }\theta = \pi /12, \mu = 0.3\). The results are shown in Figs. 21, 22, 23, 24 and 25. The results show that with the increase in radius, traffic flow will become unstable, but the maximal theoretical flux and velocity will increase. The results are agreed with the ones in Refs. [19, 40].

Fig. 21
figure 21

The traffic patterns from time \(t = 99{,}000\) to \(t = 100{,}000\) with \(a=2.5, \rho _0=\rho _\mathrm{c}=0.2, \mu =0.3, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(R=10, 20, 30, 40\), respectively

Full size image
Fig. 22
figure 22

The density profiles \(\rho (j,t)\) at time \(t = 90{,}000\) with \(a=2.5, \rho _0=\rho _\mathrm{c}=0.2, \mu =0.3, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(R=10, 20, 30, 40\), respectively

Full size image
Fig. 23
figure 23

The phase space plot at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=2.5, \rho _0=\rho _\mathrm{c}=0.2, \mu =0.3, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(R=10, 20, 30, 40\), respectively

Full size image
Fig. 24
figure 24

The hysteresis loop of flux at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=2.5, \rho _0=\rho _\mathrm{c}=0.2, \mu =0.3, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(R=10, 20, 30, 40\), respectively

Full size image
Fig. 25
figure 25

The hysteresis loop of velocity at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=2.5, \rho _0=\rho _\mathrm{c}=0.2, \mu =0.3, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(R=10, 20, 30, 40\), respectively

Full size image

Figures 26, 27, 28, 29 and 30 show the effect of friction coefficient of curved road on traffic flow. The results show that with the increasing friction coefficient \(\mu \), traffic flow will become unstable, but the maximal theoretical flux and velocity will increase. The results are in agreement with the ones in Refs. [19, 40].

Fig. 26
figure 26

The traffic patterns from time \(t = 99{,}000\) to \(t = 100{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(\mu =0.3, 0.5, 0.7, 0.9\), respectively

Full size image
Fig. 27
figure 27

The density profiles \(\rho (j,t)\) at time \(t = 90{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(\mu =0.3, 0.5, 0.7, 0.9\), respectively

Full size image
Fig. 28
figure 28

The phase space plot at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(\mu =0.3, 0.5, 0.7, 0.9\), respectively

Full size image
Fig. 29
figure 29

The hysteresis loop of flux at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(\mu =0.3, 0.5, 0.7, 0.9\), respectively

Full size image
Fig. 30
figure 30

The hysteresis loop of velocity at site 60 from time \(t = 60{,}000\) to \(t = 70{,}000\) with \(a=3, \rho _0=\rho _\mathrm{c}=0.2, R=20, k=0.14, \theta _0=\pi /4, {\varDelta }\theta =\pi /12\) for \(\mu =0.3, 0.5, 0.7, 0.9\), respectively

Full size image

6 Summary

In order to investigate the influencing mechanism of traffic flow on curved road, we propose an extended lattice hydrodynamic model for traffic flow on curved road by taking radian, friction coefficient and curvature radius of the curved road into account. We obtain the stability condition of the proposed model by the use of linear stability theory. The stability condition shows that the angle, friction coefficient and curvature radius play an important role in influencing the stability of traffic flow. The Burgers, KdV and MKdV equations are obtained to describe traffic flow behavior in the stable, metastable and unstable region, respectively. The analytical and simulation results show that enlarging the angle going into curved road may enhance the stability of traffic flow, reducing curvature radius may lead to the stabilization of traffic flow, and increasing friction coefficient could aggravate traffic jams. But the maximal theoretical flux and velocity of traffic flow increase with the increase in the curvature radius and friction coefficient, as well as the decrease in angle going into the curved road. When the angle leaving out the curved road and the radius of the curved road are fixed, the increase in the increment of radian of curved road which means enlarging the length of curved road will make traffic flow unstable.