1 Introduction

Connected and autonomous vehicles (CAVs) have received much attention recently in both academia and industry as communication and information technologies provide significant improvements for mobility, safety, and environmental sustainability [1–3]. In a CAV system, vehicle-to-vehicle (V2V) communications play an important role in the coordination between individual vehicles. For example, to avoid collisions in an autonomous vehicular flow, a wide variety of information on preceding vehicles and roadside equipment is desirable and shared by vehicles through V2V communications [4]. In this context, the opening angle of the electronic throttle (ET) of the preceding vehicles enables a following vehicle in the same platoon to react autonomously to avoid a collision by adjusting its ET. As electronic throttle control (ETC) is the core of vehicle control, ETC facilitates the performance of vehicular features such as cruise control, traction control, stability control, and pre-crash systems and other controls requiring torque management. Hence, several control strategies have been proposed to improve the performance in terms of the accuracy and responsiveness of the ETC, including linear control, nonlinear control, optimal control, and intelligent control [5, 6]. Past studies [7–9] have illustrated that the vehicle speed is related to the opening angle of the ET. It implies that the opening angle of the ET has impacts on the vehicle characteristics at microscopic level, which relate to the evolution of vehicular traffic flow at the macroscopic level. However, to the best of our knowledge, no study on traffic flow considers the ET dynamics. This motivates the construction of a theoretical model to analyze the effect of ET opening angle on traffic flow.

Traffic flow models aim to formulate the complex mechanisms behind the phenomena of vehicular traffic flow. Traffic flow models can be classified as microscopic or macroscopic models. Microscopic models are generally formulated using microscopic variables, including velocity, position, and acceleration, to capture local interactions between vehicles. Macroscopic models mainly apply aggregate variables such as density, volume, and average speed to describe the traffic flow [10]. Microscopic models can be further classified as car-following (CF) models or cellular automation (CA) models. CF models describe the interactions with preceding vehicles in the same lane based on the idea that each driver controls a vehicle under stimuli from the preceding vehicle. CF models include the Gazis–Herman–Rothery model [11] and its variants [12–14], Gipps model [15], optimal velocity (OV) model [16] and its variations [17–39], intelligent driver model [40], fuzzy-logic model [41], as well as psychophysical models [42]. On the other hand, CA models describe traffic phenomena using a stochastic discrete approach, such as Rule 184 model [43], Biham–Middleton–Levine model [44], as well as Nagel–Schreckenberg model [45] and its variants [14].

This study focuses on microscopic traffic flow modeling, with emphasis on a CF model. CF models can be generally classified as lane-discipline- and non-lane-discipline-based models. The lane-discipline-based CF models assume that vehicles follow the lane discipline and move in the middle of the lane without lateral gaps. Bando et al. [16] propose the OV model based on the assumption that the following vehicle seeks a safe velocity determined by the space headway from the leading vehicle. Thereafter, various OV-based CF models have been developed by factoring the surroundings of the following vehicle [17–25], including generalized force (GF) mode [17], full velocity difference (FVD) model [18], multiple ahead and velocity difference model [19], full velocity and acceleration difference model [20], multiple velocity difference model [21], and multiple headway, velocity and acceleration difference model [22]. In addition, results from these CF models show that the stop-and-go waves can be captured effectively. Unlike the lane-discipline-based CF models, the non-lane-discipline-based CF models allow that lanes may not be clearly demarcated on a road though multiple vehicles can travel in parallel. In this research line, Jin et al. [46] propose a non-lane-based full velocity difference CF (NLBCF) model to analyze the impact of the lateral gap on one side on the CF behavior. However, the NLBCF model cannot distinguish the right-side or the left-side lateral gaps. Consequently, Li et al. [47] propose a generalized model which considers the effects of two-sided lateral gaps of the following vehicle under non-lane-discipline environment. In addition, Li et al. [48] further study the effects of lateral gaps on the energy consumption for the electric vehicle flow under the non-lane discipline. The aforementioned studies illustrate that CF models can effectively capture the characteristics of the traffic phenomenon in the real world.

Unlike the existing CF models [16–47], this study addresses the modeling of traffic flow under connected environment with the considerations as follows. First, while the existing models focus on the interaction between vehicles in the leader–follower context, we propose to leverage the CAV environment which provides capabilities to analyze the ambient traffic conditions in the vicinity, and not just the acceleration of the leader vehicle of the leader–follower model. That is, the vehicle can obtain information on several other vehicles downstream of it, which can provide a more comprehensive understanding of the unfolding traffic conditions for it to react. Second, by leveraging the autonomous capability of the vehicles, information on the ET opening angle from all of these vehicles can directly be accessed and used as input by the vehicle of interest. The benefit of doing so is that it can react more quickly rather than the case where accelerations of the downstream vehicles are accessed and need to be processed for meaningful action. The associated time savings are especially critical when there are safety implications based on some event downstream of this vehicle, to which its immediate predecessor (its leader vehicle) also needs to react which otherwise would involve some time.

This study is motivated by the need of CF modeling in the context of CAV environment that enables the incorporation of the ET opening angle to characterize the performance of CAV traffic flow in terms of the smoothness and stability associated with the space headway, velocity, and acceleration/deceleration profiles. In particular, a new CF model is proposed based on the FVD model considering the effect of opening angle of ET. Stability analysis of the proposed CF model is performed using the perturbation method to obtain the stability condition. Numerical experiments are conducted under three scenarios: start process, stop process, and evolution process based on the FVD model and the proposed CF model. Experiment results illustrate that the proposed CF model has larger stable region compared to the FVD model. Also, it demonstrates that the performance of the proposed CF model is better than that of FVD model with respect to space headway, position, velocity, and acceleration/deceleration profiles of CAV traffic flow.

The study contributes to the literature in three aspects. First, this study is the first to consider the effect of ET opening angle on CAV traffic flow dynamics. Second, the stable region of the proposed model is analyzed rigorously. The stable region is enlarged when compared to the corresponding FVD model. Third, we demonstrate that factoring the ET opening angle in CF modeling can capture the smoothness and stability of CAV traffic flow with respect to the space headway, velocity, and acceleration/deceleration profiles. The results of this study suggest that the CAV environment can be leveraged so that vehicular characteristics at the individual level (such as ET dynamics) can be communicated to other vehicles through the connected environment and can lead to safety benefits (such as enhanced traffic stability) through the aggregate-level actions by those vehicles due to their autonomous capabilities without involving manual intervention. By contrast, past studies focus only on traffic flow characteristics (such as position, velocity, and acceleration) and do not leverage information on the dynamics of vehicular characteristics (such as electronic throttle opening angle). In summary, the conceptual novelty of this study relates to leveraging the capabilities of a CAV environment to further enhance traffic-related goals by proposing new car-following models with CAV-related capabilities.

The rest of paper is organized as follows. Section 2 presents the throttle-based FVD (T-FVD) model. Section 3 performs the stability analysis of the T-FVD model. Section 4 conducts the numerical experiments and comparisons. The final section concludes this study.

2 Derivation of the model

An ET system consists of a DC drive (powered by the chopper), a gearbox, a valve plate, a dual return spring, and a position sensor. Figure 1 shows the functional scheme of the ET. This study focuses on the effect of ET opening angle on the vehicular traffic flow [5, 6].

Fig. 1
figure 1

Schematic of electronic throttle

Full size image

As shown in Fig. 1, the driver can adjust the opening angle of ET to affect the vehicle velocity. The dynamic equations of the ET angle to vehicle velocity are as follows [8, 9]:

$$\begin{aligned} a_{i} (t)=-b(v_{i} (t)-v_0 )+c\bar{{\theta }}_{i} +d_{i} \end{aligned}$$
(1)

where \(v_{0}\) is the steady-state vehicle velocity for a throttle input \(\theta _{0}\) and \(\bar{{\theta }}_{i} =\theta _{i} -\theta _0 \) as the throttle deviation from \(\theta _{0}\); b and c vary with \(v_0 \); \(d_{i} \) is the perturbation that captures the effect of unmodeled dynamics; and \(v_{i} (t)\) and \(a_{i} (t)\) are the velocity and acceleration of the vehicle i at time t, respectively.

Fig. 2
figure 2

Car-following model

Full size image

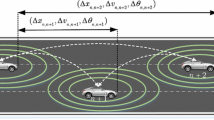
Figure 2 shows the scenario of car-following process between the leading vehicle and the following vehicle. To describe the interactions between each pair of leading and following vehicles, Jiang et al. propose the FVD model considering the effects of both positive and negative velocity difference on vehicular traffic flow as follows [18]:

$$\begin{aligned} a_{i} (t)=k[V(\Delta x_{i} (t))-v_{i} (t)]+\lambda \Delta v_{i} (t) \end{aligned}$$
(2)

where \(\Delta x_{i} (t)=x_{i+1} (t)-x_{i} (t)\) and \(\Delta v_{i} (t)=v_{i+1} (t)-v_{i} (t)\); \(x_{i} (t)\), \(v_{i} (t)\) and \(a_{i} (t)\) represent position, velocity, and acceleration of the vehicle i, respectively; \(k>0,\;\lambda >0\) are sensitivity coefficients.

And \(\Delta x_{i} (t)\) is the optimal velocity function as follows [17, 18]:

$$\begin{aligned} V(\Delta x_{i} (t))=V_1 +V_2 \tanh [C_1 (\Delta x_{i} (t)-l_c )-C_{2}] \end{aligned}$$

where \(V_1,\;V_2,\;C_1,\;C_{2}\) are constant parameters, \(l_{c}\) is the vehicle length, and \(\tanh (\cdot )\) is the hyperbolic tangent function.

Under a CAV environment, the vehicle of interest can receive and use the information on the ET opening angle from surrounding vehicles via V2V communications. It will lead to quick reaction by leveraging the autonomous capability of the vehicle, and therefore, the acceleration of the vehicle of interest will be changed accordingly. Given the above considerations, we propose a new CF model based on the FVD model to describe the effect of the ET opening angle on CAV traffic flow. This model is labeled as the throttle-based FVD (T-FVD) model hereafter. Based on Eqs. (1) and (2), the T-FVD model incorporating the dynamics of ET is formulated as follows:

$$\begin{aligned} a_{i} (t)=k[V(\Delta x_{i} (t))-v_{i} (t)]+\lambda \Delta v_{i} (t)+\kappa \Delta \theta _{i} \end{aligned}$$
(3)

where \(\Delta \theta _{i} (t)=\theta _{i+1} (t)-\theta _{i} (t)\) represents the ET opening angle difference between the vehicle \(i+1\) and vehicle i. \(\kappa >0\) is the sensitivity coefficient.

3 Stability analysis

To obtain the stability condition of the T-FVD model, we perform the stability analysis using the perturbation method that has been a classical approach used in previous studies [16–28, 49]. The stability of the T-FVD model is analyzed under the following assumption.

Assumption 1

The initial state of the vehicular traffic flow is steady, and all vehicles in the traffic flow move with the identical space headway and the optimal velocity.

Following the Assumption 1, the position solution to the steady vehicular traffic flow is

$$\begin{aligned} x_{i}^0 (t)=hi+V(h)t \end{aligned}$$
(4)

where h is the steady space headway and V(h) is the optimal velocity in uniform traffic flow. \(x_{i}^0 (t)\) is the position of the i th vehicle in steady state.

Adding a small disturbance \(y_{i} (t)\) to the steady-state solution, i.e.,

$$\begin{aligned} y_{i} (t)=x_{i} (t)-x_{i}^0 (t) \end{aligned}$$
(5)

Note that \(\Delta x_{i} =\Delta y_{i} +h, v_{i} =\dot{y}_{i} +V(h), a_{i} (t)=\ddot{y}_{i} (t)\) and substituting Eq. (5) into Eq. (3), the resulting equation is as follows:

$$\begin{aligned} \ddot{y}_{i} (t)=k[V^{\prime }(h)\Delta y_{i} -\dot{y}_{i}]+\lambda \Delta \dot{y}_{i}+\kappa \Delta \theta _{i} \end{aligned}$$
(6)

According to Eq. (1), the opening angle of ET, \(\theta _{i}\), can be rewritten as follows:

$$\begin{aligned} \theta _{i} =\frac{1}{c}(\ddot{y}_{i} +b\dot{y}-d_{i} )+\theta _{0} \end{aligned}$$
(7)

Hence

$$\begin{aligned} \Delta \theta _{i}=\frac{1}{c}(\Delta \ddot{y}_{i}+b\Delta \dot{y}_{i} ) \end{aligned}$$
(8)

Substituting Eq. (8) into Eq. (6) and linearizing the resulting equation using Taylor expansion, it follows that:

$$\begin{aligned} \ddot{y}_{i} (t)=k[V^{\prime }(h)\Delta y_{i}-\dot{y}_{i} ]+\lambda \Delta \dot{y}_{i} +\frac{\kappa }{c}(\Delta \ddot{y}_{i}+b\Delta \dot{y}_{i}) \end{aligned}$$
(9)

Set \(y_{i} (t)\) in the Fourier models, i.e., \(y_{i} (t)=A\exp (\hbox {j}\alpha i+zt)\), then substitute it in Eq. (9) to obtain

$$\begin{aligned} z^{2}= & {} kV^{\prime }(e^{\mathrm{j}\alpha }-1)-kz+\lambda z(e^{\mathrm{j}\alpha }-1)\nonumber \\&+\frac{\kappa }{c}z^{2}(e^{\mathrm{j}\alpha }-1)+\frac{b\kappa }{c}z(e^{\mathrm{j}\alpha }-1) \end{aligned}$$
(10)

Let \(z=z_1 (\hbox {j}\alpha )+z_{2} (\hbox {j}\alpha )^{2}+\cdot \;\cdot \;\cdot \) using the long wave method, and expand it to the second term of \((\hbox {j}\alpha )\), we obtain

$$\begin{aligned}&\left[ \frac{\kappa }{c}(e^{\mathrm{j}\alpha }-1)-1\right] \left[ z_1 (\hbox {j}\alpha )+z_2 (\hbox {j}\alpha )^{2}\right] ^{2}\nonumber \\&\quad =\left[ k-\left( \frac{b\kappa }{c}+\lambda \right) (e^{\mathrm{j}\alpha }-1)\right] \left[ z_1 (\hbox {j}\alpha )+z_2 (\hbox {j}\alpha )^{2}\right] \nonumber \\&\quad \quad -kV^{\prime }(e^{\mathrm{j}\alpha }-1) \end{aligned}$$
(11)

Based on Eq. (11), we combine similar items in terms of \((\hbox {j}\alpha )\). For simplicity, hereafter, we denote \(z_{1}(\hbox {j}\alpha )\) as \(z_{1}\) and \(z_{2} (\hbox {j}\alpha )\) as \(z_2\). It follows from Eq. (11) that

$$\begin{aligned} \left\{ {\begin{array}{l} 0=kz_1 -kV^{\prime } \\ 0=z_1^2 +kz_2-\left( \frac{b\kappa }{c}+\lambda \right) z_{1} -\frac{1}{2}kV^{\prime }\\ \end{array}} \right. \end{aligned}$$
(12)

Consequently

$$\begin{aligned} \left\{ {\begin{array}{l} z_1 =V^{\prime } \\ z_2 =-\frac{V^{'2}-\left( \frac{b\kappa }{c}+\lambda +\frac{k}{2}\right) V^{\prime }}{k} \\ \end{array}} \right. \end{aligned}$$
(13)

when \(z_1 >0\) and \(z_2 >0\), the stability condition is given by

$$\begin{aligned} V^{\prime }<\left( \frac{k}{2}+\lambda +\frac{b\kappa }{c}\right) \end{aligned}$$
(14)

Remark 1

Equation (3) indicates that if \(\kappa =0\), the proposed T-FVD model is deduced to the FVD model [18]. According to Eq. (14), if \(\kappa =0\), the stability condition of the proposed T-FVD model is the same as the FVD model [18]. It verifies the effectiveness of the proposed model and the correctness of the stability analysis. In addition, it implies that the FVD model is a special case of the proposed T-FVD model.

Fig. 3
figure 3

The critical curves between sensitivity coefficient and the space headway

Full size image

Figure 3 shows the critical curves between sensitivity coefficient k and the space headway with respect to different values of \(\lambda \) in the T-FVD model and FVD model. In Fig. 3, the space formed by the sensitivity coefficient k and the space headway is divided into two regions (stable region and unstable region) by the critical curve. Specifically, the region above each critical curve is the stabile region in which the traffic flow is stable; the remainder is the unstable region in which density waves emerge. As can be seen, the stable region is enlarged with the increase in the value of parameter \(\lambda \). In addition, when the value of the coefficient \(\lambda \) is the same in the T-FVD model and FVD model, i.e., \(\lambda =0.1\,\hbox {s}^{-1}\) or \(\lambda =0.3\,\hbox {s}^{-1}\), the stable region of the T-FVD model is larger than that of the FVD model. It implies that the stability region of the FVD model is improved by incorporating the dynamics of the ET opening angle.

4 Numerical experiments

Based on the foregoing theoretical analyses, numerical experiments are performed to verify the proposed T-FVD model described by Eq. (3) and demonstrate its dynamics performance. The values of parameters used in the numerical experiment are shown in Table 1. Other conditions set the same as in [18].

In addition, to investigate the dynamic performance of vehicular flow in the start and stop processes, we assume that there are eleven vehicles distributed homogeneously on a road under a periodic boundary condition with equal space headway of 7.4 m. The 11th vehicle is the first vehicle in this traffic stream. In the evolution process, we assume that there are N vehicles on a road with length L under a periodic boundary condition to investigate the performance of the traffic flow in terms of smoothness and stability. For comparison, we set the same initial disturbance as in [18]:

$$\begin{aligned} x_{1} (0)= & {} 1\,\hbox {m};\;\;x_{i} (0)=(i-1)L/N\,\hbox {m},\, \hbox { for }\, i\ne 1 \end{aligned}$$
(15)
$$\begin{aligned} v_{i} (0)= & {} V(L/N) \end{aligned}$$
(16)

The initial conditions are chosen as \(\Delta x_{i}(0)=h, i=2,.., N, x_{i}(0)=V^{-1}(h)= v_{0}\), where \(v_{0}\) is the velocity of traffic flow in the steady state. \(\Delta v_{i}\)(0) and \(\Delta \theta _{i}\)(0) can be calculated according to Eqs. (15), (16) and (1).

Table 1 The values of parameters in the CF models
Full size table

4.1 Start process

For this process, we do the following. Initially, the traffic signal is red, and all vehicles are waiting behind the signal with the uniform space headway. At time \(t=0\,\hbox {s}\), the signal changes to green and the vehicles start to move. The first vehicle starts to accelerate until it reaches the optimal speed. The other vehicles follow this vehicle to accelerate. Eventually, all vehicles travel at the same optimal velocity. For comparison, the acceleration, velocity, and position profiles of the FVD model and T-FVD model are illustrated in Figs. 4, 5, and 6, respectively.

Fig. 4
figure 4

The acceleration profile of traffic flow starting from a green traffic signal a FVD model and b T-FVD model

Full size image

Figure 4 demonstrates that the magnitude of acceleration in the T-FVD model is much less than that of the FVD model. Specifically, the maximum acceleration in the T-FVD model is about \(2\;\hbox {m/s}^{2}\), which is less than that of the FVD model (beyond \(3\;\hbox {m/s}^{2}\)). It shows that the introduction of ET opening angle reduces the magnitude of acceleration required by the CAVs. On the other hand, CAVs in the FVD model start to accelerate one by one with a transition period. In contrast, CAVs in the T-FVD model start to accelerate in a shorter time. Figure 5 indicates that the T-FVD model is more responsive than the FVD model in terms of the velocity profile. In other words, vehicles in the T-FVD model can reach the optimal velocity quickly. It implies that the information of ET opening angle can increase the responsiveness of vehicles. Here, the responsiveness of vehicular traffic flow means that vehicles react to accelerate/decelerate quickly. In addition, Fig. 6 shows that the position profile in the T-FVD model can not only start responsively but also last longer than that in FVD model. It implies that vehicles in the T-FVD model can travel far with the optimal velocity, compared with the FVD model. In summary, Figs. 4, 5 and 6 indicate that the T-FVD model enables the CAVs to have a better start performance than the FVD model with respect to the acceleration, velocity, and position profiles.

Fig. 5
figure 5

The velocity profile of traffic flow starting from a green traffic signal a FVD model and b T-FVD model

Full size image
Fig. 6
figure 6

The position profile of traffic flow starting from a green traffic signal a FVD model and b T-FVD model

Full size image

4.2 Stop process

For this process, we do the following. Initially, the traffic signal is green and all vehicles travel at the same constant velocity. At time \(t=0\,\hbox {s}\), the signal changes to red and vehicles begin to slow down. The first vehicle begins to decelerate until it comes to a complete stop. The other vehicles follow this vehicle and decelerate. Finally, all vehicles stop at the signal. To compare the performance with respect to the deceleration, velocity, and position profiles, we simulate the stop process for both the FVD and the proposed T-FVD models

Figure 7 demonstrates that the magnitude of deceleration in the T-FVD model is less than that in the FVD model. In particular, except for the leading vehicle, the maximum deceleration rate in the T-FVD model is about \(-4\;\hbox {m/s}^{2}\), which is less than that of the FVD model \((-5\;\hbox {m/s}^{2})\). It implies that the introduction of ET opening angle can reduce the magnitude of deceleration. Figure 8 demonstrates that the T-FVD model is more responsive than FVD model with respect to velocity profile. This pattern is also the same with the start process. Figure 9 shows the position profile in the T-FVD model can reach the maximum value in a shorter time, compared with the FVD model. In summary, Figs. 7, 8 and 9 indicate that the T-FVD model has a better stop performance than the FVD model with respect to the deceleration, velocity, and position profiles.

Fig. 7
figure 7

The deceleration profile of traffic flow stopping at a red traffic signal a FVD model and b T-FVD model

Full size image
Fig. 8
figure 8

The velocity profile of traffic flow stopping at a red traffic signal a FVD model and b T-FVD mode

Full size image
Fig. 9
figure 9

The position profile of traffic flow stopping at a red traffic signal a FVD model and b T-FVD model

Full size image
Fig. 10
figure 10

The velocity profile of traffic flow evolution a FVD model and b T-FVD model

Full size image
Fig. 11
figure 11

The space headway profile of traffic flow evolution a FVD model and b T-FVD model

Full size image

4.3 Evolution process

In this section, we study the performance of perturbation rejection of the proposed T-FVD model. For comparison, we use Runge–Kutta algorithm for numerical integration with the time-step \(\Delta t=0.01\hbox {s}\). The uniform random noise with the maximum amplitude \(10^{-3}\) is added to the vehicle position according to Eq. (3) with each time-step \(\Delta t\). The initial conditions are shown in Eqs. (15) and (16).

Figures 10 and 11 demonstrate the variations of space headway and velocity profiles of vehicular traffic flow at \(t=100\,\hbox {s}\), respectively. Figure 10a shows that the velocity based on the FVD model of upstream vehicular traffic flow oscillates around the constant velocity \(v_{0}\), and the downstream vehicular traffic flow moves with constant velocity \(v_{0}\). By contrast, Figure 10b shows that the velocity based on the proposed T-FVD model of vehicular traffic flow is stable around the constant velocity \(v_{0}\) both upstream and downstream. From Fig. 11a, the space headway based on the FVD model oscillates around the constant headway h upstream and gradually becomes stabilized downstream. By comparison, Fig. 11b illustrates that the space headway based on the proposed T-FVD model of vehicular traffic flow is stable around the constant headway h both upstream and downstream. Figures 10 and 11 indicate that both the smoothness and stability of the T-FVD model are improved by considering the ET dynamics, unlike with the FVD model.

Based on the theoretical analyses and numerical experiments, the comparisons demonstrate that the smoothness and stability of the T-FVD model are improved by considering the ET dynamics, compared with FVD model.

5 Conclusions

This study analyzes the effects of ET dynamics on the connected and autonomous vehicular traffic flow, and proposes the T-FVD model. Theoretical analysis proves that the FVD model is a special case of the proposed T-FVD model. Compared to the FVD model, the stability region of the T-FVD model is enlarged through the stability analysis using the perturbation method. In addition, results from numerical experiments show that the dynamic performance is improved in terms of the smoothness and stability of the T-FVD model associated with the space headway, position, velocity, and acceleration/deceleration profiles in start, stop, and evolution processes.

The findings of this study suggest that it is beneficial to incorporate the vehicle dynamics into traffic flow models to improve the dynamic performance, especially for the connected and autonomous traffic flow environments. In addition, they motivate the study of the impacts of vehicle dynamics on analyzing the formation control of vehicular traffic platoon through information and communication technologies to improve the performance of CAV systems.