1 Introduction

Nonlinear evolution equations (NLEEs) are widely used to describe complex sciences phenomena such as the marine engineering, fluid dynamics, plasma physics, chemistry and physics and many other applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. During the past several decades, many efficient methods have been proposed to obtain the exact solutions of NLEEs such as inverse scattering method [16], the homotopy perturbation method [17], Hirota direct method [18,19,20,21,22,23,24,25,26], hyperbolic function method [27], homogeneous balance method [28,29,30], F-expansion method [31], exp function method [32,33,34], the extended mapping method [35], the (G\('\)/G)-expansion method [36,37,38] and three-wave approach [39,40,41,42,43,44].

In this paper, we will research the following (3+1)-dimensional generalized shallow water equation:

$$\begin{aligned} u_{xxxy}-3\,u_x\,u_{xy}-3\,u_y\,u_{xx}+u_{yt}-u_{xz}=0. \end{aligned}$$
(1)

Equation (1) has been used in weather simulations, tidal waves, river and irrigation ows, tsunami prediction and researched in different ways. Tian [45] obtained the soliton-type solutions of Eq. (1) by using the generalized tanh algorithm method. Zayed [46] got the traveling wave solutions of Eq. (1) by using the (G\('\)/G)-expansion method. Tang [47] presented the Grammian and Pfaffian solutions of Eq. (1) by the Hirota bilinear form. Multiple soliton solutions of Eq. (1) are discussed by Zeng [1]. Next, we will discuss the new periodic solitary wave solutions for Eq. (1) by using the direct test function method. The direct test function is used instead of text function in the original Hirota bilinear method. If the bilinear equation of nonlinear evolution equations is available, then rich variety of exact solutions can be presented by using the direct test function method. These exact solutions are found to possess dynamic characteristics. This used method being simple and straightforward than the method in Refs. [45,46,47].

The paper is organized as follows: in Sect. 2, by using the auto-Bäcklund transformation and a direct test function, new periodic solitary wave solutions for the (3+1)-dimensional generalized shallow water equation are obtained. In Sect. 3, the conclusions are presented.

2 New periodic solitary wave solutions for the (3+1)-dimensional generalized shallow water equation

According to the idea of the extended variable-coefficient homogeneous balance method (EvcHB) [48], the solutions of Eq. (1) can be supposed as follows:

$$\begin{aligned} u(x,y,z,t)= & {} [\,-2\,\ln (\xi ) + \delta (\eta ) \nonumber \\&+\, \xi \, \sigma (\eta )\,]_x+u_0(x,y,z,t), \end{aligned}$$
(2)

where \(\xi =\xi (x,y,z,t)\), \(\eta =\eta (y,z,t)\) and \(u_0(x,y,z,t)\) is a special solution of Eq. (1). Substituting Eq. (2) into (1), we have the following auto-Bäcklund transformation:

$$\begin{aligned}&\xi \, \sigma (\eta )\, \xi _x^2\, (\,\xi _x\, \xi _{xy}+\xi _y\, \xi _{xx}\,)=0, \end{aligned}$$
(3)
$$\begin{aligned}&\quad -\,2\, \xi _z\, \xi _x^2+2 \,\xi _t \,\xi _y\, \xi _x+[\,3\, \xi \,\sigma (\eta )+2\,]\, \xi _y\, \xi _{xxx}\, \xi _x\nonumber \\&\quad -\, 6\, u_{0y}\, \xi _x^3+3\,\xi _y\, [\,\xi \,\sigma (\eta )\, \xi _{xx}^2-2\, \xi _x^2\, u_{0x}\,]\nonumber \\&\quad +\, 3\,\{\,[\,5\, \xi \,\sigma (\eta )-2\,]\, \xi _{xy} \,\xi _{xx}\nonumber \\&\quad +\,[\,\xi \, \sigma (\eta )+2]\, \xi _x\, \xi _{xxy}\,\}\, \xi _x=0, - 3 u_{0xy}\, \xi _x^2\end{aligned}$$
(4)
$$\begin{aligned}&\quad +\,\xi _{yt}\, \xi _x-(\,2 \,\xi _{xz}+6\, u_{0x}\, \xi _{xy}+9\, u_{0y}\, \xi _{xx}\,)\, \xi _x\nonumber \\&\quad +\, 4\, \xi _{xxxy}\, \xi _x-\xi _z\, \xi _{xx}+\xi _{xy}\,(\,\xi _t-2\, \xi _{xxx}\,)\nonumber \\&\quad -\, \frac{3}{2}\, \xi \, \sigma (\eta ) \,[\,\xi \, \sigma (\eta )-4\,]\, (\xi _{xx}\, \xi _{xxy}+\xi _{xy}\, \xi _{xxx}\,)\nonumber \\&\quad +\, \xi _y\, (\,\xi _{xt}-3\, u_{0x} \,\xi _{xx}-3\, \xi _x\, u_{0xx}+\xi _{xxxx}\,) =0, \end{aligned}$$
(5)
$$\begin{aligned}&\xi _{xyt}-3\, u_{0xy}\, \xi _{xx}-3\, \xi _{xy}\, u_{0xx}-\xi _{xxz}-3\, u_{0x}\, \xi _{xxy}\nonumber \\&\quad - 3\, u_{0y}\, \xi _{xxx}+\xi _{xxxxy}=0, \end{aligned}$$
(6)
$$\begin{aligned}&\sigma '(\eta )\, (\,\eta _t\, \xi _{xy}-\eta _z\, \xi _{xx}\,)=0, \end{aligned}$$
(7)
$$\begin{aligned}&u_{0xxxy}-3\,u_{0x}\,u_{0xy}-3\,u_{0y}\,u_{0xx}+u_{0yt}-u_{0xz}=0.\nonumber \\ \end{aligned}$$
(8)

Aiming at the new periodic solitary wave solutions, we suppose that \(\sigma (\eta )=0\), \(u_0(x,y,z,t)=0\) and a direct test function

$$\begin{aligned} \xi (x,y,z,t)= & {} k_1\,e^{\theta _1}+e^{-\theta _1}+k_2\,\tan \left( \theta _2\right) \nonumber \\&+ \,k_3\,\tan \textit{h} \left( \theta _3\right) , \end{aligned}$$
(9)

where \(\theta _i=\alpha _i\,x+\beta _i\,y+\gamma _i\,z+\delta _i\,t,i=1,2,3,4\) and \(\alpha _i\), \(\beta _i\), \(\gamma _i\), \(\delta _i\) are constants to be determined later. Substituting Eq. (9) into (3)–(8) and equating all the coefficients of different powers of \(e^{\theta _1}\), \(e^{-\theta _1}\), \(\tan \left( \theta _2\right) \), \(\tan \textit{h} \left( \theta _3\right) \) and constant term to zero, we can obtain a set of algebraic equations for \(\alpha _i\), \(\beta _i\), \(\gamma _i\), \(\delta _i\), \(k_i(i=1,2,3,4)\). Solving the system with the aid of Mathematical, we obtain the following results:

Case(1)

$$\begin{aligned} k_2 = \beta _1=\gamma _1=\alpha _3=\delta _3=0, \gamma _3=\frac{\beta _3 \alpha _1^3+\beta _3 \delta _1}{\alpha _1},\nonumber \\ \end{aligned}$$
(10)

where \(\alpha _1\), \(\delta _1\), \(\beta _3\), \(k_1\) and \(k_3\) are arbitrary constants. Substituting Eq. (10) into (9), we have

$$\begin{aligned} \xi (x,y,z,t)= & {} e^{x \alpha _1+t \delta _1} k_1+e^{-x \alpha _1-t \delta _1}\nonumber \\&+\,k_3 \tan \textit{h} [y \beta _3+\frac{z \left( \beta _3 \alpha _1^3+\beta _3 \delta _1\right) }{\alpha _1}].\nonumber \\ \end{aligned}$$
(11)

Therefore, we obtain the first new periodic solitary wave solution for Eq. (1):

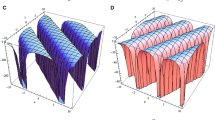
$$\begin{aligned} u_1 =-\frac{2 \left( e^{x \alpha _1+t \delta _1} k_1 \alpha _1-e^{-x \alpha _1-t \delta _1} \alpha _1\right) }{e^{x \alpha _1+t \delta _1} k_1+e^{-x \alpha _1-t \delta _1}+k_3 \tan \textit{h} \left[ y \beta _3+\frac{z \left( \beta _3 \alpha _1^3+\beta _3 \delta _1\right) }{\alpha _1}\right] }.\nonumber \\ \end{aligned}$$
(12)

The evolution and mechanical feature of Eq. (12) are shown in Figs. 1, 2.

Fig. 1
figure 1

The solitary wave solution (12) at \(k_1=k_3=\delta _1=-2\), \(\alpha _1=-1\), \(\beta _3=5\), \(z=10\), a \(t = -5\), b \(t = 0\), c \(t = 5\)

Full size image

Case(2)

$$\begin{aligned} k_3 = \beta _1=\gamma _1=\alpha _2=\delta _2=0, \gamma _2=\frac{\beta _2 \alpha _1^3+\beta _2 \delta _1}{\alpha _1},\nonumber \\ \end{aligned}$$
(13)

where \(\alpha _1\), \(\delta _1\), \(\beta _2\), \(k_1\) and \(k_2\) are arbitrary constants. Substituting Eq. (13) into (9), we have

$$\begin{aligned} \xi (x,y,z,t)= & {} e^{x \alpha _1+t \delta _1} k_1+e^{-x \alpha _1-t \delta _1}+k_2 \tan \bigg [y \beta _2\nonumber \\&+\frac{z \left( \beta _2 \alpha _1^3+\beta _2 \delta _1\right) }{\alpha _1}\bigg ]. \end{aligned}$$
(14)

Therefore, we obtain the second new periodic solitary wave solutions for Eq. (1):

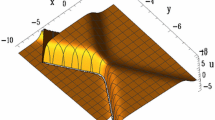
$$\begin{aligned} u_2 =-\frac{2 \left( e^{x \alpha _1+t \delta _1} k_1 \alpha _1-e^{-x \alpha _1-t \delta _1} \alpha _1\right) }{e^{x \alpha _1+t \delta _1} k_1+e^{-x \alpha _1-t \delta _1}+k_2 \tan \left[ y \beta _2+\frac{z \left( \beta _2 \alpha _1^3+\beta _2 \delta _1\right) }{\alpha _1}\right] }.\nonumber \\ \end{aligned}$$
(15)

The evolution and mechanical feature of Eq. (15) are shown in Figs. 3, 4 and 5.

Fig. 2
figure 2

The solitary wave solution (12) at \(k_1=k_3=\delta _1=-2\), \(\alpha _1=-1\), \(\beta _3=5\), \(y=-1\), a \(z = -20\), b \(z = 0\), c \(z = 20\)

Full size image
Fig. 3
figure 3

The solitary wave solution (15) at \(k_1=k_2=\delta _1=-2\), \(\alpha _1=-1\), \(\beta _2=5\), \(z=10\), a \(t = -5\), b \(t = 0\), c \(t = 5\)

Full size image
Fig. 4
figure 4

The solitary wave solution (15) at \(k_1=k_2=\delta _1=-2\), \(\alpha _1=-1\), \(\beta _2=5\), \(t=-5\), a \(x = 5\), b \(x = 10\), c \(x = 15\)

Full size image
Fig. 5
figure 5

The solitary wave solution (15) at \(k_1=k_2=\delta _1=-2\), \(\alpha _1=-1\), \(\beta _2=5\), \(z=10\), a \(x = -10\), b \(x = 0\), c \(x = 10\)

Full size image

Case(3)

$$\begin{aligned} k_1= & {} \alpha _2=\delta _2=\alpha _3=\delta _3=0, \gamma _1=\frac{\beta _1 \alpha _1^3+\beta _1 \delta _1}{\alpha _1},\nonumber \\ \gamma _2= & {} \frac{\beta _2 \alpha _1^3+\beta _2 \delta _1}{\alpha _1}, \gamma _3=\frac{\beta _3 \alpha _1^3+\beta _3 \delta _1}{\alpha _1}, \end{aligned}$$
(16)

where \(\alpha _1\), \(\delta _1\), \(\beta _1\), \(\beta _2\), \(\beta _3\), \(k_2\) and \(k_3\) are arbitrary constants. Substituting Eq. (16) into (9), we have

$$\begin{aligned} \xi (x,y,z,t)= & {} k_2 \tan \left[ y \beta _2+\frac{z \left( \beta _2 \alpha _1^3+\beta _2 \delta _1\right) }{\alpha _1}\right] \nonumber \\&+\,e^{-x \alpha _1-y \beta _1-t \delta _1-\frac{z \left( \beta _1 \alpha _1^3+\beta _1 \delta _1\right) }{\alpha _1}}\nonumber \\&+ \, k_3 \tan \textit{h} \left[ y \beta _3+\frac{z \left( \beta _3 \alpha _1^3+\beta _3 \delta _1\right) }{\alpha _1}\right] .\nonumber \\ \end{aligned}$$
(17)

Therefore, we obtain the third new periodic solitary wave solutions for Eq. (1):

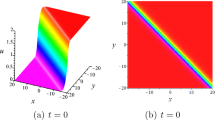
$$\begin{aligned} u_3= & {} 2 e^{-x \alpha _1-y \beta _1-t \delta _1-\frac{z \left( \beta _1 \alpha _1^3+\beta _1 \delta _1\right) }{\alpha _1}} \alpha _1/\left[ k_2 \tan \left[ y \beta _2\right. \right. \nonumber \\&\left. +\frac{z \left( \beta _2 \alpha _1^3+\beta _2 \delta _1\right) }{\alpha _1}\right] \nonumber \\&+\, e^{-x \alpha _1-y \beta _1-t \delta _1-\frac{z \left( \beta _1 \alpha _1^3+\beta _1 \delta _1\right) }{\alpha _1}}\nonumber \\&\left. +\,k_3 \tan \textit{h} \left[ y \beta _3+\frac{z \left( \beta _3 \alpha _1^3+\beta _3 \delta _1\right) }{\alpha _1}\right] \right] . \end{aligned}$$
(18)

The evolution and mechanical feature of Eq. (18) are shown in Figs. 6, 7.

Fig. 6
figure 6

The solitary wave solution (18) at \(k_3=k_2=\beta _1=\delta _1=-2\), \(\alpha _1=1\), \(\beta _2=\beta _3=-5\), \(z=10\), a \(t = -10\), b \(t = 0\), c \(t = 10\)

Full size image
Fig. 7
figure 7

The solitary wave solution (18) at \(k_2=\beta _1=\delta _1=-2\), \(k_3=0\), \(\alpha _1=1\), \(\beta _2=\beta _3=-5\), \(t=-5\), a \(y = -10\), b \(y = 0\), c \(y = 10\)

Full size image

Case(4)

$$\begin{aligned} k_1= & {} \alpha _2=\beta _2=\alpha _3=\beta _3=0, \gamma _1=\frac{\beta _1 \alpha _1^3+\beta _1 \delta _1}{\alpha _1}, \gamma _2 \nonumber \\= & {} \frac{\beta _1 \delta _2}{\alpha _1}, \gamma _3=\frac{\beta _1 \delta _3}{\alpha _1}, \end{aligned}$$
(19)

where \(\alpha _1\), \(\delta _1\), \(\beta _1\), \(\delta _2\), \(\delta _3\), \(k_2\) and \(k_3\) are arbitrary constants. Substituting Eq. (19) into (9), we have

$$\begin{aligned} \xi (x,y,z,t)= & {} k_2 \tan \left( t \delta _2+\frac{z \beta _1 \delta _2}{\alpha _1}\right) \nonumber \\&+\,k_3 \tan \textit{h} \left( t \delta _3+\frac{z \beta _1 \delta _3}{\alpha _1}\right) \nonumber \\&+ \, e^{-x \alpha _1-y \beta _1-t \delta _1-\frac{z \left( \beta _1 \alpha _1^3+\beta _1 \delta _1\right) }{\alpha _1}}. \end{aligned}$$
(20)

Therefore, we obtain the fourth new periodic solitary wave solutions for Eq.(1):

$$\begin{aligned} u_4= & {} 2 e^{-x \alpha _1-y \beta _1-t \delta _1-\frac{z \left( \beta _1 \alpha _1^3+\beta _1 \delta _1\right) }{\alpha _1}} \alpha _1/\left[ k_2 \tan \left( t \delta _2+\frac{z \beta _1 \delta _2}{\alpha _1}\right) \right. \nonumber \\&+ \, k_3 \tan \textit{h} \left( t \delta _3+\frac{z \beta _1 \delta _3}{\alpha _1}\right) \nonumber \\&\left. +\, e^{-x \alpha _1-y \beta _1-t \delta _1-\frac{z \left( \beta _1 \alpha _1^3+\beta _1 \delta _1\right) }{\alpha _1}}\right] . \end{aligned}$$
(21)

The evolution and mechanical feature of Eq. (21) are shown in Figs. 8, 9.

Fig. 8
figure 8

The solitary wave solution (21) at \(k_3=k_2=\beta _1=\delta _1=-2\), \(\alpha _1=1\), \(\delta _2=\delta _3=-5\), \(y=10\), a \(x = -20\), b \(x = 0\), c \(x = 20\)

Full size image
Fig. 9
figure 9

The solitary wave solution (21) at \(k_3=k_2=\beta _1=\delta _1=-2\), \(\alpha _1=1\), \(\delta _2=\delta _3=-5\), \(y=10\), a \(t = -10\), b \(t = 0\), c \(t = 10\)

Full size image

3 Conclusion

By using the auto-Bäcklund transformation and a direct test function, we obtain new periodic solitary wave solutions of the (3+1)-dimensional generalized shallow water equation. Moreover, the evolution and mechanical feature of solutions (12), (15), (18) and (21) are clearly presented in Figs. 1, 2, 3, 4, 5, 6, 7 , 8 and 9.

The direct test function method is reliable and effective and obtains many new periodic solitary wave solutions. The applied method will be used in further works to seek more entirely periodic solitary wave solutions of higher dimensional nonlinear evolution equations.