The dynamics of some exact solutions of the (3+1)-dimensional generalized shallow water wave equation

Abstract

The (3+1)-dimensional generalized shallow water wave equation is systematically investigated in this paper based on the Hirota bilinear method. The N-soliton solution and the higher-order kink-shaped breather solutions of the (3+1)-dimensional generalized shallow water wave equation are first proposed. Then, the line rogue wave solution and various hybrid solutions consisting of the breather, the kink-shaped soliton and the periodic solutions are discussed. Furthermore, the lump solutions of it are derived by using the long wave limit of the N-soliton solution. In addition, the diverse semi-rational solutions composed of lumps, kink solitons, line rogue wave and breathers enrich the research contents of the (3+1)-dimensional generalized shallow water wave equation. The dynamic behaviors of these exact solutions are vividly presented by their respective three-dimensional diagrams and density plots with contours.

1 Introduction

As significant mathematical models capable of describing some nonlinear phenomena, nonlinear evolution equations (NLEEs) have always been highly valued by scholars in mathematics, physics and even engineering due to their important statuses in such scientific fields as plasma physics, optical fiber communication, nonlinear atmospheric dynamics, quantum mechanics, etc. Meanwhile, the solutions to the emerging nonlinear evolution equations with nonlinear dispersion and dissipation effects are the subjects that the majority of nonlinear scientific researchers have to consider. Soliton refers to the solution with particle structural state of a class of nonlinear dispersion equations [1]. Soliton, chaos and fractal constitute the three major theories of nonlinear science, which respectively represent the three universal classes of nonlinear phenomena. The kinematic mechanism of solitons and waves has become an important research field that is active internationally since the numerical research results of the famous nonlinear shallow water wave Korteweg-de Vries (KdV) equation were published by Zabusky and Kruskal [2]. A series of methods for solving nonlinear evolution equations emerged as the times require in the theory of soliton and integrable system, such as the inverse scattering transformation (IST) [3,4,5], the homogeneous balance method [6, 7], the function expansion method [8, 9], the B$\ddot{a}$cklund transformation (BT) [10,11,12], the Darboux transformation (DT) [13,14,15] and the Hirota bilinear method [16,17,18,19]. Among them, the Hirota bilinear method is highlighted as a powerful weapon that was first proposed by Ryogo Hirota [16], to find the exact solutions of various nonlinear evolution equations. Some popular integrable equations such as the Kadomtsev-Petviashvili (KP) equation [20,21,22] and the Davey-Stewartson (DS) equation [23, 24] have been studied in detail based on these methods.

The types of exact solutions are also rich and varied, including the bright solitons, the dark solitons, the kink solitons, the breathers, the rogue waves, and the lumps [25,26,27,28,29,30,31,32,33,34,35]. Due to the combined effect of nonlinearity and dispersion, the soliton solution keeps its original stable wave packet characteristics during nonlinear wave propagation and after collision, which undoubtedly shows the amazing orderliness caused by nonlinear effects [1, 2, 25,26,27]. The breathers oscillate periodically in a certain region of the finite background during transmission [29,30,31]. In particular, the rogue waves and the lump solutions, as rational function solutions of nonlinear wave equations, have increasingly become the focus of attention due to their special structures and potential destructiveness [31,32,33,34,35]. The rogue waves were first proposed when Peregrine studied the general nonlinear Schr$\ddot{o}$dinger (NLS) equation [36] and often “come without shadow and go without trace” [37], which are interpreted as the phenomena of energy concentration in the nonlinear theory. Their peak amplitudes are usually about three times of the background waves, and they will eventually attenuate to a constant background wave. The rogue wave phenomena also exist in such fields as oceanography, optics, Bose Einstein condensate, plasma physics, atmospheric science, etc [38,39,40,41,42,43].

However, since most of the rogue wave phenomena in the ocean are described by (2+1)- or (3+1)-dimensional models, and the research on low-dimen sional nonlinear models has been relatively mature [30,31,32,33,34, 38], the research on (3+1)- and even higher-dimensional nonlinear models has become necessary. For example, the algebraic-geometrical solutions, N-soliton solution and its Wronskian form of a (3+1)-dimensional nonlinear evolution equation are solved in detail [44, 45]. The solitary wave solutions, lump-type solutions, and rogue wave solutions of the (3+1)-dimensional Jimbo-Miwa equation have been studied [46,47,48]. And the multiple-soliton solutions, multiple singular soliton solutions, Wronskian and Grammian solutions of a (3+1)-dimensional generalized Kadomtsev-Petviashvili (KP) equation are constructed [49,50,51].

This paper focuses on a (3+1)-dimensional nonlinear model, namely the (3+1)-dimensional generalized shallow water wave (gSWW) equation as

$$\begin{aligned} (u_{t}+u_{xxx})_{y}-3(u_{x}u_{y})_{x}+u_{xz}=0, \end{aligned}$$

(1.1)

where $u=u(x,y,z,t)$, which can be equivalent to the general expression of the (3+1)-dimensional generalized shallow water wave (gSWW) equation [52,53,54,55,56]

$$\begin{aligned} u_{yt}+u_{xxxy}-3u_{xx}u_{y}-3u_{x}u_{xy}-u_{xz}=0, \end{aligned}$$

(1.2)

under a scale transformation $z\rightarrow -z$. Tian et al. have obtained the soliton-typed solutions of the (3+1)-dimensional gSWW equation by using the tanh function method with symbolic computation [54]. Three functional representations of the traveling wave solutions of the equation have been derived by Zayed through the ($\frac{G'}{G}$)-expansion method [55]. Based on the Hirota bilinear method, Tang and Ma et al. calculated the solutions of the equation in Grammian and Pfaffian forms [56]. Some singular soliton solutions, hyperbolic function solutions and trigonometric function solutions of the equation are proposed by Zeng and Liu et al. through the Painlev$\acute{e}$ B$\ddot{a}$cklund transformation and the Hirota bilinear method [57]. Liu et al. used the auto-B$\ddot{a}$cklund transformation and a direct test function to obtain some periodic solitary wave solutions for the equation [58]. And Eq. (1.1) describes the propagation of shallow water waves in oceans, estuaries and reservoirs, and can be applied to weather simulation, tidal waves, rivers and irrigation flows, tsunami forecasts, etc. As we know, the higher-order kink-shaped soliton and breather solutions, the rogue wave (RW) solutions, the RW-soliton and lump-breather semi-rational solutions, and the hybrid solutions composed of different solutions of Eq. (1.1) are still to be explored. As a consequence, this paper focuses on the dynamic behaviors of new exact solutions of Eq. (1.1) heartened by the above open problems, and hopes to learn more about the new characteristics of Eq. (1.1) during the research.

The main structure of this paper is as follows. In Sect. 2, based on the Hirota bilinear method combined with a logarithmic transformation and the perturbation method, the explicit expression of the N-soliton solution and the kink-shaped multi-soliton solutions of Eq. (1.1) are derived. In Sect. 3, the higher-order breather solutions and the hybrid solutions of Eq. (1.1) are constructed under special constraints of parameters. In Sect. 4, the lump solutions and the line rogue wave solution of Eq. (1.1) are generated by taking the long wave limit [59,60,61,62,63]. In Sect. 5, various types of semi-rational solutions of Eq. (1.1) are explored. The conclusion of this paper is given in Sect. 6.

2 The bilinear form and the soliton solutions of the (3+1)-dimensional gsww equation

In order to obtain the Hirota bilinear form of Eq. (1.1), a binary differential D-operator (i.e. the Hirota derivative) [18] is introduced as

$$\begin{aligned}{} & {} \!\!\!D_{x}^{n}a(x)\cdot b(x)\equiv (\frac{\partial }{\partial x}-\frac{\partial }{\partial y})^{n}a(x)b(y)|_{y=x}\nonumber \\{} & {} \qquad \qquad \qquad \quad =\frac{\partial ^{n}}{\partial y^{n}}a(x+y)b(x-y)|_{y=0},\nonumber \\ \end{aligned}$$

(2.1)

$$\begin{aligned}{} & {} \!\!\!D_{t}^{m}D_{x}^{n}a(t,x)\cdot b(t,x)\equiv \frac{\partial ^{m}}{\partial s^{m}}\frac{\partial ^{n}}{\partial y^{n}}a(t+s,x+y)\nonumber \\{} & {} \qquad \qquad \qquad \quad b(t-s,x-y)|_{s=0,y=0},\nonumber \\ \end{aligned}$$

(2.2)

where m and n are arbitrary non-negative integers. By performing a corresponding logarithmic transformation on u

$$\begin{aligned} u=-2(\ln f)_{x}, \end{aligned}$$

(2.3)

Eq. (1.1) can be transformed into a bilinear derivative equation

$$\begin{aligned} (D_{t}D_{y}+D_{x}^{3}D_{y}+D_{x}D_{z})f\cdot f=0. \end{aligned}$$

(2.4)

This is equivalent to the bilinear expansion of Eq. (1.1), written as follows

$$\begin{aligned}{} & {} ff_{ty}-f_{t}f_{y}+ff_{xxxy}-f_{xxx}f_{y}-3f_{xxy}f_{x}\nonumber \\{} & {} \quad +3f_{xx}f_{xy}+ff_{xz}-f_{x}f_{z}=0, \end{aligned}$$

(2.5)

where $f=f(x,y,z,t)$.

By using the standard perturbation method to solve Eq. (2.4), f(x, y, z, t) is expanded into a power series according to the small parameter $\varepsilon$

$$\begin{aligned} f(x,y,z,t)=1+\varepsilon f_{1}+\varepsilon ^{2}f_{2}+\cdots +\varepsilon ^{j}f_{j}+\cdots .\nonumber \\ \end{aligned}$$

(2.6)

After substituting it into Eq. (2.4), it can be rearranged by comparing the coefficients of the same power of $\varepsilon$, then

$$\begin{aligned}{} & {} \varepsilon :f_{1,ty}+f_{1,xxxy}+f_{1,xz}=0, \end{aligned}$$

(2.7a)

$$\begin{aligned}{} & {} \varepsilon ^{2}:2(f_{2,ty}+f_{2,xxxy}+f_{2,xz})\nonumber \\{} & {} =-(D_{t}D_{y}+D_{x}^{3}D_{y}+D_{x}D_{z})f_{1}\cdot f_{1}, \end{aligned}$$

(2.7b)

$$\begin{aligned}{} & {} \varepsilon ^{3}:f_{3,ty}+f_{3,xxxy}+f_{3,xz}\nonumber \\{} & {} =-(D_{t}D_{y}+D_{x}^{3}D_{y}+D_{x}D_{z})f_{1}\cdot f_{2}, \end{aligned}$$

(2.7c)

$$\begin{aligned}{} & {} \varepsilon ^{4}:2(f_{4,ty}+f_{4,xxxy}+f_{4,xz})\nonumber \\{} & {} =-(D_{t}D_{y}+D_{x}^{3}D_{y}+D_{x}D_{z})(2f_{1}\cdot f_{3}+f_{2}\cdot f_{2}), \nonumber \\{} & {} \cdots . \end{aligned}$$

(2.7d)

The power series (2.6) can be truncated at the sum of finite terms while properly selecting the solution $f_{1}$ in the form of a linear exponential function under the conditions of the above equations, hence,

$$\begin{aligned} f(x,y,z,t)=1+\varepsilon f_{1}=1+\varepsilon e^{\eta _{1}}, \end{aligned}$$

(2.8)

where

$$\begin{aligned} \eta _{1}= & {} p_{1}x+q_{1}y+k_{1}z+\omega _{1}t+\eta _{1}^{0},\nonumber \\ \omega _{1}= & {} -\frac{p_{1}(p_{1}^{2}q_{1}+k_{1})}{q_{1}}. \end{aligned}$$

(2.9)

Since the perturbation parameter $\varepsilon$ can be absorbed by the phase constant $\eta _{1}^{0}$ of the exponent $\eta _{1}$, the exact solution of Eq. (2.4) is given as follows

$$\begin{aligned} f(x,y,z,t)=1+e^{\eta _{1}}. \end{aligned}$$

(2.10)

Further, combining the transformation (2.3), the single solitary wave solution $u_{1s}$ of Eq. (1.1) is obtained as

$$\begin{aligned} u_{1s}=-\frac{2p_{1}}{1+e^{-(p_{1}x+q_{1}y+k_{1}z+\omega _{1}t+\eta _{1}^{0})}}. \end{aligned}$$

(2.11)

Note that the arbitrary parameter $\eta _{1}^{0}$ in this expression represents the position of the soliton, which is typically taken as 0. In addition, the 1-soliton solution $u_{1s}$ has no extreme point, showing the following characteristics:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{1s}\rightarrow -2p_{1}&{}\text {for}\quad \eta _{1}\rightarrow +\infty \\ u_{1s}\rightarrow 0&{}\text {for}\quad \eta _{1}\rightarrow -\infty \end{array}\right. }. \end{aligned}$$

(2.12)

In the asymptotic dynamic behavior of the 1-soliton solution $u_{1s}$, $u_{1s}$ will degenerate into a plane wave when $p_{1}=0$, otherwise $u_{1s}$ will degenerate into a kink wave. When all the parameters in (2.11) are assigned specific values, the 1-kink soliton solution of Eq. (1.1) is shown in Fig. 1.

Fig. 1

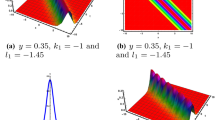
The 1-kink soliton solution of Eq. (1.1) in the (x, y)-plane at $t=0$ with parameters: $N=1$, $p_{1}=q_{1}=k_{1}=-1$, $\eta _{1}^{0}=0$. a The 3D plot. b The density plot. (Color online)

Since Eq. (2.7a) is a linear differential equation, a superposition solution of it can be given by applying the linear superposition principle

$$\begin{aligned} f_{1}= & {} e^{\eta _{1}}+e^{\eta _{2}},\quad \eta _{i}=p_{i}x+q_{i}y+k_{i}z+\omega _{i}t+\eta _{i}^{0}, \nonumber \\ \omega _{i}= & {} -\frac{p_{i}(p_{i}^{2}q_{i}+k_{i})}{q_{i}}\quad (i=1,2). \end{aligned}$$

(2.13)

After substituting (2.13) into Eq. (2.7b), the following will be obtained

$$\begin{aligned} f_{2}=e^{\eta _{1}+\eta _{2}+A_{12}}, \end{aligned}$$

(2.14)

where

$$\begin{aligned} e^{A_{12}}=\frac{p_{2}q_{1}^{2}(3p_{1}q_{2}(p_{1}-p_{2})-k_{2})-q_{1}q_{2}(3p_{1}p_{2}q_{2}(p_{1}-p_{2})-p_{1}k_{2} -p_{2}k_{1})-p_{1}q_{2}^{2}k_{1}}{p_{2}q_{1}^{2}(3p_{1}q_{2}(p_{1}+p_{2})-k_{2})+q_{1}q_{2}(3p_{1}p_{2}q_{2}(p_{1}+p_{2}) +p_{1}k_{2}+p_{2}k_{1})-p_{1}q_{2}^{2}k_{1}}. \end{aligned}$$

(2.15)

Then, by continuing to apply the perturbation method, the truncated solution of Eq. (2.4) will be transformed into

$$\begin{aligned} f(x,y,z,t)=1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{1}+\eta _{2}+A_{12}}. \end{aligned}$$

(2.16)

Thus, combining the transformation (2.3), the 2-soliton solution of Eq. (1.1) is solved as

$$\begin{aligned} u_{2s}=-2[\ln (1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{1}+\eta _{2}+A_{12}})]_{x}, \end{aligned}$$

(2.17)

where $\eta _{i}$ $(i=1,2)$ and $e^{A_{12}}$ are given in (2.13), (2.15). Under the condition that the phase constants $\eta _{i}^{0}$ $(i=1,2)$ are assigned as 0, the interactions between two kink-shaped solitons in two different cases are described (see Fig. 2a, b, e and f).

The method similar to the previous one is adopted to explain that Eq. (1.1) has the 3-soliton solution as follows

$$\begin{aligned} \begin{aligned} u_{3s}&=-2[\ln (1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{3}}+e^{\eta _{1}+\eta _{2}+A_{12}}\\&\quad +e^{\eta _{1}+\eta _{3}+A_{13}} +e^{\eta _{2}+\eta _{3}+A_{23}}\\&\quad +e^{\eta _{1}+\eta _{2}+\eta _{3}+A_{12}+A_{13}+A_{23}})]_{x}, \end{aligned} \end{aligned}$$

(2.18)

where

$$\begin{aligned} \eta _{i}= & {} p_{i}x+q_{i}y+k_{i}z+\omega _{i}t+\eta _{i}^{0}, \nonumber \\ \omega _{i}= & {} -\frac{p_{i}(p_{i}^{2}q_{i}+k_{i})}{q_{i}}\quad (i=1,2,3) \end{aligned}$$

(2.19)

$$\begin{aligned} e^{A_{ij}}= & {} \frac{\begin{aligned}p_{j}q_{i}^{2}(3p_{i}q_{j}(p_{i}{-}p_{j}){-}k_{j}){-}q_{i}q_{j}(3p_{i}p_{j}q_{j}(p_{i}\\{-}p_{j}){-}p_{i}k_{j} {-}p_{j}k_{i}){-}p_{i}q_{j}^{2}k_{i}\end{aligned}}{\begin{aligned}p_{j}q_{i}^{2}(3p_{i}q_{j}(p_{i}{+}p_{j}){-}k_{j}){+}q_{i}q_{j}(3p_{i}p_{j}q_{j}(p_{i}\\{+}p_{j}) {+}p_{i}k_{j}{+}p_{j}k_{i}){-}p_{i}q_{j}^{2}k_{i}\end{aligned}}\nonumber \\{} & {} (i<j,i,j=1,2,3). \end{aligned}$$

(2.20)

After regulating specific parameters, the 3-kink soliton solution of Eq. (1.1) is shown in Fig. 2c and g. Furthermore, the dynamic behavior of four solitons colliding with each other is also depicted (see Fig. 2d and h).

Fig. 2

The 2-, 3-, 4-kink soliton solutions of Eq. (1.1) in the (x, y)-plane at $t=0$ with parameters: a, (e)$N=2$, $p_{1}=-2$, $p_{2}=-3$, $q_{1}=\frac{1}{4}$, $q_{2}=\frac{3}{2}$, $k_{1}=k_{2}=1$, $\eta _{1}^{0}=\eta _{2}^{0}=0$; b, (f)$N=2$, $p_{1}=p_{2}=q_{1}=-q_{2}=-3$, $k_{1}=k_{2}=1$, $\eta _{1}^{0}=\eta _{2}^{0}=0$; c, (g)$N=3$, $p_{1}=p_{2}=p_{3}=-1$, $q_{1}=-\frac{1}{2}$, $q_{2}=1$, $q_{3}=-\frac{1}{9}$, $k_{1}=k_{2}=k_{3}=2$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=0$; d, (h)$N=4$, $p_{1}=p_{2}=p_{3}=p_{4}=-1$, $q_{1}=-\frac{1}{2}$, $q_{2}=1$, $q_{3}=-\frac{1}{9}$, $q_{4}=-2$, $k_{1}=k_{2}=k_{3}=k_{4}=2$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=\eta _{4}^{0}=0$. (Color online)

There is no doubt that the above method for constructing and analyzing the interactions of multi-solitary waves can be completely extended to the case of N-solitary waves. Then the N-soliton solution of Eq. (1.1) can be expressed as follows

$$\begin{aligned} u= & {} -2(\ln f)_{x}\nonumber \\= & {} -2\left[ \ln \left( \sum \limits _{\mu =0,1}e^{\sum \limits _{i=1}^{N}\mu _{i}\eta _{i}+\sum \limits _{1\le i<j}^{N}\mu _{i}\mu _{j}A_{ij}}\right) \right] _{x}, \end{aligned}$$

(2.21)

where

$$\begin{aligned}{} & {} \eta _{i}=p_{i}x+q_{i}y+k_{i}z+\omega _{i}t+\eta _{i}^{0},\nonumber \\{} & {} \omega _{i}=-\frac{p_{i}(p_{i}^{2}q_{i}+k_{i})}{q_{i}},\nonumber \\{} & {} e^{A_{ij}}{=}\frac{\begin{aligned}p_{j}q_{i}^{2}(3p_{i}q_{j}(p_{i}{-}p_{j}){-}k_{j}){-}q_{i}q_{j}(3p_{i}p_{j}q_{j}(p_{i}\\{-}p_{j}){-}p_{i}k_{j} {-}p_{j}k_{i}){-}p_{i}q_{j}^{2}k_{i}\end{aligned}}{\begin{aligned}p_{j}q_{i}^{2}(3p_{i}q_{j}(p_{i}{+}p_{j}){-}k_{j}){+}q_{i}q_{j}(3p_{i}p_{j}q_{j}(p_{i}\\{+}p_{j}) {+}p_{i}k_{j}{+}p_{j}k_{i}){-}p_{i}q_{j}^{2}k_{i}\end{aligned}}.\nonumber \\ \end{aligned}$$

(2.22)

Here, $p_{i}$, $q_{i}$, $k_{i}$ and $\eta _{i}^{0}$ are all arbitrary real or complex parameters, and subscripts i and j denote positive integers. The first summation symbol $\sum \limits _{\mu =0,1}$ behind the logarithmic sign shall take all possible combinations of $\mu _{i}=0,1$ $(i=1,2,\cdots ,N)$, which represents the addition of $2^{N}$ items. The symbol $\sum \limits _{1\le i<j}^{N}$ indicates the summation over all possible combinations of the N elements with the specific condition $1\le i<j\le N$. In addition, the formula $\omega _{i}+\frac{p_{i}(p_{i}^{2}q_{i}+k_{i})}{q_{i}}=0$ describes the nonlinear dispersion relation of Eq. (1.1). This is the critical factor that affects the periodicity and locality of the energy distribution in other rich solutions of Eq. (1.1).

Fig. 3

Sectional drawings of the 2-, 3-, 4-kink soliton solutions of Eq. (1.1) along the x-axis at different times with parameters: a $N=2$, $p_{1}=-2$, $p_{2}=-3$, $q_{1}=\frac{1}{4}$, $q_{2}=\frac{3}{2}$, $k_{1}=k_{2}=1$, $\eta _{1}^{0}=\eta _{2}^{0}=0$; b $N=3$, $p_{1}=p_{2}=p_{3}=-1$, $q_{1}=-\frac{1}{2}$, $q_{2}=1$, $q_{3}=-\frac{1}{9}$, $k_{1}=k_{2}=k_{3}=2$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=0$; c $N=4$, $p_{1}=p_{2}=p_{3}=p_{4}=-1$, $q_{1}=-\frac{1}{2}$, $q_{2}=1$, $q_{3}=-\frac{1}{9}$, $q_{4}=-2$, $k_{1}=k_{2}=k_{3}=k_{4}=2$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=\eta _{4}^{0}=0$. (Color online)

On the basis of assigning appropriate specific values to the parameters in (2.11), (2.17), (2.18), (2.21), the diagrams of the single soliton and multi-soliton solutions are demonstrated, which show the shape characteristics of kinks. Actually, $p_{i}\ne 0$ $(i=1,2,3,4)$ in formula (2.22) are the essence that causes these multi-soliton solutions to exhibit kink characteristics, and whether $p_{i}$ $(i=1,2,3,4)$ are assigned the same value also implies the diversity of the multi-soliton solutions of Eq. (1.1). The propagations of solitary waves with particle structural state can be observed intuitively from these graphics. Collisions between solitary waves are elastic because of the interaction of dispersion and nonlinear effects, that is, changes in phases are permitted, but the shapes, sizes (velocities) and directions do not change. And the interactions between these kink-shaped solitons make the amplitudes at their intersections appear a transient anomaly (see Figs. 1, 2 and 3).

3 The breather solutions and the hybrid solutions of the (3+1)-dimensional gsww equation

The shapes of the breather solutions undergo periodic oscillations during the propagation of the (3+1)-dimensional generalized shallow water wave. Their essence is in intimate relationship with multi-soliton solutions, which are generated based on the exponential function. Therefore, the hybrid solutions composed of multi-soliton solutions and breather solutions can also be discussed intensively in this section. Following the previous research [60,61,62,63], the N-soliton solution can be derived into the mth-order breather solution by first restricting the parameters in formula (2.21), (2.22) with the complex conjugate constraint

$$\begin{aligned} N= & {} 2m,\quad p_{2i}=p_{2i-1}^{*},\nonumber \\ q_{2i}= & {} q_{2i-1}^{*},\quad k_{2i}=k_{2i-1}^{*}, \end{aligned}$$

(3.1)

where $m\in N_{+}$, $i=1,2,\cdots ,m$, and then continuing to select specific values for assignment. For instance, by setting the parameters $N=2$, $p_{2}=p_{1}^{*}=2i$, $q_{2}=q_{1}^{*}=1+2i$, $k_{2}=k_{1}^{*}=-3i$, $\eta _{1}^{0}=\eta _{2}^{0}=0$, the first-order breather solution of Eq. (1.1) can be constructed as

$$\begin{aligned} u_{1b}=\frac{8e^{\zeta _{1}}\sin (\xi _{1})}{1+e^{\xi _{2}}+e^{\xi _{2}^{*}}+41e^{\zeta _{2}}}, \end{aligned}$$

(3.2)

where

$$\begin{aligned}{} & {} \zeta _{1}=-\frac{6}{5}t+y,\nonumber \\{} & {} \zeta _{2}=-\frac{12}{5}t+2y,\nonumber \\{} & {} \xi _{1}=\frac{52}{5}t+2x+2y-3z,\nonumber \\{} & {} \xi _{2}=\left( -\frac{6}{5}+\frac{52}{5}i\right) t+2ix+(1+2i)y-3iz.\nonumber \\ \end{aligned}$$

(3.3)

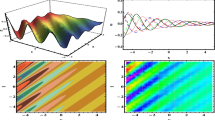
Thus it can be seen, the travel trajectory of the first-order breather solution $u_{1b}$ along the x-axis is periodic, and the cycle period is $\pi$ (see Fig. 4a, b and c). $u_{1b}$ exhibits localization simultaneously in the y-direction on the (x, y)-plane. Besides that, while taking $N=2$, $p_{2}=p_{1}^{*}=q_{1}=q_{2}^{*}=k_{2}=k_{1}^{*}=1-i$, $\eta _{1}^{0}=\eta _{2}^{0}=0$, the first-order kink-shaped breather solution of Eq. (1.1) is also shown in Fig. 4d, e and f. This breather solution not only exhibits kink feature in shape, but also exhibits oblique breathing behavior in the (x, y)-plane, with periodicity in both x and y directions.

Fig. 4

The first-order breather solution and the first-order kink-shaped breather solution of Eq. (1.1) in the (x, y)-plane at $t=0$. a, d The 3D plot. b, e The density plot with contours. c, f The sectional drawing($y=0$, $z=0$). (Color online)

When higher order cases are considered, by setting the parameters $N=4$, $p_{2}=p_{1}^{*}=k_{2}=k_{1}^{*}=-i$, $q_{2}=q_{1}^{*}=1+i$, $\eta _{1}^{0}=\eta _{2}^{0}=2\pi$, $p_{4}=p_{3}^{*}=k_{4}=k_{3}^{*}=2i$, $q_{4}=q_{3}^{*}=2-2i$, $\eta _{3}^{0}=\eta _{4}^{0}=-2\pi$ in formula (2.21), (2.22), the second-order breather solution of Eq. (1.1) can be pushed out. The diagram shows that two rows of breather waves are spread in parallel (see Fig. 5a and b). Similar to the first-order breather solution at $N=2$, the periodicity of the second-order breather solution is manifested in the x-direction on the (x, y)-plane, and the locality is manifested in the y-direction.

Fig. 5

The second-order breather solution and the second-order kink-shaped breather solution of Eq. (1.1) in the (x, y)-plane at $t=0$. a, c The 3D plot. b, d The density plot with contours. (Color online)

And the second-order kink-shaped breather solution of Eq. (1.1) can also be sought in like wise by taking $N=4$, $p_{2}=p_{1}^{*}=q_{1}=q_{2}^{*}=k_{2}=k_{1}^{*}=1-i$, $\eta _{1}^{0}=\eta _{2}^{0}=2\pi$, $p_{4}=p_{3}^{*}=q_{3}=q_{4}^{*}=2+2i$, $k_{4}=k_{3}^{*}=-2+2i$, $\eta _{3}^{0}=\eta _{4}^{0}=-2\pi$ in formula (2.21), (2.22) (see Fig. 5c and d). The second-order kink-shaped breather solution exhibits periodicity in both x and y directions, and its two kink-shaped breather waves propagate diagonally parallel to each other in the (x, y)-plane.

For $N>3$, the two groups of parameters are restricted to be conjugate, and the remaining parameters are all real numbers in formula (2.21), (2.22), then the hybrid solutions consisting of the soliton solutions and the breather solutions of Eq. (1.1) can be derived. While taking $N=3$, $p_{1}=-q_{1}=k_{1}=1$, $p_{3}=p_{2}^{*}=k_{3}=k_{2}^{*}=i$, $q_{3}=q_{2}^{*}=-1-i$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=0$, the hybrid solution of the first-order breather solution and the 1-kink soliton solution is given as follows

(3.4)

where

$$\begin{aligned}{} & {} \delta _{1}=\left( -\frac{1}{2}+\frac{3}{2}i\right) t+(1+i)x-(2+i)y+(1+i)z,\nonumber \\{} & {} \delta _{2}=\left( -\frac{1}{2}+\frac{3}{2}i\right) t+ix-(1+i)y+iz,\nonumber \\{} & {} \nu _{1}=x-y+z,\nonumber \\{} & {} \nu _{2}=-t+x-3y+z. \end{aligned}$$

(3.5)

The collision effect between two different types of solutions does not destroy the periodicity of the first-order breather solution of Eq. (1.1) (see Fig. 6a and b).

Fig. 6

The hybrid solutions of the first-order breather solution and the 1-kink soliton solution, the first-order kink-shaped breather solution and the 1-kink soliton solution of Eq. (1.1) in the (x, y)-plane at $t=0$. a, c The 3D plot. b, d The density plot with contours. (Color online)

Interestingly, when the parameters in formula (2.21), (2.22) are adjusted to the same values as above, the hybrid solution $u_{1b-1s}$ appears as the interaction solution of the first-order periodic line wave and the 1-kink soliton in the (x, z)-plane. In the dynamic behavior of this hybrid solution of Eq. (1.1), the periodic line wave, also known as the line breather, appears from a constant background wave within a finite time interval in the middle and generates the maximum amplitude at $t=0$, but it will eventually degenerate into the same constant background wave as time goes on (see Fig. 7). This first-order periodic line wave is a homoclinic orbital wave with uniformly varying wave heights in the (x, z)-plane. A key visual difference between it and the first-order breather solution of Eq. (1.1) is that the former has periodicity in space and localization in time, while the periodicity and locality of the latter are respectively reflected in the x and y directions on the (x, y)-plane. This also means that the first-order line breather solution only exists for a limited short period of time. That is, when $|t|\gg 0$, the first-order periodic line wave will be almost completely immersed in the 1-kink soliton wave and only the 1-kink soliton will appear in the diagram of this hybrid solution.

Fig. 7

The hybrid solution of the first-order periodic solution and the 1-kink soliton solution of Eq. (1.1) in the (x, z)-plane at different times with parameters: $N=3$, $p_{1}=-q_{1}=k_{1}=1$, $p_{3}=p_{2}^{*}=k_{3}=k_{2}^{*}=i$, $q_{3}=q_{2}^{*}=-1-i$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=0$. a $t=-15$. b $t=-5$. c $t=0$. d $t=10$. e $t=15$. (Color online)

Similarly, the mixed solution consisting of the first-order kink-shaped breather solution and the 1-kink soliton solution of Eq. (1.1) is also obtained under the parameters $N=3$, $p_{1}=-q_{1}=k_{1}=8$, $p_{3}=p_{2}^{*}=q_{3}=q_{2}^{*}=k_{2}=k_{3}^{*}=1+i$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=0$ (see Fig. 6c and d). These hybrid solutions are all definitely derived from the expansion of the 3-soliton solution of Eq. (1.1).

By taking $N=4$, $p_{2}=p_{1}^{*}=k_{1}=k_{2}^{*}=i$, $q_{2}=q_{1}^{*}=1+i$, $p_{3}=p_{4}=q_{3}=-q_{4}=-k_{3}=-k_{4}=-1$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=\eta _{4}^{0}=0$ in formula (2.21), (2.22), the hybrid solution of the first-order breather solution and the 2-kink soliton solution of Eq. (1.1) is shown in Fig. 8a, b and c.

Fig. 8

The hybrid solutions of the first-order breather solution and the 2-kink soliton solution, the first-order kink-shaped breather solution and the 2-kink soliton solution of Eq. (1.1) in the (x, y)-plane at different times. a, d $t=-10$. b, e $t=0$. c, f $t=10$. (Color online)

The dynamic behavior of the hybrid solution consisting of the first-order kink-shaped breather solution and the 2-kink soliton solution can also be intuitively analyzed under the parameters $N=4$, $p_{2}=p_{1}^{*}=\frac{1}{6}+i$, $q_{2}=q_{1}^{*}=\frac{5}{2}-i$, $k_{2}=k_{1}^{*}=-\frac{1}{6}-i$, $p_{3}=p_{4}=q_{3}=-q_{4}=-k_{3}=-k_{4}=-1$, $\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=\eta _{4}^{0}=0$ in Fig. 8d, e and f. These hybrid solutions are solved based on the 4-soliton solution of Eq. (1.1). One thing that can be obviously observed is that in the dynamic behavior of these hybrid solutions, the collision between the 2-kink soliton solutions and the breather solutions of Eq. (1.1) does not disrupt the periodicity in the x-direction and the localization in the y-direction of the breathers on the (x, y)-plane, and the breathers maintain their original oscillating waveforms for propagation.

4 The rational solutions of the (3+1)-dimensional gsww equation

In view of the earlier research [59,60,61,62,63], the rational solutions of nonlinear waves can be derived by taking the long wave limits of the soliton solutions based on the Hirota bilinear method. The lump solutions of the (3+1)-dimensional generalized shallow water wave equation, as some special rational function solutions localized in space, will be discussed emphatically in this section.

4.1 Case I

Consider the case of $N=2$.

The parameters in formula (2.21), (2.22) are stipulated as follows

$$\begin{aligned} N= & {} 2,\quad q_{1}=\lambda _{1}p_{1},\quad k_{1}=\gamma _{1}p_{1},\quad q_{2}=\lambda _{2}p_{2},\nonumber \\ k_{2}= & {} \gamma _{2}p_{2},\quad \eta _{1}^{0}=\eta _{2}^{0}=i\pi , \end{aligned}$$

(4.1)

and then the limits $p_{i}\rightarrow 0$ $(i=1,2)$ are performed. Hence, the f in formula (2.21) is rewritten as a polynomial function

$$\begin{aligned} f=\theta _{1}\theta _{2}+\alpha _{12}, \end{aligned}$$

(4.2)

where

$$\begin{aligned} \begin{aligned}&\theta _{i}=\frac{y\lambda _{i}^{2}+(z\gamma _{i}+x)\lambda _{i}-t\gamma _{i}}{\lambda _{i}},\quad (i=1,2),\\&\alpha _{12}=-\frac{6\lambda _{1}\lambda _{2}(\lambda _{1}+\lambda _{2})}{(\lambda _{1}-\lambda _{2}) (\gamma _{1}\lambda _{2}-\gamma _{2}\lambda _{1})}. \end{aligned} \end{aligned}$$

(4.3)

Letting $\lambda _{2}=\lambda _{1}^{*}=-i$, $\gamma _{1}=\gamma _{2}=1$, and combining the transformation (2.3), the first-order lump solution of Eq. (1.1) is solved as

$$\begin{aligned} u_{1-lump}=\frac{-4(x+z)}{(x+z)^{2}+(t+y)^{2}}. \end{aligned}$$

(4.4)

The dynamic behavior of the first-order lump solution $u_{1-lump}$ at different times is shown in Fig. 9.

Fig. 9

The first-order lump solution of Eq. (1.1) in the (x, y)-plane at different times. a $t=-30$. b $t=0$. c $t=30$. d The density plot with contours. (Color online)

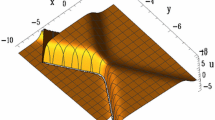
Due to the concentrated distribution of energy, it produces a local lump with two wave crests, one above the horizontal plane and the other below the horizontal plane, resulting in this lump presenting a wave peak and a wave trough. It can be intuitively found that in a finite space, $u_{1-lump}$, as a rational solution of Eq. (1.1), maintains a perfect profile around the control center of its waveform and moves on a constant background without diffusion or collapse. Nevertheless when $x\rightarrow \pm \infty$ or $y\rightarrow \pm \infty$, the first-order lump solution $u_{1-lump}$ degenerates to 0, which indicates that its asymptotic background is zero.

It is worth mentioning that when the parameters in formula (2.21), (2.22) is constrained to $p_{2}=p_{1}^{*}=q_{2}=q_{1}^{*}=k_{1}=k_{2}^{*}=1+i$, $\eta _{1}^{0}=\eta _{2}^{0}=0$, the first-order breather solution is transformed into the first-order line rogue wave (RW) solution of Eq. (1.1) as follows

$$\begin{aligned} u_{RW}=\frac{(2+2i)e^{\chi _{1}}+(2-2i)e^{\chi _{1}^{*}} -4e^{\chi _{2}}}{-1-(e^{\chi _{1}}+e^{\chi _{1}^{*}})+e^{\chi _{2}}}, \end{aligned}$$

(4.5)

where

$$\begin{aligned} \begin{aligned}&\chi _{1}=(1-i)t+(1+i)x+(1+i)y+(1-i)z,\\&\chi _{2}=2t+2x+2y+2z. \end{aligned} \end{aligned}$$

(4.6)

The first-order line rogue wave, as a finite form of the first-order line breather solution of Eq. (1.1), is generated in a constant background, rising or decaying with time evolution, and its maximum wave crest value appears at $t=0$ and $x+y=0$ (see Fig. 10). The first-order line rogue wave solution of Eq. (1.1) is localized in time and space, and the wave height at infinity of the (x, y)-plane tends to zero. Therefore, this line wave has the typical characteristic of a rogue wave solution: coming and going without a trace.

Fig. 10

The first-order line rogue wave solution of Eq. (1.1) in the (x, y)-plane at different times. a $t=-25$. b $t=10$. c $t=0$. d $t=10$. e $t=25$. (Color online)

4.2 Case II

Consider the case of N=4.

By constraining the parameters in formula (2.21), (2.22) as

$$\begin{aligned}{} & {} N=4,\quad q_{1}=\lambda _{1}p_{1},\quad k_{1}=\gamma _{1}p_{1},\nonumber \\{} & {} q_{2}=\lambda _{2}p_{2},\quad k_{2}=\gamma _{2}p_{2},\nonumber \\{} & {} q_{3}=\lambda _{3}p_{3},\quad k_{3}=\gamma _{3}p_{3},\quad q_{4}=\lambda _{4}p_{4},\quad k_{4}=\gamma _{4}p_{4},\nonumber \\{} & {} \eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=\eta _{4}^{0}=i\pi , \end{aligned}$$

(4.7)

and performing the limits $p_{i}\rightarrow 0$ $(i=1,2,3,4)$, the f in formula (2.21) is completely transformed from a exponential function to a purely rational function as follows

$$\begin{aligned}{} & {} f=\theta _{1}\theta _{2}\theta _{3}\theta _{4}+\alpha _{12}\theta _{3}\theta _{4}+\alpha _{13}\theta _{2}\theta _{4} +\alpha _{14}\theta _{2}\theta _{3}\nonumber \\{} & {} \quad +\alpha _{23}\theta _{1}\theta _{4} +\alpha _{24}\theta _{1}\theta _{3} +\alpha _{34}\theta _{1}\theta _{2}\nonumber \\{} & {} \quad +\alpha _{12}\alpha _{34}+\alpha _{13}\alpha _{24}+\alpha _{14}\alpha _{23},\nonumber \\ \end{aligned}$$

(4.8)

where

$$\begin{aligned}{} & {} \theta _{i}=\frac{y\lambda _{i}^{2}+(z\gamma _{i}+x)\lambda _{i}-t\gamma _{i}}{\lambda _{i}},\nonumber \\{} & {} \alpha _{ij}=-\frac{6\lambda _{i}\lambda _{j}(\lambda _{i}+\lambda _{j})}{(\lambda _{i}-\lambda _{j}) (\gamma _{i}\lambda _{j}-\gamma _{j}\lambda _{i})},\nonumber \\{} & {} (i<j,i,j=1,2,3,4). \end{aligned}$$

(4.9)

Taking $\lambda _{2}=\lambda _{1}^{*}=-i$, $\lambda _{4}=\lambda _{3}^{*}=-2i$, $\gamma _{1}=\gamma _{2}=\gamma _{3}=\gamma _{4}=1$, and combining the transformation (2.3), the second-order lump solution of Eq. (1.1) is presented as

$$\begin{aligned}{} & {} u_{2-lump}=(-288x^{3}-864x^{2}z-(36\rho _{1}+864z^{2})x\nonumber \\{} & {} \quad {-}288z^{3}{-}36\rho _{1}z{-}7872t {-}15360y)/(36x^{4}{+}144x^{3}z\nonumber \\{} & {} \quad +(9\rho _{1}+216z^{2})x^{2}+(144z^{3}+18\rho _{1}z+3936t\nonumber \\{} & {} \quad +7680y)x+36z^{4}+9\rho _{1}z^{2}+(3936t+7680y)z\nonumber \\{} & {} \quad + 9\rho _{2}t^{2}+360ty^{3}+144y^{4}+46720), \end{aligned}$$

(4.10)

where

$$\begin{aligned} \begin{aligned}&\rho _{1}=5t^{2}+16ty+20y^{2},\\&\rho _{2}=t^{2}+10ty+33y^{2}. \end{aligned} \end{aligned}$$

(4.11)

The intuitive diagram of the second-order lump solution $u_{2-lump}$ is also given (see Fig. 11).

Fig. 11

The second-order lump solution of Eq. (1.1) in the (x, y)-plane at $t=0$. a The 3D plot. b The density plot with contours. (Color online)

After the evolution of t, $u_{2-lump}$ only undergoes parallel shift in asymptotic motion, but its permanent lumps pattern does not change. Thus, the form of $u_{2-lump}$ at $t=0$ is discussed without losing generality. The wave crests and troughs of $u_{2-lump}$ have doubled compared to the first-order lump solution of Eq. (1.1). Additionally, when $x\rightarrow \pm \infty$ or $y\rightarrow \pm \infty$, the second-order lump solution $u_{2-lump}$ will also degenerate to zero and disappear from the field of view.

5 The semi-rational solutions of the (3+1)-dimensional gsww equation

The key to the construction of the semi-rational solutions of Eq. (1.1) lies in the application of taking the long wave limit of partial exponential functions similar to Sect. 4 and the special restrictions on the parameters in formula (2.21), (2.22).

When $N=3$, by setting the parameters in formula (2.21), (2.22) as

$$\begin{aligned} N= & {} 3,\quad q_{1}=\lambda _{1}p_{1},\quad k_{1}=\gamma _{1}p_{1},\quad q_{2}=\lambda _{2}p_{2},\nonumber \\ k_{2}= & {} \gamma _{2}p_{2},\quad \eta _{1}^{0}=\eta _{2}^{0}=i\pi , \end{aligned}$$

(5.1)

and taking the limits $p_{1}$, $p_{2}\rightarrow 0$, the f in formula (2.21) can be updated as a combination of polynomial and exponential functions

$$\begin{aligned} f= & {} (\theta _{1}\theta _{2}{+}\alpha _{13}\theta _{2}{+}\alpha _{23}\theta _{1} {+}\alpha _{13}\alpha _{23}{+}\alpha _{12})e^{\eta _{3}}\nonumber \\{} & {} {+}\theta _{1}\theta _{2}+\alpha _{12},\nonumber \\ \end{aligned}$$

(5.2)

where

$$\begin{aligned} \alpha _{i3}&{=}&{-}\frac{6(p_{3}^{2}q_{3}\lambda _{i}^{2}+p_{3}q_{3}^{2} \lambda _{i})}{-p_{3}k_{3}\lambda _{i}^{2}+(3p_{3}^{2}q_{3} {+}k_{3}{+}p_{3}\gamma _{i})q_{3}\lambda _{i}-q_{3}^{2}\gamma _{i}}, \nonumber \\{} & {} (i=1,2), \end{aligned}$$

(5.3)

and $\eta _{3}$ is the same as in (2.22), $\theta _{i}$ $(i=1,2)$, $\alpha _{12}$ are the same as in (4.3). In particular, if the parameters $\lambda _{2}=\lambda _{1}^{*}=-2i$ and the remaining parameters are all real numbers, such as $\gamma _{1}=\gamma _{2}=1$, $p_{3}=q_{3}=k_{3}=-2$, $\eta _{3}^{0}=0$, and then combining the transformation (2.3), the semi-rational solution of Eq. (1.1) consisting of the first-order lump solution and the 1-kink soliton solution can be obtained as

$$\begin{aligned}{} & {} u_{lump-1s}=((12688(x^{2}+z^{2})+(25376z+4208)x\nonumber \\{} & {} \quad +4208z+3172t^{2}+(25376y+22656)t\nonumber \\{} & {} \quad +50752y^{2}+90624y+37632)e^{\tau }\nonumber \\{} & {} \quad -12688(x+z))/((3172(x^{2}+z^{2})+(6344z\nonumber \\{} & {} \quad +4224)x+4224z+793t^{2}+(6344y+5664)t\nonumber \\{} & {} \quad +12688y^{2}+22656y+11520)e^{\tau }\nonumber \\{} & {} \quad +3172x^{2}+6344xz+3172z^{2}+793(t+4y)^{2}),\nonumber \\ \end{aligned}$$

(5.4)

where

$$\begin{aligned} \tau =10t-2x-2y-2z. \end{aligned}$$

(5.5)

The first-order lump will pass through the 1-kink soliton of Eq. (1.1) over time. Their collision is elastic, and the amplitude increases and the energy is concentrated at the intersection (see Fig. 12).

Fig. 12

The semi-rational solution consisting of the first-order lump solution and the 1-kink soliton solution of Eq. (1.1) in the (x, y)-plane at different times. a $t=-5$. b $t=0$. c $t=5$. (Color online)

By the same means, the dynamic behavior of the semi-rational solution of Eq. (1.1) consisting of the first-order line rogue wave and the 1-kink soliton is further presented. It can be seen intuitively that the collision between the first-order line rogue wave and the 1-kink soliton results in the maximum amplitude at $t=0$ and $x+z=0$ (see Fig. 13). In addition, because the line rogue wave is localized in space and time, it will degenerate into a constant plane wave when $|t|\gg 0$, that is, only the 1-kink soliton can be seen at this time, and the amplitude of the line rogue wave of Eq. (1.1) tends to zero at the infinity of the (x, z)-plane.

Fig. 13

The semi-rational solution consisting of the first-order line rogue wave solution and the 1-kink soliton solution of Eq. (1.1) in the (x, z)-plane at different times with parameters: $N=3$, $\lambda _{2}=\lambda _{1}^{*}=-2i$, $\gamma _{1}=\gamma _{2}=1$, $p_{3}=q_{3}=k_{3}=-2$, $\eta _{3}^{0}=0$. a $t=-10$. b $t=-2$. c $t=0$. d $t=5$. e $t=10$. f The sectional drawing. (Color online)

Fig. 14

The semi-rational solutions consisting of the first-order lump solution and the 2-kink soliton solution, the first-order lump solution and the first-order breather solution, the first-order lump solution and the first-order kink-shaped breather solution of Eq. (1.1) in the (x, y)-plane at $t=0$. a, b, c The 3D plot. d, e, f The density plot with contours. (Color online)

When $N=4$, the parameters are constrained in formula (2.21), (2.22) as follows

$$\begin{aligned} N= & {} 4,\quad q_{1}=\lambda _{1}p_{1},\quad k_{1}=\gamma _{1}p_{1},\quad q_{2}=\lambda _{2}p_{2}, \nonumber \\ k_{2}= & {} \gamma _{2}p_{2},\quad \eta _{1}^{0}=\eta _{2}^{0}=i\pi , \end{aligned}$$

(5.6)

and then the limits $p_{1}$, $p_{2}\rightarrow 0$ are performed. Thus, the f in formula (2.21) is rewritten as

$$\begin{aligned} f{} & {} =(\theta _{1}\theta _{2}+\alpha _{13}\theta _{2}+\alpha _{23}\theta _{1} +\alpha _{13}\alpha _{23}+\alpha _{12})e^{\eta _{3}} \nonumber \\{} & {} \quad +(\theta _{1}\theta _{2}+\alpha _{14}\theta _{2}+\alpha _{24}\theta _{1} +\alpha _{14}\alpha _{24}+\alpha _{12})e^{\eta _{4}} \nonumber \\{} & {} \quad +(\theta _{1}\theta _{2}+\alpha _{13}\theta _{2}+\alpha _{14}\theta _{2} +\alpha _{23}\theta _{1}+\alpha _{24}\theta _{1} \nonumber \\{} & {} \quad +\alpha _{13}\alpha _{23} +\alpha _{13}\alpha _{24}+\alpha _{14}\alpha _{23}+\alpha _{14}\alpha _{24} \nonumber \\{} & {} \quad +\alpha _{12})e^{\eta _{3}+\eta _{4}+A_{34}}+\theta _{1}\theta _{2}+\alpha _{12}, \nonumber \\ \end{aligned}$$

(5.7)

where

$$\begin{aligned}{} & {} \alpha _{i4}=\nonumber \\{} & {} -\frac{6(p_{4}^{2}q_{4}\lambda _{i}^{2}+p_{4}q_{4}^{2} \lambda _{i})}{-p_{4}k_{4}\lambda _{i}^{2}+(3p_{4}^{2}q_{4} +k_{4}+p_{4}\gamma _{i})q_{4}\lambda _{i}-q_{4}^{2}\gamma _{i}},\nonumber \\{} & {} (i=1,2), \end{aligned}$$

(5.8)

and $\alpha _{i3}$ $(i=1,2)$ are the same as in (5.3), $\eta _{3}$, $\eta _{4}$, $e^{A_{34}}$ are the same as in (2.22), $\theta _{i}$ $(i=1,2)$, $\alpha _{12}$ are the same as in (4.3). Here, if the parameters $\lambda _{2}=\lambda _{1}^{*}=-i$ and the remaining parameters are all real numbers as $\gamma _{1}=\gamma _{2}=p_{3}=-p_{4}=q_{3}=2q_{4}=k_{3}=-k_{4}=1$, $\eta _{3}^{0}=\eta _{4}^{0}=0$, and then combining the transformation (2.3), the semi-rational solution of Eq. (1.1) consisting of the first-order lump solution and the 2-kink soliton solution can be proposed (see Fig. 14a and d).

However, when the parameters $\lambda _{2}=\lambda _{1}^{*}=-i$, $\gamma _{1}=\gamma _{2}=1$, and the remaining two groups of parameters are restricted to be complex conjugate, two kinds of the semi-rational solutions of Eq. (1.1) can be constructed. If the remaining parameters $p_{4}=p_{3}^{*}=k_{4}=k_{3}^{*}=2i$, $q_{4}=q_{3}^{*}=2-2i$, $\eta _{3}^{0}=\eta _{4}^{0}=2\pi$, the semi-rational solution consisting of the first-order lump solution and the first-order breather solution can be derived (see Fig. 14b and e). When the remaining parameters $p_{4}=p_{3}^{*}=q_{3}=q_{4}^{*}=1+i$, $k_{4}=k_{3}^{*}=1-2i$, $\eta _{3}^{0}=\eta _{4}^{0}=2\pi$, the semi-rational solutions consisting of the first-order lump solution and the first-order kink-shaped breather solution is presented (see Fig. 14c and f). For these lump-soliton and lump-breather semi-rational solutions, when $\eta _{i}^{0}\rightarrow 0$ $(i=3,4)$, the lump will collide with the 2-kink soliton of Eq. (1.1) (see Fig. 14a and d). When $|\eta _{i}^{0}|\gg 0$ $(i=3,4)$, the lump will completely separate from the breathers of Eq. (1.1), and the periodicity and amplitude of the breather solutions remain stable (see Fig. 14b and e, c and f).

6 Conclusions

Some exact solutions of the (3+1)-dimensional generalized shallow water wave equation and the dynamic behaviors between them are systematically studied in this paper. The explicit N-soliton solution of Eq. (1.1) is derived based on the Hirota bilinear method and the standard perturbation method. The multi-soliton solutions of Eq. (1.1) exhibit kink characteristics due to $p_{i}\ne 0$ $(i=1,2,\cdots ,N)$, and the elastic collision behaviors of these solutions are discussed (see Figs. 1, 2 and 3). By adding constraints to the parameters of the original N-soliton solution, the higher-order breather solutions of Eq. (1.1) with periodic oscillation and localization on the (x, y)-plane are also solved (see Figs. 4 and 5). The hybrid solutions consisting of two types of breather solutions, the kink-shaped soliton solutions and the periodic solution (see Figs. 6, 7 and 8), and the line rogue wave solution (see Fig. 10) together enrich the dynamic behaviors between different types of solutions of Eq. (1.1). It can be seen that both the periodic solution and the line rogue wave solution grow and decay over time in a constant background.

In addition, the lump solutions (see Fig. 9, 11) are constructed by taking the long wave limit of the soliton solutions of Eq. (1.1). The difference between the line rogue wave solution and the lump solution is not only reflected in their shapes, but also in their localities, that is, the former has locality in both time and space, while the latter only has locality in space. When $N>2$, the dynamic behaviors of Eq. (1.1) are better described by the semi-rational solutions consisting of the lump, the kink-shaped solitons, the line rogue wave and the breathers (see Figs. 12, 13 and 14). Some special constraints of the parameters play an important role in affecting the diversity and the dynamic behaviors of these solutions. It$'$s worth noting that the higher-order kink-shaped soliton and breather solutions, the line rogue wave solution, the RW-soliton and lump-breather semi-rational solutions, and the hybrid solutions consisting of the breather solutions, the kink-shaped soliton solutions and the periodic solution of Eq. (1.1) have never been reported in the previous literature. The dynamic behaviors of these solutions constructed in this paper also reflect the amazing ordering caused by nonlinear actions. The research results of this paper are helpful to the research of other (3+1)-dimensional nonlinear evolution equations, enrich the theory of nonlinear dynamic systems, and help explain some nonlinear physical phenomena in nature.