1 Introduction

Nonlinear partial differential equations (PDEs) are encountered in various disciplines, such as physics, mechanics, chemistry, biology, mathematics and engineering [1–34]. The study of exact solutions of these equations plays a major role in the study of the propagation of waves. With the development of soliton theory, many useful methods for obtaining exact solutions of nonlinear PDEs have been presented. Some of them are: ansatz method [1–5], tanh method [6, 7], multiple exp-function method [8], transformed rational function method [9], first integral method [10], simplest equation method [11, 12], Kudryashov method [13, 14], modified simple equation method [15] and so on.

One of the most effective direct methods to develop the traveling wave solution of nonlinear PDEs is the trial equation method [16]. The most complete description of this method was given in [17]. This method has been successfully applied to obtain exact solutions for a variety of nonlinear PDEs [17–19].

In this paper, we consider the Davey–Stewartson (DS) equation [20–28]

$$\begin{aligned}&iq_{t}+\frac{1}{2}\delta ^{2}(q_{xx}+\delta ^{2}q_{yy}) +\lambda |q|^2q-\phi _{x}q=0,\nonumber \\&\quad \phi _{xx}-\delta ^{2}\phi _{yy}-2\lambda (|q|^{2})_{x}=0. \end{aligned}$$
(1)

The parameter \(\lambda \) characterizes the focusing or defocusing case. The Davey–Stewartson equation is the well-known example of integrable equations in two space dimensions, which arise as higher-dimensional generalizations of the nonlinear Schrödinger equation (NLSE) [20].

The nonlinear Schrödinger’s equation describes numerous nonlinear physical phenomena in the field of applied sciences such as solitons in nonlinear optical fibers, solitons in the mean-field theory of Bose-Einstein condensates, rogue waves in oceanography.

Davey and Stewartson first derived their model in the context of water waves, from purely physical considerations. In the context, q(x, y, t) is the amplitude of a surface wave packet, while \(\phi (x,y,t)\) represents the velocity potential of the mean flow interacting with the surface wave [20].

The Davey–Stewartson equations are also reduced to Hamiltonian ODEs [23], and so exact solutions could be furnished by the integrability [24] of finite-dimensional Hamiltonian systems.

The aim of this paper is to find exact solutions of the Davey–Stewartson equation by the trial equation method and the ansatz approach.

2 Trial equation method

In this section, we outline the main steps of the trial equation method [16–19] as following

Step 1. Suppose a nonlinear PDE

$$\begin{aligned} P\left( u,u_{t},u_{x},u_{tt},u_{xt},u_{xx},...\right) =0, \end{aligned}$$
(2)

can be converted to an ordinary differential equation (ODE)

$$\begin{aligned} Q\left( U,U',U'',U''',... \right) =0, \end{aligned}$$
(3)

using a traveling wave variable \(u(x,t)=U(\tau ),~~\tau =x-vt\), where \(U=U(\tau )\) is an unknown function, Q is a polynomial in the variable U and its derivatives. If all terms contain derivatives, then Eq. (3) is integrated where integration constants are considered zeros.

Step 2. Take the trial equation

$$\begin{aligned} {\left( {U'} \right) ^2} = F(U) = \sum \limits _{l = 0}^N {{a_l}{U^l},} \end{aligned}$$
(4)

where \(a_{l}, (l=0,1,...,N)\) are constants to be determined. Substituting Eq. (4) and other derivative terms such as \(U''\) or \(U'''\) in Eq. (3) yields a polynomial G(U) of U . According to the balance principle, we can determine the value of N . Setting the coefficients of G(U) to zero, we get a system of algebraic equations. Solving this system, we shall determine v and values of \({a_0},{a_1},...,{a_N}\).

Step 3. Rewrite Eq. (4) by the integral form

$$\begin{aligned} \pm (\tau - {\tau _0}) = \int {\frac{dU}{{\sqrt{F(U)} }}}. \end{aligned}$$
(5)

According to the complete discrimination system of the polynomial, we classify the roots of F(U) and solve the integral equation (5). Thus, we obtain the exact solutions to Eq. (2).

3 Soliton solutions

To find exact solutions of DS Eq. (1), first we make the transformation

$$\begin{aligned} q(x,y,t)=U(\tau )e^{i\left\{ \alpha x+\beta y+\gamma t \right\} },~~~~~\phi (x,y,t)=V(\tau ), \end{aligned}$$
(6)

where \(\tau =i\mu \left( x+y-ct\right) \), we have a relation \(c=\alpha \delta ^2+\beta \delta ^4\) and reduce system (1) to the following system of ordinary differential equations

$$\begin{aligned}&-\left( \gamma +\frac{1}{2}\alpha ^2\delta ^2+\frac{1}{2}\beta ^2\delta ^4\right) U -\frac{\mu ^{2}\delta ^{2}}{2}\left( \delta ^{2}+1\right) U''\nonumber \\&\quad +\,\,\lambda U^{3}-i\mu V'U=0, \end{aligned}$$
(7)
$$\begin{aligned}&\mu (\delta ^{2}-1)V''-2i\lambda \left( U^{2}\right) '=0. \end{aligned}$$
(8)

Integrating Eq. (8) once with respect to \(\tau \) and setting the constant of integration to be zero, we obtain

$$\begin{aligned} V'=\frac{2i\lambda }{\mu (\delta ^2-1)}U^{2}. \end{aligned}$$
(9)

Substituting (9) in Eq. (7), we have

$$\begin{aligned}&\frac{M}{2}\left( \delta ^2-1\right) U +\frac{\mu ^{2}\delta ^{2}}{2}\left( \delta ^{4}-1\right) U''\nonumber \\&-\lambda \left( \delta ^2+1\right) U^{3}=0, \end{aligned}$$
(10)

where

$$\begin{aligned} M=2\gamma +\alpha ^2\delta ^2+\beta ^2\delta ^4. \end{aligned}$$

3.1 Application of the trial solution method

Balancing \(U''\) with \(U^3\) in Eq. (10), then we get \(N=4\). Using the solution procedure of the trial equation method, we obtain the system of algebraic equations as follows:

\(U^{3}\) Coeff.:

$$\begin{aligned} \mu ^{2}\delta ^{2}(\delta ^{4}-1)a_{4}-\lambda (\delta ^2+1)=0, \end{aligned}$$
(11)

\(U^{2}\) Coeff.:

$$\begin{aligned} \frac{3}{4}\mu ^{2}\delta ^2(\delta ^4-1)a_{3}=0, \end{aligned}$$

\(U^{1}\) Coeff.:

$$\begin{aligned} \frac{M}{2}(\delta ^2-1)+\frac{\mu ^2}{2}\delta ^2(\delta ^4-1)a_{2}=0, \end{aligned}$$

\(U^{0}\) Coeff.:

$$\begin{aligned} \frac{1}{4}\mu ^{2}\delta ^2(\delta ^4-1)a_{1}=0. \end{aligned}$$

Solving the system (11) leads to the results

$$\begin{aligned}&a_{1}=0, ~~a_{2}=-\frac{M}{\mu ^{2}\delta ^{2}(\delta ^2+1)},~~a_{3}=0,\nonumber \\&\quad a_{4}=\frac{\lambda }{\mu ^{2}\delta ^{2}(\delta ^2-1)}, \end{aligned}$$
(12)

where \(a_{0}\) is an arbitrary constant.

Substituting these results in Eqs. (4) and (5), we get

$$\begin{aligned}&\pm (\tau -{\tau _0})\nonumber \\&\quad = \int {\frac{dU}{{\sqrt{a_{0}-\left( \frac{M}{\mu ^{2}\delta ^{2}(\delta ^2+1)}\right) U^2+\left( \frac{\lambda }{\mu ^{2}\delta ^{2}(\delta ^2-1)}\right) U^4} }}}.\nonumber \\ \end{aligned}$$
(13)

where \(a_{0}\) is an arbitrary real constant. Now, we discuss two cases as follows:

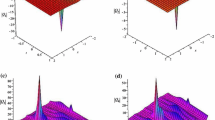
Case 1: If we set \(a_{0}=0\) in Eq. (13) and integrating with resect to U, we get the following exact soliton solutions of Eq. (1):

Solitary waves soliton solution

$$\begin{aligned}&q(x,y,t)=\pm \sqrt{\frac{M\left( \delta ^{2}-1\right) }{\lambda \left( \delta ^{2}+1\right) }} ~\text {sech}\nonumber \\&\quad \times \left( \mp \sqrt{\frac{M}{\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y \right. \right. \nonumber \\&\quad \left. \left. -\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) e^{i\left\{ \alpha x+\beta y+\gamma t \right\} },\nonumber \\&\phi (x,y,t)=\pm \sqrt{\frac{4M\delta ^2}{\delta ^{2}+1}}~\text {tanh}\nonumber \\&\quad \times \left( \mp \sqrt{\frac{M}{\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y-\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) \nonumber \\ \end{aligned}$$
(14)

Singular solitary waves soliton solution

$$\begin{aligned}&q(x,y,t)=\pm \sqrt{\frac{M\left( 1-\delta ^{2}\right) }{\lambda \left( \delta ^{2}+1\right) }} ~\text {csch}\nonumber \\&\quad \times \left( \mp \sqrt{\frac{M}{\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y \right. \right. \nonumber \\&\quad \left. \left. -\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) e^{i\left\{ \alpha x+\beta y+\gamma t \right\} },\nonumber \\&\phi (x,y,t)=\mp \sqrt{\frac{4M\delta ^2}{\delta ^{2}+1}}~\text {coth}\nonumber \\&\quad \times \left( \mp \sqrt{\frac{M}{\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y-\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) \nonumber \\ \end{aligned}$$
(15)

where

$$\begin{aligned} M=2\gamma +\alpha ^2\delta ^2+\beta ^2\delta ^4. \end{aligned}$$

These solitons are valid for

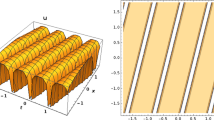
$$\begin{aligned} M\left( \delta ^{2}+1\right) >0. \end{aligned}$$

Case 2: If we set \(a_{0}=\frac{M^{2}}{4\mu ^{2}\delta ^{2}(\delta ^{4}-1)\lambda }\) in Eq. (13) and integrating with resect to U, we get the following dark soliton solution of Eq. (1)

$$\begin{aligned}&q(x,y,t)=\pm \sqrt{\frac{M\left( \delta ^{2}-1\right) }{2\lambda \left( \delta ^{2}+1\right) }} ~\text {tanh}\nonumber \\&\quad \times \left( \pm \sqrt{-\frac{M}{2\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y \right. \right. \nonumber \\&\,\,\,\left. \left. -\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) e^{i\left\{ \alpha x+\beta y+\gamma t \right\} },\nonumber \\&\phi (x,y,t)=\pm \sqrt{-\frac{2M\delta ^2}{\delta ^{2}+1}}\nonumber \\&\quad \times \left\{ \frac{1}{2}~\ln \left\{ \tanh \left( \pm \sqrt{-\frac{M}{2\delta ^{2}\left( \delta ^{2}+1\right) }}\right. \right. \right. \nonumber \\&\quad \times \left. \left. \left( x+y-\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) +1\right\} \nonumber \\&-\frac{1}{2}~\ln \left\{ \tanh \left( \pm \sqrt{-\frac{M}{2\delta ^{2}\left( \delta ^{2}+1\right) }}\right. \right. \nonumber \\&\quad \times \left. \left. \left( x+y-\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) -1\right\} \nonumber \\&-\tanh \left( \pm \sqrt{-\frac{M}{2\delta ^{2}\left( \delta ^{2}+1\right) }}\right. \nonumber \\&\quad \left. \left. \left( x+y-\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) \right\} \end{aligned}$$
(16)

where

$$\begin{aligned} M=2\gamma +\alpha ^2\delta ^2+\beta ^2\delta ^4. \end{aligned}$$

Equation (16) is valid when

$$\begin{aligned} M\left( \delta ^{2}+1\right) <0. \end{aligned}$$

3.2 Application of the ansatz approach

This subsection will utilize the ansatz approach to solving DS equation. Solitary waves soliton and singular solitary waves soliton solutions to Eq. (1) will be obtained by the aid of ansatz method.

3.2.1 Solitary waves soliton solution

For solitary waves soliton, the hypothesis is

$$\begin{aligned} U(\tau )=A~\text {sech}^{p}B\tau . \end{aligned}$$
(17)

The value of the unknown exponent p will fall out during the course of derivation of the soliton solutions. Also A and B are constants. Substituting Eq. (17) in Eq. (10) leads to

$$\begin{aligned}&+\frac{M}{2}\left( \delta ^2-1\right) A \text {sech}^{p}B\tau -\lambda \left( \delta ^2+1\right) A^3~\text {sech}^{3p}B\tau \nonumber \\&+\frac{\mu ^{2}\delta ^{2}}{2}\left( \delta ^{4}-1\right) \left\{ AB^2p^2 \text {sech}^{p}B\tau \right. \nonumber \\&\quad \left. -AB^2p(p+1)~\text {sech}^{p+2}B\tau \right\} =0. \end{aligned}$$
(18)

By virtue of balancing principle, on equating the exponents 3p and \(p+2\), from (18), gives

$$\begin{aligned} p=1. \end{aligned}$$
(19)

Next, from (18) setting the coefficients of the linearly independent functions to zero implies

\(\text {sech}^{1}\) coeff.:

$$\begin{aligned} \frac{M}{2}\left( \delta ^2-1\right) A+\frac{\mu ^{2}\delta ^{2}}{2} \left( \delta ^{4}-1\right) AB^2=0, \end{aligned}$$
(20)

\(\text {sech}^{3}\) coeff.:

$$\begin{aligned} -\lambda \left( \delta ^2+1\right) A^3-\mu ^{2}\delta ^{2}\left( \delta ^{4}-1\right) AB^2=0. \end{aligned}$$

Solving the above equations yields

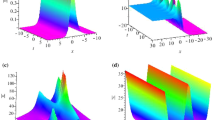
$$\begin{aligned} A=\pm \sqrt{\frac{M\left( \delta ^{2}-1\right) }{\lambda \left( \delta ^{2}+1\right) }}, ~~B=\pm \sqrt{-\frac{M}{\delta ^{2}\mu ^2\left( \delta ^{2}+1\right) }}. \end{aligned}$$
(21)

Using Eq. (9), we have the following solitary waves soliton solution of Eq. (1):

$$\begin{aligned}&q(x,y,t)=\pm \sqrt{\frac{M\left( \delta ^{2}-1\right) }{\lambda \left( \delta ^{2}+1\right) }} ~\text {sech}\nonumber \\&\quad \times \left( \mp \sqrt{\frac{M}{\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y \right. \right. \nonumber \\&\quad \left. \left. -\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) e^{i\left\{ \alpha x+\beta y+\gamma t \right\} },\nonumber \\&\phi (x,y,t)=\pm \sqrt{\frac{4M\delta ^2}{\delta ^{2}+1}}~\text {tanh}\nonumber \\&\quad \times \left( \mp \sqrt{\frac{M}{\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y-\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) \nonumber \\ \end{aligned}$$
(22)

where

$$\begin{aligned} M=2\gamma +\alpha ^2\delta ^2+\beta ^2\delta ^4. \end{aligned}$$

3.2.2 Singular solitary waves soliton solution

For singular solitary waves soliton, the hypothesis is

$$\begin{aligned} U(\tau )=A~\text {csch}^{p}\tau . \end{aligned}$$
(23)

The value of the unknown exponent p will fall out during the course of derivation of the soliton solutions. Also A and B are constants, while c is the speed of the soliton. Substituting Eq. (23) in Eq. (10) leads to

$$\begin{aligned}&+\frac{M}{2}\left( \delta ^2-1\right) A~\text {csch}^{p}B\tau -\lambda \left( \delta ^2+1\right) A^3~\text {csch}^{3p}B\tau \nonumber \\&+\frac{\mu ^{2}\delta ^{2}}{2}\left( \delta ^{4}-1\right) \left\{ AB^2p^2~\text {csch}^{p}\tau \right. \nonumber \\&\quad \left. +AB^2p(p+1)~\text {csch}^{p+2}\tau \right\} =0.\nonumber \\ \end{aligned}$$
(24)

From (24), the balancing principle yields

$$\begin{aligned} p=1. \end{aligned}$$
(25)

Next, from (24) setting the coefficients of the linearly independent functions to zero implies

$$\begin{aligned} A=\pm \sqrt{\frac{M\left( 1-\delta ^{2}\right) }{\lambda \left( \delta ^{2}+1\right) }}, ~~B=\pm \sqrt{-\frac{M}{\delta ^{2}\mu ^2\left( \delta ^{2}+1\right) }}. \end{aligned}$$
(26)

Using Eq. (9), we get the following singular solitary waves soliton solution of Eq. (1):

$$\begin{aligned}&q(x,y,t)=\pm \sqrt{\frac{M\left( 1-\delta ^{2}\right) }{\lambda \left( \delta ^{2}+1\right) }} ~\text {csch}\nonumber \\&\quad \times \left( \mp \sqrt{\frac{M}{\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y \right. \right. \nonumber \\&\quad \left. \left. -\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) e^{i\left\{ \alpha x+\beta y+\gamma t \right\} },\nonumber \\&\phi (x,y,t)=\mp \sqrt{\frac{4M\delta ^2}{\delta ^{2}+1}}~\text {coth}\nonumber \\&\quad \left( \mp \sqrt{\frac{M}{\delta ^{2}\left( \delta ^{2}+1\right) }} \left( x+y-\left\{ \alpha \delta ^2+\beta \delta ^4\right\} t\right) \right) \nonumber \\ \end{aligned}$$
(27)

where

$$\begin{aligned} M=2\gamma +\alpha ^2\delta ^2+\beta ^2\delta ^4. \end{aligned}$$

4 Conclusions

In this paper, the trial equation method and the ansatz approach have been applied to obtain the exact solutions of the DS equation. The results show that these methods are powerful tools for obtaining the exact solutions of complex nonlinear partial differential equations. It may be concluded that these methods can be easily extended to all kinds of complex nonlinear partial differential equations.