1 Introduction

A complex dynamical network (CDN) is a large set of nodes that represent dynamic systems and edges that denote connections among them [1]. In the past decades, CDN has been widely studied in various fields including metabolic networks, social relationship networks, the World Wide Web and communication networks [2–9]. Recently, synchronization in complex network of chaotic systems has attracted great attention. Synchronization of coupled chaotic systems is one of typical collective behaviors in complex networked systems due to its practical applications such as biological neural networks and communication security [10, 11]. Several types of synchronization have been investigated [12–23]. For example, by using the adaptive-impulsive control, the complete synchronization for a class of chaotic and hyperchaotic systems is investigated [14]. Tracking control and generalized projective synchronization for a class of hyperchaotic system is investigated by the adaptive control scheme [15]. Generalized outer synchronization between two complex dynamical networks is studied [18]. The hybrid function projective synchronization in CDN with time-varying delay is introduced [22].

However, most of network synchronization methods have focused on the study of chaotic systems in which the state variables are real numbers. In secure communication, synchronization of chaotic complex systems (CCSs) in which the main variables are complex numbers has been widely investigated because the doubled number of equations increases the content and security of the transmitted information [24, 25]. Since Fowler et al. [26] introduced the complex Lorenz equations, chaotic synchronization in CDN has been extensively studied; approaches include finite-time synchronization of CDN with CCS [27], and pinning synchronization of CDN with CCS [28]. Various patterns of synchronization for CCS have been investigated, including PS [29], modified PS (MPS) [30], hybrid PS [31], modified projective phase synchronization (MPPS) [32], complex PS (CPS) [33, 34] and complex FPS (CFPS) [35].

Among these methods, CFPS synchronizes the drive-response CCSs with a desired complex scaling function for both modulus and phase of their trajectories [35]. In practice, the relationship between the drive and response CCSs may evolve in different directions with a complex variable [33–35]. Hence, a complex function scaling factor should be considered in projective synchronization. In view of this, a complex function scaling matrix in networked CCS is essential to study, which we call complex modified function projective synchronization. (CMFPS). CMFPS can be represented as PS, MPS, FPS, MFPS, CPS, CMFPS and CFPS. Meanwhile, most of research on networked CCSs has not considered the influence of uncertainties and external disturbances. In many practical cases, the parameters of the dynamic system or system models cannot be exactly known; furthermore, external disturbances may influence the system. Together these complications make synchronization of CCSs a difficult task.

Among various methods, adaptive control has been widely used for uncertain CCSs [24, 36–42]. Liu et al. [42] considered CCSs with unknown parameters and external disturbances and introduced a compensator in the controller to remove the influence of external disturbances by using prior knowledge. However, in real engineering applications, prior information about uncertainties and disturbances may be difficult to use.

In one of effective ways of dealing with unknown factors, fuzzy observers can be used to compensate for unknown factors. Wu et al. [43] investigated \(\hbox {H}_{\infty }\) fuzzy adaptive control for nonlinear systems with uncertainties and disturbances. Jeong et al. [44] proposed the fuzzy disturbance observer for CDN with real variables to estimate model uncertainties and disturbances. Although fuzzy observer is an effective method for estimating unknown states and compensating for disturbing factors, most of previous studies considered dynamic systems with real variables.

In this paper, we propose adaptive complex modified function projective synchronization for a partially linearly coupled CCS of CDNs with model uncertainties and external disturbances. The main contribution is to develop adaptive controllers to achieve complex modified function projective synchronization of networked CCS by means of adaptive fuzzy logic. First, based on Lyapunov stability theory, we design an adaptive controller to achieve complex modified function projective synchronization for networked CCS. Then we propose an adaptive complex fuzzy observer (CFO) to estimate the model uncertainties and external disturbances with arbitrary small error about which there is no need for prior knowledge. Finally, we present simulation examples to demonstrate the effectiveness of the proposed method.

Notation: Throughout this paper, for any complex number \(y\), \(\bar{y}\) implies the complex conjugate of y. \(y^r\) and \(y^i\) denote the real and imaginary parts of \(y\), respectively. \(y^l\) can express \(y^r\) or \(y^i\), and \(\underline{Y}\) denotes the complex fuzzy number. \(\otimes \) is the Kronecker product, and bold face denotes matrices and vectors.

2 Problem statements

Consider a drive-response CDN consisting of \(1 + N\) identical, linearly diffusive, coupled partially linear chaotic complex systems as follows

$$\begin{aligned}&\dot{\mathbf{x}}=\mathbf M(z) x\nonumber \\&\dot{z}=f(\mathbf{x},z),\end{aligned}$$
(1)
$$\begin{aligned}&\dot{\mathbf{y}}_{i}=\mathbf{M}(z)\mathbf{y_{i}}+\mathbf{c_i} \displaystyle \sum _{k=1}^{N} a_{ ik}{\varvec{\Gamma }}\mathbf{y}_{\mathbf{k}}+\mathbf{u}_{\mathbf{i}} \end{aligned}$$
(2)

for \(i=1, 2,\ldots , N,\) where \(\mathbf{x}=[x_{1}, x_{2}, \ldots , x_{n}]^{T} \in C^{n}\) is the state variable vectors and \(z \in R\) is the state variable of the drive system. The complex matrix \(M(z)\) is dependent on the state variable \(z\). \(f:C^{n} \times R \rightarrow R\) is the known continuous nonlinear function. In the response system, \(\mathbf{y}_{i}=[y_{i1}, y_{i2}, \ldots , y_\mathrm{in}]^{T} \in C^{n}\) denotes the state vector of \(i\)-th node in the response systems and \(u_{i}\) is the controller. The positive constant \({c}_i\) is the coupling strength, \(\mathbf{A}=(a_{ ij})_{N \times N}\) is the coupling configuration matrix representing the topological structure of the network with zero row sum. \(a_{ ij}\) are defined as follows : If node \(i\) is connected to node \(j\) \((i \ne j)\), then \(a_{ ij}=a_{ ji} \ne 0\) ; otherwise, \(a_{ ij}=a_{ji}=0\). \(\mathbf{A}\) is a symmetric and irreducible matrix and \(\varvec{\Gamma } \in R^{n \times n}\) is the inner coupling matrix.

The system uncertainties, uncertain coupling strength and disturbance \(\Delta \mathbf{M}, \Delta {c}\) and \(\mathbf{d}_{i}\) are considered in the network. Then the response systems (2) can be represented as

$$\begin{aligned} \dot{\mathbf{y}}_{i}= & {} \mathbf{M}(z)\mathbf{y}_{i}+\Delta \mathbf{M}(z)\mathbf{y}_{i}+({c}_i+\Delta {c}_i) \displaystyle \sum _{k=1}^{N} a_{ ik}\varvec{\Gamma } \mathbf{y}_{k}\nonumber \\&+\, \mathbf{d}_{i}+\mathbf{u}_{i}. \end{aligned}$$
(3)

By combining three sources of uncertain terms, lumped uncertainty \(\varvec{\Omega }_{i}=[\omega _{1}, \omega _{2}, \ldots , \omega _\mathrm{in}]^{T}\) \(\in C^{n}\) is defined, and the dynamics of the response system can be rewritten as

$$\begin{aligned} \dot{\mathbf{y}}_{i}=\mathbf{M}(z)\mathbf{y}_{i}+{c}_i\displaystyle \sum _{k=1}^{N} a_{ ik} \varvec{\Gamma } \mathbf{y}_{k}+\varvec{\Omega }_{i}+\mathbf{u}_{i}. \end{aligned}$$
(4)

We define the complex-valued function projective synchronization error as follows

Definition 1

For the drive-response CDN, it is said that CMFPS can be achieved, if there exists a complex function with a full block scaling matrix \(\varvec{\Psi }(t)\) such that

$$\begin{aligned} \lim _{t \rightarrow \infty } \Vert \mathbf{e}_{i}\Vert =\lim _{t \rightarrow \infty } \Vert \mathbf{y}_{i}-\varvec{\Psi }(t)\mathbf{x}\Vert =0,\quad (i=1, \ldots , n),\nonumber \\ \end{aligned}$$
(5)

where, \(\mathbf{e}_{i}=[e_{1}, \ldots , e_{n}]^{T} \in C^{n}\) and \(\varvec{\Psi }(t)=(\psi _{ ij}(t))_{n \times n} \in C^{n \times n}\). The scaling factors \(\psi _{ ij}(t):C^n \rightarrow C\) \((i,j=1, \ldots , n)\) are complex-valued functions, which are bounded holomorphic functions and are nonzero for all t.

The dynamics of the synchronization error can be rewritten as

$$\begin{aligned} \dot{\mathbf{e}}_{i}= & {} \mathbf{M}(z)\mathbf{y}_{i}-\varvec{\Psi } \mathbf{M}(z)\mathbf{x}+{c}_i\ \displaystyle \sum _{k=1}^{N} a_{ ik}\varvec{\Gamma } \mathbf{e}_{k}\nonumber \\&+\,\varvec{\Omega }_{i} -\dot{\varvec{\Psi }}\mathbf{x}+\mathbf{u}_{i}. \end{aligned}$$
(6)

The objective is to design appropriate controllers in the response network to make CMFPS error approach the origin.

Remark 1

Most chaotic complex systems can be represented in form [1]; for example, the complex Lü system [25], the complex Chen system [45], and the complex Lorenz system [37]. Therefore, Eq. (2) can be used as a representative model for general networked CCS.

Remark 2

Previous research [27, 28, 33] ignored both model uncertainties and external disturbances. From the practical point of view, considering uncertain factors is more general and essential.

Remark 3

According to the concept of scaling factor, CMFPS can be represented as PS, MPS, FPS, MFPS, CPS, CMPS and CFPS where \(\varvec{\Psi }(t)=\alpha \) (\(\alpha \) is a constant), \(\varvec{\Psi }(t)=\hbox {diag}(\alpha )\), \(\varvec{\Psi }(t)=\alpha (t)\) (\(\alpha (t)\) is a real function), \(\varvec{\Psi }(t)=\hbox {diag}(\alpha (t))\), \(\varvec{\Psi }(t)=\beta \) (\(\beta \) is a complex number), \(\varvec{\Psi }(t)=\hbox {diag}(\beta )\) (\(\beta \) is a complex number) and \(\varvec{\Psi }(t)=\hbox {diag}(\beta (t))\) (\(\beta (t)\) is a complex function), respectively. Therefore, PS, MPS, FPS, MFPS, CPS, CMPS and CFPS are special cases of CMFPS; i.e., CMFPS covers previous work and is a more general expression.

To compensate lumped uncertainties \(\varvec{\Omega }_{i}\) in the response network, a fuzzy logic-based observer is proposed for describing complex variables. Before proceeding further, we introduce complex fuzzy number (CFN) [46, 47] and fuzzy logic systems (FLS) [44].

Definition 2

[47] If \(\underline{X}\) and \(\underline{Y}\) are real fuzzy numbers with the corresponding membership functions \(\mu (x|\underline{X})\) and \(\mu (y|\underline{Y})\) , then

$$\begin{aligned} \underline{Z}=\underline{X}+i \underline{Y}. \end{aligned}$$

is CFN with membership function

$$\begin{aligned} \mu (z|\underline{Z})=\hbox {min}(\mu (x|\underline{X}),\mu (y|\underline{Y})), \end{aligned}$$
(7)

where \(z=x+iy\). \(\mu (z|\underline{Z})\) is a mapping from the complex numbers into \([0, 1]\).

To define fuzzy complex membership function \(\mu (z|\underline{Z})\), the complex number \(\underline{Z}\) is decomposed into its real part \(\underline{X}\) and imaginary part \(\underline{Y}\) to obtain corresponding real membership functions \(\mu (x|\underline{X})\) and \(\mu (y|\underline{Y})\) . Then, based on the CFN theory, we can expand traditional fuzzy observer to a CFO.

Consider an n-input, single-output FLS with a fuzzy rule base that consists of \(M\) fuzzy if-then rules :

\(R_{l}\) : If \(v_{1}\) is \(A_{l1}\) and \(\cdots \) and \(v_{n}\) is \(A_\mathrm{in}\)

then \(w\) is \(w_{l}\),

where \(\mathbf{v}=[\ v_{1}, \ldots , v_{n} ]\ \in \underline{V} \subset C^{n}\) is the input of the FLS and \(w \in \underline{W} \subset C\) is the output of the FLS. \(A_{l1}, \ldots , A_{ln}\) are fuzzy set, and \(w_{l}\) is a fuzzy singleton number for \(l=1, \ldots , M.\)

By using a product inference engine, a singleton fuzzifier and a center-average defuzzifier, the output of the fuzzy system can be described as

$$\begin{aligned} \mathbf{w}(\mathbf{v})=\frac{\sum _{l=1}^{M}w_{l}\left( \prod _{j=1}^{n}\mu _{lj}(v_{j}|\underline{V})\right) }{\sum _{l=1}^{M}\left( \prod _{j=1}^{n}\mu _{lj}(v_{j}|\underline{V})\right) }={\varvec{\theta }}^{T}{\varvec{\xi }}(\mathbf{v}), \end{aligned}$$
(8)

where \(\mu _{lj}(v_{j}|\underline{V})\) is the membership function value of the complex fuzzy variable \(v_{j}\) , \(M\) is the number of fuzzy rules, and \({\varvec{\theta }}=[\ w_{1}, \ldots , w_{M}]\ ^{T}\) is an adjustable complex parameter vector composed of consequent parameters. Fuzzy basis function vector is defined as follows:

$$\begin{aligned} {\varvec{\xi }}({\varvec{v}})=\frac{\prod _{j=1}^{n}\mu _{lj}(v_{j}|\underline{V})}{\sum _{l=1}^{M}(\prod _{j=1}^{n}\mu _{lj}(v_{j}|\underline{V}))},\quad (l=1,\ldots ,M) \end{aligned}$$
(9)

Based on FLS, an adaptive CFO is developed to monitor lumped uncertainties \(\varvec{\Omega }_{i}\) To construct the CFO, the following dynamic observer is proposed,

$$\begin{aligned} \dot{\hat{\mathbf{y}}}_{i}=\mathbf{M}(z)\mathbf{y}_{i}+{c}_i\displaystyle \sum _{k=1}^{N}a_{ ik}\varvec{\Gamma } \mathbf{y}_{k}+\hat{\varvec{\Omega }}_{i}+\mathbf{u}_{i} +\mathbf{P}_{i}(\mathbf{y}_{i}-\hat{\mathbf{y}}_{i}), \end{aligned}$$
(10)

where \(\hat{\mathbf{y}}_{i}=[\ \hat{y}_{1}, \ldots , \hat{y}_{n} ]\ ^{T} \in C^{n}\), \(\mathbf{P}_{i}\) is \(n \times n\) a positive diagonal matrix and \(\hat{\varvec{\Omega }}_{i}=[\ \hat{\omega }_{i1}, \ldots , \hat{\omega }_{i1}]\ ^{T}\), \(\hat{\omega }_{ ij}=\theta _{ ij}^{T}\xi _{ ij}\) with \(i=1, \ldots , N\) and \(j=1, \ldots , n\). \(N\) is the number of response network. \(\theta _{ ij} \in C^{M}\) is the complex fuzzy parameter vector, \(\xi _{ ij}\) is the fuzzy basis function vector.

We define the observation error as follows

$$\begin{aligned} {\varvec{\phi }}_{i}=\mathbf{y}_{i}-\hat{\mathbf{y}}_{i}. \end{aligned}$$
(11)

From Eqs. (4) and (11), we obtain the following dynamics of the observation error

$$\begin{aligned} \dot{{\varvec{\phi }}}_{i}=-\mathbf{P}_{i}(\mathbf{y}_{i}-\hat{\mathbf{y}}_{i})+\varvec{\Omega }_{i}-\hat{\varvec{\Omega }}_{i}. \end{aligned}$$
(12)

Then, disturbance reconstruction error \(\epsilon _i\), minimum approximation error \(l_i\) and optimal parameter error \(m_i\) are defined as

$$\begin{aligned} {\varvec{\epsilon }}_{i}= & {} \varvec{\Omega }_{i}-\hat{\varvec{\Omega }}_{i}, \end{aligned}$$
(13)
$$\begin{aligned} \mathbf{l}_{i}= & {} \varvec{\Omega }_{i}-\hat{\varvec{\Omega }}_{i}^{*}, \end{aligned}$$
(14)
$$\begin{aligned} \mathbf{m}_{i}= & {} \hat{\varvec{\Omega }}_{i}^{*}-\hat{\varvec{\Omega }}_{i} \nonumber \\= & {} \left[ \ \tilde{\theta }_{i1}^{T}\xi _{i1}(\mathbf{y}), \ldots , \tilde{\theta }_\mathrm{in}^{T}\xi _\mathrm{in}(\mathbf{y})\right] \ , \end{aligned}$$
(15)

where

$$\begin{aligned}&\hat{\varvec{\Omega }}_{i}^{*}=\hat{\varvec{\Omega }}_{i}(\mathbf{y}_{i}|{\varvec{\theta }}^{*})=[\ \hat{\omega }_{i1}^{*}, \ldots , \hat{\omega }_\mathrm{in}^{*}]\ ^{T}, \end{aligned}$$
(16)
$$\begin{aligned}&\hat{\omega }_{ ij}^{*}=\hat{\omega }_{i}(\mathbf{y}_{i}|{\varvec{\theta }}^{*})=\theta _{ ij}^{*T}\xi _{ ij}(\mathbf{y}), \end{aligned}$$
(17)
$$\begin{aligned}&{\varvec{\theta }}_{ ij}^{*}=arg \hbox {min} \begin{bmatrix} \sup \limits _{x\rightarrow 0}|\omega _{ ij}(\mathbf{y}_{i}|\theta _{ ij}-\omega _{ ij}(\mathbf{y}_{i})|. \end{bmatrix} \end{aligned}$$
(18)

By the universal approximation theorem [44], a CFO \(\hat{\omega }_{ij}\) exists such that

$$\begin{aligned} |\omega _{ij}-\hat{\omega }_{ij}|< \varvec{\hat{{\epsilon }}}_{ij}, \end{aligned}$$
(19)

where \(\varvec{\hat{{\epsilon }}}_{ij}\) is an arbitrary fuzzy approximation error bound.

Before proceeding with the main result, the following lemma and assumption are required.

Lemma 1

[33] Let \(m \times m\) complex matrix \(\mathbf {H}\) be Hermitian, then

  1. (a)

    \(\mathbf{x}^T \mathbf{H} \bar{\mathbf{x}}\) is real for all \(\mathbf{x} \in C^m\);

  2. (b)

    All the eigenvalues of \(\mathbf {H}\) are real.

Assumption 1

[33] Suppose that there exists a constant \(\lambda \) such that

$$\begin{aligned} \lambda _\mathrm{max}(\mathbf{M}^{s}) \le \varvec{\lambda } \end{aligned}$$

where \(\mathbf{M}^{s}=\mathbf{M}^{T}+\bar{\mathbf{M}}\) and \(\lambda _\mathrm{max}(\mathbf{M}^{s})\) is the largest eigenvalue of Hermitian matrix \(\mathbf{M}^{s}\).

3 Main results

In this section, firstly the CMFPS of general networked CCS without uncertainties and external disturbances by the feedback control method is discussed. To achieve CMFPS, an appropriate adaptive controller is designed in the following lemma.

Lemma 2

For given complex scaling matrix \(\varvec{\Psi }(t)\), the CMFPS between the drive-response CDN (1) and (2) can be achieved if the controller and adaptation law are designed as follows

$$\begin{aligned}&\mathbf{u}_i=\mathbf{u}_{\mathbf{a}_{i}}+\mathbf{u}_{\mathbf{b}_{\mathbf{i}}}, \end{aligned}$$
(20)
$$\begin{aligned}&\mathbf{u}_{\mathbf{a}_{i}}=\varvec{\Psi } \mathbf{M}\mathbf{x}-\mathbf{M} \varvec{\Psi } \mathbf{x}+\dot{\varvec{\Psi }}\mathbf{x}, \end{aligned}$$
(21)
$$\begin{aligned}&\mathbf{u}_{\mathbf{b}_{i}}=-\hat{{\eta }}_i \mathbf{e}_i, \end{aligned}$$
(22)
$$\begin{aligned}&\dot{\hat{{\eta }}}_i={\alpha }_i \mathbf{e}_i^T \mathbf{Q} \bar{\mathbf{e}}_i. \end{aligned}$$
(23)

and \(\mathbf{Q}\) and \(\varvec{\Lambda }\) exist that satisfy

$$\begin{aligned} \varvec{\Lambda } + \mathbf{c}(\mathbf{A} \otimes \varvec{\Gamma } ^T\mathbf{Q})^s-2 \mathbf{H} \otimes \mathbf{Q}<0, \end{aligned}$$
(24)

where \({\alpha }_i\) is a positive constant and \(\mathbf{Q}\) is a positive diagonal matrix. Then CMFPS of the drive-response complex dynamical networks is achieved.

Proof

From the definition of CMFPS, the derivative of synchronization error is defined as

$$\begin{aligned} \dot{\mathbf{e}}_i=\mathbf{M}(z)\mathbf{y}_i+{c}_i\sum _{k=1}^Na_{ ik}\varvec{\Gamma } \mathbf{e}_k-\varvec{\Psi } \mathbf{M}(z)\mathbf{x}-\dot{\varvec{\Psi }}\mathbf{x}+\mathbf{u}_i. \end{aligned}$$
(25)

Substituting Eqs. (20–21) into the system (25) yields the error system

$$\begin{aligned} \dot{\mathbf{e}}_i=\mathbf{M}(z)\mathbf{e}_i+{c}_i\sum _{k=1}^Na_{ ik}\varvec{\Gamma } \mathbf{e}_k+\mathbf{u}_{\mathbf{b}_i}. \end{aligned}$$
(26)

Construct the following Lyapunov function candidate:

$$\begin{aligned} V_1=\sum _{i=1}^N \mathbf{e}_i^T\mathbf{Q}\bar{\mathbf{e}}_i + \sum _{i=1}^N \frac{1}{2{\alpha }_i}(\hat{{\eta }}_i-{\eta }_i)^2, \end{aligned}$$
(27)

The time derivative of \(V_1\) is

(28)

According to Assumption 1, the following inequality can be obtained:

$$\begin{aligned} \dot{V}_1\le & {} \sum _{i=1}^N \varvec{\lambda }_i \mathbf{e}_i^T \bar{\mathbf{e}}_i^T + {c}_i \sum _{i=1}^N\sum _{k=1}^n a_{ ik} \left( \mathbf{e}_k^T \varvec{\Gamma } ^T \mathbf{Q}\bar{\mathbf{e}}_i + \mathbf{e}_i^T\mathbf{Q} \varvec{\Gamma } \bar{\mathbf{e}}_k\right) \nonumber \\&+\,\sum _{i=1}^N +\mathbf{u}_{\mathbf{b}_i}^T\mathbf{Q}\bar{\mathbf{e}}_i+\mathbf{e}_i^T\mathbf{Q}\bar{\mathbf{u}}_{\mathbf{b}i}+\sum _{i=1}^N\frac{1}{{\alpha }_i}(\hat{{\eta }}_i-{\eta }_i)\dot{\hat{{\eta }}}_i. \nonumber \\= & {} \sum _{i=1}^N \varvec{\lambda }_i \mathbf{e}_i^T \bar{\mathbf{e}}_i^T + {c}_i \sum _{i=1}^N\sum _{k=1}^n a_{ ik}\left( \mathbf{e}_k^T \varvec{\Gamma } ^T \mathbf{Q}\bar{\mathbf{e}}_i +\mathbf{e}_i^T\mathbf{Q} \varvec{\Gamma } \bar{\mathbf{e}}_k\right) \nonumber \\&+\,\sum _{i=1}^N-2{\eta }_i\mathbf{e}_i^T\mathbf{Q}\bar{\mathbf{e}}_i \nonumber \\= & {} \mathbf{e}^T(\varvec{\Lambda }+\mathbf{c}\left( \mathbf{A} \otimes \varvec{\Gamma }^T\mathbf{Q}\right) ^s-2\mathbf{H} \otimes \mathbf{Q})\bar{e}, \end{aligned}$$
(29)

where \(\varvec{\Lambda }_1=\hbox {diag}(\varvec{\lambda }_1, \ldots , \varvec{\lambda }_n)\), \(\mathbf{c}=\hbox {diag}(c_1, \ldots , c_n)\) and \(\mathbf{H}=\hbox {diag}({\eta }_1, \ldots , {\eta }_n)\). One can choose \({\eta }_i\) to satisfy the condition \(\varvec{\Lambda }_1+\mathbf{c}(\mathbf{A}\otimes \varvec{\Gamma }^T\mathbf{Q})^s-2\mathbf{H}\otimes \mathbf{Q}\). Then, Eq. (29) can satisfy the Lyapunov stability condition, \(\dot{V}_1 \le 0\) for all errors. According to Lyapunov stability theory, the error dynamics (25) can be asymptotically stable, i.e., \(\lim _{t \rightarrow \infty } \Vert \mathbf{e}_i(t)\Vert =0\). This means that the control law (20–22) and the adaptation laws (23) can achieve CMFPS of chaotic complex response network (2). This completes the proof.

Secondly, the networked CCS with uncertainties and external disturbances is considered. The network is still subject to disturbance observation errors that cause serious degradation of system performance. The uncertainties are cancelled out by applying the adaptive CFO in the controller. The fuzzy approximation error is reduced, and the response networks are synchronized to drive CCS in the sense of CMFPS with arbitrarily small error bound. \(\square \)

Theorem 1

Consider the drive-response CDN (1), (3), the error dynamics (6) and the observer system (10). For given complex scaling function \(\varvec{\Psi }(t)\), if the robust adaptive controllers and adaptation laws for complex fuzzy observer \(\hat{\varvec{\Omega }}\) are given by

$$\begin{aligned}&\mathbf{u}_i = \mathbf{u}_{\mathbf{a}_i}+\mathbf{u}_{\mathbf{b}_i}, \end{aligned}$$
(30)
$$\begin{aligned}&\mathbf{u}_{\mathbf{a}_i}=\varvec{\Psi } \mathbf{Mx}-\mathbf{M} \varvec{\Psi } \mathbf{x}+\dot{\varvec{\Psi }}\mathbf{x}-\hat{\varvec{\Omega }}_i, \end{aligned}$$
(31)
$$\begin{aligned}&\mathbf{u}_{\mathbf{b}_i}=-\hat{{\eta }}_i \mathbf{e}_i - \hat{{\nu }}_i \mathrm{sign}(\mathbf{e}_i),\end{aligned}$$
(32)
$$\begin{aligned}&\dot{\hat{{\eta }}}_i={\alpha }_i\mathbf{e}_i^TQ\bar{\mathbf{e}}_i, \end{aligned}$$
(33)
$$\begin{aligned}&\dot{\hat{{\nu }}}_i={\beta }_i \mathbf{e}_i^TQ \mathrm{sgn}(\bar{\mathbf{e}}_i), \end{aligned}$$
(34)
$$\begin{aligned}&\dot{\theta }_{ ij}=\gamma _{i1}\bar{\xi }_{ ij}(\mathbf{y})({\varvec{\phi }}_{ ij}+\gamma _{i2}{\varvec{\epsilon }}_{ ij}), \end{aligned}$$
(35)

and \(\mathbf{Q}>0, \varvec{\Lambda }, \hat{{\varvec{\epsilon }}}_i\) and \({\nu }_i\) exist that satisfy

$$\begin{aligned}&\varvec{\Lambda } + \mathbf{c}(\mathbf{A} \otimes \varvec{\Gamma } ^T\mathbf{Q})^s-2 \mathbf{H}\otimes \mathbf{Q}<0, \end{aligned}$$
(36)
$$\begin{aligned}&\hat{{\epsilon }}_i-{\nu }_i<0, \end{aligned}$$
(37)

where \({\alpha }_i\), \({\beta }_i\), \(\gamma _{i1}\) and \(\gamma _{i2}>0\) are positive constants. Then the drive-response complex dynamic networks are synchronized in the sense of CMFPS with arbitrarily small error bound which guarantees the following robust performance.

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^{N}\int _{0}^{T} \! {\varvec{\phi }}_i^T \mathbf{P}_i\bar{{\varvec{\phi }}}_i \, \mathrm {d}t + \sum _{i=1}^{N}\int _{0}^{T} \! \mathbf{m}_i^T \varvec{\Gamma }_{i2}\bar{\mathbf{m}}_i \, \mathrm {d}t \\&\quad \le \sum _{i=1}^{N}\int _{0}^{T} \! \mathbf{e}_i(0)^T \mathbf{Q} \bar{\mathbf{e}}_i(0) \mathrm {d}t +\sum _{i=1}^{N}\int _{0}^{T}\! {\varvec{\phi }}_i(0)^T\bar{{\varvec{\phi }}}_i(0) \, \mathrm {d}t\\&\quad +\,\sum _{i=1}^{N}\int _{0}^{T}\! \frac{1}{2{\alpha }_i}(\hat{{\eta }}_i(0)-{\eta }_i(0))^2 \mathrm {d}t \\&\quad +\,\sum _{i=1}^{N}\int _{0}^{T}\! \frac{1}{2{\alpha }_i}(\hat{{\nu }}_i(0)-{\nu }_i(0))^2 \mathrm {d}t\\&\quad +\, \sum _{i=1}^{N}\int _{0}^{T}\! \frac{1}{\gamma _{i1}} \sum _{i=1}^{n} \tilde{\theta }_{ ij}^T(0)\tilde{\theta }_{ ij}(0)\mathrm{d}t \\&\quad +\, \sum _{i=1}^{N}\int _{0}^{T} \! \mathbf{l}_i^T(\varvec{\Gamma }_{i2}+\mathbf{P}_i^{-1})\bar{\mathbf{l}}_i \, \mathrm {d}t, \end{aligned} \end{aligned}$$
(38)

where \(\varvec{\Gamma }_{i2}=\mathrm{diag}(\gamma _{i2})>0\).

Proof

From Eqs. (13–15), the observation error (10) can be rewritten as

$$\begin{aligned} \dot{{\varvec{\phi }}}_{i}= & {} -\mathbf{P}_{i}(\mathbf{y}_i-\hat{\mathbf{y}}_i)+{\varvec{\epsilon }}_{i} \nonumber \\= & {} -\mathbf{P}_{i}(\mathbf{y}_i-\hat{\mathbf{y}}_i)+\mathbf{m}_i+\mathbf{l}_i. \end{aligned}$$
(39)

The definition of CMFPS, the dynamics of the synchronization error can be obtained as

$$\begin{aligned} \dot{\mathbf{e}}_i= & {} \mathbf{M}(z)y_i+{c}_i\sum _{k=1}^Na_{ ik}\varvec{\Gamma } \mathbf{e}_k-\varvec{\Psi } \mathbf{M}(z)\mathbf{x}\nonumber \\&+\,\varvec{\Omega }_i-\dot{\varvec{\Psi }}\mathbf{x}+\mathbf{u}_i. \end{aligned}$$
(40)

Substituting Eqs. (30–31) into the system (40) yields the error system

$$\begin{aligned} \dot{\mathbf{e}}_i=\mathbf{M}(z)\mathbf{e}_i+{c}_i\sum _{k=1}^Na_{ ik}\varvec{\Gamma } \mathbf{e}_k+{\varvec{\epsilon }}_i+\mathbf{u}_{\mathbf{b}_i}. \end{aligned}$$
(41)

Let us consider the following Lyapunov function candidate:

$$\begin{aligned}&V=V_1+V_2+V_3 \end{aligned}$$
(42)
$$\begin{aligned}&V_1=\sum _{i=1}^N \mathbf{e}_i^T\mathbf{Q}\bar{\mathbf{e}}_i+\sum _{i=1}^N \frac{1}{2{\alpha }_i}(\hat{{\eta }}_i-{\eta }_i)^2, \end{aligned}$$
(43)
$$\begin{aligned}&V_2=\sum _{i=1}^N \frac{1}{2{\beta }_i}(\hat{{\nu }}_i-{\nu }_i)^2, \end{aligned}$$
(44)
$$\begin{aligned}&V_3=\sum _{i=1}^N{\varvec{\phi }}_i^T\bar{{\varvec{\phi }}}_i+\sum _{i=1}^N\frac{1}{\gamma _{i1}}\sum _{j=1}^n \tilde{\theta }_{ ij}^T\bar{\tilde{\theta }}_{ ij}, \end{aligned}$$
(45)

where \({\eta }_i\) and \({\nu }_i\) are positive constants.

The time derivative of \(V\) along the trajectory of error dynamics systems is

$$\begin{aligned} \dot{V}= & {} \sum _{i=1}^N \left( \dot{\mathbf{e}}_i^T \mathbf{Q} \bar{\mathbf{e}}_i+\mathbf{e}_i^T \mathbf{Q} \dot{\bar{\mathbf{e}}}_i\right) +\sum _{i=1}^N\left( \dot{{\varvec{\phi }}}_i^T\bar{{\varvec{\phi }}}_i+{\varvec{\phi }}_i^T\dot{\bar{{\varvec{\phi }}}}_i\right) \nonumber \\&+\,\sum _{i=1}^N \frac{1}{\gamma _{i1}} \sum _{j=1}^n \left( \dot{\tilde{\theta }}_{ ij}^T\bar{\tilde{\theta }}_{ ij} +\tilde{\theta }_{ ij}^T\dot{\bar{\tilde{\theta }}}_{ ij}\right) \nonumber \\&+\,\sum _{i=1}^N\frac{1}{{\alpha }_i}(\hat{{\eta }}_i-{\eta }_i)\dot{\hat{{\eta }}}_i +\sum _{i=1}^N\frac{1}{{\beta }_i}(\hat{{\nu }}_i-{\nu }_i)\dot{\hat{{\nu }}}_i \nonumber \\= & {} \sum _{i=1}^N\left\{ \left( \mathbf{M}\mathbf{e}_i+{c}_i\sum _{k=1}^n a_{ ik} \varvec{\Gamma } \mathbf{e}_k+\mathbf{u}_{\mathbf{b}_i}+{\varvec{\epsilon }}_i\right) ^T \mathbf{Q}\bar{\mathbf{e}}_i\right. \nonumber \\&+\,\left. \mathbf{e}_i^T\mathbf{Q}\left( \overline{\mathbf{Me}}_i+{c}_i\sum _{k=1}^n a_{ ik}\Gamma \bar{\mathbf{e}}_k+\bar{\mathbf{u}}_{\mathbf{b}i}+\bar{{\varvec{\epsilon }}}_i\right) \right\} \nonumber \\&+\,\sum _{i=1}^N -2 {\varvec{\phi }}_i^T\mathbf{P}_i\bar{{\varvec{\phi }}}_i\nonumber \\&+\, \sum _{i=1}^N \left( \mathbf{l}_i^T\bar{{\varvec{\phi }}}_i+\mathbf{m}_i^T\bar{{\varvec{\phi }}}_i+{\varvec{\phi }}_i^T\bar{\mathbf{l}}_i+{\varvec{\phi }}_i^T\bar{\mathbf{m}}_i\right) \nonumber \\&+\,\sum _{i=1}^N \frac{1}{\gamma _{i1}} \sum _{j=1}^n \left( \dot{\tilde{\theta }}_{ ij}^T\bar{\tilde{\theta }}_{ ij}+\tilde{\theta }_{ ij}^T\dot{\bar{\tilde{\theta }}}_{ ij}\right) \nonumber \\&+\,\sum _{i=1}^N\frac{1}{{\alpha }_i}(\hat{{\eta }}_i-{\eta }_i)\dot{\hat{{\eta }}}_i+\sum _{i=1}^N\frac{1}{{\beta }_i}(\hat{{\nu }}_i-{\nu }_i)\dot{\hat{{\nu }}}_i \end{aligned}$$
(46)

Applying Eq. (33)–(46) yields

$$\begin{aligned} \dot{V}= & {} \sum _{i=1}^N \left\{ \mathbf{e}_i^T\mathbf{M}^s\bar{\mathbf{e}}_i+{c}_i \sum _{k=1}^n a_{ ik}\left( \mathbf{e}_k^T \Gamma ^T \mathbf{Q} \bar{\mathbf{e}}_i + \mathbf{e}_i^T\mathbf{Q}\varvec{\Gamma } \bar{\mathbf{e}}_k\right) \right. \nonumber \\&+\,\left. \left( \mathbf{u}_{\mathbf{b}_i}^T\mathbf{Q}\bar{\mathbf{e}}_i+\mathbf{e}_i^T\mathbf{Q}\bar{\mathbf{u}}_i\right) +\left( {\varvec{\epsilon }}_i^T\mathbf{Q}\bar{\mathbf{e}}_i+\mathbf{e}_i^T\mathbf{Q}\bar{{\varvec{\epsilon }}}_i\right) \right\} \nonumber \\&+\,\sum _{i=1}^N -2 {\varvec{\phi }}_i^T\mathbf{P}_i\bar{{\varvec{\phi }}}_i\nonumber \\&+\,\sum _{i=1}^N \left( \mathbf{l}_i^T\bar{{\varvec{\phi }}}_i+\mathbf{m}_i^T\bar{{\varvec{\phi }}}_i +{\varvec{\phi }}_i^T\bar{\mathbf{l}}_i +{\varvec{\phi }}_i^T\bar{\mathbf{m}}_i\right) \nonumber \\&+\,\sum _{i=1}^N \frac{1}{\gamma _{i1}} \sum _{j=1}^n \left( \dot{\tilde{\theta }}_{ ij}^T\bar{\tilde{\theta }}_{ ij}+\tilde{\theta }_{ ij}^T\dot{\bar{\tilde{\theta }}}_{ ij}\right) \nonumber \\&-\,\sum _{i=1}^N 2{\eta }_i\mathbf{e}_i^T\mathbf{Q}\bar{\mathbf{e}}_i +\sum _{i=1}^N\frac{1}{{\beta }_i}(\hat{{\nu }}_i-{\nu }_i)\dot{\hat{{\nu }}}_i. \end{aligned}$$
(47)

Here, by utilizing Lemma 1 and the definition of optimal parameter error (15), the following inequality can be obtained

$$\begin{aligned} \dot{V}_3\le & {} \mathbf{e}^T(\varvec{\Lambda } + {c}(\mathbf{A} \otimes \varvec{\Gamma } ^T\mathbf{Q})^s\nonumber \\&-\,2 \mathbf{H} \otimes \mathbf{Q})\bar{\mathbf{e}} +\sum _{i=1}^N -2 {\varvec{\phi }}_i^T\mathbf{P}_i\bar{{\varvec{\phi }}}_i\nonumber \\&+\, \sum _{i=1}^N \left( \mathbf{l}_i^T\bar{{\varvec{\phi }}}_i+{\varvec{\phi }}_i^T\bar{\mathbf{l}}_i\right) +\sum _{i=1}^N (\mathbf{u}_{\mathbf{b}_i}+{\varvec{\epsilon }}_i)^TQ\bar{\mathbf{e}}_i\nonumber \\&+\, \mathbf{e}_i^TQ (\overline{\mathbf{u}_{\mathbf{b}_i}+{\varvec{\epsilon }}_i})+\sum _{i=1}^N\frac{1}{{\beta }_i}(\hat{{\nu }}_i-{\nu }_i)\dot{\hat{{\nu }}}_i \nonumber \\&+\,\sum _{i=1}^N \frac{1}{\gamma _{i1}} \sum _{j=1}^n \left\{ \tilde{\theta }_{ ij}^T\left( \gamma _{i1}\bar{ \phi }_{ ij}\xi _{ ij}+\dot{\bar{\tilde{\theta }}}_{ ij}\right) \right. \nonumber \\&+\left( \dot{\tilde{\theta }}_{ ij}^T+\gamma _{i1}\bar{\xi }_{ ij}^T\phi _{ ij}\right) \bar{\tilde{\theta }}_{ ij}\Bigg \}. \end{aligned}$$
(48)

Substituting Eqs. (32, 34–35) into Eq. (48) yields

$$\begin{aligned} \dot{V}\le & {} \mathbf{e}^T\left( \varvec{\Lambda } + {c}(\mathbf{A} \otimes \varvec{\Gamma } ^T\mathbf{Q}\right) ^s-2 \mathbf{H} \otimes \mathbf{Q})\bar{\mathbf{e}}\nonumber \\&+\,\sum _{i=1}^N\left( \mathbf{e}_i^T\mathbf{Q}\bar{{\varvec{\epsilon }}}_i+{\varvec{\epsilon }}_i^T\mathbf{Q}\bar{\mathbf{e}}_i\right) - \sum _{i=1}^N 2{\nu }_i \mathbf{e}_i^T \mathbf{Q} \mathrm{sgn}(\bar{\mathbf{e}_i})\nonumber \\&+\,\sum _{i=1}^N \sum _{j=1}^n \left\{ -2p_i \phi _{ ij}\bar{{\phi }}_{ ij}+l_{ ij}\bar{{\phi }}_{ ij}+{\phi }_{ ij}\bar{l}_{ ij}\right. \nonumber \\&-\,\left. 2\gamma _{i2}m_{ ij}\bar{m}_{ ij}-\gamma _{i2}(m_{ ij}\bar{l}_{ ij}+l_{ ij}\bar{m}_{ ij})\right\} \nonumber \\\le & {} \mathbf{e}^T\left( \varvec{\Lambda } + {c}\left( \mathbf{A} \otimes \varvec{\Gamma } ^T\mathbf{Q}\right) ^s-2 \mathbf{H} \otimes \mathbf{Q}\right) \bar{\mathbf{e}}\nonumber \\&+\, \sum _{i=1}^N 2\left( \hat{{\epsilon }}_i-{\nu }_i\right) \mathbf{e}_i^T \mathbf{Q}\mathrm{sgn}\left( \bar{\mathbf{e}_i}\right) \nonumber \\&+\,\sum _{i=1}^N \sum _{j=1}^n \left\{ -2p_i{\phi }_{ ij}\bar{{\phi }}_{ ij}+l_{ ij}\bar{{\phi }}_{ ij}+{\phi }_{ ij}\bar{l}_{ ij}\right. \nonumber \\&-\,\left. 2\gamma _{i2}m_{ ij}\bar{m}_{ ij}-\gamma _{i2}\left( m_{ ij}\bar{l}_{ ij} +l_{ ij}\bar{m}_{ ij}\right) \right\} . \end{aligned}$$
(49)

One can choose \({\eta }_i, {\nu }_i\) to satisfy the condition that \(\varvec{\Lambda } + \mathbf{c}(\mathbf{A} \otimes \Gamma ^T\mathbf{Q})^s-2 \mathbf{H} \otimes \mathbf{Q}<0\) and \(\hat{{\epsilon }}_i-{\nu }_i<0\).

Then

$$\begin{aligned} \dot{V}\le & {} \sum _{i=1}^N \sum _{j=1}^n \left\{ -2p_i{\phi }_{ ij}\bar{{\phi }}_{ ij}+l_{ ij}\bar{{\phi }}_{ ij}+{\phi }_{ ij}\bar{l}_{ ij}\right. \nonumber \\&-\left. 2\gamma _{i2}m_{ ij}\bar{m}_{ ij}-\gamma _{i2}\left( m_{ ij}\bar{l}_{ ij} +l_{ ij}\bar{m}_{ ij}\right) \right\} . \end{aligned}$$
(50)

By applying the following inequality:

$$\begin{aligned}&{\phi }_{ ij}\bar{l}_{ ij}+\bar{{\phi }}_{ ij}l_{ ij} \le p_i{\phi }_{ ij}\bar{{\phi }}_{ ij}+p_i^{-1}l_{ ij}\bar{l}_{ ij}, \nonumber \\&\quad -\,m_{ ij}\bar{l}_{ ij}-\bar{m}_{ ij}l_{ ij} \le m_{ ij}\bar{m}_{ ij}+l_{ ij}\bar{l}_{ ij}. \end{aligned}$$
(51)

Eq. (50) becomes

$$\begin{aligned} \dot{V} \le \sum _{i=1}^N \left( -{\varvec{\phi }}_i^T\mathbf{P}_i\bar{{\varvec{\phi }}}_i-\mathbf{m}_i^T\varvec{\Gamma }_{i2}\bar{\mathbf{m}}_i+\mathbf{l}_i^T\left( \varvec{\Gamma }_{i2}+\mathbf{P}_i^{-1}\right) \bar{\mathbf{l}}_i\right) . \end{aligned}$$
(52)

Integrating both sides of Eq. (52) from \(0\) to \(T\) yields the following inequality:

$$\begin{aligned}&\sum _{i=1}^N \int _0^T {\varvec{\phi }}_i^T\mathbf{P}_i \bar{{\varvec{\phi }}}_i \mathrm {d}t + \sum _{i=1}^N \int _0^T \mathbf{m}_i^T\varvec{\Gamma }_{i2}\bar{\mathbf{m}}_i \mathrm {d}t \le V(0)-V(T) \nonumber \\&\quad +\,\sum _{i=1}^N \int _0^T \!\mathbf{l}_i^T(\varvec{\Gamma }_{i2}+\mathbf{P}_i^{-1})\bar{\mathbf{l}}_i \mathrm {d}t, \end{aligned}$$
(53)

which gives the inequality (38).

Fig. 1
figure 1

Chaotic attractors of the complex Lorenz system (a, b) and the complex Chen system (c, d)

Full size image

From inequality (38), if \(\mathbf{l}_i \in L_2\) , then \({\varvec{\phi }}_i \in L_2\) and \(\mathbf{m}_i \in L_2\); this means that \(\lim \limits _{t \rightarrow \infty }||{\varvec{\phi }}_i(t)||=0\) and \(\lim \limits _{t \rightarrow \infty }||\mathbf{m}_i(t)||=0\) by Barbalats Lemma [48]. Regardless of \(\mathbf{l}_i \notin L_2\), the \({\varvec{\phi }}_i^T\bar{{\varvec{\phi }}}_i\) is bounded by \(\mathbf{l}_i^T\bar{\mathbf{l}}_i\) with predetermined positive matrix \(\varvec{\Gamma }_{i2}+\mathbf{P}_i^{-1}\). This implies that disturbance observation error can be made arbitrarily small by adjusting predetermined factor. As a result, \(\hat{\varvec{\Omega }}_i\) can monitor \(\varvec{\Omega }_i\) with arbitrarily small error. According to Lyapunov stability theory, we can guarantee that the error dynamics (6) can be bounded. This means that the control law (30–32) and adaptation laws (33–35) can synchronize the nodes of the chaotic complex response network (3) in the sense of CMFPS. This completes the proof. \(\square \)

Remark 4

Previous literature [42] considers CCS with external disturbance. However it was assumed that the upper bound of external disturbances was known a priori. In this paper, the structure of the uncertain factor and the bounds of the disturbances can be estimated without prior information.

4 Numerical examples

In this section, two numerical examples are presented to verify the effectiveness of the proposed method. The one is a complex network that consists of \(6 + 1\) identical partially linear chaotic complex Lorenz system. The other is a drive-response network coupled with a \(20 + 1\) chaotic complex Chen system with system uncertainties and external disturbances. In the following simulations, the initial values of response systems are randomly chosen in given ranges. Because the behavior of chaotic complex system is highly sensitive to initial conditions, the behaviors of networked response systems are completely different. To verify the effectiveness of the proposed scheme, the simulation results have been illustrated.

Fig. 2
figure 2

The real and imaginary part CMFPS error in Example 1. a The real part trajectories of the error (\(e_i^r\)) by the proposed method (\(i=1, \ldots , 6\)). b The imaginary part trajectories of the \(e_i^i\) by the proposed method

Full size image

Example 1

(CMFPS of complex Lorenz system) The drive system is described by

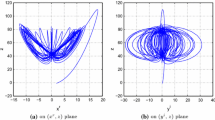
$$\begin{aligned}&\dot{\mathbf{x}}=\mathbf{M}(z)\mathbf{x} \nonumber \\&\dot{z}=-bz+1/2(\bar{x}_1x_2+x_1\bar{x}_2) \nonumber \\&\mathbf{M}(z)= \begin{bmatrix} -\sigma&\quad \! \sigma \\ (r-z)&\quad \!-a \end{bmatrix}, \end{aligned}$$
(54)

where \(\sigma =2, r=60+0.02j, a=1-0.06j\) and \(b=0.8\) with the initial condition \(\mathbf{x}_0=[2+1i,3+3i]^T\) and \(z_0=10\). With given parameters, the drive complex Lorenz system exhibits chaotic behavior as shown in Fig. 1a, b.

The response network system (2) is described as

$$\begin{aligned} \dot{\mathbf{y}}_i=\mathbf{M}(z)\mathbf{y}_i+{c}_i \sum _{k=1}^N a_{ ik} \varvec{\Gamma } \mathbf{y}_k +\mathbf{u}_i, \end{aligned}$$
(55)

where \(i=1, \ldots , 6\) and \(u_i\) is control law which is designed according to Theorem 1.

The coupling strength \(c_i=1\) and the coupling configuration matrix \(\mathbf{A}=(a_{ ij})_{6 \times 6}\) was randomly selected as zero-sum rows and the inner coupling matrix \(\varvec{\Gamma } = I_{6 \times 6}\). The initial values \(\mathbf{y}_{i0}\) were randomly chosen in \([-1, 1]\). The following complex scaling function matrix was arbitrarily selected.

$$\begin{aligned} \varvec{\Psi }= \begin{bmatrix} 2\mathrm{sin}(2t)+j\mathrm{cos}(0.5t)&\quad \! \mathrm{sin}(t)+j\mathrm{cos}(0.3t)\\ 0.5\mathrm{sin}(0.5)t+j\mathrm{cos}(t)&\quad \! \mathrm{sin}(t)+j\mathrm{cos}(2t) \end{bmatrix}. \end{aligned}$$
(56)

The input vector of the CFLS is \(\mathbf{v}_i=[y_{i1}, y_{i2}]^T\), where the range of the real part \(y_{i1}^r \in [-12, 12]\) and \(y_{i2}^r \in [-28, 33]\), and of the imaginary part \(y_{i1}^i \in [-14, 16]\) and \(y_{i2}^i \in [-37, 49]\).

Five centers of the Gaussian membership functions were chosen \(\mu _{ ij}^r\) and \(\mu _{ ij}^i\) for each real and imaginary part of input vector \(\mathbf{v}_i\) as follows

$$\begin{aligned} \mu _{ ij}^l\left( y_{ ij}^l\right) =exp \left[ \ -\left( y_{ ij}^l-c_{mj}^l\right) ^2 / \sigma _j ^{l 2}\right] \ , \end{aligned}$$
(57)
Fig. 3
figure 3

The real and imaginary part CMFPS error in Example 2. a The real part trajectories of the error (\(e_i^r\)) by the proposed method (\(i=1, \ldots , 20\)). b The imaginary part trajectories of the error (\(e_i^i\)) by the proposed method

Full size image
Fig. 4
figure 4

Time evolution of actual disturbances \(\Omega _i\) (red) and estimated disturbances \(\hat{\Omega }_i\) (blue) in Example 2. a The real and imaginary part of \(\Omega _1\) and \(\hat{\Omega }_1\) of node 1. b The real and imaginary part of \(\Omega _{20}\) and \(\hat{\Omega }_{20}\) of node 20. (Color figure online)

Full size image

where \(l\) indicates real and imaginary part of variables. We choose the center of the membership function \(c_{m1}^l\), \(c_{m2}^l\) for \(m=1, \ldots , 5\) where \({\varvec{\sigma }}_j^r=[2.548, 6.476]\) and \({\varvec{\sigma }}_j^i=[3.185, 9.130]\) with uniform distance.

For the controller and adaptation laws, we set parameters as \(\alpha _i=5\), \(\beta _i=5\), \(\hat{\eta }_0=0\), \(\hat{\nu }_0=0\), \(p_i=100\), \(\gamma _{i0}=60\) and \(\gamma _{i1}=90\).

Figure 2 shows that synchronization errors \(\mathbf{e}_i^r\) and \(\mathbf{e}_i^i\) converged to zero; therefore, CMFPS was achieved.

Example 2

(CMFPS of complex Chen system) In this example, \(20+1\) coupled complex Chen system is considered. According to general form of chaotic complex system (1), the parameters of drive system are described as \(\sigma =27\), \(r=-4\), \(a=23\) and \(b=1\) with the initial condition \(\mathbf{x}_0=[3+1j, 1+2j]^T\) and \(z_0=5\). With given parameters, the drive complex Chen system exhibits chaotic behavior as shown in Fig. 1c, d.

In the response network (3), model uncertainties \(\Delta M(z)\), \(\Delta c_i\), \(d_i\) were defined as

$$\begin{aligned}&\Delta \mathbf{M}(z)= \begin{bmatrix} -\psi _{i1}\sigma&\quad \! \psi _{i2}\sigma \\ \psi _{i3}(r-z)&\quad \! -\psi _{i4}a \end{bmatrix}, \nonumber \\&\Delta c_i=0.1, \nonumber \\&\mathbf{d}_i=[\ k_{i1}(sin(l_{i2}t)+j cos(k_{i3}t))\quad k_{i4}(sin(k_{15}t)\nonumber \\&\qquad +\,j cos(k_{i6}t))]\ ^T, \end{aligned}$$
(58)

where \(i=1, \ldots , 6\). The parameters used in the uncertain term were randomly selected in the following ranges:

\(\psi _{i1} \in [-0.1, 0.1]\), \(\psi _{i2} \in [-0.2 , 0.2]\), \(\psi _{i3} \in [-0.5 , 0.5]\), \(\psi _{i4} \in [-0.3 , 0.3]\), \(k_{i1} \in [1.5, 2.0]\), \(k_{i2} \in [2.0 , 2.5]\), \(k_{i3} \in [0.5 , 1.0]\), \(k_{i4} \in [1.5 , 2.0]\), \(k_{i5} \in [2.0 , 2.5]\), \(k_{i6} \in [1.0 , 1.5]\).

The coupling strength \(c_i=1\) and the coupling configuration matrix \(\mathbf{A}=(a_{ ij})_{20 \times 20}\) was arbitrarily selected as zero-sum rows and the inner coupling matrix \(\varvec{\Gamma } = I_{20 \times 20}\). Initial values \(\mathbf{y}_{i0}\) were randomly chosen in \([-2, 2]\). The following complex scaling function matrix was chosen.

$$\begin{aligned} \varvec{\Psi }= \begin{bmatrix} \mathrm{sin}(2t)+j\mathrm{cos}(t)&\quad \! 1.5\mathrm{sin}(t)+j\mathrm{cos}(0.5t)\\ 2\mathrm{sin}(t)+j\mathrm{cos}(1.5t)&\quad \! \mathrm{sin}(0.5t)+j\mathrm{cos}(t) \end{bmatrix}. \end{aligned}$$
(59)

The input vector of the CFLS is \(\mathbf{v}_i=[y_{i1}, y_{i2}]^T\), where the range of the real part \(y_{i1}^r \in [-28, 22]\) and \(y_{i2}^r \in [-35, 36]\), and of the imaginary part \(y_{i1}^i \in [-13, 17]\) and \(y_{i2}^i \in [-22, 21]\). We choose the center of the Gaussian membership function \(c_{m1}^l\), \(c_{m2}^l\) for \(m=1, \ldots , 5\) where \({\varvec{\sigma }}_j^r=[5.31, 7.54]\) and \({\varvec{\sigma }}_j^i=[3.186, 4.567]\) with uniform distance. According to Eqs. (30–35), the parameters of controller and adaptation laws are selected \(\alpha _i=10\), \(\beta _i=10\), \(\hat{\eta }_0=0\), \(\hat{\nu }_0=0\), \(p_i=100\), \(\gamma _{i0}=50\) and \(\gamma _{i1}=100\).

In Fig. 3, synchronization error converged to nearly zero in the sense of CMFPS. This means that the response networks are well-synchronized with the master system by proposed method. The CFO estimated overall disturbances within small bounds in Fig. 4. All of these simulation results demonstrate that the proposed method achieved adaptive CMFPS and estimates of uncertainties by using the CFO.

5 Conclusion

A complex modified function projective synchronization for networked chaotic complex systems was introduced. Firstly, based on Lyapunov stability theory, adaptive controllers were developed to achieve CMFPS for general networked chaotic complex systems. Secondly, an adaptive controller with a CFO was proposed for networked chaotic complex systems with model uncertainties and external disturbances. By using the CFO, uncertain factors existed in networks were estimated without prior information about them. The effectiveness of the proposed scheme was verified by applying it to the CMFPS of general chaotic complex Lorenz systems and the CMFPS of uncertain chaotic complex Chen systems.