1 Introduction

Synchronization and control of coupled dynamical systems have attracted much attention from scientists and engineers [1–14]. For explaining collective phenomena better, many kinds of synchronization manners are introduced, such as complete synchronization, phase synchronization, lag synchronization, projective synchronization, and so on. Projective synchronization (PS) in drive-response systems has been extensively investigated in virtue of its broad potential applications [15, 16]. According to the form of the projective factor, the concept of PS has been extended to many other forms, such as generalized projective synchronization [17, 18], modified projective synchronization [19, 20], hybrid projective synchronization [21], and function projective synchronization [7, 22]. In [13, 14, 22], the authors considered the drive-response network of 1+N coupled identical partially linear chaotic systems.

All the above research only considered the synchronization of coupled dynamical systems with real variables. On the other hand, dynamical systems with a complex variable are used to model real systems as well, for example, the complex Lorenz system [23] is used to describe and simulate rotating fluids and detuned laser [24, 25]. Recently, many researchers devoted much effort to study synchronization and control in coupled complex-variable dynamical systems [26–32]. In [27], Mahmoud et al. introduced complex Chen and Lü systems and well investigated the global synchronization of coupled identical systems. Furthermore, Mahmoud et al. [28] studied the chaos synchronization of two different complex Chen and Lü systems via active control. In [29], Nian et al. proposed the concept of module-phase synchronization and investigated the synchronization in complex dynamical systems. In [30], Hu et al. investigated hybrid projective synchronization in a chaotic complex dynamical system with respect to a scaling matrix.

It is notable that all the factors in the above projective synchronization are real numbers or real matrices, or even real valued functions. That is to say, the drive-response systems evolve in the same or inverse direction in complex plane simultaneously. For complex dynamical systems, however, in many practical situations, the drive-response systems may evolve in different directions with a constant intersection angle, for example, y=ρe jθ x, where x denotes the drive system, y denotes the response system, ρ>0 denotes the zoom rate, θ∈[0,2π) denotes the rotation angle and \(j=\sqrt{-1}\). Therefore, in [33], we investigated projective synchronization with respect to a complex factor, called complex projective synchronization (CPS), in drive-response complex-variable chaotic systems.

Motivated by the above discussions, in this paper, we will further investigate complex projective synchronization in a drive-response network of 1+N partially linearly coupled complex-variable chaotic systems. These kind of networks was first introduced in [14], in which the response systems are not only driven by the central node (drive system), but also coupled via a linear and mutual coupling scheme. Their idea comes from some practical instance, for example, in a social network or games in economic activities, and behaviors of individuals (those response systems) will be affected not only by powerful one (the drive system used in the present paper), but also those with a similar role as themselves [13, 14, 22]. The CPS in a general drive-response network is investigated via adaptive feedback control firstly, in which the outer coupling matrix only need to be symmetrical. Moreover, the CPS in a special class of drive-response networks is investigated via pinning control. Furthermore, a universal pinning control scheme is proposed via adaptive coupling strength method.

The rest of this paper is organized as follows. In Sect. 2, the model of a drive-response network coupled with partially linear complex-variable chaotic systems and some preliminaries are introduced. In Sect. 3, complex projective synchronization is investigated via adaptive control and pinning control, respectively. In Sect. 4, several numerical examples are provided to verify the effectiveness of the theoretical results. Conclusions are drawn in Sect. 5.

Notation

Throughout this paper, for Hermite matrix H, the notation H>0 (H<0) means that the matrix H is positive definite (negative definite). For any complex (real) matrix M, \(M^{s}=M^{T}+\overline{M}\). For any complex number (or complex vector) x, the notations x r and x i denote its real and imaginary parts, respectively, and \(\bar{x}\) denotes the complex conjugate of x.

2 Model description and preliminaries

Consider a drive-response network coupled with 1+N identical partially linear chaotic systems [13, 22], which can be described by

$$ \begin{array}{l} \dot{x}(t)=M(z(t))x(t),\\[6pt] \dot{z}(t)=f(x(t),z(t)), \end{array} $$
(1)
(2)

where x(t)=(x 1,x 2,…,x m )T∈C m and z(t)∈R are the drive system variables, y i (t)=(y i1,y i2,…,y im )T∈C m is the state variable of a node i in the response network. M(z(t))∈R m×m is a complex matrix function of z(t) and f:C m×R→R is a nonlinear function, ε>0 is the coupling strength and Γ∈R m×m is the inner coupling matrix. Matrix A=(a ij ) N×N is the zero-row-sum outer coupling matrix, which denotes the network topology and is defined as follows: If there is a connection from node j to node i (i≠j), then a ij ≠0; otherwise, a ij =0.

Definition 1

Matrix \(A=(a_{ik})_{i,k}^{N}\) is said to belong to class A1, denoted as A∈A1, if:

  1. (1)

    a ik ≥0, i≠k, \(a_{ii}=-\sum_{k=1,k\neq i}^{N}a_{ik}= -\sum_{i=1,i\neq k}^{N}a_{ik}\), i=1,2,…,N;

  2. (2)

    A is irreducible.

Definition 2

The drive-response network (1) and (2) is said to achieve complex projective synchronization, if there exists a complex number α such that lim t→∞∥y i (t)−αx(t)∥=0, where the norm of any complex vector x is \(\|x\|=\sqrt{x^{T}\bar{x}}\).

Without loss of generality, let α=ρ(cosθ+jsinθ), where ρ=|α| is the module of α and θ∈[0,2π) is the phase of α. Therefore, the projective synchronization is achieved when θ=0 or π. Furthermore, the complete synchronization is achieved when ρ=1 and θ=0, the antisynchronization is achieved when ρ=1 and θ=π.

Our objective here is to achieve CPS in the drive-response network (1) and (2) by applying proper controllers u i (t) on the response network. Then the controlled response network is

(3)

The following lemmas and assumption are required for deriving the main results.

Lemma 1

[34]

Let m×m complex matrix H be Hermitian, then

  1. (a)

    \(x^{T}H\overline{x}\) is real for all x∈C m;

  2. (b)

    All the eigenvalues of H are real.

Assumption 1

Suppose that there exits a constant L such that the largest eigenvalue of M s(z(t)) satisfies

$$\lambda_{\max}\bigl(M^s\bigl(z(t)\bigr)\bigr)\leq L. $$

It is easy to verified that all the chaotic systems satisfy the assumption due to z(t) is bounded.

Lemma 2

[3]

If G=(g ij ) N×N is an irreducible matrix with Rank(G)=N−1 and satisfies g ij =g ji ≥0 for i≠j, and \(\sum_{j=1}^{N} g_{ij}=0\), for all i=1,2,…,N. Then all eigenvalues of the matrix

$$ \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} g_{11}-\varepsilon&g_{12}&\cdots&g_{1N} \\ g_{21}&g_{22}&\cdots&g_{2N} \\ \vdots&\vdots&\ddots&\vdots\\ g_{N1}&g_{N2}&\cdots&g_{NN} \end{array} \right ] $$

are negative for any positive constant ε>0.

3 Main results

In this section, several sufficient conditions for achieving CPS in drive-response network (1) and (3) will be provided by adopting different control schemes. Let e i (t)=y i (t)−αx(t), then one has

(4)

Firstly, consider CPS between (1) and (3) via the following adaptive linear feedback controllers

(5)

where δ>0 is the adaptive gain.

Theorem 1

Suppose that Assumption 1 holds. The CPS in the drive-response network (1) and (3) with the controllers (5) can be achieved for a small positive constant δ.

Proof

Consider the following Lyapunov function candidate:

$$ V(t)=\sum_{i=1}^Ne_i^{T}(t) \overline{e_i(t)}+\frac{1}{2\delta} \bigl(d(t)-d^* \bigr)^2. $$

Its derivative along the trajectories of (4) is

Let \(e(t)=(e_{1}^{T},e_{2}^{T},\ldots,e_{N}^{T})^{T}\) and D=diag(d 1,…,d N ), then one has

$$ \dot{V}(t)\leq e^T(t) \bigl( \bigl(L-d^* \bigr)I_{Nm}+ \varepsilon (A\otimes \varGamma)^s \bigr)\overline{e(t)}. $$

Then one can choose a sufficiently large d ∗ such that \(\dot{V}(t)<0\). According to Lyapunov stability theory, the CPS can be achieved, therefore, the proof is completed. □

Remark 1

In Theorem 1, the outer coupling matrix A need not to be symmetric and irreducible. And synchronization speed can be adjusted by choosing proper adaptive gain δ.

Secondly, consider CPS between (1) and (3) via pinning control under the assumptions A∈A1 and Γ>0. Especially, only one node is pinned for achieving CPS.

Theorem 2

Suppose that Assumption 1 holds, A∈A1 and Γ>0. The CPS in the drive-response network (1) and (3) with the following single controller:

(6)

can be achieved if the following condition is satisfied

$$ LI_{Nm}+\varepsilon \bigl(A^s-D_1 \bigr)\otimes \varGamma<0, $$
(7)

where d 1>0 and D 1=diag(2d 1,0,…,0).

Proof

Consider the following Lyapunov function candidate:

$$ V(t)=\sum_{i=1}^Ne_i^{T}(t) \overline{e_i(t)}. $$

Its derivative along the trajectories of (4) is

Then, if condition (7) is satisfied, one has \(\dot{V}(t)<0\). According to Lyapunov stability theory, the CPS can be achieved, hence the proof is completed. □

Remark 2

Due to outer coupling matrix A∈A1, one can easily verify that matrix A s satisfies the conditions in Lemma 2 and A s−D 1<0. Then one can choose proper coupling strength ε such that condition (7) is satisfied for any given network. However, one cannot find a fixed ε such that condition (7) is satisfied for all networks. That is to say, a universal control method for all networks needs to be further explored.

Thirdly, consider CPS between (1) and (3) via pinning control and adaptive coupling strength method under the assumptions A∈A1 and Γ>0. Then the controlled response network can be rewritten as

(8)

where σ>0 is the adaptive gain.

Theorem 3

Suppose that Assumption 1 holds, A∈A1 and Γ>0. The CPS in the drive-response network (1) and (8) can be globally achieved for a small positive constant σ.

Proof

Consider the following Lyapunov function candidate:

$$ V(t)=\sum_{i=1}^Ne_i^{T}(t) \overline{e_i(t)}+\frac{\mu}{2\sigma} \bigl(\varepsilon(t)- \varepsilon^* \bigr)^2, $$

where μ and ε ∗ are positive constants to be determined. The derivative of V(t) along the trajectories of (8) can be calculated as

Due to A s−D 1<0, one can choose sufficiently small μ such that A s−D 1+μI N <0. When μ is chosen, one can choose sufficiently large ε ∗ such that LI Nm +ε(t)(A s−D 1+μI N )⊗Γ−με ∗ I Nm <0, which leads \(\dot{V}(t)<0\). Then the CPS is achieved, and the proof is completed. □

Remark 3

Clearly, for a class of networks coupled with chaotic systems satisfying assumptions A∈A1 and Γ>0, this control scheme is effective and universal. Moreover, it can also make the coupling strength as small as possible by choosing a proper initial value and an adaptive gain, which is important in applications.

Remark 4

When the size of the network is large enough, coupling strength may be chosen very large for achieving CPS of the controlled network with a single controller, and the synchronization speed may be very slow. To solve the problem, more nodes should be controlled, e.g., the first l (2≤l<N) nodes are controlled. Synchronization criterion for achieving CPS in a drive-response network with more than one controllers can be derived directly from Theorems 2 and 3.

4 Numerical simulations

Consider a drive-response network coupled with the following complex Lorenz systems:

(9)

where

$$M(z)=\left (\begin{array}{c@{\quad}c} -\sigma & \sigma \\ r-z &-a \end{array} \right ), $$

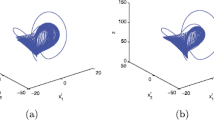
which exhibit chaotic behavior when σ=2, b=0.8, r=60+0.02j and a=1−0.06j. Figure 1 shows a chaotic attractor of the complex Lorenz system with initial values x 1(0)=1+2j, x 2(0)=3+4j, z=5, which is the synchronization orbit in the following simulations.

Fig. 1
figure 1

A chaotic attractor of the complex Lorenz system with initial values x 1(0)=1+2j, x 2(0)=3+4j, z=5

Full size image

Firstly, consider CPS in a drive-response network coupled with 1+6 identical complex Lorenz systems via adaptive feedback control, where the outer coupling matrix A is

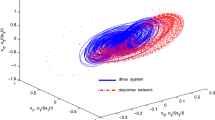
$$A=\left (\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} -4 & 3 & 0 & 2 & 0 &-1 \\ 3 &-5 & 4 & 0 & 0 &-2 \\ 0 & 4 & 1 &-2 &-3 & 0 \\ 2 & 0 &-2 &-3 & 3 & 0 \\ 0 & 0 &-3 & 3 &-2 & 2 \\ -1 &-2 & 0 & 0 & 2 & 1 \\ \end{array} \right ). $$

In numerical simulations, choose α=1+2j, ε=1, Γ=diag(1,1), δ=0.01, the initial values of d(t) as d(0)=0.2, and the initial values of complex state variables y i (t) (i=1,2,…,6) randomly. Figure 2 shows the norms of synchronization errors e i (t) and the orbit of d(t).

Fig. 2
figure 2

The norms of synchronization errors e i (t) and the orbit of d(t)

Full size image

Secondly, consider CPS in a drive-response network coupled with 1+10 identical complex Lorenz systems via only a single controller, where the outer coupling matrix A is

$$A= \left [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} -7&1&0&2&0&3&0&0&1&0\\ 0&-6&0&1&0&1&2&1&0&1\\ 3&0&-9&0&3&0&0&2&0&1\\ 1&1&0&-8&1&0&2&0&3&0\\ 0&1&0&0&-9&0&3&2&1&2\\ 0&0&3&1&0&-7&0&1&0&2\\ 2&0&0&3&0&2&-8&0&0&1\\ 0&2&3&0&2&0&1&-8&0&0\\ 1&0&3&0&1&1&0&0&-6&0\\ 0&1&0&1&2&0&0&2&1&-7 \end{array} \right ], $$

which belongs to A1. According to Eq. (9), one can easily calculate the eigenvalues of M s(z(t)): \(\lambda_{1,2}=-(\sigma+1)\pm \sqrt{(\sigma-1)^{2}+|\sigma-z+r|^{2}}\). From Fig. 1, it is found that 20≤z≤100, and then one can choose L=40 such that Assumption 1 holds.

In numerical simulations, choose α=cos(3π/5)+jsin(3π/5), Γ=diag(1,1) and d 1=10. By simple calculation, one has the largest eigenvalue of A s−D is −0.8566, and then one can choose ε=47 such that condition (7) holds. The initial values of complex state variables y i (t) (i=1,2,…,10) are chosen as y i1(0)=(1+0.5i)+j(2+0.5i) and y i2(0)=(10−0.5i)+j(11−0.5i). Figure 3 shows the norms of synchronization errors e i (t).

Fig. 3
figure 3

The norms of synchronization errors e i (t)

Full size image

Finally, consider CPS in a drive-response network coupled with 1+10 identical complex Lorenz via a single controller and adaptive coupling strength. In numerical simulations, choose σ=0.001 and the initial value of ε(t) as ε(0)=2. The other parameters are chosen the same as those in the second example. Figure 4 shows the norms of synchronization errors e i (t) and orbit of ε(t). From Fig. 4, one can see that the needed coupling strength value is much less than that calculated by inequality (7) in the second example.

Fig. 4
figure 4

The norms of synchronization errors e i (t) and the orbit of ε(t)

Full size image

5 Conclusions

Complex projective synchronization in a drive-response network coupled with identical partially linear complex-variable chaotic systems has been studied in this paper. CPS in a general drive-response network is investigated first via adaptive linear feedback control. Next, a class of special drive-response networks are well studied via pinning control. Moreover, a universal pinning control scheme is proposed via adaptive coupling strength method. According to Lyapunov stability theory, several simple and useful criteria for CPS are obtained. Numerical simulations are provided to verify the correctness and effectiveness of the derived theoretical results.