1 Introduction

In the past decades, a great variety of nonlinear dynamic systems with real variables have been proposed in many fields and extensively studied due to wide-scope potential applications in lasers, optical parametric oscillators, neuroscience, ecological systems, electrical circuits, secure communications, and cryptography [1–7]. Some natural questions arise as follows: (1) what dynamical behaviors can a complex nonlinear system exhibit, where a state complex variable includes the real part and the imaginary one? (2) How to control and synchronize the chaotic or hyperchaotic complex nonlinear systems? Fowler et al. [8] firstly introduced the complex Lorenz system. After that, some chaotic or hyperchaotic complex systems, such as the chaotic complex Chen system [9], the chaotic complex Lü system [10], the hyperchaotic complex Lü system [11], the hyperchaotic complex Lorenz system [12] and so forth, have been proposed and studied in recent years. It was found that many physical systems can be well described with the help of the complex nonlinear dynamics. Another interesting application is that the chaotic complex systems were utilized for secure communication, where the complex variables could increase the contents and security of the transmitted information [10].

So far, various types of synchronization phenomenon in the chaotic systems have been observed, such as complete synchronization (CS) [13], generalized synchronization (GS) [14], lag synchronization (LS) [15], phase synchronization (PhS) [16], Q-S synchronization [17], projective synchronization (PS) [18], etc. Amongst all kinds of chaos synchronization, projective synchronization has been especially and extensively investigated because it can obtain faster communication with its proportional feature. More recently, Chen et al. [19] proposed a new projective synchronization named function projective synchronization (FPS), where the responses of the synchronized dynamical states can synchronize up to a scaling function, but not a constant. Because the unpredictability of the scaling function in FPS can additionally enhance the security of communication, FPS of chaotic systems has attracted increasing attention [20–27]. In [22], a more general form of function projective synchronization, which is called modified function projective synchronization (MFPS), has been proposed, where the master and slave systems could be synchronized up to a scaling function matrix. The novelty feature of this synchronization phenomenon is that the scaling functions can be arbitrarily designed to different state variables by means of control. Yu and Li [23] studied adaptive generalized function projective synchronization (AGFPS) between two different uncertain chaotic systems. Sudheer and Sabir [24] investigated MFPS between two identical and mismatched hyperchaotic systems based on unidirectional OPCL coupling method. Further, they considered switched modified function projective synchronization of two identical Qi hyperchaotic systems using adaptive control method [25]. Switched synchronization of chaotic systems in which a state variable of the drive system synchronize with a different state variable of the response system is a promising type of synchronization as it provides greater security in secure communication. Wu et al. [26] presented two different hyperchaotic secure communication schemes by using generalized function projective synchronization (GFPS). In [27], robust adaptive modified function projective synchronization between two different hyperchaotic systems was introduced, where the external uncertainties are considered and the scale factors are different from each other. However, most of the existing studies mainly focus on the drive and response systems with the same order. Unfortunately, in many real systems, especially in biological and social systems, the synchronization phenomenon can also occur though the oscillators have different orders. For instance, the output from higher-order neurons always drives the neurons with lower-order in the subsystem [28]. Similar phenomena can be discovered in the human cardiovascular system [29]. Therefore, it is essential to study synchronization of strictly different dynamical systems and different order dynamical systems.

In [30, 31], reduced-order synchronization of two chaotic systems with different orders was studied. The essential feature of reduced-order synchronization is that two different dynamical systems in a master-slave configuration (the order of the master being higher than that of the slave) are synchronized such that each state of the slave system is synchronized with the corresponding one of the master. Zheng [32] investigated modified function projective synchronization (MFPS) between two different dimensional chaotic systems with unknown parameters via increased order, which could translate the problem of MFPS of chaotic systems with different dimensions into the MFPS of systems with identical dimensions by constructing auxiliary state variables. It is noted that most of the existing methods about chaos synchronization with different dimensions are only used for either reduced order or increased order. In addition, all the above-mentioned studies only involve with the chaotic systems with real variables.

Recently, several techniques and methods are introduced and applied to realize synchronization of complex chaotic systems. For example, Mahmoud et al. [11] introduced a new hyperchaotic complex Lü system and used the nonlinear control method based on Lyapunov function to synchronize the hyperchaotic attractors. In [33], an active control scheme was designed and applied to phase and antiphase synchronization of two identical hyperchaotic complex Lorenz systems. At the same time, two identical n-dimensional chaotic complex nonlinear systems with uncertain parameters were synchronized under an adaptive control scheme [34]. Liu et al. [35] investigated anti-synchronization between different chaotic complex systems by active control and nonlinear control methods, respectively. To the best of our knowledge, AGFPS between two different dimensional chaotic complex systems with unknown parameters has not been considered yet to date.

Motivated by the above discussions, adaptive generalized function projective synchronization between two different dimensional chaotic complex systems with unknown parameters via both reduced order and increased order is investigated in this paper. A universal adaptive controller and parameter update rule is devised for AGFPS of uncertain chaotic complex systems with different dimensions by means of the Lyapunov stability theory and adaptive control method. The advised scheme is simple and theoretically rigorous. Numerical simulations have shown the effectiveness of the proposed synchronization approach.

The outline of this paper is organized as follows: in Sect. 2, based on the Lyapunov stability theory and adaptive control method, a general scheme of AGFPS between two different dimensional chaotic complex systems with uncertain parameters is proposed by both reduced order and increased order. In Sect. 3, AGFPS between the hyperchaotic complex Lü system and the chaotic complex Lorenz system with fully unknown parameters is studied by the proposed synchronization scheme. Numerical simulations are used to show this process. In Sect. 4, on basis of the proposed scheme, the adaptive controllers and update parameter rules are attained for AGFPS between the uncertain chaotic complex Chen system and the uncertain hyperchaotic complex Lorenz system. Numerical simulation is employed to verify the validity of the controllers. The conclusions are finally drawn in Sect. 5.

2 A general scheme for adaptive generalized function projective synchronization between two uncertain chaotic complex systems with different dimensions

Consider the chaotic complex drive (master) and response (slave) systems given in the following form:

$$ \dot{X}(t) = F(X), $$
(1)
$$ \dot{Y}(t) = G(Y) + V(t), $$
(2)

where X(t)=(x 1,x 2,…,x m )T∈R m is an m-dimensional state complex vector for the drive system (1), Y(t)=(y 1,y 2,…,y n )T∈R n is an n-dimensional state complex vector for the response system (2), F:R m→R m and G:R n→R n are continuous nonlinear complex vector functions, and V(t)=(v 1,v 2,…,v n )T∈R n is a complex controller to be designed later. Here x j =u j1+iu j2, y k =q k1+iq k2, v k =μ k1+iμ k2, where \(i = \sqrt{ - 1}\), j=1,2,…,m, and k=1,2,…,n.

Assume that there exists a real scaling function matrix Λ(t)=(α kj (t)) n×m ∈R n×m, where α kj (t):R n→R (k=1,2,…,n; j=1,2,…,m) are continuously bounded differentiable functions, and α kj (t)≠0 for all t. Define the state error vector as

$$ \boldsymbol{e} = Y - \varLambda(t)X, $$
(3)

where e=(e 1,e 2,…,e n )T, e=e r+i e i, e k =e k1+ie k2, k=1,2,…,n. Throughout this paper, the superscripts ‘r’ and ‘i’ represent the real and imaginary parts of a complex vector or variable, respectively. Obviously, \(\boldsymbol{e}^{r} = (e_{1}^{r},e_{2}^{r}, \ldots ,e_{n}^{r})^{\mathrm{T}}\) and \(\boldsymbol{e}^{i} = (e_{1}^{i},e_{2}^{i}, \ldots ,e_{n}^{i})^{\mathrm{T}}\).

Definition 1

For the drive system (1) and the response system (2), it is said to achieve adaptive generalized function projective synchronization (AGFPS) if there exists an effective adaptive controller V(t) such that

$$\lim_{t \to\infty} \Vert\boldsymbol{e} \Vert= \lim_{t \to\infty} \bigl\Vert Y - \varLambda(t)X \bigr\Vert= 0 $$

for any initial conditions X(0) and Y(0).

To investigate AGFPS between two chaotic complex nonlinear systems with unknown parameters, the drive and response systems can be rewritten as

$$ \dot{X}(t) = F_{1}(X) + F_{2}(X)\xi, $$
(4)
$$ \dot{Y}(t) = G_{1}(Y) + G_{2}(Y)\theta+ V(t), $$
(5)

where F 1:R m→R m and G 1:R n→R n are two vectors of continuous nonlinear complex functions, F 2:R m→R m×l and G 2:R n→R n×p are continuous complex matrix functions, ξ∈R l and θ∈R p are unknown real parameter vectors of systems (4) and (5).

It is known that GFPS between the drive system and the response system with identical dimensions, i.e., m=n, has been well studied [19–27]. However, when m≠n, it means that the dimension of the drive system is not equal to that of the response system. In the existing studies, either the reduced-order synchronization [30, 31] or the increased-order synchronization [32] was considered. In this paper, we will design a general scheme for AGFPS between two different dimensional chaotic complex systems with uncertain parameters via both reduced order and increased order, i.e., m>n and m<n.

Taking the time derivative of the error vector (3) yields the error dynamical system as follows:

$$ \dot{\boldsymbol{e}} = \dot{Y} - \dot{\varLambda} (t)X - \varLambda(t)\dot{X}. $$
(6)

Substituting Eqs. (4) and (5) into Eq. (6), one can get

(7)

The above equation can be further rewritten as

(8)

Now, the problem of AGFPS between two chaotic complex systems (4) and (5) becomes the analysis of the asymptotical stability of zero solution of the error complex system (8). For this end, the key problem is how to design an effective controller V(t) and corresponding parameter update rule such that system (8) asymptotically converges to zero. In the following, we will construct the controller and corresponding parameter update rules with the help of the Lyapunov stability theory and adaptive control method. The main result is formed as Theorem 1.

Theorem 1

For given real scaling function matrix Λ(t) and arbitrary initial values X(0), Y(0), AGFPS between two chaotic complex nonlinear systems (4) and (5) can be achieved and the uncertain parameters ξ, θ can be identified if the adaptive controller is designed as follows:

$$ \everymath{\displaystyle} \left\{ \begin{array} {l} V(t) = \varLambda(t)F_{1}(X) + \varLambda (t)F_{2}(X)\tilde{\xi} - G_{1}(Y) \\[1.5mm] \hphantom{V(t) =}{}- G_{2}(Y)\tilde{\theta} + \dot{\varLambda} (t)X - K\boldsymbol{e}(t), \\[1.5mm] \eta_{j} = \varepsilon_{j}e_{j}^{2}(t), \quad \varepsilon_{j} > 0,\ j = 1,2, \ldots,n ,\end{array} \right. $$
(9)

or

$$ \everymath{\displaystyle} \left \{ \begin{array} {l} V^{r}(t) = \varLambda(t)F_{1}^{r}(X) + \varLambda (t)F_{2}^{r}(X)\tilde{\xi} - G_{1}^{r}(Y) \\[1.5mm] \hphantom{V^{r}(t)}{}- G_{2}^{r}(Y)\tilde{\theta} + \dot{\varLambda} (t)X^{r} - K^{r}\boldsymbol{e}^{r}(t) , \\ [1.5mm] V^{i}(t) = \varLambda(t)F_{1}^{i}(X) + \varLambda(t)F_{2}^{i}(X)\tilde{\xi} - G_{1}^{i}(Y) \\[1.5mm] \hphantom{V^{i}(t)}{}- G_{2}^{i}(Y)\tilde{\theta} + \dot{\varLambda} (t)X^{i} - K^{i}\boldsymbol{e}^{i}(t), \\ [1.5mm] \dot{\eta} _{j}^{r} = \varepsilon_{j}^{r} \bigl( e_{j}^{r}(t) \bigr)^{2}, \quad \varepsilon_{j}^{r} > 0,\ j = 1,2, \ldots,n , \\ [1.5mm] \dot{\eta} _{j}^{i} = \varepsilon_{j}^{i} \bigl( e_{j}^{i}(t) \bigr)^{2}, \quad \varepsilon_{j}^{i} > 0,\ j = 1,2, \ldots,n , \end{array} \right . $$
(10)

and the parameter update rules are constructed as below:

$$ \everymath{\displaystyle} \left \{ \begin{array} {l} \dot{\tilde{\xi}} = - \bigl( F_{2}^{r}(X) \bigr)^{\mathrm{T}} \bigl( \varLambda(t) \bigr)^{\mathrm{T}}\boldsymbol{e}^{r}(t) \\[1.5mm] \hphantom{\dot{\tilde{\xi}} =}{}- \bigl( F_{2}^{i}(X) \bigr)^{\mathrm{T}} \bigl( \varLambda(t) \bigr)^{\mathrm {T}} \boldsymbol{e}^{i}(t) - \boldsymbol{e}_{\xi} (t) , \\[1.5mm] \dot{\tilde{\theta}} = \bigl( G_{2}^{r}(Y) \bigr)^{\mathrm{T}}\boldsymbol{e}^{r}(t) + \bigl( G_{2}^{i}(Y) \bigr)^{\mathrm{T}}\boldsymbol{e}^{i}(t) - \boldsymbol{e}_{\theta} (t), \end{array} \right . $$
(11)

where the control gain matrix K=diag(η 1,η 2,…,η n ), K=K r+iK i, \(\eta_{j} = \eta_{j}^{{r}} + i\eta _{j}^{{i}}\), \(\boldsymbol{e}_{\xi} = \tilde{\xi} - \xi\), and \(\boldsymbol{e}_{\theta} = \tilde{\theta} - \theta\) are parameter error vectors. \(\tilde{\xi}\) and \(\tilde{\theta}\) denote the parameter estimation vectors of ξ and θ, respectively.

Proof

We introduce a positive definite Lyapunov function as follows:

(12)

where η ∗ and η Δ are positive constants to be determined later.

The time derivative of L(t) along the trajectories of the error system (8) is

(13)

Substituting Eqs. (10) and (11) into Eq. (13), one has

Since \(\dot{L}(t) < 0\), on the basis of the Lyapunov stability theory, the error vectors e r(t) and e i(t) asymptotically converge to zero, i.e., AGFPS between systems (4) and (5) is realized, and the parameter error vectors e ξ (t) and e θ (t) will tend to zero as the time t goes to infinity, which indicates that the uncertain parameters ξ and θ are also estimated. This completes the proof. □

Remark 1

The control gains η j (j=1,2,…,n) in the presented method can be automatically adapted to some suitable constants, which is different from the linear feedback [20–22]. In the linear feedback scheme, either the feedback gains of the controllers require that the system parameters must be known in advance or the fixed feedback gains are usually set maximally as possible. Unfortunately, in practical situations, the parameters may be unknown and change time to time, which results in difficult choosing the appropriate gains to stabilize the error system in the origin. Even knowing the system parameters exactly, the gains obtained may be so large that it is of no significance in some real applications.

Based on Theorem 1, we can easily derive the following corollaries.

Corollary 1

If the parameters ξ of the drive system (4) are known, AGFPS between the drive system (4) and the response system (5) can occur and the uncertain parameters θ can be estimated under the following adaptive controller and parameter update rules:

$$ \everymath{\displaystyle} \left \{ \begin{array} {l} V^{r}(t) = \varLambda(t)F_{1}^{r}(X) + \varLambda (t)F_{2}^{r}(X)\xi- G_{1}^{r}(Y) \\[1.5mm] \hphantom{V^{r}(t) =} {} - G_{2}^{r}(Y)\tilde{ \theta} + \dot{\varLambda} (t)X^{r} - K^{r} \boldsymbol{e}^{r}(t), \\[1.5mm] V^{i}(t) = \varLambda(t)F_{1}^{i}(X) + \varLambda(t)F_{2}^{i}(X)\xi- G_{1}^{i}(Y) \\[1.5mm] \hphantom{V^{i}(t) =} {} - G_{2}^{i}(Y)\tilde{ \theta} + \dot{\varLambda} (t)X^{i} - K^{i} \boldsymbol{e}^{i}(t) , \\[1.5mm] \dot{\eta} _{j}^{r} = \varepsilon_{j}^{r} \bigl( e_{j}^{r}(t) \bigr)^{2}, \quad \varepsilon_{j}^{r} > 0,\ j = 1,2, \ldots,n , \\[1.5mm] \dot{\eta} _{j}^{i} = \varepsilon_{j}^{i} \bigl( e_{j}^{i}(t) \bigr)^{2}, \quad \varepsilon_{j}^{i} > 0,\ j= 1,2, \ldots,n, \end{array} \right . $$
(14)
$$ \dot{\tilde{\theta}} = \bigl( G_{2}^{r}(Y) \bigr)^{\mathrm{T}}\boldsymbol{e}^{r}(t) + \bigl( G_{2}^{i}(Y) \bigr)^{\mathrm{T}}\boldsymbol{e}^{i}(t) - \boldsymbol{e}_{\theta} (t), $$
(15)

where the control gain matrix K=diag(η 1,η 2,…,η n ), K=K r+iK i, \(\eta_{j} = \eta_{j}^{{r}} + i\eta _{j}^{{i}}\), \(\boldsymbol{e}_{\theta} = \tilde{\theta} - \theta\) is parameter error vector, and \(\tilde{\theta}\) stands for the parameter estimation vector of θ.

Corollary 2

If the parameters θ in the response system (5) are known, GFPS between the drive system (4) and the response system (5) can be obtained and the uncertain parameters ξ can be identified by the following controller and parameter update rules:

$$ \everymath{\displaystyle} \left \{ \begin{array} {l} V^{r}(t) = \varLambda(t)F_{1}^{r}(X) + \varLambda (t)F_{2}^{r}(X)\tilde{\xi} - G_{1}^{r}(Y) \\ [1.5mm] \hphantom{V^{r}(t) =} {} - G_{2}^{r}(Y) \theta+ \dot{\varLambda} (t)X^{r} - K^{r}\boldsymbol{e}^{r}(t), \\ [1.5mm] V^{i}(t) = \varLambda (t)F_{1}^{i}(X) + \varLambda(t)F_{2}^{i}(X)\tilde{\xi} - G_{1}^{i}(Y) \\ [1.5mm] \hphantom{V^{i}(t) =} {} - G_{2}^{i}(Y) \theta+ \dot{\varLambda} (t)X^{i} - K^{i}\boldsymbol{e}^{i}(t), \\ [1.5mm] \dot{\eta} _{j}^{r} = \varepsilon_{j}^{r} \bigl( e_{j}^{r}(t) \bigr)^{2}, \quad \varepsilon_{j}^{r} > 0,\ j = 1,2, \ldots,n , \\ [1.5mm] \dot{\eta} _{j}^{i} = \varepsilon_{j}^{i} \bigl( e_{j}^{i}(t) \bigr)^{2}, \quad \varepsilon_{j}^{i} > 0,\ j = 1,2, \ldots,n, \end{array} \right . $$
(16)
$$ \everymath{\displaystyle} \begin{array}[b]{@{}rcl} \dot{\tilde{\xi}} &=& - \bigl( F_{2}^{r}(X) \bigr)^{\mathrm{T}} \bigl( \varLambda(t) \bigr)^{\mathrm {T}}\boldsymbol{e}^{r}(t) \\[1.5mm] &&{}- \bigl( F_{2}^{i}(X) \bigr)^{\mathrm{T}} \bigl( \varLambda (t) \bigr)^{\mathrm{T}}\boldsymbol{e}^{i}(t) - \boldsymbol{e}_{\xi} (t), \end{array} $$
(17)

where the control gain matrix K=diag(η 1,η 2,…,η n ), K=K r+iK i, \(\eta_{j} = \eta_{j}^{{r}} + i\eta _{j}^{{i}}\), \(\boldsymbol{e}_{\xi} = \tilde{\xi} - \xi\) is parameter error vector, and \(\tilde{\xi}\) represents the parameter estimation vectors of ξ.

The proofs of Corollaries 1 and 2 are similar to that of Theorem 1. Limited by the length of this paper, we omit them here.

3 AGFPS between the hyperchaotic complex Lü system and the chaotic complex Lorenz system with fully unknown parameters

In this section, we employ the scheme obtained in Sect. 2 to investigate AGFPS between the hyperchaotic complex Lü system and the chaotic complex Lorenz system with fully unknown parameters via reduced order, i.e., m>n. Let the hyperchaotic complex Lü system be the drive system with the subscript ‘d’ and the chaotic complex Lorenz system be the response system denoted by the subscript ‘r’. The drive and response systems are thus defined, respectively, as follows:

$$ \left\{ \begin{array}{l} \dot{x}_{d} = a(y_{d} - x_{d}) + w_{d}, \\[1.5mm] \dot{y}_{d} = by_{d} - x_{d}z_{d} + w_{d} , \\[1.5mm] \dot{z}_{d} = 1 / 2(\bar{x}_{d}y_{d} + x_{d}\bar{y}_{d}) - cz_{d} , \\[1.5mm] \dot{w}_{d} = 1 / 2(\bar{x}_{d}y_{d} + x_{d}\bar{y}_{d}) - hw_{d} , \end{array} \right. $$
(18)

and

$$ \left\{ \begin{array}{l} \dot{x}_{r} = a_{1}(y_{r} - x_{r}) + V_{1}, \\[1.5mm] \dot{y}_{r} = b_{1}x_{r} - y_{r} - x_{r}z_{r} + V_{2} , \\[1.5mm] \dot{z}_{r} = 1 / 2(\bar{x}_{r}y_{r} + x_{r}\bar{y}_{r}) - c_{1}z_{r} + V_{3} , \end{array} \right. $$
(19)

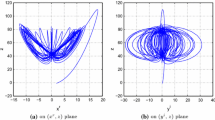
where x d =u 1+iu 2 and y d =u 3+iu 4 are the state complex variables, z d =u 5 and w d =u 6 are the state real variables for system (18); x r =q 1+iq 2 and y r =q 3+iq 4 are the state complex variables, z r =q 5 is the state real variable for system (19); an overbar ‘−’ denotes complex conjugation variables; V 1=v 1+iv 2, V 2=v 3+iv 4 and V 3=v 5 are complex and real control functions, respectively; a, b, c, h, a 1, b 1, and c 1 are unknown parameters to be identified. In particular, when a=42, b=25, c=6, and h=5, the hyperchaotic complex Lü attractors are shown in Fig. 1. When a 1=18, b 1=35, and c 1=4, the chaotic complex Lorenz system exhibits chaotic behavior, as displayed in Fig. 2.

Fig. 1
figure 1

Hyperchaotic attractors of the hyperchaotic complex Lü system (18)

Full size image
Fig. 2
figure 2

Chaotic attractors of the complex Lorenz system (19)

Full size image

Comparing systems (18) and (19) with systems (4) and (5), one can get

$$F_{1}(X_{d}) = \left( \begin{array}{c} w_{d} \\ - x_{d}z_{d} + w_{d} \\ 1 / 2(\bar{x}_{d}y_{d} + x_{d}\bar{y}_{d}) \\ 1 / 2(\bar{x}_{d}y_{d} + x_{d}\bar{y}_{d}) \end{array} \right), $$
$$F_{2}(X_{d}) = \left( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} y_{d} - x_{d} & 0 & 0 & 0 \\ 0 & y_{d} & 0 & 0 \\ 0 & 0 & - z_{d} & 0 \\ 0 & 0 & 0 & - w_{d} \end{array} \right), $$
$$\xi= \left( \begin{array}{l} a \\ b \\ c \\ h \end{array} \right), \qquad G_{1}(X_{r}) = \left( \begin{array}{c} 0 \\ - y_{r} - x_{r}z_{r} \\ 1 / 2(\bar{x}_{r}y_{r} + x_{r}\bar{y}_{r}) \end{array} \right), $$
$$G_{2}(X_{r}) = \left( \begin{array}{c@{\quad}c@{\quad}c} (y_{r} - x_{r}) & 0 & 0 \\ 0 & x_{r} & 0 \\ 0 & 0 & - z_{r} \end{array} \right), $$
$$\theta= \left( \begin{array}{l} a_{1} \\ b_{1} \\ c_{1} \end{array} \right), \qquad V(t) = \left( \begin{array}{l} V_{1}(t) \\ V_{2}(t) \\ V_{3}(t) \end{array} \right), $$

where X d =(x d ,y d ,z d ,w d )T and X r =(x r ,y r ,z r ,w r )T are the state vectors, V(t) is the controller to be determined later.

Choose arbitrarily the real scaling function matrix as follows:

$$\varLambda(t) = \left( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 3 + \sin(2t) & 1 - 2\sin(t) & 0 & 0 \\ 0 & 1.5 + \cos(0.5t) & 3 + \sin(2t) & 0 \\ 0 & 0 & 1 - 2\sin(t) & 1.5 - \cos(0.5t) \end{array} \right). $$

The error states between the response system to be controlled and the controlling drive system can be obtained as:

(20)

where e 1=e q1+ie q2, e 2=e q3+ie q4, and e 3=e q5 are complex and real error functions, respectively.

According to Eqs. (10) and (11) in Theorem 1, we can get the following adaptive controllers:

$$ \everymath{\displaystyle} \left \{ \begin{array} {@{}rcl} v_{1} &=& \bigl(3 + \sin(2t)\bigr)u_{6} + \bigl(1 - 2\sin(t)\bigr) ( - u_{1}u_{5} + u_{6}) \\[.7mm] &&{} + \bigl(3 + \sin(2t)\bigr) \tilde{a}(u_{3} - u_{1}) \\[.7mm] &&{}+ \bigl(1 - 2\sin(t)\bigr)\tilde{b}u_{3} - \tilde{a}_{1}(q_{3} - q_{1}) \\[.7mm] &&{} + 2\cos(2t)u_{1} - 2\cos(t)u_{3} - \eta_{1}^{{r}}e_{q1}, \\[.7mm] v_{2} &=& - \bigl(1 - 2\sin (t)\bigr)u_{2}u_{5} \\[.7mm] &&{} + \bigl(3 + \sin(2t)\bigr) \tilde{a}(u_{4} - u_{2}) \\[.7mm] &&{} + \bigl(1 - 2 \sin (t)\bigr)\tilde{b}u_{4} - \tilde{a}_{1}(q_{4} - q_{2}) \\[.7mm] &&{}+ 2\cos(2t)u_{2} - 2\cos(t)u_{4} - \eta_{1}^{{i}}e_{q2} , \\[.7mm] v_{3} &=& \bigl(1.5 + \cos(0.5t)\bigr) ( - u_{1}u_{5} + u_{6}) \\[.7mm] &&{} + \bigl(3 + \sin (2t)\bigr) (u_{1}u_{3} + u_{2}u_{4}) \\[.7mm] &&{} + \bigl(1.5 + \cos(0.5t)\bigr) \tilde{b}u_{3} \\[.7mm] &&{}- \bigl(3 + \sin(2t)\bigr)\tilde{c}u_{5} - ( - q_{3} - q_{1}q_{5}) - \tilde{b}_{1}q_{1} \\[.7mm] &&{} - 0.5 \sin(0.5t)u_{3} + 2\cos(2t)u_{5} - \eta _{2}^{{r}}e_{q3}, \\[.7mm] v_{4} &=& - \bigl(1.5 + \cos(0.5t)\bigr)u_{2}u_{5} \\[.7mm] &&{} + \bigl(1.5 + \cos(0.5t)\bigr)\tilde{b}u_{4} + (q_{4} + q_{2}q_{5}) - \tilde{b}_{1}q_{2}\!\!\! \\[.7mm] &&{}- 0.5\sin(0.5t)u_{4} - \eta_{2}^{{i}}e_{q4} , \\[.7mm] v_{5} &=& \bigl(2.5 - 2\sin (t) - \cos(0.5t)\bigr) (u_{1}u_{3} + u_{2}u_{4}) \\[.7mm] &&{} - \bigl(1 - 2\sin(t)\bigr)\tilde {c}u_{5} - \bigl(1.5 - \cos (0.5t)\bigr)\tilde{h}u_{6} \\[.7mm] &&{}- (q_{1}q_{3} + q_{2}q_{4}) + \tilde{c}_{1}q_{5} \\[.7mm] &&{} + \bigl( - 2\cos(t)u_{5} + 0.5 \sin(0.5t)u_{6}\bigr) - \eta_{3}^{{r}}e_{q5} , \end{array} \right . $$
(21)
$$ \left \{ \begin{array} {l} \dot{\eta} _{1}^{r} = \varepsilon_{1}^{r} \bigl( e_{q1}(t) \bigr)^{2} , \\[1.5mm] \dot{\eta} _{1}^{{i}} = \varepsilon_{1}^{{i}} \bigl( e_{q2}(t) \bigr)^{2}, \\[1.5mm] \dot{\eta} _{2}^{r} = \varepsilon_{2}^{r} \bigl( e_{q3}(t) \bigr)^{2}, \\[1.5mm] \dot{\eta} _{2}^{{i}} = \varepsilon_{2}^{{i}} \bigl( e_{q4}(t) \bigr)^{2}, \\[1.5mm] \dot{\eta} _{3}^{r} = \varepsilon_{3}^{r} \bigl( e_{q5}(t) \bigr)^{2}, \end{array} \right . $$
(22)

and the parameter update rules as follows:

$$ \left \{ \begin{array} {l} \dot{\tilde{a}} = - \bigl(3 + \sin(2t) \bigr) (u_{3} - u_{1})e_{q1} \\[1.5mm] \hphantom{\dot{\tilde{a}} =}{} - \bigl(3 + \sin (2t) \bigr) (u_{4} - u_{2})e_{q2} - e_{a} , \\[1.5mm] \dot{\tilde{b}} = - \bigl(1 - 2\sin(t)\bigr) (u_{3}e_{q1} + u_{4}e_{q2}) \\[1.5mm] \hphantom{\dot{\tilde{b}} =}{} - \bigl(1.5 + \cos(0.5t)\bigr) (u_{3}e_{q3} + u_{4}e_{q4}) - e_{b} , \\[1.5mm] \dot{\tilde{c}} = \bigl(3 + \sin (2t)\bigr)u_{5}e_{q3} \\[1.5mm] \hphantom{\dot{\tilde{c}} =}{} + \bigl(1 - 2\sin(t)\bigr)u_{5}e_{q5} - e_{c}, \\[1.5mm] \dot{\tilde{h}} = \bigl(1.5 - \cos (0.5t)\bigr)u_{6}e_{q5} - e_{h} , \\[1.5mm] \dot{\tilde{a}}_{1} = (q_{3} - q_{1})e_{q1} + (q_{4} - q_{2})e_{q2} - e_{a_{1}} , \\[1.5mm] \dot{\tilde{b}}_{1} = q_{1}e_{q3} + q_{2}e_{q4} - e_{b_{1}} , \\[1.5mm] \dot{\tilde{c}}_{1} = - q_{5}e_{q5} - e_{c_{1}}, \end{array} \right . $$
(23)

where the constants \(\varepsilon_{1}^{r} > 0\), \(\varepsilon_{1}^{{i}} > 0\), \(\varepsilon _{2}^{r} > 0\), \(\varepsilon_{2}^{{i}} > 0\), \(\varepsilon_{3}^{r} > 0\); \(e_{a} = \tilde{a} - a\), \(e_{b} = \tilde{b} - b\), \(e_{c} = \tilde{c} - c\), \(e_{h} = \tilde {h} - h\), \(e_{a_{1}} = \tilde{a}_{1} - a_{1}\), \(e_{b_{1}} = \tilde{b}_{1} - b_{1}\), and \(e_{c_{1}} = \tilde{c}_{1} - c_{1}\) are the parameter errors, and \(\tilde{a}\), \(\tilde{b}\), \(\tilde{c}\), \(\tilde{h}\), \(\tilde{a}_{1}\), \(\tilde{b}_{1}\), and \(\tilde{c}_{1}\) are the estimate variables of the uncertain parameters a, b, c, h, a 1, b 1, and c 1, respectively.

3.1 Numerical simulations

To verify and demonstrate the effectiveness and feasibility of the presented synchronization method, the simulation results have been performed. In the following simulations, the ODE45 algorithm is used to solve the systems. The unknown parameters are chosen to be a=42, b=25, c=6, h=5, a 1=18, b 1=35, and c 1=4 so that systems (18) and (19) can behave chaotically without control. The initial conditions of the drive system (18) and the response system (19) are randomly taken as x d (0)=1+0i, y d (0)=−1+2i, z d (0)=−2, w d (0)=3, x r (0)=3+4i, y r (0)=5+2i, and z r (0)=1. The initial values of all uncertain parameters are selected randomly as 0.01. Set \(\varepsilon_{1}^{r} = \varepsilon _{1}^{{i}} = \varepsilon_{2}^{r} = \varepsilon_{2}^{{i}} = \varepsilon_{3}^{r} = 15\). Simulation results are displayed in Figs. 3, 4 and 5. Figure 3 shows the time evolution of the AGFPS errors, which display the AGFPS errors e q1(t), e q2(t), e q3(t), e q4(t), and e q5(t) converge to zero after a short transient, respectively. The time evolution of the uncertain parameters is plotted in Fig. 4, from which one can see that the estimates of the unknown parameters adapt themselves to the true values, i.e., \(\tilde{a} \to 42\), \(\tilde{b} \to25\), \(\tilde{c} \to6\), \(\tilde{h} \to5\), \(\tilde{a}_{1} \to18\), \(\tilde{b}_{1} \to35\), and \(\tilde{c}_{1} \to4\) as t→∞. The control gains \(\eta _{1}^{{r}}\), \(\eta _{1}^{{i}}\), \(\eta_{2}^{{r}}\), \(\eta_{2}^{{i}}\), and \(\eta_{3}^{{r}}\) are inclined to some constants as the time t goes to infinity, which are shown in Fig. 5. All these results show that AGFPS and parameter estimation have been obtained by the adaptive control laws (21), (22), and the parameter update rules (23).

Fig. 3
figure 3

The time evolution of AGFPS errors between the drive system (18) and the response system (19)

Full size image
Fig. 4
figure 4

The estimation of the unknown parameters for the hyperchaotic complex Lü system and the chaotic complex Lorenz system

Full size image
Fig. 5
figure 5

The time evolution of the control gains

Full size image

4 AGFPS between the uncertain chaotic complex Chen system and uncertain hyperchaotic complex Lorenz system

To further illustrate the effectiveness of the proposed schemes, we consider AGFPS between the uncertain chaotic complex Chen system and the uncertain hyperchaotic complex Lorenz system via increased order, i.e., m<n, in this section. We take the chaotic complex Chen system as the drive system, which is described by

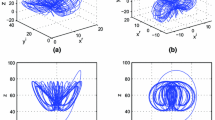
$$ \left \{ \begin{array} {l} \dot{x}_{d} = a(y_{d} - x_{d}) , \\ [1.5mm] \dot{y}_{d} = (b - a)x_{d} + by_{d} - x_{d}z_{d} , \\ [1.5mm] \dot{z}_{d} = 1 / 2(\bar{x}_{d}y_{d} + x_{d}\bar{y}_{d}) - cz_{d}, \end{array} \right . $$
(24)

where x d =u 1+iu 2 and y d =u 3+iu 4 are the state complex variables, z d =u 5 is the state real variable, a, b, and c are uncertain parameters. When a=28, b=22, and c=1, the system (24) is chaotic behavior, as depicted in Fig. 6.

Fig. 6
figure 6

Chaotic attractors of the complex Chen system (24)

Full size image

The uncertain hyperchaotic complex Lorenz system, as the response system, is given by

$$ \left \{ \begin{array} {l} \dot{x}_{r} = a_{1}(y_{r} - x_{r}) + iw_{r} + V_{1} , \\ [1.5mm] \dot{y}_{r} = b_{1}x_{r} - y_{r} - x_{r}z_{r} + iw_{r} + V_{2}, \\ [1.5mm] \dot{z}_{r} = 1 / 2(\bar{x}_{r}y_{r} + x_{r}\bar{y}_{r}) - c_{1}z_{r} + V_{3} , \\ [1.5mm] \dot{w}_{r} = 1 / 2(\bar{x}_{r}y_{r} + x_{r}\bar{y}_{r}) - h_{1}w_{r} + V_{4}, \end{array} \right . $$
(25)

where x r =q 1+iq 2 and y r =q 3+iq 4 are the state complex variables, z r =q 5 and w r =q 6 are the state real variables, a 1, b 1, c 1, and h 1 are unknown parameters to be identified, V 1=v 1+iv 2, V 2=v 3+iv 4, V 3=v 5, and V 4=v 6 are complex and real control functions, respectively. When a 1=20, b 1=40, c 1=5, and h 1=13, system (25) is a hyperchaotic system, as shown in Fig. 7.

Fig. 7
figure 7

Hyperchaotic attractors of the hyperchaotic complex Lorenz system (25)

Full size image

According to systems (4) and (5), from systems (24) and (25), we can have

$$F_{1}(X_{d}) = \left( \begin{array}{c} 0 \\ - x_{d}z_{d} \\ 1 / 2(\bar{x}_{d}y_{d} + x_{d}\bar{y}_{d}) \end{array} \right), $$
$$F_{2}(X_{d}) = \left( \begin{array}{c@{\quad}c@{\quad}c} (y_{d} - x_{d}) & 0 & 0 \\ - x_{d} & (x_{d} + y_{d}) & 0 \\ 0 & 0 & - z_{d} \end{array} \right), $$
$$\xi= \left( \begin{array}{l} a \\ b \\ c \end{array} \right), \qquad G_{1}(X_{r}) = \left( \begin{array}{c} iw_{r} \\ - y_{r} - x_{r}z_{r} + iw_{r} \\ 1 / 2(\bar{x}_{r}y_{r} + x_{r}\bar{y}_{r}) \\ 1 / 2(\bar{x}_{r}y_{r} + x_{r}\bar{y}_{r}) \end{array} \right), $$
$$G_{2}(X_{r}) = \left( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} (y_{r} - x_{r}) & 0 & 0 & 0 \\ 0 & x_{r} & 0 & 0 \\ 0 & 0 & - z_{r} & 0 \\ 0 & 0 & 0 & - w_{r} \end{array} \right), $$
$$\theta= \left( \begin{array}{l} a_{1} \\ b_{1} \\ c_{1} \\ h_{1} \end{array} \right), \qquad V(t) = \left( \begin{array}{l} V_{1}(t) \\ V_{2}(t) \\ V_{3}(t) \\ V_{4}(t) \end{array} \right), $$

where X d =(x d ,y d ,z d ,w d )T and X r =(x r ,y r ,z r ,w r )T are the state vectors, V(t) is the controller to be designed.

We take arbitrarily the following real scaling function matrix:

$$\varLambda(t) = \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 & 1 + 0.5\cos(2t) & 0 \\ 0 & 0 & 1 \\ 2 - \sin (5t) & 0 & 3 - 2\cos(t) \end{array} \right). $$

Then the synchronization errors between systems (24) and (25) can be described by

$$ \left \{ \begin{array} {l} e_{1} = x_{r} - x_{d}, \\[1.5mm] e_{2} = y_{r} - \bigl(1 + 0.5\cos(2t)\bigr)y_{d}, \\[1.5mm] e_{3} = z_{r} - z_{d} , \\[1.5mm] e_{4} = w_{r} - \bigl[ \bigl(2 - \sin(5t) \bigr)x_{d} + \bigl(3 - 2\cos(t)\bigr)z_{d} \bigr] , \end{array} \right . $$
(26)

where e 1=e q1+ie q2, e 2=e q3+ie q4, e 3=e q5, and e 4=e q6 are complex and real errors functions, respectively.

From Eqs. (10) and (11) in Theorem 1, we design the following adaptive controllers:

$$ \left \{\! \begin{array} {@{}l} v_{1} = \tilde{a}(u_{3} - u_{1}) - \tilde {a}_{1}(q_{3} - q_{1}) - \eta _{1}^{{r}}e_{q1} , \\ [1.5mm] v_{2} = \tilde{a}(u_{4} - u_{2}) - q_{6} - \tilde{a}_{1}(q_{4} - q_{2}) - \eta_{1}^{{i}}e_{q2} , \\ [1.5mm] v_{3} = - \bigl(1 + 0.5\cos(2t)\bigr)u_{1}u_{5} - \bigl(1 + 0.5\cos (2t)\bigr)\tilde{a}u_{1} \!\!\!\!\!\! \\ [1.5mm] \hphantom{v_{3} =} {}+ \bigl(1 + 0.5\cos(2t)\bigr) \tilde{b}(u_{1} + u_{3}) \\ [1.5mm] \hphantom{v_{3} =} {} + q_{3} + q_{1}q_{5} - \tilde{b}_{1}q_{1} - \sin(2t)u_{3} - \eta_{2}^{{r}}e_{q3} , \\ [1.5mm] v_{4} = - \bigl(1 + 0.5\cos (2t)\bigr)u_{2}u_{5} - \bigl(1 + 0.5\cos(2t)\bigr)\tilde{a}u_{2} \!\!\!\!\!\! \\ [1.5mm] \hphantom{v_{4} =} {} + \bigl(1 + 0.5\cos (2t)\bigr) \tilde{b}(u_{2} + u_{4}) + q_{4} \\ [1.5mm] \hphantom{v_{4} =} {} + q_{2}q_{5} - q_{6} - \tilde{b}_{1}q_{2} - \sin(2t)u_{4} - \eta_{2}^{{i}}e_{q4}, \\ [1.5mm] v_{5} = (u_{1}u_{3} + u_{2}u_{4}) - \tilde{c}u_{5} - q_{1}q_{3} - q_{2}q_{4} \\ [1.5mm] \hphantom{v_{5} =} {} + \tilde{c}_{1}q_{5} - \eta_{3}^{{r}}e_{q5}, \\ [1.5mm] v_{6} = \bigl(3 - 2\cos(t)\bigr) (u_{1}u_{3} + u_{2}u_{4}) \\ [1.5mm] \hphantom{v_{6} =} {} + \bigl(2 - \sin (5t)\bigr) \tilde{a}(u_{3} - u_{1}) - \bigl(3 - 2\cos(t)\bigr) \tilde{c}u_{5}\!\!\!\!\!\! \\ [1.5mm] \hphantom{v_{6} =} {} - q_{1}q_{3} - q_{2}q_{4} + \tilde{h}_{1}q_{6} - 5 \cos(5t)u_{1} \\ [1.5mm] \hphantom{v_{6} =} {} + 2\sin(t)u_{5} - \eta_{4}^{{r}}e_{q6}, \end{array} \right . $$
(27)
$$ \left \{ \begin{array} {l} \dot{\eta} _{1}^{r} = \varepsilon_{1}^{r} \bigl( e_{q1}(t) \bigr)^{2} , \\ [1.5mm] \dot{\eta} _{1}^{{i}} = \varepsilon_{1}^{{i}} \bigl( e_{q2}(t) \bigr)^{2} , \\ [1.5mm] \dot{\eta} _{2}^{r} = \varepsilon_{2}^{r} \bigl( e_{q3}(t) \bigr)^{2} , \\ [1.5mm] \dot{\eta} _{2}^{{i}} = \varepsilon_{2}^{{i}} \bigl( e_{q4}(t) \bigr)^{2} , \\ [1.5mm] \dot{\eta} _{3}^{r} = \varepsilon_{3}^{r} \bigl( e_{q5}(t) \bigr)^{2} , \\ [1.5mm] \dot{\eta} _{4}^{r} = \varepsilon _{4}^{r} \bigl( e_{q6}(t) \bigr)^{2} , \end{array} \right . $$
(28)

and the parameter update rules as follows:

$$ \left \{ \begin{array} {l} \dot{\tilde{a}} = - (u_{3} - u_{1})e_{q1} + \bigl(1 + 0.5\cos(2t)\bigr)u_{1}e_{q3} \\[1.5mm] \hphantom{\dot{\tilde{a}} =}{} - \bigl(2 - \sin(5t)\bigr) (u_{3} - u_{1})e_{q6} - (u_{4} - u_{2})e_{q2} \\[1.5mm] \hphantom{\dot{\tilde{a}} =}{} + \bigl(1 + 0.5 \cos(2t)\bigr)u_{2}e_{q4} - e_{a}, \\[1.5mm] \dot{\tilde{b}} = - \bigl(1 + 0.5\cos(2t)\bigr) (u_{1} + u_{3})e_{q3} \\[1.5mm] \hphantom{\dot{\tilde{b}} =}{} - \bigl(1 + 0.5\cos(2t)\bigr) (u_{2} + u_{4})e_{q4} - e_{b}, \\[1.5mm] \dot{\tilde{c}} = u_{5}e_{q5} + \bigl(3 - 2\cos(t) \bigr)u_{5}e_{q6} - e_{c}, \\[1.5mm] \dot{\tilde{a}}_{1} = (q_{3} - q_{1})e_{q1} + (q_{4} - q_{2})e_{q2} - e_{a_{1}} , \\[1.5mm] \dot{\tilde{b}}_{1} = q_{1}e_{q3} + q_{2}e_{q4} - e_{b_{1}}, \\[1.5mm] \dot{\tilde{c}}_{1} = - q_{5}e_{q5} - e_{c_{1}} , \\[1.5mm] \dot{\tilde{h}}_{1} = - q_{6}e_{q6} - e_{h_{1}}, \end{array} \right . $$
(29)

where the constants \(\varepsilon_{1}^{r} > 0\), \(\varepsilon_{1}^{{i}} > 0\), \(\varepsilon _{2}^{r} > 0\), \(\varepsilon_{2}^{{i}} > 0\), \(\varepsilon_{3}^{r} > 0\), \(\varepsilon _{4}^{r} > 0\); \(\tilde{a}\), \(\tilde{b}\), \(\tilde{c}\), \(\tilde{h}\), \(\tilde{a}_{1}\), \(\tilde{b}_{1}\), and \(\tilde{c}_{1}\) are the estimate variables of the unknown parameters, \(e_{a} = \tilde{a} - a\), \(e_{b} = \tilde{b} - b\), \(e_{c} = \tilde{c} - c\), \(e_{a_{1}} = \tilde {a}_{1} - a_{1}\), \(e_{b_{1}} = \tilde{b}_{1} - b_{1}\), \(e_{c_{1}} = \tilde{c}_{1} - c_{1}\), and \(e_{h_{1}} = \tilde{h}_{1} - h_{1}\) are the corresponding parameter errors.

4.1 Numerical simulations

Numerical simulations are performed to verify the validity of the proposed synchronization controllers (27), (28), and the parameter update rules (29). The true values of the “unknown” parameters of two uncertain systems are set as a=28, b=22, c=1, a 1=20, b 1=40, c 1=5, and h 1=13 to ensure the drive and response systems are chaotic if no controls are applied. The corresponding initial values for the drive and response systems are arbitrarily selected as (x d (0),y d (0),z d (0))=(−3+2i,4+5i,1) and (x r (0),y r (0),z r (0),w r (0))=(3−2i,−1−3i,5,0). All uncertain parameters have initial values 0.001. We take the constants \(\varepsilon_{1}^{r} = \varepsilon_{1}^{{i}} = \varepsilon_{2}^{r} = \varepsilon _{2}^{{i}} = \varepsilon_{3}^{r} = \varepsilon_{4}^{r} = 10\). Simulation results for AGFPS of the drive system (24) and the response system (25) are illustrated in Figs. 8, 9, and 10. The evolution of the AGFPS errors is plotted in Fig. 8, from which one can clearly see that the synchronization errors e q1(t), e q2(t), e q3(t), e q4(t), e q5(t), and e q6(t) tend to zero quickly. It implies that the required synchronization has been realized. Figure 9 displays the estimated values of the unknown parameters for two chaotic complex systems converge to a=28, b=22, c=1, a 1=20, b 1=40, c 1=5, and h 1=13 as t→∞, respectively. Figure 10 depicts the time evolution of the control gains \(\eta_{1}^{{r}}\), \(\eta_{1}^{{i}}\), \(\eta_{2}^{{r}}\), \(\eta_{2}^{{i}}\), \(\eta _{3}^{{r}}\), and \(\eta_{4}^{{r}}\). As shown in these figures, AGFPS between the chaotic complex Chen system (24) and the hyperchaotic complex Lorenz system (25) is obtained and all the uncertain parameters are identified successfully by the adaptive controllers (27), (28), and the parameter update rules (29).

Fig. 8
figure 8

The time evolution of AGFPS errors between the drive system (24) and the response system (25)

Full size image
Fig. 9
figure 9

The estimation of the unknown parameters for the chaotic complex Chen system and the hyperchaotic complex Lorenz system

Full size image
Fig. 10
figure 10

The time evolution of the control gains

Full size image

5 Conclusions

Considering few studies concern GFPS between two chaotic complex systems, we investigate AGFPS between two different dimensional chaotic complex systems with fully or partially unknown parameters via both reduced order and increased order. And a general scheme for AGFPS is proposed in our work. Based on the Lyapunov stability theorem and adaptive control method, a universal adaptive controller with corresponding parameter update rule is designed. By the presented synchronization scheme, one cannot only achieve AGFPS between two uncertain chaotic complex systems with different orders, but also estimate the unknown parameters. Two illustrative examples, i.e., AGFPS between the hyperchaotic complex Lü system and the chaotic complex Lorenz system with fully unknown parameters, and AGFPS between the uncertain chaotic complex Chen system and the uncertain hyperchaotic complex Lorenz system, are performed to illustrate the proposed technique. All simulation results have demonstrated the validity and feasibility of the proposed synchronization scheme.