Adaptive complex modified hybrid function projective synchronization of different dimensional complex chaos with uncertain complex parameters

Abstract

This paper focuses on the adaptive modified hybrid function projective synchronization with complex function transformation matrix (CMHFPS) for different dimensional chaotic (hyperchaotic) systems with complex variables and unknown complex parameters. The chaotic systems are considerably different from those in the existing closely related literature. Moreover, the transformation matrix in this type of chaos synchronization is not a square matrix, and its elements are complex functions. In particular, by constructing appropriate Lyapunov functions dependent on complex variables, the adaptive controllers are designed to synchronize different dimensional complex chaos (hyperchaos) with complex parameters in the sense of CMHFPS, and the complex update laws for estimating unknown complex parameters of complex chaotic systems are also given. Finally, two examples are presented to illustrate the effectiveness and feasibility of the theoretical results.

1 Introduction

In 1982, Fowler et al. [1] derived originally the Lorenz equations with complex variables and complex parameters to describe a two-layer model of the baroclinic instability as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}=\sigma (y-x),\\ \dot{y}=rx-x z-ay,\\ \dot{z}=\frac{1}{2}(\bar{x}y+x\bar{y})-b z,\\ \end{array} \right. \end{aligned}$$

(1)

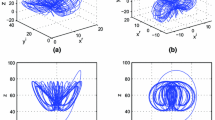
where the Rayleigh number r and parameter a are complex numbers defined by $r=r_{1}+jr_{2}, a=1-j\delta$, and $\sigma ,\,b,\,r_{1},\,r_{2},\,\delta$ are real and positive. The complex variables x, y and real variable z of Eq. (1) are related, respectively, to electric field and the atomic polarization amplitudes and the population inversion in a ring laser system of two-level atoms [2, 3], an overbar denotes complex conjugate variable and a dot represents derivative with respect to time, chaotic motion of Eq. (1) is shown in Fig. 1.

Fig. 1

Phase portraits of the attractor for complex chaotic Lorenz system (1) with complex parameters $\sigma =2,\,r=60+0.02j,\,a=1-0.06j,\,b=0.8$ and initial values $x(0)=2+0.02j,y(0)=1+0.2j,z(0)=-1$

Afterward, some research works in complex fields have been achieved on dynamics and control of chaos [4]. In 2007, Mahmoud et al. [5] studied basic properties and chaotic synchronization of the complex Lorenz model as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}=\sigma (y-x),\\ \dot{y}=rx-x z-y,\\ \dot{z}=\frac{1}{2}(\bar{x}y+x\bar{y})-b z, \end{array} \right. \end{aligned}$$

(2)

where $\sigma >0,\,r>0,\,b>0$ are real parameters. The Lorenz model (2) is embedded in (1) and can be recovered when $r_{2}=\delta =0$. In recent years, several other such examples have been proposed, notably the so-called complex Chen, Lü systems [6] and complex hyperchaotic Lorenz, Lü system [7, 8] and so on. Actually, many systems which involve complex variables have played an important role in many areas, including loading of beams and plates [9], optical systems [10], plasma physics [11], rotor dynamics [12] and high-energy accelerators [13] and secure communications [14].

Due to its importance and broad applications, the synchronization of complex chaotic systems has attracted great attention in the last few decades as well, such as global synchronization (GS) [6, 15], complete synchronization (CS) [16, 17], anti-synchronization (AS) [18], lag synchronization (LS) [19, 20], projective synchronization (PS) and modified projective synchronization (MPS) [21], modified function projective synchronization (MFPS) [22].

It is clear that the scaling matrix is always chosen as real matrix or real-valued function matrix in the above synchronization. In order to ensure that the transmitted signals have stronger anti-attack ability and anti-translated capability than that transmitted by the usual transmission model, scaling matrix has been extended to the complex domain to take into account of project synchronization very recently. Zhang et al. [23] discussed MPS with complex scaling factors (CMPS) of uncertain real chaos and complex chaos. Mahmoud et al. [24] achieved CMPS of two certain chaotic complex systems. Sun et al. [25] introduced combination synchronization with complex scaling matrix. Liu and Zhang [26] discussed FPS with complex function matrix (CFPS) of coupled chaotic complex system with known real parameters and its applications in secure communication.

It should be noted that the aforementioned papers only consider chaotic synchronization of the same dimensional complex-variable systems, and the states of the drive and response systems synchronize by a diagonal matrix, so each state variable of response system synchronizes one of drive system by a special scaling factor. As a matter of fact, the synchronization can be carried out through different dimensional oscillators, especially the systems in communication [27], biological science and social science [28], where the drive and response systems could synchronize by a desired transformation matrix, not a square matrix. By means of state transformation, multiple state variables in drive system will be involved for a corresponding state variable of response system by respective scaling factors (or functions). It is obvious that transformation matrix is arbitrary and more unpredictable than diagonal scaling matrix. Therefore, Luo and Wang [29] introduced hybrid modified function projective synchronization (MHFPS) of two different dimensional complex chaotic systems. Moreover, as the complex function transformation matrix is more unpredictable than real function transformation matrix in [29], it will greatly increase the complexity and diversity of the synchronization. As a generalization of synchronization, depending on the form of the transformation matrix, MHFPS with complex function transformation matrix (CMHFPS) contains MHFPS, MFPS, CFPS. Therefore, it is meaningful and valuable to study CMHFPS for complex chaos. To the best of our knowledge, the CMHFPS of different dimensional complex systems has rarely been explored.

Furthermore, the above discussed chaotic systems have mostly been limited to complex chaotic systems with real parameters such as system (2). There are small number of papers discussed chaos synchronization with complex parameters. For instance, Mahmoud et al. [15] discussed GS of complex nonlinear equations for detuned lasers with certain complex parameters by separating real and imaginary parts of complex variables. Recently, Liu et al. [30] discussed modified hybrid project synchronization with complex transformation matrix (CMHPS) for different dimensional hyperchaotic and chaotic complex systems with complex parameters without separating real and imaginary parts of complex parameters. However, as far as the authors know, CMHFPS of different dimensional chaotic complex systems with complex parameters is seldom reported in the literatures.

In addition, in real physical systems, parameters of systems are probably unknown or may change from time to time. In this case, it is well known that the adaptive control is an effective method to realize the synchronization of chaotic systems with unknown parameters. It is worth noting that adaptive synchronization for real systems or complex ones with real parameters have been developed [18]. However, adaptive synchronization of complex chaotic systems with uncertain complex parameters is more less. Only in [31], Liu et al. introduced adaptive complex modified projective synchronization (CMPS) of two same dimensional complex chaotic (hyperchaotic) systems with uncertain complex parameters. How to achieve CMHFPS, which covers CMPS and CMHPS, between two different dimensional complex chaotic systems with uncertain parameters via the adaptive control?

Inspired by the above discussion, in this paper, we focus on adaptive CMHFPS of different dimensional chaotic systems with complex variables and unknown complex parameters.

In more detail, the distinguishing feature of this paper are refined as follows.

First, the systems under investigation are remarkably more general than those in the closely related literature [5–8, 14, 16, 18, 19, 21–29]. This can be seen from a comparison between systems (1) and (2). A chaotic system with complex variables and unknown complex parameters produces more complex and unpredictable signals. It is well known that the adoption of chaotic systems with complex variables has been introduced for secure communication, where doubling the number of variables by introducing complex system to enhance the contents and security of the transmitted information. What is more, the system parameters are unknown complex numbers, and have more choice than real parameters, which make the systems produce more unpredictable signals.

Second, different from the real-valued function matrix in previous synchronization [22, 29], the transformation matrix is composed of complex-valued functions in CMHFPS of different dimensional complex chaos. As a generalization of synchronization, depending on the form of the transformation matrix, CMHFPS contains CFPS, CMHPS, CMPS, MHFPS, MFPS, and extend recently previous works [16, 18, 21–24, 26, 29–31].

Third, unlike the schemes proposed in the literature [5–8, 14–26, 29], we construct appropriate Lyapunov functions dependent on complex variables and do not separate real and imaginary parts of the uncertain complex parameters or complex variables. The adaptive controller is designed to synchronize different dimensional complex chaos with complex parameters in the sense of CMHFPS, and the complex update laws for estimating unknown complex parameters are also given without separating real and imaginary parts of the complex parameters.

The remainder of this paper is structured as follows. The definition of CMHFPS is introduced for different dimensional complex chaotic systems with uncertain complex parameters in Sect. 2, followed by, the general schemes of adaptive CMHFPS are designed in Sect. 3. Section 4 is devoted to simulation. The adaptive CMHFPS between complex chaotic Lorenz drive system with uncertain complex parameters and complex hyperchaotic Lorenz response system with uncertain real parameters as well as complex hyperchaotic Lü drive system with uncertain real parameters and complex Lorenz response system with uncertain complex parameters are taken as two examples to demonstrate the effectiveness and feasibility of the proposed scheme. Finally, Sect. 5 draws some conclusions.

Notation ${\mathbb {C}}^n$ stands for n dimensional complex vector space. If $\mathbf {z}\in {\mathbb {C}}^n$ is a complex vector, then $\mathbf {z}=\mathbf {z}^r+j\mathbf {z}^i$, $j=\sqrt{-1}$ is the imaginary unit, superscripts r and i stand for the real and imaginary parts of $\mathbf {z}$, respectively, $\mathbf {z}^\mathrm{{H}}$, $\mathbf {z}^\mathrm{{T}}$ are the conjugate transpose and transpose of $\mathbf {z}$, respectively and $\Vert \mathbf {z}\Vert$ implies the 2-norm of $\mathbf {z}$. If z is a complex scalar , |z| indicates the modulus of z and $\bar{z}$ is the conjugate of z, while $\mathbf {M}^\mathrm{{H}}(t)$ is the conjugate transpose of $\mathbf {M}(t)$, provided that $\mathbf {M}(t)$ is a complex matrix.

2 The definition of CMHFPS of complex chaos (hyperchaos) with complex parameters and problem descriptions

First, we consider the following general m-dimensional complex chaotic (hyperchaotic) drive system

$$\begin{aligned} \dot{\mathbf {z}}(t)= & {} \mathbf {H(z,}t), \end{aligned}$$

(3)

and n-dimensional complex chaotic (hyperchaotic) response system

$$\begin{aligned} \dot{\mathbf {w}}(t)= & {} \mathbf {R(w,}t)+\mathbf {v}(\mathbf {z},\mathbf {w},t), \end{aligned}$$

(4)

where  $\mathbf {z}=(z_1,\,z_2,\,\ldots ,\,z_m)^T \in {\mathbb {C}}^m$, $\mathbf {w}=(w_1,\,w_2,\,\ldots ,\,w_n)^\mathrm{{T}}\in {\mathbb {C}}^n$ are complex state vector, and $\mathbf {v}=\mathbf {v}^r+j\mathbf {v}^i\in {\mathbb {C}}^n$ is the control input.

Next, we introduce the definition of CMHFPS with complex function transformation matrix of complex chaotic systems with complex parameters as follows.

Definition 1

For the drive system (3) and response system (4), it is said to be CMHFPS with $\mathbf {D}(t)$ between $\mathbf {w}(t)$ and $\mathbf {z}(t)$, if there exists a controller $\mathbf {v}(\mathbf {z},\mathbf {w},t)$ such that $\lim \limits _{t\rightarrow +\infty }\Vert \mathbf {w}(t)-\mathbf {D}(t)\mathbf {z}(t)\Vert =0$, where $\mathbf {D}(t)=\mathbf {D}^{r}(t)+j\mathbf {D}^{i}(t)$, the elements of $\mathbf {D}(t)$ should be continuously differential functions with bounded.

Remark 1

The $n\times m$ matrix $\mathbf {D}(t)$ is called a complex function transformation matrix. Several kinds of function synchronization are special cases of CMHFPS, such as complex modified generalized function projective synchronization (CMGFPS), complex function projective synchronization (CFPS), modified hybrid function projective synchronization (MHFPS), modified generalized function projective synchronization (MGFPS), modified function projective synchronization (MFPS), function projective synchronization (FPS), see Table 1.

Table 1 Types of function synchronization

Remark 2

If $\mathbf {D}(t)$ is a complex constant matrix, the problem becomes CMHPS, CMPS and CPS for complex dynamical systems [23, 24, 30, 31].

The general m-dimensional complex drive chaotic system with unknown complex parameters is considered as

$$\begin{aligned} \dot{\mathbf {z}}(t)=\mathbf {H(z,}t)=\mathbf {F(z)}\mathbf {A}+\mathbf {f(z)}, \end{aligned}$$

(5)

where  $\mathbf {z}=\mathbf {z}^r+j\mathbf {z}^i\in {\mathbb {C}}^m$ and $\mathbf {z}^r=(z^{r}_{1},\,z^{r}_{2},\,\ldots ,z^{r}_{m})^\mathrm{{T}}$, $\mathbf {z}^i=(z^{i}_{1},\,z^{i}_{2},\,\ldots ,\,z^{i}_{m})^\mathrm{{T}}$. $\mathbf {A}=(a_1,\,a_2,\,\ldots ,\,a_s)^\mathrm{{T}}\in {\mathbb {C}}^s$ is a $s\times 1$ complex vector of unknown parameters, $\mathbf {F(z)}$ is a $m\times s$ complex matrix and its elements are functions of complex state variables, and $\mathbf {f}=(f_1,\,f_2,\,\ldots ,\,f_m)^\mathrm{{T}}$ is a $m\times 1$ vector of complex nonlinear function. On the other hand, the n-dimensional complex response chaotic system with the controller is depicted as

$$\begin{aligned} \dot{\mathbf {w}}(t)=\mathbf {R(w,}t)+\mathbf {v} =\mathbf {G(w)}\mathbf {B}+\mathbf {g(w)}+\mathbf {v}, \end{aligned}$$

(6)

where $\mathbf {w}=\mathbf {w}^r+j\mathbf {w}^i\in {\mathbb {C}}^n$ and $\mathbf {w}^r=(w^{r}_{1},\,w^{r}_{2},\,\ldots ,w^{r}_{n})^\mathrm{{T}}$, $\mathbf {w}^i=(w^{i}_{1},\,w^{i}_{2},\,\ldots ,\,w^{i}_{n})^\mathrm{{T}}$. $\mathbf {B}=(b_1,\,b_2,\,\ldots ,\,b_q)^\mathrm{{T}}\in {\mathbb {C}}^q$ is a $q \times 1$ complex vector of unknown parameters, $\mathbf {G(w)}$ is a $n\times q$ complex matrix and its elements are functions of complex state variables, and $\mathbf {g}=(g_1,\,g_2,\,\ldots ,\,g_n)^\mathrm{{T}}$ is a $n\times 1$ vector of complex nonlinear function. The controller $\mathbf {v}=\mathbf {v}^r+j\mathbf {v}^i\in {\mathbb {C}}^n$ needs to be designed.

Remark 3

Most of the well-studied complex chaotic and hyperchaotic systems can be written as the form of system (5), such as complex Lorenz system, complex Chen system, complex Lü system, complex Van der Pol oscillator, complex Duffing system, and complex hyperchaotic Lorenz system, complex hyperchaotic Lü system.

Remark 4

In many previous works, the numbers of variables and parameters are equal in chaotic systems. In our paper, the condition is not necessary. That is, $m\ne s$ in system (5) and $n\ne q$ in system (6).

In this paper, we discuss the CMHFPS between two different dimensional complex chaotic systems, i.e. $m>n$ or $m<n$. And CMHFPS error is defined as $\mathbf {e}(t)=\mathbf {w}(t)-\mathbf {D}(t)\mathbf {z}(t)$, where $\mathbf {e}(t)=\mathbf {e}^{r}(t)+j\mathbf {e}^{i}(t)\in {\mathbb {C}}^n$ and $\mathbf {e}^r=(e^{r}_{1},\,e^{r}_{2},\,\ldots ,e^{r}_{n})^\mathrm{{T}},\,\mathbf {e}^i=(e^{i}_{1},\,e^{i}_{2},\,\ldots ,\,e^{i}_{n})^\mathrm{{T}}$. The essential control goal is to design an adaptive controller $\mathbf {v}$ such that synchronization error tends to zero, i.e.

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }\Vert \mathbf {e}(t)\Vert =\lim \limits _{t\rightarrow +\infty }\Vert \mathbf {w}(t)-\mathbf {D}(t)\mathbf {z}(t)\Vert =0. \end{aligned}$$

(7)

3 Adaptive CMHFPS schemes of different dimensional complex chaotic systems with uncertain complex parameters

According to the definition of CMHFPS, we have

$$\begin{aligned} \dot{\mathbf {e}}(t)= & {} \dot{\mathbf {w}}(t)-\frac{\hbox {d}(\mathbf {D}(t) \mathbf {z}(t))}{\hbox {d}t}\nonumber \\= & {} \dot{\mathbf {w}}(t)-(\dot{\mathbf {D}}(t)\mathbf {z}(t) +\mathbf {D}(t)\dot{\mathbf {z}}(t)). \end{aligned}$$

(8)

Set $\mathbf {J(z},t)=\frac{\hbox {d}(\mathbf {D}(t)\mathbf {z}(t))}{\hbox {d}t} =(J_1,\,J_2,\,\ldots ,\,J_n)^\mathrm{{T}}$ is a complex vector.

Theorem 1

For given complex function transformation matrix $\mathbf {D}(t)$ and initial conditions $\mathbf {w}(0),\mathbf {z}(0)$, if the adaptive controller is designed as

$$\begin{aligned} \mathbf {v}= & {} -\,\mathbf {R(w,}\hat{\mathbf {B}},t)+\mathbf {J(z,}\hat{\mathbf {A}},t) -\mathbf {K e}\nonumber \\= & {} -\,\mathbf {G(w)}\hat{\mathbf {B}}-\mathbf {g(w)}+\dot{\mathbf {D}}(t)\mathbf {z(t)} +\mathbf {D}(t)(\mathbf {F(z)}\hat{\mathbf {A}}\nonumber \\&+\,\mathbf {f(z)})-\mathbf {K}\mathbf {e}, \end{aligned}$$

(9)

and the complex update laws of complex parameters are selected as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\hat{\mathbf {A}}}={{-(\mathbf {D}(t)\mathbf {F(z)})}^\mathrm{{H}}}~\mathbf {e}-{{\gamma }}_a~\tilde{\mathbf {A}},\\ \dot{\hat{\mathbf {B}}}={\mathbf {G}^\mathrm{{H}}}(\mathbf {w}) ~\mathbf {e}-{{\gamma }}_b~\tilde{\mathbf {B}}, \end{array} \right. \end{aligned}$$

(10)

where ${{\gamma }}_a=\mathrm {diag}\{\gamma _{a_1},\,\gamma _{a_2} ,\,\ldots ,\,\gamma _{a_s}\}$, ${{\gamma }}_b=\mathrm {diag}\{\gamma _{b_1}$, $\gamma _{b_2},\,\ldots ,\,\gamma _{b_q}\}$ and $\mathbf {K}=\mathrm {diag}\{k_1,\,k_2,\,\ldots ,\,k_n\}$ are real positive definite matrices, $k_i,(i=1,2,\ldots ,n)$ are coupling strengths, $\hat{\mathbf {A}}$, $\hat{\mathbf {B}}$ are parameter estimations of the unknown vectors $\mathbf {A}$ and $\mathbf {B}$, $\tilde{\mathbf {A}}=\hat{\mathbf {A}}-\mathbf {A}$ and $\tilde{\mathbf {B}}=\hat{\mathbf {B}}-\mathbf {B}$ are the parameter error vectors, respectively, then adaptive CMHFPS between the response system (6) and drive system (5) is achieved asymptotically, and $\hat{\mathbf {A}}$, $\hat{\mathbf {B}}$ converge to the true values of the complex constant vectors $\mathbf {A}$ and $\mathbf {B}$, respectively, (10) is called complex update laws of unknown complex parameter vectors $\mathbf {A}$ and $\mathbf {B}$.

Proof

Insertion of (5), (6) and (9) into (8) gives

$$\begin{aligned} \dot{\mathbf {e}}(t)= & {} \dot{\mathbf {w}}(t)-\frac{\hbox {d}(\mathbf {D}(t)\mathbf {z}(t))}{\hbox {d}t}\nonumber \\= & {} \dot{\mathbf {w}}(t)-\mathbf {J(z,A},t)\nonumber \\= & {} \mathbf {R(w,B},t)+[-\mathbf {R(w,}\hat{\mathbf {B}},t)+\mathbf {J(z,} \hat{\mathbf {A}},t)\nonumber \\&-\mathbf {Ke}]-\mathbf {J(z,A},t)\nonumber \\= & {} \mathbf {G(w)}\mathbf {B}+\mathbf {g(w)}-\mathbf {G(w)}\hat{\mathbf {B}} -\mathbf {g(w)}+\dot{\mathbf {D}}(t)\mathbf {z}(t)\nonumber \\&+\mathbf {D(t)}(\mathbf {F(z)}\hat{\mathbf {A}}+\mathbf {f(z)})\nonumber \\&-\mathbf {K}\mathbf {e}-\dot{\mathbf {D}}(t)\mathbf {z}(t) -\mathbf {D(t)}(\mathbf {F(z)}\mathbf {A}+\mathbf {f(z)})\nonumber \\= & {} \mathbf {D}(t)\mathbf {F(z)}(\hat{\mathbf {A}}-\mathbf {A})-\mathbf {G(w)} (\hat{\mathbf {B}}-\mathbf {B})-\mathbf {K}\mathbf {e}\nonumber \\= & {} \mathbf {D}(t)\mathbf {F(z)}\tilde{\mathbf {A}}-\mathbf {G(w)}\tilde{\mathbf {B}} -\mathbf {K}\mathbf {e}, \end{aligned}$$

(11)

where $\tilde{\mathbf {A}}=\hat{\mathbf {A}}-\mathbf {A}$ and $\tilde{\mathbf {B}}=\hat{\mathbf {B}}-\mathbf {B}$ are the parameter error vectors, respectively.

Introducing the following Lyapunov function candidate as

$$\begin{aligned} V(\mathbf {e},\tilde{\mathbf {A}},\tilde{\mathbf {B}},t)= & {} \frac{1}{2}\left( \mathbf {e^\mathrm{{H}}}\mathbf {e}+\tilde{\mathbf {A}}^\mathrm{{H}}\tilde{\mathbf {A}} +\tilde{\mathbf {B}}^\mathrm{{H}}\tilde{\mathbf {B}}\right) , \end{aligned}$$

(12)

from complex update laws (10) and $\dot{\tilde{\mathbf {A}}}=\dot{\hat{\mathbf {A}}}$, $\dot{\tilde{\mathbf {B}}}=\dot{\hat{\mathbf {B}}}$, the time derivative of the V(t) along the trajectories of the errors system (11) reads

$$\begin{aligned} \dot{V}(t)= & {} \frac{1}{2}\left[ (\dot{\mathbf {e}})^\mathrm{{H}}\mathbf {e} \!+\!\mathbf {e}^\mathrm{{H}}(\dot{\mathbf {e}}) \!+\!\dot{\tilde{\mathbf {A}}}^\mathrm{{H}}\tilde{\mathbf {A}}\!+\!\tilde{\mathbf {A}}^\mathrm{{H}}\dot{\tilde{\mathbf {A}}} +\dot{\tilde{\mathbf {B}}}^\mathrm{{H}}\tilde{\mathbf {B}}+\tilde{\mathbf {B}}^\mathrm{{H}}\dot{\tilde{\mathbf {B}}}\right] \nonumber \\= & {} \frac{1}{2}[((\mathbf {D}(t)\mathbf {F(z)})\tilde{\mathbf {A}}-\mathbf {G}(\mathbf w )\tilde{\mathbf {B}} -\mathbf {K}\mathbf {e})^\mathrm{{H}}\mathbf {e}\nonumber \\&+\,\mathbf {e}^\mathrm{{H}} (\mathbf {D}(t)\mathbf {F(z)}\tilde{\mathbf {A}} -\mathbf {G}(\mathbf w )\tilde{\mathbf {B}}-\mathbf {K}\mathbf {e})\nonumber \\&+\,({(-\mathbf {D}(t)\mathbf {F(z)})}^\mathrm{{H}}~\mathbf {e}-{{\gamma }}_a~ \tilde{\mathbf {A}})^\mathrm{{H}}~\tilde{\mathbf {A}}\nonumber \\&+\,{\tilde{\mathbf {A}}}^\mathrm{{H}}~[{(-\mathbf {D}(t)\mathbf {F(z)})}^\mathrm{{H}}~\mathbf {e} -{{\gamma }}_a~\tilde{\mathbf {A}}]\nonumber \\&+\,({\mathbf {G}^\mathrm{{H}}}(\mathbf w ) ~\mathbf {e}-{{\gamma }}_b~\tilde{\mathbf {B}})^\mathrm{{H}}\tilde{\mathbf {B}}+ {\tilde{\mathbf {B}}}^\mathrm{{H}}(\mathbf {G}^\mathrm{{H}}(\mathbf w )\mathbf {e} -{{\gamma }}_b~\tilde{\mathbf {B}})]\nonumber \\= & {} -\mathbf {e^\mathrm{{H}}}\mathbf {K}\mathbf {e} -\tilde{\mathbf {A}}^\mathrm{{H}}{{\gamma }}_a\tilde{\mathbf {A}} -\tilde{\mathbf {B}}^\mathrm{{H}}{{\gamma }}_b\tilde{\mathbf {B}}<0. \end{aligned}$$

(13)

Since $\dot{V}(t)<0$, based on the Lyapunov stability theory, the error vector $\mathbf {e}(t)\rightarrow 0$ as $t\rightarrow +\infty$. So, one arrives at CMHFPS with desired complex function transformation matrix $\mathbf {D}(t)$ between two different dimensional complex chaotic systems (5) and (6) by using the controller (9) and complex update laws (10). According to (10), when $t \rightarrow +\infty$, the parameter errors $\tilde{\mathbf {A}}$ and $\tilde{\mathbf {B}}$ also converge to zero, which shows the estimation of unknown complex parameter vectors $\hat{\mathbf {A}}$ and $\hat{\mathbf {B}}$ in both the drive and response systems also converge to the selected true values. The proof is completed. $\square$

Theorem 2

Suppose the parameter $\mathbf {B}$ of the response system (6) is known a priori. Then, for given complex function transformation matrix $\mathbf {D}(t)$ and initial conditions $\mathbf {w}(0),\mathbf {z}(0)$, if the adaptive controller is designed as

$$\begin{aligned} \mathbf {v}= & {} -\,\mathbf {R(w,B},t)+\mathbf {J(z,}\hat{\mathbf {A}},t)-\mathbf {K e}\nonumber \\= & {} -\,\mathbf {F(w)}\mathbf {B}-\mathbf {g(w)}+\dot{\mathbf {D}}(t)\mathbf {z(t)} +\mathbf {D}(t)(\mathbf {F(z)}\hat{\mathbf {A}}\nonumber \\&+\,\mathbf {f(z)})-\mathbf {K}\mathbf {e}, \end{aligned}$$

(14)

and the complex update law of complex parameter is selected as

$$\begin{aligned} \dot{\hat{\mathbf {A}}}= & {} {{-(\mathbf {D}(t)\mathbf {F(z)})}^\mathrm{{H}}}~\mathbf {e}-{{\gamma }}_a~\tilde{\mathbf {A}}, \end{aligned}$$

(15)

where ${{\gamma }}_a=\mathrm {diag}\{\gamma _{a_1}, \,\gamma _{a_2},\,\ldots ,\,\gamma _{a_s}\}$, and $\mathbf {K}=\mathrm {diag}\{k_1,\,k_2,\,\ldots ,\,k_n\}$ are real positive definite matrices, $k_i,(i=1,2,\ldots ,n)$ are coupling strengths, $\hat{\mathbf {A}}$ is parameter estimation of the unknown vector $\mathbf {A}$, $\tilde{\mathbf {A}}=\hat{\mathbf {A}}-\mathbf {A}$ is the parameter error vector, respectively, then adaptive CMHFPS between the response system (6) and drive system (5) is achieved asymptotically, and estimation $\hat{\mathbf {A}}$ converges to the true value of the complex constant vector $\mathbf {A}$.

Proof

Introduce the following Lyapunov function candidate as

$$\begin{aligned} V(\mathbf {e},\tilde{\mathbf {A}},t)= & {} \frac{1}{2}(\mathbf {e^\mathrm{{H}}}\mathbf {e} +\tilde{\mathbf {A}}^\mathrm{{H}}\tilde{\mathbf {A}}). \end{aligned}$$

(16)

Then it is similar to the proof in Theorem 1 and thus is omitted. $\square$

Theorem 3

Suppose the parameter $\mathbf {A}$ of the drive system (5) is known a priori. Then, for given complex function transformation matrix $\mathbf {D}(t)$ and initial conditions $\mathbf {w}(0),\mathbf {z}(0)$, if the adaptive controller is designed as

$$\begin{aligned} \mathbf {v}= & {} -\,\mathbf {R(w,}\hat{\mathbf {B}},t)+\mathbf {J(z,A},t)-\mathbf {K e}\nonumber \\= & {} -\,\mathbf {G(w)}\hat{\mathbf {B}}-\mathbf {g(w)}+\dot{\mathbf {D}}(t)\mathbf {z(t)} +\mathbf {D}(t)(\mathbf {F(z)}\mathbf {A}\nonumber \\&+\,\mathbf {f(z)})-\mathbf {K}\mathbf {e}, \end{aligned}$$

(17)

and the complex update law of complex parameter is selected as

$$\begin{aligned} \dot{\hat{\mathbf {B}}}= & {} {\mathbf {G}^\mathrm{{H}}}(\mathbf {w}) ~\mathbf {e}-{{\gamma }}_b~\tilde{\mathbf {B}}, \end{aligned}$$

(18)

where ${{\gamma }}_b=\mathrm {diag}\{\gamma _{b_1},\, \gamma _{b_2},\,\ldots ,\,\gamma _{b_q}\}$, and $\mathbf {K}=\mathrm {diag}\{k_1,\,k_2,\,\ldots ,\,k_n\}$ are real positive definite matrices, $k_i,(i=1,2,\ldots ,n)$ are coupling strengths, $\hat{\mathbf {B}}$ is parameter estimation of the unknown vector $\mathbf {B}$, $\tilde{\mathbf {B}}=\hat{\mathbf {B}}-\mathbf {B}$ is the parameter error vector, respectively, then adaptive CMHFPS between the response system (6) and drive system (5) is achieved asymptotically, and $\hat{\mathbf {B}}$ converges to the true value of the complex constant vector $\mathbf {B}$.

Proof

Introduce the following Lyapunov function candidate as

$$\begin{aligned} V(\mathbf {e},\tilde{\mathbf {B}},t)= & {} \frac{1}{2}(\mathbf {e^\mathrm{{H}}}\mathbf {e} +\tilde{\mathbf {B}}^\mathrm{{H}}\tilde{\mathbf {B}}). \end{aligned}$$

(19)

Then it is similar to the proof in Theorem 1 and thus is omitted. $\square$

Theorem 4

Suppose both parameter vectors $\mathbf {A}$ and $\mathbf {B}$ are known a priori. Then, for given complex function transformation matrix $\mathbf {D}(t)$ and initial conditions $\mathbf {w}(0),\mathbf {z}(0)$, if the adaptive controller is designed as

$$\begin{aligned} \mathbf {v}= & {} -\,\mathbf {R(w,B},t)+\mathbf {J(z,A},t)-\mathbf {K e}\nonumber \\= & {} -\,\mathbf {G(w)}\mathbf {B}-\mathbf {g(w)}+\dot{\mathbf {D}}(t)\mathbf {z(t)} +\mathbf {D}(t)(\mathbf {F(z)}\mathbf {A}\nonumber \\&+\,\mathbf {f(z)})-\mathbf {K}\mathbf {e}, \end{aligned}$$

(20)

where $\mathbf {K}=\mathrm {diag}\{k_1,\,k_2,\,\ldots ,\,k_n\}$ is real positive definite matrix, $k_i,(i=1,2,\ldots ,n)$ are coupling strengths, then CMHFPS between the response system (6) and drive system (5) is achieved asymptotically.

Proof

Introduce the following Lyapunov function candidate as

$$\begin{aligned} V(\mathbf {e},t)= & {} \frac{1}{2}\mathbf {e^\mathrm{{H}}}\mathbf {e}. \end{aligned}$$

Then it is similar to the proof in Theorem 1 and thus is omitted. $\square$

Remark 5

Compared with prior work [5–8, 16, 18, 21–24, 26, 29], we aim at CMHFPS scheme of complex chaotic systems with uncertain complex parameters, and design complex update laws of uncertain parameters and adaptive controller without separating the real and imaginary parts of the complex state variables or complex parameters; thus, the conclusion is very concise and easier to be applied.

Remark 6

Note that the complex function transformation matrix $\mathbf {D}(t)$ has no effect on the time derivative $\dot{V}$; thus, one can adjust complex function transformation matrix arbitrarily without altering the control robustness. Hence, the complex function transformation matrix can be used as information signal for the communication scheme. In particular, when $\mathbf {D}(t)$ is real, Theorem 1–4 are also applied to achieve MHFPS with real function transformation matrix of complex chaotic systems with uncertain parameters [29].

Remark 7

If either of the two matrices $\mathbf {A}$, $\mathbf {B}$ is complex parameter vector, then Theorem  1–4 are also be applied to realize CMHFPS of chaotic complex systems with partly complex parameters. In particular, when parameter matrices $\mathbf {A}$ and $\mathbf {B}$ are real parameter vectors, Theorem 1–4 are also applied to achieve CMHFPS of chaotic complex systems with real parameters.

4 Numerical examples

Throughout this section, in order to demonstrate the effectiveness and feasibility of the proposed synchronization scheme in Sect. 3, examples are shown for two kinds of cases: CMHFPS between two different dimensional chaotic complex systems based on the increased order for $m<n$ and reduced order for $m>n$, respectively.

4.1 Adaptive CMHFPS of complex chaotic Lorenz drive system with complex parameters and complex hyperchaotic Lorenz response system with real parameters

In order to illustrate adaptive increased order CMHFPS, it is assumed that 3-dimensional complex Lorenz system (1) with unknown complex parameters drives 4-dimensional complex hyperchaotic Lorenz system with unknown real parameters [7]. Therefore, the drive chaotic Lorenz system is given as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z}_1=a_1(z_2-z_1),\\ \dot{z}_2=a_2 z_1-a_3 z_2-z_1z_3,\\ \dot{z}_3=\frac{1}{2}(\bar{z}_1z_2+z_1\bar{z}_2)-a_4z_3,\\ \end{array} \right. \end{aligned}$$

(21)

where $z_{1}=z^{r}_{1}+jz^{i}_{1}, z_{2}=z^{r}_{2}+jz^{i}_{2}$ are complex state variables and $z_{3}$ is a real state variable, $\mathbf {A}=(a_1,\,a_2,\,a_3,\,a_4)^\mathrm{{T}}$ is unknown complex parameter vector. Equation (21) is chaotic when $a_1=2,\,{a_{2}}=60+0.02j,\,a_{3}=1-0.06j,\,a_4=0.8$, see [1] for more details.

The complex response hyperchaotic Lorenz system with the controller is written as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{w}_1=b_1(w_2-w_1)+{v}_1,\\ \dot{w}_2=b_2w_1-w_2-w_1w_3+w_{4}+{v}_2,\\ \dot{w}_3=-b_3w_3+(1/2)(\bar{w}_1w_2+w_1\bar{w}_2)+{v}_3,\\ \dot{w}_4=b_4w_1+b_5w_2+{v}_4, \end{array} \right. \end{aligned}$$

(22)

where $w_{1}=w^{r}_{1}+jw^{i}_{1}$, $w_{2}=w^{r}_{2}+jw^{i}_{2}$ and $w_{4}=w^{r}_{4}+jw^{i}_{4}$ are complex state variables, and $w_{3}$ is a real state variable, $\mathbf {B}=(b_1,\,b_2,\,b_3,\,b_4,\,b_5)^\mathrm{{T}}$ is unknown real parameter vector. Equation (22) is chaotic when $b_1=14,\,{b_{2}}=35,\,b_{3}=3,\,b_4=-5,\,b_{5}=-4$ and in the absence of the controller $\mathbf {v}=(v_1,\,v_2,\,v_3,\,v_4)^\mathrm{{T}}$, see [6] for more details.

The complex function transformation matrix is taken as

$$\begin{aligned} \mathbf {D}(t)= & {} \left( \begin{array}{ccc} 0.5\exp (j\pi t/5) &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad \exp (j\pi t/10) &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1.5\cos (\pi t/15) \\ 2\exp (j\pi t/20) &{} \quad 0 &{} \quad 0 \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$

(23)

where $\rho \exp (j\theta t)=\rho (\cos \theta t+j\sin \theta t)$. Note that $z_{3},~w_{3}\in {\mathbb {R}}$ in systems (21) and (22), we choose the scaling function $d_{33}(t)\in {\mathbb {R}}$ in (23) to make $e_3=w_3-1.5\cos (\pi t/15)z_3 \in {\mathbb {R}}$ for the convenience of real discussion.

The controller is constructed according to (9) in Theorem 1 as

$$\begin{aligned} \mathbf {v} =\left( \begin{array}{c} \scriptstyle -\hat{b}_1(w_2-w_1)+(0.1\pi j z_1+0.5\hat{a}_{1}(z_2-z_1)) \exp (j\pi t/5)-k_{1}{e}_1\\ -\hat{b}_2w_1+w_2+w_1w_3-w_{4}+(0.1\pi j z_2+(\hat{a}_2z_1-\hat{a}_{3}z_2-z_{1}z_{3}))\exp (j\pi t/10)-k_{2}{e}_2\\ \hat{b}_3w_3-\frac{1}{2}(\bar{w}_1w_2+w_1\bar{w}_2)-0.1\pi z_3\sin (\pi t/15)+ [1.5(\frac{1}{2}(\bar{z}_1z_2+z_1\bar{z}_2)-\hat{a}_4z_3)]\cos (\pi t/15)-k_{3}{e}_3\\ -\hat{b}_4w_1-\hat{b}_5w_2+(0.1\pi j z_1+2\hat{a}_{1}(z_2-z_1))\exp (j\pi t/20)-k_{4}{e}_4 \end{array} \right) ,\quad \end{aligned}$$

(24)

the complex update laws of parameters are given according to (10) as

$$\begin{aligned} \dot{\hat{\mathbf {A}}}=\left( \begin{array}{c} -(0.5\exp (-j\pi t/5)e_1+2\exp (-j\pi t/20)e_4)(\bar{z}_2-\bar{z}_1) -\gamma _{a_1}(\hat{a}_1-a_1)\\ -\exp (-j\pi t/10)\bar{z}_1e_2-\gamma _{a_2}(\hat{a}_2-a_2)\\ \exp (-j\pi t/10)\bar{z}_2e_2-\gamma _{a_3}(\hat{a}_3-a_3)\\ 1.5\cos (\pi t/15){z}_3e_3-\gamma _{a_4}(\hat{a}_4-a_4) \\ \end{array}\right) , \end{aligned}$$

(25)

and

$$\begin{aligned} \dot{\hat{\mathbf {B}}} =\left( \begin{array}{c} (\bar{w}_2-\bar{w}_1)e_1-\gamma _{b_1}(\hat{b}_1-b_1)\\ \bar{w}_1e_2-\gamma _{b_2}(\hat{b}_2-b_2)\\ -{w}_3e_3-\gamma _{b_3}(\hat{b}_3-b_3)\\ \bar{w}_1e_4-\gamma _{b_4}(\hat{b}_4-b_4)\\ \bar{w}_2e_4-\gamma _{b_5}(\hat{b}_5-b_5) \end{array} \right) . \end{aligned}$$

(26)

In the numerical simulations, the fourth-order Runge–Kutta method is applied, the true values of unknown parameters are chosen as $\mathbf {A}=(a_1,\,a_2,\,a_3,\,a_4)^\mathrm{{T}}=(2,60+0.02j,1-0.06j,0.8)^\mathrm{{T}}$ and $\mathbf {B}=(b_1,\,b_2,\,b_3,\,b_4,\,b_5)^\mathrm{{T}}=(14,35,3,-5,-4)^\mathrm{{T}}$, respectively. The initial conditions of drive system (21) and response system (22) are randomly taken as $\mathbf {z(0)} =(2+0.02j,1+0.2j,-1)^\mathrm{{T}}$ and $\mathbf {w(0)}=(-1-2j$, $-3-4j,-5,-6-7j)^\mathrm{{T}}$. The initial values of estimated parameters and control strength are $\hat{\mathbf {A}}(0)=(\hat{a}_{1}(0),\,\hat{a}_{2}(0),\, \hat{a}_{3}(0),\,\hat{a}_{4}(0))^\mathrm{{T}}=(1,\,1,\,1,\,1)^\mathrm{{T}}$, $\hat{\mathbf {B}}(0)=(\hat{b}_{1}(0),\,\hat{b}_{2}(0),\,\hat{b}_{3}(0),\, \hat{b}_{4}(0),\,\hat{b}_{5}(0))^\mathrm{{T}}=(10,\,10,\,10,\,10,\,10)^\mathrm{{T}}$, ${{\gamma }}_a=\mathrm {diag}\{\gamma _{a_1},\,\gamma _{a_2},\, \gamma _{a_3},\,\gamma _{a_4}\}=\mathrm {diag}\{16,\,6,\,5,\,18\}$, ${{\gamma }}_b=\mathrm {diag}\{\gamma _{b_1},\gamma _{b_2}, \gamma _{b_3},\gamma _{b_4},\,\gamma _{b_5}\}=\mathrm {diag}\{15,20, 6,5,18\}$ and $\mathbf {K}=\mathrm {diag}\{k_1,k_2,k_3,k_4\}=\mathrm {diag}\{1,2,3,4\}$.

Fig. 2

The CMHFPS error dynamic of systems (21) and (22) with the controller (24), complex parameter update laws (25), (26). Here $e_1=w_1-0.5\exp (j\pi t/5)z_1, e_2=w_2-\exp (j\pi t/10)z_2, e_3=w_3-1.5\cos (\pi t/15)z_3, e_4=w_4-2\exp (j\pi t/20)z_1$

Fig. 3

The identification process of unknown parameter vector $\mathbf {A}$ of drive system (21)

Fig. 4

The identification process of unknown parameter vector $\mathbf {B}$ of response system (22)

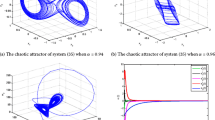
The adaptive CMHFPS errors of systems (21) and (22) converge asymptotically to zero as demonstrated in Fig. 2, where the solid line shows the real part of the error and the dotted line presents the imaginary part of the error.

The processes of parameters identification of $\hat{\mathbf {A}}$ and $\hat{\mathbf {B}}$ are shown in Figs. 3 and 4, respectively, where the red line shows the real part of the parameter and the blue line the imaginary part of the parameter. The estimated values of the unknown parameters gradually converge to the selected values $\mathbf {A}=(a_1,\,a_2,\,a_3,\,a_4)^\mathrm{{T}}=(2,60+0.02j,1-0.06j,0.8)^\mathrm{{T}}$ and $\mathbf {B}=(b_1,\,b_2,\,b_3,\,b_4,\,b_5)^\mathrm{{T}}=(14,35,3,-5,-4)^\mathrm{{T}}$ as $t\rightarrow \infty$, respectively.

As expected, the above results demonstrate that adaptive CMHFPS has been achieved between complex chaotic Lorenz drive system (21) and complex hyperchaotic Lorenz response system (22), and that all of unknown parameters in both drive and response systems are identified successfully with the designed controller (24) and the complex update laws (25) and (26) of parameters.

4.2 Adaptive CMHFPS of complex hyperchaotic Lü drive system with real parameters and complex Lorenz response system with complex parameters

In order to illustrate adaptive reduced order CMHFPS, it is assumed that 4-dimensional complex hyperchaotic Lü system with unknown real parameters [8] drives 3-dimensional complex Lorenz system (1) with unknown complex parameters. Therefore, the drive system is written as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z}_1=a_1(z_2-z_1)+z_4,\\ \dot{z}_2=a_2z_2-z_1z_3+z_{4},\\ \dot{z}_3=-a_3z_3+(1/2)(\bar{z}_1z_2+z_1\bar{z}_2),\\ \dot{z}_4=-a_4z_4+(1/2)(\bar{z}_1z_2+z_1\bar{z}_2), \end{array} \right. \end{aligned}$$

(27)

where $z_{1}=z^{r}_{1}+jz^{i}_{1}, z_{2}=z^{r}_{2}+jz^{i}_{2}$ are complex state variables and $z_{3},z_{4}$ are real state variable, $\mathbf {A}=(a_1,\,a_2,\,a_3,\,a_4)^\mathrm{{T}}$ is unknown real parameter vector. Equation (27) is chaotic when $a_1=15,\,{a_{2}}=36,\,a_{3}=4.5,\,a_4=12$, see [8] for more details.

The complex response system with the controller is given as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{w}_1=b_{1}(w_2-w_1)+v_1,\\ \dot{w}_2=b_{2}w_1-b_{3}w_{2}-w_{1}w_{3}+v_2,\\ \dot{w}_3=-b_{4}w_3+(1/2)(\bar{w}_1w_2+w_1\bar{w}_2)+v_3, \end{array} \right. \end{aligned}$$

(28)

where $w_{1}=w^{r}_{1}+jw^{i}_{1}, w_{2}=w^{r}_{2}+jw^{i}_{2}$ are complex state variables, and $w_{3}$ is a real state variable, $\mathbf {B}=(b_1,\,b_2,\,b_3,\,b_4)^\mathrm{{T}}$ is unknown complex parameter vector, and the controller $\mathbf {v}=(v_1,\,v_2,\,v_3)^\mathrm{{T}}$ is to be designed.

The complex function transformation matrix is selected as

$$\begin{aligned} \mathbf {D}(t)= & {} \left( \begin{array}{cccc} 0.5\exp (j\pi t/5) &{} 0 &{} 0 &{} 0 \\ 0 &{} \exp (j\pi t/10) &{}0 &{} 0 \\ 0 &{} 0 &{} 1.2+\sin t &{}1.2+\cos t \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$

(29)

Note that $z_{3},~z_{4},~w_{3}\in \mathbb {R}$ in systems (27) and (28), we choose the scaling functions $d_{33}(t),~d_{34}\in \mathbb {R}$ in (29) to make $e_3=w_3-(1.2+\sin t)z_3-(1.2+\cos t)z_4 \in \mathbb {R}$ for convenience of real discussion.

The controller is constructed according to (9) in Theorem 1 as

$$\begin{aligned} \left\{ \begin{array}{l} v_1=-\hat{b}_1(w_2-w_1)+(0.1\pi j z_1+0.5(\hat{a}_{1}(z_2-z_1)+z_4))\exp (j\pi t/5)-k_{1}{e}_1,\\ v_2=-\hat{b}_2w_1+\hat{b}_3w_2+w_1w_3+(0.1\pi j z_2+\hat{a}_2z_2+z_4-z_{1}z_{3})\exp (j\pi t/10)-k_{2}{e}_2,\\ v_3=\hat{b}_4w_3-\frac{1}{2}(\bar{w}_1w_2+w_1\bar{w}_2)+(1.2+\sin t)(-\hat{a}_3z_3+(1/2)(\bar{z}_1z_2+z_1\bar{z}_2))\\ \qquad \quad +(1.2+\cos t)(-\hat{a}_4z_4+(1/2)(\bar{z}_1z_2+z_1\bar{z}_2)) +z_3 \cos t-z_4 \sin t-k_{3}{e}_3, \end{array} \right. \end{aligned}$$

(30)

the complex update laws of parameters are given according to (10) as

$$\begin{aligned} \dot{\hat{\mathbf {A}}}= & {} \left( \begin{array}{c} -0.5\exp (-j\pi t/5)(\bar{z}_2-\bar{z}_1)e_1-\gamma _{a_1}(\hat{a}_1-a_1)\\ -\exp (-j\pi t/10)\bar{z}_2e_2-\gamma _{a_2}(\hat{a}_2-a_2)\\ (1.2+\sin t)z_3e_3-\gamma _{a_3}(\hat{a}_3-a_3)\\ (1.2+\cos t)z_4e_3-\gamma _{a_4}(\hat{a}_4-a_4)\\ \end{array} \right) \nonumber \\ \end{aligned}$$

(31)

and

$$\begin{aligned} \dot{\hat{\mathbf {B}}} =\left( \begin{array}{c} (\bar{w}_2-\bar{w}_1)e_1-\gamma _{b_1}(\hat{b}_1-b_1)\\ \bar{w}_1e_2-\gamma _{b_2}(\hat{b}_2-b_2)\\ -\bar{w}_2e_2-\gamma _{b_3}(\hat{b}_3-b_3)\\ -{w}_3e_3-\gamma _{b_4}(\hat{b}_4-b_4) \end{array} \right) . \end{aligned}$$

(32)

In the numerical simulations, the true values of unknown parameters are chosen as $\mathbf {A}=(a_1,\,a_2,\,a_3,\,a_4)^\mathrm{{T}}=(42,25,6,10)^\mathrm{{T}}$ and $\mathbf {B}=(b_1,\,b_2,\,b_3,\,b_4)^\mathrm{{T}}=(2,60+0.02j,1-0.06j,0.8)^\mathrm{{T}}$, respectively. The initial conditions of drive system (27) and response system (28) are randomly chosen as $\mathbf {z(0)} =(10+5j,10+6j,2,12)^\mathrm{{T}}$ and $\mathbf {w(0)}=(2+0.02j,1+0.2j,-1)^\mathrm{{T}}$. The initial values of estimated parameters and control strength are $\hat{\mathbf {A}}(0)=(\hat{a}_{1}(0),\,\hat{a}_{2}(0),\,\hat{a}_{3}(0)$, $\hat{a}_{4}(0))^\mathrm{{T}}=(15,16,17+j,18+j)^\mathrm{{T}}$, $\hat{\mathbf {B}}(0)=(\hat{b}_{1}(0),\hat{b}_{2}(0),\hat{b}_{3}(0),\hat{b}_{4}(0))^\mathrm{{T}}=(1,1,1,1+j)^\mathrm{{T}}$, ${{\gamma }}_a=\mathrm {diag}\{\gamma _{a_1},\,\gamma _{a_2},\,\gamma _{a_3}$, $\gamma _{a_4}\}=\mathrm {diag}\{16,\,8,\,10,\,18\}$, ${{\gamma }}_b=\mathrm {diag}\{\gamma _{b_1},\gamma _{b_2}$, $\gamma _{b_3},\gamma _{b_4}\}=\mathrm {diag}\{15,20,16,18\}$ and $\mathbf {K}=\mathrm {diag}\{k_1,k_2,k_3\}=\mathrm {diag}\{5,10,20\}$.

The adaptive CMHFPS errors of systems (27) and (28) converge asymptotically to zero as demonstrated in Fig. 5, where the dotted line shows the real part of the error and the solid line presents the imaginary part of the error.

Fig. 5

The CMHFPS error dynamic of systems (27) and (28) with the controller (30) and complex parameter update laws (31), (32). Here $e_1=w_1-0.5\exp (j\pi t/5)z_1, e_2=w_2-\exp (j\pi t/10)z_2, e_3=w_3-(1.2+\sin t)z_3-(1.2+\cos t)z_4$

The processes of parameters identification of $\hat{\mathbf {A}}$ and $\hat{\mathbf {B}}$ are shown in Figs. 6 and 7, respectively, where the red line shows the real part of the parameter and the blue line presents the imaginary part of the parameter. The estimated values of the unknown parameters gradually converge to the selected values $\mathbf {A}=(a_1,\,a_2,\,a_3,\,a_4)^\mathrm{{T}}=(42,25,6,10)^\mathrm{{T}}$ and $\mathbf {B}=(b_1,\,b_2,\,b_3,\,b_4)^\mathrm{{T}}=(2,60+0.02j,1-0.06j,0.8)^\mathrm{{T}}$ as $t\rightarrow \infty$, respectively.

Fig. 6

The identification process of unknown parameter vector $\mathbf {A}$ of drive system (27)

Fig. 7

The identification process of unknown parameter vector $\mathbf {B}$ of response system (28)

As expected, the above results demonstrate that adaptive CMHFPS has been achieved between complex hyperchaotic Lü drive system (27) with unknown real parameters and complex chaotic Lorenz response system (28) with unknown complex parameters, and that all of unknown parameters in both drive and response systems are identified successfully with the designed controller (30) and the complex update laws (31) and (32) of parameters.

5 Discussion and conclusions

In this paper, CMHFPS is introduced for two different dimensional chaotic systems with complex variables and complex parameters. With the present method, in the complex space, the response system is asymptotically synchronized different dimensional drive system by a desired complex function transformation matrix, not a square matrix. The adaptive controller and update laws of unknown complex parameters are designed to make the response system become a complex function projection of the drive system.

The presented synchronization scheme is simple and theoretically rigorous. It is worth pointing out that sufficient criteria on adaptive CMHFPS are derived by constructing appropriate Lyapunov functions dependent on complex variables and employing adaptive control technique. Quite different from the schemes proposed in the literature, we do not separate the real and imaginary parts of complex variables or complex parameters. This goes beyond the known results, and we hope the performed work will serve as a guideline for further studies in chaotic synchronization of complex nonlinear systems.

Moreover, the CMHFPS between complex chaotic Lorenz drive system with uncertain complex parameters and complex hyperchaotic Lorenz response system with uncertain real parameters is implemented as an example to discuss increased order synchronization, and CMHFPS between complex hyperchaotic Lü drive system with uncertain real parameters and complex Lorenz response system with uncertain complex parameters is implemented as an example to discuss reduced order synchronization, as well. Numerical results are plotted to show the rapid convergence of errors to zero and of the estimations of unknown complex parameters to the selected true values.

The CMHFPS bridges the gap between different dimensional complex chaos with complex parameters by a complex function transformation matrix. The transformation matrix is composed of complex functions, which increases the complexity and scope of the synchronization and directs high security and large variety of secure communications. What’s more, more choices of both control parameters and scaling functions are provided to realize secure communications by chaos synchronization, stronger anti-attack ability and more anti-translated capacity are strengthened for our method. Our findings indicate that the proposed scheme is particularly efficient and of wide real-world applicability, a more bright future is waiting for secure communication and information processing.