$(\mu ,\nu )-$Pseudo Almost Automorphic Solutions of Neutral Type Clifford-Valued High-Order Hopfield Neural Networks with D Operator

Abstract

The aim of this article is to study neutral type Clifford-valued high-order Hopfield neural networks with mixed delays and D operator. New criteria are established for the existence, uniqueness and global exponential stability of $(\mu ,\nu )-$pseudo almost automorphic solutions of the considered model via Banach’s fixed point principle and differential inequality techniques. An example is given to show the effectiveness of the main new criteria.

1 Introduction

Artificial Neural Networks (NNs) are a computational technique that belongs to the field of Machine Learning (ML). Their goal is to achieve a fairly simplified model of the brain. High-Order Hopfield Neural Network (HOHNN) is one of the most powerful and efficient types of NNs. The key factors that affect its success are its strong approximation ability, its fast convergence rate and its high fault tolerance capability. HOHNNs have widespread applications in various fields such as associative memory, pattern recognition, signal processing, robotics, medical image edge detection, medical event detection in electronic health records, diagnosis prediction in health care and many others. The study of high-order NNs has attracted considerable multidisciplinary research. For instance, the exponential convergence of high-order cellular NNs (CNNs) with time-varying leakage delays has been obtained in [28]; the authors of [14] discussed the existence and uniqueness of pseudo almost periodic solutions of high-order type of NNs; the authors of [29] studied the existence and exponential stability of the weighted pseudo almost periodic solutions of high-order cellular NNs with mixed delays; the dynamics of the pseudo almost automorphic solutions of HOHNNs with mixed delays has been investigated in [3]; to name but a few.

One can easily see that all the NN models considered in the above-mentioned works are under time-delay effect. The investigation of delayed NNs has become an interesting world-wide focus and several types of delays such as discrete, distributed, proportional and leakage delay have been used, see for instance [4, 5, 8, 26]. To precisely describe the dynamics of complex neural reactions, systems must contain information about the derivative of the past states. Here, we are talking about another type called “neutral-type delay”. It should be mentioned that neutral type NN models can be classified into two categories: Non-Operator-Based Neutral Functional Differential Equations (NOBNFDEs) and D-Operator-Based Neutral Functional Differential Equations (DOBNFDEs). It is important to notice that neutral type NNs with D operator have more realistic significance than non-operator-based ones in many practical applications of NN dynamics. Recently, new success stories of neutral type NNs with D operator have been provided. In [16], the global exponential stability of the anti-periodic solutions for neutral type cellular NNs with D operator has been studied. In [30], the anti-periodic solutions for neutral shunting inhibitory cellular NNs with time-varying delays and D operator have been investigated. Reference [31] dealt with the global convergence of CNNs with neutral type delays and D operator. In [32], the authors analyzed the global exponential convergence of neutral type shunting inhibitory cellular NNs with D operator. Zhang studied the oscillation dynamics of almost periodic solutions for shunting inhibitory CNNs with neutral type proportional delays and D operator in [33] and extended the results to the pseudo almost periodic solutions of the same model in [34].

On the one hand, to follow real phenomena in biological systems, researchers have proposed several classes of functions such as the class of Almost Automorphic (AA) functions in [27], the class of Pseudo Almost Automorphic (PAA) functions in [17] and the class of Weighted Pseudo Almost Automorphic (WPAA) functions which have extended to the class of $(\mu ,\nu )-$Pseudo Almost Automorphic ($(\mu ,\nu )-$PAA) functions [2]. $(\mu ,\nu )-$PAA functions have been rarely used in NN theory where the main task consists of finding an answer to the following problem: “what will be the nature of output when all the parameters of the NN model are $(\mu ,\nu )-$PAA functions?”. In [7], we found an answer to this problem by studying the dynamic oscillations of $(\mu ,\nu )-$PAA solutions of bidirectional associative memory NNs. On the other hand, Clifford introduced Clifford algebra in the 19th century. It is important associative algebras within the theories of quadratic forms, orthogonal groups and theoretical physics. As an extension of real value models, Clifford-value NNs have become active research domain due to their powerful applications in many fields such as neural computing, robotic vision, image processing, control problems and other areas. Success stories of Clifford-value NNs are reported in the following. The existence and global exponential stability of the equilibrium point of Clifford-valued recurrent NNs have been studied in [37]; sufficient conditions ensuring the existence and global stability of Clifford-valued NNs with time-varying delays have been derived in [21, 23]; the globally asymptotic almost automorphic synchronization of almost automorphic solutions of Clifford-valued recurrent NNs with mixed delays is developed in [20].

In this brief, we tried to manipulate neutral type HOHNNs in Clifford algebra with $(\mu ,\nu )-$PAA parameters. To our best knowledge, there are no public results considering the dynamic behavior of $(\mu ,\nu )-$PAA solutions of neutral type Clifford-valued NNs.

The main aim of this work is to obtain new sufficient conditions for ensuring the existence and global exponential stability of $(\mu ,\nu )-$pseudo almost automorphic solutions of neutral-type Clifford-valued HOHNNs. Most of the published articles on neutral type NNs focused on the first-order systems and analyzed real-valued, complex-valued and quaternion-valued NNs. So, this article brings several advancements listed below:

• 1. The study of the existence and uniqueness of the $(\mu ,\nu )-$pseudo almost automorphic solutions for neutral type HOHNN.

• 2. The analysis of the global exponential stability of the $(\mu ,\nu )-$pseudo almost automorphic solutions for the considered model without using the Lyapunov functional method.

• 3. The class of $(\mu ,\nu )-$PAA functions covers larger classes of functions that are very sophisticated and difficult to handle. We generalize many earlier publications [3, 5, 14].

• 4. The parameters are $(\mu ,\nu )-$PAA functions which have been considered in Clifford algebra for the first time in such context. Some previous works in the literature are significantly extended and complemented, such as [18, 19, 22].

• 5. Via direct method, we study the $(\mu ,\nu )-$PAA solutions for Clifford-valued HOHNNs without decomposing them into real-valued systems. Compared with real-valued, complex-valued and quaternion-valued HOHNNs [24, 25], the dynamical behaviors of Clifford-valued HOHNNs are the most complicated.

The outline of this paper is arranged as follows. In Sect. 2, we establish useful definitions, assumptions and lemmas. Section 3 is devoted to establish new criteria for the existence, uniqueness and global exponential stability of $(\mu ,\nu )-$PAA solutions of HOHNNs. In Sect. 4, a numerical example is given to illustrate the feasibility of the obtained results. Conclusion and meaningful remarks are drawn in Sect. 5.

2 Preliminaries

2.1 Real Clifford Algebra

In this subsection, we recall some results about real Clifford algebra. For more details, the reader may refer to [13] and the references therein. Let us denote $\mathbb {R}^m$ the $m-$dimensional real vector space. The real Clifford algebra over $\mathbb {R}^m$ is defined as

$$\begin{aligned}&\mathcal {A}=\bigg \{ \sum \limits _{A\subseteq \{1\cdots m\}}a^A e_A;\; a^A\in \mathbb {R}\bigg \},\; \hbox {where}\; e_A= e_{h_1}\cdots e_{h_\zeta }\; \hbox {with}\;A= \bigg \{h_1\cdots h_\zeta \bigg \}, \\&1\le h_1< h_2<\cdots <h_\zeta \le m \;\hbox {and}\; 1\le \zeta \le m. \end{aligned}$$

$\mathcal {A}$ equipped with m generators is defined as the Clifford algebra over the real number $\mathbb {R}$ with m multiplicative generators $e_1,\cdots ,e_m$ such that $e_i\in \mathbb {R}^m$, $e_\emptyset =e_0=1$, $e_0^2=1$ and

$$\begin{aligned} \left\{ \begin{array}{ll} e_0e_i=e_ie_0=e_i,\; &{}i=1,2,\cdots ,m,\\ e_ie_j+e_je_i=0,\; &{}i\ne j,\; i,j\in \{ 1,\cdots ,m \},\\ e_i^2=-1,\;&{}i=1,2,\cdots ,m. \end{array} \right. \end{aligned}$$

When one element is the product of multiple Clifford generators, we will write its subscripts together such as $e_{h_1}e_{h_2}=e_{h_1h_2}$ and $e_{h_1}e_{h_2}e_{h_5}=e_{h_1h_2h_5}$. It is easy to see that $\dim _\mathbb {R}\mathcal {A}=\sum \limits _{k=0}^{m} \left( {\begin{array}{c}m\\ k\end{array}}\right) =2^m.$ We also define the norm on $\mathcal {A}$ by

$$\begin{aligned} {\Vert x\Vert _\mathcal {A}=\max \limits _{1\le i\le n}\{|x^A|\},\; \hbox {for}\; x=\sum _{A}x^A e_A \in \mathcal {A},} \end{aligned}$$

and the norm on $\mathcal {A}^{n}$ by

$$\begin{aligned} {\Vert x\Vert _{\mathcal {A}^{n}}=\max \limits _{1\le i\le n}\{\Vert x_i\Vert _\mathcal {A}\},\;\hbox {for}\; x=(x_1,x_2,\cdots ,x_n)^T\in \mathcal {A}^n.} \end{aligned}$$

In the following, $\mathcal {A}^n$ denotes the $n-$dimensional real Clifford vector space.

2.2 Model Description

In this article, we deal with the following neutral type Clifford-valued HOHNNs with mixed delays:

$$\begin{aligned} \bigg [x_i(t)- q_i(t)x_i(t- r_{i}(t)) \bigg ]'= & {} -c_i(t)x_i(t)+\sum _{j=1}^{n} a_{ij}(t) f_{j} (x_{j}(t-\tau _{ij}(t))) \nonumber \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(t) g_{j}(x_{j}(t-\sigma _{ijl}(t))) g_{l}(x_{l}(t-\nu _{ijl} (t)))\nonumber \\&+\sum \limits _{j=1}^{n} \beta _{ij}(t)\int \limits _{0}^{+\infty } G_{ij}(s) h_{j}(x_{j}(t-s))ds\nonumber \\&+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}(t)\int \limits _{0}^{+\infty }P_{ijl}(t-s)k_{j}(x_{j}(s))ds \nonumber \\&\times \int \limits _{0}^{+\infty }Q_{ijl}(t-s)k_{l}(x_{l}(s))ds +I_{i}(t), \end{aligned}$$

(1)

in which n corresponds to the number of units in the NN, $x_i(\cdot )\in \mathcal {A}$ corresponds to the state vector of the $i^{th}$ unit, $c_{i}(\cdot )$ represents the rate with which the $i^{th}$ unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs, $q_i(\cdot )\in \mathcal {A}$ is the connection weights, $a_{ij}(\cdot ),\; \beta _{ij}(\cdot ) \in \mathcal {A}$ are the synaptic connection weight of the $j^{th}$ unit on the $i^{th}$ unit, $\alpha _{ijl}(\cdot ),\;p_{ijl}(\cdot )\in \mathcal {A}$ represent the second-order synaptic weights of the NNs, $f_j(\cdot ),\;g_j(.),\;h_j(\cdot ),\; k_j(\cdot )\in \mathcal {A}$ represent the activation functions of signal transmission, $G_{ij}(\cdot ),\;P_{ijl}(\cdot ),\;Q_{ijl}(\cdot ) \in \mathcal {A}$ are the transmission delay kernels, $r_i(\cdot ),\;\tau _{ij}(\cdot ),\;\sigma _{ijl}(\cdot ),\;\nu _{ijl}(\cdot ) \in \mathbb {R}^+$ are the transmission delays, $I_i(\cdot )\in \mathcal {A}$ denotes the external inputs. The initial conditions associated with (1) are of the form:

$$\begin{aligned} x_{i}(s) = \phi _{i}(s), \;s \in (-\infty , 0], \qquad i=1,2,\ldots ,n, \end{aligned}$$

(2)

where $\phi _{i}\in C\bigg ((-\infty , 0], \mathcal {A} \bigg )$ which is the set of continuous functions from $(-\infty , 0]$ to $\mathcal {A}$.

Remark 1

In (1), the functions $r_i(\cdot ),\;\tau _{ij}(\cdot ),\;\sigma _{ijl}(\cdot )$ and $\nu _{ijl}(\cdot )$ correspond to the transmission delays. In fact, time-delays exist in most NN systems because neurons cannot communicate or respond instantaneously. Sometimes they make the dynamic behaviors more complex and may destabilize the stable equilibria (see [1, 6, 11, 12]).

2.3 Notations and Definitions

Definition 1

([17]) A continuous function $f : \mathbb {R} \rightarrow \mathbb {R}^n$ is called almost automorphic if for every real sequence $(S_{n})_{n \in \mathbb {N}}$, there exists a subsequence $(s_{n})_{n \in \mathbb {N}}$ such that $g(t)=\lim \limits _{n \rightarrow \infty }f( t + s_n)$ is well defined for each $t \in \mathbb {R}$ and $\lim \limits _{n \rightarrow \infty } g( t - s_n) = f(t)$ for each $t \in \mathbb {R}$. Denote by $AA(\mathbb {R},\mathbb {R}^n)$ the set of all such functions.

Definition 2

([20]) Let $f=(f_1,f_2,\cdots ,f_n)^T:\mathbb {R} \mapsto \mathcal {A}^n$ where $f_i=\sum \limits _{A}f_i^Ae_A$. $f^A:\mathbb {R} \mapsto \mathbb {R}$ is called almost automorphic if for every $i=1,\cdots ,n$ we have $f_i^A \in AA(\mathbb {R}, \mathbb {R}^n).$ Denote by $AA(\mathbb {R}, \mathcal {A}^n)$ the set of all such functions.

Let B the Lebesgue $\sigma$-field of $\mathbb {R}$, $\mathcal {M}$ denotes the set of all positive measures $\mu$ on B satisfying $\mu (\mathbb {R})=+\infty$ and $\mu ([a,b])<+\infty$ for all $a,b\in \mathbb {R}$ $(a\le b)$.

Definition 3

For $\mu ,\nu \in \mathcal {M}$, the measures $\mu$ and $\nu$ are said to be equivalent if there exist constants $a_0$, $a_1>0$ and a bounded interval $\Omega \subset \mathbb {R}$ such that

$$\begin{aligned} a_0\nu (A)\le \mu (A)\le a_1\nu (A) \end{aligned}$$

for all $A\in B$ satisfying $A\cap \Omega =\emptyset$.

Now, we introduce a new concept of ergodicity, which generalizes those previously given in the literature.

Definition 4

Let $\mu ,\nu \in \mathcal {M}$. A bounded continuous function $f: \mathbb {R}\mapsto \mathcal {A}^n$ is said to be $(\mu ,\nu )$ ergodic if

$$\begin{aligned} \lim \limits _{r\longrightarrow + \infty }\frac{1}{\nu ([-r,r])} \int _{[-r,r]}\parallel f(t)\parallel _\mathcal {A} d\mu (t)=0. \end{aligned}$$

We denote the collection of all such functions by $\xi (\mathbb {R},\mathcal {A}^n,\mu ,\nu )$.

Let us denote $BC(\mathbb {R},\mathcal {A}^n)$ the set of bounded continued functions from $\mathbb {R}$ to $\mathcal {A}^n$, then $(BC(\mathbb {R},\mathcal {A}^n),\parallel \cdot \parallel _{*})$ is a Banach space where $\parallel \cdot \parallel _{*}$ is the norm

$$\begin{aligned} \parallel f\parallel _{*}:= \sup \limits _{t \in \mathbb {R}}\max \limits _{1 \le i\le n}\{ \Vert f_{i}(t)\Vert _\mathcal {A}\}. \end{aligned}$$

Definition 5

[7]] Let $\mu ,\nu \in \mathcal {M}$, $f \in BC(\mathbb {R},\mathcal {A}^n)$ is $(\mu ,\nu )$-pseudo almost automorphic if it can be expressed as

$$\begin{aligned} f = f_1+ f_2 \end{aligned}$$

where $f_1 \in AA(\mathbb {R},\mathcal {A}^n)$ and $f_2\in \xi (\mathbb {R},\mathcal {A}^n,\mu ,\nu ).$ The collection of such functions will be denoted by $PAA(\mathbb {R},\mathcal {A}^n,\mu ,\nu )$.

The following assumptions are fundamental in this function space:

$(A_1)$ For all $\mu ,\nu \in \mathcal {M}$, we have $\limsup \limits _{n\rightarrow \infty }\frac{\mu ([-r,r])}{\nu ([-r,r])}<\infty .$

$(A_2)$ For all $\tau \in \mathbb {R}$, there exist $\beta >0$ and a bounded interval I such that

$$\begin{aligned} \mu (\{a+\tau : a\in A\})\le \beta \mu (A) \end{aligned}$$

when $A\in B \hbox {\;satisfies\;} A\cap I=\emptyset$.

Let us state two useful theorems proved in [7] as follows.

Theorem 1

([7]) Let $\mu ,\nu \in \mathcal {M}$ satisfy $(A_2)$. Then the decomposition of a $(\mu ,\nu )$-pseudo almost automorphic function of the form $f=f_1+f_2$ where $f_1 \in AA(\mathbb {R},\mathcal {A}^n)$ and $f_2\in \xi (\mathbb {R},\mathcal {A}^n,\mu ,\nu )$ is unique.

Theorem 2

([7]) Let $\mu ,\nu \in \mathcal {M}$ satisfy $(A_1)$ and $(A_2)$. Then $PAA(\mathbb {R},\mathcal {A}^n,\mu ,\nu )$ is a Banach space.

2.4 Technical Lemmas

For $1\le i,j,l\le n$, we denote $q_{i}^*=\sup \limits _{t \in \mathbb {R}}\Vert q_{i}(t)\Vert _\mathcal {A}$, $c_{i}^*=\sup \limits _{t \in \mathbb {R}}\Vert c_{i}(t)\Vert _\mathcal {A},$ $c_{i*}=\inf \limits _{t \in \mathbb {R}}\Vert c_{i}(t)\Vert _\mathcal {A},$ $a_{ij}^*=\sup \limits _{t \in \mathbb {R}}\Vert a_{ij}(t)\Vert _\mathcal {A}$, $\alpha _{ijl}^*=\sup \limits _{t \in \mathbb {R}}\Vert \alpha _{ijl}(t)\Vert _\mathcal {A}$, $\beta _{ij}^*=\sup \limits _{t \in \mathbb {R}}\Vert \beta _{ij}(t)\Vert _\mathcal {A}$, $p_{ijl}^*= \sup \limits _{t \in \mathbb {R}}\Vert p_{ijl}(t)\Vert _\mathcal {A}$, $I_{ij}^*=\sup \limits _{t \in \mathbb {R}}\Vert I_{ij}(t)\Vert _\mathcal {A},$ $r_{i}^*=\sup \limits _{t \in \mathbb {R}}r_{i}(t),$ $\tau _{ij}^*=\sup \limits _{t \in \mathbb {R}}\tau _{ij}(t),$ $\sigma _{ijl}^*= \sup \limits _{t \in \mathbb {R}}\sigma _{ijl}(t),$ $\nu _{ijl}^*= \sup \limits _{t \in \mathbb {R}}\nu _{ijl}(t)$.

Moreover, assume that for all $1\le i,j,l \le n$, we have

$$\begin{aligned} c_i(\cdot ),\; r_i(\cdot ),\;\tau _{ij}(\cdot ), \;\sigma _{ijl}(\cdot ), \;\nu _{ijl} (\cdot )\in AA(\mathbb {R}, \mathbb {R}^n) \end{aligned}$$

and

$$\begin{aligned} q_i(\cdot ),\;a_{ij}(\cdot ),\; \alpha _{ijl}(\cdot ), \;\beta _{ij}(\cdot ), \;p_{ijl}(\cdot ), \;I_i(\cdot )\in PAA(\mathbb {R},\mathcal {A}^n,\mu ,\nu ). \end{aligned}$$

Assumption 1

For all $1\le j\le n,$ and all $u,v \in \mathbb {R}$ there exist nonnegative constants $L_j^f,\; L_j^g,\;L_j^h,\;L_j^k,\;d_j^g,\;d_j^k$ such that

$$\begin{aligned} \begin{array}{llllll} ||f_j(u)-f_j(v)||_\mathcal {A}&{}\le &{} L_j^f||u-v||_\mathcal {A},&{}||g_j(u)-g_j(v)||_\mathcal {A}&{}\le &{} L_j^g||u-v||_\mathcal {A},\\ ||g_j(u)||_\mathcal {A}&{}\le &{} d_j^g,&{}||h_j(u)-h_j(u)||_\mathcal {A}&{}\le &{} L_j^h||u-v||_\mathcal {A},\\ ||k_j(u)-k_j(u)||_\mathcal {A}&{}\le &{} L_j^k||u-v||_\mathcal {A},&{} ||k_j(u)||_\mathcal {A}&{}\le &{} d_j^k. \end{array} \end{aligned}$$

For simplicity of calculation and without loss of generality, we assume that $f_j(0)=g_j(0)=h_j(0)=0.$

Assumption 2

$G_{ij} : [0,+\infty ) \rightarrow \mathbb {R}$ is continuous and $|G_{ij}(t)| e^{\kappa _1 t}$ is integrable on $[0,+\infty )$ for a certain positive constant $\kappa _1.$ $P_{ijl} : [0,+\infty )\rightarrow \mathbb {R}$ is continuous and $|P_{ijl}(t)|e^{\kappa _2 t}$ is integrable on $[0,+\infty )$ for a certain positive constant $\kappa _2.$ $Q_{ijl} : [0,+\infty )\rightarrow \mathbb {R}$ is continuous and $|Q_{ijl}(t)|e^{\kappa _3 t}$ is integrable on $[0,+\infty )$ for a certain positive constant $\kappa _3.$

The following Lemma 1 and Lemma 2 are proved in [7].

Lemma 1

([7]) If $\phi (\cdot ) \in PAA(\mathbb {R},\mathcal {A},\mu ,\nu )$ then we have $\phi (\cdot -a ) \in PAA(\mathbb {R},\mathcal {A},\mu ,\nu )$.

Lemma 2

([7]) If $\varphi ,\psi \in PAA(\mathbb {R},\mathcal {A},\mu ,\nu )$ then we have $\varphi \times \psi \in PAA(\mathbb {R},\mathcal {A},\mu ,\nu )$.

By using Lemma 1 and Lemma 2, it is possible to prove the following lemmas.

Lemma 3

([7]) If $f(\cdot )\in C(\mathcal {A},\mathcal {A})$ satisfies the $l_f$-Lipschitz condition, $\phi (\cdot ) \in PAA (\mathbb {R},\mathcal {A},\mu ,\nu )$ and $\tau (\cdot ) \in AA(\mathbb {R},\mathcal {A},\mu ,\nu )$ then we have $f(\phi (\cdot -\tau (\cdot )))\in PAA(\mathbb {R},\mathcal {A},\mu ,\nu )$.

Lemma 4

([7]) Assume that Assumptions 1–2 hold. For all $1\le i,j\le n,$ if $\phi _j(\cdot ) \in PAA(\mathcal {A},\mathcal {A},\mu ,\nu )$ then we have

$$\begin{aligned} t\mapsto \int \limits _{0}^{+\infty } G_{ij}(s) h_{j}(\phi _{j}(\cdot -s)) ds\in PAA(\mathbb {R},\mathcal {A},\mu ,\nu ). \end{aligned}$$

Definition 6

Let $x(t)=(x_1(t),\dots ,x_n(t))^T$ be a $(\mu ,\nu )-$pseudo almost automorphic solution of the system (1) with the initial value $\varphi (t) =(\varphi _1(t),\dots ,\varphi _n(t))^T \in C\bigg ((-\infty , 0], \mathcal {A} \bigg )$ and $y(t)=(y_1(t),\dots ,y_n(t))^T$ be an arbitrary solution of the system (1) with the initial value $\psi (t) =(\psi _1(t),\dots ,\psi _n(t))^T \in C\bigg ((-\infty , 0], \mathcal {A} \bigg )$ respectively. If there exist positive constants $\lambda$ and N such that

$$\begin{aligned} \Vert x(t)-y(t) \Vert _{\mathcal {A}^n}\le & {} N \Vert \phi \Vert _\epsilon e^{- \lambda t}, \forall t>0, \end{aligned}$$

where

$$\begin{aligned} {\Vert \phi \Vert _\varepsilon =\max _{1\le i \le n}\sup _{t \in (-\infty ,0]} \bigg \Vert [\phi _i(t)-d_i(t)\phi _i(t-\tau _i(t)) ] - [x_i^*(t)- d_i(t)x^*_i(t-\tau _i(t)) ]\bigg \Vert _\mathcal {A} } \end{aligned}$$

then the $(\mu ,\nu )-$pseudo almost automorphic solution of the system (1) is said to be globally exponentially stable.

Assumption 3

For each $1\le i\le n,$ $t\in \mathbb {R},$

$$\begin{aligned} M[c_i] = \lim \limits _{T\rightarrow +\infty }\frac{1}{T}\int _{t}^{t+T}c_i(s)ds>0 \end{aligned}$$

and there exist a bounded and continuous function $\tilde{c}_i :\mathbb {R}\rightarrow (0, +\infty )$ and a positive constant $K_i$ such that

$$\begin{aligned} e^{-\int _{s}^{t}c_i(u)du}\le K_i e^{-\int _{s}^{t}\tilde{c}_i(u)du},\; \hbox {for all}\; t,s \in \mathbb {R},\; t-s\ge 0. \end{aligned}$$

Lemma 5

For $\phi =(\phi _{1},\ldots ,\phi _{n})^T \in PAA(\mathbb {R},\mathcal {A}^{n},\mu ,\nu ),$ we define the nonlinear operator $\Theta =\Theta _\phi$ as follows

$$\begin{aligned} \Theta _{\phi }(t) = \left( \begin{array}{c} \int \limits _{-\infty }^{t} e^{-\int \limits _{s}^{t}c_{1}(u) du } F_{1}(s)ds \\ \vdots \\ \int \limits _{-\infty }^{t} e^{-\int \limits _{s}^{t}c_{n}(u) du } F_{n}(s)ds\\ \end{array} \right) \end{aligned}$$

where

$$\begin{aligned} F_{i}(s)= & {} c_i(s)q_{i}(s)\phi _{i}(s-r_{i} (s))\\&\quad +\sum _{j=1}^{n} a_{ij}(s) f_{j} (\phi _{j}(s-\tau _{ij}(s)))\\&+ \sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(s) g_{j}(\phi _{j}(s-\sigma _{ijl}(s))) g_{l}(\phi _{l}(s-\nu _{ijl} (s)))\\&\quad +\sum \limits _{j=1}^{n} \beta _{ij}(s)\int \limits _{0}^{+\infty } G_{ij}(m) h_{j}(\phi _{j}(s-m))dm\\&\quad +\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}(s)\\&\quad \int \limits _{0}^{+\infty }P_{ijl}(m)k_{j}(\phi _{j}(s-m))dm \int \limits _{0}^{+\infty }Q_{ijl}(m)k_{l}(\phi _{l}(s-m))dm + I_{i}(s). \end{aligned}$$

Then $\Theta _{\phi }$ maps $PAA(\mathbb {R},\mathcal {A}^{n},\mu ,\nu )$ into itself.

Proof

Let $\phi \in PAA(\mathbb {R},\mathcal {A},\mu ,\nu ).$ Using Lemma 3, we obtain $f_{j} (\phi _{j}(s-\tau _{ij}(s)))$, $g_{j}(\phi _{j}(s-\sigma _{ijl}(s)))$ and $g_{l}(\phi _{l}(s-\nu _{ijl} (s)))$ in $PAA(\mathbb {R},\mathcal {A},\mu ,\nu )$. By using Lemma 4, we have

$$\begin{aligned} \int \limits _{0}^{+\infty } G_{ij}(m) h_{j}(x_{j}(s-m))dm,\; \int \limits _{0}^{+\infty }P_{ijl}(m)k_{j}(x_{j}(s-m))dm \;\hbox {and}\; \int \limits _{0}^{+\infty }Q_{ijl}(m)k_{l}(x_{l}(s-m))dm \end{aligned}$$

in $PAA (\mathbb {R},\mathcal {A},\mu ,\nu )$. Then, $F_i$ is a $(\mu ,\nu )-$PAA function. Via Theorem 1, we have $F_i=F_i^1+F_i^2$ with $F_i^1 \in AA(\mathbb {R},\mathcal {A}^n)$ and $F_i^2\in \xi (\mathbb {R},\mathcal {A}^n,\mu ,\nu )$.

Noting that $M[c_i]>0$ from Assumption 3 and using the theory of exponential dichotomy, we obtain that

$$\begin{aligned} \int \limits _{-\infty }^{t} e^{-\int \limits _{s}^{t}c_{i}(u) du } F_i^1(s)ds \in AA(\mathbb {R},\mathcal {A}^n) \end{aligned}$$

(3)

is a solution of the following almost automorphic differential equation

$$\begin{aligned} \dot{y}(t)=-c_i(t)y(t)+F_i^1(t),\qquad 1\le i,j \le n. \end{aligned}$$

Now, let us show that

$$\begin{aligned} \int \limits _{-\infty }^{t} e^{-\int \limits _{s}^{t}c_{i}(u) du } F_i^2(s)ds \in \xi (\mathbb {R},\mathcal {A}^n,\mu ,\nu ). \end{aligned}$$

From Assumption 3, one has

$$\begin{aligned}&\lim _{r\longrightarrow \infty } \frac{1}{\nu ([-r,r])} \int _{[-r,r]} \Vert F_{i}^{2}(t) \Vert _\mathcal {A} d\mu (t)\\&= \lim _{r\longrightarrow \infty } \frac{1}{\nu ([-r,r])} \int _{[-r,r]}\left\| \int \limits _{-\infty }^{t} e^{-\int \limits _{s}^{t}c_{i}(u) du} F_{i}^{2}(s) ds\right\| _\mathcal {A} d\mu (t) \\\le & {} \lim _{r\longrightarrow \infty } \frac{K_i}{\nu ([-r,r])} \int _{[-r,r]} \int \limits _{-\infty }^{t} e^{-(t-s)\tilde{c}_{i*}} \Vert F_{i}^{2}(s)\Vert _\mathcal {A} ds d\mu (t). \\ \end{aligned}$$

Let

$$\begin{aligned} E_{1}= & {} \lim \limits _{r\longrightarrow \infty } \frac{K_i}{\nu ([-r,r])} \int _{[-r,r]} \left( \int _{-r}^{t} \Vert e^{-(t-s)\tilde{c}_{i*}} F_{i}^{2}(s) \Vert _\mathcal {A} ds \right) d\mu (t), \\ E_{2}= & {} \lim \limits _{r\longrightarrow \infty } \frac{K_i}{\nu ([-r,r])} \int _{[-r,r]} \left( \int \limits _{- \infty }^{-r} e^{-(t-s)\tilde{c}_{i*}} \Vert F_{i}^{2}(s)\Vert _\mathcal {A} ds\right) d\mu (t) \end{aligned}$$

and $m= t-s$, then by Fubini’s theorem we obtain

$$\begin{aligned} E_{1}= & {} \lim _{r\longrightarrow \infty } \frac{K_i}{\nu ([-r,r])} \int _{[-r,r]} \left( \int _{-r}^{t} e^{-(t-s)\tilde{c}_{i*}}\Vert F_{i}^{2}(s) \Vert _\mathcal {A} ds\right) d\mu (t) \\\le & {} \lim _{r\longrightarrow \infty }\frac{K_i}{\nu ([-r,r])} \int _{[-r,r]}\left( \int \limits _{0}^{+ \infty } e^{-m \tilde{c}_{i*}}\Vert F_{i}^{2}(t-m) \Vert _\mathcal {A}dm\right) d\mu (t)\\\le & {} \int \limits _{0}^{+ \infty } e^{-m \tilde{c}_{i*}} \left( \lim _{r\longrightarrow \infty } \frac{K_i}{\nu ([-r,r])} \int _{[-r,r]} \Vert F_{i}^{2}(t-m) \Vert _\mathcal {A}d \mu (t)\right) dm\\= & {} \int \limits _{0}^{+ \infty } e^{-m \tilde{c}_{i*}} \left( \lim _{r\longrightarrow \infty } \frac{K_i}{\nu ([-r,r])} \int \limits _{-r-m}^{r-m} \Vert F_{i}^{2}(t)\Vert _\mathcal {A} d\mu _m(t)\right) dm \\\le & {} K_i \int _{0}^{+ \infty } e^{-m \tilde{c}_{i*}} \Bigg (\lim _{r\longrightarrow \infty } \frac{\nu ([-r-m,r+m] ) }{\nu ([-r,r]}\frac{\beta }{\nu ([-r-m,r+m])} \\&\times \int \limits _{[-r-m,r+m] } \Vert F_{i}^{2}(t) \Vert _\mathcal {A} d\mu (t)\Bigg ) dm. \end{aligned}$$

On the one hand we have $F_{i}^{2}\in \xi (\mathbb {R},\mathbb {R},\mu ,\nu )$ then $E_1=0$. On the other hand, we have

$$\begin{aligned} E_{2}= & {} \lim _{r\longrightarrow \infty } \frac{K_i}{\nu ([-r,r])} \int _{[-r,r]}\left( \int \limits _{- \infty }^{-r} \Vert e^{-(t-s)\tilde{c}_{i*}} F_{i}^{2}(s)\Vert _\mathcal {A} ds\right) d\mu (t)\\= & {} \lim _{r\longrightarrow \infty }\frac{K_i}{\nu ([-r,r])} \int _{[-r,r]}\left( \int \limits _{- \infty }^{-r} e^{-(t-s)\tilde{c}_{i*}} \Vert F_{i}^{2}(s)\Vert _\mathcal {A}ds\right) d\mu (t)\\\le & {} \lim _{r\longrightarrow \infty }\frac{K_i}{\nu ([-r,r])} \int \limits _{-\infty }^{- r} e^{s\tilde{c}_{i*}} \Vert F_{i}^{2}(s)\Vert _\mathcal {A} ds\int \limits _{-r}^{r} e^{- t \tilde{c}_{i*}} d\mu (t)\\= & {} \lim _{r\longrightarrow \infty } K_i \frac{\Vert F_{i}^{2}\Vert _\mathcal {A}}{ \tilde{c}_{i*}} e^{- 2r \tilde{c}_{i*}}=0. \end{aligned}$$

Combining with (3) it leads to $\Theta _{\phi }$ maps $PAA(\mathbb {R},\mathcal {A}^{n},\mu ,\nu )$ into itself. $\square$

3 Main Results

In this section, we establish new results for the existence, uniqueness and stability of $(\mu ,\nu )-$PAA solution of the system (1). For $(\phi _1,\phi _2,\cdots , \phi _n)^T \in PAA(\mathbb {R},\mathcal {A}^{n},\mu ,\nu ),$ we define the norm of $\phi$ as

$$\begin{aligned} \parallel \phi \parallel _{*}:= \max \limits _{1 \le i\le n} \sup \limits _{t \in \mathbb {R}}\bigg \{ \Vert \phi _{i}(t)\Vert _\mathcal {A}\bigg \}. \end{aligned}$$

And we consider the following Assumption:

Assumption 4

For $1\le i,j,l\le n,$ there exist strictly positive constants $M, \; \Lambda _i$ and $\Omega _i$ such that

$$\begin{aligned} {M}= & {} {\max _{1\le i \le n} \bigg \{\frac{K_i}{\tilde{c}_{i*}} I_i^*\bigg \}}\\ \Lambda= & {} \max \limits _{1 \le i \le n}\bigg \{ q_i^*+\frac{K_i}{\tilde{c}_{i*} } \bigg [c_i^*q_i^*+\sum _{j=1}^{n} a_{ij}^* L_j^f +\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^* L_j^g L_l^g+\sum \limits _{j=1}^{n} \beta _{ij}^*L_j^h \int \limits _{0}^{+\infty }|G_{ij}(u)|du\\&+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}^*L_j^kL_l^k\int \limits _{0}^{+\infty }|P_{ijl}(u)| du\int \limits _{0}^{+\infty }|Q_{ijl}(u)|du\bigg ]\bigg \}<1,\\ \Omega= & {} \max \limits _{1 \le i \le n}\bigg \{q_i^*+ \frac{K_i}{\tilde{c}_{i*}} \bigg [c_i^*q_i^*+\sum _{j=1}^{n}a_{ij}^*L_j^f+ \sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^*( L_j^g d_l^g + L_l^g d_j^g )\\&+\sum \limits _{j=1}^{n} \beta _{ij}^*L_j^h \int \limits _{0}^{+\infty }|G_{ij}(u)|du + \sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}^* \int \limits _{0}^{+\infty }|P_{ijl}(u)|du\\&\int \limits _{0}^{+\infty }|Q_{ijl}(u)|du( L_j^k d_l^k + L_l^k d_j^k )\bigg ]\bigg \}\\&\quad < 1 \end{aligned}$$

and a strictly negative constant $\Upsilon _0$ such that

$$\begin{aligned} \Upsilon _0= & {} \sup \limits _{t \in \mathbb {R}}\bigg \{-\tilde{c}_i(t)+K_i\bigg [ \frac{1}{1-q_i^* }c_i^*q_i^*+ \sum _{j=1}^{n} a_{ij}^*L_j^f \frac{1}{1-q_j^*}\\&\quad +\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^* \left( L_j^gd_l^g \frac{1}{1-q_j^*} +L_l^gd_j^g \frac{1}{1-q_j^*}\right) +\sum _{j=1}^{n}\beta _{ij}^* L_j^h\int \limits _{0}^{+\infty } |G_{ij}(u)|du\frac{ 1}{1-q_j^* }\\&\quad + \sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}^*\bigg [ L_j^kd_l^k \int \limits _{0}^{+\infty } |P_{ijl}(u)|du +L_l^k d_j^k\int \limits _{0}^{+\infty }|Q_{ijl}(u)| du\bigg ] \frac{ 1}{1-q_j^* }\bigg ]\bigg \}. \end{aligned}$$

Theorem 3

Suppose that Assumptions 1–4 hold. Then the system (1) has only one $(\mu ,\nu )-$PAA solution in the region

$$\begin{aligned} S=\bigg \{ \phi \in PAA(\mathbb {R},\mathcal {A}^{n},\mu ,\nu ): \parallel \phi - \phi _0 \parallel _{*} \le {\frac{\Lambda }{1-\Lambda }M} \bigg \}, \end{aligned}$$

where

$$\begin{aligned} \phi _0(t) = \left( \begin{array}{cc} \int _{-\infty }^{t} e^{-\int _{s}^{t}c_{1}(u)du} I_{1}(s)ds \\ \vdots \\ \int _{-\infty }^{t} e^{-\int _{s}^{t}c_{n}(u)du} I_{n}(s)ds \end{array} \right) . \end{aligned}$$

which is globally exponentially stable.

Proof

First part: existence and uniqueness of $(\mu ,\nu )-$PAA solutions Let

$$\begin{aligned} Y_i(t)=x_{i}(t)-q_{i}(t)x_{i}(t-r_{i} (t)),\; \hbox {for all}\; 1\le i\le n. \end{aligned}$$

(4)

Then, we have

$$\begin{aligned} Y'_i(t)= & {} \bigg [x_{i}(t)-q_{i}(t)x_{i}(t-r_{i}(t))\bigg ]' \nonumber \\= & {} -c_i(t)Y_i(t)-c_i(t)q_{i}(t)x_{i}(t-r_{i} (t)) +\sum _{j=1}^{n} a_{ij}(t) f_{j} (x_{j}(t-\tau _{ij}(t))) \nonumber \\&\quad +\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(t) g_{j}(x_{j}(t-\sigma _{ijl}(t))) g_{l}( x_{l}(t-\nu _{ijl}( t)))\nonumber \\&\quad +\sum \limits _{j=1}^{n} \beta _{ij}(t)\int \limits _{0}^{+\infty } G_{ij}(s) h_{j}(x_{j}(t-s))ds\nonumber \\&\quad +\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}(t)\int \limits _{0}^{+\infty }P_{ijl}(s)k_{j}(x_{j}(t-s))ds \int \limits _{0}^{+\infty }Q_{ijl}(s)k_{l}(x_{l}(t-s))ds\nonumber \\&\quad +I_{i}(t),\qquad i=1,\dots ,n. \end{aligned}$$

(5)

By using Lemma 5, we define an operator $\overline{\Theta }$ as follows:

$$\begin{aligned}&\overline{\Theta }: S \rightarrow S\\&(\phi _1\cdots ,\phi _n)^T\mapsto (\overline{\Theta }_{\phi _1}\cdots ,\overline{\Theta }_{\phi _n})^T \end{aligned}$$

such that $\overline{\Theta }_{\phi _i}=\{q_i(t)\phi _i(t-r_i(t))\}+\Theta _{\phi }(t)$ for all $\phi \in S$. One has

$$\begin{aligned} \Vert \phi _0\Vert _*= & {} \max _{1\le i \le n} \bigg \{\sup _{ t \in \mathbb {R}}\bigg \Vert \int _{-\infty }^{t} e^{-\int _{s}^{t}c_{i}(u)du} I_{i}(s)ds\bigg \Vert _\mathcal {A}\bigg \}\\\le & {} {\max _{1\le i \le n} \bigg \{ K_i \sup _{ t \in \mathbb {R}}\bigg \Vert \int _{-\infty }^{t} e^{-\int _{s}^{t}\tilde{c}_{i}(u)du} I_{i}(s)ds\bigg \Vert _\mathcal {A}\bigg \}}\\\le & {} {\max _{1\le i \le n} \bigg \{\frac{K_i}{\tilde{c}_{i*}} I_i^*\bigg \}=M} \end{aligned}$$

is the unique $(\mu ,\nu )-$pseudo almost automorphic solution of the following differential equations:

$$\begin{aligned} Y'_i (t) = -c_i (t)Y_i(t) + I_i(t),\qquad i=1,\dots ,n. \end{aligned}$$

The set $S = \bigg \{\phi \in PAA(\mathbb {R},\mathcal {A}^{n},\mu ,\nu ): \parallel \phi - \phi _0 \parallel _{*} \le {\frac{\Lambda }{1-\Lambda }M}\bigg \}$ is a closed convex subset of $PAA(\mathbb {R},\mathcal {A}^{n},\mu ,\nu )$. If $\phi \in S$, then

$$\begin{aligned} \parallel \phi \parallel _{*}\le & {} \parallel \phi - \phi _0 \parallel _{*} + \parallel \phi _0 \parallel _{*}\nonumber \\\le & {} \parallel \phi - \phi _0 \parallel _{*} + M. \end{aligned}$$

(6)

We claim that for any $\phi \in S$ the mapping $\overline{\Theta }_\phi \in S$. Note that

$$\begin{aligned} \bigg \Vert \overline{\Theta }_\varphi - \phi _0 \bigg \Vert _*= & {} \max \limits _{1 \le i \le n} \bigg \{\sup \limits _{ t \in \mathbb {R}}\bigg \Vert q_i(t)\phi _i(t-r_i (t))\\&+ \int _{-\infty }^{t} e^{-\int _{s}^{t}c_{i}(u)du}\bigg [-c_i(s)q_i(s)\phi _i(s-r_i(s))\\&+\sum _{j=1}^{n} a_{ij}(s) f_{j} (\phi _{j}(s-\tau _{ij}(s)))\\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(s) g_{j}(\phi _{j}(s-\sigma _{ijl}(s))) g_{l}(\phi _{l}(s-\nu _{ijl}(s)))\\&+\sum \limits _{j=1}^{n} \beta _{ij}(s)\int \limits _{0}^{+\infty } G_{ij}(u) h_{j}(\phi _{j}(s-u))du\\&+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}(s)\int \limits _{0}^{+\infty }P_{ijl}(u)k_{j}(\phi _{j}(s-u))du\\&\int \limits _{0}^{+\infty }Q_{ijl}(u)k_{l}(\phi _{l}(s-u))du\bigg ] ds\bigg \Vert _\mathcal {A}\bigg \}\\ \end{aligned}$$

and then we have

$$\begin{aligned} \bigg \Vert \overline{\Theta }_\varphi - \phi _0 \bigg \Vert _*\le & {} \max \limits _{1 \le i \le n}\bigg \{\sup \limits _{ t \in \mathbb {R}}\Vert q_i(t)\phi _i(t-r_i (t))\Vert _\mathcal {A}\\&\quad + \int _{-\infty }^{t} e^{-\int _{s}^{t}\tilde{c}_{i}(u)du}K_i \bigg [ \sup \limits _{ t \in \mathbb {R}}\Vert -c_i(s)q_i(s)\Vert _\mathcal {A}\sup \limits _{ t \in \mathbb {R}}\Vert \phi _i(s-r_i(s))\Vert _\mathcal {A}\\&\quad +\sum _{j=1}^{n} \sup \limits _{ t \in \mathbb {R}}\Vert a_{ij}(s)\Vert _\mathcal {A} \sup \limits _{ t \in \mathbb {R}} \Vert f_{j} (\phi _{j}(s-\tau _{ij}(s))\Vert _\mathcal {A}\\&\quad +\sum _{j=1}^{n} \sum _{l=1}^{n} \sup \limits _{ t \in \mathbb {R}}\Vert \alpha _{ijl}(s)\Vert _\mathcal {A} \sup \limits _{ t \in \mathbb {R}}\Vert g_{j}(\phi _{j}(s-\sigma _{ijl}(s)))\Vert _\mathcal {A}\sup \limits _{ t \in \mathbb {R}}\Vert g_{l}(\phi _{l}(s-\nu _{ijl}(s))\Vert _\mathcal {A}\\&\quad +\sum \limits _{j=1}^{n} \sup \limits _{ t \in \mathbb {R}}\Vert \beta _{ij}(s)\Vert _\mathcal {A}\int \limits _{0}^{+\infty } |G_{ij}(u)| \sup \limits _{ t \in \mathbb {R}}\Vert h_{j}(\phi _{j}(s-u))\Vert _\mathcal {A}du\\&\quad +\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}\sup \limits _{ t \in \mathbb {R}}\Vert p_{ijl}(s)\Vert _\mathcal {A} \int \limits _{0}^{+\infty }|P_{ijl}(u)| \sup \limits _{ t \in \mathbb {R}}\Vert k_{j}(\phi _{j}(s-u))\Vert _\mathcal {A} du\\&\quad \times \int \limits _{0}^{+\infty }|Q_{ijl}(u)|\sup \limits _{ t \in \mathbb {R}}\Vert k_{l}(\phi _{l}(s-u))\Vert _\mathcal {A}du\bigg ] ds\bigg \}. \end{aligned}$$

It leads to

$$\begin{aligned} \bigg \Vert \overline{\Theta }_\varphi - \phi _0 \bigg \Vert _*\le & {} \max \limits _{1 \le i \le n}\bigg \{q_i^* +\int _{-\infty }^{t} e^{-\int _{s}^{t}\tilde{c}_{i}(u)du}K_i \bigg [c_i^* q_i^* +\sum _{j=1}^{n} a_{ij}^* L_j^f \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^* L_j^g L_l^g +\sum \limits _{j=1}^{n} \beta _{ij}^*L_j^h \int \limits _{0}^{+\infty }|G_{ij}(u)|du \\&+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}^*L_j^kL_l^k\int \limits _{0}^{+\infty } |P_{ijl}(u)| du\int \limits _{0}^{+\infty }|Q_{ijl}(u)|du\bigg ] ds\bigg \}\Vert \phi \Vert _*\\= & {} \Lambda \Vert \phi \Vert _*. \end{aligned}$$

As $\Lambda <1,$ it implies that $\overline{\Theta }_\varphi \in S$. Next, we prove that the mapping $\overline{\Theta }$ is a contraction mapping of S. For $\phi ,\psi \in S$, we have

$$\begin{aligned} \bigg \Vert \overline{\Theta }_\phi -\overline{\Theta }_\psi \bigg \Vert _*\le & {} \max \limits _{1 \le i \le n}\bigg \{ \sup \limits _{ t \in \mathbb {R}}\bigg \Vert q_i(t)\bigg [ \phi _i(t-r_i(t))-\psi _i(t-r_i(t))\bigg ]\\&+\int _{-\infty }^{t} e^{-\int _{s}^{t}c_{i}(u)du} \bigg [-c_i(s)q_i(s)\bigg (\phi _i(s-r_i(s)) +\psi _i(s-r_i(s))\bigg )\\&+\sum _{j=1}^{n} a_{ij}(s) \bigg (f_{j} (\phi _{j}(s-\tau _{ij}(s)))- f_{j} (\psi _{j}(s-\tau _{ij}(s)))\bigg ) \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(s) \bigg (g_{j}(\phi _{j}(s-\sigma _{ijl}(s))) g_{l}(\phi _{l}(s-\nu _{ijl}(s)))\\&-g_{j}(\psi _{j}(s-\sigma _{ijl}(s))) g_{l}(\psi _{l}(s-\nu _{ijl}(s)))\bigg )\\&+\sum \limits _{j=1}^{n} \beta _{ij}(s)\int \limits _{0}^{+\infty } G_{ij}(u) \bigg ( h_{j}(\phi _{j}(s-u))- h_{j}(\psi _{j}(s-u)\bigg ) du\\&+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}(s) \bigg (\int \limits _{0}^{+\infty }P_{ijl}(u)h_j(\phi (s-u))du\int \limits _{0}^{+\infty }Q_{ijl}(u)k_l(\phi (s-u))du\\&-\int \limits _{0}^{+\infty }P_{ijl}(u)h_j(\psi (s-u))du \int \limits _{0}^{+\infty }Q_{ijl}(u)k_l(\phi (s-u))du\\&+\int \limits _{0}^{+\infty }P_{ijl}(u)h_j(\psi (s-u))du \int \limits _{0}^{+\infty }Q_{ijl}(u)k_l(\phi (s-u))du\\&-\int \limits _{0}^{+\infty }P_{ijl}(u)h_j(\psi (s-u))du \int \limits _{0}^{+\infty }Q_{ijl}(u)k_l(\psi (s-u))du\bigg ) \bigg ]ds\bigg \Vert _\mathcal {A}\bigg \}. \end{aligned}$$

It leads to

$$\begin{aligned} \bigg \Vert \overline{\Theta }_\phi -\overline{\Theta }_\psi \bigg \Vert _*\le & {} \max \limits _{1 \le i \le n}\bigg \{q_i^*+\int _{-\infty }^{t} e^{-\int _{s}^{t}\tilde{c}_{i}(u)du} K_i\bigg [c_i^*q_i^*+\sum _{j=1}^{n}a_{ij}^*L_j^f\\&+ \sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^*( L_j^g d_l^g + L_l^g d_j^g )\\&+\sum \limits _{j=1}^{n} \beta _{ij}^*L_j^h \int \limits _{0}^{+\infty } |G_{ij}(u)|du + \sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}^* \int \limits _{0}^{+\infty } |P_{ijl}(u)|du\\&\times \int \limits _{0}^{+\infty } |Q_{ijl}(u)| du( L_j^k d_l^k + L_l^k d_j^k )\bigg ]ds\bigg \}\Vert \phi -\psi \Vert _*\\ \end{aligned}$$

and then

$$\begin{aligned} \bigg \Vert \overline{\Theta }_\phi -\overline{\Theta }_\psi \bigg \Vert _*\le & {} {\max \limits _{1 \le i \le n}\bigg \{q_i^*+ \frac{K_i}{\tilde{c}_{i*}} \bigg [c_i^*q_i^*+\sum _{j=1}^{n}a_{ij}^*L_j^f+ \sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^*\left( L_j^g d_l^g + L_l^g d_j^g \right) }\\&{ +\sum \limits _{j=1}^{n} \beta _{ij}^*L_j^h \int \limits _{0}^{+\infty }\left| G_{ij}(u)\right| du + \sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}^* \int \limits _{0}^{+\infty }\left| P_{ijl}(u)\right| du}\\&{\times \int \limits _{0}^{+\infty }\left| Q_{ijl}(u)\right| du( L_j^k d_l^k + L_l^k d_j^k)\bigg ]\bigg \}\Vert \phi -\psi \Vert _*}\\= & {} {\Omega \Vert \phi -\psi \Vert _*}. \end{aligned}$$

As $\Omega <1,$ then we obtain that $\overline{\Theta }$ is a contraction. Via Theorem 2, $PAA(\mathbb {R},\mathcal {A}^n,\mu ,\nu )$ is a Banach space. Then due to Banach’s fixed point principle, $\overline{\Theta }$ possesses one and only one fixed point $x^{*}= \{x^*_i(t)\}\in S,$ such that

$$\begin{aligned} x^*_i(t)= & {} \{q_i(t) x_i^*(t-r_i (t))\}+\Theta _{x^*}(t)\\= & {} q_i(t) x_i^*(t-r_i (t))+\int _{-\infty }^{t}e^{-\int _{s}^{t}c_i(u)du}\bigg [-c_i(s)q_i(s)x^*_i(s-r_i (s))\\&+\sum _{j=1}^{n} a_{ij}(s) f_{j} (x^*_{j}(s-\tau _{ij}(s))) +\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(s) g_{j}(s- x^*_{j}(\sigma _{ijl}(s))) g_{l}( x^*_{l}(s-\nu _{ijl}( s)))\\&+\sum \limits _{j=1}^{n} \beta _{ij}(s)\int \limits _{0}^{+\infty } G_{ij}(u) h_{j}(x^*_{j}(s-u))du\\&+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}(s)\int \limits _{0}^{+\infty }P_{ijl}(u)k_{j}(x_{j}(s-u))du \int \limits _{0}^{+\infty }Q_{ijl}(u)k_{l}(x_{l}(s-u))du +I_{i}(s)\bigg ]ds. \end{aligned}$$

Then it leads to

$$\begin{aligned} \bigg [x^*_i(t)-q_i(t) x_i^*(t-r_i( t))\bigg ]'= & {} -c_i(t) x_i^*(t)+ \sum _{j=1}^{n} a_{ij}(s) f_{j} (x^*_{j}(t-\tau _{ij}(t))) \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(t)g_{j}( x^*_{j}(t-\sigma _{ijl}( t))) g_{l}( x^*_{l}(t-\nu _{ijl} (t)))\\&+\sum \limits _{j=1}^{n} \beta _{ij}(t)\int \limits _{0}^{+\infty } G_{ij}(u) h_{j}(x^*_{j}(t-u))du\\&+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}p_{ijl}(t)\int \limits _{0}^{+\infty }P_{ijl}(s)k_{j}(x^*_{j}(t-s))ds\\&\times \int \limits _{0}^{+\infty }Q_{ijl}(s)k_{l}(x^*_{l}(t-s))ds+I_{i}(t). \end{aligned}$$

Thus the system (1) has an unique $(\mu ,\nu )-$PAA solution $x^*(t)$.

Second part: global exponential stability of the $(\mu ,\nu )-$ PAA solution

In view of the first part, the system (1) has only one $(\mu ,\nu )-$pseudo almost automorphic solution denoted by $x^*(t)=(x_1^*(t),\dots ,x_n^*(t))^T$ and satisfying (2). Let $x(t)=(x_1(t),\cdots ,x_n(t))^T$ be an arbitrary solution of the system (1) with initial value $\phi (t)=(\phi _1(t),\cdots ,\phi _n(t))^T$ satisfying (2). Let

$$\begin{aligned} z_i(t)= & {} x_i(t)-x_i^*(t),\\ Z_i(t)= & {} \bigg [x_i(t)-q_i(t)x_i(t-r_i(t))\bigg ]-\bigg [x_i^*(t)-q_i(t)x^*_i(t-r_i(t))\bigg ]. \end{aligned}$$

We have

$$\begin{aligned}&Z'_{i}(t)= - c_{i}(t) Z_{i}(t)-c_i(t)q_i(t)z_i(t-r_i(t))\nonumber \\&+\sum _{j=1}^{n} a_{ij}(t) \bigg [f_{j} (x_{j}(t-\tau _{ij}(t)) - f_{j} (x_{j}^*(t-\tau _{ij}(t))\bigg ]\nonumber \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(t)\bigg [ g_{j} (x_{j}(t-\sigma _{ijl}(t)) g_{l} (x_{l}(t-\nu _{ijl}(t))))\nonumber \\&-g_{j}(x^*_{j}(t-\sigma _{ijl}(t)))g_{l}(x^*_{l}(t-\nu _{ijl}(t)))\bigg ]\nonumber \\&+\sum _{j=1}^{n}\beta _{ij} (t)\int \limits _{0}^{+\infty }G_{ij}(u)\bigg [h_j( x_j(t-u))-h_j(x_j^*(t-u)) \bigg ]du\nonumber \\&+\sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}(t)\bigg [\int \limits _{0}^{+\infty }P_{ijl}(s)k_{j}(x_{j}(t-s))ds \int \limits _{0}^{+\infty }Q_{ijl}(s)k_{l}(x_{l}(t-s))ds\nonumber \\&-\int \limits _{0}^{+\infty }P_{ijl}(s)k_{j}(x^*_{j}(t-s))ds \int \limits _{0}^{+\infty }Q_{ijl}(s)k_{l}(x^*_{l}(t-s))ds\bigg ]. \end{aligned}$$

(7)

Set

$$\begin{aligned} \Upsilon (\gamma )= & {} \sup \limits _{t \in \mathbb {R}}\bigg \{\gamma -\tilde{c}_i(t)+K_i\bigg [ \frac{e^{\gamma r_i^*}}{1-q_i^* e^{\gamma r_i^*}}c_i^*q_i^*+ \sum _{j=1}^{n} a_{ij}^*L_j^f \frac{e^{\gamma \tau _{ij}^* }}{1-q_j^*e^{\gamma r_j^*}}\nonumber \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^* \bigg ( L_j^gd_l^g \frac{e^{\gamma \sigma _{ijl}^* }}{1-q_j^*e^{\gamma r_j^*}} +L_l^gd_j^g \frac{e^{\gamma \nu _{ijl}^* }}{1-q_j^*e^{\gamma r_j^*}}\bigg )\nonumber \\&+\sum _{j=1}^{n}\beta _{ij}^* L_j^h\int \limits _{0}^{+\infty } |G_{ij}(u)|e^{\gamma u}du\frac{ 1}{1-q_j^* e^{\gamma r_j^*} }\nonumber \\&+ \sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}^*\bigg [ L_j^kd_l^k \int \limits _{0}^{+\infty } |P_{ijl}(u)|e^{\gamma u}du \nonumber \\&+L_l^k d_j^k\int \limits _{0}^{+\infty } |Q_{ijl}(u)|e^{\gamma u}du\bigg ] \frac{ 1}{1-q_j^* e^{\gamma r_j^*} }\bigg ]\bigg \},\qquad {\gamma \in [0, \min _{1\le \iota \le 3}\kappa _\iota ]}. \end{aligned}$$

(8)

From Assumption 4 and by continuity of $\Upsilon (\gamma )$ we have

$$\begin{aligned} \Upsilon (0)= & {} \sup \limits _{t \in \mathbb {R}}\bigg \{-\tilde{c}_i(t)+K_i\bigg [ \frac{1}{1-q_i^* }c_i^*q_i^*+ \sum _{j=1}^{n} a_{ij}^*L_j^f \frac{1}{1-q_j^*}\nonumber \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^* \bigg ( L_j^gd_l^g \frac{1}{1-q_j^*} +L_l^gd_j^g \frac{1}{1-q_j^*}\bigg )\nonumber \\&+\sum _{j=1}^{n}\beta _{ij}^* L_j^h\int \limits _{0}^{+\infty } |G_{ij}(u)|du\frac{ 1}{1-q_j^*}+\sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}^*\bigg [ L_j^kd_l^k \int \limits _{0}^{+\infty } |P_{ijl}(u)|du \nonumber \\&+L_l^k d_j^k\int \limits _{0}^{+\infty } |Q_{ijl}(u)|du\bigg ] \frac{ 1}{1-q_j^* }\bigg ]\bigg \}<0.\nonumber \\ \end{aligned}$$

(9)

We can choose a positive constant $\lambda$ such that $0<\lambda < \min \{\kappa _1, \kappa _2,\kappa _3, ,\tilde{c}_{1* },\dots ,\tilde{c}_{n* } \}$ satisfying $1-q_i^* e^{\lambda r_j^*}>0 ,$ and

$$\begin{aligned} \Upsilon (\lambda )= & {} \sup \limits _{t \in \mathbb {R}}\bigg \{\lambda -\tilde{c}_i(t)+K_i\bigg [ \frac{e^{\lambda r_i^*}}{1-q_i^* e^{\lambda r_i^*}}c_i^*q_i^*+ \sum _{j=1}^{n} a_{ij}^*L_j^f \frac{e^{\lambda \tau _{ij}^* }}{1-q_j^*e^{\lambda r_j^*}}\nonumber \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^* \bigg ( L_j^gd_l^g \frac{e^{\lambda \sigma _{ijl}^* }}{1-q_j^*e^{\lambda r_j^*}} +L_l^gd_j^g \frac{e^{\lambda \nu _{ijl}^* }}{1-q_j^*e^{\lambda r_j^*}}\bigg )\nonumber \\&+\sum _{j=1}^{n}\beta _{ij}^* L_j^h\int \limits _{0}^{+\infty }|G_{ij}(u)|e^{\lambda u}du\frac{ 1}{1-q_j^* e^{\lambda r_j^*} } + \sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}^*\bigg [ L_j^kd_l^k \int \limits _{0}^{+\infty } |P_{ijl}(u)|e^{\lambda u}du \nonumber \\&+L_l^k d_j^k\int \limits _{0}^{+\infty }|Q_{ijl}(u)|e^{\lambda u}du\bigg ] \frac{ 1}{1-q_j^* e^{\lambda r_j^*} }\bigg ]\bigg \}<0. \end{aligned}$$

(10)

Let

$$\begin{aligned} \Vert \phi \Vert _\varepsilon =\max _{1\le i \le n}\sup _{t \in (-\infty ,0]} \bigg \Vert [\phi _i(t)-d_i(t)\phi _i(t-\tau _i(t)) ] - [x_i^*(t)- d_i(t)x^*_i(t-\tau _i(t)) ]\bigg \Vert _\mathcal {A}. \end{aligned}$$

(11)

For any $\epsilon >0,$ we obtain

$$\begin{aligned} \Vert Z(0)\Vert _{\mathcal {A}}<(\Vert \phi \Vert _\varepsilon +\epsilon ). \end{aligned}$$

(12)

For all $t\in (-\infty ,0]$, we have

$$\begin{aligned} \Vert Z(t)\Vert _{\mathcal {A}}\le & {} (\Vert \phi \Vert _\varepsilon +\epsilon )e^{-\lambda t}\nonumber \\< & {} N(\Vert \phi \Vert _\varepsilon +\epsilon )e^{-\lambda t} \end{aligned}$$

(13)

where N is a constant satisfying $N>\max \limits _{1\le i\le n} K_i + 1$. Let us now prove that

$$\begin{aligned} \parallel Z(t) \parallel _{\mathcal {A}} < N(\Vert \phi \Vert _\varepsilon +\epsilon )e^{-\lambda t}, \qquad \forall t >0. \end{aligned}$$

(14)

If it is not the case, there exist $i\in \{1,\ldots ,n\}$ and $t_1>0$ such that

$$\begin{aligned} \parallel Z(t_{1}) \parallel _{\mathcal {A}}= N(\Vert \phi \Vert _\varepsilon +\epsilon )e^{-\lambda t_1} \end{aligned}$$

(15)

and

$$\begin{aligned} \parallel Z(t) \parallel _{\mathcal {A}} <N (\Vert \phi \Vert _\varepsilon +\epsilon )e^{-\lambda t}\qquad \forall t \in (-\infty ,t_1). \end{aligned}$$

(16)

Moreover, we have

$$\begin{aligned} e^{\lambda } \Vert z_j(\eta )\parallel _{\mathcal {A}}\le & {} e^{\lambda \eta } \Vert z_j(\eta )-q_j(\eta )z_j(\eta -r_j(\eta ))\parallel _{\mathcal {A}}+e^{\lambda \eta } \Vert q_j(\eta )z_j(\eta -r_j(\eta ))\parallel _{\mathcal {A}}\nonumber \\\le & {} e^{\lambda \eta }\Vert Z_j(\eta )\parallel _{\mathcal {A}}+e^{\lambda r_i^*} q_j^* e^{\lambda (\eta -r_j(\eta ))} \Vert z_j(\eta -r_j(\eta ))\parallel _{\mathcal {A}}\nonumber \\\le & {} (\Vert \phi \Vert _\varepsilon +\epsilon )N+e^{\lambda r_j^*} q_j^* \sup \limits _{s\in (-\infty ,t]} e^{\lambda s}\Vert z_j(s)\parallel _{\mathcal {A}}. \end{aligned}$$

(17)

For all $\eta \in (-\infty ,t],\;t\in (-\infty ,t_1),\;i \in \{1,\cdots ,n\}$, it leads to

$$\begin{aligned} e^{\lambda t} \Vert z_j(t)\Vert _{\mathcal {A}}\le & {} \sup \limits _{s \in (-\infty ,t]} e^{\lambda s} \Vert z_j(s)\Vert _{\mathcal {A}}\nonumber \\\le & {} \frac{N(\Vert \phi \Vert _\varepsilon +\epsilon )}{1- e^{\lambda q_j^* r_j^*} }. \end{aligned}$$

(18)

Multiplying Equation (7) by $e^{-\int _{0}^{s} c_{i}(u) du}$ and integrating on [0, t], we obtain

$$\begin{aligned} \displaystyle Z_{i}(t)= & {} Z_i(0)e^{-\int _{0}^{t} c_{i}(u) du}+\int \limits _{0}^{t}e^{-\int _{s}^{t} c_{i}(u) du} \bigg \{ -c_i(s)q_i(s)z_i(s-r_i(s))\nonumber \\&\displaystyle +\sum _{j=1}^{n} a_{ij}(s) \left[ f_{j} (x_{j}(s-\tau _{ij}(s)) - f_{j} (x_{j}^*(s-\tau _{ij}(s))\right] \nonumber \\&\displaystyle +\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(s) [g_{j} (x_{j}(s-\sigma _{ijl}(s)) g_{l} (x_{l}(s-\nu _{ijl}(s)))) \nonumber \\&\displaystyle -g_{j}(x^*_{j}(s-\sigma _{ijl}(s)))g_{l}(x^*_{l}(s-\nu _{ijl}(s)))]\nonumber \\&\displaystyle +\sum _{j=1}^{n}\beta _{ij} (s)\int \limits _{0}^{+\infty }G_{ij}(u)\left[ h_j( x_j(s-u))-h_j(x_j^*(s-u)) \right] du\nonumber \\&\displaystyle +\sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}(s)\bigg [\int \limits _{0}^{+\infty }P_{ijl}(u)k_{j}(x_{j}(s-u))du\nonumber \\&\displaystyle \times \int \limits _{0}^{+\infty }Q_{ijl}(u)k_{l}(x_{l}(s-u))du -\int \limits _{0}^{+\infty }P_{ijl}(u)k_{j}(x^*_{j}(s-u))du\nonumber \\&\displaystyle \times \int \limits _{0}^{+\infty }Q_{ijl}(u)k_{l}(x^*_{l}(s-u))du\bigg ]\bigg \}ds, \qquad t\in [0,t_1]. \end{aligned}$$

(19)

Using equations (8), (10)-(19), we obtain

$$\begin{aligned} \Vert Z_{i}(t_1)\Vert _{\mathcal {A}}= & {} \bigg \Vert Z_i(0)e^{-\int _{0}^{t_1} c_{i}(u) du} +\int \limits _{0}^{t_1}e^{-\int _{s}^{t_1} c_{i}(u) du} \bigg \{ -c_i(s)q_i(s)z_i(s-r_i(s))\nonumber \\&+\sum _{j=1}^{n} a_{ij}(s) (f_{j} (x_{j}(s-\tau _{ij}(s))) -f_j(x^*_{j}(s-\tau _{ij}(s))))\nonumber \\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(s) ( g_{j} (x_{j}(s-\sigma _{ijl}(s)))g_{l} (x_{l}(s-\sigma _{ijl}(s)))\nonumber \\&-g_{j} (x_{j}^*(s-\sigma _{ijl}(s)))g_{l} (x_{l}^*(s-\sigma _{ijl}(s))))\nonumber \\&+\sum _{j=1}^{n}\beta _{ij}(s) \int \limits _{0}^{+\infty }G_{ij}(u)[h_j( x_j(s-u))-h_j(x_j^*(s-u)) ]du\nonumber \\&+\sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}(s)[\int \limits _{0}^{+\infty }P_{ijl}(u)k_{j}(x_{j}(s-u))du\nonumber \\&\times \int \limits _{0}^{+\infty }Q_{ijl}(u)k_{l}(x_{l}(s-u))du -\int \limits _{0}^{+\infty }P_{ijl}(u)k_{j}(x^*_{j}(s-u))du\nonumber \\&\times \int \limits _{0}^{+\infty }Q_{ijl}(u)k_{l}(x^*_{l}(s-u))du\bigg \}ds\bigg \Vert _{\mathcal {A}}. \end{aligned}$$

Then it leads to

$$\begin{aligned} \Vert Z_{i}(t_1)\Vert _{\mathcal {A}}\le & {} (\Vert \phi \Vert _\varepsilon +\epsilon ) K_i e^{-\int \limits _{0}^{t_1} \tilde{c}_{i}(u) du}\\&+\int \limits _{0}^{t_1} e^{-\int \limits _{s}^{t_1} {\tilde{c}_{i}(u) du}} K_i \bigg \{ c_i^* q_i^* \left\| x_i(s-r_i(s))-x_i^*(s-r_i(s))\right\| _{\mathcal {A}}\\&+\sum _{j=1}^{n} a_{ij}^* \left\| f_{j} (x_{j}(s-\tau _{ij}(s)) - f_{j} (x_{j}^*(s-\tau _{ij}(s))\right\| _{\mathcal {A}}\\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^* \Vert g_{j} (x_{j}(s-\sigma _{ijl}(s)) g_{l} (x_{l}(s-\nu _{ijl}(s))))\\&-g_{j}(x^*_{j}(s-\sigma _{ijl}(s)))g_{l}(x^*_{l}(s-\nu _{ijl}(s)))\Vert _{\mathcal {A}}\\&+\sum _{j=1}^{n}\beta _{ij}^*\int \limits _{0}^{+\infty } |G_{ij}(u)|\left\| h_j( x_j(s-u))-h_j(x_j^*(s-u))\right\| _{\mathcal {A}} du\\&+\sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}^*\sup \limits _{ t \in \mathbb {R}}\bigg \Vert \int \limits _{0}^{{+\infty }}P_{ijl}(u)k_{j}(x_{j}(s-u))du\\&\int \limits _{0}^{+\infty }Q_{ijl}(u)k_{l}(x_{l}(s-u))du\\&-\int \limits _{0}^{+\infty }P_{ijl}(u)k_{j}(x^*_{j}(s-u))du \int \limits _{0}^{+\infty }Q_{ijl}(u)k_{l}(x^*_{l}(s-u))du\bigg \Vert _{\mathcal {A}}\ \bigg \}ds \end{aligned}$$

and finally it yields

$$\begin{aligned} \Vert Z_{i}(t_1)\Vert _{\mathcal {A}}\le & {} (\Vert \phi \Vert _\varepsilon +\epsilon ) e^{-\lambda t_1} K_i e^{-\int \limits _{0}^{t_1}[\tilde{c}_{i}(u) -\lambda ]du} \\&+\int \limits _{0}^{t_1 }e^{-\int _{s}^{t_1 }[\tilde{c}_i(s)-\lambda ]du} K_i\bigg \{ \frac{e^{\lambda r_i^*}}{1-q_i^* e^{\lambda r_i^*}}c_i^*q_i^*\\&+\sum _{j=1}^{n} a_{ij}^*L_j^f \frac{e^{\lambda \tau _{ij}^* }}{1-q_j^*e^{\lambda r_j^*}}\\&+\sum _{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}^* \bigg ( L_j^gd_l^g \frac{e^{\lambda \sigma _{ijl}^* }}{1-q_j^*e^{\lambda r_j^*}}\\&+L_l^gd_j^g \frac{e^{\lambda \nu _{ijl}^* }}{1-q_j^*e^{\lambda r_j^*}}\bigg )\\&+\sum _{j=1}^{n}\beta _{ij}^* L_j^h\int \limits _{0}^{+\infty } |G_{ij}(u)|e^{\lambda u}du\frac{ 1}{1-q_j^* e^{\lambda r_j^*} }\\&+ \sum _{j=1}^{n} \sum _{l=1}^{n}p_{ijl}^*\bigg [ L_j^kd_l^k \int \limits _{0}^{+\infty } |P_{ijl}(u)|e^{\lambda u}du \\&+L_l^k d_j^k\int \limits _{0}^{+\infty }|Q_{ijl}(u)|e^{\lambda u}du\bigg ] \frac{ 1}{1-q_j^* e^{\lambda r_j^*} } \bigg \}dsN(\Vert \phi \Vert _\varepsilon +\epsilon ) e^{-\lambda t_1}\\ \end{aligned}$$

and then

$$\begin{aligned} \Vert Z_{i}(t_1)\Vert _{\mathcal {A}}\le & {} (\Vert \phi \Vert _\varepsilon +\epsilon ) e^{-\lambda t_1} K_i e^{-\int _{0}^{t_1}[\tilde{c}_{i}(u) -\lambda ]du}\\&+\int \limits _{0}^{t_1 }e^{-\int _{s}^{t_1 }[\tilde{c}_i(s)-\lambda ]du} \bigg \{ \tilde{c}_i(u)-\lambda \bigg \}dsN(\Vert \phi \Vert _\varepsilon +\epsilon ) e^{-\lambda t_1}\nonumber \\\le & {} {N}(\Vert \phi \Vert _\varepsilon +\epsilon ) e^{-\lambda t_1}\bigg \{ (\frac{K_i}{N}-1) e^{-\int _{0}^{t_1}(\tilde{c}_i(u)-\lambda )du}+1 \bigg \}\nonumber \\< & {} N(\Vert \phi \Vert _\varepsilon +\epsilon ) e^{-\lambda t_1} \end{aligned}$$

which contradicts equality (15), so (14) holds. Letting $\epsilon \rightarrow 0^+$, then for all $t>0,$ we have $\Vert Z(t)\Vert _{\mathcal {A}}\le N\Vert \phi \Vert _\varepsilon e^{-\lambda t}$. Similarly, we have

$$\begin{aligned} e^{\lambda t} \Vert z_j(t)\Vert _{\mathcal {A}}\le & {} \sup \limits _{s\in (-\infty ,t]} e^{\lambda s}\Vert z_j(s)\Vert _{\mathcal {A}}\nonumber \\\le & {} \frac{N\Vert \phi \Vert _\varepsilon }{1- q_j^* e^{\lambda r_j^* }} \end{aligned}$$

and

$$\begin{aligned} \Vert z_j(t)\Vert _{\mathcal {A}}\le & {} \frac{N\Vert \phi \Vert _\varepsilon }{1- q_j^* e^{\lambda r_j^* }}e^{-\lambda t} \qquad \forall t> 0,\; j\in \{1,\cdots ,n\}. \end{aligned}$$

The $(\mu ,\nu )-$PAA solution of the system (1) is global exponentially stable. $\square$

Remark 2

In this article, we not only consider the effects of the first-order terms $a_{ij}(\cdot ),\;\beta _{ij}(\cdot )$ on NNs but also the influences of the second-order terms $\alpha _{ijl}(\cdot )$ and $p_{ijl}(\cdot )$. If $\alpha _{ijl}(\cdot )=p_{ijl}(\cdot )=0$ then the following classical (first order) neutral type Hopfiled NNs

$$\begin{aligned} \bigg [x_i(t)- q_i(t)x_i(t- r_{i}(t)) \bigg ]'= & {} -c_i(t)x_i(t)+\sum _{j=1}^{n} a_{ij}(t) f_{j} (x_{j}(t-\tau _{ij}(t))) \nonumber \\&+\sum \limits _{j=1}^{n} \beta _{ij}(t)\int \limits _{0}^{+\infty } G_{ij}(s) h_{j}(x_{j}(t-s))ds\nonumber \\&+I_{i}(t), \end{aligned}$$

(20)

has a unique $(\mu ,\nu )$-pseudo almost automorphic solution which is global exponential stable. Hence, our results generalize the results in [10].

Remark 3

If $q_i(t)=0$ then the following Hopfiled NN

$$\begin{aligned} \dot{x}_i(t)= & {} -c_i(t)x_i(t)+\sum _{j=1}^{n} a_{ij}(t) f_{j} (x_{j}(t-\tau _{ij}(t))) \nonumber \\&+\sum \limits _{j=1}^{n} \beta _{ij}(t)\int \limits _{0}^{+\infty } G_{ij}(s) h_{j}(x_{j}(t-s))ds+I_{i}(t), \end{aligned}$$

(21)

has an unique $(\mu ,\nu )$-pseudo almost automorphic solution which is global exponential stable. It is worth pointing out that our main results are also valid for the case of the non-neutral systems. Our results not only improve but also complement earlier results in [3, 5, 7, 8, 14, 29].

Remark 4

In [21], the authors considered a class of Clifford-valued neutral HOHNN with leakage delays. They studied the existence and global exponential stability of pseudo-almost periodic solutions for this class of NNs. In [22], the authors dealt with a class of inertial quaternion-valued HOHNNs with state-dependent delays. They analyzed the existence of anti-periodic solutions of the NNs. In our article, we investigate the $(\mu ,\nu )-$ pseudo almost automorphic solution for neutral-type HOHNNs. This class of functions covers larger classes of functions such as almost periodic, pseudo almost periodic, almost automorphic and pseudo almost automorphic functions. Hence, our results are not only new but also most general.

Remark 5

Although the multiplication of Clifford numbers does not satisfy the commutativity, which brings great difficulties to the study of Clifford-valued systems, we have found a method that does not decompose Clifford-valued systems into real-valued systems.

Remark 6

Pseudo almost automorphic functions play an important role in describing the dynamics of differential equations. In [3], the authors investigated the dynamics behavior of the pseudo almost automorphic solutions of a class of HOHNNs with mixed delays. Those results cannot be applicable for the systems studied in this article. Consequently, our analysis of dynamics behavior of neutral type Clifford-valued HOHNNs model with $(\mu ,\nu )-$PAA functions as coefficients and mixed delays improve the previous study in [3]. If $\mu =\nu =1,$ then the system (1) has an unique PAA solution in Clifford algebra.

Remark 7

In [7], the authors studied a class of delayed high-order Hopfield bidirectional associative memory NNs. They used fixed delays because time-varying delays are difficult to handle when dealing with $(\mu ,\nu )$-pseudo almost automorphic parameters. Hence, it is not obvious to prove the composition theorem of $(\mu ,\nu )$-pseudo almost automorphic functions i.e. $f(\phi (\cdot -\tau (\cdot )))\in PAA(\mathbb {R},\mathbb {R},\mu ,\nu ).$ In 2020, this problem has been solved in article [10].

Remark 8

In [9], the pseudo almost periodic solutions of Clifford-valued inertial neutral NNs with time-varying delays and infinite distributed delay are investigated. Then, by using the same approach we can extend the results to the space of pseudo almost automorphic functions. Our results can complement the results in [9].

4 Simulation Results

In this section, we apply our main results to a specific system and demonstrate the efficiency of our new stability criteria. Consider the following neutral type Clifford-valued HOHNNs model

$$\begin{aligned} \bigg [{x}_{i}(t)-q_{i}(t)x_{i}(t- r_{i} (t))\bigg ]'= & {} -c_i(t)x_i(t)+\sum _{j=1}^{2} a_{ij}(t) f_{j} (x_{j}(t-\tau _{ij}(t))) \nonumber \\&+\sum _{j=1}^{2} \sum _{l=1}^{2} \alpha _{ijl}(t) g_{j}(x_{j}(t-\sigma _{ijl}(t))) g_{l}(x_{l}(t-\nu _{ijl} (t)))\nonumber \\&+\sum \limits _{j=1}^{2} \beta _{ij}(t)\int \limits _{0}^{+\infty } G_{ij}(s) h_{j}(x_{j}(t-s))ds\nonumber \\&+\sum \limits _{j=1}^{2} \sum \limits _{l=1}^{2}p_{ijl}(t)\int \limits _{0}^{+\infty }P_{ijl}(t-s)k_{j}(x_{j}(s))ds\nonumber \\&\times \int \limits _{0}^{+\infty }Q_{ijl}(t-s)k_{l}(x_{l}(s))ds + I_{i}(t), \end{aligned}$$

(22)

where $x_i(t)=x_i^0(t)e_0+x_i^1(t)e_1+x_i^2(t)e_2+x_i^{12}(t)e_{12}$ and $i=1,2.$

For $1\le i\le 2,$ let ${e_0}= \left( \begin{array}{cc} 1&{}0\\ 0&{}1 \\ \end{array}\right) , e_1= \left( \begin{array}{cc} 1&{}0\\ 0&{}-1 \\ \end{array}\right) , e_2= \left( \begin{array}{cc} 0&{}1\\ 1&{}0 \\ \end{array}\right)$ and $e_{12}= \left( \begin{array}{cc} 0&{}1\\ -1&{}0 \\ \end{array}\right)$.

For $\mu ,\nu \in \mathcal {M},$ satisfying $(A_1)$ and $(A_2)$, we consider the measure $\mu (t)$ where its Radon-Nikodym derivative is $\rho _1(t)=e^{\sin t},$ and the measure $\nu (t)$ where its Radon-Nikodym derivative is

$$\begin{aligned} \rho _2(t)= {\left\{ \begin{array}{ll} e^t &{} \text {if } t\le 0,\\ 1 &{} \text {if } t>0. \end{array}\right. } \end{aligned}$$

We take the following parameters:

$$\begin{aligned} f(x_i)= & {} g(x_i) =h(x_i)=k(x_i),\; i=1,2, \\ f(x_i)= & {} \frac{|x_i^0+1|-|x_i^0+1|}{22}e_0 +\frac{1}{20}\cos x_i^1e_1+\frac{1}{27}\cos x_i^2e_2+\frac{1}{21}\cos x_i^{12}e_{12}\\\Rightarrow & {} L_{j}^{f} =L_{j}^{g} =L_{j}^{h}=L_{j}^{k}=1,d_j^g=d_j^k=0.1, \\ r_i(t)= & {} 0.5,\;\tau _{ij}(t)=\sigma _{ijl}(t)=\nu _{ijl}(t)=0.5|\cos t|. \end{aligned}$$

Let

$$\begin{aligned} G_{ij}(t)= & {} P_{ijl}(t)=Q_{ijl}(t)=e^{-t}, \;K_i=e^{0.1}\;\hbox {and}\;\kappa _\iota =0.5 \;\hbox {for}\; \iota =1,2,3.\\ c_{1}(t)= & {} (4+ \cos ^2 t)e_0,\;c_{2}(t)=(4 +\sin ^2 t)e_0, \end{aligned}$$

and

$$\begin{aligned} q_1(t)=0.12 \sin (t)e_0,\\ q_2(t)=0.12 \cos (t)e_0, \end{aligned}$$

and

$$\begin{aligned} a_{11}(t)= & {} 0.1 \sin \left( \frac{2\pi }{2+ \sin t+\sin \left( \sqrt{3}t\right) }\right) e_0+0.3 \sin \left( \sqrt{3}t\right) e_1,\\ a_{12}(t)= & {} 0.1e_0+0.1e^{-t^2}e_2,\\ a_{21}(t)= & {} 0,\;a_{22}(t)= 0.1e_0+0.1e^{-t}e_{12}, \end{aligned}$$

and

$$\begin{aligned} \alpha _{111}(t)= & {} \alpha _{121}(t)=\alpha _{122}(t)=0,\\ \alpha _{112}(t)= & {} 0.3 \cos \left( \frac{1}{2+ \sin t + \sin \sqrt{2}t}\right) e_0 +\frac{0.1}{1+t^{2}}e_{12},\\ \alpha _{211}(t)= & {} 0.6 \sin (\sqrt{5}t)e_1 + 0.3 \sin \left( \frac{1}{2+ \cos t + \sin \sqrt{5}t}\right) e_2 +\frac{0.1}{1+t}e_{12},\\ \alpha _{212}(t)= & {} \alpha _{221}(t)=\alpha _{222}(t)=0, \end{aligned}$$

and

$$\begin{aligned} \beta _{11}(t)= & {} 0.4 \sin \left( \frac{1}{2+ \cos t + \cos \sqrt{2}t}\right) e_0 + 0.4 \sin \left( \sqrt{2}t\right) e_1,\\ \beta _{12}(t)= & {} \beta _{21}(t)=0,\\ \beta _{22}(t)= & {} 0.2e_0 +0.2 \cos \left( \sqrt{7}t\right) e_1 + \frac{0.1}{1+t^2}e_{12}, \end{aligned}$$

and

$$\begin{aligned} p_{111}(t)= & {} p_{121}(t)=p_{122}(t)=0,\\ p_{112}(t)= & {} 0.2 \sin \left( \frac{1}{2+ \sin t + \sin \sqrt{2}t}\right) e_{2} + \frac{0.1}{1+t} e_{12},\\ p_{211}(t)= & {} p_{212}(t)=p_{222}(t)=0,\\ p_{221}(t)= & {} 0.4 \sin \left( \frac{1}{2+ \sin t + \sin \sqrt{2}t}\right) e_1 + \frac{0.1}{1+t} e_2, \end{aligned}$$

and

$$\begin{aligned} I_{1}(t)= & {} 0.7 \sin \left( \frac{1}{2+ \sin t + \sin \sqrt{2}t}\right) e_0 + 0.7 e_1+ 0.7 \sin t e_2+0.7\cos \left( \sqrt{2}t\right) e_{12},\\ I_{2}(t)= & {} 0.7 \cos \left( \frac{1}{2+ \cos t + \cos \sqrt{5}t}\right) e_0 + 0.7\left( \sin t+ \frac{0.3}{1+t^2}\right) e_1 \\&+0.7 \cos t\;e_2+0.7\sin \left( \sqrt{7}t\right) +e^{-t^2}e_{12}. \end{aligned}$$

We have

$$\begin{aligned} \Lambda= & {} \max \limits _{1 \le i \le 2}\bigg \{q_i^*+ \frac{K_i}{\tilde{c}_{i*} } \bigg [c_i^*q_i^*+\sum _{j=1}^{2} a_{ij}^* L_j^f +\sum _{j=1}^{2} \sum _{l=1}^{2} \alpha _{ijl}^* L_j^g L_l^g+\sum \limits _{j=1}^{2} \beta _{ij}^*L_j^h \int \limits _{0}^{+\infty } |G_{ij}(u)|du\\&+\sum \limits _{j=1}^{2} \sum \limits _{l=1}^{2}p_{ijl}^*L_j^kL_l^k\int \limits _{0}^{+\infty }|P_{ijl}(u)| du\int \limits _{0}^{+\infty }|Q_{ijl}(u)|du\bigg ]\bigg \}=0.9509<1,\\ \Omega= & {} \max \limits _{1 \le i \le 2}\bigg \{q_i^*+ \frac{K_i}{\tilde{c}_{i*}} \bigg [c_i^*q_i^*+\sum _{j=1}^{2}a_{ij}^*L_j^f+ \sum _{j=1}^{2} \sum _{l=1}^{2} \alpha _{ijl}^*( L_j^g d_l^g + L_l^g d_j^g )\\&+\sum \limits _{j=1}^{2} \beta _{ij}^*L_j^h \int \limits _{0}^{+\infty } |G_{ij}(u)|du\\&+ \sum \limits _{j=1}^{2} \sum \limits _{l=1}^{2}p_{ijl}^* \int \limits _{0}^{+\infty }|P_{ijl}(u)|du \int \limits _{0}^{+\infty }|Q_{ijl}(u)|du( L_j^k d_l^k + L_l^k d_j^k )\bigg ]\bigg \}\\= & {} 0.8825<1 \end{aligned}$$

and

$$\begin{aligned} \Upsilon _0= & {} \sup \limits _{t \in \mathbb {R}}\bigg \{-\tilde{c}_i(t)+K_i\bigg [ \frac{1}{1-q_i^* }c_i^*q_i^*+ \sum _{j=1}^{2} a_{ij}^*L_j^f \frac{1}{1-q_j^*}\\&+\sum _{j=1}^{2} \sum _{l=1}^{2} \alpha _{ijl}^* \bigg (L_j^gd_l^g \frac{1}{1-q_j^*} +L_l^gd_j^g \frac{1}{1-q_j^*}\bigg )\\&+\sum _{j=1}^{2}\beta _{ij}^* L_j^h\int \limits _{0}^{+\infty } |G_{ij}(u)|du\frac{ 1}{1-q_j^* } + \sum _{j=1}^{2} \sum _{l=1}^{2}p_{ijl}^*\bigg [ L_j^kd_l^k \int \limits _{0}^{+\infty } |P_{ijl}(u)|du\\&+L_l^k d_j^k\int \limits _{0}^{+\infty } |Q_{ijl}(u)|du\bigg ] \frac{ 1}{1-q_j^* }\bigg ]\bigg \}=-1.1779<0. \end{aligned}$$

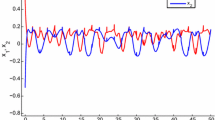
By a direct computation, we can check that all the conditions of Theorem 3 are satisfied. Therefore, the system (22) has an unique $(\mu ,\nu )-$PAA solution which is represented in Figs. 1, 2, 3 and 4.

Fig. 1

Curves of $x_i^0,\; i=1,2,$ of the system (22)

Fig. 2

Curves of $x_1^1$ and $x_2^1$ of the system (22)

Fig. 3

Curves of $x_i^2$ for $i=1,2,$ of the system (22)

Fig. 4

Curves of $x_i^{12}$ for $i=1,2,$ of the system (22)

Fig. 5

Stability of $x_i^0,\; i=1,2,$ of the system (22)

Fig. 6

Stability of $x_i^1$ for $i=1,2,$ of the system (22)

Fig. 7

Stability of $x_i^2$ for $i=1,2,$ of the system (22)

Fig. 8

Stability of $x_i^{12}$ for $i=1,2,$ of the system (22)

Besides, the unique $(\mu ,\nu )-$PAA solution of the system (22) is global exponential stable. Almost automorphy is not always as easy to identify visually. In the above example $x_i^0$, $x_i^1$, $x_i^2$ and $x_i^{12}$ with $i=1,2$ never exactly repeat themselves. They are not periodic. Figs. 5,6,7 and 8 confirm the global exponential stability of the $(\mu ,\nu )-$PAA solution for the system (22). Figures 1–8 confirm that the proposed conditions in our theoretical results are effective for the above example.

Remark 9

In the above example, $r_{i} (\cdot ),\;\tau _{ij}(\cdot ),\; \sigma _{ijl}(\cdot ),\;\nu _{ijl}(\cdot )$ represent the time-delay functions. The time-delay as an inherent feature of signal transmission between different neurons is one of the main sources for causing dynamic properties of the system (22). It should be mentioned that the presence of time-delay is a particularly harmful source of potential instability. In this example, the established criteria are straightforward to test and independent of delays, that is, the stability of the considered NN models is insensitive to the presence of the delays.

5 Conclusion

In this manuscript, neutral type Clifford-valued HOHNNs with mixed delays and D operator have been studied. By employing the fixed point theorem and differential inequalities, new sufficient conditions for the existence, uniqueness and global exponential stability of the $(\mu ,\nu )$-pseudo almost automorphic solutions have been established. To our best knowledge, this is the first paper studying the $(\mu ,\nu )$-pseudo almost automorphic solutions in Clifford algebra for such kind of NNs. As future research, there are some paths in this article that can be explored further. For instance:

• 1. In the model (1), the activation functions of signal transmission $f_j(\cdot ),\;g_j(.),\;h_j(\cdot )$ and $k_j(\cdot )$ are continuous functions. They can be considered as discontinuous functions due to the impulse behavior of firing neurons.

• 2. The concept of Stepanov like pseudo weighted almost automorphy $(WPAAS^p)$ is quite sophisticated. However, the dynamic oscillations of delayed systems with $WPAAS^p$ parameters are still relatively new. Soon, we will try to investigate dynamic oscillations of HOHNNs with $WPAAS^p$ parameters in Clifford algebra.

• 3. The study of second-order such systems [35, 36].