1 Introduction

In implementation of neural networks (NNs), the finite switching speed of neurons and amplifiers unavoidably produce time delays, which may lead to instability and oscillation in neural networks. As such, it is of great significance to investigate the mathematical properties of NNs with neutral type delays. Usually, neutral type neural networks can be described as non-operator-based neutral functional differential equations (NFDEs) ([1,2,3,4,5,6,7,8,9]) or D-operator-based NFDEs ([10,11,12,13,14]). In particular, based on the complexity of the dynamical behaviors for functional differential equations under the effect of time delays, neutral type cellular neural networks with D operator have more realistic significance than non-operator-based ones in many practical applications of neural networks dynamics. From above results, the readers can observe that most of the considered neutral type shunting inhibitory cellular neural networks (SICNNs) only touched non-operator-based NFDEs, and the dynamical behaviors of neutral type SICNNs with D operator have not been deeply studied (see [15, 16]).

In the past two decades, proportional delays occurring in nonlinear dynamic have gotten more and more attention because of its wide application in a variety of areas including probability theory on algebraic structures, electrodynamics and electric locomotive [17,18,19]. Moreover, many biological and cognitive activities (e.g., heartbeat, mastication, memorization) require repetition. For example, in many electronic circuits, oscillators are essential components and usually generate almost periodical signals (sinusoids, square waves, etc.). Consequently, almost periodic oscillations play important roles in characterizing the behaviours of nonlinear dynamiccal systems [20,21,22,23,24]. Consequently, some interesting results have been published on the existence and stability of almost periodic solution for cellular neural networks (CNNs) with proportional delays [25, 26]. However, to the best of our knowledge, no such work has been carried out on SICNNs with neutral type proportional delays and D operators.

Motivated by the above analysis, the main goal of this paper is to study the existence and generalized exponential stability of almost periodic solutions for a class of SICNNs with neutral type proportional delays and D operators, which can be described as the following NFDEs:

$$\begin{aligned}&[x _{ij} (t)-p_{ij}(t)x_{ij}( r _{ij}t)]' \nonumber \\&\quad =-a_{ij}(t)x_{ij}(t) -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(x_{kl}(q_{kl} t ))x_{ij}(t)+\,L_{ij}(t), \ t\ge t_{0}>0, \end{aligned}$$
(1.1)

where \(ij\in J=\{11, 12, \ldots , 1n, \ldots , m1, m2, \ldots , mn \},\) mn corresponds to the number of units in a neural network, \(C_{ij}\) is the cell at the (i, j) position of the lattice, \( N_r (i, j) = \Big \{C_{kl}: \max (| k - i |, | l - j |)\le r, 1 \le k \le m, 1 \le l \le n\Big \} \) is the r neighborhood of \( C_{ij}\), \( x_{ij}(t )\) designates the ijth neuron state, \(a_{ij}(t) \) represents the decay rate, f is the activation function, proportional delay factors \(q _{ij} \) and \( r_{ij} \) satisfy \(0< q _{kl}, r_{ij} < 1\), \(r _{ij } t=t -(1-r _{ij })t\) and \(q _{kl} t=t -(1-q _{kl})t\), in which \((1-r _{ij })t\) and \( (1-q _{kl})t\) are the transmission delay functions. The detailed biological description on the input \(L_{ij}(t)\) and the coefficient \( C_{ij}^{kl}(t)\) can be found in [15, 16].

The initial value conditions of SICNNs (1.1) are of the form

$$\begin{aligned} x_{ij}(s)=\varphi _{ij}(s), \ s\in [\rho _{ij}t_{0}, \ t_{0}], \ {\varphi }_{ij }\in C([\rho _{ij}t_{0}, \ t_{0}], {\mathbb {R}}) , \ ij\in J, \end{aligned}$$
(1.2)

where \(C([ \rho _{ij}, \ 1], {\mathbb {R}} )\) denotes the set of continuous functions on \([ \rho _{ij}, \ 1]\), and \(\rho _{ij} =\min \{r_{ij}, \ q_{ ij} \}\).

Contributions of the paper are summarized as follows. Firstly, basic definitions and hypotheses are imposed. By the method-of-steps, we derive that every solution of (1.1) with initial condition (1.2) exists and is unique on \([t_{0}, +\infty )\). Secondly, based on some novel differential inequality techniques, the existence and generalized exponential stability of almost periodic solutions for (1.1) will be subsequently established. Finally, the effectiveness of the obtained result is illustrated by a numerical example.

2 Preliminary Results

Throughout this paper, the following concepts and notations will be adopted:

$$\begin{aligned} x= & {} \{ x_{ij} \} =(x_{ij} )_{1\times mn}\in {\mathbb {R}}^{m n} , |x|=\{|x_{ij}|\}, \Vert x(t)\Vert =\max \limits _{ij\in J} |x_{ij}(t)|,\\ r= & {} \frac{1}{\max \limits _{ij \in J}\max \{ q_{ij}, r _{ij}\}}, W^{+}=\sup \limits _{t\in {\mathbb {R}}}|W(t)|, \ W^{-}=\inf \limits _{t\in {\mathbb {R}}}|W(t)|. \end{aligned}$$

Definition 2.1

(see [20, 21]). \(u(t)\in C({\mathbb {R}},{\mathbb {R}}^{mn})\) is said to be almost periodic on \({\mathbb {R}}\) if, for any \( \varepsilon >0\), it is possible to find a real number \(l=l(\varepsilon )>0 \) with the property that, for any interval with length \(l(\varepsilon )\), there exists a number \(\delta =\delta (\varepsilon )\) in this interval such that \(\Vert u(t+\delta )-u(t)\Vert <\varepsilon \ \text{ for } \text{ all } \ t\in {\mathbb {R}}.\)

We designate by \(AP({\mathbb {R}},\mathbb {R}^{mn})\) the set of the almost periodic functions from \({\mathbb {R}}\) to \(\mathbb {R}^{mn}\). Then \((AP({\mathbb {R}},\mathbb {R}^{mn}), \Vert \cdot \Vert _{\infty })\) is a Banach space, where \(\Vert \cdot \Vert _{\infty }\) denotes the supremum norm \(\Vert f\Vert _{\infty } := \sup \limits _{ t\in {\mathbb {R}}} \Vert f (t)\Vert \) (see [20, 21]). For all \( ij, kl \in J\), we suppose that the parameters of (1.1) and activation functions \( p_{ij}, \ a_{ij}, \ C^{kl}_{ij}, L_{ij } \in AP({\mathbb {R}},\mathbb {R})\) satisfy the following assumptions:

\((T_0)\) \(M[a_{ij}]=\lim \limits _{T\rightarrow +\infty }\frac{1}{T}\int _{t}^{t+T}a_{ij}(s)ds>0 \ \text{ for } \text{ all } t\in {\mathbb {R}} ,\) and there exist a bounded and continuous function \({\tilde{a}}_{ij} :{\mathbb {R}}\rightarrow (0, \ +\infty )\) and a positive constant \(K_{ij} \) such that

$$\begin{aligned} e ^{-\int _{s}^{t}a_{ij}(u)du}\le K_{ij} e ^{ -\int _{s}^{t}{\tilde{a}}_{ij}(u)du} \ \text{ for } \text{ all } t,s\in {\mathbb {R}} \text{ and } t-s\ge 0. \end{aligned}$$

\((T_{1})\) \( \text{ for } \text{ all } \ u , v \in {\mathbb {R}}\), there exist constants \(M ^{f} \) and \(L ^{f} \) such that

$$\begin{aligned} |f(u )-f(v )|\le L^{f} |u -v |, \ |f(u ) |\le M^{f} . \end{aligned}$$

\((T_{2})\) there exist positive constants L and \(\kappa \) such that

$$\begin{aligned} L= & {} \max \limits _{ ij\in J} \left\{ \sup \limits _{t\in {\mathbb {R}}}\left| \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du} L_{ij}(s) ds\right| \right\} > 0,\\ \end{aligned}$$
$$\begin{aligned} E_{ij}= & {} \sup \limits _{t\in \mathbb { R}} \frac{1}{{\tilde{a}}_{ij}(t)}K_{ij}\bigg [ \left| a_{ij}(t)p_{ij}(t)\right| +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl} (t)\right| ( L^{f}(\kappa +L) +|f(0)|) \bigg ]\\&<\frac{\kappa }{\kappa +L}-p_{ij}^{+},\\ \end{aligned}$$
$$\begin{aligned} F_{ij}= & {} \sup \limits _{t\in \mathbb { R}} \frac{1}{{\tilde{a}}_{ij}(t)}K_{ij}\bigg [ \left| a_{ij}(t)p_{ij}(t) \right| +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl} \ (t)\right| (M^{f} +L^{f}(\kappa +L)) \bigg ] <1-p_{ij}^{+}, \end{aligned}$$

and

$$\begin{aligned} G_{ij}= & {} \sup \limits _{t\in \mathbb { R}} \frac{1}{{\tilde{a}}_{ij}(t)} K_{ij}\bigg \{ \bigg [\left| a_{ij} (t)p_{ij} (t)\right| +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| M^{f} \bigg ]\frac{1}{1- p_{ij} ^{+} }\\&+ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| L^{f}\frac{1}{1- p_{kl} ^{+} } (\kappa +L) <1 . \end{aligned}$$

Lemma 2.1

(see [26, Lemma 2.2]). Let \(x(t)\in AP({\mathbb {R}}, \mathbb {R} ) \) and \(q\in {\mathbb {R}}\) be a constant. Then, \(x(q t)\in AP({\mathbb {R}}, \mathbb {R} )\).

Lemma 2.2

Suppose that \((T_0)\), \((T_1)\) and \((T_2)\) are satisfied. Then, every solution of (1.1) with initial condition (1.2) exists and is unique on \([t_{0}, +\infty )\).

Proof

Firstly, we show that x(t) exists and is unique on \([t_{0},\ t_{0}r]\). In fact, for \( ij\in J \), let

$$\begin{aligned} y _{ij} (t)=x _{ij} (t)-p_{ij}(t)x_{ij}( r _{ij} t ), \beta _{ij}(t)=p_{ij}(t)\varphi _{ij}( r _{ij} t ) \end{aligned}$$

and

$$\begin{aligned} A_{ij}(t)=a_{ij}(t) +\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(\varphi _{kl}(q_{kl} t )), B_{ij}(t)=-A_{ij}(t)p_{ij}(t)\varphi _{ij}( r _{ij} t ) +L_{ij}(t). \end{aligned}$$

Then

$$\begin{aligned} y _{ij} '(t)= & {} [x _{ij} (t)-p_{ij}(t)x_{ij}( r _{ij} t )]'\nonumber \\= & {} -a_{ij}(t)x_{ij}(t)-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(x_{kl}(q_{kl} t ))x_{ij}(t) +L_{ij}(t)\nonumber \\= & {} -[a_{ij}(t) +\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(\varphi _{kl}(q_{kl} t ))]x_{ij}(t) +L_{ij}(t)\nonumber \\= & {} -A_{ij}(t) y_{ij}(t) +B_{ij}(t) , \ t\in [t_{0},\ t_{0}r]. \end{aligned}$$
(2.1)

From \((T_{1})\), we can easily show that the solution y(t) of ordinary differential equations (2.1) with initial value \(y(t_{0})=\{x _{ij} (t_{0})-\beta _{ij}(t_{0})\}\) exists and is unique on \([t_{0},\ t_{0}r]\). Hence, \(x (t )=y(t)+\{\beta _{ij}(t)\}\) exists and is unique on \([t_{0},\ t_{0}r]\). Similarly, one can prove that \(x (t )=y(t)+\{\beta _{ij}(t)\}\) exists and is unique on \([t_{0}r,\ t_{0}r^{2}]\). Consequently, the Lemma 2.2 follows from the induction. \(\square \)

3 Main Results

Theorem 3.1

Under the assumptions of Lemma 2.2, system (1.1) has a unique almost periodic solution \(x^{*}(t)\). Moreover, \(x^{*}(t)\) is generalized exponential stability, i.e., there exists a positive constant \(\sigma \), which is independent of solutions of (1.1), such that for arbitrary solution x(t) of (1.1),

$$\begin{aligned} \Vert x(t)-x^{*}(t)\Vert =O\left( \frac{1}{(1+t)^{\sigma }}\right) \ \text{ as } \ t\rightarrow +\infty . \end{aligned}$$

Proof

Let

$$\begin{aligned} Y_{ij}(t)=x_{ij} (t)-p_{ij}(t)x_{ij} ( r_{ij}t), \ ij \in J. \end{aligned}$$

Then

$$\begin{aligned} Y_{ij}'(t)= & {} [x_{ij} (t)-p_{ij}(t)x_{ij} (r_{ij}t)]'\nonumber \\= & {} -a_{ij}(t)Y_{ij} (t )-a_{ij}(t)p_{ij}(t)x_{ij} (r_{ij}t) \nonumber \\&-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(x_{kl}(q_{kl} t ))x_{ij}(t) +L_{ij}(t),\ ij\in J. \end{aligned}$$
(3.1)

Let \( \varphi \in AP({\mathbb {R}},\mathbb {R}^{mn})\). In view of Lemma 2.1, we can show

$$\begin{aligned} \varphi _{ij} (r_{ij}t), \ \varphi _{kl}(q_{kl} t ) \in AP({\mathbb {R}},\mathbb {R} ), \ \ kl, \ ij\in J. \end{aligned}$$

It follows from the uniform continuity of f that

$$\begin{aligned} \sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(\varphi _{kl}(q_{kl} t ))\varphi _{ij}(t)\in AP({\mathbb {R}},\mathbb {R} ), \ \ ij\in J. \end{aligned}$$

Now, we consider the following auxiliary equations:

$$\begin{aligned} Y'_{ij}(t)= & {} -a_{ij}(t)Y_{ij} (t )-a_{ij}(t)p_{ij}(t)\varphi _{ij} (r_{ij}t)\nonumber \\&-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(\varphi _{kl}(q_{kl} t ))\varphi _{ij}(t) +L_{ij}(t), ij\in J, \ \varphi \in AP({\mathbb {R}},\mathbb {R}^{mn}).\nonumber \\ \end{aligned}$$
(3.2)

According to Lemma 1.1 in [22] and the fact that \( M[a_{ij}]>0 (ij\in J) \), one can see that the system (3.2) has exactly one almost periodic solution:

$$\begin{aligned} Y^{\varphi }(t)= & {} \left\{ Y^{\varphi }_{ij}(t)\right\} \nonumber \\= & {} \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du}\left[ -a_{ij}(s)p_{ij}(s)\varphi _{ij} ( r_{ij}s)\right. \right. \nonumber \\&\left. \left. -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)f(\varphi _{kl}(q_{kl} s ))\varphi _{ij}(s) +L_{ij}(s)\right] ds\right\} . \end{aligned}$$
(3.3)

Obviously,

$$\begin{aligned} \left\{ p_{ij}(t)\varphi _{ij} ( r_{ij}t)\right\} +Y^{\varphi }(t)\in AP({\mathbb {R}},\mathbb {R}^{mn}). \end{aligned}$$

Likewise, we can prove \(Q(t)=\{Q_{ij}(t)\}=\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du}L_{ij}(s)ds\}\) is the unique almost periodic solution of the following differential equations:

$$\begin{aligned} Y'_{ij}(t) = -a_{ij}(t)Y_{ij} (t )+L_{ij}(t), ij\in J, \end{aligned}$$

and \(\{Q_{ij}(t)\} \in AP({\mathbb {R}},\mathbb {R}^{mn})\), \(L= \Vert Q\Vert _{\infty }.\)

Set

$$\begin{aligned} \Omega =\{\varphi |\varphi \in AP({\mathbb {R}},\mathbb {R}^{mn}), \Vert \varphi -Q\Vert _{\infty } \le \kappa \} \end{aligned}$$

If \(\varphi \in \Omega \) , then

$$\begin{aligned} \Vert \varphi \Vert _{\infty } \le \Vert \varphi -Q\Vert _{\infty } +\Vert Q\Vert _{\infty } \le \kappa +L. \end{aligned}$$
(3.4)

Moreover, we define a mapping \(T:\Omega \rightarrow \Omega \) by setting

$$\begin{aligned} (T\varphi )(t)=\{p_{ij}(t)\varphi _{ij} ( r_{ij}t)\}+Y^{\varphi }(t), \ \ \ \forall \varphi \in \Omega . \end{aligned}$$

We next prove that for any \(\varphi \in \Omega , \ T \varphi \in \Omega \). Clearly, it follows from (3.3), (3.4), (\(T_{0}\)), (\(T_{1}\)) and (\(T_{2}\)) that

$$\begin{aligned}&|(T\varphi )(t)- Q(t)|\\&\quad = \left\{ \left| p_{ij}(t)\varphi _{ij} ( r_{ij}t)+\int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du}\bigg [-a_{ij}(s)p_{ij}(s)\varphi _{ij} ( r_{ij}s)\right. \right. \\&\qquad \left. \left. -\,\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)f(\varphi _{kl}(q_{kl}s))\varphi _{ij}(s) \bigg ]ds\right| \right\} \\&\quad \le \left\{ p_{ij} ^{+}\Vert \varphi \Vert _{\infty }+ \int _{-\infty }^{t}e^{-\int _{s}^{t}{\tilde{a}}_{ij}(u)du}K_{ij}\bigg [ \left| a_{ij}(s)p_{ij}(s)\right| \Vert \varphi \Vert _{\infty }\right. \\&\qquad \left. +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl} \ (s)\right| (\left| f(\varphi _{kl}(q_{kl}(s)))-f(0)\right| +|f(0)|)\Vert \varphi \Vert _{\infty } \bigg ]ds \right\} \\&\quad \le \left\{ p_{ij} ^{+}\Vert \varphi \Vert _{\infty }+\int _{-\infty }^{t}e^{-\int _{s}^{t}{\tilde{a}}_{ij}(u)du}K_{ij}\bigg [ \left| a_{ij}(s)p_{ij}(s)\right| \right. \\&\qquad \left. +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl} (s)\right| ( L^{f}\Vert \varphi \Vert +|f(0)|) \bigg ]\Vert \varphi \Vert _{\infty } \right\} \\&\quad \le \left\{ p_{ij} ^{+} +\int _{-\infty }^{t}e^{-\int _{s}^{t}{\tilde{a}}_{ij}(u)du}K_{ij}\bigg [ \left| a_{ij}(s)p_{ij}(s)\right| \right. \\&\qquad \left. +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl} (s)\right| ( L^{f}(\kappa +L) +|f(0)|)\bigg ] \right\} (\kappa +L)\\&\quad \le \left\{ p_{ij} ^{+} +\int _{-\infty }^{t}e^{-\int _{s}^{t}{\tilde{a}}_{ij}(u)du}\left( \frac{\kappa }{\kappa +L}-p_{ij}^{+}\right) {\tilde{a}}_{ij}(s)ds\right\} (\kappa +L)\\&\quad \le \{\kappa \}, \ \text{ for } \text{ all } \ t\in {\mathbb {R}}, \end{aligned}$$

which entails that \( T \varphi \in \Omega \).

Furthermore, we show that T is a contract operator. In fact, again from (3.3), (3.4), (\(T_{0}\)), (\(T_{1}\)) and (\(T_{2}\)), we obtain

$$\begin{aligned}&\left| (T\varphi )(t)-(T\psi )(t)\right| \\&\quad = \left\{ \left| ((T\varphi )(t))-(T\psi )(t))_{ij}\right| \right\} \\&\quad = \bigg \{\bigg | p_{ij}(t)[\varphi _{ij} ( r_{ij}t)-\psi _{ij} (r_{ij}t)]\\&\qquad +\int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du}\bigg [-a_{ij}(s)p_{ij}(s) (\varphi _{ij} (r_{ij}s)-\psi _{ij} (r_{ij}s))\\&\qquad -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)(f(\varphi _{kl}(q_{kl}s))\varphi _{ij}(s)-f(\psi _{kl}(q_{kl}s))\psi _{ij}(s)) \bigg ]ds \bigg |\bigg \}\\&\quad \le \bigg \{ p_{ij} ^{+}\Vert \varphi -\psi \Vert _{\infty } +\int _{-\infty }^{t}e^{-\int _{s}^{t}{\tilde{a}}_{ij}(u)du}K_{ij}\bigg [ \left| a_{ij}(s)p_{ij}(s) \right| \Vert \varphi -\psi \Vert _{\infty } \\&\qquad +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl} \ (s)\right| (\left| f(\varphi _{kl}(q_{kl}s))\right| \left| \varphi _{ij}(s)-\psi _{ij}(s)\right| \\&\qquad +\left| f(\varphi _{kl}(q_{kl}s)) - f(\psi _{kl}(q_{kl}s))\right| \left| \psi _{ij}(s)\right| ) \bigg ]ds \bigg \}\\&\quad \le \bigg \{ p_{ij} ^{+} +\int _{-\infty }^{t}e^{-\int _{s}^{t}{\tilde{a}}_{ij}(u)du}K_{ij}\bigg [ \left| a_{ij}(s)p_{ij}(s)\right| \\&\qquad +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl} \ (s)\right| (M^{f} +L^{f}(\kappa +L)) \bigg ]ds \bigg \}\Vert \varphi -\psi \Vert _{\infty }\\&\quad \le \bigg \{ p_{ij} ^{+} +\int _{-\infty }^{t}e^{-\int _{s}^{t}{\tilde{a}}_{ij}(u)du}F_{ij}{\tilde{a}}_{ij}(s) ds \bigg \}\Vert \varphi -\psi \Vert _{\infty }\\&\quad \le \bigg \{ p_{ij} ^{+} + F_{ij} \bigg \}\Vert \varphi -\psi \Vert _{\infty }, \ \text{ for } \text{ all } \ t\in {\mathbb {R}}, \varphi , \psi \in \Omega , \end{aligned}$$

which yields

$$\begin{aligned} \Vert T \varphi -T \psi \Vert _{\infty } \le \max \limits _{ ij\in J}( p_{ij} ^{+} + F_{ij})\Vert \varphi -\psi \Vert _{\infty } . \end{aligned}$$

Therefore, Theorem 0.3.1 of [27] and the fact that \( \max \limits _{ ij\in J}( p_{ij} ^{+} + F_{ij})<1\) entail that T possesses a unique fixed point \(x^{* }=\{x_{ij}^{* }(t)\}\in \Omega \) such that

$$\begin{aligned} \{x^{* }_{ij}(t)\}=x^{* }(t)=(Tx^{* })(t)=\{p_{ij}(t)x_{ij}^{* }( r_{ij}t)\}+Y^{x^{* }}(t)=\{p_{ij}(t)x_{ij}^{* }( r_{ij}t)\}+\{Y_{ij}^{x^{* }}(t)\}, \end{aligned}$$

and

$$\begin{aligned} x_{ij}^{* }(t)= & {} p_{ij}(t)x_{ij}^{* }( r_{ij}t)+Y_{ij}^{x^{* }}(t)\\= & {} p_{i}(t)x_{ij}^{*}( r_{ij}t)+\int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du}\left[ -a_{ij}(s)p_{ij}(s)x_{ij}^{* } ( r_{ij}s)\right. \\&\left. -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)f(x^{*}_{kl}(q_{kl}s))x^{*}_{ij}(s) +L_{ij}(s)\right] ds, \ i\in J, \end{aligned}$$

which, together with (3.3) leads to

$$\begin{aligned}&[x _{ij} ^{* }(t)-p_{ij}(t)x_{ij}^{* }( r _{ij}t)]' \\&\quad = -a_{ij}(t)Y_{ij}^{x^{* }}(t)-a_{ij}(t)p_{ij}(t)x_{ij}^{* } ( r_{ij}t)\\&\qquad -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(x^{*}_{kl}(q_{kl}t))x^{*}_{ij}(t) +L_{ij}(t)\\&\quad = -a_{ij}(t)x _{ij} ^{* }(t) -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(x^{*}_{kl}(q_{kl}t))x^{*}_{ij}(t) +L_{ij}(t), ij\in J , \end{aligned}$$

and \(x^{* }(t)\) is an almost periodic solution of system (1.1).

Finally, we demonstrate the global generalized exponential stability of \(x^{*}(t)\). Let \( x(t)=\{x_{ij}(t)\} \) be an arbitrary solution of (1.1) with initial value \( \phi (t)=\{\phi _{ij}(t)\} \) satisfying (1.2), and

$$\begin{aligned} z_{ij} (t)=x_{ij} (t)-x^{*}_{ij} (t), Z_{ij}(t)=z_{ij} (t)-p_{ij}(t) z_{ij} ( r_{ij}t), ij \in J. \end{aligned}$$

Then

$$\begin{aligned} Z_{ij}'(t)= & {} [z_{ij} (t)-p_{ij}(t)z_{ij} ( r_{ij}t)]'\nonumber \\= & {} -a_{ij}(t)Z_{ij} (t )-a_{ij}(t)p_{ij}(t)z_{ij} ( r_{ij}t)\nonumber \\&-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)[f(x_{kl}(q_{kl}t))x_{ij}(t)-f(x_{kl}^{*}(q_{kl}t))x^{*}_{ij}(t)] ,\ ij\in J.\qquad \end{aligned}$$
(3.5)

From \((T_{2})\), we can choose constant \(\sigma \in (0, \ \min \{ \beta , \ \min \limits _{ij\in J}{\tilde{a}}_{ij} ^{-}\}) \) such that \( e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}<1\) and

$$\begin{aligned}&\sup \limits _{t\ge \rho _{ij}t_{0}} \left\{ \sigma -{\tilde{a}}_{ij} (t)+ K_{ij} \bigg [ \left| a_{ij} (t)p_{ij} (t)\right| e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) }\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \nonumber \\&\qquad \qquad \left. + \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f} \frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \right. \nonumber \\&\qquad \qquad \left. \left. +\,L^{f}(\kappa +L)\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+}}e^{ \sigma \ln \left( \frac{ 1 }{1+ q_{kl} }\right) }\right) \bigg ] \right\} < 0 , \ ij\in J. \end{aligned}$$
(3.6)

In view of the facts that

$$\begin{aligned} \frac{\sigma }{1+t}\le \sigma , ~\ln \left( \frac{1+t}{1+r_{ij}t}\right) \le \ln \frac{1}{r_{ij}},~\ \ln \left( \frac{1+t}{1+q_{kl}t}\right) \le \ln \frac{1}{q_{kl}} \ \text{ for } \text{ all } \ t\ge 0, \end{aligned}$$

(3.6) implies that

$$\begin{aligned}&\sup \limits _{t\ge \rho _{ij}t_{0}}\left\{ \sigma \frac{1}{1+t} -{\tilde{a}}_{ij} (t)+ K_{ij} \bigg [ \left| a_{ij} (t)p_{ij} (t)\right| e^{ \sigma \ln \left( \frac{1+t }{ 1+r_{ij}t }\right) }\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \nonumber \\&\qquad \qquad \quad \left. +\,\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| (M^{f} \frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \nonumber \\&\qquad \qquad \quad \left. +L^{f}(\kappa +L)\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+}}e^{ \sigma \ln \left( \frac{1 +t}{ 1+q_{kl} t}\right) } \bigg ]\right\} \nonumber \\&\quad \le \sup \limits _{t\ge \rho _{ij}t_{0}}\left\{ \sigma \frac{1}{1+t} -{\tilde{a}}_{ij} (t)+ K_{ij} \bigg [ \left| a_{ij} (t)p_{ij} (t)\right| e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) }\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \nonumber \\&\qquad \qquad \quad \left. + \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f} \frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \right. \nonumber \\&\qquad \qquad \quad \left. \left. +\,L^{f}(\kappa +L)\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+}}e^{ \sigma \ln \left( \frac{ 1 }{1+ q_{kl} } \right) }\right) \bigg ]\right\} \nonumber \\&\quad \le \sup \limits _{t\ge \rho _{i}t_{0}}\left\{ \sigma -{\tilde{a}}_{ij} (t)+ K_{ij} \bigg [ \left| a_{ij} (t)p_{ij} (t)\right| e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) }\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \nonumber \\&\qquad \qquad \quad \left. + \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f} \frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \right. \nonumber \\&\qquad \qquad \quad \left. \left. +\,L^{f}(\kappa +L)\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+}}e^{ \sigma \ln \left( \frac{ 1 }{1+ q_{kl} } \right) }\right) \bigg ]\right\} < 0 , \ ij\in J. \end{aligned}$$
(3.7)

We trivially extend x(t) to \([r_{ij}\rho _{ij}t_{0}, \ +\infty )\) by letting \(x_{ij}(t) =\varphi _{ij}(t) = \varphi _{ij}(\rho _{ij}t_{0}) \) for \(t\in [r_{ij}\rho _{ij}t_{0}, \ \rho _{ij}t_{0}], \ ij\in J.\) Let

$$\begin{aligned} \Vert \varphi \Vert _{X}= \max \limits _{ij\in J } \sup \limits _{ t\in [\rho _{ij}t_{0}, \ t_{0}]} \left| [\varphi _{ij} (t)-x^{*}_{ij} (t)]-p_{ij}(t)[\varphi _{ij} (r_{ij}t)-x^{*}_{ij} ( r_{ij}t)] \right| . \end{aligned}$$
(3.8)

For any \(\varepsilon >0\), consider the function V(t) defined as follows:

$$\begin{aligned} V (t)=M (\Vert \varphi \Vert _{X}+\varepsilon ) e^{-\sigma \ln \left( \frac{1+ t}{1+t_{0}}\right) }, \ M= 1+\max \limits _{ij\in J}K_{ij} , \ \ \ t\ge t_{0}. \end{aligned}$$

Therefore,

$$\begin{aligned} V (q_{i j}t)= & {} M (\Vert \varphi \Vert _{X}+\varepsilon )e^{-\sigma \ln \left( \frac{1+ t}{1+t_{0}}\right) } e^{ \sigma \ln \left( \frac{1+t}{1+q_{i j}t}\right) } \nonumber \\&\quad \le V(t) e^{ \sigma \ln \frac{1 }{ q_{i j} } } \ \text{ for } \text{ all } \ t\ge t_{0}, ij \in J , \ \end{aligned}$$
(3.9)

and

$$\begin{aligned} \left| Z_{ij}(t_{0}) \right| < (\Vert \varphi \Vert _{X}+\varepsilon ) \le M (\Vert \varphi \Vert _{X}+\varepsilon )= V (t_{0}), ij\in J. \end{aligned}$$
(3.10)

Hereafter, we prove that

$$\begin{aligned} \Vert Z(t) \Vert < V (t) \quad \text{ for } \text{ all } t >t_{0} . \end{aligned}$$
(3.11)

Otherwise, there must exist \(ij\in J\) and \(\theta \in (t_{0}, \ +\infty ) \) such that

$$\begin{aligned} \left| Z_{ij}(\theta ) \right| = V (\theta )=M (\Vert \varphi \Vert _{X}+\varepsilon )e^{-\sigma \ln \left( \frac{1+ \theta }{1+t_{0}}\right) }, \end{aligned}$$
(3.12)

and

$$\begin{aligned} |Z_{kl}(t) | < V (t) \ \text{ for } \text{ all } t \in [\rho _{kl}t_{0} , \ \theta ), \ kl \in J. \end{aligned}$$
(3.13)

Consequently,

$$\begin{aligned} e^{ \sigma \ln \left( \frac{1+ \nu }{1+t_{0}}\right) } \left| z_{kl} (\nu )\right|\le & {} e^{ \sigma \ln \left( \frac{1+ \nu }{1+t_{0}}\right) }\left| z_{kl} (\nu )- p_{kl}(\nu )z_{kl} ( r_{kl} \nu )\right| + e^{ \sigma \ln \left( \frac{1+ \nu }{1+t_{0}}\right) }\left| p_{kl}(\nu )z_{kl} ( r_{kl} \nu )\right| \nonumber \\= & {} e^{ \sigma \ln \left( \frac{1+ \nu }{1+t_{0}}\right) } \left| Z_{kl} (\nu ) \right| + e^{ \sigma \ln \left( \frac{1+ \nu }{1+r_{kl}\nu }\right) }\left| p_{kl}(\nu )\right| e^{ \sigma \ln \left( \frac{1+ r_{kl}\nu }{1+t_{0}}\right) }\left| z_{kl} ( r_{kl} \nu )\right| \nonumber \\\le & {} e^{ \sigma \ln \left( \frac{1+ \nu }{1+t_{0}}\right) }\left| Z_{kl} (\nu )\right| + e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+} \sup \limits _{s\in [r_{kl}\rho _{kl}t_{0} , \ r_{kl} t]} e^{ \sigma \ln \left( \frac{1+ s}{1+t_{0}}\right) }\left| z_{kl} ( s )\right| \nonumber \\\le & {} e^{ \sigma \ln \left( \frac{1+ \nu }{1+t_{0}}\right) } \left| Z_{kl} (\nu ) \right| + e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+} \sup \limits _{s\in [ \rho _{kl}t_{0} , \ t]} e^{ \sigma \ln \left( \frac{1+ s}{1+t_{0}}\right) }\left| z_{kl} ( s )\right| \nonumber \\ \end{aligned}$$
(3.14)

and

$$\begin{aligned} e^{ \sigma \ln (\frac{1+ t}{1+t_{0}})} |z_{kl} (t)| \le \sup \limits _{s\in [\rho _{kl}t_{0}, \ t]} e^{ \sigma \ln (\frac{1+ s}{1+t_{0}})}|z_{kl} (s)|\le \frac{M (\Vert \varphi \Vert _{X}+\varepsilon ) }{1- e^{ \sigma \ln (\frac{1 }{ r_{kl} })} p_{kl} ^{+}}, \end{aligned}$$
(3.15)

where \(\nu \in [\rho _{kl}t_{0} , \ t], \ t \in [t_{0} , \ \theta ), \ kl\in J\).

We multiply both sides of (3.5) through by \(e ^{ \int _{t_{0}}^{t}a_{ij}(u)du} \) and integrating it on \( [t_{0}, \ \theta ]\). It follows that

$$\begin{aligned} |Z_{ij} (\theta )|= & {} \bigg | Z_{ij} (t_{0}) e ^{-\int _{t_{0}}^{\theta }a_{ij}(u)du}+ \int _{t_{0}}^{\theta }e ^{ -\int _{t}^{\theta }a_{ij}(u)du}\bigg [ -a_{ij}(t)p_{ij}(t)z_{ij} ( r_{ij}t) \\&-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)(f(x_{kl}(q_{kl}t))x_{ij}(t)-f(x_{kl}^{*}(q_{kl}t))x^{*}_{ij}(t))\bigg ]dt \bigg |, \end{aligned}$$

which, with the help of (3.7), (3.10), (3.13) and (3.15), entails that

$$\begin{aligned} |Z_{ij} (\theta )|\le & {} | Z_{ij} (t_{0})| K_{ij}e ^{-\int _{t_{0}}^{\theta }{\tilde{a}}_{ij}(u)du}+ \int _{t_{0}}^{\theta }e ^{ -\int _{t}^{\theta }{\tilde{a}}_{ij}(u)du}K_{ij}\bigg | -a_{ij}(t)p_{ij}(t)z_{ij} ( r_{ij}t) \\&-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)(f(x_{kl}(q_{kl}t))x_{ij}(t)-f(x_{kl}^{*}(q_{kl}t))x^{*}_{ij}(t)) \bigg |dt \\\le & {} (\Vert \varphi \Vert _{X}+\varepsilon )K_{ij}e ^{-\int _{t_{0}}^{\theta }{\tilde{a}}_{ij}(u)du}+ \int _{t_{0}}^{\theta }e ^{ -\int _{t}^{\theta }{\tilde{a}}_{ij}(u)du}K_{ij}\bigg [\left| a_{ij} (t)p_{ij} (t)\right| \left| z_{ij} ( r_{ij} t )\right| \\&+ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| f(x_{kl}(q_{kl}t))(x_{ij}(t)-x^{*}_{ij}(t))\\&+\,( f(x_{kl}(q_{kl}t))-f(x_{kl}^{*}(q_{kl}t))) x^{*}_{ij}(t) |\bigg ] ds \le (\Vert \varphi \Vert _{X}+\varepsilon )K_{ij}e ^{-\int _{t_{0}}^{\theta }{\tilde{a}}_{ij}(u)du} \\&+\, \int _{t_{0}}^{\theta }e ^{ -\int _{t}^{\theta }{\tilde{a}}_{ij}(u)du}K_{ij}\bigg [\left| a_{ij} (t)p_{ij} (t)\right| \left| z_{ij} ( r_{ij} t )\right| \\&+ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| (M^{f}\left| z_{ij}(t)\right| + L ^{f}(\kappa +L)\left| z_{kl}(q_{kl}t)\right| )\bigg ] ds \\\le & {} (\Vert \varphi \Vert _{X}+\varepsilon )K_{ij}e ^{-\int _{t_{0}}^{\theta }{\tilde{a}}_{ij}(u)du}+ \int _{t_{0}}^{\theta }e ^{ -\int _{t}^{\theta }{\tilde{a}}_{ij}(u)du}K_{ij}\\&\bigg [\left| a_{ij} (t)p_{ij} (t)\right| e^{ -\sigma \ln ( 1+ r_{ij}t )}\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\\&+ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f}e^{- \sigma \ln ( 1+ t )}\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \\&\left. +\,L^{f}(\kappa +L)e^{- \sigma \ln ( 1+ q_{kl}t )}\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+}} \right) \bigg ] dt M(\Vert \varphi \Vert _{X}+\varepsilon )e^{-\sigma \ln \left( \frac{1}{1+t_{0}}\right) } \end{aligned}$$
$$\begin{aligned}= & {} (\Vert \varphi \Vert _{X}+\varepsilon )K_{ij}e ^{ -\int _{t_{0}}^{\theta }[{\tilde{a}}_{ij}(u)-\frac{\sigma }{1+u}]du}e^{-\sigma \ln \left( \frac{1+\theta }{1+t_{0}}\right) } \\&+ \int _{t_{0}}^{\theta }e ^{ -\int _{t}^{\theta }[{\tilde{a}}_{ij}(u)-\frac{\sigma }{1+u}]du}K_{ij}\bigg [\left| a_{ij} (t)p_{ij} (t)\right| \frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}} e^{ \sigma \ln \left( \frac{1+ t}{1+ r_{ij}t}\right) }\\&+ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f} \frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \\&\left. +\,L^{f}(\kappa +L)\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+}}e^{ \sigma \ln \left( \frac{ 1+ t}{1+ q_{kl}t} \right) }\right) \bigg ] dt M(\Vert \varphi \Vert _{X}+\varepsilon )e^{-\sigma \ln \left( \frac{1+\theta }{1+t_{0}}\right) }\\\le & {} (\Vert \varphi \Vert _{X}+\varepsilon )K_{ij}e ^{ -\int _{t_{0}}^{\theta }[{\tilde{a}}_{ij}(u)-\frac{\sigma }{1+u}]du}e^{-\sigma \ln \left( \frac{1+\theta }{1+t_{0}}\right) } \\&+ \int _{t_{0}}^{\theta }e ^{ -\int _{t}^{\theta }[{\tilde{a}}_{ij}(u)-\frac{\sigma }{1+u}]du}K_{ij}\bigg [\left| a_{ij} (t)p_{ij} (t)\right| \frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}} e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) }\\&+ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f} \frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}\right. \\&\left. +\,L^{f}(\kappa +L)\frac{1}{1- e^{ \sigma \ln \left( \frac{1 }{ r_{kl} }\right) } p_{kl} ^{+}}e^{ \sigma \ln \left( \frac{ 1 }{1+ q_{kl} } \right) }\right) \bigg ] dt M(\Vert \varphi \Vert _{X}+\varepsilon )e^{-\sigma \ln \left( \frac{1+\theta }{1+t_{0}}\right) } \\\le & {} (\Vert \varphi \Vert _{X}+\varepsilon )K_{ij}e ^{ -\int _{t_{0}}^{\theta }[{\tilde{a}}_{ij}(u)-\frac{\sigma }{1+u}]du}e^{-\sigma \ln \left( \frac{1+\theta }{1+t_{0}}\right) } \\&+ \int _{t_{0}}^{\theta }e ^{ -\int _{t}^{\theta }[{\tilde{a}}_{ij}(u)-\frac{\sigma }{1+u}]du} [{\tilde{a}}_{ij}(t)-\frac{\sigma }{1+t}] dt M(\Vert \varphi \Vert _{X}+\varepsilon )e^{-\sigma \ln \left( \frac{1+\theta }{1+t_{0}}\right) }\\= & {} M(\Vert \varphi \Vert _{X}+\varepsilon )e^{-\sigma \ln \left( \frac{1+\theta }{1+t_{0}}\right) } \bigg [ 1- (1-\frac{K_{ij}}{M} )e ^{ -\int _{0}^{\theta }({\tilde{a}}_{ij}(u)-\frac{ \sigma }{1+u})du} \bigg ] \\\le & {} M(\Vert \varphi \Vert _{X}+\varepsilon )e^{-\sigma \ln \left( \frac{1+\theta }{1+t_{0}}\right) } . \end{aligned}$$

This is a clear contradiction of (3.12). Thus, (3.11) is true. Letting \(\varepsilon \longrightarrow 0^{+}\) leads to

$$\begin{aligned} \Vert Z(t)\Vert \le M \Vert \varphi \Vert _{X} e^{-\sigma \ln \left( \frac{1+ \theta }{1+t_{0}}\right) }\quad \text{ for } \text{ all } t > t_{0}. \end{aligned}$$
(3.16)

Then, using a similar theoretical derivation in the proof of (3.14) and (3.15), according to (3.16), we get

$$\begin{aligned} e^{ \sigma \ln \left( \frac{1+ t}{1+t_{0}}\right) } |z_{ij} (t)| \le \sup \limits _{s\in [\rho _{ij}t_{0}, \ t]} e^{ \sigma \ln \left( \frac{1+ s}{1+t_{0}}\right) }|z_{ij} (s)|\le \frac{M \Vert \varphi \Vert _{X} }{1- e^{ \sigma \ln \left( \frac{1 }{ r_{ij} }\right) } p_{ij} ^{+}}, \end{aligned}$$

and

$$\begin{aligned} |z_{ij} (t)| \le \frac{M \Vert \varphi \Vert _{X} }{1- e^{ \sigma \ln (\frac{1 }{ r_{ij} })} p_{ij} ^{+}} \left( \frac{1+ t_{0}}{1+t}\right) ^{\sigma }, \ \forall \ t > t_{0}, \ ij\in J. \end{aligned}$$

This ends the proof. \(\square \)

Fig. 1
figure 1

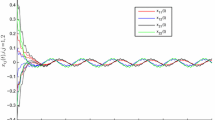
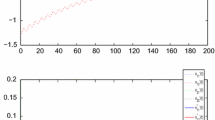
Numerical solutions of system (4.1) for three groups of different initial values

Full size image

4 An Example and Its Numerical Simulations

Example 4.1

Consider the following SICNNs with neutral type proportional delays and D operators:

$$\begin{aligned}&[x _{ij} (t)-p_{ij}(t)x_{ij}( r _{ij}t)]'\nonumber \\&\qquad \quad =-a_{ij}(t)x_{ij}(t )- \sum _{C_{kl}\in N_{1}(i,j)}C_{ij}^{kl} (t) \frac{1}{10}\arctan (x_{kl}(q_{ij} t ))x_{ij}(t) +L_{ij}(t),\qquad \end{aligned}$$
(4.1)

where \(p_{ij}(t)=\frac{1}{5}e^{-t^2}\sin (i+j)t , \ r _{ij} = \ q _{ij} = \frac{1}{2}, \ i,j=1,2, \)

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} a_{11}(t)&{}a_{12}(t) \\ a_{21}(t)&{}a_{22}(t) \end{array} \right]= & {} \left[ \begin{array}{c@{\quad }c} 0.8+ \cos 100t &{}1+1.1\sin 100t \\ 0.8+1.3\cos 100t&{}1+1.2\sin 100t \end{array} \right] , \\ \left[ \begin{array}{c@{\quad }c} C_{11}(t)&{}C_{12}(t) \\ C_{21}(t)&{}C_{22}(t) \end{array} \right]= & {} \left[ \begin{array}{c@{\quad }c} 0.01 \cos 2t &{}0.02 \cos 3t \\ 0.02 \cos 3t &{}0.01 \cos 4t \end{array} \right] ,\ \left[ \begin{array}{c@{\quad }c} L_{11}(t)&{}L_{12}(t) \\ L_{21}(t)&{}L_{22}(t) \end{array} \right] =\left\{ \frac{i+j}{100}e^{-2|t|}\sin t\right\} . \end{aligned}$$

Obviously, we can choose

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c} {\tilde{a}}_{11} &{}{\tilde{a}}_{12} \\ {\tilde{a}}_{21} &{}{\tilde{a}}_{22} \end{array} \right] =\left[ \begin{array}{c@{\quad }c} 0.8 &{}1 \\ 0.8&{}1 \end{array} \right] , K_{ij} = e^{\frac{1}{ 25}} ,M ^{f}=\frac{\pi }{20},~L^{f}=\frac{1}{10},~\kappa =0.2, \\&\sum _{C_{kl}\in N_{1}(i,j)}|{C_{ij}^{kl}}(t)|\le 0.06 , i,j=1,2 , \end{aligned}$$

such that system (4.1) satisfies \((T_{0})\), \((T_{1})\) and \((T_{2})\) and consequently it follows from Theorem 3.1 that the almost periodic solution of system (4.1) is globally generalized exponentially stable.The numerical simulations in Fig. 1 strongly support the conclusion and there are three groups of different initial values.

Remark 4.1

In this paper, it is the first time to deal with the existence and generalized exponential stability of almost periodic solutions for SICNNs involving neutral type proportional delays and D operators. Here, the criteria established in this paper are easily testable and independent of delays, that is, the considered neural network models for which stability is insensitive to the presence of the delays. On the other hand, one can see that all results obtained in [15,16,17,18,19] are invalid for system (4.1). Thus, the main results obtained in this paper are essentially new and complement some corresponding ones of the existing literature. Furthermore, the method used in this paper affords a possible approach to analysis the global generalized convergence of other cellular neural networks with neutral type proportional delays and D operators.