1 Introduction

Low-order neural networks have attracted much attention in the literature (see [6, 7, 16, 18,19,20, 22, 31, 34]). Hopfield neural networks (HNNs) are a form of low-order neural networks, introduced in 1982 by J. Hopfield (see [44, 54, 68]). In order to increase the computational power of neural networks, some investigators focused on high-order neural networks which have stronger approximation property, faster convergence rate, greater storage capacity and higher fault tolerance than low-order ones (see [15, 21, 49,50,51, 62]). One of the most typical high-order neural networks is the high-order Hopfield neural networks (HOHNNs). They have been extensively applied in psychophysics, robotics, vision and image processing. The dynamic properties of HOHNNs have been deeply discussed; the reader may refer to [12,13,14, 48, 57, 63, 64] and reference therein.

It is well known that time delay is ubiquitous in most physical, chemical and other natural system due to finite propagation speeds of signals, finite processing times in synapses and finite reaction times. In 1989, Marcus and Westervelt proposed the first neural network model with delay (see [41, 42]); since then, it has become important to consider neural networks with time delay (see [10, 17, 18, 23, 30, 37, 39, 45, 56, 59, 67, 69]). It is true that time delays are difficult to handle but have a significant impact on the dynamic behavior of neural networks.

Many phenomena process some regularity, but they are not periodic. Therefore, there exist several concepts which are more sophisticated than periodicity (see [2,3,4, 24,25,26,27,28, 32, 36, 46, 65]). The central tool in this work is the concept of asymptotic almost automorphy (AAA) which was introduced in the literature by N’Guérékata in 1980 as perturbations of almost automorphic functions by functions vanishing at infinity (see [1, 35, 38, 47]). The applications of asymptotic almost automorphy theory are involved in various research fields, especially in the domain of neural networks (see [33, 43, 55, 61]). In 2016, Brahmi et al. established various criteria of the dynamics of asymptotic almost automorphic solutions of the following model (see [15]):

$$\begin{aligned} \dot{x}_i(t)=& -a_{i}x_i(t)+ \sum \limits _{j=1}^{n}(b_{ij}(t)f_j(x_j(t))) \\ &+\sum \limits _{j=1}^{n}c_{ij}(t)g_j(x_j(t-\tau _{j})) \\ &+\sum \limits _{j=1}^{n} p_{ij}(t)\int \limits _{-\infty }^{t} r_{ij}(t-s) h_{j}(x_{j}(s))\,{\text{d}}s \\ &+ \sum \limits _{j=1}^{n} \sum \limits _{k=1}^{n}T_{ijk}(t)\phi _k(x_k(t-\tau _{k}))\phi _j(x_j(t-\tau _{j})) +J_i(t), \end{aligned}$$
(1)

where \(n\ge 2\) denotes to the number of neurons in the system, \(x_i(.)\) corresponds to the membrane potential of the neuron i,  the \(a_i\) is a positive constant rate used to reset the potential of the ith neuron to the conserve its state in isolation when it is disconnected. In addition, \(f_j(.), \;g_j(.),\; h_j(.)\) and \(\phi _j (.)\) are the activation functions of signal transmission, \(b_{ij}(.),\;c_{ij}(.),\; p_{ij}(.)\) are the connection weight of the unit j on the unit i,  \(T_{ijl}(.)\) presents the second-order connection weight of the neural networks, \(J_i(.)\) is the input unit i and \(\tau _j\ge 0\) is the transmission delay of unit j.

On the other hand, the theory of impulsive differential equations is being recognized to be not only more important than the corresponding theory of differential equations without impulses, but also represents a more natural framework for mathematical modeling of many real-world phenomena, like population dynamic systems and neural networks.

Naturally, more interesting neural network should take into account the impulsive effects, that is to say the seasonality of the changing environment (see [1, 5, 8,9,10, 16, 17, 29, 37, 40, 44, 45, 48, 52, 54, 57,58,59, 64, 66]).

For instance, Aouiti et al. studied the piecewise pseudo-almost periodic solutions for the following class of impulsive generalized high-order Hopfield neural networks with leakage delays (see [9]):

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_i(t)=-c_{i}(t)x_i(t-\rho (t))\\ \quad +\sum \limits _{j=1}^{n}a_{ij}(t)g_j(x_j(t-\tau _{ij}(t)))\\ \quad + \sum \limits _{j=1}^{n}\sum \limits _{l=1}^{n}\alpha _{ijl}(t)g_j(x_j(t-\sigma _{ij}(t)))\\ \quad \times g_l(x_l(t-\upsilon _{ij}(t))) \\ \quad +\sum \limits _{j=1}^{n} b_{ij}(t)\int \nolimits _{0}^{\infty } d_{ij}(u) g_{j}(x_{j}(t-u))\,{\text{d}}u\\ \quad +\sum \limits _{j=1}^{n}\sum \limits _{l=1}^{n}\beta _{ijl}(t)\int \nolimits _{0}^{\infty }h_{ijl}(u)g_{j}(x_{j}(t-u))\,{\text{d}}u\\ \quad \times \int \nolimits _{0}^{\infty }k_{ijl}(u)g_{l}(x_{l}(t-u))\,{\text{d}}u +J_i(t),\;t\ne t_k,\\ \quad \varDelta (x_i(t_k))=I_k(x(t_k)),\;\; k\in \mathbb {Z},\; t\in \mathbb {R},\; t=t_k, \end{array}\right. \end{aligned}$$
(2)

in which n corresponds to the number of units in a neural network, \(x_i(.)\) corresponds to the state vector of the ith unit, \(c_{i}(.)>0\) represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs, \(a_{ij}(.),\; b_{ij}(.), \alpha _{ijl}(.),\; \beta _{ijl}(.)\) are the first- and the second-order connection weights of the neural network, \(\tau _{ij}(.),\; \sigma _{ij}(.),\; \upsilon _{ij}(.)\ge 0\) correspond to the transmission delays, \(\rho (.) \ge 0\) denotes the leakage delay, \(g_j(.)\) is the activation functions of signal transmission, \(d_{ij}(.), \; h_{ijl}(.)\) and \(k_{ijl}(.)\) are the transmission delay kernels, \(J_i(.)\) denotes the external inputs. The sequence \(\{t_k\}\) has no finite accumulation point and \(I_k:\mathbb {R}^n\rightarrow \mathbb {R}, \;k\in \mathbb {Z}.\)

The impulsive HOHNNs have been the object of intensive analysis by numerous authors. However, to the best of our knowledge, there is no published paper considering the asymptotic almost automorphic solutions for impulsive HOHNNs with continuously distributed delays and variable asymptotic almost automorphic coefficients. Inspired by the above discussions, in this manuscript, we aim to challenge the analysis problem of the following system:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_i(t)=\sum \limits _{j=1}^{n}c_{ij}(t)x_j(t)+\sum \limits _{j=1}^{n}a_{ij}(t)f_j(x_j(t-\varsigma _j))\\ \quad + \sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}b_{ijl}(t)g_j(x_j(t-\sigma _j))g_l(x_l(t-\upsilon _l)) \\ \quad +\sum \limits _{j=1}^{n} d_{ij}(t)\int \nolimits _{-\infty }^{t} K_{ij}(t-s) h_{j}(x_{j}(s))\,{\text{d}}s\\ \quad +\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}r_{ijl}(t)\int \nolimits _{-\infty }^{t}P_{ijl}(t-s)k_{j}(x_{j}(s))\,{\text{d}}s\\ \quad \times \int \nolimits _{-\infty }^{t}Q_{ijl}(t-s)k_{l}(x_{l}(s))\,{\text{d}}s+\gamma _i(t),\; t\ne t_k,\\ \quad \varDelta (x_i(t_k))=\,\alpha _kx(t_k)+I_k(x(t_k))+\omega _k,\; k\in \mathbb {Z},\; t\in \mathbb {R},\; t\,=\,t_k, \end{array}\right. \end{aligned}$$
(3)

in which n corresponds to the number of units in a neural network, \(x_i(.)\) corresponds to the state vector of the ith unit, \(c_{ij}(.)\) represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs, \(a_{ij}(.),\; b_{ijl}(.),\; d_{ij}(.),\)\(r_{ijl}(.)\) are the first- and the second-order connection weights of the neural network, \(\; \varsigma _{j},\; \sigma _{j},\; \upsilon _{l}\ge 0,\) correspond to the transmission delays, \(f_j(.),\; g_j(.),\; h_j(.),\; k_j(.)\) are continuous representing the activation functions of signal transmission, \(K_{ij}(.), P_{ijl}(.)\) and \(Q_{ijl}(.)\) are the transmission delay kernels, \(\gamma _i(.)\) denotes the external inputs, \(\alpha _k \in \mathbb {R}^{2n},\)\(I_k(.)\in C(\mathbb {R},\mathbb {R}^n),\)\(\omega _k \in \mathbb {R}^n,\)\(\varDelta (x_i(t_k))=x_i(t_k^+)-x_i(t_k^-)\) are impulses at moments \(t_k\) such that \(t_1<t_2<\cdots\) is a strictly increasing sequence as \(\lim \nolimits _{n\longrightarrow \infty }t_k=+\infty .\)

The solution of (3) satisfying the initial conditions

$$\begin{aligned} x_i(s)= \phi _i(s), \; i=1,\cdots ,n, \;\;\;\; s \in (-\infty ,0]. \end{aligned}$$
(4)

where \(\phi\) is real-valued piecewise continuous functions defined on \((-\infty ,0].\)

Our motivation for this article stems from the fact that it can arise in many problems of science and engineering either directly or indirectly and that the study of asymptotic almost automorphic solutions for (3) does not exist until now. Therefore, the main purpose of this paper is to present some new criteria concerning the existence, the uniqueness and the global exponential stability of asymptotic almost automorphic solutions for a class of impulsive HOHNNs by utilizing the Banach’s fixed-point theorem and the generalized Gronwall–Bellman inequality.

Remark 1

In this work, we take into account the impulsive effects, so our results are more general than the results in [15].

Remark 2

In this work, the conditions on impulses are different from that presented in [8, 9]. Note that our model is more general than in [1, 6, 14, 15, 19, 53, 57, 60].

Remark 3

Our findings generalized some of the results reported in the literature (see [1, 16, 52, 57]) and so on, since the class of asymptotically almost automorphy contain the class of periodicity, almost periodicity, asymptotic almost periodicity and automorphy.

The rest of this paper is organized as follows: In Sect. 2, we will establish some useful assumptions, definitions and lemmas for impulsive non-autonomous dynamic systems with asymptotic almost automorphic coefficients, which will be used to obtain our main results. Section 3 is devoted to establishing some criteria for the existence, the uniqueness and the global exponential stability of asymptotic almost automorphic solution for system (3). In Sect. 4, four numerical examples are given to illustrate the feasibility of the obtained results. At last, we draw some remarks and conclusion in Sect. 5.

2 Assumptions, definitions and some new lemmas

The main aim of this article is to establish some sufficient conditions for the existence, the uniqueness and the global exponential stability of asymptotic almost automorphic solutions of (3).

Throughout this paper, the following notations were adapted:

$$\begin{aligned}&\text{for}\quad 1 \le i,j,l\le n, \quad \sup \limits _{t \in \mathbb {R}}|c_{ij}(t)| = c^{*}_{ij},\quad \sup \limits _{t \in \mathbb {R}} | a_{ij}(t)| = a^{*}_{ij},\\ &\sup \limits _{t \in \mathbb {R}} |b_{ijl}(t)| = b^{*}_{ijl},\quad \sup \limits _{t \in \mathbb {R}}| d_{ij}(t)|= d^{*}_{ij},\quad \sup \limits _{t \in \mathbb {R}} |r_{ijl}(t)| = r^{*}_{ijl},\\ &\sup \limits _{t \in \mathbb {R}}|\gamma _{i}(t)|=\gamma ^{*}_{i}. \end{aligned}$$

In order to make the paper self-contained, we introduce the following class of spaces, assumptions and definitions (for more details, see [1, 5, 11, 15, 29, 32, 38, 40, 47]).

  • \(C(\mathbb {R},\mathbb {R}^{n})\) is the set of continuous functions from \(\mathbb {R}\) to \(\mathbb {R}^{n}.\)

  • \(BC(\mathbb {R},\mathbb {R}^{n})\) denotes the set of bounded continued functions from \(\mathbb {R}\) to \(\mathbb {R}^{n}\). Note that \((BC(\mathbb {R},\mathbb {R}^{n}),\parallel . \parallel _{\infty })\) is a Banach space where \(\parallel . \parallel _{\infty }\) denotes the sup norm

    \(\parallel f \parallel _{\infty }:= \sup \nolimits _{t \in \mathbb {R}} \max \nolimits _{1 \le i \le n}\mid f_{i}(t) \mid .\)

  • \(PC(J,\mathbb {R}^n)\) is the space of piecewise continuous functions from \(J\subset \mathbb {R}\) to \(\mathbb {R}^n\) with points of discontinuity of the first kind \(t_k, \; k=\pm \,1,\pm \,2 \ldots\) and which are continuous from the left, i.e., \(x(t_k^-)=x(t_k).\)

  • \(PC_0(\mathbb {R}^+\times \mathbb {R}^n,\mathbb {R}^n)=\bigg \{\phi \in PC(\mathbb {R}^+\times \mathbb {R}^n,\mathbb {R}^n)\; \text{ such } \text{ that }\;\)

    \(\lim \nolimits _{t \rightarrow \infty }||\phi (t,x)||=0\) in t uniformly in \(x \in \mathbb {R}^n\bigg \}\).

  • \(B=\bigg \{ \{t_k\}_{k=-\infty }^\infty : t_k \in \mathbb {R},\; t_k< t_{k+1}, \; \lim \nolimits _{k \rightarrow \pm \infty }t_k=\pm \infty \bigg \},\) denote the set of all sequence unbounded and strictly increasing.

Now, we consider the following impulsive linear dynamic system:

$$\begin{aligned} \left\{ \begin{array}{ll} Z'(t)=P(t)Z(t),\; t\ne t_k,\; k\in \mathbb {Z},\\ \varDelta Z(t)=P_kZ(t),\; t= t_k, \;k\in \mathbb {Z}. \end{array} \right. \end{aligned}$$
(5)

If \(U_k(t,s)\) is the Cauchy matrix for the system

$$\begin{aligned} Z'(t)=P(t)Z(t), \;\; t_{k-1}<t<t_k, \;\{t_k\} \in B, \; k\in \mathbb {Z}, \end{aligned}$$
(6)

then the Cauchy matrix for system (5) is in the form

$$\begin{aligned} W(t,s)= \left\{ \begin{array}{l} U_{k}(t,s), \; t_{k-1}<s\le t\le t_k,\\ U_{k+1}(t,t_k+0)(I+P_k)U_k(t,s),\\ t_{k-1}< s\le t_k< t \le t_{k+1},\\ U_{k+1}(t,t_k+0)(I+P_k)U_k(t_k,t_k+0),\cdots (I+P_i)\\ \times U_i(t_i,s),\;t_{i-1}<s\le t_i< t_k<t \le t_{k+1}.\\ \end{array} \right. \end{aligned}$$

Remark 4

\(U_k(t,s)\) is a the Cauchy matrix for system (6), meaning that for \(k\in \mathbb {Z}\), the following condition is fulfilled:

$$\begin{aligned} \frac{\partial U_k(t,s)}{\partial t}= P(t)U_k(t,s), \; \;t_{k-1}< s\le t \le t_k, \;\; k\in \mathbb {Z}. \end{aligned}$$

We also assume that the following conditions (H1)–(H8) hold.

(H1):

The function \(P(t)=(c_{ij}(t))_{1 \le i,j \le n} \in C(\mathbb {R},\mathbb {R}^n)\) is asymptotically almost automorphic.

(H2):

\(\det (I+P_k)\ne 0,\) the sequence \(P_k,\) and \(t_k\) are asymptotically almost automorphic.

(H3):

The Cauchy matrix W(t, s) satisfies that there exist a positive constant K and \(\delta\) such that \(|W(t,s)|\le K e^{-\delta (t-s)},\) this further implies that:

\(|W(t+t_{n_{k}},s+t_{n_{k}})-W(t,s)|\le \tilde{M}\varepsilon e^{-\frac{\delta }{2}(t-s)},\) for any \(\varepsilon >0\) and positive constant \(\tilde{M}.\)

(H4):

The functions \(a_{ij},\;b_{ijl},\;d_{ij},\;r_{ijl}\) are almost automorphic.

(H5):

There exist positive constant numbers \(l_f^j,\;l_g^j,\;l_h^j,\;l_k^j,\;e^j,\)

\(M^j\) such that for all \(u, v\in \mathbb {R},\)\(\mid f_{j}(u)-f_{j}(v) \mid \le l_f^j \mid u-v \mid ,\)

\(\mid g_{j}(u)-g_{j}(v) \mid \le l_g^j \mid u-v \mid ,\) \(\mid h_{j}(u)-h_{j}(v) \mid \le l_h^j\mid u-v \mid ,\)

\(\mid k_{j}(u)-k_{j}(v) \mid \le l_k^j\mid u-v \mid ,\;\) \(\mid g_{j}(u) \mid \le e^j,\) \(\; \mid k_{j}(u) \mid \le M^j.\)

We suppose that \(f_{j}(0)= g_{j}(0) = h_{j}(0)= k_{j}(0)=0.\)

(H6):

For all \(i,j,l\in \{1,2,\ldots ,n\},\) the delay kernels \(K_{ij},\;P_{ijl},\)

\(Q_{ijl} : [0,+\infty ) \longrightarrow \mathbb {R}\) are continuous, integrable and there exist nonnegative constants \(K^+,P^+,Q^+, \nu ^K, \nu ^P, \nu ^Q\) such that \(| K_{ij}(t) | \le K^+ e^{-t\nu ^K},\;| P_{ijl}(t) | \le P^+ e^{-t \nu ^P},\;| Q_{ijl}(t) | \le Q^+ e^{-t\nu ^Q}.\)

(H7):

The function \(\gamma _i\) is asymptotic almost automorphic.

(H8):

The sequence \(I_k\) is asymptotic almost automorphic and there exists a positive constant L such that:

\(\mid I_{k}(u)-I_{k}(v) \mid \le L \mid u-v \mid ,\; k \in \mathbb {Z},\;u, v\in \mathbb {R}.\)

Let us recall some definitions which will be useful later.

Definition 1

A bounded piecewise continuous function

\(f \in PC(\mathbb {R},\mathbb {R}^{n})\) is called almost automorphic if

  • The sequence of impulsive moments \(\{t_k\},\; k \in \mathbb {Z}\) is an almost automorphic sequence,

  • For every real sequence \((s'_{n})_{n\in \mathbb {N}},\) there exists a subsequence \((s_{n})_{n \in \mathbb {N}}\) such that \(g(t) = \lim \nolimits _{n \rightarrow \infty } f( t + s_{n})\) is well defined for each \(t \in \mathbb {R}\) and \(\lim \nolimits _{n \rightarrow \infty } g( t - s_{n}) = f(t)\) for each \(t \in \mathbb {R}\).

Denote by \(AA(\mathbb {R},\mathbb {R}^{n})\) the set of all such functions.

Definition 2

A bounded piecewise continuous function

\(f \in PC(\mathbb {R}\times \mathbb {R}^{n},\mathbb {R}^{n})\)is called almost automorphic in t uniformly for x in compact subsets of \(\mathbb {R}^{n}\) if

  • Sequence of impulsive moments \(\{t_k\},\; k \in \mathbb {Z}\) is an almost automorphic sequence,

  • For every compact K of \(\mathbb {R}^{n}\) and for every real sequence \((s'_{n})_{n\in \mathbb {N}}\), there exists a subsequence \((s_{n})_{n \in \mathbb {N}}\) such that

    \(g(t,x) = \lim \nolimits _{n \rightarrow \infty } f( t + s_{n},x)\) is well defined for each \(t \in \mathbb {R},\)\(x \in K\) and \(\lim \nolimits _{n \rightarrow \infty } g( t - s_{n},x) = f(t,x)\) for each \(t \in \mathbb {R},\)\(x \in K.\)

Denote by \(AA(\mathbb {R}\times \mathbb {R}^{n},\mathbb {R}^{n})\) the set of all such functions.

Definition 3

A piecewise continuous function

\(f \in PC(\mathbb {R}^+,\mathbb {R}^{n})\) is called asymptotically almost automorphic if and only if it can be written as \(f=f_1+f_2\) where \(f_1 \in AA(\mathbb {R}^+,\mathbb {R}^{n})\) and \(f_2 \in PC_0(\mathbb {R}^+,\mathbb {R}^{n}).\)

The space of these kinds of functions is denoted by

\(AAA(\mathbb {R}^+,\mathbb {R}^{n}).\)

Definition 4

A piecewise continuous function

\(f \in PC(\mathbb {R}^+\times \mathbb {R}^{n},\mathbb {R}^{n})\) is called asymptotically almost automorphic if and only if it can be written as \(f=f_1+f_2\) where

\(f_1 \in AA(\mathbb {R}^+\times \mathbb {R}^{n},\mathbb {R}^{n})\) and \(f_2 \in PC_0(\mathbb {R}^+\times \mathbb {R}^{n},\mathbb {R}^{n}).\)

The space of these kinds of functions is denoted by

\(AAA(\mathbb {R}^+\times \mathbb {R}^{n},\mathbb {R}^{n}).\)

Example 1

Consider the function defined by

$$f(t)= \cos \left( \frac{1}{\sin t + \sin \sqrt{2} t}\right) +\frac{1}{1+t}, \; t \in \mathbb {R}.$$

It can be easily checked that the function f is asymptotically almost automorphic.

Indeed, the function \(t \rightarrow \cos (\frac{1}{\sin t + \sin \sqrt{2} t})\) belongs to \(AA(\mathbb {R},\mathbb {R})\), while the function \(t\rightarrow \frac{1}{1+t}\) is in \(PC_0(\mathbb {R},\mathbb {R}).\)

The function f is an example of an asymptotically almost automorphic function, which is not almost automorphic.

Definition 5

A bounded sequence\(x : \mathbb {Z}^+ \rightarrow \mathbb {R}\) is called almost automorphic if for every real sequence\((s'_{n})_{n\in \mathbb {N}}\), there exists a subsequence\((s_{n})_{n \in \mathbb {N}}\)such that\(y(m) = \lim \nolimits _{n \rightarrow \infty } x( m+ s_{n})\)is well defined for each\(m\in \mathbb {Z}^+\)and\(\lim \nolimits _{n \rightarrow \infty } y( m - s_{n}) = x(t)\)for each\(m \in \mathbb {Z}^+\).

The collection of all almost automorphic sequence which go from \(\mathbb {Z}^+\) to \(\mathbb {R}\) is denoted by \(AAS(\mathbb {Z}^+, \mathbb {R}).\)

Definition 6

A bounded sequence \(z:\mathbb {Z}^+ \rightarrow \mathbb {R}^+\) is called asymptotically almost automorphic if it can be written as \(z=z_1+z_2\) where \(z_1 \in AAS(\mathbb {Z}^+, \mathbb {R})\) and \(z_2\) is a null sequence.

The space of these kinds of sequences is denoted by

\(AAAS(\mathbb {Z}^+, \mathbb {R}).\)

Now, we propose some lemmas which will be helpful in proving the main results of this paper.

Lemma 1

If\(\varphi (.) \in AAA(\mathbb {R},\mathbb {R})\), then\(\varphi (.-h) \in AAA(\mathbb {R},\mathbb {R}).\)

Proof

(See “Appendix 1” section). \(\square\)

Lemma 2

If\(\varphi , \psi \in AAA(\mathbb {R},\mathbb {R})\), then\(\varphi \times \psi \in AAA(\mathbb {R},\mathbb {R}).\)

Proof

(See “Appendix 2” section). \(\square\)

Lemma 3

If\(f(.) \in C(\mathbb {R},\mathbb {R}^n)\) satisfies the\(l^j_f\)-Lipschitz condition, \(\phi (.) \in AAA (\mathbb {R},\mathbb {R}^n)\) and\(\varsigma \in \mathbb {R}^+\), then\(f(\phi (.-\varsigma ))\)in

\(AAA(\mathbb {R},\mathbb {R}^n).\)

Proof

(See “Appendix 3” section). \(\square\)

Lemma 4

Assume that assumptions (H5) and (H6) hold. For all \(1\le i,j\le n,\) if \(\phi _j(.) \in AAA(\mathbb {R},\mathbb {R}^n)\) then the function

$$\begin{aligned} \varPhi _{ij}: t \longmapsto \int \limits _{-\infty }^{t} K_{ij}(t-s) h_{j}(\phi _{j}(s)) \,{\text{d}}s \end{aligned}$$

belongs to \(AAA(\mathbb {R},\mathbb {R}^n).\)

Proof

(See “Appendix 4” section). \(\square\)

Corollary 1

Assume that assumptions (H5) and (H6) hold. For all\(1\le i,j,l\le n,\) if\(\phi _{j}(.) \in AAA(\mathbb {R},\mathbb {R}^n)\) then the function:

$$\begin{aligned} t \longmapsto \int \limits _{-\infty }^{t} P_{ijl}(t-s) k_{j}(\phi _{j}(s)) \,{\text{d}}s \end{aligned}$$

belongs to\(AAA(\mathbb {R},\mathbb {R}^n).\)

Corollary 2

Assume that assumptions (H5) and (H6) hold. For all\(1\le i,j,l\le n,\)if\(x_{j}(.) \in AAA(\mathbb {R},\mathbb {R}^n)\) then the function:

$$\begin{aligned} t \longmapsto \int \limits _{-\infty }^{t} Q_{ijl}(t-s) k_{l}(\phi _{l}(s)) \,{\text{d}}s \end{aligned}$$

belongs to\(AAA(\mathbb {R},\mathbb {R}^n).\)

Lemma 5

(Generalized Gronwall–Bellman inequality)

Let a nonnegative function\(x(.) \in PC (\mathbb {R},\mathbb {R}^n)\) satisfy for\(t\ge t_0\)

$$\begin{aligned} x(t)\le C(t)+ \int \limits _{t_0}^{t}u(s)x(s)\,{\text{d}}s+\sum \limits _{t_0< t_k <t} \beta _i x(t_i), \end{aligned}$$

with C(t) a positive non-decreasing function for\(t\ge t_0,\)

\(\; \beta _i \ge 0, \;u(t)\ge 0\) and\(t_i\)are the first kind discontinuity points of the function x(.). Then the following estimate holds for the functionx(.) : 

$$\begin{aligned} x(t)\le C(t) \prod \limits _{t_0< t_k <t}(1+\beta _i) e^{\int _{t_0}^{t}u(s)\,{\text{d}}s}. \end{aligned}$$

3 Main results

First, we begin by studying the existence and the uniqueness of asymptotic almost automorphic solutions. The results are based on the Banach’s fixed-point theorem.

Lemma 6

Suppose that all assumptions hold.

Define the nonlinear operator \(\varTheta\) as follows,

\(\forall \phi =(\phi _1,\ldots ,\phi _n)\in AAA(\mathbb {R},\mathbb {R}^n),\)

$$\begin{aligned} (\varTheta _\phi )_i (t):=& \int \limits _{-\infty }^{t} W(t,s)(U_\phi )_i(s)\,{\text{d}}s \\ &+ \sum \limits _{t_k<t} W(t,t_k)(I_k(\phi _i(t_k))+\omega _k), \end{aligned}$$
(7)

where

$$\begin{aligned} (U_{\phi })_i(s)& = \sum \limits _{j=1}^{n}a_{ij}(s)f_j(\phi _j(s-\varsigma _{j})) \\ &+ \sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}b_{ijl}(s)g_j(\phi _j(s-\sigma _{j}))g_l(\phi _l(s-\upsilon _{l})) \\ &+\sum \limits _{j=1}^{n} d_{ij}(s)\int \limits _{-\infty }^{s} K_{ij}(s-m) h_{j}(\phi _{j}(m))\,{\text{d}}m \\ &+\sum \limits _{j=1}^{n}\sum \limits _{l=1}^{n}r_{ijl}(s)\int \limits _{-\infty }^{s}P_{ijl}(s-m)k_{j}(\phi _{j}(m))\,{\text{d}}m \\ &\times \int \limits _{-\infty }^{s}Q_{ijl}(s-m)k_{l}(\phi _{l}(m))\,{\text{d}}m+\gamma _i(s), \end{aligned}$$
(8)

then\(\varTheta\)maps\(AAA(\mathbb {R},\mathbb {R}^n)\)into itself.

Proof

(See “Appendix 5” section). \(\square\)

Theorem 1

Under the conditions (H1)–(H8) and Lemma 6 : assume that there exist nonnegative constants r and \(\tilde{r}\) such that

$$\begin{aligned} r=& \frac{K}{\delta } \max _{1 \le i\le n}\bigg [ \sum \limits _{j=1}^{n}a_{ij}^* l_f^j + \sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}b_{ijl}^* l_g^j e^l \\ &+\sum \limits _{j=1}^{n} d_{ij}^* l_h^j \frac{K^+}{\nu ^K}+ \sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}r_{ijl}^* \frac{P^+}{\nu ^P} \frac{Q^+}{\nu ^Q} l_k^j M^l\bigg ] \\ &+ \frac{K L}{1-e^{-\delta }} <1, \end{aligned}$$
(9)
$$\begin{aligned} \tilde{r}=& \frac{K}{\delta }\max _{1 \le i\le n}\bigg [\sum \limits _{j=1}^{n}a_{ij}^* l_f^j + \sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}b_{ijl}^*(l_g^je^l+l_g^l e^j) \\ &+\sum \limits _{j=1}^{n} d_{ij}^* l_h^j \frac{K^+}{\nu ^K}+\sum \limits _{j=1}^{n} \sum \limits _{l=1}^{n}r_{ijl}^* \frac{P^+}{\nu ^P} \frac{Q^+}{\nu ^Q} (l_k^j M^l+l_k^l M^j) \bigg ] \\ &+\frac{KL}{1-e^{-\delta }} <1, \end{aligned}$$
(10)

then system (3) has a unique asymptotic almost automorphic solution in the region

$$\begin{aligned} S^*=S^{*}(\phi _{0},r)=\bigg \{ \phi \in AAA (\mathbb {R},\mathbb {R}^{n}),\Vert \phi -\phi _{0}\Vert \le \frac{r}{1-r}\bar{ R} \bigg \}, \end{aligned}$$

where

$$\begin{aligned} \bar{ R}&= K \bar{\gamma }(\frac{1}{\delta }+\frac{1}{1-e^{-\delta }}),\\ \phi _{0}(t)& = \left( \begin{array}{ll} \int \limits _{-\infty }^{t}W(t,s) \gamma _1(s)\,{\text{d}}s +\sum \limits _{t_k< t} W(t,t_k)\omega _k \\ \vdots \\ \int \limits _{-\infty }^{t}W(t,s) \gamma _n(s)\,{\text{d}}s +\sum \limits _{t_k < t} W(t,t_k)\omega _k\\ \end{array} \right) . \end{aligned}$$

Proof

(See “Appendix 6” section). \(\square\)

Second, we study the global exponential stability of asymptotic almost automorphic solutions of system (3) by using the generalized Gronwall–Bellman inequality.

Theorem 2

Suppose the conditions of Theorem 1 hold. Assume further that

$$\begin{aligned}&\frac{\ln (1+KL)}{\vartheta }+K\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\bigg [a_{ij}^*l_j^f+\sum \limits _{l=1}^{n} b_{ijl}^*( l_g^je^l+ l_g^le^j) \\ &\quad +\,d_{ij}^*\frac{K^+}{\nu ^K}l_h^j+\sum \limits _{l=1}^{n}r_{ijl}^* \frac{P^+}{\nu ^P} \frac{Q^+}{\nu ^Q} (l_k^j M^l+l_k^l M^j)\bigg ]-\delta <0 \end{aligned}$$
(11)

then the unique asymptotic almost automorphic solution of system (3) is global exponential stable.

Proof

(See “Appendix 7” section). \(\square\)

4 Numerical examples and simulations

In this section, we present some examples to illustrate the feasibility of our findings derived in the previous sections.

4.1 Example 1

Consider the following impulsive high-order Hopfield neural networks \((n=2):\)

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_i(t)=\sum \limits _{j=1}^{2}c_{ij}(t)x_j(t)+\sum \limits _{j=1}^{2}a_{ij}(t)f_j(x_j(t-\varsigma _j))\\ + \sum \limits _{j=1}^{2} \sum \limits _{l=1}^{2}b_{ijl}(t)g_j(x_j(t-\sigma _j))g_l(x_l(t-\upsilon _l)) \\ +\sum \limits _{j=1}^{2} d_{ij}(t)\int \limits _{-\infty }^{t} K_{ij}(t-s) h_{j}(x_{j}(s))\,{\text{d}}s\\ +\sum \limits _{j=1}^{2} \sum \limits _{l=1}^{2}r_{ijl}(t)\int \limits _{-\infty }^{t}P_{ijl}(t-s)k_{j}(x_{j}(s))\,{\text{d}}s\\ \times \int \limits _{-\infty }^{t}Q_{ijl}(t-s)k_{l}(x_{l}(s))\,{\text{d}}s +\gamma _i(t),\; t\ne t_k,\\ \varDelta (x_i(t_k))=\alpha _kx(t_k)+I_k(x(t_k))+\omega _k,\; t= t_k,\\ \end{array}\right. \end{aligned}$$
(12)

where \(\varsigma _{j}=\upsilon _{j}=\sigma _{j} = L=\frac{1}{40} ,\)

\(K_{ij}(t)=P_{ijl}(t)=Q_{ijl}(t) =e^{-t}.\)

For \(t \in \mathbb {R} ,\; 1 \le i,j\le 2,\) let

$$\begin{aligned} f_{j}(t)& = g_{j}(t) = h_{j}(t) = k_{j}(t)= \frac{|t+1|-|t-1|}{2}, \\ l_{f}^{j}& = l_{g}^{j} =l_{h}^{j}=l_{k}^{j}=e^j =M^j= \frac{K^+}{\nu ^K}\\ & = \frac{P^+}{\nu ^P}=\frac{Q^+}{\nu ^Q}=K=\delta =1,\\ &(c_{ij}(t))_{1 \le i,j \le 2} = \left( \begin{array}{lll} 4+\cos (t)^2 & 0 \\ 4+\sin (t)^2 & 0\\ \end{array}\right) ,\\ &(a_{ij}(t))_{1 \le i,j \le 2}\\ & = \left( \begin{array}{lll} 0.03 \sin \left(\frac{2\pi }{2+ \sin t+\sin \sqrt{3}t}\right) & 0.07+0.03e^{-t} \\ 0.05 \sin \left(\frac{2 \pi }{2+ \cos \sqrt{5}t}\right)& 0.05+0.05e^{-t} \\ \end{array}\right) ,\\ &(b_{1jl}(t))_{1 \le j,l \le 2}\\ & = \left( \begin{array}{lll} 0 & 0.03 \cos \left (\frac{1}{2+ \sin t + \sin \sqrt{2}t}\right) +\frac{0.01}{1+t^{2}}\\ 0 & 0 \\ \end{array}\right) ,\\ &(b_{2jl}(t))_{1 \le j,l \le 2}\\ &= \left( \begin{array}{lll} 0.03 \sin \left(\frac{1}{2+ \cos t + \sin \sqrt{5}t}\right ) +\frac{0.01}{1+t} &0\\ 0 & 0 \\ \end{array}\right) ,\\ &(d_{ij}(t))_{1 \le i,j \le 2}\\ & = \left( \begin{array}{lll} 0.04 \sin \left (\frac{1}{2+ \cos t + \cos \sqrt{2}t}\right) & 0.04 \cos \left (\frac{1}{2+ \sin t + \sin \sqrt{2}t}\right ) \\ 0.05 + \frac{0.1}{1+t} & 0 \\ \end{array}\right) ,\\ &(r_{1jl}(t))_{1 \le j,l \le 2}\\ & = \left( \begin{array}{lll} 0 & 0.02 \sin \left (\frac{1}{2+ \sin t + \sin \sqrt{2}t}\right) + \frac{0.01}{1+t} \\ 0 & 0 \\ \end{array}\right) ,\\ &(r_{2jl}(t))_{1 \le j,l\le 2}\\ & = \left( \begin{array}{lll} 0 & 0.04 \sin \left(\frac{1}{2+ \sin t + \sin \sqrt{2}t}\right ) + \frac{0.01}{1+t} \\ 0 & 0 \\ \end{array}\right) ,\\ &(\gamma _{i}(t))_{1 \le i\le 2} = \left( \begin{array}{l} 0.7 \sin \left(\frac{1}{2+ \sin t + \sin \sqrt{2}t}\right ) + \frac{0.3}{1+t} \\ 0.7 \cos \left (\frac{1}{2+ \cos t + \cos \sqrt{5}t}\right ) + \frac{0.3}{1+t} \\ \end{array}\right) \end{aligned}$$

and

\(\varDelta x_1(2k)=-\frac{1}{40}x_1(2k)+\frac{1}{80}\sin (x_1(2k))+\frac{1}{20},\)

\(\varDelta x_2(2k)=-\frac{1}{40}x_2(2k)+\frac{1}{80}\cos (x_2(2k))+\frac{1}{30}.\)

Then, after all calculation done we have

$$\begin{aligned}&r= \max \{ 0.319,0.33 \}<1,\; \tilde{r}=\max \{0.359, 0.379\}<1,\\ &\quad \frac{\ln \left( 1+\frac{1}{40}\right) }{\vartheta }+\sum \limits _{i=1}^{2}\sum \limits _{j=1}^{2}\sum \limits _{l=1}^{2}\left[a_{ij}^*+ 2b_{ijl}^* + d_{ij}^* +2r_{ijl}^* \right]-\delta <0. \end{aligned}$$

According to Theorems 1 and 2, system (12) has a unique asymptotic almost automorphic solution, which is globally exponentially stable.

The simulation results can be seen in the following figures:

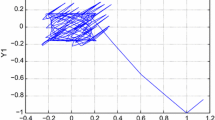
Figure 1 depicts the numeric simulation of \((x_1,x_2)\) for system (12); Fig. 2 depicts the orbit of \((x_{1},x_{2})\) for system (12).

Fig. 1
figure 1

Transient response of state variables \(x_1\) and \(x_2\) for system (12) when t in [0; 50]

Full size image
Fig. 2
figure 2

Orbit of \(x_{1}, x_{2}\) for system (12)

Full size image

4.2 Example 2

Consider the following high-order Hopfield neural networks without impulses \((n=2)\):

$$\begin{aligned} \dot{x}_i(t)& = \sum \limits _{j=1}^{2}c_{ij}(t)x_j(t)+\sum \limits _{j=1}^{2}a_{ij}(t)f_j(x_j(t-\varsigma _j)) \\ &+ \sum \limits _{j=1}^{2} \sum \limits _{l=1}^{2}b_{ijl}(t)g_j(x_j(t-\sigma _j))g_l(x_l(t-\upsilon _l)) \\ &+\sum \limits _{j=1}^{2} d_{ij}(t)\int \limits _{-\infty }^{t} K_{ij}(t-s) h_{j}(x_{j}(s))\,{\text{d}}s \\ &+\sum \limits _{j=1}^{2} \sum \limits _{l=1}^{2}r_{ijl}(t)\int \limits _{-\infty }^{t}P_{ijl}(t-s)k_{j}(x_{j}(s))\,{\text{d}}s \\ &\times \int \limits _{-\infty }^{t}Q_{ijl}(t-s)k_{l}(x_{l}(s))\,{\text{d}}s+\gamma _i(t). \end{aligned}$$
(13)

System (13) has exactly one asymptotic almost automorphic solution. The asymptotic almost automorphic solution is globally exponentially stable. The results are verified by the numerical simulations in the following figures: Fig. 3 depicts the response of state variables \((x_1,x_2)\) for system (13); Fig. 4 represents the orbit of \((x_{1},x_{2})\) for system (13).

Fig. 3
figure 3

Transient response of state variables \(x_1\) and \(x_2\) for system (13) when t in [0; 50]

Full size image
Fig. 4
figure 4

Orbit of \(x_{1},\)\(x_{2}\) for system (13)

Full size image

4.3 Example 3

Consider the following impulsive high-order Hopfield neural networks \((n=3)\):

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}_i(t)&=\sum \limits _{j=1}^{3}c_{ij}(t)x_j(t)+\sum \limits _{j=1}^{3}a_{ij}(t)f_j(x_j(t-\varsigma _j))\\ &+ \sum \limits _{j=1}^{3} \sum \limits _{l=1}^{3}b_{ijl}(t)g_j(x_j(t-\sigma _j))g_l(x_l(t-\upsilon _l)) \\ &+\sum \limits _{j=1}^{3} d_{ij}(t)\int \limits _{-\infty }^{t} K_{ij}(t-s) h_{j}(x_{j}(s))\,{\text{d}}s\\ &+\sum \limits _{j=1}^{3} \sum \limits _{l=1}^{3}r_{ijl}(t)\int \limits _{-\infty }^{t}P_{ijl}(t-s)k_{j}(x_{j}(s))\,{\text{d}}s\\ &\times \int \limits _{-\infty }^{t}Q_{ijl}(t-s)k_{l}(x_{l}(s))\,{\text{d}}s +\gamma _i(t),\; t\ne t_k,\\ \varDelta (x(t_k))&= \alpha _kx(t_k)+I_k(x(t_k))+\omega _k,\;t=t_k, \\ \end{array}\right. \end{aligned}$$
(14)

where \(\varsigma _{j}=\upsilon _{j}=\sigma _{j} = L=\frac{1}{80},\)

\(K_{ij}(t)=P_{ijl}(t)=Q_{ijl}(t) =e^{-t}.\)

For \(t \in \mathbb {R},\;i,j =1,2,3\)

$$\begin{aligned} f_{j}(t)& = g_{j}(t) = h_{j}(t) = k_{j}(t)=\sin (t)\\ l_{f}^{j}& = l_{g}^{j} =l_{h}^{j}=l_{k}^{j}=e^j =M^j= \frac{K^+}{\nu ^K}\\ & = \frac{P^+}{\nu ^P}=\frac{Q^+}{\nu ^Q}=K=\delta =1,\\ &(c_{ij}(t))_{1 \le i,j \le 3} = \left( \begin{array}{lll} 2+\cos (t) & 0 &0 \\ 2+\sin (t) & 0 & 0\\ 3+\cos (t) & 0 & 0\\ \end{array}\right) ,\\ &(a_{ij}(t))_{1 \le i,j \le 3}\\= & \left( \begin{array}{lll} 0.02 \sin \left( \frac{\pi }{2+ \sin t \sqrt{5}t}\right) & 0.01 & 0.07\\ 0.02 \sin \left( \frac{2 \pi }{2+ \cos \sqrt{5}t}\right) & 0.05\sin t+0.03 \cos \sqrt{2}t & 0.05\\ 0.05\cos \sqrt{3}t &0.04\cos \left( \frac{2\pi }{2+ \sin t+\sin \sqrt{2}t}\right) &0.01 \end{array}\right) ,\\ &(b_{1jl}(t))_{1 \le j,l \le 3}\\ & = \left( \begin{array}{lll} 0.01 \sin \left( \frac{\pi }{2+ \sin t \sqrt{5}t}\right) &0.05\sin \sqrt{5}t & 0.04\\ 0.04+e^{-t} & 0.01 \cos \sqrt{2}t &0.05 \\ 0.07 \cos \sqrt{2}t &0.01\cos \left( \frac{2\pi }{2+ \sin t+\sin \sqrt{2}t}\right) &0.02 \end{array}\right) ,\\ &(b_{2jl}(t))_{1 \le j,l \le 3} = \left( \begin{array}{lll} 0 & 0.05 \cos (t) & 0.05\\ 0 & 0.02 \cos \sqrt{2}t &0.08\sin \sqrt{5}t \\ 0 &0.02 &0.08 \end{array}\right) ,\\ &(b_{3jl}(t))_{1 \le j,l \le 3} = \left( \begin{array}{lll} 0 & 0.02 \sin (t)+e^{-t^2} & 0.02\\ 0 & 0.01 \cos \sqrt{2}t &0.03e^{-t} \\ 0 .01&0.01e^{-t} &0 \end{array}\right) ,\\ &(d_{ij}(t))_{1 \le i,j \le 3}\\ & =\left( \begin{array}{lll} 0.04 \cos \frac{1}{2+ \sin t + \sin \sqrt{2} t} & 0.01 &0.05 \cos \sqrt{3}t \\ 0.03 \cos (\sqrt{5}t) & 0.02\cos \sqrt{2}t & 0.05 \sin \sqrt{5}t \\ 0.02e^{-t}& 0. 01& 0.07 \cos \sqrt{2}t \end{array}\right) ,\\ &(r_{1jl}(t))_{1 \le j,l \le 3}\\ & = \left( \begin{array}{lll} 0.07 \cos t & 0.03 \cos (t) & 0\\ 0.05\cos (t)+\frac{0.05}{1+t^{4}} & 0 &\sin \sqrt{3}t \\ 0 &0.01e^{-t^2} &0 \end{array}\right) ,\\ &(r_{2jl}(t))_{1 \le j,l\le 3} = \left( \begin{array}{lll} 0 & 0.01 \sin (t) & 0\\ 0 & 0.08\sin \sqrt{5}t &0.02\\ 0 &0.02+\frac{0.08}{1+t^{2}} &0 \end{array}\right) ,\\ &(r_{3jl}(t))_{1 \le j,l\le 3} = \left( \begin{array}{lll} 0.01 & 0 & 0\\ 0 & 0 &0.01\sin \sqrt{5}t +e^{-t} \\ 0&0.08e^{-t} &0 \end{array}\right) ,\\ &(\gamma _{i}(t))_{1 \le i\le 3} = \left( \begin{array}{l} 0.5 +\frac{1}{1+t}\\ \frac{1}{5} \sin \left( \frac{1}{2+\sin t+\sin \sqrt{5}t}\right) + 0.1e^{-t}\\ 1 \end{array}\right) \end{aligned}$$

and

\(\varDelta x_1(2k)=-\frac{1}{80}x_1(2k)+\frac{1}{80}\sin (x_1(2k))+\frac{1}{80},\)

\(\varDelta x_2(2k)=-\frac{1}{80}x_2(2k)+\frac{1}{80}\cos (x_2(2k))+\frac{1}{40},\)

\(\varDelta x_3(2k)=-\frac{1}{80}x_3(3k)+\frac{1}{80}\cos (x_3(2k))+\frac{1}{20}.\)

Then, after all calculation done we have

$$\begin{aligned} r& = \max \{ 0.2, 0.27, 0.15\}<1,\; \tilde{r}=\max \{0.6, 0.6,0.14\}<1,\\ &\frac{\ln (1+\frac{1}{80})}{\vartheta }+\sum \limits _{i=1}^{3}\sum \limits _{j=1}^{3}\sum \limits _{l=1}^{3}\bigg [a_{ij}^*+ 2b_{ijl}^*+d_{ij}^* +2r_{ijl}^* \bigg ]-\delta <0. \end{aligned}$$

According to Theorems 1 and 2, system (14) has a unique asymptotic almost automorphic solution, which is globally exponentially stable.

The simulation results can be seen in the following figures.

Figure 5 depicts the numeric simulation of \((x_1,x_2,x_3)\) for system (14); Fig. 6 depicts the orbit of \((x_{1},x_{2})\) for system (14); Fig. 7 shows the orbit of \((x_{1},x_{3})\) for system (14); Fig. 8 shows the orbit of \((x_{2},x_{3})\) for system (14); Fig. 9 depicts the orbit of \((x_{1},x_{2},x_{3})\) for system (14).

Fig. 5
figure 5

Transient response of state variables \(x_1, x_2\) and \(x_3\) for system (14) when t in [0; 50]

Full size image
Fig. 6
figure 6

Orbit of \(x_{1},\)\(x_{2}\) for system (14)

Full size image
Fig. 7
figure 7

Orbit of \(x_{1},\)\(x_{3}\) for system (14)

Full size image
Fig. 8
figure 8

Orbit of \(x_{2},\)\(x_{3}\) for system (14)

Full size image
Fig. 9
figure 9

Orbit of \(x_{1},\)\(x_{2}\) and \(x_{3}\) for system (14)

Full size image

4.4 Example 4

Consider the following high-order Hopfield neural networks without impulses \((n=3)\):

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}_i(t)&= \sum \limits _{j=1}^{3}c_{ij}(t)x_j(t)+\sum \limits _{j=1}^{3}a_{ij}(t)f_j(x_j(t-\varsigma _j))\\ & + \sum \limits _{j=1}^{3} \sum \limits _{l=1}^{3}b_{ijl}(t)g_j(x_j(t-\sigma _j))g_l(x_l(t-\upsilon _l)) \\ & +\sum \limits _{j=1}^{3} d_{ij}(t)\int \limits _{-\infty }^{t} K_{ij}(t-s) h_{j}(x_{j}(s))\,{\text{d}}s\\ & +\sum \limits _{j=1}^{3} \sum \limits _{l=1}^{3}r_{ijl}(t)\int \limits _{-\infty }^{t}P_{ijl}(t-s)k_{j}(x_{j}(s))\,{\text{d}}s\\ &\times \int \limits _{-\infty }^{t}Q_{ijl}(t-s)k_{l}(x_{l}(s))\,{\text{d}}s+\gamma _i(t) \end{array}\right. \end{aligned}$$
(15)

System (15) has one and only one asymptotic almost automorphic solution which is globally exponentially stable.

The results are verified by the numerical simulations in the following figures:

Figure 10 depicts the response of state variables \((x_1,x_2,x_3)\) for system (15); Fig. 11 represents the orbit of \((x_{1},x_{2})\) for system (15); Fig. 12 depicts the orbit of \((x_{1},x_{3})\) for system (15); Fig. 13 shows the orbit of \((x_{2},x_{3})\) for system (15); Fig. 14 shows the orbit of \((x_{1},x_{2},x_{3})\) for system (15).

Fig. 10
figure 10

Transient response of state variables \(x_1,\)\(x_2\) and \(x_3\) for system (14) without impulses for t in [0; 50]

Full size image
Fig. 11
figure 11

Orbit of \(x_{1},\)\(x_{2}\) for system (14) without impulses

Full size image
Fig. 12
figure 12

Orbit of \(x_{1},\)\(x_{3}\) for system (14) without impulses

Full size image
Fig. 13
figure 13

Orbit of \(x_{2},\)\(x_{3}\) for system (14) without impulses

Full size image
Fig. 14
figure 14

Orbit of \(x_{1},\)\(x_{2}\) and \(x_{3}\) for system (14) without impulses

Full size image

Descriptions From Examples 1 and 3, we have the following descriptions:

  • From the orbital figures: Fig. 2 of system (12) and Figs. 6, 7, 8 and 9 of system (14), the orbits in two- and three-dimensional spaces of the asymptotic almost automorphic solutions of both systems are subject to instantaneous perturbations and change of the state abruptly. The dynamic behavior of the asymptotic almost automorphic solutions for both systems has a chaos due to the effects of the impulse.

  • The orbital figures of the two systems are good since they highlight the effect of impulse on the dynamic behavior of the asymptotic almost automorphic solution. The impulse stress the asymptotic almost automorphic solution of each system.

From Examples 2 and 4, we have the following descriptions:

  • By observing Figs. 3, 4 of system (13) and Figs. 10, 11, 12, 13 and 14 of system (15) we can see that the dynamic behavior of the asymptotic almost automorphic solution of both systems is rhythmic since we notice the absences of chaos and points of discontinuity in the behavior of the both solutions.

Roughly speaking:

  • If we do not take into account the impulsive effects then: system (12) is reduced to system (13) and system (14) is reduced to system (15).

  • Underlining a very remarkable difference between the figures of the orbits of system (12), system (14) and the figures of the orbits of system (13), system (15). The effects of the impulsion are quite profound.

Remark 5

  • Many natural phenomena cannot be accurately described as “periodic phenomena”. For examples: the time intervals of a round for a celestial body motion, the tidal flood that is a disaster for mankind, the weather during a week or a month, the earthquake which is difficult to be predicted and so on, then the concept of asymptotic almost automorphy should be adopted.

  • Our manuscript offers a theoretical basis for the design of the second-order class of neural networks with mixed time delays more effective in the resolution of optimization calculation and the control robotic manipulator thanks to the second-order synaptic terms \(b_{ijl}\) and \(r_{ijl}.\)

  • In light of Theorems 1 and 2, the existence, the uniqueness and the global exponential stability of asymptotic almost automorphic solution of system (3) are obtained, indicating that the sufficient conditions in Theorems 1 and 2 can be used to solve the optimization problem by converting object function into energy function.

  • The global exponential stability of HOHNNs can be guaranteed for the global optimal solutions. The numerical algorithms are less effective than the method of neural networks for solving the optimization problems.

  • Our criteria are of prime importance. They could be further utilized for many problems such as the control and the filtering, the non-fragile state estimation, the distributed state estimation for sensor networks and can be also extended into social networks.

5 Conclusions

The low-order Hopfield neural networks have many shortcomings. Consequently, it is indispensable to add high-order interactions to these neural networks. This motivated the extensively study on the high-order Hopfield neural networks with and/or without impulses. In this work, by using the fixed-point theorem and the generalized Gronwall–Bellman inequality, we obtain some new results of the existence, the uniqueness and the global exponential stability of asymptotic almost automorphic solutions for impulsive non-autonomous high-order Hopfield neural networks with mixed delays. Finally, four examples are given to demonstrate the effectiveness of our obtained results.