1 Introduction

Recurrent neural network, which can be applied to physical science, sociology, mathematics and communication, has been a hot topic recently. Hitherto, many excellent results have been obtained about the stability of the equilibrium point for the considered neural network [1–6].

In addition, there are increasing interests devoting the study of complex-valued recurrent neural networks (CVNNs) due to the much more extensive applications [7, 8]. CVNNs, an important kind of nonlinear complex-valued systems, can be seen as an extension of real-valued recurrent neural networks (RVNNs). Naturally, CVNNs can be also generalized to quaternion-valued recurrent neural networks (QVNNs) with quaternion-valued states, quaternion-valued connection weights, quaternion-valued activation functions and quaternion-valued output. As a special case of Clifford-valued recurrent neural networks [9], the QVNN is much more complicated than the CVNN for the non-commutativity of quaternion multiplication resulting from Hamilton rules: \(ij=-ji=k,jk=-kj=i,ki=-ik=j, i^{2}=j^{2}=k^{2}=ijk=-1\).

To the best of our knowledge, RVNNs have many applications, but they perform less well when it comes to geometrical transformations, like 2D affine transformations or 3D affine transformations. Some researchers have found that CVNNs result in improved performance on 2D affine transformations, while the performance of RVNNs is comparatively poor. Because via 2D geometrical affine operations, CVNNs enable the modeling of a point in two-dimensional space as a single entity instead of a set of two data items [10]. Furthermore, considering the three-dimensional data case, including body images and color images, which can be processed by many neurons of CVNNs. In particular, via implementing direct encoding in terms of quaternions, the processing efficiency can be increased [11]. One of benefits by QVNN is that 3D geometrical affine transformation can be represented efficiently and compactly, especially spatial rotation, which can be extensively applied to the fields of robotics, attitude control of satellites, computer graphics, ensemble control, color night vision and image impression [11–15]. Particularly, [16] designs a novel event-triggered controller for the stabilization of the considered MIMO nonlinear uncertain continuous-time systems, where the controller is approximated by a linearly parameterized neural network in the event-triggered context, based on which, the computation is reduced extensively. Moreover, the linearly parameterized neural network used in [16] is composed of appropriate neurons in the input and output layers, especially an adequate number of hidden layer neurons. Considering that the quaternionic neurons can carry three-dimensional vectors, then the number of neurons in a layer of QVNNs can be reduced to one-third number of neurons in the RVNNs resulting in much higher efficiency. Then probably, stable QVNNs can be applied to design more efficient event-triggered controllers, which deserves further investigation. All in all, QVNNs should be investigated extensively for much more efficient applications.

In addition, various approaches can be used to analyze the stability of QVNNs such as the synthesis method [17], the most popular Lyapunov function method [18–20], etc. In [18], the stability of CVNNs is concerned. Taken advantage of the bounded partial derivatives and Lipschitz conditions, a Lyapunov function is established to obtain some sufficient conditions for the global \(\mu \)-stability of the addressed CVNNs. Then, an appropriate Lyapunov–Krasovskii functional is also defined to guarantee the global \(\mu \)-stability of the considered CVNNs. In [19], the stability for switched neural networks with time-varying delay is investigated with method of Lyapunov–Krasovskii functional. By means of the linear matrix inequality technique and the average dwell time method, some sufficient conditions are given to ensure the global exponential stability of the delay-dependent neural networks. In [20], with the method of Lyapunov functional, the authors study the problem of exponential synchronization for two kinds of delayed neural networks under time-varying sampling where the sampling intervals have a upper bound. Then, based on the Lyapunov functional method, an improved method is proposed to establish some delay-dependent criteria for the exponential stability of the considered systems, which grasps the characteristic of the addressed systems.

To the best knowledge of us, time delay is also a kernel of research which may bring oscillation [21], instability and bifurcation to networks [22, 23]. Hence, it is a necessary step to study the dynamical behaviors of delayed networks [24–27]. In the past few years, many excellent results along with this area have been given by researchers [28, 29]. In [28], combined with the homeomorphism map and linear matrix inequality, the existence and uniqueness of equilibrium point are discussed for the recurrent neural networks with multiple time-varying delays, and the global asymptotic stability criteria are also proposed based on the Lyapunov–Krasovskii stability theory. What’s more, the obtained results are also applicable for recurrent neural networks with constant time delays. In [29], where the CVNN is decomposed into two real-valued systems, the global stability criteria for the delayed CVNNs are presented via establishing an appropriate Lyapunov function. Additionally, a novel adaptive global sliding mode control strategy is proposed in [30] to study the input time delay, where the stability problem for a class of linear helicopter systems with actuator faults and input time delay is investigated. Since quaternion-valued differential equations can be used in the attitude control of spacecraft [12]. Therefore, the control of linear helicopter (spacecraft) systems, such as ensemble control [31], can be potentially studied based on quaternion-valued differential equations with input time delays.

In this paper, we aim to study the global exponential stability of QVNNs with time-varying delays with the Halanay inequality technique and the matrix measure method. The considered QVNN is decomposed into four real-valued systems forming an equivalent real-valued, and without using any Lyapunov function, some criteria are given for the global exponential stability of the equilibrium point by combining the methods of Halanay inequality and matrix measure. Particularly worth mentioning is that the real-valued functions decomposed from quaternion-valued activation functions are no longer required to be derivable, which is an improvement compared with [18]. Even more, the proposed approach significantly simplifies the analytical process without the tedious integral calculations, and the final results are also compact.

The remaining part of this paper is organized as follows. In Sect. 2, the model description of QVNNs are presented and some preliminaries are also outlined briefly. In Sect. 3, some sufficient conditions for the global exponential stability of QVNNs are derived via the matrix measure method and the Halanay inequality technique. A numerical example is given in Sect. 4 to show the effectiveness of our results. Finally, Sect. 5 concludes this paper.

Notations Throughout this paper, \(\mathbb {R}^{m\times n},~\mathbb {\mathbb {C}}^{m\times n},~\mathbb {Q}^{m\times n}\) denote, respectively, the set of all \(m\times n\) real-valued, complex-valued, and quaternion-valued matrices. Function \(h(t)=h^{R}(t)+ih^{I}(t)+jh^{J}(t)+kh^{K}(t)\) denotes quaternion-valued function, where the imaginary units i, j, k obey Hamilton rules: \(ij=-ji=k,jk=-kj=i,ki=-ik=j, i^{2}=j^{2}=k^{2}=ijk=-1\) which result in the non-commutativity of the quaternion multiplication. For any \(h\in \mathbb {Q}\), \(\Vert h\Vert =\sqrt{hh^{*}}=\sqrt{(h^{R})^{2}+(h^{I})^{2}+(h^{J})^{2}+(h^{K})^{2}}\), where \(h^{*}=h^{R}-ih^{I}-jh^{J}-kh^{K}\) denotes conjugate transpose of h. For any matrix \(A=(a_{ij})_{n\times n}\in \mathbb {R}^{n\times n}\), denote \(A^{T}\) and \(\lambda _{\max }(A)(\lambda _{\min }(A))\) as the matrix transposition and maximum (minimum) eigenvalue of A, respectively, and denote \(|A|=(|a_{ij}|)_{n\times n}\). \(C([t_{0}-\tau ,t_{0}],\mathbb {R}^{n})\) represents the Banach space of continuous vector-valued functions, i.e., if \(\varphi \in C([t_{0}-\tau ,t_{0}],\mathbb {R}^{n})\), \(\varphi \) maps the interval \([t_{0}-\tau ,t_{0}]\) into \(\mathbb {R}^{n}\) along the topology of uniform convergence. In addition, denote \(\Vert \varphi \Vert _{p}=\sup _{t_{0}-\tau \le s\le t_{0}}\Vert \varphi (s)\Vert _{p}\), where \(\Vert \varphi (s)\Vert _{p}\) means the p-norm of \(\varphi (s)\in \mathbb {R}^{n}\), \(p=1,2,\infty \).

2 Preliminaries

Consider the following QVNNs with time-varying delays

$$\begin{aligned} \dot{h}(t)= & {} -Dh(t)+Af(h(t))+Bg\big (h(t-\tau (t))\big )+u,~~\nonumber \\&\quad t\ge t_{0} \end{aligned}$$
(1)

where \(h=(h_{1},h_{2},\ldots ,h_{n})^{T}\in \mathbb {Q}^{n}\) is the state vector, and \(D=\mathrm {diag}(d_{1},d_{2},\ldots , d_{n})\in \mathbb {R}^{n\times n}\) with \(d_{p}>0\) is the self-feedback connection weight matrix, for \(p=1,2,\ldots ,n\). \(A=(a_{pq})_{n\times n}\in \mathbb {Q}^{n\times n}\) and \(B=(b_{pq})_{n\times n}\in \mathbb {Q}^{n\times n}\) are, respectively, the connection weight matrices without and with time delays, \(p,q=1,2,\cdots ,n\). \(f(h(t))=\big [f_{1}(h_{1}(t)),f_{2}(h_{2}(t)),\ldots ,f_{n}(h_{n}(t))\big ]^{T}\in \mathbb {Q}^{n\times 1}\) and \(g\big (h(t-\tau (t))\big )=\big [g_{1}\big (h_{1}(t-\tau (t))\big ),g_{2}\big (h_{2}(t-\tau (t))\big ),\ldots ,g_{n}(h_{n}\big (t-\tau (t))\big )\big ]^{T}\in \mathbb {Q}^{n\times 1}\) denote, respectively, the vector-valued activation functions without and with time delays. \(0\le \tau (t)\le \tau ~(\tau >0)\) represents the transmission delay. \(u=(u_{1},u_{2},\ldots ,u_{n})\in \mathbb {Q}^{n\times 1}\) denotes the external input vector.

The initial value is given by

$$\begin{aligned}&h(s)=\phi (s)\in {\mathbb {Q}}^{n}, s\in [t_{0}-\tau ,t_{0}], \\&\phi (s)=\phi ^{R}(s)+i\phi ^{I}(s)+j\phi ^{J}(s)+k\phi ^{K}(s). \end{aligned}$$

Assumption 1

Let \(h=h^{R}+ih^{I}+jh^{J}+kh^{K},\) \(h^{R},h^{I},h^{J},h^{K}\in \mathbb {R}\). \(f_{q}(h)\) and \(g_{q}(h(t-\tau (t)))\) can be expressed similarly as

$$\begin{aligned} \begin{aligned} f_{q}(h)&=f^{R}_{q}(h^{R}(t))+if^{I}_{q}(h^{I(t)})\\&\quad +jf^{J}_{q}(h^{J}(t))+kf^{K}_{q}(h^{K}(t)), \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} g_{q}\big (h(t-\tau (t))\big )&=\,g^{R}_{q}\big (h^{R}(t-\tau (t))\big )+\,ig^{I}_{q}\big (h^{I}(t-\tau (t))\big )\\&\quad +jg^{J}_{q}\big (h^{J}(t-\tau (t))\big )\\&\quad +kg^{K}_{q}\big (h^{K}(t-\tau (t))\big ),\\ \end{aligned} \end{aligned}$$

where \(f^{l}_{q}(\cdot ),g^{l}_{q}(\cdot ): \mathbb {R}\rightarrow \mathbb {R}\), with \(q=1,2,\ldots ,n\) and \(l=R,I,J,K\) satisfying

$$\begin{aligned} \begin{aligned}&\big |f^{l}_{q}(h^{l})-f^{l}_{q}(\bar{h}^{l})\big |\le \lambda ^{l}_{q}\big |h^{l}-\bar{h}^{l}\big |,\\&\big |g^{l}_{q}(h^{l})-g^{l}_{q}(\bar{h}^{l})\big |\le \delta ^{l}_{q}\big |h^{l}-\bar{h}^{l}\big |,\quad \forall ~\bar{h}^{l}\in \mathbb {R},\\ \end{aligned} \end{aligned}$$

in which \(\lambda ^{l}_{q}\) and \(\delta ^{l}_{q}\) are constants. Let \(\lambda ^{l}=\mathrm {diag}(\lambda ^{l}_{1},\lambda ^{l}_{2},\cdots ,\lambda ^{l}_{n})\), and \(\delta ^{l}=\mathrm {diag}(\delta ^{l}_{1},\delta ^{l}_{2},\cdots ,\delta ^{l}_{n}).\)

Remark 1

On one hand, for CVNNs, choosing the appropriate activation functions is a big challenge for Liouville’s theorem, and kinds of conditions are given to restrict the complex-valued activation functions, such as the partial derivatives of real parts and imaginary parts of complex-valued activation functions exist and are continuous [18]. While in this paper, as shown in Assumption 1, such restrictions are not required any longer which is an improvement. On the other hand, despite the conditions about activation functions in Assumption 1 are not so mild as that in Assumption 2 in [18], they are indeed essential in (14) and (15) obtained by using Halanay inequality resulting in the concise analysis and calculations, which can be regarded as a tradeoff between the assumption on real and imaginary parts of quaternion-valued activation functions and the final criteria.

Based on Assumption 1, it is obtained from Eq. (1) that

$$\begin{aligned} \begin{aligned} \dot{h}(t)&=\dot{h}^{R}+i\dot{h}^{I}+j\dot{h}^{J}+k\dot{h}^{K}\\&=-Dh(t)+Af\big (h(t)\big )+Bg\big (h(t-\tau (t))\big )+u\\&=-D\big (h^{R}(t)+ih^{I}(t)+jh^{J}(t)+kh^{K}(t)\big )\\&\quad +\big (A^{R}+iA^{I}+jA^{J} +kA^{K}\big )\\&\quad \times \big (f^{R}(h^{R}(t))+if^{I}(h^{I}(t))\\&\quad +jf^{J}(h^{J}(t))+kf^{K}(h^{K}(t))\big )\\&\quad +\big (B^{R}+iB^{I}+jB^{J}+kB^{K}\big )\\&\quad \times \big (g^{R}(h^{R}(t-\tau (t)))+ig^{I}(h^{I}(t-\tau (t)))\\&\quad +jg^{J}(h^{J}(t-\tau (t)))+kg^{K}(h^{K}(t-\tau (t)))\big )\\&\quad +\big (u^{R}+iu^{I}+ju^{J}+ku^{K}\big ),\\ \end{aligned} \end{aligned}$$

considering the non-commutativity of quaternion multiplication resulting from Hamilton rules: \(ij=-ji=k,jk=-kj=i,ki=-ik=j, i^{2}=j^{2}=k^{2}=ijk=-1\), one can obtain from above equation that

$$\begin{aligned}&\dot{h}^{R}+i\dot{h}^{I}+j\dot{h}^{J}+k\dot{h}^{K}\\&\quad =-D\big (h^{R}(t)+ih^{I}(t)+jh^{J}(t)+kh^{K}(t)\big )\\&\qquad +\,\big (A^{R}+iA^{I}+jA^{J} +kA^{K}\big )\big (f^{R}(h^{R}(t))\\&\qquad +\,if^{I}(h^{I}(t))+jf^{J}(h^{J}(t))+kf^{K}(h^{K}(t))\big )\\&\qquad +\,\big (B^{R}+iB^{I}+jB^{J}+kB^{K}\big )\big (g^{R}(h^{R}(t-\tau (t)))\\&\qquad +\,ig^{I}(h^{I}(t-\tau (t))) +jg^{J}(h^{J}(t-\tau (t)))\\&\qquad +\,kg^{K}(h^{K}(t-\tau (t)))\big ) +\big (u^{R}+iu^{I}+ju^{J}+ku^{K}\big )\\&\quad =\big (-Dh^{R}+A^{R}f^{R}(h^{R}(t))-A^{I}f^{I}(h^{I}(t))\\&\qquad -\, A^{J}f^{J}(h^{J}(t)) -A^{K}f^{K}(h_{q}(t))\\&\qquad +\,B^{R}g^{R}(h^{R}(t-\tau (t))) -B^{I}g^{I}(h^{I}(t-\tau (t)))\\&\qquad -\,B^{J}g^{J}(h^{J}(t-\tau (t)))\\&\qquad -\,B^{K}g^{K}(h^{K}(t-\tau (t)))+u^{R}\big )\\&\qquad +\,i\big (-Dh^{I}+A^{R}f^{I}(h^{I}(t)) +A^{I}f^{R}(h^{R}(t))\\&\qquad +\, A^{J}f^{K}(h^{K}(t)) -A^{K}f^{J}(h^{J}(t))\\&\qquad +\,B^{R}g^{I}(h^{I}(t-\tau (t)))+B^{I}g^{R}(h^{R}(t-\tau (t)))\\&\qquad +\,B^{J}g^{K}(h^{K}(t-\tau (t)))\\&\qquad -\,B^{K}g^{J}(h^{J}(t-\tau (t))) +u^{I}\big )\\&\qquad +\,j\big (-Dh^{J}+A^{R}f^{J}(h^{J}(t))+A^{J}f^{R}(h^{R}(t))\\&\qquad -\, A^{I}f^{K}(h^{K}(t)) +A^{K}f^{I}(h^{I}(t))\\&\qquad +\,B^{R}g^{J}(h^{J}(t-\tau (t)))+B^{J}g^{R}(h^{R}(t-\tau (t)))\\&\qquad -\,B^{I}g^{K}(h^{K}(t-\tau (t)))\\&\qquad +\,B^{K}g^{I}(h^{I}(t-\tau (t))) +u^{J}\big )\\&\qquad +\,k\big (-Dh^{K}+A^{R}f^{K}(h^{K}(t))+A^{K}f^{R}(h^{R}(t))\\&\qquad +\, A^{I}f^{J}(h^{J}(t))\\&\qquad -\,A^{J}f^{I}(h^{I}(t)) +B^{R}g^{K}(h^{K}(t-\tau (t)))\\&\qquad +\,B^{K}g^{R}(h^{R}(t-\tau (t))) +B^{I}g^{J}(h^{J}(t-\tau (t)))\\&\qquad -\,B^{J}g^{I}(h^{I}(t-\tau (t))) +u^{K}\big ),\\ \end{aligned}$$

therefore, the four equations are established in the following:

$$\begin{aligned} \dot{h}^{R}&=-Dh^{R}+A^{R}f^{R}\big (h^{R}(t)\big )\nonumber \\&\quad -A^{I}f^{I}\big (h^{I}(t)\big )- A^{J}f^{J}\big (h^{J}(t)\big )-A^{K}f^{K}\big (h_{q}(t)\big )\nonumber \\&\quad +B^{R}g^{R}\big (h^{R}(t-\tau (t))\big )-B^{I}g^{I}\big (h^{I}(t-\tau (t))\big )\nonumber \\&\quad -B^{J}g^{J}\big (h^{J}(t-\tau (t))\big )\nonumber \\&\quad -B^{K}g^{K}\big (h^{K}(t-\tau (t))\big ) +u^{R}, \end{aligned}$$
(2)
$$\begin{aligned} \dot{h}^{I}&=-Dh^{I}+A^{R}f^{I}\big (h^{I}(t)\big )\nonumber \\&\quad +A^{I}f^{R}\big (h^{R}(t)\big )+ A^{J}f^{K}\big (h^{K}(t)\big )-A^{K}f^{J}\big (h^{J}(t)\big )\nonumber \\&\quad +B^{R}g^{I}\big (h^{I}(t-\tau (t))\big )\nonumber \\&\quad +B^{I}g^{R}\big (h^{R}(t-\tau (t))\big )+ B^{J}g^{K}\big (h^{K}(t-\tau (t))\big )\nonumber \\&\quad -B^{K}g^{J}\big (h^{J}(t-\tau (t))\big ) +u^{I}, \end{aligned}$$
(3)
$$\begin{aligned} \dot{h}^{J}&=-Dh^{J}+A^{R}f^{J}\big (h^{J}(t)\big ) +A^{J}f^{R}\big (h^{R}(t)\big )\nonumber \\&\quad - A^{I}f^{K}\big (h^{K}(t)\big )+A^{K}f^{I}\big (h^{I}(t)\big )\nonumber \\&\quad +B^{R}g^{J}\big (h^{J}(t-\tau (t))\big )+B^{J}g^{R}\big (h^{R}(t-\tau (t))\big )\nonumber \\&\quad - B^{I}g^{K}\big (h^{K}(t-\tau (t))\big )\nonumber \\&\quad +B^{K}g^{I}\big (h^{I}(t-\tau (t))\big ) +u^{J}, \end{aligned}$$
(4)
$$\begin{aligned} \dot{h}^{K}&=-Dh^{K}+A^{R}f^{K}\big (h^{K}(t)\big )\nonumber \\&\quad +A^{K}f^{R}\big (h^{R}(t)\big )+ A^{I}f^{J}\big (h^{J}(t)\big )-A^{J}f^{I}\big (h^{I}(t)\big )\nonumber \\&\quad +B^{R}g^{K}\big (h^{K}(t-\tau (t))\big )+B^{K}g^{R}\big (h^{R}(t-\tau (t))\big )\nonumber \\&\quad + B^{I}g^{J}\big (h^{J}(t-\tau (t))\big )\nonumber \\&\quad -B^{J}g^{I}\big (h^{I}(t-\tau (t))\big ) +u^{K}, \end{aligned}$$
(5)

and

$$\begin{aligned} \begin{aligned} A&=A^{R}+iA^{I}+jA^{J}+kA^{K},\\ B&=B^{R}+iB^{I}+jB^{J}+kB^{K},\\ u&=u^{R}+iu^{I}+ju^{J}+ku^{K}.\\ \end{aligned} \end{aligned}$$

On one hand, according to (2)–(5), one can obtain that

$$\begin{aligned} \begin{aligned} \dot{H}(t)&=-\mathfrak {D}H(t)+\hat{A}\hat{F}(H(t))\\&\quad +\hat{B}\hat{G}\big (H(t-\tau (t))\big )+U,\\ \end{aligned} \end{aligned}$$
(6)

where

$$\begin{aligned} \begin{aligned} \hat{A}&=\left( \begin{array}{cccc} A^{R} &{} -A^{I} &{} -A^{J} &{} -A^{K} \\ A^{I} &{} A^{R} &{} -A^{K} &{} A^{J} \\ A^{J} &{} A^{K} &{} A^{R} &{} -A^{I} \\ A^{K} &{} -A^{J} &{} A^{I} &{} A^{R} \end{array}\right) ,\\ \hat{B}&=\left( \begin{array}{cccc} B^{R} &{} -B^{I} &{} -B^{J} &{} -B^{K} \\ B^{I} &{} B^{R} &{} -B^{K} &{} B^{J} \\ B^{J} &{} B^{K} &{} B^{R} &{} -B^{I} \\ B^{K} &{} -B^{J} &{} B^{I} &{} B^{R} \end{array}\right) , \end{aligned} \end{aligned}$$
(7)

and

$$\begin{aligned} \begin{aligned}&H(t)=\big (\big (h^{R}(t)\big )^{T},\big (h^{I}(t)\big )^{T},\big (h^{J}(t)\big )^{T},\big (h^{K}(t)\big )^{T}\big )^{T},\\&U=\big (\big (u^{R}\big )^{T},\big (u^{I}\big )^{T},\big (u^{J}\big )^{T},\big (u^{K}\big )^{T}\big )^{T},\\&\mathfrak {D}=\mathrm {diag}\big (D,D,D,D\big ),\\&\hat{F}=\big (\big (f^{R}\big )^{T},\big (f^{I}\big )^{T}, \big (f^{J}\big )^{T},\big (f^{K}\big )^{T}\big )^{T},\\&\hat{G}=\big (\big (g^{R}\big )^{T},\big (g^{I}\big )^{T}, \big (g^{J}\big )^{T},\big (g^{K}\big )^{T}\big )^{T}.\\ \end{aligned} \end{aligned}$$

According to Assumption 1, it can be checked that

$$\begin{aligned} \begin{aligned} \big |\hat{F}(H^{l})-\hat{F}(\bar{H}^{l})\big |\le&\hat{\lambda }\big |H^{l}-\bar{H}^{l}\big |,\\ \big |\hat{G}(H^{l})-\hat{G}(\bar{H}^{l})\big |\le&\hat{\delta }\big |H^{l}-\bar{H}^{l}\big |,\quad \forall ~H^{l},\bar{H}^{l}\in \mathbb {R}^{4n},\\ \end{aligned} \end{aligned}$$

in which

$$\begin{aligned} \hat{\lambda }= & {} \mathrm {diag}\big (\lambda ^{R},\lambda ^{I},\lambda ^{J},\lambda ^{K}\big ), ~\hat{\delta }=\mathrm {diag}\big (\delta ^{R},\delta ^{I},\delta ^{J},\delta ^{K}\big ).\nonumber \\ \end{aligned}$$
(8)

On the other hand, it is obtained from (2) to (5) that

$$\begin{aligned} \dot{H}(t)= & {} -\mathfrak {D}H(t)+A_{1}\mathfrak {f}_{1}(H(t))\nonumber \\&+\,A_{2}\mathfrak {f}_{2}(H(t))+A_{3}\mathfrak {f}_{3}(H(t))+A_{4}\mathfrak {f}_{4}(H(t))\nonumber \\&+\,B_{1}\mathfrak {g}_{1}\big (H(t-\tau (t))\big ) +B_{2}\mathfrak {g}_{2}\big (H(t-\tau (t))\big )\nonumber \\&+\,B_{3}\mathfrak {g}_{3}\big (H(t-\tau (t))\big )\nonumber \\&+\,B_{4}\mathfrak {g}_{4}\big (H(t-\tau (t))\big )+U,\nonumber \\ \end{aligned}$$
(9)

where

$$\begin{aligned}&H(t)=\big (\big (h^{R}(t)\big )^{T},\big (h^{I}(t)\big )^{T},\big (h^{J}(t)\big )^{T},\big (h^{K}(t)\big )^{T}\big )^{T},\nonumber \\&\mathfrak {D}=\mathrm {diag}\big (D,D,D,D\big ),\nonumber \\&A_{1}=\mathrm {diag}\big (A^{R},A^{I},A^{J},A^{K}\big ),\nonumber \\&A_{2}=\mathrm {diag}\big (-A^{I},A^{R},A^{K},-A^{J}\big ),\nonumber \\&A_{3}=\mathrm {diag}\big (-A^{J},-A^{K},A^{R},A^{I}\big ),\nonumber \\&A_{4}=\mathrm {diag}\big (-A^{K},A^{J},-A^{I},A^{R}\big ),\nonumber \\&B_{1}=\mathrm {diag}\big (B^{R},B^{I},B^{J},B^{K}\big ),\nonumber \\&B_{2}=\mathrm {diag}\big (-B^{I},B^{R},B^{K},-B^{J}\big ),\nonumber \\&B_{3}=\mathrm {diag}\big (-B^{J},-B^{K},B^{R},B^{I}\big ),\nonumber \\&B_{4}=\mathrm {diag}\big (-B^{K},B^{J},-B^{I},B^{R}\big ),\nonumber \\&U=\big (\big (u^{R}\big )^{T},\big (u^{I}\big )^{T},\big (u^{J}\big )^{T},\big (u^{K}\big )^{T}\big )^{T},\nonumber \\&\mathfrak {f}_{1}(H(t))=\big (\big (f^{R}(h^{R}(t))\big )^{T},\big (f^{R}(h^{R}(t))\big )^{T},\nonumber \\&\quad \big (f^{R}(h^{R}(t))\big )^{T}, \big (f^{R}(h^{R}(t))\big )^{T}\big )^{T},\nonumber \\&\mathfrak {f}_{2}\big (H(t)\big )=\big (\big (f^{I}(h^{I}(t))\big )^{T},\big (f^{I}(h^{I}(t))\big )^{T},\nonumber \\&\quad \big (f^{I}(h^{I}(t))\big )^{T}, \big (f^{I}(h^{I}(t))\big )^{T}\big )^{T},\nonumber \\&\mathfrak {f}_{3}\big (H(t)\big )=\big (\big (f^{J}(h^{J}(t))\big )^{T}, \big (f^{J}(h^{J}(t))\big )^{T},\nonumber \\&\quad \big (f^{J}(h^{J}(t))\big )^{T},\big (f^{J}(h^{J}(t))\big )^{T}\big )^{T},\nonumber \\&\mathfrak {f}_{4}\big (H(t)\big )=\big (\big (f^{K}(h^{K}(t))\big )^{T},\nonumber \\&\quad \big (f^{K}(h^{K}(t))\big )^{T},\big (f^{K}(h^{K}(t))\big )^{T}, \big (f^{K}(h^{K}(t))\big )^{T}\big )^{T},\nonumber \\&\mathfrak {g}_{1}\big (H(t-\tau (t))\big )=\begin{pmatrix}\breve{g}^{R}\\ \breve{g}^{R}\\ \breve{g}^{R}\\ \breve{g}^{R}\end{pmatrix}, ~\mathfrak {g}_{2}\big (H(t-\tau (t))\big )=\begin{pmatrix}\breve{g}^{I}\\ \breve{g}^{I}\\ \breve{g}^{I}\\ \breve{g}^{I}\end{pmatrix},\nonumber \\&\mathfrak {g}_{3}\big (H(t-\tau (t))\big )=\begin{pmatrix}\breve{g}^{J}\\ \breve{g}^{J}\\ \breve{g}^{J}\\ \breve{g}^{J}\end{pmatrix}, ~\mathfrak {g}_{4}\big (H(t-\tau (t))\big )=\begin{pmatrix}\breve{g}^{K}\\ \breve{g}^{K}\\ \breve{g}^{K}\\ \breve{g}^{K}\end{pmatrix}.\nonumber \\&\breve{g}^{R}=g^{R}\big (h^{R}(t-\tau (t))\big ),\breve{g}^{I}=g^{I}\big (h^{I}(t-\tau (t))\big ),\nonumber \\&\breve{g}^{J}=g^{J}\big (h^{J}(t-\tau (t))\big ),\breve{g}^{K}=g^{K}\big (h^{K}(t-\tau (t))\big ), \end{aligned}$$

Similarly, the initial values for system (9) can be expressed in the following forms,

$$\begin{aligned} H(s)=\varPhi (s),\quad s\in [t_{0}-\tau ,t_{0}], \end{aligned}$$

where \(\varPhi (s)=\big (\big (\phi ^{R}(s)\big )^{T},\big (\phi ^{I}(s)\big )^{T},\big (\phi ^{J}(s)\big )^{T},\big (\phi ^{K}(s)\big )^{T}\big )^{T}\), and \(\phi ^{l}(s)\in C\big ([t_{0}-\tau ,t_{0}],\mathbb {R}^{n}\big )\), \(l=R,I,J,K\).

As shown above, we obtain real-valued system (9) by introducing the augmented vectors H, U, and the augmented matrices \(\mathfrak {D}\), \(A_{1}\), \(A_{2}\), \(A_{3}\), \(A_{4}\), \(B_{1}\), \(B_{2}\), \(B_{3}\), \(B_{4}\), and the augmented functions \(\mathfrak {f}_{1}\big (H(t)\big )\), \(\mathfrak {f}_{2}\big (H(t)\big )\), \(\mathfrak {f}_{3}\big (H(t)\big )\), \(\mathfrak {f}_{4}\big (H(t)\big )\), \(\mathfrak {g}_{1}\big (H(t-\tau (t))\big )\), \(\mathfrak {g}_{2}\big (H(t-\tau (t))\big )\), \(\mathfrak {g}_{3}\big (H(t-\tau (t))\big )\), \(\mathfrak {g}_{4}\big (H(t-\tau (t))\big )\).

Suppose \(\hat{H}=\big (\big (\hat{h}^{R}\big )^{T},\big (\hat{h}^{I}\big )^{T},\big (\hat{h}^{J}\big )^{T},\big (\hat{h}^{K}\big )^{T}\big )^{T}\) is an equilibrium point of real-valued system (9). By transformation \(W(t)=H(t)-\hat{H}\), one can get the following vector form of real-valued system (9):

$$\begin{aligned} \dot{W}(t)= & {} -\mathfrak {D}W(t)+A_{1}F_{1}\big (W(t)\big ) +A_{2}F_{2}\big (W(t)\big )\nonumber \\&+\,A_{3}F_{3}\big (W(t)\big )+A_{4}F_{4}\big (W(t)\big )\nonumber \\&+\,B_{1}G_{1}\big (W(t-\tau (t))\big )+B_{2}G_{2}\big (W(t-\tau (t))\big )\nonumber \\&+\,B_{3}G_{3}\big (W(t-\tau (t))\big )\nonumber \\&+\,B_{4}G_{4}\big (W(t-\tau (t))\big ), \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{aligned}&F_{1}\big (W(t)\big )=\mathfrak {f}_{1}\big (W(t)+\hat{H}\big ) -\mathfrak {f}_{1}\big (\hat{H}\big ),\\&F_{2}\big (W(t)\big )=\mathfrak {f}_{2}\big (W(t)+\hat{H}\big )-\mathfrak {f}_{2}\big (\hat{H}\big ),\\&F_{3}\big (W(t)\big )=\mathfrak {f}_{3}\big (W(t)+\hat{H}\big )-\mathfrak {f}_{3}\big (\hat{H}\big ),\\&F_{4}\big (W(t)\big )=\mathfrak {f}_{4}\big (W(t)+\hat{H}\big )-\mathfrak {f}_{4}\big (\hat{H}\big ),\\&G_{1}\big (W(t-\tau (t))\big )=\mathfrak {g}_{1}\big (W(t-\tau (t))+\hat{H}\big )-\mathfrak {g}_{1}\big (\hat{H}\big ),\\&G_{2}\big (W(t-\tau (t))\big )=\mathfrak {g}_{2}\big (W(t-\tau (t))+\hat{H}\big )-\mathfrak {g}_{2}\big (\hat{H}\big ),\\&G_{3}\big (W(t-\tau (t))\big )=\mathfrak {g}_{3}\big (W(t-\tau (t))+\hat{H}\big )-\mathfrak {g}_{3}\big (\hat{H}\big ),\\&G_{4}\big (W(t-\tau (t))\big )=\mathfrak {g}_{4}\big (W(t-\tau (t))+\hat{H}\big )-\mathfrak {g}_{4}\big (\hat{H}\big )\\ \end{aligned} \end{aligned}$$

It is clear that the stability of the origin for real-valued system (10) is equivalent to that of the equilibrium point for real-valued system (9), the real-valued system (6), as well as QVNN (1).

Definition 1

A constant vector \(\hat{h}=(\hat{h}_{1},\hat{h}_{2},\ldots ,\hat{h}_{n})^{T}\) is called an equilibrium point of QVNN (1), if

$$\begin{aligned} -D\hat{h}+Af\big (\hat{h}\big )+Bg\big (\hat{h}\big )+u=0. \end{aligned}$$

Definition 2

The unique equilibrium point \(\hat{H}\) of real-valued system (9) is said to be globally exponentially stable if there exist constants \(c_{1},c_{2}>0\) such that

$$\begin{aligned} \big \Vert H(t)-\hat{H}\big \Vert _{p}\le c_{1}\big \Vert \phi -\hat{H}\big \Vert _{p}e^{-c_{2}(t-t_{0})},~t\ge t_{0}. \end{aligned}$$

Definition 3

[32] The matrix measure of a real square matrix \(A=(a_{kj})_{n\times n}\) is defined as follows:

$$\begin{aligned} \mu _{p}(A)=\lim _{\varepsilon \rightarrow 0^{+}}\frac{\big \Vert I+\varepsilon A\big \Vert _{p}-1}{\varepsilon }, \end{aligned}$$

where \(\Vert \cdot \Vert _{p}\) is an induced matrix norm on \(\mathbb {R}^{n\times n}\), I is the identity matrix and \(p=1,2,\infty \).

Definition 4

[33] Let matrix \(A=(a_{ij})_{n\times n}\) have non-positive off-diagonal elements, then A is a non-singular M-matrix if one of the following conditions holds:

  1. (i)

    All principal minors of A are positive;

  2. (ii)

    A have all positive diagonal elements, and there exists a positive diagonal matrix \(\varLambda =\mathrm {diag}(\varLambda _{1},\varLambda _{2},\ldots ,\varLambda _{n})\) such that \(A\varLambda \) is strictly diagonally dominant; that is,

    $$\begin{aligned} a_{ii}\varLambda _{i}>\sum _{j\ne i}|a_{ij}|\varLambda _{j},\quad i=1,2,\ldots ,n, \end{aligned}$$

    which can be rewritten

    $$\begin{aligned} \sum _{j=1}^{n}a_{ij}\varLambda _{j}>0,\quad i=1,2,\cdots ,n. \end{aligned}$$

As known that several matrix norms above can be respectively presented as

$$\begin{aligned} \begin{aligned} \Vert A\Vert _{\infty }&=\max _{k}\sum ^{n}_{j=1}|a_{kj}|, \Vert A\Vert _{1}=\max _{j}\sum ^{n}_{k=1}|a_{kj}|,\\ \Vert A\Vert _{2}&=\sqrt{\lambda _{\max }(A^{T}A)}, \end{aligned} \end{aligned}$$

and the corresponding matrix measures are presented as follows

$$\begin{aligned} \begin{aligned} \mu _{\infty }(A)&=\max _{k}\left\{ a_{kk}+\sum ^{n}_{j=1,j\ne k}|a_{kj}| \right\} ,\mu _{1}(A)\\&=\max _{j}\left\{ a_{jj}+\sum ^{n}_{k=1,k\ne j}|a_{kj}|\right\} ,\\ \mu _{2}(A)&=\frac{1}{2}\lambda _{\max }(A^{T}+A).\\ \end{aligned} \end{aligned}$$

Next, a useful lemma known as Halanay inequality is given in the following which turns out to be the kernel of this paper.

Lemma 1

[32] Let \(k_{1}\) and \(k_{2}\) be constants with \(k_{1}>k_{2}>0\), and y(t) is a nonnegative continuous function defined on \([t_{0}-\tau ,+\infty )\) which satisfies the following inequality for \(t\ge t_{0}\),

$$\begin{aligned} D^{+}\big (y(t)\big )\le -k_{1}y(t)+k_{2}\bar{y}(t), \end{aligned}$$

where \(\bar{y}(t)\triangleq \sup _{t-\tau \le s\le t}y(s)\). Then the inequality

$$\begin{aligned} y(t)\le \bar{y}(t)e^{-r(t-t_{0})} \end{aligned}$$

holds for \(t\ge t_{0}\), where r is a bound on the exponential convergence rate and is the unique positive solution of \(r=k_{1}-k_{2}e^{r\tau }\), and the upper-right Dini derivative \(D^{+}y(t)\) is defined as

$$\begin{aligned} D^{+}y(t)=\overline{\lim }_{h\rightarrow 0^{+}}\frac{y(t+h)-y(t)}{h}, \end{aligned}$$

in which \(h\rightarrow 0^{+}\) means that h approaches to 0 from the right-hand side.

Remark 2

As shown above, Halanay inequality is the key of the research. In this paper, the global exponential stability problem of QVNNs is investigated. On one hand, multiplication of quaternion is not commutative due to Hamilton rules: \(ij=-ji=k,jk=-kj=i,ki=-ik=j, i^{2}=j^{2}=k^{2}=ijk=-1\); therefore, the analysis for the equation of state becomes difficult. In order to avoid the non-commutativity of quaternion multiplication, the QVNN can be decomposed into four real-valued systems, and then the vector form of the four real-valued systems is shown in (6), (9) or (10). On the other hand, without using any Lyapunov functional [8, 18, 29, 34–36], Halanay inequality is applied to the real-valued vector system (10) based on the definition of matrix norms. Then the inequality \(\big \Vert W(t)\big \Vert _{p}\le \sup _{t-\tau \le \eta \le t}\big \Vert W(\eta )\big \Vert _{p}e^{-\varpi (t-t_{0})},~~t\ge t_{0}\) is established, where \(\varpi \) is the unique positive solution of the equation \(\varpi =T_{1}-T_{2}e^{\varpi \tau }\) under the given conditions in Theorem 1, that is, \(\big \Vert W(t)\big \Vert _{p}\rightarrow 0\), \(t\rightarrow \infty \). Therefore, real-valued system (10) is globally exponentially stable.

3 Main results

In this section, some criteria for the exponential stability of QVNN (1) are presented with the matrix measure method and the Halanay inequality technique.

Theorem 1

Assume that Assumption 1 holds. Real-valued system (10) has a unique equilibrium point \(\hat{H}\) which is globally exponentially stable, if the following conditions hold:

(i) \(\mathfrak {D}-|\hat{A}|\hat{\lambda }-|\hat{B}|\hat{\delta }\) is a non-singular M-matrix;

$$\begin{aligned} \begin{aligned} (ii)~&-\mu _{p}(-\mathfrak {D})-4^{\frac{1}{p}}\lambda ^{R}\Vert A_{1}\Vert _{p}-4^{\frac{1}{p}}\lambda ^{I}\Vert A_{2}\Vert _{p}\\&\quad -4^{\frac{1}{p}}\lambda ^{J}\Vert A_{3}\Vert _{p}-4^{\frac{1}{p}}\lambda ^{K}\Vert A_{4}\Vert _{p}\\&\quad>4^{\frac{1}{p}}\delta ^{R}\Vert B_{1}\Vert _{p}+4^{\frac{1}{p}}\delta ^{I}\Vert B_{2}\Vert _{p}\\&\quad +4^{\frac{1}{p}}\delta ^{J}\Vert B_{3}\Vert _{p}+4^{\frac{1}{p}}\delta ^{K}\Vert B_{4}\Vert _{p}>0,~p=1,2,\infty ;\\ \end{aligned} \end{aligned}$$
(11)

where \(\hat{A},\hat{B},\hat{\lambda },\hat{\delta }\) are expressed by (7), (8), respectively, and \(\lambda ^{l}=\max _{1\le q\le n}\{\lambda ^{l}_{q}\}\), \(\delta ^{l}=\max _{1\le q\le n}\{\delta ^{l}_{q}\}\), and \(l=R,I,J,K\).

Proof

First, based on Assumption 1, the proof of the existence and uniqueness of the equilibrium point of real-valued system (10) can be found in Theorem 1 in [33] under (i), and thus it is omitted here. Then, the global exponential stability of the unique equilibrium point is proved in the following.

According to Lemma 1, one can obtain that

$$\begin{aligned} \begin{aligned}&D^{+}\Vert W(t)\Vert _{p}\\&\quad =\overline{\lim }_{\zeta \rightarrow 0^{+}}\frac{\Vert W(t+\zeta )\Vert _{p}-\Vert W(t)\Vert _{p}}{\zeta }\\&\quad =\overline{\lim }_{\zeta \rightarrow 0^{+}}\frac{\big \Vert W(t)+\zeta \dot{W}(t)+o(\zeta )\big \Vert _{p}-\Vert W(t)\Vert _{p}}{\zeta },\\ \end{aligned} \end{aligned}$$
(12)

where

$$\begin{aligned} \big \Vert W(t)+ & {} \zeta \dot{W}(t)+o(\zeta )\big \Vert _{p}\nonumber \\&=\big \Vert W(t)+o(\zeta )+\zeta \big [-\mathfrak {D}W(t)\nonumber \\&\quad +\,A_{1}F_{1}(W(t))+A_{2}F_{2}(W(t))\nonumber \\&\quad +\,A_{3}F_{3}(W(t))+A_{4}F_{4}(W(t))\nonumber \\&\quad +\,B_{1}G_{1}\big (W(t-\tau (t))\big )\nonumber \\&\quad +\,B_{2}G_{2}\big (W(t-\tau (t))\big )\nonumber \\&\quad +\,B_{3}G_{3}\big (W(t-\tau (t))\big )\nonumber \\&\quad +\,B_{4}G_{4}\big (W(t-\tau (t))\big )\big ]\big \Vert _{p}\nonumber \\&=\big \Vert W(t)+o(\zeta )+\zeta \big (-\mathfrak {D}\big )W(t)\nonumber \\&\quad +\,\zeta A_{1}F_{1}(W(t))+\zeta A_{2}F_{2}(W(t))\nonumber \\&\quad +\,\zeta A_{3}F_{3}(W(t))+\zeta A_{4}F_{4}(W(t))\nonumber \\&\quad +\,\zeta B_{1}G_{1}\big (W(t-\tau (t))\big )\nonumber \\&\quad +\,\zeta B_{2}G_{2}\big (W(t-\tau (t))\big )\\&\quad +\,\zeta B_{3}G_{3}\big (W(t-\tau (t))\big )\nonumber \\&\quad +\,\zeta B_{4}G_{4}\big (W(t-\tau (t))\big )\big \Vert _{p}\nonumber \\&\le \Vert o(\zeta )\Vert _{p}+\big \Vert I+\zeta \big (-\mathfrak {D}\big )\nonumber \\&\quad \times \,\big \Vert _{p}\Vert W(t)\Vert _{p}+\zeta \Vert A_{1}\Vert _{p}\Vert F_{1}(W(t))\Vert _{p}\nonumber \\&\quad +\,\zeta \Vert A_{2}\Vert _{p}\Vert F_{2}(W(t))\Vert _{p}\nonumber \\&\quad +\,\zeta \Vert A_{1}\Vert _{p}\Vert F_{1}(W(t))\Vert _{p}\nonumber \\&\quad +\,\zeta \Vert A_{2}\Vert _{p}\Vert F_{2}(W(t))\Vert _{p}\nonumber \\&\quad +\,\zeta \Vert B_{1}\Vert _{p}\big \Vert G_{1}\big (W(t-\tau (t))\big )\big \Vert _{p}\nonumber \\&\quad +\,\zeta \Vert B_{2}\Vert _{p}\big \Vert G_{2}\big (W(t-\tau (t))\big )\big \Vert _{p}\nonumber \\&\quad +\,\zeta \Vert B_{3}\Vert _{p}\big \Vert G_{3}\big (W(t-\tau (t))\big )\big \Vert _{p}\nonumber \\&\quad +\,\zeta \Vert B_{4}\Vert _{p}\big \Vert G_{4}\big (W(t-\tau (t))\big )\big \Vert _{p}.\nonumber \end{aligned}$$
(13)

Denote

$$\begin{aligned} \begin{aligned} W(t)=H(t)-\hat{H}=&\begin{pmatrix}h^{R}(t)-\hat{h}^{R}\\ h^{I}(t)-\hat{h}^{I}\\ h^{J}(t)-\hat{h}^{J}\\ h^{K}(t)-\hat{h}^{K}\end{pmatrix} =\begin{pmatrix}\tilde{h}^{R}(t)\\ \tilde{h}^{I}(t)\\ \tilde{h}^{J}(t)\\ \tilde{h}^{K}(t)\end{pmatrix},\\ \end{aligned} \end{aligned}$$

then combined with Assumption 1 and the definition of \(F_{1}(W(t))\), it is obtained that

$$\begin{aligned} \begin{aligned}&\Vert F_{1}(W(t))\Vert _{p}=\big \Vert \mathfrak {f}_{1}\big (W(t)+\hat{H}\big )-\mathfrak {f}_{1}(\hat{H})\big \Vert _{p}\\&\quad = \left\| \begin{pmatrix}f^{R}\big (\tilde{h}^{R}(t)+\hat{h}^{R}\big )-f^{R}\big (\hat{h}^{R}\big ) \\ f^{R}\big (\tilde{h}^{R}(t)+\hat{h}^{R}\big )-f^{R}\big (\hat{h}^{R}\big ) \\ f^{R}\big (\tilde{h}^{R}(t)+\hat{h}^{R}\big )-f^{R}\big (\hat{h}^{R}\big ) \\ f^{R}\big (\tilde{h}^{R}(t)+\hat{h}^{R}\big )-f^{R}\big (\hat{h}^{R}\big )\end{pmatrix}\right\| _{p}\\&\quad =\left( 4\sum ^{n}_{q=1}\big |f^{R}_{q}\big (\tilde{h}^{R}_{q}(t)+\hat{h}^{R}_{q}\big )-f^{R}_{q}(\hat{h}^{R}_{q})\big |^{p}\right) ^{\frac{1}{p}}\\&\quad \le \left( 4\sum ^{n}_{q=1}\big (\lambda ^{R}_{q}\big )^{p}\big |\tilde{h}^{R}_{q}(t)\big |^{p}\right) ^{\frac{1}{p}} \le 4^{\frac{1}{p}}\lambda ^{R}\big \Vert \tilde{h}^{R}(t)\big \Vert _{p}\\&\quad \le 4^{\frac{1}{p}}\lambda ^{R}\Vert W(t)\Vert _{p}. \end{aligned} \end{aligned}$$
(14)

Similarly, one can get that

$$\begin{aligned}&\Vert F_{2}(W(t))\Vert _{p}\le 4^{\frac{1}{p}}\lambda ^{I}\Vert W(t)\Vert _{p},\nonumber \\&\Vert F_{3}(W(t))\Vert _{p}\le 4^{\frac{1}{p}}\lambda ^{J}\Vert W(t)\Vert _{p},\nonumber \\&\Vert F_{4}(W(t))\Vert _{p}\le 4^{\frac{1}{p}}\lambda ^{K}\Vert W(t)\Vert _{p},\nonumber \\&\Vert G_{1}(W(t))\Vert _{p}\le 4^{\frac{1}{p}}\lambda ^{R}\Vert W(t-\tau (t))\Vert _{p},\\&\Vert G_{2}(W(t))\Vert _{p}\le 4^{\frac{1}{p}}\lambda ^{I}\big \Vert W\big (t-\tau (t)\big )\big \Vert _{p},\nonumber \\&\Vert G_{3}(W(t))\Vert _{p}\le 4^{\frac{1}{p}}\lambda ^{J}\big \Vert W\big (t-\tau (t)\big )\big \Vert _{p},\nonumber \\&\Vert G_{4}(W(t))\Vert _{p}\le 4^{\frac{1}{p}}\lambda ^{K}\big \Vert W\big (t-\tau (t)\big )\big \Vert _{p}.\nonumber \end{aligned}$$
(15)

Then Definition 3, (12), (13), (14) and (15) yield that

$$\begin{aligned} \begin{aligned}&D^{+}\Vert W(t)\Vert _{p}\\&\quad =\overline{\lim }_{\zeta \rightarrow 0^{+}}\frac{\Vert W(t+\zeta )\Vert _{p}-\Vert W(t)\Vert _{p}}{\zeta }\\&\quad \le \overline{\lim }_{\zeta \rightarrow 0^{+}}\frac{\Vert I+\zeta (-\mathfrak {D})\Vert _{p}-1}{\zeta }\Vert W(t)\Vert _{p}\\&\qquad +\Vert A_{1}\Vert _{p}\Vert F_{1}(W(t))\Vert _{p} +\Vert A_{2}\Vert _{p}\Vert F_{2}(W(t))\Vert _{p}\\&\qquad +\Vert A_{1}\Vert _{p}\Vert F_{1}(W(t))\Vert _{p}+\Vert A_{2}\Vert _{p}\\&\qquad \times \Vert F_{2}(W(t))\Vert _{p} +\Vert B_{1}\Vert _{p}\big \Vert G_{1}\big (W(t-\tau (t))\big )\big \Vert _{p}\\&\qquad +\Vert B_{2}\Vert _{p}\big \Vert G_{2}\big (W(t-\tau (t))\big )\big \Vert _{p}\\&\qquad +\Vert B_{3}\Vert _{p}\big \Vert G_{3}\big (W(t-\tau (t))\big )\big \Vert _{p}\\&\qquad +\Vert B_{4}\Vert _{p}\big \Vert G_{4}\big (W(t-\tau (t))\big )\big \Vert _{p}\\&\quad \le \mu _{p}(-\mathfrak {D})\Vert W(t)\Vert _{p}+4^{\frac{1}{p}}\Vert A_{1}\Vert _{p}\lambda ^{R}\Vert W(t)\Vert _{p}\\&\qquad +4^{\frac{1}{p}}\Vert A_{2}\Vert _{p}\lambda ^{I}\Vert W(t)\Vert _{p} +4^{\frac{1}{p}}\Vert A_{3}\Vert _{p}\lambda ^{J}\Vert W(t)\Vert _{p}\\&\qquad +4^{\frac{1}{p}}\Vert A_{4}\Vert _{p}\lambda ^{K}\Vert W(t)\Vert _{p}\\&\qquad +4^{\frac{1}{p}}\Vert B_{1}\Vert _{p}\delta ^{R}\big \Vert W\big (t-\tau (t)\big )\big \Vert _{p}\\&\qquad +4^{\frac{1}{p}}\Vert B_{2}\Vert _{p}\delta ^{I}\big \Vert W\big (t-\tau (t)\big )\big \Vert _{p}\\&\qquad +4^{\frac{1}{p}}\Vert B_{3}\Vert _{p}\delta ^{J}\big \Vert W\big (t-\tau (t)\big )\big \Vert _{p}\\&\qquad +4^{\frac{1}{p}}\Vert B_{4}\Vert _{p}\delta ^{K}\big \Vert W\big (t-\tau (t)\big )\big \Vert _{p}\\&\qquad \le \big (\mu _{p}(-\mathfrak {D})+4^{\frac{1}{p}}\lambda ^{R}\Vert A_{1}\Vert _{p}+4^{\frac{1}{p}}\lambda ^{I}\Vert A_{2}\Vert _{p}\\&\qquad +4^{\frac{1}{p}}\lambda ^{J}\Vert A_{3}\Vert _{p} +4^{\frac{1}{p}}\lambda ^{K}\Vert A_{4}\Vert _{p}\big )\big \Vert W(t)\big \Vert _{p}\\&\qquad +\big (4^{\frac{1}{p}}\delta ^{R}\Vert B_{1}\Vert _{p}+4^{\frac{1}{p}}\delta ^{I}\Vert B_{2}\Vert _{p}\\&\qquad +4^{\frac{1}{p}}\delta ^{J}\Vert B_{3}\Vert _{p} +4^{\frac{1}{p}}\delta ^{K}\Vert B_{4}\Vert _{p}\big )\sup _{t-\tau \le \eta \le t}\big \Vert W(\eta )\big \Vert _{p}.\\ \end{aligned} \end{aligned}$$

That is to say,

$$\begin{aligned} D^{+}\Vert W(t)\Vert _{p}\le & {} \big (\mu _{p}(-\mathfrak {D})+4^{\frac{1}{p}}\lambda ^{R}\Vert A_{1}\Vert _{p}\nonumber \\&+\,4^{\frac{1}{p}}\lambda ^{I}\Vert A_{2}\Vert _{p} +4^{\frac{1}{p}}\lambda ^{J}\Vert A_{3}\Vert _{p}\nonumber \\&+\,4^{\frac{1}{p}}\lambda ^{K}\Vert A_{4}\Vert _{p}\big )\big \Vert W(t)\big \Vert _{p}\nonumber \\&+\,\big (4^{\frac{1}{p}}\delta ^{R}\Vert B_{1}\Vert _{p}+4^{\frac{1}{p}}\delta ^{I}\Vert B_{2}\Vert _{p}\nonumber \\&+\,4^{\frac{1}{p}}\delta ^{J}\Vert B_{3}\Vert _{p} +4^{\frac{1}{p}}\delta ^{K}\Vert B_{4}\Vert _{p}\big )\nonumber \\&\times \sup _{t-\tau \le \eta \le t}\big \Vert W(\eta )\big \Vert _{p}. \end{aligned}$$
(16)

Define

$$\begin{aligned} \begin{aligned} T_{1}&=-\mu _{p}(-\mathfrak {D})-4^{\frac{1}{p}}\lambda ^{R}\Vert A_{1}\Vert _{p}\\&\quad -4^{\frac{1}{p}}\lambda ^{I}\Vert A_{2}\Vert _{p} -4^{\frac{1}{p}}\lambda ^{J}\Vert A_{3}\Vert _{p}-4^{\frac{1}{p}}\lambda ^{K}\Vert A_{4}\Vert _{p},\\ T_{2}&=4^{\frac{1}{p}}\delta ^{R}\Vert B_{1}\Vert _{p}+4^{\frac{1}{p}}\delta ^{I}\Vert B_{2}\Vert _{p}\\&\quad +4^{\frac{1}{p}}\delta ^{J}\Vert B_{3}\Vert _{p}+4^{\frac{1}{p}}\delta ^{K}\Vert B_{4}\Vert _{p},\\ \end{aligned} \end{aligned}$$

then we can get that \(T_{1}>T_{2}>0\) from (11). It follows from Lemma 1 and (16) that

$$\begin{aligned} \begin{aligned} \Vert W(t)\Vert _{p}\le \sup _{t-\tau \le \eta \le t}\Vert W(\eta )\Vert _{p}e^{-\varpi (t-t_{0})},~~t\ge t_{0}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \varpi&=T_{1}-T_{2}e^{\varpi \tau }\\&=-\mu _{p}(-\mathfrak {D})-4^{\frac{1}{p}}\lambda ^{R}\Vert A_{1}\Vert _{p}-4^{\frac{1}{p}}\lambda ^{I}\Vert A_{2}\Vert _{p}\\&\quad -4^{\frac{1}{p}}\lambda ^{J}\Vert A_{3}\Vert _{p}-4^{\frac{1}{p}}\lambda ^{K}\Vert A_{4}\Vert _{p}\\&\quad -\big (4^{\frac{1}{p}}\delta ^{R}\Vert B_{1}\Vert _{p}+4^{\frac{1}{p}}\delta ^{I}\Vert B_{2}\Vert _{p}\\&\quad +4^{\frac{1}{p}}\delta ^{J}\Vert B_{3}\Vert _{p}+4^{\frac{1}{p}}\delta ^{K}\Vert B_{4}\Vert _{p}\big )e^{\varpi \tau }.\\ \end{aligned} \end{aligned}$$
(17)

Consequently, real-valued system (10) is globally exponentially stable by Definition 2. \(\square \)

Remark 3

In fact, \(\varpi \) is the unique positive solution of the Eq. (17), i.e., \(\varpi =T_{1}-T_{2}e^{\varpi \tau }\) presented in above proof. Consider the equation

$$\begin{aligned} \theta -T_{1}+T_{2}e^{\theta \tau }=0, \end{aligned}$$

and define

$$\begin{aligned} \varDelta (\theta )=\theta -T_{1}+T_{2}e^{\theta \tau }, \quad \theta \in [0,T_{1}]. \end{aligned}$$

Based on the conditions presented in Theorem 1, it is easy to verify that \(\varDelta (0)=-T_{1}+T_{2}<0\) and \(\varDelta (T_{1})=T_{2}e^{T_{1}\tau }>0\). Moreover, \(\varDelta '(\theta )=1+T_{2}\tau e^{\theta \tau }>0\), that is, \(\varDelta (\theta )\) is a strictly monotone increasing function. Therefore, there is a unique \(\varpi \) on \((0,T_{1})\) satisfying the equation aforementioned, which is a boundary of the exponential convergence rate mentioned in Lemma 1.

Remark 4

As shown in Theorem 1, QVNN (1) is separated into four real-valued systems, forming an equivalent real-valued system. Combined with the matrix measure method and the Halanay inequality technique, some criteria for the global exponential stability of QVNN (1) are derived. Indeed, these criteria obtained from the view of matrix measure are concise, and Halanay inequality makes the analytical process more compact compared with the Lyapunov function with a lot of tedious integral calculations. For example, in [37], the authors investigate the global robust stability of the uncertain stochastic neural networks with delays combined with Lyapunov function and linear matrix inequality. In [36], the global exponential stability for CVNNs with asynchronous time delays are studied via three generalized norms, and some criteria are presented for the considered CVNNs. Furthermore, the matrix norm can only have nonnegative values, while the matrix measure can have positive values as well as negative values. In general, \(\mu _{p}(A)\ne \mu _{p}(-A)\), whereas \(\Vert A\Vert _{p}\equiv \Vert -A\Vert _{p}\), so our results are more precise than that by matrix norms in [36].

Remark 5

Due to the practical importance and extensive applications in various domain including data mining, aerospace, parallel computing, signal filtering, telecommunications and robotic, various neural networks have been investigated with different methods in the past few year mainly for the stability problem and synchronization problem. In [38–42], the authors consider the stability problem for the delayed neural networks via the methods of Lyapunov function and Lyapunov–Krasovskii functional, as well as the matrix inequalities technique with a great deal of integral calculations. For example, [39, 41] consider the stability for delayed neural networks, where the stability criteria are established by multiple Lyapunov functions and linear matrix inequalities. [38, 40–42] investigate the stability problem of the delayed neural networks with Lyapunov–Krasovskii functionals and some matrix inequalities, based on which, the obtained conditions are given in terms of high-dimensional matrices. As an extension of QVNNs, the stability problem of Clifford-valued recurrent neural networks has been studied in [9], where the Lyapunov–Krasovskii functional method and the linear matrix inequality technique are also used. While in this paper, instead of using the methods above, the Halanay inequality is applied to investigate the considered neural networks, which can help to avoid a large amount of tedious calculations and the high-dimensional matrices.

4 Example

In this section, a numerical example is provided to illustrate the effectiveness of the proposed method.

Example 1

Consider a two-dimensional QVNN with time-varying delays:

$$\begin{aligned} \dot{h}(t)=-Dh(t)+Af(h(t))+Bg\big (h(t-\tau (t))\big )+u, \end{aligned}$$
(18)

where \(h=h^{R}+ih^{I}+jh^{J}+kh^{K}\in \mathbb {Q}^{2\times 1}\),

$$\begin{aligned} \begin{aligned} A=&\left( \begin{array}{l@{\quad }c} -0.1-0.5i-0.1j-0.5k&{}~-0.4+0.2i-0.4j+0.2k\\ -0.3+0.1i-0.1j+0.1k&{}~-0.6-0.1i-0.1j-0.1k\\ \end{array}\right) \\ =&\left( \begin{array}{l@{\quad }c} -0.1&{}-0.4\\ -0.3&{}-0.6\\ \end{array} \right) +i\left( \begin{array}{l@{\quad }c} -0.5&{}0.2\\ 0.1&{}-0.1\\ \end{array} \right) +j\left( \begin{array}{l@{\quad }c} -0.1&{}-0.4\\ -0.1&{}-0.1\\ \end{array} \right) \\&+k\left( \begin{array}{l@{\quad }c} -0.5&{}0.2\\ 0.1&{}-0.1\\ \end{array} \right) \\ =&\,A^{R}+iA^{I}+jA^{J}+kA^{K},\\ B=&\left( \begin{array}{l@{\quad }c} -0.1-0.4i-0.1j-0.4k&{}~-0.4-0.1i-0.4j-0.1k\\ -0.1-0.1i-0.1j-0.1k&{}~-0.1-0.2i-0.1j-0.2k\\ \end{array} \right) \\ =&\left( \begin{array}{l@{\quad }c} -0.1&{}-0.4\\ -0.1&{}-0.1\\ \end{array} \right) +i\left( \begin{array}{l@{\quad }c} -0.4&{}-0.1\\ -0.1&{}-0.2\\ \end{array} \right) \\&+j\left( \begin{array}{l@{\quad }c} -0.1&{}-0.4\\ -0.1&{}-0.1\\ \end{array} \right) +k\left( \begin{array}{l@{\quad }c} -0.4&{}-0.1\\ -0.1&{}-0.2\\ \end{array} \right) \\ =&\,B^{R}+iB^{I}+jB^{J}+kB^{K},\\ \end{aligned} \end{aligned}$$

and \(D=\) diag(7,2), \(\tau (t)=2+\sin (2t)\), \(u=\big (-1-i-j-k~~~-2-i-2j-k\big )^{T}\). Let the activation functions \(f=g=\tanh \). It is easy to know that \(\lambda ^{R}=\frac{1}{10}\), \(\lambda ^{I}=\lambda ^{J}=\frac{1}{16}\), \(\lambda ^{k}=\frac{1}{40}\), \(\delta ^{R}=\frac{1}{10}\), \(\delta ^{I}=\delta ^{J}=\frac{1}{16}\) and \(\delta ^{K}=\frac{1}{40}\). According to the following equations,

$$\begin{aligned}&\mathfrak {D}=\mathrm {diag}\big (D,D,D,D\big ),\\&U=\left( \big (u^{R}\big )^{T},\big (u^{I}\big )^{T},\big (u^{J}\big )^{T},\big (u^{K}\big )^{T}\right) ^{T},\\&A_{1}=\mathrm {diag}\big (A^{R},A^{I},A^{J},A^{K}\big ),\\&A_{2}=\mathrm {diag}\big (-A^{I},A^{R},A^{K},-A^{J}\big ),\\&A_{3}=\mathrm {diag}\big (-A^{J},-A^{K},A^{R},A^{I}\big ),\\&A_{4}=\mathrm {diag}\big (-A^{K},A^{J},-A^{I},A^{R}\big ),\\&B_{1}=\mathrm {diag}\big (B^{R},B^{I},B^{J},B^{K}\big ),\\&B_{2}=\mathrm {diag}\big (-B^{I},B^{R},B^{K},-B^{J}\big ),\\&B_{3}=\mathrm {diag}\big (-B^{J},-B^{K},B^{R},B^{I}\big ),\\&B_{4}=\mathrm {diag}\big (-B^{K},B^{J},-B^{I},B^{R}\big ), \end{aligned}$$

one can obtain \(\mathfrak {D}-|\hat{A}|\hat{\lambda }-|\hat{B}|\hat{\delta }\) is a non-singular M-matrix which can guarantee the existence and uniqueness of the equilibrium point. Moreover, in the following we have:

  1. (i)

    When \(p=1\), with the help of MATLAB, some calculations give that \(\Vert A_{1}\Vert _{1}=\Vert A_{2}\Vert _{1}=\Vert A_{3}\Vert _{1}=\Vert A_{4}\Vert _{1}=1.0\), \(\Vert B_{1}\Vert _{1}=\Vert B_{2}\Vert _{1}=\Vert B_{3}\Vert _{1}=\Vert B_{4}\Vert _{1}=0.5\), and \(\mu _{1}(-\mathfrak {D})=-2\). Then, the equalities are obtained that

    $$\begin{aligned} T_{1}= & {} -\mu _{1}(-\mathfrak {D})-4^{1}\lambda ^{R}\Vert A_{1}\Vert _{\infty } -4^{1}\lambda ^{I}\Vert A_{2}\Vert _{1}\\&-\,4^{1}\lambda ^{J}\Vert A_{3}\Vert _{1}-4^{1}\lambda ^{K}\Vert A_{4}\Vert _{1}=1.25,\\ T_{2}= & {} 4^{1}\delta ^{R}\Vert B_{1}\Vert _{\infty }+4^{1}\delta ^{I}\Vert B_{2}\Vert _{1} +4^{1}\delta ^{J}\Vert B_{3}\Vert _{1}\\&+\,4^{1}\delta ^{K}\Vert B_{4}\Vert _{1}=0.75,\\ \end{aligned}$$

    that is, \(T_{1}>T_{2}\);

  2. (ii)

    When \(p=\infty \), via calculations with the help of MATLAB, it is obtained that \(\Vert A_{1}\Vert _{\infty }=\Vert A_{2}\Vert _{\infty }=\Vert A_{3}\Vert _{\infty }=\Vert A_{4}\Vert _{\infty }=0.9\), \(\Vert B_{1}\Vert _{\infty }=\Vert B_{2}\Vert _{\infty }=\Vert B_{3}\Vert _{\infty }=\Vert B_{4}\Vert _{\infty }=0.5\), and \(\mu _{\infty }(-\mathfrak {D})=-2\). Then, it can be obtained that

    $$\begin{aligned} T_{1}= & {} -\mu _{1}(-\mathfrak {D})-4^{1}\lambda ^{R}\Vert A_{1}\Vert _{\infty } -4^{1}\lambda ^{I}\Vert A_{2}\Vert _{1}\\&-\,4^{1}\lambda ^{J}\Vert A_{3}\Vert _{1}-4^{1}\lambda ^{K}\Vert A_{4}\Vert _{1}=1.325,\\ T_{2}= & {} 4^{1}\delta ^{R}\Vert B_{1}\Vert _{\infty }+4^{1}\delta ^{I}\Vert B_{2}\Vert _{1} +4^{1}\delta ^{J}\Vert B_{3}\Vert _{1}\\&+\,4^{1}\delta ^{K}\Vert B_{4}\Vert _{1}=0.75,\\ \end{aligned}$$

    which implies \(T_{1}>T_{2}\);

  3. (iii)

    When \(p=2\), via complex calculations with the help of MATLAB, it is obtained that the eigenvalues of \(A^{2}_{1}\) are the same as that of \(A^{2}_{2}\), \(A^{2}_{3}\), and \(A^{2}_{4}\), which are 0.0822, 0.6278, 0.2881, 0.0219, 0.0900, 0.0100, 0.2759, −0.0359, and the eigenvalues of \(B^{2}_{1}\) are the same as that of \(B^{2}_{2}\), \(B^{2}_{3}\) and \(B^{2}_{4}\), which are 0.0900, 0.0100, 0.0251, 0.1949, 0.0900, 0.0100, 0.0251, 0.1949, and then it is obtained that \(\Vert A_{1}\Vert _{2}=\Vert A_{2}\Vert _{2}=\Vert A_{3}\Vert _{2}=\Vert A_{4}\Vert _{2}=\sqrt{0.6278}=0.7923\), \(\Vert B_{1}\Vert _{2}=\Vert B_{2}\Vert _{2}=\Vert B_{3}\Vert _{2}=\Vert B_{4}\Vert _{2}=\sqrt{0.1949}=0.4415\), and \(\mu _{2}(-\mathfrak {D})=-2\). Then, one can obtain

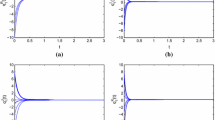
    $$\begin{aligned} T_{1}(1)= & {} -\mu _{1}(-\mathfrak {D})-4^{1}\lambda ^{R}\Vert A_{1}\Vert _{\infty } -4^{1}\lambda ^{I}\Vert A_{2}\Vert _{1}\\&-\,4^{1}\lambda ^{J}\Vert A_{3}\Vert _{1}-4^{1}\lambda ^{K}\Vert A_{4}\Vert _{1}=1.4085,\\ T_{2}(1)= & {} 4^{1}\delta ^{R}\Vert B_{1}\Vert _{\infty }+4^{1}\delta ^{I}\Vert B_{2}\Vert _{1} +4^{1}\delta ^{J}\Vert B_{3}\Vert _{1}\\&+\,4^{1}\delta ^{K}\Vert B_{4}\Vert _{1}=0.4312, \end{aligned}$$

    implying \(T_{1}>T_{2}\). Therefore, considering the above parameters, the conditions in Theorem 1 are satisfied, that is, QVNN (18) is globally exponentially stable. Fig. 1 shows the state trajectories of QVNN (18) which is simulated by MATLAB based on those necessary parameters.

Fig. 1
figure 1

State trajectories of \(h^{R}(t),h^{I}(t),h^{J}(t),h^{K}(t)\), which shows the global exponential stability of the equilibrium point of QVNN (18)

Full size image

5 Conclusion

In this paper, the global exponential stability of QVNNs with time-varying delays is investigated with the Halanay inequality technique and the method of matrix measure. By decomposing the considered QVNN into four real-valued systems, which form an equivalent real-valued system, some criteria are established for the global exponential stability of QVNN. Based on the Halanay inequality technique as well as the matrix measure method, the main results are presented. Furthermore, some strict constraints for activation functions are no longer assumed, such as the existence, continuity and boundedness of the partial derivatives for real-valued functions decomposed from quaternion-valued activation functions. Finally, a numerical example is provided to show the effectiveness and conciseness of the main results. By the algebraic feature of quaternion and the spatial structure feature of QVNNs, future works will focus on the applications of QVNNs in the design of event-triggered controllers [16] and the attitude control of spacecrafts [31], as well as the synchronization problem of a class of QVNNs [43], etc.