Nonlinear vibration response of shear deformable FGM sandwich toroidal shell segments

Abstract

The nonlinear vibration investigation of toroidal shell segment (TSS) with an analytical approach is presented in this paper. The TSS is considered as a sandwich structure with FGM core and homogeneous face sheets, or homogeneous core and FGM face sheets. The FGM sandwich TSS is surrounded by Pasternak-type of elastic foundation subjected to mechanical loads and exposed to a high-temperature environment. A third-order shear deformation shell theory (TSDT) developed by Reddy and Liu (NASA Cr. Report 4656, 1987) accounts for small strains but moderately large displacements is used to establish governing equations. Two methods using Airy stress function and displacement formulations are used separately in conjunction with Galerkin method and Runge–Kutta method to investigate the nonlinear vibration of FGM sandwich TSS. Then, the effects of material, geometric properties, mechanical condition, thermal environment, and elastic foundation on the nonlinear vibration characteristics of FGM sandwich toroidal shell segments (TSSs) are analyzed and discussed in detail. Specifically, the difference between natural frequencies calculated by using Airy stress function and displacement formulations are also described in the present study.

1 Introduction

Functionally graded materials (FGMs) are known as advanced materials usually composed of metal and ceramic constituents, in which material properties gradually vary from one interface to the other. Due to their excellent characteristics, FGM structures are widely used in various engineering applications such as space vehicles, aircraft, nuclear power plants, and other practical applications. Consequently, many researchers have studied the static and dynamic responses of FGM structures. Using the Galerkin method, Najafov et al. [2] presented an analysis of stability and torsional vibration of FGM cylindrical shells resting on elastic foundations. Babaei et al. [3, 4] and Shen [5] studied large amplitude vibrations of FGM beams, FGM cylindrical panels, and cylindrical shells, respectively.

Using higher-order shear deformations (HSDT) for linear analysis as well as nonlinear analysis has been received various attention due to the essential of analyzing thick structures. Using the sinusoidal shear deformation theory and the first-order shear deformation theory (FSDT), Kolahchi [6] studied bending, buckling, and post-buckling of nano-sandwich plates. Zhang [7] utilized a high-order shear deformation beam theory and the Ritz method to investigate the vibration and post-buckling behavior of FGM beams. Using an HSDT, Vinyas [8] studied the vibrational behavior of porous functionally graded magneto-electro-elastic circular and annular plates. Arefi et al. [9] and Arefi [10] used a TSDT to study the linear static response of functionally graded graphene nanoplatelets reinforced composite (FG-GPLRC) micro-plates and sandwich doubly curved piezoelectric micro shells, respectively. Wang et al. [11] made use of an HSDT and Navier technique to study the linear bending and vibrational characteristics of FG-GPLRC doubly curved shells. Using a TSDT and the Galerkin method, Hao et al. [12] and Liu et al. [13] presented nonlinear analyses of vibration of orthotropic FGM rectangular plates and FGM cylindrical shells, respectively. Hosseini and Kolahchi [14] suggested a mathematical model for the seismic response of submerged cylindrical shells subjected to hygrothermal load using a TSDT, the energy method, Hamilton's principle, and the differential quadrature method. Dung and Vuong [15] and Vuong and Duc [16] used the Airy stress function method to investigate the static stability and nonlinear vibration of FGM TSSs, making use of a TSDT. Also, based on a TSDT, Duc and Thiem [17] studied the nonlinear vibration of FGM cylindrical shells using the Galerkin method.

Thanks to exceptional properties such as excellent thermal and sound insulation and high strength and stiffness to weight ratio, sandwich structures have found widespread applications in various fields of engineering. The main weakness of the traditional sandwich structures is that the stresses at the face sheet-core interface are discontinuous. This drawback may cause severe damages. Due to the gradually varied mechanical properties of constituents, FGMs might be used as a solution for this problem. Therefore, many reports on static and dynamic behaviors of FGM sandwich structures have been performed. Shodja et al. [18] studied the static behaviors of FGM sandwich structures under thermomechanical loadings using stress function and the Fourier series method. They found that stress interfacial shear stress is reduced, and concentration effects are eliminated as a functionally graded coating is used. Shen and Li [19] investigated the static buckling and post-bucking behaviors of FGM sandwich plates subjected to thermal and thermomechanical loadings using an HSDT. An investigation on the thermal buckling of FGM sandwich plates is presented by Zenkour and Sobhy [20] using the sinusoidal shear deformation plate theory. Kiani and Eslami [21] studied the thermal stability of FGM sandwich plates, making use of the FSDT and the Galerkin method. Based on the three-dimensional elasticity linear theory, Li et al. [22] presented an investigation on the vibrational characteristics of FGM sandwich plates. An investigation of the natural frequencies of FGM sandwich plates with FGM core is performed by Dozio [23] using the Ritz method. Neves et al. [24] made use of an HSDT to analyze the buckling and free vibration of isotropic and FGM sandwich plates. Based on an HSDT, Kiarasi et al. [25] studied the buckling of sandwich plates with a polymeric core and two face sheets reinforced by carbon nanotubes making use of Hamilton’s principle and a Navier–Stokes method. Based on various shear deformation plate theories, Sobhy [26] studied the linear buckling and free vibration of FGM sandwich plates. The problem of three-dimensional vibration of laminated cylindrical panels with FGM layers is solved by Malekzadeh and Ghaedsharaf [27], making use of a layerwise-differential quadrature method. Shen et al. [28] presented a large amplitude vibration analysis of laminated cylindrical panels with graphene reinforcements utilizing an HSDT and a two-step perturbation technique. Sburlati [29] made use of the elastic theory to study the elastic bending behavior of circular FGM sandwich panels. The research also reveals that interface stresses are decreased when FGM core is used. Li et al. [30] used Flügge’s shell theory to investigate the free vibration of three-layer cylindrical shells with FGM core. Using the FSDT, Hamilton’s principle and the Galerkin method, Karroubi and Rahaghi [31] carried out an analysis of free vibrational responses of cylindrical sandwich shells with FGM core and piezoelectric skins. Also, based on the FSDT, Sofiyev et al. [32] studied free vibration and stability of cylindrical sandwich shells with FGM core surrounded by an elastic foundation and loaded by axial compressions making use of the Galerkin method. The problem of vibration of FGM sandwich cylindrical shells with FGM core and homogeneous face sheets is solved by Alibeigloo and Noee [33] using the differential quadrature method. Deniz [34] studied the nonlinear stability of truncated conical shells with FGM coatings loaded by axial compression using the Galerkin method. Based on the FSDT, Sofiyev and Osmancelebioglu [35] analyzed the influences of FGM coatings on the vibrational responses of sandwich truncated conical shells utilizing the Galerkin method.

Sandwich double-curved shells and sandwich TSSs also have obtained great attention from researchers. Numerous researches have been done on the static and dynamic behaviors of sandwich doubly curved shells and TSSs. The problem of nonlinear vibration of FGM sandwich doubly curved shells was solved by Dong and Dung [36] using a TSDT and by Hao et al. [37] using the improved shear deformation shell theory. Several problems of the static analysis of doubly curved sandwich shells are solved by Tornabene et al. [38], making use of the equivalent single layer theories. Fazzolari and Carrera [39] used the Principle of Virtual Displacements, the refined Equivalent Single Layer, the Zig Zag shell theory, and the Ritz method to analyze vibration responses of doubly curved sandwich shells with FGM core. Trinh and Kim [40] carried out an analytical investigation on the thermomechanical stability and vibration of FGM sandwich doubly curved shells using the classical shell theory and the Galerkin method. Vuong and Duc [41] studied the static and dynamic buckling of FGM sandwich TSSs using a TSDT. Ninh and Bich [42] investigated the vibrational characteristics of FGM sandwich TSSs resting on an elastic foundation based on the classical shell theory utilizing the Airy stress function method. To the author’s knowledge, there is no investigation on the vibration of FGM sandwich TSSs based on TSDT. Ninh and Bich [42] only used the classical thin shell theory to investigate the vibration of FGM sandwich TSSs. Vuong and Duc [16] used a TSDT to investigate the nonlinear vibration of FGM TSSs but not yet considered sandwich shells. So, in order to fill in this research gap, we use a TSDT to study the nonlinear vibration of thick FGM sandwich TSSs surrounded by the Pasternak-type elastic foundation in the thermal environment. The results of the present study may be helpful for designers to deal with thick sandwich shells.

2 Theoretical formulation

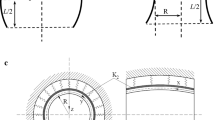
A sandwich TSS with length $L$, total thickness $h$, equatorial radius $R$, and longitudinal curvature radius $a$ is considered in Fig. 1. The TSS is defined in a coordinate system whose origin is located on the middle surface and at the end of the shell, where $x$ and $y$ are the longitudinal and circumferential direction, respectively, and $z$ axis normal to them and pointed inwards.

Fig. 1

Configuration of FGM sandwich TSSs

The sandwich TSS is constructed from three layers with a total thickness of $h$. Two face sheets of the same thickness $h_{f}$, separated by a thicker core layer of the thickness $h_{c}$. Two types of sandwich shells are considered. Sandwich shell of type A has homogeneous core (full metal) and FGM layers whereas sandwich shell of type B has FGM core and homogeneous layers (see Fig. 1). Denote $z_{1} = - h{/}2$, $z_{2} = - h{/}2 + h_{f}$, $z_{3} = h{/}2 - h_{f}$, $z_{4} = h{/}2$. The effective material properties of each type of sandwiches, such as Young modulus $E$, thermal expansion coefficient $\alpha$, and mass density $\rho$ are defined as follows.

Case 1 Sandwich shell of type A composed of homogeneous core (full metal) and two FGM face layers.

$$\begin{aligned} \left[ {E(z),\rho \left( z \right),\alpha \left( z \right)} \right] = & \left[ {E_{c} ,\rho_{c} ,\alpha_{c} } \right] - \left[ {E_{cm} ,\rho_{cm} ,\alpha_{cm} } \right] \\ & \quad \times \left\{ {\begin{array}{*{20}l} {\left( {\frac{{z - z_{1} }}{{z_{2} - z_{1} }}} \right)^{k} ,} & {z_{1} \le z \le z_{2} } \\ \begin{gathered} 1, \hfill \\ \left( {\frac{{z - z_{4} }}{{z_{3} - z_{4} }}} \right)^{k} , \hfill \\ \end{gathered} & \begin{gathered} z_{2} \le z \le z_{3} \hfill \\ z_{3} \le z \le z_{4} \hfill \\ \end{gathered} \\ \end{array} } \right. \\ \end{aligned}$$

(1)

Case 2 Sandwich shell of type B composed of FGM core, inner and outer layers are ceramic-rich and metal-rich, respectively.

$$\begin{aligned} \left[ {E(z),\rho \left( z \right),\alpha \left( z \right)} \right] = & \left[ {E_{m} ,\rho_{m} ,\alpha_{m} } \right] + \left[ {E_{cm} ,\rho_{cm} ,\alpha_{cm} } \right] \\ & \quad \times \left\{ {\begin{array}{*{20}l} {0,} & {z_{1} \le z \le z_{2} } \\ \begin{gathered} \left( {\frac{{z - z_{2} }}{{z_{3} - z_{2} }}} \right)^{k} , \hfill \\ 1, \hfill \\ \end{gathered} & \begin{gathered} z_{2} \le z \le z_{3} \hfill \\ z_{3} \le z \le z_{4} \hfill \\ \end{gathered} \\ \end{array} } \right. \\ \end{aligned}$$

(2)

where $m$ and $c$ denote metal and ceramic, respectively. $E_{m} ,\rho_{m} ,\alpha_{m} ,E_{c} ,\rho_{c} ,\alpha_{c}$ are Young modulus, mass density, and thermal expansion coefficients of metal and ceramic constituents, respectively. $E_{cm} = E_{c} - E_{m}$, $\rho_{cm} = \rho_{c} - \rho_{m}$, $\alpha_{cm} = \alpha_{c} - \alpha_{m}$. The non-negative number $k$ is the volume fraction index. The Poisson’s ratio of material constituents is assumed to be equal and to be constant, i.e. $\nu_{c} = \nu_{m} = const$ [20, 21, 36, 40, 41].

This study uses a TSDT developed by Reddy and Liu [1] to investigate the nonlinear vibration of FGM sandwich TSSs loaded by mechanical loads, exposed to a high-temperature environment, and surrounded by the Pasternak-type elastic foundation. According to this theory, the displacement components $u^{\left( 1 \right)} ,v^{\left( 1 \right)} ,w^{\left( 1 \right)}$ along the $\left( {x,y,z} \right)$ coordinates of shell is [1].

$$\begin{aligned} u^{\left( 1 \right)} \left( {x,y,z,t} \right) = & u^{\left( 0 \right)} \left( {1 - \frac{z}{a}} \right) + z\phi_{x} + z^{3} \frac{4}{{3h^{2} }}\left( { - \phi_{x} - w_{,x} } \right) \\ v^{\left( 1 \right)} \left( {x,y,z,t} \right) = & v^{\left( 0 \right)} \left( {1 - \frac{z}{R}} \right) + z\phi_{y} + z^{3} \frac{4}{{3h^{2} }}\left( { - \phi_{y} - w_{,y} } \right) \\ w^{\left( 1 \right)} \left( {x,y,z,t} \right) = & w^{\left( 0 \right)} \\ \end{aligned}$$

(3)

where $t$ is time, $\left( {u^{\left( 0 \right)} ,v^{\left( 0 \right)} ,w^{\left( 0 \right)} } \right)$ are displacements of a point on the mid-surface, and $\phi_{x} ,\phi_{y}$ are the rotations of normal to the middle surface with respect to y- and x-axes, respectively.

Basing on TSDT, the strains components ($\varepsilon_{x} ,\varepsilon_{y} ,\gamma_{xy} ,\gamma_{xz} ,\gamma_{yz}$) are expressed as [1]

$$\begin{aligned} \varepsilon_{x} = & \frac{{\partial u^{\left( 1 \right)} }}{\partial x} - \frac{{w^{\left( 1 \right)} }}{a} + \frac{1}{2}\left( {\frac{{\partial w^{\left( 1 \right)} }}{\partial x}} \right)^{2} \\ \varepsilon_{y} = & \frac{{\partial v^{\left( 1 \right)} }}{\partial y} - \frac{{w^{\left( 1 \right)} }}{R} + \frac{1}{2}\left( {\frac{{\partial w^{\left( 1 \right)} }}{\partial y}} \right)^{2} \\ \gamma_{xy} = & \frac{{\partial u^{\left( 1 \right)} }}{\partial y} + \frac{{\partial v^{\left( 1 \right)} }}{\partial x} + \frac{{\partial w^{\left( 1 \right)} }}{\partial x}\frac{{\partial w^{\left( 1 \right)} }}{\partial y} \\ \gamma_{xz} = & \frac{{\partial w^{\left( 1 \right)} }}{\partial x} + \frac{{\partial u^{\left( 1 \right)} }}{\partial z} + \frac{{u^{\left( 1 \right)} }}{a} \\ \gamma_{yz} = & \frac{{\partial w^{\left( 1 \right)} }}{\partial y} + \frac{{\partial v^{\left( 1 \right)} }}{\partial z} + \frac{{v^{\left( 1 \right)} }}{R} \\ \end{aligned}$$

(4)

Substituting Eq. (3) into Eq. (4) and ignoring higher-order terms on the assumption that $1 - \frac{z}{a} \approx 1,1 - \frac{z}{R} \approx 1$ leads to strain–displacement relations as [1]:

$$\begin{aligned} \varepsilon_{x} = & \varepsilon_{x}^{0} + z\left( {k_{x}^{\left( 0 \right)} + z^{2} k_{x}^{\left( 2 \right)} } \right) \\ \varepsilon_{y} = & \varepsilon_{y}^{0} + z\left( {k_{y}^{\left( 0 \right)} + z^{2} k_{y}^{\left( 2 \right)} } \right) \\ \gamma_{xy} = & \gamma_{xy}^{0} + z\left( {k_{xy}^{\left( 0 \right)} + z^{2} k_{xy}^{\left( 2 \right)} } \right) \\ \gamma_{xz} = & \gamma_{xz}^{0} + z^{2} k_{xz}^{\left( 1 \right)} ,\gamma_{yz} = \gamma_{yz}^{0} + z^{2} k_{yz}^{\left( 1 \right)} \\ \end{aligned}$$

(5)

where

$$\begin{aligned} \varepsilon_{x}^{0} = & \frac{{\partial u^{\left( 0 \right)} }}{\partial x} - \frac{{w^{\left( 0 \right)} }}{a} + \frac{1}{2}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}} \right)^{2} \\ \varepsilon_{y}^{0} = & \frac{{\partial v^{\left( 0 \right)} }}{\partial y} - \frac{{w^{\left( 0 \right)} }}{R} + \frac{1}{2}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial y}} \right)^{2} \\ \gamma_{xy}^{0} = & \frac{{\partial u^{\left( 0 \right)} }}{\partial y} + \frac{{\partial v^{\left( 0 \right)} }}{\partial x} + \frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial w^{\left( 0 \right)} }}{\partial y} \\ \gamma_{xz}^{0} = & & \phi_{x} + \frac{{\partial w^{\left( 0 \right)} }}{\partial x},\gamma_{yz}^{0} = \phi_{y} + \frac{{\partial w^{\left( 0 \right)} }}{\partial y} \\ k_{x}^{\left( 0 \right)} = & \frac{{\partial \phi_{x} }}{\partial x},k_{y}^{\left( 0 \right)} = \frac{{\partial \phi_{y} }}{\partial y},k_{xy}^{\left( 0 \right)} = \frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} \\ k_{xz}^{\left( 1 \right)} = & - 3c\left( {\phi_{x} + \frac{{\partial w^{\left( 0 \right)} }}{\partial x}} \right),k_{yz}^{\left( 1 \right)} = - 3c\left( {\phi_{y} + \frac{{\partial w^{\left( 0 \right)} }}{\partial y}} \right) \\ k_{x}^{\left( 2 \right)} = & - c\left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }}} \right),k_{y}^{\left( 2 \right)} = - c\left( {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }}} \right) \\ k_{xy}^{\left( 2 \right)} = & - c\left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} + 2\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right),c = \frac{4}{{3h^{2} }} \\ \end{aligned}$$

(6)

The stress–strain relations for FGM sandwich TSSs including the thermal effect using Hooke’s law, are [36, 40,41,42]

$$\begin{aligned} \sigma_{x} = & \frac{E\left( z \right)}{{1 - \nu^{2} }}\left( {\varepsilon_{x} + \nu \varepsilon_{y} } \right) - \frac{E\left( z \right)\alpha \left( z \right)\Delta T}{{1 - \nu }} \\ \sigma_{y} = & \frac{E\left( z \right)}{{1 - \nu^{2} }}\left( {\varepsilon_{y} + \nu \varepsilon_{x} } \right) - \frac{E\left( z \right)\alpha \left( z \right)\Delta T}{{1 - \nu }} \\ \sigma_{xy} = & \frac{E\left( z \right)}{{2\left( {1 + \nu } \right)}}\gamma_{xy} ,\quad \sigma_{xz} = \frac{E\left( z \right)}{{2\left( {1 + \nu } \right)}}\gamma_{xz} ,\quad \sigma_{yz} = \frac{E\left( z \right)}{{2\left( {1 + \nu } \right)}}\gamma_{yz} \\ \end{aligned}$$

(7)

where $\Delta T$ is temperature rise in comparison with thermal stress-free initial state. In the present study, the temperature change $\Delta T$ is assumed to be independent of variables $x,y,z$ and $t$.

The equations of motion of TSSs are given by [1]

$$\frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = \overline{{I_{1} }} \ddot{u} + \overline{{I_{2} }} \ddot{\phi }_{x} - \overline{{I_{3} }} \frac{{\partial \ddot{w}}}{\partial x}$$

(8)

$$\frac{{\partial N_{y} }}{\partial y} + \frac{{\partial N_{xy} }}{\partial x} = \overline{{I_{1}^{/} }} \ddot{v} + \overline{{I_{2}^{/} }} \ddot{\phi }_{y} - \overline{{I_{3}^{/} }} \frac{{\partial \ddot{w}}}{\partial y}$$

(9)

$$\begin{aligned} \frac{{\partial Q_{x} }}{\partial x} + & \frac{{\partial Q_{y} }}{\partial y} - 3c\left( {\frac{{\partial R_{x} }}{\partial x} + \frac{{\partial R_{y} }}{\partial y}} \right) \\ & \quad + c\left( {\frac{{\partial^{2} P_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} P_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} P_{y} }}{{\partial y^{2} }}} \right) + \frac{1}{R}N_{y} + \frac{1}{a}N_{x} \\ & \quad + N_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }} \\ & \quad - K_{1} w + K_{2} \left( {\frac{{\partial^{2} w}}{{\partial^{2} x}} + \frac{{\partial^{2} w}}{{\partial^{2} y}}} \right) + q = \\ I_{1} \ddot{w} + & 2\varepsilon I_{1} \dot{w} + \overline{{I_{3} }} \frac{{\partial \ddot{u}}}{\partial x} + \overline{{I_{3}^{/} }} \frac{{\partial \ddot{v}}}{\partial y}\, \\ & \quad + \overline{{I_{5} }} \frac{{\partial \ddot{\phi }_{x} }}{\partial x} + \overline{{I_{5}^{/} }} \frac{{\partial \ddot{\phi }_{y} }}{\partial y} - c^{2} I_{7} \left( {\frac{{\partial^{2} \ddot{w}}}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}}}{{\partial y^{2} }}} \right) \\ \end{aligned}$$

(10)

$$\begin{aligned} \frac{{\partial M_{x} }}{\partial x} + & \frac{{\partial M_{xy} }}{\partial y} - Q_{x} + 3cR_{x} - c\left( {\frac{{\partial P_{x} }}{\partial x} + \frac{{\partial P_{xy} }}{\partial y}} \right) \\ = & \overline{{I_{2} }} \ddot{u} + \overline{{I_{4} }} \ddot{\phi }_{x} - \overline{{I_{5} }} \frac{{\partial \ddot{w}}}{\partial x}\,\, \\ \end{aligned}$$

(11)

$$\begin{aligned} \frac{{\partial M_{y} }}{\partial y} + & \frac{{\partial M_{xy} }}{\partial x} - Q_{y} + 3cR_{y} - c\left( {\frac{{\partial P_{y} }}{\partial y} + \frac{{\partial P_{xy} }}{\partial x}} \right) \\ = & \overline{{I_{2}^{/} }} \ddot{v} + \overline{{I_{4}^{/} }} \ddot{\phi }_{y} - \overline{{I_{5}^{/} }} \frac{{\partial \ddot{w}}}{\partial y} \\ \end{aligned}$$

(12)

in which $N_{i} ,M_{i} ,P_{i} ,R_{j} ,Q_{j} ,\left( {i = x;y;xy,\,{\text{and}}\,j = x;y\,} \right)$ are the resultants defined as

$$\begin{aligned} \left( \begin{gathered} N_{i} \hfill \\ M_{i} \hfill \\ P_{i} \hfill \\ \end{gathered} \right) = & \int\limits_{ - h/2}^{h/2} {\sigma_{i} .\left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{3} \hfill \\ \end{gathered} \right)dz} ,\quad \left( {i = x;y;xy} \right) \\ \left( \begin{gathered} Q_{j} \hfill \\ R_{j} \hfill \\ \end{gathered} \right) = & \int\limits_{ - h/2}^{h/2} {\sigma_{jz} .\left( \begin{gathered} 1 \hfill \\ z^{2} \hfill \\ \end{gathered} \right)dz} ,\quad \left( {j = x;y} \right) \\ \end{aligned}$$

(13)

where $\varepsilon$ is damping coefficient. $K_{1}$ and $K_{2}$ are parameters of elastic foundation. The coefficients $I_{i} ,\overline{{I_{i} }} \,{\text{and}}\,\overline{{I_{i}^{/} }}$ are determined in “Appendix A”. Substituting Eqs. (1) and (2) into Eq. (7) and then setting the results into Eq. (13) yields

$$\begin{aligned} \left( {\begin{array}{*{20}c} {N_{x} } & {N_{y} } & {N_{xy} } \\ {M_{x} } & {M_{y} } & {M_{xy} } \\ {P_{x} } & {P_{y} } & {P_{xy} } \\ \end{array} } \right) = & \frac{1}{{1 - \nu^{2} }}\left( {\begin{array}{*{20}c} {E_{1} } & {E_{2} } & {E_{4} } \\ {E_{2} } & {E_{3} } & {E_{5} } \\ {E_{4} } & {E_{5} } & {E_{7} } \\ \end{array} } \right) \\ & \quad \left( {\begin{array}{*{20}c} {\varepsilon_{x}^{0} + \nu \varepsilon_{y}^{0} } & {\varepsilon_{y}^{0} + \nu \varepsilon_{x}^{0} } & {0.5\left( {1 - \nu } \right)\gamma_{xy}^{0} } \\ {k_{x}^{\left( 1 \right)} + \nu k_{y}^{\left( 1 \right)} } & {k_{y}^{\left( 1 \right)} + \nu k_{x}^{\left( 1 \right)} } & {0.5\left( {1 - \nu } \right)k_{xy}^{\left( 1 \right)} } \\ {k_{x}^{\left( 2 \right)} + \nu k_{y}^{\left( 2 \right)} } & {k_{y}^{\left( 2 \right)} + \nu k_{x}^{\left( 2 \right)} } & {0.5\left( {1 - \nu } \right)k_{xy}^{\left( 2 \right)} } \\ \end{array} } \right) \\ & \quad - \frac{1}{1 - \nu }\left( {\begin{array}{*{20}c} {\Phi_{1} } & {\Phi_{1} } & 0 \\ {\Phi_{2} } & {\Phi_{2} } & 0 \\ {\Phi_{4} } & {\Phi_{4} } & 0 \\ \end{array} } \right) \\ \left( {\begin{array}{*{20}c} {Q_{x} } & {Q_{y} } \\ {R_{x} } & {R_{y} } \\ \end{array} } \right) = & \frac{1}{{2\left( {1 + \nu } \right)}}\left( {\begin{array}{*{20}c} {E_{1} } & {E_{3} } \\ {E_{3} } & {E_{5} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\gamma_{xz}^{0} } & {\gamma_{yz}^{0} } \\ {k_{xz}^{2} } & {k_{yz}^{2} } \\ \end{array} } \right) \\ \end{aligned}$$

(14)

where

$$\begin{aligned} \left( \begin{gathered} E_{1} \hfill \\ E_{2} \hfill \\ E_{3} \hfill \\ E_{4} \hfill \\ E_{5} \hfill \\ E_{7} \hfill \\ \end{gathered} \right) = & \int\limits_{ - h/2}^{h/2} {E\left( z \right)\left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{2} \hfill \\ z^{3} \hfill \\ z^{4} \hfill \\ z^{6} \hfill \\ \end{gathered} \right)dz} , \\ \left( \begin{gathered} \Phi_{1} \hfill \\ \Phi_{2} \hfill \\ \Phi_{4} \hfill \\ \end{gathered} \right) = & \int\limits_{ - h/2}^{h/2} {E\left( z \right)\alpha \left( z \right)\left( \begin{gathered} 1 \hfill \\ z \hfill \\ z^{3} \hfill \\ \end{gathered} \right)\Delta Tdz} \\ \end{aligned}$$

(15)

Setting Eq. (14) into Eqs. (8) to (12) with the aid of Eq. (6) yields

$$\begin{aligned} H_{11} \left( u \right) + & H_{12} \left( v \right) + H_{13} \left( w \right) + H_{14} \left( {\phi_{x} } \right) + H_{15} \left( {\phi_{y} } \right) \\ & \quad = \overline{{I_{1} }} \ddot{u} + \overline{{I_{2} }} \ddot{\phi }_{x} - \overline{{I_{3} }} \frac{{\partial \ddot{w}}}{\partial x} \\ \end{aligned}$$

(16)

$$\begin{aligned} H_{21} \left( u \right) + & H_{22} \left( v \right) + H_{23} \left( w \right) + H_{24} \left( {\phi_{x} } \right) + H_{25} \left( {\phi_{y} } \right) \\ & \quad = \overline{{I_{1}^{/} }} \ddot{v} + \overline{{I_{2}^{/} }} \ddot{\phi }_{y} - \overline{{I_{3}^{/} }} \frac{{\partial \ddot{w}}}{\partial y} \\ \end{aligned}$$

(17)

$$\begin{aligned} H_{31} \left( u \right) + & H_{32} \left( v \right) + H_{33} \left( w \right) + H_{34} \left( {\phi_{x} } \right) + H_{35} \left( {\phi_{y} } \right) \\ + & H_{36} \left( {u,w} \right) + H_{37} \left( {v,w} \right) + H_{38} \left( {\phi_{x} ,w} \right) + H_{39} \left( {\phi_{y} ,w} \right) + q \\ & \quad = I_{1} \ddot{w} + 2\varepsilon I_{1} \dot{w} + \overline{{I_{3} }} \frac{{\partial \ddot{u}}}{\partial x} + \overline{{I_{5} }} \frac{{\partial \ddot{\phi }_{x} }}{\partial x}\, + \overline{{I_{3}^{/} }} \frac{{\partial \ddot{v}}}{\partial y} \\ & \quad + \overline{{I_{5}^{/} }} \frac{{\partial \ddot{\phi }_{y} }}{\partial y} - c^{2} I_{7} \left( {\frac{{\partial^{2} \ddot{w}}}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}}}{{\partial y^{2} }}} \right) \\ \end{aligned}$$

(18)

$$\begin{aligned} H_{41} \left( u \right) + & H_{42} \left( v \right) + H_{43} \left( w \right) + H_{44} \left( {\phi_{x} } \right) + H_{45} \left( {\phi_{y} } \right) \\ & \quad = \overline{{I_{2} }} \ddot{u} + \overline{{I_{4} }} \ddot{\phi }_{x} - \overline{{I_{5} }} \frac{{\partial \ddot{w}}}{\partial x}\,\, \\ \end{aligned}$$

(19)

$$\begin{aligned} H_{51} \left( u \right) + & H_{52} \left( v \right) + H_{53} \left( w \right) + H_{54} \left( {\phi_{x} } \right) + H_{55} \left( {\phi_{y} } \right) \\ & \quad = \overline{{I_{2}^{/} }} \ddot{v} + \overline{{I_{4}^{/} }} \ddot{\phi }_{y} - \overline{{I_{5}^{/} }} \frac{{\partial \ddot{w}}}{\partial y} \\ \end{aligned}$$

(20)

in which operators $H_{1i} ,H_{2i} ,H_{4i} ,H_{5i} \left( {i = 1 - 5} \right)$; $H_{3i} \left( {i = 1 - 9} \right)$ are defined in “Appendix B”.

Equations (16) to (20) are five governing equations in terms of five variables $u^{\left( 0 \right)} \left( {x,y} \right)$, $v^{\left( 0 \right)} \left( {x,y} \right)$, $w^{\left( 0 \right)} \left( {x,y} \right)$, $\phi_{x} \left( {x,y} \right)$ and $\phi_{y} \left( {x,y} \right)$. They are used to study the nonlinear vibration of FGM sandwich TSSs resting on the Pasternak-type elastic foundation in the thermal environment.

3 Galerkin procedure

This paper considers simply supported FGM sandwich TSSs subjected to external harmonic excitation and pre-axial compressive load. Thus, the associated boundary conditions are

$$\begin{aligned} w^{\left( 0 \right)} = & 0,\quad v^{\left( 0 \right)} = 0,\quad \phi_{y} = 0,\quad M_{x} = 0, \\ P_{x} = & 0,\quad N_{xy} = 0,\quad N_{x} = - Ph\quad {\text{at}}\quad x = 0\quad {\text{and}}\quad x = L \\ \end{aligned}$$

(21)

To solve a system of five-partial differential Eqs. (16) to (20) for five unknown functions $u^{\left( 0 \right)} \left( {x,y} \right)$, $v^{\left( 0 \right)} \left( {x,y} \right)$, $w^{\left( 0 \right)} \left( {x,y} \right)$, $\phi_{x} \left( {x,y} \right)$ and $\phi_{y} \left( {x,y} \right)$ with the boundary condition (21) the approximate solution satisfying the mentioned boundary condition is chosen as [11]

$$\begin{aligned} u^{\left( 0 \right)} = & U\left( t \right)\cos \,Mx\,\sin \,Ny \\ v^{\left( 0 \right)} = & V\left( t \right)\sin \,Mx\,\cos \,Ny \\ w^{\left( 0 \right)} = & W\left( t \right)\sin \,Mx\,\sin \,Ny \\ \phi_{x} = & \Phi_{x} \left( t \right)\cos \,Mx\,\sin \,Ny \\ \phi_{y} = & \Phi_{y} \left( t \right)\sin \,Mx\,\cos \,Ny \\ \end{aligned}$$

(22)

where $M = \frac{m\pi }{L},\,N = \frac{n}{R}$. $U\left( t \right),V\left( t \right),W\left( t \right),\Phi_{x} \left( t \right),\Phi_{y} \left( t \right)$ are unknown time-dependent functions, $m$ and $n$ are the numbers of half-waves in $x$ and $y$ directions, respectively.

Substituting Eq. (22) into Eqs. (16) to (20) then utilizing the Galerkin method leads to

$$\begin{aligned} h_{11} U + & h_{12} V + h_{13} W + h_{14} \Phi_{x} + h_{15} \Phi_{y} + h_{16} W^{2} \\ & \quad = - \overline{{I_{1} }} \ddot{U} - \overline{{I_{2} }} \ddot{\Phi }_{x} + \overline{{I_{3} }} M\ddot{W} \\ \end{aligned}$$

(23)

$$\begin{aligned} h_{21} U + & h_{22} V + h_{23} W + h_{24} \Phi_{x} + h_{25} \Phi_{y} + h_{26} W^{2} \\ & \quad = - \overline{{I_{1}^{/} }} \ddot{V} - \overline{{I_{2}^{/} }} \ddot{\Phi }_{y} + \overline{{I_{3}^{/} }} N\ddot{W} \\ \end{aligned}$$

(24)

$$\begin{aligned} h_{31} U + & h_{32} V + h_{33} W + h_{34} \Phi_{x} + h_{35} \Phi_{y} + h_{36} W^{2} \\ + & h_{37} UW + h_{38} VW + h_{39} \Phi_{x} W + h_{310} \Phi_{y} W + h_{311} W^{3} \\ + & \Phi_{{1{\text{T}}}} W - \Phi_{{2{\text{T}}}} + \frac{{4\delta_{m} \delta_{n} }}{{mn\pi^{2} }}q \\ & \quad = \left[ {I_{1} + c^{2} I_{7} \left( {M^{2} + N^{2} } \right)} \right]\ddot{W} + 2\varepsilon I_{1} \dot{W} \\ & \quad - \overline{{I_{3} }} M\ddot{U} - \overline{{I_{5} }} M\ddot{\Phi }_{x} \, - \overline{{I_{3}^{/} }} N\ddot{V} - \overline{{I_{5}^{/} }} N\ddot{\Phi }_{y} \\ \end{aligned}$$

(25)

$$\begin{aligned} h_{41} U + & h_{42} V + h_{43} W + h_{44} \Phi_{x} + h_{45} \Phi_{y} + h_{46} W^{2} \\ & \quad = - \overline{{I_{2} }} \ddot{U} - \overline{{I_{4} }} \ddot{\Phi }_{x} + \overline{{I_{5} }} M\ddot{W} \\ \end{aligned}$$

(26)

$$\begin{aligned} h_{51} U + & h_{52} V + h_{53} W + h_{54} \Phi_{x} + h_{55} \Phi_{y} + h_{56} W^{2} \\ & \quad = - \overline{{I_{2}^{/} }} \ddot{V} - \overline{{I_{4}^{/} }} \ddot{\Phi }_{y} + \overline{{I_{5}^{/} }} N\ddot{W} \\ \end{aligned}$$

(27)

where thermal parameters $\Phi_{{1{\text{T}}}} {,}\,\Phi_{{{\text{2T}}}}$ and coefficients $h_{1i} ,h_{2i} ,h_{4i} ,h_{5i} \left( {i = 1 \div 6} \right)$; $h_{3i} \left( {i = 1 \div 11} \right)$ are demonstrated in “Appendix C”.

In general, transverse nonlinear vibrations are the primary motion for the FGM sandwich shells. Following the work performed by Duc and Thiem [17], we can consider four right sides of the four Eqs. (23), (24), (26), and (27) equal zero i.e.

$$- \overline{{I_{1} }} \ddot{U} - \overline{{I_{2} }} \ddot{\Phi }_{x} + \overline{{I_{3} }} M\ddot{W} = 0$$

(28)

$$- \overline{{I_{1}^{/} }} \ddot{V} - \overline{{I_{2}^{/} }} \ddot{\Phi }_{y} + \overline{{I_{3}^{/} }} N\ddot{W} = 0$$

(29)

$$- \overline{{I_{2} }} \ddot{U} - \overline{{I_{4} }} \ddot{\Phi }_{x} + \overline{{I_{5} }} M\ddot{W} = 0$$

(30)

$$- \overline{{I_{2}^{/} }} \ddot{V} - \overline{{I_{4}^{/} }} \ddot{\Phi }_{y} + \overline{{I_{5}^{/} }} N\ddot{W} = 0$$

(31)

From Eqs. (28) to (31) and Eqs. (23), (24), (26), and (27) $\ddot{U},\ddot{V},\ddot{\Phi }_{x} ,\ddot{\Phi }_{y} ,U,V,\Phi_{x}$ and $\Phi_{y}$ can be expressed in terms of $W,\ddot{W}$. Then substituting the resulting expressions into Eq. (25) yields

$$\begin{aligned} D_{1} \ddot{W} + & D_{2} \dot{W} + \left( {D_{3} - \Phi_{1T} - PhM^{2} } \right)W \\ + & D_{4} W^{2} + D_{5} W^{3} + \Phi_{2T} + D_{6} q = 0 \\ \end{aligned}$$

(32)

where coefficients $D_{i}$ are determined in “Appendix D”.

3.1 Natural frequency of FGM sandwich TSSs

The natural frequencies of FGM sandwich TSSs can be calculated from Eq. (32) as

$$\omega_{mn} = \sqrt {\frac{{D_{3} - \Phi_{1T} - PhM^{2} }}{{D_{1} }}}$$

(33)

Using the Airy stress function method with the same way which presented in work [16], the natural frequencies of FGM sandwich TSSs are obtained as

$$\omega_{mn} = \sqrt {\frac{{B_{3} }}{{B_{1} }}}$$

(34)

where coefficients $B_{1} ,B_{3}$ can be found in “Appendix E”.

3.2 Nonlinear forced vibration of FGM sandwich TSSs

Consider FGM sandwich TSSs resting on an elastic foundation subjected to external harmonic excitation $q = Q\sin \Omega t$ and pre-axial compressive load $P$ in a thermal environment. $P,Q$ are assumed to be time independent. In this case, Eq. (32) can be written as follows

$$\begin{aligned} \frac{{d^{2} W}}{{dt^{2} }} + & g_{1} \frac{dW}{{dt}} + \omega_{mn}^{2} \left( {W + g_{2} W^{2} + g_{3} W^{3} } \right) \\ + & g_{4} \sin \Omega t + g_{5} = 0 \\ \end{aligned}$$

(35)

where coefficients $g_{i} \left( {i = 1 \div 5} \right)$ are defined in “Appendix F”. Equation (35) is used to investigate the forced vibrational characteristics of FGM sandwich shells.

3.3 Frequency-amplitude curve

In this section, the Galerkin method is used to establish the frequency-amplitude curve [17, 36, 42]. First, introduction $W = A\sin \Omega t$ into Eq. (35), then integrating the resulting equation over a quarter of vibration period leads to the frequency-amplitude relation as

$$\xi^{2} + \frac{{2g_{1} }}{{\pi \omega_{mn} }}\xi = 1 + \frac{{8g_{2} }}{3\pi }A + \frac{{3g_{3} }}{4}A^{2} - \frac{{g_{4} }}{{A\omega_{mn}^{2} }} + \frac{{4g_{5} }}{{A\pi \omega_{mn}^{2} }}$$

(36)

where $\xi = \frac{\Omega }{{\omega_{mn} }}$ refer to as frequency ratio.

In case of free vibration without damping and without temperature effect, Eq. (36) has of the form

$$\omega_{NL}^{2} = \omega_{mn}^{2} \left( {1 + \frac{{8g_{2} }}{3\pi }A + \frac{{3g_{3} }}{4}A^{2} } \right)$$

(37)

in which $\omega_{NL}$ is nonlinear frequency of free vibration of FGM sandwich TSSs.

4 Numerical analysis

4.1 Comparisons

In work [42], Ninh and Bich studied vibrational behaviors of FGM sandwich TSSs with FGM core based on the classical thin shell theory using an analytical approach. This paper extends work [42] to study the nonlinear vibration of FGM sandwich TSSs based on a TSDT. So, in this section, a comparison of the natural frequencies and nonlinear vibration response of FGM sandwich TSSs with the results in work [42] is presented. The FGM sandwich shells of type B are considered with parameters are taken as: $h = 0.06\,\,{\text{m}}$, $h_{f} {/}h = 0.1$, $R{/}h = 50$, $L{/}R = 0.5$, $a{/}R = 10$, $k = 1$, $E_{m} = 70\,{\text{GPa}}$, $E_{c} = 380\,{\text{GPa}}$, $\nu = 0.3$,$\rho_{m} = 2702\,{\text{kg/m}}^{{3}}$,$\rho_{c} = 3800\,{\text{kg/m}}^{{3}}$,$K_{2} = 0\,{\text{N/m}}$$K_{1} = 0\,{\text{N/m}}^{{3}}$,$\alpha_{m} = 23 \times 10^{ - 6} \,{\text{K}}^{ - 1}$,$\alpha_{c} = 5.4 \times 10^{ - 6} \,{\text{K}}^{ - 1}$, $\varepsilon = 0.2$, $\Delta T = 0{\text{K}}$, $P = 0\,{\text{Pa}}$, $q = 1000\,\sin 600t\,{\text{Pa}}$. The natural frequencies and nonlinear vibration responses are computed from Eqs. (33)–(35) and presented in Table 1 and Fig. 2 in comparison with the results reported by Ninh and Bich [42].

Table 1 Comparison of natural frequencies $\omega \left( {\text{rad/s}} \right)$ for FGM sandwich TSSs of type B

Fig. 2

Comparison of the nonlinear vibration response of FGM sandwich TSS $\left( {m = 1,n = 1} \right)$

It can be seen in Table 1, the natural frequencies of FGM sandwich TSSs within a TSDT are in good agreement with those of work [42] reported by Ninh and Bich using the classical thin shell theory. The information in Fig. 2 shows that the shape of the two curves is quite similar. The difference of two amplitudes is $\frac{1.1832e - 07 - 1.0329e - 7}{{1.0329e - 7}} \approx 14.5\%$. The cause of the amplitude difference is due to Ninh and Bich [42] used the classical shell theory neglecting the transverse shear deformation effects, whereas this study uses a TSDT, which has considered those effects.

In the second example, using Eq. (33) and Eq. (34), the natural frequencies of an isotropic cylindrical shell (i.e., toroidal shell segment with $a \to \infty$) are computed and tabulated in Table 2. The results are compared with those obtained by Lam and Loy [43] using the Ritz method based on Love’s first approximation thin shell theory and the results reported by Shen [5] using a two-step perturbation technique based on an HSDT. Parameters are taken as $h = 0.06\,{\text{m}}$, $R = 1\,{\text{m}}$, $L = 0.5\,{\text{m}}$, $E = 210\,{\text{GPa}}$, $\nu = 0.3$, $\rho = 7850\,{\text{kg/m}}^{{3}}$. Table 2 shows that, once again, good agreement is obtained.

Table 2 Comparison of dimensionless frequencies $\varpi = \omega \left( {h{/}\pi } \right)\sqrt {2\left( {1 + \nu } \right)\rho {/}E}$ for an isotropic cylindrical shell ($h = 0.06\,{\text{m}}$, $R = 1\,{\text{m}}$, $L = 0.5\,{\text{m}}$, $E = 210\,{\text{GPa}}$, $\,\rho = 7850\,{\text{kg/m}}^{{3}}$)

4.2 Nonlinear vibration analysis of FGM sandwich TSSs

In this section, effects of thermal environment, pre-axial compression, external pressure, elastic foundation, material and geometrical parameters, and type of sandwich on the nonlinear vibration characteristics such as linear and nonlinear vibration frequencies and nonlinear vibration response of FGM sandwich TSSs will be analyzed. The material properties are chosen as [42] $E_{m} = 70\,{\text{GPa}}$, $E_{c} = 380\,{\text{GPa}}$, $\nu_{m} = \nu_{c} = 0.3$, $\rho_{m} = 2702\,{\text{kg/m}}^{{3}}$,$\rho_{c} = 3800\,{\text{kg/m}}^{{3}}$, $\alpha_{m} = 23 \times 10^{ - 6} \,{\text{K}}^{ - 1}$,$\alpha_{c} = 5.4 \times 10^{ - 6} \,{\text{K}}^{ - 1}$. In each section, the input data will be described in corresponding tables or figures.

4.2.1 Natural frequencies

Table 3 illustrates the influences of pre-axial compression and $R{/}h$ ratio on natural frequencies of FGM sandwich TSSs of type B for mode numbers $\left( {m,n} \right) = \left( {1,3} \right)$ in case of without temperature effect and without elastic foundation. It can be seen; the natural frequency decreases as the $R{/}h$ ratio increases. It means that the thinner the shell is, the lower the natural frequency it is. The figures in Table 3 also show that the presence of pre-axial compression makes the natural frequency of FGM sandwich shells decreases. Furthermore, the natural frequencies calculated from Eq. (33) using displacement formulations are always a little higher than the corresponding ones calculated from Eq. (34) using the Airy stress function method.

Table 3 The effect of pre-axial loaded and $R{/}h$ ratio on the natural frequencies $\omega \,\left( {\text{rad/s}} \right)$ of FGM sandwich TSSs (type B) $h = 0.06\,{\text{m}}$, $h_{f} {/}h = 0.1$, $L{/}R = 0.5$, $L{/}a = 0.05$, $k = 1$

The effects of mode numbers $\left( {m,n} \right)$ and volume fraction index $\left( k \right)$ on the natural frequency of B-type FGM sandwich TSSs is tabulated in Table 4 in case of without temperature effect and without elastic foundation. The geometrical parameters are $h = 0.06\,{\text{m}}$, $h_{f} {/}h = 0.1$, $R = 100h$, $L = 0.5R$, $a = 20L$. It can be concluded that the natural frequency of B-type FGM sandwich TSS decreases as the volume fraction index $\left( k \right)$ increases. It is reasonable because, from Eq. (2), as the volume fraction index increases, the effective elastic modulus of the FGM layer decreases, the materials will be softer, and leads to the decrease of the natural frequency. Besides, Table 4 also indicated that as value $m$ in mode $\left( {m,n} \right)$ increases, the natural frequency increases.

Table 4 The effect of mode and material properties on the natural frequencies $\omega \,\left( {\text{rad/s}} \right)$ of FGM sandwich toroidal shell segments (type B) using Eq. (33)

Table 5 indicates the influences of face-sheet thickness to total thickness ratio $\left( {h_{f} {/}h} \right)$, temperature environment, elastic foundation, and type of sandwich on the natural frequency of FGM sandwich TSSs with parameters are $h = 0.06\,{\text{m}}$, $R{/}h = 100$, $L{/}R = 0.5$, $L{/}a = 0.05$, $k = 1$, $m = 1,n = 2$, $P = 0\,{\text{Pa}}$. It can be observed that as the $h_{f} {/}h$ ratio rises, the natural frequency of the A-type sandwich shell increases, while the natural frequency of the B-type sandwich shell very little reduces. This can be explained as sandwich shells of type A have softcore made by metal and stiffer face sheets made by FGM, as the $h_{f} {/}h$ ratio increases, the face-sheet thickness increases and the thickness of core layer declines, leading to the increase of stiffness of structure; while, B-type of sandwich shells have core layer made by FGM and two face sheets made by metal and ceramic, as the face-sheet thickness to total thickness ratio increases, both soft face sheet made by metal and stiff face sheet made by ceramic get thicker. The stiffness of these two face sheets compensates for each other, the stiffness of structure may be changed very little. The information in Table 5 also reveals that the natural frequency of FGM sandwich TSSs rises with the presence of elastic foundation and reduces with the presence of the thermal environment. Besides, with the same geometrical parameters, the natural frequencies of A-type sandwich shells are lower than those of B-type sandwiches.

Table 5 The effect of temperature, $h_{f} {/}h$ ratio, and elastic foundation on the natural frequencies $\omega \,\left( {\text{rad/s}} \right)$ of FGM sandwich TSSs (type A and type B) using Eq. (33)

Table 6 illustrates the effects of length to equatorial radius ratio $\left( {L{/}R} \right)$ and longitudinal curvature radius to equatorial radius ratio $\left( {a{/}R} \right)$ on the natural frequency of FGM sandwich shells in case of without temperature effect and without elastic foundation. The geometrical parameters are chosen as $h = 0.06\,{\text{m}}$, $h_{f} {/}h = 0.1$, $R{/}h = 100$, $P = 0{\text{Pa}}$, $k = 1$, $m = 1,\,n = 3$. The obtained results show that the shell is longer (i.e., $L{/}R$ ratio increases), its natural frequency is lower. For convex shells (i.e. $a > 0$), as $a{/}R$ ratio rises the natural frequency lessens. For concave shells (i.e. $a < 0$), as $a{/}R$ ratio increases the natural frequency rises. Furthermore, with the same length and equatorial radius, the cylindrical shell has a higher natural frequency than concave shell but lower than convex one.

Table 6 The effect of $L{/}a$ and $L{/}R$ ratios on the natural frequencies $\omega \,\left( {\text{rad/s}} \right)$ of FGM sandwich toroidal shell segments (type B) using Eq. (33)

4.2.2 Nonlinear frequencies

Using Eq. (37), the frequency-amplitude relations are outlined in Figs. 3, 4, 5, and 6 analyze the effects of elastic foundation and the $a{/}R$ ratio on the nonlinear frequency to linear frequency $\left( {\omega_{NL} {/}\omega_{mn} } \right)$ of FGM sandwich TSSs of type A and type B for mode numbers $\left( {m,n} \right) = \left( {1,7} \right)$. The input data is expressed in these figures. It can be observed that the lowest value of the $\omega_{NL} {/}\omega_{mn}$ ratio increases as $a{/}R$ decreases (i.e., more convex shells). However, when the vibration amplitude is large enough, the less convex shells have higher $\omega_{NL} {/}\omega_{mn}$ ratio than more convex ones. Information in Figs. 5 and 6 shows that elastic foundation enhances the $\omega_{NL} {/}\omega_{mn}$ ratio in the region of small-amplitude but reduces this ratio in the region of large-amplitude.

Fig. 3

The effect of $a{/}R$ ratio on the frequency-amplitude curves of A-type FGM sandwich shells in case of free vibration

Fig. 4

The effect of $a{/}R$ ratio on the frequency-amplitude curves of B-type FGM sandwich shells in case of free vibration

Fig. 5

The effect of elastic foundation on the frequency amplitude curves of A-type FGM sandwich shells in case of free vibration

Fig. 6

The effect of elastic foundation on the frequency amplitude curves of B-type FGM sandwich shells in case of free vibration

4.2.3 Nonlinear vibration responses

In this section, the input data is described in corresponding figures. Substitution the input data into Eq. (35), and using the Runge–Kutta method, the nonlinear vibration response of FGM sandwich TSSs is analyzed.

The effect of mode numbers $\left( {m,n} \right)$ on the nonlinear vibration responses of FGM sandwich TSSs of type A and type B excited by sinusoidal external pressure are demonstrated in Figs. 7 and 8, respectively. The input data is described in these figures. For both FGM sandwich shells of type A and type B, the vibration amplitude related to mode numbers $\left( {m,n} \right) = \left( {1,1} \right)$ is much greater than that related to other modes’ numbers. Especially, the vibration amplitude corresponding to mode numbers $\left( {m,n} \right) = \left( {3,1} \right)$ is much lower than that corresponding to the mode numbers $\left( {m,n} \right) = \left( {1,1} \right)$, $\left( {m,n} \right) = \left( {1,3} \right)$ and $\left( {m,n} \right) = \left( {1,5} \right)$. Furthermore, with the same geometrical parameters and mechanical condition, the FGM sandwich shells of type A have a higher amplitude than B-type sandwich ones. This shows that B-type FGM sandwich shells have higher dynamic load-carrying capacity than FGM sandwich of type A.

Fig. 7

The effect of mode $\left( {m,n} \right)$ on the nonlinear vibration responses of A-type FGM sandwich TSSs

Fig. 8

The effect of mode $\left( {m,n} \right)$ on the nonlinear vibration responses of B-type FGM sandwich TSSs

The influences of pressure loading on the nonlinear vibration response of both two types of FGM sandwich shells are graphically illustrated in Figs. 9 and 10. The input data is described in these figures. As expected, as the amplitude of exciting force rises, the vibration amplitude also grows.

Fig. 9

The effect of external pressure on the nonlinear vibration responses of A-type FGM sandwich TSSs

Fig. 10

The effect of external pressure on the nonlinear vibration responses of B-type FGM sandwich TSSs

Figures 11 and 12 depict the effect of volume fraction index $\left( k \right)$, presenting the contribution of material constituents in the FGM layer on the nonlinear responses of both two types of FGM sandwich TSSs. The input data is expressed in these figures. It can be observed that, as $k$ increases, the vibration amplitude of the A-type FGM sandwich shell reduces, whereas the vibration amplitude of the FGM sandwich of type B rises. This could be explained as follows: looking at Eqs. (1) and (2), one can see that when the volume fraction index $\left( k \right)$ increases, the effective elastic modulus of B-type sandwich shells reduces (the shells will be softer, leading to the rising of the vibration amplitude). In contrast, the effective elastic modulus of A-type sandwich shells rises as $\left( k \right)$ increases (the shells will be stiffer, reducing the vibration amplitude).

Fig. 11

The effect of volume fraction index on nonlinear vibration responses of A-type FGM sandwich TSSs

Fig. 12

The effect of volume fraction index on nonlinear vibration responses of B-type FGM sandwich TSSs

The influence of temperature environment on nonlinear vibration responses of FGM sandwich TSSs is graphically described in Figs. 13 and 14. The input data is depicted in these figures. The obtained result shows that temperature makes the shells to be deflected to the negative side of the $z$ coordinate axes (i.e., deflected outward).

Fig. 13

The effect of temperature environment on the nonlinear vibration responses of A-type shells

Fig. 14

The effect of temperature environment on the nonlinear vibration responses of B-type shells

Figures 15, 16, 17 and 18 illustrate the effect of length to longitudinal curvature radius ratio $\left( {L{/}a} \right)$ on the nonlinear vibration response of FGM sandwich convex shells and FGM sandwich concave shells. It can observe that the vibration amplitude grows as the absolute value of $L{/}a$ ratio increases for both two types of FGM sandwich and both convex and concave shells. Especially, the nonlinear vibration response of concave shells is very sensitive to the change of $L{/}a$ ratio.

Fig. 15

The effect of $L{/}a$ ratio on the nonlinear vibration responses of convex FGM sandwich shells of type A

Fig. 16

The effect of $L{/}a$ ratio on the nonlinear vibration responses of convex FGM sandwich shells of type B

Fig. 17

The effect of $L{/}a$ ratio on the nonlinear vibration responses of concave FGM sandwich shells of type A

Fig. 18

The effect of $L{/}a$ ratio on the nonlinear vibration response of concave FGM sandwich shells of type B

The length to equatorial radius ratio $\left( {L{/}R} \right)$ is a geometrical parameter characterizing the shallowness of TSS. The effect of this parameter on the nonlinear vibration response of FGM sandwich shells is described in Figs. 19 and 20. As can be observed, the vibration amplitude rises as the $L{/}R$ ratio increases.

Fig. 19

The effect of $L{/}R$ ratio on the nonlinear vibration responses of A-type FGM sandwich TSSs

Fig. 20

The effect of $L{/}R$ ratio on the nonlinear vibration responses of B-type FGM sandwich TSSs

Figures 21 and 22 depict the effect of equatorial radius to total thickness ratio $\left( {R{/}h} \right)$ on the nonlinear vibration response of both two types of FGM sandwich shells. It is not surprising that the vibration amplitude of both two types of FGM sandwich shell increases as $R{/}h$ rises.

Fig. 21

The effect of $R{/}h$ ratio on the nonlinear vibration responses of A-type FGM sandwich TSSs

Fig. 22

The effect of $R{/}h$ ratio on the nonlinear vibration response of B-type FGM sandwich TSSs

The effect of face sheet thickness to total thickness ratio $\left( {h_{f} {/}h} \right)$ on the vibration response of FGM sandwich TSS is described in Figs. 23 and 24. It can be observed, when the $h_{f} {/}h$ ratio grows, the vibration amplitude of the A-type FGM sandwich shell reduces, whereas the amplitude of the B-type sandwich shell is almost unchanged. This is explained as: for B-type FGM sandwich shell, as face-sheet thickness to total thickness ratio increases, both soft face sheet made by metal and stiff face sheet made by ceramic are thicker. The stiffness of these two face sheets compensates for each other; the stiffness of structure may be changed very little.

Fig. 23

The effect of $h_{f} {/}h$ ratio on the nonlinear vibration responses of A-type FGM sandwich TSSs

Fig. 24

The effect of $h_{f} {/}h$ ratio on the nonlinear vibration response of B-type FGM sandwich TSSs

Figures 25 and 26 depict the influence of pre-axial compressive load and damping coefficient on the nonlinear vibration response of A-type FGM sandwich shells. The obtained result shows that, as the value of pre-axial compressive load increases, the vibration amplitude reduces. As expected, with the presence of damping coefficient, the vibration amplitude decreases.

Fig. 25

The effect of pre-axial compressive load on the nonlinear vibration response of A-type shells

Fig. 26

The effect of damping coefficient on nonlinear the vibration response of A-type shells

5 Conclusions

Based on a third-order shear deformation shell theory developed by Reddy and Liu [1] accounts for small strains but moderately large rotations, an analytical investigation on the nonlinear vibration of FGM sandwich TSSs is presented. Using the solution in terms of Airy stress function and displacement formulations in conjunction with the Galerkin method and the Runge–Kutta method, the nonlinear vibration behaviors of FGM sandwich TSSs such as natural frequency, nonlinear free frequency, and nonlinear forced vibration response are analyzed. A comparison with existing results shows that the present approach is accurate and reliable. The effect of geometrical, material properties, elastic foundation, thermal environment on the nonlinear vibration behavior of FGM sandwich TSSs is studied and discussed in detail. Specifically, this study shows that the natural frequency of FGM sandwich TSSs calculated by using the Airy stress function method is quite similar to that calculated by using displacement formulations.

Appendices

Appendix A

$$I_{i} = \int\limits_{ - h/2}^{h/2} {\rho \left( z \right)z^{i - 1} dz} ,\quad \left( {i = 1,2,3,4,5,7} \right),$$

$$\overline{{I_{1} }} = I_{1} + \frac{{2I_{2} }}{R},\overline{{I_{1}^{/} }} = I_{1} + \frac{{2I_{2} }}{a},\overline{{I_{2} }} = I_{2} + \frac{{I_{3} }}{R} - cI_{4} - \frac{{cI_{5} }}{R},\overline{{I_{2}^{/} }} = I_{2} + \frac{{I_{3} }}{a} - cI_{4} - \frac{{cI_{5} }}{a},$$

$$\overline{{I_{3} }} = cI_{4} + \frac{{cI_{5} }}{R},\overline{{I_{3}^{/} }} = cI_{4} + \frac{{cI_{5} }}{a},\overline{{I_{4} }} = \overline{{I_{4}^{/} }} = I_{3} - 2cI_{5} + c^{2} I_{7} ,\overline{{I_{5} }} = \overline{{I_{5}^{/} }} = cI_{5} - c^{2} I_{7} .$$

Appendix B

$\begin{aligned} H_{11} \left( {u^{\left( 0 \right)} } \right) = & \frac{{E_{1} }}{{1 - \nu^{2} }}\frac{{\partial^{2} u^{\left( 0 \right)} }}{{\partial x^{2} }} + \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial^{2} u^{\left( 0 \right)} }}{{\partial y^{2} }},\quad H_{12} \left( {v^{\left( 0 \right)} } \right) = \frac{{E_{1} }}{{2\left( {1 - \nu } \right)}}\frac{{\partial^{2} v^{\left( 0 \right)} }}{\partial x\partial y},\quad H_{13} \left( {w^{\left( 0 \right)} } \right) = - \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial w^{\left( 0 \right)} }}{\partial x}, \\ & \quad + \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \nu \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right) + \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right) - \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x^{3} }} + \frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x\partial y^{2} }}} \right) \\ \end{aligned}$, $+ \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \nu \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$ $+ \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$ $- \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x^{3} }} + \frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x\partial y^{2} }}} \right)$$H_{14} \left( {\phi_{x} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + \frac{1 - \nu }{2}\frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }}} \right)$, $H_{15} \left( {\phi_{y} } \right) = \frac{{E_{2} - cE_{4} }}{{2\left( {1 - \nu } \right)}}\frac{{\partial^{2} \phi_{y} }}{\partial x\partial y}$, $H_{21} \left( {u^{\left( 0 \right)} } \right) = \frac{{E_{1} }}{{2\left( {1 - \nu } \right)}}\frac{{\partial^{2} u^{\left( 0 \right)} }}{\partial x\partial y}$, $H_{22} \left( {v^{\left( 0 \right)} } \right) = \frac{{E_{1} }}{{1 - \nu^{2} }}\frac{{\partial^{2} v^{\left( 0 \right)} }}{{\partial y^{2} }} + \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial^{2} v^{\left( 0 \right)} }}{{\partial x^{2} }}$, $H_{23} \left( {w^{\left( 0 \right)} } \right) = - \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)\frac{{\partial w^{\left( 0 \right)} }}{\partial y}$ $+ \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \nu \frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$ $+ \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$ $- \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial y^{3} }} + \frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x^{2} \partial y}}} \right)$, $H_{24} \left( {\phi_{x} } \right) = \frac{{E_{2} - cE_{4} }}{{2\left( {1 - \nu } \right)}}\frac{{\partial^{2} \phi_{x} }}{\partial x\partial y}$,$H_{25} \left( {\phi_{y} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} + \frac{1 - \nu }{2}\frac{{\partial^{2} \phi_{y} }}{{\partial x^{2} }}} \right)$, $H_{31} \left( {u^{\left( 0 \right)} } \right) = \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} u^{\left( 0 \right)} }}{{\partial x^{3} }} + \frac{{\partial^{3} u^{\left( 0 \right)} }}{{\partial x\partial y^{2} }}} \right) + \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial u^{\left( 0 \right)} }}{\partial x}$, $H_{32} \left( {v^{\left( 0 \right)} } \right) = \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} v^{\left( 0 \right)} }}{{\partial x^{2} \partial y}} + \frac{{\partial^{3} v^{\left( 0 \right)} }}{{\partial y^{3} }}} \right) + \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)\frac{{\partial v^{\left( 0 \right)} }}{\partial y}$, $H_{33} \left( {w^{\left( 0 \right)} } \right) = \left[ {\frac{{ - E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{{a^{2} }} + \frac{2\nu }{{Ra}} + \frac{1}{{R^{2} }}} \right) - K_{1} } \right]w^{\left( 0 \right)}$ $- Ph\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }}$ $+ \left[ {\frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}} - \frac{{\phi_{1} }}{1 - \nu } + K_{2} } \right]\left( {\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }}} \right)$ $- \frac{{2cE_{4} }}{{1 - \nu^{2} }}\left[ {\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \left( {\frac{1}{R} + \frac{\nu }{a}} \right)\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }}} \right]$ $- \frac{{c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{4} w^{\left( 0 \right)} }}{{\partial x^{4} }} + 2\frac{{\partial^{4} w^{\left( 0 \right)} }}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w^{\left( 0 \right)} }}{{\partial y^{4} }}} \right)$ $+ \frac{{cE_{4} }}{1 + \nu }\left[ {\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \left( {\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)^{2} + \frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x\partial y^{2} }} + \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x^{2} \partial y}}} \right]$ $+ \frac{{cE_{4} }}{{1 - \nu^{2} }}\left[ \begin{gathered} \frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x^{3} }} + \nu \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x^{2} \partial y}} + 2\left( {2\nu - 1} \right)\left( {\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)^{2} \hfill \\ - 2\nu \frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial y^{3} }} + \nu \frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x\partial y^{2} }} \hfill \\ \end{gathered} \right]$ $+ \frac{{E_{1} }}{{1 - \nu^{2} }}\left[ \begin{gathered} \left( {\frac{1}{a} + \frac{\nu }{R}} \right)\left( {\frac{1}{2}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}} \right)^{2} - w\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }}} \right) \hfill \\ + \left( {\frac{1}{R} + \frac{\nu }{a}} \right)\left( {\frac{1}{2}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial y}} \right)^{2} - w\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }}} \right) + \left( {1 - \nu } \right)\frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial w^{\left( 0 \right)} }}{\partial y} \hfill \\ \end{gathered} \right]$ $+ \frac{{E_{1} }}{{2\left( {1 - \nu^{2} } \right)}}\left[ {\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}} \right)^{2} \frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \nu \left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial y}} \right)^{2} \frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial y}} \right)^{2} \frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \nu \left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}} \right)^{2} \frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }}} \right]$, $H_{34} \left( {\phi_{x} } \right) = \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \phi_{x} }}{\partial x}$ $+ \frac{{cE_{5} - c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} \phi_{x} }}{{\partial x^{3} }} + \frac{{\partial^{3} \phi_{x} }}{{\partial x\partial^{2} y}}} \right)$ $+ \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial \phi_{x} }}{\partial x}$, $H_{35} \left( {\phi_{y} } \right) = \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \phi_{y} }}{\partial y}$ $+ \frac{{cE_{5} - c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} \phi_{y} }}{{\partial y^{3} }} + \frac{{\partial^{3} \phi_{y} }}{{\partial x^{2} \partial y}}} \right)$ $+ \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)\frac{{\partial \phi_{y} }}{\partial y}$, $H_{36} \left( {u^{\left( 0 \right)} ,w^{\left( 0 \right)} } \right) = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{{\partial u^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \nu \frac{{\partial u^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \frac{{\partial u^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$, $H_{37} \left( {v^{\left( 0 \right)} ,w^{\left( 0 \right)} } \right) = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{{\partial v^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \nu \frac{{\partial v^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \frac{{\partial v^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$, $H_{38} \left( {\phi_{x} ,w^{\left( 0 \right)} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left[ {\frac{{\partial \phi_{x} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \nu \frac{{\partial \phi_{x} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \left( {1 - \nu } \right)\frac{{\partial \phi_{x} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right]$, $H_{39} \left( {\phi_{y} ,w^{\left( 0 \right)} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left[ {\frac{{\partial \phi_{y} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \nu \frac{{\partial \phi_{y} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \left( {1 - \nu } \right)\frac{{\partial \phi_{y} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right]$, $H_{41} \left( {u^{\left( 0 \right)} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} u^{\left( 0 \right)} }}{{\partial x^{2} }} + \frac{1 - \nu }{2}\frac{{\partial^{2} u^{\left( 0 \right)} }}{{\partial y^{2} }}} \right)$, $L_{42} \left( {v^{\left( 0 \right)} } \right) = \frac{{E_{2} - cE_{4} }}{{2\left( {1 - \nu } \right)}}\frac{{\partial^{2} v^{\left( 0 \right)} }}{\partial x\partial y}$, $H_{43} \left( {w^{\left( 0 \right)} } \right) = - \left[ {\frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right) + \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}} \right]\frac{{\partial w^{\left( 0 \right)} }}{\partial x}$ $+ \frac{{E_{2} - cE_{4} }}{{2\left( {1 + \nu } \right)}}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$ $+ \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \nu \frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$ $+ \frac{{ - cE_{5} + c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x^{3} }} + \frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x\partial y^{2} }}} \right)$, $H_{44} \left( {\phi_{x} } \right) = - \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}\phi_{x}$ $+ \frac{{E_{3} - 2cE_{5} + c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + \frac{1 - \nu }{2}\frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }}} \right)$, $H_{45} \left( {\phi_{y} } \right) = \frac{{E_{3} - 2cE_{5} + c^{2} E_{7} }}{{2\left( {1 - \nu } \right)}}\frac{{\partial^{2} \phi_{y} }}{\partial x\partial y}$, $H_{51} \left( {u^{\left( 0 \right)} } \right) = \frac{{E_{2} - cE_{4} }}{{2\left( {1 - \nu } \right)}}\frac{{\partial^{2} u^{\left( 0 \right)} }}{\partial x\partial y}$, $H_{52} \left( {v^{\left( 0 \right)} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} v^{\left( 0 \right)} }}{{\partial y^{2} }} + \frac{1 - \nu }{2}\frac{{\partial^{2} v^{\left( 0 \right)} }}{{\partial x^{2} }}} \right)$, $H_{53} \left( {w^{\left( 0 \right)} } \right) = - \left[ {\frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right) + \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}} \right]\frac{{\partial w^{\left( 0 \right)} }}{\partial y}$$+ \frac{{E_{2} - cE_{4} }}{{2\left( {1 + \nu } \right)}}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial x^{2} }} + \frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$ $+ \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{{\partial w^{\left( 0 \right)} }}{\partial y}\frac{{\partial^{2} w^{\left( 0 \right)} }}{{\partial y^{2} }} + \nu \frac{{\partial w^{\left( 0 \right)} }}{\partial x}\frac{{\partial^{2} w^{\left( 0 \right)} }}{\partial x\partial y}} \right)$ $+ \frac{{ - cE_{5} + c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial y^{3} }} + \frac{{\partial^{3} w^{\left( 0 \right)} }}{{\partial x^{2} \partial y}}} \right)$, $H_{54} \left( {\phi_{x} } \right) = \frac{{E_{3} - 2cE_{5} + c^{2} E_{7} }}{{2\left( {1 - \nu } \right)}}\frac{{\partial^{2} \phi_{x} }}{\partial x\partial y}$, $H_{55} \left( {\phi_{y} } \right) = - \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}\phi_{y} + \frac{{E_{3} - 2cE_{5} + c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} + \frac{1 - \nu }{2}\frac{{\partial^{2} \phi_{y} }}{{\partial x^{2} }}} \right).$

Appendix C

$h_{11} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {M^{2} + \frac{1 - \nu }{2}N^{2} } \right)$, $h_{12} = \frac{{E_{1} MN}}{{2\left( {1 - \nu } \right)}}$, $h_{13} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)M - \frac{{cE_{4} }}{{1 - \nu^{2} }}M\left( {M^{2} + N^{2} } \right)$, $h_{14} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {M^{2} + \frac{1 - \nu }{2}N^{2} } \right)$, $h_{15} = \frac{{E_{2} - cE_{4} }}{{2\left( {1 - \nu } \right)}}MN$, $h_{16} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {2M^{3} + \frac{1 - 3\nu }{2}MN^{2} } \right)\frac{{4\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}$, $h_{21} = \frac{{E_{1} MN}}{{2\left( {1 - \nu } \right)}}$, $h_{22} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {N^{2} + \frac{1 - \nu }{2}M^{2} } \right)$, $h_{23} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)N - \frac{{cE_{4} }}{{1 - \nu^{2} }}N\left( {M^{2} + N^{2} } \right)$, $h_{24} = \frac{{E_{2} - cE_{4} }}{{2\left( {1 - \nu } \right)}}MN$, $h_{25} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {N^{2} + \frac{1 - \nu }{2}M^{2} } \right)$, $h_{26} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {2N^{3} + \frac{1 - 3\nu }{2}M^{2} N} \right)\frac{{4\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}$, $h_{31} = \frac{{cE_{4} }}{{1 - \nu^{2} }}M\left( {M^{2} + N^{2} } \right) - \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)M$, $h_{32} = \frac{{cE_{4} }}{{1 - \nu^{2} }}N\left( {M^{2} + N^{2} } \right) - \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)N$, $h_{33} = - \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}\left( {M^{2} + N^{2} } \right)$ $+ \frac{{2cE_{4} }}{{1 - \nu^{2} }}\left[ {\left( {\frac{1}{a} + \frac{\nu }{R}} \right)M^{2} + \left( {\frac{1}{R} + \frac{\nu }{a}} \right)N^{2} } \right]$ $- \frac{{c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {M^{2} + N^{2} } \right)^{2}$$- \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{{a^{2} }} + \frac{2\nu }{{Ra}} + \frac{1}{{R^{2} }}} \right)$ $- \left[ {K_{1} + K_{2} \left( {M^{2} + N^{2} } \right)} \right]$, $\delta_{m} = \left( { - 1} \right)^{m} - 1,\delta_{n} = \left( { - 1} \right)^{n} - 1$, $h_{34} = - \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}M + \frac{{cE_{5} - c^{2} E_{7} }}{{1 - \nu^{2} }}M\left( {M^{2} + N^{2} } \right) - \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)M$, $h_{35} = - \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}N + \frac{{cE_{5} - c^{2} E_{7} }}{{1 - \nu^{2} }}N\left( {M^{2} + N^{2} } \right) - \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)N$, $h_{36} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left[ {\left( {\frac{1}{a} + \frac{\nu }{R}} \right)M^{2} + \left( {\frac{1}{R} + \frac{\nu }{a}} \right)N^{2} } \right]\frac{{20\delta_{m} \delta_{n} }}{{9mn\pi^{2} }} - \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {M^{4} + N^{4} + \frac{1 + 9\nu }{2}M^{2} N^{2} } \right)\frac{{8\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}$, $h_{37} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {M^{3} + \frac{1 - 3\nu }{4}MN^{2} } \right)\frac{{16\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}$, $h_{38} = \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {N^{3} + \frac{1 - 3\nu }{4}M^{2} N} \right)\frac{{16\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}$, $h_{39} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {M^{3} + \frac{1 - 3\nu }{4}MN^{2} } \right)\frac{{16\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}$, $h_{310} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {N^{3} + \frac{1 - 3\nu }{4}M^{2} N} \right)\frac{{16\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}$, $h_{311} = \frac{{ - 3E_{1} }}{{32\left( {1 - \nu^{2} } \right)}}\left[ {M^{4} + N^{4} - \frac{{2\left( {1 - 4\nu } \right)}}{3}M^{2} N^{2} } \right]$, $h_{41} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {M^{2} + \frac{1 - \nu }{2}N^{2} } \right)$, $h_{42} = \frac{{E_{2} - cE_{4} }}{{2\left( {1 - \nu } \right)}}MN$, $h_{43} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)M$ $- \frac{{cE_{5} - c^{2} E_{7} }}{{1 - \nu^{2} }}M\left( {M^{2} + N^{2} } \right)$ $+ \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}M$, $h_{44} = \frac{{E_{3} - 2cE_{5} + c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {M^{2} + \frac{1 - \nu }{2}N^{2} } \right) + \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}$, $h_{45} = \frac{{E_{3} - 2cE_{5} + c^{2} E_{7} }}{{2\left( {1 - \nu } \right)}}MN$, $h_{46} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {2M^{3} - \frac{1 + \nu }{2}MN^{2} } \right)\frac{{4\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}$, $h_{51} = \frac{{E_{2} - cE_{4} }}{{2\left( {1 - \nu } \right)}}MN$, $h_{52} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {N^{2} + \frac{1 - \nu }{2}M^{2} } \right)$, $h_{53} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)N - \frac{{cE_{5} - c^{2} E_{7} }}{{1 - \nu^{2} }}N\left( {M^{2} + N^{2} } \right) + \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}N$, $h_{54} = \frac{{E_{3} - 2cE_{5} + c^{2} E_{7} }}{{2\left( {1 - \nu } \right)}}MN$, $h_{55} = \frac{{E_{3} - 2cE_{5} + c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {N^{2} + \frac{1 - \nu }{2}M^{2} } \right) + \frac{{E_{1} - 6cE_{3} + 9c^{2} E_{5} }}{{2\left( {1 + \nu } \right)}}$, $h_{56} = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {2N^{3} - \frac{1 + \nu }{2}M^{2} N} \right)\frac{{4\delta_{m} \delta_{n} }}{{9mn\pi^{2} }}.$

Thermal parameters: $\Phi_{{1{\text{T}}}} = \frac{{\Phi_{1} }}{1 - \nu }\left( {M^{2} + N^{2} } \right)$, $\Phi_{{{\text{2T}}}} = \frac{{\Phi_{1} }}{1 - \nu }\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{4\delta_{m} \delta_{n} }}{{mn\pi^{2} }}$ in which $\Phi_{1} = E_{c} \alpha_{c} + \frac{{E_{c} \alpha_{mc} + E_{mc} \alpha_{c} }}{h}\left( {\frac{{2h_{f} }}{k + 1} + h_{co} } \right) + \frac{{E_{mc} \alpha_{mc} }}{h}\left( {\frac{{2h_{f} }}{2k + 1} + h_{co} } \right)$ (Type A), $\Phi_{1} = E_{m} \alpha_{m} + \frac{{E_{m} \alpha_{cm} + E_{cm} \alpha_{m} }}{h}\left( {\frac{{2h_{co} }}{k + 1} + h_{f} } \right) + \frac{{E_{cm} \alpha_{cm} }}{h}\left( {\frac{{2h_{co} }}{2k + 1} + h_{f} } \right)$ (Type B).

Appendix D

$D_{1} = I_{1} + c^{2} I_{7} \left( {M^{2} + N^{2} } \right) - \overline{{I_{3} }} L_{51} M - \overline{{I_{3}^{/} }} L_{61} N - \overline{{I_{5} }} L_{71} M - \overline{{I_{5}^{/} }} L_{81} N$, $D_{2} = 2\varepsilon I_{1}$, $D_{3} = - \left( {h_{31} L_{11} + h_{32} L_{21} + h_{33} + h_{34} L_{31} + h_{35} L_{41} } \right)$, $D_{4} = - \left( {h_{31} L_{12} + h_{32} L_{22} + h_{34} L_{32} + h_{35} L_{42} + h_{36} + h_{37} L_{11} + h_{38} L_{21} + h_{39} L_{31} + h_{310} L_{41} } \right)$, $D_{5} = - \left( {h_{37} L_{12} + h_{38} L_{22} + h_{39} L_{32} + h_{310} L_{42} + h_{311} } \right)$, $D_{6} = - \frac{{4\delta_{m} \delta_{n} }}{{mn\pi^{2} }}$ in which $L_{11} = \frac{{ - \det \left( {\begin{array}{*{20}c} {h_{13} } & {h_{12} } & {h_{14} } & {h_{15} } \\ {h_{23} } & {h_{22} } & {h_{24} } & {h_{25} } \\ {h_{43} } & {h_{42} } & {h_{44} } & {h_{45} } \\ {h_{53} } & {h_{52} } & {h_{54} } & {h_{55} } \\ \end{array} } \right)}}{\Delta }$, $L_{12} = \frac{{ - \det \left( {\begin{array}{*{20}c} {h_{16} } & {h_{12} } & {h_{14} } & {h_{15} } \\ {h_{26} } & {h_{22} } & {h_{24} } & {h_{25} } \\ {h_{46} } & {h_{42} } & {h_{44} } & {h_{45} } \\ {h_{56} } & {h_{52} } & {h_{54} } & {h_{55} } \\ \end{array} } \right)}}{\Delta }$, $L_{21} = \frac{{ - \det \left( {\begin{array}{*{20}c} {h_{11} } & {h_{13} } & {h_{14} } & {h_{15} } \\ {h_{21} } & {h_{23} } & {h_{24} } & {h_{25} } \\ {h_{41} } & {h_{43} } & {h_{44} } & {h_{45} } \\ {h_{51} } & {h_{53} } & {h_{54} } & {h_{55} } \\ \end{array} } \right)}}{\Delta }$, $L_{22} = \frac{{ - \det \left( {\begin{array}{*{20}c} {h_{11} } & {h_{16} } & {h_{14} } & {h_{15} } \\ {h_{21} } & {h_{26} } & {h_{24} } & {h_{25} } \\ {h_{41} } & {h_{46} } & {h_{44} } & {h_{45} } \\ {h_{51} } & {h_{56} } & {h_{54} } & {h_{55} } \\ \end{array} } \right)}}{\Delta }$, $L_{31} = \frac{{ - \det \left( {\begin{array}{*{20}c} {h_{11} } & {h_{12} } & {h_{13} } & {h_{15} } \\ {h_{21} } & {h_{22} } & {h_{23} } & {h_{25} } \\ {h_{41} } & {h_{42} } & {h_{43} } & {h_{45} } \\ {h_{51} } & {h_{52} } & {h_{53} } & {h_{55} } \\ \end{array} } \right)}}{\Delta }$, $L_{32} = \frac{{ - \det \left( {\begin{array}{*{20}c} {h_{11} } & {h_{12} } & {h_{16} } & {h_{15} } \\ {h_{21} } & {h_{22} } & {h_{26} } & {h_{25} } \\ {h_{41} } & {h_{42} } & {h_{46} } & {h_{45} } \\ {h_{51} } & {h_{52} } & {h_{56} } & {h_{55} } \\ \end{array} } \right)}}{\Delta }$, $L_{41} = \frac{{ - \det \left( {\begin{array}{*{20}c} {h_{11} } & {h_{12} } & {h_{14} } & {h_{13} } \\ {h_{21} } & {h_{22} } & {h_{24} } & {h_{23} } \\ {h_{41} } & {h_{42} } & {h_{44} } & {h_{43} } \\ {h_{51} } & {h_{52} } & {h_{54} } & {h_{53} } \\ \end{array} } \right)}}{\Delta }$, $L_{42} = \frac{{ - \det \left( {\begin{array}{*{20}c} {h_{11} } & {h_{12} } & {h_{14} } & {h_{16} } \\ {h_{21} } & {h_{22} } & {h_{24} } & {h_{26} } \\ {h_{41} } & {h_{42} } & {h_{44} } & {h_{46} } \\ {h_{51} } & {h_{52} } & {h_{54} } & {h_{56} } \\ \end{array} } \right)}}{\Delta }$, $L_{51} = \frac{{\left( {\overline{{I_{3} }} \overline{{I_{4} }} - \overline{{I_{2} }} \overline{{I_{5} }} } \right)M}}{{\overline{{I_{1} }} \overline{{I_{4} }} - \left( {\overline{{I_{2} }} } \right)^{2} }}$, $L_{61} = \frac{{\left( {\overline{{I_{3}^{/} }} \overline{{I_{4}^{/} }} - \overline{{I_{2}^{/} }} \overline{{I_{5}^{/} }} } \right)N}}{{\overline{{I_{1}^{/} }} \overline{{I_{4}^{/} }} - \left( {\overline{{I_{2}^{/} }} } \right)^{2} }}$, $L_{71} = \frac{{\left( {\overline{{I_{1} }} \overline{{I_{5} }} - \overline{{I_{2} }} \overline{{I_{3} }} } \right)M}}{{\overline{{I_{1} }} \overline{{I_{4} }} - \left( {\overline{{I_{2} }} } \right)^{2} }}$, $L_{81} = \frac{{\left( {\overline{{I_{1}^{/} }} \overline{{I_{5}^{/} }} - \overline{{I_{2}^{/} }} \overline{{I_{3}^{/} }} } \right)N}}{{\overline{{I_{1}^{/} }} \overline{{I_{4}^{/} }} - \left( {\overline{{I_{2}^{/} }} } \right)^{2} }}$, $\Delta = \det \left( {\begin{array}{*{20}c} {h_{11} } & {h_{12} } & {h_{14} } & {h_{15} } \\ {h_{21} } & {h_{22} } & {h_{24} } & {h_{25} } \\ {h_{41} } & {h_{42} } & {h_{44} } & {h_{45} } \\ {h_{51} } & {h_{52} } & {h_{54} } & {h_{55} } \\ \end{array} } \right).$

Appendix E

$B_{1} = I_{1} - \left[ {A_{3} - A_{2} \left( {M^{2} + N^{2} } \right)} \right]\left( {C_{12} M + C_{22} N} \right) - A_{6} \left( {M^{2} + N^{2} } \right)$, $B_{3} = K_{1} + K_{2} \left( {M^{2} + N^{2} } \right)$ $+ \left[ {A_{2} \left( {M^{2} + N^{2} } \right) - A_{3} } \right]\left( {C_{11} M + C_{21} N} \right) - A_{3} \left( {M^{2} + N^{2} } \right)$ $- N^{2} \Phi_{1} - \left( {M^{2} + \nu N^{2} } \right)Ph$ + $+ A_{5} \left( {M^{2} + N^{2} } \right)^{2} + F_{11} \left( {\frac{{M^{2} }}{R} + \frac{{N^{2} }}{a}} \right)$ in which $A_{2} = \frac{{E_{1} E_{3} - E_{2}^{2} + c\left( {E_{2} E_{4} - E_{1} E_{5} } \right)}}{{E_{1} \left( {1 - \nu^{2} } \right)}}$, $A_{3} = \frac{{c\left( {E_{2} E_{4} - E_{1} E_{5} } \right)}}{{E_{1} \left( {1 - \nu^{2} } \right)}}$, $A_{5} = \frac{{E_{1} E_{5} - E_{2} E_{4} + c\left( {E_{4}^{2} - E_{1} E_{7} } \right)}}{{E_{1} \left( {1 - \nu^{2} } \right)}}$, $A_{6} = \frac{{c\left( {E_{4}^{2} - E_{1} E_{7} } \right)}}{{E_{1} \left( {1 - \nu^{2} } \right)}}$, $A_{7} = \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}}$, $A_{8} = \frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}$, $C_{11} = \frac{{v_{13} v_{22} - v_{12} v_{23} }}{{v_{11} v_{22} - v_{12} v_{21} }}$, $C_{12} = \frac{{v_{14} v_{22} - v_{12} v_{24} }}{{v_{11} v_{22} - v_{12} v_{21} }}$, $C_{21} = \frac{{v_{11} v_{23} - v_{21} v_{13} }}{{v_{11} v_{22} - v_{12} v_{21} }}$, $C_{22} = \frac{{v_{11} v_{24} - v_{21} v_{14} }}{{v_{11} v_{22} - v_{12} v_{21} }}$, $v_{11} = \left( {3cA_{8} - A_{7} } \right) - \left( {A_{2} - cA_{5} } \right)\left( {M^{2} - \frac{1 - \nu }{2}N^{2} } \right)$, $v_{12} = - \frac{1 + \nu }{2}\left( {A_{2} - cA_{5} } \right)MN$, $v_{13} = \left( {A_{3} - cA_{6} } \right)\left( {M^{3} + MN^{2} } \right) + \left( {A_{7} - 3cA_{8} } \right)M,v_{14} = - \overline{\overline{{I_{5} }}} M$, $\overline{\overline{{I_{5} }}} = \overline{{I_{5} }} - \overline{{I_{2} }} \overline{{I_{3} }} {/}\overline{{I_{1} }}$, $v_{21} = - \frac{1 + \nu }{2}\left( {A_{2} - cA_{5} } \right)MN$, $v_{22} = \left( {3cA_{8} - A_{7} } \right) - \left( {A_{2} - cA_{5} } \right)\left( {N^{2} - \frac{1 - \nu }{2}M^{2} } \right)$, $v_{23} = \left( {A_{3} - cA_{6} } \right)\left( {N^{3} + NM^{2} } \right) + \left( {A_{7} - 3cA_{8} } \right)N,v_{24} = - \overline{\overline{{I_{5}^{/} }}} N$, $\overline{\overline{{I_{5}^{/} }}} = \overline{{I_{5}^{/} }} - \overline{{I_{2}^{/} }} \overline{{I_{3}^{/} }} {/}\overline{{I_{1}^{/} }}$, $F_{11} = \frac{{E_{1} }}{{\left( {M^{2} + N^{2} } \right)^{2} }}\left( {\frac{{M^{2} }}{R} + \frac{{N^{2} }}{a}} \right).$

Appendix F

$g_{1} = \frac{{D_{2} }}{{D_{1} }}$, $g_{2} = \frac{{D_{4} }}{{D_{3} - \Phi_{1T} - PhM^{2} }}$, $g_{3} = \frac{{D_{5} }}{{D_{3} - \Phi_{1T} - PhM^{2} }}$, $g_{4} = \frac{{D_{6} }}{{D_{1} }}Q$, $g_{5} = \frac{{\Phi_{2T} }}{{D_{1} }}.$