1 Introduction

As the typical representative of novelty intelligent multifunctional structure, sandwich shell structure is made up of three important components including base layer (lower panel), viscoelastic core layer (core structure) and constraining layer (upper panel). Comparing with the traditional shell engineering structure, sandwich shell structure has excellent capacity in energy dissipation and absorption, high temperature and pressure resistances, low-weight and high structural efficiency. Based on the above excellent structural properties, sandwich shell structure has been promoted to various engineering applications including underwater submarine, launch vehicle, spacecraft and pressure vessels and so on. However, the vibration and damping performances with regard to sandwich shells have important influences in the reliability and stability of engineering structure composed of sandwich shell structure. Thus, the investigations of vibration and damping characteristic have great significance to the structural designation and safety performance evaluation of sandwich shell structure.

Yadav et al. [1] analyzed the forced vibration behaviors of sandwich shell contain cellular core and thin panels based on high-order shear deformation theory (HSDT) by employing Galerkin, incremental harmonic balance and arclength continuation methods. Yang et al. [2] proposed a three-dimensional numerical model of sandwich shallow shells under various boundary conditions for investigating its vibration characteristics by using Rayleigh–Ritz and modified three-dimensional Fourier series approaches. Li et al. [3] studied the vibration and thermal buckling behaviors of sandwich shells made up of face panels with functionally graded material (FGM) and tunable auxetic honeycomb core by employing complex modulus approach and Hamilton’s principle. Wang et al. [4] studied the vibration behaviors of sandwich cylindrical shell with composite pyramidal truss core by employing theoretically in conjunction with experimentally. Wang et al. [5, 6] put forward a semi-analytical approach for investigating the vibration behaviors of sandwich shell and panel with FGM under various boundary conditions by using modified Fourier series method based on first-order shear deformation theory (FSDT). Taati et al. [7, 8] focused on the vibration behaviors with regard to sandwich cylindrical shell which consists of carbon nanotube-reinforced face sheets and metal foam core under fluid flow by establishing fluid–structure coupling model based on classical shell theories. Yang et al. [9] discussed the vibration and damping characteristics of sandwich shells with pyramidal truss-like cores by applying finite element and Rayleigh–Ritz methods. Karimiasl et al. [10] investigated the nonlinear vibration behaviors of sandwich shell composed of magnetorheological layer flexible core layer and composite layer based on the Hamilton’s principle and Reddy’s third-order shear deformation theory. Li et al. [11] studied the free flexural vibration behaviors of sandwich shell with porous honeycomb core based on Flügge’s shell theory and Gibson’s formula in conjunction with experiments. Fu et al. [12] investigated the vibration behaviors of sandwich shells composed of functionally graded material skins and isotropic core subjected to elastic foundations by applying generalized differential quadrature approach. Sobhani et al. [13] researched the vibration characteristics of sandwich coupled shells under boundary conditions based on FSDT and Donnell’s shell theory. Kumar et al. [14] established two-dimensional finite element model for studying the vibration behaviors of sandwich shell by using first and higher order zigzag theories. Singha et al. [15] analyzed the vibration behaviors of sandwich conical shell made up of composite panels and synthetic foam core. Li et al. [16, 17] proposed an analytical model of shells that consist of hexagon honeycomb core and fiber-reinforced composite skins by employing Hamilton’s principle and Galerkin approach.

Sobhani et al. [18, 19] analyzed the circumferential vibration of sandwich coupled shell structures subjected to various elastic boundary conditions by using generalized differential quadrature strategy and Hamilton’s method. Xue et al. [20] investigated the damping and vibration performances of sandwich cylindrical shell with gradient core by means of experiments. Sofiyev et al. [21] discussed the vibration and bulking behaviors of sandwich cylindrical shell with different type coatings by applying FSDT. Chen et al. [22,23,24,25] presented a dynamics model to investigate the sandwich doubly-curved shallow shells subjected to simply supported boundary conditions by employing Navier method in conjunction with FSDT. Sayyad et al. [26,27,28] analyzed the vibration and bending behaviors of sandwich spherical and conical shells based on classical and high-order shear shell theories and Hamilton’s principle. F. Bahranifard et al. [29,30,31] investigated the dynamic characteristics of sandwich-truncated conical shells made up of face sheets and porous core by using Chebyshev–Ritz method. Li et al. [32] presented a novelty theoretical analysis model of sandwich cylindrical shell with composite pyramidal truss and damp coating subjected to elastically supported boundary conditions by applying Rayleigh–Ritz approach. Zheng et al. [33] provided an accurate numerical model of sandwich shell made up of composite panel layer and magnetorheological core by means of wave propagation technique, Hamilton’s principle and linear viscoelastic scheme. Biswal et al. [34, 35] discussed the vibration and damping behaviors of sandwich shells with three layers including base layer, viscoelastic core and constraining layer based on Hamilton’s principle by employing finite element method. Soureshjani et al. [36] proposed a semi-analytical approach for investigating the vibration characteristics with regard to coupled sandwich conical shell structures under various boundary conditions. Parand et al. [37, 38] analyzed the vibration behaviors of sandwich shell with viscoelastic interface and FGM core by employing Fourier series in conjunction with differential quadrature method. Sahu et al. [39] researched the vibration and damping behaviors of sandwich shell panels including viscoelastic core layer and functional graded layer based on FSDT by utilizing finite element method.

This paper proposes an unified numerical method for investigating the vibration and damping behaviors of sandwich shell structure including conical shell and cylindrical shell by employing the meshfree method. The sandwich shell structures are composed of based layer, viscoelastic layer and constraining layer, and the theoretical formulations of sandwich shells are derived based on energy principle and Donnel shell assumption in conjunction with FSDT. Only flexural and axial deformations are allowed in the base layer and constraining layer; only shear strains is allowed in the viscoelastic layer. Using the continuity condition in interface between the layers, the displacement components of the viscoelastic core are replaced by those of base and constraining layers. The displacement components of sandwich shell are approximated by employing Fourier series in conjunction with shape function produced by meshfree Tchebychev radial point interpolation method. The validation of the presented approach is verified by the comparison results of presented approach and existing literatures. Based on the above proposed method, the vibration and damping analyses of sandwich shells are performed by investigating the influences of the parameters including geometric dimension, boundary conditions and material properties on the vibration and modal loss factor of sandwich shell.

2 Theoretical modeling

2.1 Introduction of model

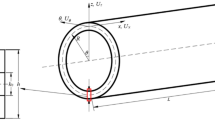
As shown in Fig. 1, sandwich conical shell structure with isotropic is made up of three layers including based layer, viscoelastic core layer and constraining layer. For convenience, the sandwich conical shell structure is described by employing orthogonal curvilinear coordinate systems, and the above coordinate systems are established at the middle surfaces of each layer. α and L denote semi-vertex and length with respect to sandwich conical shell structure of each layer; Ri0 (i = s, v, c) represents the left side of sandwich conical shell structure of each layer and the subscript characters s, v and c of Ri0 indicate base layer, viscoelastic core layer and constraining layer. Meanwhile, it is worth mentioning that the conical shell structure can be regard as cylindrical shell structure when the geometric characteristic parameter α is selected as 0.

Fig. 1
figure 1

Diagram of sandwich conical shell with viscoelastic core

Full size image

2.2 Meshfree shape function

The meshfree shape function produced by Tchebychev radial point interpolation method is applied in the proposed approach. The above meshfree shape function can be regard as the combination of the radial basis function and Tchebychev polynomials, the corresponding expression is written as follow.

$$u(x) = \sum\limits_{i = 1}^{N} {R_{i} (x)a_{i} } + \sum\limits_{j = 1}^{{N_{t} }} {\tau_{j} (x)b_{j} } = {\varvec{R}}^{T} (x){\varvec{a}} + {\varvec{T}}^{T} (x){\varvec{b}}$$
(1)

where the symbols of Ri(x) and τj(x) represent radial and Tchebychev polynomial basis functions; N and Nt denote the numbers of the above corresponding basis functions. The concrete expression of Tchebychev polynomial basis function with one-dimensional can be expressed as follows:

$${\varvec{T}}({\varvec{x}}) = \left[ {\begin{array}{*{20}c} {T_{0} (x)} & {T_{1} (x)} & \cdots & {T_{p} (x)} & \cdots \\ \end{array} } \right]^{T}$$
(2)
$$T_{k} (x) = \cos [k\cos^{ - 1} (x)]\quad ,\quad k = 0,\;1,\;2 \cdots$$
(3)

The radial basis function of meshfree shape function is determined by selecting multi-quadrics (MQ) radial basis function; the specific expression of radial basis function is described as follows:

$$R_{i} ({\varvec{x}}) = \left[ {r_{i}^{2} + (\alpha_{c} d_{c} )^{2} } \right]^{q}$$
(4)

where dc denotes nodal mean spacing and ri represents the distance between interested node and divided node. For determining the unknown variables ai and bj, the divided nodes need to be introduced into Eq. (1) for establishing a set of linear equation, the matrix expression of the above linear equation can be written as the following form:

$${\varvec{U}}_{s} = {\varvec{R}}_{0} {\varvec{a}} + {\varvec{T}}_{{N_{t} }} {\varvec{b}}$$
(5)
$${\varvec{a}} = \left[ {\begin{array}{*{20}c} {a_{1} } & {a_{2} } & \cdots & {a_{N} } \\ \end{array} } \right]^{T} ,\;\;\;\;{\varvec{b}} = \left[ {\begin{array}{*{20}c} {b_{1} } & {b_{2} } & \cdots & {b_{{N_{t} }} } \\ \end{array} } \right]^{T}$$
(6)

where the concrete expressions of the matrices Us, R0, \({\varvec{T}}_{{N_{t} }}\) can be described as follows:

$${\varvec{U}}_{s} = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \cdots & {u_{N} } \\ \end{array} } \right]^{T}$$
(7)
$${\varvec{R}}_{0} = \left[ {\begin{array}{*{20}c} {R_{1} (r_{1} )} & {R_{2} (r_{1} )} & \cdots & {R_{N} (r_{1} )} \\ {R_{1} (r_{2} )} & {R_{2} (r_{2} )} & \cdots & {R_{N} (r_{2} )} \\ \vdots & \vdots & \ddots & \vdots \\ {R_{1} (r_{N} )} & {R_{2} (r_{N} )} & \cdots & {R_{N} (r_{N} )} \\ \end{array} } \right]$$
(8)
$${\varvec{T}}_{{N_{t} }} = \left[ {\begin{array}{*{20}c} {T_{0} (x_{1} )} & {T_{1} (x_{1} )} & \cdots & {T_{{N_{t} }} (x_{1} )} \\ {T_{0} (x_{2} )} & {T_{1} (x_{2} )} & \cdots & {T_{{N_{t} }} (x_{2} )} \\ \vdots & \vdots & \ddots & \vdots \\ {T_{0} (x_{N} )} & {T_{1} (x_{N} )} & \cdots & {T_{{N_{t} }} (x_{N} )} \\ \end{array} } \right]_{{N \times N_{t} }}$$
(9)

The definition expression of rk in Ri(rk) of Eq. (8) is shown as follows:

$$r_{k} = x_{k} - x_{i}$$
(10)

In order to solving Eq. (5) advantageously, the following constraint equations need to be applied.

$$\sum\limits_{i = 1}^{N} {T_{j} ({\varvec{x}}_{i} )a_{i} } = {\varvec{T}}_{{N_{t} }}^{T} {\varvec{a}} = 0\quad ,\quad j = 1,2, \cdots ,N_{t}$$
(11)

From Eqs. (5) and (11)

$$\overline{\varvec{U}}_{s} = \left[ {\begin{array}{*{20}c} {{\varvec{U}}_{s} } \\ {\mathbf{0}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{R}}_{0} } & {{\varvec{T}}_{{N_{t} }} } \\ {{\varvec{T}}_{{N_{t} }}^{T} } & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{a}} \\ {\varvec{b}} \\ \end{array} } \right] = {\varvec{Ga}}_{0}$$
(12)

According to variable substitution, Eq. (1) can be revised as follows:

$$\begin{aligned} u(x) = & \varvec{R}^{T} (x)\varvec{a} + \varvec{T}^{T} (x)\varvec{b} = \left[ {\begin{array}{*{20}c} {\varvec{R}^{T} (x)} & {\varvec{T}^{T} (x)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \varvec{a} \\ \varvec{b} \\ \end{array} } \right] \\ = & \left[ {\begin{array}{*{20}c} {\varvec{R}^{T} (x)} & {\varvec{T}^{T} (x)} \\ \end{array} } \right]\varvec{G}^{{ - 1}} \varvec{\bar{U}}_{s} = \varvec{\bar{\Phi }}^{T} (x)\varvec{\bar{U}}_{s} \\ \end{aligned}$$
(13)
$$\begin{aligned} \varvec{\bar{\Phi }}^{T} (x) = & \left[ {\begin{array}{*{20}c} {\varvec{R}^{T} (x)} & {\varvec{T}^{T} (x)} \\ \end{array} } \right]\varvec{G}^{{ - 1}} \\ {\text{ = }} & \left[ {\begin{array}{*{20}c} {\phi _{{\text{1}}} (x)} & {\phi _{{\text{2}}} (x)} & \cdots & {\phi _{N} (x)} & {\phi _{{N{\text{ + 1}}}} (x)} & \cdots & {\phi _{{N + N_{t} }} (x)} \\ \end{array} } \right] \\ \end{aligned}$$
(14)

The shape function of nodal displacements produced by Tchebychev radial point interpolation method can be ascertained as follows:

$${\varvec{\varPhi}}^{T} (x){ = }\left[ {\begin{array}{*{20}c} {\phi_{{1}} (x)} & {\phi_{{2}} (x)} & \cdots & {\phi_{N} (x)} \\ \end{array} } \right]$$
(15)

2.3 Governing equation of sandwich shell

According to FSDT and Donnel shell assumption, the displacement components of any point of each layer are expressed as [24]

$$\left\{ {\begin{array}{*{20}c} {\overline{u}_{i} = u_{i} + z\psi_{xi} } \\ {\overline{v}_{i} = v_{i} + z\psi_{\theta i} } \\ {\overline{w}_{i} = w\;\quad \quad } \\ \end{array} } \right.\quad i = s,v,c$$
(16)

where ui, vi and w denote the displacement components of middle surface of each layer in the x, θ and z directions, respectively. For the base layer and constraining layer, the shear rotations ψxi and ψθi can be determined as follows:

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\psi_{xi} = - \frac{\partial w}{{\partial x}}\;\;} \\ {\psi_{\theta i} = - \frac{\partial w}{{R_{i} \partial \theta }}} \\ \end{array} } & {i = s,c} \\ \end{array} } \right.$$
(17)

where Ri = Ri0 + xsinα.

The displacements of the viscoelastic layer can be ascertained as the following expression based on the displacement continuity conditions of interlayer.

$$\begin{array}{*{20}c} {u_{v} = \frac{1}{2}\left( {u_{s} + u_{c} + \frac{{h_{s} }}{2}\psi_{xs} - \frac{{h_{c} }}{2}\psi_{xc} } \right)\;,} & {\psi_{xv} = \frac{1}{{h_{v} }}\left( {u_{c} - u_{s} - \frac{{h_{s} }}{2}\psi_{xs} - \frac{{h_{c} }}{2}\psi_{xc} } \right)} \\ {v_{v} = \frac{1}{2}\left( {v_{s} + v_{c} + \frac{{h_{s} }}{2}\psi_{\theta s} - \frac{{h_{c} }}{2}\psi_{\theta c} } \right)\;,} & {\psi_{\theta v} = \frac{1}{{h_{v} }}\left( {v_{c} - v_{s} - \frac{{h_{s} }}{2}\psi_{\theta s} - \frac{{h_{c} }}{2}\psi_{\theta c} } \right)} \\ \end{array}$$
(18)

Generally, the Young’s modulus of the base layer and constraining layer is much larger than the that of viscoelastic core layer. Therefore, the former only considers flexural and axial deformations, and the latter only considers shear strains. Considering Eq. (18), the strains of the viscoelastic core layer are expressed as:

$$\begin{gathered} \gamma_{xz}^{v} = \frac{1}{{h_{v} }}\left( {u_{c} - u_{s} } \right) + c_{x} \frac{\partial w}{{\partial x}} \hfill \\ \gamma_{\theta z}^{v} = \left( {\frac{1}{{h_{v} }} - \frac{\cos \alpha }{{2R_{v} }}} \right)v_{c} - \left( {\frac{1}{{h_{v} }} + \frac{\cos \alpha }{{2R_{v} }}} \right)v_{s} + c_{\theta } \frac{\partial w}{{\partial \theta }} \hfill \\ \end{gathered}$$
(19)

where

$$\begin{gathered} c_{x} = \frac{{h_{s} + h_{c} + 2h_{v} }}{{2h_{v} }} \hfill \\ c_{\theta } = \left[ {\frac{1}{{2h_{v} }}\left( {\frac{{h_{c} }}{{R_{c} }} + \frac{{h_{s} }}{{R_{s} }}} \right) + \frac{1}{{4R_{v} }}\left( {\frac{{h_{s} \cos \alpha }}{{R_{s} }} - \frac{{h_{c} \cos \alpha }}{{R_{c} }} + 4} \right)} \right] \hfill \\ \end{gathered}$$
(20)

The shear stresses with regard to the viscoelastic core layer can be written as follows:

$$\tau_{xz}^{v} = G_{{\text{v}}} \gamma_{xz}^{v} \quad \tau_{\theta z}^{v} = G_{{\text{v}}} \gamma_{\theta z}^{v}$$
(21)

where Gv denotes shear modulus with regard to the viscoelastic core layer, which consists of real and imaginary parts.

$$G_{{\text{v}}} = G_{{\text{r}}} + iG_{{\text{i}}}$$
(22)

where Gr and Gi denote the real and imaginary parts of the above shear modulus Gv, respectively.

Meanwhile, the relationships between stress and strain of the base and constraining layers are written as follows:

$$\left[ {\begin{array}{*{20}c} {\sigma_{x}^{i} } \\ {\sigma_{\theta }^{i} } \\ {\tau_{x\theta }^{i} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{11} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{x}^{i} } \\ {\varepsilon_{\theta }^{i} } \\ {\gamma_{x\theta }^{i} } \\ \end{array} } \right]\quad i = s,c$$
(23)

where the stiffness coefficients Qmn of the isotropic material are as

$$Q_{11} = \frac{{E_{i} }}{{1 - \mu_{i}^{2} }},\quad Q_{12} = \frac{{\mu_{i} E_{i} }}{{1 - \mu_{i}^{2} }},\quad Q_{66} = \frac{{E_{i} }}{{2(1 + \mu_{i} )}}$$
(24)

where Ei and μi denote Young’s modulus and Poisson’s ratios with regard to the base and constraining layers. The relationships between strain and displacement of the base and constraining layers can be determined as follows:

$$\begin{aligned} \varepsilon _{x}^{i} = & \frac{{\partial u_{i} }}{{\partial x}} - z\frac{{\partial ^{2} w}}{{\partial x^{2} }} \\ \varepsilon _{\theta }^{i} = & \frac{{\sin \alpha }}{{R_{i} }}u_{i} + \frac{1}{{R_{i} }}\frac{{\partial v_{i} }}{{\partial \theta }} + \frac{{\cos \alpha }}{{R_{i} }}w - z\frac{{\sin \alpha }}{{R_{i} }}\frac{{\partial w}}{{\partial x}} - \frac{z}{{R_{i}^{2} }}\frac{{\partial ^{2} w}}{{\partial \theta ^{2} }} \\ \gamma _{{x\theta }}^{i} = & \frac{1}{{R_{i} }}\frac{{\partial u_{i} }}{{\partial \theta }} + \frac{{\partial v_{i} }}{{\partial x}} - \frac{{\sin \alpha }}{{R_{i} }}v_{i} + 2z\frac{{\sin \alpha }}{{R_{i}^{2} }}\frac{{\partial w}}{{\partial \theta }} - \frac{{2z}}{{R_{i} }}\frac{{\partial ^{2} w}}{{\partial x\partial \theta }} \\ \end{aligned}$$
(25)

The above displacement components can be expanded as follows by introducing the meshfree TRPIM shape function.

$$\begin{gathered} u_{s} = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 0}^{M} {\phi_{m} (x)\left[ {\cos (n\theta )\tilde{U}_{mn}^{s} + \sin (n\theta )\overline{U}_{mn}^{s} } \right]e^{i\omega t} } } \hfill \\ v_{s} = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 0}^{M} {\phi_{m} (x)\left[ {\sin (n\theta )\tilde{V}_{mn}^{s} + \cos (n\theta )\overline{V}_{mn}^{s} } \right]e^{i\omega t} } } \hfill \\ u_{c} = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 0}^{M} {\phi_{m} (x)\left[ {\cos (n\theta )\tilde{U}_{mn}^{c} + \sin (n\theta )\overline{U}_{mn}^{c} } \right]e^{i\omega t} } } \hfill \\ v_{c} = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 0}^{M} {\phi_{m} (x)\left[ {\sin (n\theta )\tilde{V}_{mn}^{c} + \cos (n\theta )\overline{V}_{mn}^{c} } \right]e^{i\omega t} } } \hfill \\ w\, = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 0}^{M} {\phi_{m} (x)\left[ {\cos (n\theta )\tilde{W}_{mn} + \sin (n\theta )\overline{W}_{mn} } \right]e^{i\omega t} } } \hfill \\ \end{gathered}$$
(26)

where M and N represent the circumferential wave number and the node number which distributed in the meridional direction of shell, respectively. The symbols \({\widetilde{U}}_{mn}^{s}\), \({\widetilde{V}}_{mn}^{s}\), \({\widetilde{U}}_{mn}^{c}\), \({\widetilde{V}}_{mn}^{c}\),, \({\widetilde{W}}_{mn}\), \({\overline{U} }_{mn}^{s}\), \({\overline{V} }_{mn}^{s}\), \({\overline{U} }_{mn}^{c}\), \({\overline{V} }_{mn}^{c}\) and \({\overline{W} }_{mn}\) represent the displacement components with regard to node.

The strain energies of the sandwich shell can be described as follows:

$$\begin{gathered} U = \sum\limits_{i = s}^{c} {U_{i} } + U_{v} \;\;\;\left( {i = s,c} \right) \hfill \\ U_{i} = \frac{1}{2}\int\limits_{0}^{2\pi } {\int\limits_{0}^{L} {\int\limits_{{ - {{h_{i} } \mathord{\left/ {\vphantom {{h_{i} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{i} } \mathord{\left/ {\vphantom {{h_{i} } 2}} \right. \kern-0pt} 2}}} {\left( {\sigma_{x}^{i} \varepsilon_{x}^{i} + \sigma_{\theta }^{i} \varepsilon_{\theta }^{i} + \tau_{x\theta }^{i} \gamma_{x\theta }^{i} } \right)R_{i} {\text{d}}z{\text{d}}x{\text{d}}\theta } } } ;\;\;U_{v} = \frac{1}{2}\int\limits_{0}^{2\pi } {\int\limits_{0}^{L} {\int\limits_{{ - {{h_{v} } \mathord{\left/ {\vphantom {{h_{v} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{v} } \mathord{\left/ {\vphantom {{h_{v} } 2}} \right. \kern-0pt} 2}}} {\left( {\tau_{xz}^{v} \gamma_{xz}^{v} + \tau_{\theta z}^{v} \gamma_{\theta z}^{v} } \right)R_{v} {\text{d}}z{\text{d}}x{\text{d}}\theta } } } \hfill \\ \end{gathered}$$
(27)

The kinetic energies of the sandwich shell can be given as

$$\begin{gathered} T = \sum\limits_{i = s}^{c} {T_{i} } + T_{v} \left( {i = s,c} \right) \hfill \\ T_{i} = \frac{{\rho_{i} h_{i} }}{2}\int\limits_{0}^{2\pi } {\int\limits_{0}^{L} {\left( {\dot{u}_{i}^{2} + \dot{v}_{i}^{2} + \dot{w}^{2} } \right)R_{i} dxd\theta } } ;T_{v} = \frac{{\rho_{v} h_{v} }}{2}\int\limits_{0}^{2\pi } {\int\limits_{0}^{L} {\dot{w}^{2} R_{v} dxd\theta } } \hfill \\ \end{gathered}$$
(28)

where ρi (i = s, v, c) denotes the density of each layer.

The elastic energies stored in distributed springs of base and constraining layers can be given as

$$U_{BC} = \frac{1}{2}\sum\limits_{i = s}^{c} {\int\limits_{0}^{2\pi } {\left\{ \begin{gathered} \left[ {k_{u0} u_{i}^{2} + k_{v0} v_{i}^{2} + k_{w0} w^{2} + K_{w0} \left( {{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)} \right]_{x = 0} \hfill \\ + \left[ {k_{u1} u_{i}^{2} + k_{v1} v_{i}^{2} + k_{w1} w^{2} + K_{w1} \left( {{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)} \right]_{x = L} \hfill \\ \end{gathered} \right\}R_{i} {\text{d}}\theta } } \left( {i = s,c} \right)$$
(29)

The total Lagrangian energy function with regard to sandwich shell can be determined as follows:

$$L = T - U - U_{BC}$$
(30)

The extremum of the above Lagrangian energy function can be determined by the following derivative operation.

$$\frac{\partial L}{{\partial q}} = 0,\quad q = \tilde{U}_{mn}^{s} ,\tilde{V}_{mn}^{s} ,\tilde{U}_{mn}^{c} ,\tilde{V}_{mn}^{c} ,\tilde{W}_{mn} ,\overline{U}_{mn}^{s} ,\overline{V}_{mn}^{s} ,\overline{U}_{mn}^{c} ,\overline{V}_{mn}^{c} ,\overline{W}_{mn}$$
(31)

Substituting Eqs. (27)–(30) into Eq. (31), following governing equations are obtained.

$$\left( {{\varvec{K}} - \overline{\omega }^{2} {\varvec{M}}} \right){\varvec{U}}_{s} = {\mathbf{0}}$$
(32)

where Us is the nodal displacement vector; K and M denote mass and stiffness matrices respectively, the concrete expression of the above matrices can be found in Appendices 1 and 2. From Eq. (32), the complex eigenvalues are obtained. The definitions of real frequency ω and modal loss factor η of sandwich shells are shown as follows:

$$\omega = \sqrt {{\text{Re}} \left( {\overline{\omega }^{2} } \right)}$$
(33)
$$\eta = \frac{{{\text{Im}} \left( {\overline{\omega }^{2} } \right)}}{{{\text{Re}} \left( {\overline{\omega }^{2} } \right)}}$$
(34)

3 Numerical discussion

The validity including accuracy and reliability of the presented method is performed for demonstrating that it can be used to analyze the vibration and damping behaviors of sandwich shells including conical shell and cylindrical shell in this section.

Unless otherwise specified, the material parameters of sandwich shells in the following discussion are selected as: Es = Ec = 210 GPa, Gr = 8.582 MPa, Gi = 2.985 MPa, μs = μc = 0.3, ρs = ρc = 7850 kg/m3 and ρv = 1340 kg/m3.

3.1 Convergence and verification analyses

The computational cost and accuracy of the meshfree numerical solution are influenced by the number of divided node in the solving domain. However, it is worth noting that the computational cost and accuracy exist certain contradiction. The above contradiction can be interpreted as the computational cost and accuracy increase with the number of divided node increased. The influence of divided node number N on the natural frequencies and modal loss factor of sandwich conical shell structure are investigated; the corresponding results can be found in Fig. 2. The geometric parameters of sandwich conical shell structure are defined as: Rs = 1 m, L = 2 m, hs = hc = 2hv = 0.02 m and α = π/6.

Fig. 2
figure 2

Convergence of natural frequency and modal loss factor for a sandwich conical shell with different numbers of nodes N: a C–C and b S–S

Full size image

As shown in Fig. 2, the natural frequencies and modal loss factors of sandwich conical shell subjected to various boundary conditions have varying degree variation tendencies firstly and then remain unchanged with the number of divided node increased. The above results indicate that the proposed method has stable convergence in the process of analyzing the vibration and damping behaviors of sandwich shells under various boundary conditions.

According to the above discussion, the various boundary conditions of the proposed method are simulated by employing artificial spring technique. The crucial of artificial spring technique is select appropriate spring stiffness value in different directions. In order to determine the spring stiffness value of various boundary conditions, the effects of spring stiffness values on the natural frequencies and modal loss factors of sandwich shells including conical shell and cylindrical shell are discussed, the corresponding results are shown in Figs. 3 and 4. The geometric parameters used in this discussion can be found in Fig. 2. The left and right sides of sandwich shell structure are selected as elastic boundary and completely clamped boundary, respectively. The longitudinal mode number is selected as m = 1.

Fig. 3
figure 3

Convergence of natural frequency for a sandwich conical shell with different boundary spring stiffnesses: a n = 1, b n = 2, c n = 3 and d n = 4

Full size image
Fig. 4
figure 4

Convergence of modal loss factor for a sandwich cylindrical shell with different boundary spring stiffnesses: a n = 1, b n = 2, c n = 3 and d n = 4

Full size image

As shown in Figs. 3 and 4, the natural frequencies and modal loss factors of sandwich shells have opposite variation tendencies firstly and then keep constant with the spring stiffness values of different directions increased. The above results indicate that the solution of natural frequencies and modal loss factors of sandwich shells reach stable convergence when spring stiffness values increase to 1013.

According to the above discussion, the values of spring stiffness subjected to various boundary condition are ascertained in Table 1. It is necessary to point out that F and C denote free and clamped boundary conditions, respectively; S and SD represent simply supported and shear diaphragm boundary conditions, respectively.

Table 1 Stiffness values for different boundary springs
Full size table

Then, the validation of the presented method is performed by comparing the results calculated by the proposed method with the corresponding results from the existing literatures. The material geometric parameters are selected as: Es = Ec = 70 GPa, Gv = 0.896(1 + i0.9683) MPa, μs = μc = 0.3, ρs = ρc = 2700 kg/m3, ρv = 999 kg/m3, hs = hc = 2hv = 0.02 m, Rs = 1 m, L = 0.5 m. The comparison results of natural frequencies of sandwich cylindrical shell subjected to different boundary conditions are shown in Table 2. The material geometric parameters are consistent with Table 2 except for the following geometric parameters L = Rs = 3 m, hs = hc. The two sides of the shell are selected as simply supported boundary condition, and the axial wave number is chosen as m = 1. The comparison results of natural frequencies of sandwich cylindrical shell under various thickness ratios can be found in Table 3. As shown in Tables 2 and 3, it is not hard to see that the comparison results between proposed method and the existing literatures have good consistency.

Table 2 Comparison of natural frequencies for a sandwich cylindrical shell with various boundary conditions
Full size table
Table 3 Comparison of natural frequencies for a sandwich cylindrical shell with various thickness ratios
Full size table

3.2 Parametric analysis

According to the above convergence and verification analyses, the validation including accuracy and stability of the proposed approach is verified. The vibration and damping behaviors of sandwich shells including shell conical and cylindrical shell are investigated by analyzing the influences of some parameters on the natural frequencies and modal loss factor in this section.

First of all, the effect of semi-vertex angle on the natural frequencies (dimensionless frequency) and modal loss factors of sandwich conical shell are investigated; the corresponding results can be seen in Table 4 and Fig. 5, respectively. The definition of dimensionless frequency is shown as: \(\Omega = \omega R_{s}^{2} \sqrt {\rho_{s} /E_{s} h^{2} }\), the total thickness of sandwich conical shell is h = hs + hv + hc. The geometric parameters are selected as: Rs = 1 m, L = 1 m and hs = hc = 2hv = 0.02 m.

Table 4 Dimensionless frequencies for a sandwich conical shell with various semi-vertex angles (m = 1)
Full size table
Fig. 5
figure 5

Variation of modal loss factors for a sandwich conical shell with various semi-vertex angles (m = 1): a C–C, b C–S, c C–SD and d S–S

Full size image

From Table 4 and Fig. 5, it is easy to find that the natural frequencies and modal loss factors have opposite variation tendencies with the company of semi-vertex angle increased, the former decreases and the latter increase, respectively. Meanwhile, it is necessary to point out that the variation tendency of modal loss factors is remarkable when the semi-vertex angle increases to 70°.

Subsequently, the effects of thickness of viscoelastic core layer on the natural frequencies and modal loss factors of sandwich conical shell and cylindrical shell are investigated; the corresponding results are shown in Table 5 and Fig. 6. The above natural frequencies are nondimensionalized by means of \(\Omega = \omega R_{s}^{2} \sqrt {\rho_{s} /E_{s} h^{2} }\); the definition of thickness ratio of sandwich conical shell is set as hv/h. The thickness of base layer is consistent with the thickness of constraining layer. The geometric parameters is selected as: Rs = 1 m, L = 2 m, α = π/6 and h = 0.05 m. As shown in Table 5, it is easy to see that the thickness ratio has important effect in the vibration characteristics of sandwich conical shell. The model parameters of Fig. 6 are the same as Table 5 except the total thickness of conical shell is chosen as h = 0.1 m. From Fig. 6, the natural frequencies decrease with the thickness of viscoelastic core layer increased. However, the modal loss factors decrease firstly and then increase with the thickness of viscoelastic core layer increased.

Table 5 Dimensionless frequencies for a sandwich conical shell with various thickness ratios (m = 1)
Full size table
Fig. 6
figure 6

Variation of dimensionless frequency and modal loss factor for a sandwich conical shell with various thickness ratios (m = 1): a C–C and b C–SD

Full size image

Then, the influences of circumferential wave number on the natural frequencies and modal loss factors of sandwich shells including conical shell and cylindrical shell subjected to various boundary conditions are discussed; the corresponding results can be seen in Fig. 7. The geometric parameters of sandwich shells are selected as: Rs = 1 m, L = 2 m and hs = hc = hv = 0.02 m. From Fig. 7, it is easy to see that the natural frequencies and modal loss factors of sandwich cylindrical shell subjected to various boundary conditions attain minimum and maximum values when the circumferential wave number is set as 4. The natural frequencies and modal loss factors of sandwich conical shell subjected to C–SD and S–SD boundary conditions get minimum and maximum values when the circumferential wave number is set as 5. When sandwich conical shell under the C–C, C–S and S–S boundary conditions, the above corresponding circumferential wave number is set as 6.

Fig.7
figure 7

Variation of dimensionless frequency and modal loss factor for a sandwich shell according to circumferential wave number (m = 1): a cylindrical shell and b conical shell (α = π/6)

Full size image

Fourthly, the influences of material loss factor Gi/Gr of viscoelastic material layer on modal loss factors of sandwich shells are researched; the corresponding results are shown in Fig. 8. The geometric parameters are consistent with the corresponding parameters come from Fig. 7 except for the real part of shear modulus is chosen as Gr = 8.582 MPa. As shown in Fig. 8, the modal loss factors increased by means of linear with the material loss factor Gi/Gr increased. The influence of material loss factor on modal loss factors of sandwich shells under C–SD boundary condition is much larger than that of sandwich shells under C–C boundary condition.

Fig. 8
figure 8

Variation of modal loss factor for a sandwich shell according to material loss factor of viscoelastic material layer (m = 1): a cylindrical shell and b conical shell (α = π/6)

Full size image

Finally, the effects of various geometric parameters, circumferential wave numbers and boundary conditions on natural frequencies of sandwich shells including cylindrical shell and conical shell are performed; the corresponding results of cylindrical shell and conical shell can be found in Table 6 and Table 7. The geometric parameters are chosen as: Rs = 1 m, hv = 0.02 m and hs = hc = 0.01 m. The dimensionless definition of natural frequencies can be expressed as \(\Omega = \omega R_{s}^{2} \sqrt {\rho_{s} /E_{s} h^{2} }\). As shown in Tables 6 and 7, the structure length has significantly effect on the natural frequencies of sandwich shells compared with circumferential wave numbers and boundary conditions. According to the variation tendencies of the above natural frequencies, it can conclude that the increase of structure length will result in the decrease of stiffness of sandwich shells.

Table 6 Dimensionless frequencies for a sandwich cylindrical shell with various length ratios (m = 1)
Full size table
Table 7 Dimensionless frequencies for a sandwich conical shell with various length ratios (m = 1, α = π/6)
Full size table

4 Conclusion

A meshless method is proposed to investigate the vibration and damping characteristics of sandwich shells including cylindrical shell and conical shell. The sandwich shells are made up of three layers including base layer, viscoelastic core layer and constraining layer. The theoretical modeling of sandwich shells is deduced by employing the energy principle in framework of FSDT and Donnel shell hypothesis. The displacement components of arbitrary point locate at the sandwich shell are expanded by employing the circumferential Fourier series and the meridional direction meshfree TRPIM shape function. The convergence and validation including accuracy and stability of the proposed method are verified by comparing the results calculated by the presented approach with the corresponding results of existing literatures. Based on the above proposed method, the vibration and damping behaviors analysis of sandwich shells are carried out by investigating the influences of some parameters including geometric dimensions, material parameters and circumferential wave numbers on the natural frequencies and modal loss factors of sandwich shells. Some representative conclusions are shown as follows:

  1. (1)

    The influences of semi-vertex angle on the natural frequencies and modal loss factors of sandwich conical shell structure are opposite. The increase of semi-vertex angle leads to the decrease and increase of natural frequencies and modal loss factors, respectively.

  2. (2)

    The thickness of viscoelastic core layer has important effects on the natural frequencies and modal loss factors of sandwich shell structure.

  3. (3)

    The natural frequencies and modal loss factors of sandwich shell structure exist the extreme value phenomenon under the effects of circumferential waver number and boundary condition.

  4. (4)

    The material loss factor Gi/Gr of viscoelastic material layer and the modal loss factors of sandwich conical shell structure are positively correlated.